Кумулята
Теперь построим кумуляту — график накопленных относительных частот. Расположим его под гистограммой.
Кумулята — это экспериментальная оценка формы графика функции распределения. Теоретическая кривая будет красивой и гладкой — мы познакомились с ней в начале работы, обсуждая свой вариант задания. Экспериментальная оценка — ломаная линия, да ещё и с погрешностями. Эти случайные ошибки вызваны ограниченным, не бесконечным объёмом выборки. В любом случае, эти графики начинаются в нуле и постепенно растут до 100%.
Напомним, что значения накопленных частот должны быть привязаны к верхним границам интервалов — в соответствии со стандартами и здравым смыслом. Идея в том, что накопленная частота накапливается именно к концу интервала, а не к середине.
Построим график в виде ломаной линии:
Insert — Charts — Insert Scatter (X, Y) or Bubble Chart
Вставка — Диаграммы — Вставить точечную (X, Y) или пузырьковую диаграмму
Вставка графика Y (X)
Выбираем тип графика
Scatter — Scatter with Straight Lines
Точечная — Точечная с прямыми отрезками
Это просто ломаная линия без маркеров точек.
Ломаная линия
Выбираем данные для графика:
Select Data — Select Data Source — Legend Entries (Series) — Add
Выбрать данные — Выбор источника данных — Элементы легенды (ряды) — Добавить
В окне
Edit Series
Изменение ряда
выбираем следующие данные.
Столбец «иксов» — верхние границы:
Series X Values
Значения Х
Столбец «игреков» — накопленные частоты:
Series Y Values
Значения Y
Убираем заголовок диаграммы:
Chart Elements — Chart Title
Элементы диаграммы — Название диаграммы
Настраиваем цвет линии на графике.
Format Data Series — Series options — Fill & Line — Line
Формат ряда данных —Параметры ряда — Заливка и границы — Линия
Line — Solid line
Линия — Сплошная линия
Color — Black
Цвет — Чёрный
Width = 0.5 pt
Ширина — 0,5 пт
Если отрезков много, то ломаная линия выглядит как гладкая кривая.
Кумулята
Настроим числовые метки на вертикальной оси, чтобы выводились целые числа:
Format Axis — Axis Options — Number — Decimal places — 0
Формат оси — Параметры оси — Число — Число десятичных знаков — 0
Целочисленные метки
Установим диапазоны значений по осям.
Вертикальная ось — метки в процентах, а границы диапазона — числа. Поэтому пределы изменения будут от 0 до 1:
Category — Percentage
Категория — Процентный
Axis Options — Bounds
Параметры оси — Границы
Minimum — 0
Минимум — 0
Maximum — 1
Максимум — 1
Горизонтальная ось — в соответствии с интервалами группировки — от 190 до 310.
Кумулята
Подгоняем размеры графика и размещаем его под гистограммой. Можно сделать это вручную.
Если захочется особой точности, поработаем через меню параметров графика (числа условные).
Format Chart Area — Chart Options — Size & Properties — Size
Формат области диаграммы — Параметры диаграммы — Размер и свойства — Размер
Height — 1.8 in
Высота — 7,62 см
Width — 5.3 in
Ширина — 12,7 см
В английской версии пакета размеры измеряются в дюймах. В русской версии — в сантиметрах. Можем установить точные значения размеров вручную.
Размер диаграммы
Окончательно совмещаем маштаб гистограммы и кумуляты: начало первого интервала 190, конец последнего интервала 310. Положения этих двух меток на обоих графиках должны совпадать.
Проблемы с масштабом решаем так. Значение 190 находится в начале интервала, обозначенного 193. Значение 310 находится в конце интервала, следующего за 303.
Гистограмма и кумулята
Содержание
- Как рассчитать кумулятивную частоту в Excel
- Пример: кумулятивная частота в Excel
- Как построить CDF в Excel
- Пример: расчет и построение CDF в Excel
- Как создать кумулятивную диаграмму суммы в Excel (с примером)
- Шаг 1: введите данные
- Шаг 2: Рассчитайте совокупную сумму
- Шаг 3: Создайте гистограмму со средней линией
- Шаг 4. Настройте диаграмму (необязательно)
- Дополнительные ресурсы
- Как построить кумуляту в excel по данным таблицы
- График с накоплением в Excel.
Как рассчитать кумулятивную частоту в Excel
Таблица частот — это таблица, в которой отображается информация о частотах. Частоты просто говорят нам, сколько раз произошло определенное событие.
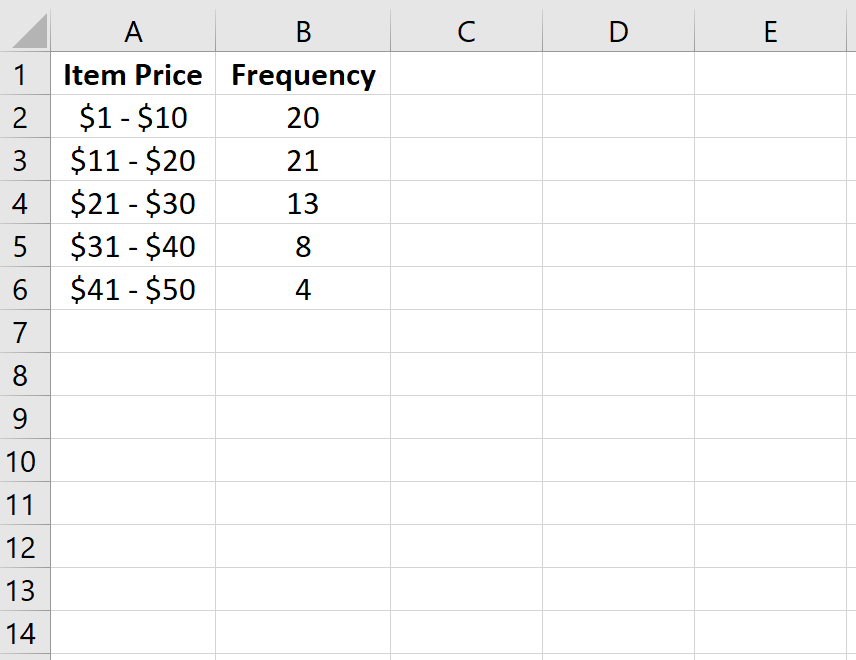
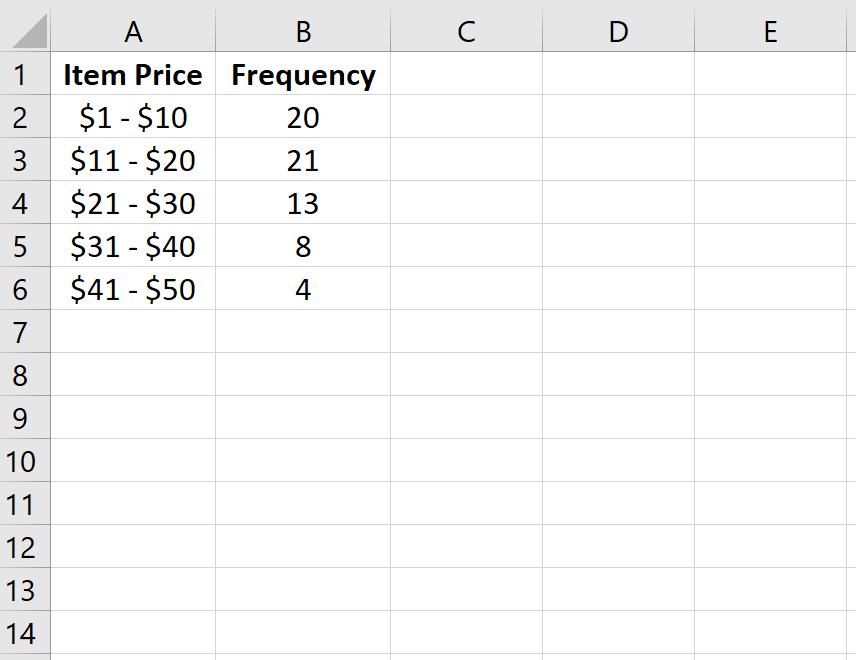
Например, в следующей таблице показано, сколько товаров было продано магазином в разных ценовых диапазонах за данную неделю:
| Цена товара | Частота | | — | — | | $1 – $10 | 20 | | $11 – $20 | 21 | | 21 – 30 долларов США | 13 | | $31 – $40 | 8 | | $41 — $50 | 4 |
В первом столбце отображается ценовой класс, а во втором столбце — частота этого класса.
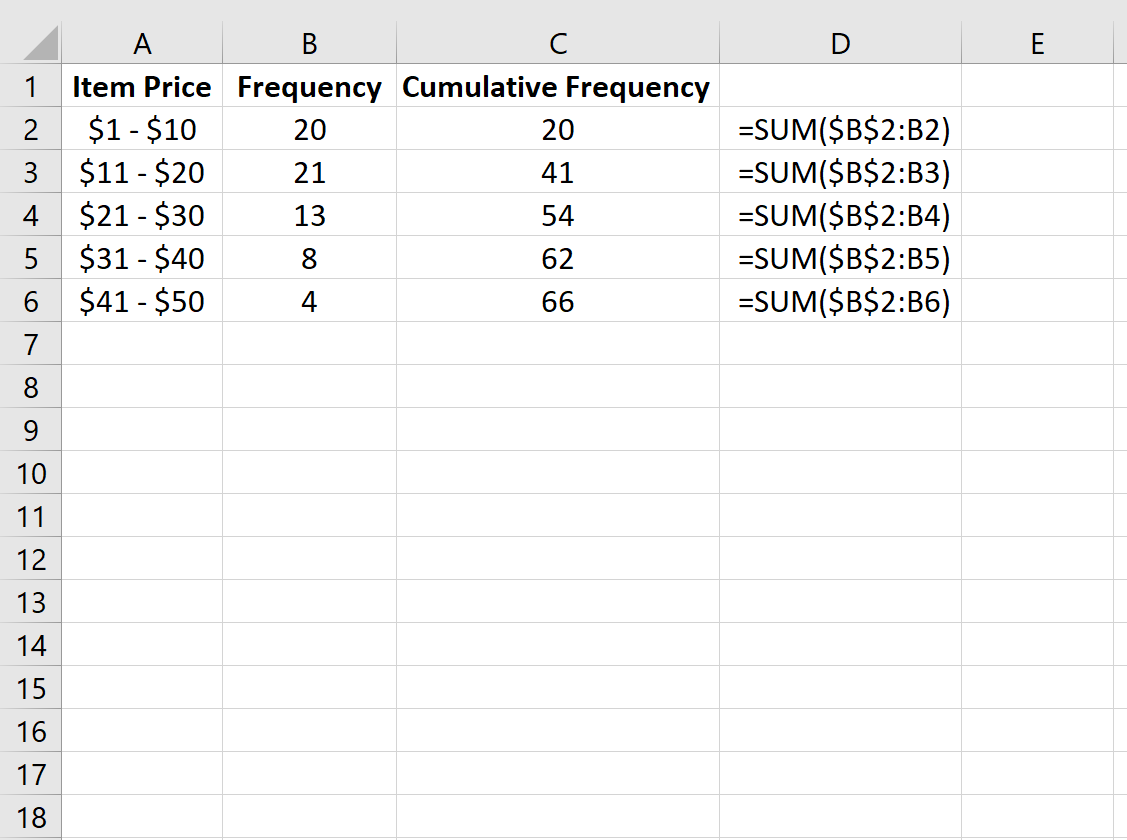
Также можно рассчитать совокупную частоту для каждого класса, которая представляет собой просто сумму частот до определенного класса.
| Цена товара | Частота | Накопленная частота | | — | — | — | | $1 – $10 | 20 | 20 | | $11 – $20 | 21 | 41 | | 21 – 30 долларов США | 13 | 54 | | $31 – $40 | 8 | 62 | | $41 — $50 | 4 | 66 |
Например, первая кумулятивная частота просто равна первой частоте 20 .
Вторая кумулятивная частота представляет собой сумму первых двух частот: 20 + 21 = 41 .
Третья кумулятивная частота представляет собой сумму первых трех частот: 20 + 21 + 13 = 54 .
В следующем примере показано, как найти совокупные частоты в Excel.
Пример: кумулятивная частота в Excel
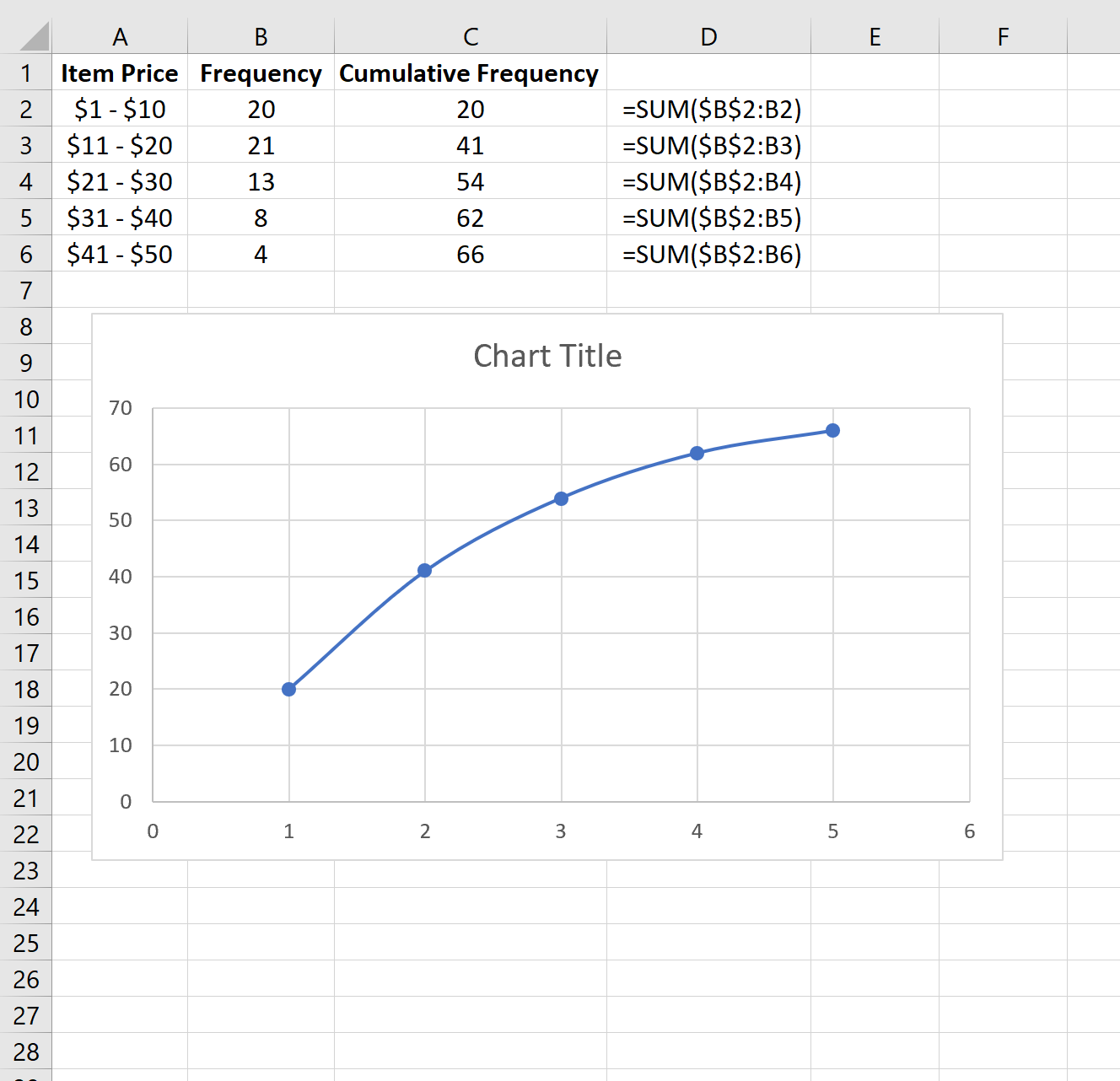
Сначала мы введем класс и частоту в столбцах A и B:
Далее мы рассчитаем совокупную частоту каждого класса в столбце C.
На изображении ниже в столбце D показаны формулы, которые мы использовали:
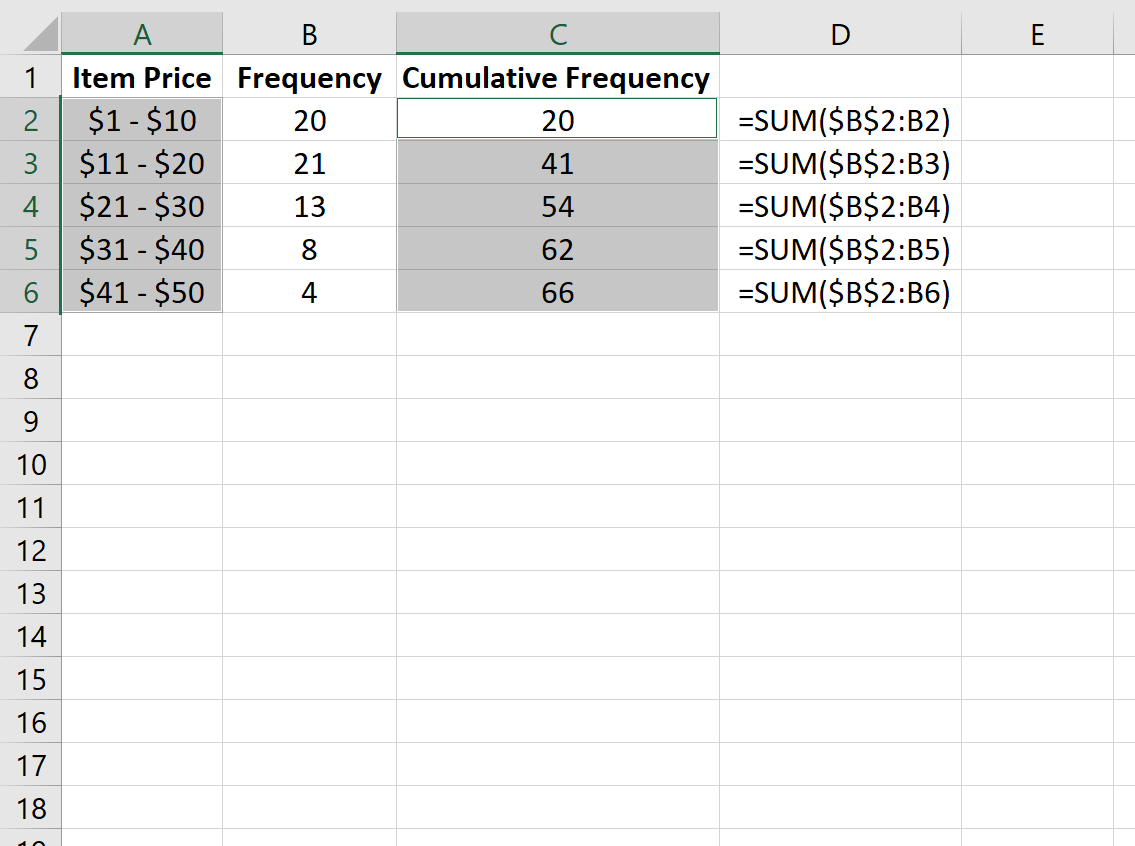
Мы также можем создать оживальную диаграмму для визуализации кумулятивных частот.
Чтобы создать оживальную диаграмму, удерживайте нажатой клавишу CTRL и выделите столбцы A и C.
Затем перейдите в группу « Диаграммы » на вкладке « Вставка » и щелкните первый тип диаграммы в « Вставить столбец» или «Гистограмма» :
На верхней ленте в Excel перейдите на вкладку « Вставка », затем в группу « Диаграммы ». Нажмите Точечная диаграмма , затем нажмите Точечная диаграмма с прямыми линиями и маркерами .
Это автоматически создаст следующий оживальный график:
Не стесняйтесь изменять оси и заголовок, чтобы сделать график более эстетичным:
Источник
Как построить CDF в Excel
Кумулятивная функция распределения (CDF) описывает вероятность того, что случайная величина примет значение, меньшее или равное некоторому числу.
Мы можем использовать следующую функцию в Excel для расчета кумулятивных вероятностей распределения:
В следующем примере показано, как рассчитать и построить CDF в Excel.
Пример: расчет и построение CDF в Excel
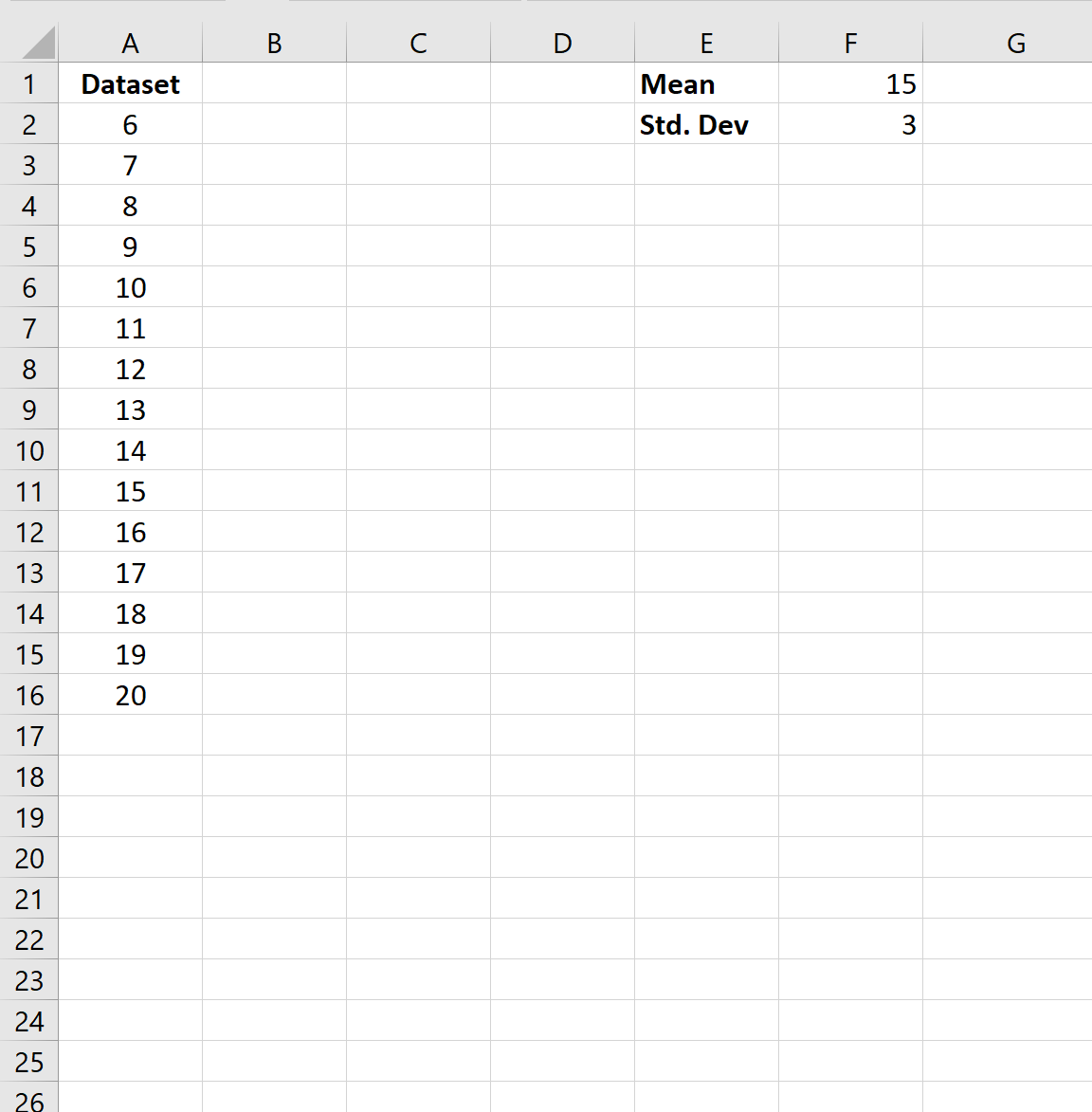
Во-первых, давайте создадим следующий набор данных в Excel:
Далее укажем среднее значение и стандартное отклонение распределения:
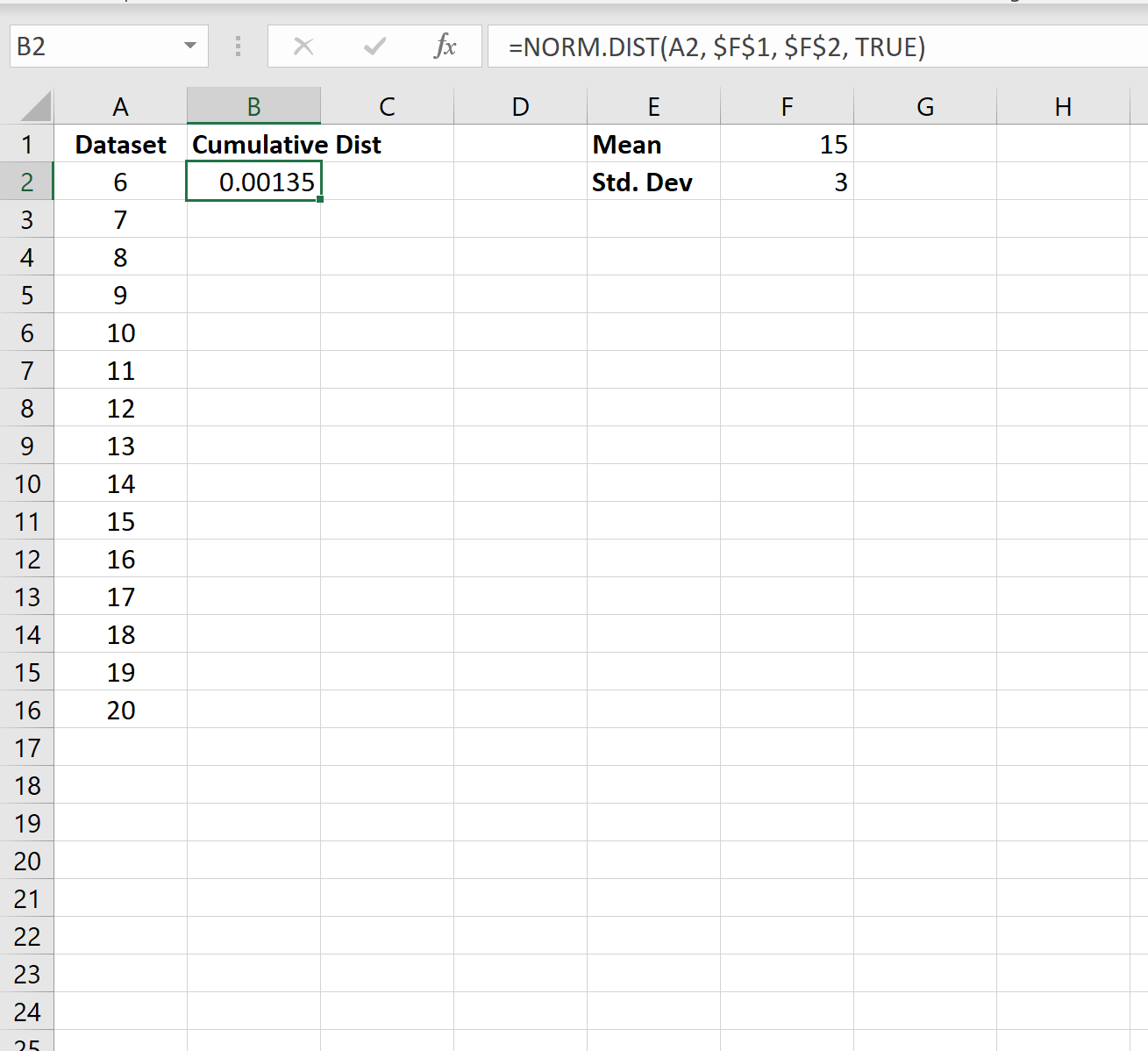
Затем мы можем рассчитать кумулятивную вероятность распределения для первого значения в наборе данных, используя следующую формулу:
Затем мы можем скопировать и вставить эту формулу в каждую другую ячейку в столбце B:
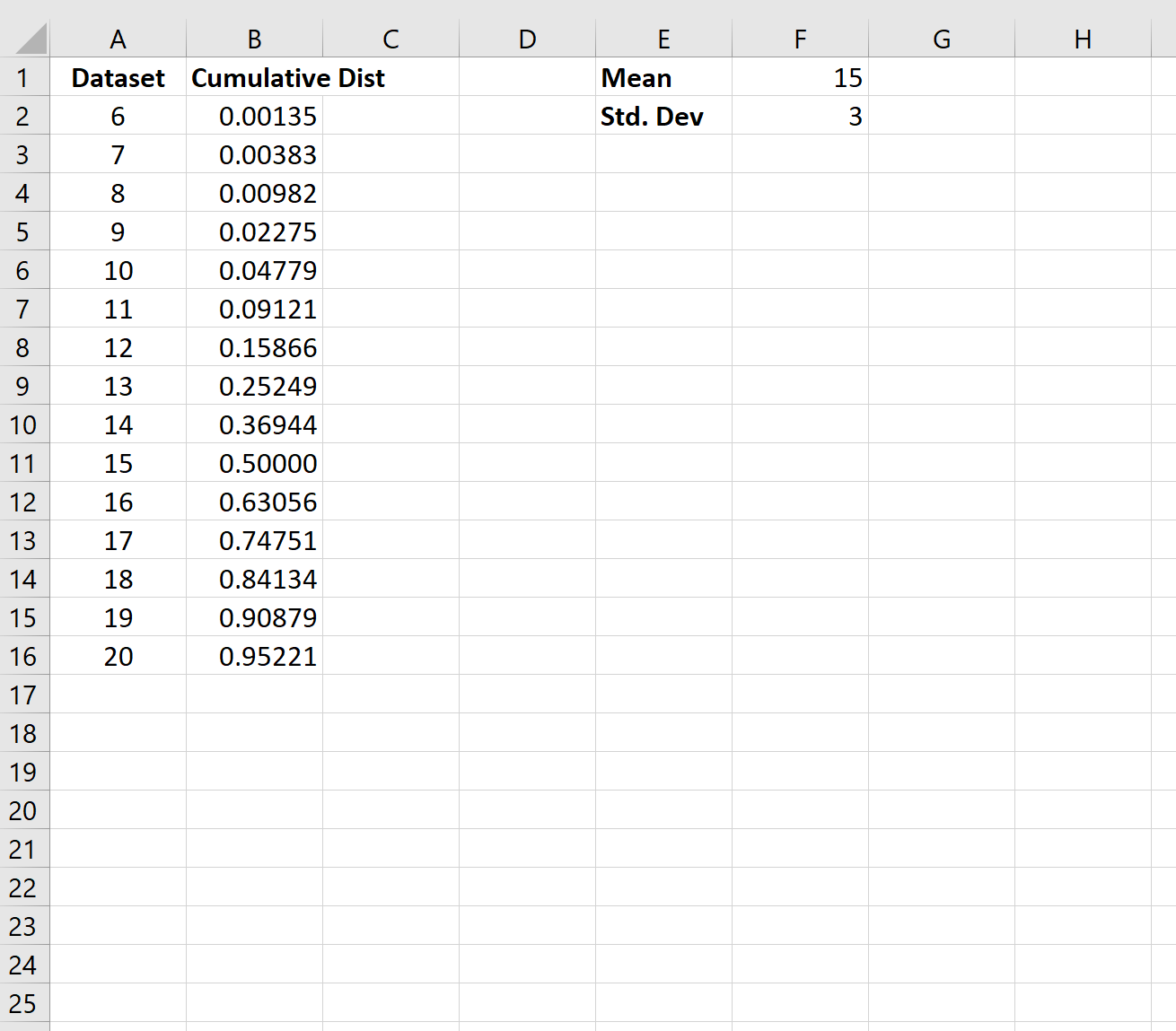
Теперь CDF завершен. Мы интерпретируем значения следующим образом:
- Вероятность того, что случайная величина примет значение, равное или меньшее 6, равна.00135 .
- Вероятность того, что случайная величина примет значение, равное или меньшее 7, равна.00383 .
- Вероятность того, что случайная величина примет значение, равное или меньшее 8, равна.00982 .
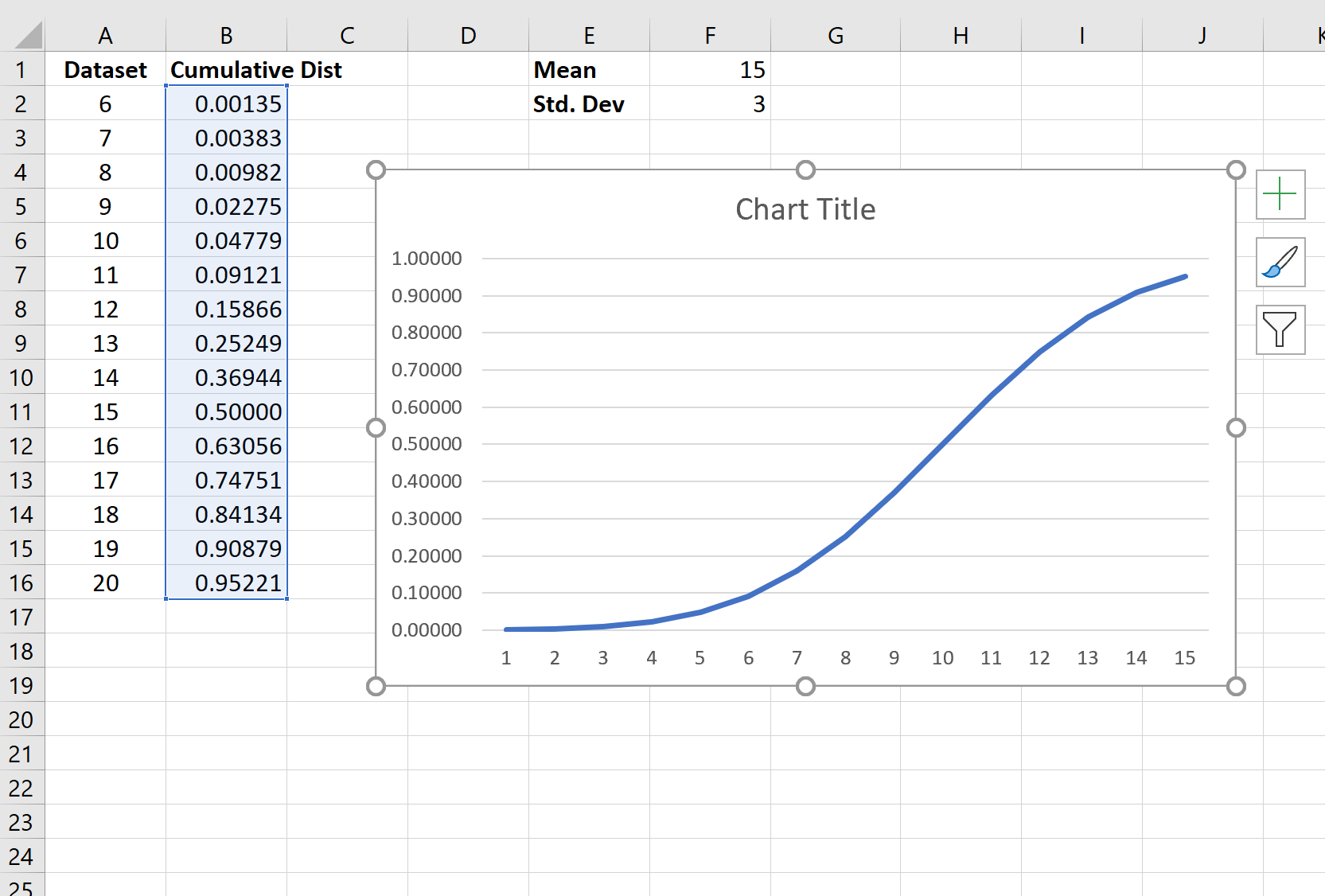
Чтобы визуализировать этот CDF, мы можем выделить каждое значение в столбце B. Затем мы можем щелкнуть вкладку « Вставка » на верхней ленте и нажать « Вставить линейную диаграмму» , чтобы создать следующую диаграмму:
Значения по оси X показывают значения из набора данных, а значения по оси Y показывают значения CDF.
Источник
Как создать кумулятивную диаграмму суммы в Excel (с примером)
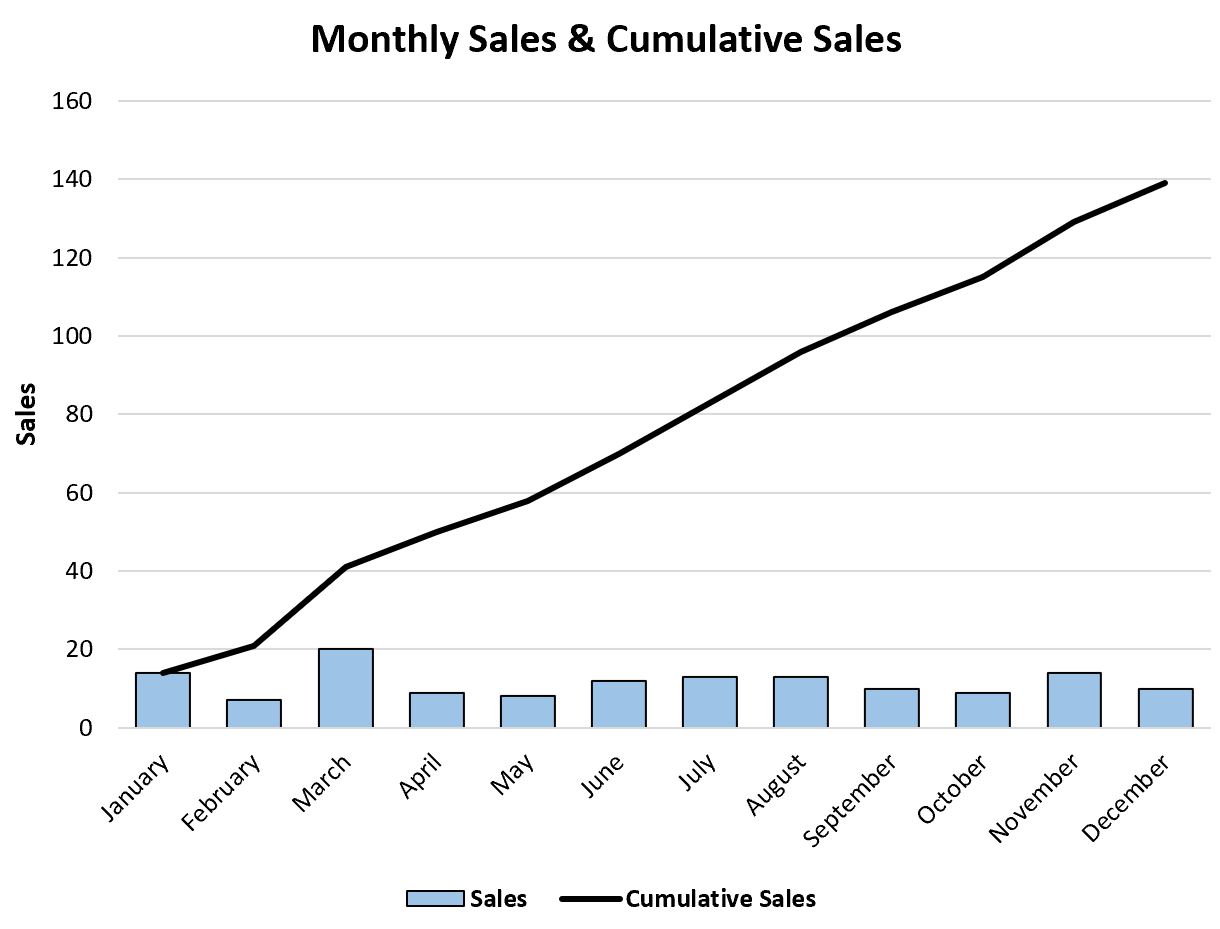
В этом руководстве представлен пошаговый пример того, как создать следующую сводную диаграмму в Excel:
Шаг 1: введите данные
Во-первых, давайте создадим следующий набор данных, который показывает общий объем продаж некоторого товара в течение каждого месяца в году:
Шаг 2: Рассчитайте совокупную сумму
Далее мы будем использовать следующую формулу для расчета совокупной суммы продаж:
Мы можем ввести эту формулу в ячейку C2 , а затем скопировать и вставить ее в каждую оставшуюся ячейку в столбце C:
Шаг 3: Создайте гистограмму со средней линией
Затем выделите диапазон ячеек A1:C13 , затем нажмите вкладку « Вставка » на верхней ленте, затем нажмите « Сгруппированный столбец » в группе « Диаграммы ».
Будет создана следующая диаграмма:
Затем щелкните правой кнопкой мыши в любом месте диаграммы и выберите « Изменить тип диаграммы» :
В появившемся новом окне нажмите Combo , а затем нажмите OK :
Диаграмма будет преобразована в гистограмму с линией:
Синие столбцы представляют продажи за каждый месяц, а оранжевая линия — совокупные продажи.
Шаг 4. Настройте диаграмму (необязательно)
Не стесняйтесь добавлять заголовок, настраивать цвета, настраивать стиль линий и настраивать ширину полос, чтобы сделать график более эстетичным:
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Источник
Как построить кумуляту в excel по данным таблицы
Для селекционера, например, важно знать, сколько зерен содержит колос выведенного (выводимого) им нового сорта пшеницы. В этой ситуации совершенно ясно, что подсчетом количества зерен только в одном колосе не обойтись. Для определения числа зерен надо воспользоваться достаточно большим количеством колосьев, скажем не менее сотни. Приведем пример математической обработки результатов селекции.
Все поле пшеницы, которое вырастил селекционер можно на математическом языке назвать генеральной совокупностью. Подсчитать количество зерен в колосьях всей генеральной совокупности, очевидно, не представляется возможным, но из всей генеральной совокупности можно выбрать, скажем, сто колосьев и подсчитать количество зерен в них. Эти сто колосьев будут называться выборкой из генеральной совокупности, и они с определенной точностью будут отражать число зерен во всем поле (генеральной совокупности). Чтобы по данным выборки иметь возможность судить обо всей генеральной совокупности, она должна быть отобрана случайно. Так в нашем случае селекционер ни в коем случае не должен отдавать предпочтение тем или иным колосьям (по размерам, внешнему виду, месту произрастания на поле и т.п.) в процессе их выборки. Наиболее целесообразно в данной ситуации совершать выбор колосьев из непрозрачного мешка наугад. У всех выбранных колосьев производится подсчет числа зерен, и результаты фиксируются в виде ряда чисел, с которыми в дальнейшем и предстоит совершать математические действия. В данном примере можно предложить следующую их последовательность.
2.1 Создание вариационного ряда.
Вариационным рядом называется ранжированный в порядке возрастания или убывания ряд вариантов с соответствующими им весами (частотами или частностями). Вариационный ряд будет дискретным, если любые его варианты отличаются на постоянную величину, и непрерывным, если варианты могут отличатся один от другого на сколь угодно малую величину.
Иными словами в вариационном ряду полученные значения располагаются в порядке их увеличения и, если значение повторяется, то рядом записывается число его повторений. Т.е. в данном примере по числу зерен в колосьях ряд может выглядеть так (таб. 2):
Теперь построим кумуляту — график накопленных относительных частот. Расположим его под гистограммой.
Кумулята — это экспериментальная оценка формы графика функции распределения. Теоретическая кривая будет красивой и гладкой — мы познакомились с ней в начале работы, обсуждая свой вариант задания. Экспериментальная оценка — ломаная линия, да ещё и с погрешностями. Эти случайные ошибки вызваны ограниченным, не бесконечным объёмом выборки. В любом случае, эти графики начинаются в нуле и постепенно растут до 100%.
Напомним, что значения накопленных частот должны быть привязаны к верхним границам интервалов — в соответствии со стандартами и здравым смыслом. Идея в том, что накопленная частота накапливается именно к концу интервала, а не к середине.
Построим график в виде ломаной линии:
Insert — Charts — Insert Scatter (X, Y) or Bubble Chart
Вставка — Диаграммы — Вставить точечную (X, Y) или пузырьковую диаграмму
Вставка графика Y (X)
Выбираем тип графика
Scatter — Scatter with Straight Lines
Точечная — Точечная с прямыми отрезками
Это просто ломаная линия без маркеров точек.
Выбираем данные для графика:
Select Data — Select Data Source — Legend Entries (Series) — Add
Выбрать данные — Выбор источника данных — Элементы легенды (ряды) — Добавить
выбираем следующие данные.
Столбец «иксов» — верхние границы:
Series X Values
Столбец «игреков» — накопленные частоты:
Series Y Values
Убираем заголовок диаграммы:
Chart Elements — Chart Title
Элементы диаграммы — Название диаграммы
Настраиваем цвет линии на графике.
Format Data Series — Series options — Fill & Line — Line
Формат ряда данных —Параметры ряда — Заливка и границы — Линия
Line — Solid line
Линия — Сплошная линия
Если отрезков много, то ломаная линия выглядит как гладкая кривая.
Настроим числовые метки на вертикальной оси, чтобы выводились целые числа:
Format Axis — Axis Options — Number — Decimal places — 0
Формат оси — Параметры оси — Число — Число десятичных знаков — 0
Установим диапазоны значений по осям.
Вертикальная ось — метки в процентах, а границы диапазона — числа. Поэтому пределы изменения будут от 0 до 1:
Axis Options — Bounds
Параметры оси — Границы
Горизонтальная ось — в соответствии с интервалами группировки — от 190 до 310.
Подгоняем размеры графика и размещаем его под гистограммой. Можно сделать это вручную.
Если захочется особой точности, поработаем через меню параметров графика (числа условные).
Format Chart Area — Chart Options — Size & Properties — Size
Формат области диаграммы — Параметры диаграммы — Размер и свойства — Размер
В английской версии пакета размеры измеряются в дюймах. В русской версии — в сантиметрах. Можем установить точные значения размеров вручную.
Окончательно совмещаем маштаб гистограммы и кумуляты: начало первого интервала 190, конец последнего интервала 310. Положения этих двух меток на обоих графиках должны совпадать.
Проблемы с масштабом решаем так. Значение 190 находится в начале интервала, обозначенного 193. Значение 310 находится в конце интервала, следующего за 303.
Одним из способов исследования рядов распределения является построение кумуляты. Она позволяет графически изобразить зависимость значения признака от накопленной частоты. Чаще всего кумулята, или полигон накопленных частот, используется для представления дискретных данных.
- — дискретный вариационный ряд;
- — линейка;
- — карандаш;
- — ластик.
Приведите имеющиеся данные в вид, необходимый для построения графика. Разделите совокупность выборки на равные части, чтобы получить равномерное положение точек графика. Чаще всего для этого используется разделение на временные промежутки: месяцы, дни, годы. Чтобы использовать такой способ, посчитайте значение признака для каждого промежутка времени, например, сколько было продано единиц продукции в каждом месяце. Если признак варьируется слабо и дискретно, используйте безынтервальный вариационный ряд (это могут быть, к примеру, оценки учащихся).
Занесите данные в таблицу, у вас получилось две строки: в первой укажите интервалы или безынтервальные значения, а во второй – частоту встречаемого признака. Добавьте еще одну строку – накопленную частоту значения признака. Заполните эту графу, последовательно прибавляя частоты из второй строки. Например, если в каждом месяце квартала последовательно было продано 5, 3, 4 единицы техники, то накопленная частота будет равна 5, 5+3, 5+3+4, то есть 5, 8, 12. Обратите внимание, каждое следующее значение накопленной частоты всегда будет равно или больше предыдущего, поэтому график никогда не будет идти вниз.
Постройте систему координат. На оси абсцисс поместите значения признака, а на оси ординат – накопленные частоты. Укажите рядом с осью название и единицу измерения.
Поставьте точки в соответствии с вашей таблицей. Для этого используйте значения первой и третьей строки, строка «частота признака» участвовать в построении не будет. Отмеряйте на оси абсцисс значение измеряемого признака, на оси ординат – накопленную частоту, а на пересечении ставьте точку. Когда все точки будут построены, соедините их ломаной линией. Эта линия и называется кумулятой ряда распределения.
Чтобы построить кумуляту в Excel, введите данные в строки или столбцы, затем нажмите «вставка» — «диаграмма». Выберите одну из подходящих точечных диаграмм, укажите нужные для построения данные (не забудьте, только две строки – значение признака и накопленная частота) и нажмите «готово». Если есть необходимость, исправьте готовую диаграмму при помощи окошка настройки.
В данной статье, на примере, рассмотрим такой вид диаграммы, как График с накоплением и в чем его отличие от обычного Графика.
Предположим у нас есть таблица, в которой отражены продажи офисных стульев за год, в штуках. Продажи осуществляли два магазина: Магазин № 1 и магазин № 2.
Это будет наша исходная таблица, на основе которой мы будем строить график с накоплением.
График с накоплением в Excel.
Перед построением графика нам необходимо выделить всю таблицу. Потом в закладке Вставка находим значок Вставить график или диаграмму с областями.
Нажимаем и получаем График с накоплением.
На графике отразились две кривые линии. Оранжевая кривая, это продажи Магазина №2. Синяя кривая, это продажи магазина №1. Для наглядности добавим Метки данных. Вызовем настройки диаграммы нажав на нее. В настройках выберем Элементы диаграммы. Поставим галочку напротив пункта Метки данных. На нашем графики отразиться количество проданных стульев соответственно месяцу года и магазину.
Вертикальная ось диаграммы показывает количество проданных стульев. При этом оранжевая кривая на графике, которая соответствует продажам Магазина №2, берет свое начало не на отметке 260 (шт.). Это количество проданных стульев данным магазинов в январе. Оранжевая кривая берет сове начало на отметке 510 (шт.). Это суммарное количество проданных стульев двумя магазинами в январе (250 шт. +.260 шт.). То есть, для оранжевой кривой, при определении координаты по вертикальной оси, начало отсчета происходит не от нулевой отметки, а от соответствующей (нижележащей) точки синей кривой.
Построим на основе исходной таблицы простой График.
Как видно, кривые продаж Магазина №1 и Магазина №2 наложились одна на одну. Проводить анализ или презентацию используя такой график не целесообразно. График с накоплением позволяет избежать данной проблемы.
При выборочном наблюдении обследованию подвергается определенная, заранее обусловленная часть совокупности, а результаты обследования распространяются на всю совокупность.
Число единиц (элементов) статистической совокупности называется ее объемом. Объем генеральной совокупности обозначается N, а объем выборочной совокупности п.
Качество результатов выборочного наблюдения зависит от того, насколько состав выборки представляет генеральную совокупность, иначе говоря, от того, насколько выборка репрезентативна (представительна).
Элементами выборки (x1 х2, . хп) являются числовые значения, называемые вариантами, которые могут быть дискретными, т.е. изолированными (например, целыми числами), или могут принимать значения из некоторого интервала (а, b).
Вариационный ряд получается из выборки упорядочением по возрастанию (или убыванию) и подсчетом частоты каждого значения. Если вариационный ряд содержит значения признака и соответствующие ему частоты,то такой ряд носит название дискретный вариационный ряд. Если нам известно, что исследуемый показатель может принимать любые значения из некоторого интервала, то строим интервальный вариационный.
Удобнее всего ряды распределения анализировать с помощью их графического изображения, позволяющего судить о форме распределения. Наглядное представление о характере изменения частот вариационного ряда дают полигон и гистограмма.
Известны следующие данные о результатах сдачи студентами экзамена (в баллах):
| 18 | 16 | 20 | 17 | 19 | 20 | 17 |
| 17 | 12 | 15 | 20 | 18 | 19 | 18 |
| 18 | 16 | 18 | 14 | 14 | 17 | 19 |
| 16 | 14 | 19 | 12 | 15 | 16 | 20 |
Необходимо построить ряд распределения числа студентов по баллу, представить графически результаты.
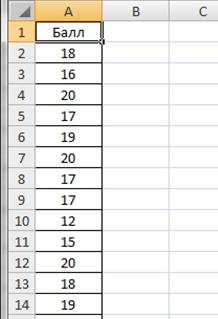
Введем данные в диапазоне A1: A29, в ячейку A1 введем текст «Балл» (рис.2.6).
Рисунок 2.6. Баллы успеваемости студентов
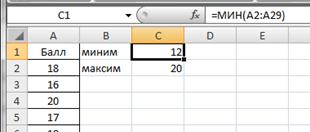
Определим наименьший и наибольший балл по выборке. Для этого введем в ячейках С1 и С2 соответственно введем формулы =МИН(A2:A29) и =МАКС(A2:A29). Получим значения 12 и 20 соответственно (рис.2.7).
Рисунок 2.7. Минимальный и максимальный балл
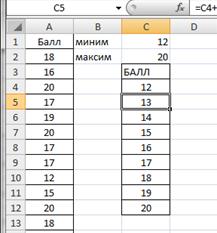
Построим вариационный ряд. Для каждого значения необходимо подсчитать частоту. Так как значения признака (балл) отличаются на единицу, то можно воспользоваться следующим способом. В ячейку С4 введем формулу =С1, в С5 соответственно С4+1. Ячейку С5 протянем маркером заполнения (правый нижний угол ячейки) вниз до С12. Результаты представлены на рисунке 2.8.
Рисунок 2.8. Значения признака
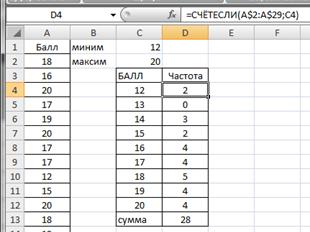
Вычислим частоту для каждого значения признака. В ячейку D4 введем формулу =СЧЕТЕСЛИ(A$2:A$29;C4) и протянем D4 маркером вниз до заполнения D12. В ячейке D13 просуммируем частоты с помощью формулы =СУММ(D4:D12).
Получим вариационный ряд (значения признака и соответствующие им частоты) на рисунке 2.9.
Рис.2.9. Частоты вариационного ряда
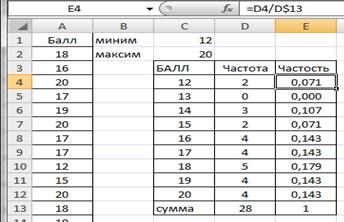
Вычислим частость (относительную частоту) для каждого значения признака. В ячейку Е4 введем формулу = D4/D$13. Протянем Е4 маркером заполнения вниз до Е12 (рис.2.10).
Рисунок 2.10. Частости ряда распределения
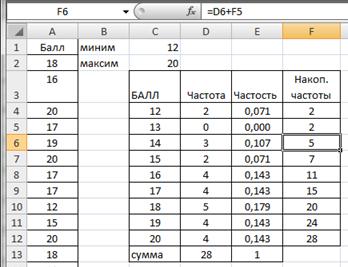
Вычислим накопленные частоты. В ячейку F4 введем формулу =D4, а в ячейку F5 – формулу = D5+F4. Протянем F5 маркером заполнения вниз до F12 (рис.2.11).
Рисунок 2.11. Накопленные частоты ряда
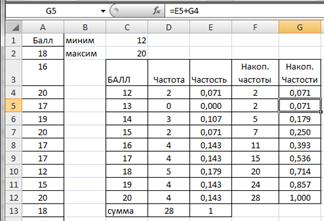
Построим эмпирическую функцию распределения, т.е. найдем наколенные частости. Выделим F4:F12 и маркером заполнения протянем вправо на соседний столбец (рис.2.12). В G4 получим формулу = Е4, в ячейке G5 формулу =Е5+ G4 и т.д.
Рисунок 2.12. Накопленные частости ряда
Построим полигон распределения частот и частостей. Выделим диапазон ячеек С4:D12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частот представлен на рисунке 2.13.
Рисунок 2.13. Полигон распределения частот
Выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон Е4:Е12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками и маркерами». Полигон распределения частостей представлен на рисунке 2.14.
Рисунок 2.14. Полигон распределения частостей
Рисунок 2.15. Гистограмма распределения частостей
Построим кумуляту частостей, для чего выделим диапазон ячеек С4:С12 и, удерживая клавишу CTRL, диапазон G4:G12. Выполним команду меню «Диаграмма» и выберем тип «Точечная», вариант «Точечная с прямыми отрезками». Кумулята представлена на рис.2.16.
Рисунок 2.16. Кумулята
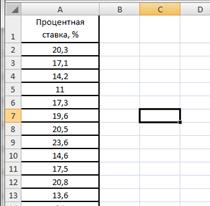
В таблице 2.7 представлены значения процентных ставок по кредитам по 30 коммерческим банкам.
Банковские процентные ставки
| № Банка | Процентная ставка, % |
| 1 | 20,3 |
| 2 | 17,1 |
| 3 | 14,2 |
| 4 | 11,0 |
| 5 | 17,3 |
| 6 | 19,6 |
| 7 | 20,5 |
| 8 | 23,6 |
| 9 | 14,6 |
| 10 | 17,5 |
| 11 | 20,8 |
| 12 | 13,6 |
| 13 | 24,0 |
| 14 | 17,5 |
| 15 | 15,0 |
| 16 | 21,1 |
| 17 | 17,6 |
| 18 | 15,8 |
| 19 | 18,8 |
| 20 | 22,4 |
| 21 | 16,1 |
| 22 | 17,9 |
| 23 | 21,7 |
| 24 | 18,0 |
| 25 | 16,4 |
| 26 | 26,0 |
| 27 | 18,4 |
| 28 | 16,7 |
| 29 | 12,2 |
| 30 | 13,9 |
Построим интервальный вариационный ряд. Для этого вычислим границы интервалов (карманов) с использованием формулы Стэрджесса.
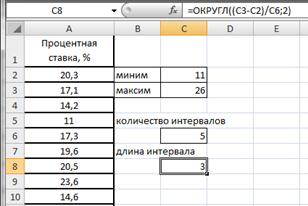
Введем данные в диапазоне A1:A31 (рис.2.17). Определим максимальное и минимальное значения (ячейки С2 и С3 соответственно) так же как и в примере 2.1. Определим число интервалов по формуле Стэрджесса, для чего в ячейку С6 введем формулу =ЦЕЛОЕ(1+3,322*LOG10(30)) (рис.2.18).
Рисунок 2.17. Процентные ставки банков
Рисунок 2.18. Число интервалов
Вычислим длину интервалов, для чего в ячейке С8 введем формулу =ОКРУГЛ((C3-C2)/C6;2) (рис.2.19).
Рисунок 2.19. Длина интервала
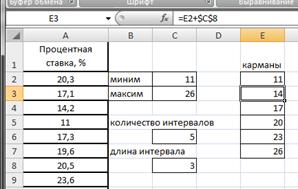
Определим нижние и верхние границы интервалов (карманы), для чего в ячейке Е2 запишем формулу =С2, в ячейке Е3 запишем ==E2+$C$8. Протянем Е3 маркером заполнения вниз до Е7 (рис.2.20).
Рисунок 2.20. Границы интервалов
Подсчитаем частоты – в интервал считаем те значения, которые больше нижней границы интервала или равны ей и меньше верхней границы.
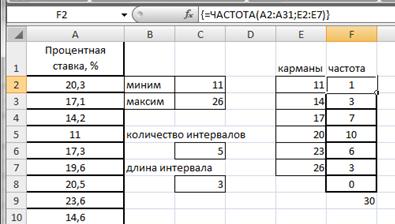
Воспользуемся функцией ЧАСТОТА. Для этого в ячейке F2 введем формулу =ЧАСТОТА(A2:A31;E2:E7). Протянем F2 маркером заполнения вниз до F8.
Формулу в этом примере необходимо ввести как формулу массива. Выделим диапазон F2:F8, нажмем клавишу F2, а затем нажмем клавиши CTRL+SHIFT+ВВОД (рис.2.21).
Если формула не будет введена как формула массива, отобразится только одно ее значение в ячейке F2.
Рисунок 2.21. Частоты значений признака
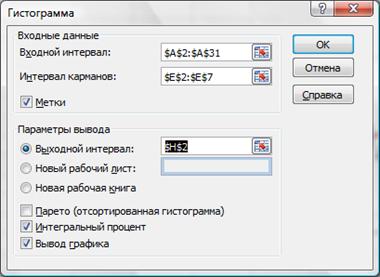
Также можно воспользоваться средством Пакета анализа (Анализ данных в Office 2007) ГИСТОГРАММА (рис.2.22). Выберем входной интервал, интервал карманов, метки, интегральный процент, поместим результаты на этом же листе (укажем ячейку $H$2).
Рисунок 2.22. Построение гистограммы
Полученная гистограмма представлена на рис.2.23.
Рис.2.23. Гистограмма частот
Замечание. Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Вариационный ряд может быть:
Рассмотрим пример построения дискретного вариационного ряда.
Пример 1. Имеются данные о количественном составе 60 семей.
Построить вариационный ряд и полигон распределения
Алгоритм построения вариационного ряда:
1) Откроем таблицы Excel.
2) Введем массив данных в диапазон А1:L5. Если вы изучаете документ в электронной форме (в формате Word, например), для этого достаточно выделить таблицу с данными и скопировать ее в буфер, затем выделить ячейку А1 и вставить данные – они автоматически займут подходящий диапазон.
3) Подсчитаем объем выборки n – число выборочных данных, для этого в ячейку В7 введем формулу =СЧЁТ(А1:L5). Заметим, что для того, чтобы в формулу ввести нужный диапазон, необязательно вводить его обозначение с клавиатуры, достаточно его выделить.
4) Определим минимальное и максимальное значение в выборке, введя в ячейку В8 формулу =МИН(А1:L5), и в ячейку В9: =МАКС(А1:L5).
Рис.1.1 Пример 1. Первичная обработка статистических данных в таблицах Excel
5) Далее, подготовим таблицу для построения вариационного ряда, введя названия для столбца интервалов (значений варианты) и столбца частот. В столбец интервалов введем значения признака от минимального (1) до максимального (6), заняв диапазон В12:В17.
6) Выделим столбец частот, введем формулу =ЧАСТОТА(А1:L5;В12:В17) и нажмем сочетание клавиш CTRL+SHIFT+ENTER
Рис.1.2 Пример 1. Построение вариационного ряда
7) Для контроля вычислим сумму частот при помощи функции СУММ (значок функции S в группе «Редактирование» на вкладке «Главная»), вычисленная сумма должна совпасть с ранее вычисленным объемом выборки в ячейке В7.
2) Название ряда диаграммы «ряд 1» можно либо изменить, воспользовавшись той же опцией «выбрать данные» вкладки «Конструктор», либо просто удалить.
Рис.1.3. Пример 1. Построение полигона частот
В реальных социально-экономических системах нельзя проводить активные эксперименты, поэтому данные обычно представляют собой наблюдения за происходящим процессом, например: курс валюты на бирже в течение месяца, урожайность пшеницы в хозяйстве за 30 лет, производительность труда рабочих за смену и т.д. Результаты наблюдений — это в общем случае ряд чисел, расположенных в беспорядке, который для изучения необходимо упорядочить (проранжи- ровать).
Операция, заключающаяся в расположении значений признака по возрастанию, называется ранжированием опытных данных.
После операции ранжирования опытные данные можно сгруппировать так, чтобы в каждой группе признак принимал одно и то же значение, которое называется вариантом (х,). Число элементов в каждой группе называется частотой варианта («,).
Размахом вариации называется число
где хтах — наибольший вариант;
x min — наименьший вариант.
Сумма всех частот равна определенному числу л, которое называется объемом совокупности:
Отношение частоты данного варианта к объему совокупности называется относительной частотой, или частостью, этого варианта:
Последовательность вариант, расположенных в возрастающем порядке, называется вариационным рядом (вариация — изменение).
Вариационные ряды бывают дискретными и непрерывными. Дискретным вариационным рядом называется ранжированная последовательность вариант с соответствующими частотами и (или) частостями.
Пример 1. В результате тестирования группа из 24 человек набрала баллы: 4, 0, 3, 4, 1, 0, 3, 1, 0, 4, 0, 0, 3, 1, 0, 1, 1, 3, 2, 3, 1, 2, 1, 2. Построить дискретный вариационный ряд.
Решение. Проранжируем исходный ряд, подсчитаем частоту и частость вариант: 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 2, 2, 2, 3, 3, 3, 3, 3, 4, 4, 4.
В результате получим дискретный вариационный ряд (табл. 3.10).
Ранжированный ряд успеваемости
Число студентов, л,
Относительная частота, А
В Excel проранжируем исходный ряд. Для этого введем все данные в диапазон А1 :А24 и воспользуемся кнопкой Щ (Сортировка по возрастанию).
Подсчитаем частоту и частость вариант. Построим таблицу в диапазоне D2:G7 (рис. 3.13).
Рис. 3.13. Контекстное меню строки состояния
Рассмотрим два варианта подсчета частот:
- 1) выделим диапазон, в котором находятся нули. Щелкнем в нижней правой части окна Excel правой кнопкой мыши и выберем в контекстном меню вид итога, который по умолчанию будет появляться в итоговой строке при выделении произвольного диапазона (см. рис. 3.13) — количество. Таким образом, последовательно выделяя диапазоны с одинаковыми значениями вариант, мы получим все частоты;
- 2) выполним команду Сервис — Анализ данных — Гистограмма. Заполним диалоговое окно в соответствии с рис. 3.14.
Рис. 3.14. Диалоговое окно инструмента пакета анализа «Гистограмма»
В результате получим таблицу с частотами вариантов и соответствующий график (рис. 3.15).
Рис. 3.15. Результаты применения инструмента «Гистограмма)
Найдем объем выборки, заполнив все частоты вариант в диапазоне ЕЗ:Е7, выделим его левой кнопкой мыши и щелкнем по кнопке ? (автосумма).
В ячейку F3 введем формулу «=ЕЗ/$Е$8», за маркер заполнения (крест в правом нижнем углу ячейки) с помощью мыши скопируем до F7 и выберем кнопку автосумма, в результате получим частоты вариантов и их сумму (1). В ячейку G3 введем частоту варианта 0 — цифру 6 (или ссылку на ячейку, ее содержащую — ЕЗ), в ячейку G4 введем формулу «=G3+E4» и скопируем ее до ячейки G7, в результате получим накопленные частоты. Таким образом, мы получили дискретный вариационный ряд. Естественно, частоты необходимо округлить, но таким образом, чтобы их сумма равнялась 1. Для этого выделим левой кнопкой мыши диапазон частот (F3:F7), щелкнув по правой кнопке, откроем контекстное меню и выполним команду Формат ячеек — Числовой — Число знаков 3 — ОК. Преобразовав обозначения, получим дискретный вариационный ряд, представленный в табл. 3.11.
Источник
17 авг. 2022 г.
читать 2 мин
В этом руководстве представлен пошаговый пример того, как создать следующую сводную диаграмму в Excel:
Давайте прыгать!
Шаг 1: введите данные
Во-первых, давайте создадим следующий набор данных, который показывает общий объем продаж некоторого товара в течение каждого месяца в году:
Шаг 2: Рассчитайте совокупную сумму
Далее мы будем использовать следующую формулу для расчета совокупной суммы продаж:
=SUM( $B$2:B2 )
Мы можем ввести эту формулу в ячейку C2 , а затем скопировать и вставить ее в каждую оставшуюся ячейку в столбце C:
Шаг 3: Создайте гистограмму со средней линией
Затем выделите диапазон ячеек A1:C13 , затем нажмите вкладку « Вставка » на верхней ленте, затем нажмите « Сгруппированный столбец » в группе « Диаграммы ».
Будет создана следующая диаграмма:
Затем щелкните правой кнопкой мыши в любом месте диаграммы и выберите « Изменить тип диаграммы» :
В появившемся новом окне нажмите Combo , а затем нажмите OK :
Диаграмма будет преобразована в гистограмму с линией:
Синие столбцы представляют продажи за каждый месяц, а оранжевая линия — совокупные продажи.
Шаг 4. Настройте диаграмму (необязательно)
Не стесняйтесь добавлять заголовок, настраивать цвета, настраивать стиль линий и настраивать ширину полос, чтобы сделать график более эстетичным:
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как подогнать кривую в Excel
Как сделать полигон частот в Excel
Как добавить горизонтальную линию на диаграмму рассеяния в Excel
Написано

Замечательно! Вы успешно подписались.
Добро пожаловать обратно! Вы успешно вошли
Вы успешно подписались на кодкамп.
Срок действия вашей ссылки истек.
Ура! Проверьте свою электронную почту на наличие волшебной ссылки для входа.
Успех! Ваша платежная информация обновлена.
Ваша платежная информация не была обновлена.
Построение полигона, гистограммы, кумуляты, огивы
Для наглядности строят различные графики статистического
распределения, и, в частности, полигон и гистограмму.
- Полигон
- Гистограмма
- Кумулята и огива
Полигон
Полигоном частот называют
ломаную, отрезки которой соединяют точки
. Для построения полигона частот на оси
абсцисс откладывают варианты
, а на оси ординат – соответствующие им
частоты
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
Полигоном относительных
частот называют ломаную, отрезки которой соединяют
точки
. Для построения полигона относительных
частот на оси абсцисс откладывают варианты
, а на оси ординат – соответствующие им
относительные частоты (частости)
. Такие точки
соединяют
отрезками прямых и получают полигон частот.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 1
Построить полигон частот и
полигон относительных частот (частостей):
Решение
Вычислим относительные
частоты (частости):
Полигон частот
Полигон относительных частот
В случае интервального ряда для
построения полигона в качестве
берутся середины интервалов.
Гистограмма
В случае интервального
статистического распределения целесообразно построить гистограмму.
Гистограммой частот
называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых
служат частичные интервалы длиною
, а высоты (в случае равных интервалов) должны
быть пропорциональны частотам. При построении гистограммы с неравными
интервалами по оси ординат наносят не частоты, а плотность частоты
. Это необходимо сделать для устранения
влияния величины интервала на распределение и иметь возможность сравнивать
частоты.
В случае построения
гистограммы относительных частот (гистограммы частостей)
высоты в случае равных интегралов должны быть пропорциональны относительной
частоте
, а в случае неравных интервалов высота
равна плотности относительной частоты
.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Пример 2
Построить гистограмму
частот и относительных частот (частостей)
Гистограмма частот
Гистограмма относительных частот
Пример 3
Построить гистограмму
частот (случай неравных интервалов).
Решение
Вычислим плотности
частоты:
Гистограмма частот
Кроме этой задачи на другой странице сайта есть
пример построения полигона и гистограммы на одном графике для интервального вариационного ряда
Кумулята и огива
При помощи кумуляты (кривой сумм) изображается ряд накопленных частот.
Накопленные частоты определяются путём последовательного суммирования частот по
группам и показывают, сколько единиц совокупности имеют значения признака не больше,
чем рассматриваемое значение. При построении кумуляты
интервального вариационного ряда по оси абсцисс откладываются варианты ряда, а
по оси ординат накопленные частоты, которые наносят на поле в виде
перпендикуляров к оси абсцисс в верхних границах интервалов. Затем эти
перпендикуляры соединяют и получают ломаную линию, т.е. кумуляту.
Если при графическом
изображении вариационного ряда в виде кумуляты оси
поменять местами, то получим огиву. То есть огива строится аналогично кумуляте с той
лишь разницей, что накопленные частоты помещают на оси абсцисс, а значения
признака — на оси ординат.
Пример 4
Построить кумулятивную
кривую:
Решение
Вычислим накопленные
частоты:
Кумулятивная кривая
Построение полигона частот
При
построении полигона частот
-
на
оси абсцисс откладываются направо в
порядке возрастания значения признака
(для дискретного рядов) или центральные
значения интервалов – середины
интервалов, -
по
оси ординат откладываются частоты, -
строим
точки, показывающие значение частоты
для каждого значения признака, -
крайние
точки полученной ломаной соединяются
с лежащими на оси абсцисс следующими
(меньшими и большими) возможными, но
фактически не наблюдающимися значениями
признака, частота которых, очевидно,
равна 0, -
замкнутая
с осью абсцисс ломаная линия представляет
полигон распределения частот.
Построение гистрограммы
Гистограмма
– столбиковая диаграмма, для построения
которой на оси абсцисс откладывают
отрезки, равные величине интервалов
вариационного ряда.
Для
построения гистограммы по оси абсцисс
откладывают величины интервалов, а
частоты изображаются прямоугольниками,
построенными на интервалах с высотой,
равной частоте в масштабе оси ординат.
В
случае неравенства интервалов гистограмма
строится не по частотам или частостям,
а по плотности распределения.
Очевидно,
что гистограмма легко может быть
преобразована в полигон распределения,
если середины верхних сторон прямоугольников
соединить отрезками прямых, при этом
середины верхних сторон двух крайних
прямоугольников соединить с осью абсцисс
в точках, отстоящих в принятом масштабе
на величину интервалов от середины
первого и последнего интервалов.
Построение кумуляты
В ряде
случаев для изображения вариационных
рядов используется кумулятивная кривая
(кумулята), она особенно удобна для
сравнения вариационных рядов. Кумулята
строится на основе накопленной частоты.
Накопленные
частоты наносятся в виде ординат;
соединяя вершины отдельных ординат
прямыми, получают ломаную линию, которая,
начиная с нуля, непрерывно поднимается
над осью абсцисс до тех пор, пока не
достигнет высоты, соответствующей общей
сумме частот.
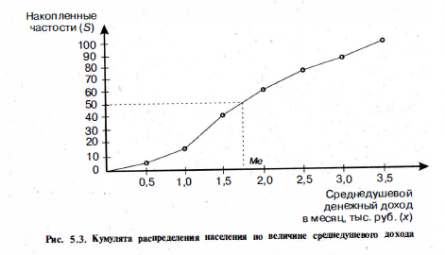
При
построении кумуляты интервального
ряда (рис. 5.3) нижней границе первого
интервала соответствует нулевая частота
(частость), верхней – вся частота (частость)
первого интервала. Верхней границе
второго интервала – сумма частот
(частостей) первого и второго интервалов
и т.д., верхней границе последнего
интервала – сумма накопленных частот
(частостей) во всех интервалах, что
соответствует общей численности
изучаемой совокупности или 100%.
11из7
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
17.02.2016629.11 Кб140308126_71740_lekcii_upravlencheskie_resheniya.rtf
- #
- #
- #
- #
- #
- #
- #
- #