Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Определение 1
Двучленным называется уравнение вида $x^{n} =A$.
Рассмотрим три случая:
- В случае если $A$ – это положительное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ – это отрицательное действительное число, то корни уравнения находятся по формуле
- В случае если $A$ – это комплексное число, то корни уравнения находятся по формуле
[x_{k} =sqrt[{n}]{A} cdot left(cos frac{2kpi }{n} +icdot sin frac{2kpi }{n} right),, , , k=0,..,n-1.]
[x_{k} =sqrt[{n}]{|A|} cdot left(cos frac{pi +2kpi }{n} +icdot sin frac{pi +2kpi }{n} right),, , , k=0,..,n-1.]
[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1.]
Пример 1
Решить уравнение: $x^{3} =8$.
Решение:
Так как $A>0$, то $x_{k} =sqrt[{3}]{8} cdot left(cos frac{2kpi }{3} +icdot sin frac{2kpi }{3} right),, , , k=0,..,2$.
При $k=0$ получаем $x_{0} =sqrt[{3}]{8} cdot left(cos 0+icdot sin 0right)=sqrt[{3}]{8} =2$.
При $k=1$ получаем
[x_{1} =sqrt[{3}]{8} cdot left(cos frac{2pi }{3} +icdot sin frac{2pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} +frac{sqrt{3} }{2} cdot i)=-1+sqrt{3} cdot i.]
При $k=2$ получаем
[x_{2} =sqrt[{3}]{8} cdot left(cos frac{4pi }{3} +icdot sin frac{4pi }{3} right)=sqrt[{3}]{8} cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=2cdot (-frac{1}{2} -frac{sqrt{3} }{2} cdot i)=-1-sqrt{3} cdot i.]
Пример 2
Решить уравнение: $x^{3} =1+i$.
«Квадратное уравнение с комплексными корнями» 👇
Решение:
Так как $A$ – комплексное число, то
[x_{k} =sqrt[{n}]{r} cdot (cos frac{varphi +2pi k}{n} +isin frac{varphi +2pi k}{n} ),, , , k=0..n-1,, , , k=0,..,2.]
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
[r=sqrt{1^{2} +1^{2} } =sqrt{1+1} =sqrt{2} ]
Вычислим аргумент исходного комплексного числа:
[varphi =arg z=arctgfrac{1}{1} =arctg1=frac{pi }{4} ]
Подставим полученные значения и получим:
[A=sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]
Уравнение перепишем в виде:
[x^{3} =sqrt{2} cdot (cos frac{pi }{4} +isin frac{pi }{4} )]
При $k=0$ получаем $x_{0} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4}{3} +icdot sin frac{pi /4}{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)=sqrt[{6}]{2} cdot left(cos frac{pi }{12} +icdot sin frac{pi }{12} right)$.
При $k=1$ получаем
[begin{array}{l} {x_{1} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+2pi }{3} +icdot sin frac{pi /4+2pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{3pi }{4} +icdot sin frac{3pi }{4} right)} end{array}]
При $k=2$ получаем
[begin{array}{l} {x_{2} =sqrt[{3}]{sqrt{2} } cdot left(cos frac{pi /4+4pi }{3} +icdot sin frac{pi /4+4pi }{3} right)=sqrt[{3}]{sqrt{2} } cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)=} \ {=sqrt[{6}]{2} cdot left(cos frac{17pi }{12} +icdot sin frac{17pi }{12} right)} end{array}]
Определение 2
Квадратным называется уравнение вида $ax^{2} +bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^{2} -4ac$, при этом
[x_{1,2} =frac{-bpm sqrt{D} }{2a} .]
Примечание 1
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Пример 3
Решить уравнение $x^{2} +2x+5=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
[D=2^{2} -4cdot 1cdot 5=4-20=-16.]
Так как $D
[x_{1,2} =frac{-2pm sqrt{-16} }{2} =frac{-2pm icdot sqrt{16} }{2} =frac{-2pm icdot 4}{2} =-1pm 2i.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
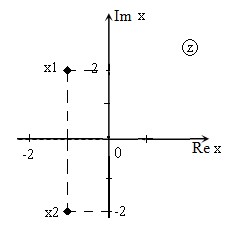
Рис. 1
Примечание 2
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Определение 3
Комплексное число вида $overline{z}=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Примечание 3
Известно, что если $x_{1,2} $ являются корнями квадратного уравнения $ax^{2} +bx+c=0$, то данное уравнение можно переписать в виде $(x-x_{1} )(x-x_{2} )=0$. В общем случае $x_{1,2} $ являются комплексными корнями.
Пример 4
Зная корни уравнения $x_{1,2} =1pm 2i$, записать исходное уравнение.
Решение:
Запишем уравнение следующим образом:
[(x-(1-2i))cdot (x-(1+2i))=0.]
Выполним умножение комплексных чисел
[x^{2} -(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0][x^{2} -x+2icdot x-x-2icdot x+1-4i^{2} =0] [x^{2} -2x+1+4=0] [x^{2} -2x+5=0]
Следовательно, $x^{2} -2x+5=0$ – искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Пример 5
Решить уравнение: $z^{2} +(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.
Решение:
Вычислим дискриминант:
[D=(1-2i)^{2} +4cdot 1cdot (1+i)=1-4i+4i^{2} +4+4i=1-4+4=1.]
Так как $D>0$, уравнение имеет два корня:
[x_{1} =frac{-(1-2i))-sqrt{1} }{2} =frac{-1+2i-1}{2} =frac{-2+2i}{2} =-1+i.] [x_{2} =frac{-(1-2i))+sqrt{1} }{2} =frac{-1+2i+1}{2} =frac{2i}{2} =i.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
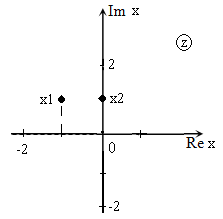
Рис. 2
Примечание 4
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты
$a$,
$b$ и
$c$ – в общем случае являются комплексными.
Его решение находим с помощью дискриминанта
$$D=b^{2}-4 a c$$
тогда
$$x_{1,2}=frac{-b pm sqrt{D}}{2 a}$$
В общем случае и дискриминант, и корни уравнения являются
комплексными числами.
Пример
Задание. Составить квадратное уравнение, которое имеет корни
$z_{1}=1-i$ и
$z_{2}=4-5i$. Решить его.
Решение. Известно, что если
$z_1$, $z_2$ – корни квадратного уравнения
$z^2+bz+c=0$, то указанное уравнение можно записать в виде
$(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что
искомое уравнение можно записать следующим образом:
$$(z-(1-i))(z-(4-5 i))=0$$
Раскрываем скобки и выполняем операции над комплексными числами:
$$z^{2}-(4-5 i) z-(1-i) z+(1-i)(4-5 i)=0$$
$$z^{2}+z(-4+5 i-1+i)+4-5 i-4 i+5 i^{2}=0$$
$z^{2}+(-5+6 i) z-(1+9 i)=0$ – искомое квадратное уравнение.
Решим полученное уравнение. Найдем дискриминант:
$$D=(-5+6 i)^{2}-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$
$$=-7-24 i$$
Так как при извлечении корня из комплексного числа в
результате получится комплексное число, то корень из
дискриминанта будем искать в виде $sqrt{D}=a+b i$. То есть
$$sqrt{-7-24 i}=a+b i Rightarrow-7-24 i=(a+b i)^{2} Rightarrow$$
$$Rightarrow-7-24 i=a^{2}+2 a b i-b^{2}$$
Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно,
получим систему для нахождения неизвестных значений $a$ и
$b$:
$$left{begin{array}{l}a^{2}-b^{2}=-7 \ 2 a b=-24end{array}right.$$
решив которую, имеем, что $a_1=3$,
$b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из
полученных пар, например, первую, получаем, что
$sqrt{D}=3-4 i$, а тогда
$$z_{1}=frac{-(-5+6 i)+(3-4 i)}{2 cdot 1}=4-5 i$$
$$z_{2}=frac{-(-5+6 i)-(3-4 i)}{2 cdot 1}=1-i$$
Ответ. $z^{2}+(-5+6 i) z-(1+9 i)=0$
Читать дальше: элементарные функции комплексного аргумента.
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Продолжаем знакомиться с комплексными числами, сегодня уже будут квадратные уравнения, но не простые, а с отрицательными числами под корнем. Да-да, вы не ошиблись, именно с отрицательными. Будем развеивать школьные мифы о том, что, если под корнем число отрицательное, то уравнение решений не имеет. Ещё как имеет, только не в области вещественных чисел. Пожалуй стоит приступать.
Начнём с простенького примерчика, выступит он у нас в качестве ознакомительного.
Посмотрим на решение.
Рассмотрим теперь полноценное квадратное уравнение.
Решим ещё один примерчик для закрепления.
На сегодня всё, было довольно необычно разбирать такие простые задания, зато посмотрели как решаются квадратные уравнения с комплексными числами, заметили что они не на много интереснее стандартных. Оставляйте в комментариях какие темы нужно ещё разобрать в дальнейшем. Спасибо за внимание.
Другие разделы:
Квадратное уравнение с комплексными корнями
Вы будете перенаправлены на Автор24
Рассмотрим решение уравнений с комплексными корнями и коэффициентами.
Двучленным называется уравнение вида $x^ =A$.
Рассмотрим три случая:
Решить уравнение: $x^ <3>=8$.
Так как $A>0$, то $x_ =sqrt[<3>] <8>cdot left(cos frac<2kpi > <3>+icdot sin frac<2kpi > <3>right),, , , k=0. 2$.
При $k=0$ получаем $x_ <0>=sqrt[<3>] <8>cdot left(cos 0+icdot sin 0right)=sqrt[<3>] <8>=2$.
При $k=1$ получаем
[x_ <1>=sqrt[<3>] <8>cdot left(cos frac<2pi > <3>+icdot sin frac<2pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=-1+sqrt <3>cdot i.]
При $k=2$ получаем
[x_ <2>=sqrt[<3>] <8>cdot left(cos frac<4pi > <3>+icdot sin frac<4pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=-1-sqrt <3>cdot i.]
Решить уравнение: $x^ <3>=1+i$.
Готовые работы на аналогичную тему
Так как $A$ – комплексное число, то
Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.
По условию $a=1,b=1$.
Вычислим модуль исходного комплексного числа:
Вычислим аргумент исходного комплексного числа:
[varphi =arg z=arctgfrac<1> <1>=arctg1=frac<pi > <4>]
Подставим полученные значения и получим:
Уравнение перепишем в виде:
При $k=0$ получаем $x_ <0>=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi /4> <3>+icdot sin frac<pi /4> <3>right)=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)=sqrt[<6>] <2>cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)$.
При $k=1$ получаем
При $k=2$ получаем
Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.
Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом
В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.
[D=2^ <2>-4cdot 1cdot 5=4-20=-16.]
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.
В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.
Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.
Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.
Зная корни уравнения $x_ <1,2>=1pm 2i$, записать исходное уравнение.
Запишем уравнение следующим образом:
[x^ <2>-(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ <2>-x+2icdot x-x-2icdot x+1-4i^ <2>=0] [x^ <2>-2x+1+4=0] [x^ <2>-2x+5=0]
Следовательно, $x^ <2>-2x+5=0$ – искомое уравнение.
Рассмотрим квадратное уравнение с комплексными коэффициентами.
Решить уравнение: $z^ <2>+(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.
Так как $D>0$, уравнение имеет два корня:
Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.
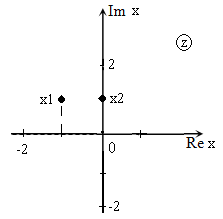
В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 13 11 2021
Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Работаем по будням с 10:00 до 20:00 по Мск
. и многие другие.
Успешной учебы! Будем рады вам помочь!
Квадратное уравнение с комплексными корнями и коэффициентами
Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты $a$, $b$ и $c$ – в общем случае являются комплексными. Его решение находим с помощью дискриминанта
В общем случае и дискриминант, и корни уравнения являются комплексными числами.
Задание. Составить квадратное уравнение, которое имеет корни $z_<1>=1-i$ и $z_<2>=4-5i$. Решить его.
Решение. Известно, что если $z_1$, $z_2$ – корни квадратного уравнения $z^2+bz+c=0$, то указанное уравнение можно записать в виде $(z-z_1)(z-z_2)=0$. А тогда, учитывая этот факт, имеем, что искомое уравнение можно записать следующим образом:
Раскрываем скобки и выполняем операции над комплексными числами:
$z^<2>+(-5+6 i) z-(1+9 i)=0$ – искомое квадратное уравнение.
Решим полученное уравнение. Найдем дискриминант:
$$D=(-5+6 i)^<2>-4 cdot 1 cdot(-(1+9 i))=-11-60 i+4+36 i=$$ $$=-7-24 i$$
Так как при извлечении корня из комплексного числа в результате получится комплексное число, то корень из дискриминанта будем искать в виде $sqrt=a+b i$. То есть
$$sqrt<-7-24 i>=a+b i Rightarrow-7-24 i=(a+b i)^ <2>Rightarrow$$ $$Rightarrow-7-24 i=a^<2>+2 a b i-b^<2>$$
Используя тот факт, что два комплексных числа будут равными, если равны их действительные и мнимые части соответственно, получим систему для нахождения неизвестных значений $a$ и $b$:
решив которую, имеем, что $a_1=3$, $b_1=-4$ или $a_2=-3$, $b_2=4$. Рассматривая любую из полученных пар, например, первую, получаем, что $sqrt=3-4 i$, а тогда
Ответ. $z^<2>+(-5+6 i) z-(1+9 i)=0$
Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.
Рассматривать будем на таком примере:
Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:
Выполним проверку того, что эти корни и права оказываются решением уравнения:
Что и требовалось доказать.
Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: 
.
Такие корни являются сопряженными комплексными корнями.
Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:
, 
,
,
,
В каждом случае получаем 2 сопряженных комплексных корня.
Решим квадратное уравнение 
.
Первым шагом определим дискриминант уравнения:
В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:
Как известно из формул дискриминанта у нас образуется 2 корня:
– сопряженные комплексные корни
Т.о., у уравнения есть 2 сопряженных комплексных корня:
,
Теперь можно решить любое квадратное уравнение!
У любого уравнения с многочленом n-ой степени 
есть ровно n корней, некоторые из них могут быть комплексными.
Как извлечь корень из произвольного комплексного числа?
Рассмотрим уравнение z n = w, либо, записав в другом виде: 
. Здесь n может принимать всякое натуральное значение, которое больше 1-цы.
В частности, при n = 2 получаем квадратный корень 
.
У уравнения типа есть ровно n корней z0, z1, z2, … zn-1, которые можно вычислить с помощью формулы:
,
где 
– это модуль комплексного числа w,
φ – его аргумент,
а параметр k принимает значения: 
.
Найдем корни уравнения: 
.
Перепишем уравнение как: 
.
В этом примере 
, 
, поэтому у уравнения будет 2 корня: z0 и z1. Детализируем общую формулу:
, 
.
Далее найдем модуль и аргумент комплексного числа :
Число w находится в 1-ой четверти, значит:
Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.
Детализируем еще немного общую формулу:
, .
Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.
Подставляем в формулу значение k = 0 и получаем 1-й корень:
.
Подставляем в формулу значение k = 1 и получаем 2-й корень:
.
Ответ: 
, 
Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.
Часто вычисленные корни нужно изобразить геометрически:
Как выполнить чертеж?
Для начала на калькуляторе вычисляем, чему равен модуль корней 
и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.
Далее берем аргумент 1-го корня 
и вычисляем, чему равен угол в градусах:
.
Отмеряем транспортиром 45° и ставим на чертеже точку z0.
Берем аргумент 2-го корня 
и переводим его тоже в градусы: 
. Отмеряем транспортиром 165° и ставим на чертеже точку z1.
По этому же алгоритму ставим точку z2.
Видно, что корни располагаются геометрически правильно с интервалом 
между радиус-векторами. Чертеж обязательно делать при помощи транспортира.
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_16_14.php
http://www.calc.ru/Chisla-Izvlecheniye-Korney-Iz-Kompleksnykh-Chisel-Kvadratnoy.html
[/spoiler]
Тема 16 действия над комплексными числами в алгебраической форме. Решение квадратных уравнений
КОНСПЕКТ 16
16.1 КОМПЛЕКСНЫЕ ЧИСЛА
Комплексным числом Zназывается
число вида
,
где
и
–
действительные числа,
–мнимая
единица.
,
а значит
Число
называетсядействительной частью(
)
комплексного числаZ,
число
называетсямнимой частью(
)комплексного числаZ
16.2 ДЕЙСТВИЯ НАД КОМПЛЕКСНЫМИ ЧИСЛАМИ,
ЗАДАННЫМИ В АЛГЕБРАИЧЕСКОЙ ФОРМЕ
СЛОЖЕНИЕ И ВЫЧИТАНИЕ
Пример
1
Сложить два комплексных числа
,
Для
того чтобы сложить два комплексных
числа нужно сложить их действительные
и мнимые части:
Пример
2
Найти разности комплексных чисел
,
если
,
Действие
аналогично сложению, единственная
особенность состоит в том, что вычитаемое
нужно взять в скобки, а затем – стандартно
раскрыть эти скобки со сменой знака:
Результат не должен смущать, у полученного
числа две, а не три части. Просто
действительная часть – составная:
.
Для наглядности ответ можно переписать
так:
.
УМНОЖЕНИЕ
Пример
3
Найти произведение комплексных чисел
,
Очевидно,
что произведение следует записать
так:
Что
напрашивается? Напрашивается раскрыть
скобки по правилу умножения многочленов.
Так и нужно сделать! Все алгебраические
действия вам знакомы, главное, помнить,
что
и
быть внимательным.
Повторим
школьное правило умножения многочленов:
Чтобы умножить многочлен на многочлен
нужно каждый член одного многочлена
умножить на каждый член другого
многочлена.
Я
распишу подробно:
Надеюсь,
всем было понятно, что
Внимание,
и еще раз внимание, чаще всего ошибку
допускают в знаках.
ДЕЛЕНИЕ
Пример
4
Даны комплексные числа
,
.
Найти частное
.
Составим
частное:
Деление
чисел осуществляется методом
умножения знаменателя и числителя на
сопряженное знаменателю выражение.
Вспоминаем
бородатую формулу
и
смотрим на нашзнаменатель:
.
В знаменателе уже есть
,
поэтому сопряженным выражением в данном
случае является
,
то есть
Согласно
правилу, знаменатель нужно умножить на
,
и, чтобы ничего не изменилось, домножить
числитель на то же самое число
:
Далее
в числителе нужно раскрыть скобки
(перемножить два числа по правилу,
рассмотренному в предыдущем пункте). А
в знаменателе воспользоваться формулой
(помним,
что
и
не путаемся в знаках!!!).
Распишу
подробно:
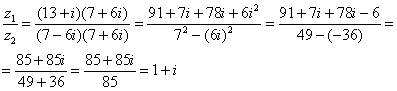
ВОЗВЕДЕНИЕ В СТЕПЕНЬ
Пример
5
Возвести в квадрат комплексное число
Здесь
можно пойти двумя путями, первый способ
это переписать степень как произведение
множителей
и
перемножить числа по правилу умножения
многочленов.
Второй
способ состоит в применение известной
школьной формулы сокращенного умножения
:
Что
делать, если комплексное число нужно
возвести, скажем, в 5-ую, 10-ую или 100-ую
степень? Ясно, что в алгебраической
форме проделать такой трюк практически
невозможно, действительно, подумайте,
как вы будете решать пример вроде
Пример
6
Возвести в степень комплексные числа
,
,
Здесь
тоже всё просто, главное, помнить
знаменитое равенство.
Если
мнимая единица возводится в четную
степень, то техника решения такова:
Если
мнимая единица возводится в нечетную
степень, то «отщипываем» одно «и»,
получая четную степень:
Если
есть минус (или любой действительный
коэффициент), то его необходимо
предварительно отделить:
16.3 РЕШЕНИЕ КВАДРАТНЫХ УРАВНЕНИЙ
Рассмотрим пример:
Нельзя
извлечь корень? Если речь идет о
действительных числах, то действительно
нельзя. В комплексных числах извлечь
корень – можно! А точнее, двакорня:
Действительно
ли найденные корни являются решением
уравнения
?
Выполним проверку:
Что
и требовалось проверить.
Часто
используется сокращенная запись, оба
корня записывают в одну строчку под
«одной гребёнкой»:
.
Такие
корни также называют сопряженными
комплексными корнями.
Как
извлекать квадратные корни из отрицательных
чисел, думаю, всем понятно:
,
,
,
,
и
т.д. Во всех случаях получаетсядвасопряженных комплексных корня.
Пример
7
Решить квадратное уравнение
Вычислим
дискриминант:
Дискриминант
отрицателен, и в действительных числах
уравнение решения не имеет. Но корень
можно извлечь в комплексных числах!
По
известным школьным формулам получаем
два корня:
–
сопряженные комплексные корни
Таким
образом, уравнение
имеет
два сопряженных комплексных корня:
,
ПРАКТИКУМ 16
ЗАДАНИЕ N 1Тема:
Действия над комплексными числами,
заданными в алгебраической формеПроизведение
комплексных чисел
и
равно …
Решение:Напоминаем, что произведение
данных комплексных чисел можно найти
по правилу умножения одночлена на
двучлен с учетом равенства
Тогда
получим:
ЗАДАНИЕ N 2Тема:
Действия над комплексными числами,
заданными в алгебраической формеПроизведение
комплексных чисел
и
равно …
Решение:Напоминаем, что произведение
данных комплексных чисел можно найти
по правилу умножения одночлена на
двучлен с учетом равенства
Тогда
получим:
ЗАДАНИЕ N 3Тема:
Действия над комплексными числами,
заданными в алгебраической формеПроизведение
комплексных чисел
и
равно …
Решение:Напоминаем, что произведение
данных комплексных чисел можно найти
по правилу умножения одночлена на
двучлен с учетом равенства
Тогда
получим:
ЗАДАНИЕ N 4Тема:
Решение уравненийКорни квадратного
уравнения
равны …
Решение:Учитывая равенство
,
мы можем найти корни данного уравнения,
принадлежащие множеству комплексных
чисел; получим:
Корнями
уравнения являются комплексные числа
и
ЗАДАНИЕ N 5Тема:
Решение уравненийКорни квадратного
уравнения
равны …
Решение:Напоминаем, что дискриминант
квадратного уравнения находится по
формуле
;
для исходного уравнения
,
но учитывая равенство
,
мы можем найти корни уравнения,
принадлежащие множеству комплексных
чисел; получим:
Корнями
уравнения являются комплексные числа
и
.
ЗАДАНИЕ N 6Тема:
Решение уравненийКорни квадратного
уравнения
равны …
Решение:Учитывая равенство
мы
можем найти корни данного уравнения,
принадлежащие множеству комплексных
чисел; получим:
Корнями
уравнения являются комплексные числа
и
.
САМОСТОЯТЕЛЬНАЯ РАБОТА 16
ЗАДАНИЕ N 1Тема:
Действия над комплексными числами,
заданными в алгебраической формеПроизведение
комплексных чисел
и
равно …
ЗАДАНИЕ N 2
Тема: Действия над комплексными
числами, заданными в алгебраической
формеПроизведение комплексных
чисел
и
равно …
ЗАДАНИЕ N 3Тема:
Действия над комплексными числами,
заданными в алгебраической формеПроизведение
комплексных чисел
и
равно …
ЗАДАНИЕ N 4
Тема: Действия над комплексными
числами, заданными в алгебраической
формеПроизведение комплексных
чисел
и
равно …
ЗАДАНИЕ N 5
Тема: Действия над комплексными
числами, заданными в алгебраической
формеПроизведение комплексных
чисел
и
равно …
ЗАДАНИЕ N 6Тема:
Решение уравненийКорни квадратного
уравнения
равны …
ЗАДАНИЕ N 7Тема:
Решение уравненийКорни квадратного
уравнения
равны …
ЗАДАНИЕ N 8Тема:
Решение уравненийКорни квадратного
уравнения
равны …
ЗАДАНИЕ N 9Тема:
Решение уравненийКорни квадратного
уравнения
равны …
ЗАДАНИЕ N 10Тема:
Решение уравненийКорни квадратного
уравнения
равны …
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
