17 авг. 2022 г.
читать 3 мин
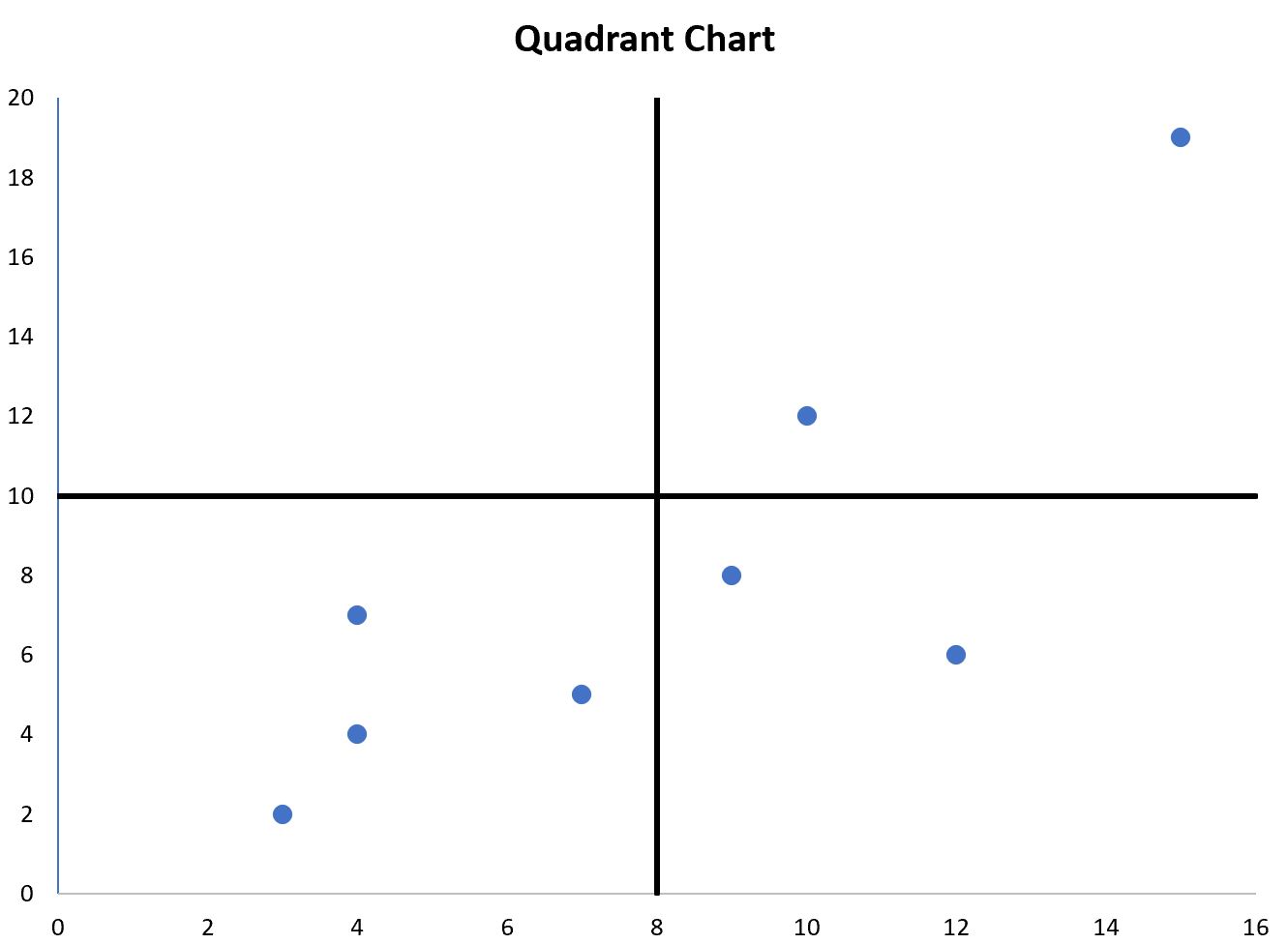
Квадрантная диаграмма — это тип диаграммы, который позволяет визуализировать точки на точечной диаграмме в четырех различных квадрантах.
В этом руководстве представлен пошаговый пример того, как создать следующую квадрантную диаграмму в Excel:
Шаг 1: введите данные
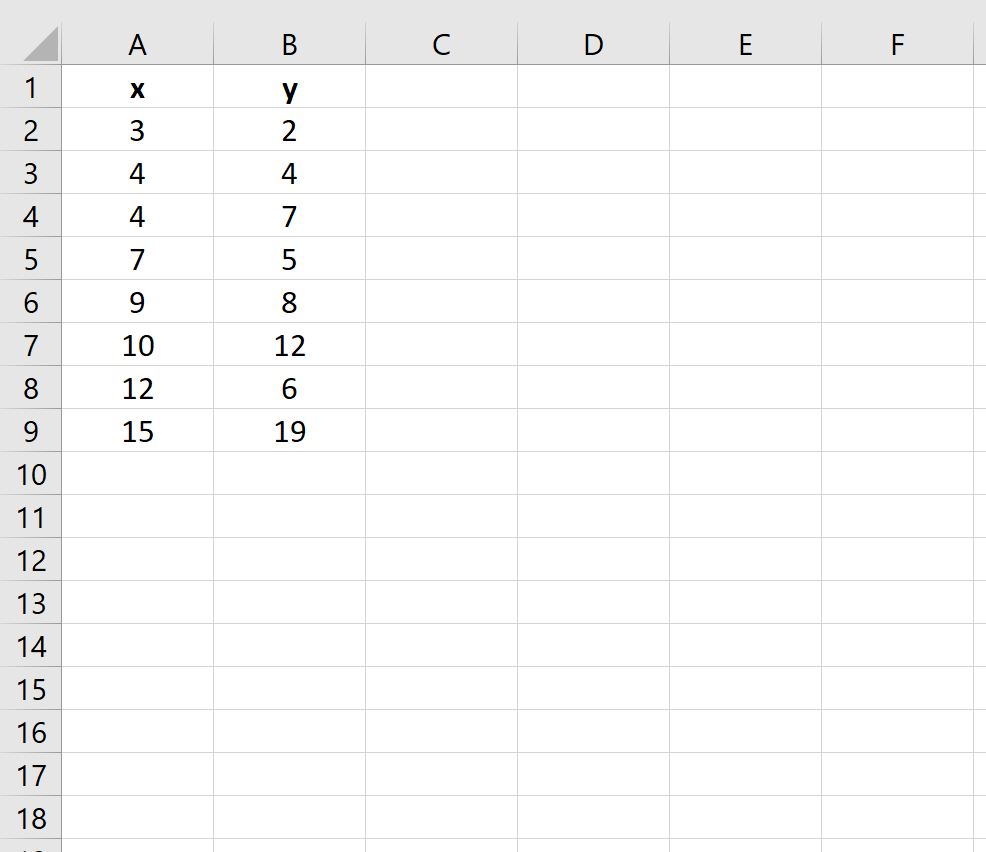
Во-первых, давайте введем следующий набор данных значений x и y в Excel:
Шаг 2: Создайте точечную диаграмму
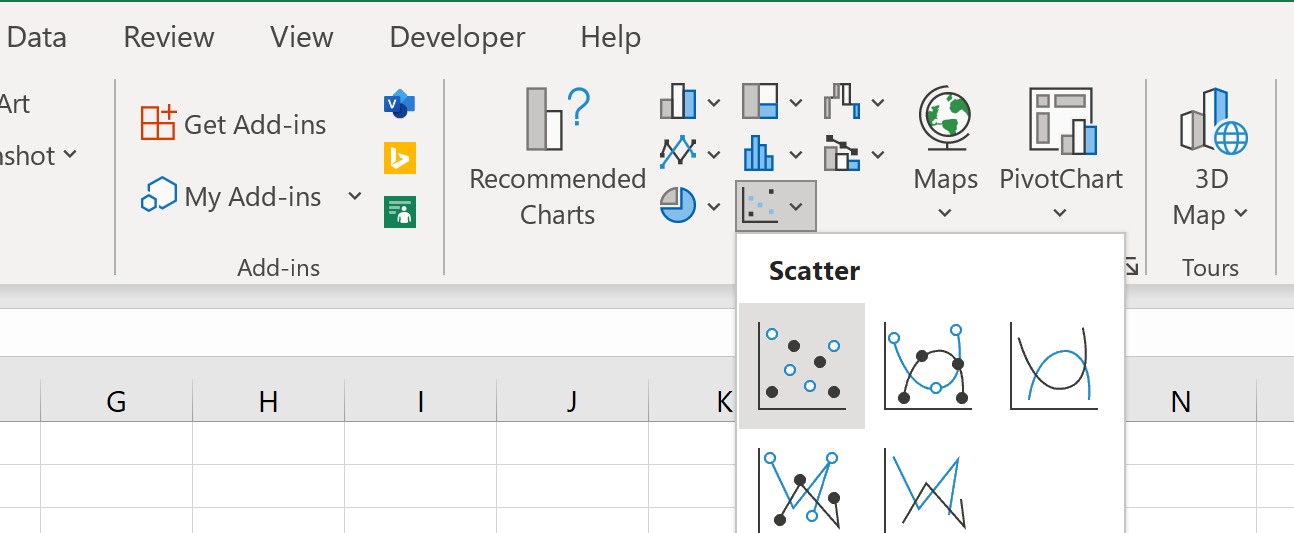
Затем выделите ячейки в диапазоне A2:B9 , затем щелкните вкладку « Вставка », затем щелкните параметр « Разброс » в группе « Диаграммы »:
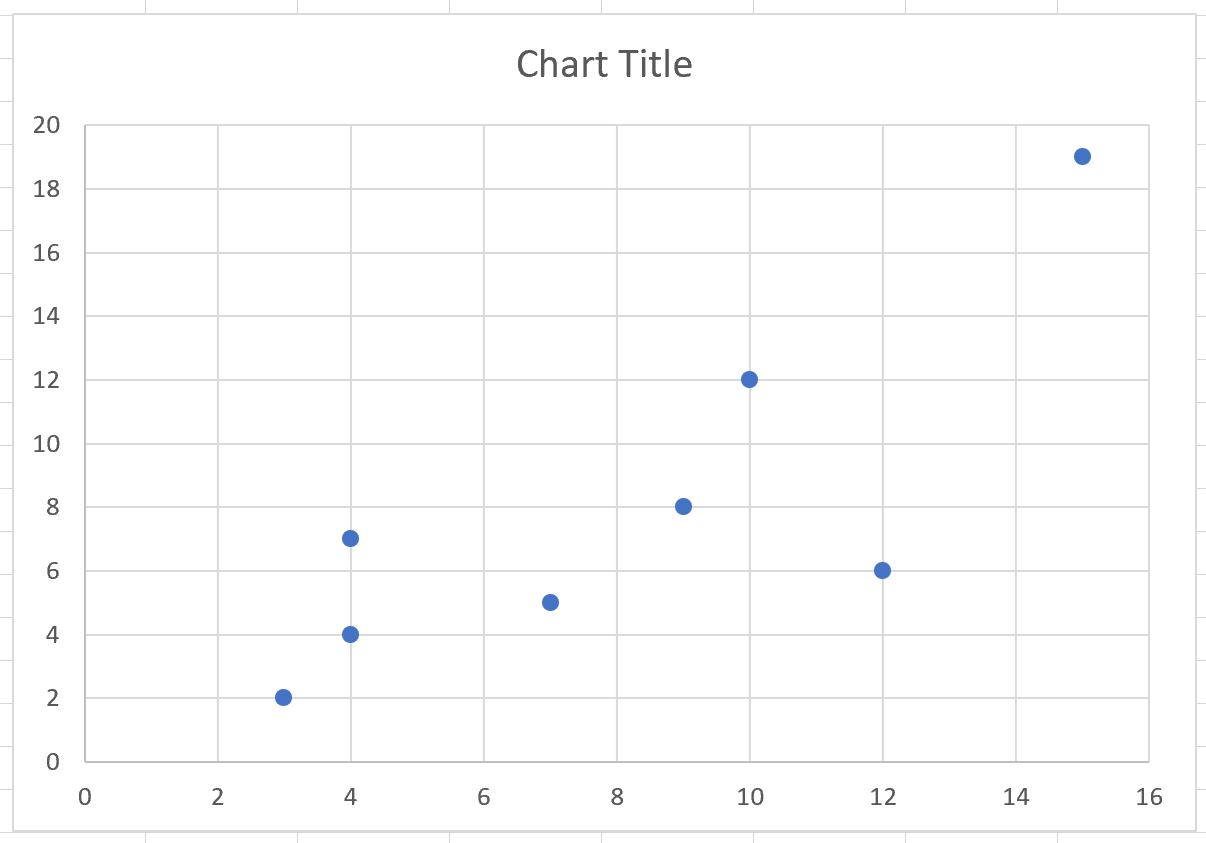
Excel автоматически вставит следующую точечную диаграмму:
Шаг 3: Создайте диаграмму квадрантов
Чтобы превратить этот точечный график в диаграмму квадрантов, мы сначала щелкнем горизонтальную и вертикальную линии сетки и удалим обе:
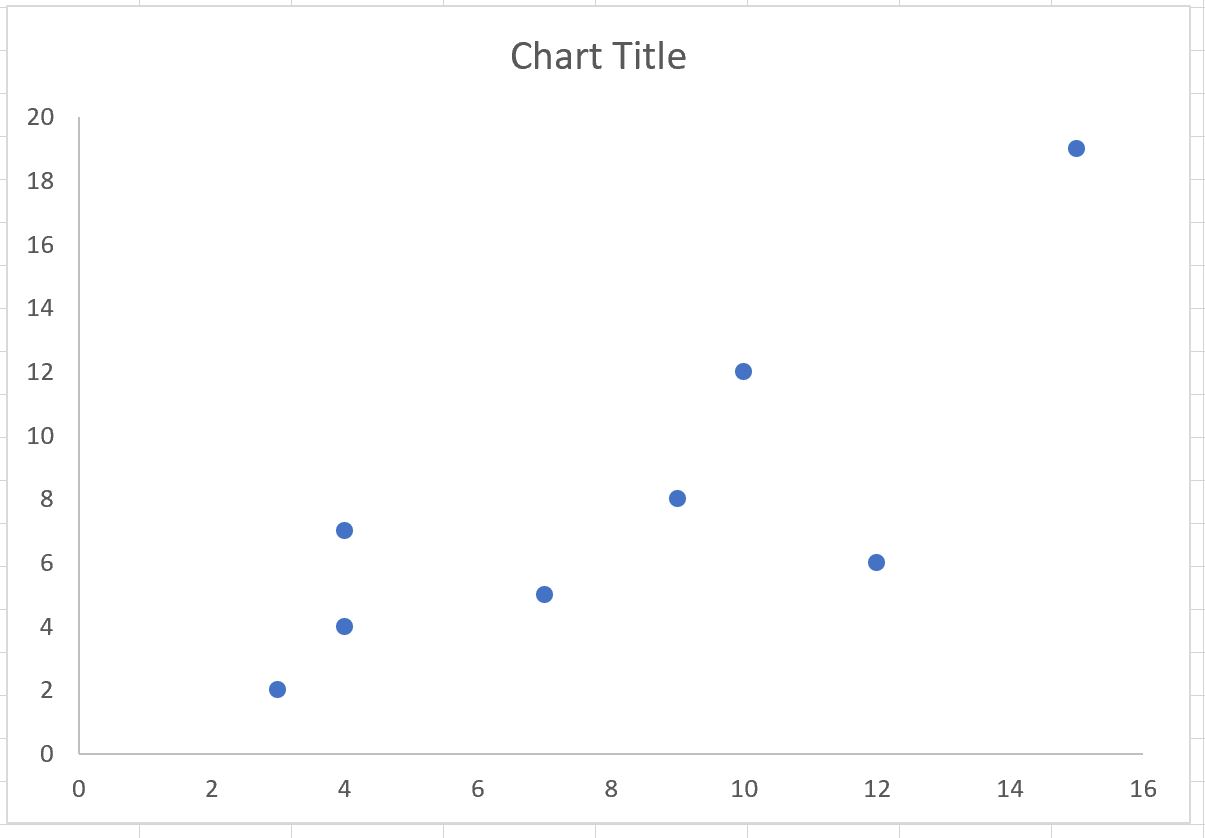
Далее нам нужно добавить вертикальную линию в середине диапазона оси X и горизонтальную линию в середине диапазона оси Y.
Вот как рассчитать значения для горизонтальной линии :
- x-values : минимальное и максимальное значения оси x
- y-values : среднее минимального и максимального значений оси y.
Вот как рассчитать значения для вертикальной линии :
- x-values : среднее минимального и максимального значений оси x.
- y-values : минимальное и максимальное значения оси y
На следующем снимке экрана показано, как рассчитать значения как для горизонтальных, так и для вертикальных линий:
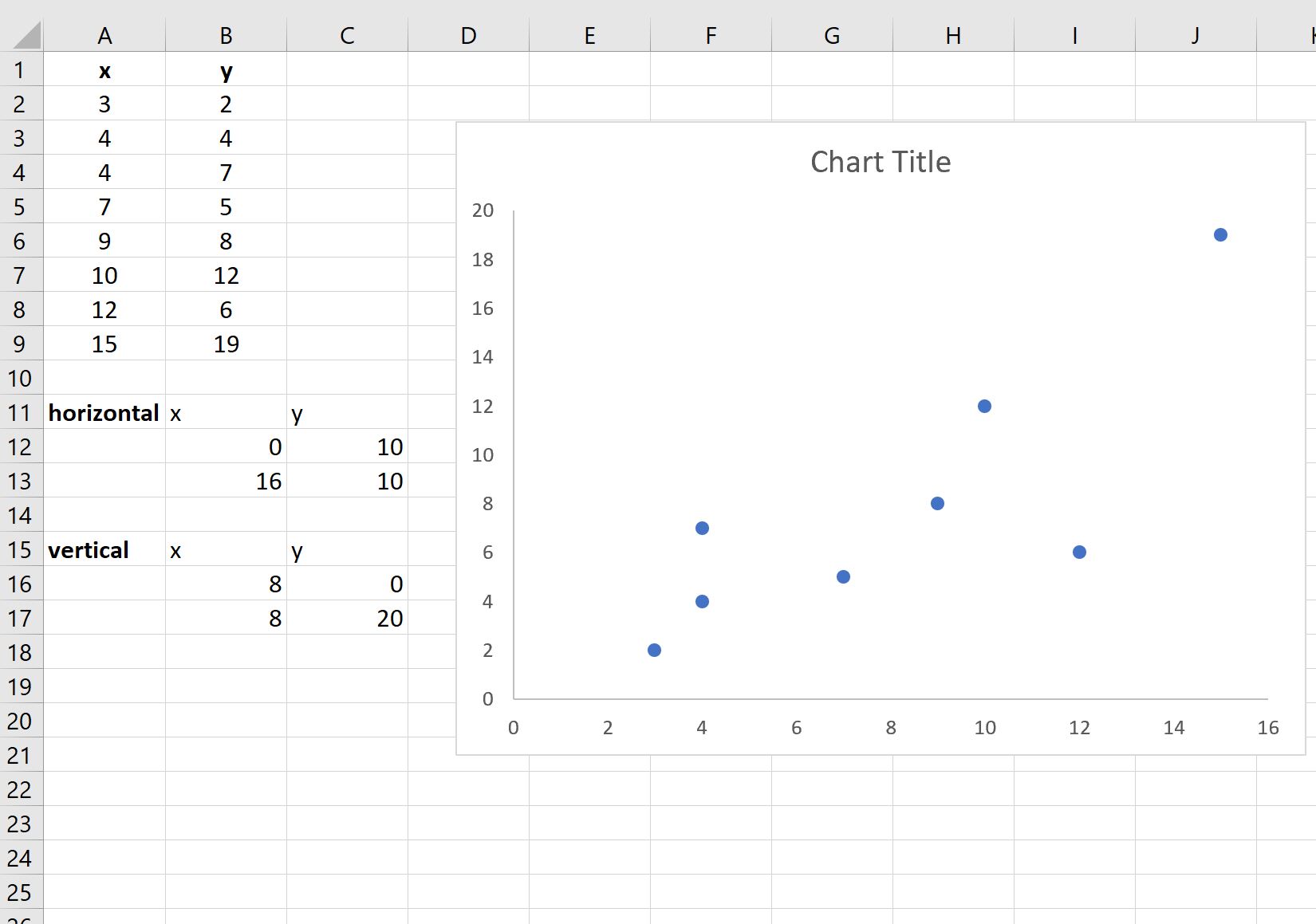
Затем щелкните правой кнопкой мыши в любом месте точечной диаграммы и выберите « Выбрать данные »:
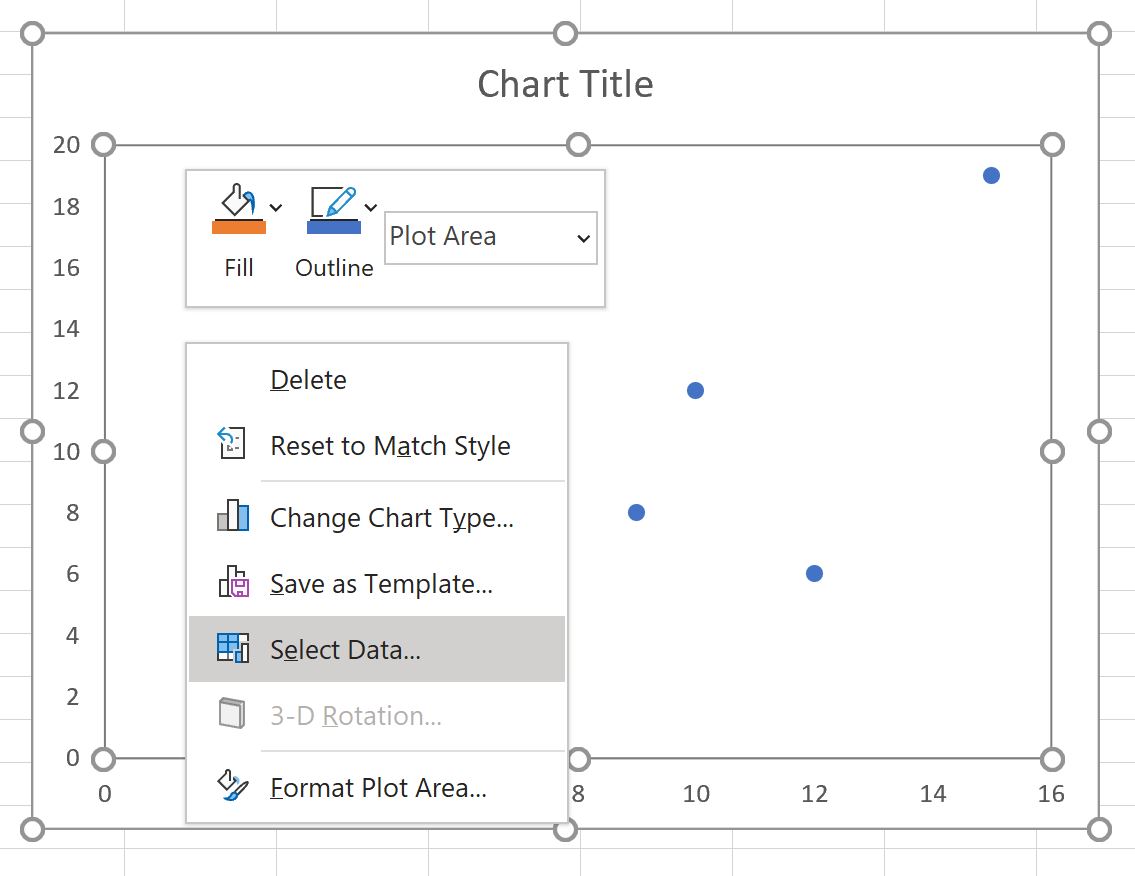
В появившемся новом окне нажмите « Добавить »:
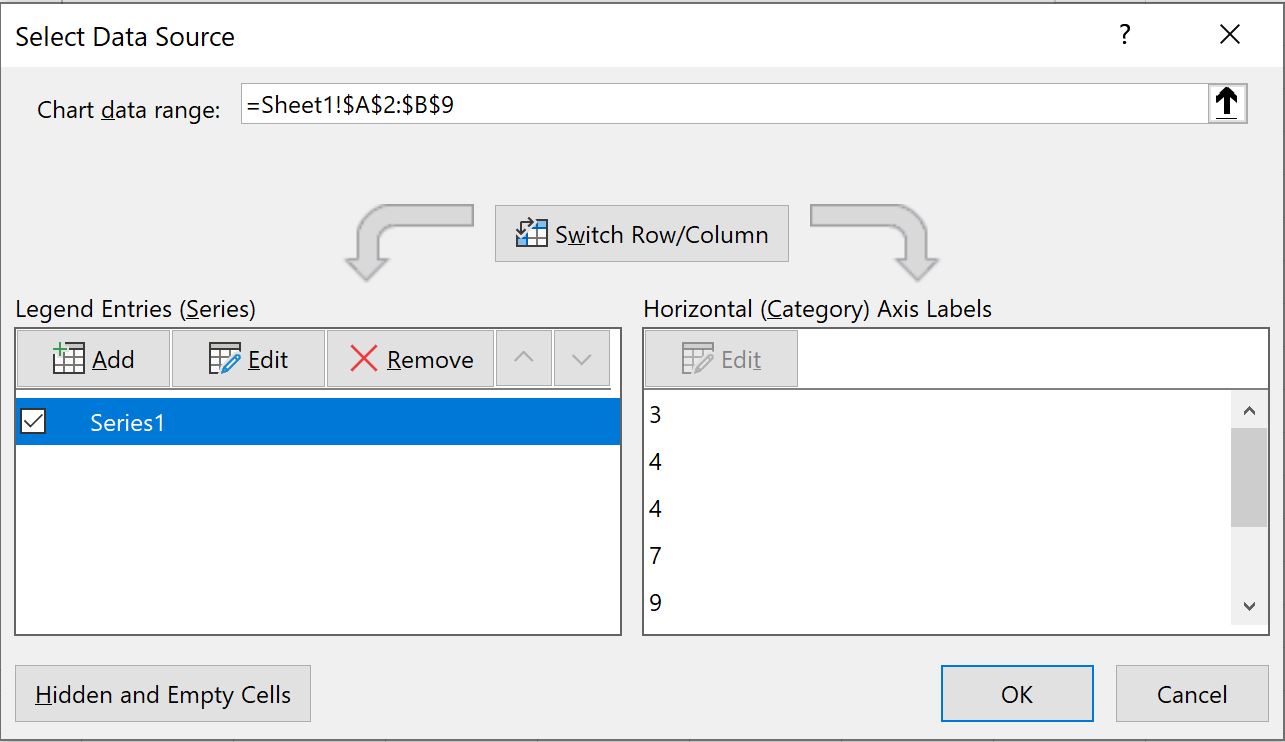
В появившемся новом окне введите любое имя в поле «Имя серии», затем выберите B12:B13 в поле « Значения серии X », затем введите C12:C13 в поле « Значения серии Y » и нажмите « ОК » :
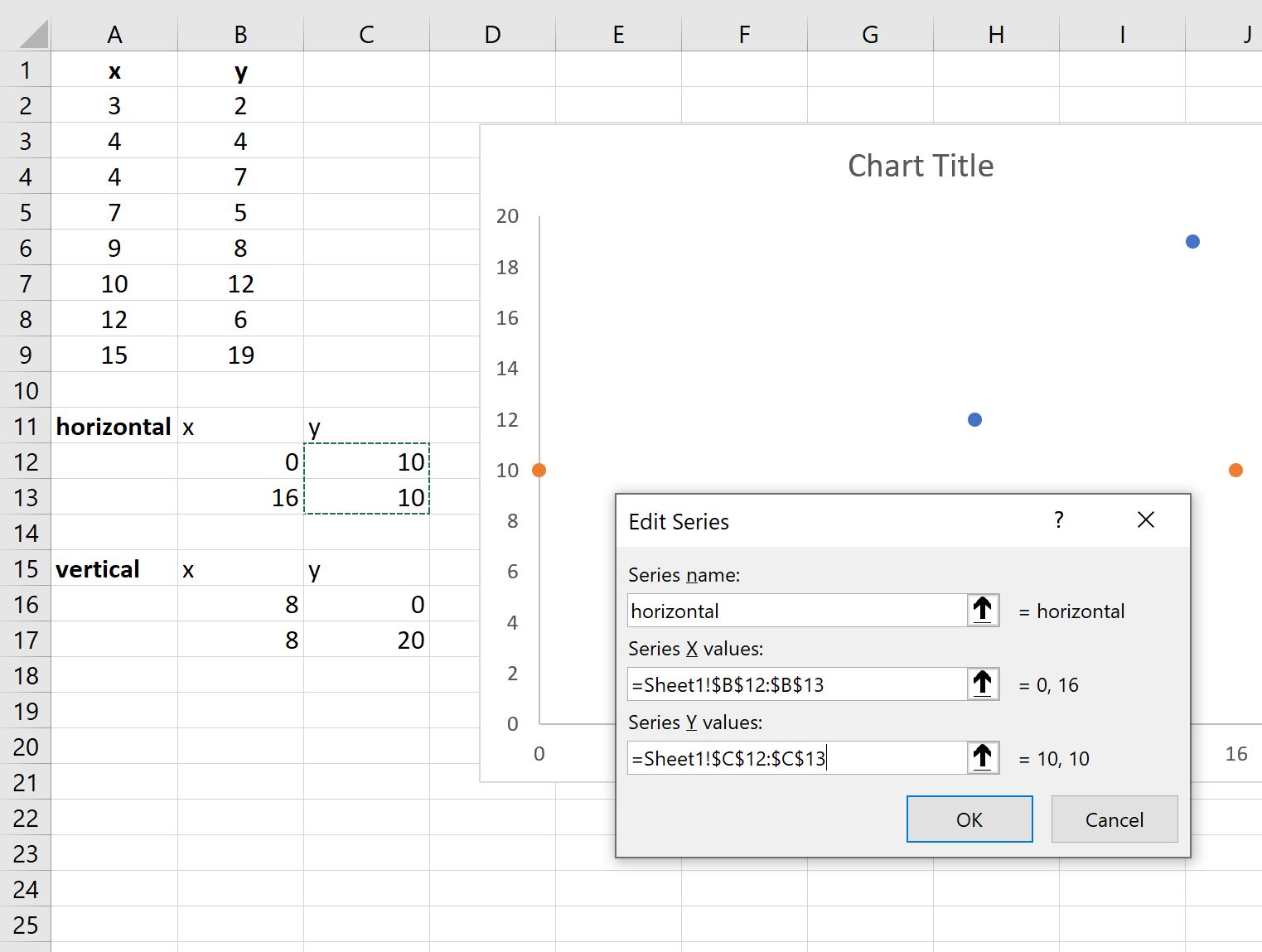
На график добавятся две оранжевые точки. Щелкните любую точку, чтобы открыть панель « Формат ряда данных» в правой части экрана.
Затем щелкните значок « Линия» , затем нажмите « Сплошная линия » и выберите «Черный» в качестве цвета :
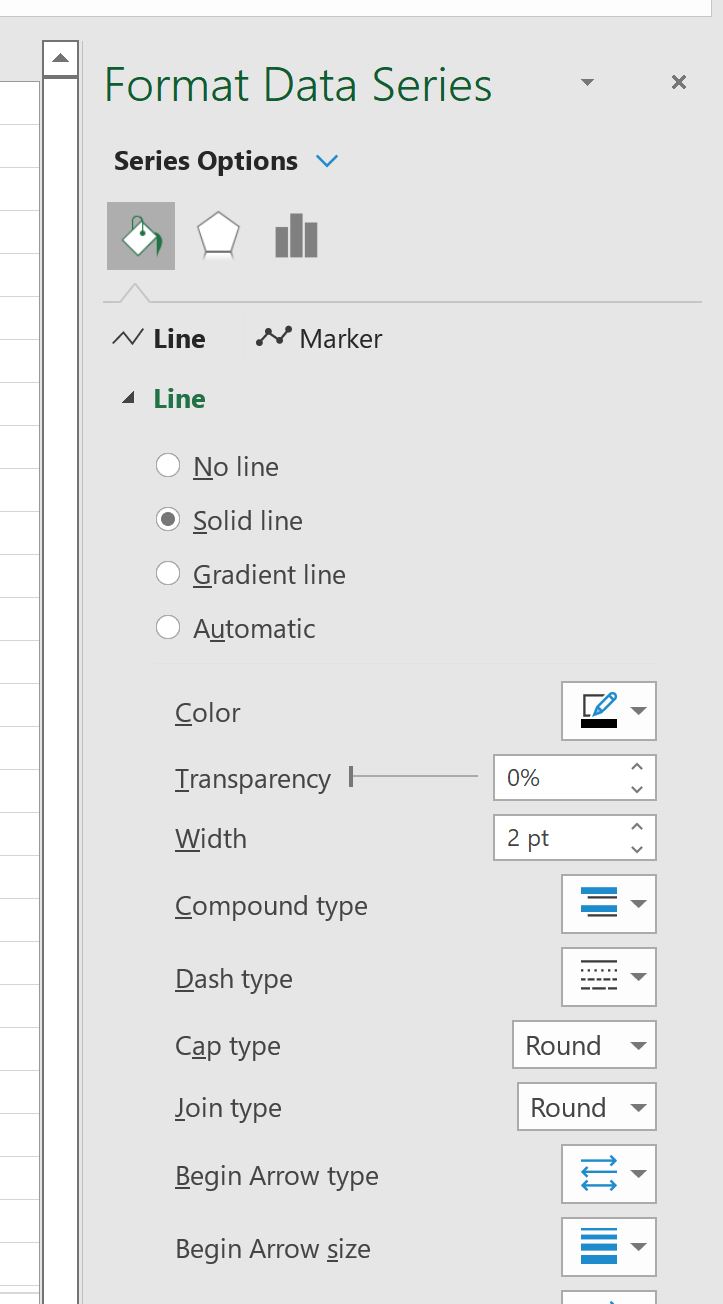
Затем нажмите значок « Маркер », затем нажмите « Нет»:
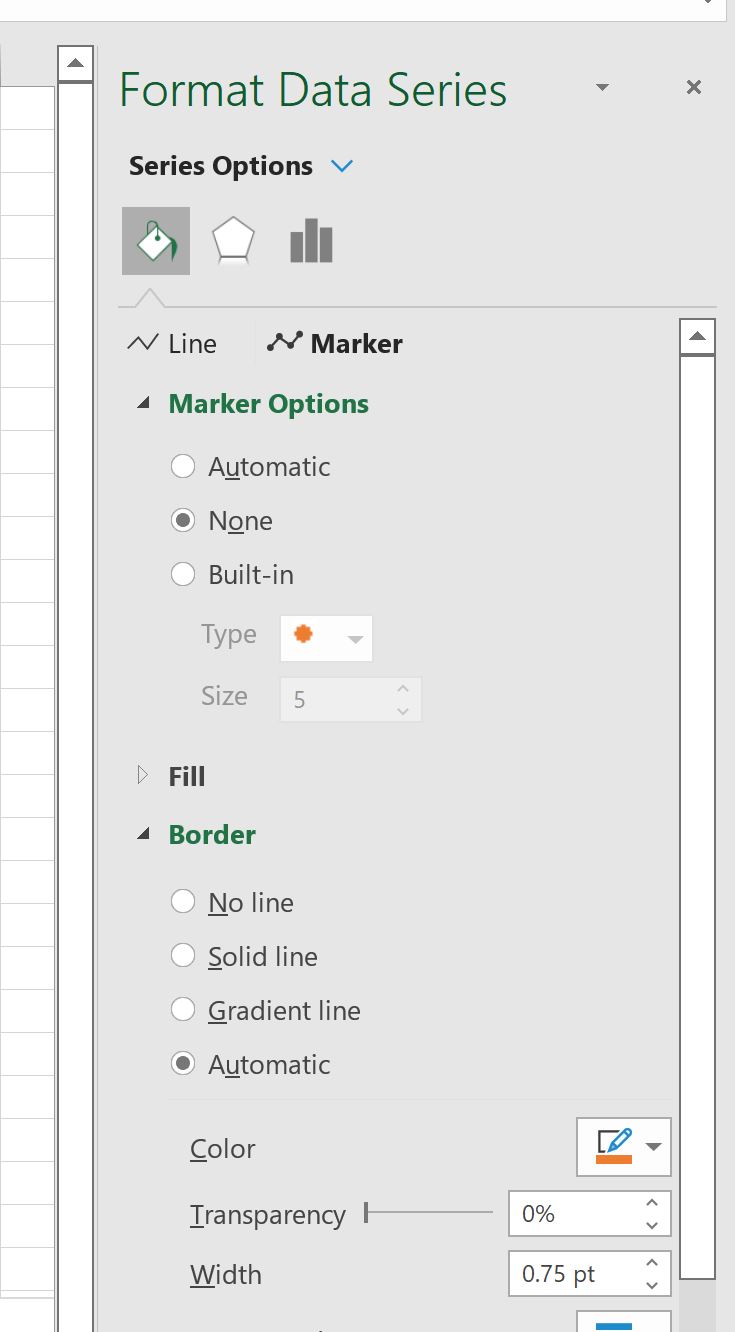
На график автоматически добавится следующая горизонтальная линия:
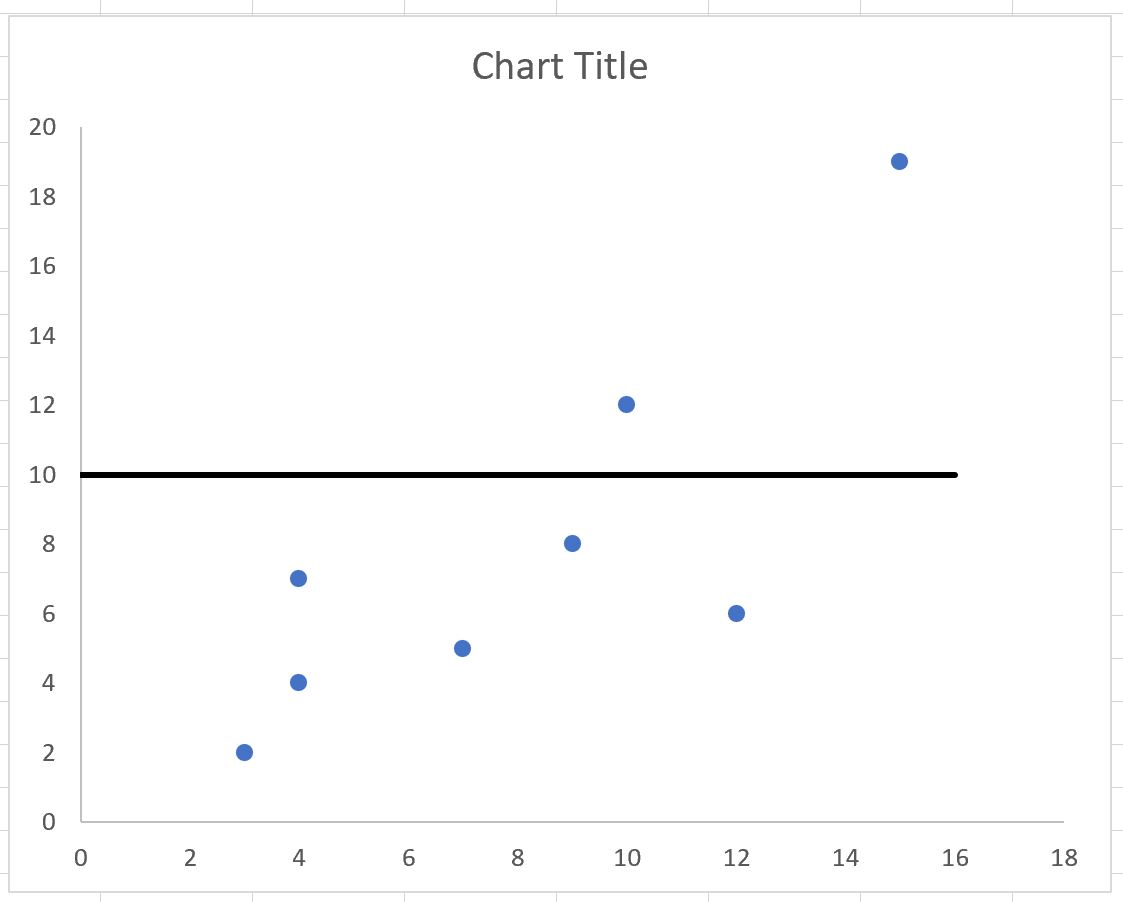
Повторите этот же процесс, чтобы добавить вертикальную линию на график.
В результате получится следующая квадрантная диаграмма:

Теперь на диаграмме четыре различных квадранта, и каждая точка на диаграмме попадает в один из четырех квадрантов.
Дополнительные ресурсы
В следующих руководствах объясняется, как создавать другие распространенные визуализации в Excel:
Как создать диаграмму Ганта в Excel
Как создать пузырьковую диаграмму в Excel
Как создать диаграмму двойного пончика в Excel
На столбиковых диаграммах статистические данные изображаются в виде вытянутых по вертикали прямоугольников. При построении столбиковых диаграмм необходимо выполнять следующие требования: 1) шкала, по которой устанавливается высота столбика, должна начинаться с нуля; 2) шкала должна быть, как правило, непрерывной; 3) основания столбиков должны быть равны между собой; столбики могут быть размещены на одинаковом расстоянии друг от друга, вплотную один к другому или наплывом, при котором один столбик частично накладывается на другой; 4) наряду с разметкой шкалы соответствующими цифровыми надписями следует снабжать и сами столбцы.
Пример. Изобразим графические данные о числе негосударственных общеобразовательных школ России за следующие учебные годы (на начало года), ед.: 1997/98 — 570; 1998/99 — 568; 1999/2000 — 607; 2000/01 — 635. Исследуем негосударственные общеобразовательные учреждения с помощью столбиковой диаграммы сравнения. На горизонтальной оси поместим основания шести столбиков на расстоянии 0,5 см друг от друга. Ширина столбиков — 1 см. Масштаб на вертикальной оси — 10 ед. на 1 см (рис. 1). На столбиковой диаграмме изображаемые величины пропорциональны длине столбцов. Из диаграммы видно, что число не государственных школ в 2000/01 учебном году составило 635 ед., что больше, чем во все предыдущие годы. Наименьшее число школ за исследуемый период времени было в 1998/99 учебном году. Из графика также видно, что число школ в 1997/98 и 1998/99 учебных годах почти не изменялось, однако далее количество негосударственных школ увеличивается с каждым годом. Можно предположить, что в следующем году их число также возрастет.
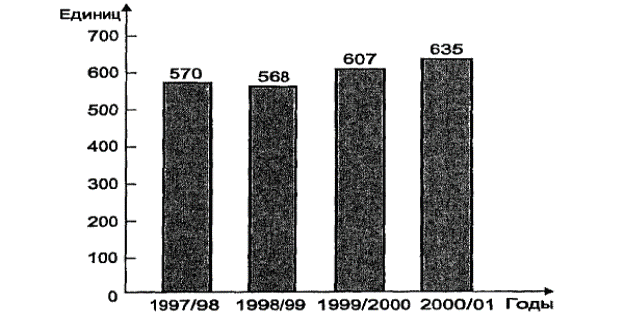
Рис. 1. Число общеобразовательных негосударственных
школ России за 1997-2001 гг.
Полосовые диаграммысостоят из прямоугольников, расположенных горизонтально (полосами, лентами). В этом случае масштабной шкалой будет горизонтальная ось. Принцип их построения тот же, что и столбиковых.
В отличие от столбиковых или полосовых диаграмм в квадратных и круговых диаграммах величина изображаемого явления выражается размером площади. Чтобы построить квадратную диаграмму, необходимо из сравниваемых статистических величин извлечь квадратные корни, а затем построить квадраты со сторонами, пропорциональными полученным результатам.
Пример.Построим квадратную диаграмму для сравнения численности учителей и учащихся в негосударственных школах за 2001 г. (на начало года). Для построения диаграммы нужно извлечь квадратные корни из следующих величин: численность учителей — 16 тыс. чел; численность учащихся — 61 тыс. чел. Это составит соответственно 4; 7,81. Чтобы построить по этим данным квадраты, необходимо выбрать масштаб. Примем 1 см за 0,8 тыс. чел. Сторонами квадратов на графике будут отрезки, пропорциональные полученным числам (рис. 2). Таким образом, квадратные диаграммы выражают размер явления своей площадью. Из графика видно, что квадрат, изображающий численность
учащихся, почти в 4 раза больше квадрата, изображающего численность учителей. Можно сделать вывод о том, что в 2001 г. на одного учителя в среднем приходилось по четыре учащихся.
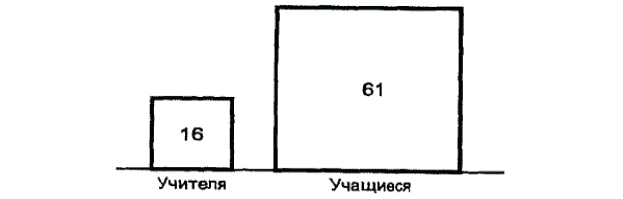
Рис. 2. Численность учащихся и учителей в негосударственных школах России
на начало 2001 года (тыс. чел.)
Круговые диаграммыстроятся аналогично. Разница состоит лишь в том, что на графике вычерчиваются круги, площади которых пропорциональны квадратным корням из изображаемых величин (рис. 3). Круги изображают исследуемые величины своей площадью. Если поместить один в другой, можно легко сравнить их площади. Из графика видно, что площадь большого круга в 7 — 8 раз больше площади малого круга. На этом основании можно сделать вывод, что в государственные вузы России в 2001 г. поступило учащихся примерно в 7 — 8 раз больше, чем в негосударственные вузы.

Рис. 3. Численность учащихся, поступивших в
государственные и негосударственные вузы России 2001 г.
Диаграммы фигур-знаковпредставляют собой графические изображения в виде рисунков, силуэтов, фигур, соответствующих содержанию статистических данных. Они отличаются от других видов диаграмм тем, что отдельные величины на них изображаются определенным количеством одинаковых по размеру и типу фигур.
Пример.Изобразим динамику производства часов в одном из регионов России за 1999 — 2002 гг. с помощью диаграммы фигур-знаков. Условно примем один рисунок за 1000 штук часов. Тогда число часов: в 1999 г. в размере 4717 шт. должно быть изображено в количестве 4,7 рисунка; в 2000 г. в размере 3672 шт. — 3,7 рисунка; в 2001 г. в размере 3987 шт. — 3,99 рисунка; в 2002 г. в размере 2189 шт. — 2,2 рисунка (рис. 4).

Рис. 4. Производство часов в одном из регионов России в 1999-2002 гг.
Секторные диаграммыудобно строить следующим образом: вся величина явления принимается за 100%, рассчитываются доли отдельных его частей в процентах. Круг разбивается на секторы пропорционально частям изображаемого целого. Таким образом, на 1% приходится 3,6°. Для получения
центральных углов секторов, изображающих доли частей целого, необходимо их процентное выражение умножить на 3,6°.
Пример.Изобразим с помощью секторной диаграммы число студентов негосударственных вузов России на начало 2000/01 учебного года по формам обучения. На дневной форме обучается 39% студентов; на вечерней — 9%; на заочной — 51%; на экстернате — 1% студентов. Построим круг произвольного радиуса. По данным о числе студентов, для построения секторов определим центральные углы: для дневной формы центральный угол составил 140,4° (39 х 3,6); для вечерней — 32,4°(9 х 3,6); для заочной — 183,6° (51 х 3,6); для экстерната — 3,6° (1 х 3,6). При помощи транспортира разделим круг на соответствующие сектора (рис. 5). Если данные о структуре какого-либо явления выражаются в абсолютных величинах, то для нахождения секторов необходимо 360° разделить на величину целого, а затем частное от деления последовательно умножить на абсолютные значения частей.
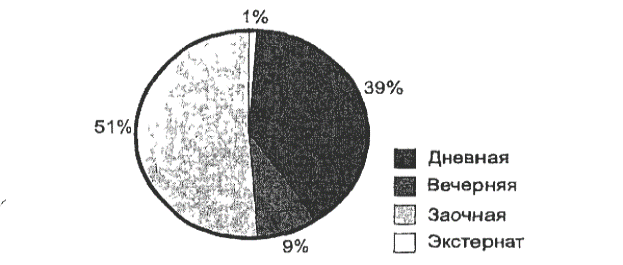
Рис. 5. Структура форм обучения студентов государственных
и негосударственных вузов России на начало 2000/01 учебного года
Для одновременного сопоставления трех величин, связанных между собой таким образом, что одна величина является произведением двух других, применяют диаграммы, называемые «знак Варзара».
Знак Варзарапредставляет собой прямоугольник, у которого одни сомножитель принят за основание, другой — за высоту, а вся площадь равна произведению.
Пример.Имеются данные по сбору яровой пшеницы в одном из регионов России в 2003 г., в котором при посевной площади 14,5 млн. га урожайность составила 1,16 т/га. В нашем случае в основание прямоугольника положена урожайность яровой пшеницы, высота — посевная площадь, а площадью прямоугольника является валовой сбор яровой пшеницы. Правильность показаний диаграммы можно проверить простыми математическими вычислениями: посевная площадь = валовой сбор /урожайность =16800000 / 1,16 = 14482758 га (рис. 6).

Рис. 6. Зависимость валового сбора яровой пшеницы от урожайности
и посевной площади в одном из регионов России 2003
Линейные диаграммышироко применяются для характеристики изменений явлений во времени, выполнения плановых заданий, а также для изучения рядов распределения, выявления связи между явлениями. Линейные диаграммы строятся на координатной сетке. Геометрическими знаками в линейных диаграммах служат точки и последовательно соединяющие их отрезки прямой, которые
складываются в ломаные кривые.
Пример.При помощи линейной диаграммы можно изобразить данные о конкурсе на вступительных экзаменах в высшие учебные заведения в России за 1996 — 2000 гг.; на одного зачисленного приходится державших экзамены: Год 1996 1997 1998 1999 2000
Конкурс, чел. 1,8 1,7 1,8 1,9 1,9
В прямоугольной системе координат нанесем на ось ординат данные о конкурсе абитуриентов (рис. 7). Масштаб: 1 см = 0,05 чел. Из графика видно, что положение кривой определяется не только данными о конкурсе, но и интервалами времени между датами. Из данных рис. 7 видно, как меняется конкурс в вузы за 1996 — 2000гг. В 1997 г. конкурс заметно снизился по сравнению с конкурсом в 1996г. Однако, с 1997г. конкурс в высшие учебные заведения возрастал и в 1999 г. превысил конкурс 1996 г. С 1999 по 2000г. конкурс в вузы России оставался неизменным.

Не нашли то, что искали? Воспользуйтесь поиском:



Диаграммы
Наиболее распространенным способом графического изображения статистической информации являются диаграммы.
Диаграммы принято подразделять по их форме на следующие виды:
- столбиковые диаграммы;
- полосовые диаграммы;
- круговые диаграммы;
- линейные диаграммы;
- фигурные диаграммы;
Другим признаком подразделения диаграмм является их содержание. По этому признаку они подразделяются на диаграммы сравнения, структурные, динамические, графики связи, графики контроля и др.
Диаграммы сравнения отражают соотношения различных исследуемых объектов в связи с каким-либо экономическим показателем. Самыми удобными графиками, на которых осуществляется сопоставление величин экономических показателей, являются столбиковые и полосовые диаграммы. Для изображения таких диаграмм применяется прямоугольная система координат. На оси абсцисс таких графиков помещается основа для определенных столбцов одинакового размера для всех исследуемых объектов. Высота каждого их столбцов должна выражать величину того экономического показателя, который отражен в определенном масштабе на оси ординат. Таковы особенности столбиковых диаграмм. Проиллюстрируем их следующей схемой (см. схему №1).
Полосовые диаграммы, в отличие от столбиковых, изображают по горизонтали: основа полос располагается на оси ординат, а экономические показатели в определенном масштабе — на оси абсцисс.
Каковы же особенности круговых и квадратных диаграмм? В ряде случаев диаграммы сравнения представляют собой круги либо квадраты; их площадь является пропорциональной величине определенных экономических показателей.
Фигурные диаграммы содержат соотношения определенных экономических показателей (объектов), которые представлены в условном виде как определенные художественные фигуры, например, головы крупного рогатого скота, какие-либо машины, и др. Такие диаграммы при первом же взгляде на них фиксируют на себе внимание, и представляют определенную числовую информацию в наиболее доходчивом виде. Структурные диаграммы (иначе-секторные) дают возможность представить состав исследуемых экономических показателей и долю (удельный вес) конкретных частей в совокупной сумме экономического показателя. В рассматриваемых диаграммах экономические явления представляются как определенные геометрические фигуры (круги или квадраты), которые разбиты на несколько секторов. Площадь круга или квадрата принимается равной ста процентам либо единице. Площадь же любого данного сектора характеризуется долей рассматриваемой части в составе ста процентов или единицы.
Динамические диаграммы характеризуют динамику, то есть изменения количественной оценки данного экономического явления в течение известных периодов времени. С этой целью могут применяться любые из рассмотренных видов диаграмм (столбиковые, полосовые, круговые, квадратные, фигурные). Вместе с тем чаще всего здесь используются линейные диаграммы (графики). На таких диаграммах изменение количественной оценки экономического явления изображается определенной линией, которая выражает непрерывность происходящего процесса. На оси абсцисс линейного графика изображаются определенные периоды времени, а на оси ординат — соответствующие величины данного экономического явления за рассматриваемые периоды времени в соответствии с принятым числовым масштабом.
Рассматриваемые линейные графики (диаграммы) применяются также и при изучении взаимосвязей между отдельными экономическими показателями. В этом случае их можно рассматривать как графики связи. В графиках связи ось абсцисс содержит числовые значения какого-либо фактора, а ось ординат — числовые значения результирующего показателя. Подобные графики характеризуют тенденцию и форму связи между экономическими показателями. Графики контроля используются в экономическом анализе в процессе рассмотрения выполнения бизнес-планов. Проиллюстрируем это следующим примером.

График контроля выполнения плана по выпуску продукции
В этом графике сплошная линия означает план по выпуску продукции, прерывистая линия — фактическое выполнение плана, Δ — отклонение фактического выполнения от плана.
Таким образом, графические способы отображения числовых данных находят большое применение в экономическом анализе и статистике. Они используются в целях наглядного отображения состава и структуры экономических явлений, выявления взаимосвязей между обобщающими показателями и влияющими на них факторами и т.д. Графические изображения имеют большое иллюстративное значение, являются доходчивыми и понятными. В отличие от аналитических таблиц графики и диаграммы наглядно представляют основополагающие тенденции развития изучаемого экономического явления, дают возможность в образной форме показать закономерности развития этого явления.
Линейная диаграмма
Линейные диаграммы используются для характеристики вариации, динамики и взаимосвязи. Линейные графики строятся на координатной сетке. Геометрическими знаками служат точки и отрезки прямой, которые их последовательно соединяют в ломаные.
Линейные диаграммы для характеристики динамики применяют в следующих случаях:
- если количество уровней ряда динамики достаточно велико. Их применение подчеркивает непрерывность процесса развития в виде непрерывной линии;
- с целью отображения общей тенденции и характера развития явления;
- при необходимости сравнения нескольких динамических рядов;
- если нужно сопоставить не абсолютные уровни явления, а темпы роста.
При изображении динамики с помощью линейной диаграммы на ось абсцисс наносят характеристики времени (дни, месяцы, кварталы, годы), а на оси ординат — значения показателя (пассажирские перевозки в России).
Перевозка пассажиров транспортом общего пользования в России
| Годы | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Млн.чел. | 47885 | 48114 | 46283 | 45037 | 45412 | 45817 |

На одном линейном графике можно построить несколько кривых, (рис. 6.6), которые позволят сравнить динамику различных показателей или одного и того же показателя в разных регионах, отраслях и др.
Для построения этого графика воспользуемся данными о динамике производства овощей и картофеля в России.
Производство овощей в России, млн.т
| Годы | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 |
| Картофель | 38,3 | 37,7 | 33,8 | 39,9 | 38,7 | 37,0 |
| Овощи | 10,0 | 9,8 | 9,6 | 11,3 | 10,7 | 11,1 |
Рис. 6.6. Динамика производства картофеля и овощей в России в 2006-2011 гг.

Логарифмическая диаграмма
Однако линейные диаграммы с равномерной шкалой искажают относительные изменения экономических показателей. Кроме того, их применение теряет наглядность и даже становится невозможным при изображении рядов динамики с резко изменяющимися уровнями, что характерно для динамических рядов за длительный период времени. В таких случаях, вместо равномерной шкалы используют полулогарифмическую сетку, в которой на одной оси наносится линейный масштаб, а на другой — логарифмический. В этом случае логарифмический масштаб наносится на ось ординат, а на оси абсцисс располагают равномерную шкалу для отсчета времени по принятым интервалам (год, квартал и пр.). Для построения логарифмической шкалы необходимо: найти логарифмы исходных чисел, начертить ординату и разделить ее на несколько равных частей. Затем нанести на ординату отрезки, пропорциональные абсолютным приростам этих логарифмов, и записать соответствующие логарифмы чисел и их антилогарифмы.
Полученные антилогарифмы дают вид искомой шкалы на ординате.
| Логарифмы чисел | Числа |
| 3,0 | 1000 |
| 2,8 | 317 |
| 2,0 | 100 |
| 1,5 | 31,7 |
| 1,0 | 10 |
Рассмотрим пример использования логарифмического масштаба для отображения динамики производства контрольно-кассовых машин в России:
| Годы | Производство, тыс.шт. | Логарифмы уровней |
| 2006 | 32,5 | 1,5119 |
| 2007 | 81,2 | 1,9096 |
| 2008 | 202,0 | 2,3054 |
| 2009 | 368,0 | 2,5658 |
| 2010 | 203,0 | 2,3075 |
| 2011 | 220,0 | 2,3424 |
Найдя минимальные и максимальные значения логарифмов производства контрольно-кассовых машин, строим масштаб с таким расчетом, чтобы все они разместились на графике. Затем находим соответствующие точки (с учетом масштаба) и соединяем их прямыми линиями. Полученный график (см. рис. 6.7.) с использованием логарифмического масштаба называется диаграммой на полулогарифмической сетке.
6.7. Динамика производства контрольно-кассовых машин в России в 2006-2011 гг.

Радиальная диаграмма
Одним из видов линейных диаграмм являются радиальные диаграммы. Они строятся в полярной системе координат с целью отражения процессов, ритмически повторяющихся во времени. Радиальные диаграммы можно разделить на два вида: замкнутые и спиральные.
В замкнутых радиальных диаграммах в качестве базы отсчета берется центр круга (рис. 6.8). Вычерчивается круг радиусом, приравненным среднемесячному показателю изучаемого явления, который делится затем на двенадцать равных секторов. Каждый радиус изображает месяц, причем расположение их аналогично циферблату часов. На каждом радиусе делается отметка согласно масштабу, выбранному исходя из данных по каждому месяцу. Если данные превышают среднегодовой уровень, то отметка делается на продолжении радиуса вне окружности. Затем отметки всех месяцев соединяются отрезками.
Рассмотрим пример построения замкнутой радиальной диаграммы по месячным данным отправления грузов железнодорожным транспортом общего пользования в России в 1997 г.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 1 | 1 | 1 |
| 68,9 | 67,6 | 776,3 | 70,7 | 71,3 | 74,2 | 76,3 | 75,7 | 79,3 | 74,9 | 74,0 | 74,2 |

Рис. 6.8. Отправление грузов железнодорожным транспортом общего пользования
В спиральных радиальных диаграммах в качестве базы отсчета берется окружность. При этом декабрь одного года соединяется с январем следующего года, что дает возможность изобразить весь ряд динамики в виде одной кривой. Особенно наглядна такая диаграмма тогда, когда наряду с сезонным ритмом наблюдается неуклонный рост уровней ряда.
Другие виды диаграмм
Столбиковая диаграмма
Среди плоскостных диаграмм наибольшее распространение получили столбиковые, полосовые или ленточные, треугольные, квадратные, круговые, секторные, фигурные.
Столбиковые диаграммы изображаются в виде прямоугольников (столбиков), вытянутых по вертикали, высота которых соответствует значению показателя (рис. 6.9).

Полосовая диаграмма
Принцип построения полосовых диаграмм тот же, что и столбиковых. Отличие заключается в том, что полосовые (или ленточные) графики представляют значение показателя не по вертикальной, а по горизонтальной оси.
Оба вида диаграмм применяются для сравнения не только самих величин, но и их частей. Для изображения структуры совокупности строят столбики (полосы) одинакового размера, принимая целое за 100%, а величину частей целого — соответствующей удельным весам (рис. 6.10).

Для изображения показателей с противоположным содержанием (импорт и экспорт, сальдо положительное и отрицательное, возрастная пирамида) строят разнонаправленные столбиковые или полосовые диаграммы.
Основу квадратных, треугольных и круговых диаграмм составляет изображение значения показателя величиной площади геометрической фигуры.
Квадратная диаграмма
Для построения квадратной диаграммы устанавливают размер стороны квадрата путем извлечения корня квадратного из значения показателя.
Так, например, для построения диаграммы на рис. 6.11 из объема услуг связи за 1997 г. в России по отправлению телеграмм
(73 млн.), пенсионных выплат (392 млн.), посылок (24 млн.) квадратные корни составили соответствено 8,5; 19,8; 4,9.
Круговая диаграмма
Круговые диаграммы строятся в виде площади кругов, радиусы которых равны корню квадратному из значений показателя.
Секторная диаграмма
Для изображения структуры (состава) совокупности используются секторные диаграммы. Круговая секторная диаграмма строится путем разделения круга на секторы пропорционально удельному весу частей в целом. Размер каждого сектора определяется величиной угла расчета (1% соответствует 3,6 0 ).
Пример. Доля продовольственных товаров в объеме розничного товарооборота России составила в 1992 г. 55%, а в 1997 г. — 49%, доля непродовольственных товаров составила соответственно 45% и 51%.
Построим два круга одинакового радиуса, а для изображения секторов определим центральные углы: для продовольственных товаров 3,6 0 *55 = 198 0 , 3,6*49 = 176,4 0 ; для непродовольственных товаров 3,6 0 *45 = 162 0 ; 3,6 0 *51 = 183,6 0 . Разделим круги на соответствующие секторы (рис. 6.12).

Треугольная диаграмма
Разновидностью диаграмм, представляющих структуру (кроме столбиковых и полосовых), является диаграмма треугольная. Она применяется для одновременного изображения трех величин, изображающих элементы или составные части целого. Треугольная диаграмма представляет собой равносторонний треугольник, каждая сторона которого является равномерной масштабной шкалой от 0 до 100. Внутри строится координатная сетка, соответствующая линиям, проводимым параллельно сторонам треугольника. Перпендикуляры из любой точки координатной сетки представляют доли трех компонентов, соответствует в сумме 100% (рис. 6.13). Точка на графике соответствует 20% (по А), 30% (по В) и 50% (по С).

Рис. 6.13. Треугольная диаграмма
Фигурная диаграмма
Диаграммы фигурные представляют собой изображение в виде рисунков, силуэтов, фигур.
Статистические графики по направлению использования характеризуются значительным разнообразием. их научная классификация предусматривает такие признаки, как общее назначение, виды, формы и типы основных элементов. Традиционно теория статистики рассматривает классификацию графиков по видам их поля. По этому принципу графические изображения разделяют на диаграммы, картограммы и картодиаграммы.
Диаграммы — это условные изображения числовых величин и их соотношений с помощью геометрических знаков.
Картограммы — изображение числовых величин и их соотношений с помощью нанесения условной штриховки или расцветки на карту — схему.
Картодиаграммы — это сочетание диаграммы с картой — схемой. При построении диаграммы устанавливается определенный масштаб, то есть соотношение между размерами величин на графике и действительной величиной изображаемого явления в натуре.
Наиболее распространенным видом статистических графиков являются диаграммы. В зависимости от способа изображения статистических данных они могут быть в одном измерения, когда эти данные изображают в виде прямых линий или полос одинаковой ширины, и в двух измерениях (плоскости), на каких данных изображают с помощью площадей геометрических фигур (прямоугольников, квадратов, кругов. ).
К первому виду диаграмм относятся линейные, столбиковые, ленточные и др .; ко второму — прямоугольные (квадратные, “Знак Варвара”), круговые, секторные, радиальные, фигурные.
Линейная диаграмма отображает размер показателя в форме линий разной длины, которые образуются в результате соединения точек в координатном поле. Одним из видов линейных диаграмм является линейный график выполнения плана и учетно-плановый график (рис. 27, 28).

Рис. 27. Линейный график динамики поголовья лошадей в хозяйстве

Рис. 28. Учетно-плановый график выполнения предприятием плана производством продукции в течение месяца: а — за декаду; б — нарастающим итогом
Применяют линейные диаграммы в основном для изучения развития явлений во времени.
Строению линейных диаграмм ставят следующие требования:
1) диаграмма должна читаться по горизонтали слева направо, по вертикали — снизу вверх;
2) на оси ординат обязательно сказывается нулевая величина. В случаях, когда соблюдение этого правила связано со значительным уменьшением масштаба и ухудшением наглядности, следует сделать разрыв по всем ординатах (при этом нулевая линия сохраняется.)
3) отрезки на оси абсцисс должны соответствовать интервалам (для рядов динамики — периода времени);
4) нулевая линия должна резко отличаться от других параллельных линий;
5) при построении диаграммы с применением процентной шкалы нужно четко выделить линию, которая означает 100%;
6) кривая линия диаграммы должна резко отличаться от линий сетки
7) цифровые показатели размещают на графике таким образом, чтобы их можно было легко прочитать;
8) площадь графика должна быть квадратной или прямоугольной. Колонке диаграммы. На этом виде диаграммы статистические
данные изображают в виде прямоугольников (столбиков) одинаковой ширины. Располагают их вертикально или горизонтально. Величину явлений характеризует высота столбика (рис. 29).

Рис. 29. Столбиковая диаграмма динамики валового производства продукции предприятием
Колонке диаграммы применяются: 1) при сравнении между собой различных явлений; 2) для изображения явлений во времени; 3) для отображения структуры явлений.
Рассмотрим основные правила построения столбиковых диаграмм:
1) ширина столбиков и расстояние между ними должны быть одинаковыми;
2) столбики располагают от меньшего к большему или наоборот (пространственная модель);
3) в основе столбиков проводится и выделяется базовая линия;
4) указывается название и цифровые данные столбиков;
5) на шкале должны быть деления, основные из которых обозначаются цифрами;
6) указывают единицу измерения.
Разновидностью столбиковой диаграммы является гистограмма, с помощью которой изображаются вариационные ряды распределения.
Ленточные диаграммы. В отличие от столбиковых, при построении ленточных диаграмм прямоугольники, которыми изображают размер явлений, располагают не по вертикали, а по горизонтали (рис. 33). Требования, предъявляемые к построению этого вида диаграмм, аналогичные требованиям к столбиковых диаграмм.

Рис. 30. Ленточная диаграмма дневной заработной платы на предприятиях
Секторные диаграммы представляют собой круг, разделенный на секторы, величины которых соответствуют (в пропорциях) изображаемым размерам явлений. Секторные диаграммы строят для отображения структуры явлений (рис. 31).
Рис. 31. Секторная диаграмма структуры посевных площадей сельскохозяйственного предприятия
Прямоугольные диаграммы. Этот вид диаграмм величину исследуемых явлений изображает в виде площадей. Прямоугольные диаграммы применяют для изображения явлений, которые изменяются во времени, а также для сравнения различных величин в пространстве.
К прямоугольных диаграмм относятся квадратные диаграммы и “Знак Варвара”.
Квадратные диаграммы используют при сравнении абсолютных величин. Для определения стороны квадрата следует добыть квадратный корень из испытуемых (диаграмованих) величин. По данным таблицы 95 проводим соответствующие расчеты, приняв масштаб 30 = 1 см. Переводим в масштабные единицы показатели, полученные после извлечения квадратного корня из величин площадей сельскохозяйственных угодий: 81,2: 30 = 2,7 см; 76,8: 30 = 2,6 см; 72,8: 30 = 2,4 см полученные числовые значения принимаются величины стороны квадрата (рис.32).
Выходные и расчетные данные для построения квадратных и круговых диаграмм
Площадь сельскохозяйственный угодий, га
Квадратный корень из размера площади
Длина радиуса, см, при масштабе 100 = 2 см
“Знак Варзара”. Используется для сравнения трех связанных между собой величин. Он представляет собой прямоугольник, в

котором длина отображает величину одного явления, ширина — другого, а площадь его характеризует произведение этих в двомасштабному сравнении: один масштаб — для основы прямоугольника, второй — для его высоты.
“Знаком Варзара” одновременно сравнивается, как уже упоминалось, три связанные между собой величины, то есть диаграмовий показатель является произведением двух других. Например, если площадь прямоугольника диаграммы иллюстрирует сбор, то одна его длина — посевную площадь, вторая — высота — урожайность. Этот вид диаграммы изображен на рисунке 33.
Рис. 32. Квадратная диаграмма размеров площадей сельскохозяйственных угодий предприятия

Рис.33. Прямоугольная диаграмма “Знак Варзара”.

Круговые диаграммы своей площади отражают величину исследуемых явлений. Они основываются на использовании площади круга для иллюстрации сравниваемых однородных величин. При их построении учитывается, что площади кругов относятся между собой как квадраты их радиусов. Для определения радиуса круга необходимо добыть квадратный корень из диаграмовои величины; на этой основе наметить его в определенном масштабе и по его величине описать круг. На рисунке 34 показано круговую диаграмму по данным таблицы 95.
Радиальные диаграммы. Этот вид диаграмм применяется для графического изображения явлений, которые изменяются в замкнутые календарные сроки. В основу их построения положен полярную систему координат, где по оси абсцисс принимается круг, за все ординат — его радиусы.
В зависимости от того, какой изображается цикл диаграмованого явления -замкнутая или продолжаемое (с периода в период) — различают радиальные диаграммы замкнутые и спиральные. Например, если весь цикл изменения изображаемого явления охватывает летний период, радиальную диаграмму строят по форме замкнутой.

Рис. 34. Круговая диаграмма размеров площадей сельскохозяйственных угодий
предприятия

Рис. 35. Радиальная диаграмма отработанных человеко-часов на предприятии в течение года
Если же изменение явления изучается в течение цикла диаграмованого периода (например, декабрь одного года соединяется с январем второго года и т.д.), ряд динамики изображается в виде сплошной кривой, которая визуально имеет вид спирали.
При построении радиальных диаграмм началом отсчета (полюсом) может быть центр окружность. Если за полюс принято центр круга, то радиальную диаграмму строят в такой последовательности: круг делят на столько частей, сколько периодов имеет диаграмований цикл (например, год — 12 мес.), И строят соответственно им радиусы (в данном случае — 12). Периоды размещают по часовой стрелке и на каждом радиусе в масштабном измерении откладывают отрезки (от центра круга), пропорциональны размерам явлений. Концы отрезков на радиусах соединяют, в результате чего образуется концентрическая ломаная линия. Пример замкнутой радиальной диаграммы с началом отсчета от центра окружности приведены на рис. 35.
Метод фигур — знаков. Этот метод изображения диаграмованих явлений предусматривает замену геометрических фигур рисунками, которые соответствуют содержанию статистических данных (рис. 36). То есть величина показателя изображается с помощью фигур (символов, рисунков): например, поголовье лошадей — в виде силуэта лошади, производство автомобилей — в виде рисунка автомобиля и т.п. Преимущества такого вида диаграмм перед геометрическим — их наглядность и доходчивость. Символическое изображение делает диаграмму выразительной и привлекательной.
Рис. 36. Динамика книжных изданий по вопросам рыночной экономики в районной библиотеке
Метод фигур — знаков (так называемый венский) имеет свои особенности и характеризуется более насыщенным содержанием, имеет принципиальное значение и требует соблюдения определенных правил построения таких диаграмм, а именно:
1) символы должны быть понятными сами по себе и не требовать детальных объяснений. Как правило, они изображают контур или силуэт диаграмованих объектов;
2) обеспечивать однозначность трактовки;
3) однозначность темы;

4) групувальни признаки располагают вертикально, а показатели, которые характеризуют, — горизонтально;
5) изображения знаков — символов должно соответствовать принципам хорошего рисунке;
6) исключительными считаются излишняя детализация и украшения;
7) стандартизация знаков — символов. Компоновка диаграммы должно осуществляться стандартизированными знаками — символами, изготовленными в типографии и монтируемые методом аппликации. Существуют специальные образцы таких знаков;
8) обязательность названия диаграммы и текстовых обозначений отдельных совокупностей (групп), которые изображается определенной фигурой; масштабное обозначения с указанием числового значения каждого знака — символа.
Полулогарифмическая графики. Этот вид статистического графика строится в системе координат. Числа, характеризующие диаграмоване явление, находятся в масштабе логарифмов. Логарифмы точек располагают на оси ординат, а дату явления (года) — на оси абсцисс (рис. 37).

Рис. 37. полулогарифмическая график динамики показателей дневной заработной платы на предприятии
Картограммы и картодиаграммы. Картограммы представляют собой контурную географическую карту или схему, на которой штриховкой различной густоты, точками или красками различной степени насыщенности изображена сравнительная интенсивность какого-либо показателя в пределах каждой единицы нанесенного на карту территориального деления. На картограммами, как правило, изображают явления, характеризующиеся относительными или средними величинами (например, количество работающих пенсионеров в общей численности работающих по регионам, мелиорованисть земель в процентах к общей площади, средняя заработная плата на предприятиях по районам области и т.д.) .
По способу изображения диаграмованих явлений различают картограммы точечные и фоновые.
В первых уровень явления показывают с помощью точек, расположенных на контурной карте территориальной единицы. Для наглядности изображения плотности или частоты появления определенного признака точкой обозначают одну или несколько единиц совокупности.
На фоновых картограммами штриховкой различной густоты или краской различной степени насыщенности изображают интенсивность какого-либо показателя в пределах территориальной единицы. Один из случаев картограмм показано на рисунке 38.
Рис. 38. Картограмма плотности поголовья коров на 100 га сельскохозяйственных угодий в хозяйствах района
Если на контурную карту наносятся статистические данные в виде диаграмм, получают картодиаграму. Ярким ее примером является географическая карта, на которой численность населения крупных городов изображена в виде кругов различной величины.
Кроме рассмотренных способов графического изображения исследуемых явлений, существуют и другие. Практическое их использование при отражении динамики явлений, их структуры и взаимосвязей рассмотрено в предыдущих главах.
Оглавление:
- 1 Как сделать квадратную диаграмму в excel? — Разбираем подробно
- 2 Подготовка данных для вафельной диаграммы
- 3 Построение вафельной диаграммы
- 4 Клонирование вафельной диаграммы
- 5 Как построить диаграмму по таблице в Excel?
- 6 Как добавить данные в диаграмму в Excel?
- 6.1 Как поменять местами оси в диаграмме Excel?
- 7 Как закрепить элементы управления на диаграмме Excel?
- 8 Как сделать диаграмму в процентах в Excel?
- 9 Диаграмма Ганта в Excel
- 10 Создание диаграмм
- 11 Редактирование диаграмм
- 11.1 Вкладка «Конструктор»
- 11.2 Вкладки «Макет» и «Формат»
- 11.3 Добавление новых данных
- 12 Новые возможности диаграмм в Excel 2013
- 12.1 Видео: Построение диаграмм в MS Office Excel
Использование новых видов визуализаций в отчетах или дашбордах всегда несет риск введения пользователей в заблуждение или снижения читабельности данных. Квадратная (или вафельная) диаграмма, не искажая понимания данных, является интересной альтернативой стандартным диаграммам Excel.
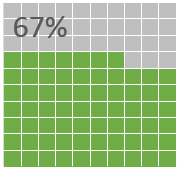
Как вы видите, вафельная диаграмма представляет из себя квадрат размером 10х10 ячеек, где 1 ячейка соответствует одному проценту из 100. Количество закрашенных ячеек соответствует значению показателя, который вы пытаетесь визуализировать. Данный вид графика будет интересен тем, кто хочет добавить новый вид диаграмм, не искажая данных и не занимая много места на дашборде.
Есть несколько способов реализации диаграмм данного вида. Описанный ниже метод использует инструменты встроенных диаграмм и хотя он сложнее в реализации (чем создание подобных графиков с помощью условного форматирования), является более гибким и позволяет внедрять квадратные диаграммы любых размеров в любое место вашего дашборда.
В сегодняшней статье мы рассмотрим шаги по созданию диаграммы – вафли и научимся быстро их дублировать для визуализации стольких метрик, сколько вам необходимо.
Подготовка данных для вафельной диаграммы
Для начала необходимо создать три диапазона данных, которые будут играть определенную роль в построении диаграммы:
Горизонтальные линии: Данный диапазон необходим для построения горизонтальных линий. В нашем случае это будет ряд от 1 до 10.
Вертикальные линии: Диапазон поможет нам построить вертикальные линии и заполняется нулями.
Значение ячейки: Данный диапазон будет определять, какие ячейки буду закрашены. Он будет содержать формулу.
В ячейки диапазона Значение ячейки вставляем формулу =МАКС(МИН(E$3*100-($B6-1)*10;10);0) и протягиваем ее вниз.
Обратите внимание на абсолютные ссылки в формуле (помечены знаком $). Это позволит быстро копировать и вставлять формулы, когда придет время дублировать диаграммы.
Формула, которую мы вставили в диапазон Значения ячейки, разбивает показатель KPI на группы, размером по 10 единиц. Обратите внимание, что после того, как мы протянули формулу, показатель 45% разбился на 5 групп, состоящих из 4 групп с целыми десятками и одна группа из неполной десятки (5%).
Если вы измените показатель на другое значение, например, 67%, формула разобьет его на 7 групп (6 – целых десяток, 1 – неполная).
На данном этапе мы имеем все данные для построения квадратной диаграммы.
Построение вафельной диаграммы
Создание вафельной диаграммы потребует от вас некоторых усилий. Но есть хорошая новость. Создав диаграмму, ее можно легко дублировать. Итак, алгоритм действий по шагам.
Строим линейчатую диаграмму с группировкой на основе данных диапазона Значения ячейки.
Копируем диапазоны Горизонтальны и вертикальные линии, выделяем диаграмму и вставляем данные.
Закрашиваем область построения в серый цвет, для этого щелкаем правой кнопкой по области построения. В выпадающем меню выбираем пункт Формат области построения. В появившейся панели Параметры области построения, переходим во вкладку Заливка и указываем понравившийся тон серого в пункте Цвет.
Далее необходимо превратить линейчатые диаграммы Горизонтальных и вертикальных линий в точечные. Для этого щелкаем по любому ряду данных правой кнопкой мыши, из выпадающего меню выбираем Изменить тип диаграммы для ряда. В появившемся диалоговом окне Изменение типа диаграммы выбираем для рядов данных Горизонтальные линии и Вертикальные линии из выпадающего списка Тип диаграммы – точечная.
Для ряда данных Горизонтальные линии необходимо добавить значения оси X. Щелкаем правой кнопкой мыши по ряду данных Горизонтальные линии, из выпадающего меню выбираем Выбрать данные. И добавляем диапазон Вертикальные линии, состоящий из нулей.
На данном этапе график должен иметь следующий вид.
Устанавливаем максимальное значение горизонтальной и вспомогательной вертикальной осей равным 10. Для этого щелкаем правой кнопкой мыши по шкале оси, из выпадающего меню выбираем Формат оси. Во всплывающей справа панели Параметры оси устанавливаем фиксированное максимальное значение равным 10. То же самое делаем для вертикальной вспомогательной оси.
Удаляем все шкалы осей. Выбираем ось и нажимаем клавишу Delete.
На следующем шаге необходимо добавить планки погрешностей, они будут играть роль разделителей. Для этого выбираем ряд данных Горизонтальные линии, щелкаем на плюсик, появившийся справа от диаграммы. Во всплывающем окне ставим галочку напротив поля Предел погрешностей. То же самое проделываем для ряда данных Вертикальные линии.
Нам понадобятся не все планки погрешностей, поэтому выделяем диаграмму, переходим во вкладку Работа с диаграммами –> Формат в группу Текущий фрагмент. Из выпадающего списка выбираем пункт Ряд «Горизонтальные линии» предел погрешностей по оси Y и нажимаем клавишу Delete. Таким же образом выделяем элемент диаграммы Ряд «Вертикальные линии» предел погрешностей по оси Xи тоже удаляем.
Из оставшегося списка выбираем элемент Ряд «Горизонтальные линии» предел погрешностей по оси X, в этой же группе вкладки Формат нажимаем Формат выделенного. В появившейся панели Параметры горизонтального предела погрешностей устанавливаем значения Направление – Плюс, Стиль края – Без точки, Величина погрешности – Фиксированное значение – 10. В этой же панели переходим во вкладку Заливка и границы и устанавливаем цвет линии Белый.
То же самое проделываем для элемента Ряд «Вертикальные линии» предел погрешностей по оси Y.
Далее щелкаем правой кнопкой по ряду данных Горизонтальные линии, в выпадающем меню выбираем Формат ряда данных, в панели Параметры ряда устанавливаем наличие маркера в положение Нет.
На этом этапе внешний вид нашей квадратной диаграммы должен иметь следующий вид.
Щелкаем правой кнопкой мыши по ряду данных Значение ячейки, выбираем из выпадающего меню пункт Формат ряда данных. В появившейся панели Параметры ряда устанавливаем Боковой зазор равным 0.
Растяните область построения графика таким образом, чтобы получился квадрат, также вы можете задать другой цвет ряду данных Значения ячейки.
Опционально, вы можете отобразить значение показателя в названии диаграммы. Для этого щелкаем по полю название диаграммы, в строке формул указываем адрес ячейки, которая содержит значение показателя.
На данном этапе вы имеете готовую вафельную диаграмму.
Клонирование вафельной диаграммы
Как мы и говорили ранее, хотя вам потребуются некоторые усилия для создания квадратной диаграммы, вам не нужно будет создавать ее каждый раз с нуля, чтобы визуализировать остальные показатели. Достаточно скопировать ее и указать новый набор данных.
Для начала вам необходимо будет продублировать диапазоны Значения ячейки.



Теперь вы можете вставить необходимое значение в только что созданный диапазон. Далее копируем нашу вафельную диаграмму и вставляем ее в любое место рабочего листа. И в конце, выделяем ряд данных Значения ячейки вновь созданной диаграммы и переносим адрес ряда данных в новый диапазон.
Вы можете повторить процесс для неограниченного количества KPI.
И помните, так как это является полноценной диаграммой, вы можете изменять ее размер по вашему усмотрению и перемещать ее куда захочется.
Как вы видите, данные графики позволяют оживить отчет или дашборд с помощью нового вида визуализации и привлечь к себе внимание. К тому же, их размеры можно сократить таким образом, чтобы они не занимали много места. Тем не менее у данной диаграммы есть один очень большой недостаток, он отображает только один показатель без трендов.
Скачать файл с примером вафельной диаграммы.
Любую информацию легче воспринимать, если она представлена наглядно. Это особенно актуально, когда мы имеем дело с числовыми данными. Их необходимо сопоставить, сравнить. Оптимальный вариант представления – диаграммы. Будем работать в программе Excel.
Так же мы научимся создавать динамические диаграммы и графики, которые автоматически обновляют свои показатели в зависимости от изменения данных. По ссылке в конце статьи можно скачать шаблон-образец в качестве примера.
Как построить диаграмму по таблице в Excel?
- Создаем таблицу с данными.
- Выделяем область значений A1:B5, которые необходимо презентовать в виде диаграммы. На вкладке «Вставка» выбираем тип диаграммы.
- Нажимаем «Гистограмма» (для примера, может быть и другой тип). Выбираем из предложенных вариантов гистограмм.
- После выбора определенного вида гистограммы автоматически получаем результат.
- Такой вариант нас не совсем устраивает – внесем изменения. Дважды щелкаем по названию гистограммы – вводим «Итоговые суммы».
- Сделаем подпись для вертикальной оси. Вкладка «Макет» — «Подписи» — «Названия осей». Выбираем вертикальную ось и вид названия для нее.
- Вводим «Сумма».
- Конкретизируем суммы, подписав столбики показателей. На вкладке «Макет» выбираем «Подписи данных» и место их размещения.
- Уберем легенду (запись справа). Для нашего примера она не нужна, т.к. мало данных. Выделяем ее и жмем клавишу DELETE.
- Изменим цвет и стиль.
Выберем другой стиль диаграммы (вкладка «Конструктор» — «Стили диаграмм»).
Как добавить данные в диаграмму в Excel?
- Добавляем в таблицу новые значения — План.
- Выделяем диапазон новых данных вместе с названием. Копируем его в буфер обмена (одновременное нажатие Ctrl+C). Выделяем существующую диаграмму и вставляем скопированный фрагмент (одновременное нажатие Ctrl+V).
- Так как не совсем понятно происхождение цифр в нашей гистограмме, оформим легенду. Вкладка «Макет» — «Легенда» — «Добавить легенду справа» (внизу, слева и т.д.). Получаем:
Есть более сложный путь добавления новых данных в существующую диаграмму – с помощью меню «Выбор источника данных» (открывается правой кнопкой мыши – «Выбрать данные»).
Когда нажмете «Добавить» (элементы легенды), откроется строка для выбора диапазона данных.
Как поменять местами оси в диаграмме Excel?
- Щелкаем по диаграмме правой кнопкой мыши – «Выбрать данные».
- В открывшемся меню нажимаем кнопку «Строка/столбец».
- Значения для рядов и категорий поменяются местами автоматически.
Как закрепить элементы управления на диаграмме Excel?
Если очень часто приходится добавлять в гистограмму новые данные, каждый раз менять диапазон неудобно. Оптимальный вариант – сделать динамическую диаграмму, которая будет обновляться автоматически. А чтобы закрепить элементы управления, область данных преобразуем в «умную таблицу».
- Выделяем диапазон значений A1:C5 и на «Главной» нажимаем «Форматировать как таблицу».
- В открывшемся меню выбираем любой стиль. Программа предлагает выбрать диапазон для таблицы – соглашаемся с его вариантом. Получаем следующий вид значений для диаграммы:
- Как только мы начнем вводить новую информацию в таблицу, будет меняться и диаграмма. Она стала динамической:
Мы рассмотрели, как создать «умную таблицу» на основе имеющихся данных. Если перед нами чистый лист, то значения сразу заносим в таблицу: «Вставка» — «Таблица».
Как сделать диаграмму в процентах в Excel?
Представлять информацию в процентах лучше всего с помощью круговых диаграмм.
Исходные данные для примера:
- Выделяем данные A1:B8. «Вставка» — «Круговая» — «Объемная круговая».
- Вкладка «Конструктор» — «Макеты диаграммы». Среди предлагаемых вариантов есть стили с процентами.
- Выбираем подходящий.
- Очень плохо просматриваются сектора с маленькими процентами. Чтобы их выделить, создадим вторичную диаграмму. Выделяем диаграмму. На вкладке «Конструктор» — «Изменить тип диаграммы». Выбираем круговую с вторичной.
- Автоматически созданный вариант не решает нашу задачу. Щелкаем правой кнопкой мыши по любому сектору. Должны появиться точки-границы. Меню «Формат ряда данных».
- Задаем следующие параметры ряда:
- Получаем нужный вариант:
Диаграмма Ганта в Excel
Диаграмма Ганта – это способ представления информации в виде столбиков для иллюстрации многоэтапного мероприятия. Красивый и несложный прием.
- У нас есть таблица (учебная) со сроками сдачи отчетов.
- Для диаграммы вставляем столбец, где будет указано количество дней. Заполняем его с помощью формул Excel.
- Выделяем диапазон, где будет находиться диаграмма Ганта. То есть ячейки будут залиты определенным цветом между датами начала и конца установленных сроков.
- Открываем меню «Условное форматирование» (на «Главной»). Выбираем задачу «Создать правило» — «Использовать формулу для определения форматируемых ячеек».
- Вводим формулу вида: =И(E$2>=$B3;E$2
Когда вам нужно построит презентабельный отчет финансовой активности предприятия, лучше использовать средства графического представления информации.
Графическое представление информации намного эффективней и быстрей усваивается человеческим зрительным восприятием информации, чем текст и цифры. Легче проводить аналитики, лучше видно ситуацию, как в целом, так и в отдельных деталях.
Простенькая диаграмма Ганта готова. Скачать шаблон с примером в качестве образца.
В программе Excel специально разрабатывались диаграммы и графики для реализации данной задачи.
Представление данных в наглядной форме диаграмм позволяет быстро оценить и проанализировать их. Как построить диаграмму в Excel? Пошаговая последовательность действий будет показана на основе приводимой ниже таблицы, показывающей помесячные доходы и налоги условного физического лица, и их соотношение в процентах.
Создание диаграмм
1. Прежде всего, необходимо выделить участок таблицы, на основе данных которого требуется построить диаграмму в эксель. В приводимом примере выделены все данные – доходы, налоги и проценты.
2. Перейти на вкладку «Вставка», и в разделе «Диаграммы» щёлкнуть желаемый вид.
3. Как видно, в разделе «Диаграммы» пользователю на выбор предлагаются разные виды диаграмм. Иконка рядом с названием визуально поясняет, как будет отображаться диаграмма выбранного вида. Если щёлкнуть любой из них, то в выпадающем списке пользователю предлагаются подвиды.
Иногда употребляют выражение «Диаграммы и графики», тем самым выделяя графический вид в отдельную категорию.
Если пользователю нужен первый из предлагаемых вариантов – гистограмма, то, вместо выполнения пп. 2 и 3, он может нажать сочетание клавиш Alt+F1.
4. При внимательном взгляде на подвиды можно заметить, что все относятся к одному из двух вариантов. Они отличаются сплошной (в зелёном прямоугольнике), или частичной (в оранжевом) закраской элементов диаграммы. Следующие два скриншота, соответствующие «зелёному» и «оранжевому» выбору, наглядно демонстрируют разницу.
Как видно, в первом случае отображаемые данные выстраиваются тремя (доходы, налоги, процент) столбиками. Второй вариант отображает их в виде закрашенных частей одного столбика.
В обоих случаях значение процента почти не видно. Это связано с тем, что на диаграммах отображается абсолютное его значение (т.е. не 14,3%, а 0,143). На фоне больших значений такое малое число еле видно.
Чтобы сделать диаграмму в экселе для данных одного типа, следует в рамках первого шага выделить именно их. На следующем скриншоте представлена диаграмма для значений процентов, которых практически не было видно на предыдущих.
Редактирование диаграмм
Закончив построение диаграмм, их можно изменить в любой момент. Одновременно с появившейся диаграммой автоматически возникает группа вкладок с общим названием «Работа с диаграммами», и происходит переход на первую из них – «Конструктор». Инструменты новых вкладок открывают широкие возможности редактирования диаграмм.
Вкладка «Конструктор»
Для отображения значений процентов часто применяется круговая диаграмма в эксель. Чтобы построить круговую диаграмму, сохранив прежние данные, нужно щёлкнуть первый слева инструмент линейки – «Изменить тип диаграммы», и выбрать желаемый подвид строки «Круговая».
На следующем скриншоте показан результат активации инструмента «Строка/Столбец», производящий взаимную замену данных на осях X и Y. Как видно, однотонная гистограмма предыдущего скриншота получила цвета, и стала гораздо привлекательней.
В разделе «Стили диаграмм» вкладки «Конструктор» можно менять стиль диаграмм. После открытия выпадающего списка этого раздела пользователю становится доступным выбор одного из 40 предлагаемых вариаций стилей. Без открытия этого списка доступно всего 4 стиля.
Очень ценен последний инструмент – «Переместить диаграмму». С его помощью диаграмму можно перенести на отдельный полноэкранный лист.
Как видно, лист с диаграммой добавляется к существовавшим листам.
Если пользователю предстоит работа по построению множества других диаграмм на основе созданной и отредактированной, то он может сохранить её для дальнейшего использования в качестве шаблона. Для этого достаточно выделить диаграмму, щёлкнуть инструмент «Сохранить как шаблон», ввести название и нажать «Сохранить». После этого запомненный шаблон будет доступен в папке «Шаблоны».
Вкладки «Макет» и «Формат»
Инструменты вкладок «Макет» и «Формат» в основном относятся к внешнему оформлению диаграммы.
Чтобы добавить название, следует щёлкнуть «Название диаграммы», выбрать один из двух предлагаемых вариантов размещения, ввести имя в строке формул, и нажать Enter.
При необходимости аналогично добавляются названия на оси диаграммы X и Y.
Инструмент «Легенда» управляет отображением и положением поясняющего текста. В данном случае это – названия месяцев. Их можно удалить или переместить влево, вверх или вниз.
Гораздо более употребителен инструмент «Подписи данных», позволяющий добавить на них числовые значения.
Если при построении диаграммы был выбран её объёмный вариант, то на вкладке «Макет» будет активен инструмент «Поворот объёмной фигуры». С его помощью можно менять угол наблюдения диаграммы.
Инструмент «Заливка фигуры» вкладки «Формат» позволяет залить любым цветом, рисунком, градиентом или текстурой фон диаграммы (как показано на скриншоте) или любой из её элементов (в данном случае – столбиков).
Для заливки соответствующего элемента он должен быть предварительно выделен.
Добавление новых данных
После создания диаграммы для одного ряда данных в некоторых случаях бывает необходимо добавить на диаграмму новые данные. Для этого сначала нужно будет выделить новый столбик – в данном случае «Налоги», и запомнить его в буфере обмена, нажав Ctrl+C. Затем щёлкнуть на диаграмме, и добавить в неё запомненные новые данные, нажав Ctrl+V. На диаграмме появится новый ряд данных «Налоги».
Новые возможности диаграмм в Excel 2013
Диаграммы рассматривались на примере широко распространённой версии Excel 2010. Так же можно работать и в Excel 2007. А вот версия 2013 года имеет ряд приятных нововведений, облегчающих работу с диаграммами:
Видео: Построение диаграмм в MS Office Excel
Did you find apk for android? You can find new Free Android Games and apps.
Использование новых видов визуализаций в отчетах или дашбордах всегда несет риск введения пользователей в заблуждение или снижения читабельности данных. Квадратная (или вафельная) диаграмма, не искажая понимания данных, является интересной альтернативой стандартным диаграммам Excel.
Как вы видите, вафельная диаграмма представляет из себя квадрат размером 10х10 ячеек, где 1 ячейка соответствует одному проценту из 100. Количество закрашенных ячеек соответствует значению показателя, который вы пытаетесь визуализировать. Данный вид графика будет интересен тем, кто хочет добавить новый вид диаграмм, не искажая данных и не занимая много места на дашборде.
Есть несколько способов реализации диаграмм данного вида. Описанный ниже метод использует инструменты встроенных диаграмм и хотя он сложнее в реализации (чем создание подобных графиков с помощью условного форматирования), является более гибким и позволяет внедрять квадратные диаграммы любых размеров в любое место вашего дашборда.
В сегодняшней статье мы рассмотрим шаги по созданию диаграммы – вафли и научимся быстро их дублировать для визуализации стольких метрик, сколько вам необходимо.
Подготовка данных для вафельной диаграммы
Для начала необходимо создать три диапазона данных, которые будут играть определенную роль в построении диаграммы:
Горизонтальные линии: Данный диапазон необходим для построения горизонтальных линий. В нашем случае это будет ряд от 1 до 10.
Вертикальные линии: Диапазон поможет нам построить вертикальные линии и заполняется нулями.
Значение ячейки: Данный диапазон будет определять, какие ячейки буду закрашены. Он будет содержать формулу.
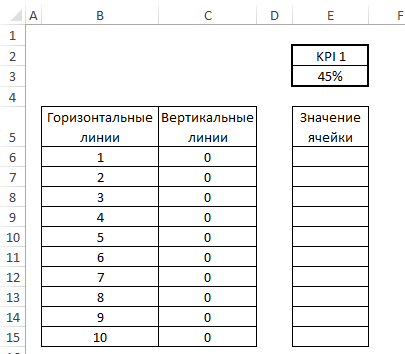
В ячейки диапазона Значение ячейки вставляем формулу =МАКС(МИН(E$3*100-($B6-1)*10;10);0) и протягиваем ее вниз.
Обратите внимание на абсолютные ссылки в формуле (помечены знаком $). Это позволит быстро копировать и вставлять формулы, когда придет время дублировать диаграммы.
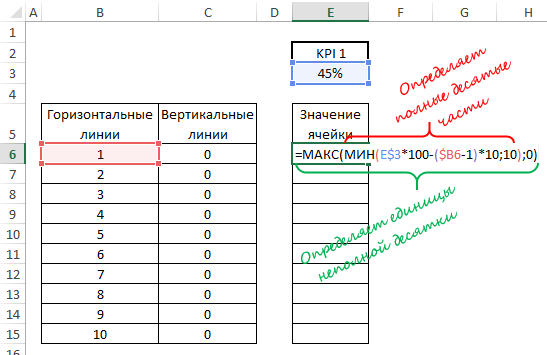
Формула, которую мы вставили в диапазон Значения ячейки, разбивает показатель KPI на группы, размером по 10 единиц. Обратите внимание, что после того, как мы протянули формулу, показатель 45% разбился на 5 групп, состоящих из 4 групп с целыми десятками и одна группа из неполной десятки (5%).
Если вы измените показатель на другое значение, например, 67%, формула разобьет его на 7 групп (6 – целых десяток, 1 – неполная).
На данном этапе мы имеем все данные для построения квадратной диаграммы.
Построение вафельной диаграммы
Создание вафельной диаграммы потребует от вас некоторых усилий. Но есть хорошая новость. Создав диаграмму, ее можно легко дублировать. Итак, алгоритм действий по шагам.
Строим линейчатую диаграмму с группировкой на основе данных диапазона Значения ячейки.
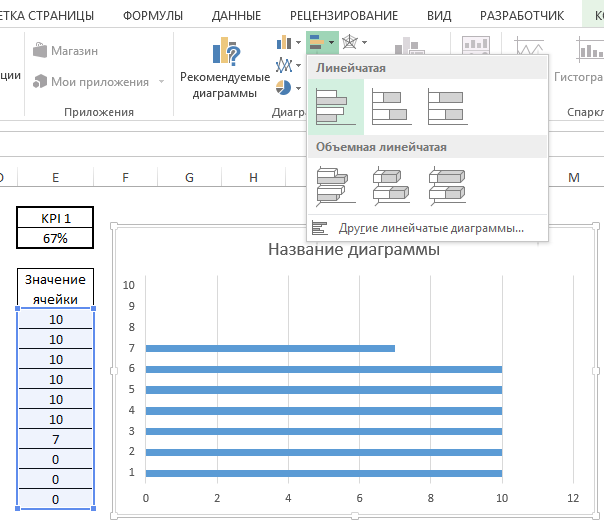
Копируем диапазоны Горизонтальны и вертикальные линии, выделяем диаграмму и вставляем данные.
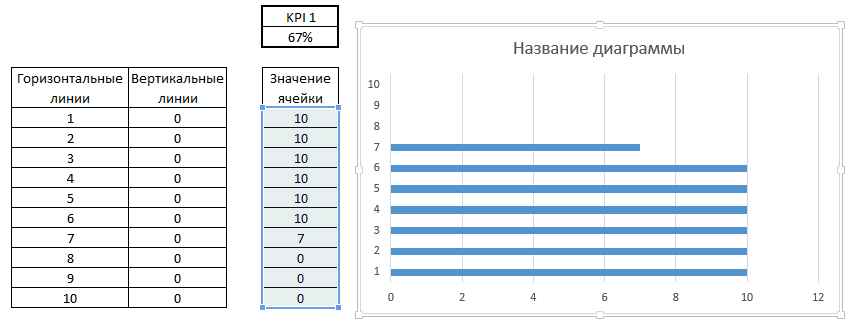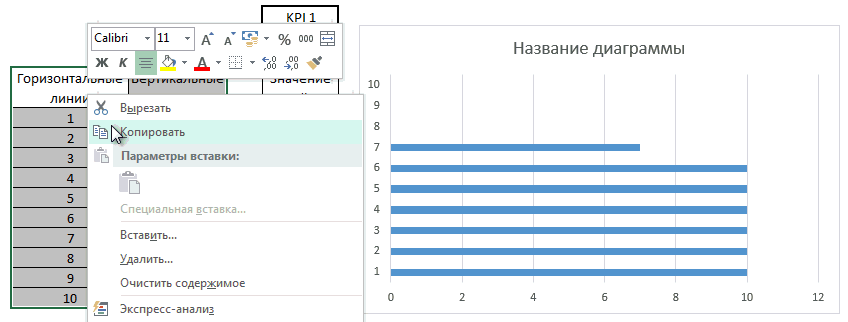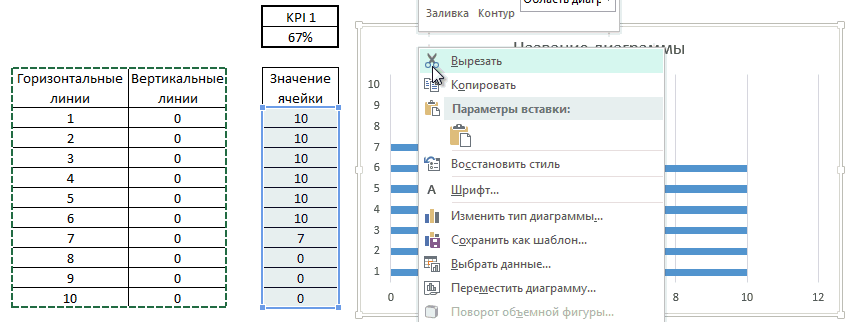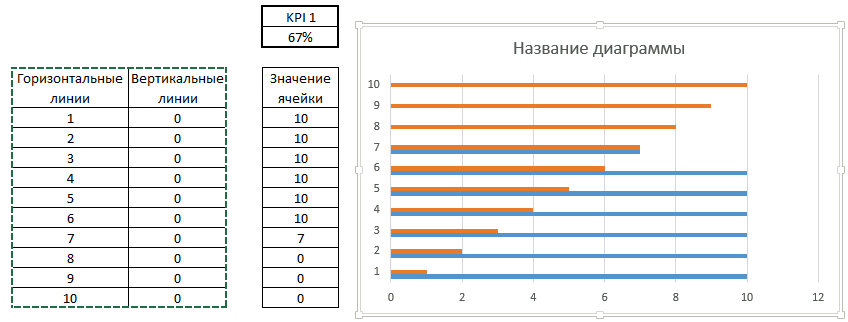
Закрашиваем область построения в серый цвет, для этого щелкаем правой кнопкой по области построения. В выпадающем меню выбираем пункт Формат области построения. В появившейся панели Параметры области построения, переходим во вкладку Заливка и указываем понравившийся тон серого в пункте Цвет.
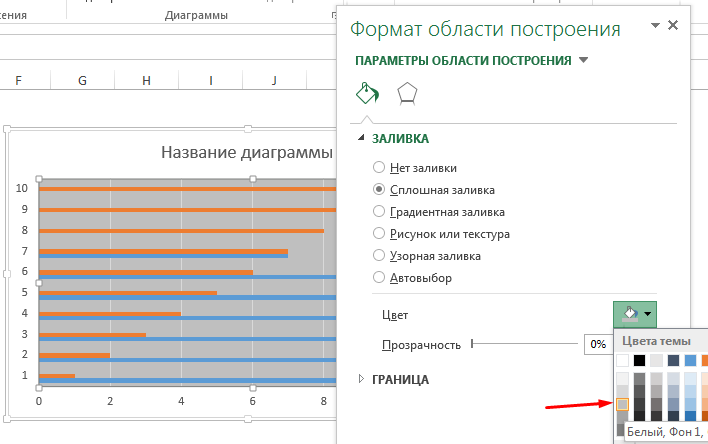
Далее необходимо превратить линейчатые диаграммы Горизонтальных и вертикальных линий в точечные. Для этого щелкаем по любому ряду данных правой кнопкой мыши, из выпадающего меню выбираем Изменить тип диаграммы для ряда. В появившемся диалоговом окне Изменение типа диаграммы выбираем для рядов данных Горизонтальные линии и Вертикальные линии из выпадающего списка Тип диаграммы – точечная.
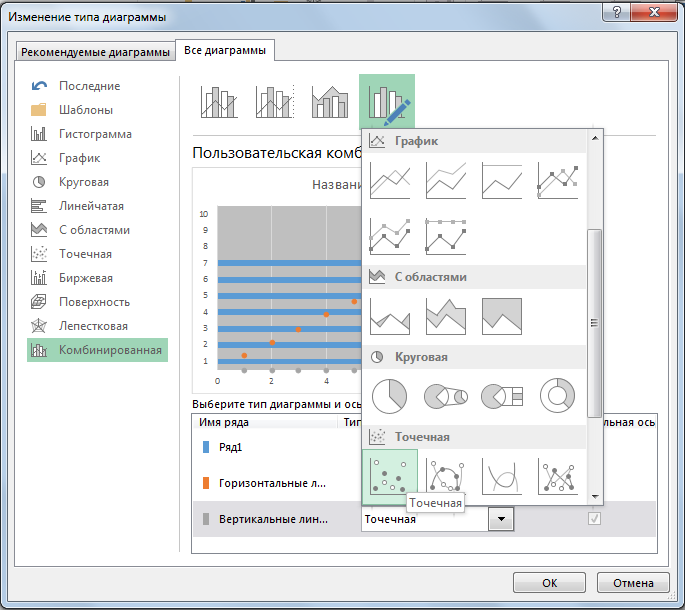
Для ряда данных Горизонтальные линии необходимо добавить значения оси X. Щелкаем правой кнопкой мыши по ряду данных Горизонтальные линии, из выпадающего меню выбираем Выбрать данные. И добавляем диапазон Вертикальные линии, состоящий из нулей.

На данном этапе график должен иметь следующий вид.
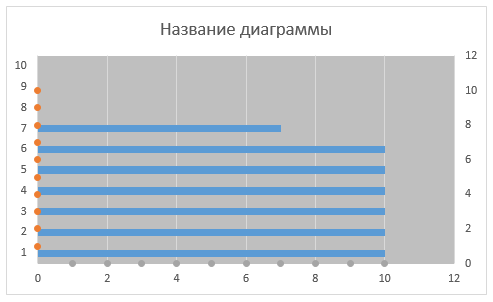
Устанавливаем максимальное значение горизонтальной и вспомогательной вертикальной осей равным 10. Для этого щелкаем правой кнопкой мыши по шкале оси, из выпадающего меню выбираем Формат оси. Во всплывающей справа панели Параметры оси устанавливаем фиксированное максимальное значение равным 10. То же самое делаем для вертикальной вспомогательной оси.
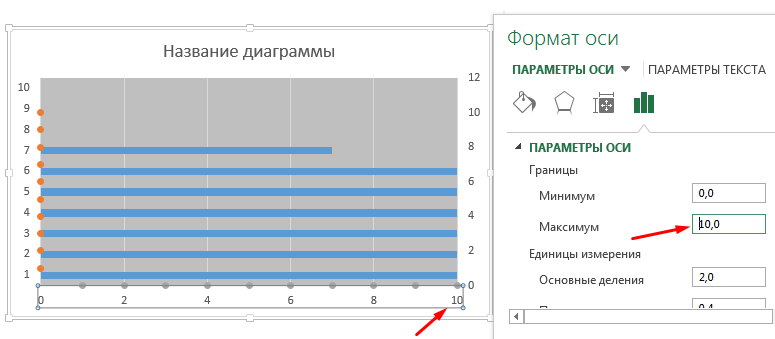
Удаляем все шкалы осей. Выбираем ось и нажимаем клавишу Delete.
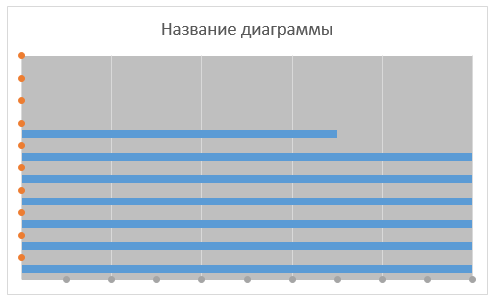
На следующем шаге необходимо добавить планки погрешностей, они будут играть роль разделителей. Для этого выбираем ряд данных Горизонтальные линии, щелкаем на плюсик, появившийся справа от диаграммы. Во всплывающем окне ставим галочку напротив поля Предел погрешностей. То же самое проделываем для ряда данных Вертикальные линии.
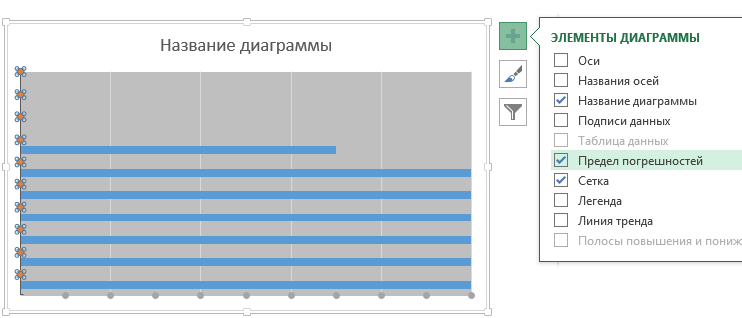
Нам понадобятся не все планки погрешностей, поэтому выделяем диаграмму, переходим во вкладку Работа с диаграммами –> Формат в группу Текущий фрагмент. Из выпадающего списка выбираем пункт Ряд «Горизонтальные линии» предел погрешностей по оси Y и нажимаем клавишу Delete. Таким же образом выделяем элемент диаграммы Ряд «Вертикальные линии» предел погрешностей по оси Xи тоже удаляем.
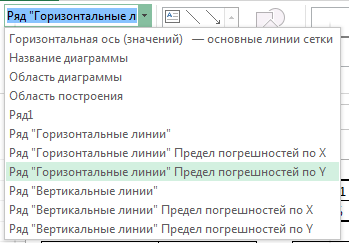
Из оставшегося списка выбираем элемент Ряд «Горизонтальные линии» предел погрешностей по оси X, в этой же группе вкладки Формат нажимаем Формат выделенного. В появившейся панели Параметры горизонтального предела погрешностей устанавливаем значения Направление – Плюс, Стиль края – Без точки, Величина погрешности – Фиксированное значение – 10. В этой же панели переходим во вкладку Заливка и границы и устанавливаем цвет линии Белый.
То же самое проделываем для элемента Ряд «Вертикальные линии» предел погрешностей по оси Y.
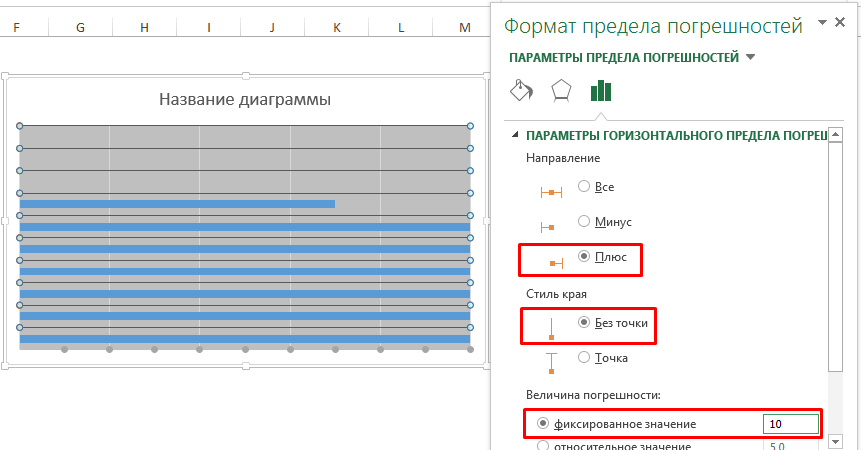
Далее щелкаем правой кнопкой по ряду данных Горизонтальные линии, в выпадающем меню выбираем Формат ряда данных, в панели Параметры ряда устанавливаем наличие маркера в положение Нет.
На этом этапе внешний вид нашей квадратной диаграммы должен иметь следующий вид.
Щелкаем правой кнопкой мыши по ряду данных Значение ячейки, выбираем из выпадающего меню пункт Формат ряда данных. В появившейся панели Параметры ряда устанавливаем Боковой зазор равным 0.

Растяните область построения графика таким образом, чтобы получился квадрат, также вы можете задать другой цвет ряду данных Значения ячейки.
Опционально, вы можете отобразить значение показателя в названии диаграммы. Для этого щелкаем по полю название диаграммы, в строке формул указываем адрес ячейки, которая содержит значение показателя.
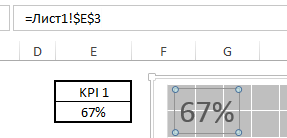
На данном этапе вы имеете готовую вафельную диаграмму.
Клонирование вафельной диаграммы
Как мы и говорили ранее, хотя вам потребуются некоторые усилия для создания квадратной диаграммы, вам не нужно будет создавать ее каждый раз с нуля, чтобы визуализировать остальные показатели. Достаточно скопировать ее и указать новый набор данных.
Для начала вам необходимо будет продублировать диапазоны Значения ячейки.
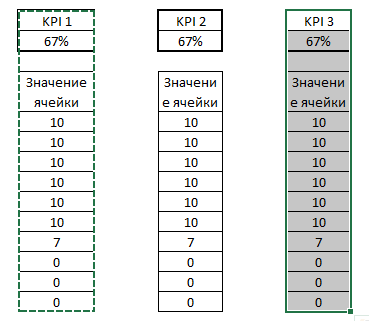
Теперь вы можете вставить необходимое значение в только что созданный диапазон. Далее копируем нашу вафельную диаграмму и вставляем ее в любое место рабочего листа. И в конце, выделяем ряд данных Значения ячейки вновь созданной диаграммы и переносим адрес ряда данных в новый диапазон.
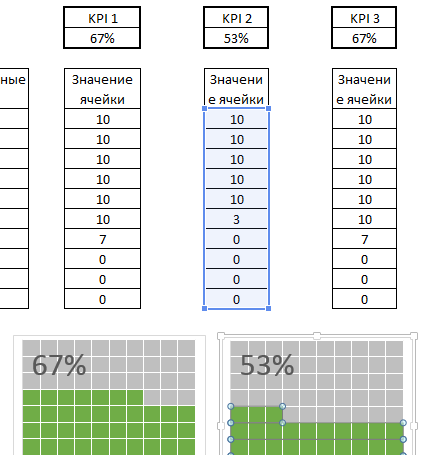
Вы можете повторить процесс для неограниченного количества KPI.
И помните, так как это является полноценной диаграммой, вы можете изменять ее размер по вашему усмотрению и перемещать ее куда захочется.
Как вы видите, данные графики позволяют оживить отчет или дашборд с помощью нового вида визуализации и привлечь к себе внимание. К тому же, их размеры можно сократить таким образом, чтобы они не занимали много места. Тем не менее у данной диаграммы есть один очень большой недостаток, он отображает только один показатель без трендов.
Скачать файл с примером вафельной диаграммы.
Рассмотрим
построение основных видов диаграмм на
конкретных
числовых примерах.
На
столбиковых
диаграммах статистические
данные
изображаются
в виде вытянутых по вертикали
прямоугольников.
При
построении столбиковых диаграмм
необходимо выполнять
следующие
требования:
1)
шкала, по которой устанавливается высота
столбика,
должна
начинаться с нуля;
2)
шкала должна быть, как правило, непрерывной;
3)
основания столбиков должны быть равны
между собой;
столбики
могут быть размещены на одинаковом
расстоянии
друг
от друга, вплотную один к другому или
наплывом, при
котором
один столбик частично накладывается
на другой;
4)
наряду с разметкой шкалы соответствующими
цифровыми
надписями
следует снабжать и сами столбцы.
Пример.
Изобразим
графические данные о числе
негосударственных
общеобразовательных школ России за
следующие
учебные годы (на начало года), ед.: 1997/98
–
570;
1998/99 – 568; 1999/2000 – 607; 2000/01 – 635.
Исследуем
негосударственные общеобразовательные
учреждения
с помощью столбиковой диаграммы
сравнения.
На
горизонтальной оси поместим основания
шести столбиков
на
расстоянии 0,5 см друг от друга. Ширина
столбиков – 1 см.
Масштаб
на вертикальной оси – 10 ед. на 1 см (рис.
5.5).
На
столбиковой диаграмме изображаемые
величины
пропорциональны
длине столбцов. Из диаграммы видно, что
число
не-
Рис.
5.5. Число общеобразовательных
негосударственных
школ
России за 1997-2001 гг.
Пример.
Построим
квадратную диаграмму для сравнения
численности
учителей и учащихся в негосударственных
школах
за 2001 г. (на начало года). Для построения
диаграммы
нужно извлечь квадратные корни из
следующих
величин:
численность учителей — 16 тыс. чел;
численность
учащихся
– 61 тыс. чел. Это составит соответственно
4; 7,81.
Чтобы
построить по этим данным квадраты,
необходимо
выбрать
масштаб. Примем 1 см за 0,8 тыс. чел.
Сторонами
квадратов на графике будут отрезки,
пропорциональные
полученным числам (рис. 5.6). Таким
образом
квадрат-
Рис.
5.6. Численность учащихся и учителей в
негосударственных
школах России на начало 2001 года (тыс.

Пример.
Изобразим
динамику производства часов в одном из
регионов
России за 1999 — 2002 гг. с помощью диаграммы
фигур-знаков.
Условно примем один рисунок за 1000 штук
часов.
Тогда число часов: в 1999 г. в размере 4717
шт.
должно
быть изображено в количестве 4,7 рисунка;
в 2000 г.
в
размере 3672 шт. – 3,7 рисунка; в 2001 г. в
размере 3987 шт
— 3,99
рисунка; в 2002 г. в размере 2189 шт. — 2,2
рисунка
(рис.
5.8).
Рис.
5.8. Производство часов в одном из регионов
России в
1999-2002
гг.

Секторные
диаграммы удобно
строить следующим образом:
вся
величина явления принимается за 100%,
рассчитываются
доли
отдельных его частей в процентах. Круг
разбивается на
секторы
пропорционально частям изображаемого
целого.
Таким
образом, на 1% приходится 3,6°. Для получения
центральных
углов секторов, изображающих доли частей
целого, необходимо их
процентное
выражение умножить на 3,6°.
Пример.
Изобразим
с помощью секторной диаграммы число
студентов
негосударственных вузов России на
начало 2000/01
учебного
года по формам обучения. На дневной
форме
обучается
39% студентов; на вечерней — 9%; на заочной
–
51%;
на экстернате – 1% студентов. Построим
круг
произвольного
радиуса. По данным о числе студентов,
для
построения
секторов определим центральные углы:
для
дневной
формы центральный угол составил 140,4″
(41,0 ¦
3,6);
для вечерней – 32,4°(9 • 3,6); для заочной
-183,6° (51 •
3,6);
для экстерната – 3,6° (1 ¦ 3,6). При помощи
транспортира
разделим круг на соответствующие сектора
(рис.
5.9).
Рис.

Рис.
5.9. Структура форм обучения студентов
государственных
и
негосударственных вузов России на
начало 2000/01
учебного
года
Если
данные о структуре какого-либо явления
выражаются в
абсолютных
величинах, то для нахождения секторов
необходимо
360° разделить на величину целого, а затем
частное
от деления последовательно умножить
на абсолютные
значения
частей.
Для
одновременного сопоставления трех
величин, связанных
между
собой таким образом, что одна величина
является
произведением
двух других, применяют диаграммы,
называемые
«знак Варзара».
Знак
Варзара представляет
собой прямоугольник, у которого
одни
сомножитель принят за основание, другой
– за высоту, а
вся
площадь равна произведению.
Пример.
Имеются
данные по сбору яровой пшеницы в одном
из
регионов России в 2003 г., в котором при
посевной
площади
14,5 млн. га урожайность составила 1,16
т/га.
В
нашем случае в основание прямоугольника
положена
урожайность
яровой пшеницы, высота — посевная
площадь, а
площадью
прямоугольника является валовой сбор
яровой
пшеницы.
Правильность показаний диаграммы можно
проверить
простыми математическими вычислениями:
посевная
площадь = валовой сбор /урожайность
=16800000 /
1,16
= 14482758 га (рис. 5.10).
Рис.

Рис.
5.10. Зависимость валового сбора яровой
пшеницы
от
урожайности и посевной площади в одном
из регаонов
России
2003 с
Линейные
диаграммы широко
применяются для
характеристики
изменений явлений во времени, выполнения
плановых
заданий, а также для изучения рядов
распределения,
выявления связи между явлениями. Линейные
диаграммы
строятся на координатной сетке.
Геометрическими
знаками
в линейных диаграммах служат точки и
последовательно
соединяющие их отрезки прямой, которые
складываются
в ломаные кривые.
Пример.
При
помощи линейной диаграммы можно
изобразить
данные
о конкурсе на вступительных экзаменах
в высшие
учебные
заведения в России за 1996 – 2000 гг.; на
одного
зачисленного
приходится державших экзамены:
Год
1996 1997 1998 1999 2000
Конкурс,
чел. 1,8 1,7 1,8 1,9 1,9
В
прямоугольной системе координат нанесем
на ось ординат
данные
о конкурсе абитуриентов (рис. 5.11). Масштаб
— 1 см
— =
0,05 чел. Из графика видно, что положение
кривой
определяется
не только данными о конкурсе, но и
интервалами
времени между датами.
Нередко
на одной линейной диаграмме приводятся
несколько
кривых,
которые дают сравнительную характеристику
дина-

Рис.
5.11. Конкурс на вступительных экзаменах
в высшие
учебные
заведения России за 1996—2000 гг. (на одного
зачисленного,
приходится державших экзамены, чел.)
мики
различных показателей или одного и того
же показателя
для
разных территорий. Методика построения
таких кривых не
отличается
от построения графика на рис. 5.11. Из
данных
рис.
5.11 видно, как меняется конкурс в вузы
за 1996 — 2000
гг.
В 1997 г. конкурс заметно снизился по
сравнению с
конкурсом
в 1996 г. Однако с 1997 г. конкурс в высшие
учебные
заведения возрастал и в 1999 г. превысил
конкурс
1996
г. С 1999 по 2000 г. конкурс в вузы России
оставался
неизменным.
Ряды
распределения чаще всего изображаются
в виде
полигона
или гистограммы.
Полигон
строят в основном для
изображения
дискретных рядов. При его построении
на оси
абсцисс
откладываются значения варьирующего
признака, а
на
оси ординат — абсолютные или относительные
численности
единиц
совокупности (частоты или частости).
Полигон на рис.
5.12
построен на основании (условных) данных
о
распределении
семей по числу детей.
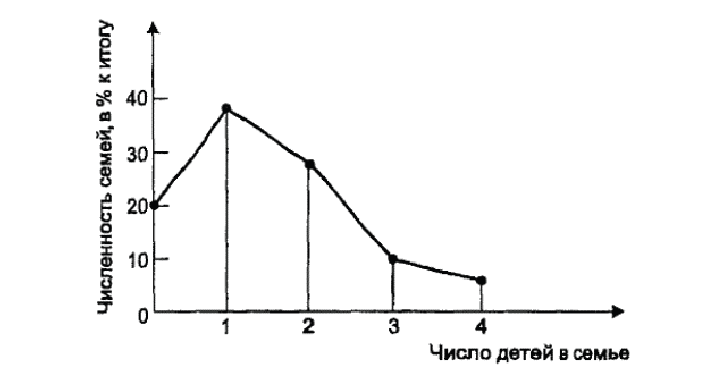
Рис.
5.12. Полигон распределения семей по числу
детей в
одном
из регионов в 2003 г.
Гистограмма
распределения применяется чаще всего
для
изображения
интервальных рядов. Для ее построения
по оси
абсцисс
откладываются интервалы признака, а по
оси ординат
— численности
единиц совокупности. На отрезках,
изображающих
интервалы, строят прямоугольники,
площади
которых
пропорциональны численностям единиц
(рис. 5.13).
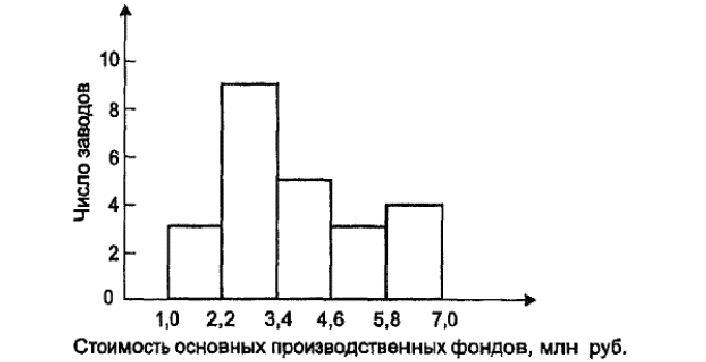
Рис.
5.13. Гистограмма распределения фирм в
одной из
отраслей
по стоимости основных производственных
фондов
В
ряде случаев для изображения вариационных
рядов
используется
кумулятивная кривая (кумулята). Для ее
построения
значения варьирующего признака
откладываются
на
оси абсцисс, а на оси ординат помещаются
накопленные
итоги
частот или частостей (рис. 5.14).

Из
Елисеевой
4.2.
Основные
виды графиков
Статистические
таблицы дополняются графиками в том
случае,
когда
ставится цель подчеркнуть какую-то
особенность данных,
провести
их сравнение. Графики являются самой
эффективной
формой
представления данных с точки зрения
восприятия.
Часто
графики используются и вне связи с
таблицей. С
помощью
графиков достигается наглядность
характеристики
структуры,
динамики, взаимосвязи явлений, их
сравнения.
Статистические
графики представляют собой условные
изображения
числовых величин и их соотношений
посредством
линий,
геометрических фигур, рисунков или
географических
карт-схем.
Графический
способ облегчает рассмотрение
статистических
данных.
На графике сразу видны пределы изменения
показателя,
сравнительная скорость изменения разных
показателей,
их колеблемость. Вместе с тем график
имеет
определенные
ограничения: прежде всего не может
включить
столько
данных, сколько может войти в таблицу;
кроме того, на
нем
показываются всегда округленные данные
— не точные, а
приблизительные.
Таким образом, график используется
только
для
изображения общей ситуации, а не деталей.
Последний
минус
— трудоемкость построения. Но этот
недостаток может
быть
преодолен применением пакетов прикладных
программ
(ППП)
для компьютерной графики, например ППП
«Harvard
graphics».
По
способу построения графики делятся на
диаграммы,
картограммы
и картодиаграммы.
Наиболее
распространенными являются диаграммы.
Они
бывают
разных видов: линейные, радиальные,
точечные,
плоскостные,
объемные, фигурные. Вид диаграммы зависит
от
вида
представляемых данных (одна переменная
или один
показатель,
несколько переменных или показателей,
количественные
или неколичественные) и задачи построения
графика.

Рис.
4.1. Динамика выбросов вредных веществ
в атмосферу
и
индекса физического объема промышленного
производства
в
Санкт-Петербурге
В
любом случае график обязательно
сопровождается
заголовком
— над или под полем графика. В заголовке
указывается,
какой показатель изображен, в каких
единицах
измерения,
по какой территории и за какое время он
определен.
Линейные
графики используются для представления
количественных
переменных: характеристики вариации
их
значений,
динамики, взаимосвязи между переменными.
Вариация
данных анализируется с помощью полигона
распределения,
кумуляты (кривой «не меньше, чем») и
огивы
(кривой
«больше, чем»). Линейные графики
используются в
решении
задач классификации данных. Линейные
графики
применяются
в анализе динамики связей. В анализе
используются
точечные диаграммы (так называемое поле
корреляции).
Линейные
графики целесообразно разделять на
используемые
для
представления данных по одной переменной
— одномерные
или
по двум переменным — двумерные. Примером
первого
является
полигон распределения, второго —•
линРис. 4.1. Динамика выбросов вредных
веществ в атмосферу
и
индекса физического объема промышленного
производства
в
Санкт-Петербурге
В
любом случае график обязательно
сопровождается
заголовком
— над или под полем графика. В заголовке
указывается,
какой показатель изображен, в каких
единицах
измерения,
по какой территории и за какое время он
определен.
Линейные
графики используются для представления
количественных
переменных: характеристики вариации
их
значений,
динамики, взаимосвязи между переменными.
Вариация
данных анализируется с помощью полигона
распределения,
кумуляты (кривой «не меньше, чем») и
огивы
(кривой
«больше, чем»). Линейные графики
используются в
решении
задач классификации данных. Линейные
графики
применяются
в анализе динамики связей. В анализе
используются
точечные диаграммы (так называемое поле
корреляции).
Линейные
графики целесообразно разделять на
используемые
для
представления данных по одной переменной
— одномерные
или
по двум переменным — двумерные. Примером
первого
является
полигон распределения, второго —•
линия регрессии.
Возможен
такой случай, когда на графике представлено
несколько переменных (показателей), а
он все-таки
не
является многомерным (рис. 4.1).
Для
того чтобы динамика двух и более
показателей была
сопоставимой,
следует обеспечить их «единый старт»,
как на
рис.
4.1, где показатели 1990 г. приняты за 100%.
 ;
;
—о——–оценка
произошедших изменений экономической
ситуации
в России;
—о—
– оценка ожидаемых изменений экономической
ситуации в
России;
—л-—
– оценка произошедших изменений личного
материального
положения;
—*—¦
-оценка ожидаемых изменений личного
материального
положения;
–
– ¦ – – – оценка благоприятности условий
для крупных покупок
Рис.
4.2. Индекс уверенности потребителя (I
кв. — февраль, II
кв.
— май, III кв. — август, IV кв. — ноябрь)
HIS
Динамика
двух показателей на одном и том же
графике может
быть
представлена и без приведения их к 100%,
если эти
показатели
связаны каким-либо функциональным
соотношением
(например, представлена динамика общего
показателя
и показателя, который является одним
из его
составляющих).
Примером такого графика является рис.
4.2.
При
графическом изображении динамики по
оси абсцисс
показывается
время (годы, кварталы, месяцы); по оси
ординат
— значения
показателей или показателя (рис. 4.3, а).
При этом
ось
ординат должна иметь начало в точке
«О». Иногда вместо
нулевой
точки в качестве начального уровня на
оси ординат
показывается
уровень какого-либо года. Это делается
втом
случае,
если изменения изображаемого показателя
значительны
— в 8—10 раз и более в течение рассматриваемого
отрезка
времени. Однако такой прием не
рекомендуется.
Правильнее
указать нулевую точку, а затем (если
нужно)
«разорвать»
ось ординат так, как это показано на
рис. 4.3, б.
Иногда
при больших изменениях показателя
прибегают к
логарифмической
шкале. Предположим, значения показателя
изменяются
от 1 до 100 (в 100 раз); это может вызвать
затруднения
при построении графика. Если перейти к
логарифмам,
то их значения для минимальных
(максимальных)
значений
показателя будут различаться не так
сильно: log 1 =
0,
log 100 = 2.
Среди
плоскостных диаграмм по частоте
использования
выделяются
столбиковые диаграммы, на которых
показатель
представляется
в виде столбика, высота которого
соответствует
значению
показателя. Пример столбиковой диаграммы
представлен
на рис. 4.4. Часто на столбиковой диаграмме
показываются
относительные величины: при сравнении
показателей
по группам, по разным совокупностям,
одна из
которых
может быть принята за 100%.
Пропорциональность
площади той или иной геометрической
фигуры
величине показателя лежит в основе
других видов
плоскостных
диаграмм: треугольных, квадратных,
прямоугольных.
В треугольной диаграмме нужно так
выбрать
стороны
и высоту треугольника, чтобы его площадь
отвечала
величине
показателя. Для построения квадратной
диаграммы
нужно
задать размер одной стороны, прямоугольной
— двух__

сторон.
Можно использовать и сравнение площадей
круга; в
этом
случае задается радиус окружности.
Ленточная
диаграмма представляет показатели в
виде
горизонтально
вытянутых прямоугольников. Как
столбиковые,
так
и ленточные диаграммы можно применять
не только для
сравнения
самих величин, но и для сравнения их
частей (рис.
4.5
и 4.6).
Особый
тип ленточных диаграмм применяется для
представления
данных с разным характером изменений:
положительным
и отрицательным (рис. 4.7).
Диаграмма,
изображенная на рис. 4.7, может использоваться,
например,
для представления регионов с разной
величиной и
характером
миграционного сальдо (положительным и
отрицательным)
предприятий, на которых повысилась и
понизилась
оплата труда и т.д.
Из
плоскостных диаграмм часто используется
секторная
диаграмма.
Она применяется для иллюстрации структуры
изучаемой
совокупности. Вся совокупность принимается
за





го
показателя. Площадь фигуры соответствует
величине
показателя
(рис. 4.10).
Если,
например, вы решите использовать фигурную
диаграмму
для
изображения структуры безработных
женщин, среди
которых
47% — молодые женщины (20—24 года) и девушки
16—19
лет, не имеющие стажа работы; 28% —
инженерно-
технические
работники и служащие со специальным
образованием
в возрасте 25—49 лет и 15% — работницы
квалифицированного
и неквалифицированного труда в возрасте
50
лет и старше, то должны изобразить три
женские фигуры,
причем
первая из них должна быть в два раза
больше второй, а
вторая
— почти в два раза больше третьей.
При
построении графика одинаково важно все
— правильный
выбор
вида графического изображения пропорций,
соблюдение
правил
оформления. Подробнее все эти вопросы
освещаются в
литературе,
рекомендованной к данной главе.
Разнообразные
виды графиков позволяют получить ППП
для
ПЭВМ
«Harvardgraphics», «Supercalc», «Statictica», «Statgraphics
»
и
др.
На
графическом представлении основаны
некоторые
процедуры классификации (группировки)
данных,
анализа
динамики: выявление тенденции, сравнение
динамики
разных
показателей и т.д.

Наконец,
сам процесс обобщения статистических
данных можно
представить
графически (рис. 4.11). Изображен весь
массив
собранных
данных, т.е. таблица «объект-признак»,
полученная
за
ряд периодов. Например, собраны данные
по промышленным
предприятиям
на данной территории по многим
характеристикам
за каждый месяц. Это можно представить
в
виде
параллелепипеда, что и сделано на рис.
4.11.
Третье
измерение может быть не временем, а
определенной
территорией,
т.е. каждая таблица «объект-признак»
относится
к
определенной территории (району, области
и т.д.). На
последующих
рисунках показано, что каждый из
подмас-сивов,
взятых
из рис. 4.12, а, может выделяться и
разрабатываться
самостоятельно
(б); на рис. 4.12, ваг показано, что данные
могут
подразделяться по регионам, по кварталам
и, наконец, по
категориям
(д). Последний рис. 4.12, е изображает
подразделение
данных по трем основаниям: по времени,
территории
и категориям.

