Эта статья открывает список уроков на тему “Линейная алгебра с примерами на Python“. Мы постараемся рассказать о базовых понятиях линейной алгебры, которые могут быть полезны тем, кто занимается машинным обучением и анализом данных, и будем сопровождать все это примерами на языке Python.
- Матрицы
- Виды матриц и способы их создания в Python
- Вектор
- Вектор-строка
- Вектор-столбец
- Квадратная матрица
- Диагональная матрица
- Единичная матрица
- Нулевая матрица
- Задание матрицы в общем виде
Матрицы
Матрицей в математике называют объект, записываемый в виде прямоугольной таблицы, элементами которой являются числа (могут быть как действительные, так и комплексные). Пример матрицы приведен ниже.
(M;=;begin{pmatrix}1&3&5\7&2&4end{pmatrix})
В общем виде матрица записывается так:
(M=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{m1}&a_{m2}&…&a_{mn}end{pmatrix})
Представленная выше матрица состоит из i-строк и j-столбцов. Каждый ее элемент имеет соответствующее позиционное обозначение, определяемое номером строки и столбца на пересечении которых он расположен: (a_{ij})- находится на i-ой строке и j-м столбце.
Важным элементом матрицы является главная диагональ, ее составляют элементы, у которых совпадают номера строк и столбцов.
Матрица в Python – это двумерный массив, поэтому задание матриц того или иного вида предполагает создание соответствующего массива. Для работы с массивами в Python используется тип данных список (англ. list). Но с точки зрения представления матриц и проведения вычислений с ними списки – не очень удобный инструмент, для этих целей хорошо подходит библиотека Numpy, ее мы и будем использовать в дальнейшей работе.
Напомним, для того, чтобы использовать библиотеку Numpy ее нужно предварительно установить, после этого можно импортировать в свой проект. По установке Numpy можно подробно прочитать в разделе “Установка библиотеки Numpy” из введения. Для того чтобы импортировать данный модуль, добавьте в самое начало программы следующую строку
import numpy as np
Если после импорта не было сообщений об ошибке, то значит все прошло удачно и можно начинать работу. Numpy содержит большое количество функций для работы с матрицами, которые мы будем активно использовать. Обязательно убедитесь в том, что библиотека установлена и импортируется в проект без ошибок.
Рассмотрим, различные варианты матриц и способы их задания в Python.
Вектор
Вектором называется матрица, у которой есть только один столбец или одна строка. Более подробно свойства векторов, их геометрическая интерпретация и операции над ними будут рассмотрены в “Главе 2 Векторная алгебра”.
Вектор-строка
Вектор-строка имеет следующую математическую запись.
(v=(1;2))
Такой вектор в Python можно задать следующим образом.
>>> v_hor_np = np.array([1, 2]) >>> print(v_hor_np ) [1 2]
Если необходимо создать нулевой или единичный вектор, то есть вектор, у которого все элементы нули либо единицы, то можно использовать специальные функции из библиотеки Numpy.
Создадим нулевую вектор-строку размера 5.
>>> v_hor_zeros_v1 = np.zeros((5,)) >>> print(v_hor_zeros_v1 ) [0. 0. 0. 0. 0.]
В случае, если требуется построить вектор-строку так, чтобы она сама являлась элементом какого-то массива, это нужно для возможности транспонирования матрицы (см. раздел “1.3 Транспонирование матрицы”), то данную задачу можно решить так.
>>> v_hor_zeros_v2 = np.zeros((1, 5)) >>> print(v_hor_zeros_v2 ) [[0. 0. 0. 0. 0.]]
Построим единичную вектор-строку в обоих из представленных для нулевого вектора-строки форм.
>>> v_hor_one_v1 = np.ones((5,)) >>> print(v_hor_one_v1) [1. 1. 1. 1. 1.]
>>> v_hor_one_v2 = np.ones((1, 5)) >>> print(v_hor_one_v2) [[1. 1. 1. 1. 1.]]
Вектор-столбец
Вектор-столбец имеет следующую математическую запись.
(v=begin{pmatrix}1\2end{pmatrix})
В общем виде вектор столбец можно задать следующим образом.
>>> v_vert_np = np.array([[1], [2]]) >>> print(v_vert_np) [[1] [2]]
Рассмотрим способы создания нулевых и единичных векторов-столбцов. Построим нулевой вектор-столбец.
>>> v_vert_zeros = np.zeros((5, 1)) >>> print(v_vert_zeros) [[0.] [0.] [0.] [0.] [0.]]
Единичный вектор-столбец можно создать с помощью функции ones().
>>> v_vert_ones = np.ones((5, 1)) >>> print(v_vert_ones) [[1.] [1.] [1.] [1.] [1.]]
Квадратная матрица
Довольно часто, на практике, приходится работать с квадратными матрицами. Квадратной называется матрица, у которой количество столбцов и строк совпадает. В общем виде они выглядят так.
(Msqr=begin{pmatrix}a_{11}&a_{12}&…&a_{1n}\a_{21}&a_{22}&…&a_{2n}\…&…&…&…\a_{n1}&a_{n2}&…&a_{nn}end{pmatrix})
Создадим следующую матрицу.
(Msqr=begin{pmatrix}1&2&3\4&5&6\7&8&9end{pmatrix})
В Numpy можно создать квадратную матрицу с помощью метода array().
>>> m_sqr_arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Как вы уже наверное заметили, аргументом функции np.array() является список Python, его можно создать отдельно и передать в функцию.
>>> m_sqr = [[1, 2, 3], [4, 5, 6], [7, 8, 9]] >>> m_sqr_arr = np.array(m_sqr) >>> print(m_sqr_arr) [[1 2 3] [4 5 6] [7 8 9]]
Но в Numpy есть еще одни способ создания матриц – это построение объекта типа matrix с помощью одноименного метода. Задать матрицу можно в виде списка.
>>> m_sqr_mx = np.matrix([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) >>> print(m_sqr_mx) [[1 2 3] [4 5 6] [7 8 9]]
Также доступен стиль Matlab, когда между элементами ставятся пробелы, а строки разделяются точкой с запятой, при этом такое описание должно быть передано в виде строки.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')
>>> print(m_sqr_mx)
[[1 2 3]
[4 5 6]
[7 8 9]]
Диагональная матрица
Особым видом квадратной матрицы является диагональная – это такая матрица, у которой все элементы, кроме тех, что расположены на главной диагонали, равны нулю.
(Mdiag=begin{pmatrix}a_{11}&0&…&0\0&a_{22}&…&0\…&…&…&…\0&0&…&a_{nn}end{pmatrix})
Диагональную матрицу можно построить вручную, задав только значения элементам на главной диагонали.
>>> m_diag = [[1, 0, 0], [0, 5, 0], [0, 0, 9]] >>> m_diag_np = np.matrix(m_diag) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Библиотека Numpy предоставляет инструменты, которые могут упростить построение такой матрицы.
Первый вариант подойдет в том случае, если у вас уже есть матрица, и вы хотите сделать из нее диагональную. Создадим матрицу размера 3 3.
>>> m_sqr_mx = np.matrix('1 2 3; 4 5 6; 7 8 9')
Извлечем ее главную диагональ.
>>> diag = np.diag(m_sqr_mx) >>> print(diag) [1 5 9]
Построим диагональную матрицу на базе полученной диагонали.
>>> m_diag_np = np.diag(np.diag(m_sqr_mx)) >>> print(m_diag_np) [[1 0 0] [0 5 0] [0 0 9]]
Второй вариант подразумевает построение единичной матрицы, ей будет посвящен следующий параграф.
Единичная матрица
Единичной матрицей называют такую квадратную матрицу, у которой элементы главной диагонали равны единицы, а все остальные нулю.
(E=begin{pmatrix}1&0&…&0\0&1&…&0\…&…&…&…\0&0&…&1end{pmatrix})
Создадим единичную матрицу на базе списка, который передадим в качестве аргумента функции matrix().
>>> m_e = [[1, 0, 0], [0, 1, 0], [0, 0, 1]] >>> m_e_np = np.matrix(m_e) >>> print(m_e_np) [[1 0 0] [0 1 0] [0 0 1]]
Такой способ не очень удобен, к счастью для нас, для построения такого типа матриц в библиотеке Numpy есть специальная функция – eye().
>>> m_eye = np.eye(3) >>> print(m_eye) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]
В качестве аргумента функции передается размерность матрицы, в нашем примере – это матрица 3 3. Тот же результат можно получить с помощью функции identity().
>>> m_idnt = np.identity(3) >>> print(m_idnt) [[ 1. 0. 0.] [ 0. 1. 0.] [ 0. 0. 1.]]
Нулевая матрица
У нулевой матрицы все элементы равны нулю.
(Z=begin{pmatrix}0&0&…&0\0&0&…&0\…&…&…&…\0&0&…&0end{pmatrix})
Пример того, как создать такую матрицу с использованием списков, мы приводить не будем, он делается по аналогии с предыдущим разделом. Что касается Numpy, то в составе этой библиотеки есть функция zeros(), которая создает нужную нам матрицу.
>>> m_zeros = np.zeros((3, 3)) >>> print(m_zeros) [[ 0. 0. 0.] [ 0. 0. 0.] [ 0. 0. 0.]]
В качестве параметра функции zeros() передается размерность требуемой матрицы в виде кортежа из двух элементов, первый из которых – число строк, второй – столбцов. Если функции zeros() передать в качестве аргумента число, то будет построен нулевой вектор-строка, это мы делали в параграфе, посвященном векторам.
Задание матрицы в общем виде
Если у вас уже есть данные о содержимом матрицы, то создать ее можно используя списки Python или функцию matrix() из библиотеки Numpy.
>>> m_mx = np.matrix('1 2 3; 4 5 6')
>>> print(m_mx)
[[1 2 3]
[4 5 6]]
Если же вы хотите создать матрицу заданного размера с произвольным содержимым, чтобы потом ее заполнить, проще всего для того использовать функцию zeros(), которая создаст матрицу заданного размера, заполненную нулями.
>>> m_var = np.zeros((2, 5)) >>> print(m_var) [[ 0. 0. 0. 0. 0.] [ 0. 0. 0. 0. 0.]]
P.S.
Вводные уроки по “Линейной алгебре на Python” вы можете найти соответствующей странице нашего сайта. Все уроки по этой теме собраны в книге “Линейная алгебра на Python”.
Если вам интересна тема анализа данных, то мы рекомендуем ознакомиться с библиотекой Pandas. Для начала вы можете познакомиться с вводными уроками. Все уроки по библиотеке Pandas собраны в книге “Pandas. Работа с данными”.
Содержание
- NumPy: матрицы и операции над ними
- 1. Создание матриц
- 2. Индексирование
- 3. Векторы, вектор-строки и вектор-столбцы
- 4. Datatypes
- 5. Математические операции
- 6. Умножение матриц и столбцов
- 7. Объединение массивов
- Задания: (Блок 1)
- Задание 1:
- Задание 2:
- Задания: (Блок 1)
- 8. Транспонирование матриц
- 9. Определитель матрицы
- 10. Ранг матрицы
- 11. Системы линейных уравнений
- 12. Обращение матриц
- 13. Собственные числа и собственные вектора матрицы
- 14. Расстояния между векторами
- p-норма
- ℓ1 норма
- ℓ2 норма
- 15. Расстояния между векторами
- 16. Скалярное произведение и угол между векторами
- 17. Комплексные числа в питоне
- Задания: (Блок 2)
- Задание 3:
- Задания: (Блок 2)
NumPy: матрицы и операции над ними
Ссылка на jupyter notebook
В этом ноутбуке из сторонних библиотек нам понадобится только NumPy.
Для удобства импортируем ее под более коротким именем:
import numpy as np
1. Создание матриц
Приведем несколько способов создания матриц в NumPy.
Самый простой способ — с помощью функции
numpy.array(list, dtype=None, …).
В качестве первого аргумента ей надо передать итерируемый объект,
элементами которого являются другие итерируемые объекты одинаковой длины
и содержащие данные одинакового типа.
Второй аргумент является опциональным и определяет тип данных матрицы.
Его можно не задавать, тогда тип данных будет определен из типа
элементов первого аргумента. При задании этого параметра будет
произведена попытка приведения типов.
Например, матрицу из списка списков целых чисел можно создать следующим
образом:
a = np.array([1, 2, 3]) # Создаем одномерный массив print(type(a)) # Prints "<class 'numpy.ndarray'>" print(a.shape) # Prints "(3,)" - кортеж с размерностями print(a[0], a[1], a[2]) # Prints "1 2 3" a[0] = 5 # Изменяем значение элемента массива print(a) # Prints "[5, 2, 3]" b = np.array([[1,2,3],[4,5,6]]) # Создаем двухмерный массив print(b.shape) # Prints "(2, 3)" print(b[0, 0], b[0, 1], b[1, 0]) # Prints "1 2 4" print(np.arange(1, 5)) #Cоздает вектор с эелементами от 1 до 4
<class 'numpy.ndarray'> (3,) 1 2 3 [5 2 3] (2, 3) 1 2 4 [1 2 3 4]
matrix = np.array([[1, 2, 3], [2, 5, 6], [6, 7, 4]]) print ("Матрица:n", matrix)
Матрица: [[1 2 3] [2 5 6] [6 7 4]]
Второй способ создания — с помощью встроенных функций
numpy.eye(N, M=None, …), numpy.zeros(shape, …),
numpy.ones(shape, …).
Первая функция создает единичную матрицу размера N×M;
если M не задан, то M = N.
Вторая и третья функции создают матрицы, состоящие целиком из нулей или
единиц соответственно. В качестве первого аргумента необходимо задать
размерность массива — кортеж целых чисел. В двумерном случае это набор
из двух чисел: количество строк и столбцов матрицы.
Примеры:
b = np.eye(5) print ("Единичная матрица:n", b)
Единичная матрица: [[1. 0. 0. 0. 0.] [0. 1. 0. 0. 0.] [0. 0. 1. 0. 0.] [0. 0. 0. 1. 0.] [0. 0. 0. 0. 1.]]
c = np.ones((7, 5)) print ("Матрица, состоящая из одних единиц:n", c)
Матрица, состоящая из одних единиц: [[1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.] [1. 1. 1. 1. 1.]]
d = np.full((2,2), 7) # Создает матрицу (1, 2) заполненую заданным значением print(d) # Prints "[[ 7. 7.] # [ 7. 7.]]" e = np.random.random((2,2)) # Создает еденичную матрицу (2, 2) заполненую случаными числами (0, 1) print(e) # Might print "[[ 0.91940167 0.08143941] # [ 0.68744134 0.87236687]]"
[[7 7] [7 7]] [[0.25744383 0.48056466] [0.13767881 0.40578168]]
Обратите внимание: размерность массива задается не двумя аргументами
функции, а одним — кортежем!
Вот так — np.ones(7, 5) — создать массив не получится, так как
функции в качестве параметра shape передается 7, а не кортеж
(7, 5).
И, наконец, третий способ — с помощью функции
numpy.arange([start, ]stop, [step, ], …), которая создает
одномерный массив последовательных чисел из промежутка
[start, stop) с заданным шагом step, и метода
array.reshape(shape).
Параметр shape, как и в предыдущем примере, задает размерность
матрицы (кортеж чисел). Логика работы метода ясна из следующего примера:
v = np.arange(0, 24, 2) print ("Вектор-столбец:n", v)
Вектор-столбец: [ 0 2 4 6 8 10 12 14 16 18 20 22]
d = v.reshape((3, 4)) print ("Матрица:n", d)
Матрица: [[ 0 2 4 6] [ 8 10 12 14] [16 18 20 22]]
Более подробно о том, как создавать массивы в NumPy, см.
документацию.
2. Индексирование
Для получения элементов матрицы можно использовать несколько способов.
Рассмотрим самые простые из них.
Для удобства напомним, как выглядит матрица d:
print ("Матрица:n", d)
Матрица: [[ 0 2 4 6] [ 8 10 12 14] [16 18 20 22]]
Элемент на пересечении строки i и столбца j можно
получить с помощью выражения array[i, j].
Обратите внимание: строки и столбцы нумеруются с нуля!
print ("Второй элемент третьей строки матрицы:", d[2, 1])
Второй элемент третьей строки матрицы: 18
Из матрицы можно получать целые строки или столбцы с помощью выражений
array[i, :] или array[:, j] соответственно:
print ("Вторая строка матрицы d:n", d[1, :]) print ("Четвертый столбец матрицы d:n", d[:, 3])
Вторая строка матрицы d: [ 8 10 12 14] Четвертый столбец матрицы d: [ 6 14 22]
Еще один способ получения элементов — с помощью выражения
array[list1, list2], где list1, list2 —
некоторые списки целых чисел. При такой адресации одновременно
просматриваются оба списка и возвращаются элементы матрицы с
соответствующими координатами. Следующий пример более понятно объясняет
механизм работы такого индексирования:
print ("Элементы матрицы d с координатами (1, 2) и (0, 3):n", d[[1, 0], [2, 3]])
Элементы матрицы d с координатами (1, 2) и (0, 3): [12 6]
# Slicing # Создадим матрицу (3, 4) # [[ 1 2 3 4] # [ 5 6 7 8] # [ 9 10 11 12]] a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]]) # Используя слайсинг, созадим матрицу b из элементов матрицы а # будем использовать 0 и 1 строку, а так же 1 и 2 столебц # [[2 3] # [6 7]] b = a[:2, 1:3] print(b) # ОБРАТИТЕ ВНИМАНИЕ НА ИЗМЕНЕНИЕ ИСХОДОЙ МАТРИЦЫ print(a[0, 1]) # Prints "2" b[0, 0] = 77 # b[0, 0] is the same piece of data as a[0, 1] print(a[0, 1]) # Prints "77"
[[2 3] [6 7]] 2 77
# Integer array indexing a = np.array([[1,2], [3, 4], [5, 6]]) print(a) print() # Пример Integer array indexing # В результате получится массив размерности (3,) # Обратите внимание, что до запятой идут индексы строк, после - столбцов print(a[[0, 1, 2], [0, 1, 0]]) # Prints "[1 4 5]" print() # По-другому пример можно записать так print(np.array([a[0, 0], a[1, 1], a[2, 0]])) # Prints "[1 4 5]"
[[1 2] [3 4] [5 6]] [1 4 5] [1 4 5]
Примеры использования слайсинга:
# Создадим новый маассив, из которого будем выбирать эллементы a = np.array([[1,2,3], [4,5,6], [7,8,9], [10, 11, 12]]) print(a) # prints "array([[ 1, 2, 3], # [ 4, 5, 6], # [ 7, 8, 9], # [10, 11, 12]])" # Создадим массив индексов b = np.array([0, 2, 0, 1]) # Выберем из каждой строки элемент с индексом из b (индекс столбца берется из b) print(a[np.arange(4), b]) # Prints "[ 1 6 7 11]" print() # Добавим к этим элементам 10 a[np.arange(4), b] += 10 print(a) # prints "array([[11, 2, 3], # [ 4, 5, 16], # [17, 8, 9], # [10, 21, 12]])
[[ 1 2 3] [ 4 5 6] [ 7 8 9] [10 11 12]] [ 1 6 7 11] [[11 2 3] [ 4 5 16] [17 8 9] [10 21 12]]
a = np.array([[1,2], [3, 4], [5, 6]]) bool_idx = (a > 2) # Найдем эллементы матрицы a, которые больше 2 # В результате получим матрицу b, такой же размерности, как и a print(bool_idx) # Prints "[[False False] print() # [ True True] # [ True True]]" # Воспользуемся полученным массивом для создания нового массива, ранга 1 print(a[bool_idx]) # Prints "[3 4 5 6]" # Аналогично print(a[a > 2]) # Prints "[3 4 5 6]"
[[False False] [ True True] [ True True]] [3 4 5 6] [3 4 5 6]
#Помните, что вы можете пользоваться сразу несколькими типами индексирования a = np.array([[1,2,3,4], [5,6,7,8], [9,10,11,12]]) row_r1 = a[1, :] row_r2 = a[1:2, :] print(row_r1, row_r1.shape) # Prints "[5 6 7 8] (4,)" print(row_r2, row_r2.shape) # Prints "[[5 6 7 8]] (1, 4)"
[5 6 7 8] (4,) [[5 6 7 8]] (1, 4)
Более подробно о различных способах индексирования в массивах см.
документацию.
3. Векторы, вектор-строки и вектор-столбцы
Следующие два способа задания массива кажутся одинаковыми:
a = np.array([1, 2, 3]) b = np.array([[1], [2], [3]])
Однако, на самом деле, это задание одномерного массива (то есть
вектора) и двумерного массива:
print ("Вектор:n", a) print ("Его размерность:n", a.shape) print ("Двумерный массив:n", b) print ("Его размерность:n", b.shape)
Вектор: [1 2 3] Его размерность: (3,) Двумерный массив: [[1] [2] [3]] Его размерность: (3, 1)
Обратите внимание: вектор (одномерный массив) и вектор-столбец
или вектор-строка (двумерные массивы) являются различными объектами в
NumPy, хотя математически задают один и тот же объект. В случае
одномерного массива кортеж shape состоит из одного числа и имеет
вид (n,), где n — длина вектора. В случае двумерных
векторов в shape присутствует еще одна размерность, равная
единице.
В большинстве случаев неважно, какое представление использовать, потому
что часто срабатывает приведение типов. Но некоторые операции не
работают для одномерных массивов. Например, транспонирование (о нем
пойдет речь ниже):
a = a.T b = b.T
print ("Вектор не изменился:n", a) print ("Его размерность также не изменилась:n", a.shape) print ("Транспонированный двумерный массив:n", b) print ("Его размерность изменилась:n", b.shape)
Вектор не изменился: [1 2 3] Его размерность также не изменилась: (3,) Транспонированный двумерный массив: [[1 2 3]] Его размерность изменилась: (1, 3)
4. Datatypes
Все элементы в массиве numpy принадлежат одному типу. В этом плане
массивы ближе к C, чем к привычным вам листам питона. Numpy имеет
множество встренных типов, подходящих для решения большинства задач.
x = np.array([1, 2]) # Автоматический выбор типа print(x.dtype) # Prints "int64" x = np.array([1.0, 2.0]) # Автоматический выбор типа print(x.dtype) # Prints "float64" x = np.array([1, 2], dtype=np.int64) # Принудительное выставление типа print(x.dtype) # Prints "int64"
int32 float64 int64
5. Математические операции
К массивам (матрицам) можно применять известные вам математические
операции. Следут понимать, что при этом у элементов должны быть схожие
размерности. Поведение в случае не совпадения размерностей хорошо
описанно в документации numpy.
x = np.array([[1,2],[3,4]], dtype=np.float64) y = np.array([[5,6],[7,8]], dtype=np.float64) arr = np.array([1, 2])
# Сложение происходит поэлеметно # [[ 6.0 8.0] # [10.0 12.0]] print(x + y) print() print(np.add(x, y)) print('С числом') print(x + 1) print('C массивом другой размерности') print(x + arr)
[[ 6. 8.] [10. 12.]] [[ 6. 8.] [10. 12.]] С числом [[2. 3.] [4. 5.]] C массивом другой размерности [[2. 4.] [4. 6.]]
# Вычитание print(x - y) print(np.subtract(x, y))
[[-4. -4.] [-4. -4.]] [[-4. -4.] [-4. -4.]]
# Деление # [[ 0.2 0.33333333] # [ 0.42857143 0.5 ]] print(x / y) print(np.divide(x, y))
[[0.2 0.33333333] [0.42857143 0.5 ]] [[0.2 0.33333333] [0.42857143 0.5 ]]
# Другие функции # [[ 1. 1.41421356] # [ 1.73205081 2. ]] print(np.sqrt(x))
[[1. 1.41421356] [1.73205081 2. ]]
6. Умножение матриц и столбцов
Напоминание теории. Операция умножения определена для двух
матриц, таких что число столбцов первой равно числу строк второй.
Пусть матрицы A и B таковы, что
A ∈ ℝn×k и
B ∈ ℝk×m. Произведением матриц
A и B называется матрица C, такая что
cij = ∑kr = 1airbrj, где cij —
элемент матрицы C, стоящий на пересечении строки с номером
i и столбца с номером j.
В NumPy произведение матриц вычисляется с помощью функции
numpy.dot(a, b, …) или с помощью метода
array1.dot(array2), где array1 и array2 —
перемножаемые матрицы.
a = np.array([[1, 0], [0, 1]]) b = np.array([[4, 1], [2, 2]]) r1 = np.dot(a, b) r2 = a.dot(b)
print ("Матрица A:n", a) print ("Матрица B:n", b) print ("Результат умножения функцией:n", r1) print ("Результат умножения методом:n", r2)
Матрица A: [[1 0] [0 1]] Матрица B: [[4 1] [2 2]] Результат умножения функцией: [[4 1] [2 2]] Результат умножения методом: [[4 1] [2 2]]
Матрицы в NumPy можно умножать и на векторы:
c = np.array([1, 2]) r3 = b.dot(c)
print ("Матрица:n", b) print ("Вектор:n", c) print ("Результат умножения:n", r3)
Матрица: [[4 1] [2 2]] Вектор: [1 2] Результат умножения: [6 6]
Обратите внимание: операция * производит над матрицами
покоординатное умножение, а не матричное!
r = a * b
print ("Матрица A:n", a) print ("Матрица B:n", b) print ("Результат покоординатного умножения через операцию умножения:n", r)
Матрица A: [[1 0] [0 1]] Матрица B: [[4 1] [2 2]] Результат покоординатного умножения через операцию умножения: [[4 0] [0 2]]
Более подробно о матричном умножении в NumPy см.
документацию.
7. Объединение массивов
Массивы можно Объединенять. Есть горизонтальное и вертикальное
объединение.
a = np.floor(10*np.random.random((2,2))) b = np.floor(10*np.random.random((2,2))) print(a) print(b) print() print(np.vstack((a,b))) print() print(np.hstack((a,b)))
[[4. 0.] [1. 4.]] [[9. 7.] [2. 6.]] [[4. 0.] [1. 4.] [9. 7.] [2. 6.]] [[4. 0. 9. 7.] [1. 4. 2. 6.]]
Массивы можно переформировать при помощи метода, который задает новый
многомерный массив. Следуя следующему примеру, мы переформатируем
одномерный массив из десяти элементов во двумерный массив, состоящий из
пяти строк и двух столбцов:
a = np.array(range(10), float) print(a) print() # Превратим в матрицу a = a.reshape((5, 2)) print(a) print() # Вернем обратно print(a.flatten()) # Другой вариант print(a.reshape((-1))) # Превратим в марицу (9, 1) print(a.reshape((-1, 1))) # Превратим в марицу (1, 9) print(a.reshape((1, -1)))
[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [[0. 1.] [2. 3.] [4. 5.] [6. 7.] [8. 9.]] [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [0. 1. 2. 3. 4. 5. 6. 7. 8. 9.] [[0.] [1.] [2.] [3.] [4.] [5.] [6.] [7.] [8.] [9.]] [[0. 1. 2. 3. 4. 5. 6. 7. 8. 9.]]
Задания: (Блок 1)
Задание 1:
Решите без использования циклов средставми NumPy (каждый пункт решается
в 1-2 строчки)
- Создайте вектор с элементами от 12 до 42
- Создайте вектор из нулей длины 12, но его пятый елемент должен быть равен 1
- Создайте матрицу (3, 3), заполненую от 0 до 8
- Найдите все положительные числа в np.array([1,2,0,0,4,0])
- Умножьте матрицу размерности (5, 3) на (3, 2)
- Создайте матрицу (10, 10) так, чтобы на границе были 0, а внтури 1
- Создайте рандомный вектор и отсортируйте его
- Каков эквивалент функции enumerate для numpy массивов?
- *Создайте рандомный вектор и выполните нормализацию столбцов (из каждого столбца вычесть среднее этого столбца, из каждого столбца вычесть sd этого столбца)
- *Для заданного числа найдите ближайший к нему элемент в векторе
- *Найдите N наибольших значений в векторе
# ваш код здесь
Задание 2:
Напишите полностью векторизованный вариант
Дан трёхмерный массив, содержащий изображение, размера (height, width,
numChannels), а также вектор длины numChannels. Сложить каналы
изображения с указанными весами, и вернуть результат в виде матрицы
размера (height, width). Считать реальное изображение можно при помощи
функции
scipy.misc.imread
(если изображение не в формате png,
установите пакет pillow:
conda install pillow
). Преобразуйте
цветное изображение в оттенки серого, использовав коэффициенты
np.array([0.299, 0.587, 0.114]).
# ваш код здесь
8. Транспонирование матриц
Напоминание теории. Транспонированной матрицей AT
называется матрица, полученная из исходной матрицы A заменой
строк на столбцы. Формально: элементы матрицы AT определяются
как aTij = aji, где aTij — элемент
матрицы AT, стоящий на пересечении строки с номером i
и столбца с номером j.
В NumPy транспонированная матрица вычисляется с помощью функции
numpy.transpose() или с помощью метода array.T, где
array — нужный двумерный массив.
a = np.array([[1, 2], [3, 4]]) b = np.transpose(a) c = a.T
print ("Матрица:n", a) print ("Транспонирование функцией:n", b) print ("Транспонирование методом:n", c)
Матрица: [[1 2] [3 4]] Транспонирование функцией: [[1 3] [2 4]] Транспонирование методом: [[1 3] [2 4]]
См. более подробно о
numpy.transpose()
и
array.T
в NumPy.
В следующих разделах активно используется модуль numpy.linalg,
реализующий некоторые приложения линейной алгебры. Более подробно о
функциях, описанных ниже, и различных других функциях этого модуля можно
посмотреть в его
документации.
9. Определитель матрицы
Напоминание теории. Для квадратных матриц существует понятие
определителя.
Пусть A — квадратная матрица. Определителем (или
детерминантом) матрицы A ∈ ℝn×n назовем
число
detA = ∑α1, α2, …, αn( − 1)N(α1, α2, …, αn)⋅aα11⋅⋅⋅aαnn,
где α1, α2, …, αn — перестановка
чисел от 1 до n,
N(α1, α2, …, αn) — число инверсий в
перестановке, суммирование ведется по всем возможным перестановкам длины
n.
Не стоит расстраиваться, если это определение понятно не до конца — в
дальнейшем в таком виде оно не понадобится.
Например, для матрицы размера 2×2 получается:
det⎛⎜⎝
a11
a12
a21
a22
⎞⎟⎠ = a11a22 − a12a21
Вычисление определителя матрицы по определению требует порядка
n! операций, поэтому разработаны методы, которые позволяют
вычислять его быстро и эффективно.
В NumPy определитель матрицы вычисляется с помощью функции
numpy.linalg.det(a), где a — исходная матрица.
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]], dtype=np.float32) det = np.linalg.det(a)
print ("Матрица:n", a) print ("Определитель:n", det)
Матрица: [[1. 2. 1.] [1. 1. 4.] [2. 3. 6.]] Определитель: -1.0
Рассмотрим одно интересное свойство определителя. Пусть у нас есть
параллелограмм с углами в точках
(0, 0), (c, d), (a + c, b + d), (a, b) (углы даны в порядке обхода по
часовой стрелке). Тогда площадь этого параллелограмма можно вычислить
как модуль определителя матрицы
⎛⎜⎝
a
c
b
d
⎞⎟⎠.
Похожим образом можно выразить и объем параллелепипеда через
определитель матрицы размера 3×3.
10. Ранг матрицы
Напоминание теории. Рангом матрицы A называется
максимальное число линейно независимых строк (столбцов) этой матрицы.
В NumPy ранг матрицы вычисляется с помощью функции
numpy.linalg.matrix_rank(M, tol=None), где M — матрица,
tol — параметр, отвечающий за некоторую точность вычисления. В
простом случае можно его не задавать, и функция сама определит
подходящее значение этого параметра.
a = np.array([[1, 2, 3], [1, 1, 1], [2, 2, 2]]) r = np.linalg.matrix_rank(a)
print ("Матрица:n", a) print ("Ранг матрицы:", r)
Матрица: [[1 2 3] [1 1 1] [2 2 2]] Ранг матрицы: 2
С помощью вычисления ранга матрицы можно проверять линейную
независимость системы векторов.
Допустим, у нас есть несколько векторов. Составим из них матрицу, где
наши векторы будут являться строками. Понятно, что векторы линейно
независимы тогда и только тогда, когда ранг полученной матрицы совпадает
с числом векторов. Приведем пример:
a = np.array([1, 2, 3]) b = np.array([1, 1, 1]) c = np.array([2, 3, 5]) m = np.array([a, b, c])
print (np.linalg.matrix_rank(m) == m.shape[0])
True
11. Системы линейных уравнений
Напоминание теории. Системой линейных алгебраических уравнений
называется система вида Ax = b, где
A ∈ ℝn×m, x ∈ ℝm×1, b ∈ ℝn×1.
В случае квадратной невырожденной матрицы A решение системы
единственно.
В NumPy решение такой системы можно найти с помощью функции
numpy.linalg.solve(a, b), где первый аргумент — матрица
A, второй — столбец b.
a = np.array([[3, 1], [1, 2]]) b = np.array([9, 8]) x = np.linalg.solve(a, b)
print ("Матрица A:n", a) print ("Вектор b:n", b) print ("Решение системы:n", x)
Матрица A: [[3 1] [1 2]] Вектор b: [9 8] Решение системы: [2. 3.]
Убедимся, что вектор x действительно является решением системы:
print (a.dot(x))
[9. 8.]
Бывают случаи, когда решение системы не существует. Но хотелось бы все
равно “решить” такую систему. Логичным кажется искать такой вектор
x, который минимизирует выражение
‖Ax − b‖2 — так мы приблизим выражение
Ax к b.
В NumPy такое псевдорешение можно искать с помощью функции
numpy.linalg.lstsq(a, b, …), где первые два аргумента такие
же, как и для функции numpy.linalg.solve(). Помимо решения
функция возвращает еще три значения, которые нам сейчас не понадобятся.
a = np.array([[0, 1], [1, 1], [2, 1], [3, 1]]) b = np.array([-1, 0.2, 0.9, 2.1]) x, res, r, s = np.linalg.lstsq(a, b, rcond=None)
print ("Матрица A:n", a) print ("Вектор b:n", b) print ("Псевдорешение системы:n", x)
Матрица A: [[0 1] [1 1] [2 1] [3 1]] Вектор b: [-1. 0.2 0.9 2.1] Псевдорешение системы: [ 1. -0.95]
12. Обращение матриц
Напоминание теории. Для квадратных невырожденных матриц определено
понятие обратной матрицы.
Пусть A — квадратная невырожденная матрица. Матрица
A − 1 называется обратной матрицей к A, если
AA − 1 = A − 1A = I,
где I — единичная матрица.
В NumPy обратные матрицы вычисляются с помощью функции
numpy.linalg.inv(a), где a — исходная матрица.
a = np.array([[1, 2, 1], [1, 1, 4], [2, 3, 6]], dtype=np.float32) b = np.linalg.inv(a)
print ("Матрица A:n", a) print ("Обратная матрица к A:n", b) print ("Произведение A на обратную должна быть единичной:n", a.dot(b))
Матрица A: [[1. 2. 1.] [1. 1. 4.] [2. 3. 6.]] Обратная матрица к A: [[ 6. 9. -7.] [-2. -4. 3.] [-1. -1. 1.]] Произведение A на обратную должна быть единичной: [[1. 0. 0.] [0. 1. 0.] [0. 0. 1.]]
13. Собственные числа и собственные вектора матрицы
Напоминание теории. Для квадратных матриц определены понятия
собственного вектора и собственного числа.
Пусть A — квадратная матрица и
A ∈ ℝn×n. Собственным вектором матрицы
A называется такой ненулевой вектор
x ∈ ℝn, что для некоторого
λ ∈ ℝ выполняется равенство
Ax = λx. При этом λ называется
собственным числом матрицы A. Собственные числа и
собственные векторы матрицы играют важную роль в теории линейной алгебры
и ее практических приложениях.
В NumPy собственные числа и собственные векторы матрицы вычисляются
с помощью функции numpy.linalg.eig(a), где a — исходная
матрица. В качестве результата эта функция выдает одномерный массив
w собственных чисел и двумерный массив v, в котором по
столбцам записаны собственные вектора, так что вектор v[:, i]
соотвествует собственному числу w[i].
a = np.array([[-1, -6], [2, 6]]) w, v = np.linalg.eig(a)
print ("Матрица A:n", a) print ("Собственные числа:n", w) print ("Собственные векторы:n", v)
Матрица A: [[-1 -6] [ 2 6]] Собственные числа: [2. 3.] Собственные векторы: [[-0.89442719 0.83205029] [ 0.4472136 -0.5547002 ]]
Обратите внимание: у вещественной матрицы собственные значения или
собственные векторы могут быть комплексными.
14. Расстояния между векторами
Вспомним некоторые нормы, которые можно ввести в пространстве
ℝn, и рассмотрим, с помощью каких библиотек и
функций их можно вычислять в NumPy.
p-норма
p-норма (норма Гёльдера) для вектора
x = (x1, …, xn) ∈ ℝn вычисляется по
формуле:
‖x‖p = (n∑i = 1|xi|p)1 ⁄ p, p ≥ 1.
В частных случаях при: * p = 1 получаем ℓ1 норму
* p = 2 получаем ℓ2 норму
Далее нам понабится модуль numpy.linalg, реализующий некоторые
приложения линейной алгебры. Для вычисления различных норм мы используем
функцию numpy.linalg.norm(x, ord=None, …), где x —
исходный вектор, ord — параметр, определяющий норму (мы
рассмотрим два варианта его значений — 1 и 2). Импортируем эту функцию:
from numpy.linalg import norm
ℓ1 норма
ℓ1 норма (также известная как манхэттенское
расстояние)
для вектора x = (x1, …, xn) ∈ ℝn
вычисляется по формуле:
‖x‖1 = n∑i = 1|xi|.
Ей в функции numpy.linalg.norm(x, ord=None, …) соответствует
параметр ord=1.
a = np.array([1, 2, -3]) print('Вектор a:', a)
Вектор a: [ 1 2 -3]
print('L1 норма вектора a:n', norm(a, ord=1))
L1 норма вектора a: 6.0
ℓ2 норма
ℓ2 норма (также известная как евклидова норма) для вектора
x = (x1, …, xn) ∈ ℝn вычисляется по
формуле:
‖x‖2 = √(n∑i = 1(xi)2).
Ей в функции numpy.linalg.norm(x, ord=None, …) соответствует
параметр ord=2.
print ('L2 норма вектора a:n', norm(a, ord=2))
L2 норма вектора a: 3.7416573867739413
Более подробно о том, какие еще нормы (в том числе матричные) можно
вычислить, см.
документацию.
15. Расстояния между векторами
Для двух векторов x = (x1, …, xn) ∈ ℝn и
y = (y1, …, yn) ∈ ℝn ℓ1 и
ℓ2 раccтояния вычисляются по следующим формулам
соответственно:
ρ1(x, y) = ‖x − y‖1 = n∑i = 1|xi − yi|
ρ2(x, y) = ‖x − y‖2 = √(n∑i = 1(xi − yi)2).
a = np.array([1, 2, -3]) b = np.array([-4, 3, 8]) print ('Вектор a:', a) print ('Вектор b:', b)
Вектор a: [ 1 2 -3] Вектор b: [-4 3 8]
print ('L1 расстояние между векторами a и b:n', norm(a - b, ord=1)) print ('L2 расстояние между векторами a и b:n', norm(a - b, ord=2))
L1 расстояние между векторами a и b: 17.0 L2 расстояние между векторами a и b: 12.12435565298214
16. Скалярное произведение и угол между векторами
a = np.array([0, 5, -1]) b = np.array([-4, 9, 3]) print ('Вектор a:', a) print ('Вектор b:', b)
Вектор a: [ 0 5 -1] Вектор b: [-4 9 3]
Скалярное произведение в пространстве ℝn для двух
векторов x = (x1, …, xn) и
y = (y1, …, yn) определяется как:
⟨x, y⟩ = n∑i = 1xiyi.
Длиной вектора x = (x1, …, xn) ∈ ℝn
называется квадратный корень из скалярного произведения, то есть длина
равна евклидовой норме вектора:
|x| = √(⟨x, x⟩) = √(n∑i = 1x2i) = ‖x‖2.
Теперь, когда мы знаем расстояние между двумя ненулевыми векторами и их
длины, мы можем вычислить угол между ними через скалярное произведение:
⟨x, y⟩ = |x||y|cos(α) ⟹ cos(α) = (⟨x, y⟩)/(|x||y|),
где α ∈ [0, π] — угол между векторами x и
y.
cos_angle = np.dot(a, b) / norm(a) / norm(b) print ('Косинус угла между a и b:', cos_angle) print ('Сам угол:', np.arccos(cos_angle))
Косинус угла между a и b: 0.8000362836474323 Сам угол: 0.6434406336093618
17. Комплексные числа в питоне
Напоминание теории. Комплексными числами называются числа вида
x + iy, где x и y — вещественные числа, а
i — мнимая единица (величина, для которой выполняется равенство
i2 = − 1). Множество всех комплексных чисел обозначается
буквой ℂ (подробнее про комплексные числа см.
википедию).
В питоне комплескные числа можно задать следующим образом (j
обозначает мнимую единицу):
a = 3 + 2j b = 1j
print ("Комплексное число a:n", a) print ("Комплексное число b:n", b)
Комплексное число a: (3+2j) Комплексное число b: 1j
С комплексными числами в питоне можно производить базовые арифметические
операции так же, как и с вещественными числами:
c = a * a d = a / (4 - 5j)
print ("Комплексное число c:n", c) print ("Комплексное число d:n", d)
Комплексное число c: (5+12j) Комплексное число d: (0.0487804878048781+0.5609756097560976j)
Задания: (Блок 2)
Задание 3:
Рассмотрим сложную математическую функцию на отрезке [1, 15]:
f(x) = sin(x / 5) * exp(x / 10) + 5 * exp(-x / 2)
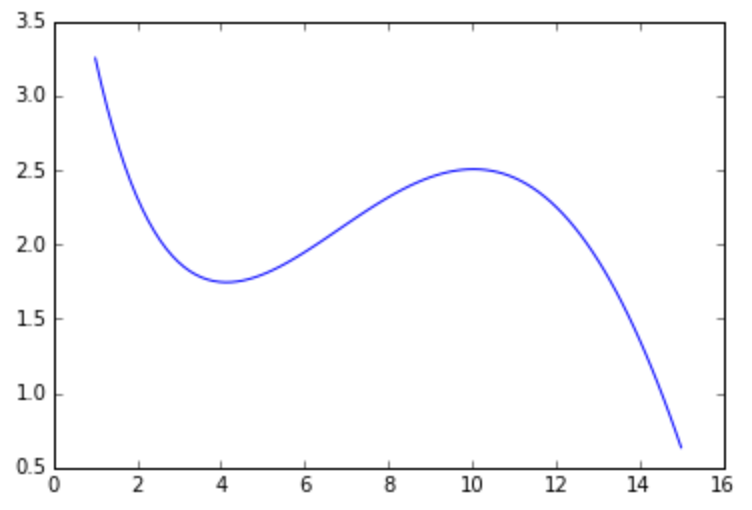
Она может описывать, например, зависимость оценок, которые выставляют
определенному сорту вина эксперты, в зависимости от возраста этого вина.
Мы хотим приблизить сложную зависимость с помощью функции из
определенного семейства. В этом задании мы будем приближать указанную
функцию с помощью многочленов.
Как известно, многочлен степени n (то есть w0 +
w1x + w2x2 + … + wnxn)
однозначно определяется любыми n + 1 различными точками, через которые
он проходит. Это значит, что его коэффициенты w0, … wn
можно определить из следующей системы линейных уравнений:
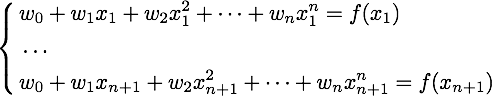
где через x1, …, xn, xn + 1 обозначены точки, через которые
проходит многочлен, а через f(x1), …, f(xn), f(xn + 1) —
значения, которые он должен принимать в этих точках.
Воспользуемся описанным свойством, и будем находить приближение функции
многочленом, решая систему линейных уравнений.
- Сформируйте систему линейных уравнений (то есть задайте матрицу
коэффициентов A и свободный вектор b) для многочлена первой степени,
который должен совпадать с функцией f в точках 1 и 15. Решите данную
систему с помощью функции scipy.linalg.solve. Нарисуйте функцию f и
полученный многочлен. Хорошо ли он приближает исходную функцию? - Повторите те же шаги для многочлена второй степени, который совпадает
с функцией f в точках 1, 8 и 15. Улучшилось ли качество
аппроксимации? - Повторите те же шаги для многочлена третьей степени, который
совпадает с функцией f в точках 1, 4, 10 и 15. Хорошо ли он
аппроксимирует функцию? Коэффициенты данного многочлена (четыре числа
в следующем порядке: w_0, w_1, w_2, w_3) являются ответом на задачу.
Округлять коэффициенты не обязательно, но при желании можете
произвести округление до второго знака (т.е. до числа вида 0.42)
Here we will discuss different ways how we can form a matrix using Python within this tutorial we will also discuss the various operation that can be performed on a matrix. we will also cover the external module Numpy to form a matrix and its operations in Python.
What is the matrix?
A matrix is a collection of numbers arranged in a rectangular array in rows and columns. In the fields of engineering, physics, statistics, and graphics, matrices are widely used to express picture rotations and other types of transformations.
The matrix is referred to as an m by n matrix, denoted by the symbol “m x n” if there are m rows and n columns.
Creating a simple matrix using Python
Method 1: Creating a matrix with a List of list
Here, we are going to create a matrix using the list of lists.
Python3
matrix = [[1, 2, 3, 4],
[5, 6, 7, 8],
[9, 10, 11, 12]]
print("Matrix =", matrix)
Output:
Matrix = [[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
Method 2: Take Matrix input from user in Python
Here, we are taking a number of rows and columns from the user and printing the Matrix.
Python3
Row = int(input("Enter the number of rows:"))
Column = int(input("Enter the number of columns:"))
matrix = []
print("Enter the entries row wise:")
for row in range(Row):
a = []
for column in range(Column):
a.append(int(input()))
matrix.append(a)
for row in range(Row):
for column in range(Column):
print(matrix[row][column], end=" ")
print()
Output:
Enter the number of rows:2 Enter the number of columns:2 Enter the entries row wise: 5 6 7 8 5 6 7 8
Time Complexity: O(n*n)
Auxiliary Space: O(n*n)
Method 3: Create a matrix using list comprehension
List comprehension is an elegant way to define and create a list in Python, we are using the range function for printing 4 rows and 4 columns.
Python3
matrix = [[column for column in range(4)] for row in range(4)]
print(matrix)
Output:
[[0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3], [0, 1, 2, 3]]
Assigning Value in a matrix
Method 1: Assign value to an individual cell in Matrix
Here we are replacing and assigning value to an individual cell (1 row and 1 column = 11) in the Matrix.
Python3
X = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
row = column = 1
X[row][column] = 11
print(X)
Output:
[[1, 2, 3], [4, 11, 6], [7, 8, 9]]
Method 2: Assign a value to an individual cell using negative indexing in Matrix
Here we are replacing and assigning value to an individual cell (-2 row and -1 column = 21) in the Matrix.
Python3
row = -2
column = -1
X[row][column] = 21
print(X)
Output:
[[1, 2, 3], [4, 5, 21], [7, 8, 9]]
Accessing Value in a matrix
Method 1: Accessing Matrix values
Here, we are accessing elements of a Matrix by passing its row and column.
Python3
print("Matrix at 1 row and 3 column=", X[0][2])
print("Matrix at 3 row and 3 column=", X[2][2])
Output:
Matrix at 1 row and 3 column= 3 Matrix at 3 row and 3 column= 9
Method 2: Accessing Matrix values using negative indexing
Here, we are accessing elements of a Matrix by passing its row and column on negative indexing.
Python3
import numpy as np
X = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
print(X[-1][-2])
Output:
8
Mathematical Operations with Matrix in Python
Example 1: Adding values to a matrix with a for loop in python
Here, we are adding two matrices using the Python for-loop.
Python3
X = [[1, 2, 3],[4, 5, 6], [7, 8, 9]]
Y = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for row in range(len(X)):
for column in range(len(X[0])):
result[row][column] = X[row][column]+ Y[row][column]
for r in result:
print(r)
Output:
[10, 10, 10] [10, 10, 10] [10, 10, 10]
Time Complexity: O(n*n)
Auxiliary Space: O(n*n)
Example 2: Adding and subtracting values to a matrix with list comprehension
Performing the Basic addition and subtraction using list comprehension.
Python3
Add_result = [[X[row][column] + Y[row][column]
for column in range(len(X[0]))]
for row in range(len(X))]
Sub_result = [[X[row][column] - Y[row][column]
for column in range(len(X[0]))]
for row in range(len(X))]
print("Matrix Addition")
for r in Add_result:
print(r)
print("nMatrix Subtraction")
for r in Sub_result:
print(r)
Output:
Matrix Addition [10, 10, 10] [10, 10, 10] [10, 10, 10] Matrix Subtraction [-8, -6, -4] [-2, 0, 2] [4, 6, 8]
Time Complexity: O(n*n)
Auxiliary Space: O(n*n)
Example 3: Python program to multiply and divide two matrices
Performing the Basic multiplication and division using Python loop.
Python3
rmatrix = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for row in range(len(X)):
for column in range(len(X[0])):
rmatrix[row][column] = X[row][column] * Y[row][column]
print("Matrix Multiplication",)
for r in rmatrix:
print(r)
for i in range(len(X)):
for j in range(len(X[0])):
rmatrix[row][column] = X[row][column] // Y[row][column]
print("nMatrix Division",)
for r in rmatrix:
print(r)
Output:
Matrix Multiplication [9, 16, 21] [24, 25, 24] [21, 16, 9] Matrix Division [0, 0, 0] [0, 1, 1] [2, 4, 9]
Time Complexity: O(n*n)
Auxiliary Space: O(n*n)
Transpose in matrix
Example: Python Program to Transpose a Matrix using loop
Transpose of a matrix is obtained by changing rows to columns and columns to rows. In other words, transpose of A[][] is obtained by changing A[i][j] to A[j][i].
Python3
X = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for row in range(len(X)):
for column in range(len(X[0])):
result[column][row] = X[row][column]
for r in result:
print(r)
Output:
[9, 6, 3] [8, 5, 2] [7, 4, 1]
Time Complexity: O(n*n)
Auxiliary Space: O(n*n)
Matrix using Numpy
Create a matrix using Numpy
Here we are creating a Numpy array using numpy.random and a random module.
Python3
import numpy as np
array = np.random.randint(10, size=(3, 3))
print(array)
Output:
[[2 7 5] [8 5 1] [8 4 6]]
Matrix mathematical operations in Python Using Numpy
Here we are covering different mathematical operations such as addition subtraction, multiplication, and division using Numpy.
Python3
x = numpy.array([[1, 2], [4, 5]])
y = numpy.array([[7, 8], [9, 10]])
print ("The element wise addition of matrix is : ")
print (numpy.add(x,y))
print ("The element wise subtraction of matrix is : ")
print (numpy.subtract(x,y))
print ("The element wise multiplication of matrix is : ")
print (numpy.multiply(x,y))
print ("The element wise division of matrix is : ")
print (numpy.divide(x,y))
Output:
The element wise addition of matrix is : [[ 8 10] [13 15]] The element wise subtraction of matrix is : [[-6 -6] [-5 -5]] The element wise multiplication of matrix is : [[ 7 16] [36 50]] The element wise division of matrix is : [[0.14285714 0.25 ] [0.44444444 0.5 ]]
Dot and cross product with Matrix
Here, we will find the inner, outer, and cross products of matrices and vectors using NumPy in Python.
Python3
X = [[1, 2, 3],[4, 5, 6],[7, 8, 9]]
Y = [[9, 8, 7], [6, 5, 4],[3, 2, 1]]
dotproduct = np.dot(X, Y)
print("Dot product of two array is:", dotproduct)
dotproduct = np.cross(X, Y)
print("Cross product of two array is:", dotproduct)
Output:
Dot product of two array is: [[ 30 24 18] [ 84 69 54] [138 114 90]] Cross product of two array is: [[-10 20 -10] [-10 20 -10] [-10 20 -10]]
Matrix transpose in Python using Numpy
To perform transpose operation in matrix we can use the numpy.transpose() method.
Python3
matrix = [[1, 2, 3], [4, 5, 6]]
print("n", numpy.transpose(matrix))
Output:
[[1 4][2 5][3 6]]
Create an empty matrix with NumPy in Python
Initializing an empty array, using the np.zeros().
Python3
a = np.zeros([2, 2], dtype=int)
print("nMatrix of 2x2: n", a)
c = np.zeros([3, 3])
print("nMatrix of 3x3: n", c)
Output:
Matrix of 2x2: [[0 0] [0 0]] Matrix of 3x3: [[0. 0. 0.] [0. 0. 0.] [0. 0. 0.]]
Slicing in Matrix using Numpy
Slicing is the process of choosing specific rows and columns from a matrix and then creating a new matrix by removing all of the non-selected elements. In the first example, we are printing the whole matrix, in the second we are passing 2 as an initial index, 3 as the last index, and index jump as 1. The same is used in the next print we have just changed the index jump to 2.
Python3
X = np.array([[6, 8, 10],
[ 9, -12, 15],
[ 12, 16, 20],
[ 15, -20, 25]])
print(X[:])
print("nSlicing Third Row-Second Column: ", X[2:3,1])
print("nSlicing Third Row-Third Column: ", X[2:3,2])
Output:
[[ 6 8 10] [ 9 -12 15] [ 12 16 20] [ 15 -20 25]] Slicing Third Row-Second Column: [16] Slicing Third Row-Third Column: [20]
Delete rows and columns using Numpy
Here, we are trying to delete rows using the np.delete() function. In the code, we first tried to delete the 0th row, then we tried to delete the 2nd row, and then the 3rd row.
Python3
a = np.array([[6, 8, 10],
[ 9, -12, 15],
[ 12, 16, 20],
[ 15, -20, 25]])
data = np.delete(a, 0, 0)
print("data after 0 th row deleted: ", data)
data = np.delete(a, 1, 0)
print("ndata after 1 st row deleted: ", data)
data = np.delete(a, 2, 0)
print("ndata after 2 nd row deleted: ", data)
Output:
data after 0 th row deleted: [[ 9 -12 15] [ 12 16 20] [ 15 -20 25]] data after 1 st row deleted: [[ 6 8 10] [ 12 16 20] [ 15 -20 25]] data after 2 nd row deleted: [[ 6 8 10] [ 9 -12 15] [ 15 -20 25]]
Add row/columns in the Numpy array
We added one more column at the 4th position using np.hstack.
Python3
ini_array = np.array([[6, 8, 10],
[9, -12, 15],
[15, -20, 25]])
column_to_be_added = np.array([1, 2, 3])
result = np.hstack((ini_array, np.atleast_2d(column_to_be_added).T))
print("nresultant arrayn", str(result))
Output:
resultant array [[ 6 8 10 1] [ 9 -12 15 2] [ 15 -20 25 3]]
На уроке рассматриваются алгоритмы работы с двумерными массивами в Python: создание матрицы, инициализация элементов, вывод, обработка элементов матрицы
Создание, вывод и ввод матрицы в Питоне
- Таким образом, получается структура из вложенных списков, количество которых определяет количество строк матрицы, а число элементов внутри каждого вложенного списка указывает на количество столбцов в исходной матрице.
- Вывод матрицы можно осуществить одним оператором, но такой простой способ не позволяет выполнять какой-то предварительной обработки элементов:
Для работы с матрицами в Python также используются списки. Каждый элемент списка-матрицы содержит вложенный список.
Рассмотрим пример матрицы размера 4 х 3:
matrix = [[-1, 0, 1], [-1, 0, 1], [0, 1, -1], [1, 1, -1]]
Данный оператор можно записать в одну строку:
matrix = [[-1, 0, 1], [-1, 0, 1], [0, 1, -1], [1, 1, -1]]
Результат:

- способ:
- способ:
1 2 3 4 5 |
def printMatrix ( matrix ): for i in range ( len(matrix) ): for j in range ( len(matrix[i]) ): print ( "{:4d}".format(matrix[i][j]), end = "" ) print () |
В примере i – это номер строки, а j – номер столбца;
len(matrix) – число строк в матрице.
1 2 3 4 5 |
def printMatrix ( matrix ): for row in matrix: for x in row: print ( "{:4d}".format(x), end = "" ) print () |
Внешний цикл проходит по строкам матрицы (row), а внутренний цикл проходит по элементам каждой строки (x).
1 2 3 4 |
from random import randint n, m = 3, 3 a = [[randint(1, 10) for j in range(m)] for i in range(n)] print(a) |
Обработка элементов двумерного массива
Нумерация элементов двумерного массива, как и элементов одномерного массива, начинается с нуля.
Т.е. matrix[2][3] — это элемент третьей строки четвертого столбца.
Пример обработки элементов матрицы:
Найти произведение элементов двумерного массива.
✍ Решение:
1 2 3 4 5 |
p = 1 for i in range(N): for j in range(M): p *= matrix[i][j] print (p) |
Пример:
Найти сумму элементов двумерного массива.
✍ Решение:
Более подходящий вариант для Python:
1 2 3 4 |
s = 0 for row in matrix: s += sum(row) print (s) |
Для поиска суммы существует стандартная функция sum.
Задание Python 8_0:
Получены значения температуры воздуха за 4 дня с трех метеостанций, расположенных в разных регионах страны:
| Номер станции | 1-й день | 2-й день | 3-й день | 4-й день |
|---|---|---|---|---|
| 1 | -8 | -14 | -19 | -18 |
| 2 | 25 | 28 | 26 | 20 |
| 3 | 11 | 18 | 20 | 25 |
Т.е. запись показаний в двумерном массиве выглядела бы так:
| t[0][0]=-8 | t[0][1]=-14 | t[0][2]=-19 | t[0][3]=-18 |
| t[1][0]=25 | t[1][1]=28 | t[1][2]=26 | t[1][3]=20 |
| t[2][0]=11 | t[2][1]=18 | t[2][2]=20 | t[2][3]=25 |
- Распечатать температуру на 2-й метеостанции за 4-й день и на 3-й метеостанции за 1-й день.
- Распечатать показания термометров всех метеостанций за 2-й день.
- Определить среднюю температуру на 3-й метеостанции.
- Распечатать, в какие дни и на каких метеостанциях температура была в диапазоне 24-26 градусов тепла.
Задание Python 8_1:
Написать программу поиска минимального и максимального элементов матрицы и их индексов.
Задание Python 8_2:
Написать программу, выводящую на экран строку матрицы, сумма элементов которой максимальна.
for i in range(N): # работаем с matrix[i][i]
for i in range(N): # работаем с matrix[i][N-1-i]
Пример:Переставить 2-й и 4-й столбцы матрицы. Использовать два способа.
✍ Решение:
for i in range(N): c = A[i][2] A[i][2] = A[i][4] A[i][4] = c
for i in range(N): A[i][2], A[i][4] = A[i][4], A[i][2]
Задание Python 8_3:
Составить программу, позволяющую с помощью датчика случайных чисел сформировать матрицу размерностью N. Определить:
In this tutorial, we will learn to create a n*n (n by n) matrix in Python. Where n is the number of rows or columns. n*n matrix has an equal number of rows and columns and is a square matrix.
For creating a matrix in Python, we need multi-dimensional data structures. Python does not have a built-in type for matrices but we can treat a nested list or list of a list as a matrix. The List is an ordered set of elements enclosed in square brackets [ ]. Each element in the list will be then treated as a row of a matrix. For example,
Input: N=2
Output: [ [1,2], [3,4] ]
To create a matrix, we require nested lists, there are different ways for creating a nested list in Python.
- By using list comprehension
-
By using next() and itertools.count() Function
We will be using these methods for creating a n*n matrix.
Approach 1: list comprehension
We will use list comprehension to store rows and columns in the list. List comprehension is a shorter syntax for writing concise codes in Python.
Algorithm
Follow the algorithm to understand the approach better.
Step 1– Define the dimension of a matrix
Step 2– Use a list comprehension to create a matrix having the defined dimensions
Step 3– Print the resulting matrix
Python Program 1
Look at the program to understand the implementation of the above-mentioned approach. This program will work for a 4×4 matrix. We have used .format() to print the values where the placeholder is mentioned.
n = 4
matrix = [list(range(1 + n * i, 1 + n * (i + 1))) for i in range(n)]
print("The created matrix of {} * {}: ".format(n,n))
for m in matrix:
print(m)The created matrix of 4 * 4:
[1, 2, 3, 4]
[5, 6, 7, 8]
[9, 10, 11, 12]
[13, 14, 15, 16]
Approach 2: next() and itertools.count()
In our program, we will use the count function to start the count of numbers and the next function will create the consecutive sublists. We will use list comprehension to handles the matrix.
Algorithm
Follow the algorithm to understand the approach better.
Step 1-Import itertools package
Step 2– Define the dimension of the matrix
Step 3– Use count() to start the count of the number
Step 4– Use a list comprehension to store rows and columns in a new list
Step 5-Use next() for creating sublists and store the matrix in the list
Step 6– Print the resulting matrix
Python Program 2
Look at the program to understand the implementation of the above-mentioned approach. This program will work for a 5X5 matrix.
import itertools
# initializing N
n = 5
temp = itertools.count(1)
matrix = [[next(temp) for i in range(n)] for i in range(n)]
print("The created matrix of {} * {}: ".format(n,n))
for m in matrix:
print(m)The created matrix of 5 * 5:
[1, 2, 3, 4, 5]
[6, 7, 8, 9, 10]
[11, 12, 13, 14, 15]
[16, 17, 18, 19, 20]
[21, 22, 23, 24, 25]
Conclusion
In this tutorial, we have learned two ways for creating square matrices in Python. We have learnt how to use list comprehension for creating a square matrix. We have also seen how to use count() and next() function in itertools package to create a matrix in Python.



