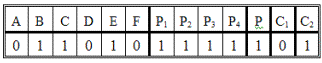Как составить легенду для клаузы

Дискретная математика:
логика, группы, графы, фракталы

Акимов О.Е.

1.4. Введение в логику высказываний

Примеры решения задач

1. Доказать методом натурального исчисления истинность следующей клаузы:

B → (C → A), B → D, C, D ⇒ A.

Доказательство:

1. Р ⇒

B

→ D, (Р₂, БП)
2. Р,

B

⇒ D, (1, УИ)
3. Р,

B

⇒

D

, (Р₄, БП)
4. Р,

B

⇒ 0, (2, 3, УО)
5. Р ⇒ B → (C → A), (Р₁, БП)
6. Р ⇒ C → A, (4, 5, УИ)
7. Р ⇒ A. (6, Р₃, БП, УИ).

2. Доказать аксиоматическим методом истинность клаузы:

A, B → D, C → D, A → (B ∨ C) ⇒ D.

Доказательство:

1. B → D, C → D, B ∨ C ⇒ D,
2.

B

∨ D,

C

∨ D, B ∨ C ⇒ D,
3. (

B

∧

C

) ∨ D, B ∨ C ⇒ D,
4. (B ∨ C) → D, B ∨ C ⇒ D,
5. B ∨ C, D ⇒ D.

3. Доказать методом Вонга истинность следующей клаузы:

B → (D → C), D, C → (A ∨ B) ⇒ A ∨ B.

Доказательство:

1. B ∨

D

∨ C, D,

C

∨ A ∨ B ⇒ A ∨ B,
1.1. B, D,

C

∨ A ∨ B,

A

⇒ B,
1.2.

D

, D,

C

∨ A ∨
B, A ⇒ B,
1.3. C, D,

C

∨ A ∨ B ⇒ A ∨
B,
1.3.1. C, D,

C

⇒ A ∨ B,
1.3.1. C, D, A,

A

⇒ B,
1.3.1. C, D, B,

A

⇒ B.

4. Доказать методом резолюций истинность следующей клаузы:

A → B, C → D, B → E, D → F, E → F, A → C ⇒
A.

Доказательство:

A

∨ B,

C

∨ D,

B

∨ E,

D

∨ F,

E

∨

F

,

A

∨ C, A ⇒ 0.

1.

C

∨ F, (Р₂, Р₄)
2.

B

∨

F

, (Р₃, Р₅)
3.

A

∨

F

, (2, Р₁)
4.

A

∨ F,(1, Р₆)
5.

A

, (3, 4) 
6. 0. (6, Р₇)

5. Пусть задана система аксиом:

А₁. 1 ⇒ А → (В → А),
А₂. 1 ⇒ (А → (В → С)) → ((А → В) → (А → С)),
А₃. 1 ⇒ (А → В) → ((А →

В

) →

А

);

и правило отделения (modus ponens — МР):

A, А → В ⇒ В.

С помощью этих аксиом и правила МР доказать справедливость закона рефлексивности:

1 ⇒ A → А.

Доказательство (символы «1 ⇒ » здесь и в следующем примере писать не будем):

1. A → ((А → A) → A), (А₁)
2. (А → ((А → A) → A)) → ((А → (А → A)) → (А → A)), (А₂)
3. (А → (А → A)) → (А → A), (1, 2, МР)
4. А → (А → A), (А₁)
5. А → A. (3, 4, МР)

6. С помощью системы аксиом предыдущего примера доказать клаузу:

X, Y, Z → X, S → (Y ∨ Z), (T ∨ U) → S ⇒
T.

Доказательство:

1. (Z → X) → ((Z →

X

) →

Z

), (А₁)
2. (Z →

X

) →

Z

, (1, Р₃, МР)
3.

X

→ (Z →

X

), (А₁)
4. Z →

X

, (3, Р₁, МР)
5. (S → (

Y

→ Z)) → ((S →

Y

) → (S → Z)), (А₂)
6. (S →

Y

) → (S → Z), (5, Р₄, МР)
7.

Y

→ (S →

Y

), (А₁)
8. S →

Y

, (7, Р₂, МР)
9. S → Z, (6, 8, МР)
10. (S → Z) → ((S →

Z

) →

S

), (А₃)
11. (S →

Z

) →

S

, (9, 10, МР)
12.

Z

→ (S →

Z

), (А₁)
13.

Z

, (2, 4, МР)
14. S →

Z

, (12, 13, МР)
15.

S

, (11, 14, МР)
16. (T ∨ U) → S = T → S, U → S, (Р₅)
17. (T → S) → ((T →

S

) →

T

), (А₃)
18. (T →

S

) →

T

, (16, 17, МР)
19.

S

→ (T →

S

), (А₁)
20. T →

S

, (15, 19, МР)
21.

T

. (18, 20, МР)

7. Составить легенды для приведенных ниже четырех клауз.

Клауза 1: A ~ C, C ~ E, E → D, D → B ⇒ A → B.

A — Падение авторитета власти.
B — Политики, не способные управлять страной.
C — Нарастание анархии в обществе.
D — Высказывание абсурдных идей.
E — Появление безответственных политиков.

«Падение авторитета власти происходит тогда и только тогда, когда нарастает анархия в обществе (A ~ C). Нарастание анархии в обществе равносильно появлению на политической арене безответственных политиков (C ~ E). Появление подобных политиков приводит к тому, что они высказывают абсурдные идеи (E → D). Высказывание политиками таких идей демонстрирует неспособность их управлять страной (D → B). Итак, падение авторитета власти приводит к появлению политиков, не способных управлять страной (A → B)».

Клауза 2: A → B, B → E, A → C, C → D, D → F, E ∧ F ⇒ A.

«Если человек занимается спортом (A), то он хочет быть здоровым (B). Хорошее здоровье (B) ведет к счастливой жизни (E). Кроме того, если человек занимается спортом (A), то он, как правило, стремится достичь высоких спортивных результатов (C). Наличие высоких результатов (C) позволяет одерживать победы на соревнованиях (D). Победы на соревнованиях (D) влекут за собой всеобщее признание (F). Однако человек не хочет жить счастливо и иметь всеобщее признание (E ∧ F). Значит, он не станет заниматься и спортом (A)».

Клауза 3: J → H, K → H, I → J, H → I, H ⇒ J ∧ K.

«Если знать язык программирования (J), то можно составить рабочую программу (H). Рабочую программу можно также получить (H) при наличии знакомого программиста (K). Овладеть языком программирования (J) можно, обучаясь в институте (I). Если программа работает (H), то ее написал выпускник такого института (I). Но программа не работает (H). Это говорит о том, что желающий получить правильный результат не знает языка программирования (J) и не имеет знакомых программистов (K)».

Клауза 4: A → B, C → D, B ∧ D → E, A, E ⇒ C.

«Все живое способно чувствовать (A → B). Всякое материальное тело занимает определенный объем (C → D). Если нечто занимает пространственный объем и способно чувствовать, то это нечто есть ни что иное, как живой организм (B ∧ D → E). Пусть существует нечто живое (A), но не являющееся организмом (E). Тогда следует вывод, что это нечто нематериально
(C)».

8. Выше приведены легенды. Запишем клаузы, отвечающие содержанию этих легенд, для чего сформулируем необходимые посылки и два следствия: одно истинное, другое ложное. С помощью таблицы истинности найдем МНФ, минимальное и все трансверсальные покрытия (последнее задание выполнено только для варианта 21).

Для варианта 21 можно предложить следующую клаузу:

A ~ B, C → A, D → B, C → E, E ⇒ C → B.
A — Где-то что-то убыло.
B — Где-то что-то прибыло.
C — “Черная дыра” существует.
D — “Белая дыра” существует.
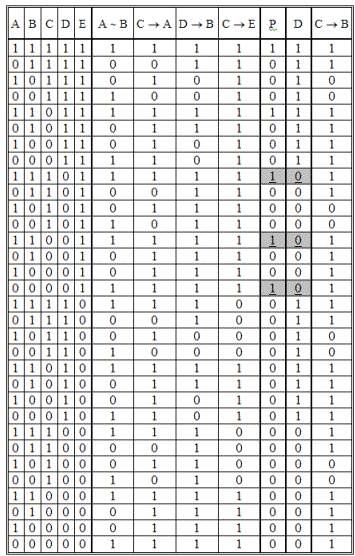
E — Невозможность ничего увидеть.

Исходную легенду допустимо трансформировать в близкую по смыслу и составить таблицу истинности (табл. 1.23): «Если в одном месте что-то убудет, то в другом что-то непременно прибудет, и наоборот (A ~ B). Если существует черная дыра, то в нее все проваливается, т.е. в ее окрестностях что-то убывает (C → A). Если существует белая дыра, то из нее в окружающее пространство должно прибывать вещество (D → B). Если существует черная дыра, то ее невозможно увидеть, так как она не излучает свет (C → E). Астроном ничего не увидел (E). Итак, белая дыра существует(D)». Это — ложное умозаключение. Истинным же заключением является, например, следующее: «Если существует черная дыра, то где-то в пространстве вселенной должно непременно появляться вещество (C → B)».

Таблица 1.23

Из табл. 1.23 видно, что три единицы обобщенной посылки (Р) не покрываются единицами ложного следствия (D); единицы же истинного следствия (C → B) целиком накрывают единицы обобщенной посылки. По табл. 1. 23 составим СДНФ:

A, B, C, D, E; A, B,

C

, D, E; A, B, C,

D

, E; A, B,

C

,

D

, E;

A

,

B

,

C

,

D

, E.

После преобразований получим следующую МДФ:

A, B, D, E; A, B, C, D, E.

Трансверсальные покрытия:

A; B, C, D, E     A, B; C, D, E     A, B, E; C, D.

Минимальное покрытие: E.

Для варианта 22 можно составить следующую клаузу:

A → B, B → C, E → (B → D), D → F ⇒
(B ∧ A ∧ E) → F.

Введем следующие обозначения:

A — Возникновение перепада напряжения в сети.
B — Перегорание предохранителя.
C — Необходимость замены предохранителя.
D — Телевизор работает нормально.
E — Телевизор подключен к сети питания.
F — Я смотрю “Новости”.

«Если в сети был перепад напряжения, то сгорит предохранитель
(P₁ = A → B). Если предохранитель сгорел, то необходима его замены
(P₂ = B → C). Если телевизор включен в сеть, то он работает нормально при условии целостности предохранителя (P₃ = E → (B → D)). Если телевизор работает нормально, я увижу “Новости”
(P₄ = D → F). Я увижу “Новости” при условии отсутствия перепада напряжения и подключения телевизора к сети питания (C₁ = (A ∧ E) → F)». 

Данное следствие является ложным. Истинным же следствием будет: «Я увижу “Новости” при условии целостности предохранителя, отсутствия перепада напряжения в сети и подключения телевизора к сети питания (C₂ = (B ∧ A ∧ E) → F)».

Выделим ту строку табл. 1.24, для которой обобщенная посылка (Р) и истинное следствие (C₂) принимают значения единицы, а ложное следствие (C₁) — значение нуля.

Таблица 1.24

Для варианта 23 допустимо составить следующую клаузу:

A → B, B → C, C → D, D → E ⇒ A → E.

A — Работа выполнена. 
B — Отпуск на рыбалку. 
C — Взять на рыбалку сына. 
D — Рыбалку провести с лодкой.
E — На рыбалку поедут все вместе.

«Если работа выполнена, то начальство отпустит на рыбалку (A → B). Если отпустят на рыбалку, то обязательно возьмут на нее и сына (B → C). Если берут сына, значит надо брать лодку (C → D). Если брать с собой лодку, то поедут все вместе (D → E). Таким образом, если работа выполнена, то все вместе едут на рыбалку (A → E)». 

Данное следствие является истинным. Ложным следствием является, очевидно, такое: «Если работа сделана, то все вместе на рыбалку не едут (A → E)».

Для варианта 24 составим следующую клаузу:

A → (B ∧ C), C → D, B → (A → E), D → (B ∨ A) ⇒ (A ∧ B) → C.

A — Уменьшение температуры.
B — Снижение давления.
C — Уменьшение объема.
D — Снижение скорости.
E — Падение уровня.

«Уменьшение температуры приводит к снижению давления и уменьшению объема (A → (B ∧ C)). Увеличение объема приводит к росту скорости потока (C → D). Повышение давления приводит к падению уровня, если при этом уменьшать температуру (B → (A → E)). Снижение скорости приводит к уменьшению давления или росту температуры (D → (B ∨ A)). Технолог Иванов рассудил так: “Мне надо повысить давление при одновременном снижении скорости потока, поэтому я должен увеличить объем и температуру” ((A ∧ C) → (B ∧ D))». 

Данное умозаключение является ложным. Истинным рассуждением будет, например, такое: «Уменьшение температуры и увеличение давления ведут к уменьшению объема
((A ∧ B) → C)».

Для варианта 25 составим клаузу:

A ∨ B ∨ C, (C ∧ D) → E, (A ∨ B) →

E

, C → D, ⇒ C → E.

A — Надеть брезентовые штаны.
B — Надеть шерстяное платье.
C — Надеть пиджак и юбку с разрезом.
D — Взять с собой сумку.
E — Великолепно смотрится.

«Я могу надеть на себя брезентовые штаны, или шерстяное платье, или пиджак и юбку с разрезом (A ∨ B ∨ C). Я буду выглядеть великолепно, если надену пиджак и юбку с разрезом и при этом возьму с собой сумку ((C ∧ D) → E). И наоборот, я буду выглядеть ужасно, если надену на себя брезентовые штаны или шерстяное платье ((A ∨ B) → E). Однако сумку надо брать обязательно, если надеть пиджак и юбку с разрезом (C → D). Итак, чтобы выглядеть великолепно, я выбираю последнее, т.е. надену на себя пиджак и юбку с разрезом (C → E)».

Данное заключение является истинным. Ложным может быть, например, такое: «Чтобы выглядеть великолепно, нужно надеть на себя брезентовые штаны (A → E)».

1. С помощью средств предыдущего примера доказать клаузу:

-X, -Y, Z -> X, S -> (Y v Z), (Т
v U) -> S => –Т

Доказательство:

1. Составить легенды для приведенных ниже четырех клауз.

Клауза 1:А ~ С, С ~ Е, Е -> D,
D -> В => А -> В

А — Падение авторитета власти.

В — Политики, не способные управлять
страной.

С — Нарастание анархии в обществе.

D—Высказывание абсурдных
идей.

Е — Появление безответственных
политиков.

«Падение авторитета власти происходит
тогда и только тогда, когда нарастает
анархия в обществе (А ~ С). Нарастание
анархии в обществе равносильно появлению
на политической арене безответственных
политиков (С ~ Е). Появление подобных
политиков приводит к тому, что они
высказывают абсурдные идеи (Е -> D).
Высказывание политиками таких идей
демонстрирует неспособность их управлять
страной (D-> В). Итак,
падение авторитета власти приводит к
появлению политиков, не способных
управлять страной (А -> В)».

Клауза 2:А -> В, В -> Е, А ->
С, С -> D, D
-> F, -(Е & F)
=> -А

«Если человек занимается спортом (А),
то он хочет быть здоровым (В). Хорошее
здоровье (В) ведет к счастливой жизни
(Е). Кроме того, если человек занимается
спортом (А), то он, как правило, стремится
достичь высоких спортивных результатов
(С). Наличие высоких результатов (С)
позволяет одерживать победы на
соревнованиях (D). Победы
на соревнованиях (D) влекут
за собой всеобщее признание (F)
. Однако, человек не хочет жить счастливо
и иметь всеобщее признание -(Е лF).
Значит, он не станет заниматься и спортом
(-А)».

Клауза 3:J->
Н, К -> Н, I -> J,
Н -> I, -Н => –J
& -К

«Если знать язык программирования (J),
то можно составить рабочую программу
(Н). Рабочую программу можно также
получить (Н) при условии наличия знакомого
программиста (К). Овладеть языком
программирования (J) можно,
обучаясь в институте (I).
Если программа работает (Н), то ее написал
выпускник такого института (I).
Но программа не работает (-Н). Это говорит
о том, что желающий получить правильный
результат не знает языка программирования
(-J) и не имеет знакомых
программистов (-К)

Клауза 4: А -> В, С -> D,
В & D -> Е, А, –E
=> -С.

«Все живое способно чувствовать (А ->
В). Всякое материальное тело занимает
определенный объем (С -> D).
Если нечто занимает пространственный
объем и способно чувствовать, то это
нечто есть ни что иное, как живой
организм_(В лD-> Е). Пусть
существует нечто живое (А), но не являющееся
организмом (Е). Тог­да следует вывод,
что это нечто нематериально (-С)».

1. 8.

Выше приведены легенды. Запишем клаузы,
отвечающие тексту или кон­тексту этих
легенд, для чего сформулируем необходимые
посылки и два следст­вия: одно истинное,
другое ложное. С помощью таблицы
истинности найдем МНФ, минимальное и
все трансверсальные покрытия (последнее
задание вы­полнено только для варианта
21).

21. Если в одном месте что-то убудет, то
в другом месте что-то прибудет — это
истина, не требующая доказательства.
Но есть такая теория, которая утверждает:
где-то в далеком космосе существуют
«черные дыры», куда все проваливается,
но оттуда ничего не появляется. Эта
теория ничего не говорит о существовании
«белых дыр», которые действовали бы
противоположно «черным». Один ино­странный
астрономический журнал сообщил координаты
«черной дыры». Рос­сийский астроном
Иванов направил туда свой мощный телескоп
и ничего не об­наружил, “Так-так, —
сказал Иванов, — но «белую дыру» я все
же открою”.

Для варианта 21 можно предложить следующую
клаузу:

А ~ В, С -> A, D
-> В, С -> Е, Е => С -> В

А—Где-то что-то убыло

В—Где-то что-то прибыло

С—“Черная дыра ” существует

D—“Белая
дыра”существует

Е—Невозможность ничего увидеть

Исходную легенду допустимо трансформировать
в близкую по смыслу и со­ставить
таблицу истинности (табл. 1.23):

«Если в одном месте что-то убудет, то в
другом что-то непременно прибудет, и
наоборот (А ~ В). Если существует
“черная дыра”, то в нее все
проваливается, то есть в ее окрестностях
что-то убывает (С -> А). Если существует
“белая дыра”, то из нее в окружающее
пространство должно прибывать вещество
(D -> В). Если
существует “черная дыра”, то ее
невозможно увидеть, так как она не
излучает свет (С -> Е). Астроном
ничего не увидел (Е). Итак, “белая
дыра” существует (D).»
Это — ложное умозаключение. Истинным
же заключением является, на­пример,
следующее: «Если существует “черная
дыра”, то где-то в пространстве
вселенной должно непременно появляться
вещество (С -> В)».

Из табл. 1.23 видно, что три единицы
обобщенной посылки (Р) не покрывают­ся
единицами ложного следствия (D);
единицы же истинного следствия (С ->
В) целиком накрывают единицы обобщенной
посылки. По табл. 1.23 составим СДНФ:

А, В, С, D, Е; А, В, С,D,
Е; А, В, С,D, Е;

А, В, С, D, Е; А, В, С,D,
Е .

После преобразований получим следующую
МДФ:

А, В, D, Е; А, В, С,D,E. Трансверсальные покрытия:

А; В, С, D, Е А, В; С,D,
Е А, В, Е; С,D.

Минимальное покрытие: Е .

l.i

Таблица 1

Для варианта 22

22. Если в цепи будет большой перепад
напряжения, то сгорит предохрани­тель,
что повлечет за собой необходимость
его замены. При целом предохрани­теле
телевизор, конечно, будет работать, но
только если он включен в сеть пита­ния.
Если телевизор работает нормально, то
я увижу сегодняшние «Новости». Итак, я
смотрю телевизионные «Новости» при
условии отсутствия перепада на­пряжения
и подключения телевизора к сети питания.

можно составить следующую клаузу:

А -> В, В -> С, Е -> (-В -> D),
D -> F
=> (-В & -А & Е) -> F

Введем следующие обозначения:

А—Возникновение перепада
напряжения в сети

В—Перегорание предохранителя

С—Необходимость замены
предохранителя

D—Телевизор работает
нормально

Е—Телевизор подключен к сети
питания

F—Я смотрю новости

«Если в сети был большой перепад
напряжения, то сгорит предохранитель
(А -> В). Если предохранитель сгорел,
необходима его замена (В -> С). Если
теле­визор включен в сеть, то телевизор
работает нормально при условии
целостно­сти предохранителя (Е ->
(-В -> D)). Если
телевизор работает нормально, я увижу
“Новости” (D ->
F). Я увижу “Новости”
при условии отсутствия перепада
напря­жения и подключения телевизора
к сети питания((-А & Е) -> F)).
Данное следст­вие яатяегся ложным.
Истинным же следствием будет: «Я увижу
“Новости” при условии целостности
предохранителя, отсутствия перепада
напряжения в сети и подключения телевизора
к сети питания ((-В & -А & Е) -> F)».
Выделим ту строку табл. 1.24, для которой
обобщенная посылка (Р) и истинное
следствие ((-В & -А & Е) -> F)
принимают значения единицы, а ложное
следствие ((-А & Е) -> F)
— зна­чение нуля.

Таблица 1.24

Для варианта 23

23. «Иван Иваныч, можно?» — «Входи,
Петров. Ну, сделал, что я тебя про­сил?»
— «Видите ли… Если бы Вы немного
прибавили…» — «Ты что, Петров! Си­доров
за эту же работу берет в два раза меньше».
— «Сидоров и сделал бы ее в два раза
хуже. Я же работаю с личным клеймом. И
потом, у меня семья — сами знае­те».
— «ладно, проси что хочешь, но денег у
меня нет». — «А как сделаю, на ры­балку
отпустите?» — «Договорились, только ты
моего Вовку с собой возьми, а то он тут
с какой-то подозрительной компанией
спутался». — «Если с Вовкой, то на Вашей
лодке». — «Вот хитрец! Хорошо, поедем
все вместе. Мне тоже не мешало бы
проветриться. Ты дело только сделай».

допустимо составить следующую простую
клаузу:

А -> В, В -> C, С
-> D, D
-> Е => А -> Е

«Если работа выполнена, то начальство
отпустит на рыбалку (А -> В). Если
отпу­стят на рыбалку, то обязательно
возьмут на нее и сына (В -> С). Если
берут сына, значит надо брать лодку (С
-> D). Если брать с
собой лодку, то поедут все вместе (D
-> Е). Таким образом, если работа
выполнена, то все вместе едут на рыбалку
(А -> Е)». Данное следствие является
истинным. ложным следствием
является,_очевидно, такое: «Если работа
сделана, то все вместе на рыбалку не
едут (А -> -Е)».

Для варианта 24

составим следующую клаузу:

А -> (В & С), С -» D, В ->
(А -> Е),D-> (ВvА) => (А & В) -> С. А — Уменьшение
температуры.

В — Снижение давления. D— Снижение скорости.

С — Уменьшение объема. Е —
Падение уровня.

«Уменьшение температуры приводит к
снижению давления и уменьшению объема
(А -> (В & С)). Увеличение объема приводит
к росту скорости потока (С -> D).
Повышение_давления приводит к падению
уровня, если при этом уме­ньшать
температуру (В -> (А -> Е)). Снижение_скорости
приводит к уменьшению давления или
росту температуры (D->
(ВvА)). Технолог Иванов
рассудил так: “Мне надо повысить
давление при одновременном снижении
скорости потока, поэтому я должен
увеличить объем и температуру” ((А &
С) -> (В &D))». Данное
умозаключение является ложным. Истинным
рассуждением будет, например, та­кое:
«Уменьшение температуры и увеличение
давления ведут к уменьшению

Для варианта 25 составим клаузу:

AvВvС, (С &D) -> Е, (AvВ) -» Е, С ->D,
=з- С -> Е.

А — Надеть брезентовые штаны. D— Взять с собой сумку.

В — Надеть шерстяное платье. Е —
Великолепно смотрится.

С — Надеть пиджак и юбку с разрезом.

«Я могу надеть на себя брезентовые штаны
или шерстяное платье или пидж и юбку с
разрезом (AvВvС). Я буду выглядеть
великолепно, если надену пи жак и юбку
с разрезом и при этом возьму с собой
сумку ((С &D) -+ Е). И наоб
рот, я буду выглядеть ужасно, если надену
на себя брезентовые штаны или ше стяное
платье ((AvВ) -> Е). Однако сумку надо брать
обязательно, если наде пиджак и юбку с
разрезом (С ->D). Итак,
чтобы выглядеть великолепно я выб раю
последнее, т.е. надену на себя пиджак и
юбку с разрезом (С -» Е)». Дани заключение
является истинным. ложным может быть,
например, такое: «Что! выглядеть
великолепно, нужно надеть на себя
брезентовые штаны (А -> Е)»,

Помогите пожалуйста написать клаузу

Запишите с использованием 4—6 различных букв клаузу, отвечающую тексту или контексту вашей легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, другое ложное.

Современный футбол — это надежная защита, хорошая скорость, напористая атака и убедительная результативность. Матвеев мне результативность обеспечит, но голы он забивает только по вдохновению, когда складывается игра. Без Федотова такой игры не получится. Он видит поле, чувствует, где находиться, но бегать не может. Скорость команде сообщит Комаров, xoтя может развалить всю защиту. Попробовать Петрова в обороне, но в паре с Матвеевым он не играет. Квасов умеет блокировать бомбардировку противника, но левой у него не получается. Надо ставить Земерова, чтобы левый край прикрыл. Однако Земеров в последнее время точный пас отдать не может. Ну нет команды! Завтра встречу точно проиграем.

Сообщения без ответов | Активные темы | Избранное

	Составление клаузы 28.01.2011, 14:55
21/01/11 53	Запишите с использованием 4 – 6 различных букв клаузу, отвечающую содержанию легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, другое ложное. С помощью таблицы истинности найдите МНФ, минимальное и все трансверсальные покрытия. В одной старой легенде рассказывается, что греческий драматург Софокл погиб при очень странных обстоятельствах. На его лысый череп орел сбросил камень, приняв его за яйцо. Если бы Софокл не сочинял трагедии, то он не уединялся бы в горах и остался бы жить до своей естественной кончины. Он мог бы сочинять свои трагедии в горах при наличии волос на голове или при отсутствии там этих странных птиц. я попыталась записать клаузу.. А – сочиняет трагедии B – уединяется в горах C – есть волосы на голове D – орлов нет E – жив не знаю правильно это или нет

Gortaur	Re: Составление клаузы 28.01.2011, 15:01
26/12/08 1813 Лейден	Это по логике такое проходят? У нас она скучнее велась… и трагедии были другого рода.

Di081	Re: Составление клаузы 28.01.2011, 15:03
21/01/11 53	да по логике)) а у нас вот так весело))) только мне что-то не очень смешно

Di081	Re: Составление клаузы 28.01.2011, 19:32
21/01/11 53	Неужели этот вопрос поставил людей из форума в тупик.. сомневаюсь — Пт янв 28, 2011 20:06:18 — Запишите с использованием 4 – 6 различных букв клаузу, отвечающую содержанию легенды, для чего сформулируйте необходимые посылки и два следствия: одно истинное, другое ложное. С помощью таблицы истинности найдите МНФ, минимальное и все трансверсальные покрытия. В одной старой легенде рассказывается, что греческий драматург Софокл погиб при очень странных обстоятельствах. На его лысый череп орел сбросил камень, приняв его за яйцо. Если бы Софокл не сочинял трагедии, то он не уединялся бы в горах и остался бы жить до своей естественной кончины. Он мог бы сочинять свои трагедии в горах при наличии волос на голове или при отсутствии там этих странных птиц. я попыталась записать клаузу.. А – сочиняет трагедии B – уединяется в горах C – есть волосы на голове D – орлов нет E – жив не знаю правильно это или нет Тут скорее или будет

Модераторы: Модераторы Математики, Супермодераторы