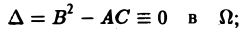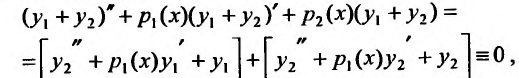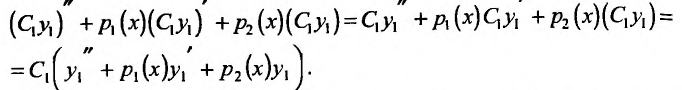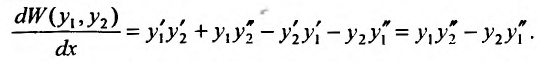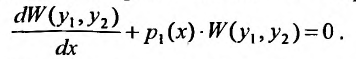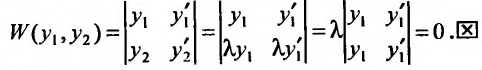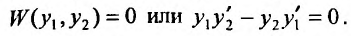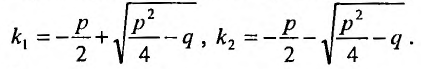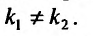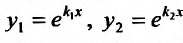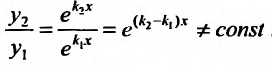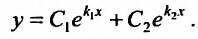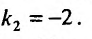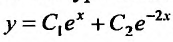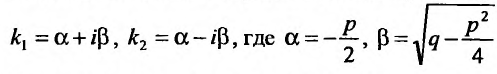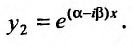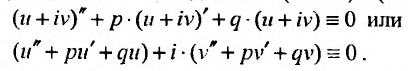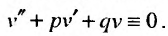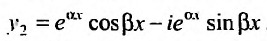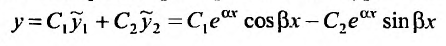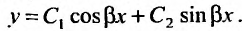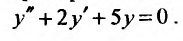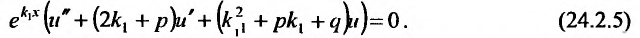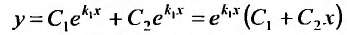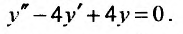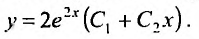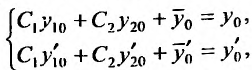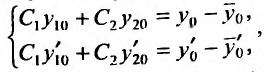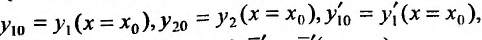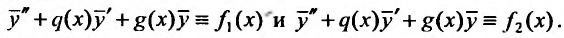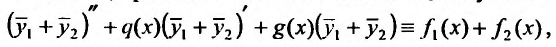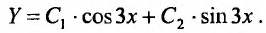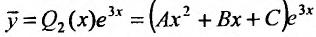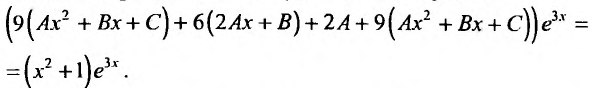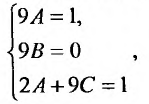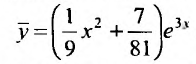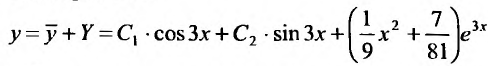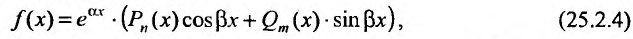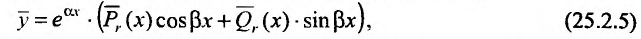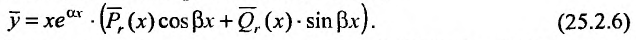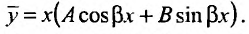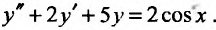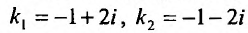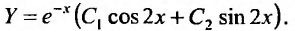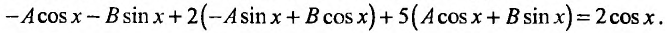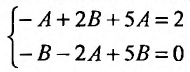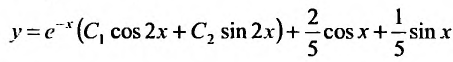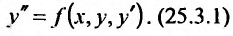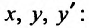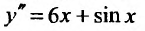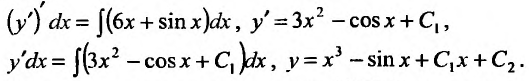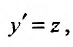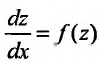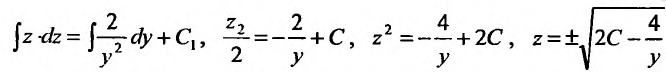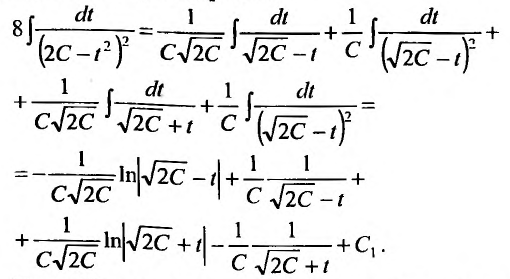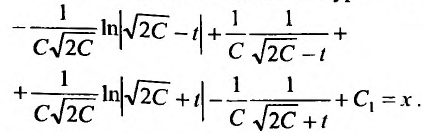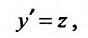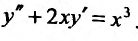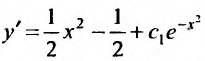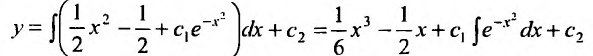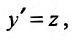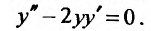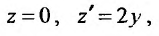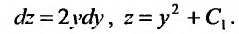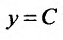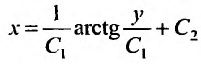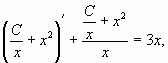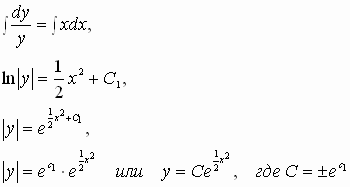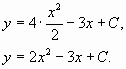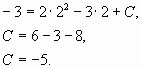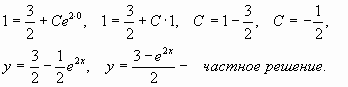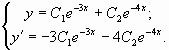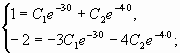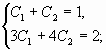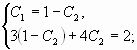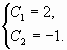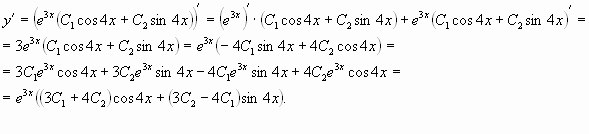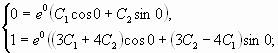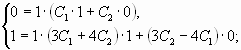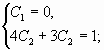Заказать задачи по любым предметам можно здесь от 10 минут
Как найти общее и частное решение линейных дифференциальных уравнений
СОДЕРЖАНИЕ ТЕКУЩЕЙ СТАТЬИ
- Линейное ДУ первого порядка
-
- Метод Бернулли
- Метод Лагранжа (вариация произвольной постоянной)
- Линейное ДУ второго порядка
-
- Метод подбора по правой части
- Метод Лагранжа (вариация произвольной постоянной)
Линейное дифференциальное уравнение – это уравнение, в котором все $y$ и его производные, входят только в первой степени и не перемножаются между собой.
В этой статье рассмотрим решение таких уравнений первого и второго порядка с неоднородной правой частью. В зависимости от порядка диффура выбирается метод его решения. Хотя есть универсальный метод вариации произвольных постоянных. Разберем все методы.
Линейное ДУ первого порядка
Линейные дифференциальные уравнения первого порядка имеют следующий вид $$y’+g(x)y=f(x),$$ где $g(x)$ и $f(x)$ некоторые функции. Для решения такого типа уравнений можно применить метод Бернулли, либо метод Лагранжа (вариация произвольной постоянной).
Метод Бернулли
- Выполняем подстановку $y=uv, y’=u’v+uv’$, где $u(x),v(x)$ некоторые функции
- Строим систему уравнений, чтобы найти $u(x)$ и $v(x)$
- Подставляем $u(x), v(x)$ в $y=uv$, чтобы получить общее решение.
| Пример 1 |
| Найти частное решение линейного дифференциального уравнения первого порядка $$y’-y tg x=frac{1}{cos x}, y(0)=0.$$ |
| Решение |
|
Первым шагом делаем подстановку $y=uv, y’=u’v+uv’$ и получаем $$u’v+uv’-uv tg x=frac{1}{cos x}.$$ Теперь выносим за скобки функцию $u$ и составляем систему уравнений: $$u’v+u(v’-v tg x)=frac{1}{cos x}$$ $$begin{cases} v’-v tg x = 0 \ u’v=frac{1}{cos x} end{cases}.$$ Сначала решаем первое уравнение методом разделяющихся переменных, чтобы из него получить $v(x)$: $$begin{cases} frac{dv}{v} = tg x dx \ u’v=frac{1}{cos x} end{cases} Rightarrow begin{cases} ln|v| = -int frac{d(cos x)}{cos x} \ u’v = frac{1}{cos x} end{cases}$$ $$begin{cases} ln|v| = -ln|cos x| \ u’v=frac{1}{cos x} end{cases} Rightarrow begin{cases} v=frac{1}{cos x} \ u’ = 1 end{cases} Rightarrow begin{cases} v=frac{1}{cos x} \ u=x+C end{cases}.$$ Таким образом подставляем найденные $u$ и $v$ в подстановку $y=uv$, чтобы получить общее решение линейного дифференциального уравнения $$y=frac{x+C}{cos x}.$$ Но по условию требуется найти частное решение, поэтому используя дополнительное условие $y(0)=0$ находим константу $C$ $$frac{0+C}{cos 0} = 0 Rightarrow C = 1.$$ Теперь зная значение $C=1$ подставляем его в общее решение и получаем ответ в виде частного решения линейного дифференциального уравнения $$y = frac{x}{cos x}.$$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$y = frac{x}{cos x}$$ |
Метод Лагранжа (вариация произвольной постоянной)
- Находим общее решение однородного уравнения
- В общем решении заменяем постоянную $C$ на функцию $C(x)$
- Находим $y’$ и подставляем его вместе с $y$ в исходное уравнение
- Получаем чему равно $C(x)$ из последнего равенства
- Подставляем $C(x)$ в ранее полученное общее решение и записываем ответ
| Пример 2 |
| Решить линейное дифференциальное уравнение первого порядка $$y’ cos^2 x + y = tg x, quad y(0)=0.$$ |
| Решение |
|
Сначала приведем уравнение к виду $y’+g(x)=f(x)$ путем деления обеих частей диффура на квадрат косинуса $$y’ + frac{y}{cos^2 x} = frac{sin x}{cos^3 x}.$$ Теперь находим общее решение однородного дифференциального уравнения $$y’+frac{y}{cos^2 x} = 0.$$ Разделяем переменные по разные стороны и интегрируем обе части: $$frac{dy}{dx}=-frac{y}{cos^2 x}$$ $$int frac{dy}{y}=-int frac{dx}{cos^2 x}$$ $$ln|y|=-tg x + C$$ $$y = Ce^{-tg x}.$$ Теперь найдем частное решение неоднородного уравнения методом Лагранжа варьируя произвольную постоянную. А именно, заменяем в полученном общем решении константу $C$ на функцию $C(x)$ $$y = C(x)e^{-tg x}.$$ Находим производную функции $$y’ = C'(x)e^{-tg x} – C(x)e^{-tg x} frac{1}{cos^2 x}.$$ Подставляем общее решение и его производную в исходное линейное дифференциальное уравнение, чтобы получить $C'(x)$ $$(C'(x)e^{-tg x} – C(x)e^{-tg x} frac{1}{cos^2 x}) cos^2 x + C(x)e^{-tg x} = tg x.$$ После упрощения получаем, что $$C'(x)e^{-tg x} cos^2 x = tg x.$$ Умножаем уравнение на $e^{tg x}$ и делим на $cos^2 x$ $$C'(x) = frac{tg x}{cos^2 x} e^{tg x}.$$ Теперь, можно получить $C(x)$, просто проинтегрировав правую часть уравнения $$C(x) = int frac{tg x}{cos^2 x} e^{tg x} dx. $$ Выполняем подведение под знак дифференциала $frac{1}{cos^2 x}$ $$C(x) = int tg x e^{tg x} d(tg x).$$ Для комфорта взятия интеграла сделаем замену $tg x = t$, а затем применяя метод интегрирования по частям найдем решение интеграла $$C(x)=int t e^t dt = begin{vmatrix} u = t qquad du=dt \ dv=e^t qquad v=e^t end{vmatrix} = te^t – int e^t dt = te^t – e^t + C.$$ Возвращаемся назад к иксам $$C(x) = te^t – e^t + C = tg x e^{tg x} – e^{tg x} + C.$$ Итак, теперь можно записать общее решение линейного дифференциального уравнения неоднородного $$ytext{о.н.} = ( tg x e^{tg x} – e^{tg x} + C)e^{-tg x} = tg x – 1 + Ce^{-tg x}.$$ По условию задачи требуется найти частное решение, значит применяем условие $y(0)=0$ и находим значение постоянной $C$ $$0 – 1 + C = 0 Rightarrow C=1.$$ Теперь можно записать окончательный ответ $$y = e^{-tg x} + tg x – 1.$$ |
| Ответ |
| $$y = e^{-tg x} + tg x – 1$$ |
Линейное ДУ второго порядка
Обычно в контрольных работах дают задачи на решение линейных дифференциальных уравнений второго порядка с постоянными коэффициентами. Поэтому разберем как решать именно такие уравнения $$y”+py’+qy=f(x).$$
Метод подбора по правой части
Общее решение линейного неоднородного уравнения складывается из общего решения однородного и частного решения неоднородного уравнений $$y_text{о.н.} = y_text{о.о.}+y_text{ч.н.}.$$ Поэтому первым делом нужно решить однородное уравнение (т.е. f(x)=0), а затем найти частное решение подобрав правую часть по таблице.
Для того, чтобы найти общее решение линейного однородного уравнения, требуется составить характеристический многочлен и найти его корни $$lambda^2 + plambda + q = 0.$$ В зависимости от получившихся корней общее решение однородного уравнения выглядит следующим образом:
- $lambda_1 neq lambda_2$, то $y_text{о.о.} = C_1 e^{lambda_1 x} + C_2 e^{lambda_2 x}$
- $lambda_1 = lambda_2$, то $y_text{о.о.} = C_1 e^{lambda_1 x} + C_2 xe^{lambda_1 x}$
- $lambda_{1,2} = alpha pm beta i$, то $y_text{о.о.} = C_1e^{alpha x}cos beta x + C_2 e^{alpha x} sin beta x$.
Далее необходимо по виду правой части подобрать частное решение $y_text{ч.н.}$. Для этого нужно воспользоваться таблицей.
| № | Правая часть | Корни характеристического многочлена | Вид частного решения |
| 1 | $$P_n (x)$$ | Число 0 не является корнем характеристического уравнения. | $$tilde{P_n}(x)$$ |
| Число 0 – корень характеристического уравнения кратности $S$. | $$x^s tilde{P_n}(x)$$ | ||
| 2 | $$P_n (x) e^{alpha x}$$ | Число $alpha$ не является корнем характеристического уравнения. | $$tilde{P_n} (x) e^{alpha x}$$ |
| Число $alpha$ является корнем характеристического уравнения кратности $S$. | $$x^s tilde{P_n} (x) e^{alpha x}$$ | ||
| 3 | $$P_n (x) cos beta x + Q_m (x) sin beta x$$ | Число $pm ibeta$ не является корнем характеристического уравнения. | $$tilde {P_n} cos beta x + tilde{Q_m} sin beta x$$ |
| Число $pm ibeta$ является корнем характеристического уравнения кратности $S$. | $$x^s (tilde {P_n} cos beta x + tilde{Q_m} sin beta x)$$ | ||
| 4 | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ | Число $alpha pm ibeta$ не является корнем характеристического уравнения. | $$e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
| Число $alpha pm ibeta$ является корнем характеристического уравнения. | $$x^s e^{alpha x}[P_n (x) cos beta x + Q_m (x) sin beta x]$$ |
Где $P_n(x)$ и $Q_m(x)$ многочлены.
| Пример 3 |
| Найти общее решение линейного дифференциального уравнения второго порядка $$y”+y’-2y=8sin 2x.$$ |
| Решение |
|
Первым делом находим общее решение однородного дифференциального уравнения $$y”+y’-2y=0.$$ Для этого составляем характеристический многочлен и находим его корни по общей формуле решения квадратных уравнений: $$lambda^2+lambda-2=0$$ $$lambda_{1,2} = frac{-1pm sqrt{1^2-4cdot 1 cdot (-2)}}{2} = frac{-1pm 3}{2}$$ $$lambda_1 = -2, quad lambda_2 = 1.$$ Теперь, используя корни, записывам $$y_text{о.о.} = C_1e^{-2 x} + C_2e^{x}.$$ Теперь нужно найти частное решение неоднородного уравнения $y_text{ч.н.}$ методом подбора правой части. Смотрим на неё и видим, что в нее входит произведение многочлена нулевой степени на косинус. Значит, частное решение будет подбирать в виде $$y_text{ч.н.} = Acos 2x + Bsin 2x,$$ где $A$ и $B$ неизвестные коэффициенты, которые требуется найти на следующем этапе решения. Найдем первую и вторую производную от частного решения: $$y’_text{ч.н.} = -2Asin 2x + 2Bcos 2x$$ $$y”_text{ч.н.} = -4Acos 2x – 4Bsin 2x$$ Теперь подставим полученные производные от $y_text{ч.н.}$ и его само в исходное дифференциальное уравнение, чтобы получить значения $A$ и $B$ методом неопределенных коэффициентов: $$-4Acos 2x – 4Bsin 2x -2Asin 2x + 2Bcos 2x – 2Acos 2x -2Bsin 2x = 8sin 2x$$ $$(2B – 6A)cos 2x + (-6B – 2A)sin 2x = 8sin 2x.$$ Теперь необходимо составить систему уравнений. Справа видим только синус, значит все что перед косинусом слева равно нулю. А всё что перед синусом равно восьми $$begin{cases} 2B-6A = 0 \ -6B-2A = 8 end{cases} Leftrightarrow begin{cases} B-3A=0 \ 3B+A=-4 end{cases} Leftrightarrow begin{cases} B = frac{6}{5} \ A=-frac{2}{5} end{cases}$$ Теперь частное решение неоднородного уравнения выглядит следующим образом $$y_text{ч.н.} = -frac{2}{5} cos 2x – frac{6}{5}sin 2x.$$ Подставляем все найденные данные в окончательную формулу, чтобы записать ответ $$y_text{о.н.} = y_text{о.о.} + y_text{ч.н.} = C_1e^{-2 x} + C_2e^{x} -frac{2}{5} cos 2x – frac{6}{5}sin 2x.$$ |
| Ответ |
| $$y = C_1e^{-2 x} + C_2e^{x} -frac{2}{5} cos 2x – frac{6}{5}sin 2x$$ |
| Пример 4 |
| Решить линейное дифференциальное уравнение $$y”-4y=e^{2x}sin 2x.$$ |
| Решение |
|
Сначала получим общее решение однородного уравнения $$y”-4y=0.$$ Составляем характеристическое уравнение и найдем его корни: $$lambda^2 – 4 = 0$$ $$(lambda – 2)(lambda + 2) = 0$$ $$lambda_1 = -2, quad lambda_2 = 2.$$ Записываем теперь решение $$y_text{о.о.} = C_1 e^{2x} + C_2 e^{-2x}.$$ Теперь выполним подбор частного решения неоднородного уравнения, основываясь на типе правой части. Она состоит из произведение экспоненты на синус, перед которым многочлен. По таблице находим, что частное решение нужно искать в виде $$y_text{ч.н.} = Ae^{2x}cos 2x + Be^{2x}sin 2x.$$ Необходимо найти коэффициенты $A$ и $B$. Для этого нужно найти вторую производную частного решения и подставить в исходное уравнение $$y’_text{ч.н.} = 2Ae^{2x}cos 2x – 2Ae^{2x}sin 2x + 2Be^{2x}sin 2x + 2Be^{2x}cos 2x = $$ $$ = (2A+2B)e^{2x}cos 2x + (2B-2A)e^{2x}sin 2x$$ $$y”_text{ч.н.} = 2(2A+2B)e^{2x}cos 2x – 2(2A+2B)e^{2x}sin 2x + 2(2B-2A)e^{2x}sin 2x + 2(2B-2A)e^{2x}cos 2x = $$ $$ = 8Be^{2x}cos 2x – 8Ae^{2x}sin 2x.$$ Подставляем в исходное ДУ: $$8Be^{2x}cos 2x – 8Ae^{2x}sin 2x – 4Ae^{2x}cos 2x – 4Be^{2x}sin 2x = e^{2x} sin 2x$$ $$(8B-4A)e^{2x}cos 2x + (-8A-4B)e^{2x}sin 2x = e^{2x}sin 2x.$$ Теперь составляем систему уравнений путем сопоставления левой и правой части. То, что слева перед синусом приравниваем к тому, что справа перед синусом. А справа косинуса нет, значит там ноль. Поэтому приравниваем скобки перед косинусом слева к нулю $$begin{cases} 8B-4A=0 \ -8A-4B = 1 end{cases} Rightarrow begin{cases} 2B-A=0 \ -8A-4B=1 end{cases} Rightarrow begin{cases} A = -frac{1}{10} \ B = -frac{1}{20} end{cases}.$$ Теперь частное решение приобретает вид $$y_text{ч.н.} = -frac{1}{10}e^{2x}cos 2x – frac{1}{20} e^{2x} sin 2x,$$ и можно записать окончательный ответ к задаче $$y_text{о.н.} = y_text{о.о.}+y_text{ч.н.} = C_1 e^{2x} + C_2 e^{-2x}-frac{1}{10}e^{2x}cos 2x – frac{1}{20} e^{2x} sin 2x.$$ |
| Ответ |
| $$y = C_1 e^{2x} + C_2 e^{-2x}-frac{1}{10}e^{2x}cos 2x – frac{1}{20} e^{2x} sin 2x$$ |
Метод Лагранжа (вариация произвольной постоянной)
Данный метод удобно применять тогда, когда правая часть не подходит под формулы из таблицы. Таким образом, метод Лагранжа становится универсальной палочкой-выручалочкой при решении данного типа задач. Алгоритм следующий:
- Находим общее решение однородного уравнения $y_text{о.о.} = C_1 y_1 + C_2 y_2$
- Заменяем константы $C_1,C_2$ на функции $C_1(x)$ и $C_2(x)$
- Решаем систему методом Крамера $begin{cases} C_1 ‘(x)y_1 + C_2 ‘(x)y_2 = 0 \ C_2 ‘(x)y’_1 + C_2 ‘(x) y’_2 = f(x) end{cases}$
- Интегрируем полученные $C’_1 (x)$ и $C’_2 (x)$
- Подставляем $C_1(x)$ и $C_2(x)$ в общее решение $y_text{о.о.}$
| Пример 5 |
| Найти общее решение линейного дифференциального уравнения второго порядка $$y”+y=frac{1}{sin x}.$$ |
| Решение |
|
Первым делом находим общее решение однородного уравнения $$y”+y=0, $$ составив характериcтический многочлен $$lambda^2 + 1 = 0, $$ и вычислив его корни $$lambda_{1,2} = pm i.$$ Записываем решение $$y_text{о.о.} = C_1 cos x + C_2 sin x.$$ Далее заменяем в нём постоянные $C_1$ и $C_2$ на функции $C_1(x)$ и соответственно $C_2(x)$. И сразу замечаем, что $y_1 = cos x$ и $y_2 = sin x$. Это пригодится для дальнейшего решения задачи при построении системы уравнений. А сейчас записываем, что $$y_text{о.о.} = C_1 (x) cos x + C_2(x) sin x.$$ Перед тем как составим систему уравнений найдем производные: $$y’_1 = -sin x$$ $$y’_2 = cos x.$$ Теперь получаем систему и решаем её методом Крамера $$begin{cases} C_1 ‘(x)cos x+C_2(x)sin x = 0 \ -C’_1 (x)sin x + C’_2(x) cos x = frac{1}{sin x} end{cases}.$$ Находим значение главного определителя $$Delta = begin{vmatrix} cos x & sin x \ -sin x & cos x end{vmatrix} = cos^2 x + sin^2 x = 1.$$ Найдем значение первого дополнительного определителя $$Delta_1 = begin{vmatrix} 0 & sin x \ frac{1}{sin x} & cos x end{vmatrix} = -1 .$$ Найдем значение второго дополнительного определителя $$Delta_2 = begin{vmatrix} cos x & 0 \ -sin x & frac{1}{sin x} end{vmatrix} = frac{cos x}{sin x}.$$ Теперь можно получить производные от искомых функций: $$C’_1(x) = frac{Delta_1}{Delta} = -1$$ $$C’_2(x) = frac{Delta_2}{Delta} = frac{cos x}{sin x}.$$ А затем путем интегрирования находим первообразные последних функций: $$C_1(x)=int (-1) dx = -x + tilde{C_1}$$ $$C_2(x)=int frac{cos x}{sin x} dx = int frac{d(sin x)}{sin x} = ln|sin x| + tilde{C_2}.$$ Теперь получим общее решение неоднородного линейного дифференциального уравнения путем подстановки найденных $C_1(x)$ и $C_2(x)$ в $y_text{о.о.}$ $$y_text{о.о.} = (-x + tilde{C_1})cos x + (ln|sin x|+tilde{C_2})sin x.$$ |
| Ответ |
| $$y = (-x + tilde{C_1})cos x + (ln|sin x|+tilde{C_2})sin x$$ |
Пример частного решения линейного дифференциального уравнения
Рассмотрим тоже самое уравнение, но решим методом вариации произвольной постоянной.
Для нахождения производных C’i составляем систему уравнений:
C’1·e -3x ·cos(2x)+C’2·e -3x ·sin(2x)=0
C’1(-2·e -3x ·sin(2x)-3·cos(2x)·e -3x ) + C’2(-3·e -3x ·sin(2x)+2·cos(2x)·e -3x ) = 8*exp(-x)
Выразим C’1 из первого уравнения:
C’1 = -c2·sin(2x)/(cos(2x))
и подставим во второе. В итоге получаем:
C’1 = -4·e 2x ·sin(2x)
C’2 = 4·cos(2x)·e 2x
Интегрируем полученные функции C’i:
C1 = -e 2x ·sin(2x)+cos(2x)·e 2x + C * 1
C2 = e 2x ·sin(2x)+cos(2x)·e 2x + C * 2
Записываем полученные выражения в виде:
C1 = (-e 2x ·sin(2x)+cos(2x)·e 2x )·cos(2x)·e -3x + C * 1e -3x ·cos(2x)
C2 = (e 2x ·sin(2x)+cos(2x)·e 2x )·e -3x ·sin(2x) + C * 2e -3x ·sin(2x)
или
C1 = -cos(2x)·e -x ·sin(2x)+cos 2 (2x)·e -x + C * 1e -3x ·cos(2x)
C2 = cos(2x)·e -x ·sin(2x)+sin 2 (2x)·e -x + C * 2e -3x ·sin(2x)
y = C1 + C2
Таким образом, общее решение дифференциального уравнения имеет вид:
Пример . y″ + 5y’ + 6 = 12cos(2x)
Cоставляем характеристическое уравнение дифференциального уравнения: r 2 +5 r + 6 = 0
Находим дискриминант: D = 5 2 – 4·1·6 = 1
Корни характеристического уравнения: r1 = -2, r2 = -3. Следовательно, фундаментальную систему решений составляют функции: y1 = e -2x , y2 = e -3x
Общее решение однородного уравнения имеет вид: y =C1·e -2x +C2·e -3x
Найдем частное решение при условии:y(0) = 1, y'(0) = 3
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = 1
Находим первую производную: y’ = -3·c2·e -3·x -2·c1·e -2·x
Поскольку y'(0) = -3·c2-2·c2, то получаем второе уравнение:
-3·c2-2·c2 = 3
В итоге получаем систему из двух уравнений:
c1+c2 = 1
-3·c2-2·c2 = 3
которую решаем или методом обратной матрицы или методом исключения переменных.
c1 = 6, c2 = -5
Тогда частное решение при заданных начальных условиях можно записать в виде: y =6·e -2x -5·e -3x
Рассмотрим правую часть: f(x) = 12·cos(2·x)
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные: y’ = -2·A·sin(2x)+2·B·cos(2x); y″ = -4·A·cos(2x)-4·B·sin(2x)
которые подставляем в исходное дифференциальное уравнение: y″ + 5y’ + 6y = (-4·A·cos(2x)-4·B·sin(2x)) + 5(-2·A·sin(2x)+2·B·cos(2x)) + 6(Acos(2x) + Bsin(2x)) = 12·cos(2·x) или -10·A·sin(2x)+2·A·cos(2x)+2·B·sin(2x)+10·B·cos(2x) = 12·cos(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему линейных уравнений:
-10A + 2B = 0
2A + 10B = 12
СЛАУ решаем методом Крамера:
A = 3 /13;B = 15 /13;
Частное решение имеет вид:
y * = 3 /13cos(2x) + 15 /13sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Пример 2 . y’’ + y = cos(x)
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами. Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 + 1 = 0
D = 0 2 – 4·1·1 = -4

Корни характеристического уравнения:
(комплексные корни):
r1 = i, r2 = -i
Следовательно, фундаментальную систему решений составляют функции:
y1 = e 0 x cos(x) = cos(x)
y2 = e 0 x sin(x) = sin(x)
Общее решение однородного уравнения имеет вид: y =C1·cos(x)+C2·sin(x)
Рассмотрим правую часть: f(x) = cos(x)
Найдем частное решение. Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) – некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k – кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) – полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i является корнем характеристического уравнения кратности k = 1(r1).
Уравнение имеет частное решение вида:
y * = x (Acos(x) + Bsin(x))
Вычисляем производные:
y’ = sin(x)(B-A·x)+cos(x)(A+B·x)
y″ = cos(x)(2·B-A·x)-sin(x)(2·A+B·x)
которые подставляем в исходное дифференциальное уравнение:
y″ + y = (cos(x)(2·B-A·x)-sin(x)(2·A+B·x)) + (x (Acos(x) + Bsin(x))) = cos(x)
или
2·B·cos(x)-2·A·sin(x) = cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
2B = 1
-2A = 0
Следовательно:
A = 0; B = 1 /2;
Частное решение имеет вид: y * = x (0cos(x) + ½ sin(x)) = ½ x sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Методические рекомендации для преподавателей математики и студентов средних специальных учебных заведений по теме “Дифференциальные уравнения”
Разделы: Математика
I. Обыкновенные дифференциальные уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную x, искомую функцию y и её производные или дифференциалы.
Символически дифференциальное уравнение записывается так:
Дифференциальное уравнение называется обыкновенным, если искомая функция зависит от одного независимого переменного.
Решением дифференциального уравнения называется такая функция 
Порядком дифференциального уравнения называется порядок старшей производной, входящей в это уравнение
1. Рассмотрим дифференциальное уравнение первого порядка
Решением этого уравнения является функция y = 5 ln x. Действительно, 

А это и значит, что функция y = 5 ln x– есть решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение второго порядка y” – 5y’ +6y = 0. Функция 
Действительно, 
Подставляя эти выражения в уравнение, получим: , – тождество.
А это и значит, что функция – есть решение этого дифференциального уравнения.
Интегрированием дифференциальных уравнений называется процесс нахождения решений дифференциальных уравнений.
Общим решением дифференциального уравнения называется функция вида ,в которую входит столько независимых произвольных постоянных, каков порядок уравнения.
Частным решением дифференциального уравнения называется решение, полученное из общего решения при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находится при определённых начальных значениях аргумента и функции.
График частного решения дифференциального уравнения называется интегральной кривой.
1.Найти частное решение дифференциального уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения, получим
Замечание. Произвольную постоянную С, полученную в результате интегрирования, можно представлять в любой форме, удобной для дальнейших преобразований. В данном случае, с учётом канонического уравнения окружности произвольную постоянную С удобно представить в виде .
– общее решение дифференциального уравнения.
Частное решение уравнения, удовлетворяющее начальным условиям y = 4 при x = 3 находится из общего подстановкой начальных условий в общее решение: 3 2 + 4 2 = C 2 ; C=5.
Подставляя С=5 в общее решение, получим x 2 +y 2 = 5 2 .
Это есть частное решение дифференциального уравнения, полученное из общего решения при заданных начальных условиях.
2. Найти общее решение дифференциального уравнения
Решением этого уравнения является всякая функция вида , где С – произвольная постоянная. Действительно, подставляя в уравнения , получим: , .
Следовательно, данное дифференциальное уравнение имеет бесконечное множество решений, так как при различных значениях постоянной С равенство определяет различные решения уравнения .
Например, непосредственной подстановкой можно убедиться, что функции являются решениями уравнения .
Задача, в которой требуется найти частное решение уравнения y’ = f(x,y) удовлетворяющее начальному условию y(x0) = y0, называется задачей Коши.
Решение уравнения y’ = f(x,y), удовлетворяющее начальному условию, y(x0) = y0, называется решением задачи Коши.
Решение задачи Коши имеет простой геометрический смысл. Действительно, согласно данным определениям, решить задачу Коши y’ = f(x,y) при условии y(x0) = y0,, означает найти интегральную кривую уравнения y’ = f(x,y) которая проходит через заданную точку M0(x0,y0).
II. Дифференциальные уравнения первого порядка
2.1. Основные понятия
Дифференциальным уравнением первого порядка называется уравнение вида F(x,y,y’) = 0.
В дифференциальное уравнение первого порядка входит первая производная и не входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется уравнением первого порядка, разрешённым относительно производной.
Общим решением дифференциального уравнения первого порядка называется функция вида , которая содержит одну произвольную постоянную.
Пример. Рассмотрим дифференциальное уравнение первого порядка .
Решением этого уравнения является функция .
Действительно, заменив в данном уравнении, его значением, получим
то есть 3x=3x
Следовательно, функция является общим решением уравнения при любом постоянном С.
Найти частное решение данного уравнения, удовлетворяющее начальному условию y(1)=1 Подставляя начальные условия x = 1, y =1 в общее решение уравнения , получим откуда C = 0.
Таким образом, частное решение получим из общего подставив в это уравнение, полученное значение C = 0 – частное решение.
2.2. Дифференциальные уравнения с разделяющимися переменными
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида: y’=f(x)g(y) или через дифференциалы , где f(x) и g(y)– заданные функции.
Для тех y, для которых , уравнение y’=f(x)g(y) равносильно уравнению, в котором переменная y присутствует лишь в левой части, а переменная x- лишь в правой части. Говорят, «в уравнении y’=f(x)g(y разделим переменные».
Уравнение вида называется уравнением с разделёнными переменными.
Проинтегрировав обе части уравнения по x, получим G(y) = F(x) + C– общее решение уравнения, где G(y) и F(x) – некоторые первообразные соответственно функций и f(x), C произвольная постоянная.
Алгоритм решения дифференциального уравнения первого порядка с разделяющимися переменными
- Производную функции переписать через её дифференциалы
- Разделить переменные.
- Проинтегрировать обе части равенства, найти общее решение.
- Если заданы начальные условия, найти частное решение.
Решить уравнение y’ = xy
Решение. Производную функции y’ заменим на
разделим переменные
проинтегрируем обе части равенства:
Ответ:
Найти частное решение уравнения
Это—уравнение с разделенными переменными. Представим его в дифференциалах. Для этого перепишем данное уравнение в виде Отсюда
Интегрируя обе части последнего равенства, найдем
Подставив начальные значения x0 = 1, y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл будет или
Составить уравнение кривой, проходящей через точку M(2;-3) и имеющей касательную с угловым коэффициентом
Решение. Согласно условию
Это уравнение с разделяющимися переменными. Разделив переменные, получим:
Проинтегрировав обе части уравнения, получим:
Используя начальные условия, x = 2 и y = – 3 найдем C:
Следовательно, искомое уравнение имеет вид
2.3. Линейные дифференциальные уравнения первого порядка
Линейным дифференциальным уравнением первого порядка называется уравнение вида y’ = f(x)y + g(x)
где f(x) и g(x) – некоторые заданные функции.
Если g(x)=0 то линейное дифференциальное уравнение называется однородным и имеет вид: y’ = f(x)y
Если то уравнение y’ = f(x)y + g(x) называется неоднородным.
Общее решение линейного однородного дифференциального уравнения y’ = f(x)y задается формулой: где С – произвольная постоянная.
В частности, если С =0, то решением является y = 0 Если линейное однородное уравнение имеет вид y’ = ky где k – некоторая постоянная, то его общее решение имеет вид: .
Общее решение линейного неоднородного дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,
т.е. равно сумме общего решения соответствующего линейного однородного уравнения и частного решения данного уравнения.
Для линейного неоднородного уравнения вида y’ = kx + b,
где k и b– некоторые числа и частным решением будет являться постоянная функция . Поэтому общее решение имеет вид .
Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’ = -2y – 3 где k = -2, b= -3 Общее решение задается формулой .
Следовательно, где С – произвольная постоянная.
Ответ:
2.4. Решение линейных дифференциальных уравнений первого порядка методом Бернулли
Нахождение общего решения линейного дифференциального уравнения первого порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных уравнений с разделенными переменными с помощью подстановки y=uv, где u и v – неизвестные функции от x. Этот метод решения называется методом Бернулли.
Алгоритм решения линейного дифференциального уравнения первого порядка
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ = u’v + uv’
3. Подставить y и y’ в данное уравнение: u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы u вынести за скобки:
5. Из скобки, приравняв ее к нулю, найти функцию
Это уравнение с разделяющимися переменными:
Разделим переменные и получим:
Откуда . .
6. Подставить полученное значение v в уравнение (из п.4):
и найти функцию Это уравнение с разделяющимися переменными:
7. Записать общее решение в виде: , т.е. .
Найти частное решение уравнения y’ = -2y +3 = 0 если y =1 при x = 0
Решение. Решим его с помощью подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’ в данное уравнение, получим
Сгруппировав второе и третье слагаемое левой части уравнения, вынесем общий множитель u за скобки
Выражение в скобках приравниваем к нулю и, решив полученное уравнение, найдем функцию v = v(x)
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения: Найдем функцию v:
Подставим полученное значение v в уравнение Получим:
Это уравнение с разделенными переменными. Проинтегрируем обе части уравнения: Найдем функцию u = u(x,c) Найдем общее решение: Найдем частное решение уравнения, удовлетворяющее начальным условиям y = 1 при x = 0:
Ответ:
III. Дифференциальные уравнения высших порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго порядка называется уравнение, содержащее производные не выше второго порядка. В общем случае дифференциальное уравнение второго порядка записывается в виде: F(x,y,y’,y”) = 0
Общим решением дифференциального уравнения второго порядка называется функция вида , в которую входят две произвольные постоянные C1 и C2.
Частным решением дифференциального уравнения второго порядка называется решение, полученное из общего при некоторых значениях произвольных постоянных C1 и C2.
3.2. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y” + py’ +qy = 0, где pи q– постоянные величины.
Алгоритм решения однородных дифференциальных уравнений второго порядка с постоянными коэффициентами
1. Записать дифференциальное уравнение в виде: y” + py’ +qy = 0.
2. Составить его характеристическое уравнение, обозначив y” через r 2 , y’ через r, yчерез 1: r 2 + pr +q = 0
3.Вычислить дискриминант D = p 2 -4q и найти корни характеристического уравнения; при этом если:
а) D > 0; следовательно, характеристическое уравнение имеет два различных действительных корня . Общее решение дифференциального уравнения выражается в виде , где C1 и C2 – произвольные постоянные.
б) D = 0; следовательно, характеристическое уравнение имеет равные действительные корни . Общее решение дифференциального уравнения выражается в виде
Общее решение
Дифференцируя общее решение, получим
Составим систему из двух уравнений
Подставим вместо ,и заданные начальные условия:
Таким образом, искомым частным решением является функция
.
2. Найти частное решение уравнения
1.
1.
2. а)
2. а)
б)
б)
в)
в)
г)
г)
Примеры решения дифференциальных уравнений с ответами
Простое объяснение принципов решения дифференциальных уравнений и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.
Алгоритм решения дифференциальных уравнений
Дифференциальные уравнения не так сильно отличаются от привычных уравнений, где необходимо найти переменную x , как кажется на первый взгляд. Всё различие лишь в том, что в дифференциальных уравнениях мы ищем не переменную, а функцию у(х) , с помощью которой можно обратить уравнение в равенство.
Дифференциальное уравнение – это уравнение, содержащее саму функцию (y=y(x)), производные функции или дифференциалы (y′, y″) и независимые переменные (наиболее распространённая – х). Обыкновенным дифференциальным уравнением называют уравнение, в котором содержится неизвестная функция под знаком производной или под знаком дифференциала.
Чтобы решить ДУ, необходимо найти множество всех функций, которые удовлетворяют данному уравнению. Это множество в большинстве случаев выглядит следующим образом:y=f(x; С), где С – произвольная постоянная.
Проверить решённое ДУ можно, подставив найденную функцию в изначальное уравнение и убедившись, что уравнение обращается в тождество (равенство).
Примеры решения дифференциальных уравнений
Задание
Решить дифференциальное уравнение xy’=y.
Решение
В первую очередь, необходимо переписать уравнение в другой вид. Пользуясь
переписываем дифференциальное уравнение, получаем
Дальше смотрим, насколько реально разделить переменные, то есть путем обычных манипуляций (перенос слагаемых из части в часть, вынесение за скобки и пр.) получить выражение, где «иксы» с одной стороны, а «игреки» с другой. В данном уравнении разделить переменные вполне реально, и после переноса множителей по правилу пропорции получаем
Далее интегрируем полученное уравнение:
В данном случае интегралы берём из таблицы:
После того, как взяты интегралы, дифференциальное уравнение считается решённым. Решение дифференциального уравнения в неявном виде называется общим интегралом дифференциального уравнения.
– это общий интеграл. Также для удобства и красоты, его можно переписать в другом виде: y=Cx, где С=Const
Ответ
Задание
Найти частное решение дифференциального уравнения
Решение
Действуем по тому же алгоритму, что и в предыдущем решении.
Переписываем производную в нужном виде, разделяем переменные и интегрируем полученное уравнение:
Получили общий интеграл.Далее, воспользуемся свойством степеней, выразим у в «общем» виде и перепишем функцию:
Если – это константа, то
0]” title=”Rendered by QuickLaTeX.com” />
– тоже некоторая константа, заменим её буквой С:
– убираем модуль и теперь константа может принимать и положительные, и отрицательные значения.
Получаем общее решение:
Ответ
Задание
Решить дифференциальное уравнение
Решение
В первую очередь необходимо переписать производную в необходимом виде:
Второй шаг – разделение переменных и перенос со сменой знака второго слагаемого в правую часть:
После разделения переменных, интегрируем уравнение, как в примерах выше.
Чтобы решить интегралы из левой части, применим метод подведения функции под знак дифференциала:
В ответе мы получили одни логарифмы и константу, их тоже определяем под логарифм.
Далее упрощаем общий интеграл:
Приводим полученный общий интеграл к виду: F(x,y)=C:
Чтобы ответ смотрелся красивее, обе части необходимо возвести в квадрат.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(0)=ln2.
Решение
Первый шаг – нахождение общего решения. То, что в исходном уравнении уже находятся готовые дифференциалы dy и dx значительно упрощает нам решение.
Начинаем разделять переменные и интегрировать уравнение:
Мы получили общий интеграл и следующий шаг – выразить общее решение. Для этого необходимо прологарифмировать обе части. Знак модуля не ставим, т.к. обе части уравнения положительные.
Получаем общее решение:
Далее необходимо найти частное решение, которое соответствует заданному начальному условию y(0)=ln2.
В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух:
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Задание
Решить дифференциальное уравнение
Решение
При внимательном разборе данного уравнения видно, что можно разделить переменные, что и делаем, после интегрируем:
В данном случае константу C считается не обязательным определять под логарифм.
Ответ
Задание
Найти частное решение дифференциального уравнения
удовлетворяющее начальному условию y(1)=e. Выполнить проверку.
Решение
Как и в предыдущих примерах первым шагом будет нахождение общего решения. Для этого начинаем разделять переменные:
Общий интеграл получен, осталось упростить его. Упаковываем логарифмы и избавляемся от них:
можно выразить функцию в явном виде.
Осталось найти частное решение, удовлетворяющее начальному условию y(1)=e.
Подставляем найденное значение константы C=1 в общее решение.
Ответ
Проверка
Необходимо проверить, выполняется ли начальное условие:
Из равенства выше видно, что начальное условие y(1)=e выполнено.
Далее проводим следующую проверку: удовлетворяет ли вообще частное решение
дифференциальному уравнению. Для этого находим производную:
Подставим полученное частное решение
и найденную производную в исходное уравнение
Получено верное равенство, значит, решение найдено правильно.
Задание
Найти общий интеграл уравнения
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Ответ
Задание
Найти частное решение ДУ.
Решение
Данное ДУ допускает разделение переменных. Разделяем переменные:
Найдем частное решение (частный интеграл), соответствующий заданному начальному условию
Подставляем в общее решение
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных. Разделяем переменные и интегрируем:
Левую часть интегрируем по частям:
В интеграле правой части проведем замену:
(здесь дробь раскладывается методом неопределенных коэффициентов)
Ответ
Задание
Решить дифференциальное уравнение
Решение
Данное уравнение допускает разделение переменных.
Разделяем переменные и интегрируем:
Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:
[spoiler title=”источники:”]
http://urok.1sept.ru/articles/527195
http://nauchniestati.ru/spravka/primery-resheniya-differenczialnyh-uravnenij-s-otvetami/
[/spoiler]
Дифференциальным уравнением с частными производными называется уравнение вида
(1)
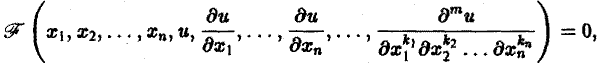
связывающее независимые переменные x1, х2, … , хn искомую функцию и = и(х1, х2,…, хn) и ее частные производные (наличие хотя бы одной производной обязательно). Здесь ki,k2,… ,кn — неотрицательные целые числа, такие, что к1 + к2 + … + кп = т.
Порядком дифференциального уравнения называется наивысший порядок входящие в уравнение частных производных. Так, если х, у — независимые переменные, и = и(х, у) — искомая функция, то
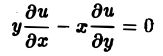
— дифференциальное уравнение 1-го порядка;
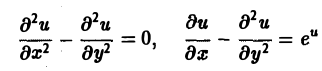
— дифференциальные уравнения 2-го порядка.
Для упрощения записи пользуются также следующими обозначениями:
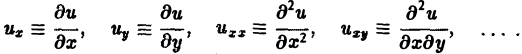
Пусть имеем дифференциальное уравнение с частными производными (1) порядка т. Обозначим через Сm(D) множество функций, непрерывных в области D вместе со всеми производными до порядка m включительно.
Определение:
Решением дифференциального уравнения (1) в некоторой области D изменения независимых переменных x1, x2…xn,. называется всякая функция и = и(х1, х2,…, xп) ∈ Сm (D) такая, что подстановка этой функции и ее производных в уравнение (1) обращает последнее в тождество по x1, x2, …., хп в области D.
Пример:
Найти решение и = и(х,у) уравнения

Равенство (2) означает, что искомая функция и не зависит опт х, но может быть любой функцией от у,
u = φ(y). (3)
Таким образом, решение (3) уравнения (2) содержит одну произвольную функцию. Это — общее решение уравнения (2).
Приме:
Найти решение u = u(z, у) уравнения

Положим 
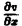


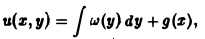
где g(x) — произвольная функция. Так как w(у) — произвольная функция, то и интеграл от нее также является произвольной функцией; обозначим его через f(у). В результате получим решение уравнения (4) в виде
u(x, y) = f(y) + g(x) (5)
(f(y)• g(x) ~ произвольные дифференцируемые функции).
Решение (5) уравнения с частными производными 2-го порядка (4) содержит уже две произвольные функции. Его называют общим решением уравнения (4), так как всякое другое решение уравнения (4) может быть получено из (5) подходящим выбором функций f и g.
Мы видим, таким образом, что уравнения с частными производными имеют целые семейства решений. Однако существуют уравнения с частными производными, множества решений которых весьма узки и, в некоторых случаях, да же пусты.
Пример:
Множество действительных решений уравнения
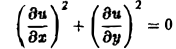
исчерпывается функцией u(x, y) = const, а уравнение
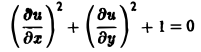
вовсе не имеет действительных решений.
Мы не ставим пока вопрос об отыскании частных решений. Позже будет выяснено, какие дополнительные условия нужно задать, чтобы с их помощью можно было выделить частное решение, т.е. функцию, удовлетворяющую как дифференциальному уравнению, так и этим дополнительным условиям.
Линейные дифференциальные уравнения с частными производными. Свойства их решений
Уравнение с частными производными называется линейным, если оно линейно относительно искомой функции и всех ее производных, входящих в уравнение; в противном случае уравнение называется нелинейным.
Пример:
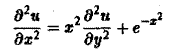
— линейное уравнение; уравнения
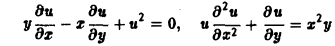
— нелинейные.
Линейное дифференциальное уравнение 2-го порядка для функции двух независимых переменных х, у в общем случае имеет вид
(1)
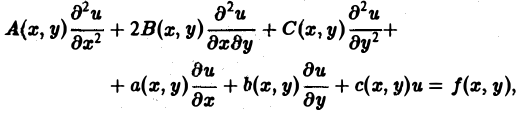
где А(х, у), В(х, у), …, с(х,у), f(x,y) — функции переменных х, у, заданные в некоторой области D плоскости хОу. Если f(x,y) ≡ 0 в D, то уравнение (1) называется однородным, в противном случае — неоднородным.
Обозначив левую часть уравнения (1) через L[u], запишем (1) в виде
L[u] = f(x, у). (2)
Соответствующее однородное уравнение запишется так:
L[u] = 0. (3)
Здесь L — линейный дифференциальный оператор, определенный на линейном пространстве C2(D) функций и = и(х, у).
Пользуясь свойством линейности оператора L, легко убедиться в справедливости следующих теорем, выражающих свойства решений линейных однородных дифференциальных уравнений с частными производными.
Теорема:
Если и(х, у) есть решение линейного однородного уравнения (3), то си(х, у), где с — любая постоянная, есть также решение уравнения (3).
Теорема:
Если и1(х, у) и и2(х, у) — решения линейного однородного уравнения (3), то сумма и1(х, у) + и2(x, у) есть также решение этого уравнения.
Следствие:
Если каждая из функций и1(х, у) и и2(х, у), u k(x, у) является решением уравнения (3), то линейная комбинация
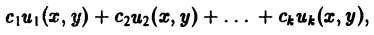
где c1, c2 …, сk — произвольные постоянные, также является решением этого уравнения.
В отличие от обыкновенного линейного однородного дифференциального уравнения, имеющего конечное число линейно независимых частных решений, линейная
комбинация которых дает общее решение этого уравнения, уравнение с частными производными может иметь бесконечное множество линейно независимых частных решений.
Пример:
Уравнение
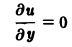
имеет общее решение k = φ(х), так что решениями его будут, например, функции 1,х,…, хn,… . В соответствии с этим в линейных задачах для уравнений с частными производными нам придется иметь дело не только с линейными комбинациями конечного числа решений, но и с рядами 
Возможны случаи, когда функция и(х, у; λ) при всех значениях параметра λ из некоторого интервала (λо, λ1), конечного или бесконечного, является решением уравнения (3). В этом случае говорят, что решения уравнения зависят от непрерывно меняющегося параметра λ. Если теперь взять функцию С(λ) такую, что первые и вторые производные интеграла
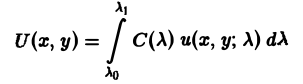
по х и по у могут быть получены с помощью дифференцирования под знаком интеграла, то этот интеграл также будет решением уравнения (3). Для линейного неоднородного уравнения
L[u] = f (4)
справедливы следующие предложения.
Теорема:
Если и(х, у) есть решение линейного неоднородного уравнения (4), a v(x, у) — решение соответствующего однородного уравнения (3), то сумма и + v есть решение неоднородного уравнения (4).
Теорема:
Принцип суперпозиции. Если и1(х, у) —решение уравнения L[u] = f1, a u2(x,y) — решение уравнения L[u] = f2, то и1 + u2 — решение уравнения L[u] = f1 + f2.
Классификация линейных дифференциальных уравнений второго порядка с двумя независимыми переменными
Определение:
Линейное дифференциальное уравнение второго порядка
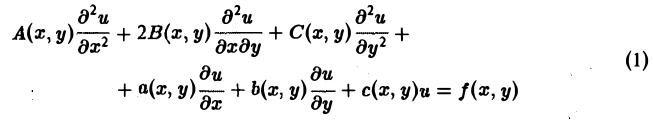
в некоторой области Q на плоскости хОу называется
1) гиперболическим в Ω, если
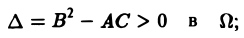
2) параболическим в Ω, если
3) эллиптическим в Ω, если
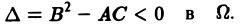
Пользуясь этим определением, легко проверить, что уравнения

— гиперболические при всех х и у, уравнение
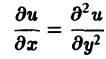
— параболическое при всех х и у, а уравнение
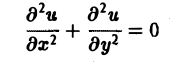
— эллиптическое при всех х и у. Уравнение
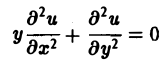
— эллиптическое при у > 0, параболическое на линии у = 0 и гиперболическое в полуплоскости у < 0.
Можно показать, что при определенных условиях на коэффициенты уравнения (1) существует неособая замена независимых переменных
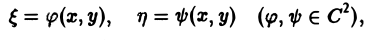
с помощью которой уравнение (1) преобразуется к более простому, каноническому виду, своему для каждого типа уравнения.
Уравнение гиперболического типа (∆ > 0) преобразуется к вшу
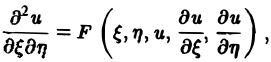
или
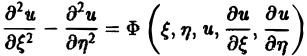
(два канонических вида уравнений гиперболического типа).
Уравнение параболического типа (∆ ≡ 0) преобразуется к виду
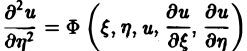
(канонический вид уравнения параболического типа).
Уравнение эллиптического типа (∆ < 0) преобразуется к виду
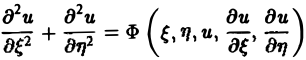
(канонический вид уравнения эллиптического типа). Здесь F и Ф — некоторые функции, зависящие от искомой функции и, ее первых производных 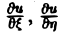
В некоторых случаях каноническая форма уравнения позволяет найти общее решение исходного уравнения.
Как правило, приведениеуравнения(1) к каноническому виду путем замены независимых переменных имеет локальный характер, т. е. осуществимо лишь в некоторой достаточно малой окрестности рассматриваемой точки Mo(xo, уo).
Когда число п независимых переменных больше двух, также различают уравнения гиперболического, параболического и эллиптического типов. Например, при п = 4 простейшая каноническая форма таких уравнений имеет вид
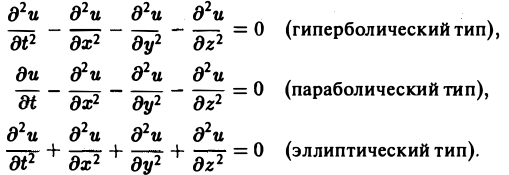
Здесь и = и(х, у, z, t).
Замечание:
В общем случае, когда число независимых переменных больше двух, приведение линейною уравнения с переменными коэффициентами
к каноническому виду возможно только в данной точке 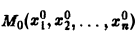
Мы ограничимся рассмотрением линейных дифференциальных уравнений 2-го порядка. К таким уравнениям приводит большое количество различных физических задач.
Так, колебательные процессы различной природы (колебания струн, мембран, акустические колебания газа в трубах, электромагнитные колебания и т. д.) описываются уравнениями гиперболического типа. Простейшим из таких уравнений является уравнение колебаний струны (одномерное волновое уравнение): (2)
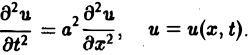
Здесь х — пространственная координата, t — время, 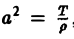
Процессы теплопроводности и диффузии приводят к уравнениям параболического типа. В одномерном случае простейшее уравнение теплопроводности имеет вид
(3)
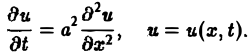
Здесь 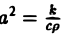
Наконец, установившиеся процессы, когда искомая функция не зависит от времени, определяются уравнениями эллиптического типа, типичным представителем которых является уравнение Лапласа
(4)
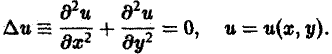
Непосредственной проверкой убеждаемся в том, что решением уравнения (2) является всякая функция и(х, t) вида
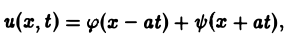
где
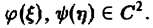
Можно показать, что решениями уравнения (3) являются функции вида
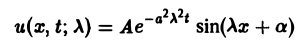
(А, а ~ произвольные постоянные, А — числовой параметр). Интегрируя решение и(х, t; λ) = 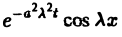
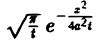
Наконец, нетрудно убедиться, что действительнозначные функции Рn(х,у) и Qn(x, у), определяемые из соотношения
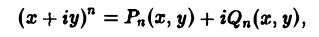
являются решениями уравнения Лапласа (4) для п = 0, 1, 2…..Этот последний результат есть частный, случай общего утверждения, что и действительная и мнимая части аналитической функции
f(z) = u(x, у) + iv(x, у)
комплексного переменного z = х + iy являются решениями уравнения Лапласа (4).
В силу линейности уравнения (4) ряды
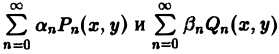
тоже будут решениями уравнения (4), если они сходятся равномерно, как и ряды, полученные из них двукратным почленным дифференцированием по каждому из аргументов х, у.
Таким образом, для простейшей — канонической — формы уравнений гиперболического, параболического и эллиптического типов мы располагаем о решениях этих уравнений некоторой информацией.
Постановка основных задач для линейных дифференциальных уравнений второго порядка
Для полного описания того или иного физического процесса мало иметь только дифференциальное уравнение процесса, надо еще задать начальное состояние этого процесса (начальные условия) и режим на границе S той области Ω, в которой процесс происходит (граничные условия). Это обусловлено неединственностью решения дифференциальных уравнений.
Пример:
Общее решение уравнения
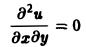
имеет вид и(х, у) = f(x) + g(y), где f(x) и g(y) — произвольные дифференцируемые функции. Поэтому чтобы выделить решение, описывающее данный физический процесс, необходимо задать дополнительные условия.
Различают три основных типа задач для дифференциальных уравнений с частными производными (число независимых переменных равно п):
а) задача Коши для уравнений гиперболического и параболического типов: задаются начальные условия, область Ω совпадает со всем пространством Rn, граничные условия отсутствуют;
б) краевая задача для уравнений эллиптического типа: задаются граничные условия на границе S области Ω, начальные условия отсутствуют;
в) смешанная задача для уравнений гиперболического и параболического типов: задаются начальные и граничные условия, Ω ≠ Rn
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Содержание:
Общие свойства линейных однородных дифференциальных уравнений:
В этой лекции мы остановимся на изучении линейных дифференциальных уравнений второго порядка, которые представляют наиболее разработанную часть теории дифференциальных уравнений. Это объясняется тем, что линейные уравнения часто описывают реальные процессы, либо дают первое приближение изучаемого явления.
Определение 24.1.1. Дифференциальное уравнение линейное относительно искомой функции
Это уравнение преобразуется к виду
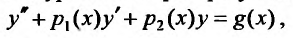
делением всех членов уравнения на коэффициент
Предположим, что коэффициенты 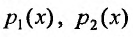
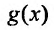
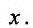
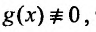
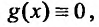
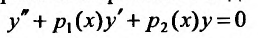
и называется линейным однородным.
Рассмотрим некоторые свойства однородных линейных дифференциальных уравнений (24.1.2).
Теорема 24.1.1. Если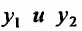
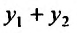
Доказательство. Так как 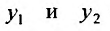
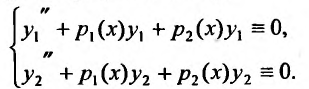
Подставляя в уравнение (24.1.2) сумму 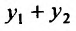
откуда и следует, что 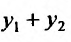
Теорема 24.1.2. Если у, – частное решение однородного уравнения (24.1.2). то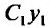
Доказательство. Так как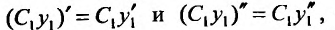
Из условия теоремы следует, что 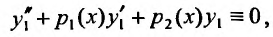
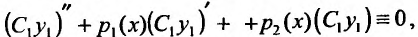
Следствие 1. Если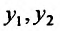
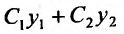
Доказательство. Действительно, 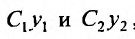
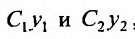
Заметим, что при сделанных предположениях относительно коэффициентов уравнения (24.1.2), оно имеет одно и только одно решение, проходящее через точку 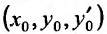
Определение 24.1.2. Определителем Вронского называется выражение 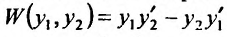
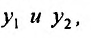
Теорема 24.1.3. Определитель Вронского вычисляется по формуле:
где С = const.
Доказательство. Для доказательства рассмотрим производную определителя
Так как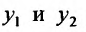
Умножая первое тождество на 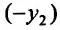
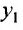
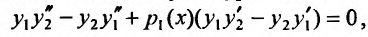
Умножив на dx, получим уравнение в дифференциальной форме: 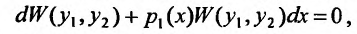
Выше мы рассматривали частные решения уравнения (24.1.2): 
Определение 24.1.3. Два ненулевые решения, 
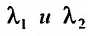
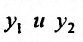
Таким образом, из определения 24.1.3 следует, что линейно зависимые (функции) решения отличаются на постоянный множитель.
Теорема 24.1.4. Если 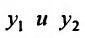
Доказательство. Действительно, если 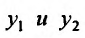
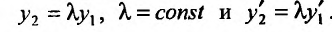
Теорема 24.1.5. Если ненулевые решения 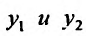
Доказательство. Предположим, что 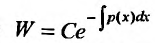
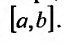
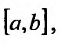
Так как 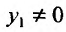
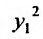
В левой части записано значение производной частного решения 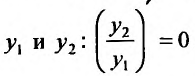
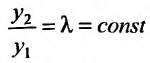
Теорема 24.1.6. Если 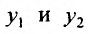
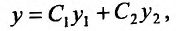
где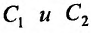
Доказательство. Из следствия 1 теоремы 24.1.2 следует, что функция 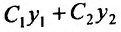
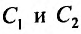
Пусть, при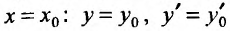
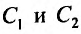
где
Так как определитель системы (24.1.6) , ,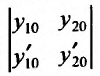
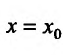
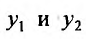
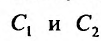
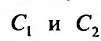
Заметим, что не существует методов для нахождения общего решения линейного однородного уравнения с переменными коэффициентами.
Однако, для уравнений с постоянными коэффициентами такой метод существует.
Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным однородным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида:
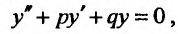
где р и q – постоянные числа. Нахождение общего решения уравнения (24.2.1) сводится к чисто алгебраическим операциям.
Вид уравнения (24.2.1) показывает, что частные решения этого уравнения следует искать, прежде всего, среди таких функций, которые в алгебраическом смысле подобны своим производным. Таким свойством обладает показательная функция. Поэтому будем искать частные решения в виде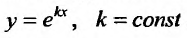
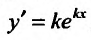
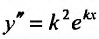
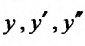
Множитель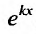
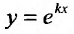
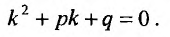
Алгебраическое квадратное уравнение (24.2.2) называют характеристическим уравнением данного дифференциального уравнения (24.2.1). Его корни находятся по формулам:
При этом могут представиться различные случаи, которые мы проанализируем подробнее.
1. Корчи характеристического уравнения действительны и различны:
В этом случае частными решениями будут функции:
так как каждому из корней соответствует частное решение. Эти решения линейно независимы, потому что их отношение не равно постоянной величине:
Тогда, в силу теоремы 24.1.6, общее решение уравнения (24.2.1) имеет вид:
Пример:
Найти общее решение уравнения:
Решение:
В силу, изложенного выше, составляем характеристическое уравнение 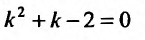
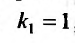
Так как корни характеристического уравнения различны, то общее решение задается функцией:
2. Корни характеристического уравнения комплексные.
Так как комплексные корни входят попарно сопряженными, то
Частные решения можно записывать в виде: 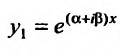
Это комплексные функции действительного аргумента, удовлетворяющие дифференциальному уравнению (24.2.1). Легко показать, что если какая-либо комплексная функция
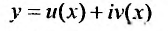
действительного аргумента удовлетворяет уравнению (24.2.1), то тгому уравнению удовлетворяют и функции 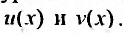
Комплексная функция равняется нулю, когда равны нулю ее действительная и мнимая части. Следовательно, 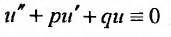
Это означает, что функции 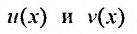
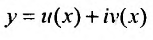
Перепишем теперь комплексные частные решения в виде суммы действительной и мнимой частей: 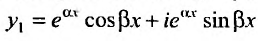
Тогда, частными решениями будут действительные функции: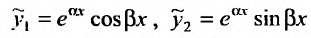
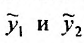
или
где 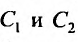
Заметим, что если в уравнении (24.2.2) р = 0,то характеристические корни чисто мнимые 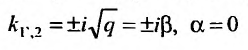
(24.2.4) имеет вид:
Пример:
Найти общее решение уравнения:
Решение:
Согласно изложенному выше, составляем характеристическое уравнение 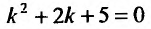
Следовательно, общее решение определяется функцией:
Пример:
Найти общее решение уравнения
Решение:
Составим характеристическое уравнение 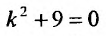
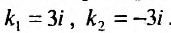
3. Корни характеристического уравнения действительные и равные: 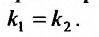
В этом случае, на основании случая 1, имеем одно частное решение 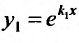
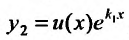
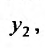
Подставляя функцию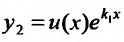
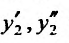
Так как 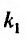
то 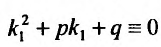
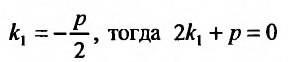
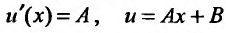
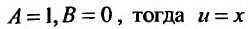
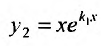
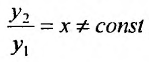
Поэтому общим решением будет функция:
Пример:
Найти общее решение уравнения:
Решение:
Составляем характеристическое уравнение 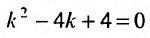
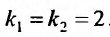
Структура общего решения линейного неоднородного уравнения второго порядка
В этом параграфе мы остановимся на изучении структуры общего решения линейного неоднородного уравнения второго порядка, т. с. уравнения вида:
Предположим, что уравнение (25.1.1) задано в области
Функция 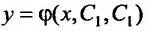
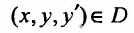
разрешимы относительно
Иначе: функция 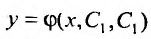
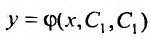
Структура общего решения уравнения (25.1.1) определяется следующей теоремой.
Теорема 25.1.1. Общее решение линейного неоднородного дифференциального уравнения (25.1.1) представляет сумму частного решения 
Доказательство. Пусть 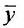
Так как 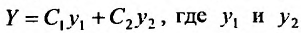
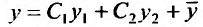
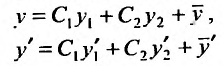
Подставляя в эти равенства начальные условия, получим систему относительно неизвестных
Эту систему можно переписать в виде:
где
Определитель последней системы является определителем Вронского, для функций 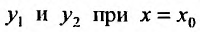
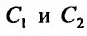
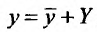
Теорема 25.1.2. Если правая часть неоднородного уравнения (25.1.1) равна сумме двух функций:
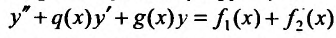
то частное решение такого уравнения можно получить как сумму частных решений аналогичных уравнений с правыми частями соответственно
Доказательство. Пусть 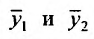
Складывая, правые и левые части тождеств, получаем:
откуда следует, что сумма 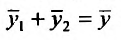
Таким образом, для решения неоднородного линейного уравнения необходимо найти общее решение соответствующего однородного и какое-либо частное решение исходного уравнения. Частное решение неоднородного линейного уравнения найти, вообще говоря, трудно Д1я уравнения (25.1.1). Мы остановимся на неоднородных линейных уравнениях с постоянными коэффициентами, т.е. уравнениях вида:
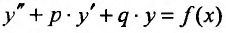
Способы нахождения частного решения линейного дифференциального уравнения второго порядка с постоянными коэффициентами и специальной правой частью
Пусть задано уравнение
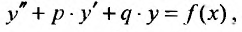
где р и q – действительные числа. Покажем, что частное решение уравнения (25.2.1) иногда можно найти, не прибегая к интегрированию, а методом неопределенных коэффициентов. Рассмотрим эти случаи.
1. Правая часть уравнения (25.1.1) представляет собой произведение показательной функции на многочлен: 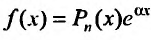
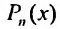
Если число а не является корнем характеристического уравнения 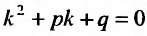
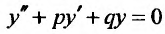
где 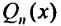
Действительно, подставляя 
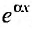
где 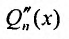
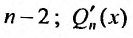
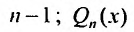
Если же число а простой корень характеристического уравнения, то частное решение следует искать в виде: 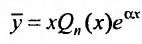
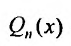
Действительно, если бы в этом случае стали искать частное решение в форме (25.2.2), то в равенстве (25.2.3) слева получили бы многочлен степени n-1, так как коэффициент при 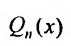
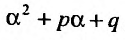
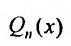
Если же число а двукратный корень характеристического уравнения, то частное решение следует искать в виде: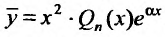
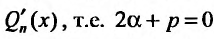
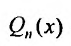
Замечание. Если правая часть уравнения (25.2.1) не содержит множителя 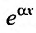
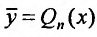
Пример №1
Найти общее решение уравнения:
Решение:
Вначале находим общее решение соответствующего однородного уравнения 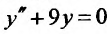
Далее ищем частное решение данного неоднородного уравнения. Так как правая часть заданного уравнения равна произведению многочлена на экспоненциальную функцию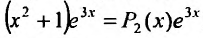
Вычисляя первую и вторую производные этого выражения и подставляя в дифференциальное уравнение, получим:
Сокращая на 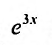
решая которую, находим: 
Общее решение заданного уравнения равно сумме общего решения соответствующего однородного уравнения и частного решения неоднородного:
1. Пусть теперь правом часть уравнения (25.2.1) представляет собой произведение многочленов на тригонометрические функции и показательную функцию’.
где 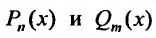
а) если число 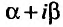
где 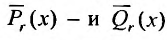
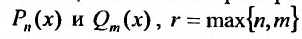
б) если число 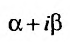
Заметим, что формы частных решений (25.2.5) и (25.2.6) сохраняются и в том случае, когда в правой части уравнения (25.2.1) один из многочленов 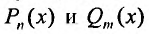
правая часть равна
Кроме того, если правая часть уравнения (25.2.1) имеет вид: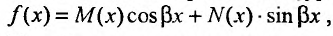
где М и N – постоянные числа, то частное решение ищем в виде:
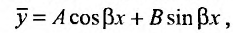
где А и В постоянные, подлежащие определению, когда 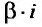
- Заказать решение задач по высшей математике
Пример №2
Найти общее решение линейного неоднородного уравнения
Решение:
Составим характеристическое уравнение соответствующего однородного уравнения: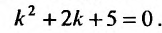
Поэтому общее решение соответствующего однородного уравнения определяется функцией:
Согласно теории, изложенной выше, частное решение неоднородного уравнения ищем в виде: 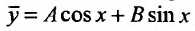
Приравнивая коэффициенты при одинаковых степенях cosx и sinx, получаем систему из двух уравнений:
Решая эту систему, находим: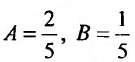
Следовательно, частное решение определяется функцией: 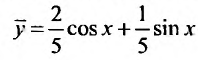
Способы решения дифференциальных уравнений второго порядка, допускающих понижение порядка
Рассмотрим дифференциальное уравнение второго порядка, разрешенное относительно производной
К простейшим интегрируемым дифференциальным уравнениям второго порядка вида (25.3.1) относятся уравнения, для которых функция, стоящая в правой части, зависит только от одного из трех аргументов
Рассмотрим также уравнения, допускающие понижение порядка, в которых функция зависит только от двух из трех аргументов:
Общее решение уравнения (25.3.2) находится двукратным интегрированием. Рассмотрим соответствующий пример.
Пример №3
Проинтегрировать дифференциальное уравнение
Решение:
Вычислим интегралы от обеих частей заданного уравнения, представив вторую производную в виде: 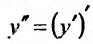
При интегрировании уравнения (25.3.3) вводится подстановка
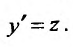
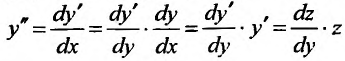
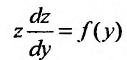
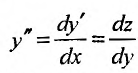
Преобразованные уравнения являются дифференциальными уравнениями первого порядка с разделяющимися переменными.
Пример №4
Найти частное решение дифференциального уравнения 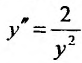
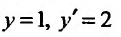
Решение:
Заданное уравнение относится к виду (25.3.3). Положим 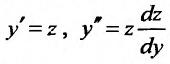
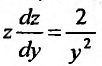
Выполним обратную подстановку 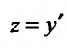
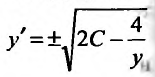
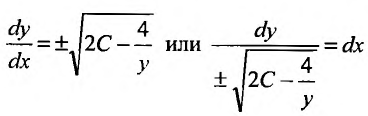
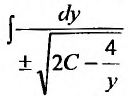
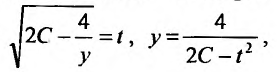
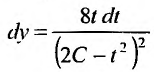
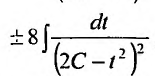
Тогда общее решение заданного уравнения будет иметь вид:
Уравнение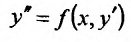
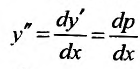
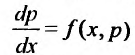
Пример №5
Проинтегрировать дифференциальное уравнение
Решение:
Положим 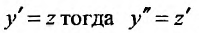
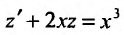
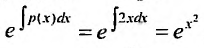
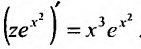
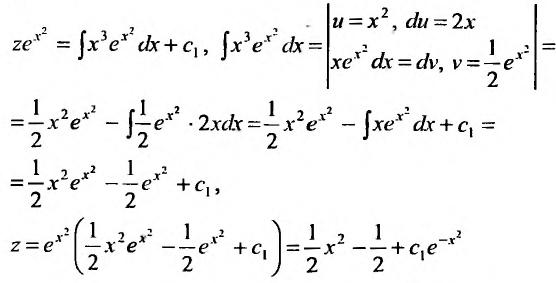
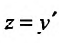
Вычислив интегралы левой и правой частей уравнения, находим общий интеграл:
Уравнение (25.3.6), 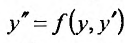
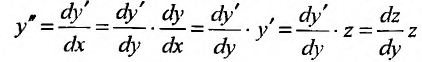
первого порядка: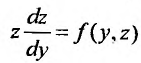
Пример №6
Проинтегрировать уравнение
Решение:
Заданное уравнение имеет вид (25.3.6). Применим подстановку 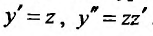
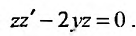
Выполнив обратную подстановку 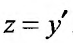
- Системы дифференциальных уравнений
- Числовые ряды
- Знакопеременные ряды
- Степенные ряды
- Предел и непрерывность функции двух переменны
- Дифференцируемость функции нескольких переменных
- Несобственные интегралы
- Дифференциальные уравнения первого порядка
I. Обыкновенные дифференциальные
уравнения
1.1. Основные понятия и определения
Дифференциальным уравнением называется
уравнение, связывающее между собой
независимую переменную x, искомую
функцию y и её производные или
дифференциалы.
Символически дифференциальное уравнение
записывается так:
F(x,y,y’)=0, F(x,y,y”)=0, F(x,y,y’,y”,.., y(n))=0
Дифференциальное уравнение называется
обыкновенным, если искомая функция зависит
от одного независимого переменного.
Решением дифференциального уравнения
называется такая функция ,
которая обращает это уравнение в тождество.
Порядком дифференциального уравнения
называется порядок старшей производной,
входящей в это уравнение
Примеры.
1. Рассмотрим дифференциальное уравнение
первого порядка
Решением этого уравнения является
функция y = 5 ln x. Действительно, ,
подставляя y’ в уравнение, получим
– тождество.
А это и значит, что функция y = 5 ln x– есть
решение этого дифференциального уравнения.
2. Рассмотрим дифференциальное уравнение
второго порядка y” – 5y’ +6y = 0. Функция
– решение этого уравнения.
Действительно, .
Подставляя эти выражения в уравнение,
получим: ,
– тождество.
А это и значит, что функция
– есть решение этого дифференциального
уравнения.
Интегрированием дифференциальных
уравнений называется процесс нахождения
решений дифференциальных уравнений.
Общим решением дифференциального
уравнения называется функция вида ,в
которую входит столько независимых
произвольных постоянных, каков порядок
уравнения.
Частным решением дифференциального
уравнения называется решение, полученное
из общего решения при различных числовых
значениях произвольных постоянных.
Значения произвольных постоянных
находится при определённых начальных
значениях аргумента и функции.
График частного решения
дифференциального уравнения называется интегральной
кривой.
Примеры
1.Найти частное решение дифференциального
уравнения первого порядка
xdx + ydy = 0, если y = 4 при x = 3.
Решение. Интегрируя обе части уравнения,
получим
Замечание. Произвольную постоянную С,
полученную в результате интегрирования,
можно представлять в любой форме, удобной
для дальнейших преобразований. В данном
случае, с учётом канонического уравнения
окружности произвольную постоянную С
удобно представить в виде .
– общее решение дифференциального
уравнения.
Частное решение уравнения,
удовлетворяющее начальным условиям y =
4 при x = 3 находится из общего
подстановкой начальных условий в общее
решение: 32 + 42= C2; C=5.
Подставляя С=5 в общее решение, получим x2
+y2 = 52.
Это есть частное решение
дифференциального уравнения, полученное из
общего решения при заданных начальных
условиях.
2. Найти общее решение дифференциального
уравнения
Решением этого уравнения является всякая
функция вида ,
где С – произвольная постоянная.
Действительно, подставляя в уравнения ,
получим: 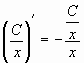
.
Следовательно, данное дифференциальное
уравнение имеет бесконечное множество
решений, так как при различных значениях
постоянной С равенство
определяет различные решения уравнения .
Например, непосредственной подстановкой
можно убедиться, что функции
являются решениями уравнения .
Задача, в которой требуется найти частное
решение уравнения y’ = f(x,y)
удовлетворяющее начальному условию y(x0)
= y0, называется задачей Коши.
Решение уравнения y’ = f(x,y),
удовлетворяющее начальному условию, y(x0)
= y0, называется решением задачи Коши.
Решение задачи Коши имеет простой
геометрический смысл. Действительно,
согласно данным определениям, решить
задачу Коши y’ = f(x,y) при условии y(x0)
= y0,, означает найти интегральную
кривую уравнения y’ = f(x,y) которая
проходит через заданную точку M0(x0,y0).
II. Дифференциальные уравнения первого
порядка
2.1. Основные понятия
Дифференциальным уравнением первого
порядка называется уравнение вида F(x,y,y’) =
0.
В дифференциальное уравнение первого
порядка входит первая производная и не
входят производные более высокого порядка.
Уравнение y’ = f(x,y) называется
уравнением первого порядка, разрешённым
относительно производной.
Общим решением дифференциального
уравнения первого порядка называется
функция вида ,
которая содержит одну произвольную
постоянную.
Пример. Рассмотрим дифференциальное
уравнение первого порядка .
Решением этого уравнения является
функция .
Действительно, заменив в данном уравнении,
его значением, получим
то есть 3x=3x
Следовательно, функция
является общим решением уравнения
при любом постоянном С.
Найти частное решение данного уравнения,
удовлетворяющее начальному условию y(1)=1
Подставляя начальные условия x = 1, y =1
в общее решение уравнения ,
получим
откуда C = 0.
Таким образом, частное решение получим из
общего
подставив в это уравнение, полученное
значение C = 0
– частное решение.
2.2. Дифференциальные уравнения с
разделяющимися переменными
Дифференциальным уравнением с
разделяющимися переменными называется
уравнение вида: y’=f(x)g(y) или через
дифференциалы ,
где f(x) и g(y)– заданные функции.
Для тех y, для которых ,
уравнение y’=f(x)g(y) равносильно уравнению,
в котором переменная y присутствует
лишь в левой части, а переменная x- лишь в
правой части. Говорят, «в уравнении y’=f(x)g(y
разделим переменные».
Уравнение вида
называется уравнением с разделёнными
переменными.
Проинтегрировав обе части уравнения
по x, получим G(y) = F(x) + C– общее
решение уравнения, где G(y) и F(x) –
некоторые первообразные соответственно
функций
и f(x), C произвольная постоянная.
Алгоритм решения дифференциального
уравнения первого порядка с разделяющимися
переменными
- Производную функции переписать через её
дифференциалы - Разделить переменные.
- Проинтегрировать обе части равенства,
найти общее решение. - Если заданы начальные условия, найти
частное решение.
Пример 1
Решить уравнение y’ = xy
Решение. Производную функции y’
заменим на
разделим переменные
проинтегрируем обе части равенства:
Ответ:
Пример 2
Найти частное решение уравнения
2yy’ = 1- 3x2,
если y0 = 3 при x0 = 1
Это—уравнение с разделенными
переменными. Представим его в
дифференциалах. Для этого перепишем данное
уравнение в виде
Отсюда
Интегрируя обе части последнего
равенства, найдем
Подставив начальные значения x0 = 1,
y0 = 3 найдем С 9=1-1+C, т.е. С = 9.
Следовательно, искомый частный интеграл
будет
или
Пример 3
Составить уравнение кривой, проходящей
через точку M(2;-3) и имеющей касательную с угловым
коэффициентом
Решение. Согласно условию
Это уравнение с разделяющимися
переменными. Разделив переменные, получим:
Проинтегрировав обе части уравнения,
получим:
Используя начальные условия, x = 2 и y
= – 3 найдем C:
Следовательно, искомое уравнение имеет
вид
2.3. Линейные дифференциальные уравнения
первого порядка
Линейным дифференциальным уравнением
первого порядка называется уравнение вида y’
= f(x)y + g(x)
где f(x) и g(x) – некоторые заданные функции.
Если g(x)=0 то
линейное дифференциальное уравнение
называется однородным и имеет вид: y’ = f(x)y
Если
то уравнение y’ = f(x)y + g(x) называется неоднородным.
Общее решение линейного однородного
дифференциального уравнения y’ = f(x)y задается формулой:
где С – произвольная постоянная.
В частности, если С =0, то решением
является y = 0 Если линейное однородное уравнение имеет
вид y’ = ky где k – некоторая постоянная, то его общее решение
имеет вид: .
Общее решение линейного неоднородного
дифференциального уравнения y’ = f(x)y + g(x) задается формулой ,
т.е. равно сумме общего решения
соответствующего линейного однородного
уравнения и частного решения
данного уравнения.
Для линейного неоднородного уравнения
вида y’
= kx + b,
где k и b–
некоторые числа и частным
решением будет являться постоянная функция
.
Поэтому общее решение имеет вид .
Пример. Решить уравнение y’ + 2y +3 = 0
Решение. Представим уравнение в виде y’
= -2y – 3 где k = -2, b= -3 Общее решение задается формулой .
Следовательно,
где С – произвольная постоянная.
Ответ:
2.4. Решение линейных дифференциальных
уравнений первого порядка методом Бернулли
Нахождение общего решения линейного
дифференциального уравнения первого
порядка y’ = f(x)y + g(x) сводится к решению двух дифференциальных
уравнений с разделенными переменными с
помощью подстановки y=uv,
где u и v – неизвестные функции от x.
Этот метод решения называется методом
Бернулли.
Алгоритм решения линейного дифференциального
уравнения первого порядка
y’ = f(x)y + g(x)
1. Ввести подстановку y=uv.
2. Продифференцировать это равенство y’ =
u’v + uv’
3. Подставить y и y’ в данное уравнение:
u’v + uv’ = f(x)uv + g(x) или u’v + uv’ + f(x)uv = g(x).
4. Сгруппировать члены уравнения так, чтобы
u вынести
за скобки:
5. Из скобки, приравняв ее к нулю, найти
функцию
Это уравнение с разделяющимися
переменными:
Разделим переменные и получим:
Откуда .
.
6. Подставить полученное значение v в уравнение
(из п.4):
и найти функцию
Это уравнение с разделяющимися переменными:
7. Записать общее решение в виде: ,
т.е. .
Пример 1
Найти частное решение уравнения y’ = -2y
+3 = 0 если y =1 при x = 0
Решение. Решим его с помощью
подстановки y=uv, .y’ = u’v + uv’
Подставляя y и y’
в данное уравнение, получим
Сгруппировав второе и третье слагаемое
левой части уравнения, вынесем общий
множитель u за
скобки
Выражение в скобках приравниваем к нулю и,
решив полученное уравнение, найдем функцию v
= v(x)
Получили уравнение с разделенными
переменными. Проинтегрируем обе части
этого уравнения:
Найдем функцию v:
Подставим полученное значение v в уравнение
Получим:
Это уравнение с разделенными переменными.
Проинтегрируем обе части уравнения:
Найдем функцию u = u(x,c)
Найдем общее решение:
Найдем частное решение уравнения,
удовлетворяющее начальным условиям y = 1 при
x = 0:
Ответ:
III. Дифференциальные уравнения высших
порядков
3.1. Основные понятия и определения
Дифференциальным уравнением второго
порядка называется уравнение, содержащее
производные не выше второго порядка. В
общем случае дифференциальное уравнение
второго порядка записывается в виде: F(x,y,y’,y”)
= 0
Общим решением дифференциального
уравнения второго порядка называется
функция вида ,
в которую входят две произвольные
постоянные C1 и C2.
Частным решением дифференциального
уравнения второго порядка называется
решение, полученное из общего
при некоторых значениях произвольных
постоянных C1 и C2.
3.2. Линейные однородные дифференциальные
уравнения второго порядка с
постоянными коэффициентами.
Линейным однородным дифференциальным
уравнением второго порядка с постоянными
коэффициентами называется уравнение вида
y” + py’ +qy = 0, где pи q–
постоянные величины.
Алгоритм решения однородных дифференциальных
уравнений второго порядка с постоянными
коэффициентами
1. Записать дифференциальное уравнение в
виде: y” + py’ +qy = 0.
2. Составить его характеристическое
уравнение, обозначив y” через r2,
y’ через r, yчерез
1:
r2 + pr +q = 0
3.Вычислить дискриминант D = p2 -4q
и найти корни характеристического
уравнения; при этом если:
а) D > 0; следовательно,
характеристическое уравнение имеет два
различных действительных корня .
Общее решение дифференциального уравнения
выражается в виде ,
где C1 и C2 – произвольные постоянные.
б) D = 0; следовательно,
характеристическое уравнение имеет равные
действительные корни .
Общее решение дифференциального уравнения
выражается в виде
в) D < 0; следовательно,
характеристическое уравнение имеет
комплексные корни,
Общее решение дифференциального уравнения
выражается, в виде
Примеры.
1. Найти частное решение дифференциального
уравнения
Решение. Составим характеристическое
уравнение
D>0,
Общее решение
Дифференцируя общее решение, получим
Составим систему из двух уравнений
Подставим вместо ,
и
заданные начальные условия:
Таким образом, искомым частным решением
является функция
.
2. Найти частное решение уравнения
Решение
<0,
Общее решение
–
частное решение.
IV. Практическая работа
Вариант 1
1. Составить уравнение кривой, проходящей
через точку M(1;2) и имеющей угловой коэффициент .
2. Найти частные решения дифференциальных
уравнений:
а)
б)
в)
г)
Вариант 2
1. Составить уравнение кривой, проходящей
через точку M(2;1) и имеющей угловой коэффициент
2. Найти частные решения дифференциальных
уравнений:
а)
б)
в)
г)
V. Ответы
|
Вариант 1 |
Вариант 2 |
|
1. |
1. |
|
2. а) |
2. а) |
|
б) |
б) |
|
в) |
в) |
|
г) |
г) |