Определение линейной зависимости
Линейная связь описывает отношение между двумя различными переменными — x и y в виде прямой линии на графике. При представлении линейной зависимости через уравнение значение y выводится через значение x, отражая их корреляцию.
Линейные отношения применяются в повседневных ситуациях, когда один фактор зависит от другого, например, повышение цены на товары снижает спрос на них. В любом случае для получения результата учитываются только две переменные.
Оглавление
- Определение линейной зависимости
- Что такое линейная зависимость?
- Уравнение линейной связи с графиком
- Линейная функция/уравнение
- Форма пересечения наклона
- Стандартная/общая форма
- Примеры
- Линейные и нелинейные отношения
- Графическое представление
- Изменение переменных
- Области применения
- Рекомендуемые статьи
- Линейная связь — это связь, в которой две переменные имеют прямую связь, что означает, что если значение x изменяется, y также должно изменяться в той же пропорции.
- Это статистический метод, позволяющий получить прямые или коррелированные значения двух переменных с помощью графика или математической формулы.
- Количество переменных, рассматриваемых в линейном уравнении, никогда не превышает двух.
- Корреляция двух переменных в повседневной жизни может быть понята с помощью этой концепции.
Что такое линейная зависимость?
Он лучше всего описывает взаимосвязь между двумя переменными (независимой и зависимой), обычно представленными x и y. В области статистики это одна из самых простых концепций для понимания.
Для линейной зависимости переменные должны образовывать прямую линию на графике каждый раз, когда значения x и y складываются вместе. С помощью этого метода можно понять, как различия между двумя факторами могут повлиять на результат и как они соотносятся друг с другом.
Возьмем реальный пример продуктового магазина, где его бюджет является независимой переменной. Независимая переменная. цель), которая измеряется в математическом, статистическом или финансовом моделировании. Читать далее, а товары, подлежащие хранению, являются зависимой переменной. Предположим, что бюджет составляет 2000 долларов США, а продуктовые товары включают 12 брендов закусок (1–2 доллара за упаковку), 12 брендов прохладительных напитков (2–4 доллара за бутылку), 5 брендов хлопьев (5–7 долларов за упаковку) и 40 брендов средств личной гигиены. ($3-$30 за продукт). Из-за бюджетных ограничений и различных цен покупка большего количества одного товара потребует покупки меньшего количества другого.
Уравнение линейной связи с графиком
Будь то графически или математически, значение y зависит от x, что дает прямую линию на графике. Вот краткая формула для понимания линейной корреляции. КорреляцияКорреляция — это статистическая мера между двумя переменными, которая определяется как изменение одной переменной, соответствующее изменению другой. Он рассчитывается как (x(i)-среднее(x))*(y(i)-среднее(y)) / ((x(i)-среднее(x))2 * (y(i)-среднее( y))2. перевод между переменными.
у = мх + б
В формуле m обозначает уклон. В то же время b является точкой пересечения оси Y или точкой на графике, пересекающей ось y с координатой x, равной нулю. Если значения m, x и b заданы, можно легко получить значение y. Можно графически изобразить то же самое, чтобы показать линейную зависимость. Давайте поймем процесс, когда значения для переменных x и y предполагаются следующим образом в сумме ниже:
- х = 2, 4, 6, 8
- у = 7, 13, 19, 25
Чтобы вычислить m, начните с поиска разности между значениями x и y, а затем представите их в виде дроби.
Следовательно, m = y2 – y1/x2 – x1
Помещая значения из значений x и y в приведенное выше уравнение,
мы получаем,
- м = 13-7/4-2
- м = 6/2
- м = 3
Следующий шаг — найти гипотетическое число (b), которое нужно добавить или вычесть в формуле, чтобы получить значение y. Как таковой,
у = мх + б
- у = 3*2 + 1
- у = 7.
Аналогично, подсчитав остальные точки, получим следующий график.
График линейной зависимости будет выглядеть так:

Практическим примером линейного уравнения может быть приготовление домашней пиццы. Здесь две переменные — это количество людей, которых нужно обслужить (постоянная или независимая переменная), и ингредиенты для пиццы (зависимая переменная). Например, предположим, что есть рецепт пиццы на четверых, но его едят только два человека. Чтобы вместить двух человек, сокращение количества ингредиентов наполовину уменьшит производительность вдвое.
Линейные и нелинейные отношения
Хотя линейные и нелинейные отношения описывают отношения между двумя переменными, обе они различаются по своему графическому представлению и тому, как переменные коррелируют.
Графическое представление
Линейная связь всегда будет отображать на графике прямую линию, отображающую отношения между двумя переменными. С другой стороны, нелинейная зависимость может создать кривую линию на графике с той же целью.
 Изменение переменных
Изменение переменных
В линейной зависимости изменение независимой переменной изменит зависимую переменную. Но это не относится к нелинейным отношениям, поскольку любые изменения одной переменной не повлияют на другую.
Области применения
Линейная зависимость лучше всего описывает ситуации, когда переменные взаимозависимы, например, физические упражнения и потеря веса. Здесь упражнения x раз в день значительно уменьшат любое количество веса.
Не существует линейной связи между переменными в нелинейной зависимости, такой как эффективность лекарства и продолжительность приема. Это связано с тем, что может быть несколько промежуточных факторов, влияющих на эффективность препарата, например:
- Если пациент принимает лекарства вовремя?
- Было ли оно принято в установленном порядке?
- Посещал ли пациент врача для периодического осмотра, как это было предложено в рецепте?
Следовательно, эффективность препарата определяется несколькими факторами, а не только продолжительностью приема, что делает зависимость нелинейной. Было проведено множество исследований, чтобы оценить жизнеспособность изучения ситуаций с точки зрения линейной корреляции. Этот Гарвардское исследование сосредоточил внимание на некоторых проблемных областях в этом отношении. Он также говорил о том, как много ситуаций неизбежно нелинейны.
Рекомендуемые статьи
В этом исчерпывающем руководстве по линейной зависимости обсуждались уравнения, примеры и отличия от нелинейная связь, вместе с ключевыми выводами. Чтобы узнать больше о его использовании в финансах, прочитайте следующие статьи:
- Регрессия
- Линейная регрессия в Excel
- Нелинейная регрессия в Excel
После
установления характера и тесноты
корреляционной связи необходимо получить
математическую модель исследуемой
зависимости в виде уравнения связи.
Если связь нелинейная, то необходимо
подобрать функцию, график которой будет
максимально приближен ко всем исходным
точкам, а если линейная – то получить
конкретное уравнение прямой.
В
данной работе, независимо от того какой
характер связи получится фактически,
будем рассчитывать уравнение прямой,
условно принимая, что связь между
исследуемыми признаками линейная. Для
этого необходимо преобразовать исходное
уравнение прямой:
![]()
Подставив
в приведенное выше уравнение все
известные значения (My,
r,
σy,
σx,
Mx)
неизвестными останутся только х и у:
![]()
В
результате преобразований:
у=3,1+0,1112x–2,798
получим конкретное
уравнение прямой:
уx
= 0,1112х + 0,3
Далее
заполняется таблица (табл. 3.7) для
построения графика. При этом значения
yx
рассчитываются по найденному выше
конкретному уравнению прямой.
Таблица 3.7
|
Х |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
|
yср |
1,625 |
1,94 |
2,48 |
3,05 |
3,44 |
3,76 |
4,28 |
|
yx |
1,63 |
2,08 |
2,52 |
2,97 |
3,41 |
3,86 |
4,3 |
|
yср–yx |
-0,005 |
-0,14 |
-0,04 |
0,08 |
0,03 |
-0,1 |
-0,02 |
На
графике изображаются исходные данные
(yср)
в виде отдельных точек и вероятные (yx
– найденные по рассчитанному уравнению)
– в виде прямой (рис. 3.3).

Рис. 3.3 Графическое
изображение корреляционной связи.
4. Регрессионный анализ
4.1. Техника и способы регрессионного анализа
В
качестве примера для аналитического
выравнивания используются данные
взаимосвязи двух сопряженных признаков:
диаметров (Д), принимаемых за X, и высот
деревьев (H), принимаемых за Y.
Таблица
4.1
Взаимосвязь
диаметров и высот (невыравненные данные)
|
№ классов |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Д (X), |
12 |
16 |
20 |
24 |
28 |
32 |
36 |
40 |
44 |
|
H (Y) м |
16,00 |
18,00 |
20,15 |
22,14 |
23,48 |
23,65 |
24,62 |
26,00 |
27,00 |
4.2 Выравнивание по уравнению прямой линии
Аналитическое
выравнивание имеет своей конечной целью
получение конкретного уравнения связи
между двумя сопряженными признаками.
В первую очередь исходные данные наносят
на систему координат и по характеру
расположения точек определяют функцию
для выравнивания. Её график должен
проходить максимально близко по отношению
ко всем исходным точкам. В данном примере
характер расположения точек линейный
следовательно выравнивание осуществляем
по уравнению прямой.
Как
известно, уравнение линейной зависимости
общего вида будет иметь вид: y
= а x+b.
Вычисление
конкретного уравнения сводится к
определению числовых значений
коэффициентов а, b,
для получения которых существует
несколько способов. Рассмотрим два,
наиболее широко применяемых способа,
характеризующихся различной точностью
и трудоемкостью:
а)
способ координат двух избранных точек,
обеспечивающий получение менее точных
результатов, но гораздо более простым
путем;
б)
способ наименьших квадратов, позволяющий
получить достаточно точные результаты
путем использования координат всех
выравниваемых точек (наблюдений).
Остановимся
на технике работ при вычислении
конкретного уравнения методом координат
избранных точек. В этом случае исходные
данные изображаются на графике, и
производится предварительное выравнивание.
Результирующая линия проводится между
точками с таким расчетом, чтобы разделить
их общее количество на две приблизительно
равные части. При этом необходимо
стремиться к такому положению, чтобы
расстояние между линией и исходными
точками было кратчайшим. Для облегчения
техники выравнивания и увеличения его
точности можно рекомендовать следующий
прием. Соединить все выравниваемые
точки и постараться провести плановую
выравнивающую линию по возможности
ближе к этим серединам. При этом желательно
провести прямую таким образом, чтобы
хотя бы две исходные точки попали на
неё. С полученной прямой линии снимаем
координаты двух любых точек исходных
данных (лежащих на проведенной прямой).
Если число наблюдений в классах известно,
то следует отдать предпочтение точкам,
обеспеченным наибольшим числом
наблюдений. В нашем примере в качестве
избранных использованы координаты
точек классов № 2 и № 6.
X2=16; Y2=18,00; X6=32; Y6=23,65.
Система двух
конкретных уравнений приобретет вид

После
подстановки координат избранных точек:
![]()
После
решения системы относительно а и b,
получим
а=0,35
b=12,4
Следовательно,
полученное конкретное уравнение связи
Y/Х
(Д/Н) будет иметь вид
у=0,35x+12,4
Для
краткости изложения в последующем
тексте полученным уравнениям присвоены
определенные номера: уравнение,
вычисленное методом координат точек,
получает номер I,
а уравнение, полученное методом наименьших
квадратов – номер II.
Пределы «работы»
полученного уравнения по диаметру от
10 см до 46 см.
Рассмотрим
технику вычислений при использовании
способа наименьших квадратов. Для
получения конкретного уравнения в этом
случае используются координаты всех
точек. Это учитывается при выведении
системы уравнений для этого метода.
Так, если записать уравнения прямой для
каждой точки, а потом просуммировать
левые и правые части всех уравнений, то
получим следующее:
y1=
ax1
+ b
y2=
ax2
+ b
y3=
ax3
+
b
……………
……………
∑y=a∑x+bn.
Так
как нам необходимо найти два неизвестных
значения (a
и b),
то в системе должно быть два уравнения.
Для получения второго уравнения системы
умножим обе части каждого уравнения на
соответствующий «х» и просуммируем
левые и правые части уравнений. Получим:
x1y1=
ax12
+ bх1
x2y2=
ax22
+ bx2
x3y3=
ax32
+
bx3
….……………
….……………
∑хy=a∑x2+b∑х.
Таким
образом, мы вывели оба уравнения системы:

Для
удобства вычислений числовых значений
указанной системы составляется
вспомогательная таблица (табл.4.2).
Таблица 4.2
Вспомогательные
расчеты для вычисления конкретного
уравнения
прямой
линии
|
Исходные данные |
ХY |
Х2 |
|
|
Х |
Y |
||
|
12 |
16,00 |
192,00 |
144 |
|
16 |
18,00 |
288,00 |
256 |
|
20 |
20,15 |
403,00 |
400 |
|
24 |
22,14 |
531,36 |
576 |
|
28 |
23,48 |
657,64 |
784 |
|
32 |
23,65 |
756,80 |
1024 |
|
36 |
24,62 |
886,32 |
1296 |
|
40 |
26,00 |
1040,00 |
1600 |
|
44 |
27,00 |
1188,00 |
1936 |
|
|
|
|
|
Подставим
итоговые данные в систему уравнений и
вычислим коэффициенты а, b,
имея в виду, что значение «n»
соответствует числу классов по X:
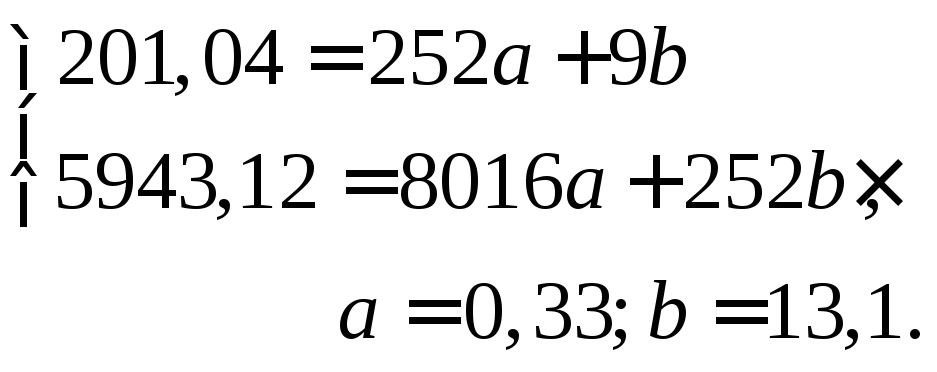
Следовательно,
конкретное уравнение будет иметь вид
Y=0,33Х+13,1
С
целью последующего анализа результатов
применения полученных уравнений
вычисляются вероятные (теоретические)
значения зависимого признака по первому
уравнению (yв1)
и второму уравнению (yв2).
Последние (yв2)
сравниваются с исходными (опытными)
данными (у). Указанные сравнения (a
= y–yв2)
производятся по всем классам X, а их
результат для
прямой линии показан
в табл.
4.3.
Таблица 4.3
Сравнение
исходных и вероятных высот деревьев,
полученных по уравнению прямой линии
|
Исходные данные |
Вероятные |
Отклонения, м |
||
|
диаметр, см |
высота, м |
Ув1 |
Ув2 |
a |
|
X |
Y |
|||
|
12 |
16,00 |
16,60 |
17,06 |
-1,06 |
|
16 |
18,00 |
18,00 |
18,38 |
-0,38 |
|
20 |
20,15 |
19,40 |
19,70 |
+0,45 |
|
24 |
22,14 |
20,80 |
21,02 |
+1,12 |
|
28 |
23,48 |
22,20 |
22,34 |
+1,14 |
|
32 |
23,65 |
23,60 |
23,66 |
-0,01 |
|
36 |
24,62 |
25,00 |
24,98 |
-0,36 |
|
40 |
26,00 |
26,40 |
26,40 |
-0,40 |
|
44 |
27,00 |
27,80 |
27,62 |
-0,62 |
|
∑-0,12 |
Приведенные
данные позволяют, прежде всего, проверить
правильность вычислений, выполненных
при получении конкретных уравнений, на
предмет обнаружения грубых арифметических
ошибок.
Правильность
вычисления уравнений связи проверяется
путем сравнения исходных значений Y
с вероятными (ув),
полученными по уравнению I
(ув1)
и уравнению II
(ув2)
Критерием правильности вычислений
уравнения I
будет совпадение вероятных значений
ув1
с
исходными значениями Y
для тех классов, в которых использованы
координаты точек в качестве исходных
для получения конкретного уравнения
I.
В нашем примере для уравнения прямой
линии значение ув1
равно
18,0, соответствует исходным данным Y
во втором классе, то есть также 18,0.
Аналогичное положение и в следующем,
шестом классе: ув1
=23,6
практически не отличается от Y
=23,65. Совпадение Y
и
![]() в остальных классах не обязательно и
в остальных классах не обязательно и
может наступить только случайно.
Некоторый
контроль правильности уравнения II
можно получить
путем
сопоставления Y
и ув2
– во
всех классах. В этом
случае
должно наблюдаться такое сочетание
знаков (плюс и минус), которое отражает
«срединное» положение выравнивающей
прямой между выравниваемыми исходными
значениями Y.
О
явной неправильности полученного
уравнения будет свидетельствовать
наличие во всех классах только +, равно
как и знаков -, а также, если в нескольких
начальных классах будут наблюдаться
отклонения с одним и тем же знаком ( +
или -), а во всех последующих классах с
противоположным, а именно:
+++++++
– – – – – – –
++++- – –
– – – -+++
Заметим,
что описанные критерии правильности и
вычислений I
и II
уравнений распространяются и на
выравнивание по всем другим линиям
связи.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Парная линейная регрессия и метод наименьших квадратов (МНК)
Краткая теория
Простейшей системой
корреляционной связи является линейная связь между двумя признаками – парная
линейная корреляция. Практическое значение ее в том, что есть системы, в
которых среди всех факторов, влияющих на результативный признак, выделяется
один важнейший фактор, который в основном определяет вариацию результативного
признака. Измерение парных корреляций составляет необходимый этап в изучении
сложных, многофакторных связей. Есть такие системы связей, при изучении которых
следует предпочесть парную корреляцию. Внимание к линейным связям объясняется
ограниченной вариацией переменных и тем, что в большинстве случаев нелинейные
формы связей для выполнения расчетов преобразуются в линейную форму.
Уравнение парной линейной
корреляционной связи называется уравнением парной регрессии и имеет вид:
где
–
среднее значение результативного признака
при
определенном значении факторного признака
;
– свободный
член уравнения;
– коэффициент
регрессии, измеряющий среднее отношение отклонения результативного признака от
его средней величины к отклонению факторного признака от его средней величины
на одну единицу его измерения – вариация
, приходящаяся на единицу вариации
.
Параметры уравнения
находят
методом наименьших квадратов (метод решения систем уравнений, при котором в
качестве решения принимается точка минимума суммы квадратов отклонений), то
есть в основу этого метода положено требование минимальности сумм квадратов
отклонений эмпирических данных
от
выровненных
:
Для нахождения минимума
данной функции приравняем к нулю ее частные производные.
В результате получим
систему двух линейных уравнений, которая называется системой нормальных
уравнений:
Решая эту систему в общем
виде, получим:
Параметры уравнения парной
линейной регрессии иногда удобно исчислять по следующим формулам, дающим тот же
результат:
или
Если
коэффициент линейной корреляции
уже
рассчитан, то легко может быть найден коэффициент
парной
регрессии:
где
,
– стандартные
отклонения.
Примеры решения задач
Задача 1
Имеются следующие данные о
цене на нефть
(ден.
ед.) и индексе акций нефтяных компаний
(усл.
ед.).
| Цена на нефть (ден. ед.) | 17,28 | 17,05 | 18,30 | 18,80 | 19,20 | 18,50 |
| Индекс акций (усл. ед.) | 537 | 534 | 550 | 555 | 560 | 552 |
- Построить
корреляционное поле. - Предполагая, что между
переменными x и y существует линейная зависимость, найти уравнение линейной
регрессии - Оценить тесноту связи.
Решение
Построим корреляционное
поле, для этого отметим в системе координат
6 точек, соответствующих данным парам значений этих признаков.
Корреляционное поле и линия регрессии
Расположение точек на
рисунке показывает, что зависимость между компонентами
и
двумерной дискретной случайной величины может
выражаться линейным уравнением регрессии
.
Составим
расчетную таблицу:
Расчетная вспомогательная таблица
|
|
|
|
|
|
|
| 1 | 17,28 | 537 | 298,5984 | 288369 | 9279,36 |
| 2 | 17,05 | 534 | 290,7025 | 285156 | 9104,7 |
| 3 | 18,3 | 550 | 334,89 | 302500 | 10065 |
| 4 | 18,8 | 555 | 353,44 | 308025 | 10434 |
| 5 | 19,2 | 560 | 368,64 | 313600 | 10752 |
| 6 | 18,5 | 552 | 342,25 | 304704 | 10212 |
| Сумма | 109,13 | 3288 | 1988,521 | 1802354 | 59847,06 |
Коэффициенты
уравнения регрессии
можно найти методом наименьших квадратов,
решив систему нормальных уравнений:
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Подставляя
в систему уравнений числовые значения, получаем:
Решая
систему уравнений, получаем:
Уравнение
парной линейной регрессии:
Коэффициент линейной корреляции
вычислим по формуле:
Вывод
Таким
образом уравнение линейной регрессии, устанавливающее зависимость между ценой
на нефть и индексом акций имеет вид
– с увеличением цены на нефть на 1 ден.ед.
цена акций увеличивается на 12,078 ед. Коэффициент корреляции очень близок к
единице – между исследуемыми величинами существует очень тесная связь.
Задача 2
По
территории региона приводятся данные за 2011 г.
Требуется:
-
Построить линейное уравнение парной регрессии
от
.
Рассчитать линейный коэффициент парной корреляции и среднюю ошибку
аппроксимации.
Оценить статистическую значимость параметров регрессии и корреляции с помощью
–критерия Фишера и
–критерия Стьюдента.
Выполнить прогноз заработной платы
при прогнозном значении среднедушевого
прожиточного минимума
, составляющем
107% от среднего уровня.
Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный
интервал.
На одном графике построить исходные данные и теоретическую прямую.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Уравнение линейной парной регрессии
1)
Для расчета параметров уравнения линейной регрессии строим расчетную таблицу:
Получено
уравнение линейной регрессии
Вывод
С
увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная
заработная плата возрастает в среднем на 1.012 руб.
Коэффициент линейной корреляции
2)
Теснота линейной связи оценивается с помощью
коэффициента корреляции
:
Коэффициент
детерминации:
Вывод
Это
означает, что 69.2% вариации заработной платы
объясняется вариацией фактора
–среднедушевого прожиточного минимума.
Средняя ошибка аппроксимации
Качество
модели можно оценить с помощью средней ошибки аппроксимации:
Вывод
Качество
построенной модели оценивается как хорошее, так как средняя ошибка
аппроксимации не превышает 8-10%.
F-критерий
3)
Рассчитаем
– критерий.
По таблице F-распределения Фишера-Снедекора, при уровне значимости α=0,05 и числе степеней свободы k1=1 и k2=12-2=10, критическое значение:
Вывод
– гипотеза о статистической незначимости
уравнения регрессии отклоняется.
Статистическая значимость параметров регрессии
Оценку
статистической значимости параметров регрессии проведем с помощью
t–статистики Стьюдента
и путем расчета
доверительного интервала каждого из показателей.
Выдвигаем
гипотезу
о статистически незначимом отличии показателей
от нуля:
для числа степеней свободы
и
составит 2,23
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Определим
случайные ошибки
Тогда:
Фактическое значение превосходит
табличное значение t–статистики.
Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Фактическое значение превосходит
табличное значение t–статистики. Нулевая
гипотеза отклоняется – то есть
не случайно отличается от нуля, а
статистически значимо.
Рассчитаем
доверительные интервалы для параметров регрессии
и
. Для этого
определим предельную ошибку для каждого показателя:
Доверительные
интервалы:
или
или
Точечный прогноз
4)
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение прожиточного минимума составит
руб., тогда прогнозное значение среднедневной
заработной платы составит:
Интервальный прогноз
5)
Ошибка прогноза составит:
Предельная
ошибка прогноза, которая в 95% случаев не будет превышена, составит:
Доверительный
интервал прогноза:
6) Построим исходные данные
и теоретическую прямую:
Корреляционное поле и прямая уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
А) линейной;
Б) степенной;
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
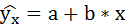
Решаем систему нормальных уравнений относительно a и b:
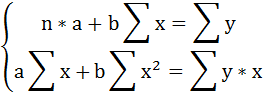
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x2 | y2 |  |
 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
 |
8,4988 | 11,1431 | х | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
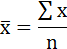
Cреднее квадратическое отклонение рассчитаем по формуле:
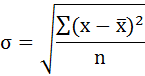
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
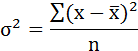
Параметры уравнения можно определить также и по формулам:
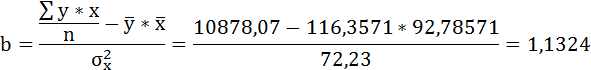
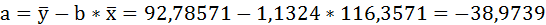
Таким образом, уравнение регрессии:
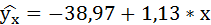
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
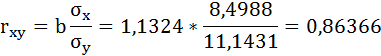
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
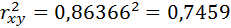
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения  .
.
Так как
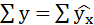 ,
,
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
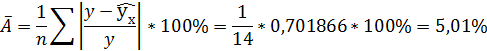
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
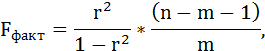
где n – число единиц совокупности;
m – число параметров при переменных х.
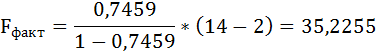
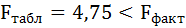
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
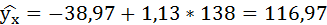
2. Степенная регрессия имеет вид:
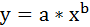
Для определения параметров производят логарифмирование степенной функции:
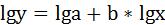
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
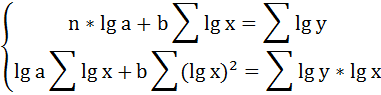
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x)2 | (lg y)2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
 |
8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х |
 |
72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
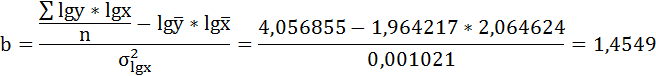
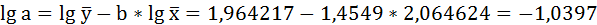
Получим линейное уравнение:
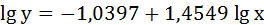
Выполнив его потенцирование, получим:
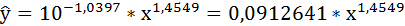
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 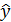 . По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
. По ним рассчитаем показатели: тесноты связи – индекс корреляции и среднюю ошибку аппроксимации.
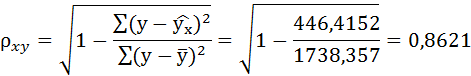
Связь достаточно тесная.
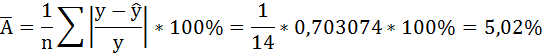
В среднем расчётные значения отклоняются от фактических на 5,02%.
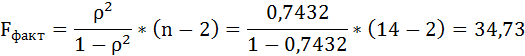
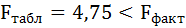
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
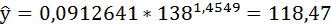
3. Уравнение равносторонней гиперболы
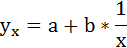
Для определения параметров этого уравнения используется система нормальных уравнений:
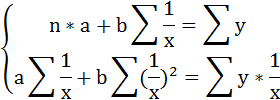
Произведем замену переменных
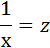
и получим следующую систему нормальных уравнений:
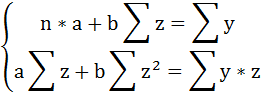
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | 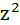 |
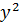 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
 |
8,4988 | 11,1431 | 0,000640820 | х | х | х |
 |
72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у |  |
 |
 |
 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
 |
8,4988 | 11,1431 | х | х | х | х |
 |
72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
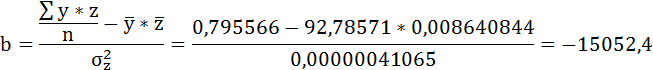
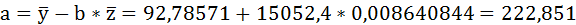
Получено уравнение:
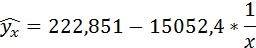
Индекс корреляции:
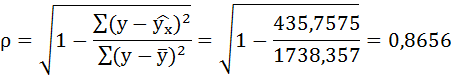
Связь достаточно тесная.
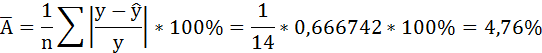
В среднем расчётные значения отклоняются от фактических на 4,76%.
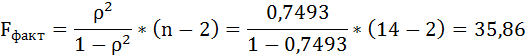
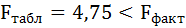
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
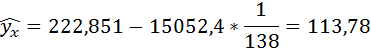
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
