Как составить линейную комбинацию векторов - Сайт, где вы сможете решить свои вопросы

Линейные комбинации векторов

Применяя
линейные операции, можно составлять
суммы векторов, умноженных на числа.

Вектор
называется линейной
комбинацией векторов
,
если он может быть представлен в виде

где
—
некоторые числа. В этом случае говорят,
что вектор
разложен
по векторам
,
а числа
называют коэффициентами
разложения.

Линейная
комбинация
с
нулевыми коэффициентами называется тривиальной.

Отметим
следующие свойства
линейных комбинаций векторов:

1.
Если векторы
—
коллинеарны, то любая их линейная
комбинация им коллинеарна.

2.
Если векторы
—
компланарны, то любая их линейная
комбинация им компланарна.

Докажем,
например, первое свойство. При умножении
вектора на число получаем (по определению)
вектор, колпинеарный данному. При
сложении двух векторов, параллельных
некоторой прямой, получаем (по определению)
вектор, параллельный той же самой прямой.
Поэтому линейная комбинация
двух
коллинеарных векторов
и
коллинеарна
им. По индукции свойство распространяется
на любое конечное число коллинеарных

векторов.

Билет
8.

§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.

Для
дальнейшего изучения свойств пространства
необходимо ввести определение ориентации
пространства. Строгая теория, касающаяся
этого понятия не очень сложна, но
достаточно суха. В связи с этим ограничимся
лишь некоторыми “качественными”
пояснениями.

Итак,
все упорядоченные некомпланарные тройки
векторов могут
быть разбиты на два непересекающихся
класса: правые тройки и левые тройки.

Определение
1:
Упорядоченная тройка некомпланарных
векторов а₁, а₂, а₃ называетсяправой,
если наблюдателю, находящемуся внутри
телесного угла, образованного этими
векторами, кратчайшие повороты
от а₁ к а₂ и
от а₂ к а₃ кажутся
происходящими против часовой стрелки.
Если повороты происходят по часовой
стрелке, то тройка – левая.

Есть
и ещё один способ разделить эти два
класса:

Правило
правой руки: Совместите
начала всех векторов тройки в одной
точке. Представьте, что в этой точке
находится ладонь Вашей правой руки.
Совместите большой палец с первым
вектором базиса, а указательный – со
вторым. Если теперь вы сможете совместить
средний палец с третьим вектором, то
рассматриваемая тройка векторов –
правая. Если нет – левая.

Выбрав
один из двух классов и назвав все входящие
в него базисы “положительными” мы
зададим ориентацию
пространства.

Далее
будем считать положительными правые
тройки векторов. Все дальнейшие
определения будем давать с учетом этого

§ 2. Скалярное произведение векторов.

Определение
2: Скалярное
произведение ставит
в соответствие паре векторов a и b число
(a,b)=|a|·|b|·cosφ_a,b.

Свойства
скалярного произведения:

1.
коммутативность: (a,b)=(b,a)

2.
(а,а)=|а|²

3.
(a,b)=0
<=> a
b

4.
Дистрибутивность: (a₁+а₂,b)=
(a₁,b)+
(a₂,b)

5.
(а, λ·b)= λ·(a,b)
λ
R.

Утверждение
1: В
декартовом базисе если а={x₁,y₁,z₁}, b={x₂,y₂,z₂},
то (a,b)=x₁·x₂+y₁·y₂+z₁·z₂.

Пример
1. Найти
угол между векторами.

§ 3. Векторное произведение векторов.

Определение
3: Векторным
произведением упорядоченной
пары векторов a и b называется
вектор [a,b],
такой что

|
[a,b]
|=S_a,b,
где S_a,b –
площадь параллелограмма, построенного
на векторах a и b.
(Если a || b,
то S_a,b=0.)
a
[a,b]
b.
a, b,
[a,b]
– правая тройка.

Свойства
векторного произведения:

[a,b]
= -[b,a]
[a,b]
= θ  a || b
[a₁+a₂,b]
= [a₁,b]+[a₂,b]
λ·[a,b]
= [λ·a,b]
= [a,λ·b]
λ
R.

Утверждение
2: В
декартовой системе координат
(базис i, j, k), a={x₁, y₁, z₁}, b={x₂, y₂,z₂}

=>
[a,b]
=

Пример
2. Вычислить
площадь параллелограмма, построенного
на векторах a и b.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Лине́йная комбина́ция — выражение, построенное на множестве элементов путём умножения каждого элемента на коэффициенты с последующим сложением результатов (например, линейной комбинацией и будет выражение вида , где и — коэффициенты)^[1]^[2]^[3].

Понятие линейной комбинации является одним из ключевых в линейной алгебре и смежных областях математики. В классическом случае линейная комбинация рассматривается в контексте векторных пространств, но существуют обобщения на произвольные модули над кольцами и бимодули^[⇨]

Определение[править | править код]

Пусть — поле (например, поле вещественных чисел) и — векторное пространство над (элементы — векторы, а элементы — скаляры).
Если $v_{1},dots ,v_{n}$ — векторы, а $a_{1},dots ,a_{n}$ — скаляры, то линейная комбинация этих векторов со скалярами в качестве коэффициентов — это:

$a_{1}v_{1}+a_{2}v_{2}+a_{3}v_{3}+cdots +a_{n}v_{n}$

Имеется некоторая двусмысленность в применении понятия «линейная комбинация», поскольку оно может относиться как к самому выражению, так и его результату. В большинстве случаев подразумевается значение, так как множество всех линейных комбинаций $v_{1},dots ,v_{n}$ всегда образует подпространство. Однако можно сказать также «две различные линейные комбинации могут дать то же самое значение» и в этом случае под линейной комбинацией следует понимать выражение. Слабо уловимая разница между этими понятиями является сущностью понятия линейной зависимости — семейство векторов линейно независимо в точности тогда, когда любая линейная комбинация векторов из (как значение) единственна (как выражение). В любом случае, даже если линейная комбинация рассматривается как выражение, всё это относится к коэффициентам для каждого $v_{i}$ ; тривиальные изменения (например, перестановки элементов или добавление элементов с нулевыми коэффициентами) не дают другой линейной комбинации.

В зависимости от ситуации, и могут быть заданы явно, или они могут быть очевидны из контекста. В последнем случае часто говорят о линейной комбинации векторов $v_{1},dots ,v_{n}$ с произвольными коэффициентами (за исключением того, что они должны принадлежать ). Или, если — подмножество , то можно говорить о линейной комбинации векторов из , где и коэффициенты, и векторы не специфицированы — за исключением того требования, что векторы должны принадлежать множеству , а коэффициенты — полю ). Наконец, можно говорить просто о линейной комбинации, где ничто не специфицировано (за исключением того, что вектора должны принадлежать множеству , а коэффициенты — полю ). В этом случае, скорее всего, речь идёт о выражениях, поскольку любой вектор в определённо является значением некоторой линейной комбинации.

По определению, линейная комбинация включает только конечное число векторов (за исключением специальных обобщений^[⇨]).
Однако множество , из которого берутся векторы, может быть бесконечным. Каждая же индивидуальная линейная комбинация включает лишь конечное число векторов из этого множества.
Также нет причин, чтобы не мог быть нулём: считается, что в этом случае результат линейной комбинации будет нулевым вектором в .

Примеры и контрпримеры[править | править код]

Векторы[править | править код]

Пусть поле — множество вещественных чисел, а пространство векторов — евклидово пространство $mathbb {R} ^{3}$ . Любой вектор в $mathbb {R} ^{3}$ является линейной комбинацией единичных векторов $e_{1}=(1,0,0),e_{2}=(0,1,0),e_{3}=(0,0,1)$ . Например, вектор $(a_{1},a_{2},a_{3})$ можно записать:

${displaystyle (a_{1},a_{2},a_{3})=(a_{1},0,0)+(0,a_{2},0)+(0,0,a_{3})}$

${displaystyle =a_{1}(1,0,0)+a_{2}(0,1,0)+a_{3}(0,0,1)}$

${displaystyle =a_{1}e_{1}+a_{2}e_{2}+a_{3}e_{3}.}$

Функции[править | править код]

Пусть — множество всех комплексных чисел, и пусть — множество всех непрерывных функций из вещественной прямой в комплексную плоскость . Взяв векторы (функции) и , определённые формулами (здесь — основание натурального логарифма и — мнимая единица):

$f(t)=e^{{it}}$

, $g(t)=e^{{-it}}$

можно получить среди прочих следующие их линейные комбинации:

$cos t={begin{matrix}{frac 12}end{matrix}}e^{{it}}+{begin{matrix}{frac 12}end{matrix}}e^{{-it}}$ ,
$2sin t=(-i)e^{{it}}+(i)e^{{-it}}$ .

С другой стороны, постоянная функция не является линейной комбинацией и ^[4].

Многочлены[править | править код]

Пусть — это , или любое поле, и пусть — множество всех многочленов с коэффициентами из .
Пусть заданы векторы (многочлены) $p_{1}=1,p_{2}=x+1,p_{3}=x^{2}+x+1$ .

Является ли многочлен x² − 1 линейной комбинацией p₁, p₂ и p₃?
Чтобы это определить, является ли многочлен $x^{2}-1$ линейной комбинацией $p_{1},p_{2},p_{3}$ можно записать комбинацию с произвольными коэффициентами $a_{1},a_{2},a_{3}$ и приравнять её к данному многочлену:

$a_{1}(1)+a_{2}(x+1)+a_{3}(x^{2}+x+1)=x^{2}-1$

Раскрыв скобки:

$(a_{1})+(a_{2}x+a_{2})+(a_{3}x^{2}+a_{3}x+a_{3})=x^{2}-1$

и приведя однородные многочлены:

$a_{3}x^{2}+(a_{2}+a_{3})x+(a_{1}+a_{2}+a_{3})=1x^{2}+0x+(-1)$

получается:

$a_{3}=1,quad a_{2}+a_{3}=0,quad a_{1}+a_{2}+a_{3}=-1$

Решением этой системы линейных уравнений является $a_{1}=-1,a_{2}=-1,a_{3}=1$ .
Таким образом, данный многочлен записывается линейной комбинацией $p_{1},p_{2},p_{3}$ :

$x^{2}-1=-1-(x+1)+(x^{2}+x+1)=-p_{1}-p_{2}+p_{3}$

Другой пример — $x^{3}-1$ , он не может быть представлен линейной комбинацией $p_{1},p_{2},p_{3}$ :

${displaystyle 0x^{3}+a_{3}x^{2}+(a_{2}+a_{3})x+(a_{1}+a_{2}+a_{3})}$

$=1x^{3}+0x^{2}+0x+(-1),$

приравняв теперь коэффициенты для $x^{3}$ , получаем противоречие 0=1 .

Линейная оболочка[править | править код]

Пусть $S={v_{1},dots ,v_{n}$ } — векторы в некотором векторном пространстве над некоторым полем . Множество всех линейных комбинаций этих векторов называется линейной оболочкой (или просто оболочкой) векторов из . Обозначения — или :

${mathrm {Sp}}(v_{1},ldots ,v_{n}):={a_{1}v_{1}+cdots +a_{n}v_{n}mid a_{1},ldots ,a_{n}subseteq K}$

Линейная независимость[править | править код]

Для некоторых наборов $v_{1},dots ,v_{n}$ векторы могут быть представлены в виде линейной комбинации неоднозначно:

$v=sum a_{i}v_{i}=sum b_{i}v_{i}$

, где $(a_{i})neq (b_{i})$

Если вычесть третий член равенства из второго и обозначить коэффициенты $c_{i}=a_{i}-b_{i}$ , получим нетривиальную комбинацию, дающую в результате нулевой вектор:

$0=sum c_{i}v_{i}.$

Если такое возможно, набор $v_{1},dots ,v_{n}$ называют линейно зависимым. В противном случае — линейно независимым. Аналогичным образом говорят о зависимости или независимости произвольного множества векторов .

Если — линейно независимо и оболочка совпадает с , говорят, что является базисом в .

Аффинная, коническая и выпуклая комбинации[править | править код]

Если наложить на коэффициенты, используемые в линейной комбинации, некоторые условия, получим понятия концепции барицентрической комбинации (или аффинной комбинации), конической комбинации и выпуклой комбинации, а также соответствующие понятия множеств таких линейных комбинаций.

Тип комбинации	Ограничения на коэффициенты	Название множества	Модель пространства
Линейная комбинация	без ограничений	Векторное подпространство	${mathbf {R}}^{n}$
Барицентрическая комбинация	$sum a_{i}=1$	Аффинное подпространство	Аффинная гиперплоскость
Коническая комбинация	$a_{i}geq 0$	Выпуклый конус	Квадрант^[en] / Октант
Выпуклая комбинация	$a_{i}geq 0$ и $sum a_{i}=1$	Выпуклое множество	Симплекс

Поскольку здесь имеют место ограничения на вид комбинаций, то получаем в результате более широкие классы объектов. Таким образом, понятия аффинных подмножеств, выпуклых конусов и выпуклых множеств выступают как обобщения понятия векторного подпространства: векторное подпространство одновременно является также и аффинным подпространством, и выпуклым конусом, и выпуклым множеством, но выпуклое множество совсем не обязательно будет векторным или аффинным подпространством или выпуклым конусом.

Эти понятия возникают, когда берут определённые линейные комбинации объектов, но не любые. Например, распределения вероятностей замкнуты относительно операции образования выпуклых комбинаций (и образуют выпуклое множество), но не конических, барицентрических или линейных. Меры множеств замкнуты относительно операции образования конических комбинаций, но не барицентрических или линейных (последние комбинации определяют заряды).

Линейную и барицентрическую комбинации можно определить для любого поля (или кольца), а коническая и выпуклая комбинации требуют понятия «положительный», так что их можно определить только над упорядоченным полем (или упорядоченным кольцом).

Если разрешено только умножение на скаляр, но не сложение, получим (не обязательно выпуклый) конус^[en]. Часто ограничиваются умножением только на положительные скаляры.

Теория операд[править | править код]

На более общем языке теории операд можно рассматривать векторные пространства как алгебры над операдой $mathbb{R} ^{infty }$ (бесконечная прямая сумма, в которой только конечное число членов ненулевые), которая параметризует линейные комбинации. (Например, вектор в таком подходе соответствует линейной комбинации $2v_{1}+3v_{2}-5v_{3}+0v_{4}+cdots$ .) Подобным же образом можно рассматривать барицентрические, конические и выпуклые комбинации как соответствующие подоперадам, у которых члены в сумме дают 1, члены которых неотрицательны, или и то, и другое; такие комбинации будут бесконечными аффинными гиперплоскостями, бесконечными гипероктантами и бесконечными симплексами.

С этой точки зрения линейная комбинация может рассматриваться как наиболее общая операция в векторном пространстве — если векторное пространство является алгеброй над операдой линейной комбинации, это в точности означает, что все возможные алгебраические операции в векторном пространстве являются линейными комбинациями.

Основные операции сложения и умножения на скаляр вместе с существованием аддитивного равенства и аддитивной инверсии нельзя скомбинировать более сложным образом, чем образованием линейной комбинации. Эти основные операции являются генерирующим множеством^[en] для операды всех линейных комбинаций.

Обобщения[править | править код]

Если — топологическое векторное пространство, то можно, если существенным образом использовать топологию , придать смысл некоторым бесконечным линейным комбинациям элементов данного пространства. Например, можно было бы говорить о $a_{1}v+a_{2}v+a_{3}v+dots$ (до бесконечности). Такие бесконечные линейные комбинации не всегда имеют смысл: обычно смысл удаётся придать лишь сходящимся комбинациям. Увеличение запаса допустимых линейных комбинаций может привести к изменению объёма понятий оболочки, линейной независимости и базиса.

Если — коммутативное кольцо, а не поле, то всё, что говорилось о линейных комбинациях выше, обобщается на этот случай без изменений. Единственная разница — такие пространства именуются модулями (а не векторными пространствами), и не все результаты, справедливые применительно к векторным пространствам, остаются справедливыми и для модулей.

Если — некоммутативное кольцо, то понятие линейной комбинации с коэффициентами из также можно ввести — с одной особенностью: поскольку модули над некоммутативным кольцом могут быть левые и правые, то и линейная комбинация может тоже быть левой и правой.

Более сложной является ситуация, когда — бимодуль над двумя кольцами $K_{L}$ и $K_{R}$ . В этом случае наиболее общий вид линейной комбинации таков:

$a_{1}v_{1}b_{1}+cdots +a_{n}v_{n}b_{n}$

где $a_{1},dots ,a_{n}$ принадлежат $K_{L}$ , ${displaystyle b_{1},dots ,b_{n}}$ принадлежат $K_{R}$ и $v_{1},dots ,v_{n}$ принадлежат .

Примечания[править | править код]

Ссылки[править | править код]

Linear Combinations and Span: Understanding linear combinations and spans of vectors, khanacademy.org.

Источник

ОПРЕДЕЛЕНИЕ 1.29

Пусть заданы векторы и числа .

Выражение называется линейной комбинацией векторов . Очевидно, что линейная комбинация векторов является вектором. Рассмотрим особый случай, когда

(1.37)

ОПРЕДЕЛЕНИЕ 1.30

Если равенство (1.37) возможно только при всех , равных нулю, то векторы называются линейно-независимыми. Если же это равенство справедливо не при всех , где , то векторы называются линейно-зависимыми.

Пусть линейно-зависимы. Тогда среди найдется хотя бы одно не равное нулю число. Пусть . Разделив обе части равенства (1.37) на , получим

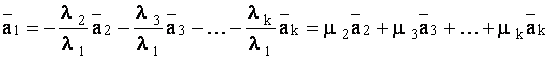где .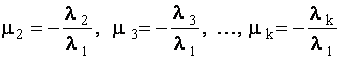

Выражение является линейной комбинацией векторов . Итак, если векторы линейно-зависимы, то хотя бы один из них является линейной комбинацией остальных.

Справедливо и обратное утверждение: если хотя бы один вектор является линейной комбинацией других векторов, то вся группа векторов линейно-зависима. Пусть, например, .

Тогда и коэффициент при отличен от нуля. Это означает, что вектора линейно-зависимы.

Примерами линейно-зависимых векторов являются любые два вектора прямой; любые три вектора плоскости; любые четыре вектора пространства (рис. 1.1.12-1.1.13).

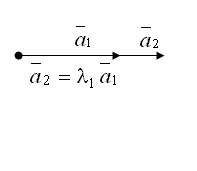
Рисунок 1.1.12

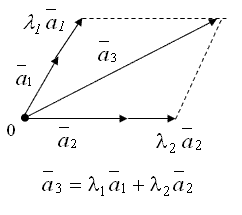
Рисунок 1.1.13

В то же время два неколлинеарных вектора и плоскости (рис. 1.1.13) или три некомпланарных вектора пространства (рис. 1.1.14) являются примерами линейно-независимых векторов.

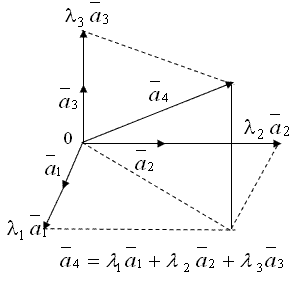
Рисунок 1.1.14

ОПРЕДЕЛЕНИЕ 1.31

Любая группа, составленная из максимального числа линейно-независимых векторов некоторого пространства , называется базисом этого пространства. Число векторов базиса называется размерностью пространства. Так, базисом на прямой (пространство ) является любой ненулевой вектор этой прямой. Размерность прямой равна единице. Базисом на плоскости (пространство ) являются любые два неколлинеарных вектора этой плоскости. Размерность плоскости равна двум. Базисом в объемном пространстве (пространство ) являются любые три некомпланарные вектора. Размерность этого пространства равна трем.

Пусть векторы образуют базис . Тогда любой вектор этого пространства является линейной комбинацией базисных векторов, то есть

(1.38)

Представление вектора в форме (1.38) называется разложением этого вектора по базисным векторам.

Числа разложения называются координатами вектора по базису . Этот факт записывается в виде .

Векторы называется компонентами вектора по базисным векторам .

Если векторы , образующие базис, имеют общее начало и вектор , где некоторая точка пространства, то числа называются также координатами этой точки. Этот факт записывают в виде .

Прямоугольная Декартова система координат
Курс математики

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Источник

Регрессия и линейные комбинации векторов

Время на прочтение
8 мин

Количество просмотров 4.8K

Недавно я помогал вести курс по линейной алгебре, который организовали Тай-Даная Брэдли и Джек Хидари. Одним из вопросов, который периодически возникал у слушателей курса, был вопрос о том, почему программистов должна заботить тема линейной комбинации векторов.

Если кто не знает о том, что это такое — поясню. Предположим, имеются векторы . Их линейной комбинацией называется выражение вида , представляющее собой сумму произведений векторов на коэффициенты .

Должен признать, что книги по математике оказывают своим читателям медвежью услугу, представляя концепцию линейной комбинации векторов не более чем теоретической идеей. В результате создаётся впечатление того, что эта концепция нужна лишь для математических доказательств, что самое ценное для практика — это умножение матриц и векторные произведения. Но, на самом деле, это не так. Линейная комбинация векторов лежит в самом сердце многих вариантов практического применения математических идей.

В некоторых случаях главной целью применения некоего алгоритма является лишь поиск «приемлемой» линейной комбинации набора векторов. Векторы — это строительные блоки (часто являющиеся базисом векторного пространства или подпространства), а набор линейных комбинаций векторов представляет собой законный способ комбинирования этих блоков. Более простые блоки допускают применение более простых и более эффективных алгоритмов, но их линейные комбинации менее выразительны. Вследствие этого и возникает компромисс.

Конкретный пример этого — регрессия. Большинство людей, говоря о регрессии, имеют в виду линейную регрессию. Речь идёт о поиске линейной функции, вроде , которая хорошо аппроксимирует некие данные. В случае с функцией от нескольких переменных имеется, например, в роли вектора входных переменных, и в роли вектора коэффициентов или весов. А сама функция тогда выглядит как .

Для того чтобы избежать сдвига функции на (что делает функцию аффинной, а не чисто линейной; с формулами чисто линейных функций проще работать, так как сдвиг функции напоминает неприятный частный случай, который нужно постоянно принимать во внимание) авторы часто добавляют к вектору входных переменных фиктивную переменную , значение которой никогда не меняется и составляет 1, и переименовывают в для того чтобы формула приобрела бы окончательный вид
. В результате задача оптимизации, которую нужно решить, учитывая то, что — это набор данных для аппроксимации, выглядит так:

В данном случае оптимизируемая функция, представляющая собой результат работы регрессии, не похожа на линейную комбинацию векторов. Но с технической точки зрения это — линейная комбинация векторов, хотя выполнена она с использованием не слишком интересного способа.

Более очевидной связь подобных задач с линейной комбинацией векторов становится тогда, когда пытаются моделировать нелинейные системы. Суть тут в том, чтобы определить класс функций, называемых базисными функциями , и допустить, чтобы аппроксимация представляла бы собой любую линейную комбинацию функций в , то есть — любую функцию в пределах :

Опять же, вместо того, чтобы умножать каждую координату входного вектора на коэффициент , мы «взвешиваем» вклад каждой базисной функции (когда нам дан весь входной вектор) в выходные данные. Если базисные функции должны дать нам единственную координату — (
), это значит, что мы возвращаемся к линейной регрессии.

В результате задача оптимизации будет заключаться в том, чтобы выбрать коэффициенты, минимизирующие ошибку аппроксимации:

Рассмотрим пример. Предположим, что нам нужно выполнить регрессию на базисных функциях, представленных квадратичными полиномами. Базис для трёх входных переменных может выглядеть так:

Любой квадратичный полином от трёх переменных может быть представлен в виде линейной комбинации этих базисных функций. Кроме того, обратить внимание на то, что если рассматривать это как базис векторного пространства, тогда вектор будет представлен набором из 10 чисел — из десяти коэффициентов полинома. Это — то же самое, что , но с другой интерпретацией того, какой смысл имеют компоненты векторов. Учитывая это, мы теперь знаем о том, как находить скалярные произведения векторов, проекции векторов, и много чего ещё, хотя всё это может и не иметь такого же геометрического смысла.

Это — не те функции, которые обычно, на практике, используются в качестве базисных функций для полиномиальной регрессии (подробнее об этом смотрите в примечаниях, приведённых в конце статьи), но благодаря этим знаниям мы уже можем сделать кое-что полезное при реализации регрессионных алгоритмов.

Простой стохастический градиентный спуск

Хотя существуют аналитические решения многих регрессионных задач (включая задачу квадратичной регрессии, хотя и с небольшим изменением), градиентный спуск — это достаточно простое решение, позволяющее продемонстрировать то, как оптимизатор может находить «приемлемые» линейные комбинации векторов. Нижеприведённый код написан на Python 3.9, этот код можно найти на GitHub.

Начнём с объявления нескольких полезных псевдонимов типов:

from typing import Callable, Tuple, List
 
Input = Tuple[float, float, float]
Coefficients = List[float]
Gradient = List[float]
Hypothesis = Callable[[Input], float]
Dataset = List[Tuple[Input, float]]

Затем объявим простой класс-обёртку для базисных функций:

class QuadraticBasisPolynomials:
    def __init__(self):
        self.basis_functions = [
            lambda x: 1,
            lambda x: x[0],
            lambda x: x[1],
            lambda x: x[2],
            lambda x: x[0] * x[1],
            lambda x: x[0] * x[2],
            lambda x: x[1] * x[2],
            lambda x: x[0] * x[0],
            lambda x: x[1] * x[1],
            lambda x: x[2] * x[2],
        ]
 
    def __getitem__(self, index):
        return self.basis_functions[index]
 
    def __len__(self):
        return len(self.basis_functions)
 
    def linear_combination(self, weights: Coefficients) -> Hypothesis:
        def combined_function(x: Input) -> float:
            return sum(
                w * f(x)
                for (w, f) in zip(weights, self.basis_functions)
            )
 
        return combined_function
 
basis = QuadraticBasisPolynomials()

Функция linear_combination возвращает функцию, которая вычисляет взвешенную сумму базисных функций. Теперь мы можем описать функции, вычисляющие ошибку для всего набора данных и для одной точки данных:

def total_error(weights: Coefficients, data: Dataset) -> float:
    hypothesis = basis.linear_combination(weights)
    return sum(
        (actual_output - hypothesis(example)) ** 2
        for (example, actual_output) in data
    )
 
 
def single_point_error(
        weights: Coefficients, point: Tuple[Input, float]) -> float:
    return point[1] - basis.linear_combination(weights)(point[0])

Сейчас можно определить градиент функции ошибки по отношению к весам и к одной точке данных. Вспомним о том, что функция ошибок выглядит так:

Здесь — это линейная комбинация базисных функций:

Так как мы реализуем алгоритм стохастического градиентного спуска, формула вычисления ошибки немного упрощается. Мы вычисляем её не для всего набора данных, а только для одного, случайным образом выбранного элемента за раз. В результате функция ошибки будет выглядеть так:

Затем мы вычисляем градиент применительно к отдельным компонентам , используя правило дифференцирования сложной функции, и учитывая, что единственный компонент линейной комбинации векторов, отличающийся ненулевым влиянием на градиент для — это компонент, содержащий . Это — один из главных плюсов использования линейной комбинации векторов, который заключается в простоте вычисления градиента:

Ещё одна сильная сторона линейности заключается в том, что этой формуле безразлично содержимое исходных базисных функций. Это будет так до тех пор, пока веса не появятся в формуле для базисных функций. Попробуйте, в качестве упражнения, изменить эту реализацию так, чтобы в каждой из точек данных применялась бы собственная радиальная базисная функция (в конце статьи есть примечание о том, почему это, в реальной жизни, может быть непросто).

def gradient(weights: Coefficients, data_point: Tuple[Input, float]) -> Gradient:
    error = single_point_error(weights, data_point)
    dE_dw = [0] * len(weights)
 
    for i, w in enumerate(weights):
        dE_dw[i] = -2 * error * basis[i](data_point[0])
 
    return dE_dw

И, наконец, реализуем ядро алгоритма градиентного спуска, в которое входят механизмы, упрощающие отладку кода:

import random
 
def print_debug_info(step, grad_norm, error, progress):
    print(f"{step}, {progress:.4f}, {error:.4f}, {grad_norm:.4f}")
 
 
def gradient_descent(
        data: Dataset,
        learning_rate: float,
        tolerance: float,
        training_callback = None,
) -> Hypothesis:
    weights = [random.random() * 2 - 1 for i in range(len(basis))]
    last_error = total_error(weights, data)
    step = 0
    progress = tolerance * 2
    grad_norm = 1.0
 
    if training_callback:
        training_callback(step, 0.0, last_error, 0.0)
 
    while abs(progress) > tolerance or grad_norm > tolerance:
        grad = gradient(weights, random.choice(data))
        grad_norm = sum(x**2 for x in grad)
         
        for i in range(len(weights)):
            weights[i] -= learning_rate * grad[i]
 
        error = total_error(weights, data)
        progress = error - last_error
        last_error = error
        step += 1
 
        if training_callback:
            training_callback(step, grad_norm, error, progress)
 
    return basis.linear_combination(weights)

Сгенерируем какой-нибудь простой набор данных и запустим оптимизацию:

def example_quadratic_data(num_points: int):
    def fn(x, y, z):
        return 2 - 4*x*y + z + z**2
 
    data = []
    for i in range(num_points):
        x, y, z = random.random(), random.random(), random.random()
        data.append(((x, y, z), fn(x, y, z)))
 
    return data
 
 
if __name__ == "__main__":
    data = example_quadratic_data(30)
    gradient_descent(
        data, 
        learning_rate=0.01, 
        tolerance=1e-06, 
        training_callback=print_debug_info
    )

Алгоритму на то, чтобы сойтись, может понадобиться несколько тысяч шагов. Сколько именно — зависит от того, как отработал генератор случайных чисел при подготовке данных. Но обычно алгоритм сходится к решению, дающему ошибку меньше 1. Вот график, на котором показана связь ошибки и шагов алгоритма градиентного спуска для задачи квадратичной регрессии.

Ошибка и шаги алгоритма

Ядра и регуляризация

Я завершу этот материал пояснениями, на которые ссылался в статье.

Настоящее полиномиальное ядро. Мы решили использовать простой набор полиномиальных функций. Это тесно связано с концепцией «ядра», но «настоящее» полиномиальное ядро использует немного другие базисные функции. Оно масштабирует некоторые из базисных функций, используя . Но зачем это делать? Ответ сводится к технике повышения эффективности вычислений, называемой «ядерным трюком». Этот «трюк», если кратко его описать, позволяет вычислять скалярное произведение двух линейных комбинаций векторов в векторном пространстве без вычисления координат данных в пространстве. Если в реализации используемого алгоритма регрессии используются только скалярные произведения векторов (что справедливо для аналитических решений регрессионных задач), то в нашем распоряжении оказываются сильные стороны нелинейного моделирования признаков и нам, при этом, не нужно тратить ресурсы на непосредственное вычисление признаков. В этой связи уместно будет обсудить гораздо больше теоретических математических вопросов (см. также: Reproducing Kernel Hilbert Space), но тут я не буду углубляться в эту тему.

Что не так с упражнением про радиальные базисные функции? В этом упражнении я предложил вам создать семейство базисных функций, по одной функции для каждой точки данных. Проблема тут заключается в том, что наличие настолько большого количества базисных функций делает пространство линейной комбинации векторов слишком выразительным. В ходе оптимизации произойдёт переобучение модели. В результате получится нечто, напоминающее справочную таблицу: каждой точке данных соответствует отдельная запись. При этом такая модель редко показывает хорошие результаты при обработке новых точек данных, которых не было в учебном наборе. Дело в том, что этих точек нет в найденной алгоритмом оптимизации «справочной таблице». На практике, для того чтобы справиться с этой проблемой, обычно, при расчёте ошибки, используют дополнительный компонент, соответствующий метрикам L1 или L2 вектора весовых коэффициентов. Это позволяет обеспечить то, что общий размер весов будет небольшим, то, что большинство весов, в случае с применением метрики L1, будут нулевыми, и то, что лишь немногие веса (самые важные) будут ненулевыми. Процесс введения «штрафов» за «размеры» линейных комбинаций векторов называют регуляризацией.

Что вы посоветовали бы почитать программистам, которые хотят с нуля освоить линейную алгебру?

Источник

Содержание

Линейные комбинации векторов в пространстве

Линейные комбинации векторов

Определение 1. Линейной комбинацией¹⁾ $n$ векторов $mathbf{a}_1,ldots,mathbf{a}_n$ называется сумма произведений этих векторов на произвольные вещественные числа, то есть выражения вида

$alpha_1mathbf{a}_1+ldots+alpha_nmathbf{a}_n$ ,

где — любые вещественные числа.

Определение 2. Векторы $mathbf{a}_1,ldots,mathbf{a}_n$ называются линейно зависимыми²⁾, если найдутся такие вещественные числа , из которых хотя бы одно отлично от нуля, что линейная комбинация векторов $mathbf{a}_1,ldots,mathbf{a}_n$ с этими числами обращается в нуль³⁾, то есть имеет место равенство:

$alpha_1mathbf{a}_1+ldots+alpha_nmathbf{a}_n=mathbf{0}$ .

Определение 3. Векторы $mathbf{a}_1,ldots,mathbf{a}_n$ называются линейно независимыми⁴⁾, если равенство нулю их линейной комбинации $alpha_1mathbf{a}_1+ldots+alpha_nmathbf{a}_n$ возможно лишь в случае, когда все числа равны нулю.

Предложение 1. Если хотя бы один из векторов $mathbf{a}_1,ldots,mathbf{a}_n$ нулевой, то эти векторы являются линейно зависимыми.

Предложение 2. Если среди $n$ векторов какие-либо $k$ ⁵⁾ векторов являются линейно зависимыми, то и все $n$ векторов являются линейно зависимыми.

Предложение 3. Система векторов линейно зависима тогда и только тогда, когда один из них представим в виде линейной комбинации остальных.

Обобщение понятия «линейная зависимость» можно посмотреть в соответствующей статье.

Линейная зависимость двух векторов

Предложение 4. Два вектора являются линейно зависимыми тогда и только тогда, когда они коллинеарны.

Линейная зависимость трех векторов

Предложение 5. Три вектора являются линейно зависимыми тогда и только тогда, когда они компланарны.

Линейная зависимость четырех векторов

Предложение 6. Любые четыре вектора в пространстве линейно зависимы.

Базис в пространстве, на плоскости и на прямой

Определение 4. Базисом в пространстве⁶⁾ называется упорядоченная тройка некомпланарных векторов.

Определение 5. Базисом на плоскости⁷⁾ называется пара неколлинеарных векторов, взятых в определенном порядке.

Определение 6. Базисом на прямой⁸⁾ называется любой ненулевой вектор на этой прямой.

Определение 7. Пусть $mathbf{e}_1,mathbf{e}_2,mathbf{e}_3$ — базис в пространстве. Если

$mathbf{a}=alpha_1mathbf{e}_1+alpha_2mathbf{e}_2+alpha_3mathbf{e}_3$ ,

то говорят, что вектор разложен по базису. Числа называются координатами⁹⁾ вектора в этом базисе. Аналогично определяются координаты на плоскости и на прямой.

Предложение 7.

Каждый вектор, параллельный какой-либо прямой, может быть разложен по базису на этой прямой.
Каждый вектор, параллельный какой-либо плоскости, может быть разложен по базису на этой плоскости.
Каждый вектор может быть разложен по базису в пространстве.

Координаты вектора в каждом случае определяются однозначно.

Предложение 8. При сложении векторов складываются их соответствующие координаты. При умножении вектора на число все его координаты умножаются на это число.

См. также

Литература

Наверх

Источник

Линейные комбинации векторов

§ 1. Ориентация пространства. Правые и левые тройки некомпланарных векторов.

§ 2. Скалярное произведение векторов.

§ 3. Векторное произведение векторов.

Определение[править | править код]

Примеры и контрпримеры[править | править код]

Векторы[править | править код]

Функции[править | править код]

Многочлены[править | править код]

Линейная оболочка[править | править код]

Линейная независимость[править | править код]

Аффинная, коническая и выпуклая комбинации[править | править код]

Теория операд[править | править код]

Обобщения[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Регрессия и линейные комбинации векторов

Простой стохастический градиентный спуск

Ядра и регуляризация

Содержание

Линейные комбинации векторов в пространстве

Линейные комбинации векторов

Линейная зависимость двух векторов

Линейная зависимость трех векторов

Линейная зависимость четырех векторов

Базис в пространстве, на плоскости и на прямой

См. также

Литература

Вам также может понравиться

Вечный огонь как найти

Как найти абонента в соц сетях

Модем определяется как cd rom как исправить windows 10

Добавить комментарий Отменить ответ