Как составить логический вопрос

Вот
почему при постановке вопросов следует
соблюдать следующие правила:

1.
Вопросы ставить необходимо корректно.
Они должны быть правильно сформулированы
по содержанию и форме. Провокационные
и неопределенные вопросы недопустимы.

2.
В соответствии с вопросом следует
предусмотреть альтернативность ответа
(«да» или «нет») на уточняющие вопросы.
Например, на вопрос: «Признает ли Петров
себя виновным в предъявленном ему
обвинении?» можно дать два альтернативных
ответа: «Да, признает» или «Нет, не
признает».

3.
Вопрос формулируется кратко и ясно.
Длинные, запутанные вопросы затрудняют
их понимание и ответ на них.

4.
Вопрос должен быть простым. Если вопрос
сложный, то его лучше разбить на несколько
простых. Например, «Были ли братья Иван
и Константин Аксаковы издателями газеты
«День»?». Это сложный вопрос следует
разбить на два простых, так как ответы
будут различными – «да», «нет». Это
связано с тем, что Иван Аксаков был
издателем газеты «День», а Константин
– нет, он был только автором многочисленных
статей в ней.

5.
В сложных разделительных вопросах
необходимо перечисление всех альтернатив.
Например, «К какому виду суда по стадии
рассмотрения дел относится данный суд:
первой или кассационной инстанции?».
Здесь не указана третья альтернатива
– суд надзорной инстанции.

6.
При формулировке вопросов следует
отличать их обычную постановку от
риторической. Риторические вопросы,
как известно, являются суждениями, так
как в них содержится утверждение или
отрицание; обычные же вопросы суждениями
не являются.

Важно
помнить, что только правильно поставленный
вопрос способен выполнить свои функции
как в научном познании, так и в дискуссии,
и в обучении.

46.
Индуктивные методы установления
причинно-следственных связей

Раскрытие
причинной связи между явлениями –
сложный, многогранный процесс, включающий
разнообраз­ные логические средства
и способы познания. В логике разработано
не­сколько научных методов установления
причинной связи между явлениями: метод
сходства, метод различия, соединенный
метод сходства и различия, метод
сопутствующих изменений и метод остатков.

Метод
сходства: если
два и более случая исследуемого явления
сходны только в одном обстоятельстве,
то это обстоятельство, вероятно, и есть
при­чина (часть причины) данного
явления. Приведем схему этого метода:

 При
условиях ABC возникает
явление а

При
условиях ADE возникает
явление а

_____При
условиях AFQ возникает
явление а____

Вероятно,
обстоятельство А есть причина а

 Для
иллюстрации данного и последующих
методов рассмотрим следую­щий пример
*. На почтамте при перевозке ценностей
было три случая хище­ния без повреждения
мешков: 6 декабря, 8 декабря, 10 декабря.
Следователь определил круг лиц,
участвовавших в эти дни в отправке
почты, и составил следующую таблицу:

Дата	Круг лиц	Происшествие
6.12	Кулдышев, Корнеев, Сандлер	Хищение
8. 12	Широглазов, Корнеев, Кузнецов	Хищение
10.12	Чуйкин, Корнеев, Кравец	Хищение

Из
этого следователь заключил, что виновником
хищения вероятнее все­го является
Корнеев, поскольку именно он и только
он занимался отправ­кой почты всякий
раз, когда происходило хищение, а все
остальные лица менялись.

Таким
образом, этот метод позволяет с большой
долей уверенности вы­двигать гипотезы
(версии). Однако он обладает рядом
недостатков, которые сходны, во-первых,
с ошибками популярной индукции, поскольку
здесь также обращается внимание по
преимуществу на сходство изучаемых
усло­вий появления некоторых явлений,
и, во-вторых, с ошибками, встречающимися
в разделительных умозаключениях. Так,
строки приведенной таблицы показывают,
что хищение совершил или Кулдышев, или
Корнеев, или Сандлер, или Кузнецов, или
Чуйкин, или Широглазов. Но известно, что
во всех разделительных умозаключениях
возможна ошибка «неполный перечень
альтернатив». Так и в данном случае
возможно, что во все эти дни работала
уборщица Хапугина, которая во время
уборки просила всех работников по­кинуть
помещение, где находились мешки с
ценностями, и на некоторое время
оставалась там одна. В таком случае то,
что Корнеев работал во все дни, когда
совершалось хищение, окажется простым
совпадением.

Таким
образом, при применении метода сходства
возможна ошибка, ко­торая получила
название «неполный перечень условий».

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

§ 3. Правила постановки вопросов

«Задай глупый вопрос, и ты получишь глупый ответ». Такое определяющее влияние вопроса на характер ответа известно с давних пор. Во время одного из своих походов Александр Ма­кедонский взял в плен десять индийских философов. Они были известны своим умением остроумно и лаконично отвечать на поставленные вопросы. Александр решил испытать пленников, задав им трудные вопросы. Пятого по счету он спросил: «Что раньше – ночь или день?». Философ ответил: «День раньше по крайней мере на день», – но увидев, что Александр не очень удовлетворен таким ответом, добавил, что не следует удивляться тому, что мудреные вопросы имеют столь же мудреные ответы[7]. Позже эту же мысль повторил немецкий философ И. Кант. «Умение ставить разумные во­просы, – остроумно заметил он, – есть уже важный и необходимый признак ума и проницательности. Если вопрос сам по себе бессмысленен и требует бесполезных ответов, то, кроме стыда для спрашивающего, он имеет иногда тот недостаток, что побуждает неосторожного слушателя к нелепым ответам и создает смешное зрелище: один (по выражению древних) козла доит, а другой держит под ним решето»[8].

Вот почему при постановке вопросов следует соблюдать следующие пра­вила:

1. Вопросы ставить необходимо корректно. Они должны быть правиль­но сформулированы по содержанию и форме. Провокационные и неопреде­ленные вопросы недопустимы.

2. В соответствии с вопросом следует предусмотреть альтернативность от­вета («да» или «нет») на уточняющие вопросы. Например, на вопрос: «При­знает ли Петров себя виновным в предъявленном ему обвинении?» можно дать два альтернативных ответа: «Да, признает» или «Нет, не признает».

3. Вопрос формулируется кратко и ясно. Длинные, запутанные вопросы затрудняют их понимание и ответ на них.

4. Вопрос должен быть простым. Если вопрос сложный, то его лучше раз­бить на несколько простых. Например, «Были ли братья Иван и Константин Аксаковы издателями газеты «День»?». Это сложный вопрос следует разбить на два простых, так как ответы будут различными – «да», «нет». Это связано с тем, что Иван Аксаков был издателем газеты «День», а Константин – нет, он был только автором многочисленных статей в ней.

5. В сложных разделительных вопросах необходимо перечисление всех альтернатив. Например, «К какому виду суда по стадии рассмотрения дел относится данный суд: первой или кассационной инстанции?». Здесь не ука­зана третья альтернатива – суд надзорной инстанции.

6. При формулировке вопросов следует отличать их обычную постановку от риторической. Риторические вопросы, как известно, являются суждения­ми, так как в них содержится утверждение или отрицание; обычные же во­просы суждениями не являются.

Важно помнить, что только правильно поставленный вопрос способен выполнить свои функции как в научном познании, так и в дискуссии, и в обучении.

Например, одним из наиболее распространенных методов исследования различных проблем общественной жизни является опрос. Цель опроса со­стоит в получении информации об объективных и субъективных (мнения, настроения, интересы и т. п.) фактах со слов опрашиваемых. Многие правовые проблемы вообще нельзя изучать, не прибегая к опросу: общественное мнение о нормах уголовного права, престиж правоохранительных органов, правовое сознание, эффективность правовой пропаганды и т. п.

Главное в этом методе – формулирование вопросов. В основе общих тре­бований, предъявляемых к формулировке вопросов, лежат рассмотренные формально-логические правила их постановки.

Во-первых, вопрос должен быть конкретным, кратким, понятным, про­стым по конструкции.

Во-вторых, вопрос должен указывать время, место и контекст, которые необходимо учитывать при ответе.

В-третьих, в вопросе не следует употреблять слова с двойным и более значений.

В-четвертых, контрольные вопросы не должны следовать сразу за основ­ными.

В-пятых, вопрос должен указывать на все возможные альтернативы отве­тов (положительные, отрицательные выборы).

В-шестых, при необходимости конкретизации ответа в вопросе можно ввести краткое предисловие.

В-седьмых, формулировка вопроса и его смысл должны учитывать личный персональный опыт опрашиваемых в той области, на которую направ­лен вопрос.

В-восьмых, нельзя вначале ставить трудные или беспокоящие опрашива­емого вопросы[9].

Как решать логические и математические задачи

Решение задач на логику — отличная гимнастика для ума детей и взрослых на каждый день.
На ЛогикЛайк более 3500 заданий с ответами и пояснениями, полноценный учебный комплекс для развития логики и способностей к математике.

Логика – это основа рационального мышления и фундамент для развития интеллекта ребенка. Решение различных логических задач дает возможность детям научиться анализировать ситуацию, находить взаимосвязи, отличать главное и второстепенное, формировать стратегию, применять в нужном месте свои знания и навыки.

Эти умения пригодятся не только в учебе, но и в реальной жизни. Рассуждая логически, ребенок может грамотно выразить свое мнение, подойти к решению той или иной задачи более осознанно, дать обоснование всевозможным явлениям, быстро сориентироваться в ситуации.

Поэтому решение логических задач должно быть неотъемлемой частью детского развития и образования. А для того, чтобы щелкать их как орешки, нужно понимать, какими приемами и методами пользоваться при решении.

Самое главное в решении логических задач

Почти у любой задачи есть несколько вариантов решения. Чтобы легко справляться даже с самыми непростыми заданиями, надо знать, какой способ будет наиболее подходящим в той или иной ситуации.

Понимание разных методов позволяет находить оптимальный вариант решения, что особенно важно в условиях ограниченного времени.

Все задачи на развитие логики можно разделить на группы:

• Математические ребусы;
• Задачи на истинность утверждений;
• Задачи на перемещение, взвешивание или переливание;
• Задачи, которые решаются с конца;
• Работа с множествами;
• Задачи на сопоставление «Кто есть кто?»

Выбор способа решения зависит от того, к какой группе относится задание.

Известные техники решения логических задач

1. Табличный метод (таблицы соответствий, истинности, совмещенные, кубические):
   таблицы создают наглядность, прозрачность рассуждений, помогают сделать верные выводы.
2. Применение законов из алгебры логики: вводятся обозначения для простых высказываний и преобразовываются в некую формулу.
3. Метод рассуждений: подходит для решения простых задач с небольшим количеством объектов. Последовательное рассуждение над каждым условием задачи приводит к правильному выводу.
4. Черчение блок-схем: способ, подходящий для решения задач на переливание, взвешивание. Рисуется схема, на которой отмечают последовательность действий и результат, полученный при их выполнении.
5. Графический метод: подходит для решения задач на объединение или пересечение множеств. Самый популярный графический метод называется «Круги Эйлера». Нарисованная геометрическая схема наглядно показывает отношение между множествами.
6. Метод «математический бильярд»: используется для решения задач на переливание жидкостей. Вычерчивается траектория движения бильярдного шара, который отталкивается от бортов стола в форме параллелограмма.

Рассмотрим подробно самые распространенные способы, которые могут использовать в решении логических задач ученики начальных классов:

Табличный метод

Условия задачи и результаты записываем в специальную таблицу. На пересечении строк и столбцов ставим «+», если утверждения не противоречат друг другу и «-», если они расходятся.

Задача:

У Сони, Маши, Антона, Кости и Юры есть домашние животные. У каждого из ребят живет или собака, или кошка, или попугай. Вот только девочки собак не держат, а у мальчиков нет попугаев. У Сони и Маши разные питомцы, а вот у Маши с Антоном – одинаковые. У Сони нет кошки. У Кости с Юрой живут одинаковые животные, а у Антона с Костей – разные. Какие животные живут у каждого?

Решение:

Чертим таблицу, где названия столбцов – имена ребят, а названия строк – животные. Ставим в каждой ячейке знаки «+» или «-», опираясь на условия задачи:

1. Девочки собак не держат (ставим «-» на пересечении этих ячеек).
2. У мальчиков нет попугаев (в этих ячейках тоже ставим «-»).
3. У Сони нет кошки (ставим «-»).
4. Значит, у Сони есть попугай (ставим «+»).
5. У Сони и Маши разные питомцы. Получается, у Маши нет попугая (ставим «-»), зато есть кошка (ставим «+»).
6. У Маши с Антоном одинаковые животные. Значит, у Антона тоже живет кошка (ставим «+») и нет собаки (ставим «-»).
7. У Антона с Костей разные питомцы, выходит, что у Кости нет кошки (ставим «-»), зато есть собака (ставим «+»).
8. У Кости с Юрой одинаковые животные, значит у Юры тоже собака (ставим «+»), а не кошка (ставим «-»).

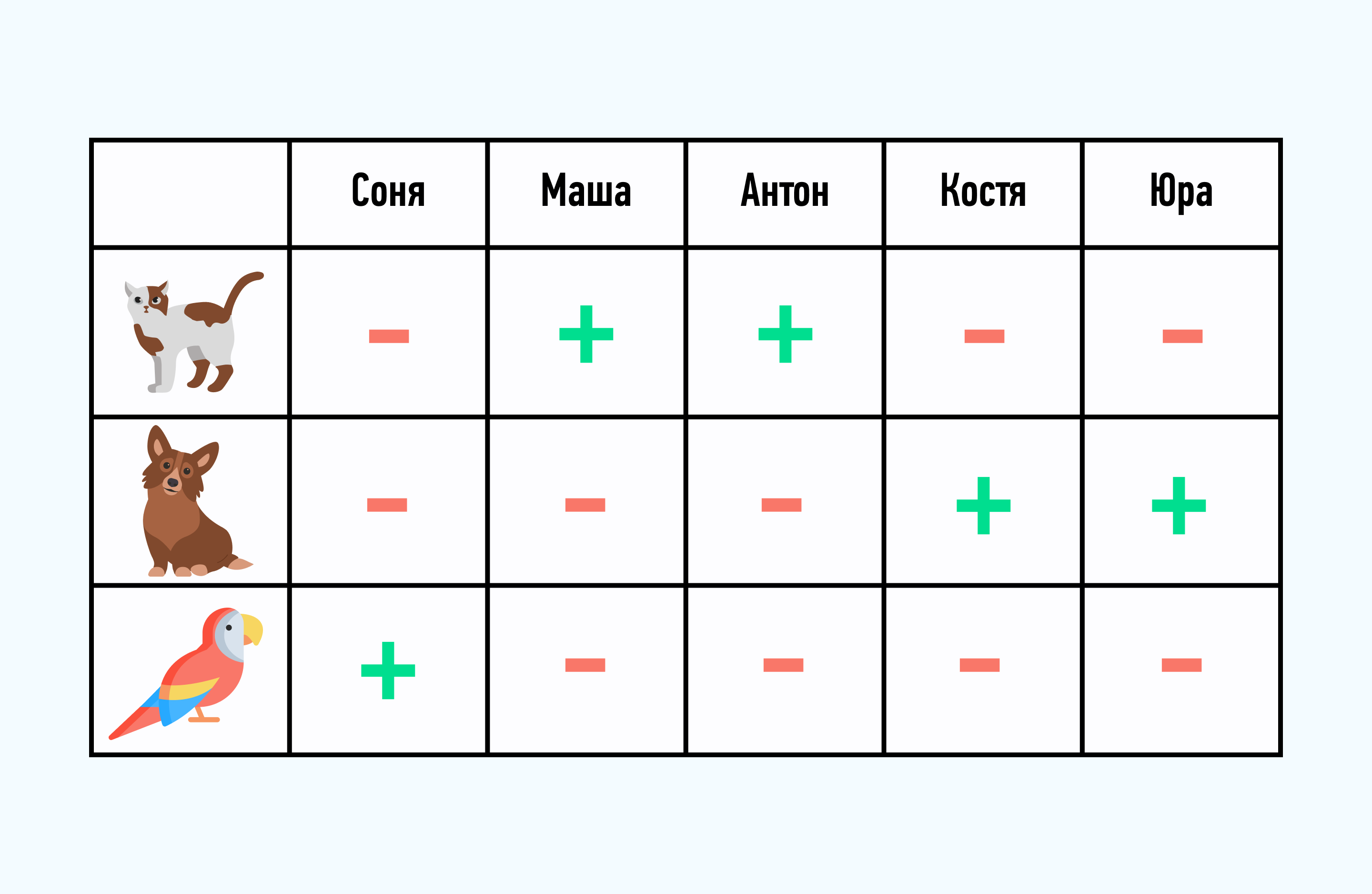
Так мы узнали, какие питомцы живут у каждого из ребят (ячейки со знаком «+»).

Ответ: У Сони попугай, у Маши и Антона кошки, у Кости и Юры собаки.

Круги Эйлера

Чтобы было легче разобраться в условиях задачи и найти решение, чертим круги, каждый из которых – отдельное множество.

Задача:

Всему классу задали на лето читать книжки. В списке литературы были такие произведения, как «Робинзон Крузо» Даниэля Дефо и «Белый клык» Джека Лондона. Известно, что 15 человек из класса прочитали «Робинзон Крузо», а остальные 11 – «Белый клык». Но среди них были 6 ребят, которые прочитали обе книги. Сколько человек прочитало только «Белый клык»?

Решение:

Чертим два круга, каждый из которых – множество детей, прочитавших определенную книгу, а пересечение кругов – дети, прочитавшие обе книги.

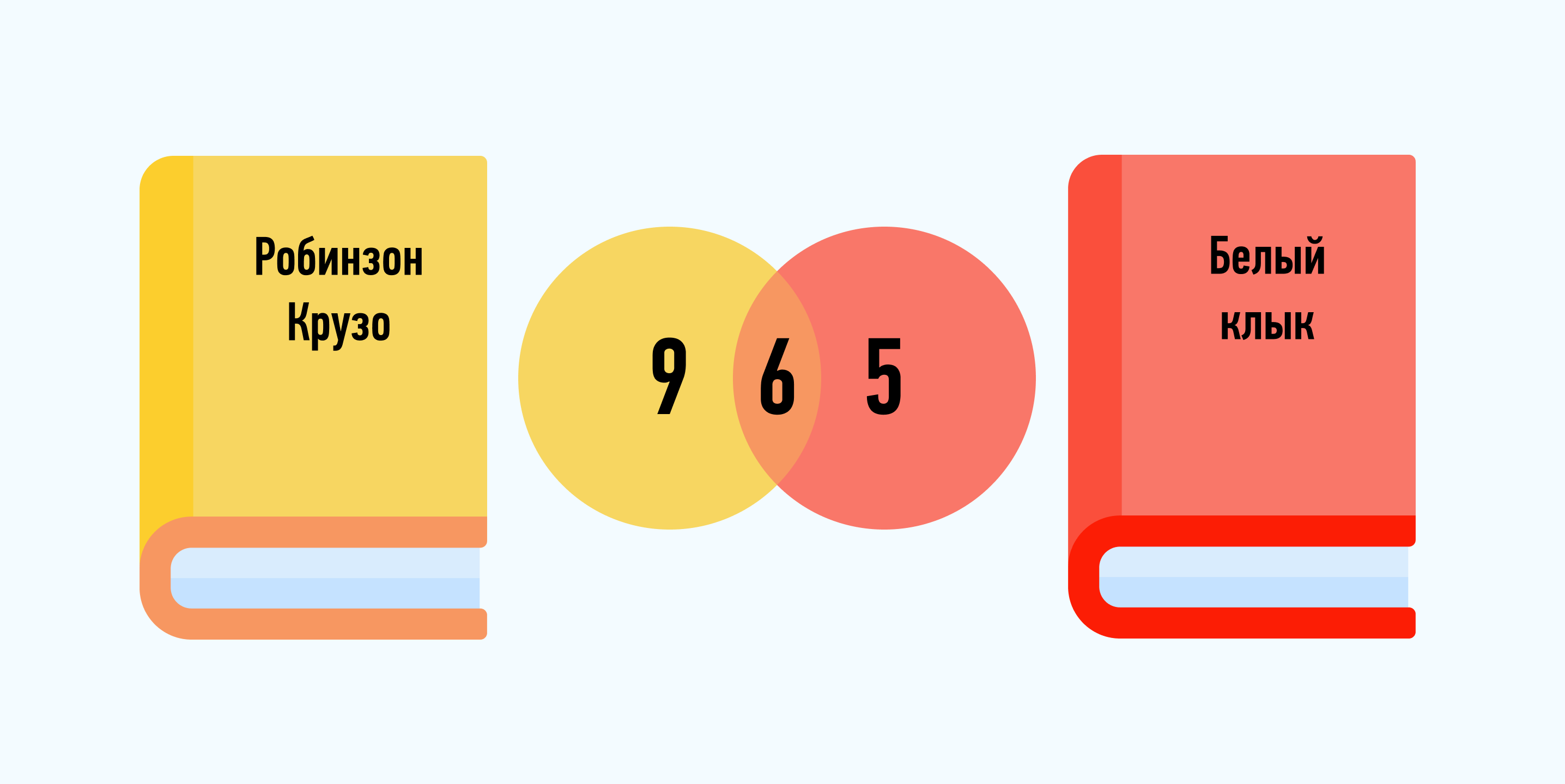
1. 15 – 6 = 9 – дети, которые прочитали только «Робинзон Крузо».
2. 11 – 6 = 5 – дети, которые читали лишь «Белый клык».

Ответ: 5 человек.

Метод рассуждений

Поочередно рассматриваем каждое из условий задачи и делаем логические выводы.

Задача:
На столе стоят вазы: голубая, зеленая, розовая и оранжевая. Третьей в ряду стоит та ваза, название цвета которой содержит больше всего букв. А зеленая стоит между оранжевой и розовой. Какая ваза стоит последней?

Решение:

1. Больше всего букв в слове «оранжевая», значит она третья по счету.
2. Если зеленая ваза стоит между оранжевой и розовой, значит, она будет второй в ряду, так как если ее поставить четвертой, то не останется места для розовой.
3. Соответственно, розовая будет стоять первой.
4. Остается голубая, она будет четвертой, то есть последней.

Ответ: голубая ваза.

Метод рассуждений «с конца»

Начинаем раскручивать клубок с конца, а затем сопоставляем результат с условиями задачи.

Задача:

Маме, папе и сыну вместе 125 лет. Когда родился сын, маме был 21 год. А папа старше мамы на 2 года. Сколько лет сейчас каждому из них?

Решение:

1. 21+2= 23 — было папе ( значит вместе родителям было 44 года)
2. (125 — 44) : 3 = 27 — возраст сына
3. 27 + 21 = 48 — возраст мамы
4. 48 + 2 = 50 — возраст папы

Ответ: 27, 48 и 50 лет.

---

Мы рассмотрели самые популярные и доступные методы, с помощью которых можно легко справиться с заданием. Главное – подобрать подходящий способ решения, который быстро приведет к правильному результату.

Для этого необходимо регулярно практиковаться и развивать свои способности. Отточить навыки решения подобных логических задач и многих других вы можете с помощью образовательной онлайн-платформы «Умназия».

Попробуйте решить вместе с ребенком задачу из раздела «логика» и переходите к регулярным занятиям на тренажере

Если вам понравилось, было весело интересно и полезно, то ждем вас на нашей онлайн платформе!
Умназия сегодня — это:

1. Онлайн тренажер развития навыков мышления — логики, внимания, эрудиции.
2. Программа «Культурный код» по развитию кругозора. Для самых любознательных и тех, кого кажется уже ничем не удивить!
3. Курсы развития памяти. Хотите чтобы Ваш ребенок без труда учил стихи, запоминал иностранные слова и всегда помнил про день рождения бабушки? На курсах покажем и расскажем как же этого достичь.
4. Пять ступеней финансовой грамотности. Увлекательная история героя, которая полностью зависит от действий ребенка и не имеет определенного результата. Сможет ли он пройти все финансовые ловушки и освоить пятую ступень?

Ждем вас, будет весело и интересно!

---

Читайте также:

• 15 сложных загадок на логику
• Загадки на логику с подвохом
• Логические загадки для детей
• Смешные логические загадки
• Загадки Эйнштейна на логику

---

4.2. Логика вопросов и ответов

В любом познавательном процессе огромную роль играет умение логически правильно строить вопросы и столь же правильно на них отвечать.

Развитие вопросно-ответной формы мышления и ведения дискуссии для ряда профессий, особенно для сотрудников ОВД, является профессионально важным.

Вопрос – это выраженная в вопросительном предложении мысль, направленная на уточнение или дополнение исходного, или базисного знания.

Логически правильно поставленный вопрос не должен допускать в своей формулировке слов, которые имеют два и более значений. Он должен быть ясным и по возможности кратким. В нем должны учитываться особенности личности адресата вопроса.

Элементы логической структуры вопроса

Ø Предпосылка – исходная информация, которая явно или неявно содержит вопрос.

Ø Оператор вопроса – требование ответа, выраженное в словах «кто», «что», «зачем» и т.д.

Ø Предмет вопроса – им может быть любой материальный или идеальный объект.

Ø Содержание вопроса – информация о предмете вопроса, которой располагает корреспондент, и требование восполнить недостающую информацию.

Ø Объем вопроса – различные возможности истинного ил ложного ответа на вопрос.

Правильно поставленные – вопросы, предпосылка которого представляет собой истинное непротиворечивое знание.

Неправильно поставленные – вопросы, предпосылка которого представляет собой неистинное противоречивое знание.

Уточняющий вопросы – вопросы, направленные на выявление истинности выраженного в нем суждения.

Восполняющие – вопросы, направленные на выяснение новых свойств у исследуемых явлений.

Простой – вопрос, не включающий в качестве составных частей других вопросов.

Сложным – вопрос, включающий в качестве составных частей другие вопросы, объединяемые логическими связками.

По отношению к обсуждаемой теме:

По существу темы – это запрос мысли, прямо или косвенно связанный с обсуждаемой темой, ответ на который уточняет либо дополняет исходную информацию.

Не по существу темы – это запрос, который не имеет непосредственного отношения к обсуждаемой теме.

Ответ – новое суждение, уточняющее или дополняющее в соответствии с поставленным вопросом исходное знание.

Правильный с точки зрения логики ответ на вопрос должен быть истинным суждением. Его формулировка должна относится к существу вопроса, то есть быть уместной и адекватной.

Ответ должен быть ясным, а так же по возможности кратким и однозначным .

По соответствию действительности:

Истинные , если выраженное в нем суждение соответствует действительности.

Ложные , если выраженное в нем суждение не соответствует действительности.

По области поиска:

Прямой – ответ взятый непосредственно из области поиска ответов, при конструировании которого не прибегают к дополнительным сведениям и рассуждениям.

Косвенный – ответ который получают из более широкой области, нежели область поиска ответа, и из которого лишь выводным путем можно получить нужную информацию.

По объему информации в ответе:

Краткий – односложный утвердительный или отрицательный ответ «да» или «нет».

Развернутый – ответ в котором повторяются все элементы вопроса.

По связи с вопросом:

Полный ответ включает информацию по всем элементам и составным частям вопроса.

Неполный ответ включает информацию относительно отдельных элементов или составных частей вопроса.

По степени точности:

Точный – под точностью имеется в виду логическая, т.е. понятийно-структурная характеристика вопроса.

Неточный выражается в двусмысленном употреблении понятий и вопросительных слов.

Источник

Решение логических задач табличным способом

Главным в предлагаемых задачах является способ решения — построение таблицы, строки которой соответствуют элементам одного из рассматриваемых в условии задачи множеств, столбцы — элементам другого, пересечение строки и столбца — комбинации двух элементов разных множеств. С помощью такой таблицы анализируются условия задачи, делаются выводы, проверяется избыточность, полнота и правильность выводов.

Задача 1. После соревнований бегунов на табло появилась надпись:
• Рустам не был вторым.
• Эдуард отстатл от Рустама на два места.
• Яков не был первым.
• Галина не была не первой ни последней.
• Карина финишировала сразу за Яковом.
Кто же победил в этих соревнованиях? Каково было распределение бегунов на финише?

Решение:
Рисуем таблицу, где столбцы –имена детей, а строки – номера мест. Читаем задачу, пошагово анализируем условие и ставим в таблицу «+», если соответствие установлено и «–», если точно соответствия нет.
Так как Рустам не был вторым и Эдуард отстал от Рустама на два места, то Эдуард не может быть ни первым, ни вторым, ни четвёртым.

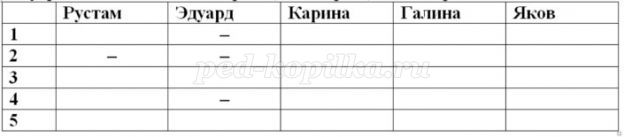
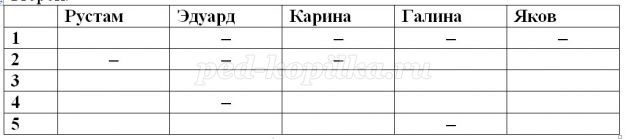
Так как Карина финишировала сразу за Яковом, то очевидно, что Яков был четвёртым, а Карина последней и тогда Галина была второй.

Итак, можно выделить
Пять простых шагов на пути поиска решения логических задач.
1. Составляйте таблицу, так как в таблице удаётся учесть все возможные варианты.
2. Внимательно читайте каждое утверждение, так как в каждом содержится что-то такое, что позволит вам исключить хотя бы один из вариантов.
3. Старайтесь отыскать ключевое утверждение, оно поможет развязать весь клубок.
4. После того как вы сравнили все утверждения и исключили из них те, невероятность которых была на поверхности, сравните утверждения между собой, установите связи и противоречия.
5. Решение можно найти простым методом последовательных исключений.

Чем больше будете тренироваться, тем лучше у вас это будет получаться. А теперь за дело.

Задача 2.
В субботний вечер Семен, Коля и Витя решили развлечься. У них был выбор: кино, рок-концерт или танцы.
• Семён любит кино, но к танцам менее нетерпим, чем к рок-музыке.
• Коля любит танцевать, но готов пойти в кино скорее, чем на рок концерт.
• Витя любит рок-музыку меньше чем танцы, но кино ему всё-таки не так неприятно, как танцы или концерт.
Поскольку вопрос решатся большинством голосов, то куда, на ваш взгляд отправились эти ребята?
Задача 3.
Трое мальчиков Костя, Фома и Марат дружили с тремя девочками – Женей, Светой и Мариной. Но вскоре компания разделилась на пары, потому, что оказалось:
• Света ненавидит ходить на лыжах.
• Костя, Женин брат часто катается со своей подружкой на лыжах
• А Фома теперь бежит на свидание к Костиной сестре.
С кем же проводит время Марат?

Задача 4.
Шестеро друзей в ожидании электрички заскочили в буфет.
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром.
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье.
• Кирилл ел то же, что и Мила, но без луковых чипсов.
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы.
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад.
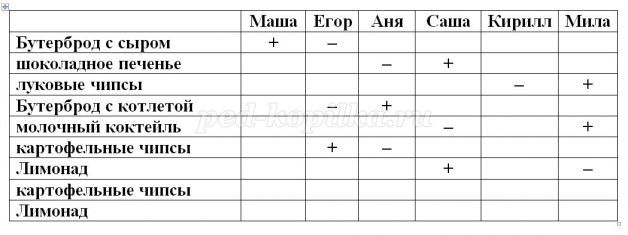
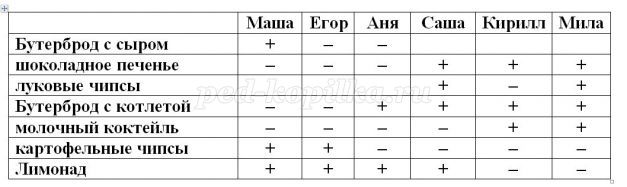
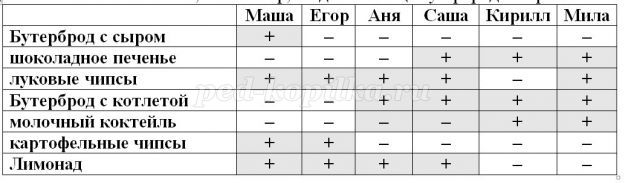
Из чего состоял завтрак каждого из друзей?

Решение: Так как
• Маша взяла то же, что и Егор, и вдобавок ещё бутерброд с сыром;
• Аня купила, то же, что и Саша, но не стала покупать шоколадное печенье;
• Кирилл ел то же, что и Мила, но без луковых чипсов;
• Егор завтракал тем же что и Аня, но бутерброду с котлетой предпочел картофельные чипсы;
• Саша ел то же, что и Мила, но вместо молочного коктейля пил лимонад, то:

Задача 5.
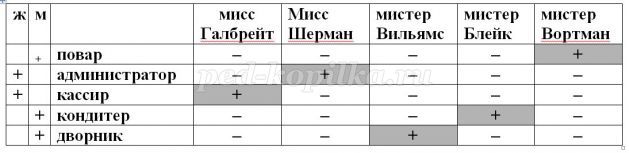
В одном небольшом кафе в смене одновременно работали 5 человек: администратор, повар, кондитер, кассир, дворник. Одновременно на работу выходили мисс Галбрейт, мисс Шерман, мистер Вильямс, мистер Вортман и мистер Блейк. При этом известно, что:
1. Повар – холостяк.
2. Кассир и администратор жили в одной комнате, когда учились в колледже.
3. Мистер Блейк и мисс Шерман встречаются только на работе.
4. Миссис Вильямс расстроилась, когда муж сказал ей, что администратор отказал ему в отгуле.
5. Вортман собирается быть шафером на свадьбе у кассира и кондитера.
Кто на какой должности в этом кафе?

Можно разделить учащихся на группы и каждой группе дать индивидуальное задание или подобрать задачи для каждого ученика.

Задача 1.
Коля, Боря, Вова и Юра заняли первые четыре места в спортивном соревновании. На вопрос, какие места они заняли, они ответили:
1) «Коля не занял ни первое, ни четвертое места».
2) “Боря занял второе место”.
3) “Вова не был последним”.
Какое место занял каждый мальчик?
Задача 2.
Три одноклассника — Влад, Тимур и Юра встретились спустя 10 лет после окончания школы. Выяснилось, что один из них стал врачом, другой — физиком, а третий — юристом. Один увлекся туризмом, другой — бегом, третий — регби.
1. Юра сказал, что, на туризм ему не хватает времени, хотя его сестра — единственный врач в семье, заядлый турист.
2. Врач сказал, что он разделяет увлечение коллеги.
3. Забавно, но у двоих из друзей в названиях их профессий и увлечений не встречается ни одна буква их имен.
Кто чем любит заниматься в свободное время и у кого какая профессия?
Задача 3.
Три друга — Иван, Дмитрий, Степан преподают различные предметы (химию, литературу, физику) в школах Москвы, Калининграда и Перми. Известно:
1) Иван работает не в Москве, а Дмитрий не в Калининграде;
2) москвич преподает не физику;
3) тот, кто работает в Калининграде, преподает химию;
4) Дмитрий преподает не литературу.
Какой предмет и в каком городе преподает каждый из товарищей?
Задача 4.
Четыре девочки Маша, Таня, София и Полина взяли в кафе сок. Каждая из них покупал только один сок, причем две из них купили сок яблочный, одна виноградный, и одна – грушевый. Известно, что у Маши и Тани разные вкусы. Разные соки взяли Маша с Софией, Полина с Софией, Полина с Машей и Таня с Софией. Кроме того известно, что Маша купила не грушевый сок. Определить, какой сок пила каждая из них.
Задача 6. (Один из вариантов «Задачи Эйнштейна»)
Пять домов стоят вдоль дороги, один за другим.
1. Доцент живёт в красном доме.
2. Гробовщик держит собак.
3. Сантехник пьёт чай.
4. Зелёный дом слева от белого.
5. Хозяин зелёного дома пьёт кофе.
6. Любитель «Примы» держит птицу.
7. Хозяин жёлтого дома курит «Беломор канал».
8. В центральном доме любят молоко.
9. Приёмщик стеклотары живёт в первом доме.
10. Курящий «Яву» сосед хозяина кошек.
11. Хозяин лошадей – сосед курящего «Беломор».
12. Любитель пива курит «Кубинские» сигары.
13. Ночной сторож предпочитает сигареты «Друг».
14. Приёмщик стеклотары живёт рядом с синим домом.
15. Курящий «Яву» сосед пьющего воду.
Кто держит рыб? (номер дома, цвет профессия, напитки)
Решение:

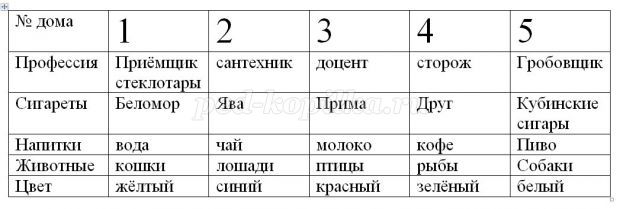
Составить логическую задачу самостоятельно.
Удачи вам!

Задачи, составленные моими учениками.
Иванова Светлана, 7«Б» кл.
На дискотеку пошли 4 девочки: Маша, Оля, Рита. На медленный танец их приглашали Сергей, Рома, Саша, Паша. Кто с кем танцевал, если:
1) Оля не танцевала с Пашей;
2) Таня не танцевала с Пашей и Романом;
3) Рита танцевала с Ромой;
4) Оле понравился Сергей, но она не танцевала с ним.

Маякова Оксана, 9«А» кл.
Бизнесмены Боря Вова Гриша и Гена зарабатывают сумасшедшие деньги, их фамилии засекречены, но удалось их узнать, правда непонятно какая кому принадлежит. Их фамилии: Иванов, Енин, Сидоров, Петров. Так же наши шпионы выяснили:
1) Боря и Петров не имеют личные самолёты.
2) Гриша и Иванов вообще ничего личного не имеют, кроме счетов в швейцарском банке.
3) Гена теперь важнее Енина, хотя Енин и имеет личный самолёт.
4) Петров важнее Енина.
У кого какая фамилия?

Конева Ксения, 9«А» кл.
Четыре подружки: Даша, Маша, Ольга и Таня ходили в магазин покупать подарки. И все подарки разные. Блокнот, альбом, брелок, и книга. На вопрос кто какие подарки купил, они ответили так:
1) Даша и Оля не знали кто купил блокнот;
2) Оля сказала, что Даша и Маша вместе с ней посещали магазин, где продают брелки.
3) Даша не покупала альбом.
Кто какой подарок купил?

Источник

Логика вопросов и ответов таблица

Перечень вопросов, рассматриваемых в теме: метод рассуждений, табличный метод, метод упрощения логических выражений.

Глоссарий по теме: для решения логических задач необходимо знать таблицы истинности логических операций и правила преобразования логических выражений (законы алгебры логики). Этот материал рассмотрен в предыдущих уроках №11,12.

Основная литература по теме урока:

Л. Л. Босова, А. Ю. Босова. Информатика. Базовый уровень: учебник для 10 класса

— М.: БИНОМ. Лаборатория знаний, 2017 (с.197—209)

Открытые электронные ресурсы по теме:

Теоретический материал для самостоятельного изучения

Исходными данными в логических задачах являются высказывания. Высказывания и взаимосвязи между ними бывают так сложны, что разобраться в них без использования специальных методов сложно. Способов решения логических задач немало, но наибольшее распространение получили метод рассуждений, табличный метод и метод упрощения логических выражений. Познакомимся с ними поочередно.

Метод рассуждений

Основная идея этого метода состоит в том, чтобы последовательно анализировать всю информацию, имеющуюся в задаче, и делать на этой основе выводы.

Пример 1. На одной улице стоят в ряд 4 дома, в каждом из которых живёт по одному человеку. Их зовут Василий, Семён, Геннадий и Иван. Известно, что все они имеют разные профессии: скрипач, столяр, охотник и врач. Известно, что:

— столяр живёт правее охотника;

— врач живёт левее охотника;

— скрипач живёт с краю;

— скрипач живёт рядом с врачом;

— Семён не скрипач и не живёт рядом со скрипачом;

— Иван живёт рядом с охотником;

— Василий живёт правее врача;

— Василий живёт через дом от Ивана.

Определим, кто где живёт.

Изобразим дома прямоугольниками и пронумеруем их:

Известно, что скрипач живёт с краю (3). Следовательно, он может жить в доме 1 или в доме 4.

Скрипач живёт рядом с врачом (4), т. е. врач может жить правее (дом 2) или левее (дом 3) скрипача.

Но врач живёт левее охотника (2), следовательно, скрипач не может жить в доме 4, т. к. в противном случае получится, что врач, живущий рядом с ним, живёт правее охотника, а это противоречит условию (2). Таким образом, скрипач живёт в доме 1, а врач — рядом с ним, в доме 2.

Так как врач живёт левее охотника (2), а столяр — правее охотника (1), то охотнику достается дом 3, а столяру — дом 4.

Так как Семён не скрипач и не живёт рядом со скрипачом (5), то он может жить в доме 3 или в доме 4.

Так как Иван живёт рядом с охотником (6), то он может жить в доме 2 или 4.

Так как Василий живёт правее врача (7), то он может жить в доме 3 или 4.

По условию (8) Василий живет через дом от Ивана, значит, в доме 1 может жить только Геннадий, в доме 2 — Иван, в доме 4 — Василий, в доме 3 — Семён.

Как видите, далеко не самая сложна задача потребовала достаточно серьезных рассуждений. Этот метод, как правило, применяется для решения простых задач.

Задачи о рыцарях и лжецах — это такой класс логических задач, в которых фигурируют персонажи:

— рыцарь — человек, всегда говорящий правду;

— лжец — человек, всегда говорящий ложь;

— обычный человек — человек, который в одних ситуациях может говорить правду, а в других лгать.

Решение подобных задач сводится к перебору вариантов и исключению тех из них, которые противоречат условию.

Пример 2. Двое жителей острова А и В разговаривали между собой в саду. Проходивший мимо незнакомец спросил у А: «Вы рыцарь или лжец?». Тот ответил, но так неразборчиво, что незнакомец не смог ничего понять. Тогда незнакомец спросил у В: «Что сказал А?».

«А сказал, что он лжец», — ответил В. Может ли незнакомец доверять ответу В? Мог ли А сказать, что он лжец?

Если А — рыцарь, то он скажет правду и сообщит, что он рыцарь.

Если А — лжец, то он скроет правду и сообщит, что он рыцарь.

Это значит, что В, утверждающий, что «А сказал, что он лжец» заведомо лжёт; он – лжец.

Определить, кем является А, в данной ситуации невозможно.

Табличный метод

Для решения логических задач, связанных с рассмотрением нескольких конечных множеств, прибегают к помощи таблиц или графов. От того, насколько удачно выбрана их структура, во многом зависит успешность решения задачи.

Пример 3. В летнем лагере в одной палатке жили Алёша, Боря, Витя и Гриша. Все они разного возраста, учатся в разных классах (с 7-го по 10-й) и занимаются в разных кружках: математическом, авиамодельном, шахматном и фотокружке. Выяснилось, что

— фотограф старше Гриши;

— Алеша старше Вити, а шахматист старше Алёши;

— в воскресенье Алёша с фотографом играли в теннис, а Гриша в то же время проиграл авиамоделисту в городки.

Определим, кто в каком кружке занимается.

В этой задаче речь идёт о высказывательной форме (предикате) вида «Ученик х занимается в кружке у». Требуется определить такие значения х и у, чтобы высказывательная форма превратилась в истинное высказывание.

Рассмотрим условия (1)-(3) и сделаем выводы: Гриша — не фотограф (1); шахматист — не Алёша и не Витя (2); Алёша — не фотограф и не авиамоделист, Гриша — не фотограф и не авиамоделист (3). Отметим это в таблице:

Мы можем сделать вывод, что Алёша занимается математикой, а Гриша — шахматами:

Из того, что Гриша — шахматист и условий (1) и (2) можем расположить учеников по возрасту (в порядке возрастания): Витя — Алёша — Гриша — фотограф. Следовательно, Боря — фотограф.

Ответ: Витя (7 класс) занимается в авиамодельном кружке, Алёша (8 класс) — в математическом, Гриша (9 класс) — в шахматном, Боря (10 класс) — в фотокружке.

Использование таблиц истинности для решения логических задач

Аппарат алгебры логики позволяет применять к широкому классу логических задач универсальные методы, основанные на формализации условий задачи.

Одним из таких методов является построение таблицы истинности по условию задачи и её анализ. Для этого следует:

1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
2. Записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций.
3. Построить таблицу истинности для полученных логических выражений.
4. Выбрать решение – набор логических переменных (элементарных высказываний), при котором значения логических выражений соответствуют условиям задачи.
5. Убедиться, что полученное решение удовлетворяет условиям задачи.

Пример 4. Три подразделения А, В, С торговой фирмы стремились получить по итогам года максимальную прибыль. Экономисты высказали следующие предположения:

1. Если А получит максимальную прибыль, то максимальную прибыль получат В и С.
2. А и С получат или не получат максимальную прибыль одновременно.
3. Необходимым условием получения максимальной прибыли подразделением С является получение максимальной прибыли подразделением В.

По завершении года оказалось, что одно из трёх предположений ложно, а остальные два истинны.

Выясним, какие из названных подразделений получили максимальную прибыль.

Рассмотрим элементарные высказывания:

А — «А получит максимальную прибыль»;

В — «В получит максимальную прибыль»;

С — «С получит максимальную прибыль».

Запишем на языке алгебры логики прогнозы, высказанные экономистами:

Вспомним, что из трёх прогнозов F₁, F₂, F₃ один оказался ложным, а два других — истинным. Эта ситуация соответствует четвёртой строке таблицы.

Ответ: максимальную прибыль получили подразделения В и С.

Метод упрощения логических выражений

Следующий формальный способ решения логических задач состоит в том, чтобы:

1. Выделить из условия задачи элементарные (простые) высказывания и обозначить их буквами.
2. Записать условие задачи на языке алгебры логики, соединив простые высказывания в составные с помощью логических операций.
3. Составить единое логическое выражение, учитывающее все требования задачи.
4. Используя законы алгебры логики, упростить полученное выражение и вычислить его значение.
5. Выбрать решение – набор логических переменных (элементарных высказываний), при котором построенное логическое выражение является истинным.
6. Убедиться, что полученное решение удовлетворяет условиям задачи.

Пример 5. На вопрос, кто из трёх учащихся изучал логику, был получен ответ: «Если изучал первый, то изучал и второй, но неверно, что если изучал третий, то изучал и второй». Кто из учащихся изучал логику?

Обозначим через А, В, С простые высказывания:

А — «Первый ученик изучал логику»;

В — «Второй ученик изучал логику»;

С — «Третий ученик изучал логику».

Из условия задачи следует истинность высказывания: .

Упростим получившееся высказывание:

Получившееся высказывание будет истинным только в случае, если С — истина, а А и В — ложь.

Источник

Примеры решения задач «Логические выражения и таблица истинности»

Для доказательства равносильности двух высказываний достаточно построить таблицу истинности для высказывания (A/ ) / (/ B) и сравнить ее с таблицей истинности эквивалентности:

А

В

A/¬B

¬AVB

(A/¬B) / (¬A /B)

Последние столбцы этих функций совпадают, значит, они равносильны. ЧТД.

№2.

Укажите, какое логическое выражение равносильно выражению

A / ¬ (¬B / C)

Ответ: 3

№3.

Постройте таблицу истинности для логического выражения:

Ответ:

Ответ:

№4.

Определите истинность следующего высказывания: «За окном светит солнце, и нет дождя».

Решение:

Нам дано сложное составное высказывание. Выделим из него простые высказывания:

А = «За окном светит солнце»

В = «За окном дождь»

Составим логическую функцию, соответствующую данному высказыванию.

построим таблицу истинности для данной логической функции.

A

B

¬B

A / ¬B

1

Ответ: логическое выражение принимает значение истина только при наборе F(1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое простое высказывание истинно, а второе ложно.

№5.

Определите истинность следующего высказывания: «Гости смеялись, шутили и не расходились по домам».

Решение:

Выделим из данного сложного высказывания простые высказывания:

А = «Гости смеялись»

В = «Гости шутили»

С = «Гости расходились по домам»

Составим логическую функцию, соответствующую данному высказыванию.

Построим таблицу истинности для данной логической функции.

A

B

C

¬C

A / B/¬C

1

Ответ: логическое выражение принимает значение истина только при наборе F(1,1,0)=1.Следовательно, данное нам высказывание истинно только тогда, когда первое и второе простые высказывания истинны, а второе ложно.

№6.

На языке алгебры логики составьте истинное тождество, соответствующее заданному условию задачи:

Школьника, Миша, остававшийся в классе на перемене, был вызван к директору по поводу разбитого в это время окна в кабинете. На вопрос директора о том, кто это сделал, мальчик ответили следующее: «Я не бил окно, и Коля тоже…»

Известно, что он либо сказал чистую правду, либо в одной части заявления соврал, а другое его высказывание истинно, либо оба факта исказил.

Решение:

А = «Окно разбил Миша»

В = «Окно разбил Коля»

Если Миша сказал чистую правду, то¬А / ¬В = 1.

Если в одной части заявления Миша соврал, а другое его высказывание истинно, то (¬А / В) / (А /¬В) = 1

Если Миша оба факта исказил, то А / В = 1.

Ответ:

Истинное тождество, соответствующее условию задачи будет выглядеть так: ¬А / ¬В /¬А / В /А / ¬ В / А / В = 1.

Источник

Логика вопросов и ответов

Вопрос— это форма мысли, посредством которой уточняется или дополняется исходное знание об объекте познавательного интереса.

Другими словами, вопрос – это требование отыскать ответ, представляющий собой истинное суждение. Сам вопрос не выражает суждения в силу того, что содержит ожидание подтверждения или отрицания и не содержит ни истины, ни лжи.

Правильно поставленный вопрос должен быть осмысленным, для этого он должен включать два явно выраженных словами элемента: 1) то, что известно (предпосылка вопроса); 2) то, что неизвестно и требуется узнать. Это составляет структуру любого осмысленного вопроса. С осмысленностью вопроса необходимо связаны его разрешимость(возможность получения искомого ответа в принципе, в информационных условиях имеющейся познавательной ситуации) и неаналитичность(отсутствие ответа или намёка на ответ в самом вопросе, в его предпосылке).

Виды вопросов

1. Вопрос может выражать требование найти все истинные ответы или только один из многих или несколько ответов. В зависимости от этого вопросы по форме бывают сильные и слабые.

Сильный вопрос характеризуется максимальной полнотой требования к ответу. Слабыйвопрос характеризуется недостаточной полнотой требований к ответу. Вопросы, которые имеют единственный ответ, называются всегда сильными вопросами.

2. По познавательной функции вопросы подразделяются на:

а) уточняющие (“ли–вопросы”),направленные на выявление истинности выраженных в них суждений-предпосылок;

б)восполняющие (“что–вопросы”),направленные на выявление новых свойств у исследуемых явлений.

3. По составу вопросы делятся на:

а) простые – не включающие в качестве составных частей другие вопросы;

б) сложные– включающие в качестве составных частей другие вопросы, объединённые логическими связками. В зависимости от типов логической связки сложные вопросы бывают дизъюнктивные, конъюнктивные, условные и смешанные.

4. Различают вопросы по отношению к обсуждаемой теме:

а)релевантные вопросы–вопросы по существу, они имеют предпосылки, связанные с обсуждаемой темой;

б) нерелевантные вопросы – вопросы не по существу темы имеют посылки, не связанные с обсуждаемой темой.

5. В зависимости от логического качества, вопросы делятся на:

а)корректные – осмысленные (предпосылка выражает истинное знание), разрешимые, информационно значимые;

б) некорректные – аналитичные или с ложной предпосылкой или неразрешимые или неопределенные (неточные, неясно сформулированные).

Если вопрос намеренно формулируется не корректно, то он называется провокационным или улавливающим.

Риторический вопрос не является вопросом в собственном смысле, является суждением, высказанным с использованием фигуры речи в форме вопроса.

Любой вопрос требует ответа (кроме риторического). Вместе с вопросом ответ формирует поле общения и является необходимой частью познавательного процесса.

Виды ответов

Ответ – новое суждение, уточняющее или дополняющее прежнее знание в соответствии с поставленным вопросом.

1. Истинные и ложные ответы. Ответ является истинным, если выраженное в нём суждение соответствует действительности. Ответ является ложным, если суждение, выраженное в нём, не соответствует действительности.

При этом информационная значимость ответа для спрашивающего и отвечающего может оцениваться по-разному, в силу различного уровня образования и информированности, но это уже внелогический фактор коммуникации.

2. По области поиска ответы делятся на:

а) прямые – берутся непосредственно из области поиска ответа, при их формулировке не прибегают к дополнительным сведениям и рассуждениям;

б) косвенные– ответы, получаемые из более широкой области, нежели область поиска ответа, требующие дополнительных рассуждений и вычислений.

3. По грамматической форме ответы могут быть краткими и развёрнутыми.

а)краткие – односложные утвердительные или отрицательные ответы, а также ответы, в которых содержится только новая информация и не воспроизводятся элементы вопроса;

б) развёрнутые – ответы, в которых повторяются элементы вопроса.

4. По объёму представленной в ответе информации ответы делятся на полные и неполные.

а) полный – ответ, включающий информацию по всем элементам сложного вопроса;

б)неполный – частичный ответ, включающий информацию по отдельным (не всем) элементам вопроса. Полный и точный ответ называют также сильным; ответ частичный и приблизительный – слабым ответом.

5. По содержанию и структуре ответ должен соответствовать поставленному вопросу. Только в этом случае ответ расценивается как корректный ответ по существу (релевантный). Если в качестве ответа приводят истинные по содержанию, но не связанные с вопросом суждения, то их расценивают какответы не по существу поставленного вопроса (нерелевантные).

Логика и этика сходятся также в том, что некорректно уходить от ответа, отвечая на вопрос вопросом, или начинать длинные рассуждения и расчёты, не получив на это согласия. Правильно в случае затруднения с ответом сообщить об этом собеседнику и попросить на подготовку ответа дополнительное время либо отказаться отвечать, сообщив причины отказа.

Вопросы для повторения

1.Какова коммуникативная сущность и логическая структура аргументации?

2.В чём особенность опровержения как вида доказательства?

3.Что такое тезис, каковы правила тезиса и к каким ошибкам ведёт их нарушение?

4.Что называется аргументами, какие виды аргументов существуют? Какие из них являются логически корректными?

5.Каковы требования к аргументам, какие ошибки возникают в доказательстве по отношению к аргументам?

6.Что называется демонстрацией в доказательстве? Каковы правила и ошибки по отношению к демонстрации?

7.Объясните понятия софизм, паралогизм, парадокс, абсурд, приведите примеры.

8.Что называется вопросом? Каковы условия осмысленности вопроса?

9.Что называется корректностью вопроса?

10.Какие вопросы называются сильными, какие слабыми?

11.Какие существуют наиболее распространённые логические и речевые ошибки в вопросах?

12.Что такое ответ? В чём состоит логическая связь ответа и вопроса?

13.Что такое косвенный ответ, когда он используется?

14.Чем краткий ответ отличается от неполного?

15.Чем полный ответ отличается от развёрнутого?

16.Какой ответ можно считать неправильным и на каких основаниях?

Резюме по теме

Аргументация и вопрос – несмотря на то, что логической основой первой является умозаключение, а второй представляет собой автономную форму мысли – связаны в процессе реального мышления самым непосредственным образом. Действительно: если нет вопроса, то незачем подбирать аргументы; если никто не сомневается в приведенном обосновании, неоткуда взяться опровержению; без спорного вопроса нет и предмета спора как конфликтной формы аргументации. Именно поэтому, чем лучше осознаны логические качества обсуждаемого вопроса, начиная с его предпосылок, тем более эффективной будет аргументация ответа. И наоборот, чем тщательнее соблюдаются логические правила аргументации, тем меньше она вызывает «лишних» вопросов, стимулирует мысль в направлении плодотворной дискуссии и достижения истины.

Источник