Лекция
Тема: Построение
логических схем с помощью базовых логических элементов
План
1. Логические
элементы.
2. Построение
логических схем.
Логическим элементом
называется дискретный преобразователь, который после обработки входных двоичных
сигналов выдает на выходе сигнал, являющийся значением одной из логических
операций.
Поскольку любая логическая операция может быть
представлена в виде комбинаций трех основных, любые устройства компьютера,
производящие обработку или хранение информации, могут быть собраны из базовых
логических элементов, как из «кирпичиков».
Логические элементы компьютера оперируют сигналами,
представляющими собой электрические импульсы. Есть импульс – логический смысл
сигнала – 1, нет импульса – 0. На входы логического элемента поступают
сигналы-значения аргументов, на выходе появляется сигнал-значение функции.
Преобразование сигнала логическим элементом задается
таблицей состояния, которая фактически является таблицей истинности,
соответствующей логической функции.
Рассмотрим условные обозначения (схемы) базовых
логических элементов, реализующих логическое умножение (конъюнктор), логическое
сложение (дизъюнктор) и отрицание (инвертор).
Логический
элемент «ИЛИ»:

 например,
например,
Логический
элемент «НЕ»:

 например,
например,
Логический
элемент «И»:


например,
ИЛИ ДРУГОЙ ВИД ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
|
Инверсия |
|
|
Конъюнкция |
|
|
Дизъюнкция |
|
Устройства компьютера (сумматоры в процессоре, ячейки
памяти в оперативной памяти и др.) строятся на основе базовых логических
элементов.
Если элемент имеет входное напряжение от 0 до 0,4В, то
оно рассматривается как логический 0, если напряжение в пределах от 0,7 до
1,5В, то оно рассматривается как 1. Примерно такие же характеристики имеет
выходное напряжение.
I.
![]() Построить
Построить
схемы
Пример 1. Составить схему
Результат:

![]()
Пример 2. Составить схему
Результат:

![]() Пример 3. Составить
Пример 3. Составить
схему
Результат:

Пример 4. Составить схему ![]()
Результат:

![]() Пример 5. Составить
Пример 5. Составить
схему
Результат:

![]()
Пример 6. Составить схему
Результат:

![]() Пример 7. Составить
Пример 7. Составить
схему
Результат:

II. Выполним задачу
обратную данной. Составим логическое выражение по заданной логической схеме:

![]()
Данное логическое
выражение можно упростить.
Операция И – логическое
умножение, ИЛИ – сложение. Запишем выражение, заменяя знаки & и U на * и +
соответственно.
![]() Упростим
Упростим
![]() , затем
, затем
запишем
![]() )
)
и тогда
логическая схема примет вид:

Вывод: Логические схемы, содержащие минимальное
количество элементов, обеспечивают большую скорость работы и увеличивают
надёжность устройства.
Алгебра логики дала конструкторам мощное средство
разработки, анализа и совершенствования логических схем. Проще, и быстрее
изучать свойства и доказывать правильность работы схемы с помощью выражающей её
формулы, чем создавать реальное техническое устройство.
По заданной логической функции ![]() построить логическую
построить логическую
схему.
Наше построение схемы, мы начнем с логической
операции, которая должна выполняться последней. В нашем случае такой операцией
является логическое сложение, следовательно, на выходе логической схемы должен
быть дизъюнктор. На него сигналы будут подаваться с двух конъюнкторов, на
которые в свою очередь подаются один входной сигнал нормальный и один
инвертированный (с инверторов).

Пример 2. Выписать
из логической схемы соответствующую ей логическую формулу:
|
А |
В |
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
1 |

Решение:

2.
Построение
логических схем.
Вариант
1.
По
заданной логической функции ![]() построить
построить
логическую схему и таблицу истинности.
Решение:


2.
Выписать из логической схемы соответствующую ей логическую формулу:
|
А |
В |
F |
|
0 |
0 |
1 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |

Решение:

Вариант
2.
1.
По заданной логической функции ![]() построить
построить
логическую схему и таблицу истинности.
Решение:


2.
Выписать из логической схемы соответствующую ей логическую формулу:
|
А |
В |
F |
|
0 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |

Решение:

По
заданной логической функции ![]() построить
построить
логическую схему и таблицу истинности.
Контрольные
вопросы:
1. Перечислите
основные логические операции.
2. Что такое
логическое умножение?
3. Что такое
логическое сложение?
4. Что такое
инверсия?
5. Что такое
таблица истинности?
6. Что такое
сумматор?
7. Что такое
полусумматор?
Литература,
ЭОР:
1.
Информатика
и информационные технологии. Учебник для 10-11 классов,Н. Д. Угринович –
2007г.;
2. Практикум по
информатике и информационным технологиям. Учебное пособие для
общеобразовательных учреждений, Н. Д. Угринович, Л. Л. Босова, Н. И. Михайлова
– 2007г.
Знания из области
математической логики можно использовать
для конструирования электронных
устройств. Нам известно, что 0 и 1 в логике
не просто цифры, а обозначение состояний
какого-то предмета нашего мира, условно
называемых “ложь” и “истина”.
Таким предметом, имеющим два фиксированных
состояния, может быть электрический
ток. Устройства, фиксирующие два
устойчивых состояния, называются
бистабильными (например, выключатель,
реле). Если вы помните, первые вычислительные
машины были релейными. Позднее были
созданы новые устройства управления
электричеством ― электронные схемы,
состоящие из набора полупроводниковых
элементов. Такие электронные схемы,
которые преобразовывают сигналы только
двух фиксированных напряжений
электрического тока (бистабильные),
стали называть логическими
элементами.
На элементарном
уровне конъюнкцию можно представить
себе в виде последовательно соединенных
выключателей, а дизъюнкцию ― в виде
параллельно соединенных выключателей:
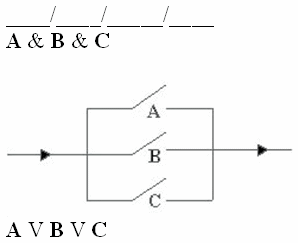
Логические элементы
имеют один или несколько входов и один
выход, через которые проходят электрические
сигналы, обозначаемые условно 0, если
“отсутствует” электрический сигнал,
и 1, если “имеется” электрический
сигнал. Простейшим логическим элементом
является инвертор,
выполняющий функцию отрицания. Если на
вход поступает сигнал, соответствующий
1, то на выходе будет 0. И наоборот. У этого
элемента один вход и один выход. На
функциональных схемах он обозначается:

Логический элемент,
выполняющий логическое сложение,
называется дизъюнктор.
Он имеет, как минимум, два входа. На
функциональных схемах он обозначается:

Логический элемент,
выполняющий логическое умножение,
называется конъюнктор. Он имеет, как
минимум, два входа. На функциональных
схемах он обозначается:

Специальных
логических элементов для импликации и
эквивалентности нет, т.к. А => В можно
заменить на ¬А V В ; А <=> В можно заменить
на (A & B)V(¬A & ¬B).
Другие логические
элементы построены из этих трех простейших
и выполняют более сложные логические
преобразования информации. Сигнал,
выработанный одним логическим элементом,
можно подавать на вход другого элемента,
это дает возможность образовывать
цепочки из отдельных логических
элементов. Например:

Эта схема
соответствует сложной логической
функции F(A,B)= ¬ (А V В).
Попробуйте
проследить изменения электрического
сигнала в этой схеме. Например, какое
значение электрического сигнала (0 или
1) будет на выходе, если на входе: А=1 и
В=0.
Такие цепи из
логических элементов называются
логическими
устройствами.
Логические устройства же, соединяясь,
в свою очередь образуют функциональные
схемы (их
еще называют структурными или логическими
схемами). По
заданной функциональной схеме можно
определить логическую формулу, по
которой эта схема работает, и наоборот.
Пример 1.
Логическая схема для функции
![]() будет
будет
выглядеть следующим образом:

Правила составления
электронных логических схем по заданным
таблицам истинности остаются такими
же, как для контактных схем.
Пример
2. Составить
логическую схему для тайного голосования
трех персон A, B, C, условия которого
определяются следующей таблицей
истинности:
|
A |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
B |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
C |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
F |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
Решение
По
таблице построим СДНФ логической функции
и упростим ее:

Правильность
полученной формулы можно проверить,
составив для нее таблицу истинности:

Значение полученной
функции совпадает с исходным, что можно
заметить, сравнивая таблицы.
Логическая
схема полученной функции имеет вид:

Рассмотрим еще
два логических элемента, которые играют
роль базовых при создании более сложных
элементов и схем.

Логический элемент
И―НЕ состоит из конъюнктора и
инвертора:
Выходная
функция выражается формулой
![]() .
.
Логический
элемент ИЛИ―НЕ состоит из дизъюнктора
и инвертора:

Выходная функция
выражается формулой
![]() .
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пример проектирования цифрового устройства «на пальцах»
Время на прочтение
3 мин
Количество просмотров 23K
Привет, Хабр! Это начало небольшого цикла из двух статей с пошаговым проектированием цифрового устройства с уклоном на практику. Минимум «воды» и максимум практики!

Для начала работы возьмем следующие выходные параметры: 0000110001110001
Примечание: существует множество способов и программ для проектирования цифровых устройств. Показанное в статье может отличаться от привычных вам. Это нормально.
Инструменты, материалы и прочее:
- Electronics Workbench
- Линейка, ручка и листок (для общих расчетов)
- Базовые знания дискретной математики, цифровой схемотехники и принципа работы представленных программ
- Условное графическое обозначение микросхем 7404 (аналог К155ЛН1), 7410 (аналог К155ЛА4), 7410 (аналог К155ЛА4) и 7420 (аналог К155ЛА1)
- Фактическое изображение микросхем 7404 (аналог К155ЛН1), 7410 (аналог К155ЛА4), 7410 (аналог К155ЛА4) и 7420 (аналог К155ЛА1)
Начало работы
1. Построение таблицы истинности и нахождение совершенной дизъюнктивной нормальной формы (СДНФ)
Первым делом необходимо составить таблицу истинности по формуле

где N – количество возможных вариантов, а i – количество выходных сигналов.
В представленном случае это будет выглядеть так:
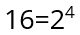
На основе полученных данных можно перейти к построению таблицы истинности. Для наглядности входные сигналы были обозначены как A, B, C и D, выходной как F.
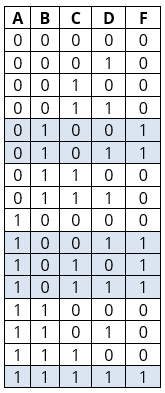
После построения таблицы истинности можно приступать к получению СДНФ. Это выполняется в два шага:
- Выделяются строчки таблицы истинности, в которых F=1.
- Выписывается конъюнкция переменных у всех выделенных строк по следующей формуле: если значение переменной равно 1, то в конъюнкцию включается сама переменная. Если значение равно 0, то включается отрицание переменной. Полученные конъюнкции нужно связать в дизъюнкцию.
По итогу выходит такая СДНФ:
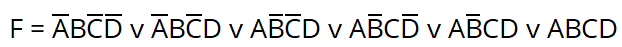
Более наглядно:
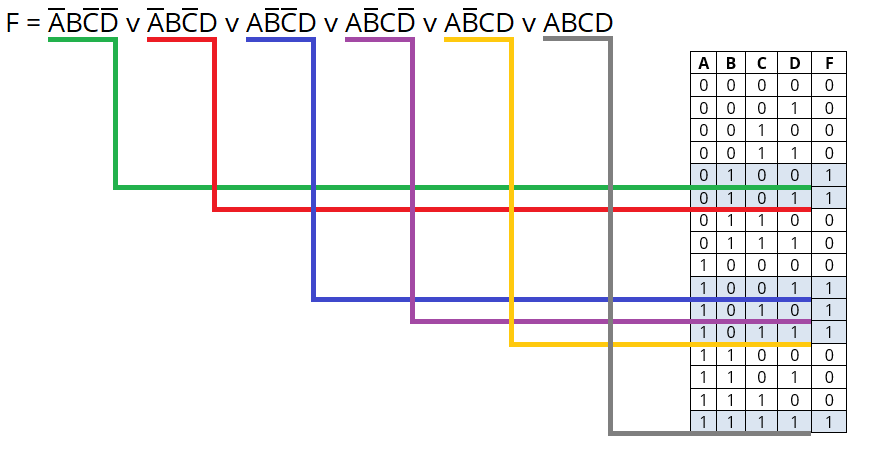
2. Создание карты Карно, минимизация и приведение к базису И-НЕ
Полученную СДНФ необходимо сократить при помощи карт Карно.
Три шага для построения карт Карно:
- так как используются четыре переменные (A, B, C и D), то строится таблица 5×5 клеток;
- таблица заполняется на основе «координат» из таблицы истинности (из строк, в которых F=1) или СДНФ (суть одна. Просто кому как удобнее);
- в заключение смежные клетки объединяются в группы. Группы не должны содержать нули. Группы должны быть кратны двум. Группы могут пересекаться.
В итоге получилось 4 группы:

Более наглядно:

Следующее действие — минимизация полученных групп. Общий принцип можно свести к следующему:
Если 11 — значение не меняется;
Если 00 — присваивается отрицание;
Если 01 (или 10) — вычеркивается.
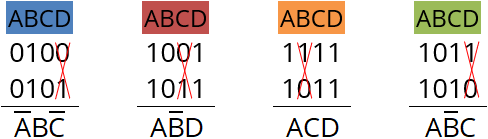
Полученные произведения связываются в дизъюнкцию:
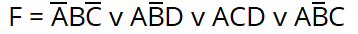
После чего составленное выражение приводится к базису И-НЕ при помощи закона де Моргана (отрицание конъюнкции есть дизъюнкция отрицаний, отрицание дизъюнкции есть конъюнкция отрицаний):
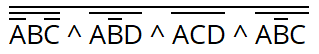
Обратите внимание на изменения — появилось двойное отрицание (по одной на «группу» и одно общее) и изменились знаки.
По желанию также можно составить логическую схему. Почему по желанию? Потому что дальше будет составление электронной схемы на основе логических элементов, а она, по своей сути, является той же самой логической схемой, но с возможностью проверки работоспособности.
Пример логической схемы:
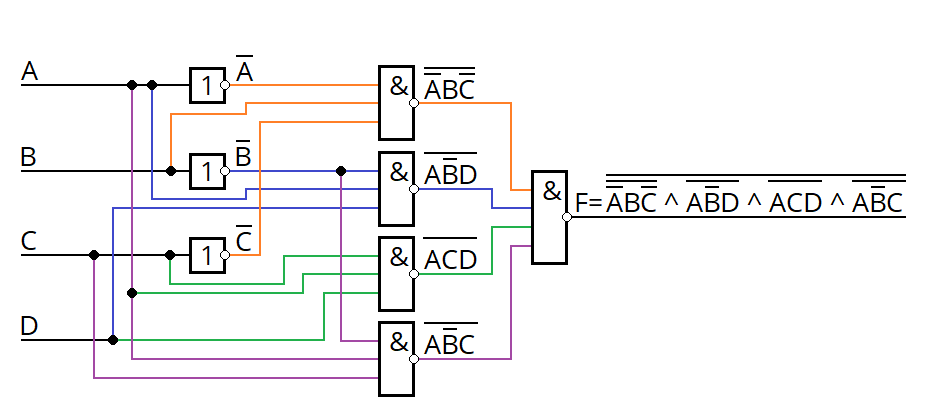
3. Электронная схема на основе логических элементов
Основные расчеты завершены. Теперь можно отложить листок с ручкой и линейкой. Переходим в Electronics Workbench.
В данном случае этот этап выступает «промежуточным» и упрощает процесс перехода от выражения в базисе И-НЕ к электронной схеме на основе микросхем.

Более наглядно:
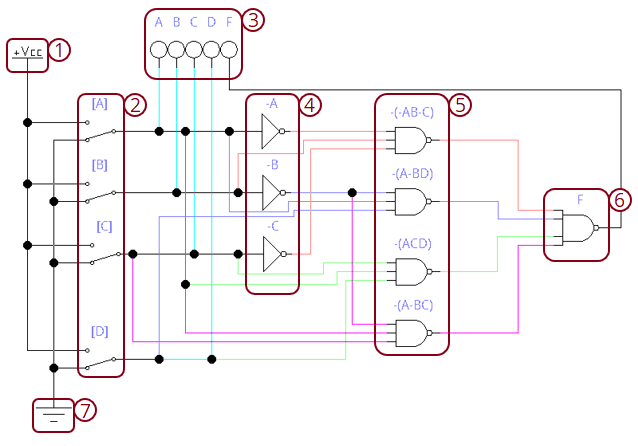
1 — Питание;
2 — Переключатели, используемые для подачи сигналов;
3 — Индикаторы (применяются для наглядной проверки работоспособности);
4 — Логические элементы типа «НЕ»;
5 — Логические элементы типа «3И-НЕ»;
6 — Логический элемент типа «4И-НЕ»;
7 — Заземление.
Как можно заметить, логические элементы электронной схемы внешне отличаются от тех, что были представлены ранее (в логической схеме). Это связано с тем, что в Electronics Workbench условное графическое обозначение логических элементов выполнено по стандартам ANSI, тогда как показанная ранее логическая схема была выполнена в соответствии ГОСТ 2.743-91.
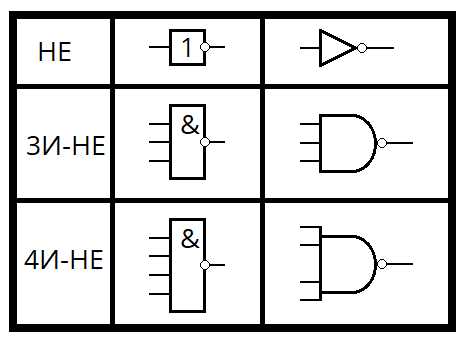
Идем дальше.
Работоспособность электронной схемы проверяется по таблице истинности. Для этого нужно нажать кнопку запуска

и начать производить переключения, проводя сравнение с таблицей истинности.
Пример:

ВАЖНО: нужно проверять каждую строчку. Выборочная проверка ничего не даст.
4. Электронная схема на основе микросхем
На базе имеющихся данных производится построение электронной схемы на основе микросхем (также по полученной схеме можно будет ориентироваться во время проектирования печатной платы).
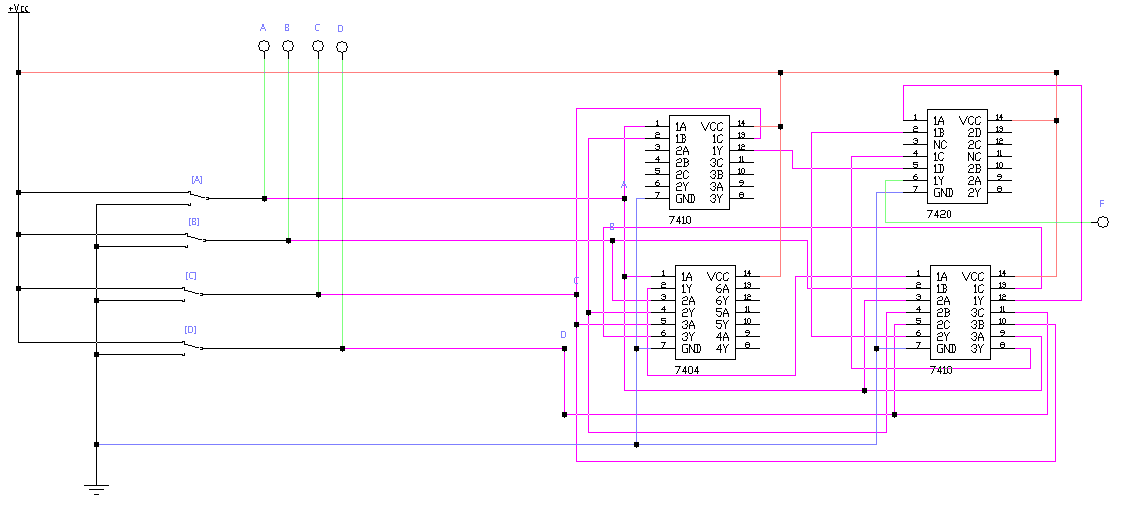
Как можно заметить, в полученной электронной схеме использовано 4 микросхемы — 7404 (аналог К155ЛН1), 7410 (аналог К155ЛА4), 7410 (аналог К155ЛА4) и 7420 (аналог К155ЛА1). Для того чтобы понять, как происходит подключение, следует обратиться к фактическому изображению микросхем.
Сначала это может показаться сложным, но со временем вы поймете, что это не так уж и трудно.
ВАЖНО: не забывайте делать проверку.
Продолжение следует…
Цели урока:
Образовательные:
- закрепить у учащихся представление об
устройствах элементной базы компьютера; - закрепить навыки построения логических схем.
Развивающие:
- формировать развитие алгоритмического
мышления; - развить конструкторские умения;
- продолжать способствовать развитию ИКТ –
компетентности;
Воспитательные:
- продолжить формирование познавательного
интереса к предмету информатика; - воспитывать личностные качества:
- активность,
- самостоятельность,
- аккуратность в работе;
Требования к знаниям и умениям:
Учащиеся должны знать:
- основные базовые элементы логических схем;
- правила составления логических схем.
Учащиеся должны уметь:
- составлять логические схемы.
Тип урока: урок закрепления
изученного материала
Вид урока: комбинированный
Методы организации учебной деятельности:
- фронтальная;
- индивидуальная;
Программно-дидактическое обеспечение:
- ПК, SMART Board, карточки с индивидуальным домашним
заданием.
Урок разработан с помощью программы Macromedia Flash.
Ход урока
I. Постановка целей урока.
Добрый день!
Сегодня мы продолжаем изучение темы
“Построение логических схем”.
Приготовьте раздаточный материал “Логические
основы ЭВМ. Построение логических схем” Приложение 1
Вопрос учителя. Назовите основные
логические элементы. Какой логический элемент
соответствует логической операции И, ИЛИ, НЕ?
Ответ учащихся. Логический элемент
компьютера – это часть электронной логической
схемы, которая реализует элементарную
логическую функцию. Основные логические
элементы конъюнктор (соответствует логическому
умножению), дизъюнктор (соответствует
логическому сложению), инвертор (соответствует
логическому отрицанию).
Вопрос учителя. По каким правилам
логические элементы преобразуют входные
сигналы. Рассмотрим элемент И. В каком случае на
выходе будет ток (сигнал равный 1).
Ответ учащихся. На первом входе есть
ток (1, истина), на втором есть (1, истина), на выходе
ток идет (1, истина).
Вопрос учителя. На первом входе есть
ток, на втором нет, однако на выходе ток идет. На
входах тока нет и на выходе нет. Какую логическую
операцию реализует данный элемент?
Ответ учащихся. Элемент ИЛИ –
дизъюнктор.
Вопрос учителя. Рассмотрим логический
элемент НЕ. В каком случае на выходе не будет тока
(сигнал равный 0)?
Ответ учащихся. На входе есть ток,
сигнал равен 1.
Вопрос учителя. В чем отличие
логической схемы от логического элемента?
Ответ учащихся. Логические схемы
состоят из логических элементов, осуществляющих
логические операции.
Проанализируем схему и определим сигнал на
выходе.
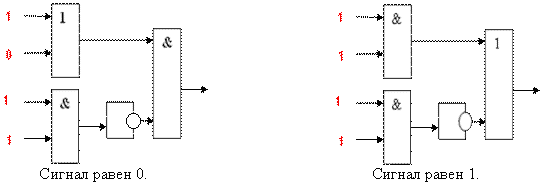
II. Закрепление изученного материала.
Почему необходимо уметь строить логические
схемы?
Дело в том, что из вентилей составляют более
сложные схемы, которые позволяют выполнять
арифметические операции и хранить информацию.
Причем схему, выполняющую определенные функции,
можно построить из различных по сочетанию и
количеству вентилей. Поэтому значение
формального представления логической схемы
чрезвычайно велико. Оно необходимо для того,
чтобы разработчик имел возможность выбрать
наиболее подходящий ему вариант построения
схемы из вентилей. Процесс разработки общей
логической схемы устройства (в том числе и
компьютера в целом), становится иерархическим,
причем на каждом следующем уровне в качестве
“кирпичиков” используются логические схемы,
созданные на предыдущем этапе.
Дома вам необходимо было построить логические
схемы, соответствующие логическим выражениям.
Вопрос учителя. Каков алгоритм
построение логических схем?
Ответ учащихся. Алгоритм построение
логических схем:
Определить число логических переменных.
Определить количество базовых логических
операций и их порядок.
Изобразить для каждой логической операции
соответствующий ей элемент (вентиль).
Соединить вентили в порядке выполнения
логических операций.
Работа со SMART Board Приложение 2
Проверка домашнего задания Приложение
1. Домашнее задание. Часть 1
Построить логическую схему для логического
выражения: ![]() .
.
- Две переменные – А и В.
- Две логические операции: &,
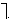
- Строим схему.
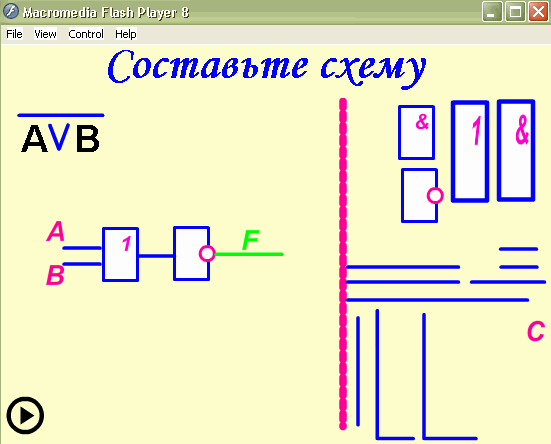
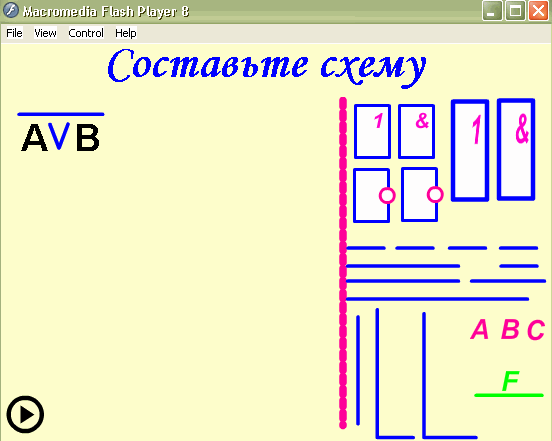
Построить логическую схему для логического
выражения: ![]()
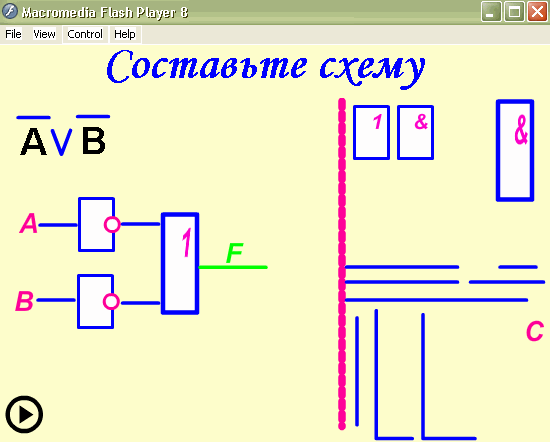
Построить логическую схему для логического
выражения: ![]()
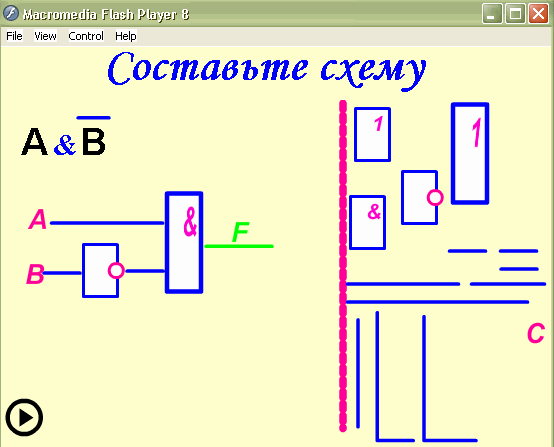
Построить логическую схему для логического
выражения: ![]()
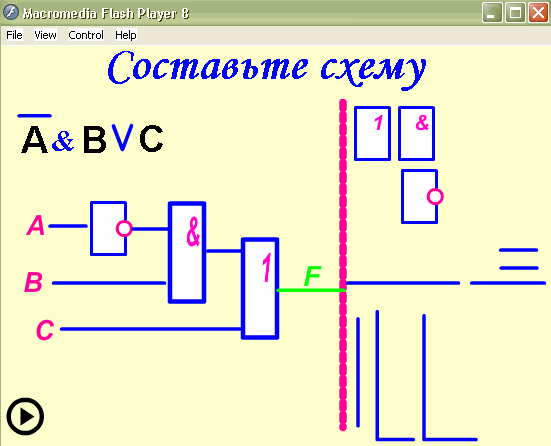
Построить логическую схему для логического
выражения: ![]()
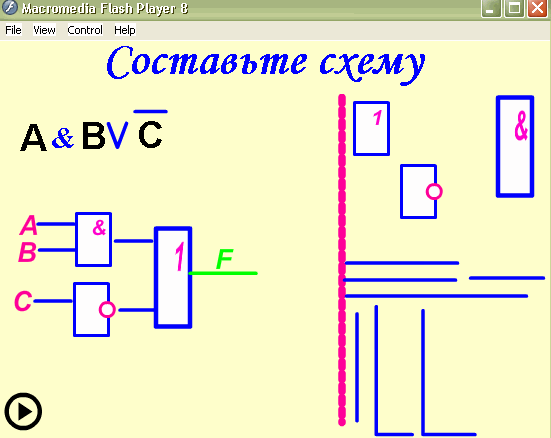
Построить логическую схему для логического
выражения: ![]()
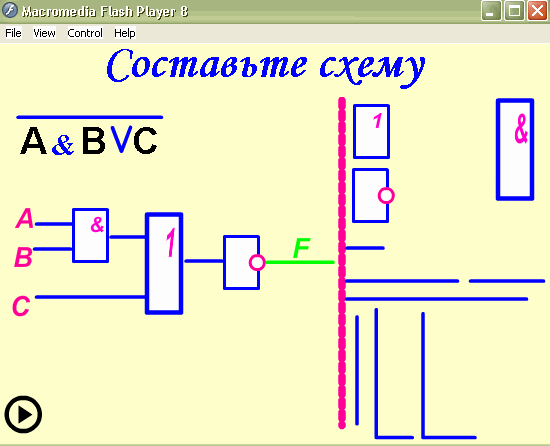
Построить логическую схему для логического
выражения: ![]()
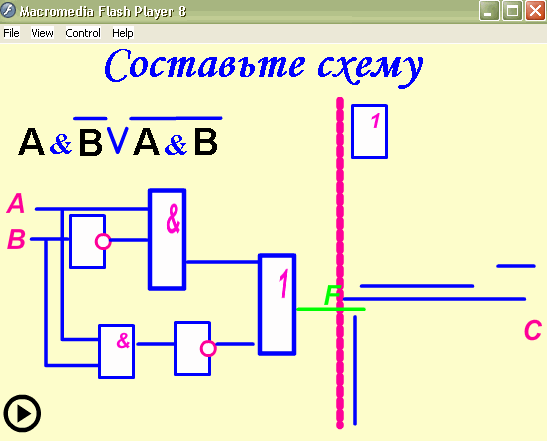
Вычислить значение данного выражения для А=1,
В=0.
Ответ F=1
III. Пропедевтика (законы логики)
Выполним задачу обратную данной. Составим
логическое выражение по заданной логической
схеме:
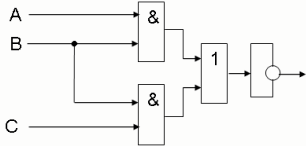
![]()
Данное логическое выражение можно упростить.
Операция И – логическое умножение, ИЛИ –
сложение. Запишем выражение, заменяя знаки & и U
на * и + соответственно.
F= ![]() (A*B+B*С) Упростим F=
(A*B+B*С) Упростим F= ![]() (B*(А+С)), затем запишем
(B*(А+С)), затем запишем ![]() и тогда
и тогда
логическая схема примет вид:
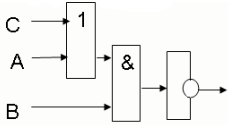
Вывод: Логические схемы, содержащие
минимальное количество элементов, обеспечивают
большую скорость работы и увеличивают
надёжность устройства.
Алгебра логики дала конструкторам мощное
средство разработки, анализа и
совершенствования логических схем. Проще, и
быстрее изучать свойства и доказывать
правильность работы схемы с помощью выражающей
её формулы, чем создавать реальное техническое
устройство.
Таким образом, цель нашего следующего урока –
изучить законы алгебры логики.
IV. Домашнее задание. Часть 2
V. Практическая работа.
Программа – тренажер “Построение логических
схем”
www.Kpolyakov.narod.ru Программа “Logic”,
Спасибо за урок!
Логические основы работы компьютера
Знания из области математической логики можно использовать для конструирования электронных устройств. Нам известно, что 0 и 1 в логике не просто цифры, а обозначение состояний какого-то предмета нашего мира, условно называемых «ложь» и «истина». Таким предметом, имеющим два фиксированных состояния, может быть электрический ток.
Логические элементы имеют один или несколько входов и один выход, через которые проходят электрические сигналы, обозначаемые условно 0, если «отсутствует» электрический сигнал, и 1, если «имеется» электрический сигнал.
Базовые логические элементы реализуют три основные логические операции: «И», «ИЛИ», «НЕ».
Логический элемент «НЕ» (инвертор)
Простейшим логическим элементом является инвертор, выполняющий функцию отрицания. Если на вход поступает сигнал, соответствующий 1, то на выходе будет 0. И наоборот.
У этого элемента один вход и один выход. На функциональных схемах он обозначается:
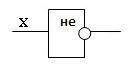 Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Говорят также, что элемент «НЕ» инвертирует значение входной двоичной переменной.
Проверь соответствие логического элемента «НЕ» логическому элементу «НЕ». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «И» (конъюнктор)
Логический элемент «И» (конъюнктор) выдает на выходе значение логического произведения входных сигналов.
Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
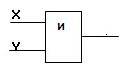 Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Сигнал на выходе конъюнктора появляется тогда и только тогда, когда поданы сигналы на все входы. На элементарном уровне конъюнкцию можно представить себе в виде последовательно соединенных выключателей. Известным примером последовательного соединения проводников является елочная гирлянда: она горит, когда все лампочки исправны. Если же хотя бы одна из лампочек перегорела, то гирлянда не работает.
Проверь соответствие логического элемента «И» логическому элементу «И». Воспользуйся тренажером Логические элементы.xlsx
Логический элемент «ИЛИ» (дизъюнктор)
Логический элемент «ИЛИ» (дизъюнктор) выдает на выходе значение логической суммы входных сигналов. Он имеет один выход и не менее двух входов. На функциональных схемах он обозначается:
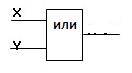 Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
Сигнал на выходе дизъюнктора не появляется тогда и только тогда, когда на все входы не поданы сигналы.
На элементарном уровне дизъюнкцию можно представить себе в виде параллельно соединенных выключателей.
Примером параллельного соединения проводников является многорожковая люстра: она не работает только в том случае, если перегорели все лампочки сразу.
Проверь соответствие логического элемента «ИЛИ» логическому элементу «ИЛИ». Воспользуйся тренажером Логические элементы.xlsx
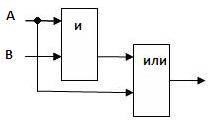
Пример 1.
Составьте логическую схему для логического выражения: F=A / B / A.
1. Две переменные – А и В.
2. Две логические операции: 1-/, 2-/.
3. Строим схему:
Пример 2.
Постройте логическую схему, соответствующую логическому выражению F=А/В/ ¬(В/А). Вычислить значения выражения для А=1,В=0.
1. Переменных две: А и В; 1 4 3 2
2. Логических операций три: / и две /; А/В/ ¬ (В/ А).
3. Схему строим слева направо в соответствии с порядком логических операций:
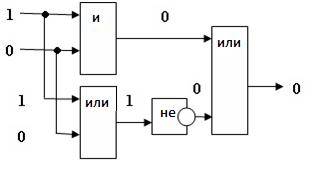
4. Вычислим значение выражения: F=1 / 0 / ¬(0 / 1)=0



