Как составить ломаную линию - Сайт, где вы сможете решить свои вопросы

Ломаная линия

Замкнутая и незамкнутая ломаная
Самопересекающаяся ломаная
Длина ломаной

Ломаная линия — это геометрическая фигура, состоящая из последовательно соединённых отрезков, в которой конец одного отрезка является началом следующего. При этом соседние (имеющие общую точку) отрезки не должны лежать на одной прямой.

Отрезки, из которых состоит ломаная, называются её звеньями, а концы этих отрезков — вершинами ломаной.

Построим ломаную из четырёх отрезков:

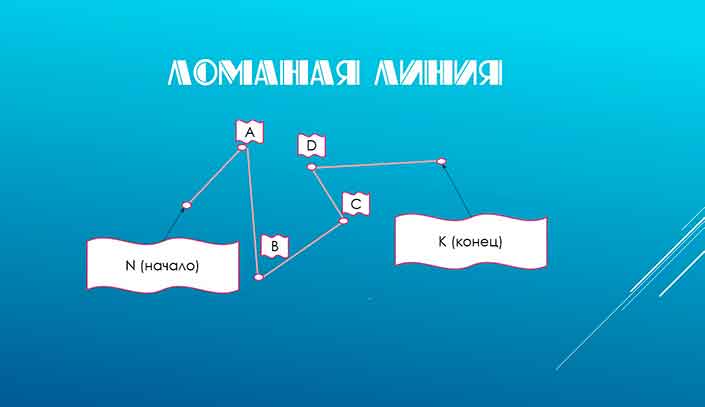
Отрезки AB, BC, CD и DE — это звенья ломаной. Точки A, B, C, D и E — вершины ломаной. Обозначение ломаной линии составляют из букв, стоящих при её вершинах, называя их по порядку. Например, говорят или пишут: ломаная ABCDE или ломаная EDCBA.

Замкнутая и незамкнутая ломаная

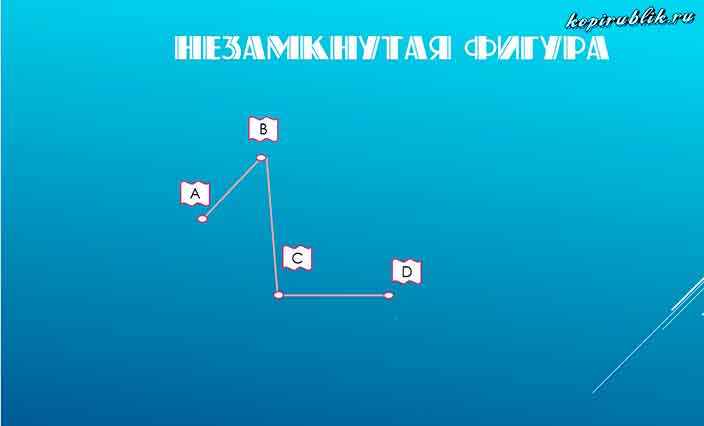
Незамкнутая ломаная — это ломаная линия, концы которой не совпадают друг с другом:

незамкнутая ломаная ABCD.

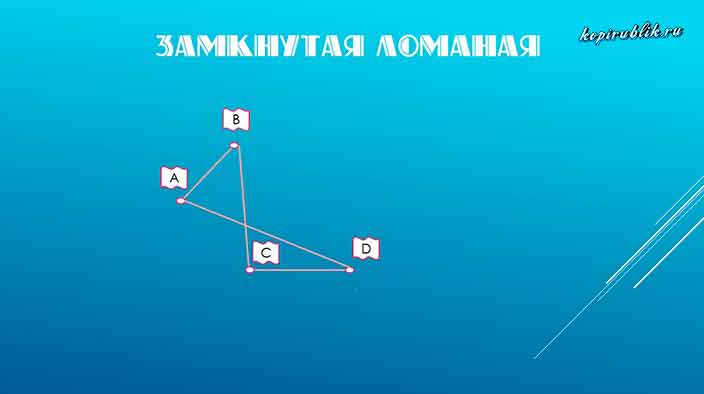
Замкнутая ломаная — это ломаная линия, концы которой совпадают друг с другом:

замкнутая ломаная ABC.

Самопересекающаяся ломаная

Замкнутые и незамкнутые ломаные линии могут быть самопересекающимися. Самопересекающаяся ломаная — это ломаная линия, звенья которой пересекают другу друга в одной или нескольких точках. Например:

точки F, T, K — точки самопересечения, то есть точки, в которых ломаная пересекает сама себя.

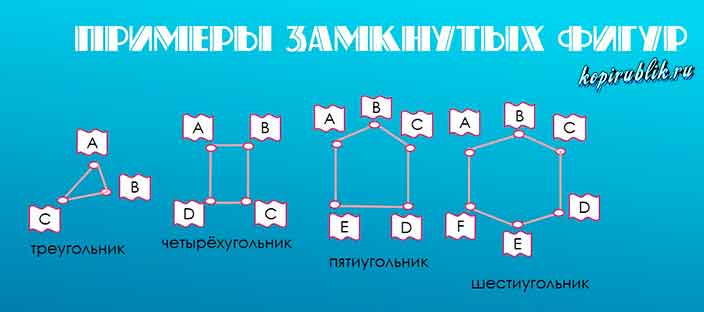
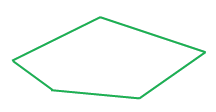
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником:

многоугольник ABCDE.

Длина ломаной

Длина ломаной — это сумма длин всех её звеньев. Длина замкнутой ломаной, не имеющий самопересечений, то есть длина многоугольника, называется периметром.

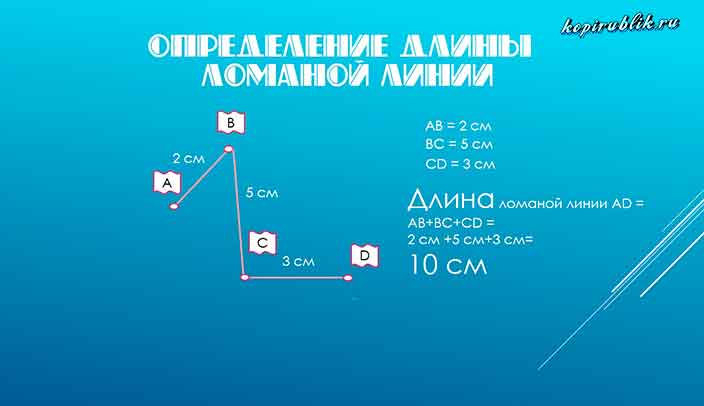
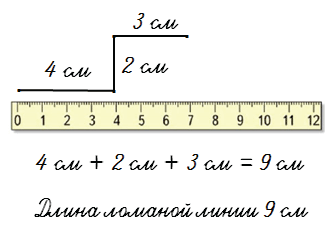
Пример 1. Найти длину ломаной из 3 звеньев.

Решение: Для нахождения длины ломаной, состоящей из трёх звеньев, надо сложить длины всех её звеньев. Длина ломаной ABCD будет равна:

AB + BC + CD = 4 см + 3 см + 2 см = 9 см.

Ответ: Длина ломаной ABCD равна 9 см.

Пример 2. Найти длину замкнутой ломаной.

Решение: Найдём периметр замкнутой ломаной, сложив длины всех её звеньев:

AB + BC + CD + DA =
3 см + 5 см + 4 см + 5 см = 17 см.

Ответ: 17 см.

Источник

Ломаная линия — что это
Обозначение ломаной линии
Из чего состоит ломаная линия
Признак замкнутости
Как измерить длину ломаной линии
Чем ломаная линия отличается от прямой
Примеры ломаных линий в быту

Ломаная линия — определение

Одним из наиболее простых и понятных геометрических терминов считают прямую линию. Есть в математике похожая фигура, но с некоторыми характерными чертами. Давайте попробуем разобраться, что такое ломаная линия и каковы её особенности.

Ломаная линия — математическая фигура, включающая в себя несколько отрезков, которые меняют направление.

Если выражаться более чётко, то это черта, которая не является прямой по всей длине, но может не иметь изгибов на отдельном отрезке.

Таким образом, фигура в обязательном порядке отвечает нескольким признакам:

состоит из отрезков, которые являются её звеньями;
конец каждого звена является началом следующего (кроме последнего);
находящиеся рядом отрезки не могут располагаться на прямой, то есть угол между ними не равен 180 градусам.

Обозначение ломаной линии

Чтобы отметить ломаную линию на чертеже вам необходимо указать наименования точек стыка, в которых она меняет направление, латинскими буквами.

Из чего состоит ломаная линия

Как вы уже успели заметить, на рисунках присутствуют звенья — отрезки, составляющие ломаную линию. А вот начальные и конечные точки этих составных частей — вершины. На картинке вершины ломаной ABCD — позиции A, B, C, D.

Признак замкнутости ломаной линии

Классификация ломаных линий прежде всего осуществляется по свойству замыкания.

Замкнутая ломаная линия — фигура, у которой конечная позиция совпадает с начальной. Иначе говоря, когда она заканчивается в том же месте, где начиналась.

Яркие представители — треугольник и квадрат, а также остальные виды многоугольников:

Незамкнутая ломаная линия — фигура, которая приходит в позицию, отличающуюся от начальной.

Время от времени, у учащихся возникает вопрос: «Как определить, замкнутая фигура или нет?». Ответ будет весьма прост:»Когда число отрезков равно количеству вершин — она замкнутая, а при наблюдающемся неравенстве — незамкнутая».

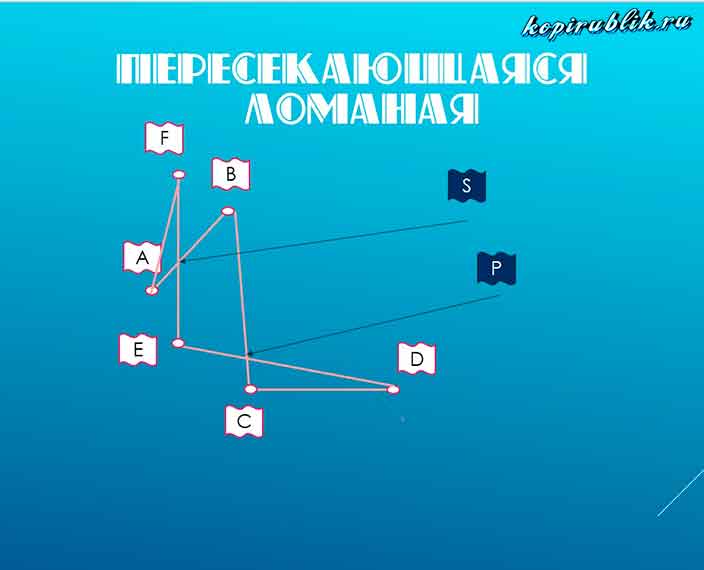
В качестве дополнительного вида рассматривают понятие самопересекающаяся ломаная линия — та, которая скрещивается на пути своего следования. Для данного термина не имеет значения сколько раз произошло пересечение.

На рисунке отмечены точки пересечения — S, P, а также вершины — A,B,C,D,E,F.

Иногда люди спрашивают — «Могут ли вершины являться точками пересечения?». Чтобы найти ответ, обратите внимание на рисунок с пересекающейся и одновременно замыкающейся — ломаной линией:

Изображение отличается от предыдущего: отрезок EB перемещён, поэтому вершина A приобрела статус точки пересечения.

Как измерить длину ломаной линии

Ломаная линия, имеющая начало и конец, имеет распространённую стандартную характеристику — длину. Имея цель сделать замер её длины, необходимо суммировать длины всех её составных частей — отрезков.

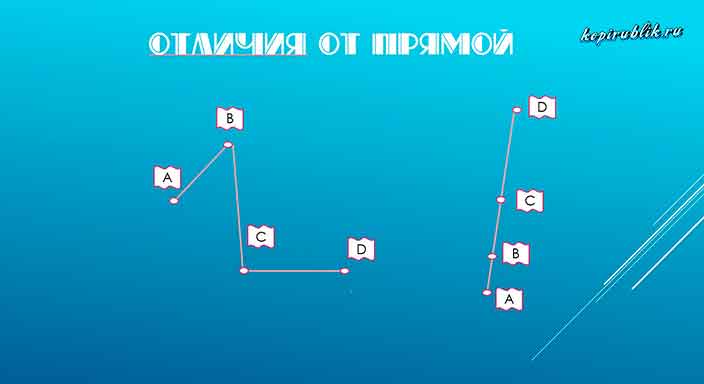
Чем ломаная линия отличается от прямой

При взгляде на рисунок очевидно: уникальный признак ломаной линии — отсутствие углов, равных 180 градусам. В остальном, фигуры одинаковые и обладают схожими свойствами, например, длиной.

Примеры ломаных линий в быту

В целях наилучшего усвоения теории, разумно на практике ознакомиться с примерами ломаных линий из жизни.

Ломаная линия— график фондового рынка. Так как отрезки графика очень маленькие, поэтому может показаться, что это кривая, но при ближайшем рассмотрении оказывается, что это не так.

Фасад дома при переводе на «язык геометрии» выглядит как замкнутая ломаная линия.

Пирамиды древнего Египта обладали формой треугольника — одной из самых популярных ломаных линий.

Также рекомендуем прочитать:

Источник

Главная
Справочники
Справочник по математике для начальной школы
Виды линий
Ломаная линия

Ломаная линия состоит из отрезков – звеньев.

Конец одного отрезка – начало другого. Никакие два соседние звена не лежат на одной прямой.

Концы каждого звена – это вершины. Их можно обозначать буквами.

Ломаная линия бывает незамкнутая.

Из незамкнутой ломаной линии можно получить замкнутую ломаную линию.

Такая замкнутая ломаная линия называется треугольником.

У нее три вершины.

У треугольника три звена.

Замкнутая ломаная линия из четырёх звеньев называется четырёхугольником.

Замкнутая ломаная линия из пяти или шести звеньев называется многоугольником.

Чтобы найти длину ломаной линий нужно измерить длину каждого звена-отрезка и сложить все длины.

Например,

Советуем посмотреть:

Точка. Кривая. Прямая линия

Отрезок. Луч

Длиннее. Короче. Уже. Шире. Одинаковые по длине и ширине

Виды линий

Правило встречается в следующих упражнениях:

1 класс

Страница 43,
Моро, Волкова, Степанова, Учебник, часть 1

Страница 45,
Моро, Волкова, Степанова, Учебник, часть 1

Страница 124,
Моро, Волкова, Степанова, Учебник, часть 1

Страница 12. ПР 3. Вариант 1,
Волкова, Проверочные работы

Страница 13. ПР 3. Вариант 2,
Волкова, Проверочные работы

Страница 41,
Моро, Волкова, Степанова, Учебник, часть 2

Страница 60,
Моро, Волкова, Степанова, Учебник, часть 2

Страница 107,
Моро, Волкова, Степанова, Учебник, часть 2

Страница 4. Урок 3,
Петерсон, Учебник, часть 2

Страница 23. Урок 12,
Петерсон, Учебник, часть 2

2 класс

Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 33,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 34,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 21. ПР 3. Вариант 2,
Моро, Волкова, Проверочные работы

Страница 66,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 83,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 78,
Моро, Волкова, Рабочая тетрадь, часть 2

Страница 109. Повторение,
Петерсон, Учебник, часть 3

Страница 112. Повторение,
Петерсон, Учебник, часть 3

3 класс

Страница 6,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 14,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 41,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 108,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 5,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 61,
Моро, Волкова, Рабочая тетрадь, часть 1

Страница 6. ПР 2. Вариант 1,
Моро, Волкова, Проверочные работы

Страница 67. Урок 22,
Петерсон, Учебник, часть 1

Страница 33. Урок 13,
Петерсон, Учебник, часть 2

4 класс

Страница 8,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1

Страница 77,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Страница 96,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2

Источник

Определение

Отрезок представляет собой часть прямой линии, которая находится между двумя точками. Эти точки называют концы отрезка.
Иными словами, отрезок – это множество точек прямой линии, находящиеся между двух известных точек, которые называют концами отрезка.

Рис. 1 Отрезок на прямой

Чтобы понять, о каком именно отрезке идет речь, называют концы этого отрезка, то есть две точки, ограничивающие его. Так, на рисунке 1 обозначен отрезок AB, лежащий на прямой a.

На одной прямой можно отметить бесконечное число отрезков. Например, на рисунке 2 изображена прямая c и точки M, O, N и P принадлежащие этой прямой. Они делят участок прямой на следующие отрезки:

Рис. 2 Несколько отрезков на прямой

Называть отрезок (то есть точки, которые являются его концами) можно как слева направо, так и справа налево. Так, в последнем примере «отрезок MN» и «отрезок NM» являются названиями одного и того же отрезка. Но принято, что при обозначении отрезка мы называем его конечные точки слева направо.

Отрезок делит прямую линию на три объекта (смотри рисунок 3):

отрезок DE
луч a с началом в точке D
луч b с началом в точке E

То есть, два конца отрезка прямой являются соответственно началами двух лучей этой же прямой.

Рис. 3 Отрезок и лучи прямой

В большинстве случаев в школьном курсе математики отрезки рассматриваются без привязки к прямой, которой они принадлежат. То есть, рисуют сам отрезок, а остальную часть прямой (образовавшиеся лучи) просто «отбрасывают».

Рис. 4 Отрезок без прямой

И наоборот, если продлить отрезок, нарисованный как на рисунке 4, в обе стороны за концы этого отрезка, то мы получим прямую, на которой лежит данный отрезок.

Если точки лежат на одной прямой с отрезком и находятся между концами этого отрезка, то говорят, что эти точки принадлежат отрезку.

Рис. 5 Отрезок и принадлежащие ему точки

Так, на рисунке 5 видно, что:

(·) C ∈AB – точка C принадлежит отрезку AB;
(·) D ∈AB – точка D принадлежит отрезку AB;
(·) E ∉AB – точка E не принадлежит отрезку AB;
(·) F ∉AB – точка F не принадлежит отрезку AB.

В последнем случае точка F хотя и лежит на одной прямой линии с отрезком AB (если вы мысленно продлите линию от точки B дальше, то увидите это), но не принадлежит ему, потому что находится не между его концами, а справа от отрезка.

Точки, которые лежат на отрезке, делят его на более короткие отрезки. На рисунке 6 видно, что точка O поделила отрезок LM на меньшие отрезки LO и OM. Каждый из этих двух меньших отрезков называются частью отрезка.

Рис. 6 Отрезок и части отрезка

Построение и измерение отрезка

Произвольный отрезок можно построить двумя способами:

Отметить часть прямой линии, обозначив края этой части точками (рисунок 7-а).
Обозначить на листе бумаги (на плоскости) две произвольные точки и соединить их между собой прямой линией (рисунок 7-б).

Рис. 7 Построение произвольного отрезка

В отличие от прямой линии и луча, которые длятся бесконечно, отрезок имеет длину, поэтому его можно измерить.

Измерить отрезок можно:

относительным способом (сравнить отрезки между собой);
абсолютным способом (определить его длину измерительным инструментом).

Сравнить отрезки между собой можно при помощи циркуля или циркуля-измерителя. Для этого нужно сперва поставить иглу на один конец отрезка, а затем вторую иглу или грифельный стержень (если используется обычный чертежный циркуль) совместить со вторым концом отрезка (рисунок 8).

После этого нужно перенести циркуль на второй отрезок и поставить одну иглу на любой его конец. Если вторая игла циркуля совпадает со вторым концом отрезка, тогда эти отрезки равны.

Рис. 8 Сравнение отрезков

На рисунке 8 видно, что:

отрезок AB равен отрезку DE (записывают просто AB=DE);
FG<AB
HK>AB

Длину отрезка измеряют линейкой с делениями или другим измерительным инструментом.

Запомните

Длина отрезка – это расстояние между концами этого отрезка.

Равные отрезки — это такие отрезки, которые имеют одинаковую длину.

На рисунке 9 измерены длины отрезков предыдущего рисунка. Проверьте, правильно ли мы сравнили эти отрезки при помощи циркуля?

Рис. 9 Измерение длины отрезка

Кроме произвольного, также требуется построить отрезок определенной длины.

Для этого на плоскости обозначают один конец отрезка (ставят точку), а затем при помощи линейки отмеряют необходимую длину отрезка (к примеру, 9 см), ставят точку второго конца отрезка и соединяют оба конца линией.

Рис. 10 Построение отрезка заданной длины

Запомните!

Отрезок — это самое короткое расстояние между двумя точками.

В этом вы можете убедиться самостоятельно на практике. Возьмите любой твердый длинный предмет, например, линейку, и шнурок. Линейка будет играть роль отрезка, а из шнурка сделайте кривую и ломаную линию, наподобие таких, какие показаны на рисунке 11, и соедините ими два конца линейки. После чего выпрямите шнурок и сравните его длину с длиной линейки.

Рис. 11 Кривая, ломаная, отрезок

Ломаная линия

Определение

Ломаная линия – это линия, которая состоит из отрезков, принадлежащих разным прямым, и эти отрезки последовательно соединены друг с другом.

Рис. 12 Ломаная линия

Вершинами ломаной линии называются концы отрезков, из которых она состоит.
Звеньями ломаной линии называются составляющие ее отрезки.
Смежные звенья – это звенья, которые имеют общие вершины.
Смежные звенья не могут принадлежать одной прямой.
Длина ломаной линии – это сумма длин всех входящих в ее состав звеньев.

На рисунке 12 видно, что:

KLMN – ломаная линия;
K, L, M, N – вершины ломаной KLMN;
KL, LM, MN – звенья ломаной KLMN;
KL и LM – смежные звенья;
LM и MN – смежные звенья;
KL и MN – не являются смежными звеньями.

Называют ломаную линию по названию ее вершин, соблюдая их последовательность. Так, называть ломаную на рисунке 11 как KLMN или NMLK – правильно, а MLKN или MNLK – не правильно.

Количество звеньев у ломаной линии может быть каким угодно, бесконечным, но самое меньшее – это два звена.

Замкнутая ломаная линия – это такая ломаная, у которой совпадают точки начала и конца, то есть, которая начинается и заканчивается в одной точке.
Разомкнутая (не замкнутая) ломаная линия начинается и заканчивается в разных точках.

Название разомкнутой ломаной начинается с названия вершины, с которой она начинается. Замкнутую ломаную можно называть, начиная с любой ее вершины.

На рисунке 12:

ABCDE
— замкнутая ломаная;
FGHKLM
— разомкнутая ломаная

Рис. 12. Замкнутая и разомкнутая ломаные линии

Самопересекающаяся ломаная линия – это такая ломаная, у которой есть хотя
бы два пересекающихся звена.

Самопересекающимися могут быть как замкнутые, так и разомкнутые ломаные.

Рис. 13. Самопересекающиеся ломаные линии

На рисунке 13 у замкнутой ломаной ABCD два пересекающихся звена: BC ∩DA, а у разомкнутой ломаной EFGHI – три: EF ∩HI и FG ∩HI.

Источник

Перейти к контенту

Математика

Время чтения 1 мин.Просмотры 16.1к.

Чтобы нарисовать геометрическую фигуру правильно, нужно знать теорию. Ломанная линия состоит из прямых отрезков, которые между собой последовательно соединены. Для закрепления знаний нужна практика. Предлагаем Вашему вниманию набор картинок с изображениями ломанных линий.

Ломаная линия из четырёх звеньев.