The short answer is
Such a grid exists
with an example of
7 16 6 3 25 5 13 22 12 24 9 11 17 14 4 20 18 21 19 1 8 10 2 15 23Quick evidence.
The first step is to identify the prime factors in the range of 1 to 25.
- 13, 17, 19, and 23 appear once each.
- 11 appears twice (11, 22).
- 7 appears three times (7, 14, 21).
- 5 appears 6 times, 3 appears 10 times, and 2 appears 22 times.
If a prime factor appears only once, it must necessarily be on the main diagonal. Similarly, if a prime factor appears exactly twice, the two numbers must be placed at the mirror images of each other (so that if one is on Row X and Col Y, the other is on Row Y and col X).
I initially thought that a prime factor cannot appear an odd number of times outside the main diagonal, but it is false (if at least three copies are available):
A .
. A
A .
Anyway, other than large primes, the only prime that appears an odd number of times is 7, so I decided to place it on the main diagonal as well as all the large primes:
7 . . . .
. 13 . . .
. . 17 . .
. . . 19 .
. . . . 23
At this point, I jumped to the prime factor 5, which has four numbers that contain 5 once (5 to 20) and one number that contains 5 twice (25). In order to make things easy, let’s just write down the exponents of the prime factor in consideration. So the mini-task here is to place four 1’s and one 2 so that the sum of the first row equals that of the first column, etc.
(From here, every step involves a varying amount of lucky pattern spotting)
One pattern that works is the following:
. . . . 2
1 . . . .
. . . . .
1 . . . .
. 1 . 1 .
I decided to place 5 and 20 on the first column, and 10 and 15 on the bottom row, in the hopes that scattering the prime factors 2’s and 3’s will make the later steps easier.
With the same intuition, I placed the remaining 7’s (14 and 21) and 11’s (11 and 22) near the center (where relatively fewer cells are occupied yet). The current grid is as follows:
7 . . . 25
5 13 22 . .
. 11 17 14 .
20 . 21 19 .
. 10 . 15 23
Now, I turned the attention to the prime factor 3. Again considering only the exponents of 3, there are six ones (3, 6, 12, 15, 21, 24), and two twos (9, 18). 15 and 21 are already placed on the grid. It took more effort to find a pattern that fits all of these, but after some trial and error with placing two 2’s first, I finally found one that works: (parenthesized (1)s are the fixed ones)
. . 1 1 .
. . . 1 1
2 . . . .
. 2 (1) . .
. . . (1) .
Intuition again tells me that it’d be better to place 9 on the first column and 18 on the second. I decided to not place other threes yet, but instead fit them together with the remaining numbers according to the powers of 2.
Current grid:
7 A B B 25
5 13 22 B B
9 11 17 14 A
20 18 21 19 A
A 10 A 15 23
The As are where 1, 2, 4, 8, 16 will be placed, and the Bs are for 3, 6, 12, 24.
Finally, let’s focus on the prime factor 2. The exponents of 2 on the current grid look like this:
0 A W X 0
0 0 1 Y Z
0 0 0 1 B
2 1 0 0 C
D 1 E 0 0
and the constraint is that we need to place 0 to 4 into A-E and 0 to 3 into W-Z.
Let’s try 4 for A. Then Y and Z must contain 2 and 3, and W and X must contain 0 and 1, in some order. By 1st row/column, D = 3. Since B and E cannot be equal, W cannot be zero, so W = 1 and X = 0.
Since B + C + E + 1 + D = (0 + 1 + 2) + 1 + 3 = 7 is odd, Z must be odd too. So Z = 3 and Y = 2.
0 4 1 0 0
0 0 1 2 3
0 0 0 1 B
2 1 0 0 C
3 1 E 0 0
4th row/col reveals C = 0, and since B > E by 3rd row/col, B = 2 and E = 1. The resulting grid satisfies all the constraints.
Now we convert these exponents into the original numbers to fill the grid, and the result is the answer at the top.
![]()
2
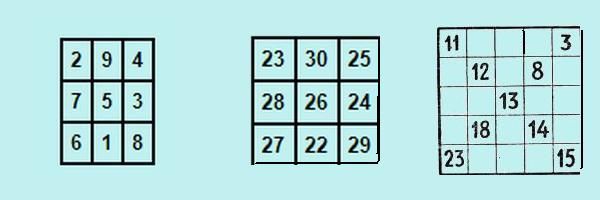
Наверняка многие любят игры с числами. На скрине первый магический квадрат изготовлен с числами от 1 до 9. В чём его магия? Сумма чисел по всем вертикалям и всем горизонталям включая угловые диагонали равна 15. Следующий магический квадрат создан из чисел от 22 до 30 по тому же принципу все суммы равны 78.
<h1>Но вопрос не об этом. Вопрос о том, как сделать магический квадрат из 5 на 5 сторон. от 1 до 25. Для удобства решения я оставила 2 диагонали. Сумма чисел в каждой равна 65</h1>
2 ответа:
![]()
3
0
Исходное состояние:
11 хх хх хх 03
хх 12 хх 08 хх
хх хх 13 хх хх
хх 18 хх 14 хх
23 хх хх хх 15
Промежуточное состояние:
11 хх 07 хх 03
хх 12 хх 08 хх
17 хх 13 хх 09
хх 18 хх 14 хх
23 хх 19 хх 15
Итоговое состояние:
11 24 07 20 03
04 12 25 08 16
17 05 13 21 09
10 18 01 14 22
23 06 19 02 15
![]()
1
0
Однако хотелось бы описать метод изготовления таких квадратов практически с любым количеством нечётных клеток. Если мне память не изменяет: метод описан в замечательной книге Я. И. Перельмана: “Занимательная математика”.

Парадокс следующего квадрата с чётной стороной, заключается ещё в том, что начиная с числа “1” можно обойти всё поле ходом шахматного коня. Об этом мало где упоминается. В далёком детстве, я случайно обнаружила это сама, увлекаясь шахматной игрой.

Читайте также
![]()
Всё просто..
Здесь рассматривается равноускоренное движение тела в гравитационном поле..
Второй закон Ньютона..
Есть только недостаток в данных: как направлен вектор скорости относительно ускорения свободного падения..
Если считать, что вектор скорости относительно горизонта – а, то необходимо разложить вектор скорости на две ортогональные составляющие в общем случае:
v cos(a) = Vx
v sin(a) – g t = Vy
h + v sin(a) t – (g t^2)/2 = 0
Если начальная скорость у тела вертикальная и направлена вверх:
Получим систему уравнений:
3 – 9,81 t = v
3 + 3 t – (9,81 t^2)/2 = 0
Из первого уравнения находим:
-4,9 t^2+3 t+3 =0
t1=1,15
t2=-0,53
Второе значение не имеет физического смысла..
Подставляем 1,15 в первое уравнение..
3 – 9,81*1,15=-8,1 м/с…
Т.е. при столкновении с землёй скорость будет направлена вертикально вниз..
![]()
Тут, к сожалению, не проканает использование формула последовательногои параллельного сопротивления, поэтому придётся честно решать через законы Кирхгофа.
Для начала малость перерисуем схему:
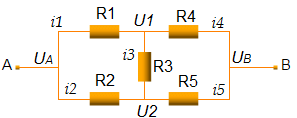
Ну и теперь, памятую законы Ома и Кирхгофа, пишем:
i1+i2 = i4+i5 (на будущее – эта сумма как раз и есть ток, который нам и надо найти)
i2+i3 = i5
i1*R1 = U1-UA
i2*R2 = U2-UA
i3*R3 = U2-U1
i4*R4 = UB-U1
i5*R5 = UB-U2
Тут 7 уравнений на 9 неизвестных – пять токов и четыре напряжения. Но штука в том, что напряжения UA, UB можно выбрать произвольно. Например, считать UA=1, UB=0. Тем самым число неизвестных снижается до числа уравнений, и система оказывается вполне себе разрешимой.
Решать её, уж не обессудьте, придётся самостоятельно, благо это не составит труда. После чего остаётся найти сумму i1+i2 – вместе с разностью напряжений между точками А и В это как раз и даст эквивалентное сопротивление вспей цепи.
![]()
Варианты:
(3+3)*3=18
3+3*3=12
3+(3*3)=12
![]()
На собеседовании нужно отвечать “ни за сколько”. Потому что в вопросе не указаны нужные исходные данные – себестоимость этой работы, площадь стекол, которые нужно вымыть, временные параметры и так далее.
А вообще говоря, если примерно взять 10 тысяч кварталов, в каждом из которых по 600 окон, тратить на каждое окно по 5 минут, брать оплату по 20 баксов в час, то получится 10 миллионов. Правда, на это уйдет 57 лет чистого мытья (без сна, еды и вообще без перерывов))
![]()
Запишем краткое условие для наглядности.
Лиса – 32 рыбки, на 24 больше, чем волк
Волк – ?
Во сколько раз лиса поймала больше волка?
Решение:
1)32-24=8 (шт.) – рыбок поймал волк.
2)32/8=4
Ответ: в 4 раза больше поймала лиса рыбы.
16
Существует несколько различных классификаций магических квадратов
пятого порядка, призванных хоть как-то их систематизировать. В книге
Мартина Гарднера [ГМ90, сс. 244-345] описан один из таких способов –
по числу в центральном квадрате. Способ любопытный, но не более того.
Сколько существует квадратов шестого порядка, до сих пор неизвестно, но их примерно 1.77 х 1019. Число огромное, поэтому нет никаких надежд пересчитать их с помощью полного перебора, а вот формулы для подсчёта магических квадратов никто придумать не смог.
Как составить магический квадрат?
Придумано очень много способов построения магических квадратов. Проще всего составлять магические квадраты нечётного порядка. Мы воспользуемся методом, который предложил французский учёный XVII века А. де ла Лубер (De La Loubère). Он основан на пяти правилах, действие которых мы рассмотрим на самом простом магическом квадрате 3 х 3 клетки.
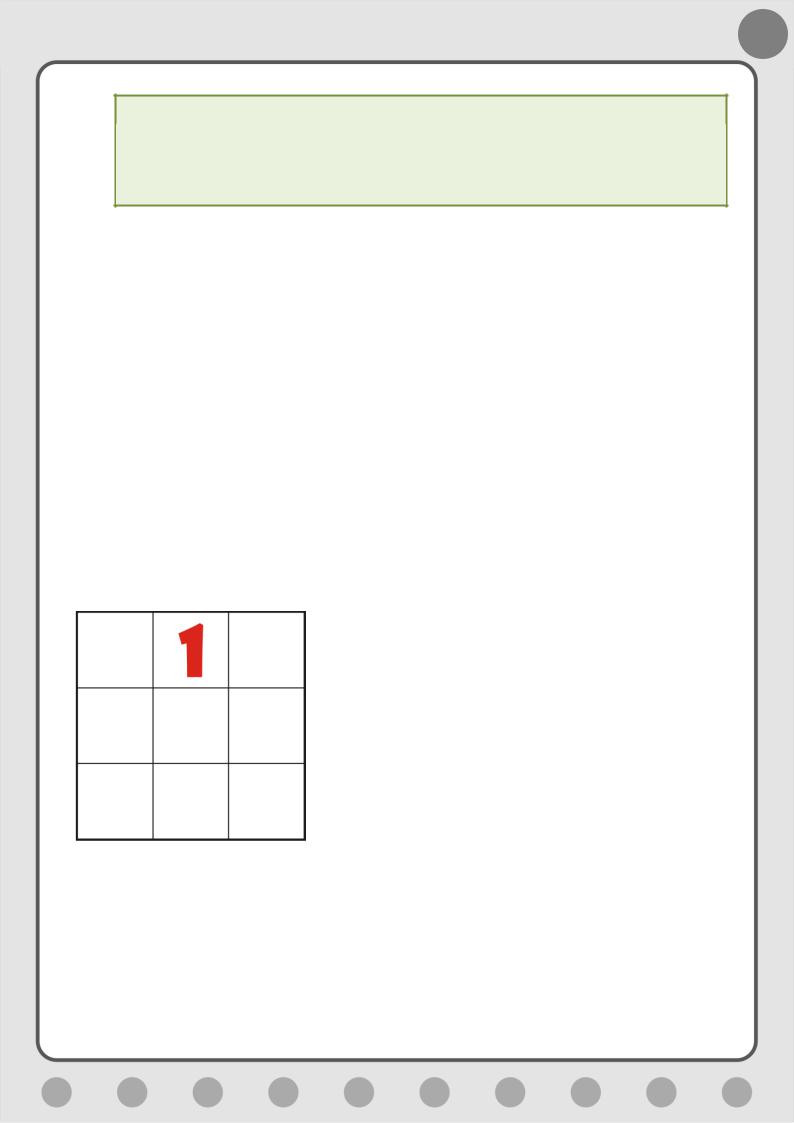
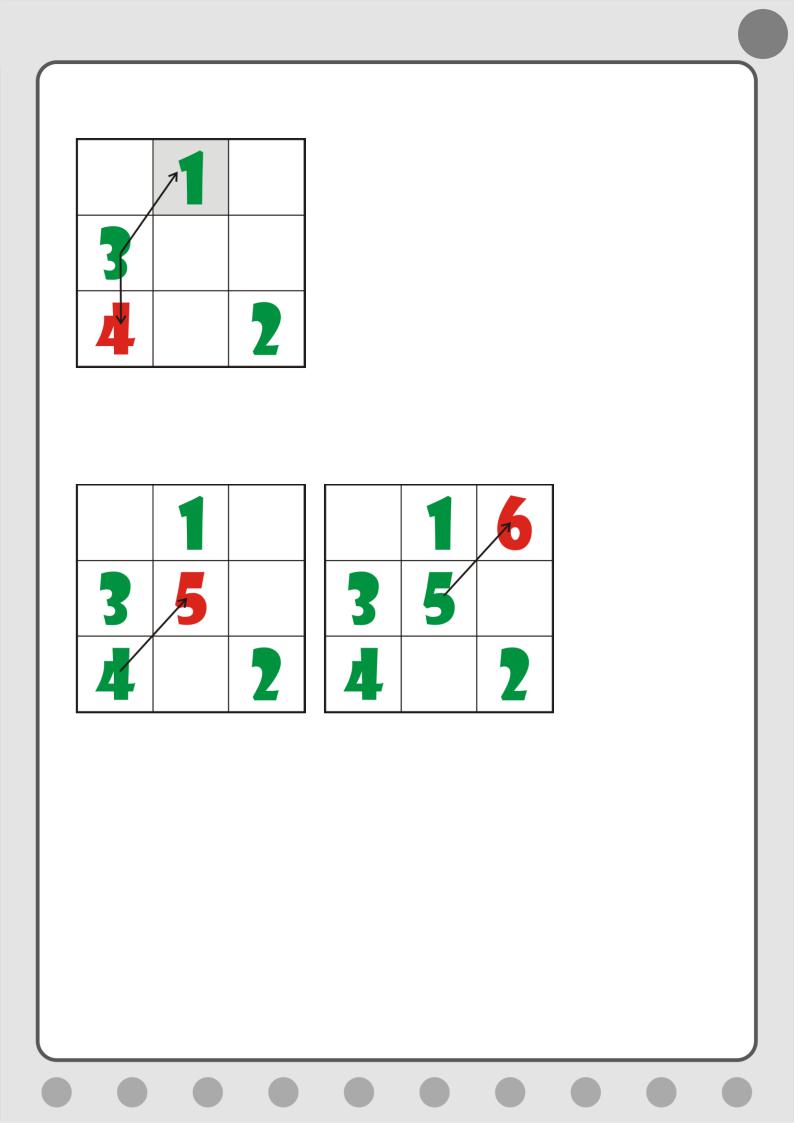
Правило 1. Поставьте 1 в среднюю колонку первой строки (Рис. 5.7).
Рис. 5.7. Первое число
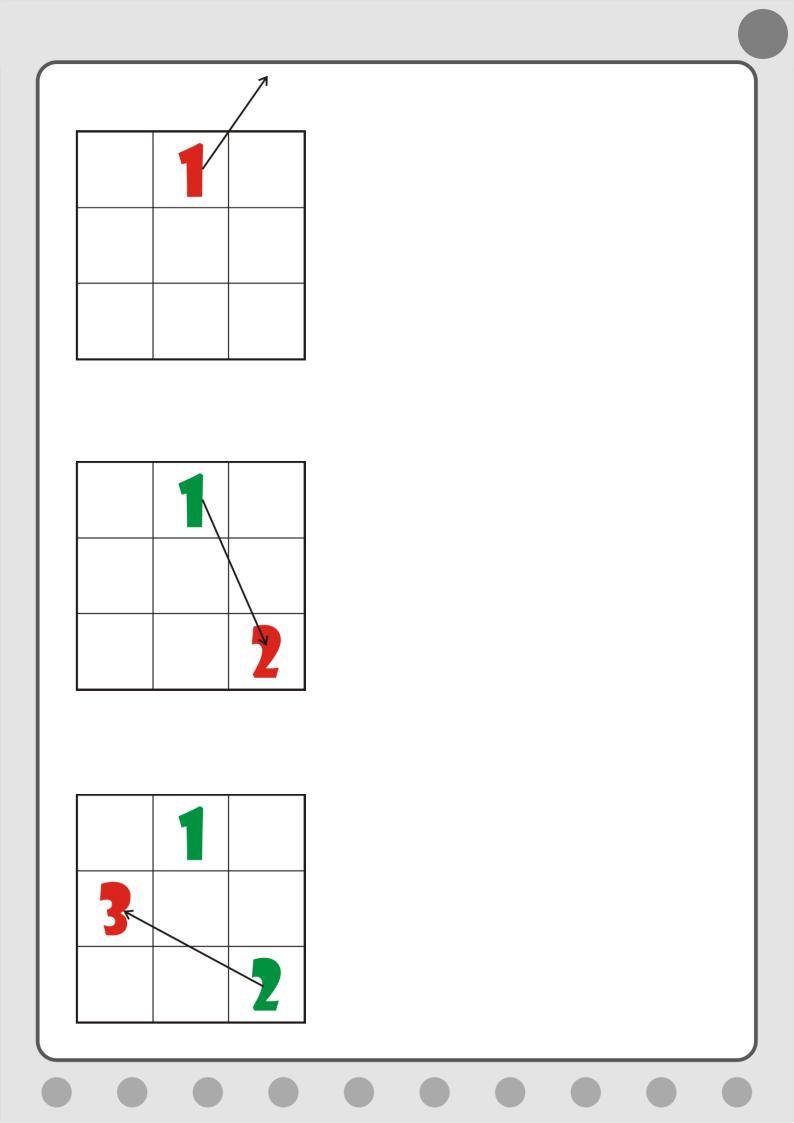
Правило 2. Следующее число поставьте, если возможно в клетку, соседнюю с текущей по диагонали правее и выше (Рис. 5.8).
17
Рис. 5.8. Пытаемся поставить второе число
Правило 3. Если новая клетка выходит за пределы квадрата сверху, то запишите число в самую нижнюю строку и в следующую колонку (Рис. 5.9).
Рис. 5.9. Ставим второе число
Правило 4. Если клетка выходит за пределы квадрата справа, то запишите число в самую первую колонку и в предыдущую строку (Рис. 5.10).
Рис. 5.10. Ставим третье число
18
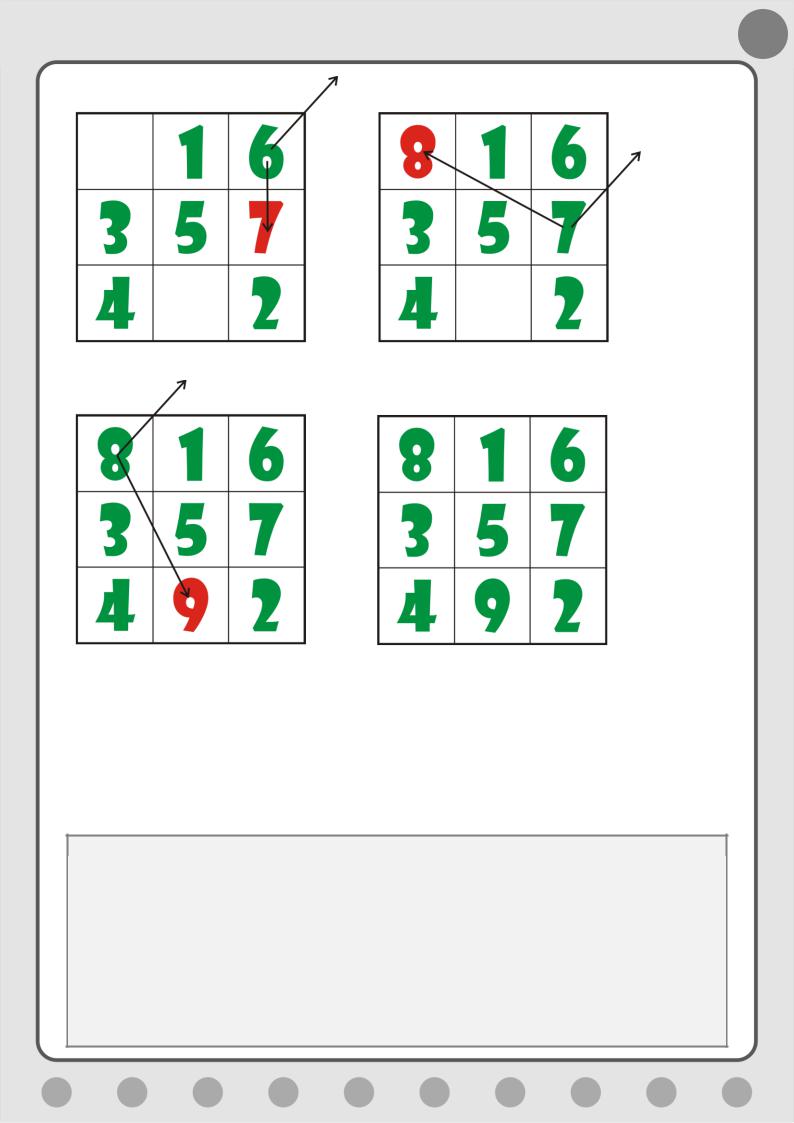
Правило 5. Если в клетке уже занята, то очередное число запишите под текущей клеткой (Рис. 5.11).
Рис. 5.11. Ставим четвёртое число
Далее переходите к Правилу 2 (Рис. 5.12).
Рис. 5.12. Ставим пятое и шестое число
Снова выполняйте Правила 3, 4, 5, пока не составите весь квадрат (Рис.
5.13).
Не правда ли, правила очень простые и понятные, но всё равно довольно утомительно расставлять даже 9 чисел. Однако, зная алгоритм построения магических квадратов, мы сможем легко перепоручить компьютеру всю рутинную работу, оставив себе только творческую, то есть написание программы.
19
Рис. 5.13. Заполняем квадрат следующими числами
Проект Магические квадраты (Magic)
Набор полей для программы Магические квадраты совершенно очевиден:
//ПРОГРАММА ДЛЯ ГЕНЕРИРОВАНИЯ
//НЕЧЕТНЫХ МАГИЧЕСКИХ КВАДРАТОВ
//ПО МЕТОДУ ДЕ ЛА ЛУБЕРА
public partial class Form1 : Form
{
//макс. размеры квадрата: const int MAX_SIZE = 27; //var
int n=0; // порядок квадрата int [,] mq; // магический квадрат
int number=0;// текущее число для записи в квадрат

20
int col=0; // текущая колонка int row=0; // текущая строка
Метод де ла Лубера годится для составления нечётных квадратов любого размера, поэтому мы можем предоставить пользователю возможность самостоятельно выбирать порядок квадрата, разумно ограничив при этом свободу выбора 27-ью клетками.
После того как пользователь нажмёт заветную кнопку btnGen Генерировать!, метод btnGen_Click создаёт массив для хранения чисел и переходит в метод generate:
//НАЖИМАЕМ КНОПКУ “ГЕНЕРИРОВАТЬ”
private void btnGen_Click(object sender, EventArgs e)
{
//порядок квадрата:
n = (int)udNum.Value;
//создаем массив:
mq = new int[n+1, n+1];
//генерируем магический квадрат: generate();
lstRes.TopIndex = lstRes.Items.Count-27;
}
Здесь мы начинаем действовать по правилам де ла Лубера и записываем первое число – единицу – в среднюю клетку первой строки квадрата (или массива, если угодно):
//Генерируем магический квадрат void generate(){
//первое число: number=1;
rule1:
//колонка для первого числа – средняя: col = n / 2 + 1;
//строка для первого числа – первая: row=1;
//заносим его в квадрат: mq[row,col]= number;
Теперь мы последовательно пристраиваем по клеткам остальные числа – от двойки до n * n:
//переходим к следующему числу:
21
nextNumber:
number++;
Запоминаем на всякий случай координаты актуальной клетки
int tc=col; int tr = row;
и переходим в следующую клетку по диагонали:
col++; row–;
Проверяем выполнение третьего правила:
rule3:
if (row < 1) row= n;
А затем четвёртого:
rule4:
if (col > n) { col=1;
goto rule3;
}
И пятого:
rule5:
if (mq[row,col] != 0) { col=tc;
row=tr+1; goto rule3;
}
Как мы узнаем, что в клетке квадрата уже находится число? – Очень просто: мы предусмотрительно записали во все клетки нули, а числа в готовом квадрате больше нуля. Значит, по значению элемента массива мы сразу же определим, пустая клетка или уже с числом! Обратите внимание, что здесь нам понадобятся те координаты клетки, которые мы запомнили перед поиском клетки для следующего числа.
Рано или поздно мы найдём подходящую клетку для числа и запишем его в соответствующую ячейку массива:

22
//заносим его в квадрат: mq[row, col] = number;
Попробуйте иначе организовать проверку допустимости перехода в но-
вую клетку!
Если это число было последним, то программа свои обязанности выполнила, иначе она добровольно переходит к обеспечению клеткой следующего числа:
//если выставлены не все числа, то if (number < n*n)
//переходим к следующему числу: goto nextNumber;
И вот квадрат готов! Вычисляем его магическую сумму и распечатываем на экране:
//построение квадрата закончено: writeMQ();
} //generate()
Напечатать элементы массива очень просто, но важно учесть выравнивание чисел разной «длины», ведь в квадрате могут быть одно-, дву- и трёхзначные числа:
//Печатаем магический квадрат void writeMQ()
{
lstRes.ForeColor = Color.Black;
string s = “Магическая сумма = ” + (n*n*n +n)/2; lstRes.Items.Add(s);
lstRes.Items.Add(“”);
// печатаем магический квадрат: for (int i= 1; i<= n; ++i){
s=“”;
for (int j= 1; j <= n; ++j){
if (n*n > 10 && mq[i,j] < 10) s += ” “; if (n*n > 100 && mq[i,j] < 100) s += ” “; s= s + mq[i,j] + ” “;
}
lstRes.Items.Add(s);
}
lstRes.Items.Add(“”); }//writeMQ()
23
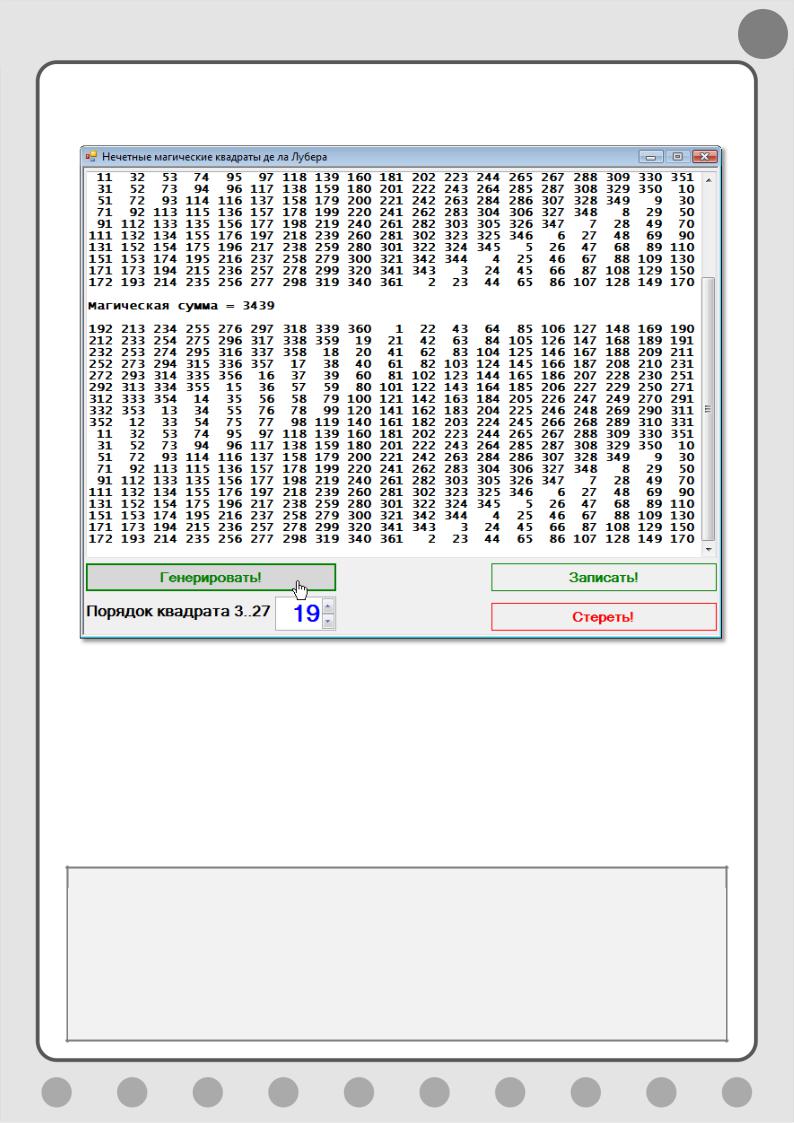
Запускаем программу – квадраты получаются быстро и на загляденье (Рис.
5.14).
Рис. 5.14. Изрядный квадратище!
В книге С.Гудман, С.Хидетниеми Введение в разработку и анализ алгорит-
мов, на страницах 297-299 мы отыщем тот же самый алгоритм, но в «сокращённом» изложении. Он не столь «прозрачен», как наша версия, но работает верно.
Добавим кнопку btnGen2 Генерировать 2! и запишем алгоритм на языке
Си-шарп в метод btnGen2_Click:
//Algorithm ODDMS
private void btnGen2_Click(object sender, EventArgs e)
{
//порядок квадрата: n = (int)udNum.Value;
//создаем массив:
mq = new int[n + 1, n + 1];
//генерируем магический квадрат: int row = 1;
24
int col = (n+1)/2;
for (int i = 1; i <= n * n; ++i)
{
mq[row, col] = i; if (i % n == 0)
{
++row;
}
else
{
if (row == 1) row = n;
else
–row;
if (col == n) col = 1;
else
++col;
}
}
//построение квадрата закончено: writeMQ();
lstRes.TopIndex = lstRes.Items.Count – 27;
}
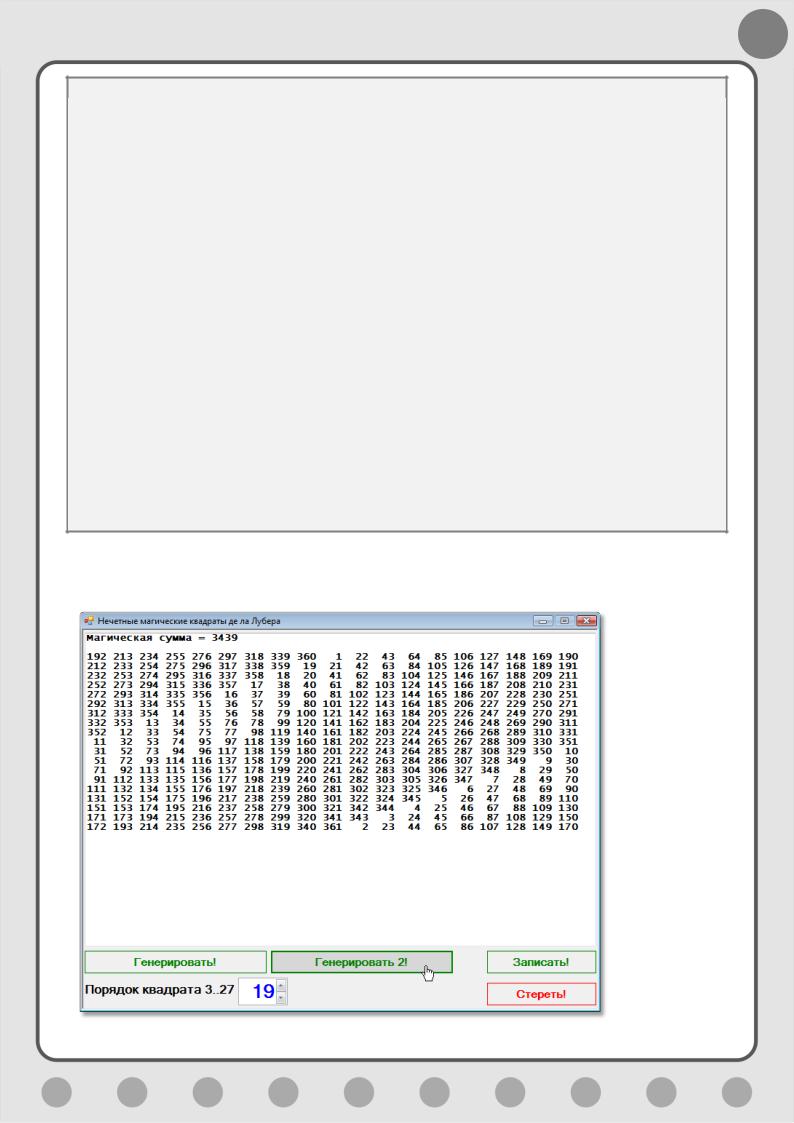
Кликаем кнопку и убеждаемся, что генерируются «наши» квадраты (Рис.
5.15).
Рис. 5.15. Старый алгоритм в новом обличии
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Network.net
Знаток
(360),
закрыт
7 лет назад
помогите решить.
Лучший ответ
Alex Kidd
Профи
(869)
7 лет назад

Остальные ответы
Катерина Березняк
Ученик
(186)
7 лет назад
начинай с диагонали 21-13-5
сумма этих чисел равна 39
далее вычитай 39 из 65
=26
дальше подбором
ps-думай головой, здесь ничего трудного нет
просто подумать надо чуток
иначе-никакого развития
Похожие вопросы
Составе магический квадрат 5х5 (магическое число 65).
Заранее спасибо!
: – ).
На этой странице сайта размещен вопрос Составе магический квадрат 5х5 (магическое число 65)? из категории
Математика с правильным ответом на него. Уровень сложности вопроса
соответствует знаниям учеников 1 – 4 классов. Здесь же находятся ответы по
заданному поиску, которые вы найдете с помощью автоматической системы.
Одновременно с ответом на ваш вопрос показаны другие, похожие варианты по
заданной теме. На этой странице можно обсудить все варианты ответов с другими
пользователями сайта и получить от них наиболее полную подсказку.
