Загрузить PDF
Загрузить PDF
Математическая модель описывает поведение какой-либо системы математическим языком. Математические модели используются не только в естественных науках и инженерном деле, но и в биологии, экономике и социологии. Математические модели могут быть самыми разными и иметь различную степень сложности.[1]
Прочтите данную статью, чтобы узнать, как создавать математические модели.
-

1
Определите, что именно необходимо узнать. Какова цель создания модели? Составьте список данных, которые необходимо определить с помощью математической модели. Прежде чем приступить к построению модели, следует поставить перед собой конкретные цели, иначе вы рискуете создать модель, которая не будет соответствовать стоящей перед вами задаче.[2]
- Хотите ли вы что-либо предсказать? Или выяснить, как управлять чем-либо? А может, вы собираетесь достичь чего-нибудь другого?[3]
- Предположим, вы хотите узнать, сколько места в вашей кладовке, чтобы определить, какое количество коробок поместится в нее. Для этого можно создать подходящую модель.
- Хотите ли вы что-либо предсказать? Или выяснить, как управлять чем-либо? А может, вы собираетесь достичь чего-нибудь другого?[3]
-

2
Определите, что вам известно. Какими исходными данными вы располагаете? Выпишите все, что вам известно. При составлении списка посмотрите, какие данные имеют первоочередное значение, а какие не столь важны.[4]
- Следует также записать любую информацию, которую можно вынести из исходных данных.
- Учтите, что для получения необходимых данных вам, возможно, придется провести некоторые измерения.
- Чтобы найти объем вашей кладовой комнаты, необходимо измерить ее высоту, ширину и длину.
-

3
Определите физические принципы, которые лежат в основе создаваемой вами модели. Следует ли учитывать такие факторы, как сила тяжести, объем, время и так далее? Запишите все факторы, которые придется принять во внимание при построении модели.[5]
- Чтобы определить, сколько места в кладовке, необходимо найти ее объем.
- Следует также помнить о том, что определенная часть объема останется незанятой, так как хранящиеся предметы могут иметь неправильную форму, и будет непросто использовать каждый сантиметр кладовки.[6]
-

4
Определите уравнения, которые понадобятся вам для решения поставленной задачи. Какие уравнения и формулы потребуются для того, чтобы найти ответ? Каким образом их следует использовать? Необходимо ясно представлять себе, как именно вы будете подставлять исходные данные в имеющиеся формулы.
- Чтобы найти объем кладовой, следует умножить ее высоту на ширину и длину: V= h x w x l[7]
- Чтобы найти объем кладовой, следует умножить ее высоту на ширину и длину: V= h x w x l[7]
-

5
Посмотрите, что уже было сделано другими. Нет никакой надобности изобретать велосипед в том случае, если кто-то уже создал модель, которая подходит вам. Загляните в учебник или посоветуйтесь со своим преподавателем. При этом следует убедиться в том, что готовую модель можно использовать в вашем случае.
- Чтобы узнать, как найти объем какого-либо тела, загляните в учебник или проконсультируйтесь с преподавателем.
-

6
Изобразите модель в виде схемы. В случае простой математической модели можно обойтись и без схемы. Однако если вы рассматриваете более сложные вопросы, схема поможет вам разобраться, как именно работает ваша модель. Попробуйте схематически изобразить создаваемую модель.[8]
- Обязательно включите в схему исходные данные — это поможет вам при дальнейшей разработке модели.
Реклама
-

1
Создайте модель. После стадии предварительной подготовки и планирования следует приступить к построению самой модели. Используйте при этом созданную ранее схему, исходные данные и другую полезную информацию. Почаще проверяйте свои действия, чтобы не допустить ошибку.[9]
- Убедитесь в том, что ваша модель действительно описывает наблюдаемые соотношения между данными величинами и процессами.
- Для создания сложной модели может понадобиться компьютерная программа.
-

2
Проверьте свою модель. Прежде чем использовать модель, необходимо проверить ее правильность. Подставьте численные данные и посмотрите, получатся ли правильные результаты. Ожидали ли вы получить именно эти результаты? Имеют ли они смысл? Воспроизводимы ли они?[10]
- Подставьте численные значения в формулу V = h x w x l и определите, имеет ли смысл полученный результат. Повторите свои действия, чтобы убедиться, что получаются воспроизводимые результаты.
-

3
Подумайте, как можно улучшить модель. Не исключено, что вам удастся улучшить свою модель, и она станет более пригодной для дальнейшего использования. Существуют ли дополнительные факторы, которые следует учесть? Обладает ли модель ограничениями, которых можно избежать? Прежде чем использовать модель в дальнейшем, подумайте над тем, как ее можно улучшить.[11]
- Например, если в кладовой необходимо оставить проход шириной 1 метр, можно учесть это в уравнении. Просто вычтите ширину прохода из общей ширины помещения. В результате уравнение приобретет следующий вид: V = h x (w-1) x l[12]
- После того, как вы определите способы улучшения своей модели, внесите в нее соответствующие изменения и вновь проверьте ее.
Реклама
- Например, если в кладовой необходимо оставить проход шириной 1 метр, можно учесть это в уравнении. Просто вычтите ширину прохода из общей ширины помещения. В результате уравнение приобретет следующий вид: V = h x (w-1) x l[12]
Советы
- Если вам что-либо неясно, посоветуйтесь со своим преподавателем математики.
- Прежде чем приступить к созданию модели, несколько раз внимательно перечитайте условие задачи.
Реклама
Об этой статье
Эту страницу просматривали 20 527 раз.
Была ли эта статья полезной?
п.1. Алгоритм решения задач с помощью систем уравнений
1. Обозначить неизвестные величины переменными («от смысла к буквам»).
2. По условию задачи записать уравнения, связывающие обозначенные переменные.
3. Решить полученную систему уравнений.
4. Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Например:
Найдите два положительных числа, если известно, что сумма квадратов этих чисел равна 185, а разность квадратов равна 57.
Шаг 1
«От смысла к буквам»:
Пусть x > 0 и y > 0 – задуманные числа.
Шаг 2
Уравнения по условию задачи:
( left{ begin{array}{ l } mathrm{x^2+y^2=185} & \ mathrm{x^2-y^2=57} & end{array}right. )
Шаг 3
Решение системы уравнений:
( left{ begin{array}{ l } mathrm{x^2+y^2=185} & \ mathrm{x^2-y^2=57} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{2x^2=185+57=242} & \ mathrm{2y^2=185-57=128} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{x^2=121} & \ mathrm{y^2=64} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=pm 11} & \ mathrm{y=pm 8} & end{array}right. )
Шаг 4
«От букв к смыслу»:
Выбираем положительные корни $$ mathrm{x=11, y=8} $$ Задуманы числа 11 и 8.
п.2. Примеры
Пример 1. Диагональ прямоугольника равна 10 см. Если меньшую сторону прямоугольника увеличить на 2 см, а большую уменьшить на 2 см, то диагональ не изменится. Найдите стороны прямоугольника.
Пусть a и b – стороны прямоугольника, a > b. Диагональ через стороны выражается по теореме Пифагора. По условию получаем: $$ left{ begin{array}{ l } mathrm{a^2+b^2=10} & \ mathrm{(a-2)^2+(b+2)^2=10^2} & end{array}right. $$ Найдём линейную зависимость между a и b из уравнения: begin{gather*} mathrm{a^2+b^2=(a-2)^2+(b+2)^2}\ mathrm{a^2+b^2=a^2-4a+4+b^2+4b+4}\ mathrm{4a-4b=8Rightarrow a-b=2Rightarrow a=b+2} end{gather*} Подставим a в верхнее уравнение системы: ( mathrm{(b+2)^2+b^2=100} ) begin{gather*} mathrm{b^2+4b+4+b^2-100=0}\ mathrm{2b^2+4b-96=0Rightarrow b^2+2b-48=0Rightarrow (b+8)(b-6)=0}\ mathrm{b_1=-8, b_2=6} end{gather*} Выбираем положительный корень: b = 6
Тогда a = b + 2 = 8
Ответ: 8 см и 6 см.
Пример 2. (задача Диофанта, III в.) Отношение двух чисел равно 3, а отношение суммы квадратов этих чисел к их сумме равно 5. Найдите эти числа.
Пусть x и y – искомые числа. По условию: $$ left{ begin{array}{ l } mathrm{frac{x}{y}=3} & \ mathrm{frac{x^2+y^2}{x+y}=5} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=3y} & \ mathrm{x^2+y^2=5(x+y)} & end{array}right. $$ Подставляем верхнее уравнение в нижнее и решаем: begin{gather*} mathrm{(3y)^2+y^2=5(3y+y)Rightarrow 9y^2+y^2=20yRightarrow 10y^2-20y=0Rightarrow}\ mathrm{Rightarrow 10y(y-2)=0Rightarrow} left[begin{array}{ l } mathrm{y_1=0} & \ mathrm{y_2=2} & end{array}right. end{gather*} Т.к. y в первом уравнении системы стоит в знаменателе, он не может быть равен 0. Получаем: begin{gather*} left{begin{array}{ l } mathrm{x=3y=6} & \ mathrm{y=2} & end{array}right. end{gather*} Ответ: 6 и 2.
Пример 3. Двое рабочих могут выполнить работу за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им понадобится 25 дней. За сколько дней каждый рабочий может выполнить задание самостоятельно?
Пусть x и y – производительность каждого рабочего, A – работа.
По условию: $$ left{ begin{array}{ l } mathrm{frac{A}{x+y}=12} & \ mathrm{frac{A}{2x}+frac{A}{2y}=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{frac{A}{2}left(frac{1}{x}+frac{1}{y}right)=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{A=frac{50}{frac{1}{x}+frac{1}{y}}=frac{50xy}{x+y}} & end{array}right. $$ Получаем уравнение: begin{gather*} mathrm{12(x+y)=frac{50xy}{x+y}Rightarrow 12(x+y)^2=50xyRightarrow 6(x+y)^2=25xy}\ mathrm{6(x^2+2xy+y^2)-25xy=0}\ mathrm{6x^2-13xy+6y^2=0 |:y^2}\ mathrm{6left(frac{x}{y}right)^2-13frac{x}{y}+6=0}\ mathrm{D=13^2-4cdot 6cdot 6=25=5^2, frac{x}{y}=frac{13pm 5}{12}=} left[begin{array}{ l } mathrm{frac23} & \ mathrm{frac32} & end{array}right. end{gather*} Пусть для определенности x > y. Тогда ( mathrm{frac{x}{y}=frac{3}{2}Rightarrow x=1,5y}. )
Работа: ( mathrm{A=12(x+y)=12(1,5y+y)=12cdot 2,5y=30y}. )
Второй рабочий может выполнить работу самостоятельно за: ( mathrm{frac{A}{y}=frac{30y}{y}=30} дней. )
Первый рабочий работает в 1,5 раза быстрей, ему понадобится ( mathrm{frac{30}{1,5}=20} дней. )
Ответ: 30 дней и 20 дней.
Пример 4. Бригада выполнила работу за 20 дней. Если бы в бригаде было на 4 человека больше, а рабочий день – на 1 ч дольше, то работа была бы выполнена за 10 дней. Если бы в бригаде было на 1 человека меньше, а рабочий день – на 1 ч короче, то работа была бы выполнена за 30 дней. Сколько человек было в бригаде, и сколько часов в день они работали?
Пусть A – вся работа, n – количество человек в бригаде, t – продолжительность рабочего дня. По условию: $$ left{ begin{array}{ l } mathrm{20nt=A} & \ mathrm{10(n+4)(t+1)=A} & \ mathrm{30(n-1)(t-1)=A} & end{array}right. $$ Исключаем A и получаем систему из двух уравнений: begin{gather*} left{begin{array}{ l } mathrm{20nt=10(n+4)(t+1)} & \ mathrm{20nt=30(n-1)(t-1)} & end{array}right.Rightarrow left{begin{array}{ l } mathrm{2nt=nt+4t+n+4} & \ mathrm{2nt=3(nt-t-n+1)} & end{array}right.Rightarrow\ Rightarrow left{begin{array}{ l } mathrm{nt=4t+n+4} & \ mathrm{nt=3t+3n-3} & end{array}right. end{gather*} Найдём линейную зависимость между n и t из уравнения: $$ mathrm{4t+n+4=3t+3n-3Rightarrow t-2n=-7Rightarrow t=2n-7}. $$ Подставим t в верхнее уравнение системы: begin{gather*} mathrm{n(2n-7)=4(2n-7)+n+4}\ mathrm{2n^2-7n=8n-28+n+4Rightarrow 2n^2-16n+24=0Rightarrow n^2-8n+12=0}\ mathrm{ (n-2)(n-6)=0Rightarrow} left[begin{array}{ l } mathrm{n_1=2} & \ mathrm{n_2=6} & end{array}right. end{gather*} Находим время ( mathrm{t=2n-7: } left[begin{array}{ l } left{begin{array}{ l } mathrm{n_1=2} & \ mathrm{t_1=-3} & end{array}right. &\ left{begin{array}{ l } mathrm{n_2=6} & \ mathrm{t_2=5} & end{array}right. end{array}right. )
Выбираем решение с ( tgt 0: left{begin{array}{ l } mathrm{n=6} & \ mathrm{t=5} & end{array}right. )
Ответ: 6 человек, 5 часов.
Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.
Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.
Пример:
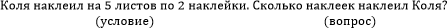
Решение любой текстовой задачи можно разделить на несколько основных этапов:
- Работа с условием
- Составление математической модели
- Проверка ответа
Работа с условием
Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.
Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?
Иллюстрация:
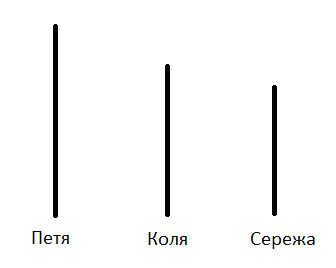
Из рисунка сразу понятен ответ: Петя выше всех.
Пример.
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?
Иллюстрация:
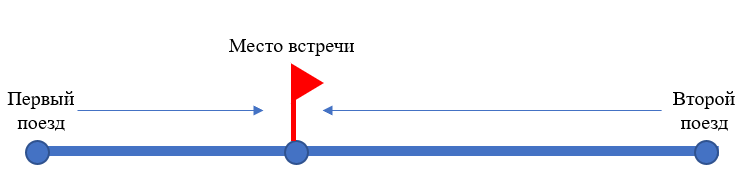
Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.
Составим математическую модель:
45х + 55х = 200
100х = 200
х = 2 ч
Ответ: 2 ч.
Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.
Математическая модель
Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.
x — число девочек
y — число мальчиков
| Реальная ситуация | Математическая модель |
|---|---|
| В классе поровну мальчиков и девочек | $ { x=y} $ |
| Девочек на 5 больше, чем мальчиков | $ { x=y+5, ; или; x-y=5,; или; x-5=y} $ |
| Мальчиков в 2 раза больше, чем девочек | $ { y=2x, ; или; frac{y}{2}=x,; или; frac{y}{x}=2} $ |
| Если в класс перейдут 3 мальчика, то девочек станет в два раза больше | $ { y=2(y+3)} $ |
Алгебраическая зависимость
Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.
При составлении уравнения особое значение играют используемые предлоги: «в» и «на».
Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?
Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.
Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.
Выразим рост мальчиков.
Петя выше Коли на 20 см: П – 20 = К
Сережа ниже Коли на 10 см: К = С + 10
Подставим в первое уравнение рост Коли: П – 20 = С + 10
Нам нужно найти, на сколько см Петя выше Сережи: П – С
П – 20 = С + 10
П – С = 20 + 10
П – С = 30
Получаем, что Петя выше Сережи на 30 см.
Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?
Решение:
Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.
Маша сделала в два раза больше снежинок, чем Коля: К = М/2
Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4
Вместе ребята сделали 12 снежинок: М + К + Р = 12
Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12
М = 4.
Маша сделала 4 снежинки.
Процентная зависимость
С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?
Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.
Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.
Так что же такое один процент?
Процент — это всегда доля какого-то числа.
100% — все число
50% — половина
25% — четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Пример:
Есть 100 яблок.
$ 1% ;от ;всех ;яблок; –frac{100}{100} = 1 ;яблоко. $
Есть 200 груш
$ 1% ;от ;всех ;груш; –frac{200}{100} = 2 ;груши. $
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.
Пример:
200 груш — 100 %
2 груши — 1 %
Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.
$ frac{200}{2}=frac{100}{1} $
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100
Эту тему мы еще подробно пройдем на курсе.
Рассмотрим несколько примеров работы с процентами в текстовых задачах.
Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов
Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?
Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек
Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?
Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?
На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:
Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880
Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880
Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.
Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.
На прошлом уроке нами была установлена взаимозависимость между математическим языком и математической моделью. Теоретический базис заложен, так что теперь самое время переходить к практике. Далее мы подробнее рассмотрим составление математической модели и простые задачи, решаемые с помощью математической модели.
На первых порах тема может даваться с трудом. Но есть хорошая новость. Составление математической модели — это во многом навык.
Чем больше типовых задач вы нарешаете, тем проще вам будет ориентироваться в моделировании.
Этапы составления математической модели
Ранее мы описывали, что этапы составления математической модели включают в себя:
| 1. Наблюдение | 2. Моделирование | 3. Предсказание |
|---|---|---|
| Анализ задачи; на основе анализа подготовка частей будущей математической модели. | Логическое объединение частей и составление математической модели. | Использование составленной математической модели для заключений по вопросу задачи. |
С практической точки зрения наибольшую сложность представляют два первых этапа — наблюдение и моделирование. Чтобы их успешно завершать, необходимо умение правильно переводить текстовые утверждения на язык математики.
Что нужно хорошо понимать. На этапе наблюдения обычно переводятся части будущего алгебраического выражения. В процессе этапа моделирования эти части объединяются.
«Типовая задача»?
Еще раз подчеркнем, что задачи для седьмого класса, решаемые с помощью математической модели, являются типовыми. Что это означает? Они отличаются одинаковостью алгоритма решения.
Логика вычислений в них зациклена. А составление математической модели от задачи к задаче также следует одной схеме.
Например, пусть дана части задачи:
«Стоимость яблочного сока $x$ рублей, а томатного — $y$ рублей. Известно, что $5$ стаканов яблочного сока стоят столько же, сколько $6$ стаканов томатного…»
То, как составлена задача, подводит нас к двум концепциям — приравниванию и умножению. Опорным для решения будет следующее алгебраическое выражение:
$$5x=6y$$
Раз задача типовая, то выражения наподобие «$ax=by$» непременно встретятся еще раз, просто уже, так скажем, не в контексте сока. Вот почему мы выше говорили про то, что составление математической модели — это навык. Оно же умение отбросить текст и увидеть алгебру за ним.
Задачи на наблюдение и моделирование
Рассмотрим далее некоторые задачи, решаемые с помощью математической модели, в которых опущен этап наблюдения — где нет вывода ответа. Это поможет освоиться в основных типах учебных задач и научит выражать важные части текста алгебраически.
Операции сложения и вычитания
Задача. Первый рабочий выполняет порученное задание за $x$ часов, второй то же задание — за $y$ часов, при этом первый работает на три часа больше, чем второй.
Решение
Между производительностью двух рабочих можно установить отношение равенства, но с учетом условия «на три часа больше». Для начала составим каркасное тождество, которое дополним далее:
$$x=y$$
«Полноправно» приравнять данные переменные мы можем, только дополнив, что первый рабочий ($x$) работает на три часа больше. Интуитивно так и хочется переписать тождество следующим образом:
$$x+3=y$$
Однако это неверное составление математической модели для данной задачи. Мало того, что по условию очевидно неравенство $x>y$, так еще и тождество с частью «$x+3$» увеличивает разрыв между значениями $x$ и $y$ на лишние три раза.
Чтобы производительность рабочих все-таки приравнять, у первого, наоборот, нужно «отобрать» три часа и «отдать» их тому, кто работает быстрее:
$$x=y+3$$
Операции умножения и деления
Задача. На двух стройках трудится одинаковое количество рабочих. На первой стройке работает 5 бригад по $x$ человек в каждой, на второй стройке — 3 бригады по $y$ человек в каждой.
РЕШЕНИЕ
Первая стройка. В одной бригаде трудится $x$ человек. По условию таких бригад пять. Откуда получаем количество человек всего, трудящихся на первой стройке: $5x$.
Вторая стройка. Здесь же в одной бригаде трудится $y$ человек. По условию имеем три бригады. Следовательно количество работников, трудящихся на второй стройке: $3y$.
Также нам известно, что на двух стройках работает одно и то же количество рабочих. Остается данные части приравнять, чтобы получить тождество:
$$5x=3y$$
Вот, буквально мгновение — и мы вновь увидели составление математической модели коэффициентного типа «$ax=bx$».
Задачи, решаемые с помощью математической модели, со смешанной арифметикой
Задача. У Кати $x$ марок, а у Димы $y$ марок. Если Катя отдаст Диме 5 марок, то у Димы станет марок вдвое больше, чем останется у Кати.
РЕШЕНИЕ
Внимание на следующие части текста задачи:
| «Отдаст пять марок…» | «Вдвое больше» |
| Сложение/вычитание | Умножение/деление |
В зависимости от того, какая часть тождества отражает данные положения, операция может быть как прямой («Катя отдаст, $x-5$»), так и обратной («Дима возьмет, $y+5$).
Разделим составление математической модели задачи на два шага.
1. Катя отдает Диме 5 марок и у нее остается $x-5$ марок. Теперь у Димы $y+5$ марок.
2. В результате у Димы марок в два раза больше.
Однако нам нужно количество марок ребят приравнять. Раз у Димы их по условию задачи больше, то для равенства с количеством марок Кати у него их должно быть меньше. Значит, мы можем либо умножить количество марок Кати на 2, либо разделить количество марок Димы на 2:
| $$2(x-5)=y+5$$ | $$x-5=frac{y+5}{2}$$ |
Составление математической модели — полные задачи
Самое время усложнить содержание задач и ввести все этапы составления математической модели, включая этап планирования. Далее мы решим ряд показательных задач, где требуется дать ответ.
Задача. В двух залах кинотеатра 460 мест. Сколько мест в большом зале, если в нем в 3 раза больше мест, чем в малом?
РЕШЕНИЕ
Заметим, что в данном случае составление математической модели задачи будет вестись в двух направлениях. С одной стороны, устанавливается алгебраическое равенство между количеством мест в залах. С другой стороны, нам известна их сумма. Составим эти выражения.
Приравнивание. Пусть количество мест в большом зале равняется $x$. Вместо того, чтобы вводить лишнюю переменную $y$ для количества мест в малом зале, выразим места малого зала через уже введенную переменную $x$ — как $frac{x}{3}$. Это краткая модель записи:
$$y=frac{x}{3}$$
Сложение. Всего в залах 460 мест. Количество мест в большом зале $x$, в малом — $frac{x}{3}$, одна треть от мест в большом. Вместе:
$$x+frac{x}{3}=460$$
Задаче требуется ответ; этапы составления математической модели должны завершаться в полном объеме. С этой целью мы и взяли за «главную» переменную количество мест в большом зале. Остается решить уравнение выше.
$$frac{4}{3}x=460\x=345$$
Ответ: 345.
Составление математической модели — задачи на движение
Задача. От пристани отошел теплоход со скоростью 22 км/ч, а от другой пристани навстречу ему через три часа отошел теплоход со скоростью 26 км/ч. Расстояние между пристанями составляет 306 км. Сколько времени в пути был каждый из теплоходов до встречи?
Для решения нам понадобится формула пути:
$$S=vt$$
Этап наблюдения
Время в пути — искомый параметр, введем его в качестве переменной $t$.
Пусть $t_1$ — это количество времени, затраченное первым теплоходом на преодоление всего своего пути. Сколько при этом затратил времени второй теплоход? На три часа меньше, ведь по условию от пристани он отошел в сравнении с первым с задержкой:
$$t_1-3$$
Этап моделирования
Каркасная модель выглядит так:
$$v_{1}t_1+ v_{2}t_2=S,$$
где $S$ — расстояние между пристанями, $v_1$ — скорость первого теплохода, $v_2$ — скорость второго, $t_1$ и $t_2$ — соответствующее время в пути.
Откуда взялась модель? Зарисуем перемещение теплоходов, что бывает иногда очень полезно при решении задач на движение. Теплоходы двигаются навстречу друг другу. Значит, в сумме они проходят расстояние между пристанями.
Доработаем модель и добавим в нее имеющиеся у нас данные:
$$22t_1+26(t_{1}-3)=306$$
Этап предсказания
Остается решить уравнение, найти значение $t_1$ и вычесть из него 3, чтобы получить $t_2$.
$$22t_1+26t_1=306+78\t_1=8$$
Первый теплоход затратил 8 часов. Второй, соответственно, 5 часов.
Ответ: 8 и 5.
Решите сами!
Показать решение
Спрятать решение
🔵 РЕШЕНИЕ
Не очевидно, но за переменную $x$ удобно взять количество учащихся в старших классах. Почему — увидите далее.
Выразим количество учащихся в начальных и средних классах также через $x$. Для этого проанализируем утверждения, заданные условием задачи.
Утверждение первое: «В начальных классах учащихся в три раза больше, чем в старших». Раз их в три раза больше, то количество учеников в начальных классах через $x$ — это $3x$.
Утверждение второе: «В начальных классах учащихся в два раза меньше, чем в средних». Количество учащихся в начальных классах мы выразили ранее как $3x$. Сколько тогда учеников в средних классах? В два раза больше, то есть $2cdot{3x}=6x$.
Остается составить модель:
$$x+3x+6x=900$$
Решаем и находим количество учеников в старших классах ($x$):
$$10x=900\x=90$$
Откуда получаем, что в начальных классах учится 270 учеников ($3x$), а в средних классах — 540 учеников ($6x$).
Ответ: 270, 540, 90.
Для использования стандартных
вычислительных алгоритмов ЛП требуется
математическая запись модели. Таким
образом, необходимо умение переводить
словесное описание задачи на язык
математических символов.
Составление математической модели
начинают с выбора переменных,
совокупность числовых значений которых
однозначно определяет один из вариантов
процесса. Следует иметь в виду, что иной
раз от удачного выбора этих переменных
зависит простота модели и, следовательно,
удобство дальнейшего ее анализа.
После выбора переменных необходимо
составить ограничения по тексту
задачи, которым эти переменные должны
удовлетворять. При этом нужно следить,
чтобы в модель были включены все
ограничительные условия и в то же время
не было ни одного лишнего или записанного
в более жесткой, чем требуется условиями
задачи, форме.
Наконец, составляется целевая функция,
которая в математической форме отражает
критерий выбора лучшего варианта.
После составления математической
модели необходимо рассмотреть
возможные пути ее упрощения и выбрать
подходящий вычислительный метод для
решения задачи.
Этап I – Выбор
переменных, необходимых для математической
модели задачи.
Введем следующие переменные переменные:
xi– площадь посеваi-ой
с/х культуры,i =
![]() ,
,
ci– число единиц удобрения, внесенных
подi-ую с/х культуру,i =
![]() ,
,
bik
– урожайностьi-ой культуры с
единицы площади посевов, на которую
внеслиkединиц удобрений.
Таким образом, решением задачи будет
являться вектор x
= (x1, x2,
…, xn),
который представляет собой способ
распределения земель междуn
посевами, а также векторc
= (c1, c2,
…, cn),
иллюстрирующий распределение единиц
удобрений по соответствующим участкам
земли.
Этап II –
Составление ограничений.
Составим ограничения, которым должны
удовлетворять переменные:
Суммарная площадь, занимаемая n
посевами, должна быть равна
фиксированному значениюS:
![]()
(1.1)
Суммарное количество внесенных
удобрений не должно превышать K
(однако, может быть и меньшеK,
так как необходимо учесть тот факт,
что внесение удобрений может навредить
посевам):
![]()
(1.2)
Учитывая тот факт, что ассортимент i
культуры зависит от ее урожайности,
запишем следующее ограничение:
![]() (1.3)
(1.3)
В данном случае под λi
понимается число единицi–ой
культуры, которое должно быть получено
в результате. Перемножая урожайность
соответствующей культурой с занимаемой
ею площадью, мы получаем в итоге реальное
количество продукции. Накладываемое
ограничение говорит о том, что реальное
количество продукции не должно быть
меньше требуемого.
Также используем в качестве ограничения
условие неотрицательности:
![]()
![]()
(1.4)
![]()
Важно отметить, что переменная xi
может принимать нулевое значение,
так как не исключена вероятность того,
что выращиваниеi–ой
культуры может повлиять на суммарный
доход таким образом, что он окажется
меньше, чем если бы эта культура не
выращивалась вовсе. И, быть может, более
выгодно будет вложить больше удобрений
во все остальные культуры.
Этап
III
– Составление целевой функции.
Составим целевую функцию, которая в
математической форме, отражает критерий
эффективности выбора лучшего варианта.
Так как необходимо найти способ
распределения земель и удобрений, при
котором суммарный доход от продажи
продукта будет максимален, то целевую
функцию можно представить в виде
разности между выгодой от продажи
каждого продукта и расходами на
удобрения:
![]()
(1.6)
Итак,
математическая модель задачи будет
иметь вид:
![]()
![]()
![]()
(1.7)
![]()
![]()
![]()
![]()
Данная математическая модель является
нелинейной. Упростим ее, введя
дополнительную булеву переменную:
если
k единиц удобрений
внесли в единицу площади подi–ую
культуру
иначе
![]()
В результате будет получена матрица,
состоящая из нулей и единиц:
|
k i |
1 |
.. |
K |
|
1 |
|||
|
.. |
|||
|
n |
При этом необходимо учесть следующие
ограничения для этой переменной:
Сумма по столбцам в каждой строке
матрицы Y не
должна превышать 1:
![]()
(1.8)
Это говорит о том, что под каждую культуру
не более одного раза вносится определенное
количество единиц удобрений.
Тогда ограничение для суммарного
количества удобрений можно переписать
следующим образом:
![]()
(1.9)
И ограничение для урожайности культур
также примет вид:
![]()
(1.10)
Целевую функцию также можно представить
в виде:
![]()
(1.11)
В результате получим видоизмененную
математическую модель:
![]()
![]()
![]()
(1.12)
![]()
![]()
![]()
![]()
![]()
Как видно, в полученной математической
модели не используются переменные ci.
Вместо этого искомый способ
распределения земель и удобрений будет
заключаться в том, что при различных
наборах значений матрицыY,
отражающих распределение единиц
удобрений на единице площади каждой
культуры, будет найдено соответствующее
распределение земель. При этом каждый
раз будет получено определенное значение
целевой функции. Выбрав в итоге
максимальное значение, мы найдём искомый
вариант оптимального распределения.
Соседние файлы в предмете Теория Принятия Решений
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
