МАТЕМАТИЧЕСКИЕ ДИКТАНТЫ НА УРОКАХ МАТЕМАТИКИ
В НАЧАЛЬНОЙ ШКОЛЕ
Математический диктант – хорошо известное средство обратной связи между учащимися и учителем. Это одна из многих оправдавших себя форм контроля знаний учеников. Выполняя задания, дети становятся более организованными и сосредоточенными. Проведение математического диктанта на этапе устного счета способствует не только развитию навыков вычисления, но и повышению их математической культуры, обогащению математического языка
Если диктанты проводятся систематически, учащиеся приучаются воспринимать задания на слух. Ценность таких навыков неоспорима – она приводит к умению слушать.
Необходимо следовать определенной методике проведения математического диктанта. Текст сначала прочитывается в целом, чтобы учащиеся знали, что от них требуется. Темп чтения определяется по темпу работы среднего ученика. Учитель выбирает такого ученика в классе, начинает читать следующее задание , когда данный ученик справился с предыдущим заданием. Необходимо следить за всем классом, реагировать на все неизбежные сбои темпа, на вопросы учащихся типа: «повторите, я не успел». Следует приучить учащихся пользоваться черновиками, где они могут делать пометки, записи в ходе диктовки.
Эффективность устного счета зависит не только от правильного определения объема и содержания этих занятий, но и от их организации: правильной постановки заданий и опроса, рационального проведения учета знаний и навыков учащихся, правильного чередования устных и письменных вычислений. Чаще всего задания предлагаются устно. Такая форма организации занятий является наиболее ценной, так как развиваются внимание и память учащихся, а главное, они подготавливаются к «жизненному» счету, где часто приходится выполнять действия над числами, воспринимаемыми на слух. Однако эта форма требует большого умственного напряжения, а поэтому сравнительно быстро утомляет детей, особенно тех, у кого преобладает зрительная память.
Наблюдающееся в школьной практике применение только этой формы занятий ведет к тому, что в устном счете участвуют не все дети. Особенно много бывает пассивных учащихся, когда диктуемые упражнения содержат большие числа или когда подряд дается много заданий на слух. Во избежание этого необходимо чисто слуховые упражнения перемежать с упражнениями на зрительное восприятие.
Основное назначение математических диктантов, помочь учителю эффективно тренировать устойчивость внимания детей, оперативную память, умение сосредоточиваться. Исходя из этих целей в диктантах даны следующие группы заданий:
- операционные, в которых нужно вычислять, решать задачи, выполнять преобразования и т.п., получив информацию на слух;
- логические, в которых требуется оценить истинность высказывания, для чего необходимо быть внимательным и сосредоточенным, уметь слушать, слышать и анализировать данные;
- направленные на усвоение математической терминологии.
Предложенные задания обеспечивают содержательным учебным материалом этап устной работы в начале урока математики, а также этап подведения итогов в конце урока. Развитию грамотной математической речи способствует наличие в каждом диктанте образцов чтения математических выражений.
Введение в математический диктант элементов игры, нестандартных заданий помогает детям, интересующимся математикой, поддерживать и развивать интерес к ней, а ребятам, у которых математика вызывает затруднения, – понять и полюбить ее.
Проведение диктанта можно организовать так:
- Учитель читает вслух задания диктанта из одного варианта. Учащиеся на листочках или в тетрадях записывают ответы. Сразу же (либо в конце урока) следует показать верные ответы, обсудить решения отдельных заданий.
- Прочитывать вслух задания диктантов могут отдельные учащиеся по указанию учителя. Это особенно полезно детям с недостаточной техникой чтения, а также тем, у кого преобладает зрительное восприятие.
- Полезно время от времени в классе давать всем ученикам тексты диктантов для самостоятельной работы с ними (записав текст диктанта и на доске). Это важно для запоминания правописания математических терминов.
- Математические диктанты можно давать и для домашней работы под руководством родителей. Это позволит каждому ученику дополнительно спокойно потренироваться в чтении математических текстов, не спеша разобраться в отдельных задачах, проверить свои знания.
Учителю читать диктант детям достаточно один раз. Это заставляет учеников быть предельно внимательными и собранными. Все вычисления и преобразования ученики выполняют только устно.
Математический диктант – одна из альтернативных форм контроля знаний, позволяющая участвовать всем учащимся сразу, а не нескольким, как при традиционном опросе.
Очень важно организовать проверку диктантов. Существует несколько видов проверки. Это запись правильных ответов на листочках с последующей сдачей их учителю на проверку, запись правильных ответов на доске, когда дети сверяют ответы со своими, взаимопроверка с соседом по парте и другие варианты, подходящие тому или иному составу учащихся. Иногда можно предложить учащимся задание на дом : составить текст математического диктанта. Оценки за работу выставляются с учетом числа верно решенных заданий. Если в диктанте 6 (или 8) заданий, оценки могут быть такими:
|
Число менее верных ответов |
6(8) |
5(7) |
4(5-6) |
4(5) |
|
Оценка |
5 |
4 |
3 |
2 |
Тема. «Числа от 1 до 10. Сложение и вычитание».
Цели. Проверить умение воспроизводить последовательность чисел от 1 до 10 и соотносить их с соответствующей группой предметов; сравнивать числа в пределах 10, читать простейшие математические записи вида 1 + 1 = 2 и др.; соотносить эти записи с конкретной иллюстрацией (рисунком); выполнять табличное сложение в пределах 10; представлять числа первого десятка ввиде суммы двух слагаемых; решать логические и текстовые задачи в одно действие.
Диктант 1
- Запишите цифрами числа: 1, 5, 7.
- Мальчик поймал 2 рыбок и выпустил их в ведро. Потом он поймал еще 3 рыбок. Нарисуйте столько рыбок, сколько всего рыбок стало в ведре.
- В семье 4 детей: сестер столько же, сколько братьев. Сколько в семье сестер?
- Запишите числа от 1 до 6.
- Запишите числа от 9 до 4.
- Заштрихуйте прямоугольник снизу вверх вертикальными линиями (прямоугольник дан на листочке).
Диктант 2
- Назовите число, которое следует за числом 9; за числом 5.
- К задуманному числу прибавили 1 и получили 7. Какое число задумали?
- Какие числа пропущены, если сумма в каждом столбце равна 8?
- Дорисуйте фигуры, чтобы количество элементов во множествах было равно.
- У старика Хоттабыча борода длиннее, чем у доктора Айболита, но короче, чем у Карабаса Барабаса. Чья борода самая длинная?
- Увеличьте: 9 на 1; 4 на 2; 7 на 1; 6 на 2.
Диктант 3
- Первое слагаемое равно 4, а второе слагаемое равно 2. Найдите значение суммы.
- Уменьшаемое равно 5, вычитаемое равно 3. Найдите значение разности.
- Увеличьте 7 на 2.
- Уменьшите 8 на 3.
- Среди чисел каждой пары найдите то число, которое больше, и обведите его в ряду чисел красным карандашом: 9 и 8; 5иЗ; 1 и 4.
- Найдите лишнюю по форме фигуру.
- Соломинка выше Пузыря, а Лапоть ниже Пузыря. Кто выше: Лапоть или Соломинка?
- Графический диктант.
Тема. «Числа от 11 до 20. Сложение и вычитание»
Цели. Проверить умение читать и записывать числа от 0 до 20; выполнять табличное сложение и вычитание в пределах 20; представлять все числа от 2 до 20 в виде суммы двух слагаемых; решать текстовые и логические задачи в одно действие.
Диктант 1
- Запишите число, которое предшествует числу 12, 13…
- Увеличьте 10 на 1.
- Уменьшите 19 на 1.
- Какое число меньше 15 на 1?
- На сколько 12 больше 7?
- Первое слагаемое 7, второе 4. Найдите сумму.
- Сколько надо прибавить к 5, чтобы получить 12?
- Чему равна сумма, если первое слагаемое 6, а второе 7?
- В гараже было 5 машин, приехало еще 3 машины. Сколько машин стало в гараже?
Диктант 2
1.10- это 7 и еще сколько?
- От какого числа надо отнять 5, чтобы получилось 7?
- Найдите значение разности чисел 15 и 9.
- Увеличьте 7 на 5.
- Уменьшаемое 12, вычитаемое 8. Найдите разность.
- У брата 5 тетрадей, у сестры столько же. Сколько тетрадей у брата и сестры вместе?
- Гребенчатый тритон линяет каждые 7 дней. Сколько раз пройдет линька у тритона за 14 дней.
Литература:
- Истомина Н.Б., Шмырева Г.Г. Дидактические карточки-задания по математике.– М. Астрель. 1979.
- Гейдман Б.П. Математика. – M.: Изд-во Московского университета, 1999.
- Волкова С.И., Столярова Н.Н. Тетрадь с математическими заданиями. – M.: Просвящение, 1993.
- Голубь В.Т.Математические диктанты 2 класс. – Воронеж. 2011.
Если с диктантом по русскому языку всё понятно, то что такое математический диктант? Ребенок приходит из школы и говорит: “Сегодня писали математический диктант. Я получил 3“. Вы понимаете о чём речь? И за что тройка? Если нет и если хотите писать такие диктанты на пятёрки, тогда эта статья для вас. В конце будут примеры диктантов для 2, 3 и 4 классов за 1 четверть.
Я своим ученикам говорю, что сейчас у нас будет устный счёт, ответы будем писать в тетрадь самостоятельно. Такая формулировка легче воспринимается для детей в начальной школе.
Математический диктант – форма работы на уроке, в которой ученики воспринимают задание на слух и записывают только ответ.
Эта такая же работа для проверки знаний учеников, как и тест или контрольная. Но диктанты пишутся быстро, от 5, максимум до 15 минут от урока.
Учитель читает задание, где надо либо написать заданное число, либо вычислить, либо решить задачу. Ученики при этом не делают никаких записей, всё считают в уме. Задание читается несколько раз, оптимально 2-3. Дети записывают только ответ в столбик или в строчку с номером задания.
Это проверка умения считать устно, но проводится она сразу со всем классом и проверяется быстро. Удобная форма работы для учителя. Раз в две недели математические диктанты пишутся в тетрадях для контрольных работ, отметки идут в дневники и в журнал.
Помимо проверки умения считать устно такие диктанты развивают:
- скорость
- мышление
- гибкость и точность мысли
- закрепляют математические навыки
- отрабатывают математическую терминологию
- умение работать самостоятельно
- самое главное – память
- внимание
- сосредоточенность
- воображение
Часто бывает, что ребенок не может воспринимать задание на слух. Задачи он читает по учебнику, решает, но когда эти же задачи ему читают, он уже не может их решить и не понимает ни условия, ни решения.
Ещё дети привыкают к привычным контрольным и самостоятельным, записанным на доске или напечатанным на листочках, поэтому математический диктант, где ничего не записано, воспринимается у них с трудом. Отсюда бывают плохие отметки за устный счёт, при том, что за письменные контрольные работы отметки всегда хорошие. Вот поэтому учитель и проводит математические диктанты, чтобы развивать быстрое и качественное умение считать устно.
Теперь главный вопрос, который волнует многих родителей:
Как готовиться к математическим диктантам
Учителю:
- Проводить минутки устного счёта в начале каждого урока
- Распечатать и показать родителям хотя бы один вариант математического диктанта за год, чтобы они хоть знали, что вы им даёте и к чему готовить своих детей. А то будет такое удивление, как в начале моей статьи: “что за диктант и за что тройка?”
- Отрабатывать сложные задания как можно чаще. Например, ученики часто “плавают” в понятиях “частное”, “уменьшаемое”, “делимое”, “слагаемое” и т.д. Не могут устно найти площадь прямоугольника, путают с периметром. Задачи на слух – вообще крах. Для этого нужно отрабатывать всё это с детьми на каждом уроке.
Школьникам и родителям:
- Тренироваться писать такие диктанты дома. Найти их можно в интернете, например, по запросу “математический диктант для 2 класса за 1 четверть“. Или купить готовое пособие (для удобства оставлю ссылки на них в конце публикации).
- Задавать ребенку чаще устные задания вида: “найди произведение 3 и 7”, “18 увеличь/уменьши на 4” и другие, по дороге в школу, на прогулке, дома после выполнения домашнего задания.
- Листочек с заданиями можно дать ребенку в качестве самостоятельной работы, если у вас нет возможности диктовать. Но необходимо ограничить время выполнения. Вам же нужно научить его считать быстро.
- Развивать умение считать в уме быстрее. Для этого подойдут самые простые примеры в пределах 10 даже для четвероклассников. Вы пишете на листочке 10-20-30 несложных примеров: 3+5, 2+6, 8-4 и т.д. Даёте ребенку на их решение две минуты. Отмечаете ошибки и время выполнения, записываете это. Говорите, что завтра ждёт такое же задание. Увидите, что завтра ребенок справится с этим лучше и быстрее, со временем ошибок не станет, а считать он будет быстрее с каждым разом. У него включится интерес и желание побить свой рекорд и превзойти самого себя. Потом перейдите к примерам на умножение. Не забывайте хвалить ребенка.
- Поговорите с учителем и выясните, какие задания он даёт на математических диктантах, спросите, в каких заданиях ошибается ваш ребенок, отработайте эти темы.
- Часто ученик не может идти дальше, потому что у него не закреплены старые темы. Не бойтесь вернуться на несколько шагов назад в первый класс. Отработайте счёт в пределах 10 и 20, состав чисел. Это основная база любого математического диктанта. Отработайте таблицу умножения. Разберите с ним, что такое сумма, разность, произведение, частное и другие математические термины, объясните, как находить произведение. Например, задавайте не 3 умножить на 2, а “найди произведение трёх и двух”.
Примеры математических диктантов за 1 четверть
2 класс
- Запиши число, в котором 3 десятка и 8 единиц
- Найди сумму чисел 40 и 5
- На сколько надо увеличить 6, чтобы получить 11?
- Уменьши 13 на 5.
- Уменьшаемое — 47, вычитаемое — 1. Найди разность.
- Вырази в сантиметрах 2 дм 9 см.
- Мама испекла 10 пирожков с картошкой и столько же с капустой. Сколько всего пирожков испекла мама?
- На двух тарелках лежало 16 конфет. На одной из них было 9 конфет. Сколько конфет на второй тарелке?
3 класс
1. Запишите самое большое однозначное число.
2. Число 45 уменьшите на 30
3. Число 18 увеличьте на 50
4. Найти сумму чисел 29 и 40
5. Найти разность чисел 70 и 1
6. Найти произведение чисел 3 и 5
7. Уменьшите 90 на 6.
8. В саду было 12 кустов смородины, крыжовника на 5 кустов меньше, чем смородины, а малины на 8 кустов больше, чем крыжовника. Сколько кустов малины было в саду?
4 класс
- Запиши число, в котором 44 десятка
- Найди произведение чисел 573 и 100.
- На сколько 1 тонна больше, чем 400 кг?
- Первый множитель 80, второй множитель 6, чему равно произведение?
- Увеличь в 4 раза число 900.
- Чему равна разность чисел 347 и 40?
- Дочери 6 лет, а мать старше её на 27 лет. Сколько лет матери?
Математические диктанты в книжном магазине Лабиринт для самоподготовки:
1-4 классы
5 класс
Диктанты для тех, у кого математика по учебнику Моро:
3 класс
4 класс
Для самостоятельной работы учащихся автора В. Голубь (не из простых!):
2 класс
3 класс
4 класс
Математический диктант
как форма проверки знаний
Важным и чрезвычайно тонким моментом учебно-воспитательного
процесса как для учителя, так и для ученика является контроль знаний.
Контроль — составная часть процесса обучения и обеспечивает учителю
получение информации о ходе познавательной деятельности учащихся в процессе
обучения, а ученикам — получение информации о своих успехах. Контроль
знаний имеет обучающее и воспитывающее значение, способствует более глубокому
изучению учащимися основ наук, совершенствованию их знаний и умений.
Математические диктанты — хорошо известная форма контроля
знаний. Учитель сам или с помощью звукозаписи задает вопросы, учащиеся
записывают под номерами краткие ответы на них. Как правило, ребятам трудно
воспринимать задания на слух. Но если диктанты проводить часто, то школьники
овладевают этим навыком. А ценность такого умения неоспорима. Иногда слуховому
восприятию нужно помочь. Для этого одновременно с чтением задания делаю запись
или чертеж на доске. В зависимости от подготовленности учащихся число заданий
увеличиваю или уменьшаю.
Прежде чем перейти к объяснению нового материала, целесообразно
убедиться, что предыдущая порция знаний учащимися усвоена. Традиционная
методика рекомендует в этом месте педагогического процесса организовать опрос
учащихся. Опрос, как форма проверки знаний, неэффективен, и прежде всего
потому, что для большей части учащихся ответ одноклассника у доски вовсе не
помогает повторить ранее изученное. Всякого рода уплотненные опросы, когда
одновременно готовятся до 10 учеников, лишь усугубляют дело: вызванные не
слушают ответ товарища на законном основании.
Опрос у доски обычно дополняют так называемым устным счетом.
Недостаток традиционного «устного счета» в том, что в нем участвуют не все
ученики. Альтернатива опроса и «устного счета» — математический диктант.
Отсюда — его место в учебном процессе: в начале урока, на котором
начинается изложение новой порции знаний. Отсюда — требование к его
содержанию: ответы на вопросы должны показывать, усвоено ли содержание ранее
изложенного материала. Математический диктант может заменить опрос по теме,
заданной для повторения. Его продолжительность обычно 10–15 минут.
Он представляет собой систему вопросов, связанных между собой.
Содержание заданий
Рассмотрим различные виды заданий, с которыми сталкиваются ученики
в диктантах.
1. Задания репродуктивного типа выполняются учащимися на
основе известных формул и теорем, определений, свойств тех или иных
математических объектов.
Репродуктивные задания позволяют
выработать основные умения и навыки, необходимые для изучения математики. И
хотя они мало способствуют развитию мышления учащихся, однако создают базу для
дальнейшего изучения математики и таким образом способствуют выполнению заданий
более высокого уровня сложности.
2. Реконструктивные задания указывают только на общий принцип решений (например, «решите
графически неравенство») или на соотнесение к тому или иному материалу
(например, «решите задачу составлением системы уравнений»). Выполнение таких
заданий возможно только после того, как ученик сам реконструирует их, соотнесет
с несколькими репродуктивными. К такого рода заданиям можно отнести задания на
построение графиков, задачи на составление уравнений, задания, при выполнении
которых учащимся приходится использовать несколько алгоритмов, формул, теорем
(например, «представьте в виде многочлена выражение (а – 2)x(а +
2) – (2 – а)2»).
Эти задания характерны тем, что, приступая к их выполнению, ученик должен
проанализировать возможные общие пути решения задачи, отыскать характерные
признаки объекта, использовать несколько репродуктивных задач. Отметим, что
познавательная деятельность ученика при выполнении этих заданий не выходит за
рамки воспроизведения знаний, но неизбежно сопровождается некоторым обобщением.
Реконструктивные задания — наиболее распространенный вид заданий,
используемый на всех этапах учебного процесса.
3. Более высоким уровнем воспроизводящей деятельности и
переходом ее в творческую характеризуются задания вариативного характера. При выполнении их ученику необходимо из всего арсенала
математических знаний отобрать нужные для решения данной задачи,
воспользоваться интуицией, найти выход из нестандартной ситуации. К такого рода
заданиям относятся так называемые задачи на сообразительность, задачи «с
изюминкой», многие задачи на доказательство, а также задачи, для решения
которых необходимо создание новых алгоритмов решения (например, «Вставьте
пропущенные одночлены так, чтобы получилось тождество а2 + 6аb + … = (… + …)2»).
Чтобы развивать мышление учащихся, формировать у них различные
виды деятельности на всех этапах обучения математике, необходимо использовать различные
виды заданий.
Математический диктант — это один из способов организации
самостоятельной деятельности учащихся. Система математических диктантов, с
одной стороны, должна обеспечивать усвоение необходимых знаний и умений, с
другой стороны, их проверку.
Виды диктантов
Математические диктанты можно разделить на следующие виды:
проверочные, обзорные, итоговые. Каждый вид математических диктантов имеет свои
особенности, свои цели, и следовательно, требования, предъявляемые к
составлению этих работ, должны быть различны.
Проверочные диктанты предназначены
для контроля усвоения отдельного фрагмента курса в период изучения темы. При их
выполнении учитель своевременно получает информацию о том, как усваивается
тема, что позволяет ему вовремя выявить ошибки, обнаружить плохо усвоивших тот
или иной материал и в зависимости от этого строить работу по изучению данной
темы. Учащиеся же получают дополнительную практику в самостоятельном решении
задач и тем самым готовятся к контрольной работе по данной теме. Поскольку
проверочные диктанты проводятся после отработки основных умений и навыков, то в
них включаются задания не только репродуктивного характера. Основа проверочных
диктантов — задания реконструктивного характера. В то же время в
проверочные диктанты не следует включать задания сложнее тех, которые
выполнялись учащимися на уроках и дома.
В процессе изучения некоторых разделов курса учитель проводит
несколько контрольных работ, дающих представление об усвоении отдельных тем,
входящих в этот раздел. Однако после завершения изучения раздела целесообразно
проверить его усвоение в целом, для этой цели можно провести обзорный
диктант, который позволит учащимся повторить материал, систематизировать
знания, установить связи между изученными вопросами. Для этого необходимо
определить, какие основные понятия должен усвоить ученик при прохождении этого
раздела, какие умения и навыки должен приобрести, какие задания уметь
выполнять, каков уровень сложности этих заданий. При этом не должно быть
заданий, отягощенных сложными тождественными преобразованиями, трудоемкой
вычислительной работой, требующих на свое выполнение много времени. Задания
должны быть четкими, конкретными, понятными. Сюда входят вопросы по проверке
изученных определений, теорем, правил, задания на решение несложных задач и
упражнений. Основу обзорных диктантов составляют задания репродуктивного
характера. Составленный таким образом диктант дает возможность учителю
проверить усвоение узловых вопросов всего раздела.
Организация повторения является важным моментом в методике
обучения математике. Повторение ранее изученного материала в связи с его
использованием при изучении нового материала является наиболее распространенным
видом повторения. Существуют и другие виды повторения, — в частности,
обзорное и итоговое повторение темы, раздела, курса.
Завершающим моментом повторения в конце года может явиться
проведение итоговых диктантов по основным содержательным линиям изученного курса.
В них следует включать задания репродуктивного и реконструктивного
характера, которые должны проверять основные умения и навыки; задания на
повторение основных теоретических вопросов: воспроизведение определений и
свойств математических объектов.
Способы проведения диктантов
Текст диктанта может быть:
а) спроецирован на доску с помощью компьютера;
б) зачитан учителем;
в) воспроизведен с помощью звукозаписи;
г) с графической записью ответа.
При чтении заданий диктанта паузы определяются по темпу работы
среднего ученика. Наблюдения показали, что достаточна пауза, равная времени
повтора текста. Следует помнить, что математический диктант проверяет не
сообразительность учащихся, а их знания. И если учащийся при ответе на вопрос
диктанта надолго задумался, он просто не знает ответ, и долгая пауза ему не
поможет.
Методика проведения
Проведение диктанта, особенно в два варианта, требует от учителя
весьма большого напряжения: надо читать в оптимальном темпе тексты заданий;
следить за классом; реагировать на неизбежные сбои («повторите», «а у меня
ручка перестала писать» и т.п.).
К тому же учащиеся нередко не понимают, какой именно из двух вариантов в данный
момент диктуется, и в результате перепутывают задания вариантов. Подобные
трудности легко преодолеваются с помощью звукозаписей, в которых задания первого
варианта читает мужской голос, а второго — женский. Ученик не реагирует на
«чужой» голос: спокойно работает пока диктуется задание другого варианта, а как
только начинается чтение задания его варианта, немедленно включается в работу.
Использование звукозаписей дисциплинирует класс: ученик понимает, что
«бездушной машине» все равно, успел ли он подготовить все необходимое к началу
диктанта, пишет ли его ручка и т.п., и сбои становятся крайне редкими. Учителю
использование звукозаписи при проведении диктанта дает возможность наблюдать за
работой учащихся, делать необходимые и убирать уже ненужные записи и рисунки с
доски и т.д.
Диктант можно провести и так.
1) Учитель полностью зачитывает текст, а учащиеся слушают, не
делая записей.
2) Учитель читает текст по фразам, делая паузы (от одной до
четырех минут), чтобы дать учащимся возможность выполнить задание.
3) Когда все задания выполнены, учитель снова читает весь
текст с небольшими остановками (это дает учащимся возможность что-то исправить
и сделать дополнения).
4) Правильные ответы записываются на доске, и ученики
самостоятельно проверяют диктант у соседа по парте. В 5–7-х классах все работы
проверяются учителем.
Организация проверки
Обычный способ проверки, когда ответы учащихся учитель собирает и
проверяет дома, малоэффективен: ребенок жаждет узнать результаты своей работы
непосредственно после завершения, на следующий день они его интересуют уже
меньше. Поэтому организовать проверку можно, например, так. Учащиеся пишут
диктант под копирку. Первый экземпляр сдается учителю сразу после слов «диктант
окончен», а копия остается у ученика и используется для проверки правильности
выполнения работы: учитель записывает на доске правильные ответы.
Весьма важно обучить учащихся правильной проверке своих
математических диктантов. Иначе некоторые ученики просто не замечают допущенных
ошибок. Можно предложить учащимся самостоятельно оценивать результаты диктанта
по указанным критериям.
Вот возможная шкала оценок для диктантов различной длины.
|
Число вопросов |
5 |
6 |
7 |
8 |
9 |
10 |
||||||||||||
|
Число |
3 |
4 |
5 |
4 |
5 |
6 |
4, |
6 |
7 |
5, |
7 |
8 |
5, |
7, |
9 |
6, |
8, |
10 |
|
Отметка |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
3 |
4 |
5 |
После того как учащиеся научатся проверять свои математические
диктанты, учитель может вообще перестать проверять их дома. Вместо самопроверки
можно делать взаимопроверку — между двумя учениками. Можно организовать
проверку и так: ученик передает свой листок другому ученику, который писал тот
же вариант. Он сверяет ответы и ставит знаки «+», «–», «?» не только в своем листке,
но и в листке товарища, и отметки ставит в обоих листках. После завершения
проверки учитель называет фамилию ученика. Ученик называет поставленную им себе
отметку, и сразу же называет поставленную ему отметку одноклассником, который
сверял ответы на его листке. Если отметки совпадают, учитель ставит ее в
журнал. Если нет, берет диктант на перепроверку.
Но, пожалуй, самым важным в организации проверки диктанта сразу
после его завершения является то, что появляется возможность обсудить все те
вопросы, которые вызвали затруднения или особенно важны для понимания нового
материала: детей, которые только что написали математический диктант,
интересует не только отметка, но и обоснование решения. Эта работа может быть
организована, например, так. Учитель предлагает сверить ответ, полученный при
выполнении первого задания, и поднять руку всем тем, кто допустил ошибку. Если
ошибок немного и само задание не такое уж важное, учащимся предлагается сверить
свои результаты по второму заданию. Если же оказалось, что решение задания
необходимо разъяснить, кто-либо из учеников или учитель дают необходимые
пояснения.
В случае необходимости учащимся по ходу проверки предлагается выполнить
аналогичное задание. При сверке ответов эффективен следующий прием. Учитель
показывает верный ответ и просит сверить с ним свои ответы. О совпадении или не
совпадении ответов должны одновременно сигнализировать все ученики. Это можно
сделать, например, с помощью карточек разных цветов; совпадение —
поднимается зеленая карточка, не совпадение — красная. Учитель видит
одновременно ответы всех учащихся и может сказать каждому, верен ли его ответ.
Разница между традиционным поднятие руки и описанным голосованием огромная: там
отвечает лишь вызванный, здесь — все. Вместо сигнальных карточек можно
использовать голосование по следующим правилам: в случае согласия поднимают
правую руку, в случае не согласия — левую. А чтобы учащиеся не забыли и не
перепутали, на доске надо написать слева слово «нет», справа — слово «да».
Поднятые руки, как и цветные карточки, позволяют учителю немедленно узнать,
правильно или не правильно каждый ученик выполнил задание.
Заключение
Процесс обучения — процесс двусторонний; для успеха обучения
требуется не только высокое качество работы учителя, но и активная деятельность
учащихся, их желание овладеть передаваемыми учителем знаниями, их интерес к
обучению, сосредоточенная и вдумчивая работа под руководством учителя. Все эти
реакции у учащихся должен вызвать к действию учитель, опираясь на свой
авторитет, на контакт с учащимися, на свою увлеченность предметом, профессией,
любовь и благожелательное отношение к детям.
Практика показывает, что реальный учебный процесс не всегда
удается организовать достаточно хорошо. Систематически применяя на своих уроках
математические диктанты наряду с другими формами проверки знаний, убеждаешься в
том, что они являются эффективным средством активизации учебной деятельности.
Но важно подчеркнуть, что в силу специфики математических диктантов
(воспринимаемые на слух вопросы; лаконичные ответы) их педагогические
возможности ограниченны. С их помощью, как правило, можно проверить, усвоили ли
учащиеся обязательный минимум знаний, но нельзя организовать углубленную
проверку. Поэтому было бы ошибкой противопоставлять диктанты другим формам
контроля. Одно и то же задание может быть как в диктанте, так и в
самостоятельной работе, но эти задания будут иметь разную дидактическую
функцию.
В самостоятельной работе от ученика требуется фиксирование хода работы, что
делает подконтрольным поиск результата. В математическом диктанте контроль
может вестись лишь по конечному результату. Надеюсь, что мой опыт заинтересует
коллег-математиков, будет полезен при обучении учащихся.
Статья подготовлена при поддержке информационно-образовательного
портала «edustudio.ru». Если Вы решили приобрести или углубить свои познания в
математике, то оптимальным решением станет обратиться в
информационно-образовательный портал «edustudio.ru». Перейдя по ссылке: «решение задач», вы сможете, не отходя от экрана монитора, посмотреть решенные
примеры, а также задать интересующий вопрос. Более подробную информацию вы
сможете найти на сайте www.edustudio.ru.
Рекомендуемая литература
1. Арутюнян Е.Б., Волович М.Б., Глазков Ю.А.,
Левитас Г.Г. Математические
диктанты для 5–9 классов. — М.: Просвещение, 1991.
2. Афанасьева Т.Л., Тапилина Л.А. Геометрия. 9 класс. (Пособие для учителя к
учебнику Л.С. Атанасяна, и др. «Геометрия. 7–9 классы»). — Волгоград:
Учитель, 2007.
3. Барышникова Н.В. Математика. 5–11 классы. Нестандартные
уроки. — Волгоград: Учитель, 2007.
4. Груденов Я.И. Совершенствование методики работы учителя
математики. — М.: Просвещение, 1990.
5. Ершова А.П., Голобородько В.В. Устные проверочные и зачетные работы по
геометрии для 7– 9 классов. — М.: Илекса, 2004.
6. Есипов Б.П. Самостоятельная работа учащихся на
уроках. — М., 1961.
7. Зив Б.Г., Алтынов П.И. Алгебра и начала анализа. Геометрия. 10–11
классы. Учебно-методическое пособие. — М., 1999.
8. Лебедев П.М. Понятие познавательной активности учащихся
и пути ее измерения//Радянська школа, 1970, № 9.
9. Левитас Г.Г. Диктанты по алгебре. 7– 11 классы.
Дидактические материалы. — М.: Илекса, 2005.
10. Левитас Г.Г. Математические диктанты. Геометрия. 7–11
классы. Дидактические материалы. — М.: Илекса, 2006.
11. Леонтьева М.Р., Суворова С.Б. Упражнения в обучении алгебре. — М.:
Просвещение,1985.
12. Манвелов С.Г. Конструирование современного урока
математики. — М.: Просвещение, 2002.
13. Ремчукова И.Б. Математика. 5–8 классы. Игровые технологии
на уроках. — Волгоград: Учитель, 2007.
14. Терский С.Б. Игра. Творчество. Жизнь. — М., 1966.
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
«Рекомендации по проведению и проверки математического диктанта»
Зачем нужны математические диктанты?
Математические диктанты – одна из форма контроля знаний. Но употребляются они всё же редко, так как учащимся трудно воспринимать задания на слух. Одной из важнейших задач в обучении является формирование у детей умения получать информацию на слух, запоминать на слух, обрабатывать и преобразовывать информацию. Из имеющихся в нашем распоряжении органов чувств, воспринимающих информацию, слуховой орган занимает второе место после зрительного, поэтому развивать его возможности у детей крайне важно. Использование математических диктантов помогает в решении этих задач.
Если диктанты проводить часто , то школьники приучаются воспринимать задания на слух. А ценность такого умения очень важна в жизни . Оно приводит к умению слушать собеседника , телепередачу , слушать лекцию.
Математические диктанты проводятся со следующими целями.
Прежде всего, они помогают контролировать знания, умения и навыки учащихся. Проанализировав диктанты, учитель получает достаточно подробную информацию об уровне усвоения пройденного как отдельными учащимися, так и классом в целом. Это позволяет оперативно устранять пробелы в подготовке учащихся.
Однако ещё более важно то, что математические диктанты играют обучающую роль. Выслушав фразу диктанта, учащиеся выполняют определенную работу – записывают алгебраическое выражение выполняют указанное построение. При этом требуется не только воспроизвести заученную формулировку, а творчески подойти к заданию.
Диктанты способствуют и развитию навыков логического мышления, и выработке умения работать с чертежными инструментами.
Известная не шаблонность постановки задачи и ограниченность времени на выполнение задания дисциплинируют учащихся, приучают к собранности, сосредоточенности, целеустремленности.
Проведение математических диктантов способствует и повышению общей грамотности учащихся.В результате систематического использования этой формы работы резко уменьшается количество ошибок в написании математических терминов.
Достоинства и недостатки математических диктантов .
недостатки математических диктантов .
-
не по любой теме можно провести диктант,
-
не все учащиеся способны хорошо воспринимать задания на слух ,
-
с их помощью можно проверить, усвоили ли учащиеся обязательный минимум знаний, но нельзя организовать углубленную проверку.
Но наряду с недостатками можно отметить и достоинства:
-
математические диктанты развивают умение воспринимать задания на слух, а это ведет к умению слушать лекцию и слушать вообще,
-
это альтернатива устного счета, который охватывает не всех учеников,
-
ответы на вопросы диктанта показывают, усвоено ли основное содержание ранее изложенного материала.
Как организовать проведение математического диктанта.
Математические диктанты являются одной из форм письменной работы. В зависимости от текста он проводится 8-15 минут. Поэтому проводить его следует либо в начале урока,либовконце.
Для диктантов лучше использовать листы бумаги (бланки ответов). Можно использовать при проведении диктанта два бланка ответов для того, чтобы ученик мог один бланк сдать учителю, а второй использовать для проверки правильности выполнения работы. Если есть закрытые доски, то можно, либо написать ответы заранее, либо вызвать два ученика к доске и их ответы проверить вместе с классом. Проверка сразу на уроке даёт возможность ещё раз закрепить изученный материал.
Во время проверки напротив правильного ответа ученик ставит «+», напротив ошибочного – «минус», напротив ответа с недочетом – «плюс, минус». Можно при проверке обменяться работами с соседом по парте.
Ó÷èòåëü äîëæåí äèêòîâàòü âîïðîñû ÷åòêî, ãðîìêî, äåëàòü äîñòàòî÷íûå ïàóçû, ÷òîáû äåòè óñïåëè çàïèñàòü îòâåòû. Âîïðîñ íåîáõîäèìî ÷èòàòü ïî äâà ðàçà, êàæäûé âàðèàíò ïî î÷åðåäè. ×òîáû äåòè íå ïóòàëè âàðèàíòû, ìîæíî âûïîëíèòü àóäèîçàïèñü òåêñòà äèêòàíòà, ïåðâûé âàðèàíò – æåíñêèì ãîëîñîì, âòîðîé – ìóæñêèì. Ó÷åíèê ñêîðî âîîáùå ïåðåñòà¸ò ðåàãèðîâàòü íà “íå ñâîé” ãîëîñ: ñïîêîéíî ðàáîòàåò, ïîêà äèêòóåòñÿ çàäàíèå äðóãîãî âàðèàíòà, è íåìåäëåííî âêëþ÷àåòñÿ â ðàáîòó, êàê òîëüêî íà÷èíàåòñÿ ÷òåíèå çàäàíèÿ åãî âàðèàíòà. Èñïîëüçîâàíèå çâóêîçàïèñåé ÷ðåçâû÷àéíî äèñöèïëèíèðóåò êëàññ: ó÷åíèê ïîíèìàåò, ÷òî ìàøèíå âñ¸ ðàâíî, óñïåë ëè îí. Ïîýòîìó ñáîè ñòàíîâÿòñÿ ðåäêèìè. Åñëè íåò òàêîé âîçìîæíîñòè, ìîæíî ñäåëàòü ñëåäóþùåå: êîãäà ó÷èòåëü äèêòóåò âîïðîñû ïåðâîãî âàðèàíòà, îí ñòàíîâèòñÿ ïåðåä ó÷àùèìèñÿ, ñèäÿùèì íà ïåðâîé ïàðòå íà ïåðâîì âàðèàíòå, à êîãäà äèêòóåò âîïðîñû âòîðîãî âàðèàíòà, îí ñòàíîâèòñÿ ïåðåä ó÷àùèìèñÿ, ñèäÿùèìè íà ïåðâîé ïàðòå íà âòîðîì âàðèàíòå, èëè êîãäà ó÷èòåëü äèêòóåò âîïðîñû ïåðâîãî âàðèàíòà, îí äåðæèò â ðóêàõ ëèñò ñ öèôðîé 1, à êîãäà äèêòóåò âîïðîñû âòîðîãî âàðèàíòà, îí äåðæèò â ðóêàõ ëèñò ñ öèôðîé 2 .
Как выставлять оценки за диктанты
Оценки за работу выставляются с учётом числа верно выполненных заданий. Целесообразно перед началом диктанта довести до сведения учащихся нормы оценок. Если в диктанте 10 заданий, оценки могут быть такими:
Например:
|
Число верных ответов |
Оценка |
|
10-9 |
5 |
|
8-6 |
4 |
|
5-3 |
3 |
|
менее 3 |
2 |
Учитель может – исходя из особенностей учащихся класса, может использовать свои подходы к оцениванию результатов диктанта. Иногда вопросы диктанта по значимости и содержанию можно разделить на “лёгкие” и “трудные”. В этом случае есть смысл каждый вопрос оценить в баллах (например, от 1 до 3 баллов), тогда итоговая оценка выставляется по сумме баллов.
Если Вы в своей работе не применяете математические диктанты, значит для этого есть причины: Много времени тратится на подготовительную работу. Проведение диктанта требует от учителя весьма большого напряжения: надо читать в оптимальном темпе тексты заданий, следить за классом, реагировать на практически неизбежные сбои.
ПРИЛОЖЕНИЕ
5 класс.
Диктант по теме: «Признаки делимости на 9 и на3.»
-
Закончите предложение: «Число делится на 9 ( 3 ), если сумма цифр числа…»
-
Пользуясь признаками делимости на 3, определите, делятся ли числа 3213, 78213, 43552, 117 ( 2511, 65031, 45083 450) на 3?
-
Пользуясь признаками делимости на 9 , определите, делятся ли числа 3213, 78213, 43552, 117( 2511, 65031, 45083 450) на 9?
-
4. Какие цифры можно подставить вместо звездочки в запись числа 641 * 2 , чтобы
это число делилось на девять (три)? -
Какие цифры можно подставить вместо звездочки в запись числа 973 * , чтобы это число не было кратно трем (девяти)?
-
Напишите наименьшее четырехзначное число, чтобы это число делилось на девять (три)?
-
Напишите наибольшее трехзначное число, чтобы это число не делилось на девять (три)?
Диктант по теме: «Процент.»
-
Закончите предложение: «Один процент – это…» (« Процентом называется…»).
-
Запишите в виде десятичной дроби 32% (25%).
-
Запишите в процентах десятичную дробь 0,25 (0,32).
-
Сколько процентов число 1 составляет от числа 5 ( 4 от 20)?
-
Как называется один процент центнера ( 0,1% от тонны)?
-
Найдите 25% от 8 км ( 40% от 15 км).
-
Найдите 15%от 25 руб. (30% от 50руб.)
8. В коробке 3 красных и 67 синих карандашей. Сколько % от всех
карандашей составляют синие (красные) карандаши?
Диктант по теме: «Прямоугольный параллелепипед.»
-
Закончите предложение: «У прямоугольного параллелепипеда противоположные грани — …» («Куб — это прямоугольный параллелепипед, …»).
-
Сколько проволоки потребуется для изготовления каркаса куба с ребром 6см ( 8см)?
-
Сколько в прямоугольном параллелепипеде вершин (ребер)?
-
Может ли только одна грань прямоугольного параллелепипеда являться квадратом (не являться квадратом) ?
-
Сколько в прямоугольном параллелепипеде граней(вершин)?
6. Используя размеры прямоугольного параллелепипеда вычислите площадь поверхности:
а = 2 м а = 6 см
в = 5 м в = 5 см
с = 4 м с = 3 см
7. Сколько в прямоугольном параллелепипеде ребер (граней)?
6 класс.
Диктант по теме: «Основное свойство пропорций.»
-
Закончите предложение: «Равенство двух отношений называют…. («Если пропорция верна, то произведение ее крайних членов равно …»).
-
Êàê íàçûâàþòñÿ ÷èñëà õ è ó (à è â ) â ïðîïîðöèè õ:à=â:ó?
-
×èñëî âîñåìíàäöàòü òàê îòíîñèòñÿ ê ÷åòûðåì, êàê äâàäöàòü ñåìü îòíîñèòñÿ ê øåñòè. Çàïèøèòå ïðîïîðöèè
-
Íàéòè íåèçâåñòíûé ÷ëåí ïðîïîðöèè: õ:14=36:7 (õ:12=36:18 ).
-
На участке дороги плиты длинной 6 м заменили новыми длиной 8 м. Сколько нужно новых плит для замены 240 старых?
-
Âåðíà ëè ïðîïîðöèÿ:
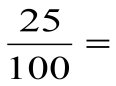
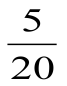 (
( 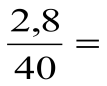
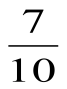 ).
).
7. Три ученика пропололи грядку за 4ч. За сколько часов выполнят
работу два (четыре) ученика?
Диктант по теме: «Умножение.»
-
Óìíîæüòå 3 íà -4 (-5 íà 0).
-
Óìíîæüòå -3 íà 0 (-8 íà -3).
-
Ðåøèòå óðàâíåíèå: õ / 6 = ( -3 ), õ / ( – 4) = 8
-
Ïðîäîëæèòå ïðåäëîæåíèå: «×òîáû óìíîæèòü îòðèöàòåëüíîå ÷èñëî íà ïîëîæèòåëüíîå, íàäî…» («×òîáû ïåðåìíîæèòü äâà îòðèöàòåëüíûõ ÷èñëà, íàäî…»).
-
Âåðíî ëè âûñêàçûâàíèå (îòâåòüòå «äà» èëè «íåò»): «Ïðîèçâåäåíèå äâóõ îòðèöàòåëüíûõ ÷èñåë — ïîëîæèòåëüíîå ÷èñëî» («Ïðîèçâåäåíèå äâóõ öåëûõ ÷èñåë íå ìîæåò áûòü ìåíüøå êàæäîãî èç ìíîæèòåëåé»).
-
Ðåøèòå óðàâíåíèå: ó ( ó – 4) = 0, õ ( õ +5) = 0
-
Âû÷èñëèòå çíà÷åíèå âûðàæåíèÿ ó*(- 16) ïðè ó=3 (11õ ïðè õ= -5 )
7 класс. Геометрия.
Диктант по теме: «Вертикальные углы.»
-
Продолжите предложение: «Два угла называются вертикальными, если…»( «Если стороны одного угла являются продолжением сторон другого угла, то такие углы…» )
-
Чему равен угол, вертикальный углу в 470( 1230 ) ?
-
У двух углов общая вершина, каждый из этих углов равен 600 (400). 0бязательно ли эти углы вертикальные?
-
Может ли при пересечении двух прямых образоваться четыре тупых (острых) угла?
-
Сумма двух углов, образованных при пересечении двух прямых, равна 1500(1700 ). Могут эти углы быть вертикальными?
-
Один из углов, которые получаются при пересечении двух прямых, равен 400 (1200 ). Найдите остальные углы.
-
Один из углов, которые получаются при пересечении двух прямых в 3 раза больше другого. Найдите эти углы.
-
Один из двух углов, который получается при пересечении двух прямых, в 8 раз меньше другого. Найти эти углы.
Диктант по теме: «Прямая и отрезок.»
Первый вариант.
-
Начертите прямую и обозначьте ее буквой а.
-
Отметьте точку D, не лежащую на прямой а.
-
Отметьте точку С, лежащую на прямой а.
-
Запишите символами предложение: «Точка С лежит на прямой b, а точка D не лежит на ней».
-
Даны две прямые а и b , пересекающиеся в точке С, и точка D,
отличная от точки С и лежащая на прямой а.
а) Выполните построение и запишите условие символами.
б) Может ли точка D лежать на прямой b?
6. На прямой b возьмите точки K, L, M. Запишите все образовавшиеся отрезки.
7. На плоскости даны три точки. Сколько прямых можно провести через эти точки так, чтобы на каждой прямой лежали хотя бы две из данных точек? Рассмотрите все возможные случаи и сделайте рисунки.
Второй вариант.
1. Начертите прямую и обозначьте её буквой b.
2. Отметьте точку М ,лежащую на прямой b.
3. Отметьте точку D, не лежащую на прямой b.
4. Используя математические символы запишите предложение : «Точка М лежит на прямой b ,а точка D не лежит на ней».
5. Начертите прямые а и b, пересекающиеся в точке К. На прямой а отметьте точку С , отличную от точки К.
а) Являются ли прямые КС и а различными прямыми ?
б) Может ли прямая b проходить через точку С?
-
На прямой а возьмите точки С, D ,Е. Запишите все образовавшиеся отрезки.
7. Сколько точек пересечения могут иметь три прямые? Рассмотрите все возможные случаи и сделайте соответствующие рисунки.
7 класс. Алгебра.
Диктант по теме: «Умножение многочленов.»
-
Ïðîäîëæèòå ïðåäëîæåíèå: «×òîáû óìíîæèòü ìíîãî÷ëåí íà ìíîãî÷ëåí, íóæíî …» («Â ðåçóëüòàòå óìíîæåíèÿ ìíîãî÷ëåíà íà ìíîãî÷ëåí …»).
-
Âûïîëíèòå äåéñòâèÿ: (3n 2 – 2) (1 – 4 n) =; (a – 2) (3 + a) =; (3 – 4c)(2c 2 – c – 1)=;(ñ + 5) (2c – 1) =.
-
Çàìåíèòå áóêâó «Ì» ìíîãî÷ëåíîì òàê, ÷òîáû ïîëó÷åííîå ðàâåíñòâî áûëî âåðíûì: 5à + Ì = 5à + 3b – 8; ( b2 – bc – Ì = b2 – bc – 7b + 5;)
-
Óìíîæüòå ìíîãî÷ëåí õ – ó ( à + â ) íà ìíîãî÷ëåí õ +ó ( à – â ).
-
Óìíîæüòå ìíîãî÷ëåí õ + ó ( à – â ) íà ìíîãî÷ëåí x 2 – õó + ó 2 (à2+ àâ + b2
-
Ïðåäñòàâüòå â âèäå ñòàíäàðòíîãî ìíîãî÷ëåíà êâàäðàò äâó÷ëåíà õ -2ó , ( à + 5â).
8класс. Алгебра.
Диктант по теме: «Функция у = х2 , ее график.»
|
1. Êàêàÿ èç ôóíêöèé íàçûâàåòñÿ êâàäðàòè÷íîé? Êàê íàçûâàåòñÿ ôóíêöèÿ ó = õ2? 2. Óêàæèòå íîìåð ôóíêöèè, êîòîðàÿ íå ÿâëÿåòñÿ êâàäðàòè÷íîé |
|
|
1 âàðèàíò 1) ó = 5õ2 + 3õ |
2 âàðèàíò 1) ó = 4õ + 3õ2 |
3. Функция задана формулой у = х2 . Чему равно ее значение при х= -5 ( 6 ).
4. Принадлежит ли точка (-3, 9), [( – 4, 15)] графику функции у = х2.
5. Значении функции у = х2 при х = 12 ( -15 ) равно 144 ( 225 ), чему оно будет равно при х = -12 ( 15 ).
6. Аргумент равен -2. Найдите значение квадратичной функции у = х2 + 3х – 5,
(у = 2х2 – х + 4 ).
7. Найдите значение аргумента квадратичной функции у = х2 – 9 (у = х2 – х – 6),
если значение функции равно 0.
Государственное учреждение образования
«Лунинская средняя школа»
ОПИСАНИЕ ОПЫТА ПЕДАГОГИЧЕСКОЙ ДЕЯТЕЛЬНОСТИ
«Математические диктанты
и их роль в учебном процессе»
Левшиц Регина Яковлевна,
учитель математики
+ 375 29 9756817;
e-mail: [email protected]
Актуальность опыта
За последние годы учителя математики провели и проводят большую работу по совершенствованию методики организации учебных занятий. Как известно, отказ от шаблонной схемы урока позволил учителю сделать урок более продуктивным, активизировать учащихся, улучшить индивидуальную работу в процессе обучения.
Работая учителем математики, я увидела, что достаточно большие сложности у учащихся вызывает восприятие информации на слух. Поэтому, я пришла к выводу, что одной из важнейших задач в обучении является формирование у детей умения получать информацию на слух, запоминать на слух, обрабатывать и преобразовывать информацию. Из имеющихся в нашем распоряжении органов чувств, воспринимающих информацию, слуховой орган занимает второе место после зрительного, поэтому развивать его возможности у детей крайне важно. Использование математических диктантов помогает в решении вышеуказанных задач.
Математические диктанты проводятся с двумя целями. Прежде всего, они помогают контролировать знания, умения и навыки учащихся. Проанализировав диктанты, учитель получает достаточно подробную информацию об уровне усвоения пройденного как отдельными учащимися, так и классом в целом. Это позволяет оперативно устранять пробелы в подготовке учащихся. Однако ещё более важно то, что математические диктанты играют обучающую роль. Выслушав фразу диктанта, учащиеся выполняют определенную работу – записывают алгебраическое выражение (равенство, неравенство, формулу), выполняют указанное построение. При этом требуется не только воспроизвести заученную формулировку, а творчески подойти к заданию. Диктанты способствуют и развитию навыков логического мышления, и выработке умения работать с чертежными инструментами.
Известная не шаблонность постановки задачи и ограниченность времени на выполнение задания дисциплинируют учащихся, приучают к собранности, сосредоточенности, целеустремленности.
Проведение математических диктантов способствует и повышению общей грамотности учащихся. Опыт показывает, что в результате систематического использования этой формы работы резко уменьшается количество ошибок в написании математических терминов.
Цели опыта:
-повышение качества знаний учащихся по математике;
-развитие у учащихся способностей воспринимать информацию на слух;
-применение знаний в нестандартных ситуациях;
-воспитание ситуации успеха;
-формировать познавательный интерес к окружающему миру, желание развиваться;
– развивать умения слушать лекцию, речь учителя, товарищей, слушать вообще.
Задачи опыта:
-повышение мотивации учащихся к изучению предмета «Математика»;
-создание условий для творчества учителя и ученика;
-формирование активной позиции ученика на уроке и проявление его творческой индивидуальности;
-создание условий для формирования навыков самоорганизации и самообразования учащихся;
-раскрытие творческого потенциала учащихся, направленного на осознанный выбор профессии, связанной с математикой.
– вовлечь учащихся в познавательный процесс и позволить им осмысленно усваивать учебный материал.
– дать рекомендации по использованию математических диктантов на уроках математики.
Планируемый результат: научить учащегося не просто слушать, а слышать, что говорит учитель. Эффективно тренировать устойчивость внимания детей, оперативную память, умение сосредотачиваться.
Ведущая идея моего опыта предполагает использование математических диктантов с целью создания на уроках математики условий для личного развития учащихся, развития их индивидуальности. Создание педагогических ситуаций общения на уроке позволяет каждому ученику проявить самостоятельность, выборность в способах работы, творчество.
Дидактические функции математических диктантов ориентированы на систему упражнений, в которой ведущими являются приемы структурного анализа и синтеза, обобщения и конкретизации, классификации, аналогии, построения умозаключений, то есть на изучение способов и приемов, которые дают возможность подготовить учеников к более высокому уровню творческой деятельности, к решению более сложных «нестандартных» задач.
Свою задачу как педагога я вижу в том, чтобы сотрудничать с учащимися, воспитывать у них желание к поиску новых знаний, хочу, чтобы учащиеся умели выражать мысли, не используя «штампы» учебника, свободно владели математической терминологией, умели слушать и понимать сказанное учителем.
Я считаю, что математические диктанты наряду с устным опросом, самостоятельными и контрольными работами являются одним из эффективных способов осуществления связи между учителем и учащимися. Проведение математических диктантов способствует развитию логического мышления, повышению их математической культуры, обогащению математической речи. Выполняя задания диктанта, ученики приучаются к организованности, учатся экономить время, формируют привычку быстро сосредотачиваться. При помощи математических диктантов можно проконтролировать не только усвоение учениками изучаемой темы, но и проверить усвоение и закрепление только что поданного материала, диктанты помогут учителю выяснить, овладели ли учащиеся соответствующими умениями и навыками.
Итак, математическим диктантам необходимо отвести надлежащую роль в системе упражнений для усвоения базовых задач. Следует лишь применять их разумно, творчески, учитывая индивидуальные особенности учителя и учеников.
Сущность педагогического опыта
Успешное усвоение знаний, умений и навыков по предмету в целом можно обеспечить, если изучение материала учащимся будет осмысленным, а для этого они должны уметь не просто делать вид, что слушают учителя, а действительно его слушать и слышать то, о чём он говорит. В связи с этим в своей педагогической практике на уроках математики я и использую математические диктанты.
В диктантах можно выделить следующие группы заданий:
– операционные, в которых нужно вычислять, решать задачи, выполнять преобразования и т.п., получив информацию на слух;
– логические, в которых требуется оценить истинность высказывания, для чего необходимо быть внимательным и сосредоточенным, уметь слушать, слышать и анализировать данные;
– направленные на усвоение математической терминологии.
Предложенные задания обеспечивают содержательным учебным материалом этап устной работы в начале урока математики, а также этап подведения итогов в конце урока. Развитию грамотной математической речи способствует наличие в каждом диктанте образцов чтения математических выражений.
Важно подчеркнуть, что в силу специфики математических диктантов (воспринимаемые на слух вопросы; лаконичные ответы) их педагогические возможности ограничены. С их помощью, как правило, можно проверить, усвоили ли учащиеся обязательный минимум знаний, но нельзя организовать углубленную проверку. Поэтому ошибкой было бы противопоставлять диктанты другим формам контроля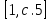 .
.
На уроках в 5 классе я использую графические диктанты. В тексте диктанта обычно приводится 10 решенных заданий, задания записаны на доске. Текст читает учитель. Темп чтения должен быть примерно таким, чтобы средний ученик успевал выполнить задание устно. Учащиеся в тетрадях записывают ответы к примерам при помощи значков _ – «верно», ^– «неверно». Сразу после выполнения диктанта, учитель показывает детям ключ к диктанту и выставляет оценки. Количество правильных ответов соответствует оценке, которую заработал учащийся за выполнение диктанта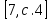 .
.
Например, графический диктант в 5 классе по теме «Повторение курса математики 1-4 класс» выглядит так:
Д-1
-
8
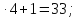
-
2+6
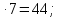
-
(2+6)
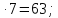
-
805:5=161;
-
2156:7=38;
-
9
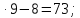
-
72:9+18-7=19;
-
60-38+5
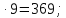
-
(74+7):(30-21)=9;
10) (36+6)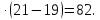
Ключ: _ _ ^ _^_^ ^ _^
Большой интерес для учащихся представляют цифровые диктанты. Суть цифрового диктанта в том, что учитель читает текст только один раз. Каждое предложение в диктанте несёт свою смысловую информацию – это может быть правило, аксиома, теорема, формула и т.д. Высказывание учителя может быть как истинным, так и, заведомо, ложным. Если ученик согласен с произнесённым высказыванием, то он ставит -1, а если нет, то -0. В диктанте приводится, обычно, 7 -8 высказываний. Я, обязательно, провожу математический диктант на том уроке, когда по плану проводится и самостоятельная работа (см. Приложение 3). Учащиеся это знают, готовятся к уроку, повторяют теоретический материал: формулы, определения, формулировки теорем. К проведению самостоятельной работы они уже подходят подготовленными теоретически, что положительно сказывается на отметке за письменную работу и способствует повышению качества знаний.
Вот пример диктанта, проводимого в 5 классе:
Натуральные числа
1.Натуральные числа используют для счёта предметов.
2. Самое первое натуральное число – это нуль.
2. Самое маленькое натуральное число – это 1.
4. Самое большое натуральное число – это десять миллионов.
5. Нельзя назвать самое большое натуральное число.
6. Для каждого натурального числа существует следующее за ним.
7. Два соседние натуральные числа отличаются на единицу.
Ответ: 1.010. 111.
Я применяю цифровые диктанты не только в 5-9 классах, но и в 10-11. Я считаю, что они дисциплинируют учащихся, заставляют старшеклассников систематически повторять формулировки правил и теорем. Начинать применение цифровых диктантов необходимо с первых уроков. Вот как может выглядеть диктант для 10 класса по теме “Аксиомы стереометрии”:
Аксиомы стереометрии
1. Прямые обозначаются одной маленькой буквой латинского алфавита.
2. В пространстве на любой плоскости выполняются все аксиомы и теоремы планиметрии.
3. Основные фигуры в пространстве – это прямые и плоскости.
4.Через любые три точки пространства проходит только одна плоскость.
5. Если две плоскости имеют общую точку, то больше общих точек у них нет .
6. Если два пункта прямой лежат в плоскости , то и вся прямая находится в этой плоскости.
7. Любую аксиому можно доказать.
Ответ: 1.100.010.
Тексты конкретных цифровых диктантов приведены в Приложении 1.
Тексты к цифровым диктантам я составляю сама. Я разрабатываю перечень вопросов по определённой теме курса алгебры или геометрии. На эти вопросы нужно чётко отвечать “да” или “нет”. Потом, в зависимости от цели урока, составляю подборку к конкретному цифровому диктанту (см. Приложение 2).
В течение 2014/2015 учебного года в 8 классе я систематически применяла цифровые диктанты на уроках. В результате, к окончанию учебного года, средний балл за четверть увеличился на 0,6 (см. Приложение 4). Поэтому я считаю, что имеет смысл, наряду с другими формами контроля, применять и математические диктанты.
Конечно, применение диктантов может вызывать определённые трудности:
-
Много времени тратится на подготовительную работу.
-
Проведение диктанта требует от учителя весьма большого напряжения: надо читать в оптимальном темпе тексты заданий, следить за классом, реагировать на практически неизбежные сбои.
-
Если требуются иллюстрации к вопросам, то к уроку нужно готовить дополнительный материал.
Этих трудностей можно избежать, если воспользоваться готовыми математическими диктантами, которые легко найти в интернете.
Созданы уникальные сборники математических диктантов для 5-6 классов и 10-11 классов со звуковым сопровождением и иллюстрацией каждого вопроса. Математический диктант записан в формате, который можно запустить на стандартном проигрывателе Windows, можно вставить в презентацию PowerPoint.
Как организовать проведение математического диктанта.
Для диктантов лучше использовать листы бумаги (бланки ответов, см. Приложение 5). Можно использовать при проведении диктанта два бланка ответов для того, чтобы ученик мог один бланк сдать учителю, а второй использовать для проверки правильности выполнения работы. Если есть закрытые доски, то можно, либо написать ответы заранее, либо вызвать два ученика к доске и их ответы проверить вместе с классом. Опять же можно использовать презентацию. Проверка сразу на уроке даёт возможность ещё раз закрепить изученный материал. Кроме того, выполнив любой вид работы, каждый ребёнок жаждет быстрее узнать результаты своей работы и оценку за неё. Вспомните: после контрольных, самостоятельных работ сколько раз мы слышали эту фразу: «Я уже сдал тетрадь, а покажите, какой там ответ или как это решается?» Если диктант проводится сразу после изучения нового материала, то можно проверить ответы, обсудить результаты.
В заключение хочу сказать, что учащимся сложно воспринимать информацию на слух. Что верно, то верно: учащимся, не привыкшим к математическим диктантам, воспринимать задания на слух действительно трудно. Но если диктанты проводятся часто и систематически, то школьники приучаются выполнять задания на слух, а ценность такого умения неоспорима.
ЛИТЕРАТУРА:
-
В.И. Жохов Математические диктанты в 6 классе // Мнемозина – 2014, с.5-12
-
Е.П. Кузнецова Математика: учебное пособие для 5 класса учреждений общего среднего образования с русским языком обучения: в 2 ч. // – Минск: Национальный институт образования– 2013. –Ч.1
-
Е.П. Кузнецова Математика: учебное пособие для 5 класса учреждений общего среднего образования с русским языком обучения : в 2 ч. // – Минск : Национальный институт образования– 2013. –Ч.2
-
Е.П. Кузнецова Алгебра: учебное пособие для 9 класса учреждений общего среднего образования с русским языком обучения // – Минск: Народная асвета – 2014
-
Л.В. Макарова Уроки-практикумы в системе работы учителя // Математика в школе – 1998 №3, с.13-15
-
П.Б. Ройтман Повышение вычислительной культуры учащихся // Пособие для учителя – 1988, с.8-14
-
В.В. Тарасова Графические диктанты // Математика Первое сентября– 2001 №47, с.4-7
-
В.В. Шлыков Геометрия: учеб. пособие для 10 класса учреждений общего среднего образования с русским языком обучения //Минск: Народная асвета – 2013
Приложение 1
Сравнение натуральных чисел, 5 класс
1. Сравнить два числа- это, значит, определить которое из них больше, а которое меньше.
2. Меньшее число расположено правее на координатном луче, а большее -левее.
3. Самое маленькое натуральное число – это 0.
4. Из двух натуральных чисел меньше то, у которого меньше разрядов.
5. Ноль больше за единицу.
6. Никто не знает самое большое натуральное число.
7. Два натуральные числа с одинаковым количеством разрядов сравнивают поразрядно.
Ответ 1.001.011.
Решение уравнений, 5 класс
1. Уравнение- это равенство, которое содержит букву, значение которой надо найти.
2. Чтобы найти неизвестное слагаемое надо к сумме прибавить известное.
3. У уравнения может быть корень, а может его и не быть.
4. 100 :4 =20.
5. Икс –это буква из белорусского алфавита.
6. При вычитании числа называют: множитель, множитель, произведение.
7. Уравнение 5х=0 не имеет решения.
Ответ: 101.000.0.
Плоские и пространственные фигуры, 7 класс
-
Слово “геометрия” в переводе с греческого означает “плоскость”.
-
Геометрия состоит из двух частей : планиметрия и алгебра.
-
Геометрические фигуры – это треугольник, квадрат, куб, шар.
-
Прямоугольный параллелепипед состоит из 6 кругов.
-
Куб можно назвать многогранником.
-
Большое влияние на развитие геометрии оказали древнегреческие учёные.
-
Точка не имеет размеров.
-
У прямой можно определить длину и ширину.
Ответ: 00.101.110.
Теорема Пифагора, 8 класс
1. Стороны прямоугольного треугольника называются : катет, гипотенуза и гипотенуза.
2. Пифагор – это великий белорусский учёный.
3. Треугольник со сторонами 3,4,5 называется персидским.
4. Катет, который лежит против угла 30 ,равен половине гипотенузы.
,равен половине гипотенузы.
5. В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
6. Гипотенуза короче чем катет.
7. Существует только одно доказательство теоремы Пифагора.
8. Треугольник со сторонами 6,8,10 является прямоуголным.
Ответ: 00.011.001.
Площадь параллелограмма и треугольника, 8 класс
1. Площадь треугольника равна призведению его смежных сторон.
2. Площадь квадрата со стороной 5см равна 20см.
3. Чтобы найти площадь параллелограмма, надо сторону поделить на высоту, проведённую к этой стороне.
4. Площадь треугольника равна половине произведения длины стороны на высоту, прведённую к этой стороне
5. Площадь измеряется в мм, см и м.
6. В прямоугольном треугольнике катет является высотой.
7. Чтобы найти площадь прямоуголного треугольника необходимо катет умножить на катет.
8. Площадь прямоугольного треугольника с катетами 8см і 2см равна 8см .
.
Ответ: 00.010.101.
Основные понятия, 10 класс
-
Планиметрия – это геометрия на плоскости.
-
К пространственным фигурам относятся: пирамида, куб, шар, цилиндр.
-
Основными понятиями стереометрии являются: точка, плоскость, кривая.
-
За изображение параллельных прямых принимают пересекающиеся прямые.
-
Многогранник состоит из многоугольников, которые называют гранями.
-
Параллелепипед – это многогранник, у которого 8 граней.
-
Прямой параллелепипед – это такой параллелепипед, у которого боковые грани прямоугольники.
Ответ : 1.100.101
Аксиомы стереометрии, 10 класс
-
Аксиома – это утверждение, которое необходимо доказать.
-
Основные фигуры стереометрии –это пункт, прямая, плоскость.
-
Плоскости обозначаются маленькими буквами латинского алфавита.
-
Существует пять аксиом, которые выражают основные свойства взаимного расположения пунктов, прямых и плоскостей.
-
Через любые три точки не лежащие на одной прямой, проходит единственая плоскость.
-
Если один пункт прямой лежит в плоскости, то и вся прямая лежит в этой плоскости.
-
Если две плоскости имеют общую точку, то они пересекаются по прямой.
Ответ: 0.100.101
Следствия из аксиом, 10 класс
1.Плоскость в пространстве можно задать при помощи трех точек, которые не лежат на одной прямой.
2. Если точка не лежит на прямой, то эта точка и прямая задают плоскость.
3. Теорема – это утверждение, которое не требует доказательства.
4.Если две плоскости имеют общую точку, то все остальные точки тоже лежат на этой прямой.
5.Через две пересекающиеся прямые нельзя провести плоскость.
6.Три точки всегда лежат в одной плоскости.
7. Аксиома – это маленькая теорема.
Ответ: 1.101.010.
Приложение 2
Перечень вопросов, которые можно использовать для составления цифрового диктанта по теме “Площадь”:
ТЕМА: Площадь.
-
Площадь многоугольника – это величина той части плоскости, которую занимает многоугольник.
-
За единицу измерения площадей принимают только квадрат со стороной 1 см.
-
Площадь многоугольника выражается только положительной величиной.
-
Верно ли, что равные многоугольники имеют равные площади?
-
Если многоугольник разбит на части, то его площадь равна сумме площадей этих частей.
-
Площадь квадрата равна кубу его стороны.
-
Площадь прямоугольника равна половине произведения его противоположных сторон.
-
Площадь прямоугольника равна произведению его соседних сторон.
-
Основание – это одна из сторон параллелограмма.
-
Высота треугольника – это перпендикуляр, опущенный из любой точки противоположной стороны к прямой, содержащей основание.
-
Площадь параллелограмма равна половине произведения высоты на основание.
-
Одну из сторон треугольника называют основанием.
-
Площадь треугольника равна половине произведения его основания на высоту.
-
Площадь прямоугольного треугольника равна произведению его катетов.
-
Если основания двух треугольников равны, то их площади относятся как высоты.
-
Если угол одного треугольника равен углу другого треугольника, то площади этих треугольников относятся как произведения сторон, заключающих равные углы.
-
Высота трапеции – это перпендикуляр, проведенный к боковой стороне.
-
Площадь трапеции равна произведению полусуммы ее оснований на высоту.
-
Площадь ромба равна произведению его диагоналей.
-
Площадь ромба можно найти по той же формуле, что и параллелограмм.
-
Теорема Пифагора используется в любых треугольниках.
-
В прямоугольном треугольнике квадрат любого катета равен сумме квадратов гипотенузы и другого катета.
-
Пифагоровы треугольники те, у которых длины сторон выражаются целыми числами.
-
Треугольник со сторонами 3, 4, 5 называют египетским треугольником.
КЛЮЧ:
«1» – 1; 3; 4; 5; 8; 9; 10; 12; 13; 16; 18; 20; 23; 24
«0» – 2; 6; 7; 11; 14; 15; 17; 19; 21; 22;
Приложение 3
Разложение квадратного трёхчлена на линейные множители
Цели:
-
Формировать представление о квадратном трёхчлене и его разложении на линейные множители;
-
Организовать деятельность, направленную на практическое применение теоремы о разложении квадратного трёхчлена на линейные множители;
-
Создать условия для развития познавательных умений – применить знания, сделать вывод, работать с учебником;
-
Способствовать воспитанию устойчивого интереса к предмету, положительного отношения к учению.
Форма урока: лекционно-практическая
Подготовительный этап: запись на доске даты, темы, устных упражнений, таблица настроения.
Ход урока
1. Проверка домашнего задания – устно;
2. Считаем устно;
3. Ответ на вопрос: что необходимо на уроке?
4. Математический диктант;
5. Самостоятельная работа;
6. Физкультминутка ;
7. Объяснение нового материала;
8. Практическое применение полученных знаний;
9. Подведение итогов урока, рефлексия.
1. Проверка домашнего задания – устно.
2. Считаем устно: назвать коэфициенты квадратного уравнения
1)5х2 +2х -4 =0; 2)-х+9х2 =0; 3)7х2 -4=0; 4) 8х2 =3х+2; 5) 0=9х2 =3х-2.
3. Ответ на вопрос: что необходимо на уроке?
Решите устно примеры и скажите, что на сегодняшнем уроке вам необходимо?
1.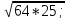 в) 40; т) 0,4.
в) 40; т) 0,4.
2. х2 =25; р) 5; н) 5;-5;
3. 7х2 =0; и) 0; о) -7;
4. 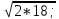 м) 6; е) -6;
м) 6; е) -6;
5. 4х2 =16. н) 4; -4; а)2; -2.
6. х2 =625 и) 25;-25; р) 15; -15;
7. 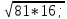 а) 18; е) 36.
а) 18; е) 36.
Ответ: внимание.
4. Математический диктант:
Ответы на вопросы диктанта проверяются сразу после его написания и обсуждаются всем классом.
1. Уравнение ах+в =0 называется квадратным.
2. Если D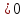 , то уравнение имеет 2 корня.
, то уравнение имеет 2 корня.
3. Дискриминант позволяет определить количество корней квадратного уравнения.
4. ах2 =0- неполное квадратное уравнение.
5. Если х2 =25, то х=5-единственное решение уравнения.
6. Квадратное уравнение является уравнением второй степени с одним неизвестным.
7. Старший коэффициент уравнения х2 +3х +4 =0 равен 0.
Ответ: 011.101.0
5. Самостоятельная работа
1.Решить уравнение: а) х2 =16; б) х2 -25=0.
2. Указать количество корней уравнения: х2 +х-3=0.
3. Решить уравнение: а) 2 х2 +3х – 5=0; б) 8 х2+2х-3=0.
4. Разложить число 58 на два множителя так ,чтобы их сумма была равна 31.
5. Решить уравнение : х2+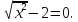
6. Физкультминутка:
Уравнение является : а) квадратным; б) линейным.
3х-5=0; 2х=3 ; х+1=0; 13 х2-11х=0; 1- х2 =0; 2 х2 =11; 5х-11=0; 6 х2-х4 +9=0; х3 +5х-17=0.
если “да”-руки вытянуть вперед;
если “нет” – хлопок в ладоши над головой.
7. Объяснение нового материала:
1. Дать определение квадратного трёхчлена, дискриминанта квадратного трёхчлена, корня квадратного трёхчлена.
2. Рассмотреть теорему о разложении квадратного трехчлена на линейные множитнли.
3. Разобрать решение примеров 1,2 из учебника.
8. Практическое применение полученных знаний
Решение на доске № 5.72, 5.73( нечётные)
9. Подведение итогов урока,рефлексия.
Таблица настроения
10. Домашнее задание № 5.72(2,4,6,8)
Приложение 4
Приложение 5
Бланк ответов.
Ф.И. ученика _______________________________
Класс__________ Дата_____________
|
№ задания |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Ответ |
18
