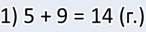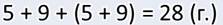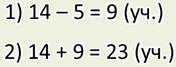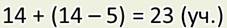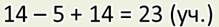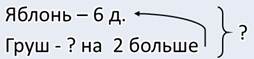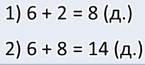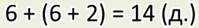Как составить математическое выражение к задаче

Чтобы составить задачу, которая приведёт к этим выражениям, например, с двумя неизвестными, нужно сначала поиграться с числами.

Берём две машины. Одна движется со скоростью 60 км/час, а вторая на 20 быстрее 80 км/час. У этих скоростей оптимальный общий множитель 48. Увеличиваем его в 10 раз получится 480 км.

Первой машине потребуется 8 часов, для преодоления этого расстояния, а второй 6 на 2 часа меньше. 480 км – это известное расстояние. Неизвестные величины — это скорость и время.

Напускаем туману. Определяемся, что скорость 1-й машины на 20 км/час меньше второй машины. Но вторая выехала на 2 часа позже и догнала первую на расстоянии 480 км. Задача готова. Нужно хитро задать вопрос. Например: Через какое время 2-я машина будет на расстоянии в 100 км от первой после из встречи.

Чтобы решить такую задачу потребуется составлять выражение. Принимать за “х” скорость первой или второй машины до встречи. За “у” время первой или второй машины также до встречи. Или обходиться одним “х”, а можно и просто обойтись числами. Но это не для составителя. Составитель оперирует известными ему числами, а “решала” составляет выражения.

Конечно это интересно. Составить хитрую математическую задачку, и чтобы её не быстро решили. А выдёргивать с интернета любой может. Я составляю сама. Бывает до взрыва мозга, а не такую легкотню, как написала выше. Например вот эта: про курагу, чернослив и инжир.

Инфоурок

›

Начальные классы

›Другие методич. материалы›Памятка”Как составить выражение к задаче”.

Памятка”Как составить выражение к задаче”.

–
Плюс!….. Плююююс! Ты где?

Привет,
Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор
с царицей Математикой.

–
Здравствуй, Минус. Как это я забыл! Включаю.

–
Здравствуйте, Дорогие Плюс и Минус!

Сегодня
я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю
вам устроить соревнование – кто сможет их решить быстрее, но при этом, конечно,
правильно.

–
Да, царица, мы Вас внимательно слушаем.

–
Мы очень внимательно слушаем.

–
Ну что же, приступим. Итак, вот первая задача:

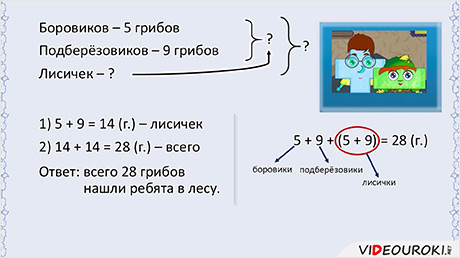
Ребята
в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек
столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли
ребята в лесу?

Ну,
Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас
смотрят, попробуют решить эту задачу.

–
Всё, я готов! Могу даже объяснить, как я решал эту задачу.

Нам
даны два числа: количество боровиков – их 5, и количество подберёзовиков – их 9.
Но неизвестно количество лисичек. Про них сказано, что их столько, сколько
боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.

В
задаче два неизвестных, значит, задача составная, то есть в ней не одно
действие, а два. В первом действии я узнаю, сколько лисичек.

А
так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то
общее количество грибов я нашёл вот так:

Ответ:
всего 28 грибов нашли ребята в лесу.

–
А я решал задачу другим способом. Вот посмотрите:

–
Да, Минус, чувствуется, что сложение – это не твой конёк. Конечно, задачу ты
решил правильно. Но при этом у тебя получилось не два, а три действия. При этом
первое и второе действия повторяются. Для этой задачи такой способ записи не
очень удобен. Хотя некоторые задачи действительно удобно записывать не по
действиям, как это сделал я, а числовым выражением. А вот, кстати,
царица Математика уже даёт нам новую задачу.

–
Тихо, Плюс, слушаем!

–
На уроке физкультуры присутствовало 14 мальчиков. А девочек – на 5 меньше.
Сколько всего учащихся присутствовало на уроке физкультуры?

–
Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

–
Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но
неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

А
в задаче надо узнать количество девочек, и только потом – сколько всего детей. Я
так и узнавал:

Ответ:
всего 23 учащихся присутствовало на уроке физкультуры.

–
А вот я записал решение этой задачи по-другому:

И
ещё можно вот так:

–
Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же
ты решил задачу другим способом – записью выражения.

–
В первой задаче он действительно был неудобен, а в этой – очень даже удобен.
Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть
те же действия, что и в твоём, и даже в той же последовательности.

Ты
первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я
записал в скобках. А то, что записано в скобках, всегда выполняется первым.

Во
втором действии к 14 прибавляем полученное в первом действии число 9. А в этой
записи слагаемые меняются местами – к 9 прибавляется 14.

И
получается, что это не другой способ решения задачи – ведь все действия
одинаковы, а другой способ записи решения. Ты решал по действиям, а я –
выражением. Способ решения одинаковый, а способ записи этого решения –
разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и
пояснений. Поэтому такая запись помогает экономить и время, и бумагу.

–
Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты
прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую
запись задачи выражением.

Ваше
величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

–
Ну что же, слушайте:

В
моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш
растёт в моём саду?

Я
хочу видеть у вас оба способа записи решения – и по действиям, и выражением.

–
Хорошо.

–
Хорошо.

–
Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш,
необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2
больше, чем яблонь.

Получаем:

Значит,
в саду царицы растёт 14 яблонь и груш.

А
вот как получилась запись выражением:

Сначала
я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я
выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при
записи по действиям – 14.

–
Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

–
Можно я начну первый.

Записывать
решение задачи можно по действиям и выражением.

–
При записи по действиям мы пишем номер действия и пояснения к каждому действию,
а при записи выражением только пояснение к значению записанного выражения.

–
При записи выражения первое действие часто записываем в скобках, и конечно, не
забываем записать ответ задачи.

–
Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете
пойти погулять в мой сад и полакомиться яблоками и грушами.

–
Ура!!!

Числовые и буквенные выражения

О чем эта статья:

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Числовые выражения: что это

Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.

Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.

Например:

• 23 + 5 = 28
• 5 — 2 = 3
• 52 * 3 = 156
• 28 : 7 = 4

Это простые числовые выражения.

Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:

• (5 * 3) — (5 * 2) = 5
• 6 : (7 — 4) = 2
• (45 + 45) : 9 = 10
• 11 * (5 * 5) = 275

Это сложные числовые выражения.

Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».

Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.

Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.

11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.

При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:

• Сначала выполняется действие, записанное в скобках.
• Затем выполняется деление/умножение.
• В последнюю очередь выполняется сложение/вычитание.

Пример 1. Найдите значение числового выражения: 3 * (2 + 8) — 4

Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)

(6 + 7) * (13 + 2) = 195

Часто бывает нужно сравнить два числовых выражения.

Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.

Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2

Сначала находим значение первого выражения:

14 больше 4
14 > 4
6 + 8 > 2 * 2

Пример 2. Сравните следующие числовые выражения:
5 * (12 — 2) — 7 и (115 + 9) — (7 — 3)

Находим значение первого выражения, соблюдая порядок выполнения арифметических действий:

43 меньше 120
43

Буквенные выражения

Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.

В буквенном выражение есть цифры, знаки арифметических действия и буквы.

Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.

Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.

У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:

• Сначала следует прочитать его полностью.
• Затем оно записывается.
• Третьим шагом идет подстановка значения неизвестного в выражение.
• А затем производится вычисление, согласно очередности выполнения арифметических действий.

Пример 1. Найдите значение выражения: 5 + x.

1. Читаем: найдите сумму числа 5 и x.
2. Подставляем вместо неизвестного x число 4.
3. Вычисляем: 5 + 4 = 9.

Пример 2. Найдите значение выражения: (4 + a) * (2 + x).

1. Читаем: найдите произведение суммы числа 4 и а и суммы числа 2 и x.
2. Подставляем вместо неизвестного a число 2.
3. Вычисляем 4 + 2 = 6.
4. Подставляем вместо неизвестного x число 5.
5. Вычисляем 2 + 5 = 10.
6. Находим произведение 6 * 10 = 60.
7. Записываем результат: (4 + 2) * (2 + 5) = 60.

Выражения с переменными

Переменная — это значение буквы в буквенном выражении.

• Например, в выражении x + a — 8
  x — переменная
  a — переменная

Если вместо переменных подставить числа, то буквенное выражение x + a — 8 станет числовым выражением. Вот так:

• подставляем вместо переменной x число 5, а вместо переменной a — число 10, получаем 5 + 10 — 8.

Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.

После подстановки значения переменных находим значение x + a — 8 = 5 + 10 — 8 = 7.

Часто можно встретить буквенные выражения, записанные следующим образом:
5x — 4a

Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.

5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a

Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.

Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.

Задание раз.

1. Сумма 6 и a.
2. Разность 8 и x.
3. Сумма x — 2 и 6
4. Разность 15 и x — y
5. Сумма 45 + 5 и 12 — 6

Задание два.

Составьте буквенное выражение:

Сумма разности b и 345 и суммы 180 и x.

Ответ: (b — 345) + (180 + x).

Задание три.
Составьте буквенное выражение:
Разность разности 30 и y и разности a и b.
Ответ: (30 — y) — (a — b).

Задание четыре.
Составьте выражение для решения задачи и найдите его значение.
Ролл «Калифорния» стоит 480 рублей — это на 40 рублей меньше, чем ролл «Филадельфия». Сколько будут стоить оба ролла?
Как решаем:
Калифорния — 480 рублей.
Филадельфия — 480 + 40.
Калифорния + Филадельфия = ?
480 + (480 + 40).
Мы помним, что выполнение арифметических действий в числовом выражении имеет строгую последовательность. Сначала — действие в скобках:
480 + 520 = 1 000.

Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.

Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?

Маша — 150 видео.
Лена — 150 + 13 видео.
Маша + Лена = ? видео.

150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.

Ответ: Маша и Лена посмотрели всего 313 видео.

Задание шесть.
Вычислите:
(500 + 300) : a — 15,
при условии, что a = 10.

Подставляем число 10 (значение переменной) вместо переменной
(500 + 300) : 10 — 15

Затем выполняем сначала арифметическое действие в скобках: 500 + 300 = 800.
Затем выполняем деление 800 : 10 = 80.
Выполняем вычитание 80 — 15 = 65.

Ответ: (500 + 300) : 10 — 15 = 65.

Задание семь.
Вычислите:
(270 — 120) * (x — 10),
при условии, что x = 45.

Как решаем: подставляем число 45 (значение переменной) вместо переменной x
(270 — 120) * (45 — 10).

Затем выполняем сначала арифметическое действие в скобках: 270 — 120 = 150.
Выполняем арифметическое действие во вторых скобках: 45 — 10 = 35.
Затем выполняем умножение 150 * 35 = 5 250

Ответ: (270 — 120) * (45 — 10) = 5 250.

Задание восемь.
Вычислите:
(50 * x) — (3 * y)
при условии, что x = 2; y = 10

Подставляем число 2 вместо переменной x
(50 * 2) — (3 * y).

Подставляем число 10 вместо переменной y
(50 * 2) — (3 * 10).

Затем выполняем сначала арифметическое действие в скобках: 50 * 2 = 100.
Выполняем арифметическое действие во вторых скобках: 3 * 10 = 30.
Затем выполняем вычитание 100 — 30 = 70

Источник

Запись решения задачи выражением

Урок 15. Математика 2 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Запись решения задачи выражением»

— Плюс. Плююююс! Ты где?

Привет, Плюс! Чего так долго? Включай скорее компьютер. Сейчас у нас будет в скайпе разговор с царицей Математикой.

— Здравствуй, Минус. Как это я забыл! Включаю.

— Здравствуйте, Дорогие Плюс и Минус!

Сегодня я хочу проверить, как вы умеете решать задачи. Я дам несколько задач и предлагаю вам устроить соревнование — кто сможет их решить быстрее, но при этом, конечно, правильно.

— Да, царица, мы Вас внимательно слушаем.

— Мы очень внимательно слушаем.

— Ну что же, приступим. Итак, вот первая задача:

Ребята в лесу собирали грибы. Они нашли 5 боровиков, 9 подберёзовиков, а лисичек столько, сколько боровиков и подберёзовиков вместе. Сколько всего грибов нашли ребята в лесу?

Ну, Плюс и Минус, я жду вашего решения. Может быть и ребята, которые на вас смотрят, попробуют решить эту задачу.

— Всё, я готов! Могу даже объяснить, как я решал эту задачу.

Нам даны два числа: количество боровиков — их 5, и количество подберёзовиков — их 9. Но неизвестно количество лисичек. Про них сказано, что их столько, сколько боровиков и подберёзовиков вместе. А ещё неизвестно, сколько всего грибов.

В задаче два неизвестных, значит, задача составная, то есть в ней не одно действие, а два. В первом действии я узнаю, сколько лисичек.

А так как боровиков и подберёзовиков вместе столько же, сколько и лисичек, то общее количество грибов я нашёл вот так:

Ответ: всего 28 грибов нашли ребята в лесу.

— А я решал задачу другим способом. Вот посмотрите:

— Да, Минус, чувствуется, что сложение — это не твой конёк. Конечно, задачу ты решил правильно. Но при этом у тебя получилось не два, а три действия. При этом первое и второе действия повторяются. Для этой задачи такой способ записи не очень удобен. Хотя некоторые задачи действительно удобно записывать не по действиям, как это сделал я, а числовым выражением. А вот, кстати, царица Математика уже даёт нам новую задачу.

— Тихо, Плюс, слушаем!

— На уроке физкультуры присутствовало 14 мальчиков. А девочек — на 5 меньше. Сколько всего учащихся присутствовало на уроке физкультуры?

— Ну что же, начинаем решать. Ребята, и вы попробуйте с нами решать!

— Я уже решил. Вот посмотрите, в задаче известно количество мальчиков, Их 14. Но неизвестно количество девочек. Ведь сказано, что их на 5 меньше, чем мальчиков.

А в задаче надо узнать количество девочек, и только потом — сколько всего детей. Я так и узнавал:

Ответ: всего 23 учащихся присутствовало на уроке физкультуры.

— А вот я записал решение этой задачи по-другому:

И ещё можно вот так:

— Но ведь ты мне только что говорил, что такой способ решения неудобен! Зачем же ты решил задачу другим способом — записью выражения.

— В первой задаче он действительно был неудобен, а в этой — очень даже удобен. Во-первых, это не другой способ решения задачи. Посмотри, в моём решении есть те же действия, что и в твоём, и даже в той же последовательности.

Ты первым действием узнаёшь, сколько девочек, и я тоже. Ведь это действие я записал в скобках. А то, что записано в скобках, всегда выполняется первым.

Во втором действии к 14 прибавляем полученное в первом действии число 9. А в этой записи слагаемые меняются местами — к 9 прибавляется 14.

И получается, что это не другой способ решения задачи — ведь все действия одинаковы, а другой способ записи решения. Ты решал по действиям, а я — выражением. Способ решения одинаковый, а способ записи этого решения — разный. Но посмотри, моя запись получилась короче. В ней нет номеров действий и пояснений. Поэтому такая запись помогает экономить и время, и бумагу.

— Ты, Плюс, как всегда. Все тебе надо складывать да экономить. Хотя, наверное, ты прав. Эта запись действительно удобная. А хотелось бы и мне попробовать такую запись задачи выражением.

Ваше величество, госпожа королева. Не могли бы Вы задать нам ещё одну задачу?

— Ну что же, слушайте:

В моём саду растёт 6 яблонь. А груш на 2больше. Сколько всего яблонь и груш растёт в моём саду?

Я хочу видеть у вас оба способа записи решения — и по действиям, и выражением.

— Ну вот что у меня получилось. Прежде, чем узнать, сколько всего яблонь и груш, необходимо узнать, сколько груш. Ведь нам это неизвестно. Сказано, что их на 2 больше, чем яблонь.

Значит, в саду царицы растёт 14 яблонь и груш.

А вот как получилась запись выражением:

Сначала я нашёл, количество груш. Но, так как это действие стоит не в начале записи, я выделил его скобками. А потом нашёл сумму чисел. Ответ такой же, как и при записи по действиям — 14.

— Хорошо. Задача решена, верно. А теперь расскажите, чему вы научились.

— Можно я начну первый.

Записывать решение задачи можно по действиям и выражением.

— При записи по действиям мы пишем номер действия и пояснения к каждому действию, а при записи выражением только пояснение к значению записанного выражения.

— При записи выражения первое действие часто записываем в скобках, и конечно, не забываем записать ответ задачи.

— Ну что же, молодцы, Плюс и Минус. Вы справились с заданием. И сейчас вы можете пойти погулять в мой сад и полакомиться яблоками и грушами.

Источник

Математика, 2 класс

Урок № 22. Решение текстовых задач. Запись решения выражением

Перечень вопросов, рассматриваемых в теме:

– Что такое встречное движение, расстояние?

– Как выполнять схематический чертёж к задачам на движение?

Глоссарий по теме:

Задача – это упражнение, которое выполняется посредством умозаключения, вычисления.

Выражение – формула, выражающая какие–либо математические отношения.

Расстояние – пространственный промежуток, разделяющий два объекта, отрезок пути.

Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):

1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова, Г.В.Бельтюкова и др. – 8-е изд. – М.: Просвещение, 2017. – с.64.
2. Математика. Рабочая тетрадь. 2 класс. Учебное пособие для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М.А.Бантова – 6-е изд., дораб. – М.: Просвещение, 2016. – с.46.
3. Для тех, кто любит математику. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 9-е изд. – М.: Просвещение, 2014. – с.28.
4. Математика. Проверочные работы. Пособие для учащихся общеобразовательных организаций. М. И. Моро, С. И. Волкова – 2-е изд. – М.: Просвещение, 2014. – с.30,31.

Теоретический материал для самостоятельного изучения

Расстояние – это путь, который прошёл какой-либо объект.

РАССТОЯНИЕ – промежуток в пространстве, разделяющий два объекта

Измеряя расстояние, мы будем использовать сокращённые записи.

1 МЕТР – 1м

1 ДЕЦИМЕТР – 1дм

1 САНТИМЕТР – 1 см

1 МИЛЛИМЕТР – 1 мм

Сегодня на уроке мы будем решать новые задачи – задачи на движение.

Длина аллеи 80 м. Два мальчика пошли навстречу друг другу. Один прошёл до встречи 45 м. Сколько прошёл до встречи другой мальчик?

Сделаем к задаче схематический чертёж.

Начертим отрезок, обозначающий длину всей дорожки, или расстояние между концами дорожки. Синей стрелкой обозначим длину дорожки. Укажем – 80 метров.

Мальчики шли навстречу друг другу с разных сторон дорожки. На чертеже это будем обозначать стрелками, которые показывают направление движения каждого мальчика.

Место встречи мальчиков будем обозначать флажком.

Теперь обозначим, что один мальчик прошёл до встречи 45 метров, а другой –

неизвестно. Поставим знак вопроса.

? м

45 м

Так выглядит схематический чертёж к задаче. По чертежу видно, что нам необходимо найти разность отрезков, выполнить вычитание.

Чтобы узнать, сколько метров до встречи прошёл второй мальчик, вычтем из длины всей дорожки длину пути, который прошёл первый мальчик.

80 – 45 = 35 (м) прошёл второй мальчик.

Второй мальчик прошёл до встречи 35 метров.

Решим вторую задачу:

Девочки измеряли длину дорожки с двух концов, идя навстречу друг другу. Одна девочка прошла до встречи 30 м, другая на 4 метра меньше. Какой длины была дорожка?

Сделаем схематический чертёж к задаче.

Итак, нам надо найти длину всей дорожки. Для этого мы должны знать, сколько метров прошла каждая девочка. Мы знаем, сколько прошла первая девочка – 30 метров. А сколько прошла вторая девочка, нам надо узнать.

Будем решать задачу в два действия. Запишем первое действие:

1) 30 – 4 = 26 (м) прошла вторая девочка.

Вторая девочка прошла до встречи двадцать шесть метров.

Теперь можем ответить на вопрос задачи. Запишем второе действие:

2) 30 + 26 = 56 (м) длина дорожки.

Длина всей дорожки была 56 метров.

Вывод: Для решения задач на движение обычно выполняют чертёж, в котором стрелками показывают направление движения объектов. Движение может быть встречным или в противоположных направлениях.

Тренировочные задания.

1.Подберите схематический чертёж к задаче

Красная Шапочка отправилась в гости к бабушке. До дома бабушки нужно пройти 100 метров. Красная Шапочка уже прошла 70 метров. Сколько ей осталось пройти?

Правильные ответы:

Вторая схема.

2.Соедините каждый чертёж с карточкой, на которой записано соответствующее решение задачи.

30 – 20

30 + 20

70 – 45

Правильные ответы:

70 – 45

30 + 20

30 – 20