Как составить математическое выражение закона действия масс

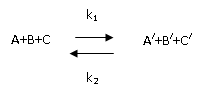
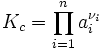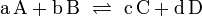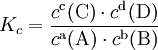Зависимость скорости химической реакции от концентрации реагирующих веществ выражает закон действующих масс:

при постоянной температуре скорость гомогенной химической реакции прямо пропорциональна произведению концентраций реагирующих веществ.

Для химической реакции A + Б = В, протекающей между двумя веществами в жидкости или газе в одну стадию, этот закон можно выразить в математической форме:

ʋ = k ∙ c(A) ∙ c(Б).

В этом выражении ʋ — скорость реакции, которая измеряется в моль/(дм³ · с); c(A) и c(Б) — концентрация вещества, соответственно А и Б; k — коэффициент пропорциональности, который называют константой скорости реакции. Значение этой константы зависит от природы реагирующих веществ, температуры, присутствия катализатора, но не зависит от концентрации реагирующих веществ.

В уравнение закона действующих масс включаются концентрации веществ, которые находятся только в гомогенной (однородной) среде (в смеси газов, в растворе).

Физический смысл закона действующих масс следует из очевидных рассуждений.

Для того чтобы между молекулами А и Б произошла химическая реакция, они должны столкнуться. Следовательно, скорость реакции пропорциональна вероятности столкновений молекул. В свою очередь, вероятность столкновения зависит от концентрации молекул, и она выше в том случае, если концентрация молекул больше. Поэтому скорость реакции зависит от концентрации веществ. Это подтверждается экспериментально.

В обобщённом виде математическое выражение закона действующих масс принимает следующую форму:

                                                ʋ = k · c^a(A) · c^b(Б).                                        (1)

В этом выражении показатели степеней a и b называют порядком химической реакции соответственно по веществу А и веществу Б. Сумма a + b представляет собой общий порядок реакции.

Порядок любой реакции устанавливается из экспериментальных данных зависимости скорости химической реакции от концентрации реагирующих веществ. Это связано с тем, что в большинстве химических реакций для получения продукта недостаточно столкновения двух частиц или распада одной частицы. Вероятность одновременного столкновения трёх молекул (ионов или атомов) ничтожно мала. Тем более невероятно столкновение большего числа частиц. Поэтому реакции имеют сложный механизм и протекают в несколько стадий. Каждая стадия — это простая, элементарная, реакция, осуществляемая столкновением двух частиц либо распадом одной частицы.

Так, реакция взаимодействия метана с хлором

включает ряд элементарных стадий. Сначала под действием света молекула хлора распадается на два атома хлора, каждый из которых имеет неспаренный электрон, то есть образуются два радикала:

Далее радикал Cl∙ взаимодействует с молекулой метана c образованием молекулы хлороводорода и метил-радикала CH₃∙:

Cl∙ + CH₄ → CH₃∙ + HCl,

который реагирует со следующей молекулой хлора, образуя хлорметан и новый хлор-радикал:

CH₃∙ + Cl₂ → CH₃Cl + Cl∙.

Такая цепочка превращений может многократно повторяться, пока она не оборвётся взаимодействием двух радикалов друг с другом.

Каждая из стадий реакции протекает со своей скоростью, а общая скорость определяется скоростью самой медленной реакции. Эту реакцию называют лимитирующей. Только для одностадийных (элементарных) реакций порядок реакции совпадает с коэффициентами в уравнении реакции. Например, для одностадийной реакции

,

или ,

её скорость можно выразить уравнением:

ʋ = c(NO₂) · c(NO₂).

Порядок этой реакции равен 2.

Если реагирующие вещества находятся в разных фазах, то реакция протекает только на поверхности раздела фаз. Поэтому концентрацию твёрдого вещества или нерастворимой в реакционной среде жидкости (например, жира, нерастворимого в водном растворе щёлочи при получении мыла) не включают в уравнение закона действующих масс. Например, для реакции

A_(г) + Б_(тв) → АБ

концентрация твёрдого вещества Б не входит в уравнение закона действующих масс, а площадь соприкосновения реагентов уже включена в значение k:

ʋ = k · с(А).

Рассмотрим на примере, как, используя закон действующих масс, можно предсказывать изменение скорости химической реакции при изменении концентрации реагирующих веществ.

При постоянной температуре скорость гомогенной химической реакции прямо пропорциональна произведению концентраций реагирующих веществ.

Константа скорости химической реакции не зависит от концентрации реагентов, но зависит от их природы и температуры, при которой протекает реакция.

Вопросы, задания, задачи

1. Назовите факторы, влияющие на скорость химических реакций. Почему скорость химических реакций изменяется в процессе их протекания?

2. От каких факторов зависит константа скорости химической реакции? Изменяется ли значение константы скорости в процессе реакции?

3. Почему в процессе протекания химической реакции её скорость изменяется?

4. Объясните, почему большинство химических реакций протекает постадийно. Каков смысл понятия «элементарная химическая реакция»?

5. Запишите выражение закона действующих масс для реакций:

• a) ;
• б) ;
• в) .

6. Во сколько раз изменится скорость гомогенной реакции:

• а) A → …;
• б) 2A → …;
• в) A + Б → …

при увеличении молярной концентрации реагента А в 6 раз?

7. Скорость элементарной химической реакции

А_(г) + 2Б_(г) = В_(г)

при концентрации вещества А, равной 0,2 моль/дм³, и концентрации вещества Б, равной 0,3 моль/дм³, составляет 3,6 ∙ 10^–5 моль/(дм³ ∙ с). Определите константу скорости этой реакции. В каких единицах она выражается?

8. В химическом реакторе объёмом 100 дм³ между газообразными веществами А и Б происходит химическая реакция

А + Б = АБ,

для которой уравнение закона действующих масс имеет вид:

ʋ = k ∙ c(A) ∙ c(Б).

В каком случае реакция протекает быстрее:

• а) количество вещества А равно 1 моль, а вещества Б — 2 моль;
• б) количество вещества А равно 2 моль, а вещества Б — 4 моль.

Как соотносятся скорости реакции в случаях а) и б)?

9. Как должна измениться (увеличиться или уменьшиться) скорость химической реакции, протекающей по уравнению

NaHCO₃ + HCl = NaCl + H₂O + CO₂↑,

если разбавить растворы исходных веществ? Обоснуйте свой ответ.

10. В химический реактор объёмом 50 дм³ ввели газообразное вещество А количеством 20 моль и газообразное вещество Б количеством 40 моль, между которыми произошла элементарная химическая реакция

А + 2Б = В.

Определите соотношение скоростей этой реакции в начальный момент и момент, к которому прореагировала половина вещества А.

Самоконтроль

1. Согласно закону действующих масс, скорость гомогенной химической реакции прямо пропорциональна:

• а) массам реагирующих веществ;
• б) массам образующихся веществ;
• в) массе катализатора;
• г) концентрациям реагирующих веществ.

2. Константа скорости реакции зависит от:

• а) природы реагирующих веществ;
• б) температуры;
• в) присутствия катализатора;
• г) концентрации реагирующих веществ.

3. При уменьшении массы порошка железа вдвое константа скорости реакции :

• а) не изменится;
• б) уменьшится вдвое;
• в) увеличится вдвое;
• г) уменьшится пропорционально изменению площади поверхности порошка.

4. Формула ʋ = k · с(А) может описывать зависимость скорости от концентрации реагирующего вещества для реакции:

• a) C_(тв) + O_2(г) = CO_2(г);
• б) BaO_(тв) + SO_2(г) = BaSO_3(тв);
• в) Zn_(тв) + H₂SO_4(р-р) = ZnSO_4(р-р) + H_2(г);
• г) N₂O_4(г) NO_2(г) + NO_2(г).

5. Увеличение в 3 раза концентрации вещества NO₂ в реакции NO₂ + NO₂ N₂O₄ приведёт к увеличению скорости в:

• а) 3 раза;
• б) 6 раз;
• в) 9 раз;
• г) 12 раз.

Математическим
выражением закона термодинамики для
равновесия химических процессов
(реакций) является закон
действующих масс, устанавливающий
связь между равновесными концентрациями
или парциальными давлениями компонентов
реакции
Действующими
массами называются:

–
парциальные равновесные давления
реагентов ();

–
равновесные концентрации веществ ();

–
числа молей ();

–
мольные доли ().

ЗДМ
при
равновесии отношение произведений
концентраций конечных продуктов, взятых
в степенях, равных их стехиометрическим
коэффициентам, к такому же произведению
концентраций исходных веществ в обратимой
реакции при данной температуре есть
величина постоянная, называемая
константой равновесия химической
реакции (К).

,

где
С_C,
С_D,
C_A,
С_В
– равновесие концентрации веществ-участников
реакции; а, в, с, d
– стехиометрические коэффициенты.

Для гомогенной газовой реакции

Рассмотрим
ЗДМ для газовой реакции

Условия:

–
все реагенты-участники реакции – газы;

–
все газы идеальные, для которых справедливо
уравнение зависимости изменения энергии
Гиббса от давления
(*);

– процесс протекает
при постоянной температуре, т.е. Т=const.

В этом случае можно
записать:

С
учетом (*), получаем:

,

или

при
условии равновесия получаем:

или
иначе,
(давления
равновесные!!!)

Например,
.
Запись константы равновесия для данной
реакции будет иметь вид:.
Единицы измерения константы равновесия
зависят от того какие единицы измерения
используются при определении равновесных
давлений, в данном случае это могут быть

Если
изменить парциальное давление, например,
–
константа равновесия останется величиной
постоянной, т.к. изменяться давления
других реагентов.

Кр
зависит от (природы вещества, температуры).

В
записи константы равновесия, как уже
отмечалось, помимо парциальных равновесных
давлений могут участвовать числа молей
компонентов-участников реакции, мольные
доли, равновесные концентрации веществ.
Тогда,
.
При этом константы равновесия при записи
помечаются соответствующими индексами:
Кр, Кс, Кn,
Кх. Эти величины связаны между собой
соотношениями:

Кр=Кс(RT)^n=Кх(Р
_общ)^n=Kn(RT/V)^n,

где
Р _общ –
общее давление равновесной газовой
смеси, V – объем газовой смеси, n
–
,n
– разность числа молей конечных и исходных
газообразных участников реакции.

Например , 2СО +
О₂ = 2СО₂

H₂
+ J₂ = 2HJ

Таким
образом, если n
в уравнении равно 0, то численное значение
константы равновесия Кр, Кс, Кn, и Кх
совпадают.

Если
величина Кр:

Кр=1
в этом случае в системе наблюдается
равновесие

Кр>1
реакция идет прямо

Кр<1
реакция протекает в обратном направлении

Кр>>1
реакция идет в прямом направлении и она
необратима

Кр<<1
реакция идет в обратном направлении и
она необратима.

Для гетерогенной реакции

Гетерогенными
называются реакции, в которых реагенты
находятся в разных агрегатных состояниях.
При этом для таких реакций с участием
газов, когда не образуются твердые и
жидкие растворы, в записи закона
действующих масс
участвуют только равновесные действующие
массы газообразных компонентов. Например,

3Fe_(тв)
+ СН_4(газ) =
Fe₃C_(тв)
+ 2Н_2(газ)

условия
равновесия G
= 0 выполняются если

из
которого следует

.

При Т=const правая
часть этого уравнения – величина
постоянная, а выражение
равно константе равновесия данной
гетерогенной реакции

где
–
равновесные парциальные давления газов.

Для реакции СО₂
+ СО 
2СО константа равновесия Кр и Кс запишутся
так

,

.

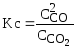
Если же вещества,
участвующие в реакции растворяются
друг в друге или в каких-то инертных
растворителях, роль которых в
пирометаллургических процессах могут
играть шлаковые или металлические фазы,
то в константу равновесия записываются
их равновесные концентрации или
термодинамические активности.

Например,

[FeO]+[C]=[Fe]+CO

Квадратная скобка
[ ] указывает, что данное вещество

является
компонентом металлической фазы

_Fe,
_FeO,
_C
– термодинамические
активности Fe, FeO и C в расплаве (жидкой
стали).

Для реакции

(MgCl₂)+CaC₂=(CaCl₂)+Mg_пар+2C_тв

.

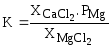
Круглые скобки (
) указывают, что MgCl₂
и CaCl₂
являются компонентами шлаковой
(солевой) фазы.
,–
мольные доли CaCl₂
и MgCl₂ в
солевом расплаве.

Константа равновесия
зависит от температуры и природы веществ.

1. влияние
   температуры на константу равновесия

Практически любой технологический
процесс проводится в условиях, отличных
от стандартных (Т
= 298,16 К,
Р = 1 атм). Поэтому
при проведении реальных термодинамических
расчетов необходимо знать температурную
зависимость (закон изменения) константы
равновесия. Это позволит установить
влияние температуры на изменение
парциальных давлений (или концентраций)
компонентов и определить направление
смещения равновесия изучаемой реакции
или процесса.

и
называется уравнением
изобары Вант-Гоффа.
Аналогично можно получить уравнение
зависимости константы равновесия от
температуры для изохорических условий.
В этом случае уравнение
изохоры Вант-Гоффа
имеет вид:
.
Так как чаще всего металлургические
процессы протекают при постоянном
давлении, то чаще всего для анализа
зависимости используютуравнение
изобары.
Проанализируем уравнение изобары,
преобразовав его в интегральную форму.
Если расчеты производятся для небольшого
интервала температур, то тепловой эффект
реакции H
в уравнении изобары можно считать
величиной постоянной. Тогда это уравнение
в интегральной форме будет иметь вид:

.
(**)

Согласно
уравнению, влияние температуры на
константу равновесия обуславливаетсязнаком
теплового эффекта.
При положительных значениях (т.е.
протекает эндотермическая реакция) положительно
и константа равновесия возрастает с
повышением температуры. В случае
экзотермической реакции – наоборот.
Это говорит о том, что при
изменении температуры давления
(концентрации) компонентов при равновесии
изменяются.
Данный общий принцип, отражающий влияние
различных факторов на положение
равновесия, носит название принципа
смещения равновесий
или принципа
Ле-Шателье,
с которым мы уже встречались при
рассмотрении вопросов подвижности
равновесия:

если
на систему, находящуюся в устойчивом
равновесии, воздействовать извне,
изменяя какое-нибудь из условий,
определяющих положение равновесия, то
в системе усилится то из направлений
процесса, течение которого ослабляет
влияние произведенного воздействия, и
положение равновесия сместится в том
же направлении.

Из уравнения Вант-Гоффа следует, что
для определения температурной зависимости
константы равновесия любой химической
реакции необходимо знать температурную
зависимость теплового эффекта
Степень влияния
температуры на константу равновесия
реакции зависит от абсолютного значения
теплового эффекта: чем больше Н,
тем сильнее влияет температура на Кр.

На рис. представлена
температурная зависимость константы
равновесия реакции в координатах lnKp –
1/T в виде прямых линий.

Определив Кр
реакции при двух температурах (Т₁
и Т₂),
можно рассчитать тепловой эффект реакции
(Н),
решая совместно уравнение (**) для двух
температур:

,

.

И вычитая одно
уравнение из другого, получим

,
откуда.

По уравнению
по известной величине К при какой-то из
двух температур Т₁или
Т₂ и
Н_{реакции}
можно найти К при другой температуре
или.

1. уравнение
   изотермы вант-гоффа

Химическая
термодинамика позволяет расчетным
путем определить полезную работу
химической реакции через изменение
функции F
и G
и тем самым судить о направлении
химического процесса.

Вант-Гофф вывел
уравнение изотермы реакции, которое
носит его имя и связывает изменение
функций F
и G
с константой равновесия реакции и
парциальными давлениями или концентрациями
веществ, участвующих в реакции.

Уравнение
изотермы Вант-Гоффа имеет вид:

для
реакций, протекающих в изохорных
условиях:

для
реакций, протекающих в изобарных
условиях:

где
F
– изменение энергии Гельмгольца реакции,
G
– изменение энергии Гиббса реакции, Кр,
Кс – константы равновесия химических
реакций, П – константа неравновесия
химических реакций.

Проанализируем
уравнение изотермы Вант-Гоффа для
изобарных процессов как наиболее часто
встречающиеся на практике.

Возьмем реакцию,
где все участники – газы:

аА + bB = dD + rR

Для реакции,
протекающей в изобарных условиях,
уравнение изотермы примет вид

,
где
– парциальные давления газов в исходной
реакционной смеси, P_D, P_R,
P_A, P_B
– парциальные
давления газов в равновесной газовой
смеси.

Поскольку
=
Кр, то при Т=const эта величина является
величиной постоянной, а константа
неравновесия П=– величина переменная, зависящая от
значений исходных давлений реагентов.

Если<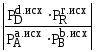
Кр, тоG<0,
реакция протекает в прямом направлении;

>
Кр, то G>0,
реакция протекает в обратном направлении;

=
Кр, то G=0,
система находится в состоянии равновесия.

1. методы
   определения константы равновесия.
   стандартное химическое сродство

Существует несколько
методов определения константы равновесия:

1. Константа
   равновесия может быть определена из
   опытных данных. Можно провести
   термодинамический процесс (осуществить
   химическую реакцию) и измерить равновесные
   давления реагентов. Путь сложный, но
   иногда используется.

2. Константу
   равновесия определяют по величинам
   стандартных электродных потенциалов
   и ЭДС гальванического элемента.

3. Определяют
   по величине произведения растворимости.

4. Так
   называемый энтропийный метод: для этого
   используют уравнение нормального
   химического сродства.

Химическим
сродством называется способность
различных веществ реагировать друг с
другом.

Количественной
мерой химического сродства является
изменение функций F
и G
для процессов (реакций), протекающих
при постоянных V и Т и Р и Т, соответственно.

Величины F
и G
не зависят от пути процесса, а зависят
только от свойств реагирующих веществ
и их термодинамического состояния; знак
F
и G
определяют направление процесса; при
равновесии эти функции имеют минимальное
значение, а их изменение (уменьшение)
при переходе из химически неравновесного
в равновесное состояние равно максимальной
работе обратимого процесса и, наконец,
эти величины (F
и G)
можно рассчитать с помощью уравнений
изотермы Вант-Гоффа.

Для того, чтобы в
одинаковых условиях сравнивать
устойчивость химических соединений,
реакционную способность веществ ввели
понятие стандартного
химического сродства.

Стандартным
химическим сродством называется
сродство, которое имеет место, когда
исходные парциальные давления или
концентрации каждого вещества,
принимающего участие в реакции, равны
единице.

В этом случае член
lnП в уравнениях изотермы становится
равным 0 и выражение для стандартного
химического сродства имеет вид

F^o=
-RTlnKc; G^o=
-RTlnKp.

Сравнивая G^o
(F^o)
разных реакций, можно оценить степень
удаления смесей веществ при Р_i=1
или С_i=1
от равновесного состояния.

Для оценки
химического сродства чаще пользуются
величиной G^o
реакции,
протекающей при стандартной температуре
298 К. Величины
образования веществ являются критерием
прочности химических соединений.
Вещество тем прочнее, чем изменение
стандартной энергии Гиббса его образования
величина более отрицательна.

Например:
=
-527934 Дж,

=
-362615 Дж.

Более прочным из
двух оксидов является ВаО, т.к.
более отрицательна, чем.

Если требуется
оценить
вещества при температуре, отличной от
стандартной, то можно воспользоваться
уравнением температурной зависимости,
приводимыми в ряде справочников.

Например:
=
-232160 + 45,31Т,
Дж/моль

= -144210 + 72,21
Т, Дж/ моль.

Расчет стандартного
химического сродства при температурах
Т, отличных от стандартной, осуществляется
с учетом температурных зависимостей
изменения функций Н
и S
химических реакций по уравнению

.

Для оценки
химического сродства при заданных
давлениях (концентрациях) участников
реакций, отличных от стандартных
значений, пользуются уравнением изотермы
Вант-Гоффа,

Таким образом,
величина константы равновесия может
быть определена по уравнению:
.
В свою очередьможет быть рассчитано:

1. С
   использованием
   _{(образования)}
   веществ,
   участвующих в реакции по уравнению

1. С
   использованием таблиц стандартных
   термодинамических характеристик
   веществ по уравнению Гиббса – Гельмгольца

.

Одновременно
уравнение Гиббса-Гельмгольца показывает,
как влияет температура на
.

Возможно несколько
ситуаций:

Условия протекания экзотермических
реакций: H<0.При этом возможность условия
самопроизвольного протекания реакции
определяется знакомG
= H
– TS

Рассмотрим, как меняется знак Gпри варьировании величиныS.

а)
ЕслиS>0,тоG
= H
– TS<0.Процесс идет самопроизвольно. Например,
протекание реакции
в
этом случаеS>0,
т.к. процесс протекает с увеличением
числа молей газообразных веществ
(вспомним, что ).
Следовательно, при H<0
и S>0
значение G
приобретает более отрицательное значение
и реакция идет самопроизвольно в прямом
направлении (рис. 14).

б) Если S=0,тоG
= H
– TS<0.Процесс идет самопроизвольно.

в) Если S<0,тоG
= H
– TS
может иметь различные знаки в
зависимости от абсолютной величины
TS:

• ..
  При этомG<0.
  Процесс идет самопроизвольно.

• При этомG=0.
  Состояние равновесия.

• При
  этомG>0.
  Процесс не идет слева направо.
  Например, протекание реакции
  в
  этом случаеS<0,
  т.к. процесс протекает с уменьшением
  числа молей газообразных веществ,
  следовательно, G
  приобретает более положительное
  значение и реакция самопроизвольно в
  прямом направлении
  не идет (рис.15).

Таким образом, экзотермические реакции
термодинамически запрещены только при
значительном уменьшении энтропии,
например, в некоторых процессах
структурирования, образования
дополнительных связей и т.д.

Условия протекания эндотермических
реакций (H>0).При этом возможность условия
самопроизвольного протекания реакции
определяется знакомG
= H
– TS

Как и в предыдущем случае, рассмотрим,
как меняется знак Gпри варьировании величиныS.

а) Если S>0,тоG
= H
– TS
может иметь различные знаки в
зависимости от абсолютной величины
TS:

• H < TS.
  При этомG<0.
  Процесс идет самопроизвольно.

• H = TS.При этомG=0.
  Состояние равновесия.

• H > TS.
  При этомG>0.
  Процесс не идет самопроизвольно
  слева направо.

б) Если S=0,
то G
= H
– TS>0.
Процесс не идет самопроизвольно
слева направо.

в) Если S<0,тоG
= H
– TS
>0. Процесс не идет самопроизвольно
слева направо.

Кинетика гомогенных процессов

Кинетикой химических реакций
называетсяучение
о скорости их протекания, механизме
химического взаимодействия
и зависимости их от различных факторов
(например,
таких как, концентрация реагирующих
веществ, температура, влияние катализаторов
и т.п.).Эти
вопросы представляют большой практический
и теоретический интерес
и являются центральными при изучении
данного раздела. Известно, что разные
реакции совершаются с самыми различными
скоростями. Некоторые, такие как
реакции разложения взрывчатых веществ,
заканчиваются в доли секунды; другие
продолжаются минутами, часами, днями,
а третьи, например, некоторые
процессы, совершающиеся в земной коре,
растягиваются на десятки, сотни и тысячи
лет. Кроме того, большое различие
существует не только в скоростях разных
реакций, нои скорость
какой-нибудь данной реакции может очень
значительно меняться в зависимости
от условий, в которых она происходит.

При практическом использовании от
скорости реакции, применяемой в
каком-нибудь производственном процессе,
будет зависеть производительность
аппарата и, следовательно, количество
вырабатываемой продукции. Поэтому очень
важно знать, с какой скоростью будет
совершаться та или
иная реакция в данных условиях и как
нужно изменить эти условия, чтобы
она протекала с желательной скоростью.
Теоретическое значение вопросов кинетики
заключаетсяв том,
что изучение их позволяет выяснить
многие важные детали химических
процессов и глубже понять механизм
взаимодействия веществ.

Физическая химия изучает системы с
позиций термодинамики и кинетики.
Сравнивая начальные и конечные состояния
системы, термодинамика предсказывает
возможность протекания реакции, а не
действительный переход безотносительно
ко времени, за которое он может произойти.
Несовпадение, в большинстве случаев,
возможного и действительного объясняют
двумя причинами:

1. Результат термодинамического анализа
(G)
является вероятностным, так как в него
входит вероятностная функция – энтропия.

2. Переход системы из одного состояния
в другое связан зачастую с преодолением
энергетического барьера, тем
большего, чем ниже температура перехода.

Таким образом, термодинамический анализ,
позволяющий оценить возможность
процесса, должен быть дополнен
кинетическим, который позволяет оценить
скорость процесса, возможность которого
доказана термодинамическим расчетом!!!

зависимость скорости реакции от
концентрации реагирующих веществ

При количественном
рассмотрении скорость
химической реакции принято характеризовать
изменением концентрации
реагирующих веществ в единицу времени.
По существу безразлично,
концентрацию какого из реагирующих
веществ рассматривать.
Концентрации
исходных веществ будут уменьшаться, а
получаемых — возрастать.Обычно скорость химической реакции при
постоянных внешних условиях не остается
постоянной, а изменяется во времени.
Это изменение можно отобразить с помощью
графической зависимости, приведенной
на рисунке. Очевидно, что по мере
расходования исходных веществ скорость
протекания процесса уменьшается. В
связи с этим численные значения скорости
реакции будут различными в определенный
промежуток или интервал времени.

Различают
среднюю скоростьреакции иистинную
скорость.

При определении средней скоростиреакции за данный промежуток времени
оперируют конечным изменением концентрации,
относящимся к промежутку времени:

.

Далее мы будем оперировать только
истинными скоростямиреакции,
которые определяются отношением
изменения концентрации к бесконечно
малому промежутку времени, или иначе,
как производная от концентрации по
времени:

.

Скорость
реакции всегда считается положительной.
Отношение
и производнаямогут быть как положительными, так и
отрицательными в зависимости от того,
представляет ли«с» концентрацию
одного из исходных или одного из продуктов
реакции. Допустим, протекает химическая
реакция:,
согласно рисунку, криваяс_в,
характеризующая изменение концентрации
исходного вещества В, убывает во времени,
таким образом,и,
следовательно, чтобы скорость была
величиной положительной необходимо в
правой части уравнения брать знак
«минус». Если же«с» представляет
концентрацию одного из получаемых
веществ, криваяс_с, то
наблюдается противоположная картина,
концентрация получаемого вещества
возрастает во времени, таким образом,и.
Следовательно, в правой части уравнения
нужно брать знак «плюс».

Допустим, рассматриваемая нами реакция
обусловлена взаимодействием только
газообразных веществ. Очевидно, что
необходимым условием, определяющим
возможность взаимодействия между двумя
молекулами, является их взаимное
столкновение, т.е. сближение до
такого расстояния, при котором электроны
и атомы одной
молекулы попадают в сферу действия
электрических полей, возбуждаемых
частицами другой молекулы. Только при
таких условиях могут произойти те
переходы электронов и перегруппировки
атомов, в результате которых образуются
новые молекулы.

Конечно, не каждое
столкновение приводит к такому
взаимодействию. Число столкновений,
испытываемых каждой молекулойгаза
в обычных условиях, очень велико и
достигает десятков миллиардов в
секунду. Отсюда следует, что в реакциях,
протекающихс
конечными скоростями (а не мгновенно),
к взаимодействию приводит только
какая-то малая часть столкновений.Возможность и
вероятность химического взаимодействия
будет зависеть от состояния молекул
(полярность) в момент столкновения и от
длительности самого столкновения.

Независимо от того, какие именно
столкновения сопровождаются
взаимодействием, можно принять, что при
постоянных внешних условиях некоторая
постоянная доля
(часть) столкновений является эффективной
для взаимодействия. Поэтому чем
больше будет происходить столкновений,тем, при прочих
равных условиях, больше будет число
случаев взаимодействия, а,
следовательно, и количество образовавшегося
нового вещества, т. е. тем скорее будет
протекать реакция.

Число столкновений
должно увеличиваться с повышением
концентрации
реагирующих веществ. Для наиболее
простых по кинетике гомогенных
реакций опыт показывает, что зависимость
скорости процесса от концентраций
реагентов, в общем виде выражают в формеосновного постулата кинетики–ОПК

при постоянной
температуре скорость данной реакции
прямо пропорциональна
произведению концентраций реагирующих
веществ, причем каждая из концентраций
участвует в степени, в простейших случаях
равной коэффициенту перед формулой
данного вещества в уравнении реакции.

Этим правилом и определяется влияние
концентрации на скорость реакции. Оно
было выражено (в несколько иной форме)
впервые Гульдбергом и Вааге (1867).Его также называютзаконом действия
масс, как и закон, выражающий
константу равновесия реакции, они тесно
связаны между собой. Для газовых реакций
это правило является строгим только в
пределах применимости законов идеальных
газов. Оно применимо также и к реакциям
в разбавленных растворах (строго только
для бесконечно разбавленных растворов).
В математической форме в применении,
например, к реакции

оно выражается в виде:

,

где k- коэффициент
пропорциональности, который для каждой
конкретной, т.е. данной реакции приT=constявляется
величиной постоянной и называетсяконстантой скорости реакции.
Ончисленно равен скорости реакции в
условиях, когда концентрация каждого
из исходных веществ равна единице.

кинетическая классификация химических
реакций

В отношении
кинетики химические реакции классифицируют
по двум признакам:

– по признаку
молекулярности
реакции;

–
по признаку порядка
реакции.

Молекулярность реакции
определяется числом молекул,
одновременным взаимодействием между
которыми осуществляется акт
химического превращения.

По этому признаку реакции разделяются
на:

– одномолекулярные (или мономолекулярные);

– двухмолекулярные (или бимолекулярные);

– трехмолекулярные (или тримолекулярные).

Можно говорить и о
более высокой молекулярности, но в
действительности одновременное
столкновение трех молекул уже является
очень маловероятным и трехмолекулярные
реакции встречаются
крайне редко. Реакций же более высокой
молекулярности практически неизвестно.

К одномолекулярнымреакциям относятся
некоторые реакции разложения молекул
и внутримолекулярных перегруппировок.
Например, газовая реакция:

.

Для простых (элементарных) одномолекулярных
реакций зависимость скорости реакции
от концентрации описывается уравнением:

,

где С –
концентрация исходного вещества. Или
иначе можно записать, что

.

Здесь kимеет размерность
обратного времени, выражается в с^-1,
мин^-1или других соответствующих
единицах.

К двухмолекулярнымреакциям относятся
такие, реализация которых происходит
при столкновении двух молекул различного
или одинакового типа:

или.

Для таких реакций:

,

где
и–
концентрации исходных веществ.

Для таких
реакций:

.

В частном
случае, когда
,
имеем:

.

Для
двухмолекулярных реакций константа
скорости kимеет размерностьили.

По аналогии, к трехмолекулярным реакциям
относят реакции, в которых для
взаимодействия необходимо одновременное
столкновение трех молекул одного или
различного видов. В общем случае уравнение
скорости простых (элементарных)
трехмолекулярных реакций имеет вид:

.

Примером трехмолекулярной реакции
рассмотренная ранее реакция
.

Порядок реакцииопределяется
по виду уравнения, выражающего зависимость
скорости реакции от концентрации
реагирующих веществ.Порядок реакции
равен сумме
показателей степеней концентраций в
уравнении, выражающем
зависимость скорости реакции от
концентраций реагирующих веществ.
Реакции разделяются на реакции:

– первого порядка,

– второго порядка,

– третьего порядка (реакции более
высоких порядков не встречаются).

Кроме того, известны так называемые
реакции нулевого порядка и некоторые
реакции, порядок которых выражаетсядробным числом. Таким образом,
порядок химической реакции изменяется
от 0 до 3, может принимать дробное значение!

Прежде такое распределение считали
совпадающим с делением по признаку
молекулярности, т.е. все
одномолекулярные реакции являются
реакциями первого порядка, и наоборот,
а все двухмолекулярные реакции
являются реакциями второго порядка, и
наоборот. Однако экспериментальные
исследования внесли свои коррективы.

Скорость химической реакции определяется
совокупностью огромного числа элементарных
актов взаимодействия между молекулами
(или атомами, или ионами). Акты эти могут
быть одинаковыми
(в простых реакциях) или различными,
происходящими параллельно или
последовательно.

Кроме того, в
некоторых случаях один из компонентов
реакции присутствует в таком большом
избытке, что расход его в реакции
практически не отражается на его
концентрации. В результате кинетика
этой реакции описывается, например,
уравнениями кинетики
реакции первого порядка, хотя реакция
является по существу бимолекулярной.

Реакциями нулевого
порядки называют процессы, в которых
скорость процессасохраняется
постоянной во времени. Это встречается
в некоторых гетерогенных системах(например, если
применять эфир, малорастворимый в воде,
и взять его в избытке, чтобы в системе
присутствовал эфирный слой, то расход
эфира будет постоянно восполняться из
эфирного слоя. Таким образом, концентрация
его в водном слое будет постоянной и,
следовательно, постоянной будет скорость
процесса
).

Реакции первого порядка

Вспомним уравнение
(уравнение для
одномолекулярных реакций), разделим
переменные и получим,
интегрируя его, получаем:

.

Обозначая через С₀начальную
концентрацию приτ=0,
определяем постоянную интегрирования.
Отсюда

или,

где
–
концентрация вещества к моменту времениτ.

Для кинетики реакций первого порядка
характерно, что в левой части уравнения
содержится только отношение концентраций.Изменение обеих концентраций в одинаковое
число раз не меняет промежутка времениτ. Следовательно, если в
одном опыте концентрация черезnминут станет вдвое меньше начальной,
то и в других опытах (при других начальных
концентрациях) в данной реакции она заnминут уменьшится тоже
в два раза. Это означает, что за одинаковые
промежутки времени прореагирует
одинаковая доля взятого количества
исходного вещества. Например, если за
первые 10 минут в реакцию вступило 5 % от
взятого количества вещества, то за
следующие 10 минут прореагируют 5 % от
оставшихся 95 % исходного вещества.

Для характеристики скорости реакций
первого порядка наряду с константой
скорости часто пользуются величиной,
называемой периодом полураспада
τ_1/2, равным промежутку
времени, в течение которого реагирует
половина взятого количества вещества.
Из уравненияили,
принимая, что,
следует, что,
следовательно,или для константы равновесия имеем.
Если решить данное уравнение для периода
полураспада, то имеем,
из данного уравнения следует, что период
полураспада в реакциях первого порядка
не зависит от начальной концентрации
реагирующего вещества и определяется
только константой скорости реакцииk.
Принимая во внимание, что,
получаем, что.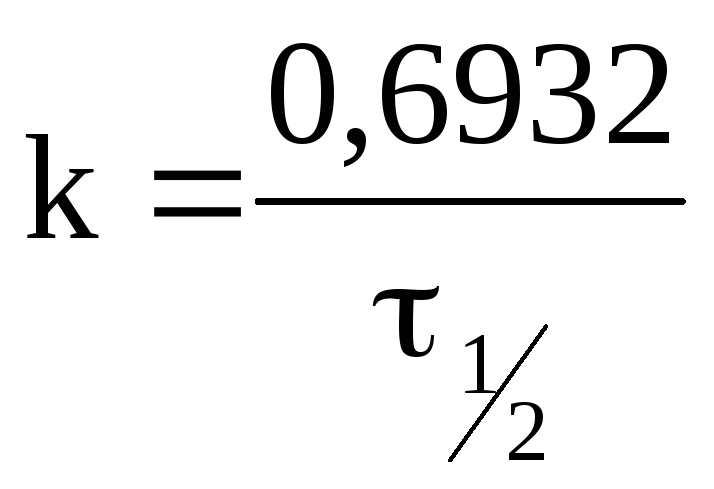
Это соотношение показывает, чтоконстанта
скорости реакции первого порядка обратно
пропорциональна периоду полураспада.

Зависимость константы скорости только
от отношения концентраций позволяет
заменять их при расчете другими
пропорциональными величинами. Часто
вместо концентраций используют отношение
количеств вещества, а в газовых реакциях
– отношение давлений.

Реакции второго порядка

Рассмотрим реакцию, протекающую по
уравнению:
.
Скорость реакции можно выразить по
основному закону кинетики через
концентрации С_Аи С_В.

.

В данном уравнении три переменные. Для
исключения одной из них выразим С_Аи С_Вчерез количество прореагировавших
веществ за время τ:

При
;

При
;,
где х – количество молей А и В,
прореагировавших к моменту времени τ.

В этом случае основной постулат кинетики:
.

После интегрирования в пределах от
до τ , отдо х, получим:

.

Решив данное
уравнение относительно k,
найдем:

.

Из данного уравнения следует, что
размерность kв уравнении
скорости второго порядка
[время^-1×концентрация^-1].
Следовательно, числовые значения
константы скорости в реакциях второго
порядка будут зависеть от того, в каких
единицах выражаются время и концентрация
реагирующих веществ.

Из данного уравнения всегда можно
определить количество прореагировавшего
х:

.

Если начальные концентрации
,
уравнениепринимает вид:

или,

или.

При
записи в общем виде индексы у концентраций
реагентов можно опуститьили.

Интегрируя в пределах от
до τ, получим:

.

В этом случае константу скорости можно
определить:

.

Данное выражение можно представить в
виде:

или.

Отложив на оси ординат
,
а на оси абсцисс время τ, получим прямую,
тангенс угла которой равенk.

Период
полураспада реакции второго порядкаопределяется по формуле:

.

В отличие
от реакции первого порядка время
половинного превращения для реакции
второго порядка обратно пропорционально
С₀.

Реакции
n-го порядка

Как мы уже знаем, сложные реакции типа
могут протекать поn-му
порядку, при этомnможет
быть целым или дробным числом. Скорость
реакцииn-го порядкапри
равных начальных концентрацияхреагирующих веществ выражается
уравнением:

Разделив
переменные, получаем:

.

Интегрируя
данное выражение в пределах от
до τ, и от С₀до С_τ, получаем

.

Данное уравнение можно представить
относительно С_τ, что позволяет
рассчитать концентрацию реагента в
любой момент времени, если известныkиn:

.

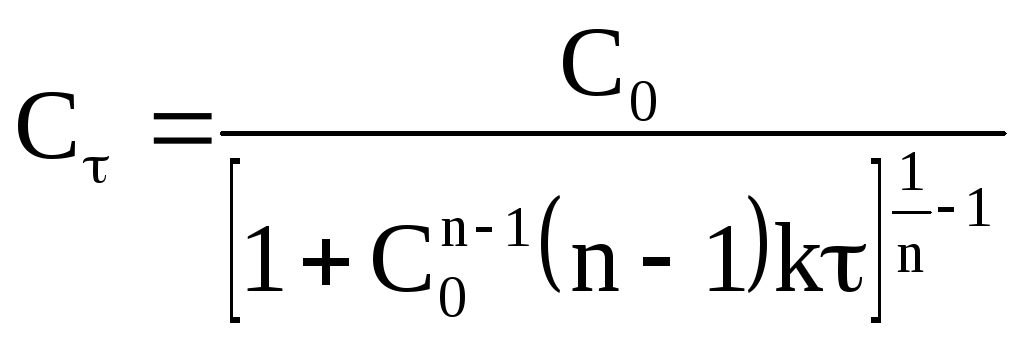
Уравнение для времени половинного
превращения можно получить, как и ранее,
приняв, что
:

.

Представленные уравнения можно
использовать для реакций n-го
порядка (кроме первого!).

n	Кинетическое уравнение	Вид зависимости	Уравнения для расчета
k
0
1
2
3

определение порядка реакции

Для определения порядка реакции
используются различные методы.

Метод подстановки (аналитический):
заключается в подстановке
экспериментальных данных в уравнения
кинетики реакции нулевого, первого,
второго и третьего порядков и определении,
которое из этих уравнений приводит к
постоянному значению константы скорости
реакции (можно считать, что уравнение
описывает процесс, если рассчитанные
по нему значения констант колеблются
около какой-то средней величины и
отклонения от среднего лежат в пределах
возможных погрешностей определения).
Если ни одно из уравнений не дает такого
результата, то реакция является сложной.

Графический метод: заключается
в построении графика, выражающего
зависимость различных функций концентрации
от времени, и определении, для которой
из них зависимость выражается прямой
линией. Так для реакции первого порядка
прямая получается в системе координат;
для реакции второго порядка;
для реакции третьего порядка.
По тангенсу угла наклона прямой можно
определить константу скорости реакции.
Для реакции нулевого порядка зависимость
концентрации от времени дает прямые,
параллельные оси абсцисс.

Метод определения периода полураспада:
основан на определении промежутка
времени, в течение которого концентрации
(или количества) исходных веществ
уменьшаются ровно в два раза. Проводя
реакцию при двух различных начальных
концентрацияхии определяя для обоих случаев периоды
полураспадаиможно определить порядок реакции.

Вспомним
уравнение для периода полураспада
реакции n-го порядка:

.

Получим
и,
разделив одно уравнение на другое,
получим:

.

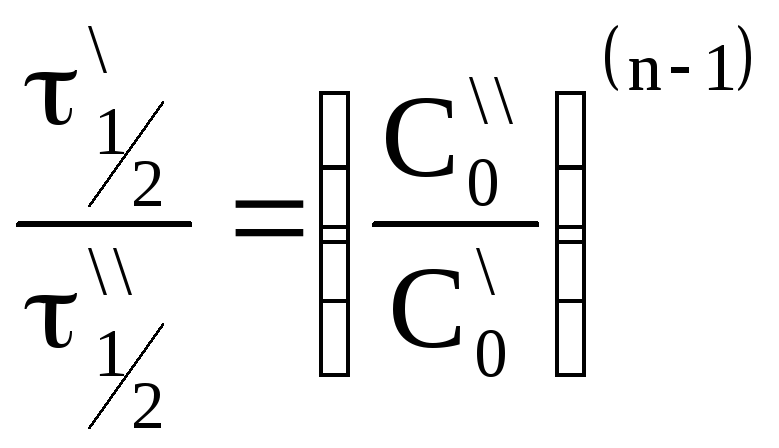
Откуда

Например,
и;
периоды полураспадаи.
Определить порядок реакции (n=1,96≈2).

Метод изоляции или метод избытка:
реагентов заключается в том, что
проводят серии опытов, в каждом из
которых изучается влияние изменения
концентрации только одного из исходных
веществ на скорость реакции. это
достигается применением всех остальных
исходных веществ в данной серии опытов
в таком избытке, что расход их в ходе
реакции существенно не меняет их
количества (концентрации), которые
поэтому можно считать постоянными.
Охватывая, таким образом, все исходные
вещества, можно установить влияние
изменения концентрации каждого из них
на скорость реакции и отсюда определить
порядок реакции и уравнение кинетики.

Рассмотреть
самостоятельно – дифференциальный
метод (разновидность графического
метода?)!

сложные реакции

Кинетика сложных реакций, состоящих из
двух или большего числа простых реакций,
в той или иной форме связанных между
собой, зависит от формы связи между
этими реакциями и от соотношения их
скоростей. Типичными по форме такой
связи являются реакции:

– параллельные;

– последовательные;

– сопряженные;

– обратимые.

Параллельные: две реакции
называются параллельными, если в обеих
в качестве исходного вещества выступает
одно и то же вещество, т.е. это реакции
вида:

Обозначим, через
начальную концентрацию вещества А,
через х – изменение его концентрации
к моменту времени τ, черезиконцентрации образовавшихся веществ
и черезиконстанты скоростей соответствующих
реакций. Тогда для скорости образования
продуктов реакции имеем:

(*)

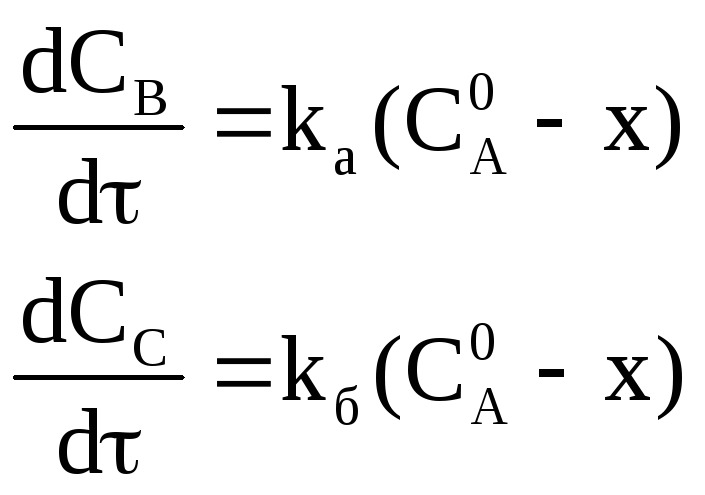
Сумма этих
скоростей определяет скорость расходования
исходных веществ:

.

С другой
стороны, отношение этих двух уравнений
(*) дает:

.

Таким образом, если в данных условиях
термодинамически возможны два или три
направления химический реакции, то
преобладание того или другого из них и
относительные количества получаемых
продуктов реакции определяются всецело
соотношением скоростей этих реакций,
а не соотношением термодинамической
устойчивости конечных продуктов.
Если реакции значительно различаются
по скорости, то обычно реакцию, обладающую
большей скоростью, называют главной
(основной), а остальные – побочными. При
не слишком большом различии в скоростях
главной реакцией называют реакцию,
приводящую к получению основного нужного
продукта, хотя бы она и обладала меньшей
скоростью.

Последовательные (или консекутивные):
две реакции называются последовательными,
если вещество, образующееся в одной
стадии, является исходным для другой,
т.е. это реакции вида:

,

где В
промежуточный продукт в процессе
получения вещества С; k₁
иk₂– константы
скоростей двух стадий превращения.

Данная схема представляет собой
простейшую последовательную реакцию,
которая происходит в две ступени, и
каждая из этих ступеней является простой
мономолекулярной реакцией. В общем же
случае ступеней может быть больше, а
стадии могут не быть мономолекулярными.

Расчет кинетики последовательных
реакций очень сложен. Отметим только,
что если одна из ступенейобладает
значительно меньшей скоростью, чем
остальные, то общая скорость реакции
определяется скоростью именно этой
реакции!!!

Зависимость концентрации веществ,
участников реакции, от времени можно
рассмотреть на примере простейшей
последовательной реакции:

Из данных графических зависимостей
следует, что в начале процесса, когда
концентрация вещества А еще сравнительно
высока, скорость первой реакции
значительна и увеличение концентрации
В происходит быстро. По мере израсходования
вещества А уменьшается и скорость
образования вещества В. Это приводит к
тому, что расход вещества В на образование
вещества С, начиная с какого-то момента
времени, уже не компенсируется в полном
степени образованием его из вещества
А и концентрация вещества В в системе
начинает уменьшаться. Вследствие этого
кривая Св проходит через максимум.
Положение таких кривых для различных
последовательных реакций неодинаково,
т.к. оно зависит от соотношения в скоростях
этих реакций, но общий характер зависимости
остается обычно таким, как он рассмотрен
нами.

Кривые на рисунке описываются уравнениями:

,

,

.

(реакции первого
порядка)

Было доказано,
что максимальная концентрация
промежуточного продукта В, достигаемая
в ходе реакции, не зависит от абсолютных
значений констант скоростейk₁
иk₂, а зависит
только от их отношения,
т.е. чем больше значение α, тем больше
должна быть концентрация Св, макс.

При k₁
>k₂скорость
образования промежуточного продукта
будет значительно выше скорости его
расходования. Таким образом, если
промежуточный продукт является целевым
и необходимо увеличить его выход, то
это может быть достигнуто увеличениемk₁, что можно достигнуть
введением в реакционную систему
селективного катализатора, который
увеличил бы скорость первой стадии при
неизменной скорости второй. Если
зависимость скоростей стадий от
температуры различна, то тот же эффект
может быть достигнут изменением
температуры.

При k₁
<k₂в этом случае
скорость превращения промежуточного
веществаВвСбудет значительно
выше скорости его возникновения изА,
а его концентрация будет весьма низкой.

С

А+В→М

А+С→N

опряженные:называются реакции
вида:

из которых
одна, например, А+В→М, протекает лишь
совместно с другой, т.е. индуцируется
последней. В таких случаях вещество Сслужит индуктором первой реакции(например, окисление
сульфата железа и йодистого водорода
перекисью водорода. Сульфат железа
окисляется независимо от присутствия
йодистого водорода, последний же в
чистом виде перекисью водорода не
окисляется, но при одновременном
окислении сульфата железа окисляется
совместно с ним). Это явление
называетсяхимической индукцией.
В этом случае вещество А, общее для обеих
реакций называетсяактором, вещество
В –акцептор, а вещество С –индуктор.

Обратимые:скорость обратимой
реакции равна разности между скоростями
прямой и обратной реакций. Если
обратиться к общему случаю реакции
вида:

то скорость
изменения (убывания) концентрации
вещества А при протекании прямой реакции
определяется уравнением:

а скорость
изменения (возрастания) ее при протекании
обратной реакции – уравнением

Если в начальном состоянии системы в
ней содержались только вещества А, В,
с, то скорость прямой реакции уменьшается
по мере течения ее в соответствии с
уменьшением этих концентраций. Таким
образом, зависимость этой скорости от
времени представляется кривой 1, если
бы не было обратной реакции, эта кривая
достигла бы оси абсцисс при израсходовании
одного их исходных компонентов. Кривая
2, относящаяся к скорости обратной
реакции, начинается в начале координат
(т.к. в начальный момент времени
концентрации продуктов реакции равны
нулю) и повышается по мере течения прямой
реакции и вызываемого ею увеличения
этих концентраций.

Общая скорость реакции в любой момент
времени равна разности скоростей прямой
и обратной реакций:

.

Очевидно, что при дальнейшем течении
реакции указанные две кривые – скоростей
прямой и обратной реакций – должны
где-то пересечься, т.е. должно быть
достигнуто такое состояние, при котором
скорости прямой и обратной реакций
станут равными между собой. После
достижения этого состояния – состояния
равновесия, концентрации каждого из
компонентов реакции будут постоянными.

Так как скорости прямой и обратной
реакций при этом будут равны по абсолютному
значению, следовательно, должны быть
равны между собой и:

.

Откуда

.

Правая часть
этого равенства представляет собой
константу равновесия Кс данной реакции
и, следовательно,

,

т.е. константа
равновесия равна отношению констант
скоростей прямой и обратной реакций.
Этот вывод четко показывает динамический
характер равновесия в химических
реакциях.

влияние температуры на скорость
ХИМИЧЕСКОЙ реакции.

энергия активации

При повышении температуры скорость
химической реакции увеличивается; это
увеличение весьма значительно. Зависимость
скорости протекания реакции от температуры
схематично представлена на рисунке.

П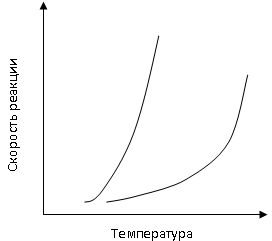ри
повышении температуры и постоянных
концентрациях реагентов скорость
химической реакции увеличивается из-за
возрастания константы скорости.

Опытные данные показывают, что если
рассматривать зависимость логарифма
константы скорости от обратного значения
абсолютной температуры, то экспериментальные
точки, относящиеся к одной реакции,
располагаются обычно практически на
одной прямой, т.е. логарифм константы
скорости реакции находится в линейной
зависимости от обратного значения
абсолютной температуры (1/Т). Искомая
зависимость выражается уравнением
Аррениуса:

,

где А и В
индивидуальные константы, характерные
для данной реакции.

Аррениусом было предложено объяснение
физического смысла постоянной А в данном
уравнении.

Вспомним
уравнение изохоры Вант-Гоффа в
дифференциальной форме:

,

которое
выражает температурный коэффициент
константы равновесия через тепловой
эффект химической реакции. Подставляя
в это уравнение вместо Кс отношение
констант скоростей прямой и обратной
реакций
,
можно получить:

.

Вант-Гофф
высказал предположение о возможности
рассматривать тепловой эффект реакции,
как разность двух энергетических величин
и,
относящихся к прямой и обратной реакциям,
отсюда.
С учетом данного равенства, уравнениеможно разложить на два уравнения вида:

и.

Интегрируя
данные уравнения при постоянстве
,
получаем:

и,

где
и–
постоянные интегрирования.

Величины
иназываютсяэнергиями активации.
Они связаны с постоянной А уравненияпростым соотношением.
Согласно представленным уравнениям,константа скорости реакции, а,
следовательно, и скорость химической
реакции сильнее изменяются с температурой
в тех реакциях, в которых энергия
активации больше. И наоборот, если в
данной реакции энергия активации
незначительна, то скорость этой реакции
слабо изменяется с температурой.
Кроме того, чем больше энергия активации
данной реакции, тем при более высоких
температурах она совершается.

Рассмотрим физический смысл энергии
активации.

В реакциях, протекающих с конечной
скоростью, число столкновений между
молекулами, приводящих к химическому
взаимодействию (число эффективных
столкновений), составляет лишь некоторую
часть от общего числа столкновений.
Эффективными считаются лишь столкновения
между молекулами, которые в момент
столкновения обладают некоторым избытком
внутренней энергии по сравнению со
средней для данной температуры величиной.
Именно этот избыток энергии, необходимый
молекулам для данной реакции в данных
условиях, и представляется энергией
активации
и.Энергия активации – это то избыточное
количество энергии (по сравнению со
средней величиной), которой должна
обладать молекула в момент столкновения,
чтобы быть способной к данному химическому
взаимодействию. Рассмотрим на примере
рисунка. На рисунке по вертикальной оси
отложена энергия активации рассматриваемой
системы молекул, а по горизонтальной –
ход реакции. Допустим прямая реакция
(переход из состояния 1 в состояние 2)
является экзотермической, то общий
запас продуктов реакции меньше, чем
исходных веществ, т.е. система в результате
этой реакции переходит на более низкий
энергетический уровень(это
также показывает, что повышение
температуры всегда сильнее увеличивает
скорость эндотермического направления
реакции, т.к. энергия активации больше.
А также, повышение температуры всегда
смещает равновесия в направлении
эндотермического процесса и тем в
большей степени, чем выше тепловой
эффект, т.е. чем больше разница в энергиях
активации прямой и обратной реакций).
Разность в энергиях этих у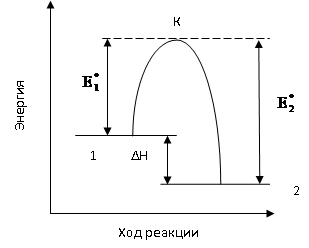ровней
равна тепловому эффекту реакции ΔН.
Уровень К определяет наименьший запас
энергии, которым должны обладать
молекулы. Чтобы их столкновение было
эффективным. Разность между этим уровнем
К и уровнем 1 представляет собой энергию
активации прямой реакции,
а разность между уровнями К и 2 – энергию
активации обратной реакции.
Таким образом, по пути из исходного
состояния в конечное система должна
преодолеть так называемыйэнергетический
барьер. Только молекулы, обладающие
в момент столкновения необходимым
избытком энергии, так называемые активные
молекулы, могут вступать в химическое
взаимодействие. Катализаторы, ускоряющие
реакцию, обычно, тем или иным путем,
снижают ее энергию активации и этим
увеличивают относительное число активных
молекул. Повышение температуры увеличивает
среднюю кинетическую энергию, что
повышает и относительное число молекул,
обладающих энергией, превосходящей
энергию уровня К. Избыточная энергия
может быть в молекуле в различных формах,
это может быть: 1) повышенная кинетическая
энергия поступательного или вращательного
движения, 2) повышенная энергия взаимного
колебания атомов или атомных групп,
составляющих молекулу, 3) повышенная
энергия движения тех или других
электронов. Для различных реакций не
все формы этой энергии равноценны.

расчеты констант скоростей и энергии
активации

Для выражения зависимости константы
скорости реакции от температуры и
определения энергии активации, а также
для расчета константы скорости при
различных температурах используют
уравнение
.
Две постоянные в данном уравнении могут
быть определены, если известны значения
констант скорости данной реакцииk₁
иk₂при двух
температурах Т₁и Т₂. Имеем
систему из двух уравнений:

с двумя
неизвестными А и В. Вычитая первое
уравнение из второго, получим:

.

Это дает
возможность непосредственно определить
А (а, следовательно, энергию активации,
т.к.
).
Подставляя полученное значение А в одно
из уравнений, рассчитывают постоянную
В. Полученное уравнение с численными
значениями постоянных А и В можно
использовать для расчета константы
скорости при промежуточных температурах.
Существует также графический способ
определения энергии активации!

Обозначим
через
константу скорости при температуреt⁰С
и черезконстанту скорости той же реакции при
температуре (t+10)⁰С.
Отношениеназывается температурным коэффициентом
скорости. Было предложено приближенное
правило, согласно которомуповышение
температуры на 10⁰С
увеличивает скорости реакций примерно
в 2-4 раза (правило Вант-Гоффа), т.о.можно принять равным примерно 2-4.

Данное правило
определяет только порядок изменения
скорости, присущий значительной части
различных химических реакций при обычных
температурах. Однако для ориентировочной
оценки возможного влияния температуры
оно нередко бывает полезным, в особенности
при отсутствии данных для более точного
расчета.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 6 ноября 2019 года; проверки требует 1 правка.

Зако́н де́йствующих масс устанавливает соотношение между массами реагирующих веществ в химических реакциях при равновесии, а также зависимость скорости химической реакции от концентрации исходных веществ. Закон действующих масс открыли в 1864—1867 годах норвежские ученые К.Гульдберг (1836—1902) и П.Вааге (1833—1900).

Закон действующих масс справедлив только для газов и жидких веществ (гомогенных систем) и не выполняется для реакций с участием твёрдых веществ (гетерогенных систем).

Закон действующих масс в химической кинетике[править | править код]

Закон действующих масс в кинетической форме (основное уравнение кинетики) гласит, что скорость элементарной химической реакции пропорциональна произведению концентраций реагентов в степенях, равных стехиометрическим коэффициентам в уравнении реакции, для элементарной реакции^[1]. Это положение сформулировано в 1864—1867 годах норвежскими учёными К. Гульдбергом и П. Вааге. Для элементарной химической реакции:

закон действующих масс может быть записан в виде кинетического уравнения вида:

где  — скорость химической реакции,  — константа скорости реакции.

Для сложных реакций в общем виде это соотношение не выполняется. Тем не менее, многие сложные реакции условно можно рассматривать как ряд последовательных элементарных стадий с неустойчивыми промежуточными продуктами, формально эквивалентный переходу из начального состояния в конечное в «один шаг». Такие реакции называют формально простыми^[2]. Для формально простых реакций кинетическое уравнение может быть получено в виде:

(для трех исходных веществ, аналогично приведённому выше уравнению). Здесь , ,  — порядок реакции по веществам , , соответственно, а сумма  — общий (или суммарный) порядок реакции. , , могут быть не равны стехиометрическим коэффициентам и не обязательно целочисленные. при определённых условиях может быть равно и нулю.

Закон действующих масс в химической термодинамике[править | править код]

В химической термодинамике закон действующих масс связывает между собой равновесные активности исходных веществ и продуктов реакции, согласно соотношению:

где

 — активность веществ. Вместо активности могут быть использованы концентрация (для реакции в идеальном растворе), парциальные давления (реакция в смеси идеальных газов), фугитивность (реакция в смеси реальных газов);

 — стехиометрический коэффициент (для исходных веществ принимается отрицательным, для продуктов — положительным);

 — константа химического равновесия. Индекс «a» здесь означает использование величины активности в формуле.

На практике в расчётах, не требующих особой точности, значения активности обычно заменяются на соответствующие значения концентраций (для реакций в растворах) либо парциальных давлений (для реакций между газами). Константу равновесия при этом обозначают или соответственно.
Впервые закон действующих масс был выведен из кинетических представлений Гульдбергом и Вааге, а термодинамический вывод его дан Вант-Гоффом в 1885 году^[3].

Пример: для стандартной реакции

константа химического равновесия определяется по формуле

Примечания[править | править код]

решение задач на химию

Timur Jumaniyazow

Ученик

(117),
закрыт

10 месяцев назад

пожалуйста помогите!
1.составьте математическое выражение закона действия масс для следующего процесса: CaO+H2SO4= CaSO4+H2O
2. Как изменится скорость реакции SO2+O2=SO3, если а) концентрацию O2 увеличить в 4 раза бn) температуру процесса повысить на 40 С (у=3)
3. В какую сторону сместится равновесие реакции : NO+O2=NO2; dH<0, если а) снизить температуру б) увеличить давление, в) внести катализатор, г) увеличить концентрацию NO?
4. Составьте выражение константы химического равновесия для процесса 3.

Действующих масс закон

Полезное