3.1 Построение математической модели.
Построим
математическую модель отстойника.
При построении
данной математической модели отстойника
необходимо принять следующие условия:
в отстойнике
осуществляется осаждение в ламинарном
режиме, поэтому скорость осаждения
водяных глобул относительно неподвижной
среды вычисляется по формуле Стокса:
![]()
(3.1)
поступление
водонефтяной эмульсии является
непрерывным, следовательно, необходимо
учитывать скорость наполнения буллита:
![]()
(3.2),
где Qприб
– расход поступающей эмульсии, D
– диаметр буллита, l
– длина буллита;
для того, чтобы
было осаждение было возможным, скорость
осаждения водяных глобул для неподвижной
среды должна быть выше скорости наполнения
буллита, так как, скорость седиментации
равна разности двух вышеупомянутых
скоростей:
![]()
(3.3)
Водонефтяная
эмульсия, осаждаемая в отстойнике,
является полидисперсной, т.е., глобулы
воды имеют разные радиусы. При условиях
технологического процесса обезвоживания
нефти возможно лишь частичное осаждение
воды в отстойнике. В связи с этим возникает
задача определения того процента
содержащейся в эмульсии воды, который
осаждается в отстойнике при текущей
скорости наполнения буллита.
Для того, чтобы
решить эту задачу, необходимо найти так
называемый критический радиус глобул
воды. Критическим радиусом будем называть
такой радиус водяных глобул, начиная с
которого возможно осаждение при текущей
скорости наполнения буллита.
Учитывая, тот
факт, что для осаждения воды необходимо,
чтобы скорость наполнения буллита не
превышала скорости осаждения глобул
воды и используя формулы (3.1) и (3.2), получим
формулу нахождения критического радиуса:
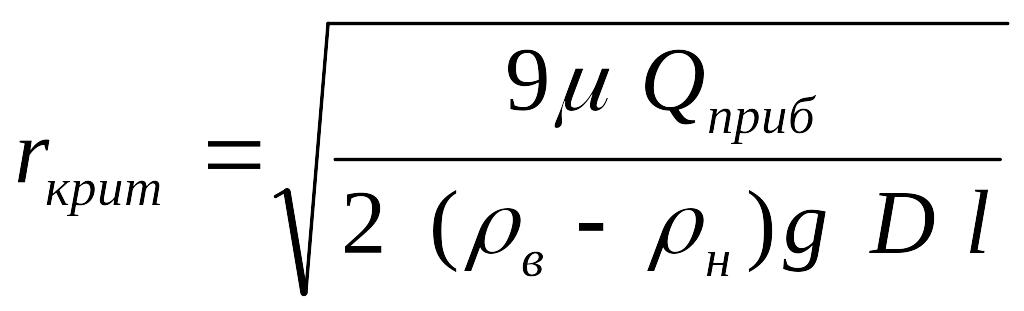
(3.4)
Будем считать,
что радиусы глобул воды в водонефтяной
эмульсии распределены по нормальному
закону.
Чтобы решить
задачу вычисления расхода отводимой
из отстойника воды и коэффициента
обводнения осветленной эмульсии,
поступающей с выхода отстойника в
электродегидратор, необходимы следующие
параметры поступающей в отстойник
эмульсии в качестве исходных данных:
– закон
распределения радиусов глобул воды в
водонефтяной
эмульсии;
– минимальный,
максимальный и критический радиусы
глобул воды
rmin,
rmax,
rкрит;
– расход
поступающей эмульсии Qприб;
– коэффициент
обводненности kобв.
Структура эмульсии
определяется плотностью распределения
глобул с радиусами, находящимися в
диапазоне rmin
– rmax:

(3.5),
где
![]()
– математическое ожидание, (3.5 а)
![]()
– среднеквадратическое
отклонение. (3.5 б)
Разделим отрезок
[rmin,
rmax]
на 6 одинаковых частей. Длина каждого
интервала равна:
![]()
(3.6).
Площадь под кривой
(3.5) в интервале ri
÷ ri+1
численно равна интегралу:

(3.7)
Отметим, что для
распределения (3.5) выполняется следующее
условие:

(3.8)
При заданных
расходе и коэффициенте обводнения
поступающей в отстойник эмульсии, можно
найти расход отводимой из отстойника
воды, расход и коэффициент обводнения
нефти, поступающей в электродегидратор
для дальнейшего обезвоживания.
Пусть в единице
объема водонефтяной эмульсии содержится
М глобул с радиусами в диапазоне rmin
– rmax.
Если
рассматривать величину Si
как вероятность того, что в водонефтяной
эмульсии содержится Si·М
глобул с радиусами ri
– ri+1,
то при достаточно большом значении М
можно считать, что в единице объема
содержится Si·М
с радиусом ri.
Будем считать,
что S0i
= foi
Δr
(3.9),
где
![]()
(3.10).
Тогда величину
foi
· М будем
рассматривать как количество глобул с
радиусом
![]()
(3.11).
Пусть n0max·М
=1, тогда
![]()
,
где n0max
– вероятность (частота) того, что в
объеме эмульсии содержатся глобулы с
радиусом r0max.
Это значит, что в структуре выбранной
эмульсии в некотором объеме содержится
М глобул с радиусами в диапазоне r0min
– r0max.
Число глобул радиусом r0i
в этом объеме будет
![]()
(3.12).
Объем воды,
образуемый глобулами радиусом r0i,
будет
равен:
![]()
(3.13).
Коэффициент
обводненности характеризуется площадью,
ограниченной кривой

,
осью r,
прямыми r
= r0min
и r
= r0min.


Рис. 3.1. График
функции V(
r
).
Прямая r
= rкрит
разбивает данную площадь на 2 части:
1) левая часть
(r0min
÷ rкрит)
соответствует неосаждаемым в отстойнике
глобулам,
2) правая часть
(rкрит
÷ r0max)
соответствует осажденным глобулам.

(3.14)

(3.15)
Коэффициент
осаждения воды с учетом коэффициента
обводнения нефтяной эмульсии будет
равен:
![]()
(3.16)
Выразим расход
воды Qв,
выходящей из отстойники и расход
осветленной эмульсии Qoe,
поступающей с отстойника на
электродегидратор:
Qв
= kобв
· kосажд
· Qприб,
(3.17)
Qoe
= Qприб
– Qв,
(3.18)
где Qприб
– расход
поступающей в отстойник водонефтяной
эмульсии.
Математическая
модель отстойника:

;
![]()
;
,
где
– математическое ожидание,
– среднеквадратическое
отклонение,
;
![]()
;
(3.34)
;
Qв
= kобв
· kосажд
· Qприб;
Qoe
= Qприб
– Qв;
Имея данную
математическую модель, можно построить
математическую модель формирования
водонефтяной эмульсии, определения
скорости седиментации и определения
оптимального межфазного уровня.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
ЛЕКЦИЯ 14
Тема 2.3
Математическое обеспечение (4 часа)
1. Назначение, состав и структура
математического обеспечения
2. Модели и алгоритмы обработки информации в
автоматизированных системах
1 Назначение, состав и структура
математического обеспечения
МО АИС является
одной из важнейших обеспечивающих подсистем АИС, наряду с ИО и ПО. Программу
работы ЭВМ легче составлять по имеющейся алгебраической формуле, поэтому
разработка МО на стадии технического проектирования системы всегда предшествует
разработке ПО. Разработкой МО занимаются специальные подразделения (отделы) со
штатом математиков, результаты их труда должны быть понятны и полезны
программистам.
МО АИС – это совокупность математических методов, моделей и
алгоритмов обработки информации, использованная при решении задач в
информационной системе (функциональных и автоматизации проектирования
информационных систем).
Иногда, написание алгоритма программы
обработки выделяют в отдельную обеспечивающую подсистему: АО (алгоритмическое
обеспечение), которое занимает промежуточное положение между МО и ПО, мы будем
включать раздел алгоритмизации в МО.
Назначение МО АИС:
1.
построение
экономико-математической модели АИС;
2.
нахождение оптимального
решения при раскрытии этой модели;
3.
проведение анализа
полученного решения.
К
средствам МО относят:
– средства моделирования процессов управления;
– типовые задачи управления;
– методы математического программирования,
математической статистики, теории массового обслуживания и др.
Техническая
документация по этому виду обеспечения АИС содержит:
– описание задач,
– задания по алгоритмизации:
– экономико-математические модели задач,
– текстовые и контрольные примеры их решения.
Персонал
составляют:
– специалисты по организации управления
объектом,
– постановщики задач управления,
– специалисты по вычислительным методам,
– проектировщики АИС.
Понятие математической модели
Понятие модели вообще и математической модели
в частности в настоящее время является одним из самых распространенных.
Между
изучаемым объектом и моделью должно быть сходство, которое позволяло бы
устанавливать степень их подобия. Модель, как правило, упрощает реальный
объект, физическое явление или процесс, однако существенные и типичные для
данного класса объектов элементы должны быть сохранены (Ex: в
физике законы, описывающие свойства газов и жидкостей выведены для их моделей –
т.е. идеальных газов и жидкостей).
В теории управления рассматриваются
поведенческие модели, т.е. сходство с системой–оригиналом должно состоять в
поведении.
Система обладает входами, через которые
в нее поступают материальные, энергетические и информационные потоки, и выходами,
благодаря которым результаты преобразования в системе поступают во внешнюю
среду.
Т.о. модель должна реагировать на изменение
входных параметров таким изменением своих параметров выхода, которое отражает
поведение оригинала.
Одной из центральных моделей теории управления
является модель «черного ящика» (что, как и в какой последовательности
происходит внутри – неважно).
Для каждого объекта-оригинала можно подобрать
очень много чем-то удачных моделей. Степень сходства может быть разной.
Модели процессов и явлений служат не только
для лучшего понимания их закономерностей, но и для проведения различных опытов
(особенно это важно в организационных системах, где очень дорого изучать
последствия разных вариантов изменения). (Ex: план поставок материальных ресурсов).
Выделение системы в качестве объекта
моделирования требует:
– наличие объекта – оригинала, состоящего из
множества элементов;
– существования наблюдателя-исследователя;
– задачи, определяющей для наблюдателя границы
рассмотрения объекта моделирования, выделения его существенных свойств.
По поводу объекта моделирования исследователь
выдвигает гипотезы – определенные предложения, предсказания, основанные
на небольшом числе опытных данных, наблюдений, догадок. При этом человек широко
использует аналогии – суждения о каком-либо частном сходстве двух
различных объектов, которые, по мнению исследователя, могут помочь в объяснении
поведения изучаемого объекта моделирования. На основе аналогий и выдвигаемых
гипотез человек вырабатывает некоторую систему представлений о свойствах
объекта моделирования, его поведении. Эта система представлений оформляется в
виде рисунков, графиков, уравнений, макетов, механизмов, т.е. строится модель
рассматриваемого объекта, выступающая абстрактным или материальным его
заменителем.
Таким образом, модель – это
представление исследуемого объекта в некоторой форме, отличной от формы его
реального существования, изучение которой дает о нем новые знания.
Моделирование – это представление объекта в виде модели для
получения информации об этом объекте путем проведения экспериментов с его
моделью.
Структура математического
обеспечения АИС
![]() МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ
МАТЕМАТИЧЕСКОЕ ОБЕСПЕЧЕНИЕ

Методы
выбора
математического Средства
Документация
обеспечения
![]()
![]()
![]() методы
методы
определения средства моделирования описание
задачи
типа
задач процессов управления
![]()
задание на
![]()
![]() методы
методы
оценки описание типовых задач
алгоритмизацию
вычислительной управления
![]()
сложности
экономико-математ.
![]() методы оптимизации
методы оптимизации
модель
![]() методы оценки моделей
методы оценки моделей
![]()
отклонений
алгоритм
![]() полученного решения методы матем. статистики
полученного решения методы матем. статистики
![]() от
от
оптимального
контрольный пример
Решения по математическому обеспечению АИС
Под математическим обеспечением АИС понимается совокупность алгоритмов расчета показателей, используемых в проектируемой информационной системе.
Для расчета необходимого Ni количества i-го товара в процессе составления задания на реализацию суммируются все сделанные заказы на данный товар (?Ni).
Проверка необходимого количества товара на складе осуществляется сравнением ?Ni с Сi (где Сi – планируемый остаток товара i на складе фирмы). Если остаток от разности этих показателей Li окажется положительным или равным нулю, задание на реализацию данного товара можно осуществлять, если же отрицательным – следует составить заявку на производство. Формализованное описание входных показателей представлено в таблице 5.
Таблица 5 – Формализованное описание входных и выходных показателей процесса запроса наличия ГП через БД.
|
№ п/п |
Наименование входного показателя |
Идентификатор входного показателя |
|
1 |
Общее заказанное количество i-ого товара всеми клиентами за рассматриваемый период. |
?Ni |
|
2 |
Остаток товара i на складе фирмы на данный момент времени. |
Сi |
|
№ п/п |
Наименование выходного показателя |
Идентификатор выходного показателя |
|
1 |
Планируемый остаток товара i после проведения задания на реализацию. |
Li= Сi -?Ni |
Для составления отгрузочных и сопроводительных документов (Накладной и Счета-фактуры) потребуется расчет общей стоимости заказа для j-го клиента c учетом налога и без его учета (таблица 6).
Таблица 6 – Формализованное описание входных и выходных показателей процесса составления товарно-транспортной накладной и счета-фактуры.
|
№ п/п |
Наименование входного показателя |
Идентификатор входного показателя |
|
1 |
Цена за единицу i-го товара |
Pi |
|
2 |
Общее заказанное количество i-ого товара j-ым клиентом за рассматриваемый период. |
?Nij |
|
3 |
Налоговая ставка для i-го товара. |
fi |
|
№ п/п |
Наименование выходного показателя |
Идентификатор выходного показателя |
|
1 |
Общая стоимость i-го товара, заказанного j-ым клиентом (без учетом налога). |
Sij= ?Nij* Pi |
|
2 |
Налог на единицу i-го товара. |
Fi= fi* Pi |
|
3 |
Общая стоимость i-го товара, заказанного j-ым клиентом (c учетом налога). |
Sij= ?Nij*Pi+ fi* ?Nij* Pi |
|
4 |
ИТОГО за все учтенные заказы для j-го клиента (по накладной и счету-фактуре). |
Ij=?Sj |
Для расчета движения готовой продукции требуется использование показателей суммы всех расходов и приходов данного вида товара за рассматриваемый период (таблица 7).
Таблица 7 – Формализованное описание входных и выходных показателей процесса расчета движения готовой продукции.
|
№ п/п |
Наименование входного показателя |
Идентификатор входного показателя |
|
1 |
Сумма всех расходов i-ого товара за рассматриваемый период. |
?Ai |
|
2 |
Остаток товара i на складе фирмы на данный момент времени. |
Сi |
|
3 |
Сумма всех приходов i-ого товара за рассматриваемый период. |
?Bi |
|
№ п/п |
Наименование выходного показателя |
Идентификатор выходного показателя |
|
1 |
Остаток товара i на складе после операций прихода и расхода товара. |
С2i= Сi+?Bi-?Ai |
Подборка по базе: Учебная практика (Проектирование и разработка информационных сис, Долинский Н.И. Практическое задание 6. Разработка управленческих, КР разработка фирменного блюда из рубленного мяса.doc, Практическое задание по предмету Моделирование экономических про, Практическая работа_ разработка технологической карты урока исто, Практическая работа № 2 (Часть 1) Раздел программы_ 2.1.4. Объек, Практическая работа_ разработка технологической карты урока обще, Задача Модель Интерпретация модели.docx, Метод разработка 6_ тренинг.docx, Практическая работа разработка технологической карты урока ифнор
МОСКОВСКАЯ ГОСУДАРСТВЕННАЯ АКАДЕМИЯ ВОДНОГО ТРАНСПОРТА
Кафедра «Судовождение»
ДОПУСКАЮ К ЗАЩИТЕ
Руководитель курсовой работы
к.т.н., доцент
А.В. Романов
_____________________ 2019 г.
КУРСОВАЯ РАБОТА
на тему: РАЗРАБОТКА МАТЕМАТИЧЕСКОЙ МОДЕЛИ ОЦЕНИВАНИЯ НАДЕЖНОСТИ АВТОМАТИЧЕСКОЙ ИДЕНТИФИКАЦИОННОЙ СИСТЕМЫ.
Дисциплина: АВТОМАТИЗАЦИЯ СУДОВОЖДЕНИЯ
Специальность 26.05.05 – «Судовождение»
Проект выполнила:
студент группы СВ-4
Стрелецкий А. А.
Руководитель курсовой работы:
Профессор кафедры СВ,
кандидат технических наук, доцент
РОМАНОВ А.В.
Москва 2019
СОДЕРЖАНИЕ.
ЗАДАНИЕ НА ВЫПОЛНЕНИЕ КУРСОВОЙ РАБОТЫ……………..……….3
РЕФЕРАТ………………………………………………………………..………4
ВВЕДЕНИЕ…………………………………………………………..………….5
1. Анализ особенностей эксплуатации и разработка структурно-эксплуатационной модели функционирования АИС…………..……………9
1.1. Анализ особенностей эксплуатации АИС…………..………….…………9
1.2. Разработка структурно-эксплуатационной модели функционирования АИС………………………………………..…….……………………..………..9
1.3. Выводы по разделу 1………………………………………………………11
2. Разработка математической модели оценивания надежности АИС и её анализ. ………………………………………..…………………………… 12
2.1. Разработка математической модели оценивания влияния быстроты решения задач на надёжность АИС…… ……………………………………..12
2.2. Анализ полученной математической модели и рекомендации по ее
использованию …………………………………………………….……………14
2.3. Выводы по разделу 2 …………………………………………………….14
3. Количественная оценка показателей эксплуатационных свойств АИС.…15
- Выбор исходных данных………………………………………..………15
- Компьютерная программа оценивания надежности АИС.……….…..15
- Анализ результатов количественного оценивания……………….….16
- Оценка влияния быстроты решения задач на надежность АИС ……..16
3.5. Выводы по разделу 3……………………………………………………………………..17
ЗАКЛЮЧЕНИЕ…………………………………………………………………18
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ..…………………….. …19
РЕФЕРАТ.
Курсовой проект 19 с., 2 рис., 4 табл., 7 источников.
ОЦЕНИВАНИЕ, АВТОМАТИЧЕСКАЯ ИДЕНТИФИКАЦИОННАЯ СИСТЕМА, МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ОЦЕНИВАНИЯ, ПОКАЗАТЕЛЬ ЭФФЕКТИВНОСТИ ФУНКЦИОНИРОВАНИЯ, РЕЖИМ,
ПРИМЕНЕНИЕ.
Объектом исследования курсового проекта является автоматическая идентификационная система.
Цель курсового проекта – разработка математической модели оценивания надежности АИС, учитывающую влияние быстроты решения задач на надежность АИС и показать возможные пути ее использования.
В процессе выполнения курсового проекта получена математическая модель оценивания эффективности функционирования автоматических идентификационных систем и рекомендации по их использованию при разработке и эксплуатации судовых АИС.
ВВЕДЕНИЕ.
Для эффективного использования АИС необходимо правильно оценивать показатели ее эксплуатационных свойств, учитывать динамику функционирования и наличие возмущающих факторов.
Одним из возможных путей такой оценки является разработка и анализ математической модели оценивания влияния эксплуатационных свойств АИС на эффективность ее функционирования.
В курсовом проекте анализируются особенности эксплуатации и функционирования АИС, а так же разрабатывается содержательная модель функционирования АИС. Разрабатывается и анализируется математическая модель оценивания показателей эксплуатационных свойств АИС. Приводятся рекомендации по ее использованию.
РЕЗОЛЮЦИЯ ИМО MSC.74(69)
(принята 12 мая 1998 года)
ПРИЛОЖЕНИЕ 3. РЕКОМЕНДАЦИИ ПО ЭКСПЛУАТАЦИОННЫМ ТРЕБОВАНИЯМ К УНИВЕРСАЛЬНОЙ СУДОВОЙ СИСТЕМЕ АВТОМАТИЧЕСКОГО ОПОЗНАВАНИЯ (AIS).
1.Назначение.
1.1. Данный стандарт определяет эксплуатационные требования к универсальным АИС.
1.2. АИС должна обеспечивать повышение уровня безопасности мореплавания посредством эффективного судовождения, защиты окружающей среды, эффективности использования Систем управления движением судов (СУДС) через выполнение следующих функциональных требований:
в режиме «судно – судно» – для предупреждения столкновений;
как средство для получения береговыми службами информации о судне и его грузе:
как инструмент СУДС – в режиме «судно-берег» (управление движением судов).
1.3. АИС должна обеспечивать суда и компетентные власти информацией от судов автоматически, и с требуемой точностью и частотой обновления, для обеспечения точного сопровождения судов. Передача данных должна осуществляться с минимальным участием судового персонала и высоким уровнем надежности.
1.4. Оборудование, в дополнение к требованиям Регламента Радиосвязи, Рекомендаций МСЭ-Р и общим требованиям, изложенным в Резолюции ИМО А.694(17), должно соответствовать следующим эксплуатационным требованиям.
2. Основные режимы работы.
2.1 АИС должна обеспечивать работу в следующих режимах:
1. «Автономный и непрерывный» – для работы во всех районах. Этот режим должен иметь возможность переключения компетентной властью с/на один из следующих режимов;
2. «Назначенный» («предписанный») – для работы в районах, где компетентной властью установлен контроль за движением судов таким образом, чтобы интервал передачи данных и/или временное положение слотов могли устанавливаться дистанционно этой властью.
3. «По запросу» или контролируемый режим – данные передаются в ответ на запрос от судна или от компетентной власти.
3. Основные функциональные требования.
3.1. В состав АИС должны входить:
связной процессор, способный управлять набором морских частот с:
1. Соответствующим методом выбора и переключения каналов, обеспечивая применение, как для ближней, так и для дальней радиосвязи.
2. Средство обработки данных от электронной системы местоопределения, обеспечивающее разрешение не хуже одной десятитысячной минуты дуги и использующее геодезическую систему координат WGS-84 .
3. Средство автоматического ввода данных от других датчиков, перечисленной в п. 6.2;
4. Средство ввода и восстановления данных вручную;
5. Средство контроля достоверности передаваемых и принимаемых данных;
6. Встроенное устройство контроля работоспособности.
3.2 АИС должна обеспечивать:
1. Автоматическое и непрерывное предоставление информации компетентной власти и другим судам, без участия судового персонала;
2. Прием и обработку информацию от других источников, включая информацию от компетентной власти и других судов;
3. Ответ с минимальной задержкой на сигналы, относящиеся к высокому приоритету и безопасности;
4. Предоставление информации о местонахождении и маневрировании c частотой обновления, достаточной для обеспечения точного сопровождения судна компетентной властью и другими судами.
4. Интерфейс пользователя.
Для обеспечения доступа, отбора и отображения информации на отдельном устройстве, АИС должна иметь интерфейс, соответствующий международным морским стандартам к интерфейсам.
5. Опознавание (идентификация).
Для целей опознавания судна и сообщений должен использоваться соответствующий идентификационный номер Морской подвижной службы (ММSI).
6. Информация.
Информация, предоставляемая АИС, должна включать:
6.1 Статическую:
ИМО номер (если имеется)
Позывной сигнал и название;
Длина и ширина судна;
Тип судна;
Расположение антенны системы место определения на судне (по отношению к носу, корме, правому, левому борту).
6.2 Динамическую:
Местоположение судна с указанием точности и целостности системы;
Время (UTC) (дата устанавливается приемным оборудованием);
Курс относительно грунта;
Скорость относительно грунта;
Курс судна;
Навигационный статус (состояние судна) (к примеру, не управляется, на якоре и т.д. – вводится вручную);
Угловая скорость поворота (где возможно);
Факультативно – Угол крена (если возможно);
Факультативно – Угол килевой и бортовой качки (если возможно).
6.3 Информацию, связанную с рейсом:
Осадка судна;
Опасный груз (тип);
Порт назначения и ЕТА (по усмотрению капитана);
Факультативно – план перехода (путевые точки).
6.4 Короткие сообщения относительно безопасности.
6.5 Частота обновления информации для автономного режима
Для различных типов информации, действующей в разное время, используется различная частота обновления (интервал)
Статическая – каждые 6 минут и по требованию;
Динамическая – в зависимости от скорости и изменения курса согласно таблице 1;
Информация, связанная с рейсом – каждые 6 минут, при изменении данных и по запросу;
Сообщение относительно безопасности – когда требуется.
Таблица 1
| Состояние судна | Интервал между сообщениями |
| Судно на якоре | 3 минуты |
| Скорость 0-14 узлов | 12 секунд |
| Скорость 0-14 узлов и меняющийся курс | 4 секунды |
| Скорость 14-23 узла | 6 секунд |
| Скорость 14-23 узла и меняющийся курс | 2 секунды |
| Скорость более 23 узлов | 3 секунды |
| Скорость более 23 узлов и меняющийся курс | 2 секунды |
Объем судовых сообщений – АИС должна обрабатывать не менее 2000 сообщений в минуту, чтобы адекватно обеспечить все эксплуатационные варианты.
6.6 Обеспечение безопасности (защиты).
Должен быть обеспечен механизм безопасности для обнаружения вывода из строя системы и предотвращения несанкционированного изменения введенных или передаваемых данных. Для предотвращения несанкционированного распространения данных следует выполнять требования Резолюции ИМО MSC/43(64) (Руководство и критерии для систем судовых сообщений)
7. Время приведения в рабочее состояние
– система должна быть готова к работе в течение 2 мин после включения.
8. Энергопитание
АИС и связанные с ней датчики должны питаться от основного источника электроэнергии на судне. Дополнительно должна иметься возможность питания АИС и связанных с ней датчиков и от альтернативного источника электроэнергии.
9. Технические характеристики.
Технические характеристики АИС, такие как изменяемая выходная мощность передатчика, рабочие частоты (международные и региональные), модуляция и антенная система, должны соответствовать Рекомендациям МСЭ-Р (M.1371, M.1024).
1. Анализ особенностей эксплуатации и разработка содержательной модели функционирования АИС.
1.1. Анализ особенностей эксплуатации АИС.
Приведенный анализ эксплуатационной документации, особенностей применения АИС в реальных условиях и опыта использования в судовождении, полученного при прохождении практики на морских судах, позволили представить процесс функционирования АИС в следующем виде.
АИС может находиться в различных состояниях (режимах).
1.2. Разработка структурно-эксплуатационной модели функционирования АИС.
В результате проведенного анализа особенностей эксплуатации и функционирования АИС, на основании соответствующей эксплуатационной документации и опыта практического применения АИС в реальных условиях, в качестве основных режимов работы следует выделить:
1) Режим ожидания (РО) – режим, при котором АИС может находиться в выключенном состоянии или во включенном, но не подготовленном к использованию основных функций.
2) Режим готовности (РГ) ‒ режим, при котором аппаратура АИС подготовлена к выполнению своих функций, аппаратура исправна и не занята измерениями навигационных параметров обнаруженных объектов.
3) Режим навигационных определений (РНО) ‒ состояние, характеризующее выполнение основных задач – обнаружение объекта и считывание его идентификационных параметров.
4) Режим воздействия помех (РВП) ‒ режим работы АИС при котором на ее функционирование влияет появившаяся помеха искусственного или естественного происхождения.
5) Режим подготовки к выключению аппаратуры (РПВА) ‒ подготовка аппаратуры к выключению и ее выключение.
6) Режим восстановления аппаратуры после отказа (РВА) ‒ режим, при котором АИС восстанавливается после отказа.
Н а основании выявленных состояний (режимов) функционирования АИС мы можем построить структурно-эксплуатационную модель функционирования в виде следующего графа состояний и переходов (рисунок 1).

РО
1
РГ
2
РНО
3
РВП
4
РВПА
5
РВА
6









a1,2
a2,3
a3,4
a4,5
a5,1
a6,1
a3,6
a4,6
a6,2
Рисунок 1. Структурно-эксплуатационная модель функционирования АИС.
Введем обозначения интенсивностей перехода АИС из одного состояния в другое.
 – интенсивность поступления заявок на подготовку аппаратуры.
– интенсивность поступления заявок на подготовку аппаратуры.
 – интенсивность поступления заявок на навигационное определение.
– интенсивность поступления заявок на навигационное определение.
 – интенсивность воздействия помех.
– интенсивность воздействия помех.
 – интенсивность поступления заявок на выключение режима навигационных определений.
– интенсивность поступления заявок на выключение режима навигационных определений.
 – интенсивность поступления заявок на выключение аппаратуры.
– интенсивность поступления заявок на выключение аппаратуры.
 – интенсивность отказов в режиме навигационных определений.
– интенсивность отказов в режиме навигационных определений.
 – интенсивность отказов в режиме воздействия помех.
– интенсивность отказов в режиме воздействия помех.
 – интенсивность восстановления в режим ожидания.
– интенсивность восстановления в режим ожидания.
 – интенсивность восстановления в режим готовности.
– интенсивность восстановления в режим готовности.
Воспользовавшись данными практического применения АИС и эксплуатационной документацией, зададим время выше перечисленных переходов для рассматриваемой системы.
Значение времени.
Таблица 2
| Т | АИС (ч) |
| Т1,2 | 0,1 |
| Т2,3 | 0,05 |
| Т3,4 | 0,001 |
| Т4,5 | 0,01 |
| Т5,1 | 0,1 |
| Т3,6 | 0,001 |
| Т4,6 | 0,001 |
| Т6,1 | 0,001 |
| Т6,2 | 6 |
Значения интенсивностей переходов нашей системы.
Таблица 3
| α | АИС (ч-1) |
 |
10 |
 |
20 |
 |
1000 |
 |
100 |
 |
10 |
 |
1000 |
 |
1000 |
 |
1000 |
 |
0,16 |
1.3. Вывод по разделу 1.
Исходя из проведенного анализа особенностей эксплуатации при применении АИС по целевому назначению, можно представить весь процесс в виде графа состояний и переходов. Под состояниями будем понимать содержания мероприятий, проводимых на АИС и операций, выполняемых АИС. Это позволило разработать эксплуатационную модель функционирования АИС.
Исходя из особенностей эксплуатации и функционирования АИС и статических данных, полученных в процессе эксплуатации, и характеристик, взятых из формуляров АИС, определены основные режимы работы, время пребывания в каждом из режимов, значения интенсивностей переходов.
2. Разработка математической модели оценивания надежности АИС и её анализ.
2.1. Разработка математической модели оценивания влияния быстроты решения задач на надёжность АИС.
Обозначим вероятности нахождения АИС в i-ом состоянии через Рi. Составим систему уравнений Колмогорова ‒ Чэпмена, соответствующую заданному графу состояний на рис.1:
1. 6,2 * Р6 + 5,1 * Р5 ‒ 1,2 * Р1 = 0;
2. 1,2 * Р1 + 6,1 * Р6 ‒ 2,3 * Р2 = 0;
3. 2,3 * Р2 ‒ 3,4 * Р3 ‒ α3,6 * Р3 = 0;
4. 3,4 * Р3 ‒ α4,6 * Р4 ‒ 4,5 * Р4 = 0;
5. 4,5 * Р4 ‒α5,1 * Р5 = 0;
6. α3,6 * Р3 + α4,6 * Р4 + α3 * Р5 ‒ 6,2 * Р6 ‒ 6,1*Р6 = 0.
Решать полученную систему уравнений необходимо с помощью нормирующего условия:
Р1+Р2+Р3+Р4+Р5+Р6 =1.
Заменив уравнение 1 нашей системы нормирующим условием, получим систему:
1. Р1+Р2+Р3+Р4+Р5+Р6 =1;
2. 1,2 * Р1 + 6,1 * Р6 ‒ 2,3 * Р2 = 0;
3. 2,3 * Р2 ‒ 3,4 * Р3 ‒ α3,6 * Р3 = 0;
4. 3,4 * Р3 ‒ α4,6 * Р4 ‒ 4,5 * Р4 = 0;
5. 4,5 * Р4 ‒α5,1 * Р5 = 0;
6. α3,6 * Р3 + α4,6 * Р4 + α3 * Р5 ‒ 6,2 * Р6 ‒ 6,1*Р6 = 0.
Обозначим показатель надежности АИС, учитывающий влияние интенсивности отказов аппаратуры через Рн. Тогда Рн будет равен 1 – Р6:
Рн =1-Р6
Решим систему уравнений относительно вероятности Р2:
Из уравнения 3 выразим вероятность Р3:
Р3=(2,3 / (3,4 +α3,6))*Р2. (1)
Из уравнения 4 выразим вероятность Р4 и подставим полученное значение вероятности Р3:
Р4=(3,4 * 2,3 /((3,4 +α3,6)*( (4,6 +α4,5))*Р2. (2)
Из уравнения 5 выразим вероятность Р5:
Р5=(4,5 * 3,4 * 2,3 /(3,4 +α3,6)* (4,5 +α4,6)*Р2. (3)
Из уравнения 6 выразим вероятность Р6:
Р6=[α3,6 * α2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 + α3,6)*(4,6 + α4,5)]*
* Р2 / (6,2 + 6,1). (4)
Из уравнения 2 найдем вероятность Р1:
Р1=Р2 * {(2,3 / 1,2) ‒ [α3,6 * 2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 + α3,6) * (4,6 + α4,5)]} / 1,2 (6,2 + 6,1). (5)
Подставим все полученные вероятности в нормирующее условие (1 уравнение системы):
< Р2*{(2,3 / 1,2) – [α3,6 * 2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 + α3,6) * (4,6 + α4,5)]} / 1,2 (6,2 + 6,1) > + < Р2 > + < (2,3 /(3,4 + α3,6))*Р2 > + < ( α3,4 * α2,3 /(3,4 + α3,6) * ( 4,6 + α4,5)) * Р2 > * Р2 / (6,2 + 6,1) > = 1. (6)
Из полученного выражения выразим вероятность Р2:
1
Р2={(2,3 / 1,2) – [α3,6 * 2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 + α3,6) * (4,6 +
α4,5)]} / 1,2 (6,2 + 6,1) + 1 +(α2,3 / (3,4 + α3,6)) + (α3,4 * α2,3 / (3,4 + α3,6)) + [α3,6 *
2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 + α3,6) * (4,6 + α4,5)] / (6,2 + 6,1). (7)
Подставив полученное выражение для вероятности Р2 в уравнение (1) получим значение вероятности Р6, тогда Рн будет равно:
Р н=1-Р6=1 ‒ [2,3 / 1,2) ‒ [α3,6 * 2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 +
н=1-Р6=1 ‒ [2,3 / 1,2) ‒ [α3,6 * 2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 +
α3,6) * (4,6 + α4,5)] * 1
{(2,3 / 1,2) ‒ [α3,6 * 2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4
+ α3,6) * (4,6 + α4,5]}/ 1,2 (6,2 + 6,1) + 1 +( α2,3 / (3,4 + α3,6)) + (α3,4 * α2,3 / (3,4
+ α3,6)) + [α3,6 * 2,3 / (3,4 + α3,6) + α4,6 * α3,4 * α2,3 / (3,4 + α3,6) * (4,6 + α4,5)]

/(6,2 + 6,1)) / (6,2 + 6,1). (8)
2.2. Анализ полученной математической модели и рекомендации по её использованию.
Данная математическая модель позволяет оценить надёжность АИС, влияние на ее работу, как нескольких отдельных факторов, так и их совокупности.
Также она позволяет определить время нахождения АИС в различных состояниях. Имеется возможность оценивать влияние отдельных параметров на различные показатели и находить их изменения в зависимости от какого-либо параметра. Также можно определить вероятности нахождения системы в различных режимах.
Определение времени нахождения АИС в различных состояниях проводится в соответствии с выражением:
Тi= 1/Ai где Ai = ∑ ai,j
Определение вероятности нахождения системы в различных режимах проводится с помощью формул, полученных в результате решения системы уравнений.
2.3. Вывод по разделу 2.
На основании построенного графа мы составили систему уравнений Колмогорова – Чэпмена, подставили нормирующее условие и выразили вероятности.
После этого провели анализ математической модели и пришли к выводу, что данная математическая модель позволяет оценить надежность АИС.
3. Количественная оценка надежности АИС.
3.1. Выбор исходных данных.
Для количественной оценки возьмём значения интенсивностей переходов АИС из i-го состояния в j-е состояние, представленных в таблицах 2 и 3, воспользуемся компьютерной программой PTC Mathcad 15.
3.2. Компьютерная программа оценивания надежности АИС.
В качестве математической программы выбрана интегральная среда PTC Mathcad 15, которая позволяет решать и анализировать широкий спектр задач. Данный выбор объясняется тем, что программа проста в использовании, построение большинства алгоритмов сводится к обычным математическим действиям, программа PTC Mathcad 15 доступна для массового пользователя, имеет встроенную систему автоматического пересчета и контроля единиц измерений в процессе вычислений, также PTC Mathcad 15 может взаимодействовать с большим количеством других компьютерных программ. Ниже приведен текст программы с уравнениями и полученными результатами для АИС.
P1=1
P2=1
P3=1
P4=1
P5=1
P6=1
Given
10 · P6 + 100 · Р5 ‒ 10 · Р1= 0
10 · P1 + 10 · Р6 ‒ 50 · P2 =0
50 · P2 ‒ 100 · P3 ‒ 0.001 · P3 = 0
100 · P3 ‒ 0.001 · P4 ‒ 100 · P4 = 0
100 · P4 ‒ 0.001 · P5 ‒ 100 · Р5 = 0
0.001 · P3 + 0.001 · Р4 + 0.001 · P5 ‒ 10 · P6 = 0
P1 + P2 + P3 + P4 + P5 + P6 = 1
Otvet = find (P1, P2, P3, P4, P5, P6)

0.143
0.143
0.143
Otvet = 0.143
0.143
0.143
3.3. Анализ результатов количественного оценивания.
Из полученных результатов видно, что быстрота решения задач системы большей частью зависит от количества поступаемых команд, и в меньшей степени от воздействия помех. Но при дальнейшем увеличении интенсивности помех и времени их воздействия, быстрота решения задач будет существенно снижаться.
3.4. Оценка влияния быстроты решения задач на надежность АИС.
Рассмотрим, как изменятся скорость решения задач в различных режимах, если будем менять α2,3, α4,6 от минимальных до максимальных значений.
Для удобства результаты отобразим на графике (рисунок 2). Покажем зависимость быстроты решения задач в режиме ожидания (в данном случае Р3) от α2,3,α4,6
α2,3,α4,6= 0.001 – 1000.. Результаты представлены в таблице:
Таблица 4
| α2,3 | α4,6 | P3 |
| 0.001 | 0.001 | 0,067 |
| 0.01 | 0.01 | 0,067 |
| 0.1 | 0.1 | 0,067 |
| 1 | 1 | 0,066 |
| 10 | 10 | 0,062 |
| 100 | 100 | 0,037 |
| 1000 | 1000 | 0,007 |
Р

Рисунок 2. График зависимости влияния быстроты решения задач на надежность АИС.
3.5. Вывод по разделу 3.
После проведенного анализа математической модели функционирования АИС, мы оценили надежность АИС воспользовавшись программой PTC Mathcad 15.
Далее провели оценку влияния быстроты решения задач на надежность АИС и построили график зависимости влияния быстроты решения задач на надежность АИС. В заключении мы пришли к следующему: при увеличении количества поступаемых команд скорость их обработки снижается согласно закону, представленному на графике (рисунок 2). Следовательно, чем меньше поступает команд, тем меньше требуется время на их обработку.
Так же следует отметить, что использование ЭВМ для оценки показателей эксплуатационных свойств представляется более эффективным и сэкономит время, так как аналитическое решение этой задачи на листе бумаги громоздко и трудоёмко.
ЗАКЛЮЧЕНИЕ.
В процессе выполнения курсовой работы был проведён анализ особенностей применения и эксплуатации АИС и на его основании разработана структурно-эксплуатационная (содержательная) модель функционирования АИС. Затем была разработана математическая модель оценивания показателей эксплуатационных свойств АИС.
Кроме того, в курсовом проекте проведён анализ математической модели и даны практические рекомендации по её использованию. Как, например, для определения времени нахождения АИС в различных состояниях, а также для определения вероятностей нахождения в данных состояниях.
Разработка и анализ подобной математической модели для конкретной АИС позволит выявить и оценить её позитивные и негативные свойства, а также наметить пути повышения эффективности её использования и обеспечения эксплуатационных качеств.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ.
- Конспект лекций по Автоматизации судовождения.
- Родионов А.И., Сазонов А.Е. Автоматизация судовождения: Учеб. Для вузов.-3-е изд., перераб. и доп.-М.: Транспорт, 1992.-192 с.
- Адерихин И.В., Лавровский В.А., Романов А.В. Курсовой проект. Требования, выполнение и защита, 2001-72 с.
- Романов А.В. Применение методов ТМО для получения количественных характеристик, исследуемых процессов судовождения: Методические рекомендации.
- Маринич А., Проценко И., Резников В., Устинов Ю., Черняев Р., Шигабутдинов А. Судовая автоматическая идентификационная система. -М.: Судостроение, 2004-180 с.
- Резолюция ИМО MSC.74(69).
- Интернет ресурсы: http://seaman-sea.ru/ais/, http://dic.academic.ru
Слайд 1«Математические модели в расчетах на ЭВМ»
Основное
содержание курса лекций и практик
Преподаватель: к.т.н., доцент
Уразбахтина Анжелика Юрьевна
2016 г

Слайд 2
Общая характеристика математических методов для инженерных расчетов
на ЭВМ
Применение математических методов и ЭВМ при
проектировании способствует повышению технического уровня и качества проектируемых объектов, сокращению сроков разработки и освоения их в производстве.
Автоматизация проектирования особенно эффективна, когда от автоматизации выполнения отдельных инженерных расчетов переходят к использованию автоматизированных информационных систем (АИС) или систем автоматизированного проектирования (САПР).

Слайд 3Задачи, решаемые с помощью математических моделей, заложенных
в АИС или САПР:
Моделирование и мониторинг
разработки месторождений;
Информационные технологии в проектировании объектов обустройства месторождений;
Стандартизация и техническое регулирование;
Комплексные решения для корпоративных информационных систем;
Моделирование последствий экологических катастроф.

Слайд 4Математические модели –
являются основой математического обеспечения (МО)
САПР или АИС.
Разработка
математических моделей и алгоритмов является творческим и сложным этапом создания АИС или САПР, от которого в наибольшей степени зависят производительность и эффективность автоматизированной системы, и качество проекта.

Слайд 5Математическое обеспечение АИС или САПР
Математическое обеспечение (МО) – это
математические модели (ММ), методы и алгоритмы, по которым разрабатывается программное обеспечение (ПО) АИС или САПР, и которые позволяют осуществлять автоматизированное проектирование.

Слайд 6Математические модели: основные понятия
Под математической моделью (ММ)
объекта и его элементов понимают систему математических
отношений, описывающих с требуемой точностью изучаемый объект и его поведение в реальных или производственных условиях.
При построении ММ используют различные математические средства описания объекта – теорию множеств, графов, вероятностей, математическую логику, математическое программирование, дифференциальные или интегральные уравнения и т.д.

Слайд 7Математические модели: основные понятия
Структура ММ – общий
вид математических отношений модели без конкретизации числовых
значений фигурирующих в ней параметров.
Математическая модель описывает зависимость между исходными (входными) данными и искомыми величинами.

Слайд 8Схема обобщенной математической модели
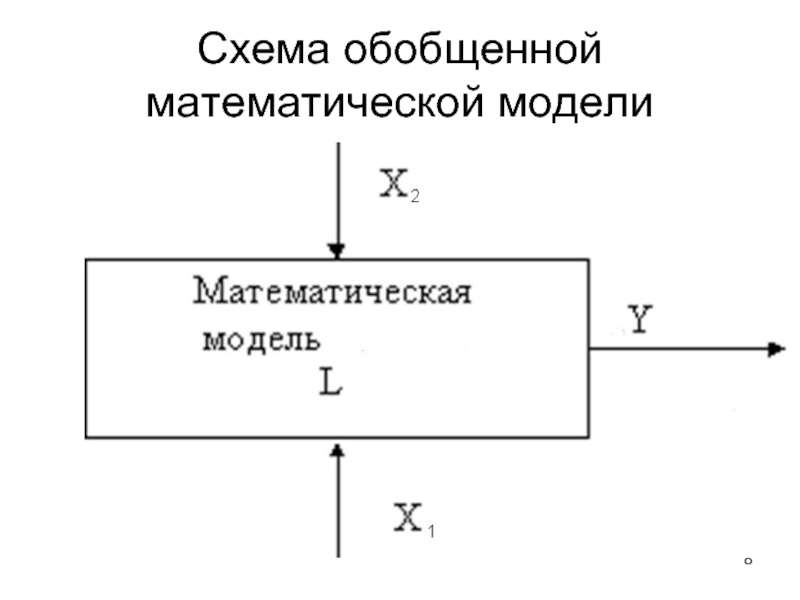
Слайд 9Данные математических моделей
X (X1,X2,…) – множество входных
данных (факторов, независимых переменных), из них: есть
группа варьируемых переменных и группа независимых переменных (констант).
L – математический оператор, определяющий операции над входными данными; это полная система математических операций, описывающих численные или логические соотношения между множествами входных и выходных данных;
Y – множество выходных данных (зависимых переменных); представляет собой совокупность критериев оценки моделируемого объекта или целевых функций улучшения объекта.

Слайд 10Математическое моделирование
по статистическим или экспериментальным данным
называется аппроксимацией или регрессионным анализом.
Цели регрессионного анализа:
определить силу влияния факторов X (X1,X2,…) на результат Y и найти неизвестные коэффициенты математической модели а,b,c и т.д.
При этом используются методы замены для преобразования нелинейных функций в линейные.

Слайд 11Входные данные математических моделей
Множество независимых переменных (констант)
из числа X (X1,X2,…) определяет среду функционирования
объекта, т.е. внешние условия, в которых будет работать проектируемый объект, эти факторы разработчик ММ изменить не может
Это могут быть:
технические параметры объекта, не подлежащие изменению в процессе проектирования;
физические возмущения среды, с которой взаимодействует объект проектирования;
тактические параметры, которые должен достигать объект проектирования.
Разделение входных параметров X (X1,X2,…) по степени важности влияния их изменений на выходные данные Y называется ранжированием.

Слайд 12Методы получения математических моделей
Получение математических моделей (ММ)
– процедура неформализованная, т.е. основные решения, касающиеся
выбора вида математических соотношений, характера используемых переменных и параметров, принимает человек (проектировщик) ММ.
Разработка ММ обычно выполняется специалистами конкретных областей с помощью традиционных экспериментальных исследований.
Методы получения математических моделей делят на теоретические и экспериментальные.

Слайд 13Теоретические методы разработки ММ –
основаны на
изучении физических закономерностей протекающих в объекте процессов,
определении соответствующего этим закономерностям математического описания, обосновании и принятии упрощающих предположений, выполнении необходимых выкладок и приведении результата к принятой форме представления модели.

Слайд 14Экспериментальные методы разработки ММ –
методы основаны на
использовании внешних проявлений свойств объекта, фиксируемых во
время эксплуатации однотипных объектов или при проведении целенаправленных экспериментов.

Слайд 15Порядок разработки ММ
1. Выбор свойств объекта, которые
подлежат отражению в модели. Он основан на
анализе возможных применений модели и определяет степень ее универсальности.
2. Сбор исходной информации о выбранных свойствах объекта (входной, выходной информации. Источниками ее являются: опыт и знания человека, разрабатывающего модель; содержание научно-технической литературы; описания прототипов – имеющихся ММ для элементов, близких по своим свойствам к исследуемому; результаты экспериментального измерения параметров и т.п.
3. Синтез структуры ММ в виде алгоритма, блок-схемы, аналитической формы, матрицы решения. Синтез структуры – это поиск и упорядочивание аналитических, логических и других зависимостей для преобразования входных параметров в выходные.
4. Расчет числовых значений параметров ММ (разработка тестового или контрольного примера). На этом этапе решается задача минимизации погрешности математической модели.
5. Оценка точности и адекватности ММ. Здесь устанавливается степень расхождения с тестовым примеров или с реальным объектом.
6. Разработка и оформление документации к ММ завершает ее проектирование.

Слайд 17Цели моделирования
ММ нужна для того, чтобы понять,
как устроен конкретный объект, какова его структура,
основные свойства, законы развития и взаимодействия
с окружающим миром (понимание);
ММ нужна для того, чтобы научиться управлять объектом (или процессом) и определить наилучшие способы управления при заданных целях и критериях (управление);
ММ нужна для того, чтобы прогнозировать прямые и косвенные последствия реализации заданных способов и форм воздействия на объект (прогнозирование).

Слайд 18Примеры целей моделирования
Какой режим эксплуатации технического объекта
выбрать для того, чтобы он был безопасным
и экономически наиболее выгодным?
2. Как составить график выполнения сотен видов взаимозависимых работ на объекте, чтобы они закончились в максимально короткие сроки?
3. Проследить (предсказать) экологические и климатические последствия прорыва крупного нефтепровода.
4. Проследить (предсказать) социальные последствия изменений цен на нефть.

Слайд 19Программное обеспечение ЭВМ, используемое на различных этапах
математического моделирования
Пакет MATLAB
Система MATLAB предназначена для
выполнения инженерных и научных расчетов и высококачественной визуализации получаемых результатов. Эта система применяется в математике, вычислительном эксперименте, математическом и имитационном моделировании.
Используя пакет MATLAB можно как из кубиков построить довольно сложную математическую модель, или написать свою программу.

Слайд 20Программное обеспечение ЭВМ, используемое на различных этапах
математического моделирования
MATHCAD
Универсальный математический пакет, предназначенный для выполнения
инженерных и научных расчетов, математического моделирования.
Ориентирован на естественный математический язык и “непрограммирующего пользователя”.
Пакет объединяет в себе: редактор математических формул, интерпретатор для вычислений, библиотеку математических функций, процессор символьных преобразований, текстовый редактор, графические средства представления результатов, возможности структурного программирования.

Слайд 21SMathStudio
программа для проведения математических вычислений и построения
графиков, позволяет работать с матрицами и векторами,
гиперболическими и тригонометрическими функциями, комплексными числами и булевыми выражениями.
Поддерживается использование примитивного программирования – циклов FOR и WHILE, условий IF и т.д. Пользователь программы имеет возможность быстрой вставки единиц измерения, может экспортировать созданные проекты в форматы HTML и MathCad или сохранять их в виде изображений BMP, GIF, JPG и PNG.
В SMathStudio есть встроенный справочник, посвященный тригонометрии, логарифмам, производным, пределам и прочим математическим понятиям.
Также в программе имеется коллекция примеров по решению математических задач.

Слайд 22EXCEL
Использование именно Excel в качестве средства разработки
математических моделей оправдывается не только высокой скоростью
моделирования.
Модели, разрабатываемые на базе этого поистине «народного» инструмента, как правило, наиболее просты в освоении, и даже их самостоятельная адаптация к меняющимся условиям может быть для более или менее квалифицированных пользователей Excel вполне посильной задачей.
К тому же, на рабочих местах использование иных программных средств может оказаться затруднительным – хотя бы в силу ресурсных ограничений (это могут быть и устаревшие компьютеры, и отсутствие локальной сети, и низкая квалификация пользователей).

Слайд 23Регрессионные математические модели
Регрессионные ММ применяются для исследования
зависимости изучаемой переменной Y от различных факторов
X и отображения их взаимосвязи в форме регрессионной математической модели.
В регрессионных моделях зависимая (объясняемая) переменная Y может быть представлена в виде функции
где – независимые (объясняющие) переменные, или факторы.
ММ регрессии можно использовать не только для анализа, но и для прогнозирования явлений различной природы.

Слайд 24Примеры регрессионных математических моделей
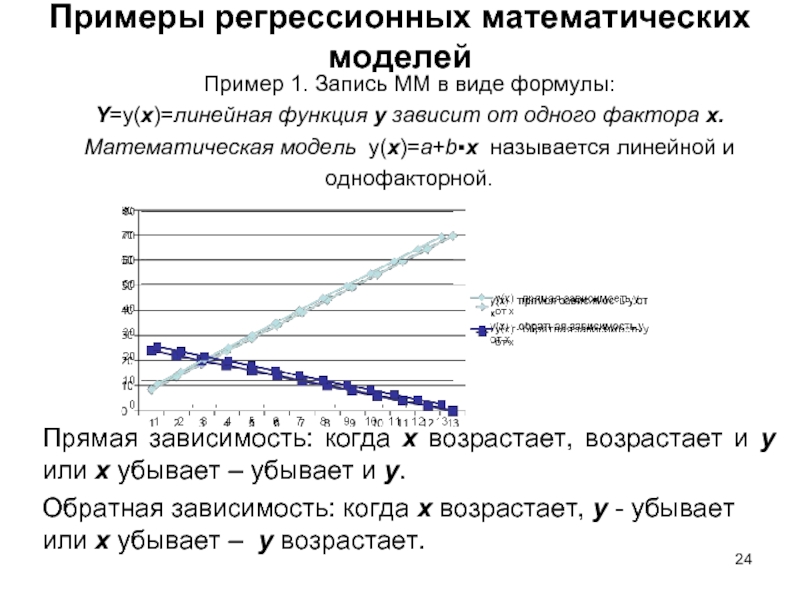
Пример 1. Запись ММ
в виде формулы:
Y=y(x)=линейная функция у зависит
от одного фактора х.
Математическая модель у(х)=а+b▪x называется линейной и однофакторной.
Прямая зависимость: когда х возрастает, возрастает и у или х убывает – убывает и у.
Обратная зависимость: когда х возрастает, у – убывает или х убывает – у возрастает.
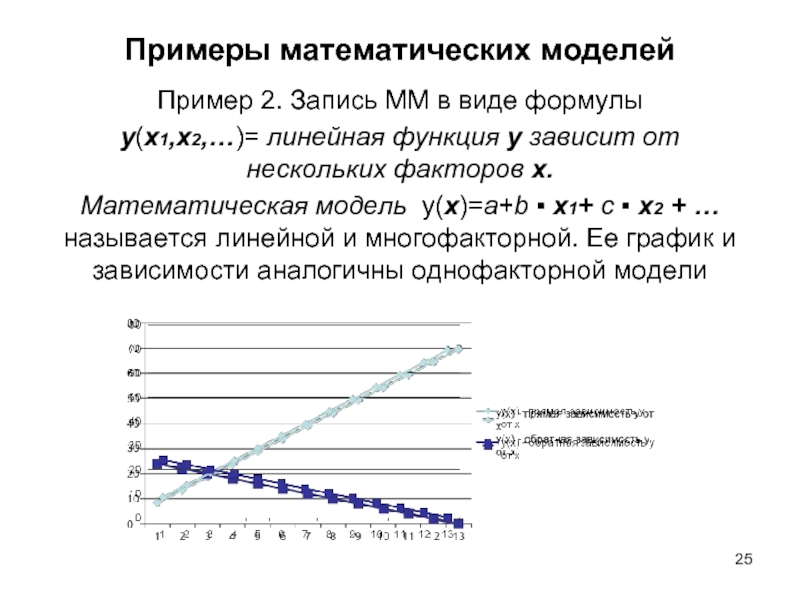
Слайд 25Пример 2. Запись ММ в виде формулы
y(x1,х2,…)= линейная функция у зависит от нескольких
факторов х.
Математическая модель у(х)=а+b ▪ x1+ с ▪ х2 + … называется линейной и многофакторной. Ее график и зависимости аналогичны однофакторной модели
Примеры математических моделей
Слайд 26Примеры математических моделей
Пример 3. Запись ММ в
виде формулы
y(x)=нелинейная функция у зависит от
одного фактора х.
Здесь может быть множество вариантов нелинейных однофакторных математических моделей:
3.1. Парабола или ее часть Y=y(x)=a+b▪x2 или y(x)=a+b▪х+с▪x2
3.2. Равносторонняя гипербола или ее часть – y(x)=a+b/x.
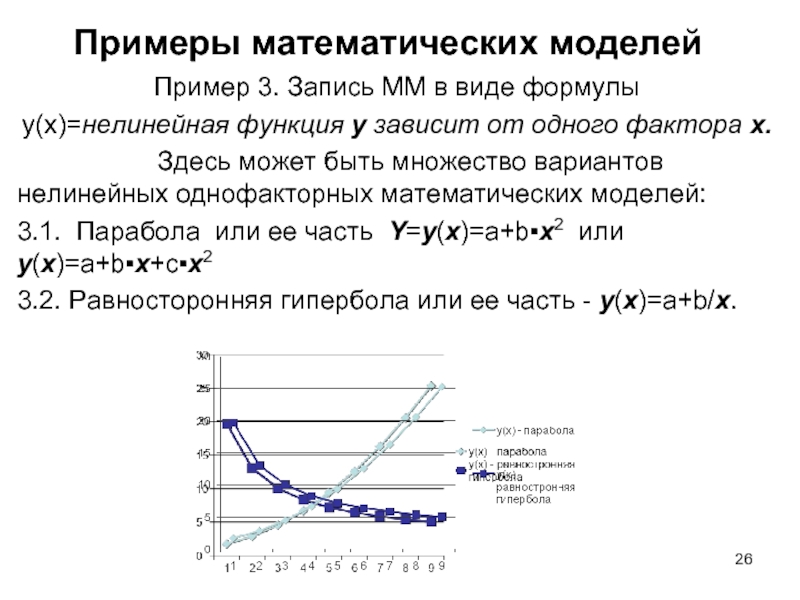
Слайд 27Примеры математических моделей
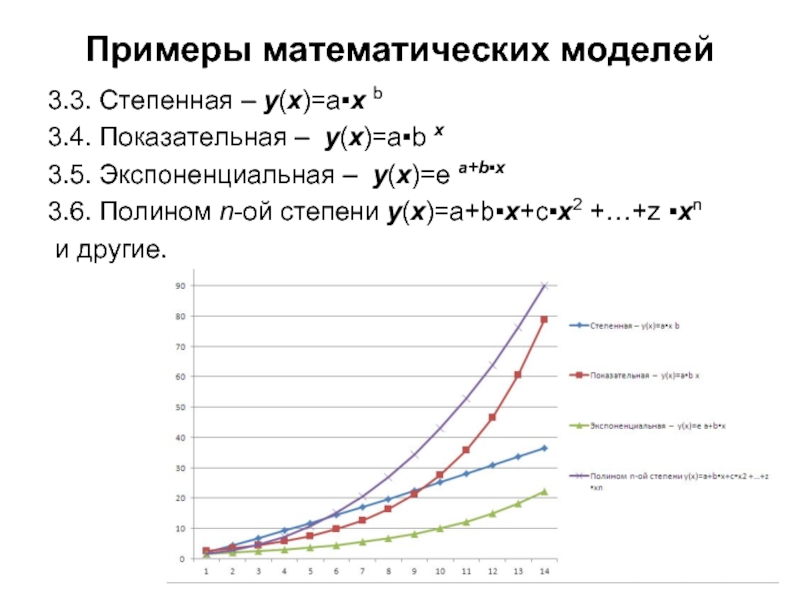
3.3. Степенная – y(x)=a▪x b
3.4. Показательная – y(x)=a▪b х
3.5.
Экспоненциальная – y(x)=е а+b▪х
3.6. Полином n-ой степени y(x)=a+b▪х+с▪x2 +…+z ▪xn
и другие.
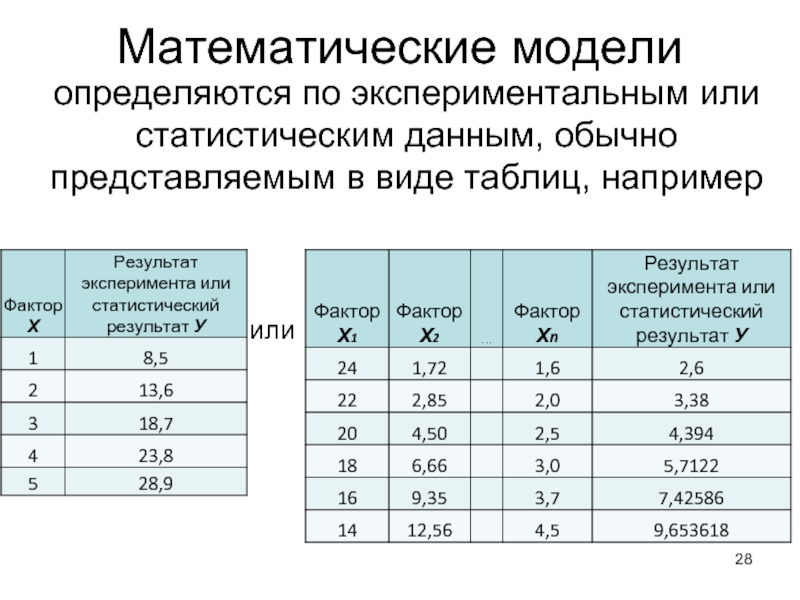
Слайд 28Математические модели
определяются по экспериментальным или статистическим
данным, обычно представляемым в виде таблиц, например
или
Слайд 29Ранжирование факторов х
1. для линейных
моделей можно производить по значению коэффициента корреляции
ry,x . Чем ближе значение | ry,x | к 1, тем сильнее влияние фактора х на результат у.
2. по значимости фактора х для правильного функционирования объекта моделирования. Значимость устанавливается путем опроса экспертов в нефтегазодобывающей промышленности.
При разработке регрессионных математических моделей проводят ранжирование факторов (X1,X2,…) . В результате ранжирования определяется – будет ли фактор хi входить в модель или нет.

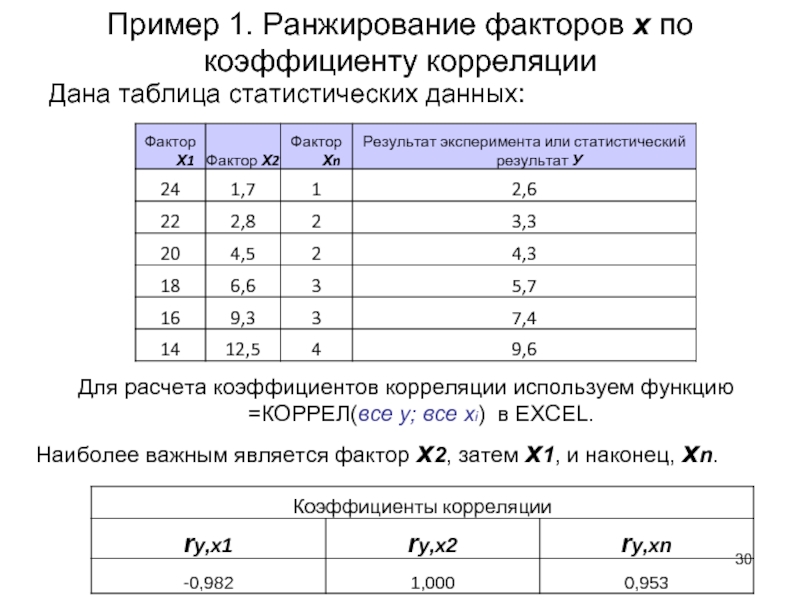
Слайд 30Пример 1. Ранжирование факторов х по коэффициенту
корреляции
Дана таблица статистических данных:
Для расчета коэффициентов корреляции
используем функцию =КОРРЕЛ(все y; все xi) в EXCEL.
Наиболее важным является фактор х2, затем х1, и наконец, xn.
Слайд 31Пример 2. Ранжирование факторов х экспертами

Слайд 32
Неизвестные а, b, c и т.п. математических
моделей находятся с помощью метода наименьших квадратов
(МНК).

Слайд 33Проверка регрессионных математических моделей
Проверка правильности ММ заключается
в разработке и проведении набора тестов, а
также в:
визуальной проверке по графикам заданного у и смоделированного умм.
сравнении сумм заданного у и смоделированного умм.
Проверке, что ∑ (заданное у – смоделированное умм)2 → min.
определении относительной погрешности аппроксимации EОТН (%) по формуле
Относительная погрешность модели должны быть меньше 7%

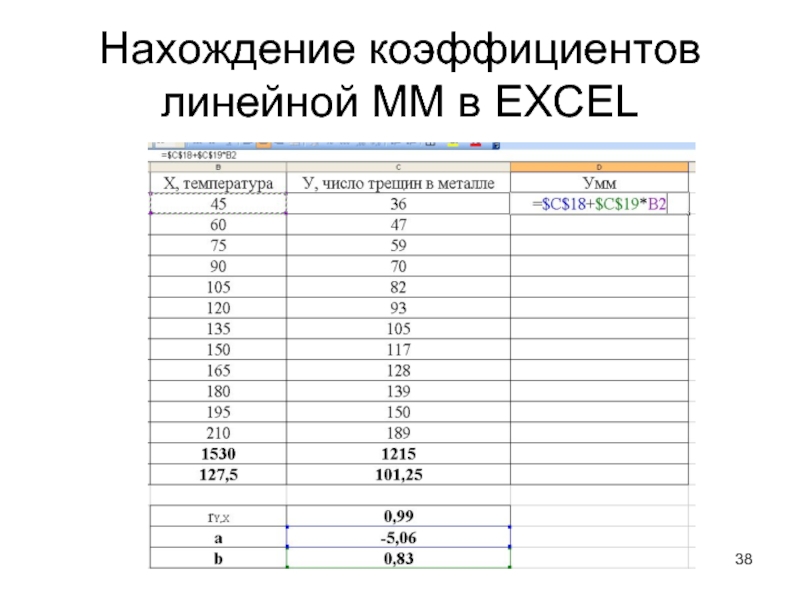
Слайд 34Нахождение коэффициентов линейной ММ в EXCEL
1. Дана
таблица с результатами наблюдений. Отранжировать таблицу по
возрастанию Х.
2. Найти сумму Х и сумму У.
3. Найти Хср и Уср (средние значения)
4. Построить график У от Х и убедиться, что требуется определить ЛИНЕЙНУЮ модель (график должен напоминать прямую линию).
5. Найти значение коэффициента корреляции rY,X и убедиться, что У существенно зависит от Х.
6. Найти коэффициент b модели с помощью функции
=ЛИНЕЙН(все У;все Х)
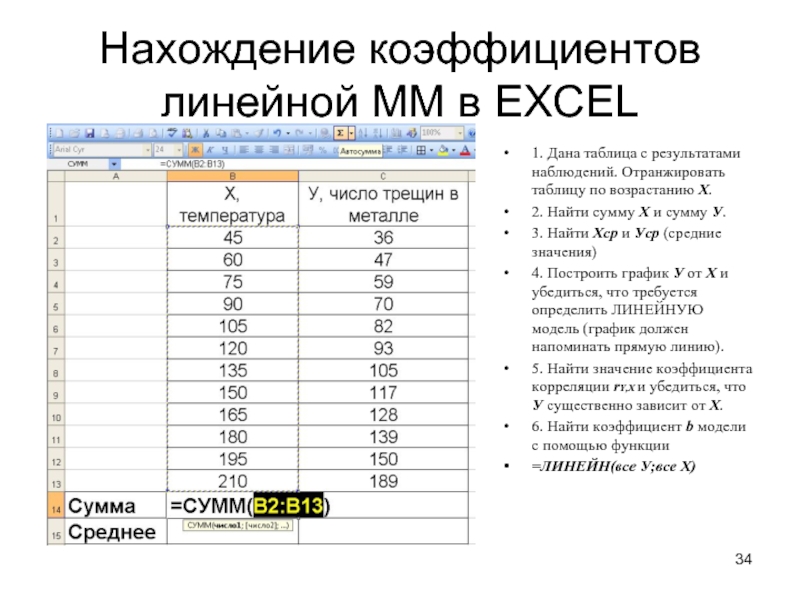
Слайд 35Нахождение коэффициентов линейной ММ в EXCEL
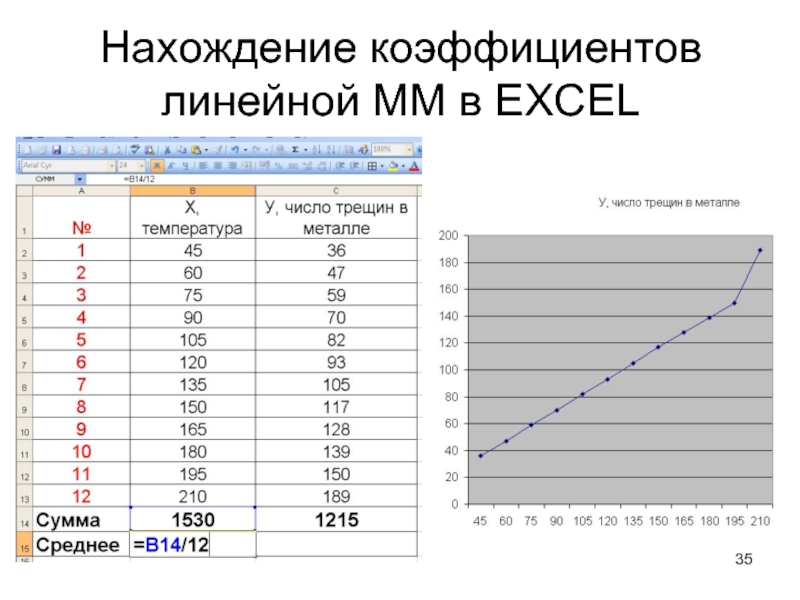
Слайд 36Нахождение коэффициентов линейной ММ в EXCEL
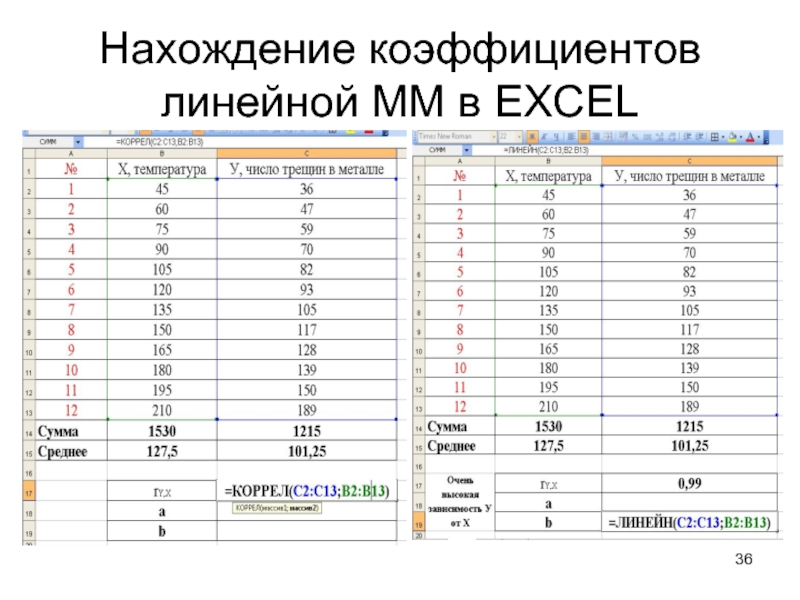
Слайд 37Нахождение коэффициентов линейной ММ в EXCEL
7. Найти
коэффициент а модели по формуле
=Уср−Хср*b
8. Вычислить столбец чисел по модели Умм=a+b*X
9. Найти сумму чисел Умм. Эта сумма должна быть приблизительно равной сумму всех У.
10. Построить на одном поле графики У и Умм. Сравнить их. Графики должны быть расположены близко друг к другу, пересекаться или даже совпадать.
11. Найти среднюю относительную ошибку аппроксимации модели Е отн. Для этого вычислить столбец значений дробей = abs(У−Умм)/У
Найти сумму и среднее этих дробей.
Если среднее значение дробей Еотн меньше 7, то признаем математическую модель хорошего качества.
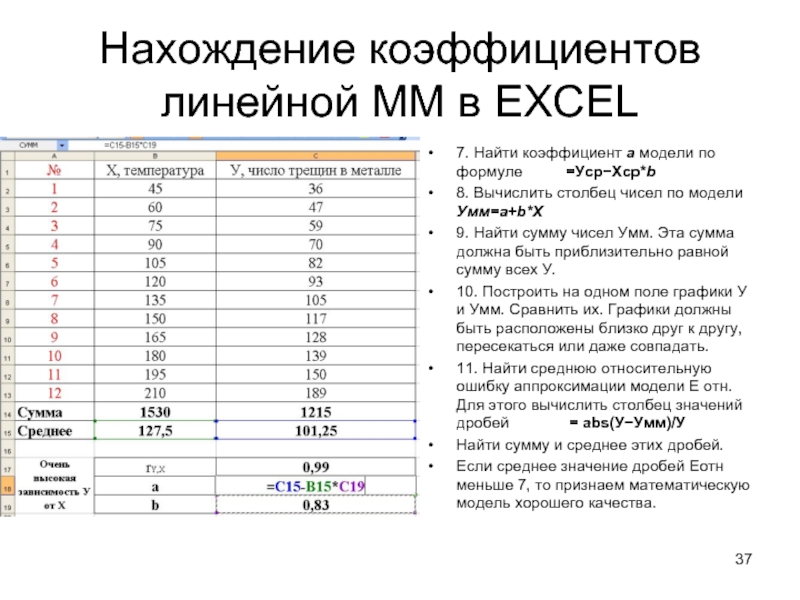
Слайд 38Нахождение коэффициентов линейной ММ в EXCEL
Слайд 39Нахождение коэффициентов линейной ММ в EXCEL
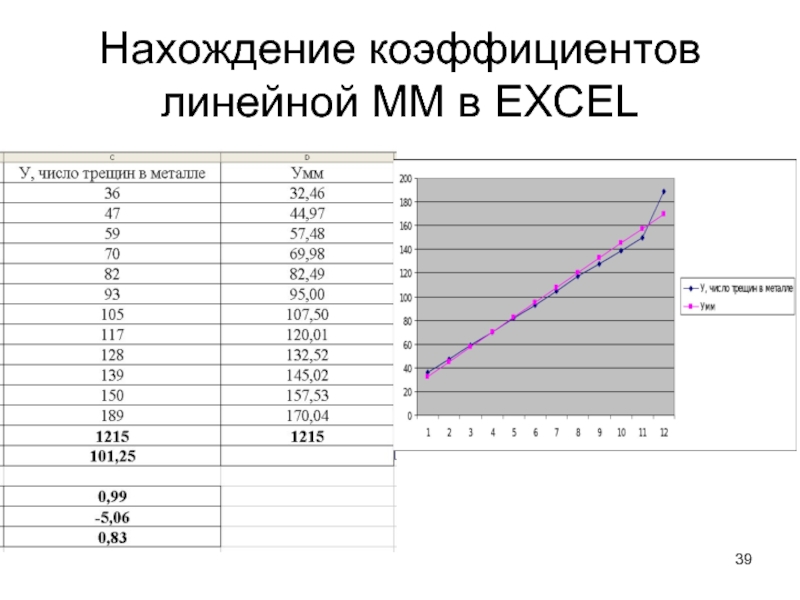
Слайд 40Нахождение коэффициентов линейной ММ в EXCEL
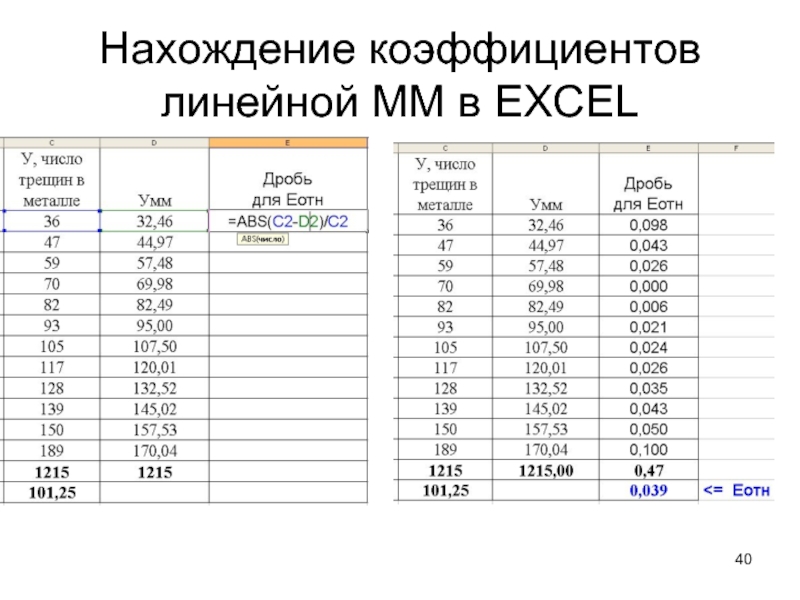
Слайд 41Нахождение коэффициентов линейной ММ в EXCEL
Так как
Еотн=0,039 и существенно меньше 7, признаем модель
хорошего качества, и выполняем с помощью модели прогноз количества трещин, которые возникнут при температуре 250 град. Для этого в формулу модели подставляем найденные коэффициенты а и b:

Слайд 42Метод наименьших квадратов (МНК) в матричной форме
для определения коэффициентов регрессионных ММ
матрица независимых факторов
х, в первый столбец этой матрицы обязательно записываются только 1. Состав остальных столбцов зависит от предполагаемой математической формулы модели.
матрица результирующих значений процесса или работы производственной системы
где

Слайд 43Применение МНК в MathCAD
покажем
на примере определения коэффициентов линейных математических моделей
a+b⋅x и c+d⋅x1+f⋅x2+k⋅xn по данным из таблиц со слайда 28.
Таким образом определили линейные математические модели 3,4+5,1⋅x и -4,796+0,176⋅x1+0,385⋅x2+1,585⋅xn

Слайд 44Применение МНК в SmathStudio
Как видно из примеров,
результаты применения МНК не зависят от использованной
программы.

Слайд 45Определение коэффициентов нелинейных однофакторных математических моделей
Дана таблица
с экспериментальными данными.
Отранжируем все данные в таблице
по возрастанию х.
Строим график у.
По графику убеждаемся, что функция ММ y(x) нелинейная.
Высказываем предположение, какая это функция (парабола, гипербола, степенная и т.д.)
Формируем матрицу Х в соответствии с выбранной нелинейной функцией.
Определяем коэффициенты модели.
Оцениваем точность модели.

Слайд 46Пример определения коэффициентов нелинейных однофакторных математических моделей
в Excel методом линеаризации
Дана таблица
График представляет собой
часть параболы, т.е. в модель введем x2
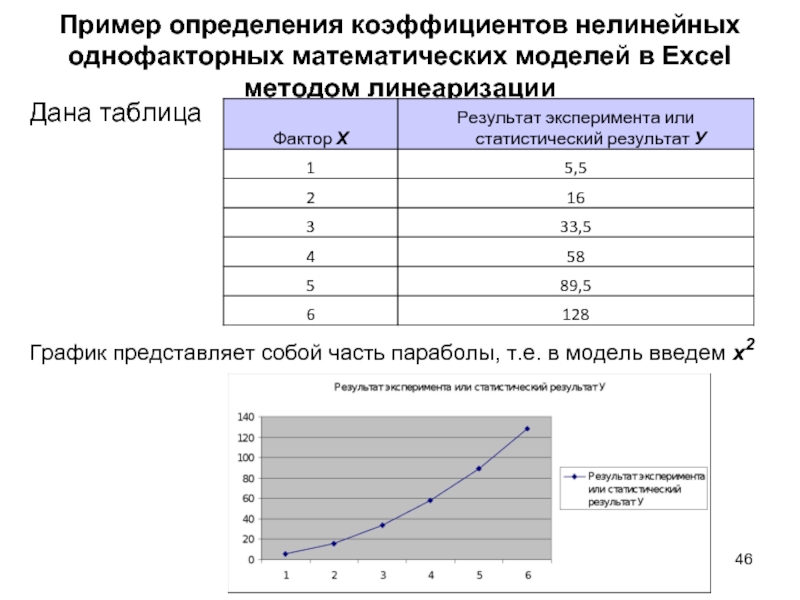
Слайд 47Пример определения коэффициентов нелинейных однофакторных математических моделей
в Excel методом линеаризации
Действия как в примерах
на слайдах 34 … 41, вместо фактора Х в расчетах участвует Х^2
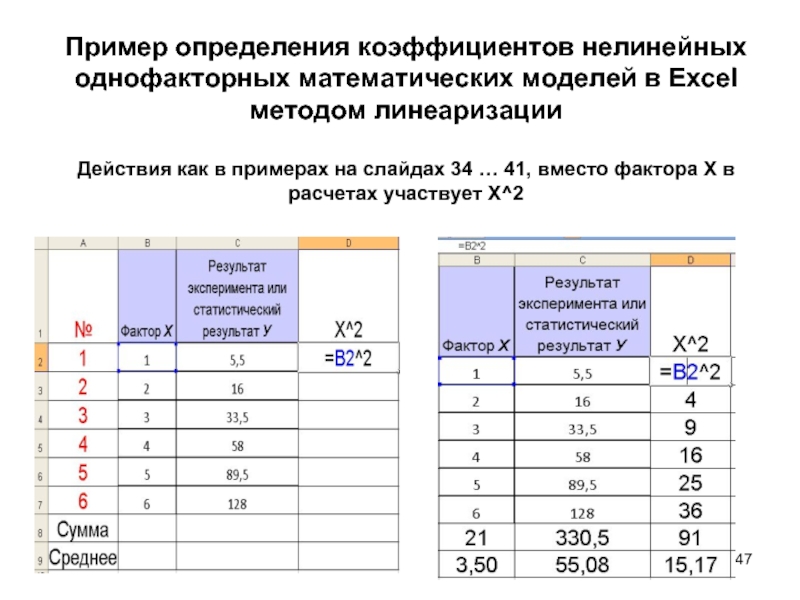
Слайд 48Пример определения коэффициентов нелинейных однофакторных математических моделей
в Excel методом линеаризации
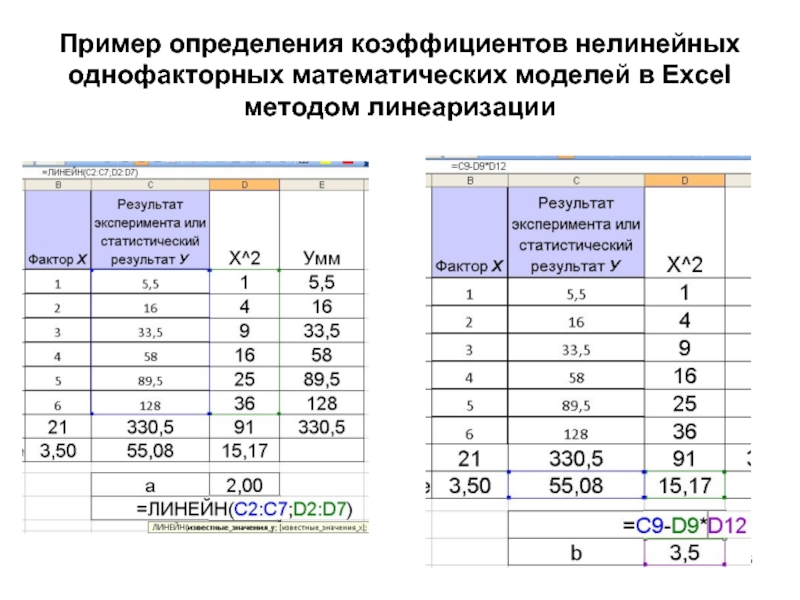
Слайд 49Пример определения коэффициентов нелинейных однофакторных математических моделей
в Excel методом линеаризации
В данном примере нелинейная
модель – идеальна (графики У и Умм совпали)
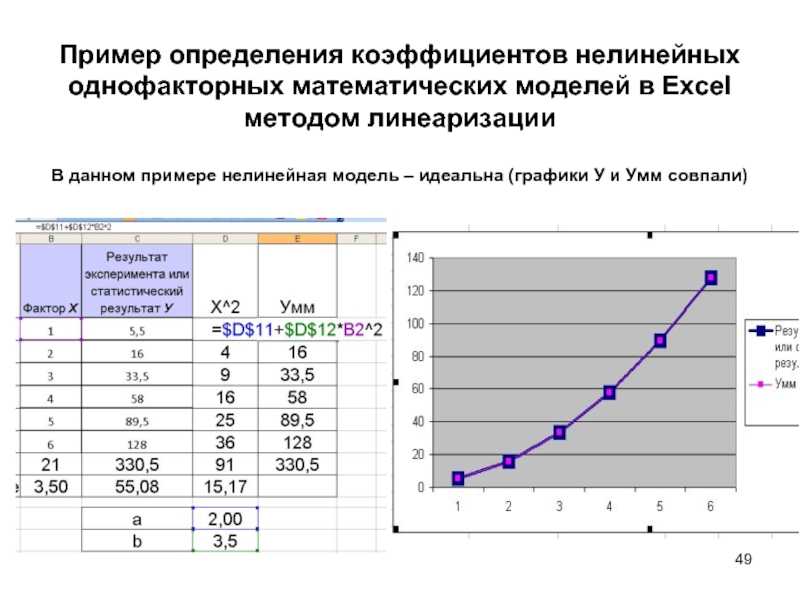
Слайд 50Пример определения коэффициентов нелинейных однофакторных математических моделей
в Excel
I. При линеаризации модели Умм=а+b/X
вместо Х
во всех расчетах используется дробь 1/Х.
II. Для степенных моделей при линеаризации используются натуральные логарифмы ln:
1) Y=a*bX
Ln(Y)=Ln(a*bX )=Ln(a)+Ln(bX )=Ln(a)+X*Ln(b),
2) Y=a*Xb
Ln(Y)=Ln(a*Xb )=Ln(a)+Ln(Xb )=Ln(a)+b*Ln(X),
и в расчетах участвуют столбцы чисел Ln(Y) и Ln(X)

Слайд 51Пример определения коэффициентов нелинейных однофакторных математических моделей
в MathCAD
В MathCAD формируем
матрицу Х.
Первый столбец в ней заполняем 1, второй столбец заполняем значениями x2.
Применяем МНК.
Получаем коэффициенты модели.
Результат – математическая модель y(x)=2+3,5×2.

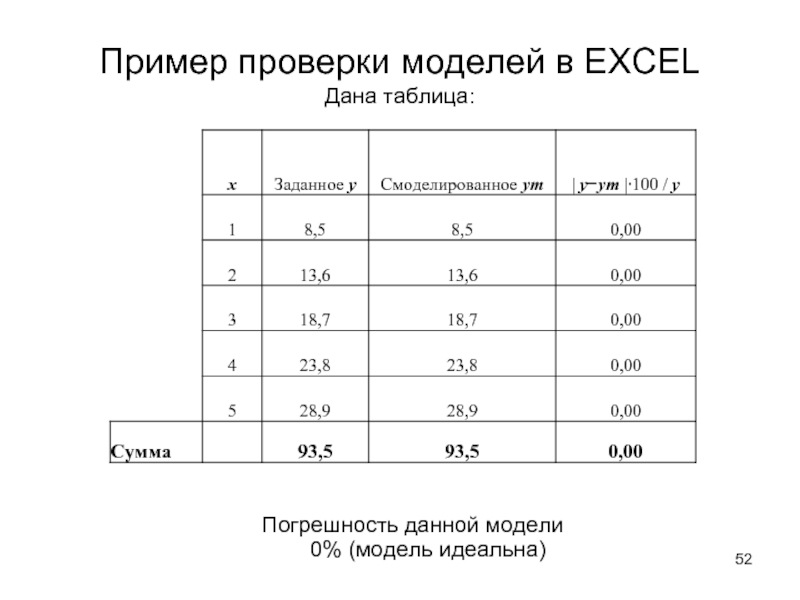
Слайд 52Пример проверки моделей в EXCEL
Дана таблица:
Погрешность данной
модели 0% (модель идеальна)
Слайд 53Фиктивные переменные в моделях
Переменные Х могут быть
не только количественными (числами), но качественными. Например,
диаметр скважины – величина числовая; расположение скважины (вертикально, наклонно, искривлено …) – параметр качественный. Качественные параметры преобразуют в числа – 0 или 1.
Например, Х=1 – вертикальное расположение; Х=0 – горизонтальное расположение.

Слайд 54Регрессионные математические модели могут быть объединены в
системы, в которые включаются и функции цели
моделирования

Слайд 55Аналитические математические модели в виде системы уравнений/неравенств
Аналитические
модели представляют собой явно выраженные зависимости выходных
параметров от входных или внутренних параметров.
Пример линеаризованной аналитической математической модели:
ММ=
где
, – параметры моделируемого объекта;
− ограничения, накладываемые на функционирование объекта окружающей средой;
– целевая функция моделирования.

Слайд 56Формулировка задачи линейного программирования (ЗЛП)
Реализуются линеаризованные математические
модели в виде систем с помощью линейного
программирования, Симплекс-метода и др.:
«Имеется некоторая величина, являющаяся линейной функцией ряда переменных, которые, в свою очередь, должны удовлетворять ограничениям, выраженным в виде системы линейных равенств или неравенств. Требуется отыскать такие неотрицательные значения переменных, удовлетворяющих системе ограничений, при которых величина, являющаяся их линейной функцией, принимала бы наименьшее или наибольшее значение.»

Слайд 57Пример решения задачи линейного программирования
Постановка задачи. Найти
минимум целевой функции:
при указанных ограничениях:
где х и y − объем добычи нефти и газа;
a и b − трудоемкость добычи нефти и газа;
– ограничение по количеству резервуаров;
– ограничение по количеству используемого оборудования;
– ограничение по количеству используемых месторождений.

Слайд 58Решение задачи линейного программирования
1. Неравенства (1)…(3) преобразовывают
в равенства:
2. Строят 3 графика по равенствам
из п. 1
3.Заштриховывают
область,
соответствующую
неравенствам (1…3)
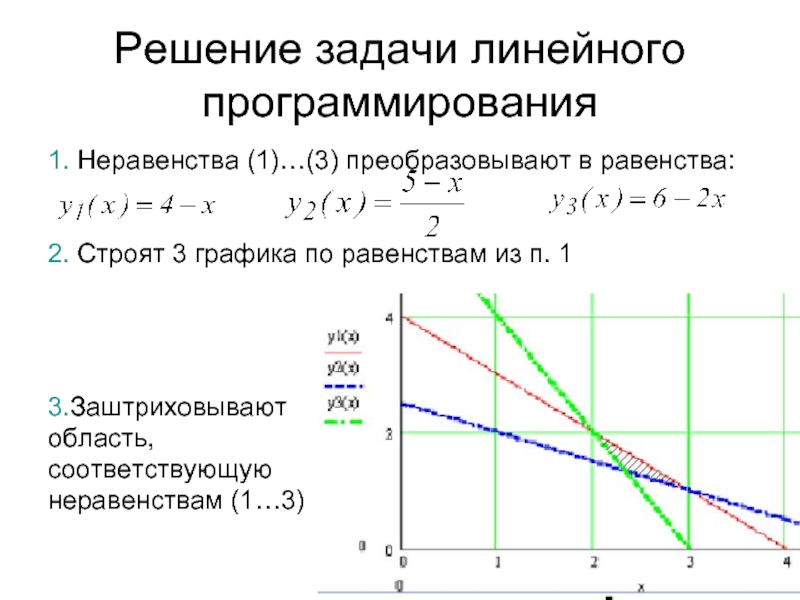
Слайд 59Решение задачи линейного программирования
4.Находят точки пересечения 3-х
графиков, их заносят в матрицы х и
у, вычисляют значения G (x, y), определяют наименьшее значение целевой функции G (x, y) и соответствующие значения х и у.
Ответ: G min=8,665 при х=2,333 и y=1,333.
Область возможных решений
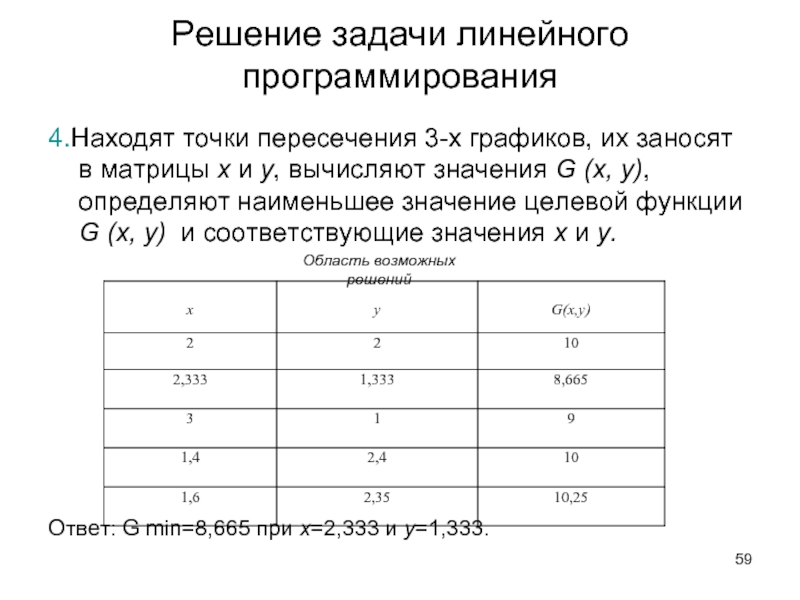
Слайд 60Рассмотрим еще примеры применения математических моделей различных
форм и записей

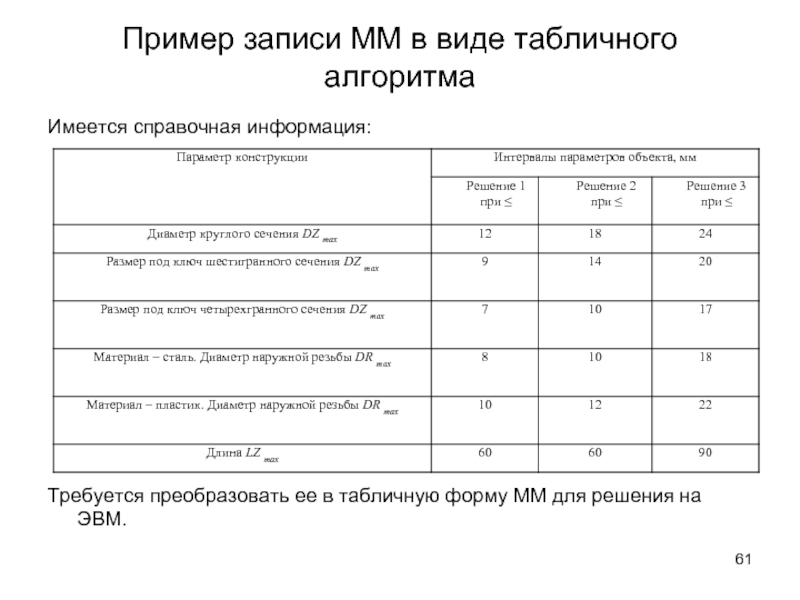
Слайд 61Пример записи ММ в виде табличного алгоритма
Имеется
справочная информация:
Требуется преобразовать ее в табличную форму
ММ для решения на ЭВМ.
Слайд 621. Составляется комплекс условий применимости (КУП) для
принятия решения:
2. где М – материал (0
– сталь, 1 – другие материалы); ФП – форма (0 – круглый, 4 – четырехгранник, 6 – шестигранник). И теперь заполняется ТА ММ.

Слайд 63Пример разработки ММ в аналитической форме и
словесного алгоритма
Постановка задачи:
Кусок проволоки данной длины
L согнуть в виде прямоугольника так, чтобы площадь прямоугольника была наибольшей.
Этап 1. Анализ требований. На рисунке представлен прямоугольник и его стороны: а – длина прямоугольника, b – ширина прямоугольника.
Периметр прямоугольника L=2a+2b
Площадь прямоугольника S=a⋅b, эта функция будет являться целевой функцией поиска значений параметров а и b.

Слайд 64Пример разработки ММ в аналитической форме и
словесного алгоритма
Этап 2. Разработка ММ. Математическая модель
(ММ) для решения задачи имеет вид:
Сформулируем словесный алгоритм:
Ввести значение L.
Вычислить Δ=L/1000.
Назначить a=Δ; S max =0; a max =0; b max =0;.
Вычислить b=(L−2a)/2.
Вычислить S= a ⋅ b.
Если S≥ S max, то a max =a; b max =b; S max =S.
Вычислить a=a+Δ.
Если a
Печать a max; b max; S max.
Конец.

Слайд 66Этап 3. Проектирование и определение спецификаций.
Спецификация параметров
к алгоритму ММ
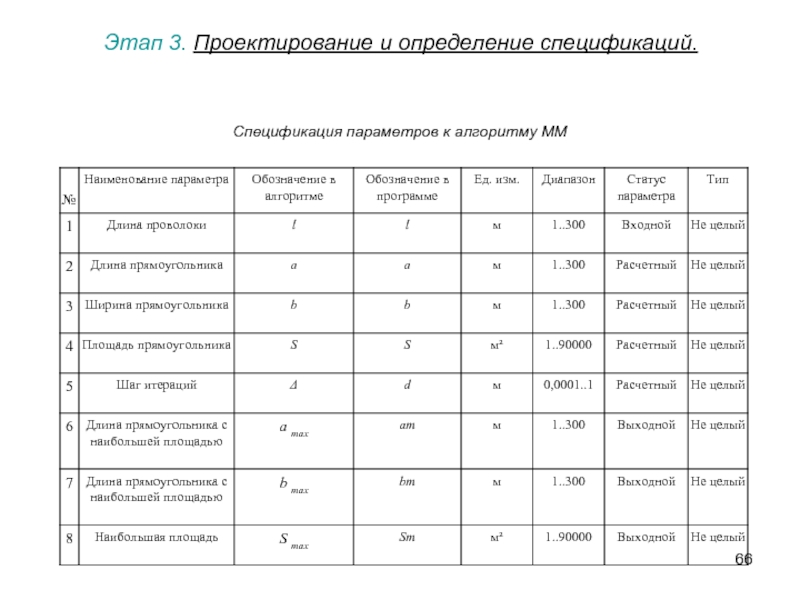
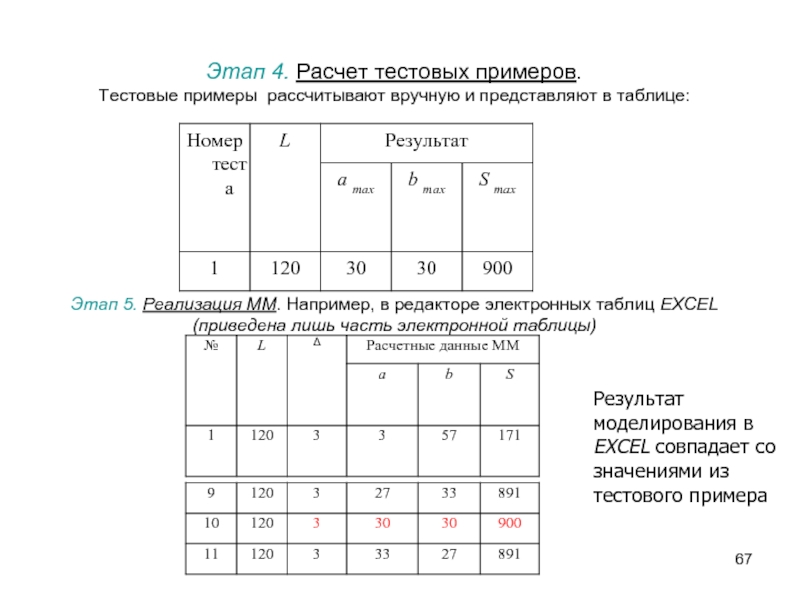
Слайд 67Этап 4. Расчет тестовых примеров.
Тестовые примеры рассчитывают
вручную и представляют в таблице:
Этап 5. Реализация
ММ. Например, в редакторе электронных таблиц EXCEL (приведена лишь часть электронной таблицы)
Результат моделирования в EXCEL совпадает со значениями из тестового примера
Слайд 68Многокритериальные ММ
В предыдущих примерах мы рассматривали одну
целевую функцию
моделирования, но в
реальных задачах их может быть несколько. Такие задачи называют многокритериальными.
Для реализации ММ на ЭВМ требуется множество целевых функции
свести к одной формуле. Например, аддитивный критерий объединяет (свертывает) несколько целевых функций в одну:
где λi − важность i -ой целевой функции для заказчика моделирования, выраженная в весовых коэффициентах; m − количество целевых функций.
Недостатки аддитивного критерия − субъективный подход к выбору весовых коэффициентов и все целевые функции должны стремиться либо к min, либо к max.
В случае, когда одни целевые функции стремятся к min, другие – к max, применяется минимаксный метод.

Слайд 69Комплексная целевая функция моделирования
где m – количество
альтернативных вариантов решения; Pi,j − текущее значение
i-го параметра для j-го варианта; λi − весовые коэффициенты значимости; max(Pi,j) или min(Pi,j) − наилучшее значение i-го параметра, наблюдаемое у множества анализируемых альтернатив; k – количество параметров проектируемого объекта, входящих в комплексную оценку.
Каждый из параметров «стремится» к своему оптимальному значению opt.
Решение сводится к поиску наибольшего значения целевой функции F из m вариантов.

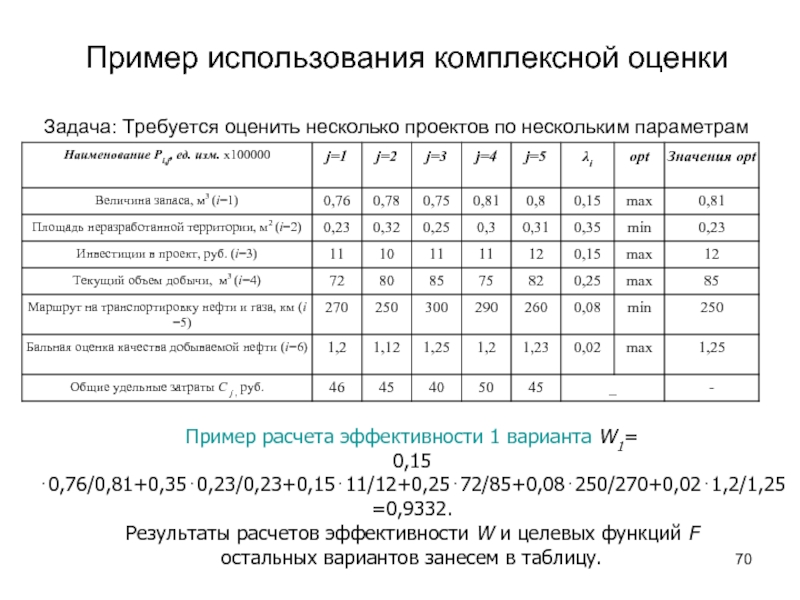
Слайд 70Пример использования комплексной оценки
Задача: Требуется оценить несколько
проектов по нескольким параметрам
Пример расчета эффективности 1
варианта W1=
0,15⋅0,76/0,81+0,35⋅0,23/0,23+0,15⋅11/12+0,25⋅72/85+0,08⋅250/270+0,02⋅1,2/1,25
=0,9332.
Результаты расчетов эффективности W и целевых функций F
остальных вариантов занесем в таблицу.
Слайд 71Пример использования комплексной оценки
Результаты расчета
Для наглядности представления
результатов моделирования строится
диаграмма значений комплексной целевой
функции по вариантам
Вывод:
лучший – 3-й вариант,
так как значение
целевой функции
здесь достигает
максимума.

Слайд 72Спасибо за внимание ☺
Следующие занятия будут практическими.
1. Перед первым практическим занятием узнайте свой
№ варианта по списку фамилий в журнале.
2. Скачайте файл «Перечень тем и заданий самостоятельной работы по ММ в расчетах на ЭВМ 2016»

