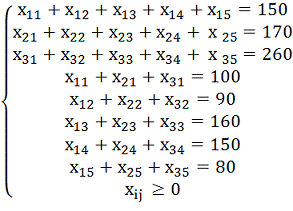Как составить математическую модель определить план - Сайт, где вы сможете решить свои вопросы

Фабрика
ООО «Мельник» специализируется на
выпуске двух сортов теста: бисквитное
и песочное. Для изготовления теста
используются такие ингредиенты как
яйца и сахар, так же затрачивается и
ресурсы труда. Для изготовления
бисквитного теста требуется 5 штук яиц
и 0,3 килограмма сахара, для изготовления
затрачивается 15 минут. А для изготовления
песочного теста потребуется 2 яйца, 0,25
килограмма сахара и 30 минут затраченного
времени. Стоимость 1 кг бисквитного
теста 30 руб., а песочного 20 руб. Общий
запас яиц равен 1000 шт., 75 кг сахара и 125
часов трудовых ресурсов.

2.1. Построение экономико-математической модели

1.
Переменные
задачи.

В
задаче требуется установить, сколько
продукции каждого вида надо производить,
поэтому искомыми величинами, а значит,
и переменными задачи являются суточные
объемы производства каждого вида
продукции:

х₁
– суточный
объем производства бисквитного
теста,
(кг);

х₂
– суточный
объем производства песочного
теста, (кг).

2.
Целевая функция.

В
условии задачи сформулирована цель –
добиться максимального дохода от
реализации продукции, т.е. критерием
эффективности служит параметр суточного
дохода, который должен стремиться к
максимуму. Чтобы рассчитать величину
суточного дохода от продажи продукции
обоих видов, необходимо знать объемы
производства, т.е. x₁
и х₂
кг продукции в сутки, а также цены на
продукцию бисквитного и песочного теста
– согласно условию 30 и 20 руб. за 1 кг
продукции соответственно. Таким образом,
доход от продажи суточного объема
производства продукции бисквитного
теста равен 30х₁
руб. в сутки, а от продажи песочного
теста – 20х₂
тыс. руб. в сутки. Поэтому запишем целевую
функцию в виде суммы дохода от продажи
продукции бисквитного и песочного
теста.

(руб.).

3.
Ограничения.

Возможные
объемы производства продукции х₁
и х₂
ограничиваются следующими условиями:

–
количество яиц, сахара и трудовых
ресурсов, израсходованных в течение
суток на производство теста обоих видов,
не может превышать запаса этих ингредиентов
на складе;

–
объем производства продукции не может
быть выражен отрицательными значениями.

Запишем
эти ограничения в математической форме.

Ограничение
по расходу яиц имеет вид:

(т/сутки).

Левая
часть ограничения – это расчет расхода
яиц на производство теста обоих видов.
Расход яиц на производство 1 кг бисквитного
теста – 5 шт.; на производство 1 кг песочного
теста – 2 шт. Тогда на производство х₁
кг бисквитного теста и х₂
кг песочного теста потребуется (5х₁
+ 2x₂)
шт. яиц. Правая часть ограничения – это
величина запаса яиц на складе – 1000 шт.

Аналогична
запись ограничения по расходу сахара:

(кг).

Так
же ограничение по трудовым ресурсам
имеет вид:

(чел.-ч.)

Неотрицательность
объемов производства задается как

Таким
образом, математическая модель задачи
имеет вид:

;

Экономико-математическая
модель задачи состоит в том, чтобы найти
такой план производства продукции
,
удовлетворяющий системе ограничений,
при котором целевая функция принимает
максимальное значение.

2.2. Определение оптимального плана производства симплексным методом

Приведем
задачу к каноническому виду. Для этого
в ограничения задачи введем дополнительные
переменные х₃,
х₄,
х₅
и перепишем условие задачи в виде
уравнений:

В
качестве базисных переменных возьмем
х₃,
х₄,
х₅,
тогда небазисные – х₁,
х₂.
Полагаем х₁
= х₂
= 0, тогда х₃
=1000, х₄=75,
х₅
=125.

1-я
итерация.

Составляем
первую симплексную таблицу, соответствующую
исходному опорному решению (таблица
3):

или

Таблица
3

c_i	БП	30	20	0	0	0	b_i
x₁	x₂	x₃	x₄	x₅
0	x₃	5	2	1	0	0	1000
0	x₄	0,3	0,25	0	1	0	75
0	x₅	0,25	0,5	0	0	1	125
_j	– 30	– 20	0	0	0	0

Все
строки таблицы, за исключением индексной,
заполняем по данным системы ограничений
и целевой функции. Элементы последней
строки рассчитываем:

и
т.д.

В
индексной строке две отрицательные
оценки, значит, найденное решение не
является оптимальным и его можно
улучшить. В качестве разрешающего
столбца следует принять столбец
переменной х₁:

,
т.е. k =1.

За
разрешающую строку принимаем строку
переменной х₃:

,
т.е. s =1.

Разрешающим
является элемент а₁₁=5,
т.е. вводим в базис переменную х₁,
выводим х₃.

2-я
итерация.

Формируем
следующую симплексную таблицу (таблица
4)

Таблица
4

c_i	БП	30	20	0	0	0	b_i
x₁	x₂	x₃	x₄	x₅
30	x₁	1	0,4	0,2	0	0	200
0	x₄	0	0,13	-0,06	1	0	15
0	x₅	0	0,4	-0,05	0	1	75
_j	0	– 8	6	0	0	6000

Из
таблицы 4 находим опорный план:

В
индексной строке таблицы 4 имеется одна
отрицательная оценка. Полученное решение
можно улучшить. Разрешающим элементом
является а₂₂=0,13

3-я
итерация.

Формируем
следующую симплексную таблицу (таблица
5).

Таблица
5

c_i	БП	30	20	0	0	0	b_i
x₁	x₂	x₃	x₄	x₅
30	x₁	1	0	0,38	-3,07	0	153,8
20	x₂	0	1	-0,4	7,7	0	115,4
0	x₅	0	0	0,13	-3,07	1	28,8
_j	0	0	2,3	61,5	0	6923

Из
таблицы 5 находим опорный план:

Так
как все оценки свободных переменных
положительные, найденное решение
является оптимальным:

Максимальная
прибыль составит 6923 рублей, при этом
необходимо произвести 153,8 кг бисквитного
теста и 115,4 кг песочного теста. В
оптимальном плане ресурсы яиц и сахара
равны нулю (х₃=х₄=0),
так как они используются полностью. А
резерв трудовых ресурсов х₅
= 28,8, что свидетельствует о излишках.

Построение
двойственной задачи

Оценки,
приписываемые каждому виду ресурсов,
должны быть такими, чтобы оценка всех
используемых ресурсов была минимальной,
а суммарная оценка ресурсов на производство
единицы продукции каждого вида – не
меньше цены единицы продукции данного
вида.

Обозначим
через y₁
– двойственную оценку дефицитности яиц,
через y₂
–сахара, y₃
– трудовых ресурсов. Тогда прямая и
двойственная задачи формулируются:

прямая
задача

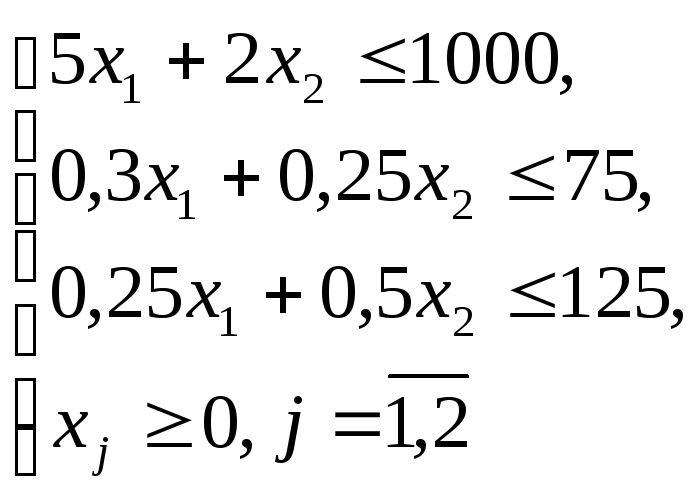
двойственная
задача

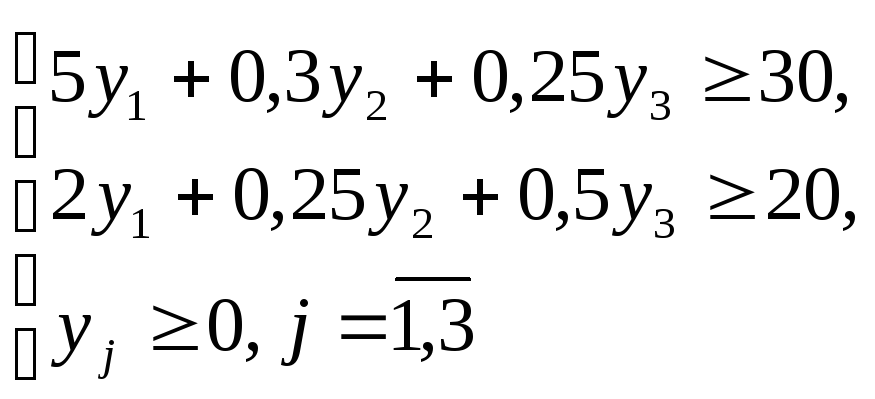
Решение
прямой задачи дает оптимальный план
производства песочного и бисквитного
теста, а решение двойственной задачи –
оптимальную систему оценок ресурсов,
используемых для производства:

Двойственные
оценки ресурсов y_i^*
– это оценочные коэффициенты _j
дополнительных переменных х₃,
х₄,
х₅
в последней симплексной таблице.

Исходя
из анализа оптимальных двойственных
оценок, можно сделать следующие выводы.

Ресурсы
яиц и сахара используются полностью.
Полному использованию этих ресурсов
соответствуют полученные оптимальные
оценки y₁,
y₂,
отличные от нуля. Значит, трудовые
ресурсы недоиспользуются (х₅
= 28,8 чел.-ч.).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Занятие 3, 4 (лекция)

Тема: Математические модели

План

Задача производственного планирования.
Общий вид задачи производственного планирования.
Простые способы записи задачи производственного планирования.
Варианты задачи производственного планирования.

Цели занятия:

На занятии вы узнаете

Понятие математической модели, аналитической и статистической модели;
Основные этапы построение математических моделей;
Примеры задач на построение математических моделей.

Порядок работы на занятии:

Прочитать текст лекции или прослушать лекцию преподавателя.
Законспектировать лекцию.
Ответить на контрольные вопросы, не заглядывая в конспект.
Проверьте свои ответы по конспекту.
Если ответы ошибочны, еще раз прочитайте лекцию и ответьте на контрольные вопросы. Будьте готовы к устному опросу и к применению знаний на практических занятиях.

В исследовании операций широко применяются как аналитические, так и статистические модели. Каждый из этих типов имеет свои преимущества и недостатки.

Аналитические модели более грубы, учитывают меньшее число факторов, всегда требуют каких-то допущений и упрощений. Зато результаты расчета по ним легче обозримы, отчетливее отражают присущие явлению основные закономерности. А, главное, аналитические модели больше приспособлены для поиска оптимальных решений.

Статистические модели, по сравнению с аналитическими, более точны и подробны, не требуют столь грубых допущений, позволяют учесть большое число факторов. Но и у них – свои недостатки: громоздкость, плохая обозримость, большой расход машинного времени, а главное, крайняя трудность поиска оптимальных решений, которые приходится искать «на ощупь», путем догадок и проб.

Наилучшие работы в области исследования операций основаны на совместном применении аналитических и статистических моделей.

Рассмотрим несколько математических моделей.

1 Задача производственного планирования

Начнем с рассмотрения простого примера. Школьный бар составляет и продает фруктовые коктейли двух видов.

Один литр коктейля “Утро” содержит 675 мл виноградного сока, 200 мл апельсинового сока и 125 мл клюквенного сока.

Коктейль “Свежесть” содержит те же соки, но в другой пропорции. Один литр “Свежести” состоит из 150 мл клюквенного, 450 мл виноградного и 400 мл апельсинового сока.

Коктейли в баре продаются порциями любого объема. Цена порции устанавливается из расчета: литр коктейля “Утро” стоит 1200 рублей, литр “Свежести” – 1000 руб.

В баре имеются запасы соков: 48 л апельсинового, 22 л клюквенного и 108 л виноградного сока.

Из трех соков можно составлять различные комбинации объемов коктейлей. Каждая такая комбинация соответствует своему производственному плану школьного бара. Производственный план представлен в данном случае двумя числами, соответствующими объемам выпуска двух коктейлей.

Некоторые планы могут оказаться невозможными (недопустимыми), для них не хватит имеющихся в наличии соков. Другие будут возможными, для них соков хватит.

Возможных, допустимых планов, конечно, чрезвычайно много. Каждому такому плану соответствует своя выручка от продажи коктейлей.

Задача состоит в нахождении наилучшего, оптимального плана, то есть такого, среди допустимых, плана, которому соответствует наибольшая выручка.

Для того чтобы решить эту задачу, запишем сначала исходные данные в удобной форме, сведем их в таблицу (табл. 1).

Таблица 1.

Коктейли

Соки (литры сока в 1 литре коктейля)

“Утро”

“Свежесть”

Запасы соков в баре (л)

виноградный

апельсиновый

клюквенный

0,675

0,200

0,125

0,450

0,400

0,150

108

Цена 1 литра коктейля (руб.)

1200

1000

В последнем столбце таблицы указано наличие соков в школьном баре. В предшествующих двух столбцах – расходы соков на изготовление 1 л коктейля. Для удобства сопоставления данные приведены в литрах сока на литр коктейля, так что сумма трех чисел в столбце равна 1 (одному литру). В.нижней строке приведены цены за один литр одного и другого коктейля.

Построим математическую модель задачи. Составление модели начинается с введения переменных. Мы хотим найти наилучший (оптимальный) производственный план. Такой план в данном случае – это пара величин, соответствующих количеству литров одного и другого коктейля.

Обозначим

посредством х₁ – количество литров коктейля “Утро”,

посредством х₂ – количество литров коктейля “Свежесть”.

Таким образом, переменные введены.

Теперь подумаем о тех ограничениях, в которых происходит составление производственного плана. Почему нельзя выбрать любой план? Потому, что запасы соков в баре ограничены. Переменные, которые мы ввели, позволят выразить эти ограничения в математической форме. Первые три строки таблицы •’ указывают расход соков на составление коктейлей и запасы соков. Каждая строка является основной для формирования неравенства по своему виду сока.

Это неравенство выражает, что суммарные расходы виноградного сока на коктейль “Утро” в количестве Х₁ литров и на коктейль “Свежесть” в количестве Х₂ литров (левая часть неравенства) не должны превосходить общих наличных запасов виноградного сока (правая часть неравенства). Аналогичное неравенство можно написать для апельсинового сока:

и для клюквенного сока:

Кроме того, количество литров коктейля не может быть отрицательной величиной, то есть

Таким образом, в целом мы получаем систему неравенств, характеризующих в математической форме условия составления плана производства коктейлей:

Такая система неравенств носит название системы ограничений задачи.

Любая пара значений переменных, то есть вектор (х₁, х₂), называется планом задачи.

Те пары значений, которые удовлетворяют всем неравенствам системы, то есть те планы, которые удовлетворяют системе ограничений, называются допустимыми планами.

Например, план (40; 50), согласно которому нужно составить 40 литров коктейля “Утро” и 50 литров коктейля “Свежесть”, является допустимым планом. Чтобы проверить его допустимость, достаточно подставить значения х₁ = 40 и х₂ = 50 в систему ограничений и убедиться, что каждое из неравенств выполнено.

Разумеется, допустимым будет и всякий план с меньшим неотрицательными объемами производства коктейлей. Отсюда следует, что допустимых планов бесконечно много.

С другой стороны, рассмотрим план (120; 50), в котором объем производства “Утро” увеличен в 3 раза, а объем производства “Свежести” оставлен прежним. Этот план – недопустимый. Он не удовлетворяет третьему неравенству системы, для его выполнения требуется 22,5 л клюквенного сока, а в наличии имеется всего 22 л. И хотя этот план удовлетворяет остальным неравенствам, запасов других соков хватает, все же выполнить этот план в тех условиях, которые указаны в задаче, не удается.

Конечно, недопустимым будет и всякий план с большим объемами производства коктейлей. Недопустимых планов бесконечно много.

Сосредоточим внимание на допустимых планах. Каждый из них дает школьному бару свой размер выручки. Чтобы ее сосчитать, нужно вспомнить о ценах за единицу готовой продукции – за литр коктейля (табл.1). Например, для плана (40; 50) выручка составит:

Z = 120040 + 100050 = 98000 (руб.) В общем случае формулу для определения выручки можно представить в следующем виде:

где z – величина выручки.

Мы хотим определить тот из допустимых планов, для которого выручка является максимальной.

Выражение для выручки представляет собой математическую запись нашей цели при решении задачи. Такое выражение называется целевой функцией задачи. Мы хотим найти наибольшее значение целевой функции на множестве допустимых планов задачи.

Математическая запись цели и условий (ограничений) задачи выглядит теперь следующим образом.

Такая запись носит название математической модели задачи. Она представляет собой соединение целевой функции (с указанием, что следует отыскать ее максимум) и системы ограничений.

Построение математической модели дает двоякую пользу. Во-первых, оно позволяет сформулировать задачу в ясной, отчетливой форме. Такая форма дает возможность быстро распознать допустимые и недопустимые планы, рассчитать соответствующую выручку.

Во-вторых, построение модели позволяет превратить содержательную экономическую задачу (в нашем примере – задачу о составлении коктейлей) в чисто математическую задачу о поиске максимального значения функции при условии, что переменные подчинены определенной системе ограничений. При решении этой математической задачи молено не знать ничего о смысле входящих в нее переменных и выражений, забыть, что речь идет о соках и коктейлях, выручке и школьном баре. Это позволяет использовать при ее решении универсальные математические методы, привлечь, если потребуется, вычислительную технику и программные средства.

Полученную математическую модель можно записать в более короткой форме с использованием матриц. Введем обозначения.

Пусть С есть двухмерный вектор-строка, соответствующий коэффициентам при переменных в целевой функции, С = (1200; 1000).

Пусть А есть матрица размерности 3×2, составленная из коэффициентов при переменных в системе ограничений:

Пусть В есть трехмерный вектор-столбец, составленный из правых частей неравенств, входящих в систему ограничений:

Пусть X есть двумерный вектор-столбец, составленный из переменных задачи:

Посредством О обозначен нулевой двумерный вектор-столбец:

Тогда, используя правила умножения матриц, математической модели можно придать следующую матричную форму:

max С X

Такая форма записи является более короткой и во многих случаях значительно более удобной для использования.

Как найти решение задачи, как вычислить оптимальный план? На какую максимальную выручку может рассчитать школьный бар? Сколько какого коктейля следует изготовить при этом? Следует ли изготавливать оба вида или выгоднее продавать лишь один вид коктейля? Все ли запасы соков будут при этом использованы? Если запасы соков изменились (часть ушла на другие нужды или прибыла новая партия соков), то как изменится оптимальный план? Насколько чувствителен оптимальный план к изменению цен на коктейли?

Если появилась возможность купить дополнительные объемы соков, то при каких ценах дополнительные затраты на их приобретение окупятся дополнительной выручкой от продажи коктейлей?

Ответы на эти вопросы (и многие другие вопросы такого рода) можно получить путем анализа математической модели. Позже мы научимся это делать для задач значительно более широкого класса, поэтому сейчас рассмотрим задачу производственного планирования в общем виде.

2 Общий вид задачи производственного планирования

В общем случае задача производственного планирования формулируется следующим образом. Предприятие распоряжается ресурсами различных типов. Среди таких ресурсов могут быть материально-вещественные (в нашем случае – соки), энергетические, трудовые, технические, финансовые и другие, не участвовавшие в нашем примере. Ресурсы каждого типа могут быть разделены на классы. Сырье – по видам сырья, трудовые – по профессиям и квалификации работников, техническим характеристикам, финансовые – по источникам финансирования и т.п. Пусть в результате такой классификации, такого разделения получилось m видов ресурсов.

Пронумеруем все виды ресурсов числами от 1 до m, буквой i будем обозначать номер вида ресурса. Таким образом, i удовлетворяет неравенству . Заметим, что ресурсы разных видов могут измеряться в различных единицах (тоннах, кубометрах, человеко-часах, рублях, штуках и др.).

Предприятие обладает некоторым запасом ресурса каждого вида. Запас ресурса i – го вида, измеренный в соответствующих ему единицах, обозначим посредством b_j. Индекс i около буквы b указывает, что запасы разных видов ресурсов могут быть различными.

Из этих запасов предприятие способно изготавливать различную продукцию (в нашем примере – коктейли). Обозначим буквой n общее число видов продукции, которые может выпустить предприятие из имеющихся ресурсов. Занумеруем все виды продукции числами от 1 до n. Буквой j будем обозначать номер вида продукции, так что выполняется неравенство . Продукция, как и ресурсы, может измеряться в различных единицах.

Пусть с_j – цена, по которой предприятие реализует каждую единицу продукции j–ro вида. Индекс j около буквы с указывает, что цена разных видов продукции может быть различной.

Производство продукции требует затрат ресурсов. Объем затрат зависит от вида ресурса, вида продукции и количества единиц продукции. Обозначим посредством а_ij норму затрат ресурса 1-го вида на производство продукции j–ro вида. Другими словами, а_ij – это количество ресурса i-го вида, затрачиваемое при производстве единицы продукции j–ro вида.

Задача производственного планирования состоят в том, чтобы определить, какую продукцию в каком объеме следует изготовить предприятию из имеющихся ресурсов с тем, чтобы доход от реализации продукции был наибольшим.

Построим математическую модель задачи. Сначала введем переменные. Посредством х_j обозначим искомый объем выпуска продукции j–ro вида. Математическую модель можно теперь записать в следующей форме:

Верхняя строка записи говорит о максимизации целевой функции. Сама целевая функция представляет собой сумму произведений цен на объем выпуска для различных видов продукции, то есть доход предприятия от продажи изготовленной продукции.

Фигурная скобка объединяет систему ограничений задачи, неравенства, входящие в систему, соответствуют различным видам ресурсов. Каждое такое неравенство говорит о том, что суммарное количество ресурса, используемое в производстве различных видов продукции, не превосходит общего запаса этого ресурса.

Рассмотрим, например, первое неравенство. В правой его части указана величина b₁ общий объем запаса ресурса первого вида. В левой его части находятся величина а_ij с одним и тем же первым индексом i=1 и различными вторыми индексами. Каждая такая величина а_ij указывает количество ресурса одного и того же первого вида, затрачиваемого на производство одной единицы продукции j–ro вида. Величина а_ij умножается на объем x_j произведенной продукции j–ro вида. Такое произведение дает затраты ресурса первого вида на производство всего количества произведенной продукции j–ro вида. Затем все эти затраты ресурса суммируются по всем видам продукции, таким образом, в левой части первого неравенства – суммарные затраты первого вида ресурса на производство всех видов продукции в соответствующих объемах. В правой части неравенства – общее количество первого вида ресурса, имеющееся в наличии. Само неравенство требует, чтобы расходуемый объем первого ресурса был не больше объема запаса этого ресурса. Аналогичный смысл, но для других видов ресурсов, имеют другие неравенства системы ограничений.

В последней строке системы ограничений указано, что количества производимой продукции не могут быть отрицательными. Заметим, что равенство нулю здесь не запрещено, то есть некоторые (или даже все) видs продукции предприятие может и не выпускать, хотя они и доступны для выпуска по имеющимся ресурсам.

Экономическая задача поиска плана производства продукции, дающего наибольший доход, превращается в математическую задачу поиска максимального значения целевой функции от n переменных при условии, что значения этих переменных подчинены системе ограничений, имеющих форму неравенств.

Всякий набор значений переменных (х₁х₂,…х_n) называется планом задачи.

Те планы, которые удовлетворяют системе ограничений, называются допустимыми планами.

Оптимальным планом; называется тот из допустимых планов, который дает наибольшее значение целевой функции среди всех ее значений на допустимых планах. Само это наибольшее значение целевой функции, то есть значение целевой функции на оптимальном плане, называется оптимумом задачи.

Решить задачу производственного планирования – значит найти оптимальный план и оптимум для ее математической модели.

3. Простые способы записи задачи производственного планирования.

Математическую модель задачи можно записать в другой, более компактной форме с использованием знака суммирования . В этой записи модель примет следующий вид:

Здесь выражение (i=l,…,m) в правой части записи указывает, что при каждом конкретном значении индекса i, лежащем в пределах от I до m, в систему входит свое неравенство, соответствующее этому значению i.

Аналогично, выражение (j=1,…,n) говорит о том, что неравенство представляет собой целую совокупность из n неравенств, каждое из которых получается при своем значении индекса j.

Особенно удобной и краткой является матричная форма записи:

Заметим, что переставлять местами сомножители в произведении матриц нельзя, если это сделать, может получиться совсем другой результат, а может и вообще перемножение матриц оказаться неосуществимым. Для правильного, корректного перемножения матриц их размерности должны быть согласованы. Поэтому важно, что в одних случаях мы рассматриваем именно вектор-строку, а в других – именно вектор-столбец. Отметим также, что хотя В и X – оба векторы-столбцы, но их размерности (их длина) различны. Размерность столбца В равна m, а размерность X равна n.

4. Варианты задачи производственного планирования

Мы рассмотрели простой вид задачи производственного планирования.

Возможны и другие, более сложные ее виды. Однако, и в этих случаях математическая модель строится без труда.

Например, по всем или некоторым видам продукции предприятие может иметь договоры с другими предприятиями – потребителями этой продукции. В соответствии с этими договорами предприятие должно выпустить течение месяца продукцию того или иного вида в объеме, не меньшем заданного. Пусть продукцию j–ro вида предприятие должно изготовить в объеме, не меньшем заданной величины dj. Тогда к системе ограничений следует дописать неравенство

Далее, предприятие может не только продавать продукцию, но и покупать продукцию других предприятий для своих производственных нужд. Для того, чтобы учесть затраты на покупку такой продукции, следует величину этих затрат, то есть произведение цены на объем покупки, ввести в целевую функцию со знаком “минус”.

Для того, чтобы учесть возможности использования такой продукции в производственном процессе, следует оформить соответствующее ограничение, в правой части которого вместо наличного объема ресурса будет находиться купленный объем продукции, используемый в качестве одного из ресурсов.

Если предприятие производит некоторую продукцию исключительно для собственных нужд (полуфабрикат), то такую продукцию можно рассматривать как покупаемую предприятием у себя самого по нулевой цене, с соответствующими естественными изменениями в модели.

Эти и многие другие дополнительные производственные условия легко могут быть учтены в математической модели. Они приводят лишь к расширению модели, увеличению числа ограничений и переменных, но не приводят к ее качественному принципиальному изменению.

5. Вопросы и упражнения

Опишите содержание задачи производственного планирования.

Сформулируйте математическую модель задачи производственного планирования. Объясните смысл входящих в нее обозначений, целевой функции, ограничений.
Что такое план задачи? Какие планы называются допустимыми, а какие – недопустимыми? Какой план называется оптимальным? Что такое оптимум задачи? В чем различие между оптимальным планом и оптимумом?
Модель задачи производственного планирования записывается в компактной форме (с помощью знака ), в матричной форме?
Приведите примеры (три конкретных примера) различных допустимых планов и три примера недопустимых планов для задачи о школьном баре.

Является ли допустимым план (0; 0)? Каким объемам выпуска коктейлей он соответствует? Какую выручку он приносит бару?

Предположим, что половина запасов каждого сока в баре оказалась с просроченной датой использования и непригодной к употреблению. Какие из Ваших допустимых планов сохранили свою допустимость? Остались ли недопустимые планы недопустимыми?

Предположим, что школьный бар обязался продавать 10 литров коктейля “Утро” и 15 литров коктейля “Свежесть” соседнему детскому саду, как ввести в математическую модель эти дополнительные условия? Будет ли теперь план (0;0) допустимым?
Предположим, что у школьного бара появилась возможность увеличить запасы апельсинового сока, покупая его по цене 800 руб. за литр. Бар стремится максимизировать прибыль, т.е. разность между выручкой от продажи коктейлей и затратами на покупку сока. Купленный сок вместе с имеющими запасами можно использовать для приготовления коктейлей, как изменится математическая модель в связи с изменившимися условиями?
В условиях предыдущего пункта предположим, что у бара появилась дополнительная возможность продавать не только коктейли, но и клюквенный сок по цене 1100 руб за литр, как изменится математическая модель в связи с этой новой ситуацией?
Кондитерская фабрика производит три вида карамели: сибирскую, праздничную и студенческую, для производства карамели используются три вида сырья: сахар, патока и фруктовое пюре. Для производства 1 тонны сибирской карамели требуется 500 кг сахара, 300кг патоки и 200 кг фруктового пюре. Чтобы изготовить 1 тонну праздничной карамели, необходимо 700 кг сахара, 200 кг патоки и 100 кг фруктового пюре. Для приготовления 1 тонны студенческой карамели требуется 600 кг сахара, 100 кг патоки и 300 кг фруктового пюре. На фабрике имеется 1000 тонн сахара, 1200 тонн патоки и 800 тонн фруктового пюре. Прибыль от реализации одной томны карамели составляет 4 млн.руб. для сибирской, 3 млн.руб. для праздничной и 2,5 млн.руб. – для студенческой карамели.

Требуется построить математическую модель для определения плана производства карамели, обеспечивающую фабрике прибыль от ее реализации.

Предположим, что кондитерская фабрика может выпускать еще один вид карамели – петербургскую. Для производства 1 тонны петербургской карамели требуется 400 кг сахара, 300 кг патоки и 300 кг фруктового пюре, прибыль от реализации тонны петербургской карамели составляет 3,5 млн.руб. Как изменится математическая модель в этой новой ситуации?
Предположим, что кондитерская фабрика имеет возможность покупать патоку по цене 1,4 млн.руб. за тонну и продавать сахар по цене 1 млн.руб. за тонну. Внесите соответствующие изменения в математическую модель.
Фабрика производит два вида красок: первый – для наружных, а второй – для внутренних работ. Для производства красок используются два ингредиента: А и В. Максимально возможные суточные запасы этих ингредиентов составляют 6 и 8 т соответственно. Известны расходы А и В на 1 т соответствующих красок (табл. 1.1). Изучение рынка сбыта показало, что суточный спрос на краску 2-го вида никогда не превышает спроса на краску 1-го вида более чем на 1 т. Кроме того, установлено, что спрос на краску 2-го вида никогда не превышает 2 т в сутки. Оптовые цены одной тонны красок равны: 3 тыс. руб. для краски 1-го вида; 2 тыс. руб. для краски 2-го вида.

Необходимо построить математическую модель, позволяющую установить, какое количество краски каждого вида надо производить, чтобы доход от реализации продукции был максимальным.

Таблица 1.1

Параметры задачи о производстве красок

Ингредиенты

Расход ингредиентов, т ингр./т краски

Запас, т ингр./сутки

Краска 1-го вида

Краска 2-го вида

Занятие 5 (лекция)

Тема: Задача о диете

1. Общий вид задачи о диете.

Мы рассмотрим так называемую задачу производственного планирования и ее математическую модель. Рассмотрим теперь другую задачу, относящуюся к другой области экономических исследований, не к области производства, а к области потребления. Это – так называемая задача о диете, задача о составлении наиболее экономного рациона, наиболее экономной корзины продуктов питания.

Человек в течение месяца может потреблять любые из n видов продуктов питания (хлеб, молоко, рыбу, яйца и т.д.). Пронумеруем все эти виды продуктов числами от 1 до n. Пусть j– номер продукта питания. 1j n. Продукты могут измеряться в разных единицах (килограммах, литрах, штуках). Обозначим посредством c_j цену единицы j-го продукта питания.

Каждый продукт содержит различные полезные вещества, полезные характеристики. Это – необходимые человеку белки, жиры, углеводы, различные микроэлементы, разнообразные витамины, калории. Пусть общее число видов таких полезных составляющих равно m. Пронумеруем их числами от 1 до m, порядковый номер такой полезной составляющей будем обозначать посредством i, так что 1im. Разные полезные составляющие измеряются в различных единицах. Посредством b_i обозначим то количество единиц i– й составляющей, которое человеку необходимо потребить в течение месяца.

Обозначим посредством a_ij то количество единиц i– го полезного вещества (например, витамина А), которое содержится в одной единице j– го продукта питания (например, в одном килограмме мяса).

Задача состоит в том, чтобы рассчитать наиболее экономную диету, то есть продовольственный рацион наименьшей стоимости, содержащий, тем не менее, все необходимые человеку полезные вещества в нужных объемах. Построим математическую модель для решения этой задачи.

Сначала следует ввести переменные. Нам необходимо определить рацион, то есть установить, сколько какого продукта питания необходимо приобретать человеку для потребления. В соответствии с этим и введем переменные. Обозначим посредством x_j; искомое количество единиц j– го продукта питания, 1jn.

Математическую модель задачи о диете можно записать теперь следующим образом:

В верхней строке модели указана минимизация целевой функции. Сама целевая функция представляет собой сумму произведений цен на объем покупаемых для потребления продуктов питания. Таким образом цель, формализованная в виде минимизации целевой функции – это найти набор объемов продуктов питания наименьшей суммарной стоимости.

Система ограничений представляет собой систему неравенств. Неравенства указывают, что общее количество полезных веществ, содержащихся во всех потребляемых объемах продуктов питания, должны быть не меньше заданной границы.

Рассмотрим, например, первое неравенство систем ограничений. Левая часть неравенства представляет собой сумму произведений. В этих произведениях первый сомножитель имеет один и тот же первый индекс i = 1, но различные вторые индексы j. Следовательно, во всех этих случаях речь идет об одном и том же первом полезном веществе, но о разных продуктах питания. Величина a_ij равна количеству первого полезного вещества в одной единице j– го продукта питания. После умножения этой величины на x_jполучим количество первого полезного вещества, содержащегося во всем потребляемом объеме j– го продукта питания. Суммирование по всем продуктам питания дает количество первого полезного вещества, содержащегося во всем потребляемом рационе. Это левая часть первого неравенства. Требуется, чтобы она была больше или равна правой части, в которой указан наименьший допустимый объем потребления первого полезного вещества. Первое неравенство требует, таким образом, чтобы рацион обеспечивал потребление первого полезного вещества не ниже некоторой границы.

Мы рассмотрели подробно смысл первого неравенства. Аналогичный смысл имеют остальные неравенства системы ограничений. В последней строке системы указано, что потребляемые объемы продуктов питания должны быть неотрицательны. Допускается, что они могут быть равны 0, то есть некоторые из потенциально возможных продуктов питания в рацион могут не войти. Но отрицательными они быть не могут.

Как и для задачи производственного планирования, построение математической для задачи о диете означает переход к решению математической задачи. Решение математической задачи сводится к поиску минимума некоторого выражения (целевой функции) при условии, что переменные удовлетворяют системе неравенств (системе ограничений). При решении математической задачи можно отвлечься от содержательного смысла входящих в нее символов, от того, что некоторые из них – это объемы продуктов питания, другие – объемы полезных веществ, третьи – цены, что перед нами задача о наиболее экономном рационе. Именно это и позволяет использовать при ее решении универсальные и мощные математические средства.

Две рассмотренные нами экономические задачи – задача производственного планирования и задача о диете, существенно отличаются друг от друга по содержанию. В одной речь идет о производстве, в другой – о потреблении. Однако рассмотрение их математических моделей показывает, что они весьма похожи друг на друга. Общей является сама структура модели: в обоих случаях имеется целевая функция, экстремальное значение которой требуется найти, и система ограничений в виде системы неравенств. Целевая функция и выражения, стоящие в левых частях неравенств, в обоих случаях являются линейными функциями от многих переменных. Различия между моделями состоят в том, что в них требуется отыскать разные экстремумы целевой функции: в одном случае – максимум, а в другом – минимум. Кроме того, знаки неравенств в системе ограничений повернуты в разные стороны. Как мы увидим дальше, эти различия не являются принципиальными. Одну математическую модель можно легко перестроить в другую. Математические методы, применяемые для решения этих задач, оказываются одинаковыми.

Терминология, используемая в связи с этими моделями, тоже одинакова. Вектор значений переменных называется планом задачи. Те планы, которые удовлетворяют системе ограничений, называются допустимыми планами. Тот из допустимых планов, на котором целевая функция достигает своего минимального значения на множестве всех допустимых планов, называется оптимальным планом. Само это минимальное значение целевой функции носит название оптимума задачи.

2. Простые способы записи задачи о диете.

Как и для задачи производственного планирования, здесь также можно использовать различные формы компактной записи модели.

Например, можно записать ее в такой форме:

Можно воспользоваться и матричной формой записи задачи. Используя те матричные обозначения, которые были введены в связи с моделью задачи производственного планирования, нашу новую модель можно представить в следующей матричной форме:

3. Варианты задачи о диете.

Заметим, что мы рассмотрели простой вид задачи о диете. Возможны и другие, более сложные его виды. Так, например, кроме полезных веществ в продуктах питания могут содержаться и вредные вещества, потребление которых следует ограничить. Ограничения, связанные с такими вредными веществами, без труда могут быть введены в модель. Для этого следует для каждого такого вещества задать предельно допустимый объем его потребления b_k . затем в систему ограничений для каждого вредного вещества следует ввести новое неравенство, совершенно аналогичное предыдущим (левая часть которого указывает содержание данного вредного вещества во всех продуктах питания вместе взятых), и которое заканчивается знаком b_k. Так же следует поступить и для тех веществ, которые в небольших количествах являются полезными, но чрезмерное потребление, которых приносит вред. Для таких веществ следует ввести в систему два неравенства, одно из которых требует обеспечить потребление этого вещества в объеме, не ниже заданной нижней границы, а другое – в объеме, не выше заданной верхней границы.

Если некоторое вещество требуется потреблять в строго заданном количестве, то для него соответствующее ограничение будет не неравенством, а равенством.

Таким образом, в общем случае в математической модели задачи о диете могут присутствовать как неравенства со знаком , так и неравенства со знаком , а также равенства со знаком =.

Вопросы и упражнения

Опишите содержание задачи о диете.
Сформулируйте математическую модель задачи о диете. Объясните смысл входящих в нее обозначений, целевой функции, ограничений.
В чем сходство и в чем различие между математическими моделями задачи производственного планирования и задачи о диете?
Человеку для нормальной жизнедеятельности необходимо ежемесячно потреблять 3,5 кг. Белка, 1,7 кг. Жиров, 15кг. Углеводов, 250г. Минеральных солей.

В таблице указано количество граммов этих полезных веществ, содержащихся в килограмме потребляемых продуктов, а также цена за 1кг. Каждого продукта.

Полезные вещества

Содержание (г) полезного вещества в 1кг. продукта

Мясо

Молоко

Масло

Картофель

Крупа

Белки

200

140

Жиры

800

Углеводы

240

700

Мин. соли

Цена 1кг. Продукта (тыс.руб.)

3,8

0,8

5,4

1,2

0,9

Построить математическую модель для составления месячного рациона наименьшей стоимости, обеспечивающего месячное потребление человеком полезных веществ в необходимых объемах.

Источник

Методы решения задач математического моделирования

ОГЛАВЛЕНИЕ

Введение

1. теоретическая часть

.1
Определение основных понятий математического моделирования и характеристика
этапов создания математической модели

.2
Характеристика типовых задач математического моделирования и подходов к их
решению

.3 Определение
и характеристика линейного программирования

.4
Характеристика симплекс-метода как основного аппарата решения задач линейного
программирования

.5 Основные
этапы, особенности и методы решения транспортной задачи

2. Практическая часть

2.1 Составление
математической модели задачи планирования производства

.2 Решение
задачи планирования производства геометрическим способом

.3 Решение
задачи планирования производства симплекс-методом

.4 Решение
задачи планирования производства с помощью табличного процессора MS Excel

.5
Составление математической модели транспортной задачи

.6 Нахождение
опорного плана транспортной задачи методом северо-западного угла

2.7 Нахождение
опорного плана транспортной задачи методом наименьшего элемента

.8 Решение
транспортной задачи методом потенциалов

.9 Решение
транспортной задачи при помощи табличного процессора Excel

Заключение

Литература

Приложение 1

Приложение 2

Введение

Различные технико-экономические и экономические производственные задачи,
начиная от оптимальной загрузки станка и раскройки стального листа или полотна
ткани до анализа межотраслевого баланса и оценки темпов роста экономики страны
в целом, приводят к необходимости решения тех или иных задач линейного
программирования.

На сегодняшний день это является важным инструментом экономического
анализа: позволяет получить четкое представление о состоянии предприятия,
охарактеризовать и количественно описать его внутреннюю структуру и внешние
связи. Таким образом, экономико-математическое моделирование работы предприятия,
фирмы, основанное на анализе его деятельности, должно обогащать этот анализ
результатами и выводами, полученными после решения соответствующих задач.

Часто эксперимент с математической моделью может заменить реальный
эксперимент, который либо слишком дорог, либо невозможен по тем или иным
причинам. Все это и дает весомую актуальность применению задач линейного
программирования в современных экономических условиях.

Главной целью решения транспортной задачи является планирование наиболее
рациональных путей и способов транспортировки товаров.

Транспорт играет исключительно важную роль в экономике любой страны,
обеспечивая межпроизводственные связи в различных отраслях промышленности. В
условиях жесткой конкуренции каждое предприятие вынуждено минимизировать свои
расходы, значительную часть которых составляет именно транспортные расходы.

Целью данной курсовой работы является изучение методов решения задач
математического моделирования на примере задач планирования производства и
транспортной задачи.

Из поставленной цели вытекают следующие задачи:

1. Изучение теоретической части материала.

2. Создание математических моделей задач планирования производства и
транспортных задач

. Решение задачи планирования производства аналитическим и
программным методами.

. Решение транспортной задачи различными методами и программным
способом.

1. теоретическая часть

1.1
Определение основных понятий математического моделирования и характеристика
этапов создания математической модели

Под моделированием понимают процесс построения, изучения и применения
моделей.

Модель – это материальный тип или мысленно представляемый объект, который в
процессе исследования замещает объект-оригинал так, что его непосредственное
изучение даёт новые знания об объекте оригинале.

Математическая модель – математическое описание физического объекта процесса
или явления, выражающее состояние его внутренней динамики взаимодействия и
свойства, это приближенное описание какого-либо класса явлений, выраженное с
помощью математической символики.

В математических методах широко применяются как аналитические, так и
статистические модели.

Аналитические модели более грубы, учитывать меньшее число факторов, всегда
требует каких-то допущений и упрощений.

Статистические модели по сравнению с аналитическими более точны и подробны, не
требуют столь грубых допущений, позволяют учесть большее количество факторов.

Операции – всякое мероприятие, система действий, объединенных единым замыслом и
направлением к достижению какой-либо цели. Операция является управляемым мероприятием,
то есть от нас зависти, каким способом выбрать некоторые параметры,
характеризующие ее организацию.

Исследование операций – совокупность прикладных математических методов,
используемых для решения практических организационных задач.

Решение – это всякий определенный набор зависящих от нас
параметров.

Оптимальным – называется решения, по тем или иным признакам
предпочтительнее перед другими.

Допустимыми решения – это решения, удовлетворяющие системе ограничений и
требованию неотрицательности.

Допустимый план – такой вариант плана, который удовлетворяет всем
заданным ограничениям задачи, но не обязательно оптимальный.

Оптимальный план – допустимый план, который удовлетворяет условиям
максимизации или минимизации (в зависимости от условия задачи).

Целевая функция – функция переменных, от которых зависит достижение
оптимального состояния системы.

Математическое моделирование – мощный метод изучения внешнего
мира, а также прогнозирования и управления.

Процесс математического моделирования можно подразделить на четыре этапа.

· Первый этап – формулировка законов, связывающих основные объекты модели.
Этот этап требует широкого знания фактов, относящихся к изучаемым явлениям, и
глубокого проникновения в их взаимосвязи.

· Второй этап – исследование математических задач, к которым
приводят построенные математические модели.

· Третий этап – выяснение того, удовлетворяет ли принятая
гипотетическая модель критерию практики.

· Четвертый этап – последующий анализ модели в связи с
накоплением данных об изучаемых явлениях и модернизации модели

Основные этапы математического моделирования

1) Построение модели. На этом этапе задается некоторый
«нематематический» объект – явление природы, конструкция, экономический план,
производственный процесс и т. д. При этом, как правило, четкое описание
ситуации затруднено. Сначала выявляются основные особенности явления и связи
между ними на качественном уровне. Затем найденные качественные зависимости
формулируются на языке математики, то есть строится математическая модель. Это
самая трудная стадия моделирования.

2) Решение математической задачи, к
которой приводит модель. На этом этапе большое внимание уделяется разработке алгоритмов и
численных методов решения задачи на ЭВМ, при помощи которых результат может
быть найден с необходимой точностью и за допустимое время.

3) Интерпретация полученных следствий
из математической модели. Следствия, выведенные из модели на языке математики, интерпретируются на
языке, принятом в данной области.

4) Проверка адекватности модели. На этом этапе выясняется,
согласуются ли результаты эксперимента с теоретическими следствиями из модели в
пределах определенной точности.

5) Модификация модели. На этом этапе происходит либо
усложнение модели, чтобы она была более адекватной действительности, либо ее
упрощение ради достижения практически приемлемого решения.

Классификация моделей

Классифицировать модели можно по разным критериям.
Например, по характеру решаемых проблем модели могут быть разделены на
функциональные и структурные. В первом случае все величины, характеризующие
явление или объект, выражаются количественно. При этом одни из них
рассматриваются как независимые переменные, а другие – как функции от этих
величин. Математическая модель обычно представляет собой систему уравнений
разного типа (дифференциальных, алгебраических и т. д.), устанавливающих
количественные зависимости между рассматриваемыми величинами. Во втором случае
модель характеризует структуру сложного объекта, состоящего из отдельных
частей, между которыми существуют определенные связи. Как правило, эти связи не
поддаются количественному измерению. Для построения таких моделей удобно
использовать теорию графов.

Граф – это математический объект,
представляющий собой некоторое множество точек (вершин) на плоскости или в
пространстве, некоторые из которых соединены линиями (ребрами).

По характеру исходных данных и результатов предсказания модели могут быть
разделены на детерминистические и вероятностно-статистические. Модели первого
типа дают определенные, однозначные предсказания. Модели второго типа основаны
на статистической информации, а предсказания, полученные с их помощью, имеют
вероятностный характер.

1.2
Характеристика типовых задач математического моделирования и подходов к их
решению

Задачи моделирования делятся на две категории: прямые и обратные.

Прямые задачи отвечают на вопрос, что будет, если при заданных условиях мы
выберем какое-то решение из множества допустимых решений. В частности, чему
будет равен, при выбранном решении критерий эффективности.

Обратные задачи отвечают на вопрос: как выбрать решение из множества
допустимых решений, чтобы критерий эффективности обращался в максимум или
минимум.

Если число допустимых вариантов решения невелико, то можно вычислить
критерий эффектности для каждого из них, сравнить между собой полученные
значения и непосредственно указать один или несколько оптимальных вариантов.
Такой способ нахождения оптимального решения называется “простым
перебором”. Когда число допустимых вариантов решения велико, то поиск
оптимального решения простым перебором затруднителен, а зачастую практически
невозможен. В этих случаях применяются методы “направленного”
перебора, обладающие той особенностью, что оптимальное решение находится рядом
последовательных попыток или приближений, из которых каждое последующие
приближает нас к искомому оптимальному.

Модели принятия оптимальных решений отличаются универсальностью. Их можно
классифицировать как задачи минимизации (максимизации) критерия эффективности,
компоненты которого удовлетворяют системе ограничений (равенств и/или)
неравенств.

Их можно разделить на:

принятие решений в условиях определенности – исходные данные – детерминированные;
принятие решений в условиях неопределенности – исходные данные – случайные
величины.

Таблица 1.2.1

Классификация задач оптимизации

Исходные данные	Переменные	Зависимости	Задача
Детерминированные	Непрерывные	Линейные	Линейного программирования
	Целочисленные	Линейные	Целочисленного программирования
	Непрерывные, целочисленные	Нелинейные	Нелинейного программирования
Случайные	Непрерывные	Линейные	Стохастическое программирование

А по критерию эффективности:

· одноцелевое принятие решений (один критерий эффективности);

· многоцелевое принятие решений (несколько критериев эффективности).

Наиболее разработан и широко используется на практике аппарат
одноцелевого принятия решений в условиях определенности, который получил
название математического программирования. В этом “детерминированном”
случаи, когда все условия операции известны заранее. тогда, обратная задача
будет включает в себя критерий эффективности и некоторые известные заранее
факторы (ограничения) позволяющие выбрать множество допустимых решений.

В общем виде обратная детерминированная задача будет
выглядеть следующим образом.

При заданном комплексе ограничений найти такое оптимальное
решение, принадлежащее множеству допустимых решений, которое обращает критерий
эффективности в максимум (минимум).

Метод поиска экстремума и связанного с ним оптимального решения должен
всегда исходить из особенности критерия эффективности и вида ограничений,
налагаемых на решение.

Реальные задачи содержит помимо выше перечисленных факторов, еще одну
группу – неизвестные факторы. Тогда обратную задачу можно сформулировать
следующим образом.

При заданном комплексе ограничений, с учетом неизвестных
факторов, найти такое оптимальное решение, принадлежащее множеству допустимых
решений, которое, по возможности, обеспечивает максимальное (минимальное)
значение критерий эффективности.

Это уже другая, не чисто математическая задача. Наличие неопределенных
факторов переводит эту задачу в новое качество: она превращается в задачу о
выборе решений в условиях неопределенности.

1.3
Определение и характеристика линейного программирования

Линейное программирование – это направление математической программирования,
изучающая методы решения экстремальный задач, которые характеризуются линейной
зависимостью между переменными и линейным критерием.

Линейное программирование – наиболее разработанный и широко применяемый
раздел математического программирования. Это объясняется следующим:

· математические модели очень большого числа экономических задач линейны
относительно искомых переменных;

· эти типы задач в настоящее время наиболее изучены;

· для них разработаны специальные конечные методы, с помощью
которых эти задачи решаются, и соответствующие стандартные программы для их
решения на ЭВМ;

· многие задачи линейного программирования, будучи решенными,
нашли уже сейчас широкое практическое применение в народном хозяйстве;

· некоторые задачи, которые в первоначальной формулировке не
являются линейными, после ряда дополнительных ограничений и допущений могут
стать линейными или могут быть приведены к такой форме, что их можно решать
методами линейного программирования.

Необходимым условием постановки задачи линейного программирования
являются ограничения на наличие ресурсов, величину спроса, производственную
мощность предприятия и другие производственные факторы.

Сущность линейного программирования состоит в нахождении точек
наибольшего или наименьшего значения некоторой функции при определенном наборе
ограничений, налагаемых на аргументы и образующих систему ограничений,
которая имеет, как правило, бесконечное множество решений. Каждая совокупность
значений переменных (аргументов функции F), которые удовлетворяют системе
ограничений, называется допустимым планом задачи линейного
программирования. Функция F, максимум или минимум которой определяется,
называется целевой функцией задачи. Допустимый план, на котором
достигается максимум или минимум функции F, называется оптимальным
планом задачи.

Система ограничений, определяющая множество планов, диктуется условиями
производства. Задачей линейного программирования является выбор из множества
допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим
образом:

Имеются какие-то переменные х = (х₁, х₂, … х_n)
и функция этих переменных f(x) = f (х₁, х₂, … х_n),
которая носит название целевой функции. Ставится задача: найти экстремум
(максимум или минимум) целевой функции f(x) при условии, что переменные x
принадлежат некоторой области G:

В зависимости от вида функции f(x) и области G и различают
разделы математического программирования: квадратичное программирование,
выпуклое программирование, целочисленное программирование и т.д. Линейное
программирование характеризуется тем, что а) функция f(x) является
линейной функцией переменных х₁, х₂, … х_nб)
область G определяется системой линейных равенств или неравенств.

Математическая модель любой задачи линейного программирования включает в
себя:

· максимум или минимум целевой функции (критерий оптимальности);

· систему ограничений в форме линейных уравнений и неравенств;

· требование неотрицательности переменных.

Возникновение и развитие Линейного программирования связано с экономикой.
Предположение о линейности экономических зависимостей несколько ограничивает
возможности Линейного программирования, однако простота и наглядность линейных
моделей, с достаточной степенью точности описывающих экономические процессы,
позволяет применять эти модели в различных видах экономической деятельности.

1.4
Характеристика симплекс-метода как основного аппарата решения задач линейного
программирования

Симплекс-метод является основным в линейном программировании.
Решение задачи начинается с рассмотрений одной из вершин многогранника условий.
Если исследуемая вершина не соответствует максимуму (минимуму), то переходят к
соседней, увеличивая значение функции цели при решении задачи на максимум и
уменьшая при решении задачи на минимум. Таким образом, переход от одной вершины
к другой улучшает значение функции цели. Так как число вершин многогранника
ограничено, то за конечное число шагов гарантируется нахождение оптимального
значения или установление того факта, что задача неразрешима.

Допустим, предприятие предполагает выпускать два вида продукции и , для производства которых
используется сырьё трех видов.

Производство обеспечено сырьем каждого вида в количествах: , , кг. На изготовление единицы изделия требуется затратить сырья каждого
вида , , кг., соответственно, а для единицы
изделия – , , кг. Прибыль от реализации единицы
изделия составляет ден.ед., для единицы изделия – ден.ед. (табл.1.4.1).

Таблица 1.4.1

Вид сырья	Продукция	Ограничения по сырью
	А₁	А₂
1-й	a₁₁	a₁₂	b₁
2-й	a₂₁	a₂₂	b₂
3-й	a₃₁	a₃₂	b₃
Прибыль	c₁	c₂

Составляем математическую модель:

математический
моделирование производство транспортный

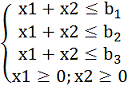(1.4.1)

Введем базисные переменные и преобразуем исходную задачу к виду:

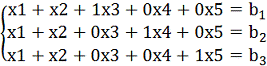(1.4.2)

Решим систему уравнений относительно базисных переменных x3, x4, x5.

Таблица 1.4.2

Итерация № 0

Базис		Х1	Х2	Х3	Х4	Х5	Свободные члены	Отношение
Х3	C1							596/5
Х4	C2							264/3
Х5	C3							640/2
Z			0	0	0	0	–

При составлении исходной симплекс таблицы, коэффициенты при переменных
функции Z записываются с противоположными
знаками, а свободный член со своим знаком.

– вектор, составленный из координат соответствующих базисных
переменных.

Текущий план не оптимален, так как в индексной строке находятся
отрицательные коэффициенты.

Будем считать что Z2
наименьший элемент, а строку с наименьшим отношением свободного члена к
соответствующему элементу выбранного столбца – строку Х4.

Ведущий столбец Х2, так как ( – наименьшее отрицательное число.

За ведущую выберем строку 2, так как отношение свободного члена к
соответствующему элементу выбранного столбца для 2 строки является наименьшим.

Разрешающий элемент .

Разделим элементы строки 2 на разрешающий элемент ().

От элементов строки 1 отнимаем соответствующие элементы строки 2,
умноженные на .

От элементов строки 3 отнимаем соответствующие элементы строки 2,
умноженные на .

От элементов строки Z
отнимаем соответствующие элементы строки 3, умноженные на .

Заменяем базисную переменную Х5 на Х1.

Количество итераций будет продолжаться до тех пор, пока в строке Z остаются отрицательные элементы.

Порядок работы с симплекс таблицей

Первая симплекс-таблица подвергается преобразованию, суть которого
заключается в переходе к новому опорному решению.

Алгоритм перехода к следующей таблице такой:

· просматривается последняя строка (индексная) таблицы и среди
коэффициентов этой строки (исключая столбец свободных членов Y0) выбирается
наименьшее отрицательное число при отыскании max, либо наибольшее
положительное при задачи на min. Если такового нет, то исходное базисное
решение является оптимальным и данная таблица является последней;

· просматривается столбец таблицы, отвечающий выбранному
отрицательному (положительному) коэффициенту в последней строке- ключевой
столбец, и в этом столбце выбираются положительные коэффициенты. Если
таковых нет, то целевая функция неограниченна на области допустимых значений
переменных и задача решений не имеет;

· среди выбранных коэффициентов столбца выбирается тот, для
которого абсолютная величина отношения соответствующего свободного члена
(находящегося в столбце свободных членов) к этому элементу минимальна. Этот коэффициент
называется разрешающим, а строка в которой он находится ключевой;

· в дальнейшем базисная переменная, отвечающая строке
разрешающего элемента, должна быть переведена в разряд свободных, а
свободная переменная, отвечающая столбцу разрешающего элемента, вводится в
число базисных. Строится новая таблица, содержащая новые названия базисных
переменных:

· разделим каждый элемент ключевой строки (исключая
столбец свободных членов) на разрешающий элемент и полученные значения запишем
в строку с измененной базисной переменной новой симплекс таблицы.

· строка разрешающего элемента делится на этот элемент и полученная строка
записывается в новую таблицу на то же место.

· в новой таблице все элементы ключевого столбца = 0,
кроме разрезающего, он всегда равен 1.

· столбец, у которого в ключевой строке имеется 0,в новой таблице будет
таким же.

· строка, у которой в ключевом столбце имеется 0,в новой таблице будет такой
же.

· в остальные клетки новой таблицы записывается результат
преобразования элементов старой таблицы

В результате получают новую симплекс-таблицу, отвечающую новому базисному
решению.

Следует просмотреть строку целевой функции (индексную), если в ней
нет отрицательных значений (в задачи на нахождение максимального значения),
либо положительных (в задачи на нахождение минимального значения) кроме
стоящего на месте Y0 (свободного столбца), то значит, что оптимальное
решение получено. В противном случае, переходим к новой симплекс таблице по
выше описанному алгоритму. Рассмотрим порядок решения задачи с помощью
симплекс-таблиц на примере.

1.5
Основные этапы, особенности и методы решения транспортной задачи

Под названием “транспортная задача” объединяется широкий круг задач с
единой математической моделью. Данные задачи относятся к задачам линейного программирования
и могут быть решены симплексным методом. Однако матрица системы ограничений
транспортной задачи настолько своеобразна, что для ее решения разработаны
специальные методы. Эти методы, как и симплексный метод, позволяют найти
начальное опорное решение, а затем, улучшая его, получить оптимальное решение.

Предположим что на три базы , , поступил однородный груз в
количествах: соответственно. Груз требуется развезти в пять пунктов: в пункт в пункт в пункт в пункт в пункт

Таблица 1.5.1

Пункт направления	B₁	B₂	B₃	B₄	B₅	Запасы, a_i
A₁	c₁₁	c₁₂	c₁₃	c₁₄	c₁₅	A₁
A₂	c₂₁	c₂₂	c₂₃	c₂₄	c₂₅	A₂
A₃	c₃₁	c₃₂	c₃₃	c₃₄	c₃₅	A₃
Потребности, b_j	b₁	b₂	b₃	b₄	b₅

Составим математическую модель данной задачи:

Целевая функция:

(1.5.1)

Ограничения:

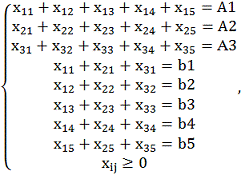(1.5.2)

–
количество груза, отправляемого с базы в пункт

Одним
из способов решения транспортных задач является метод северо-западного угла. На
каждом этапе метода максимально возможным числом заполняют левую верхнюю клетку
оставшейся части таблицы. Заполнение происходит таким образом, что полностью
выносится груз из или
полностью удовлетворяется потребность .

Методы
решения транспортных задач

Так
как транспортная задача является задачей линейного программирования, то её
можно решать симплекс-методом, но в силу своей особенности её можно решить гораздо
проще.

Условия
задачи удобно располагать в таблице, вписывая в ячейки количество перевозимого
груза из Аi в Bj груза X_ij ≥ 0, а в маленькие клетки –
соответствующие тарифы C_ij.(рис. 1.5.1)

Рисунок
1.5.1

Затем
решение задачи разбивается на два этапа:

· Определение опорного плана (Это решение можно найти, используя метод
“северо-западного угла” или метод “минимального элемента”.)

· Нахождение оптимального решения путем последовательных операций. Метод
северо-западного угла

Сущность метода заключается в том, что на каждом шаге заполняется левая
верхняя (северо-западная) клетка оставшейся части таблицы, причем максимально
возможным числом: либо полностью выносится груз из Аi, либо полностью
удовлетворяется потребность Вj. Процедура продолжается до тех пор, пока на
каком-то шаге не исчерпаются запасы аi и не удовлетворятся все потребности bj.
В заключении проверяют, удовлетворяют ли найденные компоненты плана Х_ij
горизонтальным и вертикальным уравнениям.

Метод наименьшего элемента

Сущность метода в том, что на каждом шаге заполняется та клетка
оставшейся части таблицы, которая имеет наименьший тариф; в случае наличия
нескольких таких равных тарифов заполняется любая из них. В остальном действуют
аналогично предыдущему способу.

Метод потенциалов

Соотношения определяют систему из m+n-1 линейных уравнений с m+n
известными, имеющую бесчисленное множество решений; для её определённости
одному неизвестному присваивают произвольное значение (обычно альфа равное 0),
тогда все остальные неизвестные определяются однозначно.

Критерий оптимальности

Если известны потенциалы решения Х0 транспортной задачи и для всех
незаполненных ячеек выполняются условия α_i+β_j ≤ C_ij, то Х0 является оптимальным
планом транспортной задачи.

Если план не оптимален, то необходимо перейти к следующему плану
(таблице) так, чтобы транспортные расходы не увеличивались.

Цикл перерасчёта таблицы – это последовательность ячеек, удовлетворяющая
условиям:

· Одна ячейка пустая, все остальные занятые.

· Любые две соседние ячейки находятся в одной строке или в
одном столбце.

· Никакие три соседние ячейки не могут быть в одной строке или
в одном столбце.

Пустой ячейке присваивают знак “+”, остальным – поочерёдно знаки
“-” и “+”.

Для перераспределения плана перевозок с помощью цикла перерасчёта сначала
находят незаполненную ячейку (r, s), в которой αr+βs > Crs, и строят соответствующий
цикл; затем в минусовых клетках находят число X = min(X_ij). Далее
составляют новую таблицу по следующему правилу:

· В плюсовых клетках добавляем Х.

· Из минусовых клеток вычитаем Х.

· Все остальные клетки вне цикла остаются без изменения.

Получим новую таблицу, дающую новое решение Х, такое, что F (X₁)
≤ F (X₀); оно снова проверяется на оптимальность через
конечное число шагов, обязательно найдем оптимальный план транспортной задачи,
ибо он всегда существует.

2. Практическая часть

2.1 Составление математической модели задачи планирования
производства

Задача. Предприятие предполагает выпускать два вида продукции А1 и А2, для
производства которых используется сырьѐ трех видов. Производство
обеспечено сырьем каждого вида в количествах: b1, b2, b3 кг. На изготовление
единицы изделия А1 требуется затратить сырья каждого вида а11, а21, а31 кг,
соответственно, а для единицы изделия А2 – а12, а22, а32 кг. Прибыль от
реализации единицы изделия А1 составляет с1 ден.ед., для единицы изделия А2 –
с2 ден.ед.

Требуется составить план производства изделий А1 и А2 обеспечивающий
максимальную прибыль предприятия от реализации готовой продукции.

Таблица 2.1.1

Исходная таблица

Вид сырья	Продукция	Ограничения по сырью
	А1	А2
1-й	4	1	240
2-й	2	3	180
3-й	1	5	251
Прибыль	40	30

Математическая модель

Пусть x1-количество изделий А₁;
Х2-количество изделий А₂;

Ограничения:

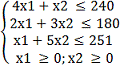
Целевая функция: Z= 40×1 + 30×2 → max

2.2 Решение задачи
планирования производства геометрическим способом

Найдем область допустимых решений

Посмотрим прямые:

x1+x2=240

x1+3×2=180

x1+5×2=251

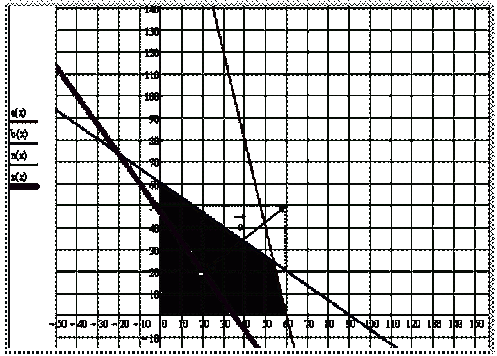
Рисунок 2.2.1

Многоугольник OABCD- область
допустимых решений.

Построим прямую уровня

Возьмем из области допустимых решений произвольную точку М(20; 20),
подставим в целевую функцию:

Z: 40
*20 + 30 * 20 = 1400

x1 +
30×2 = 1400 – уравнение прямой уровня.

Результаты расчётов приведены на рис. 2.2.1.

Определим направление перемещения прямой уровня

α (40; 30) – координаты вектора, в направлении которого
нужно перемещать прямую уровня до пересечения с последней граничной точкой
области допустимых решений.

Эта точка С.

Найдём её координаты:

Найдем максимальную прибыль

*54+30*24=2880

Ответ: Для достижения максимальной прибыли 2880 ден.ед. следует производить 54
ед. продукции вида А₁ и 24. продукции вида А₂.

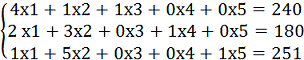
Z= 40×1 + 30×2 + 0x₃ + 0x₄ + 0x₅ → max

Решим систему уравнений относительно базисных переменных: x₃,
x₄, x₅.

Полагая, что свободные переменные равны 0, получим первый опорный план:

= (0,0,240,180,251)

Таблица 2.3.1

Итерация № 0

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены	Отношение
X₃	0	4	1	1	0	0	240	240/4
X₄	0	2	3	0	1	0	180	180/2
X₅	0	1	5	0	0	1	251	251/1
Z	-40	-30	0	0	0	0	–

При составлении исходной симплекс таблицы (Табл. 2.3.1), коэффициенты при
переменных функции 𝑍 записываются с противоположными знаками, а свободный
член со своим знаком.

Сб – вектор, составленный из координат соответствующих базисных
переменных.

Текущий план не оптимален, так как в индексной строке находятся
отрицательные коэффициенты.

Ведущий столбец X1, так как -40 – наименьшее отрицательное число.

За ведущую выберем строку 1, так как отношение свободного члена к
соответствующему элементу выбранного столбца для 3 строки является наименьшим.

Таблица 2.3.2

Разрешающий элемент 4

Базис	Сб	X₁	X₂	X₃	X₄	X₅		Отношение
X₃	0	4	1/4	1/4	0	0	60	60
X₄	0	2	3	0	1	0	180	90
X₅	0	1	5	0	0	1	251	251
Z	-40	-30	0	0	0	0	–

От элементов строки 2 отнимаем соответствующие элементы строки 1,
умноженные на 2.

От элементов строки 3 отнимаем соответствующие элементы строки 1,
умноженные на 1.

От элементов строки 𝑍 отнимаем соответствующие элементы
строки 1, умноженные на -40 (Табл. 2.3.2)

Заменяем базисную переменную X3 на X1

Таблица 2.3.3

Итерация № 1

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены	Отношение
X₁	0	1	0,25	0,25	0	0	60	240
X₄	0	0	2,5	-0,5	1	0	60	24
X₅	40	0	4,75	-0,25	0	1	191	40,21
Z	0	-20	10	0	0	2400	0

Текущий опорный план не оптимален, так как в индексной строке находятся
отрицательные коэффициенты (Табл. 2.3.3).

За ведущий выберем столбец 2, так как -20 наименьший элемент в 𝑍 строке.

Разрешающий элемент 2,5

Разделим элементы строки 2 на 2,5(Табл. 2.3.3).

Таблица 2.3.4

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены	Отношение
X₁	0	1	0,25	0,25	0	0	60	240
X₄	20	0	1	-0,2	0,4	0	24	24
X₅	40	0	4,75	-0,25	0	1	191	40,21
Z	0	-20	10	0	0	2400	0

От элементов строки 1 отнимаем соответствующие элементы строки 2,
умноженные на 0,25.

От элементов строки 3 отнимаем соответствующие элементы строки 2,
умноженные на 4,75.

От элементов строки 𝑍 отнимаем соответствующие элементы
строки 2, умноженные на -20

Таблица 2.3.5

Базис	Сб	X₁	X₂	X₃	X₄	X₅	Свободные члены
X₁	0	1	0	0,3	-0,1	0	54
X₂	20	0	1	-0,2	0,4	0	24
X₅	40	0	0	0,7	-1,9	1	77
Z	0	0	6	8	0	2880

X2 = (54, 24, 77, 0, 0)

𝑍(X2) = 40*54 + 30*24 = 2880 (Табл. 2.3.5).

Ответ: Для достижения максимальной прибыли 2880 ден.ед. следует производить 54
ед. продукции вида А1 и 24 ед. продукции вида А2. (ответ совпадает с ответом
полученным графическим способом).

2.4 Решение задачи планирования
производства с помощью табличного процессора MS Excel

) Ввод данных

Вводим данные таблицы 3 в ячейки EXCEL (рис. 2.4.1.).

· В ячейках B3: С5 введены
виды продукции.

· В ячейках B6: C6 находится прибыль от реализации
единицы изделия A1 и А2.

· В ячейках D3: D5 находятся ограничения по сырью.

2) Записываем формулы для вычисления ограничений

Введем формулы в ячейки B7: B9

· B7: =B10*B3+B11*C3

· B8: =B10*B4+B11*C4

· B9: =B10*B5+B11*C5

3) Записываем формулу для вычисления целевой функции

Целевая функция находится в ячейке E2

· В ячейку E2 введем формулу:
=B10*B6+B11*C6

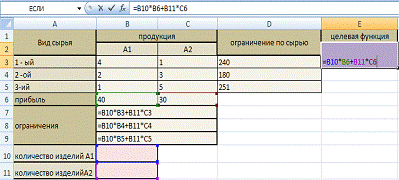
Рисунок 2.4.1

) Заполнение окна процедуры «Поиск решения»

· Целевая функция: E2 ($E$2);

· Вид поиска: max;

· Изменяемые ячейки: B10: B11 ($B$10:$B$11);

· В поле «Ограничения» добавим заданные ограничения:

$B$10:$B$11 = целое;

$B$10:$B$11 >= 0;

$B$7 <= $D$3

$B$8 <= $D$4

$B$9 <= $D$5

· В окне «Параметры» установить «Линейная модель». Результаты заполнения
окна показаны на (рис.2.4.2), (рис. 2.4.3).

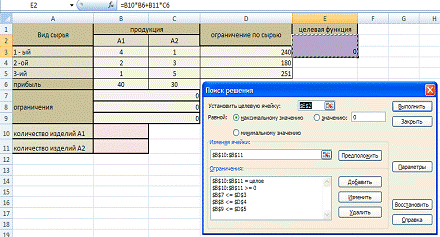
Рисунок 2.4.2

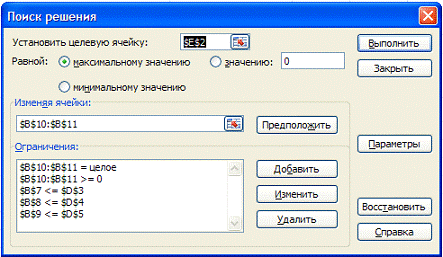
Рисунок 2.4.3

5) Выполнив процедуру «Поиск решения» получим следующие результаты (рис.
2.4.4):

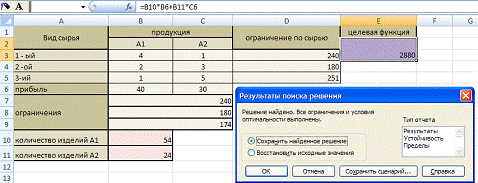
Рисунок 2.4.4

2.5 Составление математической модели
транспортной задачи

Задача На три базы А1, А2, А3 поступил однородный груз в количествах: а1, a2, а3 соответственно. Груз требуется
развести в пять пунктов: b1 в
пункт В1, b2в пункт В3, b3 в пункт В3, b4 в
пункт В4, b5 в пункт В5.

Спланировать перевозки так, чтобы их общая стоимость была минимальной.

Математическая модель транспортной задачи:

Пусть Хij –
количество груза, отправляемого с базы Аi в пункт Вj.

Целевая функция:

Таблица 2.5.1

Исходная таблица

Пункт направления	В1	В2	В3	В4	В5	Запасы, а_i
A1	2	10	15	14	4	150
A2	3	7	12	5	8	170
A3	21	18	6	13	16	260
Потребности	100	90	160	150	80	580

Ограничения:

2.6
Нахождение опорного плана транспортной задачи методом северо-западного угла

Используя метод северо-западного угла, построим первый опорный
план транспортной задачи (Табл. 2.6.1).

Таблица 2.6.1

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2[100]	10[50]	15	14	4	150
A2	3	7[40]	12[130]	5	8	170	21	18	6[30]	13[150]	16[80]	260
Потребности	100	90	160	150	80	580

В результате получен первый опорный план, который является допустимым,
так как все грузы из баз вывезены, потребность магазинов удовлетворена, а план
соответствует системе ограничений транспортной задачи.

. Подсчитаем число занятых клеток таблицы, их 7, а должно быть m + n – 1
= 7. Следовательно, опорный план является невырожденным.

Значение целевой функции для этого опорного плана равно:

(x) = 2*100 + 10*50 + 7*40 + 12*130 + 6*30 + 13*150 + 16*80 = 5950

2.7 Нахождение опорного плана
транспортной задачи методом наименьшего элемента

Используя метод наименьшего элемента, построим первый опорный план
транспортной задачи (Табл. 2.7.1).

Таблица 2.7.1

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2[100]	10	15	14	4[50]	150
A2	3	7[20]	12	5[150]	8	170
A3	21	18[70]	6[160]	13	16[30]	260
Потребности	100	90	160	150	80	580

Значение целевой функции для этого опорного плана равно:

(x) = 2*100 + 4*50 + 7*20 + 5*150 + 18*70 + 6*160 + 16*30 = 3990

2.8 Решение транспортной задачи методом
потенциалов

Проверим оптимальность опорного плана. Найдем предварительные
потенциалы u_i, v_i. по занятым клеткам таблицы, в
которых u_i + v_i = c_ij, полагая, что u₁
= 0.

Таблица 2.8.1

	v₁=2	v₂=10	v₃=15	v₄=22	v₅=25
u₁=0	2[100]	10[50]	15	14	4
u₂=-3	3	7[40]	12[130]	5	8
u₃=-9	21	18	6[30]	13[150]	16[80]

Опорный план не является оптимальным, так как существуют оценки свободных
клеток, для которых u_i + v_i > c_ij(Табл.
2.8.1).

Выбираем максимальную оценку свободной клетки (1;5): 4

Для этого в перспективную клетку (1;5) поставим знак «+», а в остальных
вершинах многоугольника чередующиеся знаки «-», «+», «-» (Табл. 2.8.2).

Таблица 2.8.2

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2[100]	10[50][-]	15	14	4[+]	150
A2	3	7[40][+]	12[130][-]	5	8	170
A3	21	18	6[30][+]	13[150]	16[80][-]	260
Потребности	100	90	160	150	80	580

Цикл приведен в таблице (1,5; 1,2; 2,2; 2,3; 3,3; 3,5;).

Из грузов х_ij стоящих в минусовых клетках, выбираем
наименьшее, т.е.

у = min (1, 2) = 50

Прибавляем 50 к объемам грузов, стоящих в плюсовых клетках и вычитаем 50
из Х_ij, стоящих в минусовых клетках. В результате получим новый
опорный план (Табл. 2.8.3).

Таблица 2.8.3

Пункт направления	B1	B2	B3	B4	B5	Запасы
1	2[100]	10	15	14	4[50]	150
2	3	7[90]	12[80]	5	8	170
3	21	18	6[80]	13[150]	16[30]	260
Потребности	100	90	160	150	80	580

Проверим оптимальность опорного плана. Найдем предварительные потенциалы
u_i, v_i. по занятым клеткам таблицы, в которых u_i
+ v_i = c_ij, полагая, что u₁ = 0.

Таблица 2.8.4

	v₁=2	v₂=-11	v₃=-6	v₄=1	v₅=4
u₁=0	2[100]	10	15	14	4[50]
u₂=18	3	7[90]	12[80]	5	8
u₃=12	21	18	6[80]	13[150]	16[30]

Опорный план не является оптимальным, так как существуют оценки свободных
клеток, для которых u_i + v_i > c_ij (Табл.
2.8.4).

Выбираем максимальную оценку свободной клетки (2;1): 3

Для этого в перспективную клетку (2;1) поставим знак «+», а в остальных
вершинах многоугольника чередующиеся знаки «-», «+», «-» (Табл. 2.8.5).

Таблица 2.8.5

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2[100][-]	10	15	14	4[50][+]	150
A2	3[+]	7[90]	12[80][-]	5	8	170
A3	21	18	6[80][+]	13[150]	16[30][-]	260
Потребности	100	90	160	150	80

Цикл приведен в таблице (2,1; 2,3; 3,3; 3,5; 1,5; 1,1;).

Из грузов х_ij стоящих в минусовых клетках, выбираем
наименьшее, т.е. у = min (3, 5) = 30. Прибавляем 30 к объемам грузов, стоящих в
плюсовых клетках и вычитаем 30 из Х_ij, стоящих в минусовых клетках.
В результате получим новый опорный план (Табл. 2.8.6).

Таблица 2.8.6

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2[70]	10	15	14	4[80]	150
A2	3[30]	7[90]	12[50]	5	8	170
A3	21	18	6[110]	13[150]	16	260
Потребности	100	90	160	150	80	580

Проверим оптимальность опорного плана. Найдем предварительные потенциалы
u_i, v_i. по занятым клеткам таблицы, в которых u_i
+ v_i = c_ij, полагая, что u₁ = 0.

Таблица 2.8.7

	v₁=2	v₂=6	v₃=11	v₄=18	v₅=4
u₁=0	2[70]	10	15	14	4[80]
u₂=1	3[30]	7[90]	12[50]	5	8
u₃=-5	21	18	6[110]	13[150]	16

Опорный план не является оптимальным, так как существуют оценки свободных
клеток, для которых u_i + v_i > c_ij(Табл.
2.8.7).

Выбираем максимальную оценку свободной клетки (2;4): 5

Для этого в перспективную клетку (2;4) поставим знак «+», а в остальных
вершинах многоугольника чередующиеся знаки «-», «+», «-» (Табл. 2.8.8).

Таблица 2.8.8

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2[70]	10	15	14	4[80]	150
A 2	3[30]	7[90]	12[50][-]	5[+]	8	170
A 3	21	18	6[110][+]	13[150][-]	16	260
Потребности	100	90	160	150	80	580

Цикл приведен в таблице (2,4; 2,3; 3,3; 3,4;).

Из грузов х_ij стоящих в минусовых клетках, выбираем
наименьшее, т.е. у = min (2, 3) = 50. Прибавляем 50 к объемам грузов, стоящих в
плюсовых клетках и вычитаем 50 из Х_ij, стоящих в минусовых клетках.
В результате получим новый опорный план (Табл. 2.8.9).

Таблица 2.8.9

Пункт направления	B1	B2	B3	B4	B5	Запасы
A1	2[70]	10	15	14	4[80]	150
A2	3[30]	7[90]	12	5[50]	8
A3	21	18	6[160]	13[100]	16	260
Потребности	100	90	160	150	80	580

Проверим оптимальность опорного плана. Найдем предварительные потенциалы
u_i, v_i. по занятым клеткам таблицы, в которых u_i
+ v_i = c_ij, полагая, что u₁ = 0.

Таблица
2.8.10

	v₁=2	v₂=6	v₃=-3	v₄=4	v₅=4
u₁=0	2[70]	10	15	14	4[80]
u₂=1	3[30]	7[90]	12	5[50]	8
u₃=9	21	18	6[160]	13[100]	16

Опорный план является оптимальным, так все оценки свободных клеток
удовлетворяют условию u_i + v_i <= c_ij(Табл.
2.8.10).

Минимальные затраты составят:

(x) = 2*70 + 4*80 + 3*30 + 7*90 + 5*50 + 6*160 + 13*100 = 3690

2.9
Решение транспортной задачи при помощи табличного процессора Excel

) Ввод данных

· Вводим данные таблицы 2.5.1 в ячейки EXCEL (рис 2.9.1).

· В ячейки B2: F4 введены стоимости перевозок.

· В ячейках H7: H9 находится количество имеющегося в
наличии товара.

· В ячейках B11: F11 находятся запросы пунктов
назначения.

· Ячейки B7: F9 – рабочие (изменяемые) ячейки, в
которых будут вычисляться значения переменных задачи X_ij.

· В ячейках G7: G9 нужно записать формулы для
вычисления левых частей ограничений

§ в G7 должна быть сумма ячеек B7: F7;

§ в G8 должна быть сумма ячеек B8: F8;

§ в G9 должна быть сумма ячеек B9: F9.

· Формулы для вычисления левых частей ограничений введем в ячейки B10: F10:

§ в B10 должна быть сумма ячеек B7: B9;

§ в C10 должна быть сумма ячеек C7: C9;

§ в D10 должна быть сумма ячеек D7: D9;

§ в E10 должна быть сумма ячеек E7: E9;

§ в F10 должна быть сумма ячеек F7: F9;

· Целевую функцию поместим в ячейку G2:

§ H4: СУММПРОИЗВ(B2:F4; B7:F9).

· Таблица исходных данных имеет вид (рис. 2.9.1):

Рисунок 2.9.1.

2) Заполнение окна процедуры «Поиск решения»

· Целевая функция: G2 ($G$2);

· Значение целевой функции: min;

· Изменяемые ячейки: B7: F9($B$7: $F$9);

· Ограничения задачи:

$B$10:
$F410 = $B411: $F$11

$B$7: $F$9 = целое

$B$7: $F$90

$G$7: $G$9
= $H$7: $H$9

В
окне «Параметры» установить «Линейная модель».

Результаты
заполнения окна показаны на рис. 2.9.2.

Рисунок
2.9.2

3) Выполнив
процедуру «Поиск решения» получим следующие результаты (рис. 2.9.3):

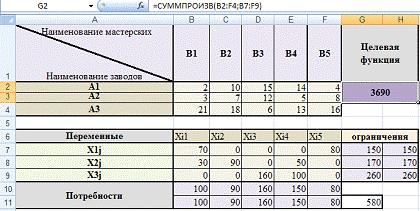
Рисунок 2.9.3

Таким образом из A1
следует отвезти 70 ед. товара в B1 и
80 ед. товара в B5; из A2 отвезти 30 ед. товара в B1, 90 ед. товара в B2 и 50 ед. товара в В4; из A3 отвезти 160 ед. товара в B3 и 100 ед. товара в B4. При этом суммарная стоимость
транспортных расходов составит 3690 рубля.

Заключение

Необходимость решения задач линейного программирования на современных
предприятиях очевидна. Построение и решение экономико-математических, а также
транспортных задач позволяет, в свою очередь, решать различные
технико-экономические и экономические производственные задачи, которые
позволяют найти наиболее рациональные путеи и способы транспортировки товаров и
минимизировать сумму транспортных расходов.

Целью моей курсовой работы было изучение методов решения задач
математического моделирования.

В ходе работы, я изучила основных понятий математического моделирования.
Научилась составлять математическую модель задачи плана производства, решать
задачу геометрическим способом и симплекс-методом, составлять математическую
модель транспортной задачи, находить опорный план методом северного – западного
угла и методом наименьшего элемента, находить оптимальный план перевозок
методом потенциалов, решать задачи программным способом с помощью табличного
процессора MS Excel

При выполнении курсовой работы была рассмотрена производственная и
транспортная задача и произведено решение двумя различными способами:
аналитическим и программным. При сравнении ответов выяснилось, что оба способа
дали одинаковые результаты, что доказывает правильность полученного
оптимального плана.

Данная работа, может послужить примером материалов для самостоятельного
изучения методов решения задач математического моделирования.

Я считаю, что цель поставленная в курсовой работе полностью достигнута,
задачи выполнены, актуальность доказана.

Литература

1. Кузнецов
А.В., Новикова Г.И., Холод И.И. – «Сборник задач по математическому
программированию». Минск, Высшая школа, 1985 г.

2. Кузнецов
А.В., Новикова Г.И., Холод И.И. – «Высшая математика. Математическое
программирование». Минск, Высшая школа, 2001 г.

. Красс
М.С., Чупрынов Б.П. ”Основы математики и ее приложения в экономическом
образовании”, Издательство “Дело”, Москва 2001г.

. Лященко
И.Н. Линейное и нелинейное программирование. / Лященко И.Н., Карагодова Е.А.,
Черникова Н.В., Шор Н.З.. – К.: «Высшая школа», 1975, 372с.

5. <http://www.edu.ru>

. <http://www.rfst.fsoft.ru>

Приложение 1

Задача. Предприятие предполагает выпускать два вида продукции А₁ и А₂,
для производства которых используется сырьё трех видов. Производство обеспечено
сырьем каждого вида в количествах: b₁, b₂, b₃ кг. На изготовление единицы изделия
А₁ требуется затратить сырья каждого вида а₁₁, а₂₁,
а₃₁кг, соответственно, а для единицы изделия А₂ – а₁₂,
а₂₂, а₃₂кг. Прибыль от реализации единицы изделия А₁
составляет с₁ ден.ед., для единицы изделия А₂ – с₂
ден.ед. Данные для решения задачи представлены в таблице 1

Требуется составить план производства изделий А₁ и А₂обеспечивающий
максимальную прибыль предприятия от реализации готовой продукции.

Необходимо:

· Решить задачу геометрически (графики построить в системе Mathcad);

· Решить задачу симплекс-методом;

· Решить задачу программным способом с помощью табличного
процессора MS Excel.

Таблица 1

Вид сырья	Продукция	Ограничения по сырью
	B₁	B₂
1-й	4	1	240
2-й	2	3	180
3-й	1	5	251
прибыль	40	30

Приложение 2

Задача. На три базы А₁, А₂, А₃ поступил
однородный груз в количествах: а_1, а₂, а₃соответственно.
Груз требуется развезти в пять пунктов: b₁в пункт В₁, b₂в пункт В₂, b₃в пункт В₃, b₄в пункт В₄, b₅в пункт В₅. Данные для решения задачи представлены
в таблице 2

Таблица 2

Пункт направления	B1	B2	B3	B4	B5	Запасы, a_i
A1	2	10	15	14	4	150
A2	3	7	12	5	8	170
A3	21	18	6	13	16	260
Потребности, b_j	100	90	160	150	80	580

Спланировать перевозки таким образом, чтобы их общая стоимость была
минимальной.

Необходимо:

· Найти опорный план методом северо-западного угла;

· Найти опорный план методом наименьшего элемента;

· Найти оптимальный план перевозок методом потенциалов;

· Решить задачу программным способом с помощью табличного
процессора MS Excel.

Источник

2.1. Построение экономико-математической модели

2.2. Определение оптимального плана производства симплексным методом

Методы решения задач математического моделирования

Введение

1. теоретическая часть

1.1 Определение основных понятий математического моделирования и характеристика этапов создания математической модели

Основные этапы математического моделирования

Классификация моделей

1.2 Характеристика типовых задач математического моделирования и подходов к их решению

1.3 Определение и характеристика линейного программирования

1.4 Характеристика симплекс-метода как основного аппарата решения задач линейного программирования

1.5 Основные этапы, особенности и методы решения транспортной задачи

2. Практическая часть

2.1 Составление математической модели задачи планирования производства

2.2 Решение задачи планирования производства геометрическим способом

2.4 Решение задачи планирования производства с помощью табличного процессора MS Excel

2.5 Составление математической модели транспортной задачи

<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" height="211" src="https://www.bibliofond.ru/wimg/10/524602.files/image077.gif" />

2.7 Нахождение опорного плана транспортной задачи методом наименьшего элемента

2.8 Решение транспортной задачи методом потенциалов

2.9 Решение транспортной задачи при помощи табличного процессора Excel

Заключение

Литература

Приложение 1

Приложение 2

Вам также может понравиться

Как исправить невозможно исправить ошибки у вас отложены held битые пакеты

Как найти латинские буквы в айфоне

Если не помнишь куда положил как найти

Добавить комментарий Отменить ответ

1.1
Определение основных понятий математического моделирования и характеристика
этапов создания математической модели

1.2
Характеристика типовых задач математического моделирования и подходов к их
решению

1.3
Определение и характеристика линейного программирования

1.4
Характеристика симплекс-метода как основного аппарата решения задач линейного
программирования

1.5
Основные этапы, особенности и методы решения транспортной задачи

2.1 Составление математической модели задачи планирования
производства

2.2 Решение задачи
планирования производства геометрическим способом

2.4 Решение задачи планирования
производства с помощью табличного процессора MS Excel

2.5 Составление математической модели
транспортной задачи

2.7 Нахождение опорного плана
транспортной задачи методом наименьшего элемента

2.8 Решение транспортной задачи методом
потенциалов

2.9
Решение транспортной задачи при помощи табличного процессора Excel