Как составить математическую модель ситуации по условию - Сайт, где вы сможете решить свои вопросы

Тема: Математический
язык. Математическая модель

Урок: Математическая
модель и текстовые задачи

Цель: повторение пройденного
на прошлом уроке, составление словесной и математической модели реальной
ситуации.

На прошлом уроке мы выучили
три основных этапа решения текстовых задач с помощью математических моделей. На
этом уроке мы закрепим эту тему, решая более сложные текстовые задачи с помощью
математического моделирования.

I.
Повторение этапов решения текстовых задач

Повторим, что при решении
текстовых задач осуществляется переход от словесного описания к математическому
описанию. В процессе решения таких задач выделяются три этапа:

1й: Составление
математической модели;

2й: Работа с математической
моделью;

3й: Получение ответа на
вопрос задачи.

II.
Рассмотрим первый пример решения текстовых задач.

Задача 1: В
одном доме на 86 квартир больше, чем в другом. Сколько квартир в каждом доме,
если в двух домах 792 квартиры?

Первый этап: Составим
математическую модель, для чего введем переменные.

Пусть –
число квартир в первом доме. Исходя из условия, ()
– это число квартир во втором доме. Тогда общее количество квартир есть
равно .
По условию это число квартир равняется 792. Получаем уравнение:

Второй этап: необходимо
решить полученное уравнение и найти .

Третий этап: в
задаче необходимо ответить на вопрос: сколько квартир в одном доме и сколько в
другом доме.

В одном доме у нас квартир.

А во втором доме квартир.

Ответ: число
квартир в одном доме 353 и 439 в другом доме.

III.
Второй приме решения текстовых задач

Задача 2:
В двух залах кинотеатра 460 мест. Сколько мест в большом зале, если в нём в три
раза больше мест, чем в малом?

Первый этап: Пусть –
число мест в малом зале. По условию задачи в большом зале мест в три раза
больше, тогда –
число мест в большом зале. Общее количество мест равно .
В задаче сказано, что общее количество мест равно 460.

Второй этап: Решим
уравнение.

Третий этап: Необходимо
ответить на вопрос: сколько мест в большом зале?

Нам нужно найти .
Мы получили значение =
115, значит:

Ответ: в
большом зале 345 мест.

IV.
Третий пример решения текстовых задач

Задача 3:
Маме и дочке вместе 35 лет. Сколько лет дочке, если она на 25 лет моложе мамы?

Первый этап: Пусть –
число лет дочки. Тогда –
число лет мамы. По условию задачи маме и дочке вместе 35 лет. Значит,

Второй этап: Решим
уравнение.

Третий этап: Ответим
на вопрос, сколько лет дочке.

Мы обозначили возраст дочери
через ,
и нашли, что =
5.

Ответ: дочке
5 лет.

V.
Четвертый пример решения текстовых задач

Задача 4: На
двух книжных полках всего 48 книг. Сколько книг на первой полке, если известно,
что их в два раза больше, чем на второй полке?

Первый этап: Пусть –
число книг на первой полке, их в два раза больше, чем на второй полке.
Значит, –
число книг на второй полке. Тогда:

Второй этап: Решим
уравнение.

Третий этап: Необходимо
узнать, сколько книг на первой полке. Мы обозначили их число через ,
значит, ответ на вопрос задачи следующий: на первой полке 32 книги.

Ответ: на
первой полке 32 книги.

Итак, мы рассмотрели метод
математического моделирования на примере четырех задач. В каждой задаче была
составлена математическая модель, решено соответствующее уравнение и получен
ответ.

Рекомендованное домашнее
задание

1. №№ 3.15, 3.17, Мордкович
А.Г. Алгебра 7.

2. Решить задачу:

В папке «Video» размещалось
втрое больше фильмов, чем мультфильмов. После удаления трех фильмов и
скачивания пяти мультиков, их соотношение стало два к одному. Сколько фильмов
было в папке изначально?

3. Решить задачу:

На клумбе росли лилии и
тюльпаны, причем лилий было в два раза больше. После того, как посадили еще
пять тюльпанов, и выкопали две лилии, их количество сравнялось. Сколько лилий
было на клумбе изначально?

Список рекомендованной
литературы

1. Мордкович А.Г. Алгебра 7.
4 издание. М.: Мнемозина. 2012 г.

2. Мерзляк А.Г., Полонский
В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ

Рекомендованные ссылки на
ресурсы интернет

1. Школьный помощник

2. В помощь учащимся

3. Методическая копилка
учителя информатики

Источник

Цели изучения

Содержание работы

Методика работы (общая характеристика)

Конкретные примеры заданий

Систематическое

развитие понятия числа, выработка умений выполнять устно и письменно арифметические

действия над числами, переводить практические задачи на язык математики, подготовка

учащихся к изучению систематических курсов алгебры и геометрии.

Курс строится на индуктивной основе с привлечением элементов дедуктивных

рассуждений. Теоретический материал курса излагается на наглядно-интуитивном уровне,

математические методы и законы формулируются в виде правил.

В ходе изучения курса учащиеся развивают навыки вычислений с натуральными

числами, овладевают навыками действий с обыкновенными и десятичными дробями,

получают начальные представления об использовании букв для записи выражений и

свойств арифметических действий, составлении уравнений, продолжают знакомство с

геометрическими понятиями, приобретают навыки построения геометрических фигур и

измерения геометрических величин.

Математический язык, математическое предложение, перевод математической записи на обычный язык, чтение выражения.

Математическая модель, составление математической модели данной ситуации. Наличие умений составлять задачи по математической модели; решать задачи с использованием математической модели; давать оценку информации, фактам, процессам, определять их актуальность; составить набор карточек с заданиями.

Работа с раздаточным материалом.

1) Разработка принципа систематичности и последовательности в

обучении математике с позиций психологической теории деятельности,

предложенная нами, позволяет выстроить систему знаний того или иного

раздела курса на основе такого системообразующего фактора как предметная

деятельность учащихся;

2)Методологическая схема изучения числовой линии курса математики

5-6 классов способствует результативному применению

метода учебных задач в процессе обучения на этапе введения новых знаний.

Решение задачи, выделяя три этапа математического моделирования. 595. На одной автостоянке было в 4 раза меньше машин, чем на другой. Когда со второй стоянки на первую перевели 12 автомобилей, машин на стоянках стало поровну. Сколько машин было на каждой стоянке первоначально?

1. Составление математической модели. На этом этапе переводим текст задачи с обыденного языка на математический язык. В результате получаем математическую модель ситуации, описанной в условии задачи.

Пусть на первой автостоянке стояло x автомобилей. Тогда на второй 4х автомобилей. После перевода со второй стоянки на первую 12 автомобилей, на первой стало х + 12, а на второй 4х – 12 автомобилей. Зная, что машин на стоянках стало поровну, составим уравнение:

4х – 12 = х + 12

2. Работа с математической моделью. На этом этапе надо решить составленное уравнение.

Решение:

4х – 12 = х + 12

3х = 24

х = 8

3. Ответ на вопрос задачи.

На первой стоянке было 8 автомобилей, а на второй 32.

Ответ: 8 автомобилей, 32 автомобиля.

Цельюизучения курса алгебры в 7 – 9 классах является развитие вычислительных умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования задач, осуществление функциональной подготовки школьников. Курс характеризуется повышением теоретического уровня обучения, постепенным усилием роли теоретических обобщений и дедуктивных заключений. Прикладная направленность раскрывает возможность изучать и решать практические задачи.

Математический язык. Математическая модель.

Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной.

Линейные и квадратные уравнения как математические модели реальных ситуаций. Рациональные уравнения, математическая модель реальной ситуации, решение задач на составление уравнений. Свободное решение задач на числа, выделяя основные этапы моделирования. Использование для решения познавательных задач справочной литературы.

Работа с конспектом, с книгой и наглядными пособиями по группам.

Методы обучения: методы организации и осуществления учебно-познавательной деятельности: словесный (диалог, рассказ и др.); наглядный (опорные схемы, презентации и др.); практический (упражнения, практические работы, решение задач, моделирование и др.); исследовательский; метод стимулирования и мотивации: интереса к учению, долга и ответственности в учении; метод контроля и самоконтроля в обучении: фронтальная устная проверка, индивидуальный устный опрос, письменный контроль и др.

Решение задачи, выделяя три этапа математического моделирования.

Пример 1. Перегон в 60 км поезд должен был проехать с постоянной скоростью за определенное расписанием время. Простояв у семафора перед перегоном 5 мин, машинист вынужден был увеличить скорость прохождения перегона на 10 км/ч, чтобы наверстать к окончанию прохождения перегона потерянные 5 мин. С какой скоростью поезд должен был пройти перегон по расписанию?
Решение.
Первый этап. Составление математической модели (Перевод задачи с естественного языка на язык математических терминов). Пусть х км/ч — скорость поезда по расписанию. Так как протяженность перегона равна 60 км, то время, отведенное расписанием на прохождение перегона, составляет ч.

Фактически поезд прошел перегон в 60 км со скоростью (х + 10) км/ч, значит, время, затраченное на прохождение перегона, равно ч.
Из двух величин — ч и ч первая больше второй на 5 мин, т. е. на ч. Значит, мы приходим к уравнению

Математическая модель задачи составлена. Это — рациональное уравнение.

Второй этап. Работа с составленной моделью.
Имеем

Преобразуем левую часть уравнения

Приравняв числитель этой дроби нулю, получим квадратное уравнение – х

2 – 10х + 7200 = 0 или, переходя к более удобной записи, х2 + 10х – 7200 = 0.
Применяя известную формулу, находим

Оба значения удовлетворяют условию

, следовательно, эти значения — корни составленного рационального уравнения.
Третий этап. Ответ на вопрос задачи. (перевод полученного результата на язык, на котором была сформулирована задача).
Спрашивается, с какой скоростью поезд должен был пройти перегон по расписанию? Именно эту величину мы обозначили. Значение нас явно не устраивает, поскольку скорость движения поезда не может выражаться отрицательным числом. Значит, выбираем значение х = 80, это и есть ответ на вопрос задачи.

О т в е т: 80 км/ч.

формирование представлений о математике как универсальном языке науки, средстве моделирования явлений и процессов, об идеях и методах математики;

развитие логического мышления, пространственного воображения, алгоритмической культуры, критичности мышления на уровне, необходимом для будущей профессиональной деятельности, а также последующего обучения в высшей школе;

овладение математическими знаниями и умениями, необходимыми в повседневной жизни, для изучения школьных естественнонаучных дисциплин на базовом уровне, для получения образования в областях, не требующих углубленной математической подготовки;

воспитание средствами математики культуры личности, понимания значимости математики для научно-технического прогресса, отношения к математике как к части общечеловеческой культуры через знакомство с историей развития математики, эволюцией математических идей.

− решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;

составлять уравнения и неравенства по условию задачи;

использовать для приближенного решения уравнений и неравенств графический метод;

изображать на координатной плоскости множества решений простейших уравнений и их систем;

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

построения и исследования простейших математических моделей.

Планируется использование элементов следующих педагогических технологий в преподавании предмета:

технологии полного усвоения;

технологии обучения на основе решения задач;

технологии обучения на основе схематичных и знаковых моделей;

технологии проблемного обучения;

проектно – исследовательские технологии

Большинство жизненных задач решаются как алгебраические уравнения: приведением их к самому простому виду, т.е. к составлению единой математической модели. Метод введения новой переменной позволяет при решении тригонометрических, показательных, логарифмических уравнений и неравенств перейти к составлению единой, более простой модели: квадратному уравнению или неравенству.

Пример 1. Решить уравнение4х + 2х+1 – 24 = 0.

Решение.

1. Первый этап. Составление математической модели.

Заметив, что 4х = (22)х = 22х = (2х)2, а 2х+1 = 2·2х, перепишем заданное уравнение в виде (2х)2 + 2·2х – 24 = 0.

Есть смысл ввести новую переменную: у = 2х; тогда уравнение примет вид у2 + 2у – 24 = 0. Математическая модель составлена. Это – квадратное уравнение. 2. Второй этап. Работа с составленной моделью. Решив квадратное уравнение у2 + 2у – 24 = 0 относительно у, находим: у1 = 4, у2 = -6.

3. Третий этап. Ответ на вопрос задачи.

Так как у = 2х, Значит, нам остается решить два уравнения: 2х = 4; 2х = -6.

Из первого уравнения находим: х = 2; второе уравнение не имеет корней, поскольку при любых значениях х выполняется неравенство 2х > 0.

Ответ: 2.

Пример 2. Задача на нахождение наибольших и наименьших значений величин.

Бак, имеющий вид прямоугольного параллелепипеда с квадратным основанием, должен вмещать 500 литров воды. При какой стороне основания площадь поверхности бака (без крышки) будет наименьшей?

Решение. Первый этап. Составление математической модели.

1) Оптимизируемая величина (О. В.) — площадь поверхности бака, поскольку в задаче требуется выяснить, когда эта площадь будет наименьшей. Обозначим О. В. буквой S.

2) Площадь поверхности зависит от измерений прямоугольного параллелепипеда. Объявим независимой переменной (Н. П.) сторону квадрата, служащего основанием бака; обозначим ее буквой х. Ясно, что х > 0. Других ограничений нет, значит, 0 < х < +оо. Таковы реальные границы изменения независимой переменной: X = (0; Н-оо).

3) Если бак вмещает 500 л воды, то объем V бака равен 500 дм3. Если h – высота бака, то V = x2h, откуда находим h= Поверхность бака состоит из квадрата со стороной х и четырех прямоугольников со сторонами х и . Значит,

S = х2 + 4 • · x= х2+ .

Итак, S = X2 + , где х € (0; +) (мы учли, что V = 500)

Математическая модель задачи составлена.

Второй этап. Работа с составленной моделью.

На этом этапе для функции S = х2 + , где х € (0; +)

надо найти у/наим. Для этого нужна производная функции:

S’ = 2х – ;

S’ =.

На промежутке (0; +оо) критических точек нет, а стационарная точка только одна: S’ = 0 при х = 10.

Заметим, что при х< 10 выполняется неравенство S’ < 0, а при х > 10 выполняется неравенство S’ > 0. Значит, х = 10 — единственная стационарная точка, причем точка минимума функции на заданном промежутке, а потому, согласно теореме из пункта 1, в этой точке функция достигает своего наименьшего значения.

Третий этап. Ответ на вопрос задачи.

В задаче спрашивается, какой должна быть сторона основания, чтобы бак имел наименьшую поверхность. Мы выяснили, что сторона квадрата, служащего основанием такого бака, равна 10 дм.

Ответ: 10 дм.

Источник

Модель

Когда мы передаем какую-то информацию, мы ее упрощаем. То есть передаем не всё, а только самое важное. Причём степень подробности, т.е. выделения важного, определяется целью.

Вам звонит друг и спрашивает: «Ты где?» Если вы знаете, что он заболел и сидит дома, то ответите: «В школе» (Рис. 1).

Рис. 1. Ответ на вопрос в зависимости от ситуации

А если сейчас перемена и вы знаете, что он пошёл в столовую? Вряд ли ответ «В школе» можно назвать полезным и содержательным. Скорее всего, вы ответите: «В 305 кабинете» (Рис. 2).

Рис. 2. Ответ на вопрос в зависимости от ситуации

На один и тот же вопрос можно давать ответы с разной степенью точности в зависимости от ситуации или цели. В жизни для описания того или иного события или задачи не нужно учитывать все возможные факторы. Более того, все учесть невозможно. То есть всегда необходимо упростить ситуацию, выделить главное, чтобы её описать. По-другому говорят «составить модель».

Математическая модель

Мы постоянно сталкиваемся с моделями. План зрительного зала – это модель настоящего зала. Она упрощает задачу – найти место в зале (Рис. 3).

Рис. 3. План зрительного зала – модель

Ту же самую функцию выполняют карта страны или мира (Рис. 4).

Рис. 4. Карта мира – тоже модель

Когда мы идем по улице и смотрим на номера домов, то знаем, что 19-й дом будет после 15-го и 17-го. Мы это понимаем, потому что в голове у нас есть модель – натуральные числа и порядок, по которому они расположены (Рис. 5).

Рис. 5. Модель нумерации номеров домов

Когда мы хотим решить какую-то задачу, найти какую-нибудь величину, мы тоже упрощаем. Реальные объекты мы обозначаем числами или буквами (переменными). В таком случае говорят, что мы строим математическую модель.

Построение математической модели

Задача 1

В одной вазе 10 яблок, во второй – 12 (Рис. 6). Сколько всего яблок в двух вазах?

Рис. 6. Иллюстрация к задаче 1

Решение

Если вы ответили , значит, вы уже успели построить математическую модель и с её помощью решить задачу.

Ответ: 22.

Без модели эта задача решается так. В одной вазе 10 яблок, во второй – 12. Ссыпаем их в одну вазу и руками пересчитываем (Рис. 7).

Рис. 7. Решение задачи без построения математической модели

Но мы поступаем не так. Все яблоки разные (разного цвета, размера), но нас интересует только их количество. Поэтому яблоки в обеих вазах мы заменяем числами, их количеством: 10 и 12.

Теперь нам не надо складывать яблоки вместе, а остается сложить только числа 10 и 12 и получить 22.

Это и есть математическая модель, математическое упрощение реальности. Действия мы произвели с моделью, но выводы сделали относительно реальной ситуации.

Кроме того, что модель упростила решение, мы с помощью нее решили сразу много реальных задач. Например, в одном дворе 10 машин, во втором – 12 (Рис. 8). Сколько всего машин?

Рис. 8. С помощью одной математической модели решаются многие реальные задачи

В одной комнате 10 человек, в другой – 12. Сколько всего человек? Везде один и тот же ответ: .

Алгоритм решения задач при помощи математической модели

Обратите внимание: если записать количества словами – «десять» и «двенадцать», то сложить не получится. А если записать в правильном виде (т.е. в десятичной записи): , то для решения есть своя техника – сложение в столбик.

То есть цель составления математической модели – переписать задачу с русского языка на математический в таком виде, для которого есть своя техника выполнения работ.

На математике мы будем изучать много техник решения для различных математических конструкций. Зачем это нужно? Овладев техникой решения математической конструкции, мы можем решить любую задачу, которая сводится к этой конструкции.

Этот же приём мы используем в жизни: вместо того чтобы таскать кирпичи руками на 3-й, 4-й, 5-й этажи, мы придумали механизм – лебедку, которая облегчает нашу задачу и позволяет поднять кирпичи на любой этаж (Рис. 9).

Рис. 9. Лебедка позволяет не таскать кирпичи

Иногда может казаться, что изучаемая техника решения задач (решение уравнений, неравенств и т.д.) сама по себе бессмысленна. Если вас будет мучить эта мысль, попробуйте разобрать часы и посмотреть на детали, из которых они состоят. Каждая из них по отдельности кажется бесполезной для определения времени. А вот собранные вместе эти детали позволяют решить важную задачу – узнать время (Рис. 10).

Рис. 10. Собранные вместе детали позволяют определить время

Но этот урок мы посвятим не технике решения, а более важному этапу решения задач – составлению математической модели (т.е. переписыванию условия с русского языка на математический).

Чтобы решить какую-то задачу, обычно поступают так:

Переходят от реальной ситуации к модели.
Решают модель по некоторому алгоритму.
Возвращаются от модели к реальной ситуации.

Уравнения в математических моделях

Очень часто математическая модель содержит уравнение. Уравнение – это аналог ситуации, когда объект неизвестен, но кое-что мы про него знаем.

Задача 2. В двух вазах 17 яблок, причем во второй на 3 больше, чем в первой. Сколько яблок в каждой вазе? (Рис. 11)

Рис. 11. Иллюстрация к задаче 2

Решение

Для решения этой задачи мы составляем математическую модель. От яблок мы переходим к числам. Яблоки в каждой вазе мы заменяем числом (т.е. количеством).

Т.к. нам неизвестно количество яблок в одной вазе, то мы вводим переменную . В одной вазе яблок, во второй – на 3 больше, т.е. .

Таким образом,

– количество яблок в первой вазе.
– количество яблок во второй вазе.

Тогда всего яблок: .

Вот мы и построили математическую модель. Мы не думаем больше о яблоках, а только о том, как решить это уравнение:

Корень уравнения , тогда .

Мы решили модель. Теперь возвращаемся к реальной ситуации и получаем ответ: 7 – это количество яблок в первой вазе и 10 – во второй.

Ответ: .

Для решения этой же задачи мы могли составить другую модель.

Пусть:

– количество яблок в первой вазе.
– количество яблок во второй вазе.

Тогда у нас есть два условия: в двух вазах 17 яблок: и во второй вазе яблок на 3 больше, чем в первой: . Причём эти условия должны выполняться одновременно.

В таких случаях говорят о системе уравнений и записывают следующим образом:

Фигурная скобка означает, что оба условия должны выполняться одновременно.

Обратите внимание, что для любой модели ответ в задаче получится один и тот же (при условии, что модель составлена и решена правильно).

В ответвлении вы можете подробнее узнать о системах уравнений.

Системы уравнений

Рассмотрим такой пример. Если сыщик знает про одного преступника, что тот высокий, а про второго, что тот блондин, то эти два условия не объединены в систему, они относятся к разным неизвестным – к разным преступникам.

Рис. 1. Пример условий, которые не объединены в систему

Если это информация про одного и того же преступника, то это уже система. Оба условия выполняются одновременно. Одну информацию можно использовать для уточнения другой. Преступник – высокий блондин.

Рис. 2. Пример условий, которые объединены в систему

Рассмотрим ещё один пример. Пусть нам известно, что дом находится на ул. Гоголя. Вариантов, где точно расположен дом, много – целая улица. Дом находится на проспекте Мира. То же самое – вариантов много.

Но если эта информация относится к одному и тому же дому, то сразу понятно, что дом находится на перекрестке (Рис. 3). Два условия объединены в систему.

Рис. 3. Ещё один пример условий, которые объединены в систему

Итак, система – это объединение нескольких условий так, чтобы они выполнялись одновременно.

Теперь рассмотрим систему уравнений в математике.

Задача 1. Два человека вскопали огород площадью . Сколько вскопал каждый, если они вскопали одинаковую площадь?

Рис. 4. Иллюстрация к задаче 1

Решение

Запишем условие уравнением: , где – площадь, которую вскопал первый человек, – площадь, которую вскопал второй человек.

Решение такого уравнения – пара чисел. Их бесконечно много. Например, один вскопал , другой – . Или один вскопал все , другой – ничего (Рис. 5).

Рис. 5. Иллюстрация к задаче 1

Запишем условие, что два человека вскопали равные площади (Рис. 6), уравнением: .

Здесь тоже бесконечно много решений.

Рис. 6. Иллюстрация к задаче 1

А если речь идет про один и тот же огород, про одних и тех же людей, то эти два условия выполняются одновременно. Двое вскопали огород , причем поровну.

Уравнения нужно объединить в систему. Договорились обозначать это фигурной скобкой:

Здесь уже только одно решение – каждый вскопал по : .

Эта пара чисел является решением каждого из уравнений системы.

Ответ: .

Пример составления математической модели

Задача 3

Смешали два водно-солевых раствора с концентрацией и получили 400 граммов раствора с концентрацией . Сколько взяли граммов каждого раствора?

Решение

Запишем условие в другом виде.

Смешали два раствора и получили 400 граммов раствора:
В первом растворе содержится соли:
Во втором растворе содержится соли:

В смеси с одной стороны,

а с другой,

Получаем еще одно условие: .

То есть

Для того чтобы не переписывать так длинно, введем удобные обозначения , а ещё лучше ввести – :

Тогда получим систему уравнений:

Что мы сделали? Мы записали условие задачи на математическом языке. В таком виде легко будет найти ответ, решив систему уравнений.

Почему мы можем работать с неизвестными переменными

Обратите внимание, что во всех задачах мы использовали один и тот же приём – обозначали неизвестную за и переписывали условие на математическом языке, используя это обозначение. То есть мы ещё не знаем, чему равен , но уже его используем.

Этот метод мы применяем для решения любой задачи: не знаем, что ищем, но делаем некоторые допущения, без которых невозможно было бы даже приступить к решению.

Например, детектив, прежде чем искать преступника, делает предположение – это человек. Он ещё не знает – мужчина или женщина, какой рост, вес, цвет кожи и т.д. (Рис. 1).

Рис. 1. Прежде чем искать преступника, необходимо сделать предположение

Как иначе искать отпечатки пальцев на ручке, если не предполагать, что это человек? Сделав такое предположение, детектив позволяет себе начать думать о решении и использовать «технику»: по размерам отпечатков искать размер обуви, по пеплу искать марку сигарет и т.д. (Рис. 2).

Рис. 2. По размеру отпечатка можно определить размер обуви

В алгебре своя техника, которую мы будем изучать на уроках, – решение уравнений, систем и т.д. Но если использовать только числа и не вводить переменные, то не получится «забежать вперёд», т.е. составить уравнение или систему, которая позволит решить задачу.

Математические модели для задач, которые сводятся к линейным уравнениям

Для решения задач нам нужно сделать следующее.

Составить математическую модель (т.е. переписать условие на математическом языке).
Решить полученное уравнение или систему.

Как решать полученную систему уравнений – это техника, о которой мы будем говорить позже, поскольку это отдельная задача.

Научившись решать какой-то тип уравнений или их систем, мы научимся решать целый класс задач. Например, мы умеем решать линейные уравнения: где – числа, – переменная. Поэтому мы умеем решать все задачи, условие которых можно переписать в таком виде.

Рассмотрим три такие задачи.

Задача 1

Автомобиль 3 часа ехал с некоторой постоянной скоростью, затем увеличил скорость на 20 км/ч и проехал так 5 часов.

С какой скоростью автомобиль ехал первые3 часа, если весь путь составил 750 км?

Задача 2

Килограмм апельсинов стоит на 10 рублей больше, чем килограмм яблок. Сколько стоит килограмм яблок и килограмм апельсинов, если за 2 кг яблок и 3 кг апельсинов заплатили 500 руб?

Задача 3

Второй рабочий делает в час на 5 деталей меньше первого. Если он проработает 7 часов, а потом его сменит первый и проработает 3 часа, то вместе они сделают 235 деталей.

Сколько деталей делает каждый рабочий в час?

Из определения скорости вы можем выразить пройденный путь: где – путь, – скорость, – время.

Пусть – скорость за 3 часа, тогда:

Пусть – цена за яблок, тогда:

Пусть – количество деталей в час у первого рабочего, тогда:

У нас были совершенно разные задачи, но, составив математическую модель, мы увидели, что все эти задачи сводятся примерно к одинаковым уравнениям. Поэтому мы учимся решать не уравнения к каждой конкретной задаче, а сразу некоторый тип уравнений.

Например, в задачах, рассмотренных выше, мы везде получили линейные уравнения: где – числа, – переменная.

Такие уравнения мы уже умеем решать, значит, умеем решать и все такие задачи.

Модель на уроках математики и физики

Обратите внимание: в учебниках по математике вам сразу даются задачи в математической модели, в них выделено всё важное.

Например: моторная лодка прошла против течения реки 160 км и вернулась в пункт отправления, затратив на обратный путь на 8 часов меньше времени.

Известно, что в неподвижной воде лодка движется со скоростью 15 км/ч.

Найдите скорость течения реки. Ответ дайте в км/ч.

Нам не даны размеры лодки, мощность мотора, ширина реки, наличие ветра и его скорость и т.д.

Подразумевается, что для решения достаточно данных в условии значений: длина пути, время, скорости движения лодки и течения реки (Рис. 1). То есть задача уже упрощена.

Рис. 1. Для решения задачи достаточно данных в условии значений

Нам остаётся текстовую модель реальной ситуации переписать на математическом языке, составить математическую модель и решить её.

На уроках по физике вам будут попадаться задачи, в которых саму модель ещё надо будет составить (например, пренебречь трением между каким-то телами или массой лёгкого объекта). И только после того, как будет составлена модель, можно будет составлять математическую модель и её решать. Собственно, физическая часть решения задачи – это как раз составление модели. И сложность заключается в том, что мы должны выделить самое важное и отбросить неважное до того, как решим задачу.

Дальше остается техника, для которой как раз и нужна математика. То есть математики создают удобные инструменты и отрабатывают технику работы с этими инструментами, а физики выбирают, какие инструменты понадобятся для решения той или иной физической задачи, а какие – нет (Рис. 2).

Рис. 2. Математики создают удобные инструменты для решения задач, а физики выбирают, какие из инструментов понадобятся

Математические модели для текстовых задач

В завершении рассмотрим задачу, которая не застанет вас врасплох, если вы умеете составлять и решать математические модели.

Задача 4. Кирпич весит килограмм и еще полкирпича. Сколько весит кирпич?

Рис. 12. Иллюстрация к задаче 4

Эта задача нацелена на то, чтобы вы ответили сходу и дали неправильный ответ. Конечно же, ответ «полтора килограмма» неверный. А потом, когда рассказчик вам даст правильный ответ, вы должны восхититься этим фокусом. На самом деле восхищаться здесь нечем. Математическая модель дает нам очень быстрое решение.

Решение (с использованием математической модели)

Нам неизвестна масса кирпича, поэтому обозначим ее. Пусть – масса кирпича. Тогда масса половины кирпича .

Тогда условие задачи перепишем в следующем виде: .

Это и есть наша математическая модель. Так как она сохраняет только важное для задачи, то здесь лишние слова нас не вводят в заблуждение, и мы легко решаем эту смоделированную задачу, т.е. уравнение:

Итак, – это решение нашей модели – уравнения. Таким образом, масса кирпича равна кг.

Ответ: 2.

Можно решить эту задачу и без математического моделирования.

Кирпич весит килограмм и еще полкирпича. Кладем это всё на весы. Кирпич мы можем расколоть на две половины. Мы можем с обеих сторон убрать полкирпича (Рис. 13).

Рис. 13. Раскололи кирпич пополам и убрали с обеих чаш по половине

То есть мы уже поняли, что полкирпича весит килограмм. Значит, весь кирпич весит 2 кг.

Но здесь на последнем шаге мы снова применили математическую модель, а собирались без нее.

Доведем дело до конца по-честному. Раз полкирпича весит столько же, сколько гиря, то добавим слева полкирпича, а справа гирю. Склеим снова кирпич. Таким образом, масса кирпича 2 кг (Рис. 14).

Рис. 14. Добавили слева полкирпича, а справа – гирю и склеили кирпич

Заключение

На этом уроке мы рассмотрели два этапа решения текстовых задач – составление математической модели (переписывание условия задачи на математическом языке) и техника (расчёт полученной модели). И подробно остановились на первом этапе, потренировались составлять математические модели к разным задачам.

Список рекомендованной литературы

Никольский С.М., Решетников Н.Н., Потапов М.К., Шевкин А.В. Алгебра. 7 класс. Учебник. ФГОС, изд-во «Просвещение», 2017.
Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. Алгебра. 7 класс. Учебник, изд-во «Просвещение», 2014.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра. 7 класс. Учебник, изд-во «Просвещение», 2013.

Рекомендованные ссылки на ресурсы сети Интернет

Интернет-портал yaklass.ru (Источник)
Интернет-портал school-assistant.ru (Источник)
Интернет-портал edufuture.biz (Источник)

Домашнее задание

В одной кассе кинотеатра продали на билетов больше, чем в другой. Сколько билетов продали в каждой кассе, если всего было продано билета?
Двое рабочих изготовили деталей, причем первый изготовил на деталей больше, чем второй. Сколько деталей изготовил каждый рабочий?
На путь по течению реки пароход затратил ч, а на обратный путь – ч. Скорость течения км/ч. Какова скорость парохода в стоячей воде?

Источник

Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.

Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.

Пример:

Решение любой текстовой задачи можно разделить на несколько основных этапов:

Работа с условием
Составление математической модели
Проверка ответа

Работа с условием

Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.

Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?

Иллюстрация:

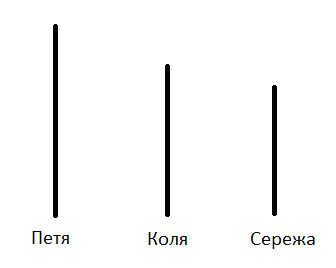
Из рисунка сразу понятен ответ: Петя выше всех.

Пример.

Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?

Иллюстрация:

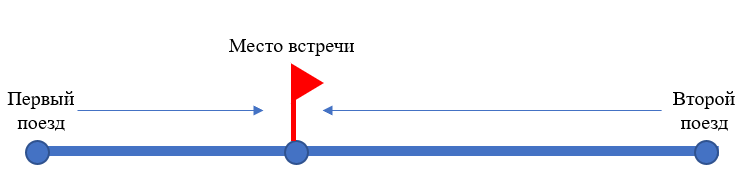
Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.

Составим математическую модель:

45х + 55х = 200

100х = 200

х = 2 ч

Ответ: 2 ч.

Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.

Математическая модель

Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.

x — число девочек

y — число мальчиков

Реальная ситуация	Математическая модель
В классе поровну мальчиков и девочек	$ { x=y} $
Девочек на 5 больше, чем мальчиков	$ { x=y+5, ; или; x-y=5,; или; x-5=y} $
Мальчиков в 2 раза больше, чем девочек	$ { y=2x, ; или; frac{y}{2}=x,; или; frac{y}{x}=2} $
Если в класс перейдут 3 мальчика, то девочек станет в два раза больше	$ { y=2(y+3)} $

Алгебраическая зависимость

Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.

При составлении уравнения особое значение играют используемые предлоги: «в» и «на».

Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?

Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.

Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.

Выразим рост мальчиков.

Петя выше Коли на 20 см: П – 20 = К

Сережа ниже Коли на 10 см: К = С + 10

Подставим в первое уравнение рост Коли: П – 20 = С + 10

Нам нужно найти, на сколько см Петя выше Сережи: П – С

П – 20 = С + 10

П – С = 20 + 10

П – С = 30

Получаем, что Петя выше Сережи на 30 см.

Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?

Решение:

Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.

Маша сделала в два раза больше снежинок, чем Коля: К = М/2

Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4

Вместе ребята сделали 12 снежинок: М + К + Р = 12

Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12

М = 4.

Маша сделала 4 снежинки.

Процентная зависимость

С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?

Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.

Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.

Так что же такое один процент?

Процент — это всегда доля какого-то числа.

100% — все число

50% — половина

25% — четверть

Чтобы найти 1%, необходимо поделить всё число на 100.

Пример:

Есть 100 яблок.

$ 1% ;от ;всех ;яблок; –frac{100}{100} = 1 ;яблоко. $

Есть 200 груш

$ 1% ;от ;всех ;груш; –frac{200}{100} = 2 ;груши. $

Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.

Пример:

200 груш — 100 %

2 груши — 1 %

Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.

$ frac{200}{2}=frac{100}{1} $

Исходя из правил работы с дробями, получаем правила работы с пропорцией.

1. Внутри одной дроби можно сокращать значения.

2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100

Эту тему мы еще подробно пройдем на курсе.

Рассмотрим несколько примеров работы с процентами в текстовых задачах.

Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов

Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?

Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек

Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?

Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?

На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:

Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880

Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880

Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.

Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.

Источник

Содержание

Что такое математическая модель?
Понятие математической модели.
Составление (построение) математической модели задачи.
Если Вам нравится этот сайт.
22. Текстовые задачи Читать 0 мин.
22.112. Математическая модель

Что такое математическая модель?

Понятие математической модели.

Математическая модель — очень простое понятие. И очень важное. Именно математические модели связывают математику и реальную жизнь.

Говоря простым языком, математическая модель — это математическое описание любой ситуации. И всё. Модель может быть примитивной, может быть и суперсложной. Какая ситуация, такая и модель.)

В любом (я повторяю — в любом!) деле, где нужно чего-нибудь посчитать да рассчитать — мы занимаемся математическим моделированием. Даже если и не подозреваем об этом.)

Например, нам нужно посчитать расходы (Р) на покупки в магазине. Надо купить две булки (Б) и три пачки масла (М). Мы знаем цену булки (ЦБ) и цену масла (ЦМ). Легко можно записать:

Вот эта запись и будет математической моделью расходов на наши покупки. Модель не учитывает цвет упаковки, срок годности, вежливость кассиров и т.п. На то она и модель, а не реальная покупка. Но расходы, т.е. то, что нам надо — мы узнаем точно. Если модель правильная, конечно.

Представлять, что такое математическая модель полезно, но этого мало. Самое главное — уметь эти модели строить.

Составление (построение) математической модели задачи.

Составить математическую модель — это значит, перевести условия задачи в математическую форму. Т.е. превратить слова в уравнение, формулу, неравенство и т.д. Причём превратить так, чтобы эта математика строго соответствовала исходному тексту. Иначе у нас получится математическая модель какой-то другой, неведомой нам задачи.)

Говоря конкретнее, нужно установить математическую связь между всеми данными задачи.

Задач в мире — бесконечное количество. Поэтому предложить чёткую пошаговую инструкцию по составлению математической модели любой задачи — невозможно.

Но можно выделить три основных момента, на которые нужно обратить внимание.

1. В любой задаче есть текст, как ни странно.) В этом тексте, как правило, имеется явная, открытая информация. Числа, значения и т.п.

2. В любой задаче имеется скрытая информация. Это текст, который предполагает наличие дополнительных знаний в голове. Без них — никак. Кроме того, математическая информация частенько скрывается за простыми словами и. проскакивает мимо внимания.

3. В любой задаче должно быть дана связь данных между собой. Эта связь может быть дана открытым текстом (что-то равно чему-то), а может быть и скрыта за простыми словами. Но простые и понятные факты частенько упускаются из виду. И модель никак не составляется.

Сразу скажу: чтобы применить эти три момента, задачу приходится читать (и внимательно!) несколько раз. Обычное дело.

А теперь — примеры.

Начнём с простой задачки:

Петрович вернулся с рыбалки и гордо предъявил семье улов. При ближайшем рассмотрении оказалось, что 8 рыбин родом из северных морей, 20% всех рыбин — из южных, а из местной реки, где рыбачил Петрович — нет ни одной. Сколько всего рыбин купил Петрович в магазине «Морепродукты»?

Все эти слова нужно превратить в какое-то уравнение. Для этого нужно, повторюсь, установить математическую связь между всеми данными задачи.

С чего начинать? Сначала вытащим из задачи все данные. Начнём по порядочку:

Обращаем внимание на первый момент.

Какая здесь явная математическая информация? 8 рыбин и 20%. Не густо, да нам много и не надо.)

Обращаем внимание на второй момент.

Ищем скрытую информацию. Она здесь есть. Это слова: «20% всех рыбин«. Здесь нужно понимать, что такое проценты и как они считаются. Иначе задача не решается. Это как раз та дополнительная информация, которая должна быть в голове.

Здесь ещё имеется математическая информация, которую совершенно не видно. Это вопрос задачи: «Сколько всего рыбин купил. « Это ведь тоже какое-то число. И без него никакая модель не составится. Поэтому обозначим это число буквой «х». Мы пока не знаем, чему равен икс, но такое обозначение очень нам пригодится. Подробнее, что брать за икс и как с ним обращаться, написано в уроке Как решать задачи по математике? Вот так сразу и запишем:

х штук — общее количество рыб.

В нашей задаче южные рыбы даны в процентах. Надо их перевести в штуки. Зачем? Затем, что в любой задаче модели надо составлять в однотипных величинах. Штуки — так всё в штуках. Если даны, скажем часы и минуты — всё переводим во что-нибудь одно — или только часы, или только минуты. Не суть важно во что. Важно, чтобы все величины были однотипными.

Возвращаемся к раскрытию информации. Кто не знает, что такое процент, никогда не раскроет, да. А кто знает, тот сразу скажет, что проценты здесь от общего числа рыб даны. А нам это число неизвестно. Ничего не выйдет!

Общее количество рыб (в штуках!) мы не зря буквой «х» обозначили. Посчитать южных рыб в штуках не получится, но записать-то мы сможем? Вот так:

0,2·х штук — количество рыб из южных морей.

Вот теперь мы скачали всю информацию с задачи. И явную, и скрытую.

Обращаем внимание на третий момент.

Ищем математическую связь между данными задачи. Эта связь настолько проста, что многие её не замечают. Такое часто бывает. Здесь полезно просто записать собранные данные в кучку, да и посмотреть, что к чему.

Что у нас есть? Есть 8 штук северных рыб, 0,2·х штук — южных рыб и х рыб — общее количество. Можно связать эти данные как-то воедино? Да легко! Общее количество рыб равно сумме южных и северных! Ну кто бы мог подумать. ) Вот и записываем:

Вот это уравнение и будет математической моделью нашей задачи.

Прошу заметить, что в этой задаче нас не просят ничего складывать! Это мы сами, из головы, сообразили, что сумма южных и северных рыб даст нам общее количество. Вещь настолько очевидная, что проскакивает мимо внимания. Но без этой очевидности математическую модель не составить. Вот так.

Теперь уже можно применить всю мощь математики для решения этого уравнения). Именно для этого и составлялась математическая модель. Решаем это линейное уравнение и получаем ответ.

Составим математичесскую модель ещё одной задачки:

Спросили Петровича: «А много ли у тебя денег?» Заплакал Петрович и отвечает: «Да всего чуть-чуть. Если я потрачу половину всех денег, да половину остатка, то всего-то один мешок денег у меня и останется. » Сколько денег у Петровича?

Опять работаем по пунктам.

1. Ищем явную информацию. Тут её не сразу и обнаружишь! Явная информация — это один мешок денег. Есть ещё какие-то половинки. Ну, это во втором пункте разберём.

2. Ищем скрытую информацию. Это половинки. Чего? Не очень понятно. Ищем дальше. Есть ещё вопрос задачи: «Сколько денег у Петровича?» Обозначим количество денег буквой «х»:

И вновь читаем задачу. Уже зная, что у Петровича х денег. Вот тут уже и половинки сработают! Записываем:

0,5·х — половина всех денег.

Остаток будет тоже половина, т.е. 0,5·х. А половину от половины можно записать так:

0,5·0,5·х = 0,25х — половина остатка.

Теперь вся скрытая информация выявлена и записана.

3. Ищем связь между записанными данными. Здесь можно просто читать страдания Петровича и записывать их математически):

Если я потрачу половину всех денег.

Запишем этот процесс. Всех денег — х. Половина — 0,5·х. Потратить — это отнять. Фраза превращается в запись:

да половину остатка.

Отнимем ещё половину остатка:

то всего-то один мешок денег у меня и останется.

А вот и равенство нашлось! После всех вычитаний один мешок денег остаётся:

Вот она, математическая модель! Это опять линейное уравнение, решаем, получаем:

Вопрос на соображение. Четыре — это чего? Рубля, доллара, юаня? А в каких единицах у нас деньги в математической модели записаны? В мешках! Значит, четыре мешка денег у Петровича. Тоже неплохо.)

Задачки, конечно, элементарные. Это специально, чтобы уловить суть составления математической модели. В некоторых задачах может быть гораздо больше данных, в которых легко запутаться. Это часто бывает в т.н. компетентностных задачах. Как вытаскивать математическое содержание из кучи слов и чисел показано на примерах здесь.

В задачах на движение требуется держать в голове формулу-ключ: связь расстояния, скорости и времени. По ссылке можно посмотреть примеры составления модели и решения таких задач.

В задачах на работу надо чётко понимать формулу-ключ: связь времени, производительности труда и объёма работы. Там имеются свои фишки, с которыми можно ознакомиться по ссылке.

Для того, чтобы свободнее ориентироваться в построении математических моделей очень полезно порешать обратные задачи. Т.е. по заданной модели придумать условие задачи. Это, кстати, не так просто.) Тема может быть совершенно любой, фантазия ограничена только математикой. Вот примеры таких заданий:

Составить задачу по математической модели:

х + (х+10) + (х-30) + 20 = 120

Я специально не раскрываю скобки и не привожу подобные — так проще.

Попробуйте придумать задачку, а потом можете найти в уроке Как решать задачи по математике исходную задачу для этой модели. И сравните, для интереса.)

Еще пример, посложнее:

Составить задачу по математической модели:

Исходная задача и её решение приведены в уроке Решение задач на движение. Кстати, по ссылке подробно написано, как эту математическую модель составить.

Составить задачу по математической модели:

1 = 5 · (х + 2х + 2х + 3х + 4х)

Эта задача и её решение расписаны в уроке Задачи на работу.

Ещё одно замечание. В классических школьных задачах (трубы заполняют бассейн, куда-то плывут катера и т.п.) все данные, как правило, подобраны очень тщательно. Там выполняются два правила:
— информации в задаче хватает для её решения,
— лишней информации в задаче не бывает.

Это подсказка. Если осталась какая-то неиспользованная в математической модели величина — задумайтесь, нет ли ошибки. Если данных никак не хватает — скорее всего, не вся скрытая информация выявлена и записана.

В компетентностных и прочих жизненных задачах эти правила строго не соблюдаются. Нету подсказки. Но и такие задачи можно решать. Если, конечно, потренироваться на классических.)

Если Вам нравится этот сайт.

Кстати, у меня есть ещё парочка интересных сайтов для Вас.)

Вот здесь можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)

А вот здесь можно познакомиться с функциями и производными.

Источник

22. Текстовые задачи Читать 0 мин.

22.112. Математическая модель

Пример:

Решение любой текстовой задачи можно разделить на несколько основных этапов:

Работа с условием
Составление математической модели
Проверка ответа

Работа с условием

Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?

Из рисунка сразу понятен ответ: Петя выше всех.

Пример.

Составим математическую модель:

Математическая модель

x — число девочек

y — число мальчиков

Реальная ситуация	Математическая модель
В классе поровну мальчиков и девочек	$ < x=y>$
Девочек на 5 больше, чем мальчиков	$ < x=y+5, ; или; x-y=5,; или; x-5=y>$
Мальчиков в 2 раза больше, чем девочек	$ < y=2x, ; или; frac<2>=x,; или; frac=2> $
Если в класс перейдут 3 мальчика, то девочек станет в два раза больше	$ < y=2(y+3)>$

Алгебраическая зависимость

Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.

При составлении уравнения особое значение играют используемые предлоги: «в» и «на».

Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?

Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.

Выразим рост мальчиков.

Петя выше Коли на 20 см: П – 20 = К

Сережа ниже Коли на 10 см: К = С + 10

Подставим в первое уравнение рост Коли: П – 20 = С + 10

Нам нужно найти, на сколько см Петя выше Сережи: П – С

Получаем, что Петя выше Сережи на 30 см.

Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.

Маша сделала в два раза больше снежинок, чем Коля: К = М/2

Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4

Вместе ребята сделали 12 снежинок: М + К + Р = 12

Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12

Маша сделала 4 снежинки.

Процентная зависимость

Так что же такое один процент?

Процент — это всегда доля какого-то числа.

Чтобы найти 1%, необходимо поделить всё число на 100.

Пример:

$ 1% ;от ;всех ;яблок; –frac<100> <100>= 1 ;яблоко. $

Пример:

Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.

Исходя из правил работы с дробями, получаем правила работы с пропорцией.

1. Внутри одной дроби можно сокращать значения.

2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100

Эту тему мы еще подробно пройдем на курсе.

Рассмотрим несколько примеров работы с процентами в текстовых задачах.

Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?

Источник

Модель

Математическая модель

Построение математической модели

Алгоритм решения задач при помощи математической модели

Уравнения в математических моделях

Пример составления математической модели

Математические модели для задач, которые сводятся к линейным уравнениям

Математические модели для текстовых задач

Что такое математическая модель?

Понятие математической модели.

Составление (построение) математической модели задачи.

Если Вам нравится этот сайт.

22. Текстовые задачи <img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" src="https://reshutest.ru/resources/img/ico-wristwatch.svg" />Читать 0 мин.

22.112. Математическая модель

Вам также может понравиться

Как найти фото с телеграмма на андроид

Как найти вершину трапеции по точкам

Как найти знак в строке питон

Добавить комментарий Отменить ответ

22. Текстовые задачи Читать 0 мин.