Как составить математическую модель задачи пример

1. Примеры составления математических моделей

Пример
1.5.1.

Пусть
некоторый экономический регион производит
несколько (n) видов продуктов исключительно
своими силами и только для населения
данного региона. Предполагается, что
технологический процесс отработан, а
спрос населения на эти товары изучен.
Надо определить годовой объем выпуска
продуктов, с учетом того, что этот объем
должен обеспечить как конечное, так и
производственное потребление.

Составим
математическую модель этой задачи. По
ее условию даны: виды продуктов, спрос
на них и технологический процесс;
требуется найти объем выпуска каждого
вида продукта.

Обозначим
известные величины:

c_i
– спрос населения на i-й
продукт (i=1,…,n);
a_ij
– количество i-го
продукта, необходимое для выпуска
единицы j -го продукта по данной технологии
( i=1,…,n
; j=1,…,n);

Обозначим
неизвестные величины:

х_i
– объем
выпуска i-го
продукта (i=1,…,n);
совокупность с
=( c₁
,…,c_n
) называется
вектором спроса, числа a_ij
– технологическими коэффициентами, а
совокупность х
=( х₁
,…,х_n
) – вектором
выпуска.

По
условию задачи вектор х
распределяется
на две части: на конечное потребление
(вектор с)
и на воспроизводство (вектор х-с
). Вычислим
ту часть вектора х
которая идет
на воспроизводство. По нашим обозначениям
для производства х_j
количества j-го товара идет a_ij
· х_j
количества i-го
товара.

Тогда
сумма a_i1
· х₁
+…+ a_in
· х_n
показывает ту величину i-го
товара, которая нужна для всего выпуска
х =(
х₁
,…,х_n
).

Следовательно,
должно выполняться равенство:

.

Распространяя это рассуждение на все
виды продуктов, приходим к искомой
модели:

Решая эту систему из n линейных уравнений
относительно х₁ ,…,х_nи найдем требуемый вектор выпуска.

Для того, чтобы написать эту модель в
более компактной (векторной) форме,
введем обозначения:

Квадратная ()
—матрицаАназывается технологической
матрицей. Легко проверить, что наша
модель теперь запишется так:х-с=Ахили

(1.6)

Мы получили классическую модель «Затраты
– выпуск», автором которой является
известный американский экономист В.
Леонтьев.

Пример
1.5.2.

Нефтеперерабатывающий
завод располагает двумя сортами нефти:
сортом А
в количестве 10 единиц, сортом В
— 15 единиц. При переработке из нефти
получаются два материала: бензин
(обозначим Б)
и мазут (М).
Имеется три варианта технологического
процесса переработки:

I:
1ед.А
+ 2ед.В
дает 3ед.Б
+ 2ед.М

II: 2ед.А
+ 1ед.В
дает 1ед.Б
+ 5ед.М

III: 2ед.А
+ 2ед.В
дает 1ед.Б
+ 2ед.М

Цена
бензина — 10 долл. за единицу, мазута —
1 долл. за единицу.

Требуется определить наиболее выгодное
сочетание технологических процессов
переработки имеющегося количества
нефти.

Перед моделированием уточним следующие
моменты. Из условия задачи следует, что
«выгодность» технологического процесса
для завода следует понимать в смысле
получения максимального дохода от
реализации своей готовой продукции
(бензина и мазута). В связи с этим понятно,
что «выбор (принятие) решения» завода
состоит в определении того, какую
технологию и сколько раз применить.
Очевидно, что таких возможных вариантов
достаточно много.

Обозначим
неизвестные величины:

х_i– количество
использованияi-го технологического
процесса(i=1,2,3).
Остальные параметры
модели (запасы сортов нефти, цены бензина
и мазута)известны.

Теперь одно конкретное решение завода
сводится к выбору одного вектора х=(
х₁ ,х₂ ,х₃),
для которого выручка завода равна(32х₁+15х₂
+12х₃)долл. Здесь 32 долл.
– это доход, полученный от одного
применения первого технологического
процесса (10 долл. ·3ед.Б+ 1 долл. ·2ед.М= 32 долл.). Аналогичный смысл имеют
коэффициенты 15 и 12 для второго и третьего
технологических процессов соответственно.
Учет запаса нефти приводит к следующим
условиям:

для сорта А:

для сорта В:,

где в первом неравенстве коэффициенты
1, 2, 2 – это нормы расхода нефти сорта А
для одноразового применения технологических
процессов I,II,IIIсоответственно.
Коэффициенты второго неравенства имеют
аналогичный смысл для нефти сорта В.

Математическая модель в целом имеет
вид:

Найти такой вектор х = ( х₁
,х₂ ,х₃),
чтобы максимизировать

f(x) =32х₁+15х₂
+12х₃

при выполнении условий:

.

Сокращенная форма этой записи такова:

при ограничениях

(1.7)

Мы получили так называемую задачу
линейного программирования.

Модель (1.7.) является примером оптимизационной
модели детерминированного типа (с вполне
определенными элементами).

Пример1.5.3.

Инвестору
требуется определить наилучший набор
из акций, облигаций и других ценных
бумаг для приобретения их на некоторую
сумму с целью получения определенной
прибыли с минимальным риском для себя.
Прибыль на каждый доллар, вложенный в
ценную бумагу j
– го вида, характеризуется двумя
показателями: ожидаемой прибылью и
фактической прибылью. Для инвестора
желательно, чтобы ожидаемая прибыль на
один доллар вложений была для всего
набора ценных бумаг не ниже заданной
величины b.

Заметим,
что для правильного моделирования этой
задачи от математика требуются
определенные базовые знания в области
портфельной теории ценных бумаг.

Обозначим
известные параметры задачи:

n
– число разновидностей ценных бумаг;
а_j
– фактическая прибыль (случайное число)
от j-го вида ценной бумаги ;
–
ожидаемая прибыль отj-го
вида ценной бумаги.

Обозначим
неизвестные величины:

y_j
— средства,
выделенные для приобретения ценных
бумаг вида j.

По
нашим обозначениям вся инвестированная
сумма выражается как
.

Для упрощения модели введем новые
величины

.

Таким образом, х_i— это
доля от всех средств, выделяемая для
приобретения ценных бумаг видаj.

Ясно, что

Из условия задачи видно, что цель
инвестора — достижение определенного
уровня прибыли с минимальным риском.
Содержательно риск — это мера отклонения
фактической прибыли от ожидаемой.
Поэтому его можно отождествить с
ковариацией
прибыли
для ценных бумаг вида i и вида j. Здесь М
— обозначение математического ожидания.

Математическая модель исходной задачи
имеет вид:

при ограничениях

,,,. (1.8)

Мы получили известную модель Марковица
для оптимизации структуры портфеля
ценных бумаг.

Модель (1.8.) является примеров оптимизационной
модели стохастического типа (с элементами
случайности).

Пример1.5.4.

На базе торговой организации имеется
n типов одного из товаров ассортиментного
минимума. В магазин должен быть завезен
только один из типов данного товара.
Требуется выбрать тот тип товара, который
целесообразно завести в магазин. Если
товар типа jбудет пользоваться
спросом, то магазин от его реализации
получит прибыльр_j, если
же он не будет пользоваться спросом –
убытокq_j.

Перед
моделированием обсудим некоторые
принципиальные моменты. В данной задаче
лицом, принимающим решение (ЛПР), является
магазин. Однако исход (получение
максимальной прибыли) зависит не только
от его решения, но и от того, будет ли
завезенный товар пользоваться спросом,
т. е. будет ли выкуплен населением
(предполагается, что по какой-то причине
у магазина нет возможности изучить
спрос населения). Поэтому население
может рассматриваться как второе ЛПР,
выбирающее тип товара согласно своего
предпочтения. Наихудшим для магазина
«решением» населения является: «завезенный
товар не пользуется спросом». Так что,
для учета всевозможных ситуаций, магазину
нужно считать население своим «противником»
(условно), преследующим противоположную
цель – минимизировать прибыль магазина.

Итак,
имеем задачу принятия решения с двумя
участниками, преследующими противоположные
цели. Уточним, что магазин выбирает один
из типов товаров для продажи (всего n
вариантов решений), а население — один
из типов товаров, который пользуется
наибольшим спросом (n
вариантов решений).

Для
составления математической модели
нарисуем таблицу с n
строками и n
столбцами (всего n²
клеток) и условимся, что строки
соответствуют выбору магазина, а столбики
— выбору населения. Тогда клетка (i,
j) соответствует
той ситуации, когда магазин выбирает
i-й
тип товара (i-ю
строку), а население выбирает j-й
тип товара (j-ю
столбик). В каждую клетку запишем числовую
оценку (прибыль или убыток) соответствующей
ситуации с точки зрения магазина:

Числа q_iнаписаны с минусом
для отражения убытка магазина; в каждой
ситуации «выигрыш» населения (условно)
равен «выигрышу» магазина, взятому с
обратным знаком.

Сокращенный вид этой модели таков:

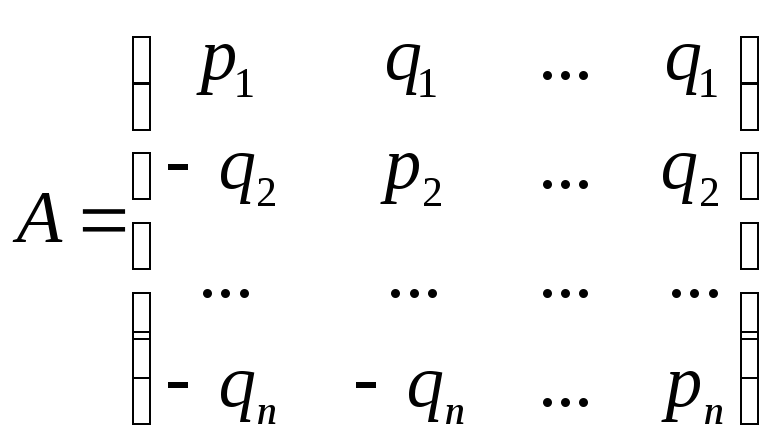(1.9)

Мы получили так называемую матричную
игру. Модель (1.9.) является примером
игровых моделей принятия решения.

п.1. Алгоритм решения задач с помощью систем уравнений

1. Обозначить неизвестные величины переменными («от смысла к буквам»).
2. По условию задачи записать уравнения, связывающие обозначенные переменные.
3. Решить полученную систему уравнений.
4. Истолковать результат в соответствии с условием задачи («от букв к смыслу»).

Например:
Найдите два положительных числа, если известно, что сумма квадратов этих чисел равна 185, а разность квадратов равна 57.

п.2. Примеры

Пример 1. Диагональ прямоугольника равна 10 см. Если меньшую сторону прямоугольника увеличить на 2 см, а большую уменьшить на 2 см, то диагональ не изменится. Найдите стороны прямоугольника.

Пусть a и b – стороны прямоугольника, a > b. Диагональ через стороны выражается по теореме Пифагора. По условию получаем: $$ left{ begin{array}{ l } mathrm{a^2+b^2=10} & \ mathrm{(a-2)^2+(b+2)^2=10^2} & end{array}right. $$ Найдём линейную зависимость между a и b из уравнения: begin{gather*} mathrm{a^2+b^2=(a-2)^2+(b+2)^2}\ mathrm{a^2+b^2=a^2-4a+4+b^2+4b+4}\ mathrm{4a-4b=8Rightarrow a-b=2Rightarrow a=b+2} end{gather*} Подставим a в верхнее уравнение системы: ( mathrm{(b+2)^2+b^2=100} ) begin{gather*} mathrm{b^2+4b+4+b^2-100=0}\ mathrm{2b^2+4b-96=0Rightarrow b^2+2b-48=0Rightarrow (b+8)(b-6)=0}\ mathrm{b_1=-8, b_2=6} end{gather*} Выбираем положительный корень: b = 6
Тогда a = b + 2 = 8
Ответ: 8 см и 6 см.

Пример 2. (задача Диофанта, III в.) Отношение двух чисел равно 3, а отношение суммы квадратов этих чисел к их сумме равно 5. Найдите эти числа.

Пусть x и y – искомые числа. По условию: $$ left{ begin{array}{ l } mathrm{frac{x}{y}=3} & \ mathrm{frac{x^2+y^2}{x+y}=5} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=3y} & \ mathrm{x^2+y^2=5(x+y)} & end{array}right. $$ Подставляем верхнее уравнение в нижнее и решаем: begin{gather*} mathrm{(3y)^2+y^2=5(3y+y)Rightarrow 9y^2+y^2=20yRightarrow 10y^2-20y=0Rightarrow}\ mathrm{Rightarrow 10y(y-2)=0Rightarrow} left[begin{array}{ l } mathrm{y_1=0} & \ mathrm{y_2=2} & end{array}right. end{gather*} Т.к. y в первом уравнении системы стоит в знаменателе, он не может быть равен 0. Получаем: begin{gather*} left{begin{array}{ l } mathrm{x=3y=6} & \ mathrm{y=2} & end{array}right. end{gather*} Ответ: 6 и 2.

Пример 3. Двое рабочих могут выполнить работу за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им понадобится 25 дней. За сколько дней каждый рабочий может выполнить задание самостоятельно?

Пусть x и y – производительность каждого рабочего, A – работа.
По условию: $$ left{ begin{array}{ l } mathrm{frac{A}{x+y}=12} & \ mathrm{frac{A}{2x}+frac{A}{2y}=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{frac{A}{2}left(frac{1}{x}+frac{1}{y}right)=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{A=frac{50}{frac{1}{x}+frac{1}{y}}=frac{50xy}{x+y}} & end{array}right. $$ Получаем уравнение: begin{gather*} mathrm{12(x+y)=frac{50xy}{x+y}Rightarrow 12(x+y)^2=50xyRightarrow 6(x+y)^2=25xy}\ mathrm{6(x^2+2xy+y^2)-25xy=0}\ mathrm{6x^2-13xy+6y^2=0 |:y^2}\ mathrm{6left(frac{x}{y}right)^2-13frac{x}{y}+6=0}\ mathrm{D=13^2-4cdot 6cdot 6=25=5^2, frac{x}{y}=frac{13pm 5}{12}=} left[begin{array}{ l } mathrm{frac23} & \ mathrm{frac32} & end{array}right. end{gather*} Пусть для определенности x > y. Тогда ( mathrm{frac{x}{y}=frac{3}{2}Rightarrow x=1,5y}. )
Работа: ( mathrm{A=12(x+y)=12(1,5y+y)=12cdot 2,5y=30y}. )
Второй рабочий может выполнить работу самостоятельно за: ( mathrm{frac{A}{y}=frac{30y}{y}=30} дней. )
Первый рабочий работает в 1,5 раза быстрей, ему понадобится ( mathrm{frac{30}{1,5}=20} дней. )
Ответ: 30 дней и 20 дней.

Пример 4. Бригада выполнила работу за 20 дней. Если бы в бригаде было на 4 человека больше, а рабочий день – на 1 ч дольше, то работа была бы выполнена за 10 дней. Если бы в бригаде было на 1 человека меньше, а рабочий день – на 1 ч короче, то работа была бы выполнена за 30 дней. Сколько человек было в бригаде, и сколько часов в день они работали?

Пусть A – вся работа, n – количество человек в бригаде, t – продолжительность рабочего дня. По условию: $$ left{ begin{array}{ l } mathrm{20nt=A} & \ mathrm{10(n+4)(t+1)=A} & \ mathrm{30(n-1)(t-1)=A} & end{array}right. $$ Исключаем A и получаем систему из двух уравнений: begin{gather*} left{begin{array}{ l } mathrm{20nt=10(n+4)(t+1)} & \ mathrm{20nt=30(n-1)(t-1)} & end{array}right.Rightarrow left{begin{array}{ l } mathrm{2nt=nt+4t+n+4} & \ mathrm{2nt=3(nt-t-n+1)} & end{array}right.Rightarrow\ Rightarrow left{begin{array}{ l } mathrm{nt=4t+n+4} & \ mathrm{nt=3t+3n-3} & end{array}right. end{gather*} Найдём линейную зависимость между n и t из уравнения: $$ mathrm{4t+n+4=3t+3n-3Rightarrow t-2n=-7Rightarrow t=2n-7}. $$ Подставим t в верхнее уравнение системы: begin{gather*} mathrm{n(2n-7)=4(2n-7)+n+4}\ mathrm{2n^2-7n=8n-28+n+4Rightarrow 2n^2-16n+24=0Rightarrow n^2-8n+12=0}\ mathrm{ (n-2)(n-6)=0Rightarrow} left[begin{array}{ l } mathrm{n_1=2} & \ mathrm{n_2=6} & end{array}right. end{gather*} Находим время ( mathrm{t=2n-7: } left[begin{array}{ l } left{begin{array}{ l } mathrm{n_1=2} & \ mathrm{t_1=-3} & end{array}right. &\ left{begin{array}{ l } mathrm{n_2=6} & \ mathrm{t_2=5} & end{array}right. end{array}right. )
Выбираем решение с ( tgt 0: left{begin{array}{ l } mathrm{n=6} & \ mathrm{t=5} & end{array}right. )
Ответ: 6 человек, 5 часов.

Повторение этапов решения текстовых задач

Повторим, что при решении текстовых задач осуществляется переход от словесного описания к математическому описанию. В процессе решения таких задач выделяются три этапа:

1-й: Составление математической модели;

2-й: Работа с математической моделью;

3-й: Получение ответа на вопрос задачи.

Первый пример решения текстовых задач

Задача 1: В одном доме на 86 квартир больше, чем в другом. Сколько квартир в каждом доме, если в двух домах 792 квартиры?

Первый этап: Составим математическую модель, для чего введем переменные.

Пусть  – число квартир в первом доме. Исходя из условия, () – это число квартир во втором доме. Тогда общее количество квартир есть равно . По условию это число квартир равняется 792. Получаем уравнение:

Второй этап: необходимо решить полученное уравнение и найти .

Третий этап: в задаче необходимо ответить на вопрос: сколько квартир в одном доме и сколько в другом доме.

В одном доме у нас  квартир.

А во втором доме  квартир.

Ответ: число квартир в одном доме 353 и 439 в другом доме.

Второй пример решения текстовых задач

Задача 2: В двух залах кинотеатра 460 мест. Сколько мест в большом зале, если в нём в три раза больше мест, чем в малом?

Первый этап: Пусть  – число мест в малом зале. По условию задачи в большом зале мест в три раза больше, тогда  – число мест в большом зале. Общее количество мест равно . В задаче сказано, что общее количество мест равно 460.

Второй этап: Решим уравнение.

Третий этап: Необходимо ответить на вопрос: сколько мест в большом зале?

Нам нужно найти . Мы получили значение  = 115, значит:

Ответ: в большом зале 345 мест.

Третий пример решения текстовых задач

Задача 3: Маме и дочке вместе 35 лет. Сколько лет дочке, если она на 25 лет моложе мамы?

Первый этап: Пусть – число лет дочки. Тогда  – число лет мамы. По условию задачи маме и дочке вместе 35 лет. Значит,

Второй этап: Решим уравнение.

Третий этап: Ответим на вопрос, сколько лет дочке.

Мы обозначили возраст дочери через , и нашли, что  = 5.

Ответ: дочке 5 лет.

Задача 4: На двух книжных полках всего 48 книг. Сколько книг на первой полке, если известно, что их в два раза больше, чем на второй полке?

Первый этап: Пусть  – число книг на первой полке, их в два раза больше, чем на второй полке. Значит, – число книг на второй полке. Тогда:

Второй этап: Решим уравнение.

Третий этап: Необходимо узнать, сколько книг на первой полке. Мы обозначили их число через , значит, ответ на вопрос задачи следующий: на первой полке 32 книги.

Ответ: на первой полке 32 книги.

Итак, мы рассмотрели метод математического моделирования на примере четырех задач. В каждой задаче была составлена математическая модель, решено соответствующее уравнение и получен ответ.

Список рекомендованной литературы

1. Мордкович А.Г. Алгебра 7. 4 издание. М.: Мнемозина. 2001 г.
2. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебра 7. М.: ВЕНТАНА-ГРАФ
3. Колягин Ю.М., Ткачёва М.В., Фёдорова Н.Е. и др. Алгебра 7 .М.: Просвещение. 2006 г.

Рекомендованные ссылки на ресурсы интернет

1. Школьный помощник (Источник).
2. В помощь учащимся (Источник).
3. Методическая копилка учителя информатики (Источник).

Рекомендованное домашнее задание

1. №№ 95, 97, 100-102. Мордкович А.Г. Алгебра 7. 4 издание. М.: Мнемозина. 2001 г.

2. Решить задачу:

В папке «Video» размещалось втрое больше фильмов, чем мультфильмов. После удаления трех фильмов и скачивания пяти мультиков, их соотношение стало два к одному. Сколько фильмов было в папке изначально?

3. Решить задачу:

На клумбе росли лилии и тюльпаны, причем лилий было в два раза больше. После того, как посадили еще пять тюльпанов, и выкопали две лилии, их количество сравнялось. Сколько лилий было на клумбе изначально?