Здравствуйте, уважаемые читатели!
Известно, что одним из самых сложных заданий ЕГЭ по химии является расчетная задача (№ 34 в формате ЕГЭ-2022) на нахождение массовой доли вещества в смеси (растворе). В процессе решения этой задачи ученику приходится пройти, как минимум, через 8-10 этапов, половина из которых основаны на логике и математике. Как правило, именно эти этапы вызывают наибольшие трудности и создают 34 задаче ореол “нерешаемости”. Одним из используемых при этом базовых логико-математических приемов является материальный баланс. Проанализировав задачи реальных ЕГЭ по химии за несколько лет, я выделила 3 направления (или разновидности) использования матбаланса:
1.Нахождение количественных характеристик
А) раствора (смеси ) ,полученного в результате реакции
Пример: 100 г 16,25% раствора хлорного железа смешали со 100 г 10,6% раствора Na2CO3. Найти массу полученного раствора.
Б) раствора (смеси ), взятого в качестве исходного для рассматриваемой реакции
- -по данным материального баланса
Пример: 100 г 16,25% раствора хлорного железа смешали с насыщенным раствором Na2CO3. В результате реакции выделилось 0,05 моль газа и образовалось 123,88 г раствора. Найти растворимость Na2CO3.
- -по данным элементного анализа
Пример: Смесь, содержащую оксид фосфора(V) и оксид калия, сплавили, затем растворили в горячей воде. В результате получили 447,4 г раствора, в котором массовая доля атомов водорода составляет 7,6%. Найти массу исходной смеси оксидов
В) по прореагировавшему реагенту, взятому в избытке
Пример: К 1000 г раствора иодида калия добавили 425г 40%-ного раствора нитрата серебра. После завершения реакции массовая доля нитрата серебра в образовавшемся растворе составила 8,44%. Найти концентрацию иодида в растворе
2. Использование в задаче приема «разделение раствора на порции»
а) независимое нахождение концентрации реагентов в отдельных, последовательно рассматриваемых пробах
Пример: Полученный раствор бромида кальция и хлорида меди(II) разлили по трем колбам. К 200 г раствора в первой колбе добавили 785 г 30%-ного раствора нитрата серебра. При этом массовая доля нитрата серебра в растворе уменьшилась вдвое. К 340 г раствора во второй колбе добавили избыток раствора иодида калия, в результате чего в осадок выпало 64,94 г соли. Вычислите массовую долю каждой из солей в третьей колбе.
б) взаимосвязанное нахождение концентрации одного реагента в отдельных, параллельно рассматриваемых пробах
Пример: 189,6 г 36,7% раствора сульфита аммония разлили в две колбы. К раствору в первой колбе добавили избыток концентрированной азотной кислоты. Выделился бурый газ. К раствору во второй колбе добавили 120 г соляной кислоты, также взятой в избытке. При этом объём газа, выделившегося из второй колбы, оказался в 4 раза меньше объёма газа, выделившегося из первой колбы. Определите массовую долю соли в конечном растворе во второй колбе.
3. Выпадение осадка из раствора вследствие его охлаждения
А)осадок – безводная соль
Пример: Растворимость калийной селитры при 20 град С составляет 30 г/100 г воды.,при 50 град С – 85 г/100 г воды. 370 г раствора селитры, насыщенного при 50 град, охладили до 20 град. Найти массу выпавшего осадка.
Б) осадок – кристаллогидрат
Пример: Коэффициент растворимости хлорида меди (2) при 100 град С – 110 г/100 г воды, при 20 град С – 72, 7 г . 420 г насыщенного при 100 град раствора соли охладили до 20 град и выделившийся осадок дигидрата хлорида меди отделили. Найти массу осадка.
Рассмотрение всех указанных вариаций применения матбалансов в решении 34 задачи планирую провести на вебинаре 25 декабря. Наряду с приведенными в статье примерами будут разобраны более 10 задач из сборников ЕГЭ-2023 и 5 авторских задач условной тематики “олеум+кристаллогидраты”. Вебинар – двухчасовой, будет его видеозапись.
Зарегистрироваться на вебинар можно по ссылке: https://forms.gle/ordjXGoK4qBn2dvh8
Всего доброго!
Материальный
баланс ХТП является следствием закона
сохранения массы вещества (а точнее –
следствием сохранения элементов при
химических превращениях).
Это
означает, что масса веществ, поступивших
на технологическую операцию – приход,
равна массе полученных веществ – расходу.
Материальный баланс должен соблюдаться
для ХТП всех типов: синтеза, разделения,
очистки целевых продуктов. Данные о
материальном балансе позволяют дать
оценку целесообразности осуществления
процесса в заданных условиях. Эти данные
нужны как при проектировании новых, так
и при анализе работы существующих
производств. По данным материального
баланса рассчитывают технологические
показатели процесса: выход целевого
продукта, степень превращения сырья,
селективность процесса, расходные
коэффициенты по сырью и т.д. Материальный
баланс является необходимым элементом
при расчете энергетического и
эксергетического балансов.
Материальный
баланс сводят, пользуясь уравнениями
основной и побочных реакций. Когда
учитывают не все происходящие побочные
реакции и полученные побочные продукты,
а лишь наиболее важные из них, материальный
баланс имеет приблизительный характер.
Существуют три основные формы составления
материального баланса. В виде системы
уравнений, таблицы и поточной диаграммы.
Уравнение
материального баланса в общем виде:
GAO
+ GBO
+ … = GR
+ …+ GD
+…+
GA
+ GB
+
G,
где
GAO
,
GBO
– массы исходных реагентов (сырья).
GR –
масса целевого продукта,
GD
– масса побочного продукта,
GА
,
GВ
–
массы непрореагировавших веществ,
G –
невязка баланса.
Невязка
баланса является следствием потерь
сырья и продуктов при проведении
процесса, неточности эксперимента и
расчета, а также принятых допущений.
Чаще
всего материальный баланс процесса
представляют в виде таблицы:
|
Приход |
Расход |
||||
|
Наименование |
Масс. |
% |
Наименование |
Масс. |
% |
|
Реагент |
… |
… |
Целевой |
… |
… |
|
Реагент |
… |
… |
Побочный |
… |
… |
|
Реагент |
… |
… |
|||
|
Реагент |
… |
… |
|||
|
Невязка |
… |
… |
|||
|
Всего |
… |
100 |
Всего |
… |
100 |
В
таблицу материального баланса, кроме
обязательных масс и массовых процентов
введенных и получающихся веществ,
включают еще и объемы веществ, находящихся
в газовой фазе, приведенные к нормальным
условиям. Массовые проценты в столбце
“Расход” рассчитывают по отношению к
сумме масс введенных реагентов в столбце
“Приход”, т.е. массу всех введенных
реагентов принимают за 100%.
Может случиться, что из-за погрешностей
эксперимента и допущений, принятых при
расчете, масса полученных веществ
окажется больше массы введенных. Тогда
невязка баланса будет иметь отрицательное
значение. Материальный баланс составляют
на заданный базис. Обычно базисом
является масса сырья или целевого
продукта (кг,
т)
или продолжительность процесса (ч,
сутки).
В лабораторных исследованиях составляют
баланс за время проведения опыта.
В
дальнейшем производят пересчет на
заданный базис, пользуясь коэффициентом
пересчета. Коэффициент пересчета
показывает, во сколько раз нужно изменить
массы веществ, входящих в материальный
баланс, при переходе на другой базис.
Так, если в материальном балансе,
составленном за время проведения опыта,
получили GR
грамм целевого продукта, а заданный
базис расчета – 1000
г целевого продукта, коэффициент
пересчета равен 1000
/ GR.
В
названии таблицы материального баланса
указывают, для какого процесса и реактора
произведен расчет, а также принятый
базис расчета.
Поточная
диаграмма это блок-схема (рис.1.3).
Материальные потоки изображают в виде
полос, ширина которых пропорциональна
массе в выбранном масштабе. Основным
преимуществом данного способа изображения
является его наглядность.

Рис.1.3.
Поточная диаграмма колонны синтеза
аммиака:
1
– свежий газ;
2
– циркулирующий газ;
3
– жидкий аммиак и растворенные в нем
газы;
4
– отдувочные газы
1.2.8.
Расходные
коэффициенты по сырью.
К основным показателям ХТП относятся
расходные коэффициенты, характеризующие
затраты сырья, воды, топлива, электроэнергии,
пара на единицу массы целевого продукта.
В связи с большим вкладом затрат на
реагенты (сырье) в себестоимость продуктов
в химической технологии особое значение
имеют расходные коэффициенты по
реагентам. Различают теоретические и
практические расходные коэффициенты.
Теоретический расходный коэффициент
стех
рассчитывают,
пользуясь стехиометрическим уравнением,
описывающим химическое превращение
(1.18):




где

и

– массы реагента и продукта из уравнения
реакции
MA
и MP
– молекулярные массы реагента и продукта
а
и р
–
стехиометрические коэффициенты.
Теоретический
расходный коэффициент характеризует
минимальный расход сырья на получение
единицы массы продукта.
Практический
расходный коэффициент
отражает реальный расход поступившего
в процесс сырья на получение единицы
массы продукта, т.е. его рассчитывают
как отношение массы поступившего в
процесс сырья

к массе получившегося продукта GР:

Расходные
коэффициенты рассчитывают по всем
реагентам. Практические расходные
коэффициенты всегда больше стехиометрических
из-за неполноты превращения сырья, а
также из-за расходования сырья на
побочные реакции. Данные для расчета
практических расходных коэффициентов
берут из материального баланса процесса.
Практический расходный коэффициент по
реагенту можно найти, зная теоретический
расходный коэффициент и выход целевого
продукта по этому реагенту:

где
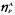
– выход Р
по реагенту А
в долях единицы.
Соседние файлы в папке методички митхт
- #
- #
- #
- #
- #
- #
- #
Методичка ОХТ_2006. Методическое пособие по практическим занятиям для студентов специальностей 148 01 01 Химическая технология производства и переработки неорганических материалов
| Название | Методическое пособие по практическим занятиям для студентов специальностей 148 01 01 Химическая технология производства и переработки неорганических материалов |
| Анкор | Методичка ОХТ_2006.doc |
| Дата | 23.10.2017 |
| Размер | 1.11 Mb. |
| Формат файла | |
| Имя файла | Методичка ОХТ_2006.doc |
| Тип | Методическое пособие #9744 |
| страница | 3 из 9 |
| Подборка по базе: Учебное пособие ENGLISH TOPICS .doc, Технологии искусственного интеллекта Учебно-методическое пособие, Рекомендации к практическим_Организационная культура.docx, Учебное пособие по АФХД посл.doc, Новое пособие по WORD. Лабораторный практикум Часть 2.doc, Методическое пособие-сборка схем.pdf, Учебное пособие Лукьянец Н.Г.2.pdf, Оператор товарный – пособие 2.doc, Методическое пособие.pdf, Учебные материалы к практическим занятиям.pdf
2. материальный баланс химико-технологических процессов Материальный баланс основан на законе сохранения массы вещества, согласно которому масса веществ, поступивших в замкнутую систему, равна массе веществ на выходе из нее. Применительно к материальному балансу любого технологического процесса это означает, что масса веществ, поступивших на технологическую операцию, – приход, равна массе всех веществ, получившихся в результате ее, – расходу. Материальный баланс может быть представлен уравнением, левую часть которого составляет масса всех видов сырья и материалов, поступающих на переработку (Σmприх), а правую – масса получаемых продуктов плюс производственные потери (Σmрасх): Уравнение материального баланса может быть представлено в следующем виде: m + m + m + m = m + m+ m + m+ m7, (25) где m1 и m2 массы поступившего газообразного, жидкого и твердого сырья и вспомогательного материала; m3, m4, m5 полученные целевой продукт, побочный продукт, отход соответственно; m6 непрореагировавшее сырье; m7 – производственные потери. Слагаемые прихода и расхода, число которых зависит от состава производственных потоков, называют статьями материального баланса. Материальный баланс – зеркало технологического процесса, отражающее расходные коэффициенты по сырью, наличие твердых отходов, газообразных выбросов, жидких стоков, состав образующихся продуктов. Чем подробнее изучен процесс, тем более полно можно составить материальный баланс. Составляют его по уравнению основной суммарной реакции с учетом параллельных и побочных реакций. Поскольку на практике приходится иметь дело не с чистыми веществами, а с сырьем сложного химического состава, то для составления материального баланса следует учитывать массу всех компонентов, входящих в его состав. Для этого пользуются данными химических анализов. Стехиометрические коэффициенты в химических уравнениях показывают количество моль компонентов, вступивших в химическое взаимодействие. Их можно выразить в массовых величинах, умножая стехиометрические коэффициенты на молярную массу. Например, окисление диоксида серы описывается уравнением SO2 + 0,5O2 SO3. Молярные массы, г/моль или кг/кмоль: SO2 – 64; O2 – 32; SO3 – 80, и это же уравнение с «массовыми» стехиометрическими коэффициентами будет иметь вид 64SO2 + 16O2 80SO3. В такой записи очевиден материальный баланс: суммарная масса исходных веществ равна массе продукта. Рассмотрим пример: в производстве азотной кислоты определить количество HNO3, образующейся из 1 т аммиака. В химико-технологическом процессе протекают следующие реакции: (принимаем, что NH3 полностью окисляется до NO); окисление оксида азота хемосорбция диоксида азота В абсорбционную колонну подается кислород, и образующийся оксид азота повторно окисляется до NO2 по реакции (27). Таким образом, образование азотной кислоты представлено стехиометрическими уравнениями (2628). Умножим первое из них на 1, второе – на 3, третье – на 2 и сложим их. Получим суммарное стехиометрическое уравнение (брутто-уравнение) Конечно, такая реакция не известна. Но стехиометрическое уравнение показывает, в каких соотношениях реагенты вступают во взаимодействие друг с другом, и этому определению отвечает уравнение (29). Умножим стехиометрические коэффициенты в (29) на мольные массы соответствующих компонентов (г/моль или кг/кмоль) (NH3 – 17; O2 – 32; HNO3 – 63; Н2О – 18) и получим Из уравнения (30) видно, что для производства 63 кг азотной кислоты надо затратить 17 кг аммиака, а на 1 т (1 000 кг) азотной кислоты пойдет 17 1000 / 63 = 270 кг NH3. Удобство записи суммарного стехиометрического уравнения очевидно. Сожжено 100 м 3 газовой смеси, содержащей 50 об. % пропана и 50 об. % бутана. Избыток воздуха по отношению к теоретически необходимому для сгорания составляет 20%. Составить материальный баланс процесса горения и рассчитать состав продуктов сгорания (об. %). При расчете принимаем, что воздух является смесью одного объема кислорода и 3,76 объема азота (т. е. молярное отношение О2 : N2 составляет 1 : 3,76). Объем 1 кмоль О2, N2 при н. у. равен 22,4 м 3 . Уравнения реакций горения имеют следующий вид: Исходя из состава воздуха и с учетом его избытка при сжигании газовой смеси, запишем общее уравнение реакции, принимая во внимание, что молярное соотношение пропана и бутана в смеси такое же, как объемное соотношение (т. е. 1 : 1): воздух для воздух для избыток воздуха сжигания пропана сжигания бутана Данное уравнение можно записать в следующем виде: Результаты материального баланса представлены в табл. 1. Стехиометрические балансы могут быть представлены в виде уравнений, согласно которым можно рассчитать степень превращения реагентов и их концентрацию в данный момент времени (табл. 2). где стехиометрический коэффициент; абсолютное значение стехиометрического коэффициента (для исходных веществ 0). Обозначим количество исходных веществ (в моль) перед началом реакции через na 0, nb 0, …, ni 0, …, а количество исходных веществ в данный момент реакции na, nb, …, ni, … . Когда исходные реагенты берутся в стехиометрическом соотношении, степени превращения каждого из них одинаковы. Если же исходные реагенты вступают в реакции не в стехиометрическом соотношении, то значение степени превращения х зависит от того, для какого вещества эта величина рассчитывается. Следовательно, так как соотношения количеств исходных реагентов могут быть нестехиометрическими, расчет будем вести по степени превращения одного, произвольно выбранного, исходного реагента, например K. хk = . В соответствии со стехиометрическим уравнением (31), когда превращению подвергается 1 моль исходного вещества K, одновременно превращение претерпевает число молей исходного вещества I, равное ni 0 ni = nk 0 хk. Nj = . (32) В числителе и знаменателе выражения (32) написан знак «+», так как вместо i использовано i (для исходных веществ i |
|||
| Т, С | 50 | 100 | 150 |
| Кр | 17,29 | 0,9042 | 0,0948 |
реакции получения хлористого изопропила из стехиометрической смеси пропилена и хлористого водорода по уравнению
Общее давление Р = 1 атм.
Рассчитать степень превращения пропилена = x.
Принимаем, что в реакцию вступают 1 моль пропилена и 1 моль хлористого водорода. После установления равновесия будет (1 – x) моль пропилена, (1 – x) моль хлористого водорода и x моль хлористого изопропила. Всего
Материальный и тепловой балансы химического процесса (стр. 1 )
| Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 |
МАТЕРИАЛЬНЫЙ И ТЕПЛОВОЙ БАЛАНСЫ ХИМИЧЕСКОГО ПРОЦЕССА
Материальный и тепловой балансы химического процесса: составляются на основе законов сохранения массы и энергии.
Уравнения материального и теплового балансов служат основой расчета реакционного объема аппарата (при заданной степени превращения) или степени превращения в реакторе (при заданных условиях). При расчете чаще всего пользуются выражением общего баланса, составленного по одному из исходных веществ, участвующих в химическом процессе. Вид уравнения зависит от типа реактора, в котором протекает процесс химического превращения веществ. Материальный баланс представляет собой основу для вывода зависимости связи между степенью превращения, скоростью и временем химического процесса, которая является необходимым элементом его расчета и носит название характеристического уравнения реактора. Если химическое превращение вещества протекает в неизотермических условиях, тепловой баланс процесса следует рассматривать совместно с его материальным балансом.
1. Общий материальный баланс реакционной системы равен сумме материальных балансов по каждому из реагирующих веществ:
где М — общее количество реакционной смеси, кмоль; t — время реакции, с;. D Мобщ — изменение общего количества реакционной смеси, кмоль×с-1.
2. Общее уравнение материального баланса для i-ro вещества, участвующего в реакции:
где Mi — количество i-го вещества в системе, кмоль; DMi — изменение количества i-го вещества, кмоль×с-1; ri —скорость химической реакции, выраженная по i-му веществу, кмоль×м-3×с-1; V — реакционный объем, м3.
3. Уравнения материального баланса для различных типов. химических реакторов.
Периодически действующий реактор идеального смешения:
где Ci — концентрация i-го вещества в системе, кмоль×м-3.
Непрерывнодействующий реактор идеального смешения:
,
где , —концентрация i-го вещества в системе на входе в реактор и выходе из него, соответственно, кмоль×м-3; ri — скорость химической реакции по i-му веществу в системе, кмоль×м-3×с-1.
Каскад n непрерывнодействующих реакторов идеального смешения:
,
.где ,- концентрация i-ro вещества в системе на выходе из п-го реактора, кмоль×м-3; rin —скорость реакции по i-му веществу в n-м реакторе, кмоль×м-3×с-1
Непрерывнодействующий реактор идеального вытеснения:
где S — площадь поперечного сечения потока реагирующей системы, м2; L — длина реактора, м.
Полунепрерывнодействующий реактор идеального смешения:
По i-му веществу для этого реактора имеем:
где , — концентрация i-го вещества в системе на входе в реактор и выходе из него, соответственно, кмоль×м-3; —скорость химической реакции по i-му веществу в системе на выходе из реактора, кмоль×м-3×с-1.
4. Общий вид уравнения теплового баланса:
где U — внутренняя энергия реакционной системы, кДж-кмоль”1; / — энтальпия системы, кДж×кмоль-1; . — коэффициент теплопередачи, Вт(м2×К)-1; F — площадь поверхности теплопередачи, м2; Тр — температура реакции, К или °С; Тх—температура теплоносителя (хладоагента), К или °С; р — давление в системе, Па.
5. Уравнения теплового баланса для различных типов химических реакторов.
Периодически действующий реактор идеального смешения при V = const:
где сu — удельная теплоемкость смеси реагирующих веществ при постоянном объеме, кДж(кмоль×К)-1; DHr — тепловой эффект реакции, кДж×кмоль-1.
Непрерывнодействующий реактор идеального смешения с внешним теплообменом:
,
где u0 — объемная скорость подачи реагирующих веществ, м3×с-1; Со — начальная концентрация реагирующих веществ, кмоль×м-3; х — степень превращения; То—начальная температура реакционной смеси, К или °С; Т1 — конечная температура реакционной смеси, К или °С; ср — удельная теплоемкость смеси реагирующих веществ при постоянном давлении, кДж(кг×К)-1
Непрерывнодействующий реактор идеального вытеснения с внешним теплообменом при постоянных температуре и составе по поперечному сечению потока:
где S — площадь поперечного сечения, м2; Rr — гидравлический радиус, м..
Непрерывнодействующий реактор идеального смешения, работающий в автотермическом режиме:
Адиабатический yепрерывнодействующий реактор идеального вытеснения с теплообменом между реагентом и продуктами реакции (система теплообменник — реактор):
где =С0(DНr)/(rcp),
u0rcp(T0-)+KF((T1–T0),
где — разность температур в адиабатическом реакторе при х = 1;.. Т0 — температура исходной смеси на входе в реактор, К или °С; — температура исходной смеси на входе в теплообменник, К или oС.
Непрерывнодействующий реактор идеального вытеснения с внутренним теплообменом между исходными веществами и реакционной смесью (при подогреве исходных веществ):
где Ti— температура реакционной смеси во внутреннем подогревателе, К или °С.
Пример 2-1. В реакторе идеального смешения происходят следующие реакции:
где D — целевой продукт реакции; СRа = CSo = СТo = CDo = 0 — начальные концентрации промежуточных и конечных продуктов.
Начальная концентрация исходного вещества СА = 1 кмоль × м-3; текущие концентрации веществ (в кмоль × м-3); СА = 0,44; Св=1,06; СR = 0,05; CS = 0,33; СT = 0,14. Скорость подачи исходных веществ u0 = 5 × 10-3 м3 × с-1.
Определить производительность реактора GB по веществу В:
Решение. Составляем материальный баланс для реактора смешения. На основании стехиометрических соотношений реакций (а) и (г); (а) и (б); (а), (б), (в) и (г); (г) запишем:
CBo-CB = (3/2)CT + 2C’R+ C’S + CD, (3)
Комбинируя уравнения (1), (2), (4) и (5), а также (2) — (5), получаем:
CAo-CA = CR + CS + CD, (6)
CBo-CB=(3/2)CT + 2CR + 3CS-2CD. (7)
Из уравнения (6) определяем концентрацию продукта D:
CD = 1 – (0,44 + 0,05 + 0,33) = 0,18 кмоль × м-3.
Тогда производительность по продукту D будет равна:
Из уравнения (7) определяем концентрацию исходного вещества В
СВо= (3/2) 0,14 + 2 × 0,05 – 2 × 0,18+ 1,06 = 2 кмоль × м-3,
а затем производительность по веществу В:
Пример 2-2. В реакторе идеального смешения, работающем в адиабатических условиях, происходят реакции:
2R®S, (в)
где R — продукт реакции.
Начальные концентрации исходных веществ и продуктов (в кмоль × м-3): САо = 0,1; СВо=0,3; CRo = CDa = СРо =CSo = 0. Текущие концентрации взаимодействующих веществ (в кмоль х м-3): СА = 0,016; СР = 0,028; CS = 0,012; CD = 0,034.
Тепловой эффект реакции —DНr= 1,5 × 108 Дж (кмоль × В) -1. Плотность смеси r = 860 кг× м-3, теплоемкость смеси ср = = 2,85 × 103 Дж(кг×К)-1, скорость подачи u0 = 2,6×10-2×м3 ×с-1.
Определить производительность реактора по продукту R и температуру на выходе реактора, если начальная температура 12 °С (285 К).
Решение. Составляем уравнения материального и теплового баланса. Из стехиометрических соотношений уравнений реакции (а), (б) и (в) следует:
Тогда из уравнений (1) и (3) получим:
= 0,026 кмоль • м -3.
Из уравнений (2) и (3) находим:
СB = СВо — (СAо — СA) — 2СР = 0,30 — (0,1 —0,016) —2 • 0,028 =
= 0,160 кмоль • м -3.
Таким образом, производительность реактора по продукту R:
GR = CRu0 = 0,026 • 2,6 •10 -2 = 6,76•10 -4 кмоль • с -1.
где QP = (—DНr) (CBo —CB) u0 — тепловой поток, который выделяется в результате реакций; QH = cppu0 DT— тепловой поток, который затрачивается на нагревание реакционной смеси при адиабатических условиях работы реактора идеального смешения.
Из уравнения (4) после преобразования получаем:
Следовательно, температура на выходе из реактора равна 285 + 8,6 = 393,6 К или 20,6 °С.
Пример 2-3. В реакторе идеального вытеснения, работающем т адиабатических условиях, происходит жидкофазная реакция первого порядка
Константа скорости реакции kA (в с -1):
Начальные концентрации веществ (в кмоль×м-3): СAо=4,5; СB = 0. Тепловой эффект реакции—DHr=2×107 Дж(кмоль×А)-1, теплоемкость реакционной смеси ср:=2,2×103 Дж(кг×К)-1, плотность реакционной смеси r = 850 кг×м-3, температура исходной смеси Т0 = 300 К, скорость подачи uо= 10-3 м3 × с-1, объем реактора V = 5 м3.
Определить производительность реактора по продукту В и температуру смеси на выходе.
Решение. Тепловой баланс:
где QP = (—DHr) (СAо—CA) uо – тепловой поток, который выделяется в результате реакции; QH = срruо (Tк — Т0) – тепловой поток, который затрачивается на нагревание исходных веществ и продуктов реакции; Тк – температура реакционной смеси на выходе из реактора; Т0 – температура исходной смеси, подаваемой в реактор.
Характеристическое уравнение для необратимой реакции первого порядка, протекающей в реакторе идеального вытеснения:
, (1)
Так как процесс протекает при адиабатических условиях, константа скорости реакции будет изменяться по ходу реакции. Используем метод конечных разностей:
, (2)
где ki = 1013ехр(—1,2-104 Ti-1).
Для определения концентрации вещества А на выходе из реактора проводим последовательные приближения по Ti при шаге DT = 2 К. Тогда из уравнения материального баланса
определяем для каждого значения Тi соответствующее значение и по уравнению (2) рассчитываем сумму до значения i = n, при котором t= V/V0 =5/(1 •=5 × 103 с. Расчеты сведены в табл. 2-1. Из табл. 2-1 получаем при Ti=23 = 344 К:
c.
Тогда производительность реактора по продукту В:
= 1/2 (4,500 — 0,386) •= 2,06 •кмоль • с.
Пример 2-4. Установка состоит из следующих последовательно соединенных реакторов: идеального смешения (V1 = 2 м3), идеального вытеснения (V2 = 2 м3) и идеального смешения (V3 = 3 м3). Начальная концентрация вещества САo = = 1 кмоль • м -3, скорость подачи uо = 5×10-2 м3×с-1, скорость реакции (-rA) =5,1 • 10-3CA0,28. В начальный момент времени продукт в системе отсутствует. Плотность реакционной смеси не меняется.
Определить концентрацию исходного вещества после каждого реактора и рассчитать графически производительность установки по продукту, если известно, что 1 моль исходного вещества дает 2 моль продукта.
Решение. Составляем материальный баланс по веществу А для 1-го реактора смешения:
Для нахождения времени пребывания в реакторе идеального вытеснения интегрируем кинетическое уравнение:
,
Составляем материальный баланс по веществу А для 2-го реактора смешения:
.
Уравнение материального баланса в химии
Материальный баланс реакционного процесса
Основой расчетов химико-технологических процессов являются материальные и тепловые балансы. К расчетам материального баланса следует отнести определение выхода основного и побочных продуктов, расходных коэффициентов по сырью, производственных потерь. Только определив материальные потоки, можно произвести конструктивные расчеты производственного оборудования и коммуникаций, оценить экономическую эффективность и целесообразность процесса. Составление материального баланса необходимо как при проектировании нового, так и при анализе работы действующего производства.
Материальный баланс может быть представлен уравнением, левую часть которого составляет масса всех видов сырья и материалов поступающих на переработку S G, а правую – масса получаемых продуктов S G плюс производственные потери G пот
Основой материального баланса являются законы сохранения массы вещества и стехиометрических соотношений.
Материальный баланс составляют по уравнению основной суммарной реакции с учетом побочных реакций согласно закону сохранения массы вещества. Общая масса всех поступающих в аппарат материалов, то есть приход, равен общей массе выходящих материалов , то есть расходу. Материальный баланс составляют на единицу массы основного продукта (кг, т) или единицу времени (ч, сутки).
Теоретический материальный баланс рассчитывают на основе стехиометрического уравнения реакции. Для его составления достаточно знать уравнение реакции и молекулярные массы компонентов.
Практический материальный баланс учитывает состав исходного сырья и готовой продукции, избыток одного из компонентов сырья, степень превращения, потери и т.д.
Методика расчета практического материального баланса реактора на примере окисления метанола в формальдегид. Сложность расчета материальных потоков обусловлена наличием нескольких целевых, побочных и параллельных реакций с образованием соответствующих веществ. Расчет материального баланса реактора проводим на основе схемы химико-технологического процесса представленного на рис. 10.
Расчет полного материального баланса реактора представляет собой составление балансов по каждому из исходных, целевых, побочных веществ и их суммировании по приходу и расходу.
[spoiler title=”источники:”]
http://pandia.ru/text/78/161/9489.php
http://macp.web.tstu.ru/12/pr_12_05.html
[/spoiler]
