Как составить матрицу гессе - Сайт, где вы сможете решить свои вопросы

Гессиан функции — симметрическая квадратичная форма^[1], описывающая поведение функции во втором порядке.

Для функции , дважды дифференцируемой в точке $xin mathbb{R} ^{n}$

$H(x)=sum _{{i=1}}^{n}sum _{{j=1}}^{n}a_{{ij}}x_{i}x_{j}$

или

$H(z)=sum _{{i=1}}^{n}sum _{{j=1}}^{n}a_{{ij}}z_{i}overline {z}_{j}$

где $a_{{ij}}=partial ^{2}f/partial x_{i}partial x_{j}$ (или $a_{{ij}}=partial ^{2}f/partial z_{i}partial overline {z}_{j}$ ) и функция задана на -мерном вещественном пространстве $mathbb {R} ^{n}$ (или комплексном пространстве $mathbb{C}^n$ ) с координатами $x_{1},ldots ,x_{n}$ (или $z_{1},ldots ,z_{n}$ ). В обоих случаях гессиан — квадратичная форма, заданная на касательном пространстве, не меняющаяся при линейных преобразованиях переменных. Гессианом также часто называют и определитель матрицы ${displaystyle (a_{ij}),}$ см. ниже.

Матрица Гессе[править | править код]

Матрица этой квадратичной формы образована вторыми частными производными функции. Если все производные существуют, то

$H(f)={begin{bmatrix}{frac {partial ^{2}f}{partial x_{1}^{2}}}&{frac {partial ^{2}f}{partial x_{1},partial x_{2}}}&cdots &{frac {partial ^{2}f}{partial x_{1},partial x_{n}}}\\{frac {partial ^{2}f}{partial x_{2},partial x_{1}}}&{frac {partial ^{2}f}{partial x_{2}^{2}}}&cdots &{frac {partial ^{2}f}{partial x_{2},partial x_{n}}}\\vdots &vdots &ddots &vdots \\{frac {partial ^{2}f}{partial x_{n},partial x_{1}}}&{frac {partial ^{2}f}{partial x_{n},partial x_{2}}}&cdots &{frac {partial ^{2}f}{partial x_{n}^{2}}}end{bmatrix}}$

Определитель этой матрицы называется определителем Гессе, или просто гессианом^{[источник не указан 3820 дней]}.

Матрицы Гессе используются в задачах оптимизации методом Ньютона.
Полное вычисление матрицы Гессе может быть затруднительно, поэтому были разработаны квазиньютоновские алгоритмы, основанные на приближённых выражениях для матрицы Гессе. Наиболее известный из них — алгоритм Бройдена — Флетчера — Гольдфарба — Шанно.

Симметрия матрицы Гессе[править | править код]

Смешанные производные функции f — это элементы матрицы Гессе, стоящие не на главной диагонали. Если они непрерывны, то порядок дифференцирования не важен:

${frac {partial }{partial x_{i}}}left({frac {partial f}{partial x_{j}}}right)={frac {partial }{partial x_{j}}}left({frac {partial f}{partial x_{i}}}right)$

Это можно также записать как

$f_{{x_{i}x_{j}}}=f_{{x_{j}x_{i}}},quad forall i,jin {1,ldots ,n}.$

В этом случае матрица Гессе симметрична.

Критические точки функции[править | править код]

Если градиент (её векторная производная) равен нулю в некоторой точке $x_{0}$ , то эта точка называется критической. Достаточным условием существования экстремума в этой точке является знакоопределённость гессиана f (понимаемого в данном случае как квадратичная форма), а именно:

Вариации и обобщения[править | править код]

Вектор-функции[править | править код]

Если — вектор-функция, то есть

$f=(f_{1},f_{2},dots ,f_{n}),$

то её вторые частные производные образуют не матрицу, а тензор ранга 3, который можно рассматривать как массив из матриц Гессе:

${displaystyle H(f)=left(H(f_{1}),ldots ,H(f_{n})right).}$

При n = 1 данный тензор вырождается в обычную матрицу Гессе.

Окаймлённый гессиан[править | править код]

При решении задачи нахождения условного экстремума функции ${displaystyle f:mathbb {R} ^{n}rightarrow mathbb {R} }$ с ограничениями

${displaystyle left{{begin{array}{c}g_{1}(x)=0,\vdots \g_{m}(x)=0,end{array}}right.}$

где $x in mathbb{R}^n$ , m<n , для проверки достаточных условий экстремума можно использовать так называемый окаймлённый гессиан функции Лагранжа , который будет иметь вид^[2]

${displaystyle left({begin{array}{cc}{dfrac {partial ^{2}L}{partial x^{2}}}&{dfrac {partial ^{2}L}{partial xpartial lambda }}\left({dfrac {partial ^{2}L}{partial xpartial lambda }}right)^{mathrm {T} }&{dfrac {partial ^{2}L}{partial lambda ^{2}}}end{array}}right)=left({begin{array}{cccccc}{dfrac {partial ^{2}L}{partial x_{1}^{2}}}&ldots &{dfrac {partial ^{2}L}{partial x_{1}partial x_{n}}}&{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{1}}}\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial ^{2}L}{partial x_{n}partial x_{1}}}&ldots &{dfrac {partial ^{2}L}{partial x_{n}^{2}}}&{dfrac {partial g_{1}}{partial x_{n}}}&ldots &{dfrac {partial g_{m}}{partial x_{n}}}\{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{1}}{partial x_{n}}}&0&ldots &0\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial g_{m}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{n}}}&0&ldots &0end{array}}right).}$

Проверка достаточных условий экстремума заключается в вычислении знаков детерминантов определённого набора подматриц окаймлённого гессиана. Именно, если существуют ${displaystyle x^{*}in mathbb {R} ^{n}}$ и ${displaystyle lambda ^{*}in mathbb {R} ^{m}}$ такие, что ${displaystyle nabla L(x^{*},lambda ^{*})=0}$ и

${displaystyle (-1)^{m}{mbox{det}}left({begin{array}{cccccc}{dfrac {partial ^{2}L}{partial x_{1}^{2}}}&ldots &{dfrac {partial ^{2}L}{partial x_{1}partial x_{p}}}&{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{1}}}\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial ^{2}L}{partial x_{p}partial x_{1}}}&ldots &{dfrac {partial ^{2}L}{partial x_{p}^{2}}}&{dfrac {partial g_{1}}{partial x_{p}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}\{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{1}}{partial x_{p}}}&0&ldots &0\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial g_{m}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}&0&ldots &0end{array}}right)>0}$

для , то в точке $x^{*}$ функция имеет строгий условный минимум. Если же

${displaystyle (-1)^{p}{mbox{det}}left({begin{array}{cccccc}{dfrac {partial ^{2}L}{partial x_{1}^{2}}}&ldots &{dfrac {partial ^{2}L}{partial x_{1}partial x_{p}}}&{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{1}}}\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial ^{2}L}{partial x_{p}partial x_{1}}}&ldots &{dfrac {partial ^{2}L}{partial x_{p}^{2}}}&{dfrac {partial g_{1}}{partial x_{p}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}\{dfrac {partial g_{1}}{partial x_{1}}}&ldots &{dfrac {partial g_{1}}{partial x_{p}}}&0&ldots &0\vdots &ddots &vdots &vdots &ddots &vdots \{dfrac {partial g_{m}}{partial x_{1}}}&ldots &{dfrac {partial g_{m}}{partial x_{p}}}&0&ldots &0end{array}}right)>0}$

для , то в точке $x^{*}$ функция имеет строгий условный максимум^[3].

История[править | править код]

Понятие введено Людвигом Отто Гессе (1844), который использовал другое название. Термин «гессиан» был введён Джеймсом Джозефом Сильвестром.

См. также[править | править код]

Якобиан
Критическая точка (математика)
Лемма Морса
Критерий Сильвестра — критерий положительной или отрицательной определённости квадратной матрицы

Примечания[править | править код]

↑ Гессиан. Дата обращения: 2 апреля 2016. Архивировано 15 апреля 2016 года.
↑ Hallam, Arne Econ 500: Quantitative Methods in Economic Analysis I. Iowa State (7 октября 2004). Дата обращения: 14 апреля 2021. Архивировано 19 апреля 2021 года.
↑ Neudecker, Heinz. Matrix Differential Calculus with Applications in Statistics and Econometrics / Heinz Neudecker, Jan R. Magnus. — New York : John Wiley & Sons, 1988. — P. 136. — ISBN 978-0-471-91516-4.

Ссылки[править | править код]

Камынин Л.И. Математический анализ. Т. 1, 2. – 2001.
Кудрявцев Л.Д «Краткий курс математического анализа. Т.2. Дифференциальное и интегральное исчисления функций многих переменных. Гармонический анализ», ФИЗМАТЛИТ, 2002, — 424 с. — ISBN 5-9221-0185-4. Или любое другое издание.
Голубицкий М., Гийемин В. Устойчивые отображения и их особенности, — М.: Мир, 1977.

Источник

Экстремумы функции трёх переменных

Плюс одно измерение. Рассмотрим функцию трёх переменных , внутреннюю точку её области определения и -окрестность данной точки, которая представляет собой шар с центром в точке радиуса .

Определение: если в некоторой -окрестности точки выполнено неравенство ( – точка -шара, отличная от ), то функция имеет минимум в точке ; если же – то максимум.

Вполне, кстати, понятное и не такое уж абстрактное определение.

Всё очень похоже. Если дифференцируемая функция имеет экстремум в точке , то обязательно выполняются условия . Но с другой стороны, если в какой-либо точке производные 1-го порядка равны нулю, то это ещё не значит, что там есть экстремум.

Алгоритм решения сохраняется прежним:

Найти экстремумы функции

Решение: переключаем передачу на частные производные функции трёх переменных:

Чтобы найти стационарные точки, составим и решим следующую систему:

Аккуратно расположим переменные в обычном порядке и, кроме того, разделим последнее уравнение на 2:

Систему можно решить методом Гаусса, нозачем такие сложности? Из 3-го уравнения выразим и подставим его в первые два уравнения:

Из 1-го уравнения выразим и подставим во 2-е уравнение:

Таким образом, – стационарная точка. Здесь, напоминаю, не помешает подставить найденное решение в каждое уравнение исходной системы и убедиться в выполнении условий .

Проверка достаточного условия экстремума осуществляется несколько по-другому. Сначала нужно найти все частные производные 2-го порядка, вычислить их в точке и составить так называемую матрицу Гессе:

Да не пугайтесь вы так =) Данная матрица является симметричной (или симметрической). Это значит, что её элементы симметричны относительно главной диагонали, на которой в данном случае расположены «однобуквенные» частные производные . Уловили закономерность?

Далее нужно вычислить угловые миноры. Это определители, которые «разрастаются» из левого верхнего угла:

1) Если , то функция достигает минимума в точке .

2) Если (так и только так!), то функция достигает максимума в точке .

3) Если получилось что-то другое и при этом , то – седловая точка. Здесь это уже во многом условное название.

4) Если , то признак не даёт ответа о характере точки .

Внимательные читатели заметили, что эту схему в варианте «два на два» мы использовали и в предыдущем параграфе – только оформление «детское» было. Но не будем отвлекаться.

В нашем примере все производные 2-го порядка равны константам:

а значит, они равны константам и в точке . Составим матрицу Гессе:

и вычислим её угловые миноры:

Вывод: функция достигает максимума в точке .

Для удобства вычислений скопирую функцию:

Аналогичное задание для закрепления материала:

Исследовать функцию на экстремум

Краткое решение и ответ рядом.

Рассмотренный алгоритм исследования распространяется и на функции бОльшего количества переменных. Я бы мог расписать его в общем виде, но заметная часть аудитории просто на дух не переносит общие формулы с нагромождением цифр и индексов. Поэтому разберём ещё случай функции 4 переменных, а дальше – будет понятно.

Чтобы исследовать на экстремум дифференцируемую функцию четырёх аргументов, нужно найти частные производные 1-го порядка и решить систему:

Предположим, что в результате решения найдена стационарная точка . Далее нужно найти частные производные 2-го порядка, вычислить их в точке и составить матрицу Гессе:

после чего вычислить её угловые миноры .

Если все миноры положительны, то в точке – минимум, если знакочередуются в следующем порядке: (и именно в таком!), то в точке – максимум. Если имеет место другой случай, но , то – седловая точка; если же , то признак не даёт ответа о характере точки .

Ну и для совсем продвинутых читателей сообщу, что это есть не что иное, как проверка квадратичной формы полного дифференциала 2-го порядка на знакоопределённостьметодом Сильвестра(для функций 2, 3, 4 и бОльшего количества переменных).

Удачных вам исследований!

На следующих уроках мы познакомимся с условными экстремумами, задачей нахождения минимального и максимального значений функции, а также известнейшим приложением темы – Методом наименьших квадратов.

Как наберётесь сил – приходите ещё! =)

Решения и ответы:

Пример 2: Решение: найдём стационарные точки:

– стационарная точка.
Проверим выполнение достаточного условия экстремума:
, в частности:

, значит, в точке нет экстремума.
Ответ: экстремумы отсутствуют

Пример 3: Решение: найдём стационарные точки:

Из 1-го уравнения выразим: – подставим во 2-е уравнение:

Матрица Гессе

Гессиан функции — симметрическая квадратичная форма описывающая поведение функции во втором порядке.

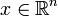
xin R^n

Для функции f дважды дифференцируемой в точке

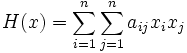(или 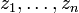). В обоих случаях гессиан — квадратичная форма, заданная на касательном пространстве, не меняющаяся при линейных преобразованиях переменных.

Содержание

Матрица Гессе

$H(f) = begin<bmatrix>frac<partial^2 f> <partial x_1^2>&amp; frac<partial^2 f> <partial x_1,partial x_2>&amp; cdots &amp; frac<partial^2 f> <partial x_1,partial x_n>\ \ frac<partial^2 f> <partial x_2,partial x_1>&amp; frac<partial^2 f> <partial x_2^2>&amp; cdots &amp; frac<partial^2 f> <partial x_2,partial x_n>\ \ vdots &amp; vdots &amp; ddots &amp; vdots \ \ frac<partial^2 f> <partial x_n,partial x_1>&amp; frac<partial^2 f> <partial x_n,partial x_2>&amp; cdots &amp; frac<partial^2 f> <partial x_n^2>end<bmatrix>» width=»» height=»» /> Определитель этой матрицы называется определитель Гессе или также Гессианом. Матрицы Гессе используются в задачах оптимизации в методе Ньютона. Полное вычисление матрицы Гессе может быть затруднительно, поэтому были разработаны квазиньютоновские алгоритмы, основанные на приближенных выражениях для матрицы Гессе. Наиболее известный такой алгоритм — алгоритм Бройдена — Флетчера — Гольдфарба — Шанно (англ.). <h3>Симметрия Гессиана</h3> Смешанные производные функции f — это элементы матрицы Гессе, стоящие не на главной диагонали. Если они непрерывны, то порядок дифференцирования не важен (теорема Клеро), например <img decoding=$

то её вторые частные производные образуют не матрицу, а тензор ранга 3.

История

Понятие введено Гессе (1844) который использовал другое название. Термин «Гессиан» был введён Сильвестром.

См. также

Ссылки

Кудрявцев Л.Д «Краткий курс математического анализа. Т.2. Дифференциальное и интегральное исчисления функций многих переменных. Гармонический анализ», ФИЗМАТЛИТ, 2002, — 424 с. — ISBN 5-9221-0185-4

Wikimedia Foundation . 2010 .

Полезное

Смотреть что такое «Матрица Гессе» в других словарях:

Гессе матрица — [Hessian matrix] матрица вторых частных производных функций нескольких переменных: Определитель этой матрицы называется гессианом. Характеристика матрицы Гессе (ее отрицательная или положительная определенность и полуопределенность) служит… … Экономико-математический словарь

Гессе матрица — Матрица вторых частных производных функций нескольких переменных: Определитель этой матрицы называется гессианом. Характеристика матрицы Гессе (ее отрицательная или положительная определенность и полуопределенность) служит условием для… … Справочник технического переводчика

Определитель Гессе — Гессиан функции симметрическая квадратичная форма описывающая поведение функции во втором порядке. Для функции f дважды дифференцируемой в точке или где (или … Википедия

Гессиан функции — Гессиан функции симметрическая квадратичная форма[источник?], описывающая поведение функции во втором порядке. Для функции , дважды дифференцируемой в точке или где … Википедия

ОВРАЖНЫХ ФУНКЦИЙ МЕТОДЫ МИНИМИЗАЦИИ — численные методы отыскания минимумов функций многих переменных. Пусть задана ограниченная снизу дважды непрерывно дифференцируемая по своим аргументам функция для к рой известно, что при нек ром векторе ( знак транспонирования) она принимает… … Математическая энциклопедия

Седловая точка — функции z=x2 y2 (обозначена красным) … Википедия

Метод одной касательной — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия

Метод Ньютона — Метод Ньютона, алгоритм Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном… … Википедия

Метод Гаусса — Ньютона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия

Метод Ньютона-Рафсона — Метод Ньютона (также известный как метод касательных) это итерационный численный метод нахождения корня (нуля) заданной функции. Метод был впервые предложен английским физиком, математиком и астрономом Исааком Ньютоном (1643 1727), под именем… … Википедия

Вычисление матриц Якоби и Гессе

Пусть задана система функций от переменных. Матрицей Якоби или якобианом данной системы функций называется матрица, составленная из частных производных этих функций по всем переменным.

Если в некоторой точке очень сложно или невозможно вычислить частные производные, , то для вычисления матрицы Якоби применяются методы численного дифференцирования.

Вычисление матрицы Гессе

Матрицей Гессе функции переменных называется матрица, составленная из вторых производных функции по всем переменным

Если в некоторой точке очень сложно или невозможно вычислить частные производные, , то для вычисления матрицы Гессе применяются методы численного дифференцирования.

Методы вычисления матрицы Якоби

Прямое вычисление частных производных

Для вычисления матрицы Якоби в заданной необходимо найти частные производные всех функций системы по всем переменным. Для вычисления производной применяются методы вычисления первой производной.

Формула для элемента якобиана при использовании правой разностной производной:

Формула для элемента якобиана при использовании центральной разностной производной:

Вычисление якобиана с использованием правой разностной производной требует вычислять значения функций в точках. Если использовать центральную производную, то нужно находить значения функций в точках. С другой, стороны погрешность правой производной имеет порядок а центральной — . В большинстве случаев вычисление значения функции — это затратная по времени операция, поэтому используется правая разностная производная.

Оценка погрешности метода

Основная проблема при вычислении каждого элемента матрицы Якоби — как правильно выбрать шаг метода . Шаг выбирается независимо для каждого элемента матрицы.

Проанализируем зависимость погрешности метода от величины шага в случае использования правой разностной производной. Для сокращения записи введём обозначения . Остаточный член в соотношении имеет вид . Если , то Если значения и заданы с погрешностями , то погрешность будет содержать ещё одно слагаемое . Таким образом, оценка суммарной погрешности имеет вид . Эта оценка достигает минимума при . При этом . Оценка погрешности имеет один глобальный миниум. Поэтому выбор очень маленького шага не привидёт к росту точности. При величине шага, близкой к погрешность имеет порядок .

Метод Бройдена

Чаще всего вычисление якобиана является одной из подзадач в различных методах оптимизации и решения систем нелинейных уравнений. При решении систем нелинейных уравнений методом Ньютона требуется вычислять якобиан на каждой итерации. Вычисление якобиана требует вычисления функций в точках. Это сложная и затратная по времени операция. Суть метода Бройдена состоит в том, чтобы вычислить якобиан аналитически или с помощью метода конечных разностей на первой итерации, а после этого на каждой итерации обновлять якобиан, не вычисляя значения функций и их производных.

Пусть задана система нелинейных уравнений , где . Тогда якобиан на -ой итерации выражается по формуле

После этого следующее приближение вычисляется по формуле

Методы вычисления матрицы Гессе

Как и матрица Якоби, матрица Гессе может быть вычислена с помощью разностной аппроксимации производных. , где — вектор переменных, а и — единичные вектора. Эта формула требует вычисления значений функции в точках. Погрешность формулы имеет порядок .

Численный эксперимент

В качестве примера рассчитаем с помощью вышеизложенного метода матрицу Гессе функции в точке (1, 1)

Источник

From Wikipedia, the free encyclopedia

In mathematics, the Hessian matrix or Hessian is a square matrix of second-order partial derivatives of a scalar-valued function, or scalar field. It describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named after him. Hesse originally used the term “functional determinants”.

Definitions and properties[edit]

Suppose ${displaystyle f:mathbb {R} ^{n}to mathbb {R} }$ is a function taking as input a vector ${displaystyle mathbf {x} in mathbb {R} ^{n}}$ and outputting a scalar If all second-order partial derivatives of exist, then the Hessian matrix of is a square matrix, usually defined and arranged as

${displaystyle mathbf {H} _{f}={begin{bmatrix}{dfrac {partial ^{2}f}{partial x_{1}^{2}}}&{dfrac {partial ^{2}f}{partial x_{1},partial x_{2}}}&cdots &{dfrac {partial ^{2}f}{partial x_{1},partial x_{n}}}\[2.2ex]{dfrac {partial ^{2}f}{partial x_{2},partial x_{1}}}&{dfrac {partial ^{2}f}{partial x_{2}^{2}}}&cdots &{dfrac {partial ^{2}f}{partial x_{2},partial x_{n}}}\[2.2ex]vdots &vdots &ddots &vdots \[2.2ex]{dfrac {partial ^{2}f}{partial x_{n},partial x_{1}}}&{dfrac {partial ^{2}f}{partial x_{n},partial x_{2}}}&cdots &{dfrac {partial ^{2}f}{partial x_{n}^{2}}}end{bmatrix}}.}$

That is, the entry of the ith row and the jth column is

${displaystyle (mathbf {H} _{f})_{i,j}={frac {partial ^{2}f}{partial x_{i},partial x_{j}}}.}$

If furthermore the second partial derivatives are all continuous, the Hessian matrix is a symmetric matrix by the symmetry of second derivatives.

The determinant of the Hessian matrix is called the Hessian determinant.^[1]

The Hessian matrix of a function is the transpose of the Jacobian matrix of the gradient of the function ; that is: ${displaystyle mathbf {H} (f(mathbf {x} ))=mathbf {J} (nabla f(mathbf {x} ))^{T}.}$

Applications[edit]

Inflection points[edit]

If is a homogeneous polynomial in three variables, the equation f=0 is the implicit equation of a plane projective curve. The inflection points of the curve are exactly the non-singular points where the Hessian determinant is zero. It follows by Bézout’s theorem that a cubic plane curve has at most inflection points, since the Hessian determinant is a polynomial of degree

Second-derivative test[edit]

The Hessian matrix of a convex function is positive semi-definite. Refining this property allows us to test whether a critical point is a local maximum, local minimum, or a saddle point, as follows:

If the Hessian is positive-definite at then attains an isolated local minimum at If the Hessian is negative-definite at then attains an isolated local maximum at If the Hessian has both positive and negative eigenvalues, then is a saddle point for Otherwise the test is inconclusive. This implies that at a local minimum the Hessian is positive-semidefinite, and at a local maximum the Hessian is negative-semidefinite.

For positive-semidefinite and negative-semidefinite Hessians the test is inconclusive (a critical point where the Hessian is semidefinite but not definite may be a local extremum or a saddle point). However, more can be said from the point of view of Morse theory.

The second-derivative test for functions of one and two variables is simpler than the general case. In one variable, the Hessian contains exactly one second derivative; if it is positive, then is a local minimum, and if it is negative, then is a local maximum; if it is zero, then the test is inconclusive. In two variables, the determinant can be used, because the determinant is the product of the eigenvalues. If it is positive, then the eigenvalues are both positive, or both negative. If it is negative, then the two eigenvalues have different signs. If it is zero, then the second-derivative test is inconclusive.

Equivalently, the second-order conditions that are sufficient for a local minimum or maximum can be expressed in terms of the sequence of principal (upper-leftmost) minors (determinants of sub-matrices) of the Hessian; these conditions are a special case of those given in the next section for bordered Hessians for constrained optimization—the case in which the number of constraints is zero. Specifically, the sufficient condition for a minimum is that all of these principal minors be positive, while the sufficient condition for a maximum is that the minors alternate in sign, with the minor being negative.

Critical points[edit]

If the gradient (the vector of the partial derivatives) of a function is zero at some point then has a critical point (or stationary point) at The determinant of the Hessian at is called, in some contexts, a discriminant. If this determinant is zero then is called a degenerate critical point of or a non-Morse critical point of Otherwise it is non-degenerate, and called a Morse critical point of

The Hessian matrix plays an important role in Morse theory and catastrophe theory, because its kernel and eigenvalues allow classification of the critical points.^[2]^[3]^[4]

The determinant of the Hessian matrix, when evaluated at a critical point of a function, is equal to the Gaussian curvature of the function considered as a manifold. The eigenvalues of the Hessian at that point are the principal curvatures of the function, and the eigenvectors are the principal directions of curvature. (See Gaussian curvature § Relation to principal curvatures.)

Use in optimization[edit]

Hessian matrices are used in large-scale optimization problems within Newton-type methods because they are the coefficient of the quadratic term of a local Taylor expansion of a function. That is,

${displaystyle y=f(mathbf {x} +Delta mathbf {x} )approx f(mathbf {x} )+nabla f(mathbf {x} )^{mathrm {T} }Delta mathbf {x} +{frac {1}{2}},Delta mathbf {x} ^{mathrm {T} }mathbf {H} (mathbf {x} ),Delta mathbf {x} }$

where nabla f is the gradient ${displaystyle left({frac {partial f}{partial x_{1}}},ldots ,{frac {partial f}{partial x_{n}}}right).}$ Computing and storing the full Hessian matrix takes ${displaystyle Theta left(n^{2}right)}$ memory, which is infeasible for high-dimensional functions such as the loss functions of neural nets, conditional random fields, and other statistical models with large numbers of parameters. For such situations, truncated-Newton and quasi-Newton algorithms have been developed. The latter family of algorithms use approximations to the Hessian; one of the most popular quasi-Newton algorithms is BFGS.^[5]

Such approximations may use the fact that an optimization algorithm uses the Hessian only as a linear operator and proceed by first noticing that the Hessian also appears in the local expansion of the gradient:

${displaystyle nabla f(mathbf {x} +Delta mathbf {x} )=nabla f(mathbf {x} )+mathbf {H} (mathbf {x} ),Delta mathbf {x} +{mathcal {O}}(|Delta mathbf {x} |^{2})}$

Letting for some scalar this gives

${displaystyle mathbf {H} (mathbf {x} ),Delta mathbf {x} =mathbf {H} (mathbf {x} )rmathbf {v} =rmathbf {H} (mathbf {x} )mathbf {v} =nabla f(mathbf {x} +rmathbf {v} )-nabla f(mathbf {x} )+{mathcal {O}}(r^{2}),}$

that is,

${displaystyle mathbf {H} (mathbf {x} )mathbf {v} ={frac {1}{r}}left[nabla f(mathbf {x} +rmathbf {v} )-nabla f(mathbf {x} )right]+{mathcal {O}}(r)}$

so if the gradient is already computed, the approximate Hessian can be computed by a linear (in the size of the gradient) number of scalar operations. (While simple to program, this approximation scheme is not numerically stable since has to be made small to prevent error due to the term, but decreasing it loses precision in the first term.^[6])

Notably regarding Randomized Search Heuristics, the evolution strategy’s covariance matrix adapts to the inverse of the Hessian matrix, up to a scalar factor and small random fluctuations.
This result has been formally proven for a single-parent strategy and a static model, as the population size increases, relying on the quadratic approximation.^[7]

Other applications[edit]

The Hessian matrix is commonly used for expressing image processing operators in image processing and computer vision (see the Laplacian of Gaussian (LoG) blob detector, the determinant of Hessian (DoH) blob detector and scale space). It can be used in normal mode analysis to calculate the different molecular frequencies in infrared spectroscopy.^[8] It can also be used in local sensitivity and statistical diagnostics.^[9]

Generalizations[edit]

Bordered Hessian[edit]

A bordered Hessian is used for the second-derivative test in certain constrained optimization problems. Given the function considered previously, but adding a constraint function such that the bordered Hessian is the Hessian of the Lagrange function ^[10]

${displaystyle mathbf {H} (Lambda )={begin{bmatrix}{dfrac {partial ^{2}Lambda }{partial lambda ^{2}}}&{dfrac {partial ^{2}Lambda }{partial lambda partial mathbf {x} }}\left({dfrac {partial ^{2}Lambda }{partial lambda partial mathbf {x} }}right)^{mathsf {T}}&{dfrac {partial ^{2}Lambda }{partial mathbf {x} ^{2}}}end{bmatrix}}={begin{bmatrix}0&{dfrac {partial g}{partial x_{1}}}&{dfrac {partial g}{partial x_{2}}}&cdots &{dfrac {partial g}{partial x_{n}}}\[2.2ex]{dfrac {partial g}{partial x_{1}}}&{dfrac {partial ^{2}Lambda }{partial x_{1}^{2}}}&{dfrac {partial ^{2}Lambda }{partial x_{1},partial x_{2}}}&cdots &{dfrac {partial ^{2}Lambda }{partial x_{1},partial x_{n}}}\[2.2ex]{dfrac {partial g}{partial x_{2}}}&{dfrac {partial ^{2}Lambda }{partial x_{2},partial x_{1}}}&{dfrac {partial ^{2}Lambda }{partial x_{2}^{2}}}&cdots &{dfrac {partial ^{2}Lambda }{partial x_{2},partial x_{n}}}\[2.2ex]vdots &vdots &vdots &ddots &vdots \[2.2ex]{dfrac {partial g}{partial x_{n}}}&{dfrac {partial ^{2}Lambda }{partial x_{n},partial x_{1}}}&{dfrac {partial ^{2}Lambda }{partial x_{n},partial x_{2}}}&cdots &{dfrac {partial ^{2}Lambda }{partial x_{n}^{2}}}end{bmatrix}}={begin{bmatrix}0&{dfrac {partial g}{partial mathbf {x} }}\left({dfrac {partial g}{partial mathbf {x} }}right)^{mathsf {T}}&{dfrac {partial ^{2}Lambda }{partial mathbf {x} ^{2}}}end{bmatrix}}}$

If there are, say, constraints then the zero in the upper-left corner is an block of zeros, and there are border rows at the top and border columns at the left.

The above rules stating that extrema are characterized (among critical points with a non-singular Hessian) by a positive-definite or negative-definite Hessian cannot apply here since a bordered Hessian can neither be negative-definite nor positive-definite, as ${displaystyle mathbf {z} ^{mathsf {T}}mathbf {H} mathbf {z} =0}$ if is any vector whose sole non-zero entry is its first.

The second derivative test consists here of sign restrictions of the determinants of a certain set of n-m submatrices of the bordered Hessian.^[11] Intuitively, the constraints can be thought of as reducing the problem to one with n-m free variables. (For example, the maximization of ${displaystyle fleft(x_{1},x_{2},x_{3}right)}$ subject to the constraint ${displaystyle x_{1}+x_{2}+x_{3}=1}$ can be reduced to the maximization of ${displaystyle fleft(x_{1},x_{2},1-x_{1}-x_{2}right)}$ without constraint.)

Specifically, sign conditions are imposed on the sequence of leading principal minors (determinants of upper-left-justified sub-matrices) of the bordered Hessian, for which the first leading principal minors are neglected, the smallest minor consisting of the truncated first rows and columns, the next consisting of the truncated first rows and columns, and so on, with the last being the entire bordered Hessian; if is larger than then the smallest leading principal minor is the Hessian itself.^[12] There are thus n-m minors to consider, each evaluated at the specific point being considered as a candidate maximum or minimum. A sufficient condition for a local maximum is that these minors alternate in sign with the smallest one having the sign of ${displaystyle (-1)^{m+1}.}$ A sufficient condition for a local minimum is that all of these minors have the sign of ${displaystyle (-1)^{m}.}$ (In the unconstrained case of m=0 these conditions coincide with the conditions for the unbordered Hessian to be negative definite or positive definite respectively).

Vector-valued functions[edit]

If is instead a vector field ${displaystyle mathbf {f} :mathbb {R} ^{n}to mathbb {R} ^{m},}$ that is,

${displaystyle mathbf {f} (mathbf {x} )=left(f_{1}(mathbf {x} ),f_{2}(mathbf {x} ),ldots ,f_{m}(mathbf {x} )right),}$

then the collection of second partial derivatives is not a matrix, but rather a third-order tensor. This can be thought of as an array of Hessian matrices, one for each component of :

${displaystyle mathbf {H} (mathbf {f} )=left(mathbf {H} (f_{1}),mathbf {H} (f_{2}),ldots ,mathbf {H} (f_{m})right).}$

This tensor degenerates to the usual Hessian matrix when

Generalization to the complex case[edit]

In the context of several complex variables, the Hessian may be generalized. Suppose ${displaystyle fcolon mathbb {C} ^{n}to mathbb {C} ,}$ and write ${displaystyle fleft(z_{1},ldots ,z_{n}right).}$ Then the generalized Hessian is ${displaystyle {frac {partial ^{2}f}{partial z_{i}partial {overline {z_{j}}}}}.}$ If satisfies the n-dimensional Cauchy–Riemann conditions, then the complex Hessian matrix is identically zero.

Generalizations to Riemannian manifolds[edit]

Let (M,g) be a Riemannian manifold and nabla its Levi-Civita connection. Let be a smooth function. Define the Hessian tensor by

${displaystyle operatorname {Hess} (f)in Gamma left(T^{*}Motimes T^{*}Mright)quad {text{ by }}quad operatorname {Hess} (f):=nabla nabla f=nabla df,}$

where this takes advantage of the fact that the first covariant derivative of a function is the same as its ordinary differential. Choosing local coordinates ${displaystyle left{x^{i}right}}$ gives a local expression for the Hessian as

${displaystyle operatorname {Hess} (f)=nabla _{i},partial _{j}f dx^{i}!otimes !dx^{j}=left({frac {partial ^{2}f}{partial x^{i}partial x^{j}}}-Gamma _{ij}^{k}{frac {partial f}{partial x^{k}}}right)dx^{i}otimes dx^{j}}$

where $Gamma^k_{ij}$ are the Christoffel symbols of the connection. Other equivalent forms for the Hessian are given by

${displaystyle operatorname {Hess} (f)(X,Y)=langle nabla _{X}operatorname {grad} f,Yrangle quad {text{ and }}quad operatorname {Hess} (f)(X,Y)=X(Yf)-df(nabla _{X}Y).}$

Notes[edit]

^ Binmore, Ken; Davies, Joan (2007). Calculus Concepts and Methods. Cambridge University Press. p. 190. ISBN 978-0-521-77541-0. OCLC 717598615.
^ Callahan, James J. (2010). Advanced Calculus: A Geometric View. Springer Science & Business Media. p. 248. ISBN 978-1-4419-7332-0.
^ Casciaro, B.; Fortunato, D.; Francaviglia, M.; Masiello, A., eds. (2011). Recent Developments in General Relativity. Springer Science & Business Media. p. 178. ISBN 9788847021136.
^ Domenico P. L. Castrigiano; Sandra A. Hayes (2004). Catastrophe theory. Westview Press. p. 18. ISBN 978-0-8133-4126-2.
^ Nocedal, Jorge; Wright, Stephen (2000). Numerical Optimization. Springer Verlag. ISBN 978-0-387-98793-4.
^ Pearlmutter, Barak A. (1994). “Fast exact multiplication by the Hessian” (PDF). Neural Computation. 6 (1): 147–160. doi:10.1162/neco.1994.6.1.147. S2CID 1251969.
^ Shir, O.M.; A. Yehudayoff (2020). “On the covariance-Hessian relation in evolution strategies”. Theoretical Computer Science. Elsevier. 801: 157–174. doi:10.1016/j.tcs.2019.09.002.
^ Mott, Adam J.; Rez, Peter (December 24, 2014). “Calculation of the infrared spectra of proteins”. European Biophysics Journal. 44 (3): 103–112. doi:10.1007/s00249-014-1005-6. ISSN 0175-7571. PMID 25538002. S2CID 2945423.
^ Liu, Shuangzhe; Leiva, Victor; Zhuang, Dan; Ma, Tiefeng; Figueroa-Zúñiga, Jorge I. (March 2022). “Matrix differential calculus with applications in the multivariate linear model and its diagnostics”. Journal of Multivariate Analysis. 188: 104849. doi:10.1016/j.jmva.2021.104849.
^ Hallam, Arne (October 7, 2004). “Econ 500: Quantitative Methods in Economic Analysis I” (PDF). Iowa State.
^ Neudecker, Heinz; Magnus, Jan R. (1988). Matrix Differential Calculus with Applications in Statistics and Econometrics. New York: John Wiley & Sons. p. 136. ISBN 978-0-471-91516-4.
^ Chiang, Alpha C. (1984). Fundamental Methods of Mathematical Economics (Third ed.). McGraw-Hill. p. 386. ISBN 978-0-07-010813-4.

External links[edit]

“Hessian of a function”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. “Hessian”. MathWorld.

Источник

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Введение
- 1.1 Постановка математической задачи
  - 1.1.1 Вычисление матрицы Якоби
  - 1.1.2 Вычисление матрицы Гессе
2 Методы вычисления матрицы Якоби
- 2.1 Прямое вычисление частных производных
  - 2.1.1 Оценка погрешности метода
- 2.2 Метод Бройдена
3 Методы вычисления матрицы Гессе
4 Численный эксперимент
5 Рекомендации программисту
6 Заключение
7 Список литературы

Введение

Постановка математической задачи

Вычисление матрицы Якоби

Пусть задана система функций от переменных. Матрицей Якоби или якобианом данной системы функций называется
матрица, составленная из частных производных этих функций по всем переменным.

$J=begin{bmatrix} frac{partial y_1}{partial x_1} & cdots & frac{partial y_1}{partial x_m} \ vdots & ddots & vdots \ frac{partial y_n}{partial x_1} & cdots & frac{partial y_n}{partial x_m} end{bmatrix}.$

Если в некоторой точке очень сложно или невозможно вычислить частные производные, $frac{partial y_i}{partial x_j}$ , то для вычисления матрицы Якоби применяются методы численного дифференцирования.