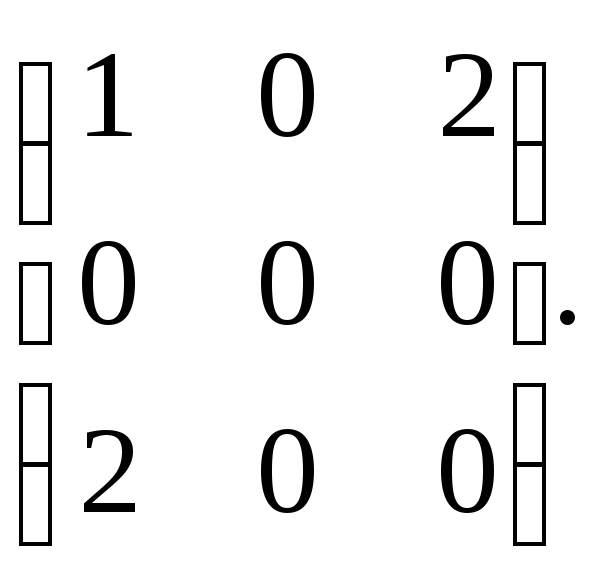
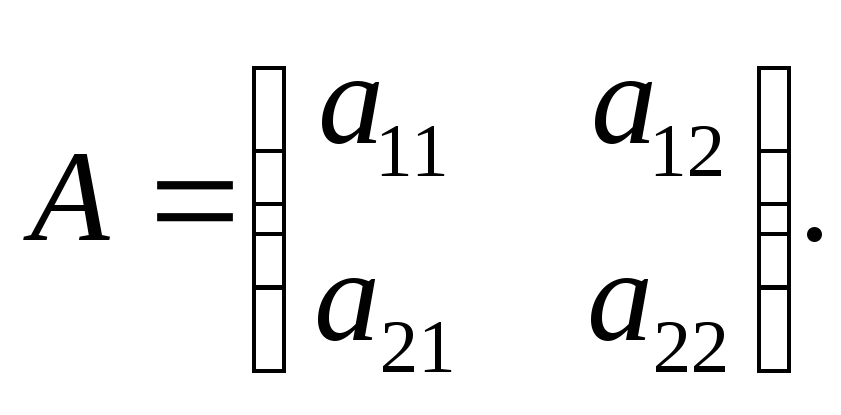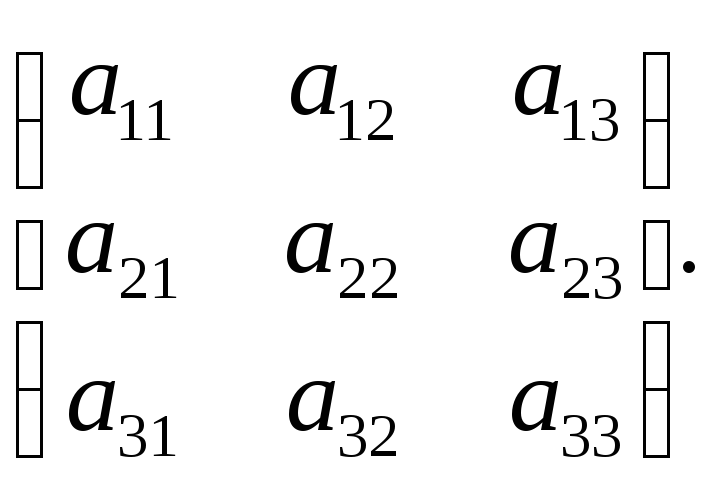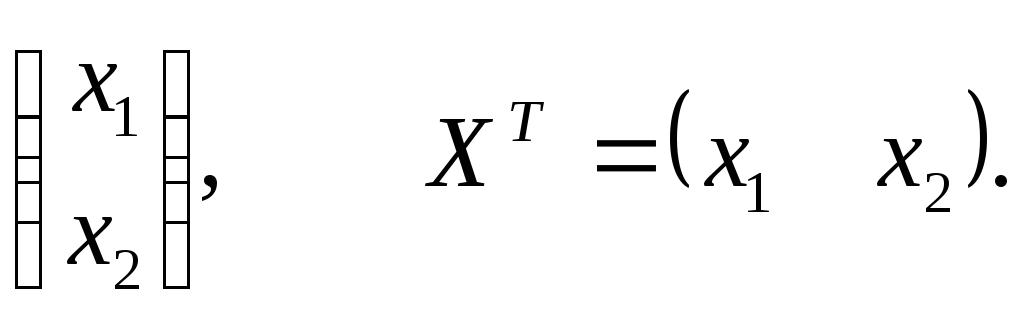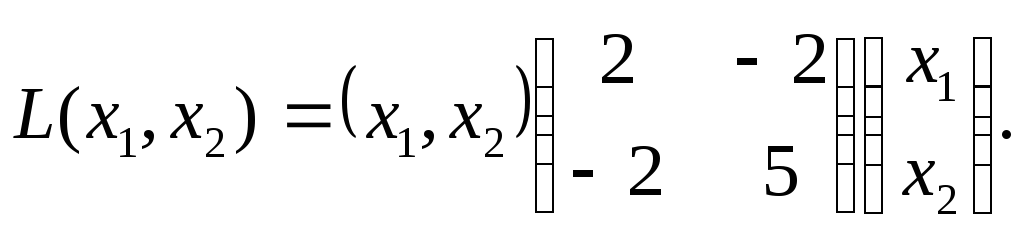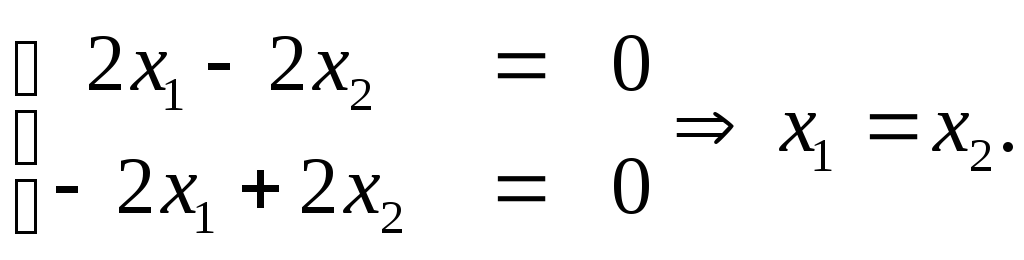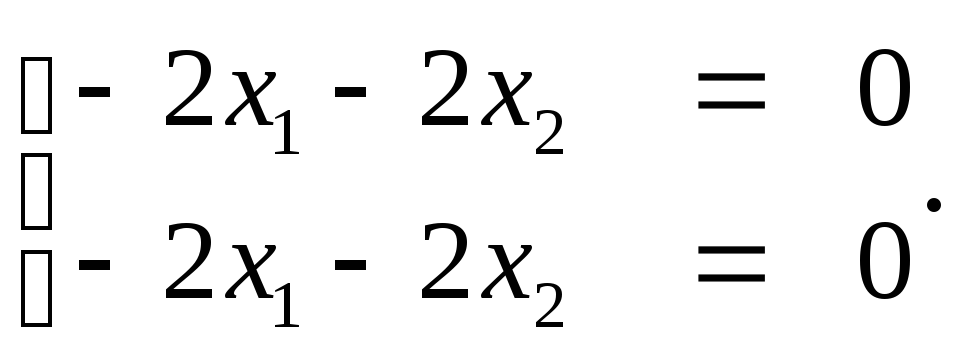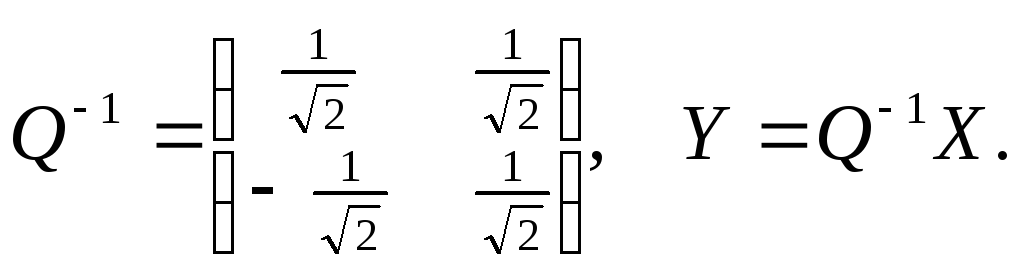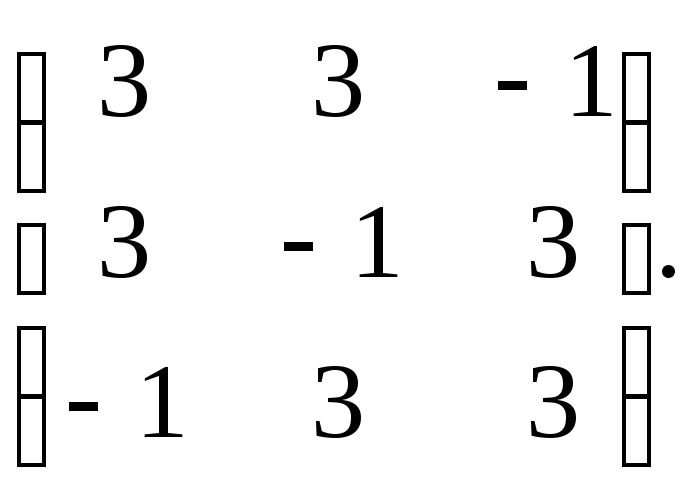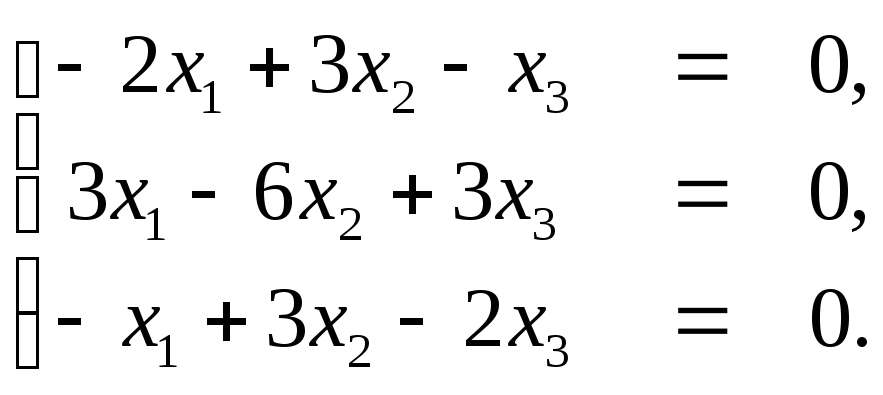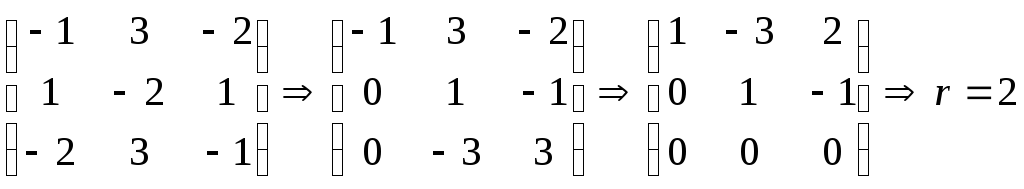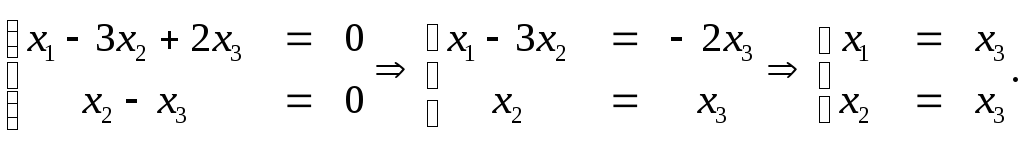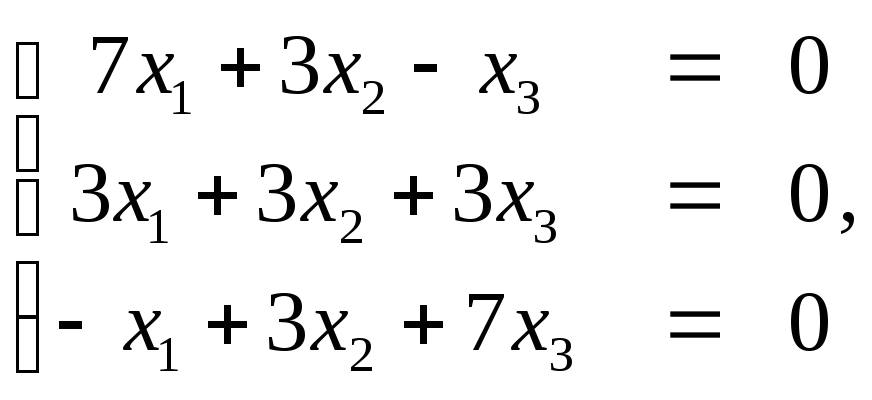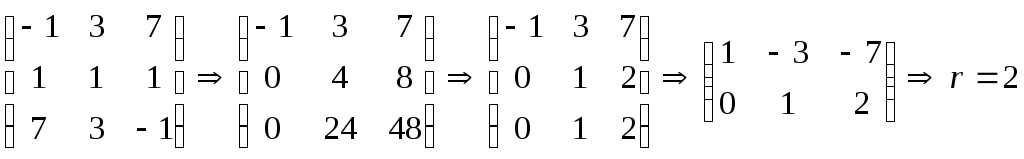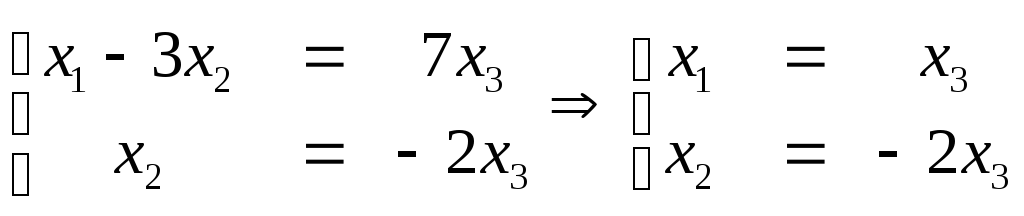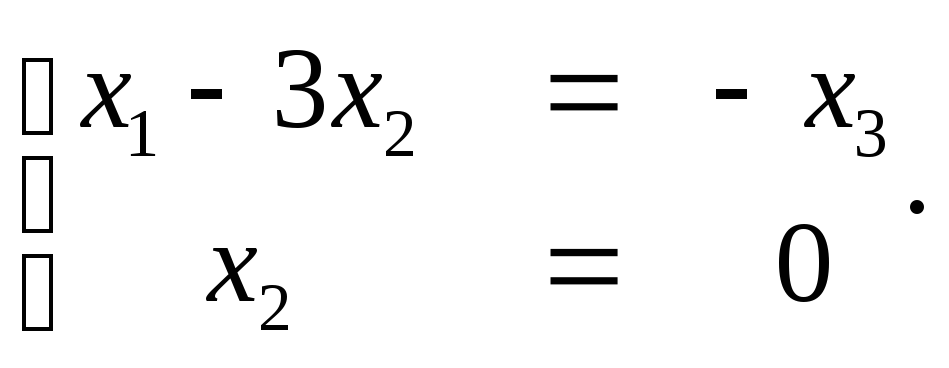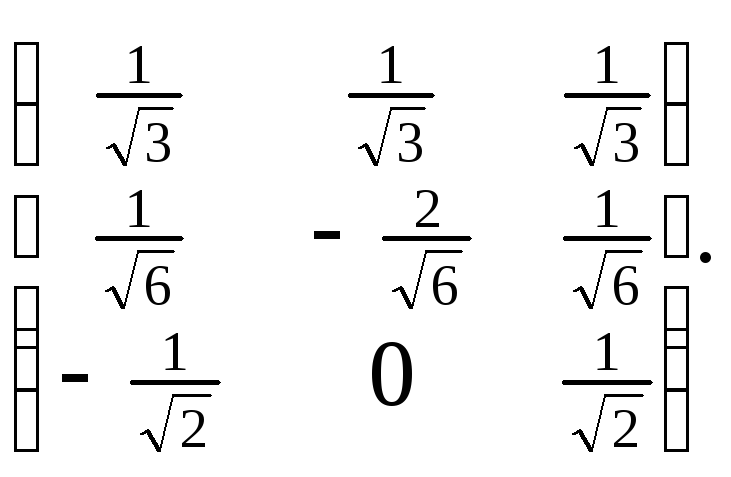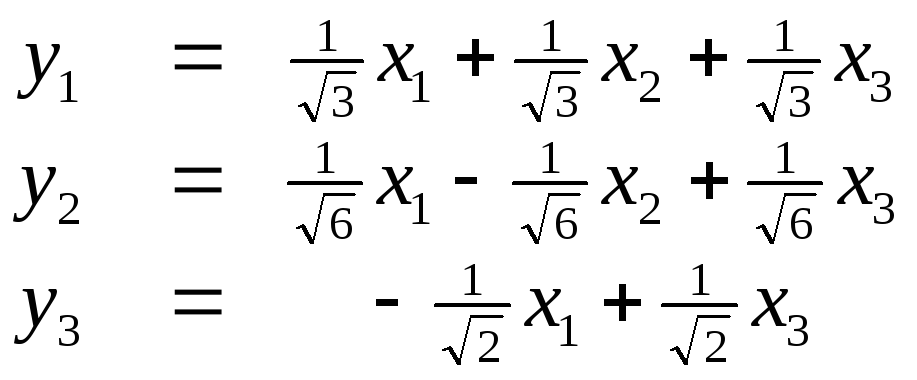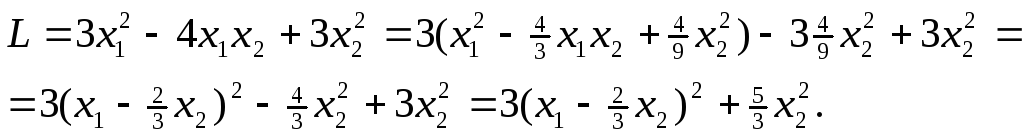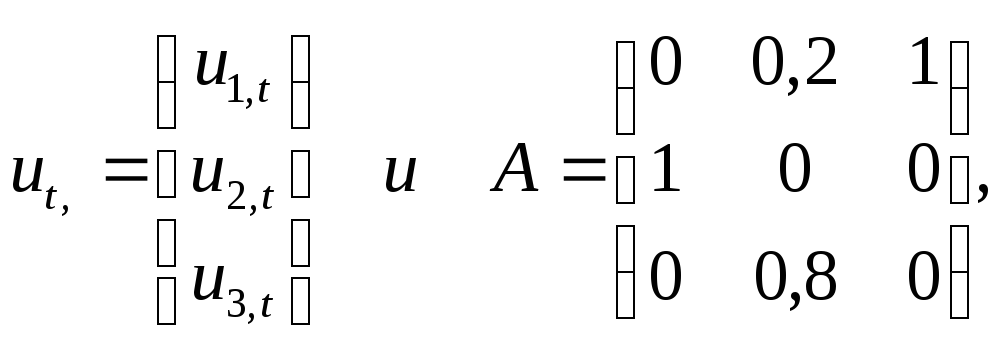Задание 1. Составить матрицу квадратичной формы .
Решение. В общем виде квадратичная форма аргументов и
задаётся следующим образом:
,
Где являются элементами матрицы
квадратичной формы. Сравнивая заданную квадратичную форму с общим её видом, получим, что
,
,
,
,
,
, т. е.

Ответ: 
Задание 2. Восстановить квадратичную форму по заданной матрице . Каждая ли из заданных матриц может соответствовать некоторой квадратичной форме? Почему?
А) 

Решение. Матрица квадратичной формы должна быть симметрической, т. е. .
а) Матрица 
, т. е. она не является симметрической.
Б) Матрице 
,
,
,
,
,
. Следовательно, квадратичная форма примет вид
.
Ответ: .
Задание 3. Задана квадратичная форма . Найти квадратичную форму
, полученную из данной линейным преобразованием:
,
.
Решение. При невырожденном линейном преобразовании
матрица
квадратичной формы преобразуется в матрицу
.
Выпишем матрицу заданной квадратичной формы: 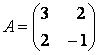

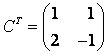
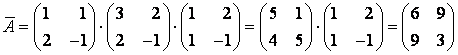
т. е. .
Можно сделать проверку полученного результата непосредственной подстановкой в заданную квадратичную форму формулы преобразования координат:
.
Ответ: .
Задание 4. Привести к каноническому виду квадратичную форму .
Решение. Выпишем матрицу квадратичной формы:
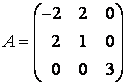
квадратичной формы происходит в ОНБ из собственных векторов. Если
– матрица перехода к такому базису, то координаты вектора
в разных базисах связаны между собой соотношением:

Где в столбцах матрицы находятся координаты векторов ОНБ из собственных векторов, соответствующих собственным значениям.
Составим характеристическое уравнение:
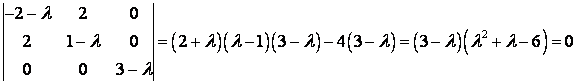
Значит, собственные значения ,
,
.
Найдём собственные векторы, соответствующие найденным собственным значениям.
При :

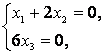
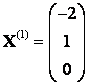
При :

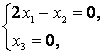
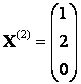
При :
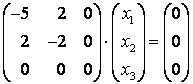
Из системы следует, что – свободная переменная. Примем
, тогда
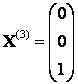
Векторы ,
,
попарно ортогональны (в этом легко убедиться непосредственно!), тогда ОНБ составят векторы
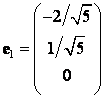
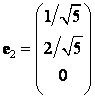
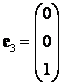
Матрица перехода от ОНБ
к ОНБ
примет вид:
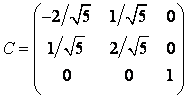
Замечание. О том чтобы матрица оказалась симметрической, следует помнить при построении собственных векторов
,
И
.
Формулы перехода от координат к координатам
:
,
,
.
Канонический вид заданной квадратичной формы:
.
Подстановкой приведенных формул преобразования координат в заданную квадратичную форму можно убедиться в правильности проведенных вычислений.
Ответ: .
Задание 5. Установить знакоопределённость квадратичной формы .
Решение.
Метод 1. Если все собственные значения , то квадратичная форма
положительно определённая; если все
– отрицательно определённая. Найдём собственные значения квадратичной формы. Для этого составим её матрицу:
И характеристическое уравнение:
Его корни ,
, т. е. все
, а следовательно, квадратичная форма положительно определённая.
Метод 2. Знакоопределённость квадратичной формы можно установить и с помощью критерия Сильвестра, в соответствии с которым квадратичная форма положительно определённая, если все главные диагональные миноры матрицы положительны, т. е.
,
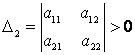

,
,
, …, то квадратичная форма – отрицательно определённая.
Для данной квадратичной формы имеем:
,
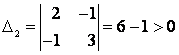
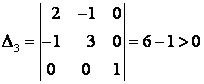
Ответ: квадратичная форма положительно определённая.
| < Предыдущая | Следующая > |
|---|
| Матричная форма записи данной квадратичной формы |
Расчет квадартичной формы достаточно простая задача, по крайней мере описательная часть примитивна до невозможности и алгоритм расчета, когда известна матрица, заключается в расчете каждого из элемента по формуле
где, 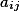
Но все примитивное, не значит удобное и при вычислении квадратичной формы легко ошибиться. Наш калькулятор поможет не делать ошибок в вычислениях.
Как и во всех калькуляторах, матрица может содержать не только вещественные числа, но и комплексные.
При вводе данных, у нас есть два поля:
первое, это матрица;
второе, это способ именования каждого из элемента.
Если мы во втором поле напишем какой то символ (a,b,c….) то каждый элемент будет именоваться
Рассмотрим несколько примеров.
Ввводим элементы матрицы через пробел (можно каждую строку начинать с новой строки)
и получаем следующие результаты
Расчет в комплексном поле
Удачных расчетов!!
Вычисление матрицы квадратичной формы
| Матричная форма записи данной квадратичной формы |
Расчет квадартичной формы достаточно простая задача, по крайней мере описательная часть примитивна до невозможности и алгоритм расчета, когда известна матрица, заключается в расчете каждого из элемента по формуле
(Q(x)=sum_{{i,j=1}}^{n}a_{{ij}}x_{i}x_{j})
где, 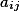
(A=begin{pmatrix}a_{11}&a_{12}&cdots&a_{1n}\a_{21}&a_{22}&cdots&a_{2n}\vdots&vdots&ddots&vdots\a_{m1}&a_{m2}&cdots&a_{mn}end{pmatrix})
Но все примитивное, не значит удобное и при вычислении квадратичной формы легко ошибиться. Наш калькулятор поможет не делать ошибок в вычислениях.
Как и во всех калькуляторах, матрица может содержать не только вещественные числа, но и комплексные.
При вводе данных, у нас есть два поля:
первое, это матрица;
второе, это способ именования каждого из элемента.
Если мы во втором поле напишем какой то символ (a,b,c….) то каждый элемент будет именоваться
Рассмотрим несколько примеров.
Вводим элементы матрицы через пробел (можно каждую строку начинать с новой строки)
и получаем следующие результаты
(begin{pmatrix}x_{0}&x_{1}&x_{2}\end{pmatrix}*begin{pmatrix}1&1&2\1&3&0\2&0&1\end{pmatrix}*begin{pmatrix}x_{0}\x_{1}\x_{2}\end{pmatrix}=\=(1)x_{0}^2+(2)x_{0}x_{1}+(4)x_{0}x_{2}+(3)x_{1}^2+(1)x_{2}^2)
(begin{pmatrix}a_{0}&a_{1}&a_{2}\end{pmatrix}*begin{pmatrix}2&2&-1\2&-5&3\-1&3&8\end{pmatrix}*begin{pmatrix}a_{0}\a_{1}\a_{2}\end{pmatrix}=\=(2)a_{0}^2+(4)a_{0}a_{1}+(-2)a_{0}a_{2}+(-5)a_{1}^2+(6)a_{1}a_{2}+(8)a_{2}^2)
Расчет в комплексном поле
(begin{pmatrix}s_{0}&s_{1}&s_{2}&s_{3}\end{pmatrix}*begin{pmatrix}i&4&2-i&-2\-i&2&2-i&i+7\2i-9&0.4-i&11&-6\1&0&-i&2i\end{pmatrix}*begin{pmatrix}s_{0}\s_{1}\s_{2}\s_{3}\end{pmatrix}=\=(i)s_{0}^2+(4-1i)s_{0}s_{1}+(-7+1i)s_{0}s_{2}+(-1)s_{0}s_{3}+(2)s_{1}^2+(2.4-2i)s_{1}s_{2}+(7+1i)s_{1}s_{3}+(11)s_{2}^2+(-6-1i)s_{2}s_{3}+(2i)s_{3}^2)
Удачных расчетов!!
-
Квадратичные формы
-
Матрица квадратичной формы
Определение.
Квадратичной формой Ĺ(х1,х2,…,хп)
от n переменных называется сумма, каждый
член которой является или квадратом
одной из переменных или произведением
двух разных переменных, взятых с
некоторыми коэффициентами – действительными
числами.
Мы будем рассматривать квадратичные
формы с двумя переменными
(5.1.1)
и с
тремя переменными
(5.1.2)
Квадратичные
формы можно записать в матричной форме,
введя в рассмотрение матрицу А квадратичной
формы. Для (5.1.1) матрица имеет вид
Для (5.1.2) матрица записывается в виде:
А=
То
есть матрица квадратичной формы является
симметрической матрицей. Для переменных
вводится матрица-столбец Х и
транспонированная
–
матрица – строка. Тогда квадратичная
форма может быть записана в виде
произведения трех матриц
( 5.1.3)
Пример.
Дана квадратичная
форма
Записать ее в матричной форме.
Решение.
Матрица квадратичной формы составляется
следующим образом: элементы главной
диагонали равны коэффициентам при
квадратах переменных, остальные элементы
равны половине коэффициента при
произведении х1х2:
А=
Матрица Х=
Таким
образом,
Пример.
Написать матрицу квадратичной формы
Решение.
На главной диагонали располагаем
элементы при квадратах переменных
а11=3,
а22=1,
а33=6,
остальные элементы а12=а21=5/2,
а13=а31=-2,
а23=а32=0.
Следовательно,
А=
Ранг матрицы квадратичной формы называют
рангом квадратичной формы. Если ранг
совпадает с числом переменных квадратичной
формы, то ее называют невырожденной.
Если ранг меньше, то квадратичная форма
– вырожденная.
Пример.
Является ли невырожденной квадратичная
форма L(х1,х2,х3
) = х21+4х1х3?
Решение.
Составим матрицу квадратичной формы
А=
Найдем ранг матрицы А. Так как величина
ранга не зависит от элементарных
преобразований матрицы, то отбрасывая
нулевую строку, найдем минор второго
порядка М2=
то есть ранг меньше трех переменных,
входящих в квадратичную форму.
Следовательно, данная квадратичная
форма вырожденная.
-
Канонический вид квадратичной формы
В
квадратичной форме
можно выполнить линейное преобразование
переменных
невырожденная
квадратная матрица n-ого порядка. Учитывая
линейное преобразование переменных,
получим равенство:
(5.2.1)
Здесь
использовано свойство
.
Новая матрица квадратичной формы
( 5.2.2)
Первоначальная квадратичная форма и
полученная из нее (5.2.1) с помощью
невырожденного линейного преобразования
называются эквивалентными квадратичными
формами.
Пример.
Дана квадратичная форма
.
Найти эквивалентную квадратичную форму
L(y1,y2),
используя линейное преобразование
переменных х1=у1-2у2,
х2=у1+у2.
Решение.
По условию матрица данной квадратичной
формы А=
Заданное линейное преобразование в
матричной форме
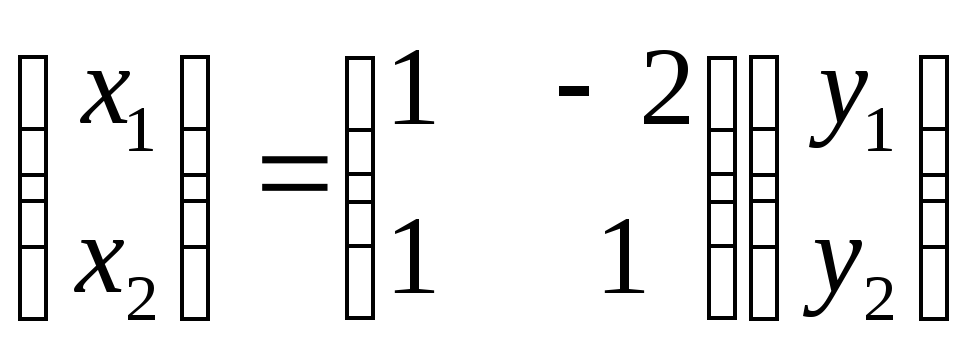
Следовательно,
матрица С=
Теперь
по формуле (5.2.2) новая матрица получается
Ответ.
Квадратичная форма, эквивалентная
данной
Определение.
Квадратичная форма имеет канонический
вид, если все коэффициенты
,
т.е.
и ее матрица является диагональной.
В примере после линейного преобразования
квадратичная форма приняла канонический
вид.
Справедливо следующее утверждение:
любая квадратичная форма с помощью
невырожденного линейного преобразования
переменных может быть приведена к
каноническому виду. Возможны два способа
приведения квадратичных форм к
каноническому виду.
Первый
способ. Идея
метода состоит в том, что путем
тождественных преобразований в
квадратичной форме последовательно
выделяются полные квадраты по всем
переменным.
Пример.
Привести к каноническому виду квадратичную
форму
Решение.
Выделим полный квадрат по переменной
х1:
Введя
новые переменные у1=х1–получим
канонический вид
Пример.
Привести к каноническому виду
квадратичную форму
Решение.
Сначала сгруппируем все слагаемые,
содержащие х1,
и затем дополним их до полного квадрата:
Теперь
полный квадрат по х1
оставляем неизменным, а среди оставшихся
слагаемых объединяем все члены, содержащие
х2,
и выделяем полный квадрат:
Обозначим
у1=х1+2х2+2х3,
у2=х2+х3,
у3=х3,
в результате
получаем канонический вид
Второй
способ. Матрица
квадратичной формы всегда симметрическая,
поэтому она имеет действительные
собственные значения и сводится к
диагональному виду с помощью линейного
ортогонального преобразования Х=QY,
где Q
– ортогональная матрица (см. пример в
4.4.1)
Если
квадратичная форма зависит от двух
переменных L=L(x1,x2)
и λ1,λ2
собственные значения ее матрицы , то
канонический вид квадратичной формы
Если
L=L(x1,x2,x3)
и ее матрица имеет собственные значения
λ1,
λ2,
λ3
, то кононический вид в новых переменных
Чтобы найти линейное преобразование
переменных, приводящих квадратичную
форму к каноническому виду, нужно найти
собственные векторы, нормировать их и
записать матрицу Q.
Пример.
Привести к каноническому виду квадратичную
форму
Решение.
Матрица данной квадратичной формы
А=.
Характеристическое уравнение
.
Собственные
значения λ1=1,λ2=5.
Квадратичная форма в новом базисе из
собственных векторов имеет канонический
вид
Найдем
собственные векторы. Для этого в систему
уравнений вида (4.3.2)
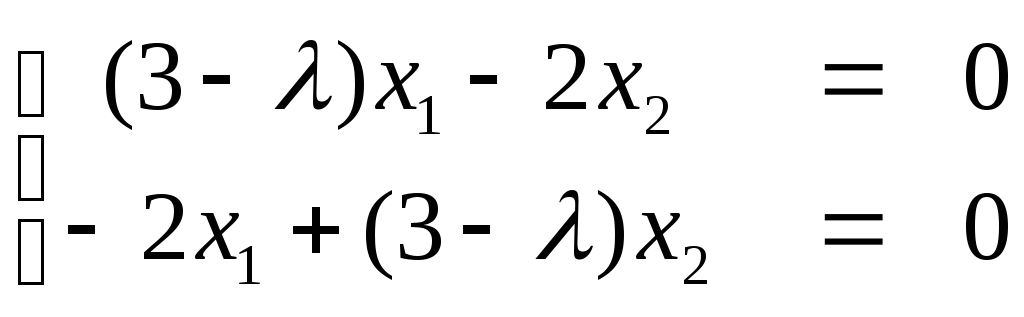
подставим собственные значения.
а)
При λ=λ1=1
получим
Пусть
х2=1
и х1=1.
Тогда е1=(1,1).
б)
При λ=λ2=5
система имеет вид
Таким
образом, х1=-х2
и за второй собственный вектор можно
взять е2=(-1,1).
Очевидно, что е1е2=0
– векторы ортогональны. Нормируя е1,
е2,
запишем ортонормированный базис:
е1=(
Матрица
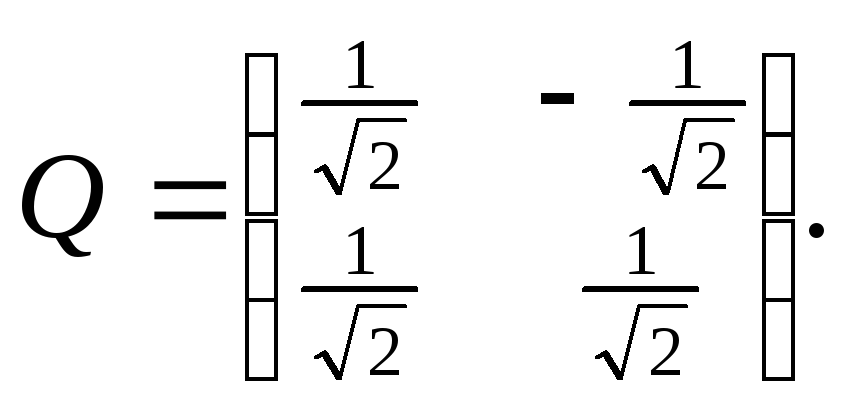
преобразование координат получено.
Заметим,
что в случае ортогональных преобразований
легко получить обратное преобразование
переменных, воспользовавшись свойством
Обратная
матрица равна
Поэтому выполняются соотношения
Ответ.
Канонический
вид
Пример.
Привести квадратичную форму к
каноническому виду и найти ортогональное
преобразование переменных, если
Решение.
Матрица квадратичной формы А=
Характеристическое уравнение
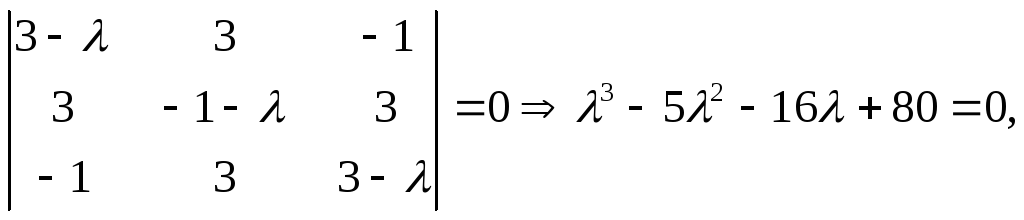
корни
которого λ1=5,
λ2=-4
, λ3=4
Тогда канонический вид квадратичной
формы
Заметим,. что нумерация собственных
значений произвольная. Например, если
взять
то
канонический вид будет
Для каждого такого
варианта обозначений меняется
соответственно расположение (нумерация)
базисных собственных векторов (то есть
система координат), а смысл квадратичной
формы не меняется.
Найдем теперь ортонормированный базис
и преобразование переменных. Составим
систему уравнений:
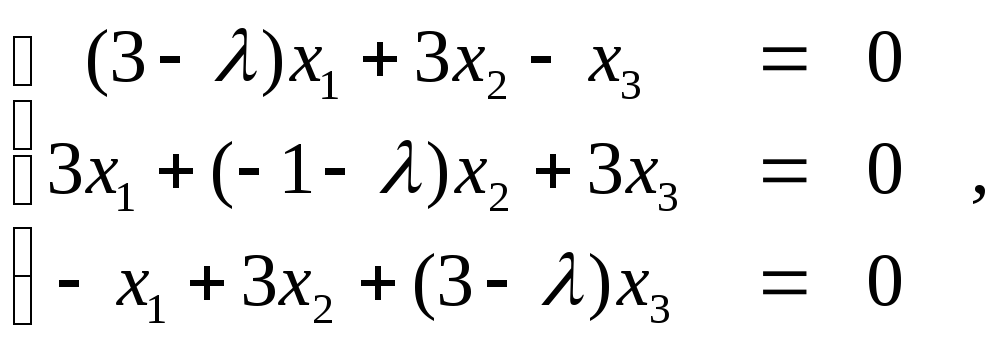
последовательно подставим собственные
значения.
а)
При λ=5 система
примет вид
Выпишем
матрицу системы и подвергнем ее
элементарным преобразованиям:
Получим систему эквивалентную исходной:
Если
х3=k
– любое число, не равное нулю, то множество
собственных векторов (k,k,k).
Пусть k=1,
тогда е1=(1,1,1).
б)
При λ=-4 имеем систему
Преобразуем
матрицу системы
По
последней матрице запишем систему
уравнений
При х3=k,
где k≠0,
множество собственных векторов (k,
-2k,
k).
Возьмем k=1,
тогда е2=(1,
-2, 1).
в)
При λ=4
получим систему уравнений
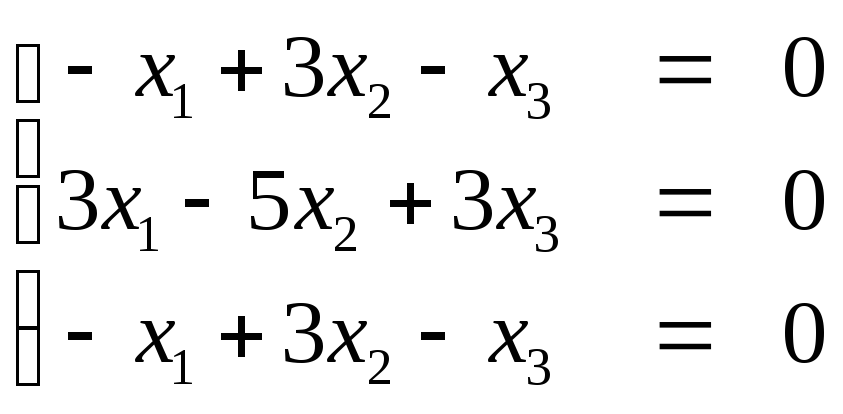
Здесь первое и третье уравнения
одинаковые, поэтому запишем матрицу
системы в виде:
Откуда следует, что
Если х3=k,
где k≠0,
то множество собственных векторов (-k,
0, k).
Пусть k=1,
тогда е3=(-1,0,1).
Получили собственные векторы е1=(1,1,1),
е2=(1,-2,1),
е3=(-1,
0, 1). Легко увидеть, что они попарно
ортогональны. Запишем ортонормированный
базис:
Ортогональная
матрица Q=
Транспонируя
матрицу Q, получим матрицу:
=
И
так как
записываем ортогональное преобразование
переменных
(*)
Ответ.
Квадратичная форма имеет канонический
вид
в базисе из собственных векторов и может
быть получена с помощью преобразования
координат в виде (*).
Отметим
некоторые свойства квадратичных форм:
-
Канонический
вид квадратичной формы не определяется
однозначно, так как зависит от выбора
системы координат (базисных векторов). -
В
каноническом виде число слагаемых с
положительными (отрицательными)
коэффициентами не зависит от способа
приведения формы к каноническому виду. -
Ранг матрицы квадратичной формы не
меняется при линейных преобразованиях
переменных. Ранг всегда равен количеству
ненулевых коэффициентов в канонической
форме. -
Квадратичная форма называется
положительно (отрицательно) определенной,
если при всех значениях переменных, из
которых хотя бы одно отлично от нуля,
выполняется
>0,
<0.
Например,положительно
определенная форма, а
отрицательно определенная.
5. Если все
собственные значения матрицы квадратичной
формы положительны, то
>0
положительно определена. Если все
собственные значения отрицательны, то
<
0- отрицательно определенная форма.
6. Знакоопределенность
квадратичной формы может быть установлена
с помощью критерия Сильвестра: если все
главные миноры матрицы квадратичной
формы положительны, то квадратичная
форма положительно определена. Если
все главные миноры матрицы нечетного
порядка положительны, то квадратичная
форма отрицательно определена.
Продемонстрируем
на примере перечисленные свойства.
Пример.
Дана квадратичная форма
Ее канонический вид
получен с помощью собственных значений
λ1=1 ,λ2=5. Приведем теперь
эту форму к каноническому виду по первому
способу с помощью выделения полных
квадратов.
Таким образом
Канонический вид квадратичной формы
зависит от выбора линейного преобразования
переменных, то есть от выбора системы
координат. Если, например, взять L=1, то
уравнения
являются уравнениями одного и того же
эллипса в разных системах координат.
Пример.
В предыдущем примере мы обратили внимание
на то, что канонический вид квадратичной
формы можно записать разными способами:
Во всех этих записях число слагаемых с
положительными и отрицательными
коэффициентами одно и то же.
Пример. Исследовать на знакоопределенность
квадратичную форму
Решение. Составим матрицу данной
квадратичной формы А=
и вычислим главные угловые миноры
М1=3>0,
М2=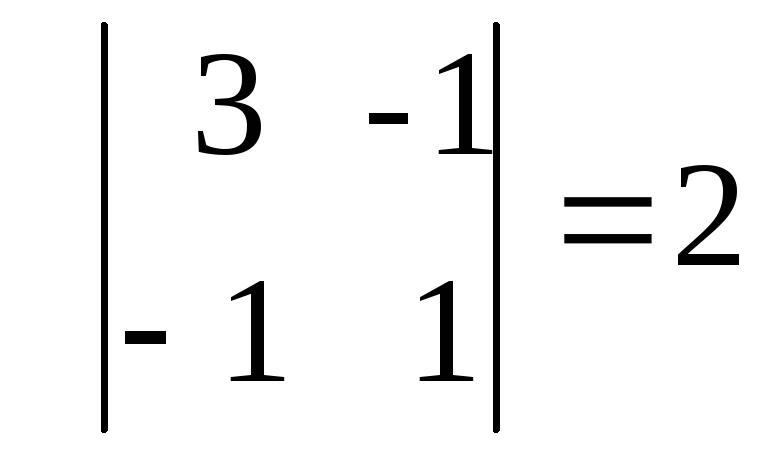
М3=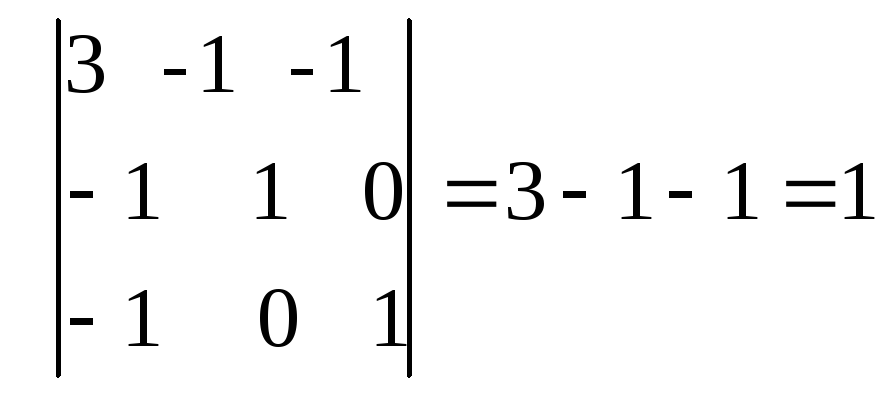
Следовательно,
по критерию Сильвестра квадратичная
форма положительно определенная.
В заключение рассмотрим экономический
смысл понятий собственного значения и
собственного вектора. Предположим, что
на некотором предприятии в начале года
заменяют 20 % оборудования, проработавшего
два года, и все оборудование, проработавшее
три года. То оборудование, которое было
в эксплуатации один год, не заменяется.
Для анализа и прогнозирования экономических
параметров работы предприятия надо
знать устойчивое, т.е. не изменяющееся
из года в год, распределение количества
единиц работающего оборудования. Введем
следующие обозначения:
количество
единиц оборудования, проработавшего i
лет к началу года t, тогда
Это равенство означает, что не заменяется
новое оборудование прошлого года,
заменяется 20 % оборудования, проработавшего
два года к началу предыдущего года и
все оборудование, проработавшее три
года к началу предыдущего года.
Это равенство означает, что два года
проработает то оборудование, которое
к началу предыдущего года эксплуатировалось
один год.
т.е. три года эксплуатируют то оборудование,
которое к началу года проработало два
сезона и не было заменено. Введем матрицы
тогда все
предыдущие рассуждения описываются
уравнением
Если нас интересует устойчивое
распределение, то
и приходится решать уравнение
Если справедливо предположение о том,
что оборудование заменяется пропорционально
количеству единиц техники, находящейся
на предприятии, то приходится искать
распределение, которое является решением
уравнения
Задача отыскания таких λ , при которых
существует ненулевое решение уравнения
и приводит к понятию собственного
вектора и собственного значения
оператора.
Упражнения для
самостоятельного решения
-
Привести
к каноническому виду квадратичную
форму L=х2–у2-4ху
путем выделения полного квадрата. Какую
кривую определяет уравнение L(x,y)=1? -
Привести
к каноническому виду квадратичную
форму, выделяя полные квадраты, L= -
Привести
к каноническому виду квадратичную
форму, определив собственные значения
ее матрицы
Ответы: 1.
2.
3.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
- Квадратичные формы и их определение
- Квадратичные формы
Квадратичные формы и их определение
Определение. Квадратичной формой L (x1, x2, …, xn) от n переменных называется сумма, каждый член которой является или квадратом одной из переменных, или произведением двух различных переменных, взятых с некоторым коэффициентом, то есть

Допускаем, что в квадратичной форме (2.44) aij — действительные числа. Распишем квадратичную форму (2.44), разбив слагаемые, содержащие произведения переменных, на две равные части:
Матрица

или A = {aij} (i, j = 1, 2, …, n) является симметричной, так как aij = aji, называется матрицей квадратичной формы (2.44).
Рангом квадратичной формы называется ранг ее матрицы. Квадратичная форма называется невырожденной, если ее матрица невырожденная.
Если 
Выражение XT AX представляет собой квадратичную форму в матричном виде.
Пример 1. Записать в матричном виде квадратичную форму
Решение. Матрица данной квадратичной формы имеет вид
А =
Значит,
Квадратичная форма называется канонической (или другими словами, имеет канонический вид), если все aij = 0, когда i ≠ j. Тогда квадратичная форма будет иметь вид
Рассмотрим следующую теорему.
ТЕОРЕМА 1. Произвольная квадратичная форма приводится к каноническому виду.
Доказательство. Пусть задана квадратичная форма (2.44) с матрицей (2.45) в базисе 
Матрица B является матрицей перехода от базиса

к некоторому базису

Примечание. Действительная квадратная матрица называется ортогональной, если сумма квадратов элементов каждого столбца равна единице и сумма произведений соответствующих элементов из двух разных столбцов равна нулю. Необходимое и достаточное условие ортогональности матрицы В является условие ВT ⋅ B = Е.
Пусть X и Y являются векторами-столбцами из координат вектора 
или

Примечание. При доказательстве данной теоремы использовали транспонирование произведения матриц по формуле (СY)T = YT ⋅ CT.
Заметим, что в канонической форме (2.48) λ1, λ2, …, λn являются собственными числами матрицы A.
Пример 2. Привести квадратичную форму 
Решение. Матрица данной квадратичной формы имеет вид 

Характеристическое уравнение данной системы имеет вид

Решив данное уравнение, находим λ1 = 6, λ2 = 1. Значит канонический вид данной квадратичной формы является 
Найдем ортогональную матрицу.
Столбцами ортогональной матрицы, которая приводит квадратичную форму к каноническому виду, является ортонормированный собственные вектор-столбец матрицы A.
Сначала найдем нормированный собственный вектор-столбец матрицы A с собственным значением λ1 = 6. Для этого из системы (2.49) имеем систему для нахождения координат вектора:
Из данной системы находим x2 = 2x1 или u2 = 2u1. Значит, при произвольном u1, отличном от нуля, столбец 


Аналогично находим вектор-столбец матрицы A с собственным значением λ2 = 1, а именно из системы:
Находим x1 = –2x2 или при произвольном s, отличном от нуля, столбец 

Замечание. Легко проверить, что 
Рассмотрим на примере еще один метод приведения квадратичной формы к каноническому виду.
Метод Лагранжа приведения квадратичной формы к каноническому виду заключается в последовательном выделении полных квадратов.
Пример 3. Привести к каноническому виду квадратичную форму

Итак, невырожденное линейное преобразование
приводит данную квадратичную форму к каноническому виду
Канонический вид квадратичной формы не является однозначным, так как одна и та же квадратичная форма может быть приведена к каноническому виду многими способами. Однако полученные разными способами квадратичные формы имеют ряд общих свойств.
Сформулируем одно из этих свойств, которое выражает закон инерции квадратичных форм, и заключается в следующем: все канонические формы, к которым приводится данная квадратичная форма, имеют:
1) одно и то же число нулевых коэффициентов;
2) одно и то же число положительных коэффициентов;
3) одно и то же число отрицательных коэффициентов.
Определение 1. Квадратичная форма L (x1, x2, …, xn) называется положительно определенной, если для всех действительных значений x1, x2, …, xn используется неравенство L (x1, x2, …, xn) > 0.
Определение 2. Если L (x1, x2, …, xn) является положительно определенной формой, то квадратичная формаL (x1, x2, …, xn) < 0 называется отрицательно определенной.
Необходимые и достаточные условия положительной (отрицательной) определенности квадратичной формы дает следующая теорема.
ТЕОРЕМА 2. Для того чтобы квадратичная форма L = XT AX была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения λi (i = 1, 2, …, n) матрицы A были положительными (отрицательными).
Данную теорему приводим без доказательства.
Во многих случаях для установления знакоопределенности квадратичной формы удобно применять критерии Сильвестра.
ТЕОРЕМА 3. Для того чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы этой формы были положительными, то есть


Следует заметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака “минус” для минора первого порядка.
Например, квадратичная форма L в примере 2 является положительно определенной на основании теоремы 2, так как корни характеристического уравнения λ1 = 6 и λ2 = 1 являются положительными.
Второй способ. Так как главные миноры матрицы A

Квадратичные формы
Однородный многочлен второй степени относительно переменных
называется квадратичной формой от этих переменных. Если взять 
или
где
Выражение (1.28), а следует и квадратичная форма (1.26) полностью определяется матрицей 
Выполняя замену базиса, квадратичную форму (1.26) можно привести к виду:
где 


Выражение (1.29) называется каноническим видом квадратичной формы (1.26).
Рассмотрим квадратичную форму 

Тогда квадратичную форму можно записать так:
Квадратичная форма 



Если 

Решение примеров:
Пример 1.99
Квадратичная форма
положительно определенной.
Квадратичная форма
отрицательно определенная.
Квадратичная форма
неопределенной.
Квадратичная форма
является отрицательно определенной.
Пример 1.100
Используя теорию квадратичных форм, привести к каноническому виду уравнения линии второго порядка
Решение. Уравнение линии запишем в виде 
Сложим характеристическое уравнение матрицы 

Корни уравнения 


Свойства квадратичной формы (1.30) связаны с собственными числами матрицы
Пример 1.101
Привести к каноническому виду уравнения линии 
Решение. Группа старших членов этого уравнения квадратическую форму 
Собственными значениями будут числа 




Лекции:
- Преобразование выражений, содержащих переменную под знаком логарифма
- Метод неопределенных коэффициентов
- Несобственный интеграл первого рода
- Функциональные ряды. Область сходимости. Равномерная сходимость
- Производные тригонометрических функций
- Интегралы, зависящие от параметра
- Умножение логарифмов: пример решения
- Вычислить определитель матрицы
- Геометрический и физический смысл производной
- Найти фундаментальную систему решений


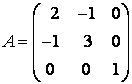
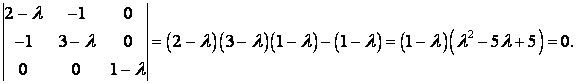
=sum%20_{{i,j=1}}^{n}a_{{ij}}x_{i}x_{j})

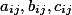
x_{0}^2}+(2)x_{0}x_{1}+(4)x_{0}x_{2}+(3)x_{1}^2}+(1)x_{2}^2})
a_{0}^2}+(4)a_{0}a_{1}+(-2)a_{0}a_{2}+(-5)a_{1}^2}+(6)a_{1}a_{2}+(8)a_{2}^2})
s_{0}^2+(4-1i)s_{0}s_{1}+(-7+1i)s_{0}s_{2}+(-1)s_{0}s_{3}+(2)s_{1}^2+(2.4-2i)s_{1}s_{2}+(7+1i)s_{1}s_{3}+(11)s_{2}^2+(-6-1i)s_{2}s_{3}+(2i)s_{3}^2)