В данной статье пойдет речь о таком понятии, как ранг матрицы и необходимых дополнительных понятиях. Мы приведем примеры и доказательства нахождения ранга матрицы, а также расскажем, что такое минор матрицы, и почему он так важен.
Минор матрицы
Чтобы понять, что такое ранг матрицы, необходимо разобраться с таким понятием, как минор матрицы.
Минор k-ого порядка матрицы — определитель квадратной матрицы порядка k×k, которая составлена из элементов матрицы А, находящихся в заранее выбранных k-строках и k-столбцах, при этом сохраняется положение элементов матрицы А.
Проще говоря, если в матрице А вычеркнуть (p-k) строк и (n-k) столбцов, а из тех элементов, которые остались, составить матрицу, сохраняя расположение элементов матрицы А, то определитель полученной матрицы и есть минор порядка k матрицы А.
Из примера следует, что миноры первого порядка матрицы А и есть сами элементы матрицы.
Можно привести несколько примеров миноров 2-ого порядка. Выберем две строки и два столбца. Например, 1-ая и 2 –ая строка, 3-ий и 4-ый столбец.
При таком выборе элементов минором второго порядка будет -1302=(-1)×2-3×0=-2
Другим минором 2-го порядка матрицы А является 0011=0
Предоставим иллюстрации построения миноров второго порядка матрицы А:
Минор 3-го порядка получается, если вычеркнуть третий столбец матрицы А:
003112-1-40=0×1×0+0×2×(-1)+3×1×(-4)-3×1×(-1)-0×1×0-0×2×(-4)=-9
Иллюстрация, как получается минор 3-го порядка матрицы А:
Для данной матрицы миноров выше 3-го порядка не существует, потому что
k≤min(p, n)=min (3, 4)=3
Сколько существует миноров k-ого порядка для матрицы А порядка p×n?
Число миноров вычисляют по следующей формуле:
Cpk×Cnk, где Сpk=p!k!(p-k)! и Cnk=n!k!(n-k)! — число сочетаний из p по k, из n по k соответственно.
После того, как мы определились, что такое миноры матрицы А, можно переходить к определению ранга матрицы А.
Ранг матрицы: методы нахождения
Ранг матрицы — наивысший порядок матрицы, отличный от нуля.
Rank (A), Rg (A), Rang (A).
Из определения ранга матрицы и минора матрицы становиться понятно, что ранг нулевой матрицы равен нулю, а ранг ненулевой матрицы отличен от нуля.
Нахождение ранга матрицы по определению
Метод перебора миноров — метод, основанный на определении ранга матрицы.
Алгоритм действий способом перебора миноров:
Необходимо найти ранг матрицы А порядка p×n. При наличии хотя бы одного элемента, отличного от нуля, то ранг матрицы как минимум равен единице (т.к. есть минор 1-го порядка, который не равен нулю).
Далее следует перебор миноров 2-го порядка. Если все миноры 2-го порядка равны нулю, то ранг равен единице. При существовании хотя бы одного не равного нулю минора 2-го порядка, необходимо перейти к перебору миноров 3-го порядка, а ранг матрицы, в таком случае, будет равен минимум двум.
Аналогичным образом поступим с рангом 3-го порядка: если все миноры матрицы равняются нулю, то ранг будет равен двум. При наличии хотя бы одного ненулевого минора 3-го порядка, то ранг матрицы равен минимум трем. И так далее, по аналогии.
Найти ранг матрицы:
А=-11-1-202260-443111-7
Поскольку матрица ненулевая, то ее ранг минимум равен единице.
Минор 2-го порядка -1122=(-1)×2-1×2=4 отличен от нуля. Отсюда следует, что ранг матрицы А не меньше двух.
Перебираем миноры 3-го порядка: С33×С53=15!3!(5-3)!= 10 штук.
-11-12264311=(-1)×2×11+1×6×4+(-1)×2×3-(-1)×2×4-1×2×11-(-1)×6×3=0
-11-2220431=(-1)×2×1+1×0×4+(-2)×2×3-(-2)×2×4-1×2×1-(-1)×0×3=0
-1-1-22604111=(-1)×6×1+(-1)×0×4+(-2)×2×11-(-2)×6×4-(-1)×2×1-(-1)×0×11=0
-11-2220431=(-1)×2×1+1×0×4+(-2)×2×3-(-2)×2×4-1×2×1-(-1)×0×3=0
-1-1026-4411-7=(-1)×6×(-7)+(-1)×(-4)×4+0×2×11-0×6×4-(-1)×2×(-7)-(-1)×(-4)×11=0
1-1026-4311-7=1×6×(-7)+(-1)×(-4)×3+0×2×11-0×6×3-(-1)×2×(-7)-1×(-4)×11=0
1-2020-431-7=1×0×(-7)+(-2)×(-4)×3+0×2×1-0×0×3-(-2)×2×(-7)-1×(-4)×1=0
-1-2060-4111-7=(-1)×0×(-7)+(-2)×(-4)×11+0×6×1-0×0×11-(-2)×6×(-7)-(-1)×(-4)×1=0
Миноры 3-го порядка равны нулю, поэтому ранг матрицы равен двум.
Ответ: Rank (A) = 2.
Нахождение ранга матрицы методом окаймляющих миноров
Метод окаймляющих миноров — метод, который позволяет получить результат при меньшей вычислительной работе.
Окаймляющий минор — минор Mok(k+1) -го порядка матрицы А, который окаймляет минор M порядка k матрицы А, если матрица, которая соответствует минору Mok , «содержит» матрицу, которая соответствует минору М.
Проще говоря, матрица, которая соответствует окаймляемому минору М, получается из матрицы, соответствующей окаймляющему минору Mok , вычеркиванием элементов одной строки и одного столбца.
Найти ранг матрицы:
А=120-13-2037134-21100365
Для нахождения ранга берем минор 2-го порядка М=2-141
Записываем все окаймляющие миноры:
12-1-207341,20-10374-21,2-13071411,12-1341006,20-14-21036,2-13411065.
Чтобы обосновать метод окаймляющих миноров, приведем теорему, формулировка которой не требует доказательной базы.
Если все миноры, окаймляющие минор k-ого порядка матрицы А порядка p на n, равны нулю, то все миноры порядка (k+1) матрицы А равна нулю.
Алгоритм действий:
Чтобы найти ранг матрицы, необязательно перебирать все миноры, достаточно посмотреть на окаймляющие.
Если окаймляющие миноры равняются нулю, то ранг матрицы нулевой. Если существует хотя бы один минор, который не равен нулю, то рассматриваем окаймляющие миноры.
Если все они равны нулю, то Rank(A) равняется двум. При наличии хотя бы одного ненулевого окаймляющего минора, то приступаем к рассматриванию его окаймляющих миноров. И так далее, аналогичным образом.
Найти ранг матрицы методом окаймляющих миноров
А=210-134210-12111-40024-14
Как решить?
Поскольку элемент а11 матрицы А не равен нулю, то возьмем минор 1-го порядка. Начнем искать окаймляющий минор, отличный от нуля:
2142=2×2-1×4=02041=2×1-0×4=2
Мы нашли окаймляющий минор 2-го порядка не равный нулю 2041.
Осуществим перебор окаймляющих миноров — (их(4-2)×(5-2)=6 штук).
210421211=0; 20-1410211=0; 20341-121-4=0;210421002=0; 20-1410024=0; 20341-102-14=0
Ответ: Rank(A) = 2.
Нахождение ранга матрицы методом Гаусса (с помощью элементарных преобразований)
Вспомним, что представляют собой элементарные преобразования.
Элементарные преобразования:
- путем перестановки строк (столбцов) матрицы;
- путем умножение всех элементов любой строки (столбца) матрицы на произвольное ненулевое число k;
путем прибавления к элементам какой-либо строки (столбца) элементов, которые соответствуют другой стоки (столбца) матрицы, которые умножены на произвольное число k.
Нахождение ранга матрицы методом Гаусса — метод, который основывается на теории эквивалентности матриц: если матрица В получена из матрицы А при помощи конечного числа элементарных преобразований, то Rank(A) = Rank(B).
Справедливость данного утверждения следует из определения матрицы:
- в случае перестановки строк или столбцов матрицы ее определитель меняет знак. Если он равен нулю, то и при перестановке строк или столбцов остается равным нулю;
- в случае умножения всех элементов какой-либо строки (столбца) матрицы на произвольное число k, которое не равняется нулю, определитель полученной матрицы равен определителю исходной матрицы, которая умножена на k;
в случае прибавления к элементам некоторой строки или столбца матрицы соответствующих элементов другой строки или столбца, которые умножены на число k, не изменяет ее определителя.
Суть метода элементарных преобразований: привести матрицу ,чей ранг необходимо найти, к трапециевидной при помощи элементарных преобразований.
Для чего?
Ранг матриц такого вида достаточно просто найти. Он равен количеству строк, в которых есть хотя бы один ненулевой элемент. А поскольку ранг при проведении элементарных преобразований не изменяется, то это и будет ранг матрицы.
Проиллюстрируем этот процесс:
- для прямоугольных матриц А порядка p на n, число строк которых больше числа столбцов:
А~1b12b13⋯b1n-1b1n01b23⋯b2n-2b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01000⋯00⋮⋮⋮⋮⋮⋮000⋯00, Rank(A)=n
или
А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k
- для прямоугольных матриц А порядка p на n, число строк которых меньше числа столбцов:
А~1b12b13⋯b1pb1p+1⋯b1n01b23⋯b2pb2p+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bpp+1⋯bpn, Rank(A)=p
или
А~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0
- для квадратных матриц А порядка n на n:
А~1b12b13⋯b1n-1b1n01b23⋯b2n-1b2n⋮⋮⋮⋮⋮⋮000⋯1bn-1n000⋯01, Rank(A)=n
или
A~1b12b13⋯b1kb1k+1⋯b1n01b23⋯b2kb2k+1⋯b2n⋮⋮⋮⋮⋮⋮⋮⋮000⋯1bkk+1⋯bkn000⋯00⋯0⋮⋮⋮⋮⋮⋮⋮⋮000⋯00⋯0, Rank(A)=k, k<n
Найти ранг матрицы А при помощи элементарных преобразований:
А=21-26300-11-12-75-24-1572-411
Как решить?
Поскольку элемент а11 отличен от нуля, то необходимо умножить элементы первой строки матрицы А на 1а11=12:
А=21-26300-11-12-75-24-1572-411~
Прибавляем к элементам 2-ой строки соответствующие элементы 1-ой строки, которые умножены на (-3). К элементам 3-ей строки прибавляем элементы 1-ой строки, которые умножены на (-1):
~А(1)=112-13300-11-12-75-24-1572-411~А(2)==112-133+1(-3)0+12(-3)0+(-1)(-3)-1+3(-3)1+1(-3)-1+12(-3)2+(-1)(-1)-7+3(-1)5+1(-5)-2+12(-5)4+(-1)(-5)-15+3(-5)7+1(-7)2+12(-7)-4+(-1)(-7)11+3(-7)=
=112-130-323-100-323-100-929-300-323-10
Элемент а22(2) отличен от нуля, поэтому мы умножаем элементы 2-ой строки матрицы А на А(2) на 1а22(2)=-23:
А(3)=112-1301-22030-323-100-929-300-323-10~А(4)=112-1301-22030-32+1323+(-2)32-10+203×320-92+1929+(-2)92-30+203×920-32+1323+(-2)32-10+203×32==112-1301-2203000000000000
- К элементам 3-ей строки полученной матрицы прибавляем соответствующие элементы 2-ой строки ,которые умножены на 32;
- к элементам 4-ой строки — элементы 2-ой строки, которые умножены на 92;
- к элементам 5-ой строки — элементы 2-ой строки, которые умножены на 32.
Все элементы строк равны нулю. Таким образом, при помощи элементарных преобразований ,мы привели матрицу к трапецеидальному виду, откуда видно, что Rank (A(4))=2 . Отсюда следует, что ранг исходной матрицы также равен двум.
Если проводить элементарные преобразования, то не допускаются приближенные значения!
Перед тем как начать знакомство с темой, необходимо повторить правила нахождения определителей второго, третьего и высших порядков. Также необходимо знать, что детерминант 1-го порядка — число. Рассмотрим 2 метода вычисления ранга матриц.
Онлайн-калькулятор
Метод окаймляющих миноров
Для нахождения ранга матрицы данным методом требуется уметь находить миноры матриц.
Рангом матрицы QQ называется наивысший порядок миноров, среди которых есть хотя бы один отличный от 00.
При этом ранг матрицы не может превышать порядка матрицы: 0⩽rang Qm×n⩽min(m,n)0leqslant rang Q_{mtimes n}leqslant min (m, n).
Обозначить ранг матрицы QQ можно следующим образом: rang Qrang Q или r(Q)r(Q).
Если ранг матрицы QQ равен rr, то это означает, что в матрице QQ имеется отличный от нуля минор порядка rr. При этом всякий минор порядка больше, чем rr равен нулю.
Исходя из определения ранга матрицы, следует, что если все миноры первого порядка (т. е. элементы матрицы QQ) равны 00, то rang Q=0rang Q=0. Если один из миноров первого порядка отличен от 00, а все миноры второго порядка равны 00, то rang Q=1rang Q=1. Если все миноры kk-го порядка равны 00, или миноров kk-го порядка не существует, то rang Q=k−1rang Q=k-1.
Рассмотрим примеры нахождения ранга матриц данным методом.
Пример 1
Найти ранг матрицы методом окаймляющих миноров
F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Данная матрица имеет размер 3×33times3, поэтому ее ранг не может быть больше 33, т.е. rang F⩽3rang Fleqslant3.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang F≥1rang Fgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣0321∣=0⋅1−2⋅3=0−6=−6begin{vmatrix}0&3\2&1end{vmatrix}=0cdot1-2cdot3=0-6=-6. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang F≥2rang Fgeq2.
Перейдем к проверке миноров 3-го порядка. Минор 3-го порядка — определитель матрицы FF, поскольку она состоит из 3 строк и 3 столбцов: ∣03−1210−2−10∣=0begin{vmatrix}0&3&-1\2&1&0\-2&-1&0end{vmatrix}=0. Значит, ранг матрицы FF равен 22, или rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом окаймляющих миноров
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Данная матрица имеет размер 5×45times4. Из чисел 55 и 44 минимальным является 44, поэтому ее ранг не может быть больше 44, а значит rang K⩽4rang Kleqslant4.
Перейдем к вычислению ранга матрицы.
Среди миноров 1-го порядка (т.е. элементов определителя) есть хотя бы один, не равный 00, поэтому rang K≥1rang Kgeq1.
Перейдем к проверке миноров 2-го порядка. Например, на пересечении строк №1 и №2 и столбцов №1 и №2 получим минор: ∣21−12∣=2⋅2−(−1)⋅1=4+1=5begin{vmatrix}2&1\-1&2end{vmatrix}=2cdot2-(-1)cdot1=4+1=5. Значит, среди миноров 2-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥2rang Kgeq2.
Перейдем к проверке миноров 3-го порядка. Например, на пересечении строк №1, №3 и №5 и столбцов №2, №3 и №4 получим минор:
∣1−233−153−31∣=1⋅(−1)⋅1+(−2)⋅5⋅3+3⋅(−3)⋅3−3⋅(−1)⋅3−(−2)⋅1⋅3−1⋅5⋅(−3)=−1−30−27+9+6+15=−28begin{vmatrix}1&-2&3\3&-1&5\3&-3&1end{vmatrix}=1cdot(-1)cdot1+(-2)cdot5cdot3+3cdot(-3)cdot3-3cdot(-1)cdot3-(-2)cdot1cdot3-1cdot5cdot(-3)=-1-30-27+9+6+15=-28.
Значит, среди миноров 3-го порядка есть хотя бы один, не равный 00 и поэтому rang K≥3rang Kgeq3.
Перейдем к проверке миноров 4-го порядка. Например, на пересечении строк №1, №2, №3 и №4 и столбцов №1, №2, №3 и №4 получим минор:
∣21−23−121213−15−2−212∣=2(−1)1+1∣2123−15−212∣−(−1)2+1∣1−233−15−212∣+(−1)3+1∣1−23212−212∣−2(−1)4+1∣1−232123−15∣=2(−1)2∣2123−15−212∣−(−1)3∣1−233−15−212∣+(−1)4∣1−23212−212∣−2(−1)5∣1−232123−15∣=2∣2123−15−212∣+∣1−233−15−212∣+∣1−23212−212∣+2∣1−232123−15∣=2(−4+6−10−4−10−6)−2+9+20−6−5+12+2+6+8+6−2+8+2(5−6−12−9+2+20)=−56+56+0=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2end{vmatrix}=2(-1)^{1+1}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{2+1}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{3+1}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{4+1}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-1)^{2}begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}-(-1)^{3}begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+(-1)^{4}begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}-2(-1)^{5}begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2begin{vmatrix}2&1&2\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\3&-1&5\-2&1&2end{vmatrix}+begin{vmatrix}1&-2&3\2&1&2\-2&1&2end{vmatrix}+2begin{vmatrix}1&-2&3\2&1&2\3&-1&5end{vmatrix}=2(-4+6-10-4-10-6)-2+9+20-6-5+12+2+6+8+6-2+8+2(5-6-12-9+2+20)=-56+56+0=0.
Остальные миноры 4-го порядка также равны нулю:
∣21−23−121213−1543−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\4&3&-3&1end{vmatrix}=0,
∣21−23−1212−2−21243−31∣=0begin{vmatrix}2&1&-2&3\-1&2&1&2\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣21−2313−15−2−21243−31∣=0begin{vmatrix}2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0,
∣−121213−15−2−21243−31∣=0begin{vmatrix}-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{vmatrix}=0.
Значит, ранг матрицы KK равен 33, или rang K=3rang K=3.
Данный метод не всегда удобен, поскольку связан с вычислением большого количества определителей. Рассмотрим метод нахождения ранга матриц, который наиболее часто применяется на практике.
Метод Гаусса (метод элементарных преобразований)
Метод основан на элементарных преобразованиях матриц, под которыми будем понимать такие преобразования, в результате которых сохраняется эквивалентность матриц:
- перестановка местами любых двух рядов (строк или столбцов) матрицы;
- умножение любого ряда матрицы (строки или столбца) на некоторое число, отличное от нуля;
- прибавление к любому ряду (строке или столбцу) матрицы другого ряда (строки или столбца), умноженного на некоторое число, отличное от нуля.
Рангом матрицы называется количество ненулевых строк матрицы после ее приведения к ступенчатому виду при помощи элементарных преобразований над строками и столбцами.
Рассмотрим суть данного метода на примерах.
Пример 1
Найти ранг матрицы методом Гаусса F=(03−1210−2−10)F=begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}.
Приведем матрицу FF с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(03−1210−2−10)∼(21003−1−2−10)begin{pmatrix}0&3&-1\2&1&0\-2&-1&0end{pmatrix}sim begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 1:
(21003−1−2−10)∼(21003−1000)begin{pmatrix}2&1&0\0&3&-1\-2&-1&0end{pmatrix}simbegin{pmatrix}2&1&0\0&3&-1\0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу FF к ступенчатому виду. В ней остались 2 ненулевые строки, следовательно, rang F=2rang F=2.
Пример 2
Найти ранг матрицы методом Гаусса
K=(21−23−121213−15−2−21243−31)K=begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Приведем матрицу KK с помощью элементарных преобразований к ступенчатому виду.
Поменяем местами строки №1 и №2:
(21−23−121213−15−2−21243−31)∼(−121221−2313−15−2−21243−31)begin{pmatrix}2&1&-2&3\-1&2&1&2\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}.
Поменяем местами строки №2 и №4:
(−121221−2313−15−2−21243−31)∼(−1212−2−21213−1521−2343−31)begin{pmatrix}-1&2&1&2\2&1&-2&3\1&3&-1&5\-2&-2&1&2\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}.
Поменяем местами строки №3 и №4:
(−1212−2−21213−1521−2343−31)∼(−1212−2−21221−2313−1543−31)begin{pmatrix}-1&2&1&2\-2&-2&1&2\1&3&-1&5\2&1&-2&3\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}.
Поменяем местами строки №4 и №5:
(−1212−2−21221−2313−1543−31)∼(−1212−2−21221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\1&3&-1&5\4&3&-3&1end{pmatrix}sim begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №2 строку №1, умноженную на -2:
(−1212−2−21221−2343−3113−15)∼(−12120−6−1−221−2343−3113−15)begin{pmatrix}-1&2&1&2\-2&-2&1&2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №3 строку №1, умноженную на 2:
(−12120−6−1−221−2343−3113−15)∼(−12120−6−1−2050743−3113−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\2&1&-2&3\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}.
Прибавим к строке №4 строку №1, умноженную на 4:
(−12120−6−1−2050743−3113−15)∼(−12120−6−1−205070111913−15)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\4&3&-3&1\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}.
Прибавим к строке №5 строку №1, умноженную на 1:
(−12120−6−1−205070111913−15)∼(−12120−6−1−20507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\1&3&-1&5end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №2 строку №3, умноженную на 1:
(−12120−6−1−20507011190507)∼(−12120−1−150507011190507)begin{pmatrix}-1&2&1&2\0&-6&-1&-2\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}.
Прибавим к строке №5 строку №3, умноженную на -1:
(−12120−1−150507011190507)∼(−12120−1−150507011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&5&0&7end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №3 строку №2, умноженную на 5:
(−12120−1−150507011190000)∼(−12120−1−1500−532011190000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&5&0&7\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №2, умноженную на 11:
(−12120−1−1500−532011190000)∼(−12120−1−1500−53200−10640000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&11&1&9\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}.
Прибавим к строке №4 строку №3, умноженную на -2:
(−12120−1−1500−53200−10640000)∼(−12120−1−1500−53200000000)begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&-10&64\0&0&0&0end{pmatrix}sim begin{pmatrix}-1&2&1&2\0&-1&-1&5\0&0&-5&32\0&0&0&0\0&0&0&0end{pmatrix}.
С помощью элементарных преобразований мы привели матрицу KK к ступенчатому виду. В ней остались 3 ненулевые строки, следовательно, rang K=3rang K=3.
Любым из рассмотренных методов можно найти ранг матрицы.
Наши эксперты готовы оказать вам помощь с решением задачи онлайн по самым низким ценам!
Тест по теме «Ранг матрицы»
Лекция №6 Ранг матрицы и ранг системы векторов.
Основные понятия темы:
1.Ранг матрицы и ранг системы векторов.
2.Методы вычисления ранга матрицы.
3.Ортогональные системы векторов.
1. Понятие ранга матрицы.
Рассмотрим матрицу порядка m x n
|
a11 |
a12 |
… |
a1n |
|
a21 |
a22 |
… |
a2n |
|
A |
… |
||
|
… |
… |
… |
|
|
am2 |
… |
||
|
am1 |
amn |
Если в ней взять произвольные k строк и k столбцов ( k m, k n ), то на их пересечении расположена квадратная матрица k–го порядка. Ее определитель называется минором Mk матрицы A, k- порядок минора.
Определение. Рангом матрицы A называется наивысший из порядков миноров матрицы, отличных от нуля.
Или по-другому, рангом матрицы r(A)
называется такое число r, что у матрицы имеется по крайней мере один минор Mr r–го порядка, отличный от 0, а все миноры (r+1)–го и высших порядков равны 0.

Например, ранг матрицы
|
3 |
2 |
1 |
0 |
||
|
0 |
1 |
5 |
0 |
||
|
A |
4 |
||||
|
0 |
0 |
0 |
|||
|
6 |
3 |
2 |
0 |
||
равен 3, т.к. матрица имеет минор 3-го порядка, отличный от 0:
00 4
Аминор 4-го порядка равен нулю:
|
2 |
1 |
0 |
|||
|
3 |
|||||
|
M 4 |
0 |
1 |
5 |
0 |
|
|
0 |
0 |
4 |
0 |
||
|
6 |
3 |
2 |
0 |
||
Других миноров 4-го порядка у матриц нет. Принимая условно, что ранг нулевой матрицы равен 0, очевидно, что ранг может принимать
значения 0 r(A) min(m, n) .
Свойства ранга матрицы:
при последующих преобразованиях матрицы, называемых элементарными, ранг матрицы не меняется:
1) при транспонировании матрицы (замена строк столбцами, не меняя их порядка)
2)при перестановке строк и столбцов
3)при умножении любой строки (или столбца) на отличный от нуля множитель
4)при прибавлении к одной строке (столбцу) другой строки (столбца), умноженной на любой множитель, отличный от нуля
5)при вычеркивании нулевой строки (или нулевого столбца)
6)при вычеркивании строки (столбца), являющейся линейной комбинацией других строк (столбцов); в частности строки (столбца), пропорциональной другой строке (столбцу).
Методы вычисления ранга матрицы.
На элементарных преобразованиях матрицы основан первый метод нахождения ранга матрицы – метод элементарных преобразований. По этому методу с помощью элементарных преобразований данная матрица А преобразовывается в другую матрицу B, ранг который равен рангу матрицы А. Такая матрица В называется эквивалентной матрице А.( A B )
Теорема 1. Эквивалентные матрицы имеют один и тот же ранг.
Применяя последовательно элементарные преобразования, преобразовывают матрицу постепенно к ступенчатой, которая имеет следующий вид:
b
11
00
…
В 00
…
0
Где b11,b22,b33,…,brr
b12 b13 …
b22 b23 …
0 b33 …
… … …
0 0 …
0 0 …
… … …
0 0 …
0 .
b1r b2r b3r
…
brr
0
…
0
…
…
…
…
…
…
…
…
b1n b2n b3n
…
brn
0
…
0
Теорема 2. Ранг ступенчатой матрицы B равен r, r(B)=r, т.е. числу ненулевых строк.
Метод окаймления для нахождения ранга матрицы.
Метод окаймления основан на следующей теореме.
Теорема 3. Если у матрицы существует минор r –го порядка Mr, отличный от 0, а все миноры
(r +1) – го порядка Mr+1, содержащие Mr , отличный от 0, (окаймляющие миноры), равны
0, то ранг матрицы равен r.
По второму методу окаймления сначала вычислим минор второго порядка M2, расположенный на пересечении первых двух строк и столбцов матрицы. Если равен 0, то переходим к вычислению других миноров второго порядка. Если все миноры второго
порядка (их очевидно у матрицы будет Cn2 Cm2 штук) равны 0, то r(A) = 1. Если хотя бы один
минор M 2 0 , то далее составляем миноры M3 третьего порядка, содержащие M2 (окаймляющие миноры). Если все окаймляющие миноры M3 равны 0, то r(A) = 2.
Если хотя бы один минор M3 0 то составляют миноры 4-го порядка, окаймляющие M3 т.д. Процесс нахождения ранга заканчивается тогда, когда найдется минор Mr (r-го порядка),
отличный от 0, а все миноры Mr+1, окаймляющие отличный от 0 минор Mr, равны
0, то ранг матрицы А равен r.
Понятие базисного минора. Теорема о базисном миноре матрицы.
Определение. Любой отличный от нуля, минор матрицы, порядок которого равен ее рангу, называется базисным минором.
Соседние файлы в папке Теория по линалу
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Элементарные преобразования матриц:
Рассмотрим прямоугольную матрицу:

состоящую из m строк и n столбцов. В п.3.2 отмсчалось, что каждую строку матрицы можно рассматривать как n-мсрный вектор, а каждый столбец – как m-мерный вектор. Тогда матрицу А можно записать в виде:
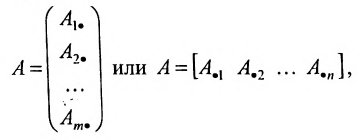
и, следовательно, данную матрицу можно рассматривать как систему вектор строк или вектор столбцов. Б указанных системах вектор-строк и вектор-столбцов можно выделять линейно независимые (зависимые) векторы. Тогда будем говорить, что строки (столбцы) матрицы линейно независимы (зависимы), если соответствующие им векторы независимы (зависимы).
Определения
Определение: Рангом системы строк (соответственно столбцов) матрицы А называется наибольшее число линейно независимых среди них.
Поскольку легко доказать, что ранг системы строк матрицы равен рангу системы её столбцов, то справедливо следующее
Определение: Рангом матрицы, обозначаемым r(А), называется максимальное число линейно независимых строк (столбцов) матрицы.
При транспонировании матрицы ранг её не изменяется.
Другой метод определения ранга матрицы связан с понятием определителя.
Выделим в матрице А любые k строк и k столбцов. Элементы, стоящие на их пересечении, образуют квадратную матрицу, определитель которой называется минором k-го порядка матрицы А. Ясно, что величина к должна удовлетворять двум условиям: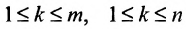 . Полагая последовательно k = 1,2,…,l, где
. Полагая последовательно k = 1,2,…,l, где
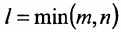 , составляем при каждом k все миноры k-то порядка матрицы А. Тогда можно сформулировать еще одно определение ранга матрицы.
, составляем при каждом k все миноры k-то порядка матрицы А. Тогда можно сформулировать еще одно определение ранга матрицы.
Определение: Рангом матрицы, обозначаемым r(А), называется порядок самого старшего минора этой матрицы, не равного нулю.
Из определения следует, что если ранг матрицы А равен l, то среди всех её миноров существует хотя бы один минор l-го порядка, отличный от нуля, но все миноры (l+1)-го порядков либо равны нулю, либо не могут быть составлены.
Вычисление ранга матрицы путём перебора всех её миноров весьма трудоёмко. Существует, однако, более простой способ вычисления ранга матрицы, основанный на упрощении структуры матрицы с помощью элементарных преобразований. Элементариыми преобразованиями матрицы называют следующие преобразования:
- обмен местами двух строк или двух столбцов матрицы;
- умножение всех элементов строки или столбца матрицы на произвольное число
 , не равное нулю;
, не равное нулю; - прибавление ко всем элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), предварительно умноженных на одно и то же число;
- исключение из матрицы строки или столбца, состоящего из нулей.
Матрицы называются эквивалентными, если от одной из них к другой можно перейти путём конечного числа элементарных преобразований.
Ступенчатой матрицей называется матрица, удовлетворяющая тому свойству, что если в какой-либо из сё строк первый отличный от нуля элемент стоит на l-м месте, то во всех следующих строках на первых l местах стоят нули:
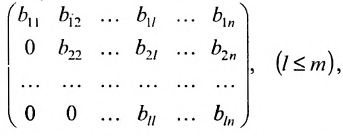
где элементы 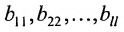 отличны от нуля, а все элементы, стоящие под ними, равны нулю.
отличны от нуля, а все элементы, стоящие под ними, равны нулю.
Для вычисления ранга матрицы приводят её с помощью цепочки элементарных преобразований к ступенчатому виду. Тогда ранг матрицы совпадает с числом её ненулевых диагональных элементов.
Теоремы о ранге матриц. Свойства ранга матриц
Относительно ранга матриц можно сформулировать следующие теоремы:
Теорема: Если матрица имеет минор порядка r, отличный от нуля, для которого все содержащие его миноры порядка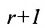 (окаймляющие миноры) равны нулю, то ранг этой матрицы равен r.
(окаймляющие миноры) равны нулю, то ранг этой матрицы равен r.
Вычисление ранга матрицы при помощи метода окаймления нужно вести от низших порядков к высшим. Сначала ищем минор первого порядка (т.е. элемент матрицы) или сразу второго порядка, отличный от нуля. Затем вычисляем окаймляющие его миноры следующего порядка, пока не найдём среди них отличного от нуля и т.д., пока не найдем минор порядка l, отличный от нуля, для которого либо все окаймляющие его миноры порядка l+1 равны нулю, либо такие миноры не могут быть составлены.
Теорема: Элементарные преобразования не меняют ранга матрицы.
Доказательство теоремы следует из определения ранга матрицы и свойств определителей.
Пример:
Найти ранг матрицы: 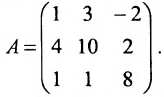
Решение:
Минор первого порядка в левом верхнем углу равен 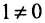 . Окаймляющий его минор второго порядка:
. Окаймляющий его минор второго порядка:
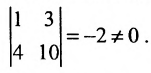 Вычисляем окаймляющий его минор третьего порядка:
Вычисляем окаймляющий его минор третьего порядка: 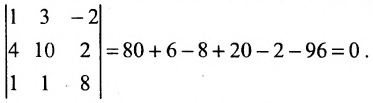
Значит ранг матрицы равен 2.
Пример:
Найти ранг матрицы:

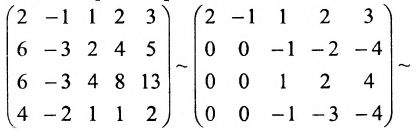
Решение:
При помощи элементарных преобразований приведём данную матрицу к ступенчатому виду. На первом шаге умножим последовательно первую строку на 3, 3, 2 и вычтем из второй, третьей, четвёртой строк соответственно:
В эквивалентной матрице прибавим к третьей строке вторую и вычтем вторую из четвёртой строки:

(поменяем местами третью и четвертую строки)

(поменяем местами третий, четвёртый и пятый столбцы со вторым и опустим строки, состоящие из нулей) 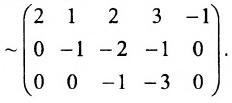 Преобразовали матрицу к ступеньчатому виду, у которой на диагонали три ненулевых элемента. Ранг матрицы равен 3.
Преобразовали матрицу к ступеньчатому виду, у которой на диагонали три ненулевых элемента. Ранг матрицы равен 3.
Отмстим некоторые свойства ранга матриц.
- Ранг суммы двух (или нескольких) матриц не больше суммы их рангов.
- Любую матрицу ранга r можно представить в виде суммы r матриц ранга 1, но нельзя представить в виде суммы менее чем r таких матриц.
- Любую матрицу С ранга r можно представить в виде произведения
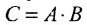 , где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк.
, где А состоит из r линейно независимых столбцов, г B -из r линейно независимых строк. - Ранг произведения матриц порядка n удовлетворяет неравенству
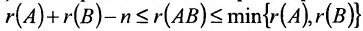 .
.
Определение системы m линейных уравнений с n неизвестными
Системой m линейных уравнений с n неизвестными 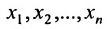 называется система вида:
называется система вида:
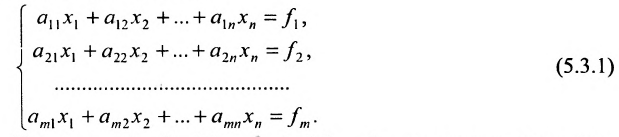
Числа 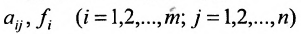 называются соответственно коэффициентами системы и ее свободными членами. Первый индекс i коэффициента
называются соответственно коэффициентами системы и ее свободными членами. Первый индекс i коэффициента 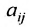 соответствует номеру уравнения, в которое входит этот коэффициент, а второй индекс – номеру неизвестной
соответствует номеру уравнения, в которое входит этот коэффициент, а второй индекс – номеру неизвестной 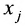 , при которой стоит этот коэффициент. Индекс свободного члена
, при которой стоит этот коэффициент. Индекс свободного члена 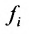 соответствует номеру уравнения, содержащего
соответствует номеру уравнения, содержащего 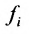 .
.
С помощью знака суммирования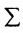 систему (5.3.1) можно записать в виде:
систему (5.3.1) можно записать в виде:

Матрица
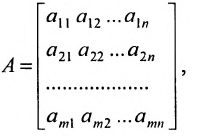
составленная из коэффициентов системы 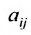 , называется матрицей
, называется матрицей
системы. Если к этой матрице добавить столбец свободных членов, то получим расширенную матрицу системы: 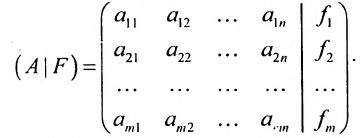 Обозначив матрицу-столбец неизвестных
Обозначив матрицу-столбец неизвестных 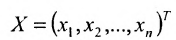 и матрицу-столбец свободных членов
и матрицу-столбец свободных членов 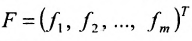 , систему (5. 3.1) можно записать в матричной форме:
, систему (5. 3.1) можно записать в матричной форме:
 где
где 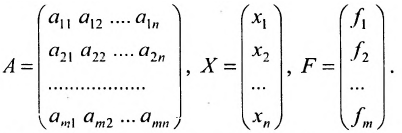
Используется также табличная форма записи системы (5.3.1):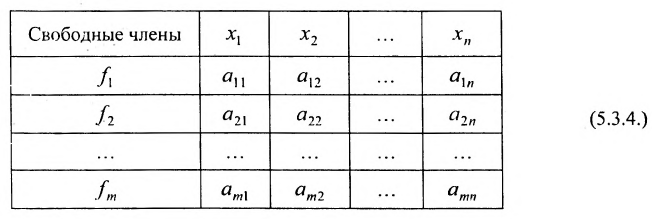
Отметим, что (5.3.1), (5.3.2), (5.3.3), (5.3.4)- различные виды записи одной и той же системы линейных уравнений.
Решением системы (5.3.1) называется любой упорядоченный набор действительных чисел 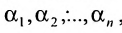 , который при подстановке в (5.3.1) вместо неизвестных
, который при подстановке в (5.3.1) вместо неизвестных 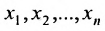 , обращает каждое из уравнений системы в верное равенство.
, обращает каждое из уравнений системы в верное равенство.
Система уравнений (5.3.1) называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений. Совместная система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.
Две системы уравнений с одинаковыми наборами неизвестных 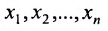 называются равносильными, если они имеют одно и то же множество решений.
называются равносильными, если они имеют одно и то же множество решений.
Отмстим, что для любой системы (5.3.1) возможны только три случая:
- система (5.3.1) имеет единственное решение;
- система (5.3.1) имеет бесчисленное множество решений;
- система (5.3.1) несовместна.
Множество всех решений системы (5.3.1) называется ее общим решением.
Решить систему (5.3.1) – значит найти ее общее решение.
Пример:
Пусть задана система
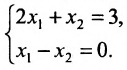
Тогда эту систему можно записать в матричном виде:
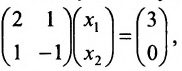
или в виде таблицы:

Система определенная, так как она имеет единственное решение 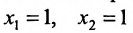 . Других решений быть не может, так как прямые
. Других решений быть не может, так как прямые
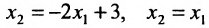 на координатной плоскости
на координатной плоскости 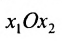 пересекаются в единственной точке.
пересекаются в единственной точке.
Экономические задачи, приводящие к системе линейных уравнений
Предположим, что производственные мощности для изготовления n различных видов продукции установлены в т цехах. Пусть 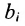 представляет собой суммарную мощность цеха i, и
представляет собой суммарную мощность цеха i, и 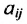 — часть производственного аппарата цеха i, которая необходима для производства единицы продукции вида j. Тогда обозначив через
— часть производственного аппарата цеха i, которая необходима для производства единицы продукции вида j. Тогда обозначив через 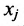 количество выпущенной продукции, получим систему уравнений, показывающих. как можно использовать имеющиеся мощности в полном объёме.
количество выпущенной продукции, получим систему уравнений, показывающих. как можно использовать имеющиеся мощности в полном объёме.
Широкий круг задач экономики приводит к составлению системы уравнений. Так в примере 4.3.2 составлялась система линейных уравнений (4.3.1) балансовой модели для трёх отраслей. В общем случае под балансовой моделью понимается система уравнений, каэ/сдое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.
При построении балансовых моделей используется понятие чистой (или технологической) отрасли, т.е. условной отрасли, объединяющей всё производство данного продукта независимо от ведомственной (административной) подчинённости и форм собственности предприятий и фирм. Всё народное хозяйство представляется в виде совокупности п отраслей, каждая из которых рассматривается как производящая и как потребляющая.
Если обозначить через:
то систему уравнений баланса можно записать в виде:

или в матричной форме:

где Х- вектор-столбец валовой продукции; Y- вектор-столбец конечной продукции; А – матрица коэффициентов прямых затрат.
Основу экономико-математической модели межотраслевого баланса составляет технологическая матрица А, содержащая коэффициенты прямых затрат на производство единицы продукции:
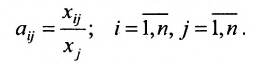
Коэффициент!,! прямых затрат являются довольно стабильной величиной во времени.
Переписав матричное уравнение (5.4.2) в виде EX-AX = Y или (E-A)X = Y, (5.4.3) получим стандартную форму записи системы уравнений.
Определение ранга матрицы
Рассмотрим прямоугольную матрицу (4.1). Если в этой матрице выделить произвольно 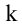 строк и
строк и 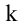 столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу
столбцов, то элементы, стоящие на пересечении выделенных строк и столбцов, образуют квадратную матрицу 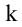 -го порядка. Определитель этой матрицы называется минором
-го порядка. Определитель этой матрицы называется минором 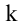 -го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел
-го порядка матрицы А. Очевидно, что матрица А обладает минорами любого порядка от 1 до наименьшего из чисел 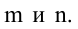 Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен
Среди всех отличных от нуля миноров матрицы А найдется по крайней мере один минор, порядок которого будет наибольшим. Наибольший из порядков миноров данной матрицы, отличных от нуля, называется рангом матрицы. Если ранг матрицы А равен 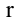 , то это означает, что в матрице А имеется отличный от нуля минор порядка
, то это означает, что в матрице А имеется отличный от нуля минор порядка 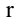 , но всякий минор порядка, большего чем
, но всякий минор порядка, большего чем 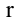 , равен нулю. Ранг матрицы А обозначается через
, равен нулю. Ранг матрицы А обозначается через 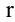 (А).
(А).
Очевидно, что выполняется соотношение
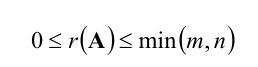
Ранг матрицы находится либо методом окаймления миноров, либо методом элементарных преобразований. При вычислении ранга матрицы первым способом следует переходить от миноров низших порядков к минорам более высокого порядка. Если уже найден минор D 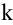 -го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (
-го порядка матрицы А, отличный от нуля, то требуют вычисления лишь миноры (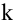 +1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен
+1)-го порядка, окаймляющие минор D, т.е. содержащие его в качестве минора. Если все они равны нулю, то ранг матрицы равен 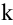 .
.
Элементарными называются следующие преобразования матрицы:
- перестановка двух любых строк (или столбцов),
- умножение строки (или столбца) на отличное от нуля число,
- прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.
Две матрицы называются эквивалентными, если одна из них получается из другой с помощью конечного множества элементарных преобразований.
Эквивалентные матрицы не являются, вообще говоря, равными, но их ранги равны. Если матрицы А и В эквивалентны, то это записывается так: А ~ В.
Канонической матрицей называется матрица, у которой в начале главной диагонали стоят подряд несколько единиц (число которых может равняться нулю), а все остальные элементы
равны нулю, например, 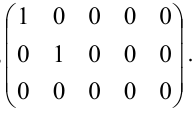
При помощи элементарных преобразований строк и столбцов любую матрицу можно привести к канонической. Ранг канонической матрицы равен числу единиц на ее главной диагонали.
- Заказать решение задач по высшей математике
Пример:
Найти методом окаймления миноров ранг матрицы 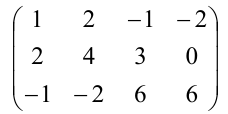
Решение:
Начинаем с миноров 1-го порядка, т.е. с элементов матрицы А. Выберем, например, минор (элемент) 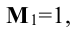 расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор
расположенный в первой строке и первом столбце. Окаймляя при помощи второй строки и третьего столбца, получаем минор 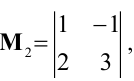 отличный от нуля.
отличный от нуля.
Переходим теперь к минорам 3-го порядка, окаймляющим 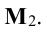 Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:
Их всего два (можно добавить второй столбец или четвертый). Вычисляем их:
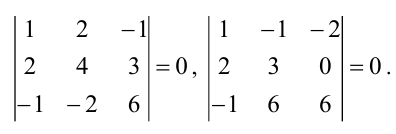
Таким образом, асе окаймляющие миноры третьего порядка оказались равными нулю. Ранг матрицы А равен двум.
Пример:
Найти ранг матрицы 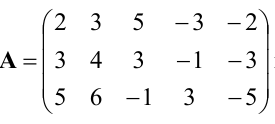 и привести ее к каноническому виду.
и привести ее к каноническому виду.
Решение:
Из второй строки вычтем первую и переставим эти строки: 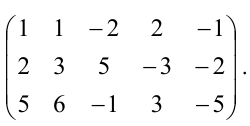
Теперь из второй и третьей строк вычтем первую, умноженную соответственно на 2 и 5: 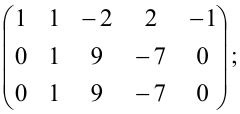
из третьей строки вычтем первую; получим матрицу 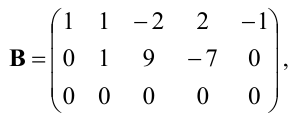 которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и
которая эквивалентна матрице А, так как получена из нее с помощью конечного множества элементарных преобразований. Очевидно, что ранг матрицы В равен 2, а следовательно, и 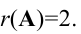 Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
Матрицу В легко привести к канонической. Вычитая первый столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы первой строки, кроме первого, причем элементы остальных строк не изменяются. Затем, вычитая второй столбец, умноженный на подходящие числа, из всех последующих, обратим в нуль все элементы второй строки, кроме второго, и получим каноническую матрицу:
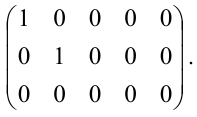
Вычисление ранга матрицы
Для исследования разрешимости систем линейных уравнений важную роль играет понятие ранга матрицы. Рассмотрим прямоугольную матрицу А 
Выделим k произвольных строк и k произвольных столбцов этой матрицы. Определитель k-го порядка, составленный из элементов матрицы А, расположенных на пересечении выделенных строк и столбцов, называется минором k-го порядка матрицы А.
Рангом матрицы А называется наибольший порядок ее миноров, отличных от нуля. Обозначение: rank А, 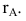
Базисным минором матрицы называется всякий отличный от нуля ее минор, порядок которого равен рангу матрицы.
Рассмотрим некоторые методы вычисления ранга матрицы.
Метод окаймляющих миноров
Минор порядка k+1, содержащий в себе минор порядка k, называется окаймляющим минором.
Вычисляя ранг матрицы, удобнее переходить от миноров меньших порядков к минорам больших порядков. Если найден минор k-го порядка, отличный от нуля, а все окаймляющие его миноры порядка k+1 равны нулю, то ранг матрицы равен k.
- Определители второго и третьего порядков и их свойства
- Метод Гаусса – определение и вычисление
- Прямая линия на плоскости и в пространстве
- Плоскость в трехмерном пространстве
- Кратный интеграл
- Ряды в математике
- Дифференциальные уравнения с примерами
- Обратная матрица – определение и нахождение
Содержание
Ранг
Ранг — это неотрицательное целое число!
Понятие ранга возникает естественным образом при решении систем линейных уравнений.
П
Пример. Решить систему уравнений
$$
left{
begin{array}{rrrl}
2x_1&-3x_2&-x_3=&3 \
4x_1&-3x_2&-5x_3=&6 \
6x_1&-6x_2&-6x_3=&9.
end{array}
right.
$$
Наблюдательный читатель сразу обратит внимание на «излишнесть» последнего уравнения: оно получается суммой двух первых, т.е. является их следствием. Таким образом, это уравнение можно спокойно выбросить из системы без ущерба для задачи. Приведенный пример тривиален, ситуации могут оказаться не такими очевидными.
П
Пример. Решить систему уравнений
$$
left{
begin{array}{rrrrl}
x_1&+2x_2&+3x_3&-x_4&=1 \
2x_1&+3x_2&+x_3&+x_4&=1 \
3x_1&+2x_2&+x_3&-x_4&=1 \
2x_1&+2x_2&+2x_3&-x_4&=1 \
5x_1&+5x_2&+2x_3& &=2. \
end{array}
right.
$$
Система является переопределенной: число неизвестных меньше числа определяющих их уравнений. Как правило, подобные системы решений не имеют (несовместны). Попробуем убедиться в этом применив для решения системы метод Гаусса.
$$
rightarrow
left{
begin{array}{rrrrr}
x_1&+2x_2&+3x_3&-x_4&=1 \
&-x_2&-5x_3&+3x_4&=-1 \
&-4x_2&-8x_3&+2x_4&=-2 \
&-2x_2&-4x_3&+x_4&=-1 \
&-5x_2&-13x_3&+5x_4 &=-3 \
end{array}
right.
quad rightarrow
$$
$$
rightarrow quad
left{
begin{array}{rrrrr}
x_1&+2x_2&+3x_3&-x_4&=1 \
&-x_2&-5x_3&+3x_4&=-1 \
&&12x_3&-10x_4&=2 \
&&6x_3&-5x_4&=1 \
&&12x_3&-10x_4 &=2 \
end{array}
right.
$$
Получившаяся система эквивалентна исходной (либо обе несовместны, либо обе имеют одинаковые решения). Однако в новой системе очевидно три последних уравнения фактически совпадают, и, таким образом, два из них можно безнаказанно выбросить из системы, не испортив ее множество решений. Получается, что исходная переопределенная система на самом деле «маскирует» систему «недоопределенную»:
$$
left{
begin{array}{rrrrr}
x_1&+2x_2&+3x_3&-x_4=&1 \
&-x_2&-5x_3&+3x_4=&-1 \
&&6x_3&-5x_4=&1,
end{array}
right.
$$
состоящую из уравнений в количестве меньшем, чем определяемые ими неизвестные. Как правило, такие системы совместны и имеют бесконечное множество решений. Так оно и получается в нашем примере. Фактически, мы привели уже систему к трапециевидному виду и осталось только извлечь из этого вида все множество решений обратным ходом метода Гаусса. Ответом в примере является множество1)
$$
x_1=frac{1+5t}{6}, x_2=frac{1-7t}{6}, x_3=frac{1+5t}{6},x_4=t quad npu quad forall t in mathbb R .
$$
Мы однако, обратим сейчас внимание на другое обстоятельство. Оказалось, что исходная система может быть сокращена на «излишние» уравнения — без ущерба для ее множества решений. Похоже, что в этой системе «реальных» уравнений всего три, а два оставшихся должны являться их следствиями. Так оно и есть: если сложить первое и третье уравнения системы, то поучится удвоенное четвертое, а если сложить второе и третье — получится пятое. Вывод: четвертое и пятое уравнения системы оказываются лишними.
♦
Задача. Для заданной системы линейных уравнений
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=b_1,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=b_2,\
dots & & & dots & \
a_{m1}x_1 &+a_{m2}x_2&+ ldots&+a_{mn}x_n &=b_m.
end{array} right.
$$
определить сколько в ней будет существенных уравнений.
Это искомое число и будет называться рангом. На самом деле, поставленная задача тут же усложняется: во-первых, интересует какие именно уравнения можно из системы выбросить, а какие нельзя, и, во-вторых, сколькими параметрами можно описать множество решений этой системы — если это множество бесконечно (как было в предыдущем примере). Оказывается, на оба эти вопроса тоже помогает ответить понятие ранга — как некоторой целочисленной характеристики системы уравнений.
К тому же понятию можно подойти с другой стороны.
П
Пример. Рассмотрим систему из последнего примера и перепишем ее в виде:
$$
x_1 underbrace{left( begin{array}{r} 1 \ 2 \ 3 \ 2 \ 5
end{array} right)}_{A_{[1]}} +
x_2 underbrace{left( begin{array}{r} 2 \ 3 \ 2 \ 2 \ 5
end{array} right)}_{A_{[2]}}+
x_3 underbrace{left( begin{array}{r} 3 \ 1 \ 1 \ 2 \ 2
end{array} right)}_{A_{[3]}} +
x_4 underbrace{left( begin{array}{r} -1 \ 1 \ -1 \ -1 \ 0
end{array} right)}_{A_{[4]}} =
underbrace{left( begin{array}{r} 1 \ 1 \ 1 \ 1 \ 2
end{array} right)}_{mathcal B} .
$$
Задачу решения системы уравнений можно переформулировать «на языке столбцов»: при заданных столбцах $ A_{[1]}, A_{[2]}, A_{[3]}, A_{[4]} $ и $ {mathcal B} $ подобрать такие числа $ x_1,x_2,x_3,x_4 $ чтобы сумма $ x_1 A_{[1]}+ x_2 A_{[2]}+ x_3 A_{[3]}+ x_4 A_{[4]} $ оказалась равной $ {mathcal B} $. Хотя это и нелегко увидеть, но тем не менее можно формально проверить, что столбец $ A_{[1]} $ можно выразить через $ A_{[2]}, A_{[3]}, A_{[4]} $ по формуле:
$$ A_{[1]} =frac{7}{5}A_{[2]}- A_{[3]}- frac{6}{5}A_{[4]} . $$
В результате система уравнений переписывается в виде
$$
left( x_2 + frac{7}{5} x_1 right) A_{[2]} + left( x_3 – x_1 right) A_{[3]}+
left( x_4 – frac{6}{5} x_1 right) A_{[4]} = mathcal B ,
$$
и получается, что она реально содержит только 3 переменные, именно
$$
y_2= x_2 + frac{7}{5} x_1, y_3=x_3 – x_1, y_4 = x_4 – frac{6}{5} x_1 .
$$
Если новая система
$$ y_2A_{[2]} + y_3 A_{[3]}+ y_4 A_{[4]}= mathcal B $$
имеет хотя бы одно решение относительно неизвестных $ y_2,y_3,y_4 $, то исходная система тоже будет совместной и иметь бесконечное число решений (за счет того, что при обратном переходе к неизвестным $ x_1, x_2, x_3, x_4 $ появляется неоднозначность за счет отсутствия ограничений на $ x_1 $).
♦
Задача. Для заданной системы линейных уравнений
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=b_1,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=b_2,\
dots & & & dots & \
a_{m1}x_1 &+a_{m2}x_2&+ ldots&+a_{mn}x_n &=b_m.
end{array} right.
$$
определить сколько в ней будет существенных неизвестных.
Это искомое число тоже будет называться рангом. Единство в названии разных объектов оказывается оправданным: это два подхода к одному и тому же понятию (в приведенных выше решениях примера именно так и оказалось — число существенных уравнений системы совпало с числом существенных переменных).
Для доказательства этого факта обратим сначала внимание на то обстоятельство, что мы, фактически действовали над коэффициентами системы уравнений, привлекая переменные только на самом последнем этапе. Так, в первом решении мы действовали только над строками матрицы коэффициентов, а во втором решении — только над ее столбцами.
Ранг системы строк (столбцов)
В настоящем и последующих пунктах мы будем рассматривать примеры и формулировать утверждения, ориентируясь на случай вещественных чисел, в частности, коэффициенты уравнений и искомые решения будем представлять во множестве $ mathbb R_{} $. Следует понимать, что все результаты будут справедливыми и для случая комплексных чисел.
В настоящем пункте мы, на время, отвлечемся от систем уравнений и рассмотрим множества строк ( $ 1 times N $-матриц) и столбцов ($ Ntimes 1 $-матриц) с числовыми (вещественными) элементами. Поскольку принципиальная разница между этими двумя объектами несущественна, мы будем говорить
обобщенно о рядах, имея в виду каждый раз что-то определенное: либо строки
$ A^{[1]}, A^{[2]},dots $ либо столбцы $ A_{[1]}, A_{[2]}, dots $
Рассмотрим систему2) $ n_{} $ рядов (строк или столбцов)
$$
{ A_1,dots,A_n } .
$$
Выражение
$$
alpha_1A_1+dots+alpha_nA_n
$$
при фиксированных числах $ alpha_1,dots,alpha_n $ называется линейной комбинацией рядов $ A_1,dots,A_n $. Множество всевозможных линейных комбинаций рядов $ A_1,dots,A_n $ называется их линейной оболочкой:
$$
mathcal L(A_1,dots,A_n)=left{ alpha_1A_1+dots+alpha_nA_n big| {alpha_1,dots,alpha_n} subset mathbb R right}.
$$
Система рядов $ { A_1,dots,A_n } $ называется линейно зависимой (л.з.) если существуют числа
$ alpha_1,dots,alpha_n $, хотя бы одно из которых отлично от нуля, такие что
$$
alpha_1A_1+dots+alpha_nA_n=mathbb O .
$$
Если же последнее равенство возможно только при $ alpha_1=0,dots, alpha_n=0 $,
то система рядов называется линейно независимой (л.н.з.).
Т
Теорема 1. а) Если система $ { A_1,dots,A_n } $ содержит хотя бы один нулевой ряд, то она л.з.
б) Если система $ { A_1,dots,A_n } $ л.н.з., то и любая ее подсистема л.н.з.
в) При $ n>1 $ система $ { A_1,dots,A_n } $ л.з. тогда и только тогда,
когда по меньшей мере один ее ряд линейно выражается через остальные,
т.е. существуют $ jin mathbb N $ и константы $ gamma_1,dots,gamma_{j-1},
gamma_{j+1},dots,gamma_{n} $ такие, что
$$ A_j=gamma_1A_1+dots+gamma_{j-1}A_{j-1}+
gamma_{j+1}A_{j+1}+dots + gamma_{n}A_{n} .$$
П
Пример. Найти все значения параметра $ color{Red}{lambda} $, при которых строка $ B=(7,-2,{color{Red}{lambda}} ) $ выражается через строки
$$A_1=(2,3,5), A_2=(3,7,8), A_3=(1,-6,1) .$$
Решение. Составим уравнение
$ B=gamma_1A_1+gamma_2A_2+gamma_3A_3 $
и попытаемся подобрать неопределенные параметры $ gamma_j $ ему удовлетворяющие.
$$
left{
begin{array}{rrrrr}
2gamma_1&+3gamma_2&+gamma_3=&7 \
3gamma_1&+7gamma_2&-6gamma_3=&-2 \
5gamma_1&+8gamma_2&+gamma_3=& color{Red}{lambda}
end{array}right.
$$
Мы получили систему линейных уравнений для определения неизвестных постоянных $ gamma_1,gamma_2, gamma_3 $. Решаем ее по методу Гаусса:
$$
left{
begin{array}{rrrrc}
gamma_1&+4gamma_2&-7gamma_3=&-9, \
&gamma_2&-3gamma_3=&-5, \
&&0=&{color{Red}{lambda}} -15.
end{array}right.
$$
Последнее уравнение обращается в истинное равенство только при $ lambda=15 $. При этом значении параметра система уравнений будет совместна. Например, одним из решений будет
$ gamma_1=6, gamma_2=-2,gamma_3=1 $.
Ответ. $ {color{Red}{lambda}} =15 $.
Т
Теорема 2. Если каждый из рядов системы $ { A_1,dots,A_n } $ линейно
выражается через ряды системы $ {B_1,dots,B_k } $ и при этом во второй системе рядов меньше, чем в первой, т.е. $ k<n $, то первая система будет линейно зависимой.
Доказательство
☞
ЗДЕСЬ.
Рангом системы рядов $ { A_1,dots,A_n } $ называется число рядов в ее максимальной линейно независимой подсистеме:
$$mathfrak{r}=operatorname{rank} { A_1,dots,A_n } ;$$
дополнительно полагают, что ранг системы, состоящей только из нулевых рядов, равен нулю:
$$ operatorname{rank} {mathbb O,dots,mathbb O} = 0 . $$
Т
Теорема 3. Ранг системы рядов $ { A_1,dots,A_n } $ равен $ mathfrak{r}ge 1 $ тогда и только тогда, когда в этой системе существует $ mathfrak{r} $ линейно независимых рядов, через которые выражается каждый ряд системы.
Эта теорема позволяет дать другое определение ранга.
Рангом системы рядов $ { A_1,dots,A_n } $ называется число $ mathfrak{r}_{} $
таких линейно независимых рядов системы, через которые линейно выражается каждый ряд системы.
Любая совокупность $ mathfrak{r} $ линейно независимых рядов
системы $ { A_1,dots,A_n } $ ранга $ mathfrak{r}ne 0 $ называется базисом этой системы.
Т
Теорема 4. При фиксированном базисе системы $ { A_1,dots,A_n } $ любой ряд из ее линейной оболочки $ mathcal L(A_1,dots,A_n) $ представúм в виде линейной комбинации базисных рядов и такое представление единственно.
Доказательство первой части тривиально. Докажем единственность представления. Предположим, для упрощения записи индексов, что базисными рядами являются первые $ mathfrak r_{} $ рядов системы, т.е.
$ {A_1,dots, A_{mathfrak r_{}} } $. Если какой-то ряд $ X in mathcal L(A_1,dots,A_n) $ имеет два представления в виде линейной комбинации базисных рядов:
$$ X=x_1A_1+dots+ x_{mathfrak r_{}}A_{mathfrak r_{}}=y_1A_1+dots+ y_{mathfrak r_{}}A_{mathfrak r_{}} , $$
то получаем
$$ (x_1-y_1)A_1+dots+ (x_{mathfrak r_{}}-y_{mathfrak r_{}})A_{mathfrak r_{}}= mathbb O . $$
Первая возможность: ряды $ {A_1,dots, A_{mathfrak r_{}} } $ линейно зависимы, но тогда это противоречит предположению. Следовательно, остается единственная возможность:
$$ x_1=y_1,dots, x_{mathfrak r_{}}=y_{mathfrak r_{}} . $$
♦
Представление ряда $ X in mathcal L(A_1,dots,A_n) $ в виде линейной комбинации базисных рядов
$ {A_{j_1},dots, A_{j_{mathfrak r_{}}} } $
называется разложением ряда по данному базису; числа из линейной комбинации
$$X= x_1A_{j_1}+dots+ x_{mathfrak r_{}} A_{j_{mathfrak r_{}}} $$
называются координатами ряда $ X_{} $ в данном базисе. Предыдущая теорема утверждает, что при фиксированном базисе, координаты любого ряда $ X in mathcal L(A_1,dots,A_n) $ определяются единственным образом. Справедливо и обратное: задав набор (ряд) чисел $ {x_j} $ в количестве, совпадающем с количеством базисных рядов, мы однозначно определим ряд из $ mathcal L(A_1,dots,A_n) $.
Т
Теорема 5. Любую линейно независимую подсистему
$$
{ A_{i_1},A_{i_2},dots,A_{i_k} }
$$
системы рядов $ { A_1,dots,A_n } $ можно дополнить до базиса этой системы.
П
Пример. Найти какой-нибудь базис системы строк
$$A_1=(5,2,-3,1), A_2=(4,1,-2,3), A_3=(1,1,-1,-2), A_4=(3,4,-1,2)$$
и все строки системы, не входящие в этот базис, выразить через
базисные.
Решение. Воспользуемся предыдущей теоремой. Строка $ A_1 $ ненулевая,
возьмем ее в качестве первой строки искомого базиса и попытаемся дополнить
оставшимися строками до базиса. Если $ operatorname{rank}=1 $, то
все оставшиеся строки должны линейно выражаться через $ A_1 $, в частности
$ A_2=gamma A_1 $ при подходящем числе $ gamma $. Однако система линейных
уравнений
$$4=5 gamma, 1=2gamma, -2=-3gamma, 3=gamma$$
несовместна, так что предположение неверно. Итак, $ mathfrak{r}>1 $ и строки $ A_1,A_2 $
л.н.з.
Если $ operatorname{rank}=2 $, то строки $ A_3,A_4 $ должны линейно выражаться
через $ A_1,A_2 $. Из двух составленных систем уравнений:
$$
left{
begin{array}{rrrr}
5gamma_1&+4gamma_2=&1 \
2gamma_1&+ gamma_2=&1 \
-3gamma_1&-2gamma_2=&-1 \
gamma_1&+3gamma_2=&-2
end{array}right. quad u quad
left{
begin{array}{rrrr}
5gamma_1&+4gamma_2=&3 \
2gamma_1&+ gamma_2=&4 \
-3gamma_1&-2gamma_2=&-1 \
gamma_1&+3gamma_2=&2
end{array}right.
$$
первая совместна и имеет решение $ gamma_1=1,gamma_2=-1 $; вторая же
несовместна. Итак, $ operatorname{rank} >2 $ и строки $ A_1,A_2,A_4 $ л.н.з.
В системе осталась только одна строка $ A_3 $, но поскольку уже установлена
ее линейная зависимость от $ A_1,A_2 $, то ее включение в уже построенную
подсистему не может увеличить ранга.
Ответ. Базис системы составляют, например, строки $ A_1,A_2,A_4 $;
при этом $ A_3=A_1-A_2 $.
Установим теперь, какие действия над системой не изменяют ее ранга.
Т
Теорема 6. Если систему дополнить
рядом, линейно выражающимся через ряды системы, то ранг системы
не изменится. Точно так же ранг системы не меняется при удалении
ряда, линейно выражающегося через остальные ряды системы.
=>
Если каждый из рядов системы $ { A_1,dots,A_n } $ линейно
выражается через ряды системы $ {B_1,dots,B_k } $, то
$$operatorname{rank} { A_1,dots,A_n }le operatorname{rank} { B_1,dots,B_k } , . $$
Результат последней теоремы можно усилить, введя следующее определение.
Элементарными преобразованиями системы рядов
называются следующие
-
перестановка местами двух любых рядов;
-
умножение ряда на число $ cne 0 $;
-
прибавление к одному ряду любого другого ряда.
Т
Теорема 7. Элементарные преобразования не меняют ранга системы рядов.
Ранг матрицы
определяется для произвольной (не обязательно квадратной) матрицы $ A_{} $ как наибольший порядок ее отличных от нуля миноров. Иначе говоря: $ operatorname{rank} (A)_{} ={mathfrak r}in {mathbb N} $ тогда и только тогда, когда существует ее минор порядка $ {mathfrak r}_{} $, отличный от нуля, а все миноры более высокого порядка равны нулю. Кроме того, полагают: $ operatorname{rank} ({mathbb O}_{mtimes n}) = 0_{} $.
Матрицу $ A_{} $ порядка $ mtimes n_{} $ можно рассматривать как состоящую из набора своих строк или набора своих столбцов. Так, например:
$$
A= left[ A_{[1]}mid A_{[2]} mid dots mid A_{[m]} right] quad npu quad
A_{[j]}=left(begin{array}{c} a_{1j} \ a_{2j} \ vdots \ a_{mj} end{array} right) ;
$$
здесь $ mid_{} $ означает конкатенацию. В следующем пункте мы покажем тождественность определения ранга матрицы определению ранга системы составляющих ее рядов (строк или столбцов).
Метод окаймляющих миноров
Очевидно, что если все миноры порядка $ mathfrak{r}+1 $ для матрицы $ A_{m times n} $ равны нулю,
то и все миноры бóльшего порядка должны быть равны нулю. Но, оказывается,
для проверки условия $ operatorname{rank} (A) =mathfrak{r} $ нет необходимости вычислять и
все миноры порядка $ mathfrak{r}+1 $.
Для произвольного минора матрицы $ A_{} $ порядка $ k< min (m,n) $
$$Aleft( begin{array}{llll}
alpha_1 & alpha_2 & dots & alpha_k \
beta_1 & beta_2 & dots & beta_k
end{array}
right) npu
quad
left{begin{array}{lllll}
1le &alpha_1 <&alpha_2 <& dots < alpha_k & le m \
1le &beta_1 <&beta_2 <& dots < beta_k & le n.
end{array}
right.
$$
его окаймляющим минором называется минор $ (k+1)_{} $-го порядка, получающийся приписыванием еще одной строки и одного столбца:
$$Aleft( begin{array}{lllll}
alpha_1 & alpha_2 & dots & alpha_k & alpha_{k+1}\
beta_1 & beta_2 & dots & beta_k & beta_{k+1}
end{array}
right) npu
quad alpha_{k+1}ne alpha_{j}, beta_{k+1}ne beta_{j} .
$$
П
Пример. Для $ 6times 7 $-матрицы окаймление минора с элементами, выделенными зелеными звездами ( т.е. при $ alpha_1=2, alpha_2=3 $ , $ alpha_3=6, beta_1=3,beta_2=4,beta_3=6 $),

возможно любым из способов, отраженным на схеме красными квадратами:

Т
Теорема [Кронекер]. Если матрица $ A_{} $ имеет некоторый минор порядка $ mathfrak r $ отличным от нуля, а все окаймляющие этот минор миноры порядка
$ mathfrak r+1 $ равны нулю, то $ operatorname{rank} (A) =mathfrak{r} $.
Доказательство
☞
ЗДЕСЬ.
Метод окаймляющих миноров вычисления ранга матрицы
1.
Ищем минор первого порядка (т.е. элемент матрицы $ a_{jk}^{} $), отличный от нуля (если такого нет, то $ operatorname{rank} (A)=0_{} $);
2.
ищем минор второго порядка, содержащий $ a_{jk}^{} $ и отличный от нуля:
$$ A left( begin{array}{cc}
j & j_2 \
k & k_2
end{array}
right)=
left| begin{array}{cc}
a_{jk} & a_{jk_2} \
a_{j_2k} & a_{j_2k_2}
end{array}
right| $$
(если такого нет, то $ operatorname{rank} (A)=1_{} $ );
3.
продолжаем процесс окаймления до тех пор, пока не найдем такой минор $ mathfrak{r}_{} $-го порядка, который сам отличен от нуля, а все окаймляющие его $ (mathfrak{r}+1)^{} $-го порядка равны нулю. Тогда $ operatorname{rank} (A)=mathfrak{r}^{} $.
=>
Ранг матрицы равен рангу системы ее строк (и рангу системы ее столбцов).
Доказательство. Пусть $ operatorname{rank} (A)=mathfrak{r} $. Тогда, по определению, существует
по крайней мере один минор $ mathfrak{r} $-го порядка, отличный от нуля, а все миноры более высокого порядка (если такие имеются) равны нулю. Отсюда, в частности, следует, что все миноры $ (mathfrak{r}+1) $-го порядка,
окаймляющие данный, равны нулю. По теореме Кронекера ранг системы
строк (столбцов) равен $ mathfrak{r} $, т.е. равен $ operatorname{rank} (A) $.
П
Пример. Вычислить ранг матрицы
$$
left( begin{array}{rrrrr}
3 & 4 & -1 &5& -2 \
1 & 5 & -2 &3& 4 \
2 & -1 & 1 &2& 3 \
3 & -7 & 4 &1& -7 \
0 & 11 & -5 &4& -4
end{array}
right).
$$
Решение. Для проверки условия $ mathfrak{r}_{}>0 $ достаточно найти хотя бы один ненулевой элемент матрицы:
$$
left( begin{array}{rrrrr}
3 & * & * &*& * \
ast & * & * &*& * \
ast & * & * &*& * \
ast & * & * &*& * \
ast & * & * &*& *
end{array}
right) .
$$
Далее, для проверки условия $ mathfrak{r}_{}>1 $ пытаемся подобрать ненулевой
минор второго порядка, окаймляя выбранный минор первого порядка:
$$
left( begin{array}{rrrrrr}
3 & 4 & & * &*& * \
1 & 5 & & * &*& * \
ast & * & & * &*& * \
ast & * & &* &*& * \
ast & * & &* &*& *
end{array}
right).
$$
Из всех окаймляющих этот минор миноров третьего порядка:
$$
left( begin{array}{rrrrr}
3 & 4 & -1 &*& * \
1 & 5 & -2 &*& * \
2 & -1 & 1 & * &*\
ast & * & * &*& * \
ast & * & * &*& *
end{array}
right),
left( begin{array}{rrrrr}
3 & 4 & -1 &*& * \
1 & 5 & -2 & * & * \
ast & * & * &*& * \
3 & 7 &4 &*& * \
ast & * & * &*& *
end{array}
right),
left( begin{array}{rrrrr}
3 & 4 & -1 &*& * \
1 & 5 & -2 & * & * \
ast & * & * &*& * \
ast & * & * &*& * \
0 & 11 & -5 & * &* \
end{array}
right),
$$
$$
left( begin{array}{rrrrr}
3 & 4 & * &5& * \
1 & 5 & * &3& * \
2 & -1 & * &2 & * \
ast & * & * &*& * \
ast & * & * &*& *
end{array}
right),
left( begin{array}{rrrrr}
3 & 4 & * &5& * \
1 & 5 & * &3& * \
ast & * & * &*& * \
3 & -7 & * &1& * \
ast & * & * &*& *
end{array}
right),
left( begin{array}{rrrrr}
3 & 4 & * &5& * \
1 & 5 & * &3& * \
ast & * & * &*& * \
ast & * & * &*& * \
0 &11 & * & 4& * \
end{array}
right),
$$
$$
left( begin{array}{rrrrr}
3 & 4 & * &*& -2 \
1 & 5 & * &*&4 \
2 & -1 & * &*&3 \
ast & * & * & * & * \
ast & * & * & * & *
end{array}
right),
left( begin{array}{rrrrr}
3 & 4 & * &* & -2 \
1 & 5 & * &* &4 \
ast & * & * & *& * \
3 & -7 & * &*&-7 \
ast & * & * & * & *
end{array}
right),
left( begin{array}{rrrrr}
3 & 4 & * &*& -2 \
1 & 5 & * &*&4 \
ast & * & * &*& * \
ast & * & * &*& * \
0 & 11 & * &*&-4 \
end{array}
right)
$$
два последних отличны от нуля. (Подчеркнем: нас интересовал
хотя бы один отличный от нуля минор; если бы нам повезло его угадать
сходу, то не нужно было бы вычислять все остальные миноры третьего
порядка.) Это означает, что $ mathfrak{r}_{}ge 3 $.
Окаймляем какой-нибудь из ненулевых миноров третьего порядка.
Оказывается, что все $ 4_{} $ минора четвертого порядка равны нулю.
Ответ. Ранг матрицы равен $ 3_{} $.
?
Найти ранги матриц
$$
{mathbf a)} left( begin{array}{ccccc}
color{Red}{alpha} & 1 & 1 & 1 & 1\
1 & color{Red}{alpha} & 1 & 1 & 1\
1 & 1 & color{Red}{alpha} & 1 & 1\
1 & 1 & 1 & color{Red}{alpha} & 1
end{array}
right) , quad {mathbf b)} left( begin{array}{rrrrr}
color{Red}{alpha} & 1 & 3 & 4 & 1\
1 & color{Red}{alpha} & -1 & 1 & 5\
lambda & color{Red}{alpha} & 4 & 3 & -4\
1 & 1 & 7 & 7 & -3
end{array}
right)
$$
в зависимости от значений параметра $ color{Red}{alpha} $.
Ответ.
$ {mathbf a)} mathfrak{r}_{}=1 $ при $ color{Red}{alpha} =1 $, и $ mathfrak{r}_{}=4 $ при $ color{Red}{alpha} ne 1 $;
$ {mathbf b)} mathfrak{r}_{}=3 $ при $ color{Red}{alpha} =1 $ или $ color{Red}{alpha} =1/4 $, и $ mathfrak{r}_{}=4 $ при $ color{Red}{alpha} ne 1 $ или $ color{Red}{alpha} ne 1/4 $.
Любой отличный от нуля минор матрицы $ A $ порядка $ mathfrak{r}= operatorname{rank} (A) $ называется базисным минором этой матрицы. Строки (столбцы) матрицы $ A $, из элементов которых этот минор составлен, образуют базис системы строк (столбцов) матрицы.
Метод элементарных преобразований
Этот метод основан на последней теореме из
☞
ПУНКТА: элементарные преобразования системы строк матрицы не изменяют ее ранга. Поэтому имеет смысл преобразовать исходную систему к такому виду, для которого величина ранга будет очевидна.
1.
Ищем ненулевой элемент матрицы $ a_{jk}^{} $ (если такого нет, то $ operatorname{rank} (A_{})=0 $);
2.
перестановкой строк и столбцов матрицы, добиваемся, чтобы ненулевой элемент $ a_{jk}^{} $ попал в левый верхний угол;
3.
применяя метод исключения Гаусса, добиваемся, чтобы все элементы первого столбца полученной матрицы, кроме верхнего, обратились в нуль;
4.
к полученной в результате исключения подматрице порядка $ (m-1)times (n-1) $ применяем процедуры пунктов
1-3
.
Процесс заканчивается, когда матрица оказывается приведенной к виду:
$$
left( begin{array}{lllllll}
b_{11} & b_{12} & dots & b_{1{mathfrak r}} & b_{1,{mathfrak r}+1} & dots & b_{1n} \
0 & b_{22} & dots & b_{2{mathfrak r}} & b_{2,{mathfrak r}+1} & dots & b_{2n} \
vdots & & ddots & & & & vdots \
0 & 0 & dots & b_{{mathfrak r}{mathfrak r}} & b_{{mathfrak r},{mathfrak r}+1} & dots &
b_{{mathfrak r}n} \
0 & 0 & dots & 0 & 0 & dots & 0 \
vdots & & & & & & vdots \
0 & 0 & dots & 0 & 0 & dots & 0
end{array}
right) quad npu quad b_{11}ne 0,b_{22}ne 0,dots,b_{{mathfrak r}{mathfrak r}}ne 0.
$$
Тогда $ operatorname{rank} ={mathfrak r}_{} $ (числу оставшихся ненулевых строк).
П
Пример. Вычислить ранг матрицы
$$
left( begin{array}{rrrrr}
2 & 3 & 5 &-3& -2 \
3 & 4 & 3 &-1& -3 \
5 & 6 & -1 &3& -5
end{array}
right).
$$
Решение. Элементарными преобразованиями строк матрицы, приводим ее к трапециевидной (ступенчатой):
$$
rightarrow
left( begin{array}{rrrrr}
2 & 3 & 5 &-3& -2 \
1 & 1 & -2 &2& -1 \
5 & 6 & -1 &3& -5
end{array}
right) rightarrow
left( begin{array}{rrrrr}
1 & 1 & -2 &2& -1 \
2 & 3 & 5 &-3& -2 \
5 & 6 & -1 &3& -5
end{array}
right) rightarrow
$$
$$
rightarrow
left( begin{array}{rrrrr}
1 & 1 & -2 &2& -1 \
0 & 1 & 9 &-7& 0 \
0 & 1 & 9 &-7& 0
end{array}
right)
rightarrow
left( begin{array}{rrrrr}
1 & 1 & -2 &2& -1 \
0 & 1 & 9 &-7& 0 \
0 & 0 & 0 &0& 0
end{array}
right).
$$
Получили две ненулевые строки.
Ответ. Ранг матрицы равен $ 2_{} $.
?
Найти ранги матриц по методу элементарных преобразований:
$$
{mathbf a)} left( begin{array}{rrrr}
17 & 51 & 27 & 31\
93 & 25 & 14 & 121\
94 & 27 & 15 & 120\
18 & 53 & 28 & 30
end{array}
right), quad
{mathbf b)}
left( begin{array}{rrrrrr}
8 & 5 & 3 & 7 & 1& 2\
4 & 6 & 7 & 9 & 11& 12\
3 & 0 & -1 & 2 & 7& 1\
15 & 11 & 9 & 13 & 19& 15\
17 & 10 & 2 & -5 & 6& 3
end{array}
right) .
$$
Матрицы ранга 1
Простейшими ненулевыми матрицами являются матрицы ранга $ 1_{} $ или одноранговые матрицы. Вид их довольно прост: все их столбцы (строки) должны быть пропорциональны.
П
Пример.
$$
left(begin{array}{rrr}
1 & -5 & – 3 \
2 & -10 & -6 \
-1 & 5 & 3 \
1/2 & -5/2 & -3/2
end{array}
right) ; quad
left(begin{array}{rrrr}
1 & -5 & – 3 & -18\
0 & 0 & 0 & 0\
-2 & 10 & 6 & 36
end{array}
right) ; quad
left(begin{array}{rrrr}
0 & 1 \
0 & 0
end{array}
right) .
$$
Т
Теорема. $ operatorname{rank}(A_{mtimes n}) = 1 $ тогда и только тогда, когда матрицу $ A_{} $ можно представить в виде произведения
$$ A= left(begin{array}{c}
u_1\
u_2\
vdots \
u_m
end{array}
right) (v_1,dots,v_n)=left[u_jv_kright]_{j=1,dots,m;k=1,dots,n} $$
при хотя бы одной паре индексов $ j_{} $ и $ k_{} $ таких, что $ u_jne 0, v_k ne 0 $.
Т
Теорема. Любая матрица ранга $ mathfrak r_{} $ может быть представлена в виде суммы $ mathfrak r_{} $ матриц ранга $ 1_{} $, но не может быть представлена в виде суммы меньшего числа матриц ранга $ 1_{} $.
П
Пример. Представить матрицу
$$
left(begin{array}{rrr}
3 & 2 & 5 \
2 & 3 & 4 \
-5 & 0 & -7 \
1 & 4 & 1
end{array}
right)
$$
в виде суммы матриц ранга $ 1_{} $.
Решение.
$$
left(begin{array}{rrr}
3 & 2 & 5 \
2 & 3 & 4 \
-5 & 0 & -7 \
1 & 4 & 1
end{array}
right) =
left(begin{array}{rrr}
3 & 2 & 5 \
0 & 0 & 0 \
0 & 0 & 0 \
0 & 0 & 0
end{array}
right)+
left(begin{array}{rrr}
0 & 0 & 0 \
2 & 3 & 4 \
0 & 0 & 0 \
0 & 0 & 0
end{array}
right)+left(begin{array}{rrr}
0 & 0 & 0 \
0 & 0 & 0 \
-5 & 0 & -7 \
0 & 0 & 0
end{array}
right)+
left(begin{array}{rrr}
0 & 0 & 0 \
0 & 0 & 0 \
0 & 0 & 0 \
1 & 4 & 1
end{array}
right)
$$
и каждая матрица в правой части имеет ранг $ 1_{} $. Ранг исходной матрицы равен $ 3_{} $, с ненулевым минором
$$
left|begin{array}{rrr}
3 & 2 & 5 \
2 & 3 & 4 \
1 & 4 & 1
end{array}
right| .
$$
Следовательно третья строка матрицы может быть выражена в виде линейной комбинации оставшихся:
$$
(-5, 0, -7)=-3cdot (3,2,5)+2 cdot (2,3,4) .
$$
Поэтому
$$
left(begin{array}{rrr}
3 & 2 & 5 \
2 & 3 & 4 \
-5 & 0 & -7 \
1 & 4 & 1
end{array}
right) =
left(begin{array}{rrr}
3 & 2 & 5 \
0 & 0 & 0 \
-9 & -6 & -15\
0 & 0 & 0
end{array}
right)+
left(begin{array}{rrr}
0 & 0 & 0 \
2 & 3 & 4 \
4 & 6 & 8 \
0 & 0 & 0
end{array}
right)+
left(begin{array}{rrr}
0 & 0 & 0 \
0 & 0 & 0 \
0 & 0 & 0 \
1 & 4 & 1
end{array}
right) .
$$
♦
Представление матрицы в виде суммы матриц ранга $ 1 $ возможно разными способами. Так, к примеру, симметричная матрица $ A_{} $ всегда может быть представлена в виде суммы симметричных же одноранговых матриц:
$$
left(begin{array}{rrr}
2 & 2 & -1 \
2 & -1 & 2 \
-1& 2 & 2
end{array}
right)=
$$
$$
=left(begin{array}{rrr}
-1/2 & 1 & -1/2 \
1 & -2 & 1 \
-1/2& 1 & -1/2
end{array}
right)+
left(begin{array}{rrr}
3/2 & 0 & -3/2 \
0 & 0 & 0 \
-3/2& 0 & 3/2
end{array}
right)+
left(begin{array}{rrr}
1 & 1 & 1 \
1 & 1 & 1 \
1 & 1 & 1
end{array}
right) , .
$$
Исключительное прикладное значение имеет разложение произвольной матрицы $ A_{mtimes n} $ в сумму одноранговых матриц, известное как сингулярное разложение (singular value decomposition,SVD).
Применение для решения систем линейных уравнений
Рассмотрим снова общую систему линейных уравнений
$$
left{
begin{array}{lllll}
a_{11}x_1 &+a_{12}x_2&+ ldots&+a_{1n}x_n &=b_1,\
a_{21}x_1 &+a_{22}x_2&+ ldots&+a_{2n}x_n &=b_2,\
dots & & & dots & \
a_{m1}x_1 &+a_{m2}x_2&+ ldots&+a_{mn}x_n &=b_m.
end{array} right.
$$
Матрица, получающаяся конкатенацией матрицы $ A_{} $ и столбца правых частей $ {mathcal B}_{} $ этой системы, т.е.
$$
[A|{mathcal B}] =
left(
begin{array}{rrrrl}
a_{11} & a_{12} & dots & a_{1n} & b_1 \
a_{21} & a_{22} & dots & a_{2n} & b_2 \
dots &&& & dots \
a_{m1} & a_{m2} & dots & a_{mn} & b_m
end{array}
right)_{mtimes (n+1)}
$$
называется расширенной матрицей системы линейных уравнений.
Т
Теорема [Кронекер, Капелли]. Система совместна тогда и только тогда, когда ранг матрицы этой системы совпадает с рангом ее расширенной матрицы:
$$ operatorname{rank}(A) = operatorname{rank} [A|{mathcal B}] . $$
При выполнении этого условия, система имеет единственное решение, если число неизвестных $ n_{} $ совпадает с общим значением ранга $ mathfrak r_{} $, и бесконечное множество решений, если $ n > mathfrak r_{} $.
§
Более подробно изложено
☞
ЗДЕСЬ
Неравенства для ранга
Т
Теорема 1. Для любых матриц $ A_{} $ и $ B_{} $ одинакового порядка имеет место неравенство:
$$
operatorname{rank} (A + B) le operatorname{rank} (A) + operatorname{rank} (B) .
$$
Т
Теорема 2. Для любых матриц
$ A_{mtimes n}^{} $ и $ B_{ntimes ell}^{} $ имеет место неравенство Сильвестра:
$$
operatorname{rank} (A) + operatorname{rank} (B) – n le operatorname{rank} (AB) le min (operatorname{rank} (A), operatorname{rank} (B)) .
$$
=>
Если $ A_{} $ и $ B_{} $ — квадратные матрицы $ n_{} $-го
порядка и $ det B ne 0_{} $, то
$$ operatorname{rank} (AB) = operatorname{rank} (A)^{} , .$$
Ранг симметричной матрицы
Ранг квадратичной формы
определяется
☞
ЗДЕСЬ.
Ранг линейного отображения
рассматривается
☞
ЗДЕСЬ.
Задачи
Источники
[1]. Бохер М. Введение в высшую алгебру. М.-Л. ГТТИ, 1933
[2]. Kronecker L. Bemerkungen zur Determinanten-Theorie. J. reine angew. Math. Bd. 72, 1870, S. 152-175
