Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2023 года; проверки требуют 2 правки.
Ма́трицей поворо́та (или матрицей направляющих косинусов) называется ортогональная матрица[1], которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в двумерном пространстве[править | править код]
В двумерном пространстве поворот можно описать одним углом 
- или
.
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
Координаты (x′,y′) в результате поворота точки (x, y) имеют вид:
Конкретные знаки в формулах зависят от того, является ли система координат правосторонней или левосторонней, и выполняется ли вращение по или против часовой стрелки. Верхний знак указан для обычного соглашения: правосторонняя система координат и положительное направление вращения против часовой стрелки (тот же знак верен для левосторонней координатной системы при выборе положительного направления вращения по часовой стрелке; в оставшихся двух комбинациях — нижний знак).
Матрица поворота в трёхмерном пространстве[править | править код]
Любое вращение в трёхмерном пространстве может быть представлено как композиция поворотов вокруг трёх ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трёх матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол 
- Вращение вокруг оси
:
- Вращение вокруг оси
:
- Вращение вокруг оси
:
- Матрица поворота последовательности поворотов в некотором оговорённом порядке:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси[2]. Например, при повороте на угол 






Матрица поворота в n-мерном пространстве[править | править код]
Совершенно аналогично могут быть записаны матрицы поворота конечномерного пространства любой более высокой размерности.
Надо только иметь в виду, что для размерностей пространства, не равных трём, невозможно указать единственную прямую, ортогональную двум данным прямым, а поэтому нельзя говорить о вращении вокруг какой-то оси, можно же говорить о вращении в какой-то плоскости[3]. Все точки при повороте в пространстве любой размерности, начиная с 2, всегда движутся параллельно некоторой (двумерной) плоскости.
Итак, аналогично трёхмерному случаю (с приведенной оговоркой) можем написать матрицу поворота в любой координатной плоскости для любой размерности пространства.
Например:
— матрица поворота в 5-мерном пространстве в плоскости 
— матрица поворота в 7-мерном пространстве в плоскости 
Изменение оси поворота[править | править код]
Пусть 




где 

где 

Перестановочность поворотов[править | править код]
Если 





то 


При этом последовательность поворотов можно поменять, видоизменив поворот 
где матрица 



поскольку 

Выражение матрицы поворота через углы Эйлера[править | править код]
Последовательные повороты около осей 



Ось 







.
В случае, если повороты задаются в другой последовательности, матрица поворота находится перемножением матриц для вращения вокруг соответствующих декартовых осей координат, например:
- 1) Поворот около осей:
- 2) Соответственно:
- 3)
- 4)
- 5)
- 6)
- 7)
- 8)
- 9)
- 10)
- 11)
- 12)
Матрица поворота вокруг произвольной оси[править | править код]
Пусть ось вращения задана единичным вектором 

Тогда матрица поворота в декартовых координатах имеет вид:
Выражение матрицы поворота через кватернион[править | править код]
Если задан кватернион 
Свойства матрицы поворота[править | править код]
Если 


Примечания[править | править код]
См. также[править | править код]
- Матрица перехода
- Поворот
Литература[править | править код]
- Лурье А. И. Аналитическая механика. — М.:Физматлит. — 1961. — 824 с.
Ссылки[править | править код]
- Поворот плоскости. Матрица поворота
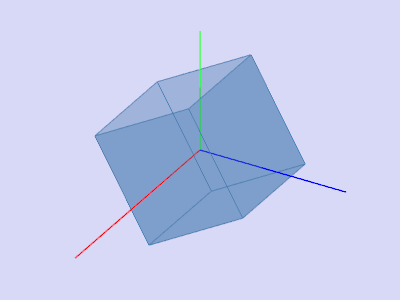
Вращение фигуры в 3-х мерном пространстве
Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в трёхмерном пространстве
Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:
Вращение вокруг оси y:
Вращение вокруг оси z:
После преобразований мы получаем формулы:
По оси Х
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;
По оси Y
x’=x*cos(L)+z*sin(L);
y’=y;
z’=-x*sin(L)+z*cos(L);
По оси Z
x’=x*cos(L)-y*sin(L);
y’=-x*sin(L)+y*cos(L);
z’=z;
Все три поворота делаются независимо друг от друга, т.е. если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Матрица поворота на угол
В двумерном пространстве поворот можно описать одним углом 
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:

Координаты (x’,y’) в результате поворота точки (x,y) имеют вид:


Положительным углам при этом соответствует вращение вектора против часовой стрелки в обычной, правосторонней системе координат, и по часовой стрелке в левосторонней системе координат.
[править] Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
· Вращение вокруг оси x:

· Вращение вокруг оси y:

· Вращение вокруг оси z:

Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть на плоскость вращении со стороны полупространства, где значения координат оси, вокруг которой осуществляется поворот, положительные. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Свойства матрицы поворота.
Свойства матрицы поворота
Если 

·
·
·
· 
· 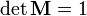
· если строки (или столбцы матрицы) рассматривать как координаты векторов 
o
o
o
· Матрица обратного поворота получается обычным транспонированием матрицы прямого поворота, т. о. 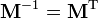
24. Алгоритм Брезенхема для растеризации отрезка.
Алгоритм Брезенхе́ма (англ. Bresenham’s line algorithm) — это алгоритм, определяющий, какие точки двумерного растра нужно закрасить, чтобы получить близкое приближение прямой линии между двумя заданными точками. Это один из старейших алгоритмов в машинной графике — он был разработан Джеком Е. Брезенхэмом (Jack E. Bresenham) в компании IBM в 1962 году. Алгоритм широко используется, в частности, для рисования линий на экране компьютера. Существует обобщение алгоритма Брезенхэма для построения кривых 2-го порядка.
Алгоритм
Отрезок проводится между двумя точками — (x ,y ) и (x1,y1), где в этих парах указаны колонка и строка, соответственно, номера которых растут вправо и вниз. Сначала мы будем предполагать, что наша линия идёт вниз и вправо, причём горизонтальное расстояние x1 − x превосходит вертикальное y1 − y , т.е. наклон линии от горизонтали — менее 45°. Наша цель состоит в том, чтобы для каждой колонки x между x и x1, определить, какая строка y ближе всего к линии, и нарисовать точку (x,y).
Общая формула линии между двумя точками:
Поскольку мы знаем колонку x, то строка y получается округлением к целому следующего значения:
Однако, вычислять точное значение этого выражения нет необходимости. Достаточно заметить, что y растёт от y и за каждый шаг мы добавляем к x единицу и добавляем к y значение наклона
которое можно вычислить заранее. Более того, на каждом шаге мы делаем одно из двух: либо сохраняем тот же y, либо увеличиваем его на 1.
Что из этих двух выбрать — можно решить, отслеживая значение ошибки, которое означает — вертикальное расстояние между текущим значением y и точным значением y для текущего x. Всякий раз, когда мы увеличиваем x, мы увеличиваем значение ошибки на величину наклона s, приведённую выше. Если ошибка превысила 0.5, линия стала ближе к следующему y, поэтому мы увеличиваем y на единицу, одновременно уменьшая значение ошибки на 1. В реализации алгоритма, приведённой ниже, plot(x,y) рисует точку, а abs возвращает абсолютную величину числа:
function line(x0, x1, y0, y1) int deltax := abs(x1 – x0) int deltay := abs(y1 – y0) real error := 0 real deltaerr := deltay / deltax int y := y0 for x from x0 to x1 plot(x,y) error := error + deltaerr if error >= 0.5 y := y + 1 error := error – 1.0
Проблема такого подхода — в том, что с вещественными величинами, такими как error и deltaerr, компьютеры работают относительно медленно. Кроме того, при вычислениях с плавающей точкой может накапливаться ошибка. По этим причинам, лучше работать только с целыми числами. Это можно сделать, если умножить все используемые вещественные величины на deltax. Единственная проблема — с константой 0.5 — но в данном случае достаточно умножить обе части неравенства на 2. Получаем следующий код:
Умножение на 2 для целых чисел реализуется битовым сдвигом влево.
Теперь мы можем быстро рисовать линии, направленные вправо-вниз с величиной наклона меньше 1. Осталось распространить алгоритм на рисование во всех направлениях. Это достигается за счёт зеркальных отражений, т.е. заменой знака (шаг в 1 заменяется на -1), обменом переменных x и y, обменом координат начала отрезка с координатами конца.
[править] Рисование линий
Реализация на C++:
vo > -deltaY) if(error2 = 0) drawpixel(X1 + x, Y1 + y) drawpixel(X1 + x, Y1 – y) drawpixel(X1 – x, Y1 + y) drawpixel(X1 – x, Y1 – y) error = 2 * (delta + y) – 1 if ((delta 0) && (error > 0)) delta += 1 – 2 * –y continue x++ delta += 2 * (x – y) y–
Алгоритм сглаживания Ву.
Алгоритм Ву — это алгоритм разложения отрезка в растр со сглаживанием. Был предложен У Сяолинем (Xiaolin Wu, отсюда устоявшееся в русском языке название алгоритма) в статье, опубликованной журналом Computer Graphics в июле 1991 года. Алгоритм сочетает высококачественное устранение ступенчатости и скорость, близкую к скорости алгоритма Брезенхема без сглаживания.
Алгоритм
Горизонтальные и вертикальные линии не требуют никакого сглаживания, поэтому их рисование выполняется отдельно. Для остальных линий алгоритм Ву проходит их вдоль основной оси, подбирая координаты по неосновной оси аналогично алгоритму Брезенхема. Отличие состоит в том, что в алгоритме Ву на каждом шаге устанавливается не одна, а две точки. Например, если основной осью является Х, то рассматриваются точки с координатами (х, у) и (х, у+1). В зависимости от величины ошибки, которая показывает как далеко ушли пиксели от идеальной линии по неосновной оси, распределяется интенсивность между этими двумя точками. Чем больше удалена точка от идеальной линии, тем меньше ее интенсивность. Значения интенсивности двух пикселей всегда дают в сумме единицу, то есть это интенсивность одного пикселя, в точности попавшего на идеальную линию. Такое распределение придаст линии одинаковую интенсивность на всем ее протяжении, создавая при этом иллюзию, что точки расположены вдоль линии не по две, а по одной.
Результат работы алгоритма
Реализация в псевдокоде (только для линии по x):
function plot(x, y, c) is // рисует точку с координатами (x, y) // и яркостью c (где 0 ≤ c ≤ 1) function ipart(x) is return целая часть от x function round(x) is return ipart(x + 0.5) // округление до ближайшего целого function fpart(x) is return дробная часть x function draw_line(x1,y1,x2,y2) is if x2 BColor) and (C<>Color) then
PutPixel (x, y, Color);
PixelFill (x+1, y, BColor, Color);
PixelFill (x, y+1, BColor, Color);
PixelFill (x-1, y, BColor, Color);
PixelFill (x, y-1, BColor, Color);
Этот алгоритм не оптимизирован относительно использования стековой памяти и является одним из самых медленных алгоритмов закрашивания (в среднем только один из четырёх вызовов используется для закрашивания). Алгоритм не может заполнить области, ограниченные цветом заполнения. Можно построить подобный алгоритм и без рекурсии, если вместо стека использовать массивы.
Алгоритм закрашивания линиями.
| Данный алгоритм получил широкое распространение в компьютерной графике. От приведенного ранее он отличается тем, что на каждом шаге закрашивания рисуется горизонтальная линия, которая размещается между пикселями контура. Данный алгоритм также рекурсивный, однако количество вложенных вызовов гораздо меньше (пропорционально длине линии). Схема алгоритма такова (см.рис.): |  |
1.Имеется затравочная точка с координатами (xst, yst) и начальное направление действия рекурсивных вызовов dir=1. Параметры левой и правой границы вначале совпадают с координатой затравочной точки: xPL = xst, xPR = xst. Вызывается процедура LineFill, в которой:
2.Находятся xL и xR – левая и правая границы, между которыми проводится текущая горизонтальная линия.
3.Делается приращение у=у+dir и, между xL и xR, анализируется цвет пикселей над линией. Если он не совпадает с цветом заполнения, процедура LineFill вызывается рекурсивно с dir = 1 и xPL = xL, xLR = xR.
4.Делается приращение y=y–dir и, начиная от xL до предыдущего значения xPL анализируется цвет пикселей под линией. Если цвет пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR.
5.Продолжая по той же горизонтали от предыдущего xPR до xR анализируется цвет под линией. Если цвет какого-либо пикселя отличается от цвета заполнения, процедура вызывается рекурсивно с dir = –1 и xPL = xL, xPR = xR.
Ниже приведен пример реализации этого алгоритма на языке С++:
void LineFill (int x, int y, int dir, int xPL, int xPR)
// в этой переменной будет храниться цвет пикселя
// УСТАНАВЛИВАЕМ ТЕКУЩИЕ ГРАНИЦЫ xL И xR
color = GetPixel (–xL,y);
// xL=xL-1 помещается в вызов функции
while (color != bcolor); // bcolor – цвет границы
color = GetPixel (++xR,y);
while (color !=bcolor);
Line (xL,y, xR,y, Mycolor);
//это может быть любая функция рисования линии
// АНАЛИЗИРУЕМ ПИКСЕЛИ НАД ЛИНИЕЙ
Описание алгоритма
Алгоритм разделяет плоскость на 9 частей прямыми, которые образуют стороны прямоугольника. Каждой из 9 частей присваивается четырёхбитный код. Биты (от младшего до старшего) значат «левее», «правее», «ниже», «выше». Иными словами, у тех трёх частей плоскости, которые слева от прямоугольника, младший бит равен 1, и так далее.
Алгоритм определяет код конечных точек отрезка. Если оба кода равны нулю, то отрезок полностью находится в прямоугольнике. Если битовое И кодов не равно нулю, то отрезок не пересекает прямоугольник (т.к. это значит, что обе конечные точки отрезка находятся с одной стороны прямоугольника). В прочих случаях, алгоритм выбирает конечную точку, находящуюся вне прямоугольника, находит ближайшую к ней точку пересечения отрезка с одной из линий, образующей стороны прямоугольника, и использует эту точку пересечения как новую конечную точку отрезка. Укороченный отрезок снова пропускается через алгоритм.
Реализация алгоритма для трёхмерной модели идентична двумерной реализации, за исключением того, что вместо четырёхразрядного кода применяется шестиразрядный (дополнительные два бита глубины).
28. Алгоритм разбиения средней точкой.
Последнее изменение этой страницы: 2016-04-21; Нарушение авторского права страницы
Что такое матрица поворота?
Матрица поворота используется для поворота точек вокруг
системы координат. В то время как отдельные точки привязываются к новым координатам,
расстояния между ними не меняются.
Все вращения определяются через тригонометрические функции синус и косинус.
Для двумерной системы координат, матрица вращения такая:
Если угол А равен 0, то на выходе получаем единичную матрицу:
Если угол А равен +90 градусов, то матрица такова:
Если угол А равен -90 градусов, то матрица такова:
Углы поворота, взятые с обратным знаком равны транспонированию матрицы.
Если матрица вращения умножена на транспонированную,
в результате будет единичная матрица
Как матрицы вращения влияют на систему координат?
Матрицы вращения влияют на систему координат следующим образом:
По договоренности положительные углы создают вращение по часовой стрелке,
если смотреть из центра координат в положительном направлении оси вращения.
Следуя этому правилу, в праворукой декартовой системе координат,
мы увидим следующие три вида:
Так как вращение на положительный угол создает вращение по часовой стрелке,
можно создать набор координат для каждого такого вращения.
Для упрощения рассмотрим поворот на +90:
Можно упростить так:
В матрице это будет так:
Это и есть те три базовые матрицы, которые используются в OpenGL.
Поворот системы координат
Василиса ЯВИКС — интеллектуальная поисковая система. Завтра уже здесь!
Ма́трицей поворо́та (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в двумерном пространстве
В двумерном пространстве поворот можно описать одним углом θ со следующей матрицей линейного преобразования в декартовой системе координат:
Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:
Координаты (x′,y′) в результате поворота точки (x, y) имеют вид:
Конкретные знаки в формулах зависят от того, является ли система координат правосторонней или левосторонней, и выполняется ли вращение по или против часовой стрелки. Верхний знак указан для обычного соглашения: правосторонняя система координат и положительное направление вращения против часовой стрелки (тот же знак верен для левосторонней координатной системы при выборе положительного направления вращения по часовой стрелке; в оставшихся двух комбинациях — нижний знак).
Матрица поворота в трёхмерном пространстве
Любое вращение в трёхмерном пространстве может быть представлено как композиция поворотов вокруг трёх ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трёх матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве с неподвижной системой координат являются:
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Например, при повороте на угол α∘ вокруг оси ось переходит в : ∘⋅. Аналогично, ∘⋅ и ∘⋅. Правая система координат связана с выбором правого базиса (см. правило буравчика).
Матрица поворота в -мерном пространстве
Совершенно аналогично могут быть записаны матрицы поворота конечномерного пространства любой более высокой размерности.
Надо только иметь в виду, что для размерностей пространства, не равных трём, невозможно указать единственную прямую, ортогональную двум данным прямым, а поэтому нельзя говорить о вращении вокруг какой-то оси, можно же говорить о вращении в какой-то плоскости. Все точки при повороте в пространстве любой размерности, начиная с 2, всегда движутся параллельно некоторой (двумерной) плоскости.
Итак, совершенно аналогично трёхмерному случаю (с приведенной оговоркой) можем написать матрицу поворота в любой координатной плоскости для любой размерности пространства.
— матрица поворота в 5-мерном пространстве в плоскости ,
— матрица поворота в 7-мерном пространстве в плоскости .
- При таком подходе знаки перед синусами расставлять даже легче, поскольку они определяются порядком перечисления осей плоскости вращения: какая названа первой, в той строке перед синусом минус.
- Легко видеть, что матрица поворота в плоскости совпадает (что естественно) с матрицей поворота в плоскости и т. д. с точностью до замены угла поворота на противоположный.
- Поэтому такие матрицы с переставленными индексами очевидно не независимы, и для получения произвольного поворота достаточно включить в композицию каждую плоскость только один раз, то есть, скажем, только α, а не α и α.
- Исходя из этого, нетрудно сосчитать их общее количество: −, где n — размерность пространства.
Изменение оси поворота
Пусть — матрица поворота вокруг оси с ортом на угол α, — матрица поворота вокруг оси с ортом на тот же угол, причем
где — матрица поворота, изменяющая орт оси поворота . Тогда
где — транспонированная матрица.
Перестановочность поворотов
Если — матрица поворота вокруг оси с ортом на угол α, — матрица поворота вокруг оси с ортом на угол β,то ⋅ — матрица, описывающая поворот, являющийся результатом двух последовательно осуществленных поворотов ( и ), поскольку
При этом последовательность поворотов можно поменять, видоизменив поворот :
где матрица — матрица поворота на угол α вокруг оси c ортом повернутым с помощью поворота :
поскольку ⋅, так как матрица поворота является ортогональной матрицей ( — единичная матрица). Заметим, что коммутативности поворотов в обычном смысле нет, то есть
Выражение матрицы поворота через углы Эйлера
Последовательные повороты около осей на угол прецессии (α), угол нутации (β) и на угол собственного вращения (γ) приводят к следующему выражению для матрицы поворота:
Ось — ось X, повёрнутая первым поворотом (на α), — ось Z, повёрнутая первым и вторым поворотом (на α и β). Вследствие перестановочности поворотов приведённая матрица соответствует поворотам на углы γ, β, α вокруг осей Z, X, Z:
В случае, если повороты задаются в другой последовательности, матрица поворота находится перемножением матриц для вращения вокруг соответствующих декартовых осей координат, например:
- 1) Поворот около осей:
- 2) Соответственно:
- 3)
- 4)
- 5)
- 6)
- 7)
- 9)
- 10)
- 11)
- 12)
Матрица поворота вокруг произвольной оси
Пусть ось вращения задана единичным вектором , а угол поворота θ.
Тогда матрица поворота в декартовых координатах имеет вид:
Выражение матрицы поворота через кватернион
Если задан кватернион, то соответствующая матрица поворота имеет вид:
Свойства матрицы поворота
Если — матрица, задающая поворот вокруг оси → на угол φ, то:
- →→∀→
- →→
- →→−φ→⋅→→φ
- −φ (след матрицы вращения), где n — размерность пространства (размер матрицы).
- (матрица имеет единичный определитель).
- Матрица обратного поворота получается обычным транспонированием матрицы прямого поворота, т. о. −.
- Для трёхмерного пространства (матриц ×): если строки (или столбцы матрицы) рассматривать как координаты векторов →→→, то верны следующие соотношения):
- →→→
- →⋅→→⋅→→⋅→
- →×→→→×→→→×→→
- Первые два свойства, означающие условие ортогональности матрицы, верны и для произвольной размерности пространства (размера матрицы).
Примечания
- Ортогональность матрицы означает, что её обратная матрица равна транспонированной матрице: A−1 = AT.
- То есть если смотреть на плоскость вращения со стороны полупространства, где значения координат оси, вокруг которой осуществляется поворот, положительные.
- О вращении в плоскости можно говорить и для трёхмерного пространства, например, вращение вокруг оси есть вращение в плоскости ; однако для трёхмерного пространства возможно и то и другое представление, и поэтому обычно, если вопрос сводится к случаю только этой размерности, выбирают представление (и обозначения) вращения вокруг оси как интуитивно несколько более простое.
- Для всех n строк (столбцов).
Литература
- Лурье А. И. Аналитическая механика. — М.:Физматлит. — 1961. — 824 с.
Ссылки
- Поворот плоскости. Матрица поворота
Операторы извлечения и вставки в поток, страница 2
1. Перегрузкаоператора присваивания.
2. Перегрузкабинарных операторов.
3. Перегрузкаунарных операторов.
4. Перегрузкаоператоров ++ и —.
5. Перегрузкаоператора вызова функции.
6. Перегрузкаоператора преобразования типа.
Вычисление вектора по координатам его концов
Проекции вектора можновычислить по координатам начала (точка А) и конца (точка В) использую следующуюформулу:
Вычисление координат конца вектора
Координаты конца (точка В) вектора можно вычислить по координатам начала(точка А) и проекциям вектора АВ использую следующую формулу:
Вычисление модуля вектора
Модуль вектора (длину)можно вычислить по теореме Пифагора:
Вычисление расстояния между двумя точками
Расстояние D междудвумя точка A и B можновычислить по теореме Пифагора:
Вычисление площади треугольника
Площадь S треугольника со сторонами a,b и с можно вычислить по формуле Герона:
Вычисление скалярного произведения векторов
Скалярное произведение векторов и можновычислить по следующей формуле:
Вычисление угла между векторами
Угол между векторами и можновычислить по следующей формуле:
Поворот вектора на заданный угол
Проекции вектора ,повёрнутого относительно вектора на угол , можно вычислить по следующей формуле:
Вычисление вектора, перпендикулярного заданному вектору
Проекции вектора ,перпендикулярного вектору , можно вычислить последующей формуле:
Не трудно видеть, что скалярное произведение векторов и в этом случае равно нулю
Умножение вектора на число
Умножение вектора начисло К можно выполнить по следующей формуле:
Нетрудно видеть, что вектор в К раз длиннее вектора и параллелен вектору
Вычисления прямой, проходящей через две заданные точки
Уравнение прямой ,проходящей через точки и имеетвид:
Откуда легко получить:
Вычисление коэффициентов прямой, перпендикулярной заданной прямой
Две прямые и перпендикулярны друг другу, если:
Если прямая известна, то коэффициенты и прямой можно вычислить по следующим формулам:
Прямая проходитчерез точку , если:
Вычисление детерминанта
Детерминант матрицы размером 2´2 можно вычислить по следующей формуле:
Пересечение двух прямых
Задачу нахождения точки пересечения двух прямыхна плоскости можно свести к решению двух линейных уравнений с двумянеизвестными методом Крамера:
Вычисления прямой, перпендикулярной заданному вектору и проходящей череззаданную точку
Прямая перпендикулярнавектору с проекциями , если:
Прямая проходитчерез точку , если:
Вычисления прямой, параллельной заданному вектору и проходящей через заданнуюточку
Прямая перпендикулярнавектору с проекциями , если:
Прямая проходитчерез точку , если:
Преобразования прямоугольных координат
Получим формулы, связывающие координаты точки при переходе от одной прямоугольной системы координат к другой прямоугольной системе координат. Рассмотрим три типа преобразований:
а) параллельный перенос;
б) поворот системы координат;
в) зеркальное отражение в оси абсцисс (изменение направления оси ординат на противоположное).
В каждом случае координаты точки в старой и новой системах координат связаны формулой (2.8). Поэтому достаточно найти вектор переноса начала координат и матрицу перехода от базиса к базису .
а) При параллельном переносе системы координат (рис.2.11,а) базис не изменяется, поэтому матрица перехода является единичной: . Находим координаты вектора переноса начала координат: . Тогда формулу (2.8) можно записать в виде
б) При повороте системы координат на угол (рис.2.11,6) начало новой системы координат совпадает с началом старой, поэтому вектор переноса нулевой: . Разлагая новые базисные векторы по старому базису, получаем Составим матрицу перехода, записывая координаты векторов по столбцам: . Тогда формулу (2.8) можно записать в виде
в) При зеркальном отражении в оси абсцисс (изменении направления оси ординат на противоположное) (рис.2.11,в) начало новой системы координат совпадает с началом старой, поэтому вектор переноса нулевой: . Разлагая новые базисные векторы по старому базису, получаем (так как ), или . Составим матрицу перехода, записывая координаты векторов по столбцам: . Тогда формулу (2.8) можно записать в виде .
Аналогично определяется зеркальное отражение в оси ординат (изменение направления оси абсцисс на противоположное).
Покажем, что любое преобразование прямоугольной системы координат сводится к последовательному применению рассмотренных преобразований, т.е. к композиции преобразований систем координат. Действительно, пусть на плоскости заданы две прямоугольные системы координат и . Сначала, если точки и не совпадают, выполним параллельный перенос старой системы координат на вектор , при этом получим систему координат .
Затем при помощи поворота на угол совместим вектор с вектором , при этом получим систему координат , где вектор либо совпадает с вектором , либо противоположен ему . В первом случае, когда обе системы и одноименные, никаких преобразований делать уже не надо, так как полученная система координат совпадает с заданной (рис.2.12,а). Во втором случае, когда системы и разноименные, для получения системы достаточно изменить направление оси ординат на противоположное, т.е.
выполнить зеркальное отражение в оси (рис.2.12,6). Формулы, связывающие старые и новые координаты точки, имеют вид:
– при одноименных системах координат (рис.2.12,а):
– при разноименных системах координат (рис.2.12,6):
Таким образом, любое преобразование прямоугольной системы координат на плоскости сводится к композиции преобразований, каждое из которых является либо параллельным переносом, либо поворотом, либо зеркальным отражением в оси координат.
1. Для рассмотренных преобразований координат точек нетрудно получить выражения новых координат через старые:
Для преобразования (2.9) аналогичные формулы имеют вид:
2. При и из соотношений (2.10) получается преобразование изменяющее названия координатных осей (зеркальное отражение в прямой, содержащей биссектрису первого координатного угла).
3. Справедливо утверждение: любое преобразование прямоугольной системы координат на плоскости может быть представлено в виде композиции зеркальных отражений в некоторых прямых.
Для доказательства достаточно показать, что рассмотренные выше преобразования — параллельный перенос (рис.2.11,а) и поворот (рис.2.11,6) — можно представить при помощи композиции зеркальных отражений.
Действительно, параллельный перенос системы координат вдоль оси абсцисс (на вектор ) можно получить при помощи двух отражений: первое — относительно оси ординат (получим систему координат ) , а второе — относительно прямой , проходящей через точку на оси абсцисс параллельно оси ординат (рис.2.13,а).
Аналогично выполняется сдвиг вдоль оси ординат. Поэтому любой параллельный перенос сводится к композиции зеркальных отражений.
Чтобы получить поворот на угол , нужно выполнить два зеркальных отражения (рис.2.13,6): первое — относительно оси ординат (получим систему ), а второе — относительно биссектрисы угла между векторами и .
4. Утверждение пункта 3 можно уточнить: любое преобразование прямоугольной системы координат на плоскости может быть представлено в виде композиции не более трех зеркальных отражений в некоторых прямых.
5. Преобразования координат (2.7) и (2.8) называются ортогональными, если матрица перехода ортогональная, т.е. . Нетрудно но показать, что преобразования (2.9),(2.10) ортогональные, поэтому любое преобразование прямоугольной системы координат является ортогональным.
Пример 2.5. Известны координаты точек и в прямоугольной системе координат на плоскости. Найти координаты точки в прямоугольной системе координат , полученной при помощи зеркального отражения в некоторой прямой системы (рис.2.14).
Решение. Находим вектор переноса начала системы координат , его длину и угол между векторами и , так как .
Ось симметрии при зеркальном отражении является серединным перпендикуляром к отрезку , поэтому угол , который образует ось симметрии с положительным направлением оси абсцисс , равен .
Отражение в оси представим в виде композиции следующих преобразований: параллельного переноса на вектор ; поворота на угол ; зеркального отражения в оси абсцисс (рис.2.12,6). Старые и новые координаты точки связаны формулой (2.10) при . Учитывая, что и
Подставляя старые координаты точки , получаем ее новые координаты:
Следовательно, точка имеет одинаковые координаты в обеих системах, т.е. точка лежит на оси симметрии .
Преобразования прямоугольных координат в пространстве
Получим формулы, связывающие координаты точки при переходе от одной прямоугольной системы координат в пространстве к другой прямоугольной системе координат.
Рассмотрим три типа преобразований прямоугольной системы координат:
а) параллельный перенос;
б) поворот вокруг координатной оси;
в) зеркальное отражение в координатной плоскости (изменение направления одной координатной оси на противоположное).
В каждом случае координаты точки в старой и новой системах координат связаны формулой (2.7). Поэтому достаточно найти вектор переноса начала координат и матрицу перехода от базиса к базису .
а) При параллельном переносе системы координат базис не изменяется, поэтому матрица перехода является единичной: . Находим координаты вектора переноса начала координат: . Тогда формулу (2.7) можно записать в виде
б) При повороте системы координат на угол (рис.2.11,б) вокруг оси аппликат начало новой системы координат совпадает с началом старой, поэтому вектор переноса нулевой: . Разлагая новые базисные векторы по старому базису, получаем
Составим матрицу перехода , записывая координаты векторов по столбцам. Тогда формулу (2.7) можно записать в виде
Очевидно, что система координат на плоскости при этом преобразовании поворачивается на угол .
в) При зеркальном отражении в плоскости (изменении направления оси аппликат на противоположное) начало новой системы координат совпадает с началом старой, поэтому вектор переноса нулевой: . Разлагая новые базисные векторы по старому базису, получаем
Составим матрицу перехода
Тогда формулу (2.7) можно записать в виде
Аналогично определяются зеркальные отражения в других координатных плоскостях (изменение направлений осей абсцисс или ординат на противоположные).
Матрицы переходов в пунктах «а», «б» и «в» ортогональные (см. пункт 5 замечаний 2.3).
Как и в случае преобразований на плоскости, можно показать, что любое преобразование прямоугольной системы координат в пространстве сводится к композиции преобразований, каждое из которых является либо параллельным переносам, либо поворотам вокруг координатной оси, либо зеркальным отражением в координатной плоскости.
Углы Эйлера
Используя композицию, получим формулы преобразования координат точки в пространстве при переходе от старой прямоугольной системы к новой , имеющей то же начало и ту же ориентацию (т.е. новая система координат получается из старой поворотом вокруг начала координат ). Обе системы координат изображены на рис.2.15 (полужирными и двойными линиями соответственно).
Чтобы от системы перейти к системе нужно выполнить три поворота. Сначала проведем через точку перпендикуляр (линию узлов) к плоскости . Направление на этом перпендикуляре выберем так, чтобы ориентация системы координат совпадала бы с ориентацией системы координат . Если оси и совпадают, то ось выбирается совпадающей с осью .
Если оси и противоположно направлены, то и ось выбирается противоположно направленной оси . Затем последовательно сделаем три поворота:
– первый поворот выполним вокруг оси на угол от оси до оси (получим систему координат , оси и которой изображены штриховыми линиями на рис.2.15);
– второй поворот выполним вокруг оси на угол от оси до оси , при этом ось примет положение (получим систему координат , ось которой Рис.2.15 изображена двойной штриховой линией на рис.2.15);
– третий поворот выполним вокруг оси на угол от оси до оси .
Указанные углы называются углами Эйлера, в частности, угол называется углом прецессии, угол — углом нутации, а угол — углом чистого вращения.
Согласно пункту «б», запишем матрицы переходов от базиса к базису для указанных поворотов соответственно:
По свойству 1 (см. разд.2.2.1) получаем матрицу перехода от базиса прямоугольной системы координат к базису прямоугольной системы координат :
Отсюда следуют формулы для преобразования прямоугольных координат точки
Поскольку каждая из матриц ортогональная, то и их произведение также является ортогональной матрицей (см. пункт 5 замечаний 2.3).
Пример 2.6. Прямоугольная система координат получена из стандартной системы координат при помощи поворота на угол вокруг прямой, проходящей через начало координат и образующей равные углы с координатными осями (на рис.2.16 эта прямая изображена одной точкой , поскольку перпендикулярна плоскости рисунка). Требуется найти углы Эйлера.
Решение. Составим матрицу перехода от базиса к базису .
Сравнивая с матрицей , заключаем, что (так как и ); (так как и ); (так как и ).
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
[spoiler title=”источники:”]
http://pcznatok.ru/kompjutery/matrica-povorota-na-ugol.html
http://glonass-std.ru/sistemy-navigatsii/povorot-sistemy-koordinat.html
[/spoiler]
Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.
Матрица поворота в трёхмерном пространстве
Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:
Вращение вокруг оси y:
Вращение вокруг оси z:
После преобразований мы получаем формулы:
По оси Х
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;
По оси Y
x’=x*cos(L)+z*sin(L);
y’=y;
z’=-x*sin(L)+z*cos(L);
По оси Z
x’=x*cos(L)-y*sin(L);
y’=-x*sin(L)+y*cos(L);
z’=z;
Все три поворота делаются независимо друг от друга, т.е. если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.
Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси. Правая система координат связана с выбором правого базиса (см. правило буравчика).

Матрица преобразований (направляющих косинусов) |
||||
|
Рассмотрим теперь КЭ в составе рамы, расположенный под углом |
α к оси Х в |
|||
|
общей системе осей координат. |
||||
|
Необходимо перейти от матрицы реакций [r]’j в местной системе осей координат к |
||||
|
матрице [r] в общей системе координат. |
||||
|
Задачу решаем следующим образом. В начале построим матрицу [c]j, которая |
||||
|
преобразует перемещения КЭ {z}j в общей системе осей координат в перемещения {v}j, |
||||
|
по выражению |
{v}j = [c]j {z}j |
|||
|
Y |
||||
|
Z3 |
||||
|
V3 |
V4 |
|||
|
К |
Z4 |
|||
|
Z2 |
Z6 =V6 |
|||
|
V2 |
V1 |
|||
|
Н |
Z1 |
|||
|
a |
Z3 =V3 |
|||
|
X |
||||
|
V1 = Z1 cosα + Z2 sinα |
||||
|
V2 = -Z1 sinα + Z2 cosα |
||||
|
V3 = Z3 |
||||
|
V6 = Z6 |
||||
|
V4 = Z4 cosα + Z5 sinα |
||||
|
V5 = -Z4 sinα + Z5 cosα |
В матричной форме приведенная выше запись будет иметь вид
éV1 êêV2
êêV3
êV4 êêV5
êëV6
|
ù |
é cosα |
sinα |
0 |
0 |
0 |
0ù |
éZ1 |
ù |
||
|
ú |
ê |
cosα |
0 |
0 |
0 |
ú |
ê |
ú |
||
|
ú |
ê– sinα |
0ú |
êZ2 |
ú |
||||||
|
ú |
ê |
0 |
0 |
1 |
0 |
0 |
0ú |
êZ |
3 |
ú |
|
ú |
= ê |
0 |
0 |
0 |
cosα |
sinα |
ú |
× ê |
ú, |
|
|
ú |
ê |
0ú |
êZ4 |
ú |
||||||
|
ú |
ê |
0 |
0 |
0 |
– sinα |
cosα |
0ú |
êZ |
5 |
ú |
|
ú |
ê |
0 |
0 |
0 |
0 |
ú |
ê |
ú |
||
|
ú |
ê 0 |
1ú |
êZ |
6 |
ú |
|||||
|
û |
ë |
û |
ë |
û |
|
или в блочной форме |
éс |
0 ù |
||||
|
[c]j = ê |
н |
ú, |
||||
|
ë |
0 |
cк û |
||||
|
где для жесткого узла |
é соsa |
sina |
0ù |
|||
|
[c]н,к = |
ê– sina |
cosa |
0ú, |
|||
|
ê |
0 |
0 |
ú |
|||
|
ê |
1ú |
|||||
|
для шарнирного узла |
ë |
û |
||||
|
é cosa |
sinaù |
|||||
|
[c]н,к = |
||||||
|
ê |
ú. |
|||||
|
ë– sina |
cosaû |
Так как мы рассматриваем плоские упругие системы, то векторы узловых усилий и узловых перемещений, как для отдельного элемента, так и для сооружения в целом,
связаны между собой линейно
|
{S}j’ = [r]j’{V}j |
– в местной системе осей координат. |
|
|
{S}j = [r]j {Z}j |
– в общей системе осей координат |
|
|
Кроме того |
{V}j = [c]j{Z}j, |
|
|
Аналогично |
||
{S}j’ = [c]j{S}j,
где {S}’,{S}-узловые усилия КЭ соответственно, в местной и общей системах осей координат.
Тогда
{S}j = [c]j-1 {S}j’ = [c]j-1[r]j’{V}j = [c]j-1[r]j’[c]j{Z}j.
Для матрицы направляющих косинусов выполняется равенство
[c]j-1 = [c]jT,
Тогда
{S}j = [c]jT [r]j’ [c]j{Z}.
Обозначим
[r]j = [c]jT [r]j’ [c]j – это выражение и является формулой для вычисления матрицы жесткости КЭ в общей системе осей координат.
При формировании матриц жесткости отдельных элементов [r]j’ должны быть зафиксированы начало и конец каждого стержня, так как от этого зависит знак угла a, определяющего ориентацию стержня в общей системе осей координат ХОY.
Соседние файлы в папке СФ
- #
- #
- #
- #
- #
- #
Матрица направляющих косинусов
- Матрица направляющих косинусов
-
Содержание
- 1 Матрица поворота в двумерном пространстве
- 2 Матрица поворота в трёхмерном пространстве
- 3 Свойства матрицы поворота
- 4 См. также
- 5 Литература
- 6 Ссылки
Матрицей поворота (или матрицей направляющих косинусов) называется матрица, умножение любого вектора на которую не меняет его длины.
Матрица поворота в двумерном пространстве
В двумерном пространстве поворот можно описать одним углом θ. Положительным углам соответствует вращение против часовой стрелки.
Матрица поворота вектора в декартовой системе координат:
Сам поворот происходит путём умножения вектора (описывающего вращаемую точку) на матрицу:
.
Матрица поворота в трёхмерном пространстве
Матрицами вращения вокруг оси декартовой правосторонней системы координат на угол α в трёхмерном пространстве являются:
- Вращение вокруг оси x:
,
- Вращение вокруг оси y:
,
- Вращение вокруг оси z:
,
В трёхмерном пространстве для описания поворота можно использовать
- матрицу поворота 3×3,
- три угла, например, углы Эйлера (γ,β,α),
- угол поворота θ и единичный вектор оси вращения
,
- кватернион.
Матрицы поворота вектора в декартовой системе координат, соответствующие этим двум способам задания поворота:
и
Свойства матрицы поворота
Если
— матрица, задающая поворот вокруг оси
на угол φ, то:
См. также
- Матрица перехода
Литература
- Лурье А. И. Аналитическая механика — М.:Физматлит — 1961 г. — 824 с.
Ссылки
- Поворот плоскости. Матрица поворота
Wikimedia Foundation.
2010.
Полезное
Смотреть что такое “Матрица направляющих косинусов” в других словарях:
-
Матрица поворота — Проверить информацию. Необходимо проверить точность фактов и достоверность сведений, изложенных в этой статье. На странице обсуждения должны быть пояснения … Википедия
-
Матрица вращения — Содержание 1 Матрица поворота в двумерном пространстве 2 Матрица поворота в трёхмерном пространстве … Википедия
-
Складывание рамок — … Википедия


































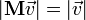

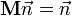

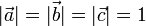

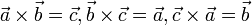






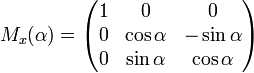
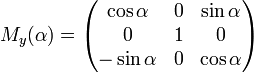
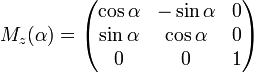
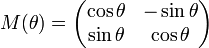
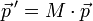 .
.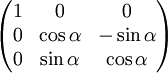 ,
,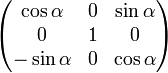 ,
,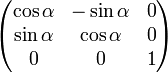 ,
,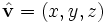 ,
,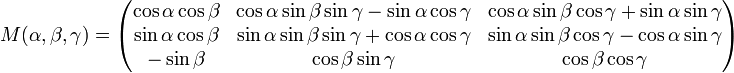
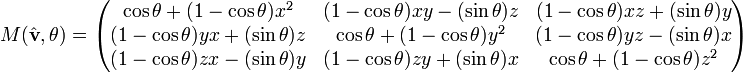
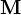 — матрица, задающая поворот вокруг оси
— матрица, задающая поворот вокруг оси 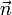 на угол
на угол 