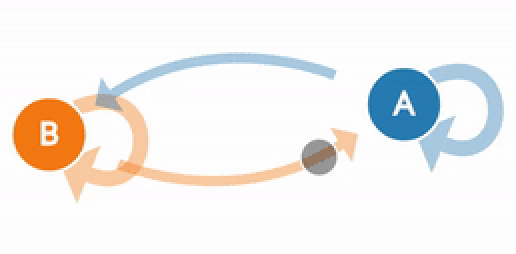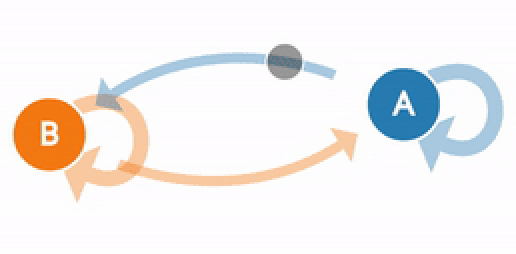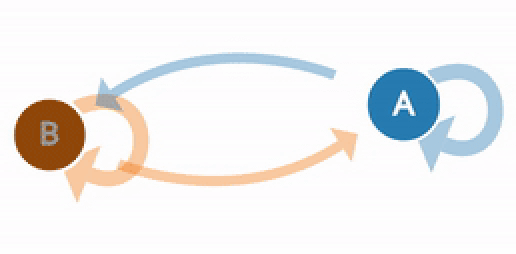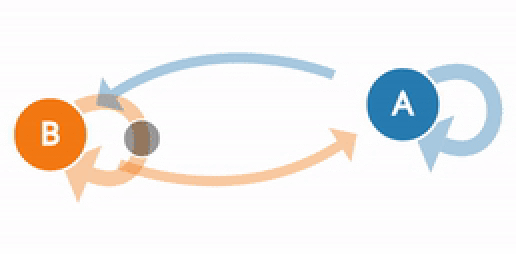
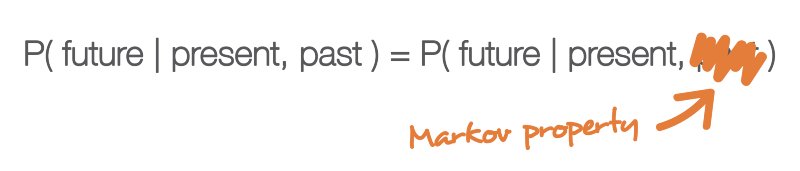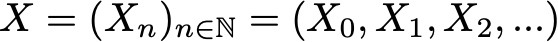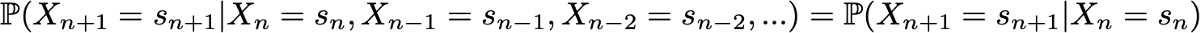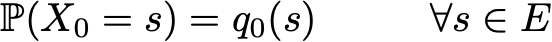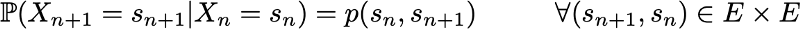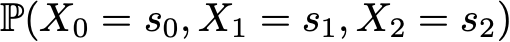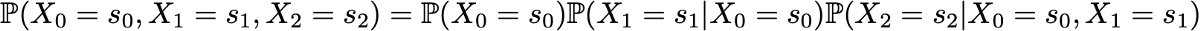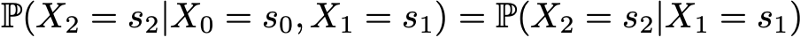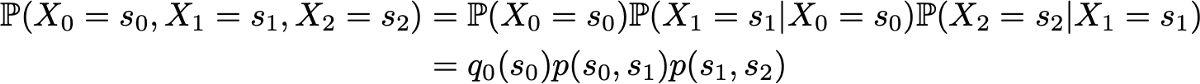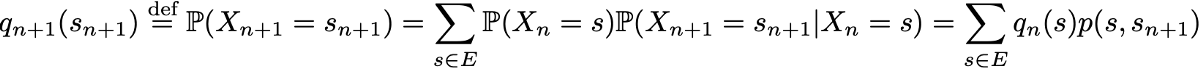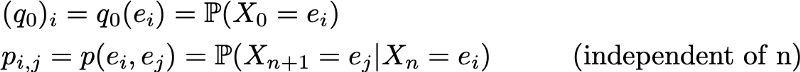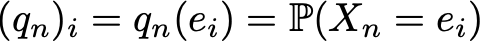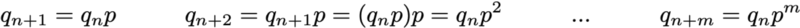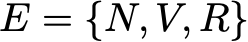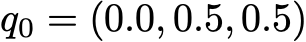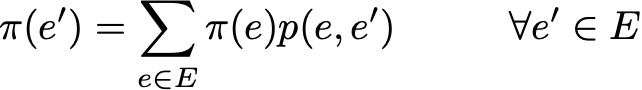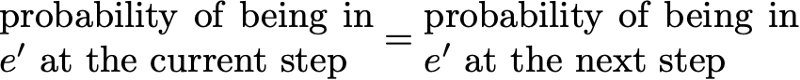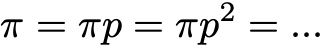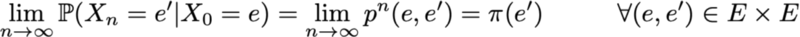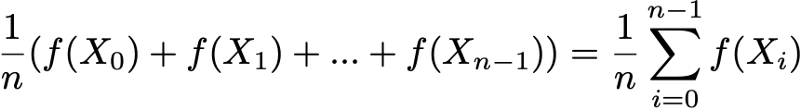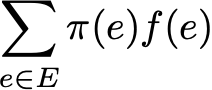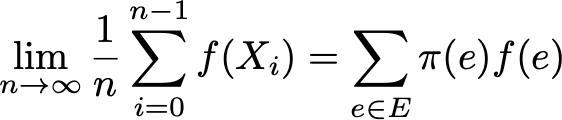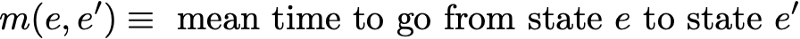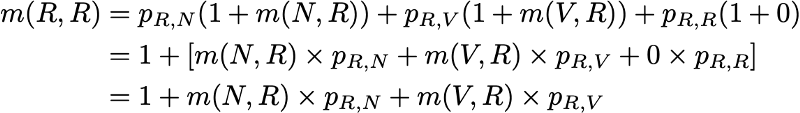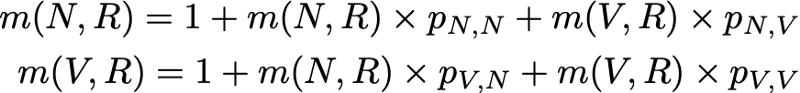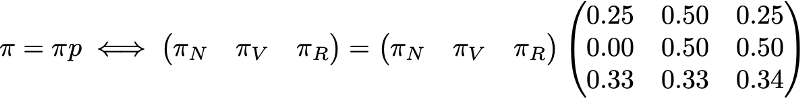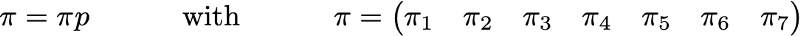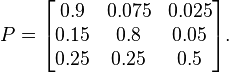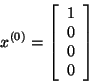В 1998 году Лоуренс Пейдж, Сергей Брин, Раджив Мотвани и Терри Виноград опубликовали статью «The PageRank Citation Ranking: Bringing Order to the Web», в которой описали знаменитый теперь алгоритм PageRank, ставший фундаментом Google. Спустя чуть менее двух десятков лет Google стал гигантом, и даже несмотря на то, что его алгоритм сильно эволюционировал, PageRank по-прежнему является «символом» алгоритмов ранжирования Google (хотя только немногие люди могут действительно сказать, какой вес он сегодня занимает в алгоритме).
С теоретической точки зрения интересно заметить, что одна из стандартных интерпретаций алгоритма PageRank основывается на простом, но фундаментальном понятии цепей Маркова. Из статьи мы увидим, что цепи Маркова — это мощные инструменты стохастического моделирования, которые могут быть полезны любому эксперту по аналитическим данным (data scientist). В частности, мы ответим на такие базовые вопросы: что такое цепи Маркова, какими хорошими свойствами они обладают, и что с их помощью можно делать?
Краткий обзор
В первом разделе мы приведём базовые определения, необходимые для понимания цепей Маркова. Во втором разделе мы рассмотрим особый случай цепей Маркова в конечном пространстве состояний. В третьем разделе мы рассмотрим некоторые из элементарных свойств цепей Маркова и проиллюстрируем эти свойства на множестве мелких примеров. Наконец, в четвёртом разделе мы свяжем цепи Маркова с алгоритмом PageRank и увидим на искусственном примере, как цепи Маркова можно применять для ранжирования узлов графа.
Примечание. Для понимания этого поста необходимы знания основ вероятностей и линейной алгебры. В частности, будут использованы следующие понятия: условная вероятность, собственный вектор и формула полной вероятности.
Что такое цепи Маркова?
Случайные переменные и случайные процессы
Прежде чем вводить понятие цепей Маркова, давайте вкратце вспомним базовые, но важные понятия теории вероятностей.
Во-первых, вне языка математики случайной величиной X считается величина, которая определяется результатом случайного явления. Его результатом может быть число (или «подобие числа», например, векторы) или что-то иное. Например, мы можем определить случайную величину как результат броска кубика (число) или же как результат бросания монетки (не число, если только мы не обозначим, например, «орёл» как 0, а «решку» как 1). Также упомянем, что пространство возможных результатов случайной величины может быть дискретным или непрерывным: например, нормальная случайная величина непрерывна, а пуассоновская случайная величина дискретна.
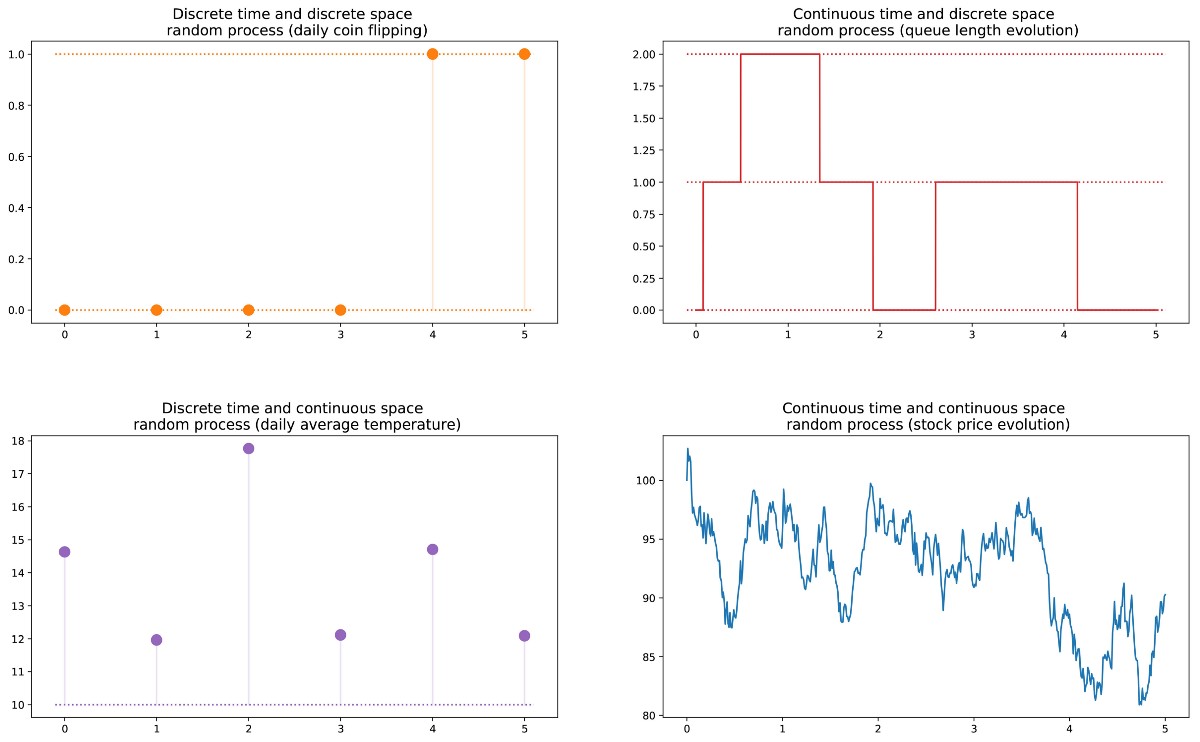
Далее мы можем определить случайный процесс (также называемый стохастическим) как набор случайных величин, проиндексированных множеством T, которое часто обозначает разные моменты времени (в дальнейшем мы будем считать так). Два самых распространённых случая: T может быть или множеством натуральных чисел (случайный процесс с дискретным временем), или множеством вещественных чисел (случайный процесс с непрерывным временем). Например, если мы будем бросать монетку каждый день, то зададим случайный процесс с дискретным временем, а постоянно меняющаяся стоимость опциона на бирже задаёт случайный процесс с непрерывным временем. Случайные величины в разные моменты времени могут быть независимыми друг от друга (пример с подбрасыванием монетки), или иметь некую зависимость (пример со стоимостью опциона); кроме того, они могут иметь непрерывное или дискретное пространство состояний (пространство возможных результатов в каждый момент времени).
Разные виды случайных процессов (дискретные/непрерывные в пространстве/времени).
Марковское свойство и цепь Маркова
Существуют хорошо известные семейства случайных процессов: гауссовы процессы, пуассоновские процессы, авторегрессивные модели, модели скользящего среднего, цепи Маркова и другие. Каждое из этих отдельных случаев имеет определённые свойства, позволяющие нам лучше исследовать и понимать их.
Одно из свойств, сильно упрощающее исследование случайного процесса — это «марковское свойство». Если объяснять очень неформальным языком, то марковское свойство сообщает нам, что если мы знаем значение, полученное каким-то случайным процессом в заданный момент времени, то не получим никакой дополнительной информации о будущем поведении процесса, собирая другие сведения о его прошлом. Более математическим языком: в любой момент времени условное распределение будущих состояний процесса с заданными текущим и прошлыми состояниями зависит только от текущего состояния, но не от прошлых состояний (свойство отсутствия памяти). Случайный процесс с марковским свойством называется марковским процессом.
Марковское свойство обозначает, что если мы знаем текущее состояние в заданный момент времени, то нам не нужна никакая дополнительная информация о будущем, собираемая из прошлого.
На основании этого определения мы можем сформулировать определение «однородных цепей Маркова с дискретным временем» (в дальнейшем для простоты мы их будем называть «цепями Маркова»). Цепь Маркова — это марковский процесс с дискретным временем и дискретным пространством состояний. Итак, цепь Маркова — это дискретная последовательность состояний, каждое из которых берётся из дискретного пространства состояний (конечного или бесконечного), удовлетворяющее марковскому свойству.
Математически мы можем обозначить цепь Маркова так:
где в каждый момент времени процесс берёт свои значения из дискретного множества E, такого, что
Тогда марковское свойство подразумевает, что у нас есть
Снова обратите внимание, что эта последняя формула отражает тот факт, что для хронологии (где я нахожусь сейчас и где я был раньше) распределение вероятностей следующего состояния (где я буду дальше) зависит от текущего состояния, но не от прошлых состояний.
Примечание. В этом ознакомительном посте мы решили рассказать только о простых однородных цепях Маркова с дискретным временем. Однако существуют также неоднородные (зависящие от времени) цепи Маркова и/или цепи с непрерывным временем. В этой статье мы не будем рассматривать такие вариации модели. Стоит также заметить, что данное выше определение марковского свойства чрезвычайно упрощено: в истинном математическом определении используется понятие фильтрации, которое выходит далеко за пределы нашего вводного знакомства с моделью.
Характеризуем динамику случайности цепи Маркова
В предыдущем подразделе мы познакомились с общей структурой, соответствующей любой цепи Маркова. Давайте посмотрим, что нам нужно, чтобы задать конкретный «экземпляр» такого случайного процесса.
Сначала заметим, что полное определение характеристик случайного процесса с дискретным временем, не удовлетворяющего марковскому свойству, может быть сложным занятием: распределение вероятностей в заданный момент времени может зависеть от одного или нескольких моментов в прошлом и/или будущем. Все эти возможные временные зависимости потенциально могут усложнить создание определения процесса.
Однако благодаря марковскому свойству динамику цепи Маркова определить довольно просто. И в самом деле. нам нужно определить только два аспекта: исходное распределение вероятностей (то есть распределение вероятностей в момент времени n=0), обозначаемое
и матрицу переходных вероятностей (которая даёт нам вероятности того, что состояние в момент времени n+1 является последующим для другого состояния в момент n для любой пары состояний), обозначаемую
Если два этих аспекта известны, то полная (вероятностная) динамика процесса чётко определена. И в самом деле, вероятность любого результата процесса тогда можно вычислить циклически.
Пример: допустим, мы хотим знать вероятность того, что первые 3 состояния процесса будут иметь значения (s0, s1, s2). То есть мы хотим вычислить вероятность
Здесь мы применяем формулу полной вероятности, гласящую, что вероятность получения (s0, s1, s2) равна вероятности получения первого s0, умноженного на вероятность получения s1 с учётом того, что ранее мы получили s0, умноженного на вероятность получения s2 с учётом того, что мы получили ранее по порядку s0 и s1. Математически это можно записать как
И затем проявляется упрощение, определяемое марковским допущением. И в самом деле, в случае длинных цепей мы получим для последних состояний сильно условные вероятности. Однако в случае цепей Маркова мы можем упростить это выражение, воспользовавшись тем, что
получив таким образом
Так как они полностью характеризуют вероятностную динамику процесса, многие сложные события можно вычислить только на основании исходного распределения вероятностей q0 и матрицы переходной вероятности p. Стоит также привести ещё одну базовую связь: выражение распределения вероятностей во время n+1, выраженное относительно распределения вероятностей во время n
Цепи Маркова в конечных пространствах состояний
Представление в виде матриц и графов
Здесь мы допустим, что во множестве E есть конечное количество возможных состояний N:
Тогда исходное распределение вероятностей можно описать как вектор-строку q0 размером N, а переходные вероятности можно описать как матрицу p размером N на N, такую что
Преимущество такой записи заключается в том, что если мы обозначим распределение вероятностей на шаге n вектором-строкой qn, таким что его компоненты задаются
тогда простые матричные связи при этом сохраняются
(здесь мы не будем рассматривать доказательство, но воспроизвести его очень просто).
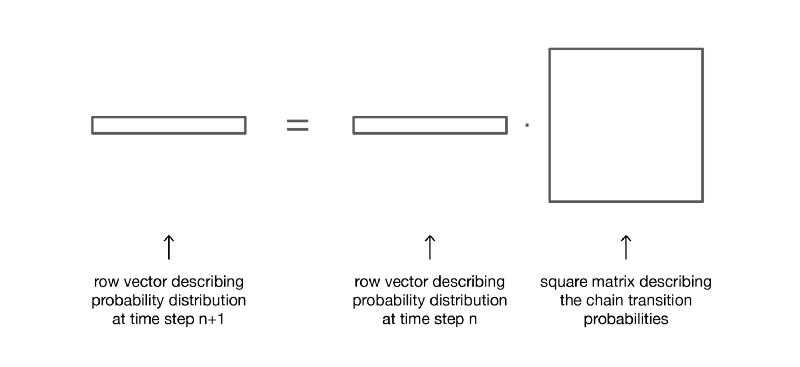
Если умножить справа вектор-строку, описывающий распределение вероятностей на заданном этапе времени, на матрицу переходных вероятностей, то мы получим распределение вероятностей на следующем этапе времени.
Итак, как мы видим, переход распределения вероятностей из заданного этапа в последующий определяется просто как умножение справа вектора-строки вероятностей исходного шага на матрицу p. Кроме того, это подразумевает, что у нас есть
Динамику случайности цепи Маркова в конечном пространстве состояний можно с лёгкостью представить как нормированный ориентированный граф, такой что каждый узел графа является состоянием, а для каждой пары состояний (ei, ej) существует ребро, идущее от ei к ej, если p(ei,ej)>0. Тогда значение ребра будет той же вероятностью p(ei,ej).
Пример: читатель нашего сайта
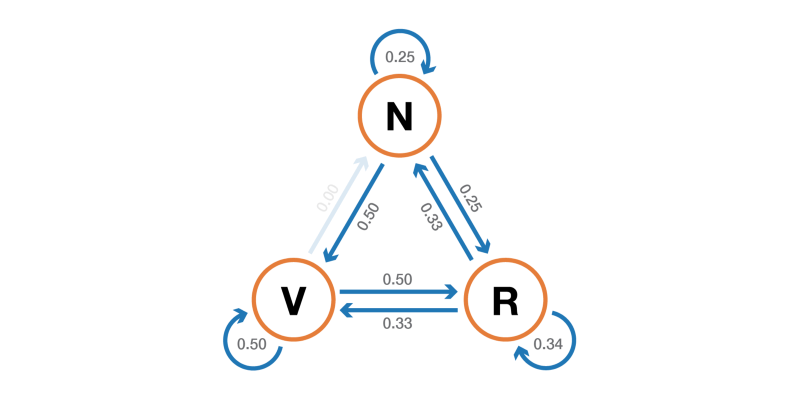
Давайте проиллюстрируем всё это простым примером. Рассмотрим повседневное поведение вымышленного посетителя сайта. В каждый день у него есть 3 возможных состояния: читатель не посещает сайт в этот день (N), читатель посещает сайт, но не читает пост целиком (V) и читатель посещает сайт и читает один пост целиком (R ). Итак, у нас есть следующее пространство состояний:
Допустим, в первый день этот читатель имеет вероятность 50% только зайти на сайт и вероятность 50% посетить сайт и прочитать хотя бы одну статью. Вектор, описывающий исходное распределение вероятностей (n=0) тогда выглядит так:
Также представим, что наблюдаются следующие вероятности:
- когда читатель не посещает один день, то имеет вероятность 25% не посетить его и на следующий день, вероятность 50% только посетить его и 25% — посетить и прочитать статью
- когда читатель посещает сайт один день, но не читает, то имеет вероятность 50% снова посетить его на следующий день и не прочитать статью, и вероятность 50% посетить и прочитать
- когда читатель посещает и читает статью в один день, то имеет вероятность 33% не зайти на следующий день (надеюсь, этот пост не даст такого эффекта!), вероятность 33% только зайти на сайт и 34% — посетить и снова прочитать статью
Тогда у нас есть следующая переходная матрица:
Из предыдущего подраздела мы знаем как вычислить для этого читателя вероятность каждого состояния на следующий день (n=1)
Вероятностную динамику этой цепи Маркова можно графически представить так:
Представление в виде графа цепи Маркова, моделирующей поведение нашего придуманного посетителя сайта.
Свойства цепей Маркова
В этом разделе мы расскажем только о некоторых самых базовых свойствах или характеристиках цепей Маркова. Мы не будем вдаваться в математические подробности, а представим краткий обзор интересных моментов, которые необходимо изучить для использования цепей Маркова. Как мы видели, в случае конечного пространства состояний цепь Маркова можно представить в виде графа. В дальнейшем мы будем использовать графическое представление для объяснения некоторых свойств. Однако не стоит забывать, что эти свойства необязательно ограничены случаем конечного пространства состояний.
Разложимость, периодичность, невозвратность и возвратность
В этом подразделе давайте начнём с нескольких классических способов характеризации состояния или целой цепи Маркова.
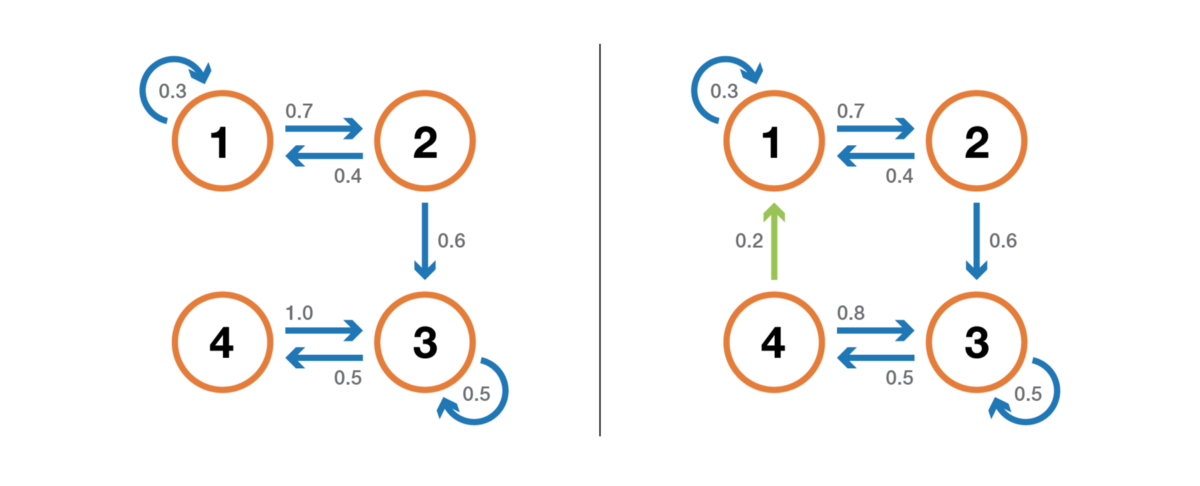
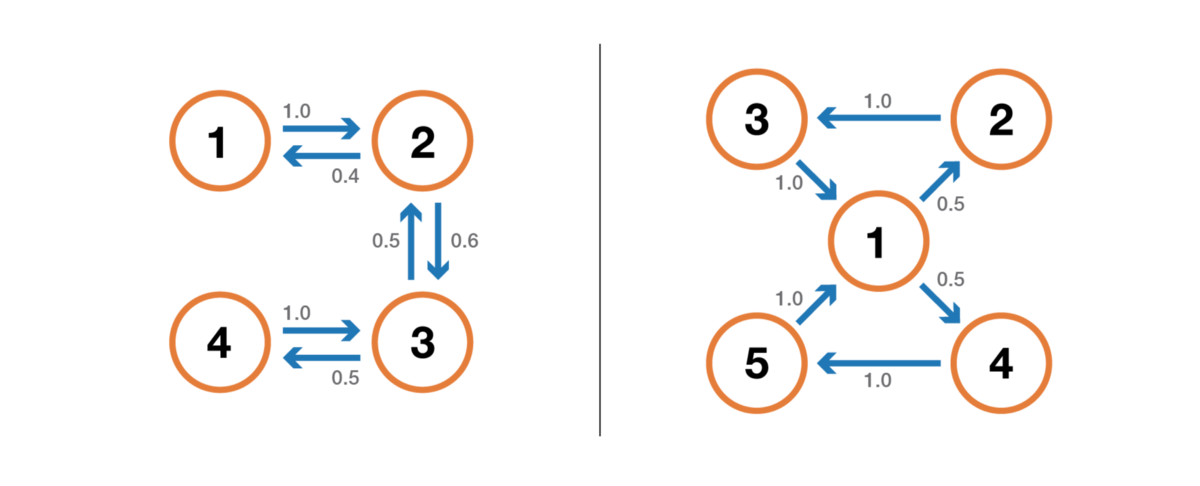
Во-первых, мы упомянем, что цепь Маркова неразложима, если можно достичь любого состояния из любого другого состояния (необязательно, что за один шаг времени). Если пространство состояний конечно и цепь можно представить в виде графа, то мы можем сказать, что граф неразложимой цепи Маркова сильно связный (теория графов).
Иллюстрация свойства неразложимости (несокращаемости). Цепь слева нельзя сократить: из 3 или 4 мы не можем попасть в 1 или 2. Цепь справа (добавлено одно ребро) можно сократить: каждого состояния можно достичь из любого другого.
Состояние имеет период k, если при уходе из него для любого возврата в это состояние нужно количество этапов времени, кратное k (k — наибольший общий делитель всех возможных длин путей возврата). Если k = 1, то говорят, что состояние является апериодическим, а вся цепь Маркова является апериодической, если апериодичны все её состояния. В случае неприводимой цепи Маркова можно также упомянуть, что если одно состояние апериодическое, то и все другие тоже являются апериодическими.
Иллюстрация свойства периодичности. Цепь слева периодична с k=2: при уходе из любого состояния для возврата в него всегда требуется количество шагов, кратное 2. Цепь справа имеет период 3.
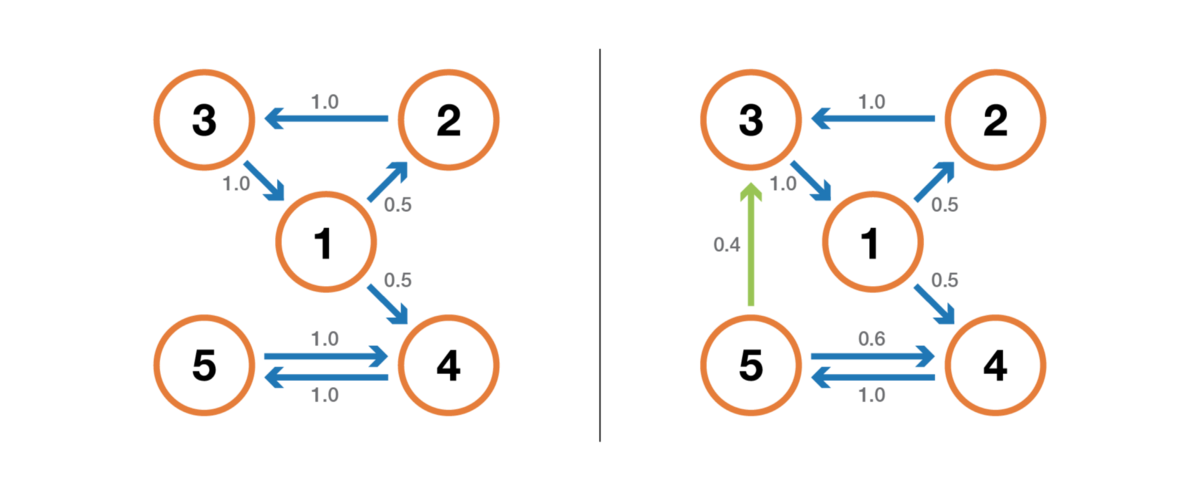
Состояние является невозвратным, если при уходе из состояния существует ненулевая вероятность того, что мы никогда в него не вернёмся. И наоборот, состояние считается возвратным, если мы знаем, что после ухода из состояния можем в будущем вернуться в него с вероятностью 1 (если оно не является невозвратным).
Иллюстрация свойства возвратности/невозвратности. Цепь слева имеет такие свойства: 1, 2 и 3 невозвратны (при уходе из этих точек мы не можем быть абсолютно уверены, что вернёмся в них) и имеют период 3, а 4 и 5 возвратны (при уходе из этих точек мы абсолютно уверены, что когда-нибудь к ним вернёмся) и имеют период 2. Цепь справа имеет ещё одно ребро, делающее всю цепь возвратной и апериодической.
Для возвратного состояния мы можем вычислить среднее время возвратности, которое является ожидаемым временем возврата при покидании состояния. Заметьте, что даже вероятность возврата равна 1, то это не значит, что ожидаемое время возврата конечно. Поэтому среди всех возвратных состояний мы можем различать положительные возвратные состояния (с конечным ожидаемым временем возврата) и нулевые возвратные состояния (с бесконечным ожидаемым временем возврата).
Стационарное распределение, предельное поведение и эргодичность
В этом подразделе мы рассмотрим свойства, характеризующие некоторые аспекты (случайной) динамики, описываемой цепью Маркова.
Распределение вероятностей π по пространству состояний E называют стационарным распределением, если оно удовлетворяет выражению
Так как у нас есть
Тогда стационарное распределение удовлетворяет выражению
По определению, стационарное распределение вероятностей со временем не изменяется. То есть если исходное распределение q является стационарным, тогда оно будет одинаковых на всех последующих этапах времени. Если пространство состояний конечно, то p можно представить в виде матрицы, а π — в виде вектора-строки, и тогда мы получим
Это снова выражает тот факт, что стационарное распределение вероятностей со временем не меняется (как мы видим, умножение справа распределения вероятностей на p позволяет вычислить распределение вероятностей на следующем этапе времени). Учтите, что неразложимая цепь Маркова имеет стационарное распределение вероятностей тогда и только тогда, когда одно из её состояний является положительным возвратным.
Ещё одно интересное свойство, связанное с стационарным распределением вероятностей, заключается в следующем. Если цепь является положительной возвратной (то есть в ней существует стационарное распределение) и апериодической, тогда, какими бы ни были исходные вероятности, распределение вероятностей цепи сходится при стремлении интервалов времени к бесконечности: говорят, что цепь имеет предельное распределение, что является ничем иным, как стационарным распределением. В общем случае его можно записать так:
Ещё раз подчеркнём тот факт, что мы не делаем никаких допущений об исходном распределении вероятностей: распределение вероятностей цепи сводится к стационарному распределению (равновесному распределению цепи) вне зависимости от исходных параметров.
Наконец, эргодичность — это ещё одно интересное свойство, связанное с поведением цепи Маркова. Если цепь Маркова неразложима, то также говорится, что она «эргодическая», потому что удовлетворяет следующей эргодической теореме. Допустим, у нас есть функция f(.), идущая от пространства состояний E к оси (это может быть, например, цена нахождения в каждом состоянии). Мы можем определить среднее значение, перемещающее эту функцию вдоль заданной траектории (временное среднее). Для n-ных первых членов это обозначается как
Также мы можем вычислить среднее значение функции f на множестве E, взвешенное по стационарному распределению (пространственное среднее), которое обозначается
Тогда эргодическая теорема говорит нам, что когда траектория становится бесконечно длинной, временное среднее равно пространственному среднему (взвешенному по стационарному распределению). Свойство эргодичности можно записать так:
Иными словами, оно обозначает, что в пределе ранее поведение траектории становится несущественным и при вычислении временного среднего важно только долговременное стационарное поведение.
Вернёмся к примеру с читателем сайта
Снова рассмотрим пример с читателем сайта. В этом простом примере очевидно, что цепь неразложима, апериодична и все её состояния положительно возвратны.
Чтобы показать, какие интересные результаты можно вычислить с помощью цепей Маркова, мы рассмотрим среднее время возвратности в состояние R (состояние «посещает сайт и читает статью»). Другими словами, мы хотим ответить на следующий вопрос: если наш читатель в один день заходит на сайт и читает статью, то сколько дней нам придётся ждать в среднем того, что он снова зайдёт и прочитает статью? Давайте попробуем получить интуитивное понятие о том, как вычисляется это значение.
Сначала мы обозначим
Итак, мы хотим вычислить m(R,R). Рассуждая о первом интервале, достигнутом после выхода из R, мы получим
Однако это выражение требует, чтобы для вычисления m(R,R) мы знали m(N,R) и m(V,R). Эти две величины можно выразить аналогичным образом:
Итак, у нас получилось 3 уравнения с 3 неизвестными и после их решения мы получим m(N,R) = 2.67, m(V,R) = 2.00 и m(R,R) = 2.54. Значение среднего времени возвращения в состояние R тогда равно 2.54. То есть с помощью линейной алгебры нам удалось вычислить среднее время возвращения в состояние R (а также среднее время перехода из N в R и среднее время перехода из V в R).
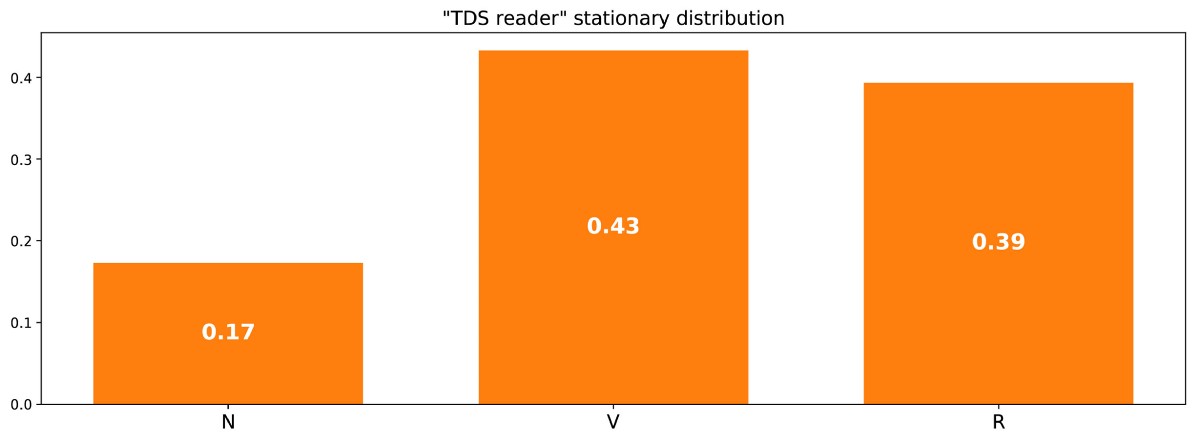
Чтобы закончить с этим примером, давайте посмотрим, каким будет стационарное распределение цепи Маркова. Чтобы определить стационарное распределение, нам нужно решить следующее уравнение линейной алгебры:
То есть нам нужно найти левый собственный вектор p, связанный с собственным вектором 1. Решая эту задачу, мы получаем следующее стационарное распределение:
Стационарное распределение в примере с читателем сайта.
Можно также заметить, что π( R ) = 1/m(R,R), и если немного поразмыслить, то это тождество довольно логично (но подробно об этом мы говорить не будем).
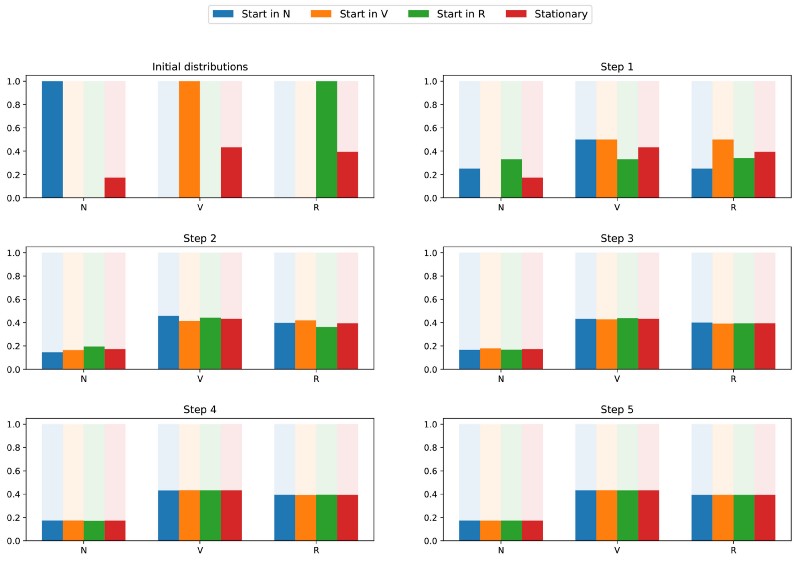
Поскольку цепь неразложима и апериодична, это означает, что в длительной перспективе распределение вероятностей сойдётся к стационарному распределению (для любых исходных параметров). Иными словами, каким бы ни было исходное состояние читателя сайта, если мы подождём достаточно долго и случайным образом выберем день, то получим вероятность π(N) того, что читатель не зайдёт на сайт в этот день, вероятность π(V) того, что читатель зайдёт, но не прочитает статью, и вероятность π® того, что читатель зайдёт и прочитает статью. Чтобы лучше уяснить свойство сходимости, давайте взглянем на следующий график, показывающий эволюцию распределений вероятностей, начинающихся с разных исходных точек и (быстро) сходящихся к стационарному распределению:
Визуализация сходимости 3 распределений вероятностей с разными исходными параметрами (синяя, оранжевая и зелёная) к стационарному распределению (красная).
Классический пример: алгоритм PageRank
Настало время вернуться к PageRank! Но прежде чем двигаться дальше, стоит упомянуть, что интерпретация PageRank, данная в этой статье, не единственно возможная, и авторы оригинальной статьи при разработке методики не обязательно рассчитывали на применение цепей Маркова. Однако наша интерпретация хороша тем, что очень понятна.
Произвольный веб-пользователь
PageRank пытается решить следующую задачу: как нам ранжировать имеющееся множество (мы можем допустить, что это множество уже отфильтровано, например, по какому-то запросу) с помощью уже существующих между страницами ссылок?
Чтобы решить эту задачу и иметь возможность отранжировать страницы, PageRank приблизительно выполняет следующий процесс. Мы считаем, что произвольный пользователь Интернета в исходный момент времени находится на одной из страниц. Затем этот пользователь начинает случайным образом начинает перемещаться, щёлкая на каждой странице по одной из ссылок, которые ведут на другую страницу рассматриваемого множества (предполагается, что все ссылки, ведущие вне этих страниц, запрещены). На любой странице все допустимые ссылки имеют одинаковую вероятность нажатия.
Так мы задаём цепь Маркова: страницы — это возможные состояния, переходные вероятности задаются ссылками со страницы на страницу (взвешенными таким образом, что на каждой странице все связанные страницы имеют одинаковую вероятность выбора), а свойства отсутствия памяти чётко определяются поведением пользователя. Если также предположить, что заданная цепь положительно возвратная и апериодичная (для удовлетворения этим требованиям применяются небольшие хитрости), тогда в длительной перспективе распределение вероятностей «текущей страницы» сходится к стационарному распределению. То есть какой бы ни была начальная страница, спустя длительное время каждая страница имеет вероятность (почти фиксированную) стать текущей, если мы выбираем случайный момент времени.
В основе PageRank лежит такая гипотеза: наиболее вероятные страницы в стационарном распределении должны быть также и самыми важными (мы посещаем эти страницы часто, потому что они получают ссылки со страниц, которые в процессе переходов тоже часто посещаются). Тогда стационарное распределение вероятностей определяет для каждого состояния значение PageRank.
Искусственный пример
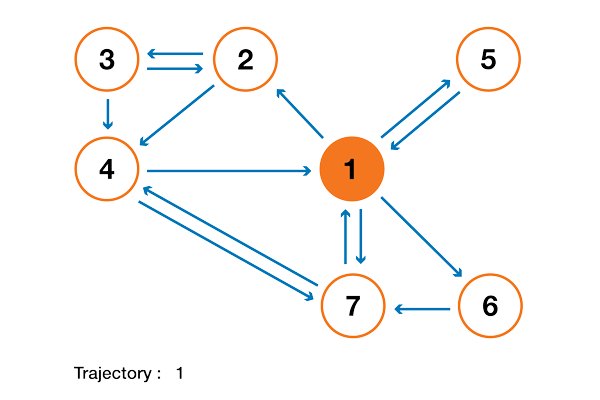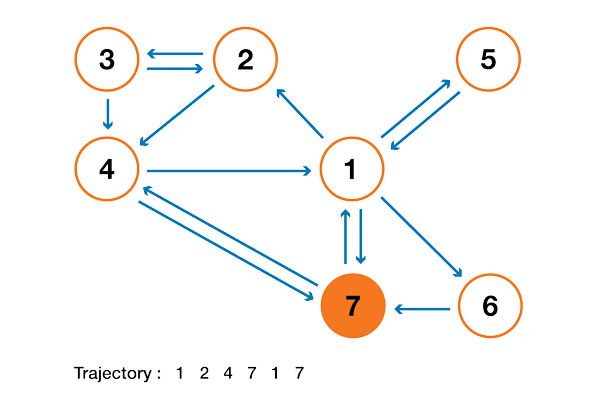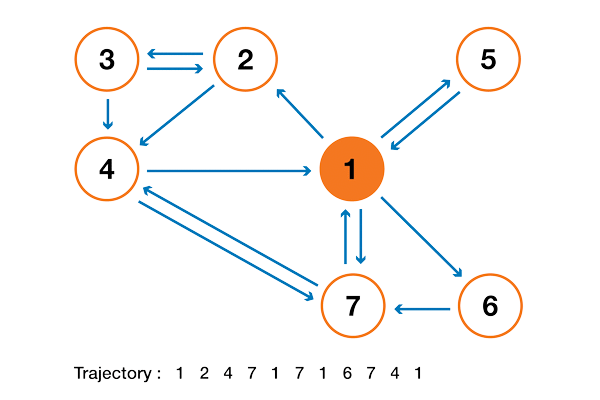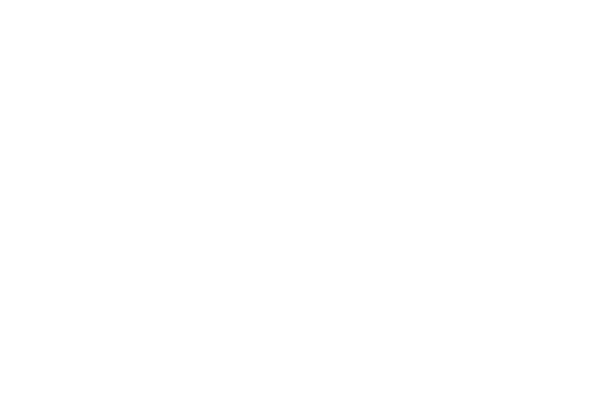
Чтобы это стало намного понятнее, давайте рассмотрим искусственный пример. Предположим, что у нас есть крошечный веб-сайт с 7 страницами, помеченными от 1 до 7, а ссылки между этими страницами соответствуют следующему графу.
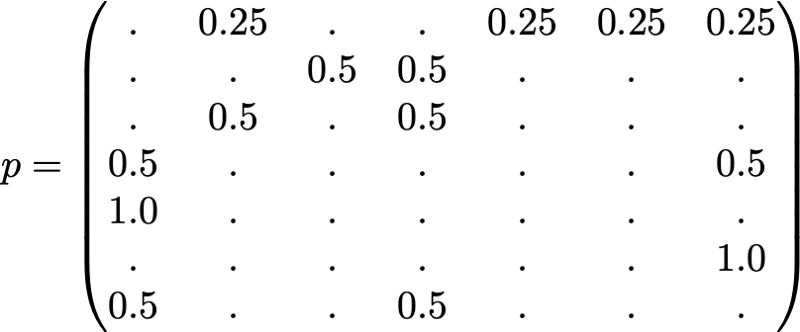
Ради понятности вероятности каждого перехода в показанной выше анимации не показаны. Однако поскольку подразумевается, что «навигация» должна быть исключительно случайной (это называют «случайным блужданием»), то значения можно легко воспроизвести из следующего простого правила: для узла с K исходящими ссылками (странице с K ссылками на другие страницы) вероятность каждой исходящей ссылки равна 1/K. То есть переходная матрица вероятностей имеет вид:
где значения 0.0 заменены для удобства на “.”. Прежде чем выполнять дальнейшие вычисления, мы можем заметить, что эта цепь Маркова является неразложимой и апериодической, то есть в длительной перспективе система сходится к стационарному распределению. Как мы видели, можно вычислить это стационарное распределение, решив следующую левую задачу собственного вектора
Сделав так, мы получим следующие значения PageRank (значения стационарного распределения) для каждой страницы
Значения PageRank, вычисленные для нашего искусственного примера из 7 страниц.
Тогда ранжирование PageRank этого крошечного веб-сайта имеет вид 1 > 7 > 4 > 2 > 5 = 6 > 3.
Выводы
Основные выводы из этой статьи:
- случайные процессы — это наборы случайных величин, часто индексируемые по времени (индексы часто обозначают дискретное или непрерывное время)
- для случайного процесса марковское свойство означает, что при заданном текущем вероятность будущего не зависит от прошлого (это свойство также называется «отсутствием памяти»)
- цепь Маркова с дискретным временем — это случайные процессы с индексами дискретного времени, удовлетворяющие марковскому свойству
- марковское свойство цепей Маркова сильно облегчает изучение этих процессов и позволяет вывести различные интересные явные результаты (среднее время возвратности, стационарное распределение…)
- одна из возможных интерпретаций PageRank (не единственная) заключается в имитации веб-пользователя, случайным образом перемещающегося от страницы к странице; при этом показателем ранжирования становится индуцированное стационарное распределение страниц (грубо говоря, на самые посещаемые страницы в устоявшемся состоянии должны ссылаться другие часто посещаемые страницы, а значит, самые посещаемые должны быть наиболее релевантными)
В заключение ещё раз подчеркнём, насколько мощным инструментом являются цепи Маркова при моделировании задач, связанных со случайной динамикой. Благодаря их хорошим свойствам они используются в различных областях, например, в теории очередей (оптимизации производительности телекоммуникационных сетей, в которых сообщения часто должны конкурировать за ограниченные ресурсы и ставятся в очередь, когда все ресурсы уже заняты), в статистике (хорошо известные методы Монте-Карло по схеме цепи Маркова для генерации случайных переменных основаны на цепях Маркова), в биологии (моделирование эволюции биологических популяций), в информатике (скрытые марковские модели являются важными инструментами в теории информации и распознавании речи), а также в других сферах.
Разумеется, огромные возможности, предоставляемые цепями Маркова с точки зрения моделирования и вычислений, намного шире, чем рассмотренные в этом скромном обзоре. Поэтому мы надеемся, что нам удалось пробудить у читателя интерес к дальнейшему изучению этих инструментов, которые занимают важное место в арсенале учёного и эксперта по данным.
Цепь Маркова – череда событий, в которой каждое последующее событие зависит от предыдущего. В статье мы подробнее разберём это понятие.
Цепь Маркова – это распространенный и довольно простой способ моделирования случайных событий. Используется в самых разных областях, начиная генерацией текста и заканчивая финансовым моделированием. Самым известным примером является SubredditSimulator. В данном случае Цепь Маркова используется для автоматизации создания контента во всем subreddit.
Цепь Маркова понятна и проста в использовании, т. к. она может быть реализована без использования каких-либо статистических или математических концепций. Цепь Маркова идеально подходит для изучения вероятностного моделирования и Data Science.
Сценарий
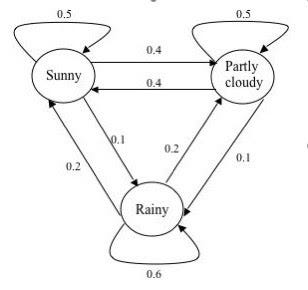
Представьте, что существует только два погодных условия: может быть либо солнечно, либо пасмурно. Всегда можно безошибочно определить погоду в текущий момент. Гарантированно будет ясно или облачно.
Теперь вам захотелось научиться предсказывать погоду на завтрашний день. Интуитивно вы понимаете, что погода не может кардинально поменяться за один день. На это влияет множество факторов. Завтрашняя погода напрямую зависит от текущей и т. д. Таким образом, для того чтобы предсказывать погоду, вы на протяжении нескольких лет собираете данные и приходите к выводу, что после пасмурного дня вероятность солнечного равна 0,25. Логично предположить, что вероятность двух пасмурных дней подряд равна 0,75, так как мы имеем всего два возможных погодных условия.
Теперь вы можете прогнозировать погоду на несколько дней вперед, основываясь на текущей погоде.
Этот пример показывает ключевые понятия цепи Маркова. Цепь Маркова состоит из набора переходов, которые определяются распределением вероятностей, которые в свою очередь удовлетворяют Марковскому свойству.
Обратите внимание, что в примере распределение вероятностей зависит только от переходов с текущего дня на следующий. Это уникальное свойство Марковского процесса – он делает это без использования памяти. Как правило, такой подход не способен создать последовательность, в которой бы наблюдалась какая-либо тенденция. Например, в то время как цепь Маркова способна сымитировать стиль письма, основанный на частоте использования какого-то слова, она не способна создать тексты с глубоким смыслом, так как она может работать только с большими текстами. Именно поэтому цепь Маркова не может производить контент, зависящий от контекста.
Модель
Формально, цепь Маркова – это вероятностный автомат. Распределение вероятностей переходов обычно представляется в виде матрицы. Если цепь Маркова имеет N возможных состояний, то матрица будет иметь вид N x N, в которой запись (I, J) будет являться вероятностью перехода из состояния I в состояние J. Кроме того, такая матрица должна быть стохастической, то есть строки или столбцы в сумме должны давать единицу. В такой матрице каждая строка будет иметь собственное распределение вероятностей.
Общий вид цепи Маркова с состояниями в виде окружностей и ребрами в виде переходов.
Примерная матрица перехода с тремя возможными состояниями.
Цепь Маркова имеет начальный вектор состояния, представленный в виде матрицы N x 1. Он описывает распределения вероятностей начала в каждом из N возможных состояний. Запись I описывает вероятность начала цепи в состоянии I.
Этих двух структур вполне хватит для представления цепи Маркова.
Мы уже обсудили, как получить вероятность перехода из одного состояния в другое, но что насчет получения этой вероятности за несколько шагов? Для этого нам необходимо определить вероятность перехода из состояния I в состояние J за M шагов. На самом деле это очень просто. Матрицу перехода P можно определить вычислением (I, J) с помощью возведения P в степень M. Для малых значений M это можно делать вручную, с помощью повторного умножения. Но для больших значений M, если вы знакомы с линейной алгеброй, более эффективным способом возведения матрицы в степень будет сначала диагонализировать эту матрицу.
Цепь Маркова: заключение
Теперь, зная, что из себя представляет цепь Маркова, вы можете легко реализовать её на одном из языков программирования. Простые цепи Маркова являются фундаментом для изучения более сложных методов моделирования.
Оригинал
Материалы по теме:
- От новичка до профи в машинном обучении за 3 месяца
- Собеседование для Data Scientists: вопросы и ответы
- Как правильно искать и читать научные статьи?
Переходные вероятности. Матрица перехода.
Переходной
вероятностью
называют
условную вероятность того, что из
состояния
в итоге следующего испытания система
перейдет в состояние
.
Таким образом, индекс
относится к предшествующему, а
– к последующему состоянию.
Будем считать, что
число состояний конечно и равно k.
Матрицей
перехода
системы называют матрицу, которая
содержит все переходные вероятности
этой системы:
,
где
представляют вероятности перехода за
один шаг.
Отметим некоторые
особенности матрицы перехода.
-
Элементы
каждой строки матрицы представляют
собой вероятности всех возможных
переходов за один шаг из выбранного
состояния, в том числе и вероятность
отсутствия перехода (элемент строки с
равными индексами) -
Элементы
столбцов задают вероятности всех
переходов системы за один шаг в заданное
состояние -
Так
как в каждой строке матрицы помещены
вероятности событий (т.е. вероятности
перехода из состоянияв любое возможное состояние
),
которые образуют полную группу, то
сумма вероятностей этих событий равна
единице:
-
По
главной диагонали матрицы перехода
стоят вероятности
того, что система не выйдет из состояния,
а останется в нем.
Равенство Маркова
Обозначим через
вероятность того, что в результате n
шагов (испытаний) система перейдет из
состояния
в состояние
.
Например,
–
вероятность перехода за 10 шагов из
третьего состояния в шестое. Отметим,
что при n
= 1 эта вероятность сводится просто к
переходной вероятности
.
Возникает вопрос,
как, зная переходные вероятности
,
найти вероятности перехода состояния
в состояние
за n
шагов. С этой целью вводится в рассмотрение
промежуточное (между
и
) состояние r.
Другими словами, полагают, что из
первоначального состояния
за m
шагов система перейдет в промежуточное
состояние r
с вероятностью
,
после чего за оставшиеся n
– m
шагов из промежуточного состояния r
она перейдет в конечное состояние
с вероятностью
.
Используя формулу полной вероятности,
можно показать, что справедлива формула
Эту формулу называют
равенством
Маркова.
Зная все переходные
вероятности
,
т.е. зная матрицу перехода
из состояния в состояние за один шаг,
можно найти вероятности
перехода из состояние в состояние за
два шага, а значит, и саму матрицу перехода
,
далее – по известной матрице
– найти
и т.д.
Действительно,
полагая в равенстве Маркова n
= 2, m
= 1 получим
или
.
В матричном виде это можно записать как
.
Полагая n=3,
m
=2, получим
.
В общем случае справедливо соотношение
.
Пример.
Пусть матрица перехода
равна
Требуется найти
матрицу перехода
.
Умножая матрицу
саму на себя, получим
.
Для
практических применений чрезвычайно
важным является вопрос о расчете
вероятности
нахождения системы
в том или ином состоянии в конкретный
момент времени.
Решение этого вопроса требует знания
начальных условий, т.е. вероятностей
нахождения системы в определенных
состояниях в начальный момент времени.
Начальным распределением вероятностей
марковской цепи называется распределение
вероятностей состояний в начале процесса
.
Здесь через
обозначена вероятность нахождения
системы в состоянии
в начальный момент времени. В частном
случае, если начальное состояние системы
в точности известно (например
),
то начальная вероятность
,
а все остальные равны нулю.
Если
для однородной цепи Маркова заданы
начальное распределение вероятностей
и матрица перехода, то вероятности
состояний системы на n-м
шаге
вычисляются
по рекуррентной формуле
.
Для иллюстрации
приведем простой пример. Рассмотрим
процесс функционирования некоторой
системы (например, прибора). Пусть прибор
в течение одних суток может находиться
в одном из двух состояний – исправном
(
)
и неисправном (
).
В результате массовых наблюдений за
работой прибора составлена следующая
матрица перехода
,
где
– вероятность того, что прибор останется
в исправном состоянии;
–
вероятность перехода прибора из
исправного в неисправное состояние;
–
вероятность перехода прибора из
неисправного в исправное состояние;
–
вероятность того, что прибор останется
в состоянии “неисправен”.
Пусть вектор
начальных вероятностей состояний
прибора задан соотношением
,
т.е.
(в начальный момент прибор был
неисправен). Требуется определить
вероятности состояния прибора через
трое суток.
Решение:
Используя матрицу перехода, определим
вероятности состояний после первого
шага (после первых суток):
.
Вероятности
состояний после второго шага (вторых
суток) равны
Наконец,
вероятности состояний после третьего
шага (третьих суток) равны
.
Таким образом,
вероятность того, что прибор будет
находиться в исправном состоянии равна
0,819, и того, что в неисправном –
соответственно 0,181.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
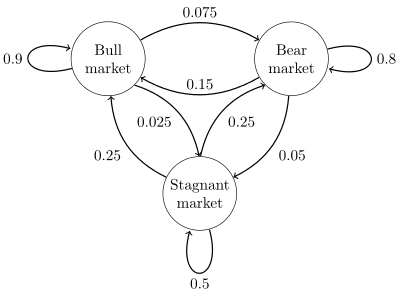
Цепь Маркова используют многие современные компании и организации. Она помогает прогнозировать погоду и разрабатывать маркетинговые стратегии, находит применение в различных приложениях для решения реальных задач конечных автоматов, таких как DFA.

В Python эта концепция представлена в системе вероятностного автомата. Изменения состояния системы называются переходами. Вероятности, связанные с различными изменениями состояния, называются вероятностями перехода. Вероятностный автомат превращает вероятность каждого перехода в функцию перехода и формирует переходную матрицу.
Как создать цепь Маркова
Представим себе такую ситуацию:
“Когда Си Джей грустит (что для нее не очень характерно), она либо отправляется на пробежку, либо поглощает мороженое, либо укладывается спать”.
Для создания цепи Маркова нам потребуется сначала создать переходную матрицу, в которой будут перечислены вероятности каждого перехода состояния. Другими словами, мы должны представить текущее состояние сегодняшним действием Си Джей, в то время как следующее состояние — ее завтрашним действием.
Вероятность перехода состояния будем рассматривать как вероятность того, что Си Джей выполнит одно из трех конкретных действий сегодня, а следующее действие, тоже одно, — завтра. Например, Си Джей отправится на пробежку сегодня, а завтра будет спать. Связав таким образом все вероятности перехода состояния, мы получим переходную матрицу, которая поможет создать цепь Маркова, описывающую конкретную ситуацию.
Наша матрица перехода — это матрица N x N, предполагающая, что N — это количество вероятных состояний. Итак, сначала мы должны определить количество состояний в нашей задаче. Поскольку нам дано три действия, которые Си Джей совершает, когда ей грустно, у нас есть 3 состояния. При этом важно учитывать, что Си Джей не может выполнять все 3 действия одновременно. Другими словами, она не может в одно и то же время спать и есть мороженое, так как ключевые слова в постановке задачи — либо одно действие, либо другое.
Главная идея цепи Маркова заключается в том, что существует только одно текущее состояние и, следовательно, один переход в одно следующее состояние. Это важное замечание поможет нам отслеживать наши вероятности.
Как уже говорилось выше, мы выделили 3 действия, которые совершает Си Джей, когда ей грустно, чтобы определить значение N, или количество состояний. Теперь мы должны создать переходную матрицу связанных вероятностей 3 х 3.
Пошаговый алгоритм процесса создания переходной матрицы
Предположим, что Си Джей грустит. В этом случае, как указано в задаче, нужно рассмотреть 3 вероятных состояния Си Джей:

- Отправляется на пробежку.
- Ест мороженое.
- Спит.
Если текущее состояние “спит”, то можно вычислить вероятность следующего состояния:
- “спит” — 20%;
- “отправляется на пробежку” — 60%;
- “ест мороженое” — 20%.
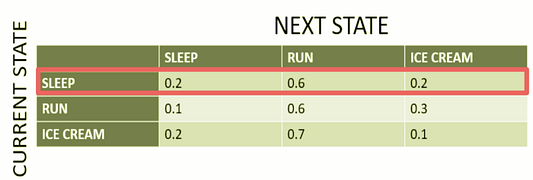
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей спит в течение сегодняшнего дня.
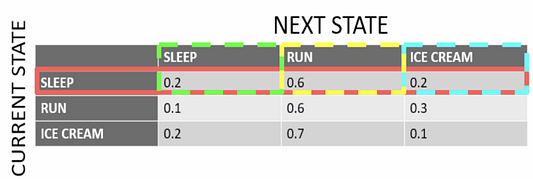
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей спит. Вы можете видеть вероятность каждого перехода, например, когда Си Джей спит сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,6; съест мороженое — 0,2. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “собирается на пробежку”, то вероятность следующего состояния составит:
- “спит” — 10%;
- “собирается на пробежку” — 60%;
- “ест мороженое” — 30%.
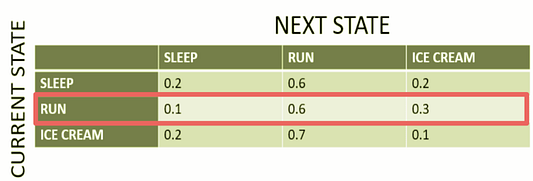
Мы выделили красным цветом строку, на которой сосредоточились, поскольку текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей собирается на пробежку в течение сегодняшнего дня.
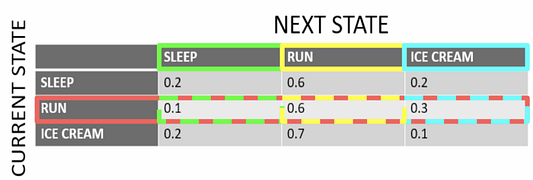
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей собирается на пробежку. Вы можете видеть вероятности каждого перехода, например, когда Си Джей собирается на пробежку в текущий день, вероятность того, что на следующий день она будет спать, равна 0,1; пойдет на пробежку — 0,6; съест мороженое — 0,3. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “ест мороженое”, то вероятность следующего состояния составит:
- “спит” — 20%;
- “собирается на пробежку” — 70%;
- “ест мороженое” — 10%.
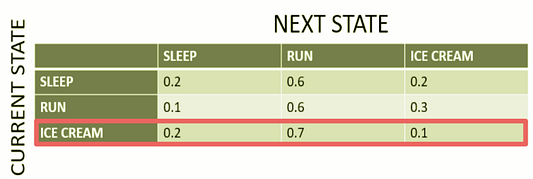
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей ест мороженое в течение сегодняшнего дня.

Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей ест мороженое. Вы можете видеть вероятность каждого перехода, например, когда Си Джей ест мороженое сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,7; съест мороженое — 0,1. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Ниже приведена конечная переходная матрица.
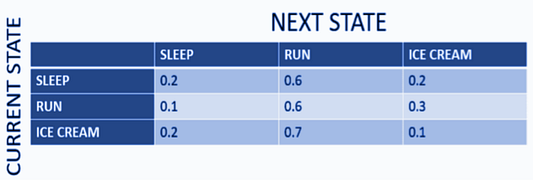
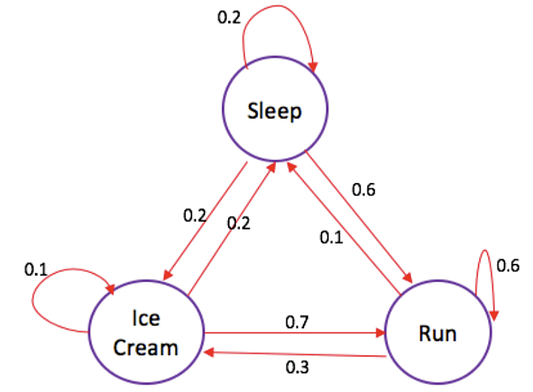
Используя конечную переходную матрицу, мы можем создать цепь Маркова. Для этого отметим все 3 состояния, представляющие ситуацию в настоящее время. Затем создадим переходы между состояниями. Направление стрелки определяет переход от текущего к следующему состоянию. Используя значения из нашей матрицы, подставляем их к соответствующим переходам состояния. Когда текущее состояние равно следующему состоянию, это означает, что Си Джей выполняет одно и то же действие в течение текущего и следующего дня. В этом случае стрелка возвращается к текущему состоянию, поскольку нет перехода в другое состояние.
Дополнительное упражнение
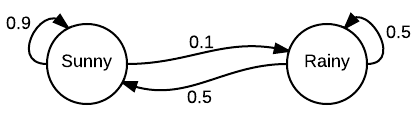
Теперь давайте еще раз взглянем на цепь Маркова, которая моделирует погоду (она была представлена в начале этого поста).
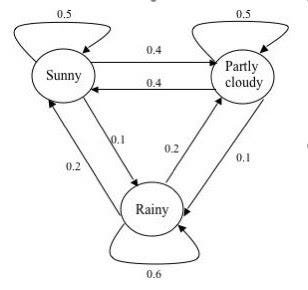
Попытайтесь на основе описанного выше алгоритма создать свою собственную переходную матрицу. Когда закончите, прокрутите страницу вниз, чтобы увидеть конечный результат!
Конечная переходная матрица
Ниже представлена переходная матрица цепи Маркова, которая моделирует погоду. Чтобы ее создать, мы использовали тот же алгоритм, что описан выше, только в обратном направлении.
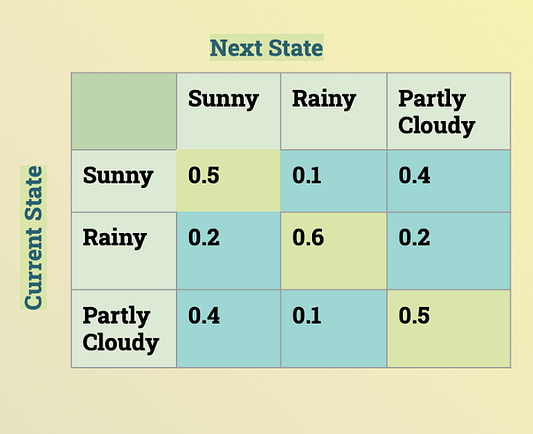
Заключение
Как вы видели в приведенных выше примерах, цепь Маркова можно использовать в прогнозировании погоды, а также в разработке маркетинговой стратегии, основанной на предположении вероятного поведения потребителя. На основе цепей Маркова созданы такие приложения, как Google PageRank, Subreddit, генератор текстов, автозаполнение слов и предложений. Компании могут использовать эту концепцию для принятия сложных решений, поскольку она позволяет увидеть различные потенциальные решения в доступной визуализированной форме.
Читайте также:
- Машинное обучение без данных
- ИИ-технологии на службе у инфлюенс-маркетинга
- Математические операции над массивами и матрицами
Читайте нас в Telegram, VK и Яндекс.Дзен
Перевод статьи Elda Cervantes, The Markov Chain
Источник: Nuances of Programming
Цепь Маркова используют многие современные компании и организации. Она помогает прогнозировать погоду и разрабатывать маркетинговые стратегии, находит применение в различных приложениях для решения реальных задач конечных автоматов, таких как DFA.
В Python эта концепция представлена в системе вероятностного автомата. Изменения состояния системы называются переходами. Вероятности, связанные с различными изменениями состояния, называются вероятностями перехода. Вероятностный автомат превращает вероятность каждого перехода в функцию перехода и формирует переходную матрицу.
Как создать цепь Маркова
Представим себе такую ситуацию:
“Когда Си Джей грустит (что для нее не очень характерно), она либо отправляется на пробежку, либо поглощает мороженое, либо укладывается спать”.
Для создания цепи Маркова нам потребуется сначала создать переходную матрицу, в которой будут перечислены вероятности каждого перехода состояния. Другими словами, мы должны представить текущее состояние сегодняшним действием Си Джей, в то время как следующее состояние — ее завтрашним действием.
Вероятность перехода состояния будем рассматривать как вероятность того, что Си Джей выполнит одно из трех конкретных действий сегодня, а следующее действие, тоже одно, — завтра. Например, Си Джей отправится на пробежку сегодня, а завтра будет спать. Связав таким образом все вероятности перехода состояния, мы получим переходную матрицу, которая поможет создать цепь Маркова, описывающую конкретную ситуацию.
Наша матрица перехода — это матрица N x N, предполагающая, что N — это количество вероятных состояний. Итак, сначала мы должны определить количество состояний в нашей задаче. Поскольку нам дано три действия, которые Си Джей совершает, когда ей грустно, у нас есть 3 состояния. При этом важно учитывать, что Си Джей не может выполнять все 3 действия одновременно. Другими словами, она не может в одно и то же время спать и есть мороженое, так как ключевые слова в постановке задачи — либо одно действие, либо другое.
Главная идея цепи Маркова заключается в том, что существует только одно текущее состояние и, следовательно, один переход в одно следующее состояние. Это важное замечание поможет нам отслеживать наши вероятности.
Как уже говорилось выше, мы выделили 3 действия, которые совершает Си Джей, когда ей грустно, чтобы определить значение N, или количество состояний. Теперь мы должны создать переходную матрицу связанных вероятностей 3 х 3.
Пошаговый алгоритм процесса создания переходной матрицы
Предположим, что Си Джей грустит. В этом случае, как указано в задаче, нужно рассмотреть 3 вероятных состояния Си Джей:
- Отправляется на пробежку.
- Ест мороженое.
- Спит.
Если текущее состояние “спит”, то можно вычислить вероятность следующего состояния:
- “спит” — 20%;
- “отправляется на пробежку” — 60%;
- “ест мороженое” — 20%.
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей спит в течение сегодняшнего дня.
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей спит. Вы можете видеть вероятность каждого перехода, например, когда Си Джей спит сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,6; съест мороженое — 0,2. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “собирается на пробежку”, то вероятность следующего состояния составит:
- “спит” — 10%;
- “собирается на пробежку” — 60%;
- “ест мороженое” — 30%.
Мы выделили красным цветом строку, на которой сосредоточились, поскольку текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей собирается на пробежку в течение сегодняшнего дня.
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей собирается на пробежку. Вы можете видеть вероятности каждого перехода, например, когда Си Джей собирается на пробежку в текущий день, вероятность того, что на следующий день она будет спать, равна 0,1; пойдет на пробежку — 0,6; съест мороженое — 0,3. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Если текущее состояние “ест мороженое”, то вероятность следующего состояния составит:
- “спит” — 20%;
- “собирается на пробежку” — 70%;
- “ест мороженое” — 10%.
Мы выделили красным цветом строку, на которой сосредоточились, так как текущее состояние (как указано в заголовке строки слева) заключается в том, что Си Джей ест мороженое в течение сегодняшнего дня.
Столбцы представляют следующее состояние, учитывая, что текущее состояние заключается в том, что Си Джей ест мороженое. Вы можете видеть вероятность каждого перехода, например, когда Си Джей ест мороженое сегодня, вероятность того, что на следующий день она будет спать, равна 0,2; отправится на пробежку — 0,7; съест мороженое — 0,1. Три разных столбца выделены разными цветами, чтобы изолировать 3 разностные вероятности перехода состояний.
Ниже приведена конечная переходная матрица.
Используя конечную переходную матрицу, мы можем создать цепь Маркова. Для этого отметим все 3 состояния, представляющие ситуацию в настоящее время. Затем создадим переходы между состояниями. Направление стрелки определяет переход от текущего к следующему состоянию. Используя значения из нашей матрицы, подставляем их к соответствующим переходам состояния. Когда текущее состояние равно следующему состоянию, это означает, что Си Джей выполняет одно и то же действие в течение текущего и следующего дня. В этом случае стрелка возвращается к текущему состоянию, поскольку нет перехода в другое состояние.
Дополнительное упражнение
Теперь давайте еще раз взглянем на цепь Маркова, которая моделирует погоду (она была представлена в начале этого поста).
Попытайтесь на основе описанного выше алгоритма создать свою собственную переходную матрицу. Когда закончите, прокрутите страницу вниз, чтобы увидеть конечный результат!
Конечная переходная матрица
Ниже представлена переходная матрица цепи Маркова, которая моделирует погоду. Чтобы ее создать, мы использовали тот же алгоритм, что описан выше, только в обратном направлении.
Заключение
Как вы видели в приведенных выше примерах, цепь Маркова можно использовать в прогнозировании погоды, а также в разработке маркетинговой стратегии, основанной на предположении вероятного поведения потребителя. На основе цепей Маркова созданы такие приложения, как Google PageRank, Subreddit, генератор текстов, автозаполнение слов и предложений. Компании могут использовать эту концепцию для принятия сложных решений, поскольку она позволяет увидеть различные потенциальные решения в доступной визуализированной форме.
Читайте также:
Читайте нас в Telegram, VK
Перевод статьи Elda Cervantes, The Markov Chain