Как составить матрицу поворота - Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 18 апреля 2023 года; проверки требуют 2 правки.

Ма́трицей поворо́та (или матрицей направляющих косинусов) называется ортогональная матрица^[1], которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.

Обычно считают, что в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.

Матрица поворота в двумерном пространстве[править | править код]

В двумерном пространстве поворот можно описать одним углом ;theta со следующей матрицей линейного преобразования в декартовой системе координат:

$M(theta )={begin{pmatrix}cos {theta }&mp sin {theta }\pm sin {theta }&cos {theta }end{pmatrix}}$

или

${displaystyle M(theta )=exp left({theta }cdot {begin{bmatrix}0&mp 1\pm 1&0end{bmatrix}}right)}$

Поворот выполняется путём умножения матрицы поворота на вектор-столбец, описывающий вращаемую точку:

${displaystyle {begin{bmatrix}x'\y'\end{bmatrix}}={begin{bmatrix}cos theta &mp sin theta \pm sin theta &cos theta \end{bmatrix}}{begin{bmatrix}x\y\end{bmatrix}}.}$

Координаты (x′,y′) в результате поворота точки (x, y) имеют вид:

{displaystyle x'=xcos theta mp ysin theta ,}

{displaystyle y'=pm xsin theta +ycos theta .}

Конкретные знаки в формулах зависят от того, является ли система координат правосторонней или левосторонней, и выполняется ли вращение по или против часовой стрелки. Верхний знак указан для обычного соглашения: правосторонняя система координат и положительное направление вращения против часовой стрелки (тот же знак верен для левосторонней координатной системы при выборе положительного направления вращения по часовой стрелке; в оставшихся двух комбинациях — нижний знак).

Матрица поворота в трёхмерном пространстве[править | править код]

Любое вращение в трёхмерном пространстве может быть представлено как композиция поворотов вокруг трёх ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трёх матриц поворота.

Матрицами вращения вокруг оси декартовой системы координат на угол varphi в трёхмерном пространстве с неподвижной системой координат являются:

Вращение вокруг оси :

${displaystyle M_{x}(varphi )={begin{pmatrix}1&0&0\0&cos varphi &-sin varphi \0&sin varphi &cos varphi end{pmatrix}}.}$

Вращение вокруг оси :

${displaystyle M_{y}(varphi )={begin{pmatrix}cos varphi &0&sin varphi \0&1&0\-sin varphi &0&cos varphi end{pmatrix}}.}$

Вращение вокруг оси :

${displaystyle M_{z}(varphi )={begin{pmatrix}cos varphi &-sin varphi &0\sin varphi &cos varphi &0\0&0&1end{pmatrix}}.}$

Матрица поворота последовательности поворотов в некотором оговорённом порядке:

${displaystyle M_{x}(alpha )*M_{y}(beta )*M_{z}(gamma )={begin{pmatrix}1&0&0\0&cos alpha &-sin alpha \0&sin alpha &cos alpha end{pmatrix}}{begin{pmatrix}cos beta &0&sin beta \0&1&0\-sin beta &0&cos beta end{pmatrix}}{begin{pmatrix}cos gamma &-sin gamma &0\sin gamma &cos gamma &0\0&0&1end{pmatrix}}={begin{pmatrix}cos beta cos gamma &-sin gamma cos beta &sin beta \sin alpha sin beta cos gamma +sin gamma cos alpha &-sin alpha sin beta sin gamma +cos alpha cos gamma &-sin alpha cos beta \sin alpha sin gamma -sin beta cos alpha cos gamma &sin alpha cos gamma +sin beta sin gamma cos alpha &cos alpha cos beta end{pmatrix}}.}$

Положительным углам при этом соответствует вращение вектора против часовой стрелки в правой системе координат, и по часовой стрелке в левой системе координат, если смотреть против направления соответствующей оси^[2]. Например, при повороте на угол ${displaystyle alpha =90^{circ }}$ вокруг оси ось переходит в : ${displaystyle M_{z}(90^{circ })cdot mathbf {e} _{x}=mathbf {e} _{y}}$ . Аналогично, ${displaystyle M_{y}(90^{circ })cdot mathbf {e} _{z}=mathbf {e} _{x}}$ и ${displaystyle M_{x}(90^{circ })cdot mathbf {e} _{y}=mathbf {e} _{z}}$ . Правая система координат связана с выбором правого базиса (см. правило буравчика).

Матрица поворота в n-мерном пространстве[править | править код]

Совершенно аналогично могут быть записаны матрицы поворота конечномерного пространства любой более высокой размерности.

Надо только иметь в виду, что для размерностей пространства, не равных трём, невозможно указать единственную прямую, ортогональную двум данным прямым, а поэтому нельзя говорить о вращении вокруг какой-то оси, можно же говорить о вращении в какой-то плоскости^[3]. Все точки при повороте в пространстве любой размерности, начиная с 2, всегда движутся параллельно некоторой (двумерной) плоскости.

Итак, аналогично трёхмерному случаю (с приведенной оговоркой) можем написать матрицу поворота в любой координатной плоскости для любой размерности пространства.

Например:

$M_{1,2}(alpha )={begin{pmatrix}cos alpha &-sin alpha &0&0&0\sin alpha &cos alpha &0&0&0\0&0&1&0&0\0&0&0&1&0\0&0&0&0&1end{pmatrix}}$

— матрица поворота в 5-мерном пространстве в плоскости $x_{1}x_{2}$ ,

$M_{2,4}(alpha )={begin{pmatrix}1&0&0&0&0&0&0\0&cos alpha &0&-sin alpha &0&0&0\0&0&1&0&0&0&0\0&sin alpha &0&cos alpha &0&0&0\0&0&0&0&1&0&0\0&0&0&0&0&1&0\0&0&0&0&0&0&1end{pmatrix}}$

— матрица поворота в 7-мерном пространстве в плоскости $x_{2}x_{4}$ .

Изменение оси поворота[править | править код]

Пусть — матрица поворота вокруг оси с ортом на угол ;alpha , ;M' — матрица поворота вокруг оси с ортом ;n' на тот же угол, причем

где ;M'' — матрица поворота, изменяющая орт оси поворота . Тогда

$M'=M''cdot Mcdot M''^{;T},$

где $;M''^{{;T}}$ — транспонированная матрица ;M'' .

Перестановочность поворотов[править | править код]

Если $;M_{1}$ — матрица поворота вокруг оси с ортом на угол ;alpha , $;M_{2}$ — матрица поворота вокруг оси с ортом на угол ;beta ,
то $M_{2}cdot M_{1}$ — матрица, описывающая поворот, являющийся результатом двух последовательно осуществленных поворотов ( $;M_{1}$ и $;M_{2}$ ), поскольку

$(M_{2}cdot M_{1})cdot r=M_{2}cdot (M_{1}cdot r).$

При этом последовательность поворотов можно поменять, видоизменив поворот $;M_{1}$ :

$M_{2}cdot M_{1}=M'_{1}cdot M_{2},$

где матрица $;M'_{1}$ — матрица поворота на угол ;alpha вокруг оси c ортом ;n', повернутым с помощью поворота $;M_{2}$ :

$n'=M_{2}cdot n,qquad M'_{1}=M_{2}cdot M_{1}cdot M_{2}^{T},$

поскольку $M_{2}^{T}cdot M_{2}=E$ , так как матрица поворота является ортогональной матрицей ( — единичная матрица). Заметим, что коммутативности поворотов в обычном смысле нет, то есть

$M_{2}cdot M_{1}neq M_{1}cdot M_{2}.$

Выражение матрицы поворота через углы Эйлера[править | править код]

Последовательные повороты около осей на угол прецессии ( alpha ), угол нутации ( beta ) и на угол собственного вращения ( gamma ) приводят к следующему выражению для матрицы поворота:

${displaystyle M(alpha ,beta ,gamma )={begin{pmatrix}cos alpha cos gamma -sin alpha cos beta sin gamma &-cos alpha sin gamma -sin alpha cos beta cos gamma &sin alpha sin beta \sin alpha cos gamma +cos alpha cos beta sin gamma &-sin alpha sin gamma +cos alpha cos beta cos gamma &-cos alpha sin beta \sin beta sin gamma &sin beta cos gamma &cos beta end{pmatrix}}.}$

Ось ;X' — ось X, повёрнутая первым поворотом (на ;alpha ), ;Z'' — ось Z, повёрнутая первым и вторым поворотом (на ;alpha и ;beta ). Вследствие перестановочности поворотов приведённая матрица соответствует поворотам на углы ;gamma , ;beta , ;alpha вокруг осей Z, X, Z:

${displaystyle M(alpha ,beta ,gamma )=M_{Z}(alpha )cdot M_{X}(beta )cdot M_{Z}(gamma )}$

В случае, если повороты задаются в другой последовательности, матрица поворота находится перемножением матриц для вращения вокруг соответствующих декартовых осей координат, например:

1) Поворот около осей:
2) Соответственно:
3)
4)
5)
6)
7)
8)
9)
10)
11)
12)

Матрица поворота вокруг произвольной оси[править | править код]

Пусть ось вращения задана единичным вектором , а угол поворота theta .

Тогда матрица поворота в декартовых координатах имеет вид:

$M({hat {mathbf {v} }},theta )={begin{pmatrix}cos theta +(1-cos theta )x^{2}&(1-cos theta )xy-(sin theta )z&(1-cos theta )xz+(sin theta )y\(1-cos theta )yx+(sin theta )z&cos theta +(1-cos theta )y^{2}&(1-cos theta )yz-(sin theta )x\(1-cos theta )zx-(sin theta )y&(1-cos theta )zy+(sin theta )x&cos theta +(1-cos theta )z^{2}end{pmatrix}}$

Выражение матрицы поворота через кватернион[править | править код]

Если задан кватернион , то соответствующая матрица поворота имеет вид:

$Q={begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}end{bmatrix}}.$

Свойства матрицы поворота[править | править код]

Если — матрица, задающая поворот вокруг оси на угол varphi , то:

Примечания[править | править код]

См. также[править | править код]

Матрица перехода
Поворот

Литература[править | править код]

Лурье А. И. Аналитическая механика. — М.:Физматлит. — 1961. — 824 с.

Ссылки[править | править код]

Поворот плоскости. Матрица поворота

Источник

Привет меня зовут Давид, а вот я собственной персоной отрендеренный своим самописным рендером:

К сожалению я не смог найти более качественную бесплатную модель, но все равно выражаю благодарность заморскому скульптору запечатлевшему меня в цифре! И как вы уже догадались, речь пойдет о написании CPU — рендера.

Идея

С развитием шейдерных языков и увеличением мощностей GPU все больше людей заинтересовались программированием графики. Появились новые направления, такие как например Ray marching со стремительным ростом своей популярности.

В преддверии выхода нового монстра от NVidia я решил написать свою (ламповую и олдскульную) статью про основы рендеринга на CPU. Она является отражением моего личного опыта написания рендера, и в ней я попытаюсь довести понятия и алгоритмы с которыми я столкнулся в процессе кодинга. Стоит понимать, что производительность данного софта будет весьма низкая в силу непригодности процессора для выполнения подобных задач.

Выбор языка изначально падал на c++ или rust, но я остановился на c# из-за простоты написания кода и широких возможностей для оптимизации. Итоговым продуктом данной статьи будет рендер, способный выдавать подобные картинки:

Все модели, использованные мной здесь, распространяются в открытом доступе, не занимайтесь пиратством и уважайте труд художников!

Математика

Само собой куда же писать рендеры без понимания их математических основ. В этом разделе я изложу только те концепции, которые я использовал в коде. Тем кто не уверен в своих знаниях пропускать данный раздел не советую, без понимания этих основ трудно будет понять дальнейшее изложение. Так же я рассчитываю, что тот кто решил изучать computation geometry будет иметь базовые знания в линейной алгебре, геометрии, а так же тригонометрии(углы, вектора, матрицы, скалярное произведение). Для тех кто хочет понять вычислительную геометрию глубже, могу порекомендовать книгу Е. Никулина «Компьютерная геометрия и алгоритмы машинной графики».

Повороты вектора. Матрица поворота

Поворот — это одно из основных линейных преобразований векторного пространства. Так же оно является еще и ортогональным преобразованием, так как сохраняет длины преобразованных векторов. В двумерном пространстве существует два типа поворотов:

Поворот относительно начала координат
Поворот относительно некоторой точки

Здесь я рассмотрю только первый тип, т.к. второй является производным от первого и отличается лишь сменой системы координат вращения (системы координат мы разберем далее).

Давайте выведем формулы для вращения вектора в двумерном пространстве. Обозначим координаты исходного вектора — {x, y}. Координаты нового вектора, повернутого на угол f, обозначим как {x’ y’}.

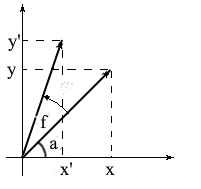
Мы знаем, что длина у этих векторов общая и поэтому можем использовать понятия косинуса и синуса для того, чтобы выразить эти вектора через длину и угол относительно оси OX:

Заметьте, что мы можем использовать формулы косинуса и синуса суммы для того, чтобы разложить значения x’ и y’. Для тех, кто подзабыл я напомню эти формулы:

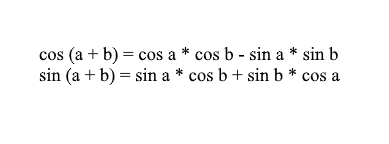
Разложив координаты повернутого вектора через них получим:

Здесь нетрудно заметить, что множители l * cos a и l * sin a – это координаты исходного вектора: x = l * cos a, y = l * sin a. Заменим их на x и y:

Таким образом мы выразили повернутый вектор через координаты исходного вектора и угол его поворота. В виде матрицы это выражение будет выглядеть так:

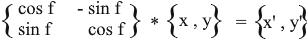
Умножьте и проверьте что результат эквивалентен тому, что мы вывели.

Поворот в трехмерном пространстве

Мы рассмотрели поворот в двумерном пространстве, а так же вывели матрицу для него. Теперь возникает вопрос, а как получить подобные преобразования для трех измерений? В двумерном случае мы вращали вектора на плоскости, здесь же бесконечное количество плоскостей относительно которых мы можем это сделать. Однако существует три базовых типа вращений, при помощи которых можно выразить любой поворот вектора в трехмерном пространстве — это XY, XZ, YZ вращения.

XY вращение.

При таком повороте мы вращаем вектор относительно оси OZ координатной системы. Представьте, что вектора — это вертолётные лопасти, а ось OZ — это мачта на которой они держаться. При XY вращении вектора будут поворачиваться относительно оси OZ, как лопасти вертолета относительно мачты.

Заметьте, что при таком вращении z координаты векторов не меняются, а меняются x и x координаты — поэтому это и называется XY вращением.

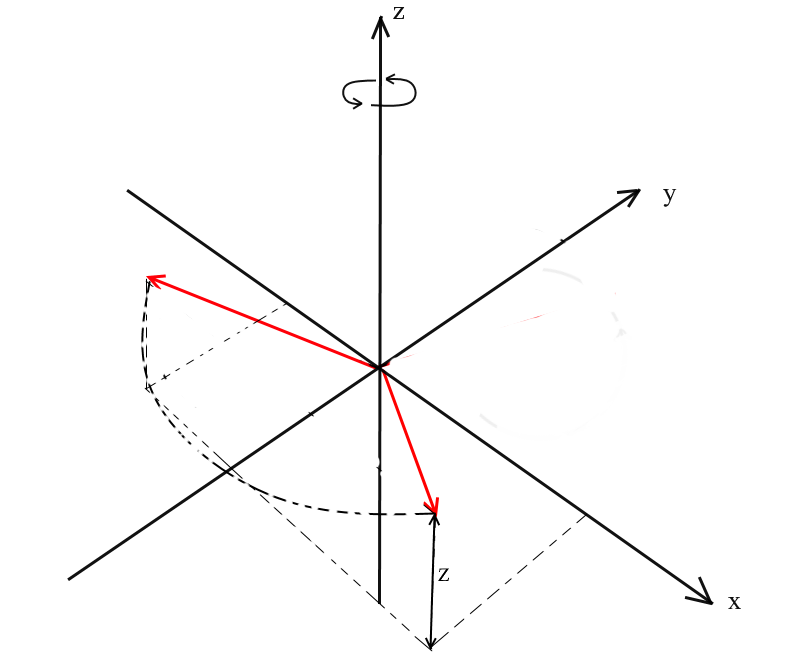
Нетрудно вывести и формулы для такого вращения: z — координата остается прежней, а x и y изменяются по тем же принципам, что и в 2д вращении.

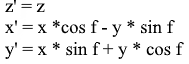
То же в виде матрицы:

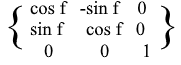
Для XZ и YZ вращений все аналогично:

Проекция

Понятие проекции может варьироваться в зависимости от контекста в котором его используют. Многие, наверное, слышали про такие понятия, как проекция на плоскость или проекция на координатную ось.

В том понимании которое мы используем здесь проекция на вектор — это тоже вектор. Его координаты – точка пересечения перпендикуляра опущенного из вектора a на b с вектором b.

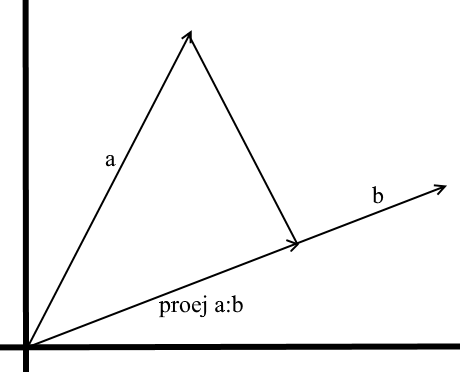
Для задания такого вектора нам нужно знать его длину и направление. Как мы знаем прилегающий катет и гипотенуза в прямоугольном треугольнике связаны отношением косинуса, поэтому используем его, чтобы выразить длину вектора проекции:

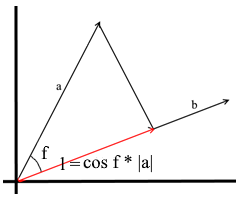
Направление вектора проекции по определению совпадает с вектором b, значит проекция определяется формулой:

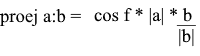
Здесь мы получаем направление проекции в виде единичного вектора и умножаем его на длину проекции. Несложно понять, что результатом будет как раз-таки то, что мы ищем.

Теперь представим все через скалярное произведение:

Получаем удобную формулу для нахождения проекции:

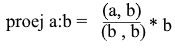
Системы координат. Базисы

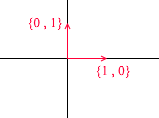
Многие привыкли работать в стандартной системе координат XYZ, в ней любые 2 оси будут перпендикулярны друг другу, а координатные оси можно представить в виде единичных векторов:

На деле же систем координат бесконечное множество, каждая из них является базисом. Базис n-мерного пространства является набором векторов {v1, v2 …… vn} через которые представляются все вектора этого пространства. При этом ни один вектор из базиса нельзя представить через другие его вектора. По сути каждый базис является отдельной системой координат, в которой вектора будут иметь свои, уникальные координаты.

Давайте разберем, что из себя представляет базис для двумерного пространства. Возьмём для примера всем знакомую декартову систему координат из векторов X {1, 0}, Y {0, 1}, которая является одним из базисов для двумерного пространства:

Любой вектор на плоскости можно представить в виде суммы векторов этого базиса с некими коэффициентами или же в виде линейной комбинации. Вспомните, что вы делаете когда записываете координаты вектора — вы пишете x — координату, а далее — y. Таким образом вы на самом деле определяете коэффициенты разложения по векторам базиса.

Теперь возьмём другой базис:

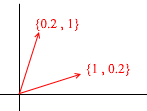
Через его вектора также можно представить любой 2д вектор:

А вот такой набор векторов не является базисом двухмерного пространства:

В нем два вектора {1,1} и {2,2} лежат на одной прямой. Какие бы их комбинации вы не брали получать будете только вектора, лежащие на общей прямой y = x. Для наших целей такие дефектные не пригодятся, однако, понимать разницу, я считаю, стоит. По определению все базисы объединяет одно свойство – ни один из векторов базиса нельзя представить в виде суммы других векторов базиса с коэффициентами или же ни один вектор базиса не является линейной комбинацией других. Вот пример набора из 3-х векторов который так же не является базисом:

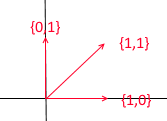
Через него можно выразить любой вектор двумерной плоскости, однако вектор {1, 1} в нем является лишним так как сам может быть выражен через вектора {1, 0} и {0,1} как {1,0} + {0,1}.

Вообще любой базис n-мерного пространства будет содержать ровно n векторов, для 2д это n соответственно равно 2.

Перейдем к 3д. Трехмерный базис будет содержать в себе 3 вектора:

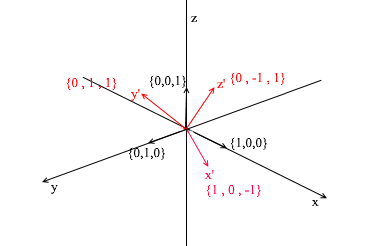
Если для двумерного базиса достаточно было двух векторов не лежащих на одной прямой, то в трехмерном пространстве набор векторов будет базисом если:

1)2 вектора не лежат на одной прямой
2)3-й не лежит на плоскости образованной двумя другими.

С данного момента базисы, с которыми мы работаем будут ортогональными (любые их вектора перпендикулярны) и нормированными (длина любого вектора базиса — 1). Другие нам просто не понадобятся. К примеру стандартный базис

удовлетворяет этим критериям.

Переход в другой базис

До сих пор мы записывали разложение вектора как сумму векторов базиса с коэффициентами:

Снова рассмотрим стандартный базис – вектор {1, 3, 6} в нем можно записать так:

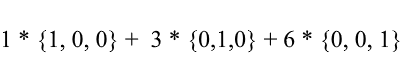
Как видите коэффициенты разложения вектора в базисе являются его координатами в этом базисе. Разберем следующий пример:

Этот базис получен из стандартного применением к нему XY вращения на 45 градусов. Возьмем вектор a в стандартной системе имеющий координаты {0 ,1, 1}

Через вектора нового базиса его можно разложить таким образом:

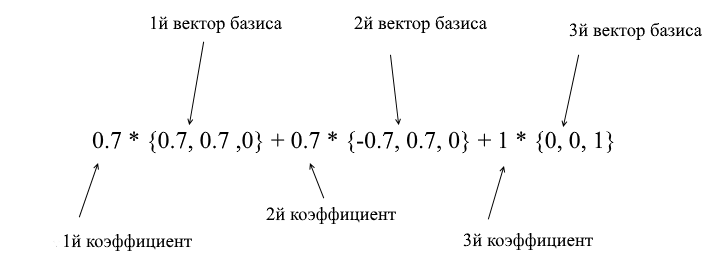
Если вы посчитаете эту сумму, то получите {0, 1, 1} – вектор а в стандартном базисе. Исходя из этого выражения в новом базисе вектор а имеет координаты {0.7, 0.7, 1} – коэффициенты разложения. Это будет виднее если взглянуть с другого ракурса:

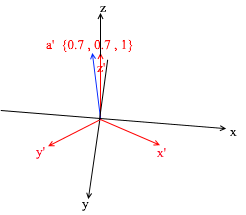
Но как находить эти коэффициенты? Вообще универсальный метод — это решение довольно сложной системы линейных уравнений. Однако как я сказал ранее использовать мы будем только ортогональные и нормированные базисы, а для них есть весьма читерский способ. Заключается он в нахождении проекций на вектора базиса. Давайте с его помощью найдем разложение вектора a в базисе X{0.7, 0.7, 0} Y{-0.7, 0.7, 0} Z{0, 0, 1}

Для начала найдем коэффициент для y’. Первым шагом мы находим проекцию вектора a на вектор y’ (как это делать я разбирал выше):

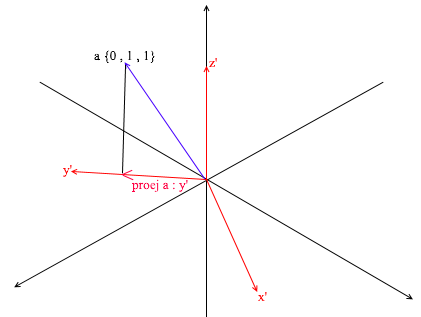
Второй шаг: делим длину найденной проекции на длину вектора y’, тем самым мы узнаем “сколько векторов y’ помещается в векторе проекции” – это число и будет коэффициентом для y’, а также y — координатой вектора a в новом базисе! Для x’ и z’ повторим аналогичные операции:

Теперь мы имеем формулы для перехода из стандартного базиса в новый:

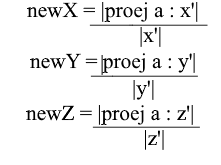
Ну а так как мы используем только нормированные базисы и длины их векторов равны 1 отпадет необходимость делить на длину вектора в формуле перехода:

Раскроем x-координату через формулу проекции:

Заметьте, что знаменатель (x’, x’) и вектор x’ в случае нормированного базиса так же равен 1 и их можно отбросить. Получим:

Мы видим, что координата x базисе выражается как скалярное произведение (a, x’), координата y соответственно – как (a, y’), координата z – (a, z’). Теперь можно составить матрицу перехода к новым координатам:

Системы координат со смещенным центром

У всех систем координат которые мы рассмотрели выше началом координат была точка {0,0,0}. Помимо этого существуют еще системы со смещенной точкой начала координат:

Для того, чтобы перевести вектор в такую систему нужно сначала выразить его относительно нового центра координат. Сделать это просто — вычесть из вектора этот центр. Таким образом вы как бы «передвигаете» саму систему координат к новому центу, при этом вектор остается на месте. Далее можно использовать уже знакомую нам матрицу перехода.

Пишем геометрический движок. Создание проволочного рендера.

Ну вот, думаю тому кто прошел раздел с математикой и не закрыл статью можно промывать мозги более интересными вещами! В этом разделе мы начнем писать основы 3д движка и рендеринга. Вообще рендеринг — это довольно сложная процедура, которая включает в себя много разных операций: отсечение невидимых граней, растеризация, расчет света, обработку различных эффектов, материалов(иногда даже физику). Все это мы частично разберем в дальнейшем, а сейчас мы займемся более простыми вещами — напишем проволочный рендер. Суть его в том, что он рисует объект в виде линий, соединяющих его вершины, поэтому результат выглядит похожим на сеть из проволок:

Полигональная графика

Традиционно в компьютерной графике используется полигональное представление данных трехмерных объектов. Таким образом представляются данные в форматах OBJ, 3DS, FBX и многих других. В компьютере такие данные хранятся в виде двух множеств: множество вершин и множество граней(полигонов). Каждая вершина объекта представлена своей позицией в пространстве — вектором, а каждая грань(полигон) представлена тройкой целых чисел которые являются индексами вершин данного объекта. Простейшие объекты(кубы, сферы и т.д.) состоят из таких полигонов и называются примитивами.

В нашем движке примитив будет основным объектом трехмерной геометрии — все остальные объекты будут наследоваться от него. Опишем класс примитива:

    abstract class Primitive
    {
        public Vector3[] Vertices { get; protected set; }
        public int[] Indexes { get; protected set; }
    }

Пока все просто — есть вершины примитива и есть индексы для формирования полигонов. Теперь можно использовать этот класс чтобы создать куб:

   public class Cube : Primitive
      {
        public Cube(Vector3 center, float sideLen)
        {
            var d = sideLen / 2;
            Vertices = new Vector3[]
                {
                    new Vector3(center.X - d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X - d , center.Y - d, center.Z) ,
                    new Vector3(center.X - d , center.Y , center.Z - d) ,
                    new Vector3(center.X - d , center.Y , center.Z) ,
                    new Vector3(center.X + d , center.Y - d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y - d, center.Z) ,
                    new Vector3(center.X + d , center.Y + d, center.Z - d) ,
                    new Vector3(center.X + d , center.Y + d, center.Z + d) ,
                };

            Indexes = new int[]
                {
                    1,2,4 ,
                    1,3,4 ,
                    1,2,6 ,
                    1,5,6 ,
                    5,6,8 ,
                    5,7,8 ,
                    8,4,3 ,
                    8,7,3 ,
                    4,2,8 ,
                    2,8,6 ,
                    3,1,7 ,
                    1,7,5
                };
        }
    }

int Main()
{
        var cube = new Cube(new Vector3(0, 0, 0), 2);
}

Реализуем системы координат

Мало задать объект набором полигонов, для планирования и создания сложных сцен необходимо расположить объекты в разных местах, поворачивать их, уменьшать или увеличивать их в размере. Для удобства этих операций используются так называемые локальные и глобальная системы координат. Каждый объект на сцене имеет свои свою собственную систему координат — локальную, а так же собственную точку центра.

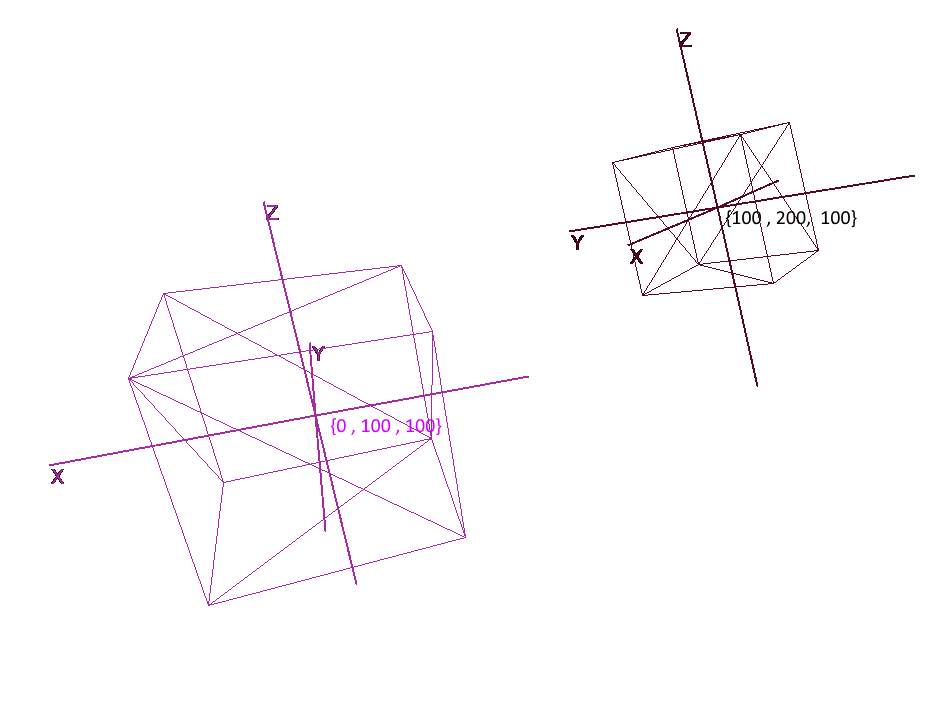
Представление объекта в локальных координатах позволяет легко производить любые операции с ним. Например, для перемещения объекта на вектор a достаточно будет сдвинуть центр его системы координат на этот вектор, для вращения объекта — повернуть его локальные координаты.

При работе с объектом мы будем производить операции с его вершинами в локальной системе координат, при рендеринге будем предварительно переводить все объекты сцены в единую систему координат — глобальную. Добавим системы координат в код. Для этого создадим объект класса Pivot (стержень, точка опоры) который будет представлять локальный базис объекта и его центральную точку. Перевод точки в систему координат представленную Pivot будет производиться в 2 шага:

1)Представление точки относительно центра новых координат
2)Разложение по векторам нового базиса

Наоборот же, чтобы представить локальную вершину объекта в глобальных координатах необходимо выполнить эти действия в обратном порядке:

1)Разложение по векторам глобального базиса
2)Представление относительно глобального центра

Напишем класс для представления систем координат:

    public class Pivot
    {
        //точка центра
        public Vector3 Center { get; private set; }
        //вектора локального базиса - локальные координатные оси
        public Vector3 XAxis { get; private set; }
        public Vector3 YAxis { get; private set; }
        public Vector3 ZAxis { get; private set; }

        //Матрица перевода в локальные координаты
        public Matrix3x3 LocalCoordsMatrix => new Matrix3x3
            (
                XAxis.X, YAxis.X, ZAxis.X,
                XAxis.Y, YAxis.Y, ZAxis.Y,
                XAxis.Z, YAxis.Z, ZAxis.Z
            );

        //Матрица перевода в глобальные координаты
        public Matrix3x3 GlobalCoordsMatrix => new Matrix3x3
            (
                XAxis.X , XAxis.Y , XAxis.Z,
                YAxis.X , YAxis.Y , YAxis.Z,
                ZAxis.X , ZAxis.Y , ZAxis.Z
            );

        public Vector3 ToLocalCoords(Vector3 global)
        {
            //Находим позицию вектора относительно точки центра и раскладываем в локальном базисе
            return LocalCoordsMatrix * (global - Center);
        }
        public Vector3 ToGlobalCoords(Vector3 local)
        {
            //В точности да наоборот - раскладываем локальный вектор в глобальном базисе и находим позицию относительно глобального центра
            return (GlobalCoordsMatrix * local)  + Center;
        }

        public void Move(Vector3 v)
        {
            Center += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            XAxis = XAxis.Rotate(angle, axis);
            YAxis = YAxis.Rotate(angle, axis);
            ZAxis = ZAxis.Rotate(angle, axis);
        }
    }

Теперь используя данный класс добавим в примитивы функции вращения, передвижения и увеличения:

    public abstract class Primitive
    {
        //Локальный базис объекта
        public Pivot Pivot { get; protected set; }
        //Локальные вершины
        public Vector3[] LocalVertices { get; protected set; }
        //Глобальные вершины
        public Vector3[] GlobalVertices { get; protected set; }
        //Индексы вершин
        public int[] Indexes { get; protected set; }

        public void Move(Vector3 v)
        {
            Pivot.Move(v);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] += v;
        }

        public void Rotate(float angle, Axis axis)
        {
            Pivot.Rotate(angle , axis);

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }

        public void Scale(float k)
        {
            for (int i = 0; i < LocalVertices.Length; i++)
                LocalVertices[i] *= k;

            for (int i = 0; i < LocalVertices.Length; i++)
                GlobalVertices[i] = Pivot.ToGlobalCoords(LocalVertices[i]);
        }
    }

Вращение и перемещение объекта с помощью локальных координат

Рисование полигонов. Камера

Основным объектом сцены будет камера — с помощью нее объекты будут рисоваться на экране. Камера, как и все объекты сцены, будет иметь локальные координаты в виде объекта класса Pivot — через него мы будем двигать и вращать камеру:

Для отображения объекта на экране будем использовать немудреный способ перспективной проекции. Принцип на котором основан этом метод заключается в том, что чем дальше от нас расположен объект тем меньше он будет казаться. Наверное многие решали когда-то в школе задачу про измерение высоты дерева находящимся на некотором расстоянии от наблюдателя:

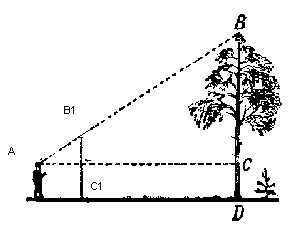
Представьте, что луч от верхней точки дерева падает на некую проекционную плоскость находящуюся на расстоянии C1 от наблюдателя и рисует на ней точку. Наблюдатель видит эту точку и хочет по ней определить высоту дерева. Как вы могли заметить высота дерева и высота точки на проекционной плоскости связанны отношением подобных треугольников. Тогда наблюдатель может определить высоту точки используя это отношение:

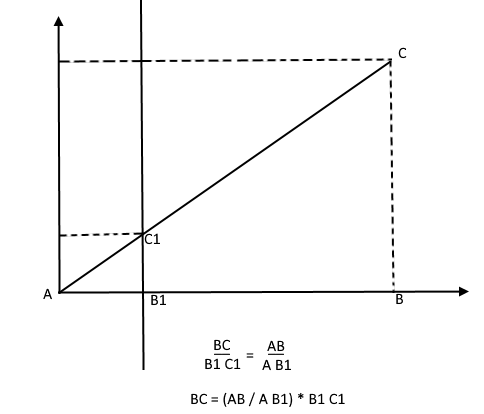
Наоборот же, зная высоту дерева он может найти высоту точки на проекционной плоскости:

Теперь вернемся к нашей камере. Представьте, что к оси z координат камеры прикреплена проекционная плоскость на расстоянии z’ от начала координат. Формула такой плоскости z = z’, ее можно задать одним числом — z’. На эту плоскость падают лучи от вершин различных объектов. Попадая на плоскость луч будет оставлять на ней точку. Соединяя такие точки можно нарисовать объект.

Такая плоскость будет представлять экран. Координату проекции вершины объекта на экран будем находить в 2 этапа:

1)Переводим вершину в локальные координаты камеры
2)Находим проекцию точки через отношение подобных треугольников

Проекция будет 2-мерным вектором, ее координаты x’ и y’ и будут определять позицию точки на экране компьютера.

Класс камеры 1

public class Camera
{
    //локальные координаты камеры
    public Pivot Pivot { get; private set; }
    //расстояние до проекционной плоскости
    public float ScreenDist { get; private set; }

    public Camera(Vector3 center, float screenDist)
    {
        Pivot = new Pivot(center);
        ScreenDist = screenDist;
    }
    public void Move(Vector3 v)
    {
        Pivot.Move(v);
    }
    public void Rotate(float angle, Axis axis)
    {
        Pivot.Rotate(angle, axis);
    }
    public Vector2 ScreenProection(Vector3 v)
    {
        var local = Pivot.ToLocalCoords(v);
        //через подобные треугольники находим проекцию
        var delta = ScreenDist / local.Z;
        var proection = new Vector2(local.X, local.Y) * delta;
        return proection;
    }
}

Данный код имеет несколько ошибок, о исправлении которых мы поговорим далее.

Отсекаем невидимые полигоны

Спроецировав таким образом на экран три точки полигона мы получим координаты треугольника который соответствует отображению полигона на экране. Но таким образом камера будет обрабатывать любые вершины, включая те, чьи проекции выходят за область экрана, если попытаться нарисовать такую вершину велика вероятность словить ошибок. Камера так же будет обрабатывать полигоны которые находятся позади нее (координаты z их точек в локальном базисе камеры меньше z’) — такое «затылковое» зрение нам тоже ни к чему.

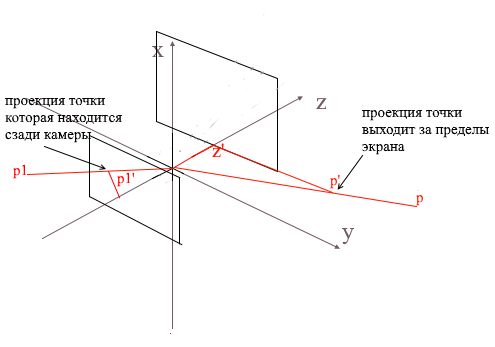
Для отсечения невидимых вершин в open gl используются метод усекающей пирамиды. Заключается он в задании двух плоскостей — ближней(near plane) и дальней(far plane). Все, что лежит между этими двумя плоскостями будет подлежать дальнейшей обработке. Я же использую упрощенный вариант с одной усекающей плоскостью — z’. Все вершины, лежащие позади нее будут невидимыми.

Добавим в камеру два новых поля — ширину и высоту экрана.
Теперь каждую спроецированную точку будем проверять на попадание в область экрана. Так же отсечем точки позади камеры. Если точка лежит сзади или ее проекция не попадает на экран то метод вернет точку {float.NaN, float.NaN}.

Код камеры 2

public Vector2 ScreenProection(Vector3 v)
{
    var local = Pivot.ToLocalCoords(v);
    //игнорируем точки сзади камеры
    if (local.Z < ScreenDist)
    {
        return new Vector2(float.NaN, float.NaN);
    }
    //через подобные треугольники находим проекцию
    var delta = ScreenDist / local.Z;
    var proection = new Vector2(local.X, local.Y) * delta;
    //если точка принадлежит экранной области - вернем ее
    if (proection.X >= 0 && proection.X < ScreenWidth && proection.Y >= 0 && proection.Y < ScreenHeight)
    {
        return proection;
    }
    return new Vector2(float.NaN, float.NaN);
}

Переводим в экранные координаты

Здесь я разъясню некоторый момент. Cвязан он с тем, что во многих графических библиотеках рисование происходит в экранной системе координат, в таких координатах начало — это верхняя левая точка экрана, x увеличивается при движении вправо, а y — при движении вниз. В нашей проекционной плоскости точки представлены в обычных декартовых координатах и перед отрисовкой необходимо переводить эти координаты в экранные. Сделать это нетрудно, нужно только сместить начало координат в верхний левый угол и инвертировать y:

Код камеры 3

public Vector2 ScreenProection(Vector3 v)
{
    var local = Pivot.ToLocalCoords(v);
    //игнорируем точки сзади камеры
    if (local.Z < ScreenDist)
    {
        return new Vector2(float.NaN, float.NaN);
    }
    //через подобные треугольники находим проекцию
    var delta = ScreenDist / local.Z;
    var proection = new Vector2(local.X, local.Y) * delta;
    //этот код нужен для перевода проекции в экранные координаты
    var screen = proection + new Vector2(ScreenWidth / 2, -ScreenHeight / 2);
    var screenCoords = new Vector2(screen.X, -screen.Y);
    //если точка принадлежит экранной области - вернем ее
    if (screenCoords.X >= 0 && screenCoords.X < ScreenWidth && screenCoords.Y >= 0 && screenCoords.Y < ScreenHeight)
    {
        return screenCoords;
    }
    return new Vector2(float.NaN, float.NaN);
}

Корректируем размер спроецированного изображения

Если вы используете предыдущий код для того, чтобы нарисовать объект то получите что-то вроде этого:

Почему — то все объекты рисуются очень маленькими. Для того, чтобы понять причину вспомните как мы вычисляли проекцию — умножали x и y координаты на дельту отношения z’ / z. Это значит, что размер объекта на экране зависит от расстояния до проекционной плоскости z’. А ведь z’ мы можем задать сколь угодно маленьким значением. Значит нам нужно корректировать размер проекции в зависимости от текущего значения z’. Для этого добавим в камеру еще одно поле — угол ее обзора.

Он нам нужен для сопоставления углового размера экрана с его шириной. Угол будет сопоставлен с шириной экрана таким образом: максимальный угол в пределах которого смотрит камера — это левый или правый край экрана. Тогда максимальный угол от оси z камеры составляет o / 2. Проекция, которая попала на правый край экрана должна иметь координату x = width / 2, а на левый: x = -width / 2. Зная это выведем формулу для нахождения коэффициента растяжения проекции:

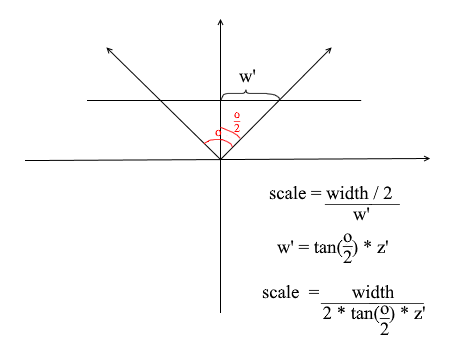
Код камеры 4

public float ObserveRange { get; private set; }
public float Scale => ScreenWidth / (float)(2 * ScreenDist * Math.Tan(ObserveRange / 2));
public Vector2 ScreenProection(Vector3 v)
{
    var local = Pivot.ToLocalCoords(v);
    //игнорируем точки сзади камеры
    if (local.Z < ScreenDist)
    {
        return new Vector2(float.NaN, float.NaN);
    }
    //через подобные треугольники находим проекцию и умножаем ее на коэффициент растяжения
    var delta = ScreenDist / local.Z * Scale;
    var proection = new Vector2(local.X, local.Y) * delta;
    //этот код нужен для перевода проекции в экранные координаты
    var screen = proection + new Vector2(ScreenWidth / 2, -ScreenHeight / 2);
    var screenCoords = new Vector2(screen.X, -screen.Y);
    //если точка принадлежит экранной области - вернем ее
    if (screenCoords.X >= 0 && screenCoords.X < ScreenWidth && screenCoords.Y >= 0 && screenCoords.Y < ScreenHeight)
    {
        return screenCoords;
    }
    return new Vector2(float.NaN, float.NaN);
}

Вот такой простой код отрисовки я использовал для теста:

Код рисования объектов

public DrawObject(Primitive primitive , Camera camera)
{
    for (int i = 0; i < primitive.Indexes.Length; i+=3)
    {
        var color = randomColor();
        // индексы вершин полигона
        var i1 = primitive.Indexes[i];
        var i2 = primitive.Indexes[i+ 1];
        var i3 = primitive.Indexes[i+ 2];
        // вершины полигона
        var v1 = primitive.GlobalVertices[i1];
        var v2 = primitive.GlobalVertices[i2];
        var v3 = primitive.GlobalVertices[i3];
        // рисуем полигон
        DrawPolygon(v1,v2,v3 , camera , color);
    }
}

public void DrawPolygon(Vector3 v1, Vector3 v2, Vector3 v3, Camera camera , color)
{
    //проекции вершин
    var p1 = camera.ScreenProection(v1);
    var p2 = camera.ScreenProection(v2);
    var p3 = camera.ScreenProection(v3);
    //рисуем полигон
    DrawLine(p1, p2 , color);
    DrawLine(p2, p3 , color);
    DrawLine(p3, p2 , color);
}

Давайте проверим рендер на сцене и кубов:

И да, все прекрасно работает. Для тех, кому разноцветные кубики не кажутся пафосными я написал функцию парсинга моделей формата OBJ в объекты типа Primitive, залил фон черным и отрисовал несколько моделей:

Результат работы рендера

Растеризация полигонов. Наводим красоту.

В прошлом разделе мы написали проволочный рендер. Теперь мы займемся его модернизацией — реализуем растеризацию полигонов.

По простому растеризировать полигон — это значит закрасить его. Казалось бы зачем писать велосипед, когда есть уже готовые функции растеризации треугольника. Вот что будет если нарисовать все дефолтными инструментами:

Современное искусство, полигоны сзади нарисовались поверх передних, одним словом — каша. К тому же как таким образом текстурировать объекты? Да, никак. Значит нам нужно написать свой имба-растерайзер, который будет уметь в отсечение невидимых точек, текстуры и даже в шейдеры! Но для того чтобы это сделать стоит понять как вообще красить треугольники.

Алгоритм Брезенхема для рисования линии.

Начнем с линий. Если кто не знал алгоритм Брезенхема — это основной алгоритм рисования прямых в компьютерной графике. Он или его модификации используется буквально везде: рисование прямых, отрезков, окружностей и т.п. Кому интересно более подробное описание — читайте вики. Алгоритм Брезенхема

Имеется отрезок соединяющий точки {x1, y1} и {x2, y2}. Чтобы нарисовать отрезок между ними нужно закрасить все пиксели которые попадают на него. Для двух точек отрезка можно найти x-координаты пикселей в которых они лежат: нужно лишь взять целые части от координат x1 и x2. Чтобы закрасить пиксели на отрезке запускаем цикл от x1 до x2 и на каждой итерации вычисляем y — координату пикселя который попадает на прямую. Вот код:

void Brezenkhem(Vector2 p1 , Vector2 p2)
{
    int x1 = Floor(p1.X);
    int x2 = Floor(p2.X);
    if (x1 > x2) {Swap(x1, x2); Swap(p1 , p2);}
    float d = (p2.Y - p1.Y) / (x2 - x1);
    float y = p1.Y;
    for (int i = x1; i <= x2; i++)
    {
        int pixelY = Floor(y);
        FillPixel(i , pixelY);
        y += d;
    }
}

Картинка из вики

Растеризация треугольника. Алгоритм заливки

Линии рисовать мы умеем, а вот с треугольниками будет чуть посложнее(не намного)! Задача рисования треугольника сводится к нескольким задачам рисования линий. Для начала разобьем треугольник на две части предварительно отсортировав точки в порядке возрастания x:

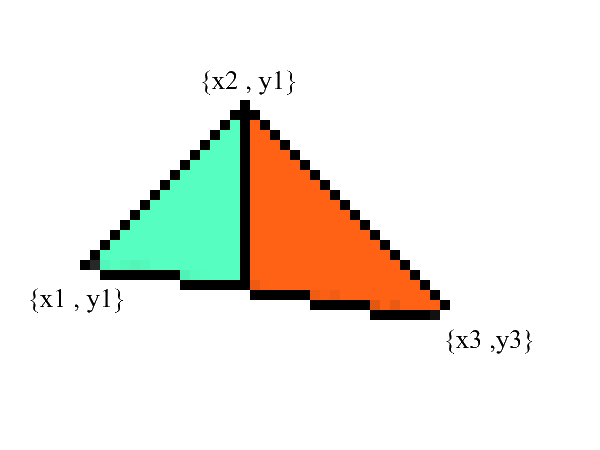
Заметьте — теперь у нас есть две части в которых явно выражены нижняя и верхняя границы. все что осталось — это залить все пиксели находящиеся между ними! Сделать это можно в 2 цикла: от x1 до x2 и от x3 до x2.

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    //хардкодим BubbleSort для упорядочивания по x
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    //узнаем на сколько увеличивается y границ при увеличении x
    //избегаем деления на 0: если x1 == x2 значит эта часть треугольника - линия
    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;

    //верхняя граница должна быть выше нижней
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    //изначально у координаты границ равны y1
    var up = v1.Y;
    var down = v1.Y;

    for (int i = (int)v1.X; i <= (int)v2.X; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta;
        down += downDelta;
    }

    //все то же самое для другой части треугольника
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);
    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;

    if (upDelta < downDelta) Swap(upDelta, downDelta);

    up = v3.Y;
    down = v3.Y;

    for (int i = (int)v3.X; i >=(int)v2.X; i--)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i, g);
        }
        up += upDelta;
        down += downDelta;
    }
}

Несомненно этот код можно отрефакторить и не дублировать цикл:

void Triangle(Vector2 v1 , Vector2 v2 , Vector2 v3)
{
    if (v1.X > v2.X) { Swap(v1, v2); }
    if (v2.X > v3.X) { Swap(v2, v3); }
    if (v1.X > v2.X) { Swap(v1, v2); }

    var steps12 = max(v2.X - v1.X , 1);
    var steps13 = max(v3.X - v1.X , 1);
    var steps32 = max(v2.X - v3.X , 1);
    var steps31 = max(v1.X - v3.X , 1);

    var upDelta = (v2.Y - v1.Y) / steps12;
    var downDelta = (v3.Y - v1.Y) / steps13;
    if (upDelta < downDelta) Swap(upDelta , downDelta);

    TrianglePart(v1.X , v2.X , v1.Y , upDelta , downDelta);

    upDelta = (v2.Y - v3.Y) / steps32;
    downDelta = (v1.Y - v3.Y) / steps31;
    if (upDelta < downDelta) Swap(upDelta, downDelta);

    TrianglePart(v3.X, v2.X, v3.Y, upDelta, downDelta);
}

void TrianglePart(float x1 , float x2 , float y1  , float upDelta , float downDelta)
{
    float up = y1, down = y1;
    for (int i = (int)x1; i <= (int)x2; i++)
    {
        for (int g = (int)down; g <= (int)up; g++)
        {
            FillPixel(i , g);
        }
        up += upDelta; down += downDelta;
    }
}

Отсечение невидимых точек.

Для начала подумайте каким образом вы видите. Сейчас перед вами экран, а то что находится позади него скрыто от ваших глаз. В рендеринге работает примерно такой же механизм — если один полигон перекрывает другой рендер нарисует его поверх перекрытого. Наоборот же, закрытую часть полигона рисовать он не будет:

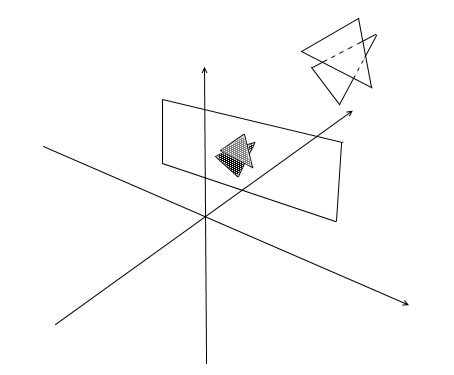
Для того, чтобы понять видима точки или нет, в рендеринге применяют механизм zbuffer-а(буфера глубины). zbuffer можно представить как двумерный массив (можно сжать в одномерный) с размерностью width * height. Для каждого пикселя на экране он хранит значение z — координаты на исходном полигоне откуда эта точка была спроецирована. Соответственно чем ближе точка к наблюдателю, тем меньше ее z — координата. В конечном итоге если проекции нескольких точек совпадают растеризировать нужно точку с минимальной z — координатой:

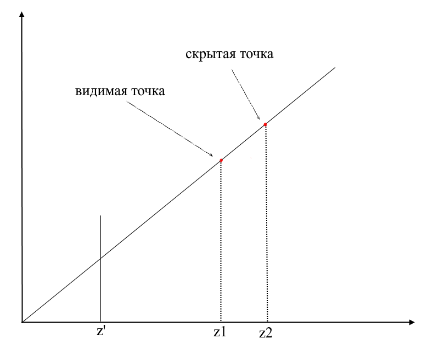
Теперь возникает вопрос — как находить z-координаты точек на исходном полигоне? Это можно сделать несколькими способами. Например можно пускать луч из начала координат камеры, проходящий через точку на проекционной плоскости {x, y, z’}, и находить его пересечение с полигоном. Но искать пересечения крайне затратная операция, поэтому будем использовать другой способ. Для рисования треугольника мы интерполировали координаты его проекций, теперь, помимо этого, мы будем интерполировать также и координаты исходного полигона. Для отсечения невидимых точек будем использовать в методе растеризации состояние zbuffer-а для текущего фрейма.

Мой zbuffer будет иметь вид Vector3[] — он будет содержать не только z — координаты, но и интерполированные значения точек полигона(фрагменты) для каждого пикселя экрана. Это сделано в целях экономии памяти так как в дальнейшем нам все равно пригодятся эти значения для написания шейдеров! А пока что имеем следующий код для определения видимых вершин(фрагментов):

Код

public void ComputePoly(Vector3 v1, Vector3 v2, Vector3 v3 , Vector3[] zbuffer)
{
    //находим проекцию полигона
    var v1p = Camera.ScreenProection(v1);
    var v2p = Camera.ScreenProection(v2);
    var v3p = Camera.ScreenProection(v3);

    //упорядочиваем точки по x - координате
    //Заметьте, также меняем исходные точки - они должны соответствовать проекциям
    if (v1p.X > v2p.X) { Swap(v1p, v2p); Swap(v1p, v2p); }
    if (v2p.X > v3p.X) { Swap(v2p, v3p); Swap(v2p, v3p); }
    if (v1p.X > v2p.X) { Swap(v1p, v2p); Swap(v1p, v2p); }

    //считаем количество шагов для построения линии алгоритмом Брезенхема
    int x12 = Math.Max((int)v2p.X - (int)v1p.X, 1);
    int x13 = Math.Max((int)v3p.X - (int)v1p.X, 1);

    //теперь помимо проекций будем интерполировать и исходные точки
    float dy12 = (v2p.Y - v1p.Y) / x12; var dr12 = (v2 - v1) / x12;
    float dy13 = (v3p.Y - v1p.Y) / x13; var dr13 = (v3 - v1) / x13;

    Vector3 deltaUp, deltaDown; float deltaUpY, deltaDownY;
    if (dy12 > dy13) { deltaUp = dr12; deltaDown = dr13; deltaUpY = dy12; deltaDownY = dy13;}
    else { deltaUp = dr13; deltaDown = dr12; deltaUpY = dy13; deltaDownY = dy12;}

    TrianglePart(v1 , deltaUp , deltaDown , x12 , 1 , v1p , deltaUpY , deltaDownY , zbuffer);
    //вторую часть треугольника аналогично - думаю вы поняли
}
public void ComputePolyPart(Vector3 start, Vector3 deltaUp, Vector3 deltaDown,
    int xSteps, int xDir, Vector2 pixelStart, float deltaUpPixel, float deltaDownPixel , Vector3[] zbuffer)
{
    int pixelStartX = (int)pixelStart.X;
    Vector3 up = start - deltaUp, down = start - deltaDown;
    float pixelUp = pixelStart.Y - deltaUpPixel, pixelDown = pixelStart.Y - deltaDownPixel;
    for (int i = 0; i <= xSteps; i++)
    {
        up += deltaUp; pixelUp += deltaUpPixel;
        down += deltaDown; pixelDown += deltaDownPixel;
        int steps = ((int)pixelUp - (int)pixelDown);
        var delta = steps == 0 ? Vector3.Zero : (up - down) / steps;
        Vector3 position = down - delta;
        for (int g = 0; g <= steps; g++)
        {
            position += delta;
            var proection = new Point(pixelStartX + i * xDir, (int)pixelDown + g);
            int index = proection.Y * Width + proection.X;
            //проверка на глубину
            if (zbuffer[index].Z == 0 || zbuffer[index].Z > position.Z)
            {
                zbuffer[index] = position;
            }
        }
    }
}

Анимация шагов растеризатора(при перезаписи глубины в zbuffer-е пиксель выделяется красным):

Для удобства я вынес весь код в отдельный модуль Rasterizer:

Класс растеризатора

    public class Rasterizer
    {
        public Vertex[] ZBuffer;
        public int[] VisibleIndexes;
        public int VisibleCount;
        public int Width;
        public int Height;
        public Camera Camera;

        public Rasterizer(Camera camera)
        {
            Shaders = shaders;
            Width = camera.ScreenWidth;
            Height = camera.ScreenHeight;
            Camera = camera;

        }
        public Bitmap Rasterize(IEnumerable<Primitive> primitives)
        {
            var buffer = new Bitmap(Width , Height);
            ComputeVisibleVertices(primitives);
            for (int i = 0; i < VisibleCount; i++)
            {
                var vec = ZBuffer[index];
                var proec = Camera.ScreenProection(vec);
                buffer.SetPixel(proec.X , proec.Y);
            }
            return buffer.Bitmap;
        }
        public void ComputeVisibleVertices(IEnumerable<Primitive> primitives)
        {
            VisibleCount = 0;
            VisibleIndexes = new int[Width * Height];
            ZBuffer = new Vertex[Width * Height];
            foreach (var prim in primitives)
            {
                foreach (var poly in prim.GetPolys())
                {
                    MakeLocal(poly);
                    ComputePoly(poly.Item1, poly.Item2, poly.Item3);
                }
            }
        }
        public void MakeLocal(Poly poly)
        {
            poly.Item1.Position = Camera.Pivot.ToLocalCoords(poly.Item1.Position);
            poly.Item2.Position = Camera.Pivot.ToLocalCoords(poly.Item2.Position);
            poly.Item3.Position = Camera.Pivot.ToLocalCoords(poly.Item3.Position);

        }
    }

Теперь проверим работу рендера. Для этого я использую модель Сильваны из известной RPG «WOW»:

Не очень понятно, правда? А все потому что здесь нет ни текстур ни освещения. Но вскоре мы это исправим.

Текстуры! Нормали! Освещение! Мотор!

Почему я объединил все это в один раздел? А потому что по своей сути текстуризация и расчет нормалей абсолютно идентичны и скоро вы это поймете.

Для начала рассмотрим задачу текстуризации для одного полигона. Теперь помимо обычных координат вершин полигона мы будем хранить еще и его текстурные координаты. Текстурная координата вершины представляется двумерным вектором и указывает на пиксель изображения текстуры. В интернете я нашел хорошую картинку чтобы показать это:

Заметьте, что начало текстуры (левый нижний пиксель) в текстурных координатах имеет значение {0, 0}, конец (правый верхний пиксель) — {1, 1}. Учитывайте систему координат текстуры и возможность выхода за границы картинки когда текстурная координата равна 1.

Сразу создадим класс для представления данных вершины:

  public class Vertex
    {
        public Vector3 Position { get; set; }
        public Color Color { get; set; }
        public Vector2 TextureCoord { get; set; }
        public Vector3 Normal { get; set; }

        public Vertex(Vector3 pos , Color color , Vector2 texCoord , Vector3 normal)
        {
            Position = pos;
            Color = color;
            TextureCoord = texCoord;
            Normal = normal;
        }
    }

Зачем нужны нормали я объясню позже, пока что просто будем знать, что у вершин они могут быть. Теперь для текстуризации полигона нам необходимо каким-то образом сопоставить значение цвета из текстуры конкретному пикселю. Помните как мы интерполировали вершины? Здесь нужно сделать то же самое! Я не буду еще раз переписывать код растеризации, а предлагаю вам самим реализовать текстурирование в вашем рендере. Результатом должно быть корректное отображение текстур на модели. Вот, что получилось у меня:

текстурированная модель

Вся информация о текстурных координатах модели находятся в файле OBJ. Для того, чтобы использовать это изучите формат: Формат OBJ.

Освещение

С текстурами все стало гораздо веселее, но по настоящему весело будет когда мы реализуем освещение для сцены. Для имитации «дешевого» освещения я буду использовать модель Фонга.

Модель Фонга

В общем случае этот метод имитирует наличие 3х составляющих освещения: фоновая(ambient), рассеянная(diffuse) и зеркальная(reflect). Сумма этих трех компонент в итоге даст имитацию физического поведения света.

Модель Фонга

Для расчета освещения по Фонгу нам будут нужны нормали к поверхностям, для этого я и добавил их в классе Vertex. Где же брать значения этих нормалей? Нет, ничего вычислять нам не нужно. Дело в том, что великодушные 3д редакторы часто сами считают их и предоставляют вместе с данными модели в контексте формата OBJ. Распарсив файл модели мы получаем значение нормалей для 3х вершин каждого полигона.

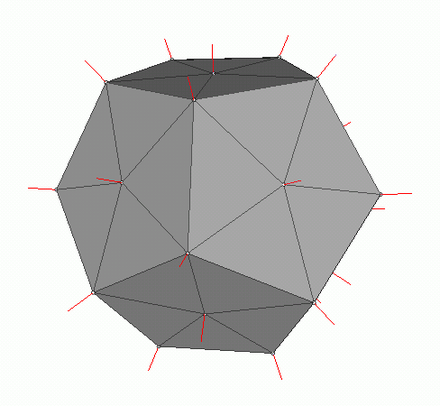
Картинка из вики

Для того, чтобы посчитать нормаль в каждой точке на полигоне нужно интерполировать эти значения, мы уже умеем делать это. Теперь разберем все составляющие для вычисления освещения Фонга.

Фоновый свет (Ambient)

Изначально мы задаем постоянное фоновое освещение, для нетекстурированных объектов можно выбрать любой цвет, для объектов с текстурами я делю каждую из компонент RGB на некий коэффициент базового затенения (baseShading).

Рассеянный свет (Diffuse)

Когда свет падает на поверхность полигона он равномерно рассеивается. Для расчета diffuse значения на конкретном пикселе учитывается угол под которым свет падает на поверхность. Чтобы рассчитать этот угол можно применить скалярное произведение падающего луча и нормали(само собой вектора перед этим нужно нормализировать). Этот угол будет умножаться на некий коэффициент интенсивности света. Если скалярное произведение отрицательно — это значит, что угол между векторами больше 90 градусов. В этом случае мы начнем рассчитывать уже не осветление, а, наоборот, затенение. Стоит избегать этого момента, сделать это можно с помощью функции max.

Код

public interface IShader
    {
        void ComputeShader(Vertex vertex, Camera camera);
    }

    public struct Light
    {
        public Vector3 Pos;
        public float Intensivity;
    }

public class PhongModelShader : IShader
    {
        public static float DiffuseCoef = 0.1f;
        public Light[] Lights { get; set; }

        public PhongModelShader(params Light[] lights)
        {
            Lights = lights;
        }
        public void ComputeShader(Vertex vertex, Camera camera)
        {
            if (vertex.Normal.X == 0 && vertex.Normal.Y == 0 && vertex.Normal.Z == 0)
            {
                return;
            }
            var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
            foreach (var light in Lights)
            {
                var ldir = Vector3.Normalize(light.Pos - gPos);
                var diffuseVal = Math.Max(VectorMath.Cross(ldir, vertex.Normal), 0) * light.Intensivity;
                vertex.Color = Color.FromArgb(vertex.Color.A,
                    (int)Math.Min(255, vertex.Color.R * diffuseVal * DiffuseCoef),
                    (int)Math.Min(255, vertex.Color.G * diffuseVal * DiffuseCoef,
                    (int)Math.Min(255, vertex.Color.B * diffuseVal * DiffuseCoef));
            }
        }
    }

Давайте применим рассеянный свет и рассеем тьму:

Зеркальный свет (Reflect)

Для расчета зеркальной компоненты нужно учитывать точку из которой мы смотрим на объект. Теперь мы будем брать скалярное произведение луча от наблюдателя и отраженного от поверхности луча умноженное на коэффициент интенсивности света.

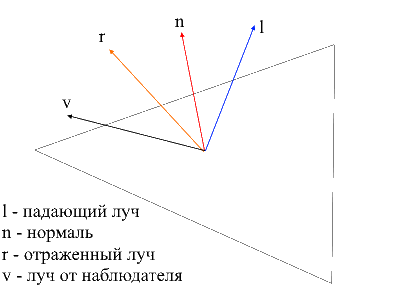
Найти луч от наблюдателя к поверхности легко — это будет просто позиция обрабатываемой вершины в локальных координатах. Для того, чтобы найти отраженный луч я использовал следующий способ. Падающий луч можно разложить на 2 вектора: его проекцию на нормаль и второй вектор который можно найти вычитанием из падающего луча этой проекции. Чтобы найти отраженный луч нужно из проекции на нормаль вычесть значение второго вектора.

код

    public class PhongModelShader : IShader
    {
        public static float DiffuseCoef = 0.1f;
        public static float ReflectCoef = 0.2f;
        public Light[] Lights { get; set; }

        public PhongModelShader(params Light[] lights)
        {
            Lights = lights;
        }
        public void ComputeShader(Vertex vertex, Camera camera)
        {
            if (vertex.Normal.X == 0 && vertex.Normal.Y == 0 && vertex.Normal.Z == 0)
            {
                return;
            }
            var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
            foreach (var light in Lights)
            {
                var ldir = Vector3.Normalize(light.Pos - gPos);
                //Следующие три строчки нужны чтобы найти отраженный от поверхности луч
                var proection = VectorMath.Proection(ldir, -vertex.Normal);
                var d = ldir - proection;
                var reflect = proection - d;
                var diffuseVal = Math.Max(VectorMath.Cross(ldir, -vertex.Normal), 0) * light.Intensivity;
                //луч от наблюдателя
                var eye = Vector3.Normalize(-vertex.Position);
                var reflectVal = Math.Max(VectorMath.Cross(reflect, eye), 0) * light.Intensivity;
                var total = diffuseVal * DiffuseCoef + reflectVal * ReflectCoef;
                vertex.Color = Color.FromArgb(vertex.Color.A,
                    (int)Math.Min(255, vertex.Color.R * total),
                    (int)Math.Min(255, vertex.Color.G * total),
                    (int)Math.Min(255, vertex.Color.B * total));
            }
        }
    }

Теперь картинка выглядит следующим образом:

Тени

Конечной точкой моего изложения будет реализация теней для рендера. Первая тупиковая идея которая зародилась у меня в черепушке — для каждой точки проверять не лежит ли между ней и светом какой-нибудь полигон. Если лежит — значит не нужно освещать пиксель. Модель Сильваны содержит 220к с лихвой полигонов. Если так для каждой точки проверять пересечение со всеми этими полигонами, то нужно сделать максимум 220000 * 1920 * 1080 * 219999 вызовов метода пересечения! За 10 минут мой компьютер смог осилить 10-у часть всех вычислений (2600 полигонов из 220000), после чего у меня случился сдвиг и я отправился на поиски нового метода.

В интернете мне попался очень простой и красивый способ, который выполняет те же вычисления в тысячи раз быстрее. Называется он Shadow mapping(построение карты теней). Вспомните как мы определяли видимые наблюдателю точки — использовали zbuffer. Shadow mapping делает тоже самое! В первом проходе наша камера будет находиться в позиции света и смотреть на объект. Таким образом мы сформируем карту глубин для источника света. Карта глубин — это знакомый нам zbuffer. Во втором проходе мы используем эту карту, чтобы определять вершины которые должны освещаться. Сейчас я нарушу правила хорошего кода и пойду читерским путем — просто передам шейдеру новый объект растеризатора и он используя его создаст нам карту глубин.

Код

public class ShadowMappingShader : IShader
{
    public Enviroment Enviroment { get; set; }
    public Rasterizer Rasterizer { get; set; }
    public Camera Camera => Rasterizer.Camera;
    public Pivot Pivot => Camera.Pivot;
    public Vertex[] ZBuffer => Rasterizer.ZBuffer;
    public float LightIntensivity { get; set; }

    public ShadowMappingShader(Enviroment enviroment, Rasterizer rasterizer, float lightIntensivity)
    {
        Enviroment = enviroment;
        LightIntensivity = lightIntensivity;
        Rasterizer = rasterizer;
        //я добвил события в объекты рендера, привязав к ним перерасчет карты теней
        //теперь при вращении/движении камеры либо при изменение сцены шейдер будет перезаписывать глубину
        Camera.OnRotate += () => UpdateDepthMap(Enviroment.Primitives);
        Camera.OnMove += () => UpdateDepthMap(Enviroment.Primitives);
        Enviroment.OnChange += () => UpdateDepthMap(Enviroment.Primitives);
        UpdateVisible(Enviroment.Primitives);
    }
    public void ComputeShader(Vertex vertex, Camera camera)
    {
        //вычисляем глобальные координаты вершины
        var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
        //дистанция до света
        var lghDir = Pivot.Center - gPos;
        var distance = lghDir.Length();
        var local = Pivot.ToLocalCoords(gPos);
        var proectToLight = Camera.ScreenProection(local).ToPoint();
        if (proectToLight.X >= 0 && proectToLight.X < Camera.ScreenWidth && proectToLight.Y >= 0
            && proectToLight.Y < Camera.ScreenHeight)
        {
            int index = proectToLight.Y * Camera.ScreenWidth + proectToLight.X;
            if (ZBuffer[index] == null || ZBuffer[index].Position.Z >= local.Z)
            {
                vertex.Color = Color.FromArgb(vertex.Color.A,
                    (int)Math.Min(255, vertex.Color.R + LightIntensivity / distance),
                    (int)Math.Min(255, vertex.Color.G + LightIntensivity / distance),
                    (int)Math.Min(255, vertex.Color.B + LightIntensivity / distance));
            }
        }
        else
        {
            vertex.Color = Color.FromArgb(vertex.Color.A,
                    (int)Math.Min(255, vertex.Color.R + (LightIntensivity / distance) / 15),
                    (int)Math.Min(255, vertex.Color.G + (LightIntensivity / distance) / 15),
                    (int)Math.Min(255, vertex.Color.B + (LightIntensivity / distance) / 15));
        }
    }
    public void UpdateDepthMap(IEnumerable<Primitive> primitives)
    {
        Rasterizer.ComputeVisibleVertices(primitives);
    }
}

Для статичной сцены достаточно будет один раз вызвать построение карты глубин, после во всех фреймах использовать ее. В качестве тестовой я использую менее полигональную модель пушки. Вот такое изображение получается на выходе:

Многие из вас наверное заметили артефакты данного шейдера(необработанные светом черные точки). Опять же обратившись в всезнающую сеть я нашел описание этого эффекта с противным названием «shadow acne»(да простят меня люди с комплексом внешности). Суть таких «зазоров» заключается в том, что для определения тени мы используем ограниченное разрешение карты глубин. Это значит, что несколько вершин при рендеринге получают одно значение из карты глубин. Такому артефакту наиболее подвержены поверхности на которые свет падает под пологим углом. Эффект можно исправить, увеличив разрешение рендера для света, однако существует более элегантный способ. Заключается он в том, чтобы добавлять определенный сдвиг для глубины в зависимости от угла между лучом света и поверхностью. Это можно сделать при помощи скалярного произведения.

Улучшенные тени

public class ShadowMappingShader : IShader
{
    public Enviroment Enviroment { get; set; }
    public Rasterizer Rasterizer { get; set; }
    public Camera Camera => Rasterizer.Camera;
    public Pivot Pivot => Camera.Pivot;
    public Vertex[] ZBuffer => Rasterizer.ZBuffer;
    public float LightIntensivity { get; set; }

    public ShadowMappingShader(Enviroment enviroment, Rasterizer rasterizer, float lightIntensivity)
    {
        Enviroment = enviroment;
        LightIntensivity = lightIntensivity;
        Rasterizer = rasterizer;
        //я добвил события в объекты рендера, привязав к ним перерасчет карты теней
        //теперь при вращении/движении камеры либо при изменение сцены шейдер будет перезаписывать глубину
        Camera.OnRotate += () => UpdateDepthMap(Enviroment.Primitives);
        Camera.OnMove += () => UpdateDepthMap(Enviroment.Primitives);
        Enviroment.OnChange += () => UpdateDepthMap(Enviroment.Primitives);
        UpdateVisible(Enviroment.Primitives);
    }
    public void ComputeShader(Vertex vertex, Camera camera)
    {
        //вычисляем глобальные координаты вершины
        var gPos = camera.Pivot.ToGlobalCoords(vertex.Position);
        //дистанция до света
        var lghDir = Pivot.Center - gPos;
        var distance = lghDir.Length();
        var local = Pivot.ToLocalCoords(gPos);
        var proectToLight = Camera.ScreenProection(local).ToPoint();
        if (proectToLight.X >= 0 && proectToLight.X < Camera.ScreenWidth && proectToLight.Y >= 0
            && proectToLight.Y < Camera.ScreenHeight)
        {
            int index = proectToLight.Y * Camera.ScreenWidth + proectToLight.X;
            var n = Vector3.Normalize(vertex.Normal);
            var ld = Vector3.Normalize(lghDir);
            //вычисляем сдвиг глубины
            float bias = (float)Math.Max(10 * (1.0 - VectorMath.Cross(n, ld)), 0.05);
            if (ZBuffer[index] == null || ZBuffer[index].Position.Z + bias >= local.Z)
            {
                vertex.Color = Color.FromArgb(vertex.Color.A,
                    (int)Math.Min(255, vertex.Color.R + LightIntensivity / distance),
                    (int)Math.Min(255, vertex.Color.G + LightIntensivity / distance),
                    (int)Math.Min(255, vertex.Color.B + LightIntensivity / distance));
            }
        }
        else
        {
            vertex.Color = Color.FromArgb(vertex.Color.A,
                    (int)Math.Min(255, vertex.Color.R + (LightIntensivity / distance) / 15),
                    (int)Math.Min(255, vertex.Color.G + (LightIntensivity / distance) / 15),
                    (int)Math.Min(255, vertex.Color.B + (LightIntensivity / distance) / 15));
        }
    }
    public void UpdateDepthMap(IEnumerable<Primitive> primitives)
    {
        Rasterizer.ComputeVisibleVertices(primitives);
    }
}

Бонус

Играем с нормалями

Я подумал, стоит ли интерполировать значения нормалей, если можно посчитать среднее между 3мя нормалями полигона и использовать для каждой его точки. Оказывается, что интерполяция дает куда более естественный и гладкий материал картинки.

Двигаем свет

Реализовав простой цикл получим набор отрендеренных картинок с разными позициями света на сцене:

            float angle = (float)Math.PI / 90;
            var shader = (preparer.Shaders[0] as PhongModelShader);
            for (int i = 0; i < 180; i+=2)
            {
                shader.Lights[0] = = new Light()
                    {
                        Pos = shader.Lights[0].Pos.Rotate(angle , Axis.X) ,
                        Intensivity = shader.Lights[0].Intensivity
                    };
                Draw();
            }

Производительность

Для теста использовалась следующие конфигурации:

Модель Сильваны: 220к полигонов.
Разрешение экрана: 1920×1080.
Шейдеры: Phong model shader
Конфигурация компьютера: cpu — core i7 4790, 8 gb ram

FPS рендеринга составлял 1-2 кадр/сек. Это далеко не realtime. Однако стоит все же учитывать, что вся обработка происходила без использования многопоточности, т.е. на одном ядре cpu.

Заключение

Я считаю себя новичком в 3д графике не исключаю ошибок допущенных мною в ходе изложения. Единственное на что я опираюсь — это практический результат, полученный в процессе создания. Все поправки и оптимизации(если таковые будут) вы можете оставить в комментариях, я с радостью их прочту. Ссылка на репозиторий проекта.

Источник

Матрица поворота в двумерном пространстве

В
двумерном пространстве поворот можно
описать одним углом

со
следующей матрицей линейного
преобразования
в декартовой
системе координат:

Поворот
выполняется путём умножения матрицы
поворота на вектор-столбец,
описывающий вращаемую точку:

Координаты
(x’,y’) в результате поворота точки (x,y)
имеют вид:

Положительным
углам при этом соответствует вращение
вектора против часовой стрелки в обычной,
правосторонней
системе координат,
и по часовой стрелке в левосторонней
системе координат.

[Править] Матрица поворота в трёхмерном пространстве

Матрицами
вращения вокруг оси декартовой
системы координат
на угол α
в трёхмерном пространстве являются:

Вращение
вокруг оси x:

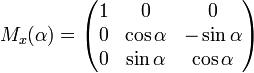
Вращение
вокруг оси y:

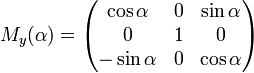
Вращение
вокруг оси z:

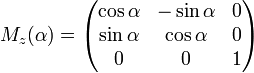
Положительным
углам при этом соответствует вращение
вектора против часовой стрелки в правой
системе координат,
и по часовой стрелке в левой системе
координат, если смотреть на плоскость
вращении со стороны полупространства,
где значения координат оси, вокруг
которой осуществляется поворот,
положительные. Правая система координат
связана с выбором правого базиса
(см. правило
буравчика).

Свойства
матрицы поворота.

Свойства матрицы поворота

Если

—
матрица, задающая поворот вокруг оси

на
угол ϕ,
то:

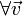
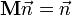
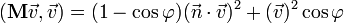
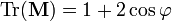
(след
матрицы
вращения)
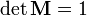
(матрица
имеет единичный определитель).
если
строки (или столбцы матрицы) рассматривать
как координаты векторов

,
то верны следующие соотношения):
Матрица
обратного поворота получается обычным
транспонированием
матрицы прямого поворота, т. о.

.

Алгоритм
Брезенхема для растеризации отрезка.

Алгоритм
Брезенхе́ма
(англ. Bresenham’s
line algorithm)
— это алгоритм, определяющий, какие
точки двумерного
растра нужно закрасить, чтобы получить
близкое приближение прямой линии между
двумя заданными точками.
Это один из старейших алгоритмов в
машинной
графике
— он был разработан Джеком Е. Брезенхэмом
(Jack E. Bresenham) в компании IBM
в 1962
году. Алгоритм широко используется, в
частности, для рисования линий на экране
компьютера. Существует обобщение
алгоритма Брезенхэма
для построения кривых 2-го порядка.

Алгоритм

Отрезок
проводится между двумя точками — (x₀,y₀)
и (x₁,y₁),
где в этих парах указаны колонка и
строка, соответственно, номера которых
растут вправо и вниз. Сначала мы будем
предполагать, что наша линия идёт вниз
и вправо, причём горизонтальное расстояние
x₁
− x₀
превосходит вертикальное y₁
− y₀,
т.е. наклон линии от горизонтали — менее
45°. Наша цель состоит в том, чтобы для
каждой колонки x
между x₀
и x₁,
определить, какая строка y
ближе всего к линии, и нарисовать точку
(x,y).

Общая
формула линии между двумя точками:

Поскольку
мы знаем колонку x,
то строка y
получается округлением к целому
следующего значения:

Однако,
вычислять точное значение этого выражения
нет необходимости. Достаточно заметить,
что y
растёт от y₀
и за каждый шаг мы добавляем к x
единицу и добавляем к y
значение наклона

которое
можно вычислить заранее. Более того, на
каждом шаге мы делаем одно из двух: либо
сохраняем тот же y,
либо увеличиваем его на 1.

Что
из этих двух выбрать — можно решить,
отслеживая значение
ошибки,
которое означает — вертикальное
расстояние между текущим значением y
и точным значением y
для текущего x.
Всякий раз, когда мы увеличиваем x,
мы увеличиваем значение ошибки на
величину наклона s,
приведённую выше. Если ошибка превысила
0.5, линия стала ближе к следующему y,
поэтому мы увеличиваем y
на единицу, одновременно уменьшая
значение ошибки на 1. В реализации
алгоритма, приведённой ниже, plot(x,y)
рисует точку, а abs
возвращает абсолютную
величину
числа:

function
line(x0, x1, y0, y1)

int
deltax := abs(x1 – x0)

int
deltay := abs(y1 – y0)

real
error := 0

real
deltaerr := deltay / deltax

int
y := y0

for
x from
x0 to
x1

plot(x,y)

error
:= error + deltaerr

if
error >= 0.5

y
:= y + 1

error
:= error – 1.0

Проблема
такого подхода — в том, что с вещественными
величинами, такими как error
и deltaerr,
компьютеры работают относительно
медленно. Кроме того, при вычислениях
с плавающей точкой может накапливаться
ошибка. По этим причинам, лучше работать
только с целыми числами. Это можно
сделать, если умножить все используемые
вещественные величины на deltax.
Единственная проблема — с константой
0.5 — но в данном случае достаточно
умножить обе части неравенства на 2.
Получаем
следующий
код:

function
line(x0, x1, y0, y1)

int
deltax := abs(x1 – x0)

int
deltay := abs(y1 – y0)

int
error := 0

int
deltaerr := deltay

int
y := y0

for
x from
x0 to
x1

plot(x,y)

error
:= error + deltaerr

if
2 * error >= deltax

y
:= y + 1

error
:= error – deltax

Умножение
на 2 для целых чисел реализуется битовым
сдвигом влево.

Теперь
мы можем быстро рисовать линии,
направленные вправо-вниз с величиной
наклона меньше 1. Осталось распространить
алгоритм на рисование во всех направлениях.
Это достигается за счёт зеркальных
отражений, т.е. заменой знака (шаг в 1
заменяется на -1), обменом переменных x
и y,
обменом координат начала отрезка с
координатами конца.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

In linear algebra, a rotation matrix is a transformation matrix that is used to perform a rotation in Euclidean space. For example, using the convention below, the matrix

${displaystyle R={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta end{bmatrix}}}$

rotates points in the xy plane counterclockwise through an angle θ about the origin of a two-dimensional Cartesian coordinate system. To perform the rotation on a plane point with standard coordinates v = (x, y), it should be written as a column vector, and multiplied by the matrix R:

${displaystyle Rmathbf {v} ={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}={begin{bmatrix}xcos theta -ysin theta \xsin theta +ycos theta end{bmatrix}}.}$

If x and y are the endpoint coordinates of a vector, where x is cosine and y is sine, then the above equations become the trigonometric summation angle formulae. Indeed, a rotation matrix can be seen as the trigonometric summation angle formulae in matrix form. One way to understand this is say we have a vector at an angle 30° from the x axis, and we wish to rotate that angle by a further 45°. We simply need to compute the vector endpoint coordinates at 75°.

The examples in this article apply to active rotations of vectors counterclockwise in a right-handed coordinate system (y counterclockwise from x) by pre-multiplication (R on the left). If any one of these is changed (such as rotating axes instead of vectors, a passive transformation), then the inverse of the example matrix should be used, which coincides with its transpose.

Since matrix multiplication has no effect on the zero vector (the coordinates of the origin), rotation matrices describe rotations about the origin. Rotation matrices provide an algebraic description of such rotations, and are used extensively for computations in geometry, physics, and computer graphics. In some literature, the term rotation is generalized to include improper rotations, characterized by orthogonal matrices with a determinant of −1 (instead of +1). These combine proper rotations with reflections (which invert orientation). In other cases, where reflections are not being considered, the label proper may be dropped. The latter convention is followed in this article.

Rotation matrices are square matrices, with real entries. More specifically, they can be characterized as orthogonal matrices with determinant 1; that is, a square matrix R is a rotation matrix if and only if R^T = R⁻¹ and det R = 1. The set of all orthogonal matrices of size n with determinant +1 is a representation of a group known as the special orthogonal group SO(n), one example of which is the rotation group SO(3). The set of all orthogonal matrices of size n with determinant +1 or −1 is a representation of the (general) orthogonal group O(n).

In two dimensions[edit]

A counterclockwise rotation of a vector through angle θ. The vector is initially aligned with the x-axis.

In two dimensions, the standard rotation matrix has the following form:

${displaystyle R(theta )={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta \end{bmatrix}}.}$

This rotates column vectors by means of the following matrix multiplication,

${displaystyle {begin{bmatrix}x'\y'\end{bmatrix}}={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta \end{bmatrix}}{begin{bmatrix}x\y\end{bmatrix}}.}$

Thus, the new coordinates (x′, y′) of a point (x, y) after rotation are

${displaystyle {begin{aligned}x'&=xcos theta -ysin theta ,\y'&=xsin theta +ycos theta ,end{aligned}}.}$

Examples[edit]

For example, when the vector

${displaystyle mathbf {hat {x}} ={begin{bmatrix}1\0\end{bmatrix}}}$

is rotated by an angle θ, its new coordinates are

${displaystyle {begin{bmatrix}cos theta \sin theta \end{bmatrix}},}$

and when the vector

${displaystyle mathbf {hat {y}} ={begin{bmatrix}0\1\end{bmatrix}}}$

is rotated by an angle θ, its new coordinates are

${displaystyle {begin{bmatrix}-sin theta \cos theta \end{bmatrix}}.}$

Direction[edit]

The direction of vector rotation is counterclockwise if θ is positive (e.g. 90°), and clockwise if θ is negative (e.g. −90°). Thus the clockwise rotation matrix is found as

${displaystyle R(-theta )={begin{bmatrix}cos theta &sin theta \-sin theta &cos theta \end{bmatrix}}.}$

The two-dimensional case is the only non-trivial (i.e. not one-dimensional) case where the rotation matrices group is commutative, so that it does not matter in which order multiple rotations are performed. An alternative convention uses rotating axes,^[1] and the above matrices also represent a rotation of the axes clockwise through an angle θ.

Non-standard orientation of the coordinate system[edit]

A rotation through angle θ with non-standard axes.

If a standard right-handed Cartesian coordinate system is used, with the x-axis to the right and the y-axis up, the rotation R(θ) is counterclockwise. If a left-handed Cartesian coordinate system is used, with x directed to the right but y directed down, R(θ) is clockwise. Such non-standard orientations are rarely used in mathematics but are common in 2D computer graphics, which often have the origin in the top left corner and the y-axis down the screen or page.^[2]

See below for other alternative conventions which may change the sense of the rotation produced by a rotation matrix.

Common rotations[edit]

Particularly useful are the matrices

${displaystyle {begin{bmatrix}0&-1\[3pt]1&0\end{bmatrix}},quad {begin{bmatrix}-1&0\[3pt]0&-1\end{bmatrix}},quad {begin{bmatrix}0&1\[3pt]-1&0\end{bmatrix}}}$

for 90°, 180°, and 270° counter-clockwise rotations.

A 180° rotation (middle) followed by a positive 90° rotation (left) is equivalent to a single negative 90° (positive 270°) rotation (right). Each of these figures depicts the result of a rotation relative to an upright starting position (bottom left) and includes the matrix representation of the permutation applied by the rotation (center right), as well as other related diagrams. See “Permutation notation” on Wikiversity for details.

Relationship with complex plane[edit]

Since

${displaystyle {begin{bmatrix}0&1\-1&0end{bmatrix}}^{2} = {begin{bmatrix}-1&0\0&-1end{bmatrix}} =-I,}$

the matrices of the shape

${displaystyle {begin{bmatrix}x&y\-y&xend{bmatrix}}}$

form a ring isomorphic to the field of the complex numbers . Under this isomorphism, the rotation matrices correspond to circle of the unit complex numbers, the complex numbers of modulus 1.

If one identifies $mathbb {R} ^{2}$ with through the linear isomorphism the action of a matrix of the above form on vectors of $mathbb {R} ^{2}$ corresponds to the multiplication by the complex number x + iy, and rotations correspond to multiplication by complex numbers of modulus 1.

As every rotation matrix can be written

${displaystyle {begin{pmatrix}cos t&sin t\-sin t&cos tend{pmatrix}},}$

the above correspondence associates such a matrix with the complex number

${displaystyle cos t+isin t=e^{it}}$

(this last equality is Euler’s formula).

In three dimensions[edit]

A positive 90° rotation around the y-axis (left) after one around the z-axis (middle) gives a 120° rotation around the main diagonal (right).
In the top left corner are the rotation matrices, in the bottom right corner are the corresponding permutations of the cube with the origin in its center.

Basic rotations[edit]

A basic rotation (also called elemental rotation) is a rotation about one of the axes of a coordinate system. The following three basic rotation matrices rotate vectors by an angle θ about the x-, y-, or z-axis, in three dimensions, using the right-hand rule—which codifies their alternating signs. Notice that the right-hand rule only works when multiplying . (The same matrices can also represent a clockwise rotation of the axes.^{[nb 1]})

${displaystyle {begin{alignedat}{1}R_{x}(theta )&={begin{bmatrix}1&0&0\0&cos theta &-sin theta \[3pt]0&sin theta &cos theta \[3pt]end{bmatrix}}\[6pt]R_{y}(theta )&={begin{bmatrix}cos theta &0&sin theta \[3pt]0&1&0\[3pt]-sin theta &0&cos theta \end{bmatrix}}\[6pt]R_{z}(theta )&={begin{bmatrix}cos theta &-sin theta &0\[3pt]sin theta &cos theta &0\[3pt]0&0&1\end{bmatrix}}end{alignedat}}}$

For column vectors, each of these basic vector rotations appears counterclockwise when the axis about which they occur points toward the observer, the coordinate system is right-handed, and the angle θ is positive. R_z, for instance, would rotate toward the y-axis a vector aligned with the x-axis, as can easily be checked by operating with R_z on the vector (1,0,0):

${displaystyle R_{z}(90^{circ }){begin{bmatrix}1\0\0\end{bmatrix}}={begin{bmatrix}cos 90^{circ }&-sin 90^{circ }&0\sin 90^{circ }&quad cos 90^{circ }&0\0&0&1\end{bmatrix}}{begin{bmatrix}1\0\0\end{bmatrix}}={begin{bmatrix}0&-1&0\1&0&0\0&0&1\end{bmatrix}}{begin{bmatrix}1\0\0\end{bmatrix}}={begin{bmatrix}0\1\0\end{bmatrix}}}$

This is similar to the rotation produced by the above-mentioned two-dimensional rotation matrix. See below for alternative conventions which may apparently or actually invert the sense of the rotation produced by these matrices.

General rotations[edit]

Other rotation matrices can be obtained from these three using matrix multiplication. For example, the product

${displaystyle {begin{aligned}R=R_{z}(alpha ),R_{y}(beta ),R_{x}(gamma )&={overset {text{yaw}}{begin{bmatrix}cos alpha &-sin alpha &0\sin alpha &cos alpha &0\0&0&1\end{bmatrix}}}{overset {text{pitch}}{begin{bmatrix}cos beta &0&sin beta \0&1&0\-sin beta &0&cos beta \end{bmatrix}}}{overset {text{roll}}{begin{bmatrix}1&0&0\0&cos gamma &-sin gamma \0&sin gamma &cos gamma \end{bmatrix}}}\&={begin{bmatrix}cos alpha cos beta &cos alpha sin beta sin gamma -sin alpha cos gamma &cos alpha sin beta cos gamma +sin alpha sin gamma \sin alpha cos beta &sin alpha sin beta sin gamma +cos alpha cos gamma &sin alpha sin beta cos gamma -cos alpha sin gamma \-sin beta &cos beta sin gamma &cos beta cos gamma \end{bmatrix}}end{aligned}}}$

represents a rotation whose yaw, pitch, and roll angles are α, β and γ, respectively. More formally, it is an intrinsic rotation whose Tait–Bryan angles are α, β, γ, about axes z, y, x, respectively.
Similarly, the product

${displaystyle {begin{aligned}\R=R_{z}(gamma ),R_{y}(beta ),R_{x}(alpha )&={begin{bmatrix}cos gamma &-sin gamma &0\sin gamma &cos gamma &0\0&0&1\end{bmatrix}}{begin{bmatrix}cos beta &0&sin beta \0&1&0\-sin beta &0&cos beta \end{bmatrix}}{begin{bmatrix}1&0&0\0&cos alpha &-sin alpha \0&sin alpha &cos alpha \end{bmatrix}}\&={begin{bmatrix}cos beta cos gamma &sin alpha sin beta cos gamma -cos alpha sin gamma &cos alpha sin beta cos gamma +sin alpha sin gamma \cos beta sin gamma &sin alpha sin beta sin gamma +cos alpha cos gamma &cos alpha sin beta sin gamma -sin alpha cos gamma \-sin beta &sin alpha cos beta &cos alpha cos beta \end{bmatrix}}end{aligned}}}$

represents an extrinsic rotation whose (improper) Euler angles are α, β, γ, about axes x, y, z.

These matrices produce the desired effect only if they are used to premultiply column vectors, and (since in general matrix multiplication is not commutative) only if they are applied in the specified order (see Ambiguities for more details). The order of rotation operations is from right to left; the matrix adjacent to the column vector is the first to be applied, and then the one to the left.^[3]

Conversion from rotation matrix to axis–angle[edit]

Every rotation in three dimensions is defined by its axis (a vector along this axis is unchanged by the rotation), and its angle — the amount of rotation about that axis (Euler rotation theorem).

There are several methods to compute the axis and angle from a rotation matrix (see also axis–angle representation). Here, we only describe the method based on the computation of the eigenvectors and eigenvalues of the rotation matrix. It is also possible to use the trace of the rotation matrix.

Determining the axis[edit]

A rotation R around axis u can be decomposed using 3 endomorphisms P, (I − P), and Q (click to enlarge).

Given a 3 × 3 rotation matrix R, a vector u parallel to the rotation axis must satisfy

{displaystyle Rmathbf {u} =mathbf {u} ,}

since the rotation of u around the rotation axis must result in u. The equation above may be solved for u which is unique up to a scalar factor unless R = I.

Further, the equation may be rewritten

{displaystyle Rmathbf {u} =Imathbf {u} implies left(R-Iright)mathbf {u} =0,}

which shows that u lies in the null space of R − I.

Viewed in another way, u is an eigenvector of R corresponding to the eigenvalue λ = 1. Every rotation matrix must have this eigenvalue, the other two eigenvalues being complex conjugates of each other. It follows that a general rotation matrix in three dimensions has, up to a multiplicative constant, only one real eigenvector.

One way to determine the rotation axis is by showing that:

${displaystyle {begin{aligned}0&=R^{mathsf {T}}0+0\&=R^{mathsf {T}}left(R-Iright)mathbf {u} +left(R-Iright)mathbf {u} \&=left(R^{mathsf {T}}R-R^{mathsf {T}}+R-Iright)mathbf {u} \&=left(I-R^{mathsf {T}}+R-Iright)mathbf {u} \&=left(R-R^{mathsf {T}}right)mathbf {u} end{aligned}}}$

Since (R − R^T) is a skew-symmetric matrix, we can choose u such that

${displaystyle [mathbf {u} ]_{times }=left(R-R^{mathsf {T}}right).}$

The matrix–vector product becomes a cross product of a vector with itself, ensuring that the result is zero:

${displaystyle left(R-R^{mathsf {T}}right)mathbf {u} =[mathbf {u} ]_{times }mathbf {u} =mathbf {u} times mathbf {u} =0,}$

Therefore, if

${displaystyle R={begin{bmatrix}a&b&c\d&e&f\g&h&i\end{bmatrix}},}$

then

${displaystyle mathbf {u} ={begin{bmatrix}h-f\c-g\d-b\end{bmatrix}}.}$

The magnitude of u computed this way is ‖u‖ = 2 sin θ, where θ is the angle of rotation.

This does not work if R is symmetric. Above, if R − R^T is zero, then all subsequent steps are invalid. In this case, it is necessary to diagonalize R and find the eigenvector corresponding to an eigenvalue of 1.

Determining the angle[edit]

To find the angle of a rotation, once the axis of the rotation is known, select a vector v perpendicular to the axis. Then the angle of the rotation is the angle between v and Rv.

A more direct method, however, is to simply calculate the trace: the sum of the diagonal elements of the rotation matrix. Care should be taken to select the right sign for the angle θ to match the chosen axis:

{displaystyle operatorname {tr} (R)=1+2cos theta ,}

from which follows that the angle’s absolute value is

${displaystyle |theta |=arccos left({frac {operatorname {tr} (R)-1}{2}}right).}$

Rotation matrix from axis and angle[edit]

The matrix of a proper rotation R by angle θ around the axis u = (u_x, u_y, u_z), a unit vector with u²
_x + u²
_y + u²
_z = 1, is given by:^[4]

${displaystyle R={begin{bmatrix}cos theta +u_{x}^{2}left(1-cos theta right)&u_{x}u_{y}left(1-cos theta right)-u_{z}sin theta &u_{x}u_{z}left(1-cos theta right)+u_{y}sin theta \u_{y}u_{x}left(1-cos theta right)+u_{z}sin theta &cos theta +u_{y}^{2}left(1-cos theta right)&u_{y}u_{z}left(1-cos theta right)-u_{x}sin theta \u_{z}u_{x}left(1-cos theta right)-u_{y}sin theta &u_{z}u_{y}left(1-cos theta right)+u_{x}sin theta &cos theta +u_{z}^{2}left(1-cos theta right)end{bmatrix}}.}$

A derivation of this matrix from first principles can be found in section 9.2 here.^[5] The basic idea to derive this matrix is dividing the problem into few known simple steps.

First rotate the given axis and the point such that the axis lies in one of the coordinate planes (xy, yz or zx)
Then rotate the given axis and the point such that the axis is aligned with one of the two coordinate axes for that particular coordinate plane (x, y or z)
Use one of the fundamental rotation matrices to rotate the point depending on the coordinate axis with which the rotation axis is aligned.
Reverse rotate the axis-point pair such that it attains the final configuration as that was in step 2 (Undoing step 2)
Reverse rotate the axis-point pair which was done in step 1 (undoing step 1)

This can be written more concisely as

${displaystyle R=(cos theta ),I+(sin theta ),[mathbf {u} ]_{times }+(1-cos theta ),(mathbf {u} otimes mathbf {u} ),}$

where [u]_× is the cross product matrix of u; the expression u ⊗ u is the outer product, and I is the identity matrix. Alternatively, the matrix entries are:

${displaystyle R_{jk}={begin{cases}cos ^{2}{frac {theta }{2}}+sin ^{2}{frac {theta }{2}}left(2u_{j}^{2}-1right),quad &{text{if }}j=k\2u_{j}u_{k}sin ^{2}{frac {theta }{2}}-varepsilon _{jkl}u_{l}sin theta ,quad &{text{if }}jneq kend{cases}}}$

where ε_jkl is the Levi-Civita symbol with ε₁₂₃ = 1. This is a matrix form of Rodrigues’ rotation formula, (or the equivalent, differently parametrized Euler–Rodrigues formula) with^{[nb 2]}

${displaystyle mathbf {u} otimes mathbf {u} =mathbf {u} mathbf {u} ^{mathsf {T}}={begin{bmatrix}u_{x}^{2}&u_{x}u_{y}&u_{x}u_{z}\[3pt]u_{x}u_{y}&u_{y}^{2}&u_{y}u_{z}\[3pt]u_{x}u_{z}&u_{y}u_{z}&u_{z}^{2}end{bmatrix}},qquad [mathbf {u} ]_{times }={begin{bmatrix}0&-u_{z}&u_{y}\[3pt]u_{z}&0&-u_{x}\[3pt]-u_{y}&u_{x}&0end{bmatrix}}.}$

In $mathbb {R} ^{3}$ the rotation of a vector x around the axis u by an angle θ can be written as:

${displaystyle R_{mathbf {u} }(theta )mathbf {x} =mathbf {u} (mathbf {u} cdot mathbf {x} )+cos left(theta right)(mathbf {u} times mathbf {x} )times mathbf {u} +sin left(theta right)(mathbf {u} times mathbf {x} )}$

If the 3D space is right-handed and θ > 0, this rotation will be counterclockwise when u points towards the observer (Right-hand rule). Explicitly, with a right-handed orthonormal basis,

${displaystyle R_{mathbf {u} }(theta ){boldsymbol {alpha }}=cos left(theta right){boldsymbol {alpha }}+sin left(theta right){boldsymbol {beta }},quad R_{mathbf {u} }(theta ){boldsymbol {beta }}=-sin left(theta right){boldsymbol {alpha }}+cos left(theta right){boldsymbol {beta }},quad R_{mathbf {u} }(theta )mathbf {u} =mathbf {u} .}$

Note the striking merely apparent differences to the equivalent Lie-algebraic formulation below.

Properties[edit]

For any n-dimensional rotation matrix R acting on ${displaystyle mathbb {R} ^{n},}$

${displaystyle R^{mathsf {T}}=R^{-1}}$

(The rotation is an orthogonal matrix)

It follows that:

A rotation is termed proper if det R = 1, and improper (or a roto-reflection) if det R = –1. For even dimensions n = 2k, the n eigenvalues λ of a proper rotation occur as pairs of complex conjugates which are roots of unity: λ = e^±iθ_j for j = 1, …, k, which is real only for λ = ±1. Therefore, there may be no vectors fixed by the rotation (λ = 1), and thus no axis of rotation. Any fixed eigenvectors occur in pairs, and the axis of rotation is an even-dimensional subspace.

For odd dimensions n = 2k + 1, a proper rotation R will have an odd number of eigenvalues, with at least one λ = 1 and the axis of rotation will be an odd dimensional subspace. Proof:

${displaystyle {begin{aligned}det left(R-Iright)&=det left(R^{mathsf {T}}right)det left(R-Iright)=det left(R^{mathsf {T}}R-R^{mathsf {T}}right)=det left(I-R^{mathsf {T}}right)\&=det(I-R)=left(-1right)^{n}det left(R-Iright)=-det left(R-Iright).end{aligned}}}$

Here I is the identity matrix, and we use det(R^T) = det(R) = 1, as well as (−1)ⁿ = −1 since n is odd. Therefore, det(R – I) = 0, meaning there is a null vector v with (R – I)v = 0, that is Rv = v, a fixed eigenvector. There may also be pairs of fixed eigenvectors in the even-dimensional subspace orthogonal to v, so the total dimension of fixed eigenvectors is odd.

For example, in 2-space n = 2, a rotation by angle θ has eigenvalues λ = e^iθ and λ = e^−iθ, so there is no axis of rotation except when θ = 0, the case of the null rotation. In 3-space n = 3, the axis of a non-null proper rotation is always a unique line, and a rotation around this axis by angle θ has eigenvalues λ = 1, e^iθ, e^−iθ. In 4-space n = 4, the four eigenvalues are of the form e^±iθ, e^±iφ. The null rotation has θ = φ = 0. The case of θ = 0, φ ≠ 0 is called a simple rotation, with two unit eigenvalues forming an axis plane, and a two-dimensional rotation orthogonal to the axis plane. Otherwise, there is no axis plane. The case of θ = φ is called an isoclinic rotation, having eigenvalues e^±iθ repeated twice, so every vector is rotated through an angle θ.

The trace of a rotation matrix is equal to the sum of its eigenvalues. For n = 2, a rotation by angle θ has trace 2 cos θ. For n = 3, a rotation around any axis by angle θ has trace 1 + 2 cos θ. For n = 4, and the trace is 2(cos θ + cos φ), which becomes 4 cos θ for an isoclinic rotation.

Examples[edit]

The 2 × 2 rotation matrix

$Q={begin{bmatrix}0&1\-1&0end{bmatrix}}$

corresponds to a 90° planar rotation clockwise about the origin.

The transpose of the 2 × 2 matrix

$M={begin{bmatrix}0.936&0.352\0.352&-0.936end{bmatrix}}$

is its inverse, but since its determinant is −1, this is not a proper rotation matrix; it is a reflection across the line 11y = 2x.

The 3 × 3 rotation matrix

${displaystyle Q={begin{bmatrix}1&0&0\0&{frac {sqrt {3}}{2}}&{frac {1}{2}}\0&-{frac {1}{2}}&{frac {sqrt {3}}{2}}end{bmatrix}}={begin{bmatrix}1&0&0\0&cos 30^{circ }&sin 30^{circ }\0&-sin 30^{circ }&cos 30^{circ }\end{bmatrix}}}$

corresponds to a −30° rotation around the x-axis in three-dimensional space.

The 3 × 3 rotation matrix

${displaystyle Q={begin{bmatrix}0.36&0.48&-0.80\-0.80&0.60&0.00\0.48&0.64&0.60end{bmatrix}}}$

corresponds to a rotation of approximately −74° around the axis (−1/2,1,1) in three-dimensional space.

The 3 × 3 permutation matrix

$P={begin{bmatrix}0&0&1\1&0&0\0&1&0end{bmatrix}}$

is a rotation matrix, as is the matrix of any even permutation, and rotates through 120° about the axis x = y = z.

The 3 × 3 matrix

$M={begin{bmatrix}3&-4&1\5&3&-7\-9&2&6end{bmatrix}}$

has determinant +1, but is not orthogonal (its transpose is not its inverse), so it is not a rotation matrix.

The 4 × 3 matrix

$M={begin{bmatrix}0.5&-0.1&0.7\0.1&0.5&-0.5\-0.7&0.5&0.5\-0.5&-0.7&-0.1end{bmatrix}}$

is not square, and so cannot be a rotation matrix; yet M^TM yields a 3 × 3 identity matrix (the columns are orthonormal).

The 4 × 4 matrix

${displaystyle Q=-I={begin{bmatrix}-1&0&0&0\0&-1&0&0\0&0&-1&0\0&0&0&-1end{bmatrix}}}$

describes an isoclinic rotation in four dimensions, a rotation through equal angles (180°) through two orthogonal planes.

The 5 × 5 rotation matrix

$Q={begin{bmatrix}0&-1&0&0&0\1&0&0&0&0\0&0&-1&0&0\0&0&0&-1&0\0&0&0&0&1end{bmatrix}}$

rotates vectors in the plane of the first two coordinate axes 90°, rotates vectors in the plane of the next two axes 180°, and leaves the last coordinate axis unmoved.

Geometry[edit]

In Euclidean geometry, a rotation is an example of an isometry, a transformation that moves points without changing the distances between them. Rotations are distinguished from other isometries by two additional properties: they leave (at least) one point fixed, and they leave “handedness” unchanged. In contrast, a translation moves every point, a reflection exchanges left- and right-handed ordering, a glide reflection does both, and an improper rotation combines a change in handedness with a normal rotation.

If a fixed point is taken as the origin of a Cartesian coordinate system, then every point can be given coordinates as a displacement from the origin. Thus one may work with the vector space of displacements instead of the points themselves. Now suppose (p₁, …, p_n) are the coordinates of the vector p from the origin O to point P. Choose an orthonormal basis for our coordinates; then the squared distance to P, by Pythagoras, is

${displaystyle d^{2}(O,P)=|mathbf {p} |^{2}=sum _{r=1}^{n}p_{r}^{2}}$

which can be computed using the matrix multiplication

${displaystyle |mathbf {p} |^{2}={begin{bmatrix}p_{1}cdots p_{n}end{bmatrix}}{begin{bmatrix}p_{1}\vdots \p_{n}end{bmatrix}}=mathbf {p} ^{mathsf {T}}mathbf {p} .}$

A geometric rotation transforms lines to lines, and preserves ratios of distances between points. From these properties it can be shown that a rotation is a linear transformation of the vectors, and thus can be written in matrix form, Qp. The fact that a rotation preserves, not just ratios, but distances themselves, is stated as

${displaystyle mathbf {p} ^{mathsf {T}}mathbf {p} =(Qmathbf {p} )^{mathsf {T}}(Qmathbf {p} ),}$

${displaystyle {begin{aligned}mathbf {p} ^{mathsf {T}}Imathbf {p} &{}=left(mathbf {p} ^{mathsf {T}}Q^{mathsf {T}}right)(Qmathbf {p} )\&{}=mathbf {p} ^{mathsf {T}}left(Q^{mathsf {T}}Qright)mathbf {p} .end{aligned}}}$

Because this equation holds for all vectors, p, one concludes that every rotation matrix, Q, satisfies the orthogonality condition,

${displaystyle Q^{mathsf {T}}Q=I.}$

Rotations preserve handedness because they cannot change the ordering of the axes, which implies the special matrix condition,

Equally important, it can be shown that any matrix satisfying these two conditions acts as a rotation.

Multiplication[edit]

The inverse of a rotation matrix is its transpose, which is also a rotation matrix:

${displaystyle {begin{aligned}left(Q^{mathsf {T}}right)^{mathsf {T}}left(Q^{mathsf {T}}right)&=QQ^{mathsf {T}}=I\det Q^{mathsf {T}}&=det Q=+1.end{aligned}}}$

The product of two rotation matrices is a rotation matrix:

${displaystyle {begin{aligned}left(Q_{1}Q_{2}right)^{mathsf {T}}left(Q_{1}Q_{2}right)&=Q_{2}^{mathsf {T}}left(Q_{1}^{mathsf {T}}Q_{1}right)Q_{2}=I\det left(Q_{1}Q_{2}right)&=left(det Q_{1}right)left(det Q_{2}right)=+1.end{aligned}}}$

For n > 2, multiplication of n × n rotation matrices is generally not commutative.

${displaystyle {begin{aligned}Q_{1}&={begin{bmatrix}0&-1&0\1&0&0\0&0&1end{bmatrix}}&Q_{2}&={begin{bmatrix}0&0&1\0&1&0\-1&0&0end{bmatrix}}\Q_{1}Q_{2}&={begin{bmatrix}0&-1&0\0&0&1\-1&0&0end{bmatrix}}&Q_{2}Q_{1}&={begin{bmatrix}0&0&1\1&0&0\0&1&0end{bmatrix}}.end{aligned}}}$

Noting that any identity matrix is a rotation matrix, and that matrix multiplication is associative, we may summarize all these properties by saying that the n × n rotation matrices form a group, which for n > 2 is non-abelian, called a special orthogonal group, and denoted by SO(n), SO(n,R), SO_n, or SO_n(R), the group of n × n rotation matrices is isomorphic to the group of rotations in an n-dimensional space. This means that multiplication of rotation matrices corresponds to composition of rotations, applied in left-to-right order of their corresponding matrices.

Ambiguities[edit]

Alias and alibi rotations

The interpretation of a rotation matrix can be subject to many ambiguities.

In most cases the effect of the ambiguity is equivalent to the effect of a rotation matrix inversion (for these orthogonal matrices equivalently matrix transpose).

Alias or alibi (passive or active) transformation

The coordinates of a point P may change due to either a rotation of the coordinate system CS (alias), or a rotation of the point P (alibi). In the latter case, the rotation of P also produces a rotation of the vector v representing P. In other words, either P and v are fixed while CS rotates (alias), or CS is fixed while P and v rotate (alibi). Any given rotation can be legitimately described both ways, as vectors and coordinate systems actually rotate with respect to each other, about the same axis but in opposite directions. Throughout this article, we chose the alibi approach to describe rotations. For instance,

$R(theta )={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta \end{bmatrix}}$

represents a counterclockwise rotation of a vector v by an angle θ, or a rotation of CS by the same angle but in the opposite direction (i.e. clockwise). Alibi and alias transformations are also known as active and passive transformations, respectively.

Pre-multiplication or post-multiplication

The same point P can be represented either by a column vector v or a row vector w. Rotation matrices can either pre-multiply column vectors (Rv), or post-multiply row vectors (wR). However, Rv produces a rotation in the opposite direction with respect to wR. Throughout this article, rotations produced on column vectors are described by means of a pre-multiplication. To obtain exactly the same rotation (i.e. the same final coordinates of point P), the equivalent row vector must be post-multiplied by the transpose of R (i.e. wR^T).

Right- or left-handed coordinates

The matrix and the vector can be represented with respect to a right-handed or left-handed coordinate system. Throughout the article, we assumed a right-handed orientation, unless otherwise specified.

Vectors or forms

The vector space has a dual space of linear forms, and the matrix can act on either vectors or forms.

Decompositions[edit]

Independent planes[edit]

Consider the 3 × 3 rotation matrix

${displaystyle Q={begin{bmatrix}0.36&0.48&-0.80\-0.80&0.60&0.00\0.48&0.64&0.60end{bmatrix}}.}$

If Q acts in a certain direction, v, purely as a scaling by a factor λ, then we have

{displaystyle Qmathbf {v} =lambda mathbf {v} ,}

so that

{displaystyle mathbf {0} =(lambda I-Q)mathbf {v} .}

Thus λ is a root of the characteristic polynomial for Q,

${displaystyle {begin{aligned}0&{}=det(lambda I-Q)\&{}=lambda ^{3}-{tfrac {39}{25}}lambda ^{2}+{tfrac {39}{25}}lambda -1\&{}=(lambda -1)left(lambda ^{2}-{tfrac {14}{25}}lambda +1right).end{aligned}}}$

Two features are noteworthy. First, one of the roots (or eigenvalues) is 1, which tells us that some direction is unaffected by the matrix. For rotations in three dimensions, this is the axis of the rotation (a concept that has no meaning in any other dimension). Second, the other two roots are a pair of complex conjugates, whose product is 1 (the constant term of the quadratic), and whose sum is 2 cos θ (the negated linear term). This factorization is of interest for 3 × 3 rotation matrices because the same thing occurs for all of them. (As special cases, for a null rotation the “complex conjugates” are both 1, and for a 180° rotation they are both −1.) Furthermore, a similar factorization holds for any n × n rotation matrix. If the dimension, n, is odd, there will be a “dangling” eigenvalue of 1; and for any dimension the rest of the polynomial factors into quadratic terms like the one here (with the two special cases noted). We are guaranteed that the characteristic polynomial will have degree n and thus n eigenvalues. And since a rotation matrix commutes with its transpose, it is a normal matrix, so can be diagonalized. We conclude that every rotation matrix, when expressed in a suitable coordinate system, partitions into independent rotations of two-dimensional subspaces, at most n/2 of them.

The sum of the entries on the main diagonal of a matrix is called the trace; it does not change if we reorient the coordinate system, and always equals the sum of the eigenvalues. This has the convenient implication for 2 × 2 and 3 × 3 rotation matrices that the trace reveals the angle of rotation, θ, in the two-dimensional space (or subspace). For a 2 × 2 matrix the trace is 2 cos θ, and for a 3 × 3 matrix it is 1 + 2 cos θ. In the three-dimensional case, the subspace consists of all vectors perpendicular to the rotation axis (the invariant direction, with eigenvalue 1). Thus we can extract from any 3 × 3 rotation matrix a rotation axis and an angle, and these completely determine the rotation.

Sequential angles[edit]

The constraints on a 2 × 2 rotation matrix imply that it must have the form

$Q={begin{bmatrix}a&-b\b&aend{bmatrix}}$

with a² + b² = 1. Therefore, we may set a = cos θ and b = sin θ, for some angle θ. To solve for θ it is not enough to look at a alone or b alone; we must consider both together to place the angle in the correct quadrant, using a two-argument arctangent function.

Now consider the first column of a 3 × 3 rotation matrix,

${begin{bmatrix}a\b\cend{bmatrix}}.$

Although a² + b² will probably not equal 1, but some value r² < 1, we can use a slight variation of the previous computation to find a so-called Givens rotation that transforms the column to

${begin{bmatrix}r\0\cend{bmatrix}},$

zeroing b. This acts on the subspace spanned by the x– and y-axes. We can then repeat the process for the xz-subspace to zero c. Acting on the full matrix, these two rotations produce the schematic form

$Q_{xz}Q_{xy}Q={begin{bmatrix}1&0&0\0&ast &ast \0&ast &ast end{bmatrix}}.$

Shifting attention to the second column, a Givens rotation of the yz-subspace can now zero the z value. This brings the full matrix to the form

$Q_{yz}Q_{xz}Q_{xy}Q={begin{bmatrix}1&0&0\0&1&0\0&0&1end{bmatrix}},$

which is an identity matrix. Thus we have decomposed Q as

$Q=Q_{xy}^{-1}Q_{xz}^{-1}Q_{yz}^{-1}.$

An n × n rotation matrix will have (n − 1) + (n − 2) + ⋯ + 2 + 1, or

${displaystyle sum _{k=1}^{n-1}k={frac {1}{2}}n(n-1)}$

entries below the diagonal to zero. We can zero them by extending the same idea of stepping through the columns with a series of rotations in a fixed sequence of planes. We conclude that the set of n × n rotation matrices, each of which has n² entries, can be parameterized by 1/2n(n − 1) angles.

xzx_w	xzy_w	xyx_w	xyz_w
yxy_w	yxz_w	yzy_w	yzx_w
zyz_w	zyx_w	zxz_w	zxy_w
xzx_b	yzx_b	xyx_b	zyx_b
yxy_b	zxy_b	yzy_b	xzy_b
zyz_b	xyz_b	zxz_b	yxz_b

In three dimensions this restates in matrix form an observation made by Euler, so mathematicians call the ordered sequence of three angles Euler angles. However, the situation is somewhat more complicated than we have so far indicated. Despite the small dimension, we actually have considerable freedom in the sequence of axis pairs we use; and we also have some freedom in the choice of angles. Thus we find many different conventions employed when three-dimensional rotations are parameterized for physics, or medicine, or chemistry, or other disciplines. When we include the option of world axes or body axes, 24 different sequences are possible. And while some disciplines call any sequence Euler angles, others give different names (Cardano, Tait–Bryan, roll-pitch-yaw) to different sequences.

One reason for the large number of options is that, as noted previously, rotations in three dimensions (and higher) do not commute. If we reverse a given sequence of rotations, we get a different outcome. This also implies that we cannot compose two rotations by adding their corresponding angles. Thus Euler angles are not vectors, despite a similarity in appearance as a triplet of numbers.

Nested dimensions[edit]

A 3 × 3 rotation matrix such as

${displaystyle Q_{3times 3}={begin{bmatrix}cos theta &-sin theta &{color {CadetBlue}0}\sin theta &cos theta &{color {CadetBlue}0}\{color {CadetBlue}0}&{color {CadetBlue}0}&{color {CadetBlue}1}end{bmatrix}}}$

suggests a 2 × 2 rotation matrix,

${displaystyle Q_{2times 2}={begin{bmatrix}cos theta &-sin theta \sin theta &cos theta end{bmatrix}},}$

is embedded in the upper left corner:

${displaystyle Q_{3times 3}=left[{begin{matrix}Q_{2times 2}&mathbf {0} \mathbf {0} ^{mathsf {T}}&1end{matrix}}right].}$

This is no illusion; not just one, but many, copies of n-dimensional rotations are found within (n + 1)-dimensional rotations, as subgroups. Each embedding leaves one direction fixed, which in the case of 3 × 3 matrices is the rotation axis. For example, we have

${displaystyle {begin{aligned}Q_{mathbf {x} }(theta )&={begin{bmatrix}{color {CadetBlue}1}&{color {CadetBlue}0}&{color {CadetBlue}0}\{color {CadetBlue}0}&cos theta &-sin theta \{color {CadetBlue}0}&sin theta &cos theta end{bmatrix}},\[8px]Q_{mathbf {y} }(theta )&={begin{bmatrix}cos theta &{color {CadetBlue}0}&sin theta \{color {CadetBlue}0}&{color {CadetBlue}1}&{color {CadetBlue}0}\-sin theta &{color {CadetBlue}0}&cos theta end{bmatrix}},\[8px]Q_{mathbf {z} }(theta )&={begin{bmatrix}cos theta &-sin theta &{color {CadetBlue}0}\sin theta &cos theta &{color {CadetBlue}0}\{color {CadetBlue}0}&{color {CadetBlue}0}&{color {CadetBlue}1}end{bmatrix}},end{aligned}}}$

fixing the x-axis, the y-axis, and the z-axis, respectively. The rotation axis need not be a coordinate axis; if u = (x,y,z) is a unit vector in the desired direction, then

${displaystyle {begin{aligned}Q_{mathbf {u} }(theta )&={begin{bmatrix}0&-z&y\z&0&-x\-y&x&0end{bmatrix}}sin theta +left(I-mathbf {u} mathbf {u} ^{mathsf {T}}right)cos theta +mathbf {u} mathbf {u} ^{mathsf {T}}\[8px]&={begin{bmatrix}left(1-x^{2}right)c_{theta }+x^{2}&-zs_{theta }-xyc_{theta }+xy&ys_{theta }-xzc_{theta }+xz\zs_{theta }-xyc_{theta }+xy&left(1-y^{2}right)c_{theta }+y^{2}&-xs_{theta }-yzc_{theta }+yz\-ys_{theta }-xzc_{theta }+xz&xs_{theta }-yzc_{theta }+yz&left(1-z^{2}right)c_{theta }+z^{2}end{bmatrix}}\[8px]&={begin{bmatrix}x^{2}(1-c_{theta })+c_{theta }&xy(1-c_{theta })-zs_{theta }&xz(1-c_{theta })+ys_{theta }\xy(1-c_{theta })+zs_{theta }&y^{2}(1-c_{theta })+c_{theta }&yz(1-c_{theta })-xs_{theta }\xz(1-c_{theta })-ys_{theta }&yz(1-c_{theta })+xs_{theta }&z^{2}(1-c_{theta })+c_{theta }end{bmatrix}},end{aligned}}}$

where c_θ = cos θ, s_θ = sin θ, is a rotation by angle θ leaving axis u fixed.

A direction in (n + 1)-dimensional space will be a unit magnitude vector, which we may consider a point on a generalized sphere, Sⁿ. Thus it is natural to describe the rotation group SO(n + 1) as combining SO(n) and Sⁿ. A suitable formalism is the fiber bundle,

${displaystyle SO(n)hookrightarrow SO(n+1)to S^{n},}$

where for every direction in the base space, Sⁿ, the fiber over it in the total space, SO(n + 1), is a copy of the fiber space, SO(n), namely the rotations that keep that direction fixed.

Thus we can build an n × n rotation matrix by starting with a 2 × 2 matrix, aiming its fixed axis on S² (the ordinary sphere in three-dimensional space), aiming the resulting rotation on S³, and so on up through Sⁿ⁻¹. A point on Sⁿ can be selected using n numbers, so we again have 1/2n(n − 1) numbers to describe any n × n rotation matrix.

In fact, we can view the sequential angle decomposition, discussed previously, as reversing this process. The composition of n − 1 Givens rotations brings the first column (and row) to (1, 0, …, 0), so that the remainder of the matrix is a rotation matrix of dimension one less, embedded so as to leave (1, 0, …, 0) fixed.

Skew parameters via Cayley’s formula[edit]

When an n × n rotation matrix Q, does not include a −1 eigenvalue, thus none of the planar rotations which it comprises are 180° rotations, then Q + I is an invertible matrix. Most rotation matrices fit this description, and for them it can be shown that (Q − I)(Q + I)⁻¹ is a skew-symmetric matrix, A. Thus A^T = −A; and since the diagonal is necessarily zero, and since the upper triangle determines the lower one, A contains 1/2n(n − 1) independent numbers.

Conveniently, I − A is invertible whenever A is skew-symmetric; thus we can recover the original matrix using the Cayley transform,

${displaystyle Amapsto (I+A)(I-A)^{-1},}$

which maps any skew-symmetric matrix A to a rotation matrix. In fact, aside from the noted exceptions, we can produce any rotation matrix in this way. Although in practical applications we can hardly afford to ignore 180° rotations, the Cayley transform is still a potentially useful tool, giving a parameterization of most rotation matrices without trigonometric functions.

In three dimensions, for example, we have (Cayley 1846)

${displaystyle {begin{aligned}&{begin{bmatrix}0&-z&y\z&0&-x\-y&x&0end{bmatrix}}mapsto \[3pt]quad {frac {1}{1+x^{2}+y^{2}+z^{2}}}&{begin{bmatrix}1+x^{2}-y^{2}-z^{2}&2xy-2z&2y+2xz\2xy+2z&1-x^{2}+y^{2}-z^{2}&2yz-2x\2xz-2y&2x+2yz&1-x^{2}-y^{2}+z^{2}end{bmatrix}}.end{aligned}}}$

If we condense the skew entries into a vector, (x,y,z), then we produce a 90° rotation around the x-axis for (1, 0, 0), around the y-axis for (0, 1, 0), and around the z-axis for (0, 0, 1). The 180° rotations are just out of reach; for, in the limit as x → ∞, (x, 0, 0) does approach a 180° rotation around the x axis, and similarly for other directions.

Decomposition into shears[edit]

For the 2D case, a rotation matrix can be decomposed into three shear matrices (Paeth 1986):

${displaystyle {begin{aligned}R(theta )&{}={begin{bmatrix}1&-tan {frac {theta }{2}}\0&1end{bmatrix}}{begin{bmatrix}1&0\sin theta &1end{bmatrix}}{begin{bmatrix}1&-tan {frac {theta }{2}}\0&1end{bmatrix}}end{aligned}}}$

This is useful, for instance, in computer graphics, since shears can be implemented with fewer multiplication instructions than rotating a bitmap directly. On modern computers, this may not matter, but it can be relevant for very old or low-end microprocessors.

A rotation can also be written as two shears and scaling (Daubechies & Sweldens 1998):

${displaystyle {begin{aligned}R(theta )&{}={begin{bmatrix}1&0\tan theta &1end{bmatrix}}{begin{bmatrix}1&-sin theta cos theta \0&1end{bmatrix}}{begin{bmatrix}cos theta &0\0&{frac {1}{cos theta }}end{bmatrix}}end{aligned}}}$

Group theory[edit]

Below follow some basic facts about the role of the collection of all rotation matrices of a fixed dimension (here mostly 3) in mathematics and particularly in physics where rotational symmetry is a requirement of every truly fundamental law (due to the assumption of isotropy of space), and where the same symmetry, when present, is a simplifying property of many problems of less fundamental nature. Examples abound in classical mechanics and quantum mechanics. Knowledge of the part of the solutions pertaining to this symmetry applies (with qualifications) to all such problems and it can be factored out of a specific problem at hand, thus reducing its complexity. A prime example – in mathematics and physics – would be the theory of spherical harmonics. Their role in the group theory of the rotation groups is that of being a representation space for the entire set of finite-dimensional irreducible representations of the rotation group SO(3). For this topic, see Rotation group SO(3) § Spherical harmonics.

The main articles listed in each subsection are referred to for more detail.

Lie group[edit]

The n × n rotation matrices for each n form a group, the special orthogonal group, SO(n). This algebraic structure is coupled with a topological structure inherited from ${displaystyle operatorname {GL} _{n}(mathbb {R} )}$ in such a way that the operations of multiplication and taking the inverse are analytic functions of the matrix entries. Thus SO(n) is for each n a Lie group. It is compact and connected, but not simply connected. It is also a semi-simple group, in fact a simple group with the exception SO(4).^[6] The relevance of this is that all theorems and all machinery from the theory of analytic manifolds (analytic manifolds are in particular smooth manifolds) apply and the well-developed representation theory of compact semi-simple groups is ready for use.

Lie algebra[edit]

The Lie algebra so(n) of SO(n) is given by

${displaystyle {mathfrak {so}}(n)={mathfrak {o}}(n)=left{Xin M_{n}(mathbb {R} )mid X=-X^{mathsf {T}}right},}$

and is the space of skew-symmetric matrices of dimension n, see classical group, where o(n) is the Lie algebra of O(n), the orthogonal group. For reference, the most common basis for so(3) is

${displaystyle L_{mathbf {x} }={begin{bmatrix}0&0&0\0&0&-1\0&1&0end{bmatrix}},quad L_{mathbf {y} }={begin{bmatrix}0&0&1\0&0&0\-1&0&0end{bmatrix}},quad L_{mathbf {z} }={begin{bmatrix}0&-1&0\1&0&0\0&0&0end{bmatrix}}.}$

Exponential map[edit]

Connecting the Lie algebra to the Lie group is the exponential map, which is defined using the standard matrix exponential series for e^A^[7] For any skew-symmetric matrix A, exp(A) is always a rotation matrix.^{[nb 3]}

An important practical example is the 3 × 3 case. In rotation group SO(3), it is shown that one can identify every A ∈ so(3) with an Euler vector ω = θu, where u = (x, y, z) is a unit magnitude vector.

By the properties of the identification ${displaystyle mathbf {su} (2)cong mathbb {R} ^{3}}$ , u is in the null space of A. Thus, u is left invariant by exp(A) and is hence a rotation axis.

According to Rodrigues’ rotation formula on matrix form, one obtains,

${displaystyle {begin{aligned}exp(A)&=exp {bigl (}theta (mathbf {u} cdot mathbf {L} ){bigr )}\&=exp left({begin{bmatrix}0&-ztheta &ytheta \ztheta &0&-xtheta \-ytheta &xtheta &0end{bmatrix}}right)\&=I+sin theta mathbf {u} cdot mathbf {L} +(1-cos theta )(mathbf {u} cdot mathbf {L} )^{2},end{aligned}}}$

where

${displaystyle mathbf {u} cdot mathbf {L} ={begin{bmatrix}0&-z&y\z&0&-x\-y&x&0end{bmatrix}}.}$

This is the matrix for a rotation around axis u by the angle θ. For full detail, see exponential map SO(3).

Baker–Campbell–Hausdorff formula[edit]

The BCH formula provides an explicit expression for Z = log(e^Xe^Y) in terms of a series expansion of nested commutators of X and Y.^[8] This general expansion unfolds as^{[nb 4]}

${displaystyle Z=C(X,Y)=X+Y+{tfrac {1}{2}}[X,Y]+{tfrac {1}{12}}{bigl [}X,[X,Y]{bigr ]}-{tfrac {1}{12}}{bigl [}Y,[X,Y]{bigr ]}+cdots .}$

In the 3 × 3 case, the general infinite expansion has a compact form,^[9]

for suitable trigonometric function coefficients, detailed in the Baker–Campbell–Hausdorff formula for SO(3).

As a group identity, the above holds for all faithful representations, including the doublet (spinor representation), which is simpler. The same explicit formula thus follows straightforwardly through Pauli matrices; see the 2 × 2 derivation for SU(2). For the general n × n case, one might use Ref.^[10]

Spin group[edit]

The Lie group of n × n rotation matrices, SO(n), is not simply connected, so Lie theory tells us it is a homomorphic image of a universal covering group. Often the covering group, which in this case is called the spin group denoted by Spin(n), is simpler and more natural to work with.^[11]

In the case of planar rotations, SO(2) is topologically a circle, S¹. Its universal covering group, Spin(2), is isomorphic to the real line, R, under addition. Whenever angles of arbitrary magnitude are used one is taking advantage of the convenience of the universal cover. Every 2 × 2 rotation matrix is produced by a countable infinity of angles, separated by integer multiples of 2π. Correspondingly, the fundamental group of SO(2) is isomorphic to the integers, Z.

In the case of spatial rotations, SO(3) is topologically equivalent to three-dimensional real projective space, RP³. Its universal covering group, Spin(3), is isomorphic to the 3-sphere, S³. Every 3 × 3 rotation matrix is produced by two opposite points on the sphere. Correspondingly, the fundamental group of SO(3) is isomorphic to the two-element group, Z₂.

We can also describe Spin(3) as isomorphic to quaternions of unit norm under multiplication, or to certain 4 × 4 real matrices, or to 2 × 2 complex special unitary matrices, namely SU(2). The covering maps for the first and the last case are given by

${displaystyle mathbb {H} supset {qin mathbb {H} :|q|=1}ni w+mathbf {i} x+mathbf {j} y+mathbf {k} zmapsto {begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}end{bmatrix}}in mathrm {SO} (3),}$

and

${displaystyle mathrm {SU} (2)ni {begin{bmatrix}alpha &beta \-{overline {beta }}&{overline {alpha }}end{bmatrix}}mapsto {begin{bmatrix}{frac {1}{2}}left(alpha ^{2}-beta ^{2}+{overline {alpha ^{2}}}-{overline {beta ^{2}}}right)&{frac {i}{2}}left(-alpha ^{2}-beta ^{2}+{overline {alpha ^{2}}}+{overline {beta ^{2}}}right)&-alpha beta -{overline {alpha }}{overline {beta }}\{frac {i}{2}}left(alpha ^{2}-beta ^{2}-{overline {alpha ^{2}}}+{overline {beta ^{2}}}right)&{frac {i}{2}}left(alpha ^{2}+beta ^{2}+{overline {alpha ^{2}}}+{overline {beta ^{2}}}right)&-ileft(+alpha beta -{overline {alpha }}{overline {beta }}right)\alpha {overline {beta }}+{overline {alpha }}beta &ileft(-alpha {overline {beta }}+{overline {alpha }}beta right)&alpha {overline {alpha }}-beta {overline {beta }}end{bmatrix}}in mathrm {SO} (3).}$

For a detailed account of the SU(2)-covering and the quaternionic covering, see spin group SO(3).

Many features of these cases are the same for higher dimensions. The coverings are all two-to-one, with SO(n), n > 2, having fundamental group Z₂. The natural setting for these groups is within a Clifford algebra. One type of action of the rotations is produced by a kind of “sandwich”, denoted by qvq^∗. More importantly in applications to physics, the corresponding spin representation of the Lie algebra sits inside the Clifford algebra. It can be exponentiated in the usual way to give rise to a 2-valued representation, also known as projective representation of the rotation group. This is the case with SO(3) and SU(2), where the 2-valued representation can be viewed as an “inverse” of the covering map. By properties of covering maps, the inverse can be chosen ono-to-one as a local section, but not globally.

Infinitesimal rotations[edit]

The matrices in the Lie algebra are not themselves rotations; the skew-symmetric matrices are derivatives, proportional differences of rotations. An actual “differential rotation”, or infinitesimal rotation matrix has the form

where dθ is vanishingly small and A ∈ so(n), for instance with A = L_x,

${displaystyle dL_{x}={begin{bmatrix}1&0&0\0&1&-dtheta \0&dtheta &1end{bmatrix}}.}$

The computation rules are as usual except that infinitesimals of second order are routinely dropped. With these rules, these matrices do not satisfy all the same properties as ordinary finite rotation matrices under the usual treatment of infinitesimals.^[12] It turns out that the order in which infinitesimal rotations are applied is irrelevant. To see this exemplified, consult infinitesimal rotations SO(3).

Conversions[edit]

We have seen the existence of several decompositions that apply in any dimension, namely independent planes, sequential angles, and nested dimensions. In all these cases we can either decompose a matrix or construct one. We have also given special attention to 3 × 3 rotation matrices, and these warrant further attention, in both directions (Stuelpnagel 1964).

Quaternion[edit]

Given the unit quaternion q = w + xi + yj + zk, the equivalent pre-multiplied (to be used with column vectors) 3 × 3 rotation matrix is ^[13]

${displaystyle Q={begin{bmatrix}1-2y^{2}-2z^{2}&2xy-2zw&2xz+2yw\2xy+2zw&1-2x^{2}-2z^{2}&2yz-2xw\2xz-2yw&2yz+2xw&1-2x^{2}-2y^{2}end{bmatrix}}.}$

Now every quaternion component appears multiplied by two in a term of degree two, and if all such terms are zero what is left is an identity matrix. This leads to an efficient, robust conversion from any quaternion – whether unit or non-unit – to a 3 × 3 rotation matrix. Given:

${displaystyle {begin{aligned}n&=wtimes w+xtimes x+ytimes y+ztimes z\s&={begin{cases}0&{text{if }}n=0\{frac {2}{n}}&{text{otherwise}}end{cases}}\end{aligned}}}$

we can calculate

${displaystyle Q={begin{bmatrix}1-s(yy+zz)&s(xy-wz)&s(xz+wy)\s(xy+wz)&1-s(xx+zz)&s(yz-wx)\s(xz-wy)&s(yz+wx)&1-s(xx+yy)end{bmatrix}}}$

Freed from the demand for a unit quaternion, we find that nonzero quaternions act as homogeneous coordinates for 3 × 3 rotation matrices. The Cayley transform, discussed earlier, is obtained by scaling the quaternion so that its w component is 1. For a 180° rotation around any axis, w will be zero, which explains the Cayley limitation.

The sum of the entries along the main diagonal (the trace), plus one, equals 4 − 4(x² + y² + z²), which is 4w². Thus we can write the trace itself as 2w² + 2w² − 1; and from the previous version of the matrix we see that the diagonal entries themselves have the same form: 2x² + 2w² − 1, 2y² + 2w² − 1, and 2z² + 2w² − 1. So we can easily compare the magnitudes of all four quaternion components using the matrix diagonal. We can, in fact, obtain all four magnitudes using sums and square roots, and choose consistent signs using the skew-symmetric part of the off-diagonal entries:

${displaystyle {begin{aligned}t&=operatorname {tr} Q=Q_{xx}+Q_{yy}+Q_{zz}quad ({text{the trace of }}Q)\r&={sqrt {1+t}}\w&={tfrac {1}{2}}r\x&=operatorname {sgn} left(Q_{zy}-Q_{yz}right)left|{tfrac {1}{2}}{sqrt {1+Q_{xx}-Q_{yy}-Q_{zz}}}right|\y&=operatorname {sgn} left(Q_{xz}-Q_{zx}right)left|{tfrac {1}{2}}{sqrt {1-Q_{xx}+Q_{yy}-Q_{zz}}}right|\z&=operatorname {sgn} left(Q_{yx}-Q_{xy}right)left|{tfrac {1}{2}}{sqrt {1-Q_{xx}-Q_{yy}+Q_{zz}}}right|end{aligned}}}$

Alternatively, use a single square root and division

${displaystyle {begin{aligned}t&=operatorname {tr} Q=Q_{xx}+Q_{yy}+Q_{zz}\r&={sqrt {1+t}}\s&={tfrac {1}{2r}}\w&={tfrac {1}{2}}r\x&=left(Q_{zy}-Q_{yz}right)s\y&=left(Q_{xz}-Q_{zx}right)s\z&=left(Q_{yx}-Q_{xy}right)send{aligned}}}$

This is numerically stable so long as the trace, t, is not negative; otherwise, we risk dividing by (nearly) zero. In that case, suppose Q_xx is the largest diagonal entry, so x will have the largest magnitude (the other cases are derived by cyclic permutation); then the following is safe.

${displaystyle {begin{aligned}r&={sqrt {1+Q_{xx}-Q_{yy}-Q_{zz}}}\s&={tfrac {1}{2r}}\w&=left(Q_{zy}-Q_{yz}right)s\x&={tfrac {1}{2}}r\y&=left(Q_{xy}+Q_{yx}right)s\z&=left(Q_{zx}+Q_{xz}right)send{aligned}}}$

If the matrix contains significant error, such as accumulated numerical error, we may construct a symmetric 4 × 4 matrix,

${displaystyle K={frac {1}{3}}{begin{bmatrix}Q_{xx}-Q_{yy}-Q_{zz}&Q_{yx}+Q_{xy}&Q_{zx}+Q_{xz}&Q_{zy}-Q_{yz}\Q_{yx}+Q_{xy}&Q_{yy}-Q_{xx}-Q_{zz}&Q_{zy}+Q_{yz}&Q_{xz}-Q_{zx}\Q_{zx}+Q_{xz}&Q_{zy}+Q_{yz}&Q_{zz}-Q_{xx}-Q_{yy}&Q_{yx}-Q_{xy}\Q_{zy}-Q_{yz}&Q_{xz}-Q_{zx}&Q_{yx}-Q_{xy}&Q_{xx}+Q_{yy}+Q_{zz}end{bmatrix}},}$

and find the eigenvector, (x, y, z, w), of its largest magnitude eigenvalue. (If Q is truly a rotation matrix, that value will be 1.) The quaternion so obtained will correspond to the rotation matrix closest to the given matrix (Bar-Itzhack 2000) (Note: formulation of the cited article is post-multiplied, works with row vectors).

Polar decomposition[edit]

If the n × n matrix M is nonsingular, its columns are linearly independent vectors; thus the Gram–Schmidt process can adjust them to be an orthonormal basis. Stated in terms of numerical linear algebra, we convert M to an orthogonal matrix, Q, using QR decomposition. However, we often prefer a Q closest to M, which this method does not accomplish. For that, the tool we want is the polar decomposition (Fan & Hoffman 1955; Higham 1989).

To measure closeness, we may use any matrix norm invariant under orthogonal transformations. A convenient choice is the Frobenius norm, ‖Q − M‖_F, squared, which is the sum of the squares of the element differences. Writing this in terms of the trace, Tr, our goal is,

Find Q minimizing Tr( (Q − M)^T(Q − M) ), subject to Q^TQ = I.

Though written in matrix terms, the objective function is just a quadratic polynomial. We can minimize it in the usual way, by finding where its derivative is zero. For a 3 × 3 matrix, the orthogonality constraint implies six scalar equalities that the entries of Q must satisfy. To incorporate the constraint(s), we may employ a standard technique, Lagrange multipliers, assembled as a symmetric matrix, Y. Thus our method is:

Differentiate Tr( (Q − M)^T(Q − M) + (Q^TQ − I)Y ) with respect to (the entries of) Q, and equate to zero.

Consider a 2 × 2 example. Including constraints, we seek to minimize

${displaystyle {begin{aligned}&left(Q_{xx}-M_{xx}right)^{2}+left(Q_{xy}-M_{xy}right)^{2}+left(Q_{yx}-M_{yx}right)^{2}+left(Q_{yy}-M_{yy}right)^{2}\&quad {}+left(Q_{xx}^{2}+Q_{yx}^{2}-1right)Y_{xx}+left(Q_{xy}^{2}+Q_{yy}^{2}-1right)Y_{yy}+2left(Q_{xx}Q_{xy}+Q_{yx}Q_{yy}right)Y_{xy}.end{aligned}}}$

Taking the derivative with respect to Q_xx, Q_xy, Q_yx, Q_yy in turn, we assemble a matrix.

${displaystyle 2{begin{bmatrix}Q_{xx}-M_{xx}+Q_{xx}Y_{xx}+Q_{xy}Y_{xy}&Q_{xy}-M_{xy}+Q_{xx}Y_{xy}+Q_{xy}Y_{yy}\Q_{yx}-M_{yx}+Q_{yx}Y_{xx}+Q_{yy}Y_{xy}&Q_{yy}-M_{yy}+Q_{yx}Y_{xy}+Q_{yy}Y_{yy}end{bmatrix}}}$

In general, we obtain the equation

so that

where Q is orthogonal and S is symmetric. To ensure a minimum, the Y matrix (and hence S) must be positive definite. Linear algebra calls QS the polar decomposition of M, with S the positive square root of S² = M^TM.

${displaystyle S^{2}=left(Q^{mathsf {T}}Mright)^{mathsf {T}}left(Q^{mathsf {T}}Mright)=M^{mathsf {T}}QQ^{mathsf {T}}M=M^{mathsf {T}}M}$

When M is non-singular, the Q and S factors of the polar decomposition are uniquely determined. However, the determinant of S is positive because S is positive definite, so Q inherits the sign of the determinant of M. That is, Q is only guaranteed to be orthogonal, not a rotation matrix. This is unavoidable; an M with negative determinant has no uniquely defined closest rotation matrix.

Axis and angle[edit]

To efficiently construct a rotation matrix Q from an angle θ and a unit axis u, we can take advantage of symmetry and skew-symmetry within the entries. If x, y, and z are the components of the unit vector representing the axis, and

${displaystyle {begin{aligned}c&=cos theta \s&=sin theta \C&=1-cend{aligned}}}$

then

$Q(theta )={begin{bmatrix}xxC+c&xyC-zs&xzC+ys\yxC+zs&yyC+c&yzC-xs\zxC-ys&zyC+xs&zzC+cend{bmatrix}}$

Determining an axis and angle, like determining a quaternion, is only possible up to the sign; that is, (u, θ) and (−u, −θ) correspond to the same rotation matrix, just like q and −q. Additionally, axis–angle extraction presents additional difficulties. The angle can be restricted to be from 0° to 180°, but angles are formally ambiguous by multiples of 360°. When the angle is zero, the axis is undefined. When the angle is 180°, the matrix becomes symmetric, which has implications in extracting the axis. Near multiples of 180°, care is needed to avoid numerical problems: in extracting the angle, a two-argument arctangent with atan2(sin θ, cos θ) equal to θ avoids the insensitivity of arccos; and in computing the axis magnitude in order to force unit magnitude, a brute-force approach can lose accuracy through underflow (Moler & Morrison 1983).

A partial approach is as follows:

${displaystyle {begin{aligned}x&=Q_{zy}-Q_{yz}\y&=Q_{xz}-Q_{zx}\z&=Q_{yx}-Q_{xy}\r&={sqrt {x^{2}+y^{2}+z^{2}}}\t&=Q_{xx}+Q_{yy}+Q_{zz}\theta &=operatorname {atan2} (r,t-1)end{aligned}}}$

The x-, y-, and z-components of the axis would then be divided by r. A fully robust approach will use a different algorithm when t, the trace of the matrix Q, is negative, as with quaternion extraction. When r is zero because the angle is zero, an axis must be provided from some source other than the matrix.

Euler angles[edit]

Complexity of conversion escalates with Euler angles (used here in the broad sense). The first difficulty is to establish which of the twenty-four variations of Cartesian axis order we will use. Suppose the three angles are θ₁, θ₂, θ₃; physics and chemistry may interpret these as

${displaystyle Q(theta _{1},theta _{2},theta _{3})=Q_{mathbf {z} }(theta _{1})Q_{mathbf {y} }(theta _{2})Q_{mathbf {z} }(theta _{3}),}$

while aircraft dynamics may use

${displaystyle Q(theta _{1},theta _{2},theta _{3})=Q_{mathbf {z} }(theta _{3})Q_{mathbf {y} }(theta _{2})Q_{mathbf {x} }(theta _{1}).}$

One systematic approach begins with choosing the rightmost axis. Among all permutations of (x,y,z), only two place that axis first; one is an even permutation and the other odd. Choosing parity thus establishes the middle axis. That leaves two choices for the left-most axis, either duplicating the first or not. These three choices gives us 3 × 2 × 2 = 12 variations; we double that to 24 by choosing static or rotating axes.

This is enough to construct a matrix from angles, but triples differing in many ways can give the same rotation matrix. For example, suppose we use the zyz convention above; then we have the following equivalent pairs:

(90°,	45°,	−105°)	≡	(−270°,	−315°,	255°)	multiples of 360°
(72°,	0°,	0°)	≡	(40°,	0°,	32°)	singular alignment
(45°,	60°,	−30°)	≡	(−135°,	−60°,	150°)	bistable flip

Angles for any order can be found using a concise common routine (Herter & Lott 1993; Shoemake 1994).

The problem of singular alignment, the mathematical analog of physical gimbal lock, occurs when the middle rotation aligns the axes of the first and last rotations. It afflicts every axis order at either even or odd multiples of 90°. These singularities are not characteristic of the rotation matrix as such, and only occur with the usage of Euler angles.

The singularities are avoided when considering and manipulating the rotation matrix as orthonormal row vectors (in 3D applications often named the right-vector, up-vector and out-vector) instead of as angles. The singularities are also avoided when working with quaternions.

Vector to vector formulation[edit]

In some instances it is interesting to describe a rotation by specifying how a vector is mapped into another through the shortest path (smallest angle). In $mathbb {R} ^{3}$ this completely describes the associated rotation matrix. In general, given x, y ∈ ⁿ, the matrix

${displaystyle R:=I+yx^{mathsf {T}}-xy^{mathsf {T}}+{frac {1}{1+langle x,yrangle }}left(yx^{mathsf {T}}-xy^{mathsf {T}}right)^{2}}$

belongs to SO(n + 1) and maps x to y.^[14]

Uniform random rotation matrices[edit]

We sometimes need to generate a uniformly distributed random rotation matrix. It seems intuitively clear in two dimensions that this means the rotation angle is uniformly distributed between 0 and 2π. That intuition is correct, but does not carry over to higher dimensions. For example, if we decompose 3 × 3 rotation matrices in axis–angle form, the angle should not be uniformly distributed; the probability that (the magnitude of) the angle is at most θ should be 1/π(θ − sin θ), for 0 ≤ θ ≤ π.

Since SO(n) is a connected and locally compact Lie group, we have a simple standard criterion for uniformity, namely that the distribution be unchanged when composed with any arbitrary rotation (a Lie group “translation”). This definition corresponds to what is called Haar measure. León, Massé & Rivest (2006) show how to use the Cayley transform to generate and test matrices according to this criterion.

We can also generate a uniform distribution in any dimension using the subgroup algorithm of Diaconis & Shashahani (1987). This recursively exploits the nested dimensions group structure of SO(n), as follows. Generate a uniform angle and construct a 2 × 2 rotation matrix. To step from n to n + 1, generate a vector v uniformly distributed on the n-sphere Sⁿ, embed the n × n matrix in the next larger size with last column (0, …, 0, 1), and rotate the larger matrix so the last column becomes v.

As usual, we have special alternatives for the 3 × 3 case. Each of these methods begins with three independent random scalars uniformly distributed on the unit interval. Arvo (1992) takes advantage of the odd dimension to change a Householder reflection to a rotation by negation, and uses that to aim the axis of a uniform planar rotation.

Another method uses unit quaternions. Multiplication of rotation matrices is homomorphic to multiplication of quaternions, and multiplication by a unit quaternion rotates the unit sphere. Since the homomorphism is a local isometry, we immediately conclude that to produce a uniform distribution on SO(3) we may use a uniform distribution on S³. In practice: create a four-element vector where each element is a sampling of a normal distribution. Normalize its length and you have a uniformly sampled random unit quaternion which represents a uniformly sampled random rotation. Note that the aforementioned only applies to rotations in dimension 3. For a generalised idea of quaternions, one should look into Rotors.

Euler angles can also be used, though not with each angle uniformly distributed (Murnaghan 1962; Miles 1965).

For the axis–angle form, the axis is uniformly distributed over the unit sphere of directions, S², while the angle has the nonuniform distribution over [0,π] noted previously (Miles 1965).

[edit]

^ Note that if instead of rotating vectors, it is the reference frame that is being rotated, the signs on the sin θ terms will be reversed. If reference frame A is rotated anti-clockwise about the origin through an angle θ to create reference frame B, then R_x (with the signs flipped) will transform a vector described in reference frame A coordinates to reference frame B coordinates. Coordinate frame transformations in aerospace, robotics, and other fields are often performed using this interpretation of the rotation matrix.
^ Note that

${displaystyle mathbf {u} otimes mathbf {u} ={bigl (}[mathbf {u} ]_{times }{bigr )}^{2}+{mathbf {I} }}$

so that, in Rodrigues’ notation, equivalently,

${displaystyle mathbf {R} =mathbf {I} +(sin theta )[mathbf {u} ]_{times }+(1-cos theta ){bigl (}[mathbf {u} ]_{times }{bigr )}^{2}.}$
^ Note that this exponential map of skew-symmetric matrices to rotation matrices is quite different from the Cayley transform discussed earlier, differing to the third order,

${displaystyle e^{2A}-{frac {I+A}{I-A}}=-{tfrac {2}{3}}A^{3}+mathrm {O} left(A^{4}right).}$

Conversely, a skew-symmetric matrix A specifying a rotation matrix through the Cayley map specifies the same rotation matrix through the map exp(2 artanh A).
^ For a detailed derivation, see Derivative of the exponential map. Issues of convergence of this series to the right element of the Lie algebra are here swept under the carpet. Convergence is guaranteed when ‖X‖ + ‖Y‖ < log 2 and ‖Z‖ < log 2. If these conditions are not fulfilled, the series may still converge. A solution always exists since exp is onto^{[clarification needed]} in the cases under consideration.

Notes[edit]

^ Swokowski, Earl (1979). Calculus with Analytic Geometry (Second ed.). Boston: Prindle, Weber, and Schmidt. ISBN 0-87150-268-2.
^ W3C recommendation (2003). “Scalable Vector Graphics – the initial coordinate system”.
^ “Rotation Matrices” (PDF). Retrieved 30 November 2021.
^ Taylor, Camillo J.; Kriegman, David J. (1994). “Minimization on the Lie Group SO(3) and Related Manifolds” (PDF). Technical Report No. 9405. Yale University.
^ Cole, Ian R. (January 2015). Modelling CPV (thesis). Loughborough University. hdl:2134/18050.
^ Baker (2003); Fulton & Harris (1991)
^ (Wedderburn 1934, §8.02)
^ Hall 2004, Ch. 3; Varadarajan 1984, §2.15
^ (Engø 2001)
^ Curtright, T L; Fairlie, D B; Zachos, C K (2014). “A compact formula for rotations as spin matrix polynomials”. SIGMA. 10: 084. arXiv:1402.3541. Bibcode:2014SIGMA..10..084C. doi:10.3842/SIGMA.2014.084. S2CID 18776942.
^ Baker 2003, Ch. 5; Fulton & Harris 1991, pp. 299–315
^ (Goldstein, Poole & Safko 2002, §4.8)
^ Shoemake, Ken (1 July 1985). “Animating rotation with quaternion curves”. SIGGRAPH Comput. Graph. Association for Computing Machinery. 19 (3): 245–254. doi:10.1145/325334.325242. Retrieved 3 January 2023.
^ Cid, Jose Ángel; Tojo, F. Adrián F. (2018). “A Lipschitz condition along a transversal foliation implies local uniqueness for ODEs”. Electronic Journal of Qualitative Theory of Differential Equations. 13 (13): 1–14. arXiv:1801.01724. doi:10.14232/ejqtde.2018.1.13.

References[edit]

Arvo, James (1992), “Fast random rotation matrices”, in David Kirk (ed.), Graphics Gems III, San Diego: Academic Press Professional, pp. 117–120, Bibcode:1992grge.book…..K, ISBN 978-0-12-409671-4
Baker, Andrew (2003), Matrix Groups: An Introduction to Lie Group Theory, Springer, ISBN 978-1-85233-470-3
Bar-Itzhack, Itzhack Y. (Nov–Dec 2000), “New method for extracting the quaternion from a rotation matrix”, Journal of Guidance, Control and Dynamics, 23 (6): 1085–1087, Bibcode:2000JGCD…23.1085B, doi:10.2514/2.4654, ISSN 0731-5090
Björck, Åke; Bowie, Clazett (June 1971), “An iterative algorithm for computing the best estimate of an orthogonal matrix”, SIAM Journal on Numerical Analysis, 8 (2): 358–364, Bibcode:1971SJNA….8..358B, doi:10.1137/0708036, ISSN 0036-1429
Cayley, Arthur (1846), “Sur quelques propriétés des déterminants gauches”, Journal für die reine und angewandte Mathematik, 1846 (32): 119–123, doi:10.1515/crll.1846.32.119, ISSN 0075-4102, S2CID 199546746; reprinted as article 52 in Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, vol. I (1841–1853), Cambridge University Press, pp. 332–336
Diaconis, Persi; Shahshahani, Mehrdad (1987), “The subgroup algorithm for generating uniform random variables”, Probability in the Engineering and Informational Sciences, 1: 15–32, doi:10.1017/S0269964800000255, ISSN 0269-9648, S2CID 122752374
Engø, Kenth (June 2001), “On the BCH-formula in so(3)”, BIT Numerical Mathematics, 41 (3): 629–632, doi:10.1023/A:1021979515229, ISSN 0006-3835, S2CID 126053191
Fan, Ky; Hoffman, Alan J. (February 1955), “Some metric inequalities in the space of matrices”, Proceedings of the American Mathematical Society, 6 (1): 111–116, doi:10.2307/2032662, ISSN 0002-9939, JSTOR 2032662
Fulton, William; Harris, Joe (1991), Representation Theory: A First Course, Graduate Texts in Mathematics, vol. 129, New York, Berlin, Heidelberg: Springer, ISBN 978-0-387-97495-8, MR 1153249
Goldstein, Herbert; Poole, Charles P.; Safko, John L. (2002), Classical Mechanics (third ed.), Addison Wesley, ISBN 978-0-201-65702-9
Hall, Brian C. (2004), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction, Springer, ISBN 978-0-387-40122-5 (GTM 222)
Herter, Thomas; Lott, Klaus (September–October 1993), “Algorithms for decomposing 3-D orthogonal matrices into primitive rotations”, Computers & Graphics, 17 (5): 517–527, doi:10.1016/0097-8493(93)90003-R, ISSN 0097-8493
Higham, Nicholas J. (October 1, 1989), “Matrix nearness problems and applications”, in Gover, Michael J. C.; Barnett, Stephen (eds.), Applications of Matrix Theory, Oxford University Press, pp. 1–27, ISBN 978-0-19-853625-3
León, Carlos A.; Massé, Jean-Claude; Rivest, Louis-Paul (February 2006), “A statistical model for random rotations”, Journal of Multivariate Analysis, 97 (2): 412–430, doi:10.1016/j.jmva.2005.03.009, ISSN 0047-259X
Miles, Roger E. (December 1965), “On random rotations in R³“, Biometrika, 52 (3/4): 636–639, doi:10.2307/2333716, ISSN 0006-3444, JSTOR 2333716
Moler, Cleve; Morrison, Donald (1983), “Replacing square roots by pythagorean sums”, IBM Journal of Research and Development, 27 (6): 577–581, doi:10.1147/rd.276.0577, ISSN 0018-8646
Murnaghan, Francis D. (1950), “The element of volume of the rotation group”, Proceedings of the National Academy of Sciences, 36 (11): 670–672, Bibcode:1950PNAS…36..670M, doi:10.1073/pnas.36.11.670, ISSN 0027-8424, PMC 1063502, PMID 16589056
Murnaghan, Francis D. (1962), The Unitary and Rotation Groups, Lectures on applied mathematics, Washington: Spartan Books
Cayley, Arthur (1889), The collected mathematical papers of Arthur Cayley, vol. I (1841–1853), Cambridge University Press, pp. 332–336
Paeth, Alan W. (1986), “A Fast Algorithm for General Raster Rotation” (PDF), Proceedings, Graphics Interface ’86: 77–81
Daubechies, Ingrid; Sweldens, Wim (1998), “Factoring wavelet transforms into lifting steps” (PDF), Journal of Fourier Analysis and Applications, 4 (3): 247–269, doi:10.1007/BF02476026, S2CID 195242970
Pique, Michael E. (1990), “Rotation Tools”, in Andrew S. Glassner (ed.), Graphics Gems, San Diego: Academic Press Professional, pp. 465–469, ISBN 978-0-12-286166-6
Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), “Section 21.5.2. Picking a Random Rotation Matrix”, Numerical Recipes: The Art of Scientific Computing (3rd ed.), New York: Cambridge University Press, ISBN 978-0-521-88068-8

Shepperd, Stanley W. (May–June 1978), “Quaternion from rotation matrix”, Journal of Guidance and Control, 1 (3): 223–224, doi:10.2514/3.55767b
Shoemake, Ken (1994), “Euler angle conversion”, in Paul Heckbert (ed.), Graphics Gems IV, San Diego: Academic Press Professional, pp. 222–229, ISBN 978-0-12-336155-4
Stuelpnagel, John (October 1964), “On the parameterization of the three-dimensional rotation group”, SIAM Review, 6 (4): 422–430, Bibcode:1964SIAMR…6..422S, doi:10.1137/1006093, ISSN 0036-1445, S2CID 13990266 (Also NASA-CR-53568.)
Varadarajan, Veeravalli S. (1984), Lie Groups, Lie Algebras, and Their Representation, Springer, ISBN 978-0-387-90969-1 (GTM 102)
Wedderburn, Joseph H. M. (1934), Lectures on Matrices, AMS, ISBN 978-0-8218-3204-2

External links[edit]

“Rotation”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Rotation matrices at Mathworld
Math Awareness Month 2000 interactive demo (requires Java)
Rotation Matrices at MathPages
(in Italian) A parametrization of SOn(R) by generalized Euler Angles
Rotation about any point

Источник

Матрицей поворота (или матрицей направляющих косинусов) называется ортогональная матрица, которая используется для выполнения собственного ортогонального преобразования в евклидовом пространстве. При умножении любого вектора на матрицу поворота длина вектора сохраняется. Определитель матрицы поворота равен единице.
Обычно считают, что, в отличие от матрицы перехода при повороте системы координат (базиса), при умножении на матрицу поворота вектора-столбца координаты вектора преобразуются в соответствии с поворотом самого вектора (а не поворотом координатных осей; то есть при этом координаты повернутого вектора получаются в той же, неподвижной системе координат). Однако отличие той и другой матрицы лишь в знаке угла поворота, и одна может быть получена из другой заменой угла поворота на противоположный; та и другая взаимно обратны и могут быть получены друг из друга транспонированием.

Матрица поворота в трёхмерном пространстве

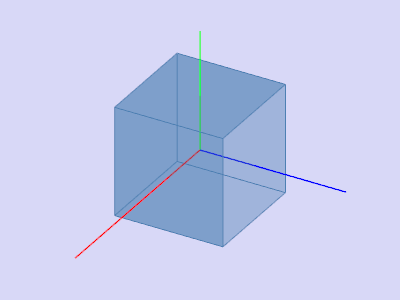
Любое вращение в трехмерном пространстве может быть представлено как композиция поворотов вокруг трех ортогональных осей (например, вокруг осей декартовых координат). Этой композиции соответствует матрица, равная произведению соответствующих трех матриц поворота.
Матрицами вращения вокруг оси декартовой системы координат на угол α в трёхмерном пространстве являются:
Вращение вокруг оси x:

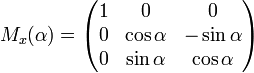
Вращение вокруг оси y:

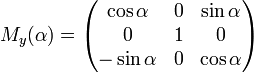
Вращение вокруг оси z:

После преобразований мы получаем формулы:
По оси Х
x’=x;
y’:=y*cos(L)+z*sin(L) ;
z’:=-y*sin(L)+z*cos(L) ;

По оси Y
x’=x*cos(L)+z*sin(L);
y’=y;
z’=-x*sin(L)+z*cos(L);

По оси Z
x’=x*cos(L)-y*sin(L);
y’=-x*sin(L)+y*cos(L);
z’=z;

Все три поворота делаются независимо друг от друга, т.е. если надо повернуть вокруг осей Ox и Oy, вначале делается поворот вокруг оси Ox, потом применительно к полученной точки делается поворот вокруг оси Oy.

Источник