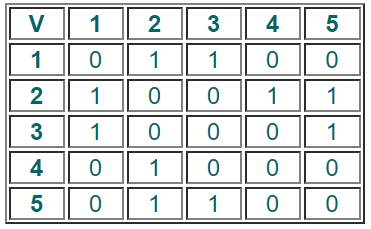
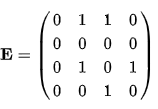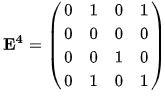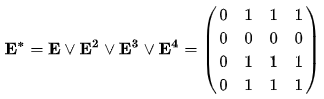Матрица
смежности S –
это
квадратная матрица, в которой и число
строк, и число столбцов равно n –
числу вершин графа. В ячейки матрицы
смежности записываются некоторые числа
в зависимости от того, соединены
соответствующие вершины рёбрами или
нет, и от типа графа.
Матрица
смежности для неориентированного графа
Элемент
матрицы смежности sij неориентированного
графа определяется следующим образом:
–
равен единице, если вершины vi и vj смежны;
–
равен нулю, если вершины vi и vj не
смежны.
Если
на диагонали матрицы стоят 1, то это
показывает наличие петель.
|
Пример |
Пример |
Таким
образом, матрица
смежности неориентированного
графа симметрична относительно главной
диагонали.
Матрица
смежности для ориентированного графа
Элемент
матрицы смежности sij ориентированного
графа определяется следующим образом:
–
равен единице, если из вершины vi в
вершину vj входит
дуга;
–
равен нулю, если из вершины vi в
вершину vj дуга
не входит.
Если
на диагонали матрицы стоят 1, то это
показывает наличие петель.
|
Пример |
Пример
|
Таким
образом, матрица
смежности ориентированного
графа не симметрична.
9.4. Список ребер
|
Пример
|
9.1-9.4
|
Пример
Матрицы
|
9.5. Матрица достижимости
Матрица
достижимости простого ориентированного
графа G=(V,E) — бинарная матрица замыкания
по транзитивности отношения E (оно
задаётся матрицей смежности графа).
Таким образом, в матрице достижимости
хранится информация о существовании
путей между вершинами орграфа.
Возведение
в степень матрицы смежности орграфа
показывает, за сколько шагов (величина
степени) можно достичь некой вершины.
Способы
построения матрицы достижимости:
-
Перемножение
матриц -
Алгоритм
Уоршелла -
Связанные
понятия
|
Пример Дан
Матрица Матрица Матрица Матрица Если Получим матрицу
Если
|
|||
|
Пример
|
- 1. Представление матрицы смежности
- 2. Пример матрицы смежности
- 3. Плюсы матрицы смежности
- 4. Минусы матрицы смежности
- 5. Код матрицы смежности
- 6. Матрица смежности в C++
- 7. Матрица смежности в Java
- 8. Матрица смежности в Python
Матрица смежности
– это способ представления графа G = {V, E} в виде матрицы логических значений.
Представление матрицы смежности
Размер матрицы VxV, где V – количество вершин в графе, а значение записи Aij равно 1 или 0, в зависимости от того, существует ли ребро от вершины i до вершины j.
Пример матрицы смежности
Изображение ниже показывает график и его эквивалентную матрицу смежности.
В случае неориентированного графа матрица симметрична относительно диагонали, потому что у каждого ребра (i, j) также есть ребро (j, i).
Плюсы матрицы смежности
Основные операции, такие как добавление ребра, удаление ребра и проверка наличия ребра от вершины i до вершины j, являются чрезвычайно эффективными по времени операциями. Операциями с постоянным временем.
Если граф плотный и число ребер велико, матрица смежности должна стать первым выбором. Даже если граф и матрица смежности разрежены, мы можем представить ее, используя структуры данных для разреженной матрицы.
Однако самое большое преимущество исходит от использования матриц. Последние достижения в области аппаратного обеспечения позволяют нам выполнять даже дорогостоящие матричные операции на графическом процессоре (GPU).
Выполняя операции над смежной матрицей, мы можем получить важную информацию о природе графа и взаимосвязи между его вершинами.
Минусы матрицы смежности
Из-за требования к пространству матрицы смежности VxV может быть недостаточно памяти. Но обычно графы не имеют слишком много соединений, и это главная причина, почему списки смежности являются лучшим выбором для большинства задач.
Хотя базовые операции просты, такие операции, как inEdges и outEdges, дороги при использовании представления матрицы смежности.
Код матрицы смежности
Если вы знаете, как создавать двумерные массивы, значит вы также знаете, как создать матрицу смежности.
Матрица смежности в C++
#include <iostream> using namespace std; class Graph { private: bool** adjMatrix; int numVertices; public: Graph(int numVertices) { this->numVertices = numVertices; adjMatrix = new bool*[numVertices]; for (int i = 0; i < numVertices; i++) { adjMatrix[i] = new bool[numVertices]; for (int j = 0; j < numVertices; j++) adjMatrix[i][j] = false; } } void addEdge(int i, int j) { adjMatrix[i][j] = true; adjMatrix[j][i] = true; } void removeEdge(int i, int j) { adjMatrix[i][j] = false; adjMatrix[j][i] = false; } bool isEdge(int i, int j) { return adjMatrix[i][j]; } void toString() { for (int i = 0; i < numVertices; i++) { cout << i << " : "; for (int j = 0; j < numVertices; j++) cout << adjMatrix[i][j] << " "; cout << "n"; } } ~Graph() { for (int i = 0; i < numVertices; i++) delete[] adjMatrix[i]; delete[] adjMatrix; } }; int main(){ Graph g(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.toString(); /* Outputs 0: 0 1 1 0 1: 1 0 1 0 2: 1 1 0 1 3: 0 0 1 0 */ }Матрица смежности в Java
public class Graph { private boolean adjMatrix[][]; private int numVertices; public Graph(int numVertices) { this.numVertices = numVertices; adjMatrix = new boolean[numVertices][numVertices]; } public void addEdge(int i, int j) { adjMatrix[i][j] = true; adjMatrix[j][i] = true; } public void removeEdge(int i, int j) { adjMatrix[i][j] = false; adjMatrix[j][i] = false; } public boolean isEdge(int i, int j) { return adjMatrix[i][j]; } public String toString() { StringBuilder s = new StringBuilder(); for (int i = 0; i < numVertices; i++) { s.append(i + ": "); for (boolean j : adjMatrix[i]) { s.append((j?1:0) + " "); } s.append("n"); } return s.toString(); } public static void main(String args[]) { Graph g = new Graph(4); g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); System.out.print(g.toString()); /* Outputs 0: 0 1 1 0 1: 1 0 1 0 2: 1 1 0 1 3: 0 0 1 0 */ } }Матрица смежности в Python
class Graph(object): def __init__(self, size): self.adjMatrix = [] for i in range(size): self.adjMatrix.append([0 for i in range(size)]) self.size = size def addEdge(self, v1, v2): if v1 == v2: print("Same vertex %d and %d" % (v1, v2)) self.adjMatrix[v1][v2] = 1 self.adjMatrix[v2][v1] = 1 def removeEdge(self, v1, v2): if self.adjMatrix[v1][v2] == 0: print("No edge between %d and %d" % (v1, v2)) return self.adjMatrix[v1][v2] = 0 self.adjMatrix[v2][v1] = 0 def containsEdge(self, v1, v2): return True if self.adjMatrix[v1][v2] > 0 else False def __len__(self): return self.size def toString(self): for row in self.adjMatrix: for val in row: print('{:4}'.format(val)), print def main(): g = Graph(5) g.addEdge(0, 1); g.addEdge(0, 2); g.addEdge(1, 2); g.addEdge(2, 0); g.addEdge(2, 3); g.toString() if __name__ == '__main__': main()
В чем особенности представления графа матрицей смежности
Содержание:
-
Матрица смежности для графов
- В чем особенности представления
- Списки смежности и списки ребер, плюсы и минусы
- Классификация графов
- Способы представления графа, алгоритмы обхода
- Как построить граф по матрице смежности
Матрица смежности для графов
Матрица смежности графа является квадратной матрицей с элементами, каждый из которых имеет одно из двух значений: 0 или 1.
Простой пример матрицы смежности изображен на рисунке.
Данная матрица является двоичной квадратной, то есть количество строк в единичном случае соответствует количеству столбцов, а также строки и столбы имеют значения либо 1, либо 0. Первая строка и первый столбец, не состоящие в матрице, а записанные для легкости восприятия, содержат номера, на пересечении которых расположен каждый из элементов, и они определяют индексное значение последних. Достаточно просто выполнить построение матрицы данного типа, зная соответствующий ей граф.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
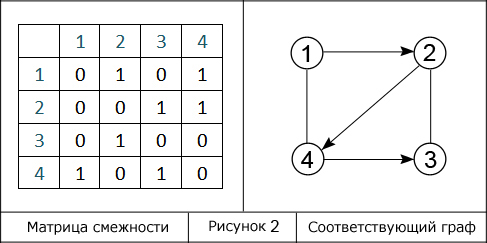
В левой стороне на рисунке представлена аналогичная матрица смежности с размерностью 4х4. Числа, выделенные синим цветом, допустимо рассматривать в виде вершин смешанного графа, записанного в правой стороне – того, представлением которого является матрица.
Отобразить граф можно путем вычисления по матрице смежности числа его вершин и применения специального правила. В том случае, когда из одной вершины в другую проход свободен, то есть имеется ребро, в ячейку записывают 1, в противном случае – 0. Таким образом:
если из i в j существует ребро, то (A[i][j]:=1), в противном случае (A[i][j]:=0.)
Заметим, что для элементов, расположенных на главной диагонали, характерно нулевое значение. Это является следствием отсутствия у графа петель. Однако, в информатике нет ограничений для записи некоторых или всех элементов на главной диагонали в виде единиц.
В чем особенности представления
В программе матрицу смежности задают с помощью обычного двумерного массива. Его размерность соответствует n x n, где n является числом вершин графа.
В том случае, когда граф неизвестен заранее, а определен пользователем, необходимо вводить двумерный массив вручную. Это объясняется условиями работы конкретного языка программирования. При необходимости предоставления графа в виде матрицы смежности требуется (O(|V|^{2})) памяти, так как ее размер соответствует квадрату числа всех вершин.
Если количество ребер графа в сравнении с числом вершин является небольшим, значения многих элементов матрицы смежности будут соответствовать нулю. Таким образом, применение рассматриваемой методики нецелесообразно, в связи с наличием для подобных графов наиболее эффективных способов представления.
Списки смежности и списки ребер, плюсы и минусы
Относительно памяти, списки смежности менее требовательны по сравнению с матрицами смежности. Объем памяти для их хранения составляет (O(|V|+|E|)). Такой перечень целесообразно представить как таблицу с двумя столбцами и строками в количестве, не превышающем число вершин в графе. Для примера можно рассмотреть граф смешанного типа:
В данном случае, граф состоит из 6 вершин (|V|) и 5 ребер (|E|). Из последних 2 ребра являются направленными и 3 ненаправленными. При этом из каждой вершины выходит, как минимум одно ребро в другую вершину. Таким образом, список смежности рассматриваемого графа содержит |V| строк.
В i строке и 1 столбце указана вершина выхода, а в i строке и 2 столбце – вершина входа. Например, из вершины 5 выходят два ребра, входящие в вершины 1 и 4.
В процессе программной реализации списка смежности число вершин и ребер задают с помощью клавиатуры. Можно установить лимиты, то есть задать пару констант, одна из которых определяет максимально допустимое число вершин (Vmax), другая – ребер (Emax). Затем следует использовать три одномерных целочисленных массива:
- terminal[1..Emax] – для хранения вершин, содержащих ребра;
- next [1..Emax] – включает указатели на элементы массива terminal;
- head[1..Vmax] – состоит из указателей на начало подсписков, то есть такие вершины, записанные в массив terminal, с которых начинается процесс перечисления всех вершин, смежных одной i-ой вершине.
Примечание
Допустимым действием является выделение в программе двух ключевых частей. К ним относят ввод ребер для дальнейшего добавления их в список смежности и вывод полученного списка смежности на экран.
В первую очередь выполняют запрос на ввод суммы вершин (n) и ребер (m) графа (данная информация должна быть у пользователя). Следующим шагом является запуск цикла ввода ребер, то есть смежных вершин. Условие в этом цикле нужно для того, чтобы узнать, какое введено ребро.
Если введено направленное ребро, то функция add вызывается 1 раз, иначе – 2, тем самым внося сведения, что есть ребро как из вершины v в вершину u, так и из u в v. По окончанию формирования списка смежности происходит его отображение программой на экране.
Вывод на экран осуществляется:
- по циклу от 1 до n, где n – является количеством вершин;
- согласно вложенному в него циклу, который прекращает свою работу тогда, когда указатель на следующий элемент для i-ой вершины отсутствует, то есть все смежные ей вершины уже выведены.
Функция add производит добавление ребер в изначально пустой список смежности:
(Add(v, u))
(k:=k+1)
(terminal[k]:=u)
(next[k]:=head[v])
(head[v]:=k)
Действия реализуются, согласно алгоритму с формальными параметрами, вспомогательной переменной k и тремя одномерными целочисленными массивами:
- значение переменной k увеличивается на 1;
- в k-ый элемент массива terminal добавляют конечную для какого-либо ребра вершина (u);
- в строке №3 для k-ого элемента массива next определяется адрес следующего элемента массива terminal;
- массив head заполняют указателями на стартовые элементы, которые являются началом подсписка (строки в таблице) смежных вершин с некоторой i-ой вершиной.
В ячейке, где пересекаются i-ая строка и 2-ой столбец, могут быть записи нескольких элементов в соответствии с несколькими смежными вершинами. Можно обозначить каждую строку из списка смежности его подсписком. В результате выведенный список смежности будет включать элементы подсписков, отсортированные в обратном порядке. Обычно порядок вывода смежных вершин (в подсписках) не имеет принципиального значения.
Список со строками, содержащими запись двух смежных вершин и вес ребра, которое их соединяет, называют списком ребер графа. В качестве примера можно рассмотреть связный граф G=(V, E). Множество ребер E следует сгруппировать следующим образом:
- d – подмножество, включающее только неориентированные ребра графа G;
- k – подмножество, включающее только ориентированные ребра графа G.
Допустим, какая-либо величина p равна количеству всех ребер, которые включены в подмножество d, а s – то же самое относительно k. Тогда для графа G высотой списка ребер будет являться величина:
s+p*2
Таким образом, число строк из списка ребер в любом случае должно соответствовать величине, определенной по итогам сложения ориентированных ребер с неориентированными, умноженными на 2. Рассматриваемый способ представления графа предполагает хранение в каждой строке пары смежных вершин, а неориентированное ребро, которое соединяет вершины v и u, идет как из v в u, так и из u в v.
Например, имеется некий граф смешанного типа с 5 вершинами и 4 ребрами, каждому из которых соответствует определенное целое значение (для наглядности оно составлено из номеров вершин):
Граф содержит 3 направленных ребра и 1 ненаправленное. Путем подстановки значений в формулу можно определить высоту списка ребер: 3+1*2=5
На рисунке изображен список ребер для рассматриваемого графа. Таблица в размерах составляет n×3, где n= s+p*2=3+1*2=5. Элементы в первом столбце расположены по возрастанию, во втором – порядок расположения элементов определен первым, а в третьем – зависит от двух предыдущих.
Список ребер реализуется программой. Процесс схож с операциями при реализации списка смежностей. В первую очередь организуют ввод данных, которые с помощью особой функции распределяются среди массивов. Затем происходит вывод полученного списка смежности на экран. В связи с необходимостью в использовании дополнительного массива, функция добавления ребер организована по-другому.
Максимально допустимое число вершин в графе определено с помощью константы Vmax, а количество ребер – Emax. Вторая константа инициализируется формулой Vmax*(Vmax-1)/2, вычисляющей количество ребер в полном графе при известном числе вершин.
Далее, в программах описываются 5 массивов:
- terminal – массив вершин, включающий ребра;
- weight – массив весов ребер;
- head[i]=k – для хранения i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – является первой вершиной, смежной с i-ой, а weight[k] – вес инцидентного ей ребра;
- last[i]=k – для хранения i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – является последней вершиной, смежной с i-ой, а weight[k] – вес инцидентного ей ребра;
- point[i]=k – хранит для i-ой вершины номер k-ого элемента массивов terminal и weight, где terminal[k] – следующая вершина, смежная с i-ой, а weight[k] – вес инцидентного ей ребра.
По результатам ввода числа вершин (n) и ребер (m) графа будет запущен цикл, каждый этап которого сопровождается вводом пользователем с клавиатуры пары смежных вершин и веса ребра, расположенного между ними. Если ребро ориентированное, функция записи в список ребер (Add) вызывается единожды, при неориентированном ребре – дважды. Суммарное количество вызовов функции определяется по формуле:
s+(p*2)
где s – является ориентированными ребрами графа
p – неориентированные ребра
По итогам формирования списка ребер следует умножить на 2 переменную m. Это связано с тем, что при чисто неориентированном графе высота списка составляет:
0+(m*2)
Завершающим этапом является отображение на экране результирующей конструкции. В связи с тем, что на номер первой вершины, смежной с i-ой вершиной, указывает элемент head[i], каждая новая итерация внешнего цикла начинается с взятия этого номера (k=head[i]). Внутренний цикл прекращает реализацию в том случае, когда отсутствует смежная с i-ой вершины (k станет равной нулю), а внешний – по окончанию вывода списка ребер.
Ключевые действия, включая добавление ребра, удаление ребра, проверку наличия ребра от вершины i до вершины j, отличаются высокой эффективностью и являются операциями с постоянным временем. В том случае, когда граф плотный, а количество ребер большое, матрица смежности представляет собой наиболее целесообразное решение. Даже когда граф и матрица смежности разрежены, можно представить ее с помощью структур данных для разреженной матрицы.
Главное достоинство методики заключается в применении матриц. Благодаря передовым разработкам в сфере аппаратного обеспечения, представляется возможным реализовывать даже дорогостоящие матричные операции на графическом процессоре (GPU). В процессе выполнения операций со смежной матрицей можно получить ценные данные о природе графа и том, как связаны его вершины.
К минусам матрицы смежности можно отнести риски возникновения недостатка объема памяти по причине наличия требований к пространству матрицы смежности VxV. Однако, зачастую графы не обладают чрезмерно большим числом соединений, что является основным поводом выбрать списки смежности для решения распространенных задач.
С другой стороны, несмотря на простоту базовых операций, существуют такие операции, как inEdges и outEdges, которые отличаются дороговизной при использовании для представления матрицы смежности.
Классификация графов
Ярким примером графа является схема метро или некий другой маршрут. Программисты знакомы с компьютерной сетью, которая также представляет собой граф. Общим в этих примерах является наличие точек, соединенных линиями.
В случае компьютерной сети точками являются отдельные серверы, а линиями – разные типы электрических сигналов. В метрополитене точки можно принять за станции, а линии – за туннели, проложенные между станциями. Согласно теории графов, точки представляют собой вершины или узлы, а линии – ребра или дуги.
Граф является совокупностью вершин, которые соединены ребрами.
В математике преимущественно рассматривают не содержание, а структуру вещей, отделяя ее от всего остального. Данный прием позволяет определять какие-либо объекты, как графы. В случае компьютерной сети можно отметить наличие определенной топологии и возможности условного представления в виде некоторого количества компьютеров и соединительных путей. На рисунке изображена полносвязная топология:
Фактически такая топология является графом. Пять компьютеров представляют собой вершины, а соединения или пути передачи сигналов являются ребрами. Ели выполнить замену компьютеров на вершины, то в результате получится математический объект или граф с 10 ребрами и 5 вершинами. Нумерацию вершин допустимо выполнять произвольно.
В рассматриваемом примере не используются петли, то есть такие ребра, которые выходят из вершины и сразу же водят в нее. В теории графов существует ряд обозначений:
- G=(V, E), здесь G – граф, V – его вершины, E – ребра;
- |V| – порядок (число вершин);
- |E| – размер графа (число рёбер).
Применительно к рисунку:
|V|=5, |E|=10.
Классификация графов:
- связные, в которых между какой-либо парой вершин расположено от одного и более путей;
- несвязные – хотя бы с одной вершиной, не связанной с другими.
В том случае, когда из любой вершины доступна другая вершина, граф является неориентированным и связным. При невыполнении данного условия для связного графа, его называет ориентированным или орграфом.
Примечание
Степень вершины определяется числом ребер, которые соединяют ее с другими вершинами.
В сумме все степени графа соответствуют удвоенному количеству всех его ребер. К примеру, на рисунке изображен граф со суммой степеней, равной 20:
Орграф отличается от неориентированного графа возможностью перемещаться из вершины h в вершину s без промежуточных вершин лишь тогда, когда ребро выходит из h и входит в s, но не наоборот. Форма записи ориентированного графа:
G=(V, A)
где V – является вершинами, A – определяет направленные ребра.
К третьему типу относят смешанные графы. Такие графы включают направленные и ненаправленные ребра. Формальная запись смешанного графа:
G=(V, E, A)
Источник: kvodo.ru
На рисунке изображен граф с направленными [(e, a), (e, c), (a, b), (c, a), (d, b)] и ненаправленными [(e, d), (e, b), (d, c)…] дугами. Предположим, что имеются два графа:
Данные графы эквиваленты друг другу, так как без изменений в структуре одного графа можно построить второй. Такие графы являются изоморфными, то есть обладают следующим свойством: какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На приведенном выше рисунке изображена пара изоморфных графов.
В случае, когда каждое ребро графа соответствует некоторому значению в виде веса ребра, граф является взвешенным. При решении задач можно встретить примеры, когда за вес принимают длину, цену маршрута и другие виды измерений. При графическом изображении графа принято указывать весовые значения около ребер.
Путь – последовательность вершин, каждая из которых связана с последующей с помощью ребра.
При совпадении первой и последней вершины путь называют циклом. Длина пути равна количеству составляющих его ребер. К примеру, на рисунке путь является последовательностью [(e), (a), (b), (c)]. Этот путь представляет собой подграф, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.
Способы представления графа, алгоритмы обхода
Граф, как и другие распространенные типы математических объектов, можно представить на компьютере, то есть сохранить в его памяти. Наиболее известные способы интерпретации графов:
- матрица смежности;
- матрица инцидентности;
- список смежности;
- список ребер.
Первые два метода заключаются в хранении графа в виде двумерного массива или матрицы. Размеры этих массивов определяются числом вершин и/или ребер в определенном графе. Таким образом, размер матрицы смежности – n×n (где n – число вершин), а матрицы инцидентности – n×m (n – число вершин, m – число ребер в графе).
В процессе решения многих задач с применением графов требуется обходить все вершины и ребра, то есть дуги. Обойти граф – значит, пройти все его вершины точно по одному разу. Алгоритмы обхода:
- в глубину;
- в ширину.
Реализация алгоритма обхода заключается в последовательном посещении вершин и исследовании ребер. Не посещенную вершину называют новой. После посещения вершину считают открытой до момента исследования всех инцидентных ей ребер. По итогу манипуляций вершина становится закрытой.
Обход в глубину выполняют, согласно следующим правилам:
- при нахождении в вершине х следует перемещаться в какую-либо другую вершину, не посещенную ранее, с одновременным запоминанием первой дуги;
- в том случае, когда невозможно переместиться в ранее не посещенную вершину из вершины х, требуется вернуться в вершину z, из которой впервые удалось попасть в х, и продолжить обход в глубину из вершины z.
Примечание
Поиск в ширину отличается тем, что за активную принимается такая открытая вершина, которая была посещена последней. В том случае, когда выполняется обход в глубину, чем позднее будет посещена вершина, тем раньше она будет использована.
В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке:
Обход следует начинать со стартовой вершины 1. Она является активной и единственной, которая открыта. Другие вершины: 2,3,4,5,6 – новые. Вершина 1 обладает тремя инцидентными ребрами – 1–2, 1–4 и 1–6. Можно начать с ребра 1–2. В результате его прохождения открывается вершина 2. Она обладает одним инцидентным ребром 2–1, которое просмотрено. Вершина 2 была просмотрена, в результате чего она преобразуется в закрытую.
Затем по ребру 2–1 можно вернуться в вершину 1. По ребру 1– 4 легко попасть в вершину 4, которая становится открытой. Вершина 4 обладает четырьмя инцидентными ребрами: 4–1, 4–3, 4–5, 4–6. Таким образом, ребро 4–1 просмотрено.
Далее следует рассмотреть ребро 4–3. С его помощью удобно попасть в вершину 3, которая в результате становится открытой. Вершина 3 обладает одним инцидентным ребром 3–4. Данная вершина просмотрена. В результате вершина 3 закрыта, а по ребру 3–4 можно вернуться в вершину 4. Затем следует рассмотреть ребро 4 – 5.
Вершина 5 обладает двумя инцидентными ей ребрами: просмотренным (4–5) и ребром 5–6, по которому можно попасть в вершину 6. Вершина 6 обладает тремя инцидентными ей ребрами: просмотренным 6–5, 6–1 и 6–4. С помощью ребра 6–1 можно попасть в просмотренную вершину 1. По ребру 6–4 просто попасть в просмотренную вершину 4. В результате все вершины графа просмотрены. Порядок посещения вершин: 1, 2, 4, 3, 5, 6.
Основной особенностью и отличием поиска в ширину является выбор в виде активной вершины – такой, которая посещалась раньше, чем остальные. Таким образом, можно сформулировать ключевое свойство обхода в ширину: чем ближе вершина к старту, тем раньше она будет посещена.
Вершина используется путем просмотра одновременно всех вершин, которые ранее не были просмотрены и являются смежными с рассматриваемой вершиной. В результате поиск реализуют по всем вероятным направлением сразу. В первую очередь посещается вершина А, далее смежные с ней вершины, удаленные от А на 1.
Затем посещаются вершины, которые расположены на расстоянии 2 от А, и так далее. Чем ближе вершина к стартовой вершине, тем раньше она будет посещена. Поиск в ширину направлен на определение наиболее короткого из возможных путей.
В качестве примера можно рассмотреть неориентированный граф, изображенный на рисунке:
Обход следует начать со стартовой вершины 1, которая является просмотренной. Вершины 2, 4, 6 и стартовая вершина – смежные. Данные вершины можно отметить, как просмотренные, и поместить в очередь. При рассмотрении вершины 2 можно заметить, что она не обладает смежными вершинами.
Затем нужно рассмотреть вершину 4 с двумя смежными вершинами 3 и 5. Их можно поместить в очередь и отметить, как просмотренные. В результате просмотрены все вершины графа. Порядок посещения вершин: 1, 2, 4, 6, 3, 5.
Как построить граф по матрице смежности
Данная методика отличается удобством, что позволяет представлять плотные графы с количеством ребер (|E|), которое приблизительно соответствует числу вершин в квадрате (|V|2). В процессе требуется заполнить матрицу размером |V| x |V| следующим образом:
A[i][j] = 1 (Если существует ребро из i в j)
A[i][j] = 0 (Иначе)
Метод допустим к применению в случае ориентированных и неориентированных графов. Во втором варианте матрица A имеет вид симметричной, то есть A[i][j] == A[j][i]. Это объясняется тем, что при существовании ребра между i и j, оно является и ребром из i в j, и ребром из j в i. С помощью данного свойства сокращают практически вдвое объем требуемой памяти, в связи с тем, что элементы хранятся лишь в верхней части матрицы, над главной диагональю.
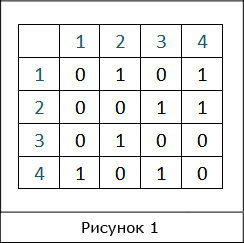
Матрица смежности графа — это квадратная матрица, в которой каждый элемент принимает одно из двух значений: 0 или 1. Прежде чем отобразить граф через матрицу смежности, рассмотрим простой пример такой матрицы (рис. 1).
Это двоичная квадратная матрица, т. к. число строк в ней равно числу столбцов, и любой из ее элементов имеет значение либо 1, либо 0. Первая строка и первый столбец (не входят в состав матрицы, а показаны здесь для легкости ее восприятия) содержат номера, на пересечении которых находится каждый из элементов, и они определяют индексное значение последних. Имея в наличии лишь матрицу такого типа, несложно построить соответствующий ей граф.
Слева на рисунке изображена все та же матрица смежности, имеющая размерность 4×4. Числа, выделенные синим, можно рассматривать как вершины смешанного графа, расположенного справа – того, представлением которого является матрица.
Для графического отображения графа необходимо уметь вычислять по матрице смежности количество его вершин, а также обладать знанием следующего правила. Когда из одной вершины в другую проход свободен (имеется ребро), тогда в ячейку заноситься 1, иначе – 0. Немного формализовав только что сказанное, получим: если из i в j существует ребро, то A[i][j]:=1, в противном случае A[i][j]:=0. Как видно, все элементы на главной диагонали равны нулю, это следствие отсутствия у графа петель. Но ни что не мешает, чтобы некоторые или все элементы главной диагонали были единицами.
В программе матрица смежности задается при помощи обычного двумерного массива, имеющего размерность n×n, где n – число вершин графа.
На языке C++, описать ее можно, например, так:
int graph[n][n] = {
{0, 1, 0, 1},
{0, 0, 1, 1},
{0, 1, 0, 0},
{1, 0, 1, 0}};
В Паскале способ описания практически аналогичен:
const graph: array[1..n,1..n] of integer = ( (0, 1, 0, 1), (0, 0, 1, 1), (0, 1, 0, 0), (1, 0, 1, 0));
В случае если граф неизвестен заранее, а определяется пользователем, то нужно организовать ручной ввод двумерного массива, так как это предусматривает конкретный язык программирования.
Чтобы представить граф в виде матрицы смежности понадобиться O(|V|2) памяти, поскольку ее размер, как уже отмечалось, равен квадрату числа всех вершин. И если количество ребер графа, в сопоставлении с количеством вершин, невелико, то значения многих элементов матрицы смежности будут нулевыми, следовательно, использование данного метода нецелесообразно, т. к. для подобных графов имеются наиболее оптимальные способы их представления.
( 1 оценка, среднее 5 из 5 )
Что такое матрица смежности?
Матрица смежности – это вид представления графа в виде матрицы, когда пересечение столбцов и строк задаёт дуги. Используя матрицу смежности, можно задать вес дуг и ориентацию. Каждая строка и столбец матрицы соответствуют вершинам, номер строки соответствует вершине, из которой выходит дуга, а номер столбца – в какую входит дуга.
Примеры матриц смежности
| Граф из 3 соединённых вершин | Граф с ориентированной дугой | Граф из 4 вершин без дуг |
|---|---|---|
0, 1, 1, 1, 0, 1, 1, 1, 0, |
0, 1, 0, 0, |
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, |

|

|

|
| Ссылка на граф | Ссылка на граф | Ссылка на граф |
Использование Матрицы смежности в сервисе Граф Онлайн
Видео справка
Сервис Граф Онлайн предоставляет вам возможность создать Создать граф по матрице смежности.
Также вы можете редактировать существующую матрицу смежности. Для этого вам необходимо выбрать меню Граф -> Матрица смежности.
Для того чтобы использовать матрицу смежности вам необходимо ввести её в правильном формате.
Формат ввода матрицы смежности
Вводя матрицу смежности вам необходимо руководствоваться следующими правилами:
- Матрица должна быть квадратная – число строк равно числу столбцов.
- Каждая новая строка вводится с новой строки.
- Каждое значение разделяется замятой (,)
- Вес дуг должен быть положительным числом. Значение 0 значит что дуги не существует.
А теперь рассмотрим основные ошибки ввода матриц смежности
Основные ошибки ввода матриц смежности
| Неправильная матрица | Причина ошибки | Правильная матрица |
|---|---|---|
5,5,5,5,5 5,5,5,5,5 5,5,5,5,5 |
Матрица не квадратная: число строк – 3, а число столбцов – 5 |
5,5,5,5,5 5,5,5,5,5 5,5,5,5,5 5,5,5,5,5 5,5,5,5,5 |
0,1,1,1,0,1,0,0,0 1,0,1,0,0,1,1,1,0 1,1,0,1,1,0,1,0,0 1,0,1,0,1,1,1,1,0 0,0,1,1,0,1,0,0,0 1,1,0,1,1,0,1,1,1 0,1,1,1,0,1,0,0,1 0,0,0,0,0,1,1,1,0 |
Матрица не квадратная: число строк – 8, а число столбцов – 9 |
0,1,1,1,0,1,0,0,0 1,0,1,0,0,1,1,1,0 1,1,0,1,1,0,1,0,0 1,0,1,0,1,1,1,1,0 0,0,1,1,0,1,0,0,0 1,1,0,1,1,0,1,1,1 0,1,1,1,0,1,0,0,1 0,0,0,0,0,1,1,1,0 0,0,0,0,0,0,0,0,0 |
1, 0, 0 1, 2, 0 -2, 1, 0 0, -2, 0 1, 3, 0 |
Матрица не квадратная, также содержит отрицательные значения |
1, 0, 0 1, 2, 0 2, 1, 0 |
1 2, 1 3, 1 4, 4 5, 5 2, 6 3, |
Введена не матрица смежности, а отношение между вершинами. Необходимо ввести матрицу смежности для этого графа. |
0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, |
∞,10,9,10 10,∞,∞,∞ ∞,5,∞.8 10,∞,∞,∞ |
Вместо символа ∞ используйте 0. |
0,10,9,10 10,0,0,0 0,5,0.8 10,0,0,0 |
-, 8, -, 1, -, -, -, -, 4, 7, 2, -, -, -, -, -, 4, 2, -, -, 9, -, 7, -, -, -, -, -, -, 6, inf , -, -, -, -, -, |
Вместо символа – или inf используйте 0. |
0, 8, 0, 1, 0, 0, 0, 0, 4, 7, 2, 0, 0, 0, 0, 0, 4, 2, 0, 0, 9, 0, 7, 0, 0, 0, 0, 0, 0, 6, 0, 0, 0, 0, 0, 0, |