The most basic MATLAB® data structure is the matrix. A matrix is a two-dimensional, rectangular array of data elements arranged in rows and columns. The elements can be numbers, logical values (true or false), dates and times, strings, categorical values, or some other MATLAB data type.
Even a single number is stored as a matrix. For example, a variable containing the value 100 is stored as a 1-by-1 matrix of type double.
Name Size Bytes Class Attributes A 1x1 8 double
Constructing a Matrix of Data
If you have a specific set of data, you can arrange the elements in a matrix using square brackets. A single row of data has spaces or commas in between the elements, and a semicolon separates the rows. For example, create a single row of four numeric elements. The size of the resulting matrix is 1-by-4 because it has one row and four columns. A matrix of this shape is often referred to as a row vector.
Now create a matrix with the same numbers, but arrange them in two rows. This matrix has two rows and two columns.
Specialized Matrix Functions
MATLAB has many functions that help create matrices with certain values or a particular structure. For example, the zeros and ones functions create matrices of all zeros or all ones. The first and second arguments of these functions are the number of rows and number of columns of the matrix, respectively.
The diag function places the input elements on the diagonal of a matrix. For example, create a row vector A containing four elements. Then, create a 4-by-4 matrix whose diagonal elements are the elements of A.
A = [12 62 93 -8]; B = diag(A)
B = 4×4
12 0 0 0
0 62 0 0
0 0 93 0
0 0 0 -8
Concatenating Matrices
You can also use square brackets to append existing matrices. This way of creating a matrix is called concatenation. For example, concatenate two row vectors to make an even longer row vector.
A = ones(1,4); B = zeros(1,4); C = [A B]
To arrange A and B as two rows of a matrix, use the semicolon.
To concatenate several matrices, they must have compatible sizes. In other words, when you concatenate matrices horizontally, they must have the same number of rows. When you concatenate them vertically, they must have the same number of columns.
For example, create two matrices that both have two rows. Horizontally append the second matrix to the first by using square brackets.
C = 2×5
1 1 1 0 0
1 1 1 0 0
An alternative way to concatenate compatible matrices is to use concatenation functions, such as horzcat, vertcat, and cat. Horizontally append the second matrix to the first by using horzcat.
D = 2×5
1 1 1 0 0
1 1 1 0 0
Generating a Numeric Sequence
The colon is a handy way to create matrices whose elements are sequential and evenly spaced. For example, create a row vector whose elements are the integers from 1 to 10.
A = 1×10
1 2 3 4 5 6 7 8 9 10
You can use the colon operator to create a sequence of numbers within any range, incremented by one.
A = 1×6
-2.5000 -1.5000 -0.5000 0.5000 1.5000 2.5000
To change the value of the sequence increment, specify the increment value in between the starting and ending range values, separated by colons.
To decrement, use a negative number.
You can also increment by noninteger values. If an increment value does not evenly partition the specified range, MATLAB automatically ends the sequence at the last value it can reach before exceeding the range.
A = 1×6
1.0000 1.2000 1.4000 1.6000 1.8000 2.0000
Expanding a Matrix
You can add one or more elements to a matrix by placing them outside of the existing row and column index boundaries. MATLAB automatically pads the matrix with zeros to keep it rectangular. For example, create a 2-by-3 matrix and add an additional row and column to it by inserting an element in the (3,4) position.
A = 2×3
10 20 30
60 70 80
A = 3×4
10 20 30 0
60 70 80 0
0 0 0 1
You can also expand the size by inserting a new matrix outside of the existing index ranges.
A = 5×6
10 20 30 0 0 0
60 70 80 0 0 0
0 0 0 1 0 0
0 0 0 0 2 3
0 0 0 0 4 5
To expand the size of a matrix repeatedly, such as within a for loop, it is a best practice to preallocate space for the largest matrix you anticipate creating. Without preallocation, MATLAB has to allocate memory every time the size increases, slowing down operations. For example, preallocate a matrix that holds up to 10,000 rows and 10,000 columns by initializing its elements to zero.
If you need to preallocate additional elements later, you can expand it by assigning outside of the matrix index ranges or concatenate another preallocated matrix to A.
Empty Arrays
An empty array in MATLAB is an array with at least one dimension length equal to zero. Empty arrays are useful for representing the concept of “nothing” programmatically. For example, suppose you want to find all elements of a vector that are less than 0, but there are none. The find function returns an empty vector of indices, indicating that it did not find any elements less than 0.
A = [1 2 3 4]; ind = find(A<0)
ind = 1x0 empty double row vector
Many algorithms contain function calls that can return empty arrays. It is often useful to allow empty arrays to flow through these algorithms as function arguments instead of handling them as a special case. If you do need to customize empty array handling, you can check for them using the isempty function.
Related Topics
- Array Indexing
- Reshaping and Rearranging Arrays
- Multidimensional Arrays
- Create String Arrays
- Represent Dates and Times in MATLAB
This topic contains an introduction to creating matrices and performing basic matrix calculations in MATLAB®.
The MATLAB environment uses the term matrix to indicate a variable containing real or complex numbers arranged in a two-dimensional grid. An array is, more generally, a vector, matrix, or higher dimensional grid of numbers. All arrays in MATLAB are rectangular, in the sense that the component vectors along any dimension are all the same length. The mathematical operations defined on matrices are the subject of linear algebra.
Creating Matrices
MATLAB has many functions that create different kinds of matrices. For example, you can create a symmetric matrix with entries based on Pascal’s triangle:
Or, you can create an unsymmetric magic square matrix, which has equal row and column sums:
Another example is a 3-by-2 rectangular matrix of random integers. In this case the first
input to randi describes the range of possible values for the
integers, and the second two inputs describe the number of rows and columns.
A column vector is an m-by-1 matrix, a row vector is a 1-by-n matrix, and a scalar is a 1-by-1 matrix. To define a matrix manually, use square brackets [ ] to denote the beginning and end of the array. Within the brackets, use a semicolon ; to denote the end of a row. In the case of a scalar (1-by-1 matrix), the brackets are not required. For example, these statements produce a column vector, a row vector, and a scalar:
u = [3; 1; 4] v = [2 0 -1] s = 7
u =
3
1
4
v =
2 0 -1
s =
7
For more information about creating and working with matrices, see Creating, Concatenating, and Expanding Matrices.
Adding and Subtracting Matrices
Addition and subtraction of matrices and arrays is performed element-by-element, or element-wise. For example, adding A to B and then subtracting A from the result recovers B:
Addition and subtraction require both matrices to have compatible dimensions. If the dimensions are incompatible, an error results:
Error using + Matrix dimensions must agree.
For more information, see Array vs. Matrix Operations.
Vector Products and Transpose
A row vector and a column vector of the same length can be multiplied in either order. The result is either a scalar, called the inner product, or a matrix, called the outer product:
u = [3; 1; 4]; v = [2 0 -1]; x = v*u
For real matrices, the transpose operation interchanges aij and aji. For complex matrices, another consideration is whether to take the complex conjugate of complex entries in the array to form the complex conjugate transpose. MATLAB uses the apostrophe operator (') to perform a complex conjugate transpose, and the dot-apostrophe operator (.') to transpose without conjugation. For matrices containing all real elements, the two operators return the same result.
The example matrix A = pascal(3) is symmetric, so A' is equal to A. However, B = magic(3) is not symmetric, so B' has the elements reflected along the main diagonal:
For vectors, transposition turns a row vector into a column vector (and vice-versa):
If x and y are both real column vectors, then the product x*y is not defined, but the two products
and
produce the same scalar result. This quantity is used so frequently, it has three different names: inner product, scalar product, or dot product. There is even a dedicated function for dot products named dot.
For a complex vector or matrix, z, the quantity z' not only transposes the vector or matrix, but also converts each complex element to its complex conjugate. That is, the sign of the imaginary part of each complex element changes. For example, consider the complex matrix
z = [1+2i 7-3i 3+4i; 6-2i 9i 4+7i]
z = 1.0000 + 2.0000i 7.0000 - 3.0000i 3.0000 + 4.0000i 6.0000 - 2.0000i 0.0000 + 9.0000i 4.0000 + 7.0000i
The complex conjugate transpose of z is:
ans = 1.0000 - 2.0000i 6.0000 + 2.0000i 7.0000 + 3.0000i 0.0000 - 9.0000i 3.0000 - 4.0000i 4.0000 - 7.0000i
The unconjugated complex transpose, where the complex part of each element retains its sign, is denoted by z.':
ans = 1.0000 + 2.0000i 6.0000 - 2.0000i 7.0000 - 3.0000i 0.0000 + 9.0000i 3.0000 + 4.0000i 4.0000 + 7.0000i
For complex vectors, the two scalar products x'*y and y'*x are complex conjugates of each other, and the scalar product x'*x of a complex vector with itself is real.
Multiplying Matrices
Multiplication of matrices is defined in a way that reflects composition of the underlying linear transformations and allows compact representation of systems of simultaneous linear equations. The matrix product C = AB is defined when the column dimension of A is equal to the row dimension of B, or when one of them is a scalar. If A is m-by-p and B is p-by-n, their product C is m-by-n. The product can actually be defined using MATLAB for loops, colon notation, and vector dot products:
A = pascal(3); B = magic(3); m = 3; n = 3; for i = 1:m for j = 1:n C(i,j) = A(i,:)*B(:,j); end end
MATLAB uses an asterisk to denote matrix multiplication, as in C = A*B. Matrix multiplication is not commutative; that is, A*B is typically not equal to B*A:
X =
15 15 15
26 38 26
41 70 39
Y =
15 28 47
15 34 60
15 28 43
A matrix can be multiplied on the right by a column vector and on the left by a row vector:
Rectangular matrix multiplications must satisfy the dimension compatibility conditions. Since A is 3-by-3 and C is 3-by-2, you can multiply them to get a 3-by-2 result (the common inner dimension cancels):
However, the multiplication does not work in the reverse order:
Error using * Incorrect dimensions for matrix multiplication. Check that the number of columns in the first matrix matches the number of rows in the second matrix. To perform elementwise multiplication, use '.*'.
You can multiply anything with a scalar:
When you multiply an array by a scalar, the scalar implicitly expands to be the same size as the other input. This is often referred to as scalar expansion.
Identity Matrix
Generally accepted mathematical notation uses the capital letter I to denote identity matrices, matrices of various sizes with ones on the main diagonal and zeros elsewhere. These matrices have the property that AI = A and IA = A whenever the dimensions are compatible.
The original version of MATLAB could not use I for this purpose because it did not distinguish between uppercase and lowercase letters and i already served as a subscript and as the complex unit. So an English language pun was introduced. The function
returns an m-by-n rectangular identity matrix and eye(n) returns an n-by-n square identity matrix.
Matrix Inverse
If a matrix A is square and nonsingular (nonzero determinant), then
the equations AX =
I and XA =
I have the same solution X. This solution is called
the inverse of A and is denoted A-1. The inv function and the expression
A^-1 both compute the matrix inverse.
X =
3.0000 -3.0000 1.0000
-3.0000 5.0000 -2.0000
1.0000 -2.0000 1.0000
ans =
1.0000 0 0
0.0000 1.0000 -0.0000
-0.0000 0.0000 1.0000
The determinant calculated by det is a measure of the scaling factor of the linear transformation
described by the matrix. When the determinant is exactly zero, the matrix is
singular and no inverse exists.
Some matrices are nearly singular, and despite the fact that an
inverse matrix exists, the calculation is susceptible to numerical errors. The cond function computes the condition number for
inversion, which gives an indication of the accuracy of the results from
matrix inversion. The condition number ranges from 1 for a
numerically stable matrix to Inf for a singular matrix.
It is seldom necessary to form the explicit inverse of a matrix. A frequent misuse of
inv arises when solving the system of linear equations Ax =
b. The best way to solve this equation, from the standpoint of both
execution time and numerical accuracy, is to use the matrix backslash operator
x = Ab. See mldivide for more information.
Kronecker Tensor Product
The Kronecker product, kron(X,Y), of two matrices is the larger matrix formed from all possible products of the elements of X with those of Y. If X is m-by-n and Y is p-by-q, then kron(X,Y) is mp-by-nq. The elements are arranged such that each element of X is multiplied by the entire matrix Y:
[X(1,1)*Y X(1,2)*Y . . . X(1,n)*Y
. . .
X(m,1)*Y X(m,2)*Y . . . X(m,n)*Y]
The Kronecker product is often used with matrices of zeros and ones to build up repeated copies of small matrices. For example, if X is the 2-by-2 matrix
and I = eye(2,2) is the 2-by-2 identity matrix, then:
ans =
1 0 2 0
0 1 0 2
3 0 4 0
0 3 0 4
and
ans =
1 2 0 0
3 4 0 0
0 0 1 2
0 0 3 4
Aside from kron, some other functions that are useful to replicate arrays are repmat, repelem, and blkdiag.
Vector and Matrix Norms
The p-norm of a vector x,
is computed by norm(x,p). This operation is defined for any value of p > 1, but the most common values of p are 1, 2, and ∞. The default value is p = 2, which corresponds to Euclidean length or vector magnitude:
v = [2 0 -1]; [norm(v,1) norm(v) norm(v,inf)]
ans =
3.0000 2.2361 2.0000
The p-norm of a matrix A,
can be computed for p = 1, 2, and ∞ by norm(A,p). Again, the default value is p = 2:
A = pascal(3); [norm(A,1) norm(A) norm(A,inf)]
ans = 10.0000 7.8730 10.0000
In cases where you want to calculate the norm of each row or column of a matrix, you can use vecnorm:
ans =
1.7321 3.7417 6.7823
Using Multithreaded Computation with Linear Algebra Functions
MATLAB supports multithreaded computation for a number of linear algebra and element-wise numerical functions. These functions automatically execute on multiple threads. For a function or expression to execute faster on multiple CPUs, a number of conditions must be true:
-
The function performs operations that easily partition into sections that execute concurrently. These sections must be able to execute with little communication between processes. They should require few sequential operations.
-
The data size is large enough so that any advantages of concurrent execution outweigh the time required to partition the data and manage separate execution threads. For example, most functions speed up only when the array contains several thousand elements or more.
-
The operation is not memory-bound; processing time is not dominated by memory access time. As a general rule, complicated functions speed up more than simple functions.
The matrix multiply (X*Y) and matrix power (X^p) operators show significant increase in speed on large double-precision arrays (on order of 10,000 elements). The matrix analysis functions det, rcond, hess, and expm also show significant increase in speed on large double-precision arrays.
Related Topics
- Systems of Linear Equations
- Factorizations
- Eigenvalues
- Singular Values
External Websites
- Matrix Methods of Linear Algebra (MathWorks Teaching Resources)
Эта тема содержит введение в создание матриц и выполнение основных матричных вычислений в MATLAB®.
Среда MATLAB использует термин матрица, чтобы указать на переменное, содержащее вещественные или комплексные числа, расположенные в двумерной сетке. Массив является, в более общем плане, вектором, матрицей или более высокой размерной сеткой чисел. Все массивы в MATLAB являются прямоугольными, в том смысле, что векторы компонента по любому измерению являются всеми одинаковыми длина. Математические операции, заданные на матрицах, являются предметом линейной алгебры.
Создание матриц
MATLAB имеет много функций, которые создают различные виды матриц. Например, можно создать симметрическую матрицу с записями на основе треугольника Паскаля:
Или, можно создать несимметричную матрицу магического квадрата, которая имеет равные суммы строки и столбца:
Другим примером является 3 2 прямоугольная матрица случайных целых чисел. В этом случае первый вход к randi описывает область значений возможных значений для целых чисел, и вторые два входных параметров описывают количество строк и столбцов.
Вектор-столбцом является m-by-1 матрица, вектор-строка является 1 n матрицей, и скаляр является матрицей 1 на 1. Чтобы задать матрицу вручную, используйте квадратные скобки [ ] обозначить начало и конец массива. В скобках используйте точку с запятой ; обозначить конец строки. В случае скаляра (матрица 1 на 1), не требуются скобки. Например, эти операторы производят вектор-столбец, вектор-строку и скаляр:
u = [3; 1; 4] v = [2 0 -1] s = 7
u =
3
1
4
v =
2 0 -1
s =
7
Для получения дополнительной информации о создании и работе с матрицами, смотрите Создание, конкатенацию и расширение матрицы.
Сложение и вычитание матриц
Сложение и вычитание матриц и массивов выполняются поэлементно или поэлементные. Например, добавление A к B и затем вычитание A от результата восстанавливает B:
Сложение и вычитание требуют, чтобы обе матрицы имели совместимые размерности. Если размерности несовместимы, ошибка заканчивается:
Error using + Matrix dimensions must agree.
Для получения дополнительной информации см. Массив по сравнению Матричные операции.
Векторные произведения и транспонирование
Вектор-строка и вектор-столбец той же длины могут быть умножены в любом порядке. Результатом является или скаляр, названный скалярным произведением, или матрица, названная векторным произведением:
u = [3; 1; 4]; v = [2 0 -1]; x = v*u
Для действительных матриц транспонировать операция обменивается a i j и a j i. Для комплексных матриц другой фактор состоит в том, взять ли сопряженное комплексное число комплексных записей в массиве, чтобы сформировать комплексное сопряженное транспонирование. MATLAB использует оператор апострофа (') выполнять комплексное сопряженное транспонирование и оператор точечного апострофа (.') транспонировать без спряжения. Для матриц, содержащих все действительные элементы, эти два оператора возвращают тот же результат.
Матрица в качестве примера A = pascal(3) симметрично, таким образом, A' равно A. Однако B = magic(3) не симметрично, таким образом, B' отразили элементы по основной диагонали:
Для векторов перемещение превращает вектор-строку в вектор-столбец (и наоборот):
Если x и y оба действительные вектор-столбцы, затем продукт x*y не задан, но эти два продукта
и
приведите к тому же скалярному результату. Это количество используется так часто, оно имеет три различных имени: скалярное произведение, скалярное произведение или скалярное произведение. Существует даже специализированная функция для названных скалярных произведений dot.
Для комплексного вектора или матрицы, z, количество z' не только транспонирует вектор или матрицу, но также и преобразует каждый комплексный элемент в его сопряженное комплексное число. Таким образом, знак мнимой части каждого комплексного элемента изменения. Например, рассмотрите комплексную матрицу
z = [1+2i 7-3i 3+4i; 6-2i 9i 4+7i]
z = 1.0000 + 2.0000i 7.0000 - 3.0000i 3.0000 + 4.0000i 6.0000 - 2.0000i 0.0000 + 9.0000i 4.0000 + 7.0000i
Комплексное сопряженное транспонирование z :
ans = 1.0000 - 2.0000i 6.0000 + 2.0000i 7.0000 + 3.0000i 0.0000 - 9.0000i 3.0000 - 4.0000i 4.0000 - 7.0000i
Неспрягаемый комплекс транспонирует, где комплексная часть каждого элемента сохраняет свой знак, обозначается z.':
ans = 1.0000 + 2.0000i 6.0000 - 2.0000i 7.0000 - 3.0000i 0.0000 + 9.0000i 3.0000 + 4.0000i 4.0000 + 7.0000i
Для комплексных векторов, эти два скалярных произведения x'*y и y'*x сопряженные комплексные числа друг друга и скалярное произведение x'*x из комплексного вектора с собой действительно.
Умножение матриц
Умножение матриц задано способом, который отражает состав базовых линейных преобразований и позволяет компактное представление систем одновременных линейных уравнений. Матричное произведение C = AB задан, когда размерность столбца A равна размерности строки B, или когда один из них является скаляром. Если A является m-by-p, и B является p-by-n, их продукт, C является m-by-n. Продукт может на самом деле быть задан с помощью MATLAB for циклы, colon обозначение и векторные скалярные произведения:
A = pascal(3); B = magic(3); m = 3; n = 3; for i = 1:m for j = 1:n C(i,j) = A(i,:)*B(:,j); end end
MATLAB использует звездочку, чтобы обозначить умножение матриц, как в C = A*B. Умножение матриц не является коммутативным; то есть, A*B обычно не равно B*A:
X =
15 15 15
26 38 26
41 70 39
Y =
15 28 47
15 34 60
15 28 43
Матрица A может быть умножена справа вектор-столбцом и слева вектором-строкой:
Прямоугольные умножения матриц должны удовлетворить условиям совместимости размерности. Начиная с A имеет размер 3х3 и C 3 2, можно умножить их, чтобы добраться 3 2 результат (общие внутренние отмены размерности):
Однако умножение не работает в обратном порядке:
Error using * Incorrect dimensions for matrix multiplication. Check that the number of columns in the first matrix matches the number of rows in the second matrix. To perform elementwise multiplication, use '.*'.
Можно умножить что-либо со скаляром:
Когда вы умножаете массив на скаляр, скаляр неявно расширяется, чтобы быть одного размера с другим входом. Это часто упоминается как скалярное расширение.
Единичная матрица
Общепринятое математическое обозначение использует прописную букву I, чтобы обозначить единичные матрицы, матрицы различных размеров с единицами на основной диагонали и нулях в другом месте. Эти матрицы имеют свойство, что A I = A и I A = A каждый раз, когда размерности совместимы.
Исходная версия MATLAB не могла использовать I с этой целью, потому что это не различало прописные и строчные буквы, и i уже служил индексом и как комплексной единицей. Таким образом, английская игра слов языка была введена. Функция
возвращает m-by-n прямоугольная единичная матрица и eye(n) возвращает n-by-n квадратная единичная матрица.
Обращение матриц
Если матричный A является квадратным и несингулярным (ненулевой определитель), затем уравнения A X = I и X A =, I имеет то же решение X. Это решение называется инверсией A и обозначается A-1. inv функционируйте и выражение A^-1 оба вычисляют обратную матрицу.
X =
3.0000 -3.0000 1.0000
-3.0000 5.0000 -2.0000
1.0000 -2.0000 1.0000
ans =
1.0000 0 0
0.0000 1.0000 -0.0000
-0.0000 0.0000 1.0000
Определитель, вычисленный det мера масштабного коэффициента линейного преобразования, описанного матрицей. Когда определитель ниже нуля, матрица сингулярна, и никакая инверсия не существует.
Некоторые матрицы почти сингулярны, и несмотря на то, что обратная матрица существует, вычисление восприимчиво к числовым ошибкам. cond функция вычисляет число обусловленности для инверсии, которая дает индикацию относительно точности результатов матричной инверсии. Число обусловленности лежит в диапазоне от 1 для численно устойчивой матрицы к Inf для сингулярной матрицы.
Редко необходимо сформировать явную инверсию матрицы. Частое неправильное употребление inv возникает при решении системы линейных уравнений A x = b. Лучший способ решить это уравнение, с точки зрения и времени выполнения и числовой точности, состоит в том, чтобы использовать матричный оператор обратной косой черты x = Ab. Смотрите mldivide для получения дополнительной информации.
Продукт тензора Кронекера
Кронекеров продукт, kron(X,Y), из двух матриц большая матрица, сформированная из всех возможных продуктов элементов X с теми из Y. Если X m-by-n и Y p-by-q, затем kron(X,Y) mp-by-nq. Элементы располагаются таким образом что каждый элемент X умножается на целый матричный Y:
[X(1,1)*Y X(1,2)*Y . . . X(1,n)*Y
. . .
X(m,1)*Y X(m,2)*Y . . . X(m,n)*Y]
Кронекеров продукт часто используется с матрицами нулей и единиц, чтобы создать повторенные копии маленьких матриц. Например, если X матрица 2 на 2
и I = eye(2,2) единичная матрица 2 на 2, затем:
ans =
1 0 2 0
0 1 0 2
3 0 4 0
0 3 0 4
и
ans =
1 2 0 0
3 4 0 0
0 0 1 2
0 0 3 4
Кроме kron, некоторые другие функции, которые полезны, чтобы реплицировать массивы, repmat, repelem, и blkdiag.
Векторные и матричные нормы
p – норма векторного x,
вычисляется norm(x,p). Эта операция задана для любого значения p> 1, но наиболее распространенные значения p равняются 1, 2, и ∞. Значением по умолчанию является p = 2, который соответствует Евклидовой длине или векторной величине:
v = [2 0 -1]; [norm(v,1) norm(v) norm(v,inf)]
ans =
3.0000 2.2361 2.0000
p – норма матричного A,
может быть вычислен для p = 1, 2, и ∞ norm(A,p). Снова, значением по умолчанию является p = 2:
A = pascal(3); [norm(A,1) norm(A) norm(A,inf)]
ans = 10.0000 7.8730 10.0000
В случаях, где вы хотите вычислить норму каждой строки или столбца матрицы, можно использовать vecnorm:
ans =
1.7321 3.7417 6.7823
Используя многопоточное вычисление с функциями линейной алгебры
MATLAB поддерживает многопоточный расчет во многой линейной алгебре и поэлементных числовых функциях. Эти функции автоматически выполняются на нескольких потоках. Для функции или выражения, чтобы выполниться быстрее на нескольких центральных процессорах, много условий должны быть верными:
-
Функция выполняет операции, что легко раздел в разделы, которые выполняются одновременно. Эти разделы должны смочь выполниться с небольшой связью между процессами. Они должны потребовать немногих последовательных операций.
-
Размер данных является достаточно большим так, чтобы любые преимущества параллельного выполнения перевесили время, требуемое разделить данные и управлять отдельными потоками выполнения. Например, большинство функций убыстряется только, когда массив содержит несколько тысяч элементов или больше.
-
Операция не ограничена памятью; время вычислений не во власти времени доступа к памяти. Как правило сложные функции ускоряют больше, чем простые функции.
Матрица умножает (X*Y) и матричная степень (X^p) операторы показывают значительное увеличение скорости на больших массивах с двойной точностью (порядка 10 000 элементов). Функции анализа матрицы det, rcond, hess, и expm также покажите значительное увеличение скорости на больших массивах с двойной точностью.
Похожие темы
- Системы линейных уравнений
- Факторизации
- Собственные значения
- Сингулярные значения
Main Content
Array creation, combining, reshaping, rearranging,
and indexing
Matrices and arrays are the fundamental representation of information and data in MATLAB®. You can create common arrays and grids, combine existing arrays,
manipulate an array’s shape and content, and use indexing to access array
elements. For an overview of matrix and array manipulation, watch Working with Arrays.
Functions
expand all
Create and Combine Arrays
zeros |
Create array of all zeros |
ones |
Create array of all ones |
rand |
Uniformly distributed random numbers |
true |
Logical 1 (true) |
false |
Logical 0 (false) |
eye |
Identity matrix |
diag |
Create diagonal matrix or get diagonal elements of matrix |
blkdiag |
Block diagonal matrix |
cat |
Concatenate arrays |
horzcat |
Concatenate arrays horizontally |
vertcat |
Concatenate arrays vertically |
repelem |
Repeat copies of array elements |
repmat |
Repeat copies of array |
combinations |
Generate all element combinations of arrays |
Create Grids
Determine Size, Shape, and Order
length |
Length of largest array dimension |
size |
Array size |
ndims |
Number of array dimensions |
numel |
Number of array elements |
isscalar |
Determine whether input is scalar |
isvector |
Determine whether input is vector |
ismatrix |
Determine whether input is matrix |
isrow |
Determine if input is row vector |
iscolumn |
Determine if input is column vector |
isempty |
Determine whether array is empty |
issorted |
Determine if array is sorted |
issortedrows |
Determine if matrix or table rows are sorted |
isuniform |
Determine if vector is uniformly spaced |
Reshape and Rearrange
Indexing
colon |
Vector creation, array subscripting, and for-loopiteration |
end |
Terminate block of code or indicate last array index |
ind2sub |
Convert linear indices to subscripts |
sub2ind |
Convert subscripts to linear indices |
Topics
- Creating, Concatenating, and Expanding Matrices
Create a matrix or construct one from other matrices.
- Array Indexing
Access elements of an array by specifying their indices or by checking whether
elements meet a condition.- Find Array Elements That Meet a Condition
- Access Data in Cell Array
- Access Data in Tables
- Structure Arrays
- Comma-Separated Lists
- Indexing into Function Call Results
- Removing Rows or Columns from a Matrix
Remove matrix rows or columns.
- Reshaping and Rearranging Arrays
Change the shape or arrangement of elements in an existing array.
- Multidimensional Arrays
Create and manipulate arrays with three or more dimensions.
If you look at the MATLAB, Vector and Matrix are two basic fundamentals components. So, we need to become familiar with the matrix, vector, how to generate them, different MATLAB matrix operations and functions…
In the last tutorial, I described the MATLAB Vector with their functions and mathematical manipulations on the MATLAB command window.
Let’s start this complete tutorial about MATLAB matrix operations.
Table of Content:
- Introduction about the Matrix in MATLAB
- Creating and Generating the Matrix in MATLAB
- Transpos of the Matrix
- Determinant of the Matrix
- Inverse of the Matrix
- MATLAB Matrix Operation
- Matrix Functions in MATLAB
-
- Getting all Diagonal Elements of the Matrix
- Finding out Eigenvalue of the Matrix
- Determining the Rank of the Matrix
- Creating a Zero Matrix
- Generating an Identity Matrix
- Creating a Ones Matrix
- Finding a Size of the Matrix
INTRODUCTION
The definition of the Matrix is a two-dimensional array which consists of both the rows and columns.
In the MATLAB matrix, the rows and columns are created by using the commas (,) / line-spaces ( ) and semicolon (;) respectively.
The matric is represented by the square brackets ‘[ ]’.
Creating and Generating the Matrix in MATLAB
In the generation of the matrix section, we are studying ‘How to create the Matrix [Rows and Columns] in MATLAB?’.
The last tutorials I shared ‘How to create the vector in MATLAB?’. This tutorial is about creating the Matrix rows and columns with the detail explanation.
For creating MATLAB Matrix, you must have four points to remember.
- Start with the open square bracket ‘[‘
- Create the rows in the matrix by using the commas (,) or line-spaces ( )
- Create the columns in the matrix by using the semi-colon ( ; )
- End with the close square bracket ‘]’
Let’s look at the general representation of matrix with the row and column…
The general representation of Row Matrix is…
A = [x1, x2, x3, ....... xn] or [x1 x2 x3 ....... xn] This is (1 × n) vector i.e. a single row consisting the n th term elements.
The general representation of Column Matrix is…
A = [x1; x2; x3; ....... xm] This is (m × 1) vector i.e. a single row consisting the m th term elements.
Note: Row matrix and column matrix are nothing but the vectors.
For example,
How to generate or create N×M Matrix in MATLAB?
Solution: The 3×3 matrix must have 3 rows and 3 columns. These rows and columns are created with the help of space and semicolon.
The matrix in MATLAB:
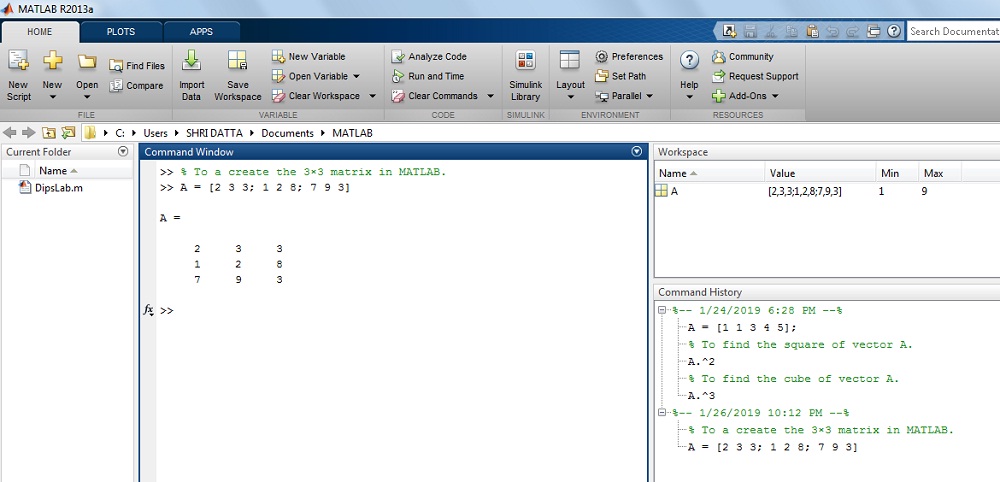
>> Matrix A is...>> A= [2 3 3; 1 2 8; 7 9 3]
A =
2 3 3
1 2 8
7 9 3
The output on MATLAB Window:
In this section, we have seen how to create and generate the matrix.
Moving to the next part…
TRANSPOSING OF MATRIX
What is the Transpose of the Matrix?
Transpose method is a mathematical operation where…
- The elements of the row are converted into the elements of the column. (or)
- The elements of the column are converted into the elements of the row.
The transpose of the Matrix is represented by an apostrophe or single quote (‘) or power of T like as [ ]’ 0r [ ]T.
Note: The representation of the transpose of the Matrix is the same as the representation of the transpose of the vector.
Here is a general syntax for Transpose of the Matrix.
Transpose of matrix A (A’) is
A = [x1 x2 x3; x4 x5 x6; x7 x8 x9]'= [x1 x4 x7; x2 x5 x8; x3 x6 x9]
Transpose of matrix B (B’) is
B = [x1 x4 x7; x2 x5 x8; x3 x6 x9]' = [x1 x2 x3; x4 x5 x6; x7 x8 x9]
If you perform transpose operation twice on the matrix, it will give the same matrix.
i.e.
A = (A')'
Let’s take a mathematics example…
How to determine the transpose of the given below matrix D?
where D = [2 0 1; 9 6 8; 4 1 1]
Solution: You can use the transpose method to change the row vector into a column vector.
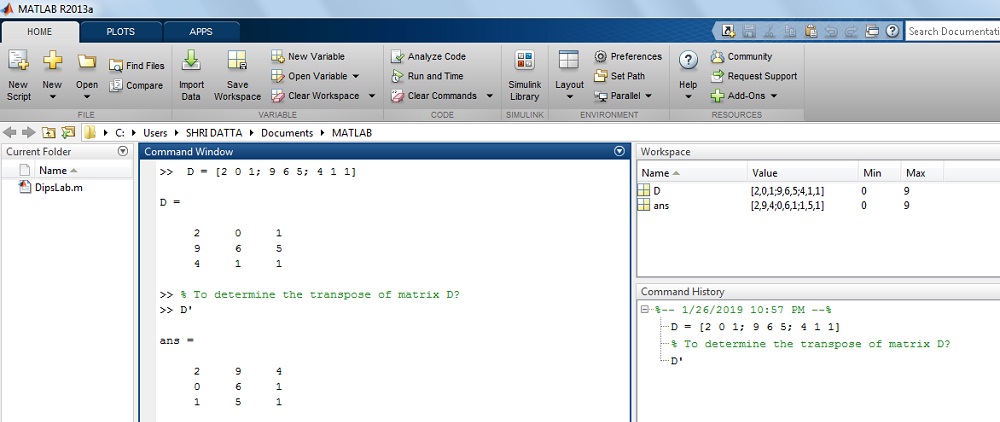
>> D =
2 0 19 6 8
4 1 1
>> By using the transpose method,
>> D' =
2 9 40 6 1
1 8 1
The output on the MATLAB Window:
Looks like its pretty simple till now. Isn’t it?
DETERMINANT OF MATRIX
What is a determinant of the Matrix?
It is a special number calculated from the square matrix. If you are not aware of determinant if the matrix, you can check here.
Note: You can calculate the matrix determinant only where if it is square matrix means the number of rows and the number of columns will be the same.
In MATLAB, we can easily determine the ‘Determinant of Matrix’ by using the ‘det’ function. You don’t need to do any mathematical operation explicitly.
The general Syntax is,
x = det(x) Return the determinant of matrix 'x'Where, x is matrix.
Example,
How to find the determinate of matrix ‘P’ in MATLAB?
Where, P = [1 5 3; 1 2 9; 7 8 5]
Solution: The given value of matrix ‘P’ is
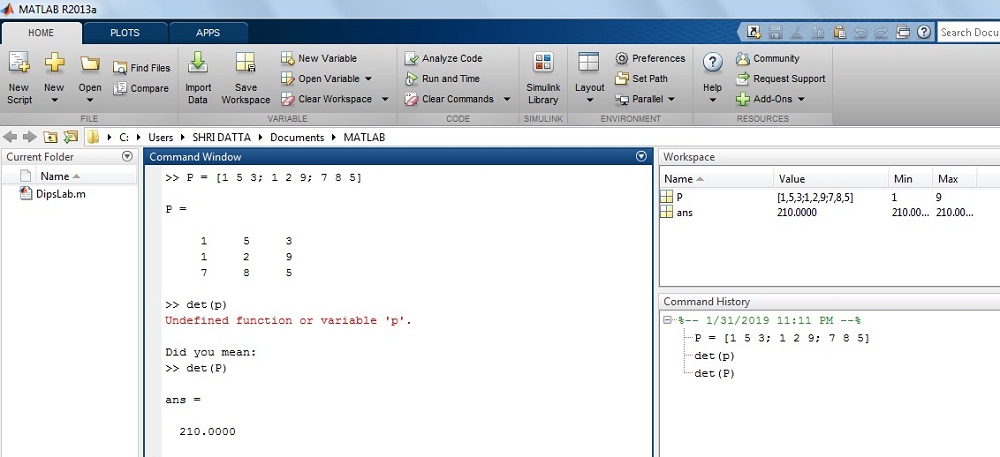
>> P = [1 5 3; 1 2 9; 7 8 5]
>> P =1 5 3
1 2 9
7 8 5
>> det(P)
ans =
210.0000
The output on MATLAB Window:
INVERSE OF MATRIX
What is Inverse of the Matrix?
If the multiplication of the matrix A and matrix B is the Identity matrix, matrix B is the inverse of matrix A.
If you are interested to know how to calculate the inverse of matrix mathematically, check this link.
In MATLAB, the inverse of the matrix is calculating by using the ‘inv’ function. The representation of inverse matrix is ‘matrix power of -1’ or []-1
The general Syntax is…
x = inv(x) Return the inverse value of matrix 'x'Where, x is matrix.
Example.
How to calculate the inverse of the matrix M in MATLAB?
Where, M=[1 2 2; 9 7 6; 5 4 6]
Solution: By using the inverse function,
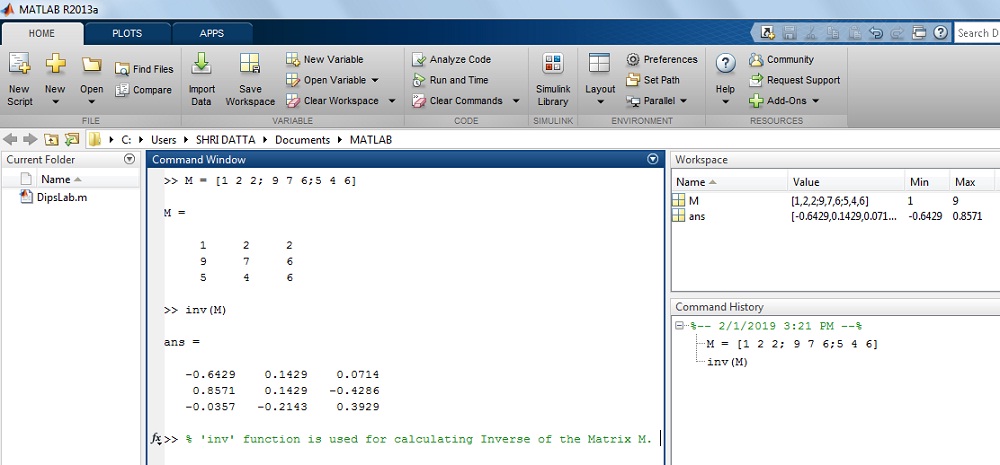
>> M=[1 2 2; 9 7 6; 5 4 6]>> M=
1 2 2
9 7 6
5 4 6
>> inv(M)
ans =
-0.6429 0.1429 0.0714
0.8571 0.1429 -0.4286
-0.0357 -0.2143 0.3929
The output on MATLAB Window:
This is all about a simple function to calculate the inverse of the matrix in MATLAB.
MATLAB MATRIX OPERATIONS [Mathematical]
Earlier we have seen the different types of mathematical functions and their short abbreviations. In this section, we will perform same mathematical operations on Matrix.
In the MATLAB environment, the mathematical operations (functions) on Matrix are the same as Vector.
What are the different mathematical operations we can perform on the matrix in MATLAB?
| Mathematical Arithmetic Operation | Notation andSyntax for Matrix |
| Addition | + |
| Subtraction | – |
| Multiplication | .* |
| Division | ./ |
| Exponential or power | .^ |
MATRIX FUNCTIONS in MATLAB
The MATLAB provides the various functions for mathematical matrix manipulation.
We will see those MATLAB matrix functions one by one…
1. How to find Diagonal element of the Matrix in MATLAB?
In the MATLAB command window, ‘diag’ syntax is used to get the diagonal elements of the matrix.
The general Syntax:
x = diag(x) Return the diagonal value of matrix 'x'Where, x is matrix.
Example
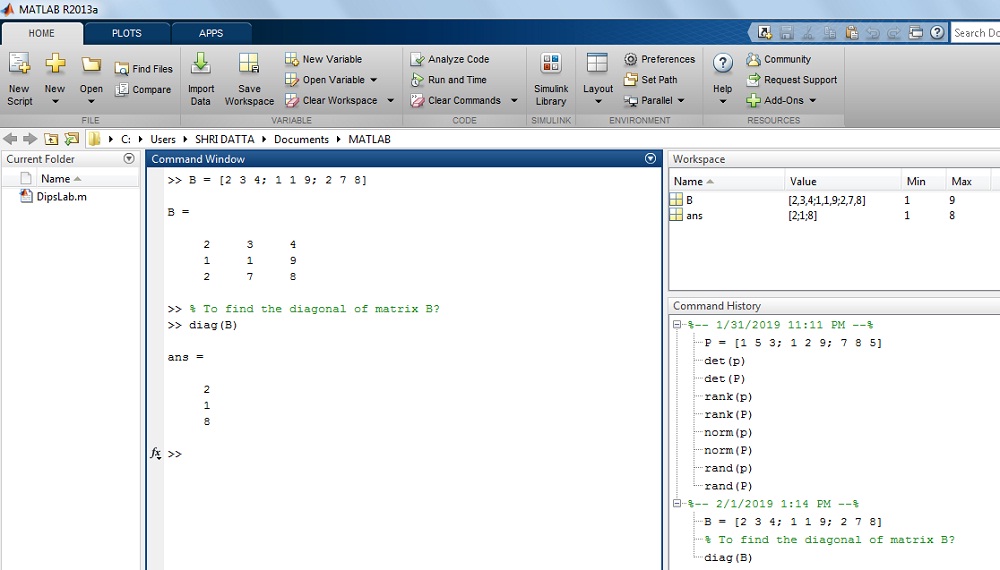
How to get all the diagonal elements of Matrix B in MATLAB?
Where, B = [2 3 4; 1 1 9; 2 7 8]
Solution: The given value of matrix B is
>> B = [2 3 4; 1 1 9; 2 7 8]>> B =
2 3 4
1 1 9
2 7 8
>> diag(B)
ans =
2
1
8
The result on MATLAB display:
2. How to determine the Eigen-value of the Matrix in MATLAB?
What is Eigen-Value of Matrix and how to calculate it?
Note: This video is just for your understanding. You don’t need to do any mathematical operations to find the eigenvalue of the matrix in MATLAB.
In MATLAB, it is pretty easy.
The eigenvalue of the matrix calculated by using the ‘eig’ syntax in MATLAB.
The general Syntax is,
x = eig(x) Return the eigen value of matrix 'x'Where, x is matrix.
Example.
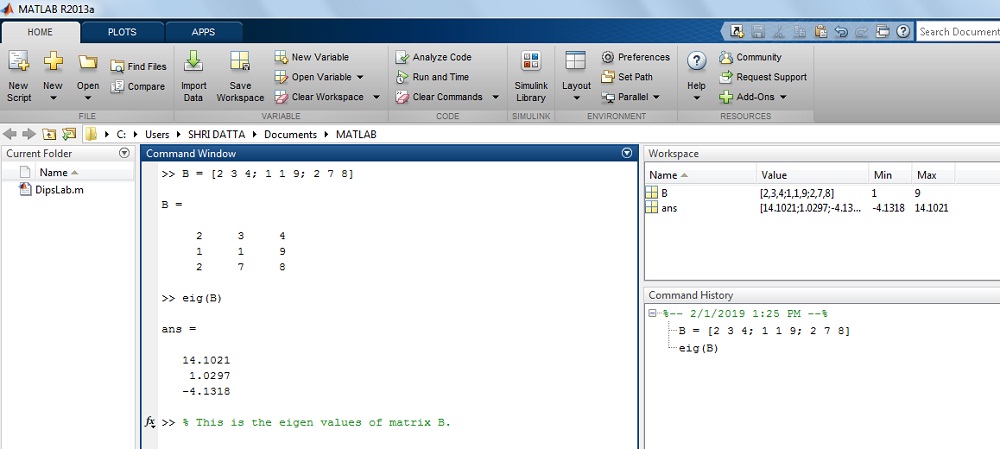
How to find the eigenvalue of Matrix B in MATLAB?
Where, B = [2 3 4; 1 1 9; 2 7 8]
Solution:
>> B = [2 3 4; 1 1 9; 2 7 8]>> B =
2 3 4
1 1 9
2 7 8
ans =14.1021
1.0297
-4.1318
The result on MATLAB display:
3. How to find the Rank of the Matrix in MATLAB?
What is the rank of the matrix?
The rank of a matrix is defined as the maximum number of linearly independent column vectors in the matrix. It is similar to the maximum number of linearly independent row vectors in the given matrix.
Here is video if you are interested in finding rank of the matrix in general.
In MATLAB to find the Rank matrix, ‘rank’ function is used.
The general Syntax is..
x = rank(x) Return the rank of matrix 'x'Where, x is matrix.
Example.
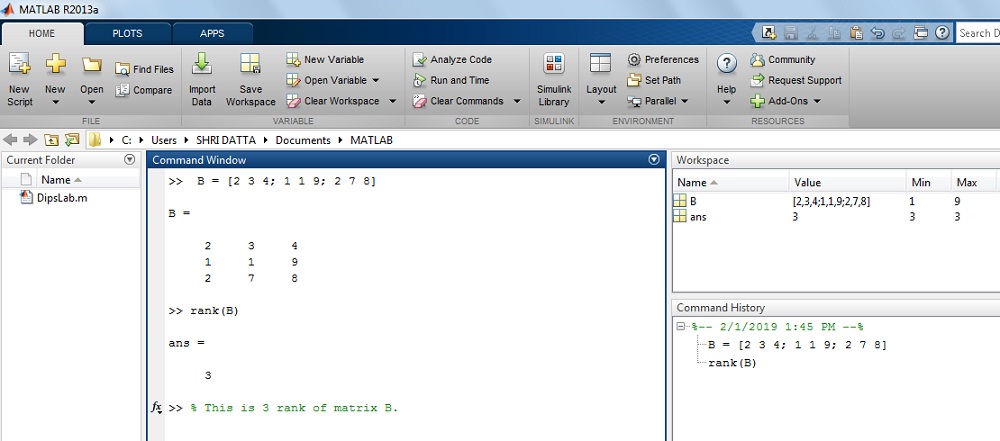
How to find out the rank of Matrix B in MATLAB?
Where, B = [2 3 4; 1 1 9; 2 7 8]
Solution: For the given matrix B,
>> B = [2 3 4; 1 1 9; 2 7 8]>> B =
2 3 4
1 1 9
2 7 8
>>rank(B)
ans =
3
The result on MATLAB display:
4. How to create Zero Matrix using zeros function in MATLAB?
What is Zero Matrix?
In the zero matrix, all the elements of the matrix are zero.
In the case of MATLAB, zeros function is used to create all zero in rows and columns of the matrix.
The general Syntax is…
x = zeros(x) Return the zeros of matrix 'x'Where, x is matrix.
Example.
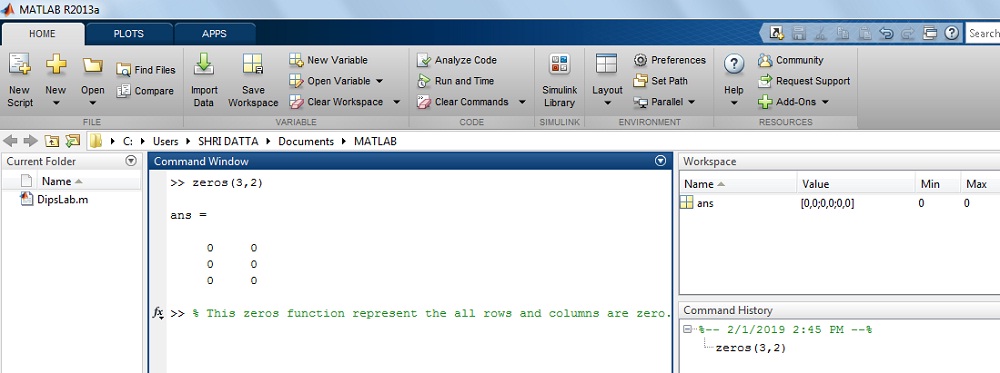
How to create a zero matrix in MATLAB?
Where, matrix A is 3 by 2 matrix,
Solution: The matrix A is
>> A= zeros(3,2)ans =
0 0
0 0
0 0
The result on MATLAB display:
5. How to create Identity matrix using eye Function in MATLAB?
The eyes function in MATLAB is used to create the identity matrix.
The general Syntax is…
x = eye(x) Return the eye of matrix 'x'Where, x is matrix.
Example.
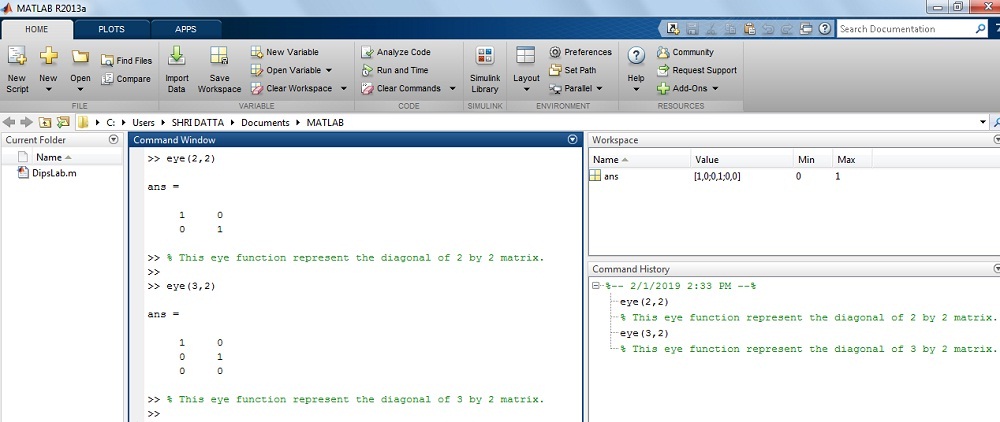
How to generate the Identify Matrix by using the eye function in MATLAB?
Where matrix A is 2 by 2 matrix.
Solution: The matrix A is…
>> eye(2,2)ans =
1 0
0 1
The result on MATLAB display:
6. How to create Matrix with all elements as one using ones function in MATLAB
In MATLAB, the ‘ones’ function is useful for creating the matrix with all elements one.
The general Syntax is…
x = ones(a) Return the ones of matrix 'x'Where, 'a' is a size of the matrix
Example.
How to generate the matrix with all elements one in MATLAB?
Where, matrix A is 2 by 2.
Solution:
>> A = ones(2)ans =
1 1
1 1
Or
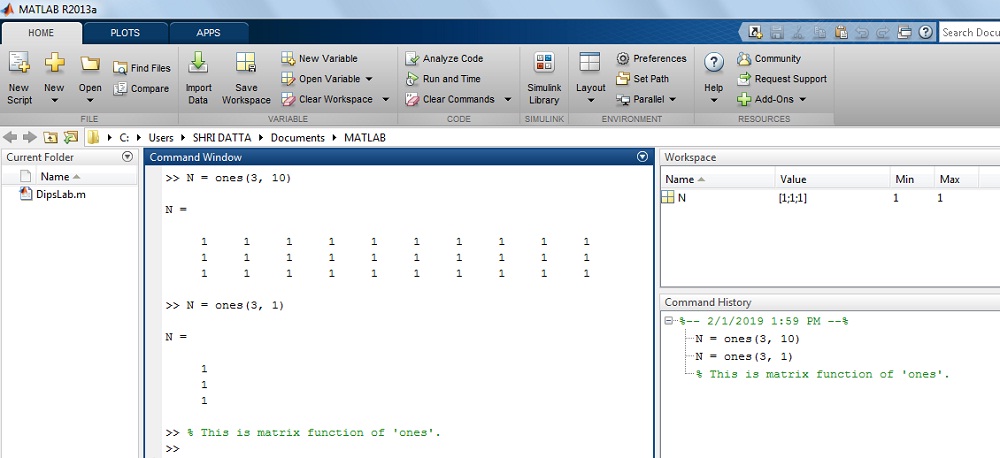
>> N = ones(3,1)
N =
1
1
1
The result on MATLAB display:
7. How to find the size of the matrix in MATLAB?
In MATLAB, we can find out the number of columns and rows with the help of ‘size’ function.
The general Syntax is,
s = size(x) Return the size of matrix 'x'Where, x is matrix.
Example,
How to determine the size of matrix C in MATLAB?
Where, C = [2 7 3; 9 5 4; 1 0 7]
Solution: The given value of matrix C,
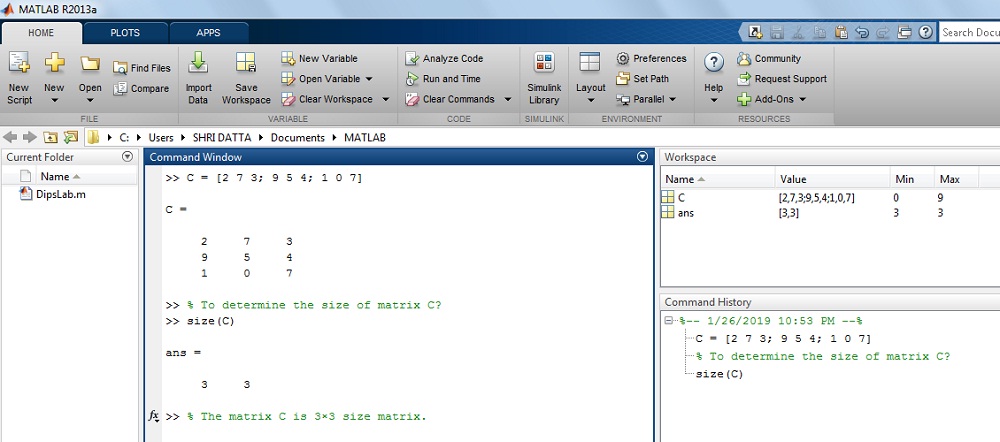
>> C = [2 7 3; 9 5 4; 1 0 7]>> C =
2 7 3
9 5 4
1 0 7
>> size(C)
ans =
3 3
The result on MATLAB display:
On this Matrix MATLAB tutorial, I tied my best covering all the basics of the matrix. And also explained mathematical operations and functions of the matrix by solving examples on the command window of MATLAB Software.
Check my all other MATLAB tutorials and keep exploring. I will be sharing more of such tutorials, stay tuned.
If you have any query related to different MATLAB matrix operations, feel free to ask by commenting below. If you like this tutorial please comment your feedback and also share it with your friends and students.
I have completed master in Electrical Power System. I work and write technical tutorials on the PLC, MATLAB programming, and Electrical on DipsLab.com portal.
Sharing my knowledge on this blog makes me happy. And sometimes I delve in Python programming.