Как составить механический алгоритм

Виды алгоритмов и их реализация

• механические алгоритмы, или иначе
  детерминированные, жесткие (алгоритм
  работы машины, двигателя и т.п.).
  Механические алгоритмы задают
  определенные действия, обозначая их в
  единственной и достоверной
  последовательности, обеспечивая тем
  самым однозначный требуемый или искомый
  результат, если выполняются те условия
  процесса, для которых разработан
  алгоритм;

• гибкие алгоритмы, например,
  стохастические, т.е. вероятностные и
  эвристические.

• вероятностные(стохастические)алгоритмыдают программу решения
  задачи несколькими путями или способами,
  приводящими к вероятному достижению
  результата;

• эвристические алгоритмы(от греч
  слова «эврика») – такие алгоритмы, в
  которых достижение конечного результата
  программы действий однозначно не
  предопределено, так же как не обозначена
  вся последовательность действий, не
  выявлены все действия исполнителя. К
  эвристическим алгоритмам относят
  инструкции и предписания. В этих
  алгоритмах используются универсальные
  логические процедуры и способы принятия
  решений, основанные на аналогиях,
  ассоциациях и прошлом опыте решения
  схожих задач;

• линейные алгоритмы– наборы команд
  (указаний), выполняемых последовательно
  во времени друг за другом;

• разветвляющиеся алгоритмы–
  алгоритмы, содержащие хотя бы одно
  условие, в результате проверки которого
  ЭВМ обеспечивает переход на один из
  двух возможных шагов;

• циклические алгоритмы– алгоритмы,
  предусматривающие многократное
  повторение одного и того же действия
  над новыми исходными данными. К
  циклическим алгоритмам сводится
  большинство методов вычислений, перебора
  вариантов.

Цикл программы– последовательность
команд (серия, тело цикла), которая может
выполняться многократно до удовлетворения
некоторого условия.

Цикломназывается многократно
повторяемый участок вычислений.

Вычислительный процесс, содержащий
один или несколько циклов, называется
циклическим. По количеству выполнения
циклы делятся на циклы с определенным
(заранее заданным) числом повторений;
циклы с неопределенным числом повторений.

Количество повторений последних зависит
от соблюдения некоторого условия
задающего необходимость выполнения
цикла. При этом условие может проверяться
в начале цикла – тогда речь идет о цикле
с предусловием, или в конце – тогда это
цикл с постусловием.

Зацикливание – неверно задано условие
окончания цикла, которое всегда будет
истинным – при этом тело цикла будет
выполняться бесконечно.

Вспомогательный (подчиненный) алгоритм– алгоритм, ранее разработанный и
целиком используемый при алгоритмизации
конкретной задачи. В некоторых случаях
при наличии одинаковых последовательностей
указаний (команд) для различных данных
с целью сокращения записи также выделяют
вспомогательный алгоритм.

Форма записи алгоритма

На практике наиболее распространены
следующие формы представления алгоритмов:

• словесно-формульная (запись на
  естественном языке);

• графическая (изображения из графических
  символов);

• псевдокод (полуформализованные описания
  алгоритмов на алгоритмическом языке);

• программная (тексты на языках
  программирования);

• с помощью граф-схем;

• с помощью сетей Петри.

Лекция: Править]Виды алгоритмов

Особую роль выполняют прикладные алгоритмы, предназначенные для решения определённых прикладных задач. Алгоритм считается правильным, если он отвечает требованиям задачи (например, даёт физически правдоподобный результат). Алгоритм (программа) содержит ошибки, если для некоторых исходных данных он даёт неправильные результаты, сбои, отказы или не даёт никаких результатов вообще. Последний тезис используется в олимпиадах по алгоритмическому программированию, чтобы оценить составленные участниками программы.

Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:

• Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т.п.);

• Гибкие алгоритмы, например стохастические, т.е. вероятностные и эвристические. Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.

• Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.

• Эвристический алгоритм (от греческого слова “эврика”) – это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.

• Линейный алгоритм – набор команд (указаний), выполняемых последовательно во времени друг за другом.

• Разветвляющийся алгоритм – алгоритм, содержащий хотя бы одно условие, в результате проверки которого может осуществляться разделение на несколько параллельных ветвей алгоритма.

• Циклический алгоритм – алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов. Цикл программы – последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторого условия.

• Вспомогательный (подчиненный) алгоритм (процедура) – алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм. На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.

• Структурная блок-схема, граф-схема алгоритма – графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков – графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия. Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации.

Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему – набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации “.

Свойства алгоритма

Понятие информации

Алгоритм — точное предписание исполнителю совершить определенную последовательность действий для достижения поставленной цели за конечное число шагов.

Одним из фундаментальных понятий в информатике является понятие алгоритма. Происхождение самого термина «алгоритм» связано с математикой. Это слово происходит от Algorithmi — латинского написания имени Мухаммеда аль-Хорезми (787 — 850) выдающегося математика средневекового Востока. В своей книге «Об индийском счете» он сформулировал правила записи натуральных чисел с помощью арабских цифр и правила действий над ними столбиком. В дальнейшем алгоритмом стали называть точное предписание, определяющее последовательность действий, обеспечивающую получение требуемого результата из исходных данных.

Алгоритм может быть предназначен для выполнения его человеком или автоматическим устройством. Создание алгоритма, пусть даже самого простого, — процесс творческий. Он доступен исключительно живым существам, а долгое время считалось, что только человеку. В XII в. был выполнен латинский перевод его математического трактата, из которого европейцы узнали о десятичной позиционной системе счисления и правилах арифметики многозначных чисел. Именно эти правила в то время называли алгоритмами.

Данное выше определение алгоритма нельзя считать строгим — не вполне ясно, что такое «точное предписание» или «последовательность действий, обеспечивающая получение требуемого результата».

Поэтому обычно формулируют несколько общих свойств алгоритмов, позволяющих отличать алгоритмы от других инструкций.

Такими свойствами являются:

* Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.

* Определенность — каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.

* Результативность (конечность) — алгоритм должен приводить к решению задачи за конечное число шагов.

* Массовость — алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.

На основании этих свойств иногда дается определение алгоритма, например: “Алгоритм — это последовательность математических, логических или вместе взятых операций, отличающихся детерменированностью, массовостью, направленностью и приводящая к решению всех задач данного класса за конечное число шагов”.

Такая трактовка понятия “алгоритм” является неполной и неточной.

Во-первых, неверно связывать алгоритм с решением какой-либо задачи. Алгоритм вообще может не решать никакой задачи.

Во-вторых, понятие “массовость” относится не к алгоритмам как к таковым, а к математическим методам в целом. Решение поставленных практикой задач математическими методами основано на абстрагировании — мы выделяем ряд существенных признаков, характерных для некоторого круга явлений, и строим на основании этих признаков математическую модель, отбрасывая несущественные признаки каждого конкретного явления. В этом смысле любая математическая модель обладает свойством массовости. Если в рамках построенной модели мы решаем задачу и решение представляем в виде алгоритма, то решение будет “массовым” благодаря природе математических методов, а не благодаря “массовости” алгоритма.

Виды алгоритмов

Виды алгоритмов как логико-математических средств отражают указанные компоненты человеческой деятельности и тенденции, а сами алгоритмы в зависимости от цели, начальных условий задачи, путей ее решения, определения действий исполнителя подразделяются следующим образом:

* Механические алгоритмы, или иначе детерминированные, жесткие (например, алгоритм работы машины, двигателя и т.п.);

* Гибкие алгоритмы, например стохастические, т.е. вероятностные и эвристические. Механический алгоритм задает определенные действия, обозначая их в единственной и достоверной последовательности, обеспечивая тем самым однозначный требуемый или искомый результат, если выполняются те условия процесса, задачи, для которых разработан алгоритм.

* Вероятностный (стохастический) алгоритм дает программу решения задачи несколькими путями или способами, приводящими к вероятному достижению результата.

* Эвристический алгоритм (от греческого слова “эврика”) — это такой алгоритм, в котором достижение конечного результата программы действий однозначно не предопределено, так же как не обозначена вся последовательность действий, не выявлены все действия исполнителя. К эвристическим алгоритмам относят, например, инструкции и предписания. В этих алгоритмах используются универсальные логические процедуры и способы принятия решений, основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.

Линейный алгоритм — набор команд (указаний), выполняемых последовательно во времени друг за другом.

* Разветвляющийся алгоритм — алгоритм, содержащий хотя бы одно условие, в результате проверки которого ЭВМ обеспечивает переход на один из двух возможных шагов.

* Циклический алгоритм — алгоритм, предусматривающий многократное повторение одного и того же действия (одних и тех же операций) над новыми исходными данными. К циклическим алгоритмам сводится большинство методов вычислений, перебора вариантов.

Цикл программы — последовательность команд (серия, тело цикла), которая может выполняться многократно (для новых исходных данных) до удовлетворения некоторого условия.

Вспомогательный (подчиненный) алгоритм (процедура) — алгоритм, ранее разработанный и целиком используемый при алгоритмизации конкретной задачи. В некоторых случаях при наличии одинаковых последовательностей указаний (команд) для различных данных с целью сокращения записи также выделяют вспомогательный алгоритм.

На всех этапах подготовки к алгоритмизации задачи широко используется структурное представление алгоритма.

Структурная (блок-, граф-) схема алгоритма — графическое изображение алгоритма в виде схемы связанных между собой с помощью стрелок (линий перехода) блоков — графических символов, каждый из которых соответствует одному шагу алгоритма. Внутри блока дается описание соответствующего действия.

Графическое изображение алгоритма широко используется перед программированием задачи вследствие его наглядности, т.к. зрительное восприятие обычно облегчает процесс написания программы, ее корректировки при возможных ошибках, осмысливание процесса обработки информации. алгоритм свойство программировани

Можно встретить даже такое утверждение: “Внешне алгоритм представляет собой схему — набор прямоугольников и других символов, внутри которых записывается, что вычисляется, что вводится в машину и что выдается на печать и другие средства отображения информации “. Здесь форма представления алгоритма смешивается с самим алгоритмом.

Требования, предъявляемые к алгоритму

Первое правило — при построении алгоритма прежде всего необходимо задать множество объектов, с которыми будет работать алгоритм. Формализованное (закодированное) представление этих объектов носит название данных. Алгоритм приступает к работе с некоторым набором данных, которые называются входными, и в результате своей работы выдает данные, которые называются выходными. Таким образом, алгоритм преобразует входные данные в выходные. Это правило позволяет сразу отделить алгоритмы от “методов” и “способов”. Пока мы не имеем формализованных входных данных, мы не можем построить алгоритм.

Второе правило — для работы алгоритма требуется память. В памяти размещаются входные данные, с которыми алгоритм начинает работать, промежуточные данные и выходные данные, которые являются результатом работы алгоритма. Память является дискретной, т.е. состоящей из отдельных ячеек. Поименованная ячейка памяти носит название переменной. В теории алгоритмов размеры памяти не ограничиваются, т. е. считается, что мы можем предоставить алгоритму любой необходимый для работы объем памяти. В школьной “теории алгоритмов” эти два правила не рассматриваются. В то же время практическая работа с алгоритмами (программирование) начинается именно с реализации этих правил.

В языках программирования распределение памяти осуществляется декларативными операторами (операторами описания переменных). В языке Бейсик не все переменные описываются, обычно описываются только массивы. Но все равно при запуске программы транслятор языка анализирует все идентификаторы в тексте программы и отводит память под соответствующие переменные.

Третье правило — дискретность. Алгоритм строится из отдельных шагов (действий, операций, команд). Множество шагов, из которых составлен алгоритм, конечно.

Четвертое правило — детерменированность. После каждого шага необходимо указывать, какой шаг выполняется следующим, либо давать команду остановки. Пятое правило — сходимость (результативность). Алгоритм должен завершать работу после конечного числа шагов. При этом необходимо указать, что считать результатом работы алгоритма.

Алгоритм — неопределяемое понятие теории алгоритмов. Алгоритм каждому определенному набору входных данных ставит в соответствие некоторый набор выходных данных, т.е. вычисляет (реализует) функцию.

В старой трактовке вместо слова «порядок» использовалось слово «последовательность», но по мере развития параллельности в работе компьютеров слово «последовательность» стали заменять более общим словом «порядок». Это связано с тем, что работа каких-то инструкций алгоритма может быть зависима от других инструкций или результатов их работы. Таким образом, некоторые инструкции должны выполняться строго после завершения работы инструкций, от которых они зависят. Независимые инструкции или инструкции, ставшие независимыми из-за завершения работы инструкций, от которых они зависят, могут выполняться в произвольном порядке, параллельно или одновременно, если это позволяют используемые процессор и операционная система.

10. История развития ЭВМ. Поколения ЭВМ.
Начиная с 1950 года, каждые 7-10 лет кардинально обновлялись конструктивно-технологические и программно-алгоритмические принципы построения и использования ЭВМ. В связи с этим правомерно говорить о поколениях вычислительных машин. Условно каждому поколению можно отвести 10 лет.

ЭВМ проделали большой эволюционный путь в смысле элементной базы (от ламп к микропроцессорам) а также в смысле появления новых возможностей, расширения области применения и характера их использования.

Деление ЭВМ на поколения — весьма условная, нестрогая классификация вычислительных систем по степени развития аппаратных и программных средств, а также способов общения с ЭВМ.

К первому поколению ЭВМ относятся машины, созданные на рубеже 50-х годов: в схемах использовались электронные лампы. Команд было мало, управление — простым, а показатели объема оперативной памяти и быстродействия — низкими. Быстродействие порядка 10-20 тысяч операций в секунду. Для ввода и вывода использовались печатающие устройства, магнитные ленты, перфокарты и перфоленты.

Ко второму поколению ЭВМ относятся те машины, которые были сконструированы в 1955-65 гг. В них использовались как электронные лампы, так и транзисторы. Оперативная память была построена на магнитных сердечниках. В это время появились магнитные барабаны и первые магнитные диски. Появились так называемые языки высокого уровня, средства которых допускают описание всей последовательности вычислений в наглядном, легко воспринимаемом виде. Появился большой набор библиотечных программ для решения различных математических задач. Машинам второго поколения была свойственна программная несовместимость, которая затрудняла организацию крупных ‑­

информационных систем, поэтому в середине 60х годов наметился переход к созданию ЭВМ, программно совместимых и построенных на микроэлектронной технологической базе.

Третье поколение ЭВМ. Это машины, создаваемые после 60х годов, обладающих единой архитектурой, т.е. программно совместимых. Появились возможности мультипрограммирования, т.е. одновременного выполнения нескольких программ. В ЭВМ третьего поколения применялись интегральные схемы.

Четвертое поколение ЭВМ. Это нынешнее поколение ЭВМ, разработанных после 1970 г. Машины 4го поколения проектировались в расчёте на эффективное использование современных высокоуровневых языков и упрощение процесса программирования для конечного пользователя.

В аппаратурном отношении для них характерно использование больших интегральных схем как элементной базы и наличие быстродействующих запоминающих устройств с произвольной выборкой, объемом несколько Мбайт.

Машины 4-го поколения- многопроцессорные, многомашинные комплексы, работающие на внеш. память и общее поле внеш. устройств. Быстродействие достигает десятков миллионов операций в сек, память — нескольких млн. слов.

Переход к пятому поколению ЭВМ уже начался. Он заключается в качественном переходе от обработки данных к обработке знаний и в повышении основных параметров ЭВМ. Основной упор будет сделан на «интеллектуальность».

На сегодняшний день реальный «интеллект», демонстрируемый самыми сложными нейронными сетями, находится ниже уровня дождевого червя, однако, как бы ни были ограничены возможности нейронных сетей сегодня, множество революционных открытий, могут быть не за горами.

‑­

3. Алгоритм и его свойства .

Алгоpитм — заранее заданное понятное и точное предписание возможному исполнителю
совершить определенную последовательность действий для получения решения
задачи за конечное число шагов.

Исполнитель алгоритма — это некоторая абстрактная или реальная (техническая,
биологическая или биотехническая) система, способная выполнить действия,
предписываемые алгоритмом.

Исполнителя хаpактеpизуют:

• среда;
• элементарные действия;
• система команд;
• отказы.

Среда (или обстановка) — это “место обитания” исполнителя.

Система команд . Каждый исполнитель может выполнять команды
только из некоторого строго заданного списка — системы команд исполнителя.
Для каждой команды должны быть заданы условия применимости (в
каких состояниях среды может быть выполнена команда) и описаны результаты
выполнения команды . После вызова команды исполнитель совершает
соответствующее элементарное действие .

Отказы исполнителя возникают, если команда вызывается
при недопустимом для нее состоянии среды.

Основные свойства алгоритмов :

1.   Понятность для исполнителя — исполнитель алгоритма
должен понимать, как его выполнять. Иными словами, имея алгоритм и произвольный
вариант исходных данных, исполнитель должен знать, как надо действовать
для выполнения этого алгоритма.

2.   Дискретность (прерывность, раздельность) —
алгоpитм должен представлять процесс решения задачи как последовательное
выполнение простых (или ранее определенных) шагов (этапов).

3.   Определенность — каждое правило алгоритма
должно быть четким, однозначным и не оставлять места для произвола. Благодаря
этому свойству выполнение алгоритма носит механический хаpактеp и не требует
никаких дополнительных указаний или сведений о решаемой задаче.

4.   Результативность (или конечность) состоит
в том, что за конечное число шагов алгоpитм либо должен приводить к решению
задачи, либо после конечного числа шагов останавливаться из-за невозможности
получить решение с выдачей соответствующего сообщения, либо неограниченно
продолжаться в течение времени, отведенного для исполнения алгоритма, с
выдачей промежуточных результатов.

5.   Массовость означает, что алгоpитм решения
задачи pазpабатывается в общем виде, т.е. он должен быть применим для некоторого
класса задач, различающихся лишь исходными данными. При этом исходные данные
могут выбираться из некоторой области, которая называется областью применимости
алгоритма.

Виды алгоритмов

Алгоритмы как логико-математические средства отражают указанные компоненты
человеческой деятельности и тенденции, а сами алгоритмы, в зависимости
от цели, начальных условий задачи, Петей ее решения, определения действий
исполнителя подразделяются следующим образом:

•  механические алгоритмы (детерминированные, жесткие, например,
алгоритм работы машины, двигателя). Механический алгоритм задает определенные
действия, обозначая их в единственной и достоверной последовательности,
обеспечивая тем самым однозначный требуемый или искомый результат, если
выполняются те условия процесса, задачи, для которых разработан алгоритм;

•  гибкие алгоритмы:

•  вероятностные (стохастические) алгоритмы дают программу решения
задачи несколькими путями или способами, приводящими к вероятному достижению
результата;

•  эвристические алгоритмы – это алгоритмы, в которых достижение
конечного результата программы действий однозначно не определено, так же
как не обозначена вся последовательность действий исполнителя. К эвристическим
алгоритмам относят, например, инструкции и предписания. В этих алгоритмах
используются универсальные логические процедуры и способы принятия решений,
основанные на аналогиях, ассоциациях и прошлом опыте решения схожих задач.

•  линейные алгоритмы – наборы команд (указаний), выполняемых
последовательно во времени друг за другом;

•  разветвляющиеся алгоритмы – алгоритмы, содержащие хотя бы
одно условие, в результате проверки которого компьютер обеспечивает переход
на один из двух возможных шагов;

•  циклические алгоритмы – алгоритмы, предусматривающие многократное
повторение одного и того же действия (одних и тех же операций) над новыми
исходными данными. К циклическим алгоритмам сводится большинство методов
вычислений, перебора вариантов;

•  вспомогательные (подчиненные) алгоритмы (процедуры) – алгоритмы,
ранее разработанные и целиком используемые при алгоритмизации конкретной
задачи. В некоторых случаях при наличии одинаковых последовательностей
указаний (команд) для различных данных с целью сокращения записи так же
выделяют вспомогательные алгоритмы.

Алгоритмы можно представлять как некоторые структуры, состоящие из отдельных базовых (т.е.
основных) элементов .

Логическая структура любого алгоритма может быть представлена комбинацией
трех базовых структур: следование,   ветвление,   цикл.

Характерной особенностью базовых структур является наличие в них одного
входа и одного выхода.

1. Базовая структура  “следование”. Образуется
последовательностью действий, следующих одно за другим:

Школьный алгоритмический язык	Язык блок-схем
действие 1 действие 2 . . . . . . . . . действие n

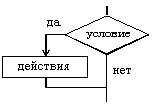
2. Базовая структура  “ветвление” .
Обеспечивает в зависимости от результата проверки условия ( да или нет )
выбор одного из альтернативных путей работы алгоритма. Каждый из путей
ведет к общему выходу , так что работа алгоритма будет
продолжаться независимо от того, какой путь будет выбран. Структура ветвление существует
в четырех основных вариантах:

• если—то;
• если—то—иначе;
• выбор;
• выбор—иначе.

Школьный алгоритмический язык	Язык блок-схем
1. если—то
если условие   то действия все
2. если—то—иначе
если условие   то действия 1   иначе действия 2 все
3. выбор
выбор   при условие 1: действия 1   при условие 2: действия 2   . . . . . . . . . . . .   при условие N: действия N все
4. выбор—иначе
выбор   при условие 1: действия 1   при условие 2: действия 2   . . . . . . . . . . . .   при условие N: действия N   иначе действия N+1 все

Примеры структуры ветвление

Школьный алгоритмический язык	Язык блок-схем
если x > 0   то y := sin(x) все
если a > b   то a := 2*a; b := 1   иначе b := 2*b все
выбор   при n = 1: y := sin(x)   при n = 2: y := cos(x)   при n = 3: y := 0 все
выбор   при a > 5: i := i+1   при a = 0: j := j+1   иначе i := 10; j:=0 все

3. Базовая структура  “цикл”. Обеспечивает многократное
выполнение некоторой совокупности действий, которая называется телом
цикла . Основные разновидности циклов представлены в таблице:

Школьный алгоритмический язык	Язык блок-схем
Цикл типа пока . Предписывает выполнять тело цикла до тех пор, пока выполняется условие, записанное после слова пока.
нц пока условие   тело цикла   (последовательность действий) кц
Цикл типа для . Предписывает выполнять тело цикла для всех значений       некоторой переменной (параметра цикла) в заданном диапазоне.
нц для i от i1 до i2   тело цикла   (последовательность действий) кц

Примеры структуры цикл

Школьный алгоритмический язык	Язык блок-схем
нц пока i <= 5   S := S+A[i]   i := i+1 кц
нц для i от 1 до 5   X[i] := i*i*i   Y[i] := X[i]/2 кц

Особенностью итерационного цикла является то, что число
повторений операторов тела цикла заранее неизвестно. Для его организации
используется цикл типа   пока . Выход из итерационного
цикла осуществляется в случае выполнения заданного условия.

На каждом шаге вычислений происходит последовательное приближение
к искомому результату и проверка условия достижения последнего.

Пример. Составить алгоритм вычисления бесконечной суммы
 

с заданной точностью    (для
данной знакочередующейся бесконечной суммы требуемая точность будет достигнута,
когда очередное слагаемое станет по абсолютной величине меньше ).

Алгоритм на школьном АЯ

Блок-схема алгоритма

алг Сумма ( арг вещ x, Eps, рез вещ S)   дано | 0 < x < 1   надо | S = x – x**2/2 + x**3/3 – … нач цел i, вещ m, p   ввод x, Eps   S := 0; i := 1 | начальные значения   m := 1; p := -1   нц пока abs(m) > Eps   p := -p*x | p – числитель           | очередного слагаемого   m := p/i  | m – очередное слагаемое   S := S + m  | S – частичная сумма   i := i + 1  | i – номер           | очередного слагаемого   кц   вывод S кон

Пример вложенных циклов   для  

Вычислить сумму элементов заданной матрицы А(5,3).
 

Матрица А

S := 0; нц для i от 1 до 5   нц для j от 1 до 3     S:=S+A[i,j]   кц кц

Пример вложенных циклов   пока  

Вычислить произведение тех элементов заданной матрицы A(10,10), которые
расположены на пересечении четных строк и четных столбцов.  

i:=2; P:=1 нц пока i <= 10   j:=2   нц пока j <= 10     P:=P*A[i,j]     j:=j+2   кц   i:=i+2 кц

Алгоритм, в состав которого входит итерационный цикл, называется итеpационным
алгоpитмом. Итерационные алгоритмы используются при реализации
итерационных численных методов.

В итерационных алгоритмах необходимо обеспечить обязательное достижение
условия выхода из цикла ( сходимость итерационного процесса ).
В противном случае произойдет “зацикливание” алгоритма,
т.е. не будет выполняться основное свойство алгоритма — результативность .