Наибольший общий
делитель всех коэффициентов многочлена
с целыми коэффициентами называется его
содержанием.Многочлен называетсяпримитивным, если его содержание
равно 1.
Теорема (лемма
Гаусса). Произведение примитивных
многочленов вновь примитивный многочлен.
Доказательство:
Пусть![]()
![]()
![]()
![]() многочленыgиhпримитивные, и простое числоpделит все коэффициенты многочленаf.
многочленыgиhпримитивные, и простое числоpделит все коэффициенты многочленаf.
Предположим, чтоk–
номер первого коэффициента многочленаg, который не делится
наp, аs– номер последнего коэффициента
многочленаh, который
не делится наp. Тогда
в равенстве
![]()
число,
стоящее слева и все слагаемые суммы,
стоящей справа, кроме одного
![]() делятся наp. Противоречие.
делятся наp. Противоречие.
Следовательно, такого простого числаpнет и наибольший
общий делитель коэффициентов многочленаfравен 1. ■
Теорема(признак
Эйзенштейна). Если существует такое
простое числоp, которое
делит все коэффициенты многочлена с
целыми коэффициентами![]() кроме старшего
кроме старшего![]() но для которого свободный член
но для которого свободный член![]() не делится на
не делится на![]() то многочлен
то многочлен![]() неприводим.
неприводим.
Доказательство:Предположим противное, что многочлен![]() представлен в виде произведения двух
представлен в виде произведения двух
многочленов с целыми коэффициентами
![]() где
где![]()
Тогда
![]()
Произведение
![]() делится наp, но не
делится наp, но не
делится на![]() В силу простоты числаp,
В силу простоты числаp,
это означает, что один из сомножителей
делится наp, скажем![]() а другой нет. Аналогичные рассуждения
а другой нет. Аналогичные рассуждения
при рассмотрении равенства
![]()
но с
учетом того, что
![]() не делится наp, приводят
не делится наp, приводят
к выводу, что![]() делится наp. Продолжив
делится наp. Продолжив
рассуждения, получим:![]() делится наp, а
делится наp, а
следовательно,![]() делится наp. Противоречие
делится наp. Противоречие
с условием. Значит наше предположение
неверно и теорема доказана. ■
Теорема.Если![]() – рациональный корень многочлена с
– рациональный корень многочлена с
целыми коэффициентами![]() то
то![]() делится наp,
делится наp,![]() делится наqи для
делится наqи для
любого целого числаm![]() делится на
делится на![]() В частности,
В частности,![]() делится на
делится на![]() а
а![]() делится на
делится на![]()
Доказательство:![]() тогда
тогда
![]()
Из этого равенства
следует, что
![]() делится наp. Но
делится наp. Но![]() т.е. по теореме Евклида
т.е. по теореме Евклида![]() делится наp. Аналогично,
делится наp. Аналогично,
так как![]() делится наq,
делится наq,![]() то
то![]() делится наq.
делится наq.
Разделим
![]() на
на![]() Получим
Получим
![]()
Домножим обе части
равенства на
![]() Тогда
Тогда
![]()
и нетрудно доказать,
что
![]()
Подставим в обе части
тождества вместо хчислоm.
Получим
![]()
т.е.
![]() делится нацело на
делится нацело на![]()
![]() иqвзаимно просты,
иqвзаимно просты,
поэтому![]() делится на
делится на![]() ■
■
Пример.Доказать,
что уравнение![]() не имеет рациональных корней.
не имеет рациональных корней.
Решение:Если![]() – рациональный корень, тоpможет равняться 1 или -1, аqсоответственно 1, 2, 4, 8 (знак корня относим
– рациональный корень, тоpможет равняться 1 или -1, аqсоответственно 1, 2, 4, 8 (знак корня относим
к числителю). Рациональным корнем может
быть только одно из чисел 1,![]() Пусть
Пусть![]() Тогда
Тогда![]() Из числа подозреваемых исключаем 1, а
Из числа подозреваемых исключаем 1, а
также![]() (так какf(1) не делится
(так какf(1) не делится
на![]() С помощью числаf(2) =
С помощью числаf(2) =
53 аналогичным образом убедимся, что и
остальные числа не удовлетворяют условиюf(2) делится на![]() т.е. не являются корнями уравнения.
т.е. не являются корнями уравнения.
Упражнения и задачи
-
Доказать,
что уравнение
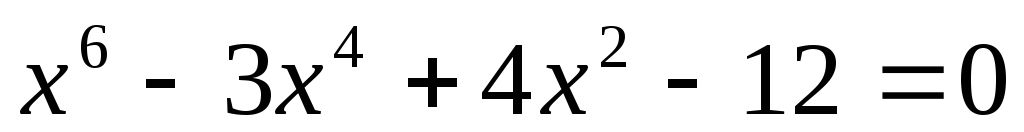 не имеет рациональных корней.
не имеет рациональных корней. -
Найти
все рациональные корни многочленов:
а)
![]() б)
б)![]()
в)
![]() г)
г)![]()
§2.1.12 Многочлены с рациональными коэффициентами
Теорема.Многочлен с рациональными коэффициентами
можно представить в виде произведения
примитивного многочлена с целыми
коэффициентами и несократимой рациональной
дроби и притом единственным образом.
Доказательствотеоремы существования. Пустьb– наименьший общий знаменатель
коэффициентов многочлена![]() с рациональными коэффициентами,а– содержание многочлена
с рациональными коэффициентами,а– содержание многочлена![]() с целыми коэффициентами. Тогда
с целыми коэффициентами. Тогда![]() где
где![]() – примитивный многочлен с целыми
– примитивный многочлен с целыми
коэффициентами. Отсюда![]()
Доказательство теоремы
единственности. Пусть
![]() и
и![]() где
где![]() и
и![]() – примитивные многочлены. Тогда
– примитивные многочлены. Тогда
![]()
Отсюда
![]() так какad– содержание
так какad– содержание
многочлена![]() аbc– содержание
аbc– содержание
многочлена![]() и эти многочлены равны. Следовательно,
и эти многочлены равны. Следовательно,![]() и
и![]() Оба
Оба
представления совпали. Заметим, что в
равенстве![]() числаbиdположительны по построению. Докажем,
числаbиdположительны по построению. Докажем,
что![]() Из равенства
Из равенства![]() и условия
и условия![]() по теореме Евклида следует, чтоаделится нас, т.е.
по теореме Евклида следует, чтоаделится нас, т.е.![]() Подставив это значениеав равенство
Подставив это значениеав равенство![]() ,
,
получим![]() илиbделится наd.
илиbделится наd.
А из того, что иаdделится наb,![]() следует, чтоdделится
следует, чтоdделится
наb. Положительные
числаdиbделятся друг на друга, значит они равны,![]() отсюда
отсюда![]() ■
■
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Как составить уравнение с целыми коэффициентами
Нам уже известны формулы для решения квадратных уравнений. А что делать, если встретится уравнение более высокой степени ? Оказы вается, что для уравнений третьей и четвёртой степени есть формулы, позволяющие найти корни (но они редко используются на практике ввиду их громоздкости), а для уравнений пятой степени и выше доказано, что таких формул не существует. Таким образом, у нас не выйдет в общем случае решить уравнение третьей или более высокой степени. Но существует ряд приёмов, позволяющих решить некоторые специальные виды уравнений. К их рассмотрению мы сейчас и перейдём.
Решите уравнение: `x^3 +4x^2 — 2x-3=0`.
Заметим, что `x=1` является корнем уравнения (значение многочлена при `x=1` равно сумме коэффициентов многочлена). Тогда по теореме Безу многочлен `x^3 +4x^2 -2x -3` делится на многочлен `x-1`. Выполнив деление, получаем:
`x^3 +4x^2 -2x -3=0 hArr (x-1)(x^2 + 5x +3) =0 hArr`
Обычно кубические уравнения решают именно так: подбирают один корень, выполняют деление уголком, после чего остаётся решить только квадратное уравнение. А что делать, если у нас уравнение четвёртой степени? Тогда придётся подбирать корень два раза. После подбора первого корня и деления останется кубическое уравнение, у которого надо будет подобрать ещё один корень. Возникает вопрос. Что делать, если такие «простые» числа как `+-1`, `+-2` не являются корнями уравне ния? Неужели тогда надо перебирать всевозможные числа? Ответ на этот вопрос даёт следующее утверждение.
Если несократимая дробь `p//q` (`p` — целое, `q` — натуральное) является корнем многочлена с целыми коэффициентами , то сво бодный член делится на `p` , а старший коэффициент делится на `q`.
Пусть несократимая дробь `p//q` — корень многочлена (8). Это означает, что
`a_n (p/q)^n +a_(n-1)(p/q)^(n-1) + a_(n-2) (p/q)^(n-2)+ . «+a_2 (p/q)^2 +a_1(p/q)+0=0`.
Умножим обе части на `q^n`, получаем:
`a_n p^n + a_(n-1) p^(n-1) q+a_(n-2) p^(n-2) q^2 + . + a_2 p^2 q^(n-2) +a_1 pq^(n-1)+a_0q^n=0`.
Перенесём в правую часть, а из оставшихся слагаемых вынесем `p` за скобки:
Справа и слева в (14) записаны целые числа. Левая часть делится на `p=>` правая часть также делится на `p`. Числа `p` и `q` взаимно просты (т. к. дробь `p//q` несократимая), откуда следует, что `a_0 vdotsp`.
Аналогично доказывается, что `a_n vdotsq`. Теорема доказана.
Как правило, предлагаемые вам уравнения имеют целые корни, поэтому в большинстве задач используется следующее: если у многочлена с целыми коэффициентами есть целые корни, то они являются делителями свободного члена.
а) `x^4+4x^3-102x^2-644x-539=0`; (15)
б) `6x^4-35x^3+28x^2+51x+10=0`. (16)
а) Попробуем найти целые корни уравнения. Пусть `p` — корень. Тогда `539vdotsp`; чтобы найти возможные значения `p`, разложим число `539` на простые множители:
Поэтому `p` может принимать значения:
Подстановкой убеждаемся, что `x=-1` является корнем уравнения. Разделим многочлен в левой части (15) уголком на `x+1` и получим:
Далее подбираем корни у получившегося многочлена третьей степени. Получаем `x=-7`, а после деления на `(x+7)` остаётся `(x+1)(x+7)(x^2-4x-77)=0`. Решая квадратное уравнение, находим окончательное разложение левой части на множители:
1) После того, как найден первый корень, лучше сначала выполнить деление уголком, и только потом приступать к поиску последующих корней. Тогда вычислений будет меньше.
2) В разложении многочлена на множители множитель `(x+7)` встретился дважды. Тогда говорят, что `(–7)` является корнем кратности два. Аналогично говорят о корнях кратности три, четыре и т. д.
б) Если уравнение имеет рациональный корень `x_0=p/q`, то `10vdotsp`, `6vdotsq`, т. е. `p in<+-1;+-2;+-5;+-10>`; `qin<1;2;3;6>`.Возможные варианты для `x_0`:
Начинаем перебирать числа из этого списка. Первым подходит число `x=5/2`. Делим многочлен в левой части (16) на `(2x-5)` и получаем
Заметим, что для получившегося кубического уравнения выбор рациональных корней заметно сузился, а именно, следующие числа могут быть корнями: `x_0=+-1,+-2,+-1/3,+-2/3`, причём мы уже знаем, что числа `+-1` и `+-2` корнями не являются (так как мы их подставляли раньше, и они не подошли). Находим, что `x=-2/3` — корень; делим `3x^3-10x^2-11x-2` на `3x+2` и получаем:
Решаем квадратное уравнение: `x^2-4x-1=0 iff x=2+-sqrt5`.
К сожалению, уравнения не всегда имеют рациональные корни. Тогда приходится прибегать к другим методам.
Разложите на множители:
а) `x^4+4=x^4+4x^2+4-4x^2=(x^2+2)^2-(2x)^2=`
Таким образом, сумму четвёртых степеней, в отличие от суммы квадратов, можно разложить на множители:
в) Вынесем `x^2` за скобки и сгруппируем:
Обозначим `x+2/x=t`. Тогда `x^2+4+4/x^2=t^2`, `x^2+4/x^2=t^2-4`, выражение в скобках принимает вид:
В итоге получаем:
Этот приём иногда используется для решения уравнений четвёртой степени; в частности, с его помощью решают возвратные уравнения (см. пример 12 е).
г)* Можно убедиться, что никакой из рассмотренных выше методов не помогает решить задачу, а именно: рациональных корней уравнение не имеет (числа `+-1` и `+-2` – не корни); вынесение числа `x^2` за скобки и группировка слагаемых приводит к выражению
Если здесь обозначить `4x-13/x=t`, то `x^2-2/x^2` через `t` рационально не выражается.
Прибегнем к методу неопределённых коэффициентов. Пусть
Попробуем подобрать коэффициенты `a`, `b`, `c`, `d` так, чтобы (17) обратилось в верное равенство. Для этого раскроем скобки в правой части и приведём подобные слагаемые:
Приравняем в (18) коэффициенты при одинаковых степенях в обеих частях уравнения. Получим систему уравнений:
Мы будем пытаться найти целочисленные решения системы (19). Найти все решения системы (19) не проще, чем решить исходную задачу, однако нахождение целочисленных решений – разумеется, если они есть – нам по силам.
Рассмотрим четвёртое уравнение. Возможны только два принципиально различных случая:
2) `b=2` и `d=-1`. Рассмотрим каждый из них. Подставляем значения `b` и `d` в первые три уравнения:
Из первого и третьего уравнений системы получаем `c=5/3`; `a=-17/3`, что не удовлетворяет второму уравнению, поэтому система решений не имеет; пара чисел `b=1` и `d=-2` не подходит.
Эта система имеет одно решение `a=-7`, `c=3`. Значит, числа `a=-7`, `b=2`, `c=3`, `d=-1` являются решением системы (19), поэтому
Далее каждый из квадратных трёхчленов можно разложить на множители.
Во многих ситуациях степень уравнения можно понизить с помощью замены переменных.
Решение уравнений высших степеней
В общем случае уравнение, имеющее степень выше 4 , нельзя разрешить в радикалах. Но иногда мы все же можем найти корни многочлена, стоящего слева в уравнении высшей степени, если представим его в виде произведения многочленов в степени не более 4 -х. Решение таких уравнений базируется на разложении многочлена на множители, поэтому советуем вам повторить эту тему перед изучением данной статьи.
Чаще всего приходится иметь дело с уравнениями высших степеней с целыми коэффициентами. В этих случаях мы можем попробовать найти рациональные корни, а потом разложить многочлен на множители, чтобы потом преобразовать его в уравнение более низкой степени, которое будет просто решить. В рамках этого материала мы рассмотрим как раз такие примеры.
Уравнения высшей степени с целыми коэффициентами
Все уравнения, имеющие вид a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 , мы можем привести к уравнению той же степени с помощью умножения обеих частей на a n n — 1 и осуществив замену переменной вида y = a n x :
a n x n + a n — 1 x n — 1 + . . . + a 1 x + a 0 = 0 a n n · x n + a n — 1 · a n n — 1 · x n — 1 + … + a 1 · ( a n ) n — 1 · x + a 0 · ( a n ) n — 1 = 0 y = a n x ⇒ y n + b n — 1 y n — 1 + … + b 1 y + b 0 = 0
Те коэффициенты, что получились в итоге, также будут целыми. Таким образом, нам нужно будет решить приведенное уравнение n-ной степени с целыми коэффициентами, имеющее вид x n + a n x n — 1 + … + a 1 x + a 0 = 0 .
Схема решения уравнения
Вычисляем целые корни уравнения. Если уравнение имеет целые корни, нужно искать их среди делителей свободного члена a 0 . Выпишем их и будем подставлять в исходное равенство по очереди, проверяя результат. Как только мы получили тождество и нашли один из корней уравнения, то можем записать его в виде x — x 1 · P n — 1 ( x ) = 0 . Здесь x 1 является корнем уравнения, а P n — 1 ( x ) представляет собой частное от деления x n + a n x n — 1 + … + a 1 x + a 0 на x — x 1 .
Подставляем остальные выписанные делители в P n — 1 ( x ) = 0 , начав с x 1 , поскольку корни могут повторяться. После получения тождества корень x 2 считается найденным, а уравнение может быть записано в виде ( x — x 1 ) ( x — x 2 ) · P n — 2 ( x ) = 0 .Здесь P n — 2 ( x ) будет частным от деления P n — 1 ( x ) на x — x 2 .
Продолжаем и дальше перебирать делители. Найдем все целые корни и обозначим их количество как m . После этого исходное уравнение можно представить как x — x 1 x — x 2 · … · x — x m · P n — m ( x ) = 0 . Здесь P n — m ( x ) является многочленом n — m -ной степени. Для подсчета удобно использовать схему Горнера.
Если у нас исходное уравнение имеет целые коэффициенты, мы не можем получить в итоге дробные корни.
У нас в итоге получилось уравнение P n — m ( x ) = 0 , корни которого могут быть найдены любым удобным способом. Они могут быть иррациональными или комплексными.
Покажем на конкретном примере, как применяется такая схема решения.
Условие: найдите решение уравнения x 4 + x 3 + 2 x 2 — x — 3 = 0 .
Решение
Начнем с нахождений целых корней.
У нас есть свободный член, равный минус трем. У него есть делители, равные 1 , — 1 , 3 и — 3 . Подставим их в исходное уравнение и посмотрим, какие из них дадут в итоге тождества.
При x , равном единице, мы получим 1 4 + 1 3 + 2 · 1 2 — 1 — 3 = 0 , значит, единица будет корнем данного уравнения.
Теперь выполним деления многочлена x 4 + x 3 + 2 x 2 — x — 3 на ( х — 1 ) в столбик:
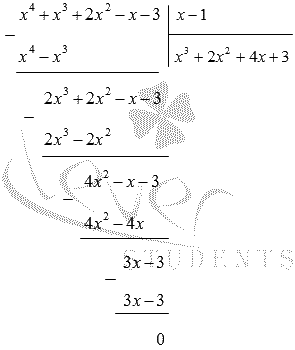
Значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
Перебираем возможные делители дальше, но подставляем их в равенство x 3 + 2 x 2 + 4 x + 3 = 0 :
1 3 + 2 · 1 2 + 4 · 1 + 3 = 10 ≠ 0 ( — 1 ) 3 + 2 · ( — 1 ) 2 + 4 · — 1 + 3 = 0
У нас получилось тождество, значит, мы нашли еще один корень уравнения, равный — 1 .
Делим многочлен x 3 + 2 x 2 + 4 x + 3 на ( х + 1 ) в столбик:
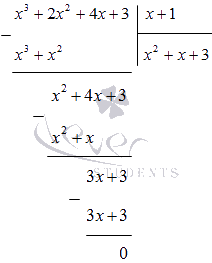
x 4 + x 3 + 2 x 2 — x — 3 = ( x — 1 ) ( x 3 + 2 x 2 + 4 x + 3 ) = = ( x — 1 ) ( x + 1 ) ( x 2 + x + 3 )
Подставляем очередной делитель в равенство x 2 + x + 3 = 0 , начиная с — 1 :
— 1 2 + ( — 1 ) + 3 = 3 ≠ 0 3 2 + 3 + 3 = 15 ≠ 0 ( — 3 ) 2 + ( — 3 ) + 3 = 9 ≠ 0
Равенства, полученные в итоге, будут неверными, значит, у уравнения больше нет целых корней.
Оставшиеся корни будут корнями выражения x 2 + x + 3 .
D = 1 2 — 4 · 1 · 3 = — 11 0
Из этого следует, что у данного квадратного трехчлена нет действительных корней, но есть комплексно сопряженные: x = — 1 2 ± i 11 2 .
Уточним, что вместо деления в столбик можно применять схему Горнера. Это делается так: после того, как мы определили первый корень уравнения, заполняем таблицу.
| x i | коэффициенты многочлена | ||||
| 1 | 1 | 2 | — 1 | — 3 | |
| 1 | 1 | 1 + 1 · 1 = 2 | 2 + 2 · 1 = 4 | — 1 + 4 · 1 = 3 | — 3 + 3 · 1 = 0 |
В таблице коэффициентов мы сразу можем увидеть коэффициенты частного от деления многочленов, значит, x 4 + x 3 + 2 x 2 — x — 3 = x — 1 x 3 + 2 x 2 + 4 x + 3 .
После нахождения следующего корня, равного — 1 , мы получаем следующее:
| x i | коэффициенты многочлена | |||
| 1 | 2 | 4 | 3 | |
| 1 | 1 | 2 + 1 · ( — 1 ) = 1 | 4 + 1 · ( — 1 ) = 3 | 3 + 3 · ( — 1 ) = 0 |
Далее мы приходим к разложению x — 1 x + 1 x 2 + x + 3 = 0 . Потом, проверив оставшиеся делители равенства x 2 + x + 3 = 0 , вычисляем оставшиеся корни.
Ответ: х = — 1 , х = 1 , x = — 1 2 ± i 11 2 .
Условие: решите уравнение x 4 — x 3 — 5 x 2 + 12 = 0 .
Решение
У свободного члена есть делители 1 , — 1 , 2 , — 2 , 3 , — 3 , 4 , — 4 , 6 , — 6 , 12 , — 12 .
Проверяем их по порядку:
1 4 — 1 3 — 5 · 1 2 + 12 = 7 ≠ 0 ( — 1 ) 4 — ( — 1 ) 3 — 5 · ( — 1 ) 2 + 12 = 9 ≠ 0 2 4 · 2 3 — 5 · 2 2 + 12 = 0
Значит, x = 2 будет корнем уравнения. Разделим x 4 — x 3 — 5 x 2 + 12 на х — 2 , воспользовавшись схемой Горнера:
| x i | коэффициенты многочлена | ||||
| 1 | — 1 | — 5 | 0 | 12 | |
| 2 | 1 | — 1 + 1 · 2 = 1 | — 5 + 1 · 2 = — 3 | 0 — 3 · 2 = 3 | 12 — 6 · 2 = 0 |
В итоге мы получим x — 2 ( x 3 + x 2 — 3 x — 6 ) = 0 .
Проверяем делители дальше, но уже для равенства x 3 + x 2 — 3 x — 6 = 0 , начиная с двойки.
2 3 + 2 2 — 3 · 2 — 6 = 0
Значит, 2 опять будет корнем. Разделим x 3 + x 2 — 3 x — 6 = 0 на x — 2 :
| x i | коэффициенты многочлена | |||
| 1 | 1 | — 3 | — 6 | |
| 2 | 1 | 1 + 1 · 2 = 3 | — 3 + 3 · 2 = 3 | — 6 + 3 · 2 = 0 |
В итоге получим ( x — 2 ) 2 · ( x 2 + 3 x + 3 ) = 0 .
Проверка оставшихся делителей смысла не имеет, поскольку равенство x 2 + 3 x + 3 = 0 быстрее и удобнее решить с помощью дискриминанта.
Решим квадратное уравнение:
x 2 + 3 x + 3 = 0 D = 3 2 — 4 · 1 · 3 = — 3 0
Получаем комплексно сопряженную пару корней: x = — 3 2 ± i 3 2 .
Ответ: x = — 3 2 ± i 3 2 .
Условие: найдите для уравнения x 4 + 1 2 x 3 — 5 2 x — 3 = 0 действительные корни.
Решение
x 4 + 1 2 x 3 — 5 2 x — 3 = 0 2 x 4 + x 3 — 5 x — 6 = 0
Выполняем домножение 2 3 обеих частей уравнения:
2 x 4 + x 3 — 5 x — 6 = 0 2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0
Заменяем переменные y = 2 x :
2 4 · x 4 + 2 3 x 3 — 20 · 2 · x — 48 = 0 y 4 + y 3 — 20 y — 48 = 0
В итоге у нас получилось стандартное уравнение 4 -й степени, которое можно решить по стандартной схеме. Проверим делители, разделим и получим в итоге, что оно имеет 2 действительных корня y = — 2 , y = 3 и два комплексных. Решение целиком здесь мы не будем приводить. В силу замены действительными корнями данного уравнения будут x = y 2 = — 2 2 = — 1 и x = y 2 = 3 2 .
Ответ: x 1 = — 1 , x 2 = 3 2
Советуем также ознакомиться с материалами, посвященными решению кубических уравнений и уравнений четвертой степени.
Рациональные корни многочленов с целыми коэффициентами. Алгебраические и трансцендентные числа

Рациональные корни многочленов с целыми коэффициентами
Прежде, чем дать общую формулировку теоремы о рациональных корнях многочленов с целыми коэффициентами , решим следующую задачу.
Задача . Найти все корни уравнения
Решение . Предположим, что рассматриваемое уравнение имеет корень, являющийся рациональным числом. Тогда, поскольку каждое рациональное число можно представить в виде несократимой дроби
 ,
,
где m – число целое, а n – число натуральное, то выполняется равенство:
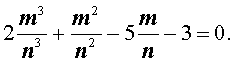
Умножая это равенство на n 3 , получаем равенство:
| 2m 3 + m 2 n – 5 m n 2 – – 3n 3 = 0. |
(1) |
Теперь преобразуем равенство (1):
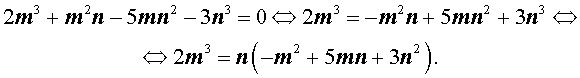
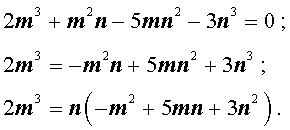
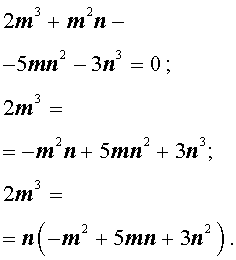
Отсюда вытекает, что число 2m 3 нацело делится на число n . А из этого, в свою очередь, следует, что, поскольку числа m и n не имеют общих простых делителей, то число n является делителем числа 2 . Таким образом, число n равно 1 или 2 .
Теперь преобразуем равенство (1) по-другому:
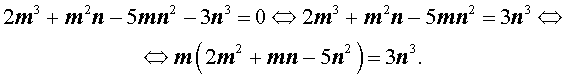
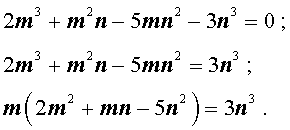
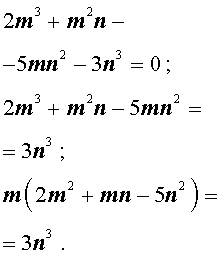
Значит, число 3n 3 нацело делится на число m . А из этого, в свою очередь, следует, что, так как числа m и n не имеют общих простых делителей, то число m является делителем числа 3. Таким образом, число m может быть равно: – 1, 1, – 3 или 3 .
Далее, рассматривая все возможные комбинации чисел m и n , получаем, что дробь

может принимать только следующие значения:
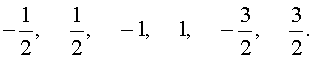
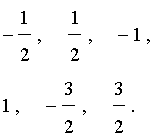
Таким образом, если у исходного уравнения и есть рациональный корень, то искать его нужно среди полученных шести чисел. Других рациональных корней у исходного уравнения быть не может.
Подставляя поочередно каждое из этих чисел в исходное уравнение, получаем, что корнем уравнения является лишь число 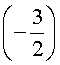 .
.
Оставляя читателю проверку того, что другие числа корнями исходного уравнения не являются, покажем, что число 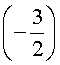 действительно является его корнем:
действительно является его корнем:
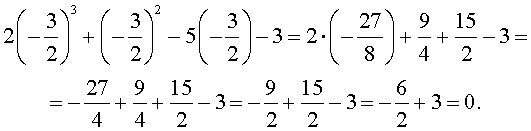
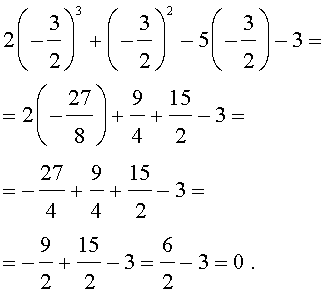
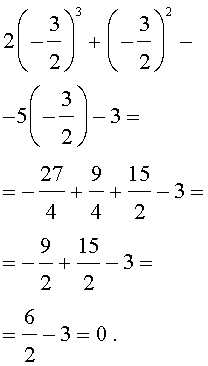
Ответ . Число 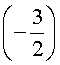 является единственным рациональным корнем исходного уравнения.
является единственным рациональным корнем исходного уравнения.
Замечание . Для того, чтобы найти все остальные корни исходного уравнения, нужно, воспользовавшись теоремой Безу, разделить многочлен
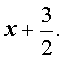
В результате деления получится квадратный трехчлен
Теорема . Если рациональное число (несократимая дробь)
 ,
,
где m – число целое, а n – число натуральное, является корнем многочлена k -ой степени
которого являются целыми числами, то числитель дроби m является делителем коэффициента ak , а знаменатель дроби n является делителем коэффициента a0 .
Коэффициент a0 называют старшим коэффициентом многочлена, а коэффициент ak – свободным членом многочлена.
Алгебраические и трансцендентные числа
Определение . Действительное число называют действительным алгебраическим числом , если существует многочлен с целочисленными коэффициентами, корнем которого это число является. Если же такой многочлен не существует, то указанное число называют действительным трансцендентным числом .
Замечание . Числа π и e – наиболее известные примеры действительных трансцендентных чисел.
Утверждение . Каждое рациональное число является алгебраическим числом.
Доказательство . Каждое рациональное число представимо в виде несократимой дроби
 ,
,
где m – число целое, а n – число натуральное. Но указанная дробь является корнем уравнения первой степени
что и требовалось доказать.
Следствие . Каждое действительное трансцендентное число является иррациональным числом.
источники:
http://zaochnik.com/spravochnik/matematika/systems/reshenie-uravnenij-vysshih-stepenej/
http://www.resolventa.ru/spr/algebra/ratroot.htm
Содержание:
Многочлен – это сумма одночленов, причем сам одночлен – это частный случай многочлена.
История многочелена:
Живший в 1050-1122 гг Омар Хаям известен в мире как мастер рубай. Однако имя Омара Хаяма также упоминается наряду с именами гениальных математиков. Именно Омар Хаям впервые представил общую формулу корней уравнения кубического многочлена 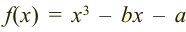
Многочлены от одной переменной и действия над ними
Определение многочленов от одной переменной и их тождественное равенство
Рассмотрим одночлен и многочлен, которые зависят только от одной переменной, например, от переменной 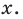
По определению одночлена числа и буквы (в нашем случае одна буква — 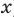 ) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида
) в нем связаны только двумя действиями — умножением и возведением в натуральную степень. Если в этом одночлене произведение всех чисел записать перед буквой, а произведение всех степеней буквы записать как целую неотрицательную степень этой буквы (то есть записать одночлен в стандартном виде), то получим выражение вида 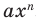 , где
, где 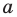 — некоторое число. Поэтому одночлен от одной переменной
— некоторое число. Поэтому одночлен от одной переменной 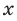 — это выражение вида
— это выражение вида 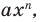 где
где 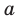 — некоторое число,
— некоторое число, 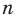 — целое неотрицательное число. Если
— целое неотрицательное число. Если 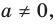 то показатель степени
то показатель степени 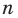 переменной
переменной 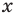 называется степенью одночлена. Например,
называется степенью одночлена. Например, 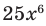 — одночлен шестой степени,
— одночлен шестой степени, 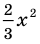 — одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку
— одночлен второй степени. Если одночлен является числом, не равным нулю, то его степень считается равной нулю. Для одночлена, заданного числом 0, понятие степени не определяется (поскольку 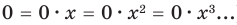 ).
).
По определению многочлен от одной переменной 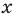 — это сумма одночленов от одной переменной
— это сумма одночленов от одной переменной 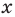 . Поэтому
. Поэтому
многочленом от одной переменной 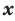 : называется выражение вида
: называется выражение вида
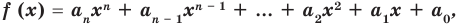 (1)
(1)
где коэффициенты 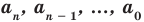 — некоторые числа.
— некоторые числа.
Если 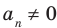 , то этот многочлен называют многочленом
, то этот многочлен называют многочленом 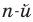 степени от переменной
степени от переменной 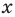 . При этом член
. При этом член 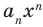 называют старшим членом многочлена
называют старшим членом многочлена 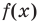 , число
, число 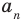 — коэффициентом при старшем члене, а член
— коэффициентом при старшем члене, а член 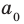 — свободным членом. Например,
— свободным членом. Например, 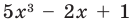 — многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
— многочлен третьей степени, у которого свободный член равен 1, а коэффициент при старшем члене равен 5.
Заметим, что иногда нумерацию коэффициентов многочлена начинают с начала записи выражения (1), и тогда общий вид многочлена 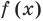 записывают так:
записывают так:
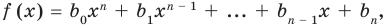
где 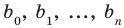 — некоторые числа.
— некоторые числа.
Теорема 1. Одночлены 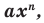 где
где 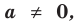 и
и 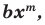 где
где 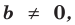 , тождественно равны тогда и только тогда, когда
, тождественно равны тогда и только тогда, когда 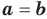 и
и 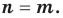 Одночлен
Одночлен 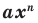 тождественно равен нулю тогда и только тогда, когда
тождественно равен нулю тогда и только тогда, когда 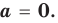
Поскольку равенство одночленов
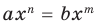 (2)
(2)
выполняется при всех значениях 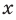 (по условию эти одночлены тождественно равны), то, подставляя в это равенство
(по условию эти одночлены тождественно равны), то, подставляя в это равенство 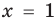 , получаем, что
, получаем, что 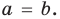 Сокращая обе части равенства (2) на
Сокращая обе части равенства (2) на 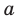 (где
(где 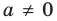 по условию), получаем
по условию), получаем 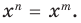 При
При 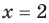 из этого равенства имеем:
из этого равенства имеем: 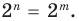 Поскольку 2
Поскольку 2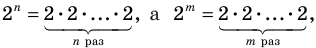 то равенство
то равенство 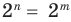 возможно только тогда, когда
возможно только тогда, когда 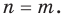 Таким образом, из тождественного равенства
Таким образом, из тождественного равенства 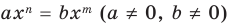 получаем, что
получаем, что 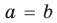 и
и 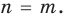 Если известно, что
Если известно, что 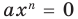 для всех
для всех 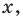 то при
то при 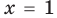 получаем
получаем 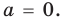 Поэтому одночлен
Поэтому одночлен 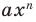 тождественно равен нулю при
тождественно равен нулю при 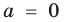 (тогда
(тогда 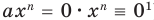 ).
).
Далее любой одночлен вида 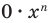 будем заменять на 0.
будем заменять на 0.
Теорема 2. Если многочлен 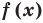 тождественно равен нулю (то есть принимает нулевые значения при всех значениях
тождественно равен нулю (то есть принимает нулевые значения при всех значениях 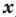 ), то все его коэффициенты равны нулю.
), то все его коэффициенты равны нулю.
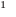 Значком
Значком 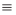 обозначено тождественное равенство многочленов.
обозначено тождественное равенство многочленов.
Для доказательства используем метод математической индукции. Пусть 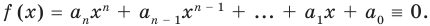
При 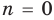 имеем
имеем 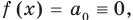 поэтому
поэтому 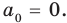 То есть в этом случае утверждение теоремы выполняется.
То есть в этом случае утверждение теоремы выполняется.
Предположим, что при 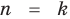 это утверждение также выполняется: если многочлен
это утверждение также выполняется: если многочлен 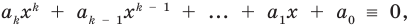 то
то 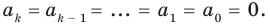
Докажем, что данное утверждение выполняется и при 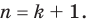 Пусть
Пусть 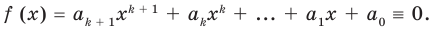 (3)
(3)
Поскольку равенство (3) выполняется при всех значениях  , то, подставляя в это равенство
, то, подставляя в это равенство 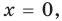 получаем, что
получаем, что 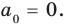 Тогда равенство (3) обращается в следующее равенство:
Тогда равенство (3) обращается в следующее равенство: 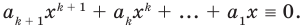 Вынесем
Вынесем  в левой части этого равенства за скобки и получим
в левой части этого равенства за скобки и получим
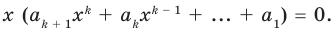 (4)
(4)
Равенство (4) должно выполняться при всех значениях  . Для того чтобы оно выполнялось при
. Для того чтобы оно выполнялось при 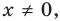 должно выполняться тождество
должно выполняться тождество
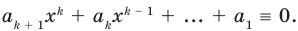 В левой части этого тождества стоит многочлен со степенями переменной от
В левой части этого тождества стоит многочлен со степенями переменной от 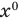 до
до 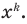 Тогда по предположению индукции все его коэффициенты равны нулю:
Тогда по предположению индукции все его коэффициенты равны нулю: 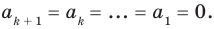 Но мы также доказали, что
Но мы также доказали, что 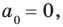 поэтому наше утверждение выполняется и при
поэтому наше утверждение выполняется и при 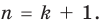 Таким образом, утверждение теоремы справедливо для любого целого неотрицательного
Таким образом, утверждение теоремы справедливо для любого целого неотрицательного 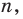 то есть для всех многочленов.
то есть для всех многочленов.
Многочлен, у которого все коэффициенты равны нулю, обычно называют нулевым многочленом, или нуль-многочленом, и обозначают 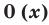 или просто
или просто 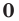 (поскольку
(поскольку 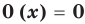 ).
).
Теорема 3. Если два многочлена 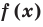 и
и 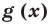 тождественно равны, то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
тождественно равны, то они совпадают (то есть их степени одинаковы и коэффициенты при одинаковых степенях равны).
Пусть многочлен 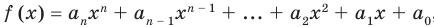 , а многочлен
, а многочлен 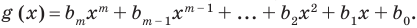 Рассмотрим многочлен
Рассмотрим многочлен 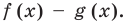 Поскольку многочлены
Поскольку многочлены 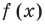 и
и 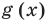 по условию тождественно равны, то многочлен
по условию тождественно равны, то многочлен 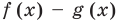 тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
тождественно равен 0. Таким образом, все его коэффициенты равны нулю.
Но 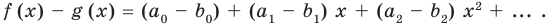 Тогда
Тогда 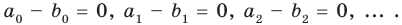 Отсюда
Отсюда 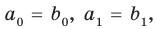
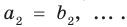 Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например,
Как видим, если допустить, что у какого-то из двух данных многочленов степень выше, чем у второго многочлена (например, 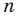 больше
больше 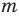 ), то коэффициенты разности будут равны нулю. Поэтому начиная с (
), то коэффициенты разности будут равны нулю. Поэтому начиная с (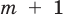 -го номера все коэффициенты
-го номера все коэффициенты 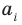 также будут равны нулю. То есть действительно многочлены
также будут равны нулю. То есть действительно многочлены 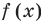 и
и 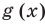
имеют одинаковую степень и соответственно равные коэффициенты при одинаковых степенях.
Теорема 3 является основанием так называемого метода неопределенных коэффициентов. Покажем его применение на следующем примере.
Пример:
Докажите, что выражение 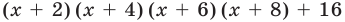
является полным квадратом.
Решение:
► Данное выражение может быть записано в виде многочлена четвертой степени, поэтому оно может быть полным квадратом только многочлена второй степени вида 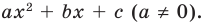 Получаем тождество:
Получаем тождество:
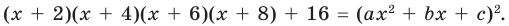 (5)
(5)
Раскрывая скобки в левой и правой частях этого тождества и приравнивая коэффициенты при одинаковых степенях 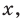 получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
получаем систему равенств. Этот этап решения удобно оформлять в следующем виде:
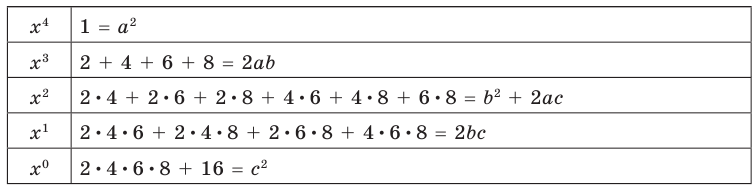
Из первого равенства получаем 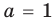 или
или 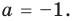
При 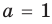 из второго равенства имеем а из третьего —
из второго равенства имеем а из третьего — 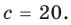 Как видим, при этих значениях
Как видим, при этих значениях 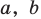 и
и 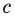 последние два равенства также выполняются. Следовательно, тождество (5) выполняется при
последние два равенства также выполняются. Следовательно, тождество (5) выполняется при 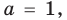
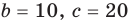 (аналогично можно также получить
(аналогично можно также получить 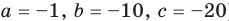 ). Таким образом,
). Таким образом, 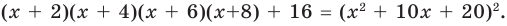
Действия над многочленами. Деление многочлена на многочлен с остатком
Сложение и умножение многочленов от одной переменной выполняется с помощью известных правил сложения и умножения многочленов. В результате выполнения действий сложения или умножения над многочленами от одной переменной всегда получаем многочлен от той же переменной.
Из определения произведения двух многочленов вытекает, что старший член произведения двух многочленов равен произведению старших членов множителей, а свободный член произведения равен произведению свободных членов множителей. Отсюда получаем, что степень произведения двух многочленов равна сумме степеней множителей.
При сложении многочленов одной степени получаем многочлен этой же степени, хотя иногда можно получить многочлен меньшей степени. Например, 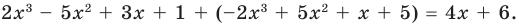 При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей степени слагаемого.
При сложении многочленов разных степеней всегда получаем многочлен, степень которого равна большей степени слагаемого.
Например, 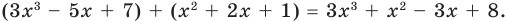 Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что целое число
Деление многочлена на многочлен определяется аналогично делению целых чисел. Напомним, что целое число 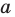 делится на целое число
делится на целое число 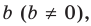 если существует такое целое число
если существует такое целое число 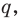 что
что 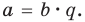
Определение: Многочлен  делится на многочлен
делится на многочлен 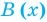 (где
(где 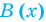 — не нулевой многочлен), если существует такой многочлен
— не нулевой многочлен), если существует такой многочлен  что
что 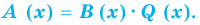
Как и для целых чисел, операция деления многочлена на многочлен выполняется не всегда, поэтому во множестве многочленов вводится операция деления с остатком. Говорят, что
многочлен  делится на многочлен
делится на многочлен  (где
(где  — не нулевой многочлен) с остатком, если существует такая пара многочленов
— не нулевой многочлен) с остатком, если существует такая пара многочленов  и
и  что
что  причем степень остатка
причем степень остатка  меньше степени делителя
меньше степени делителя  (в этом случае многочлен
(в этом случае многочлен  называют неполным частным.)
называют неполным частным.)
Например, поскольку 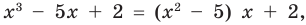 то при делении многочлена
то при делении многочлена 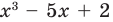 на многочлен
на многочлен 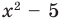 получаем неполное частное
получаем неполное частное 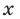 : и остаток 2.
: и остаток 2.
Иногда деление многочлена на многочлен удобно выполнять «уголком», как и деление многозначных чисел, пользуясь следующим алгоритмом.
Пример №1
Разделим многочлен 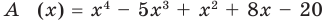 на многочлен
на многочлен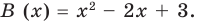
Решение:
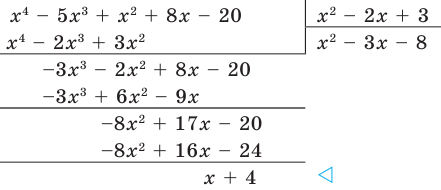 Докажем, что полученный результат действительно является результатом деления
Докажем, что полученный результат действительно является результатом деления 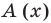 на
на 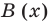 с остатком.
с остатком.
Если обозначить результат выполнения первого шага алгоритма через 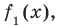 второго шага — через
второго шага — через 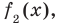 третьего — через
третьего — через 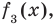 то операцию деления, выполненную выше, можно записать в виде системы равенств:
то операцию деления, выполненную выше, можно записать в виде системы равенств:
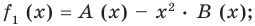 (1)
(1)
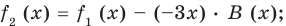 (2)
(2)
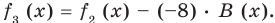 (3)
(3)
Сложим почленно равенства (1), (2), (3) и получим
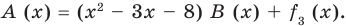 (4)
(4)
Учитывая, что степень многочлена 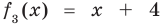 меньше степени делителя
меньше степени делителя 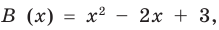 обозначим
обозначим 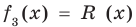 (остаток), а
(остаток), а 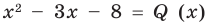 (неполное частное). Тогда из равенства (4) имеем:
(неполное частное). Тогда из равенства (4) имеем: 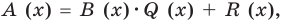 то есть
то есть 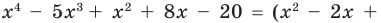
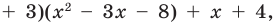 а это и означает, что мы разделили
а это и означает, что мы разделили 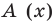 на
на 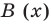 с остатком.
с остатком.
Очевидно, что приведенное обоснование можно провести для любой пары многочленов 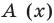 и
и 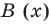 в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого
в случае их деления столбиком. Поэтому описанный выше алгоритм позволяет для любых делимого 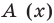 и делителя
и делителя 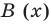 (где
(где 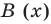 — не нулевой многочлен) найти неполное частное
— не нулевой многочлен) найти неполное частное 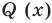 и остаток
и остаток 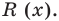
Отметим, что в случае, когда степень делимого 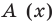 меньше степени делителя
меньше степени делителя 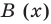 , считают, что неполное частное
, считают, что неполное частное 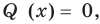 а остаток
а остаток 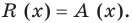
Теорема Безу. Корни многочлена. Формулы Виета
Рассмотрим деление многочлена 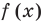 на двучлен
на двучлен 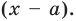 Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен
Поскольку степень делителя равна 1, то степень остатка, который мы получим, должна быть меньше 1, то есть в этом случае остатком будет некоторое число R. Таким образом, если разделить многочлен 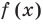 на двучлен
на двучлен 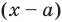 , то получим
, то получим
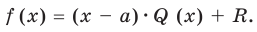
Это равенство выполняется тождественно, то есть при любом значении 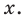 При
При 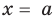 имеем
имеем 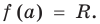 Полученный результат называют теоремой Безу
Полученный результат называют теоремой Безу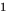 .
.
Теорема 1 (теорема Безу). Остаток от деления многочлена 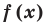 на двучлен
на двучлен 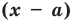 равен
равен 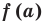 (то есть значению многочлена при
(то есть значению многочлена при 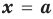 ).
).
Пример №2
Докажите, что 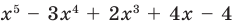 делится на
делится на 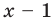 без остатка.
без остатка.
Решение:
► Подставив в 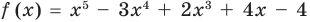 вместо
вместо 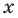 значение 1, получаем:
значение 1, получаем: 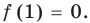 . Таким образом, остаток от деления
. Таким образом, остаток от деления 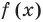 на
на  равен 0, то есть
равен 0, то есть 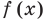 делится на
делится на  без остатка. <]
без остатка. <]
Определение: Число 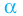 называют корнем многочлена
называют корнем многочлена 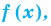 если
если
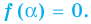
Если многочлен 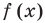 делится на
делится на  то
то 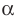 — корень этого многочлена.
— корень этого многочлена.
 Безу Этьен (1730-1783) — французский математик, внесший значительный вклад в развитие теории алгебраических уравнений.
Безу Этьен (1730-1783) — французский математик, внесший значительный вклад в развитие теории алгебраических уравнений.
Действительно, если 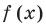 делится на
делится на 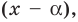 то
то  и поэтому
и поэтому 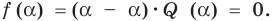 Таким образом,
Таким образом, 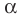 — корень многочлена
— корень многочлена 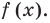
Справедливо и обратное утверждение. Оно является следствием теоремы Безу.
Теорема 2. Если число 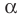 является корнем многочлена
является корнем многочлена 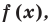 то этот многочлен делится на двучлен
то этот многочлен делится на двучлен 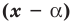 без остатка.
без остатка.
По теореме Безу остаток от деления 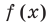 на
на  равен
равен 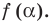 Но по условию
Но по условию 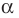 — корень
— корень 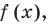 таким образом,
таким образом, 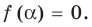
Обобщением теоремы 2 является следующее утверждение.
Теорема 3. Если многочлен 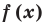 имеет попарно разные корни
имеет попарно разные корни 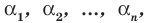 то он делится без остатка на произведение
то он делится без остатка на произведение 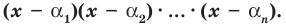
Для доказательства используем метод математической индукции.
При 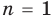 утверждение доказано в теореме 2.
утверждение доказано в теореме 2.
Допустим, что утверждение справедливо при 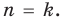 То есть если
То есть если 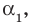
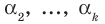 попарно разные корни многочлена
попарно разные корни многочлена 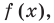 то он делится на произведение
то он делится на произведение 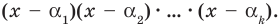 Тогда
Тогда
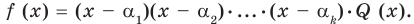 (1)
(1)
Докажем, что утверждение теоремы справедливо и при 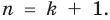 Пусть
Пусть 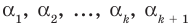 — попарно разные корни многочлена
— попарно разные корни многочлена 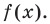 Поскольку
Поскольку 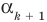 — корень
— корень 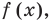 то
то 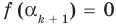 . Принимая во внимание равенство (1), которое выполняется согласно допущению индукции, получаем:
. Принимая во внимание равенство (1), которое выполняется согласно допущению индукции, получаем:
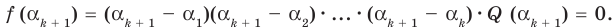
По условию все корни 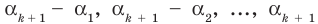 разные, поэтому ни одно из чисел
разные, поэтому ни одно из чисел 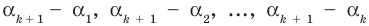 не равно нулю. Тогда
не равно нулю. Тогда 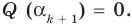 Таким образом,
Таким образом, 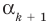 — корень многочлена
— корень многочлена 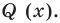 Тогда по теореме 2 многочлен
Тогда по теореме 2 многочлен 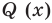 делится на
делится на 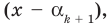 то есть
то есть 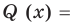
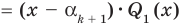 и из равенства (1) имеем
и из равенства (1) имеем

Это означает, что 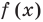 делится на произведение
делится на произведение
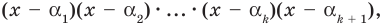 то есть теорема доказана и при
то есть теорема доказана и при 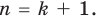
Таким образом, теорема справедлива для любого натурального 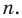
Следствие. Многочлен степени 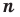 имеет не больше
имеет не больше 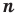 разных корней.
разных корней.
Допустим, что многочлен 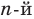 степени имеет
степени имеет 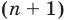 разных корней:
разных корней: 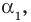
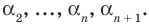 Тогда
Тогда 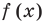 делится на произведение
делится на произведение 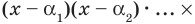
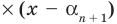 многочлен степени
многочлен степени 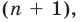 но это невозможно. Поэтому многочлен
но это невозможно. Поэтому многочлен 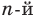 степени не может иметь больше чем
степени не может иметь больше чем 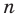 корней.
корней.
Пусть теперь многочлен 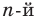 степени
степени 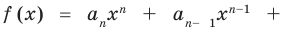
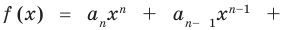 имеет
имеет 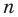 разных корней
разных корней 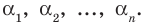 Тогда этот многочлен делится без остатка на произведение
Тогда этот многочлен делится без остатка на произведение 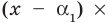
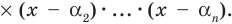 Это произведение является многочленом той же
Это произведение является многочленом той же
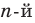 степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
степени. Таким образом, в результате деления можно получить только многочлен нулевой степени, то есть число. Таким образом,
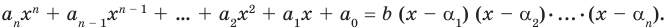 (2)
(2)
Если раскрыть скобки в правой части равенства (2) и приравнять коэффициенты при старших степенях, то получим, что 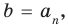 то есть
то есть
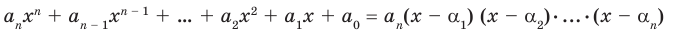 (3)
(3)
Сравнивая коэффициенты при одинаковых степенях 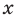 в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
в левой и правой частях тождества (3), получаем соотношения между коэффициентами уравнения и его корнями, которые называют формулами Виета:
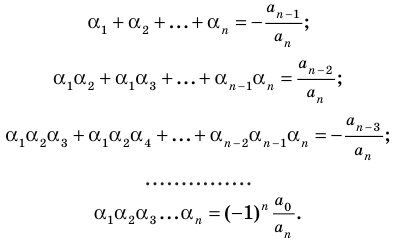 (4)
(4)
Например, при 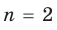 имеем:
имеем:
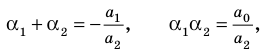
а при 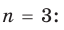
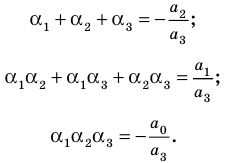 (5)
(5)
Выполнение таких равенств является необходимым и достаточным
условием того, чтобы числа 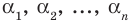 были корнями многочлена
были корнями многочлена
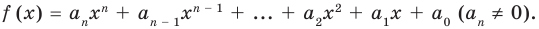
Формулы (3) и (4) справедливы не только для случая, когда все корни многочлена 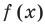 разные. Введем понятие кратного корня многочлена.
разные. Введем понятие кратного корня многочлена.
Если многочлен 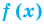 делится без остатка на
делится без остатка на 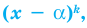 но не делится без остатка на
но не делится без остатка на 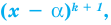 то говорят, что число
то говорят, что число  является корнем кратности
является корнем кратности  многочлена
многочлена 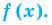
Например, если произведение  записать в виде многочлена, то для этого многочлена число
записать в виде многочлена, то для этого многочлена число 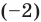 является корнем кратности 3, число 1 — корнем кратности 2, а число
является корнем кратности 3, число 1 — корнем кратности 2, а число 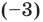 — корнем кратности 1.
— корнем кратности 1.
При использовании формул Виета в случае кратных корней необходимо каждый корень записать такое количество раз, которое равно его кратности.
Пример №3
Проверьте справедливость формул Виета для многочлена 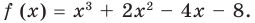
Решение:
► 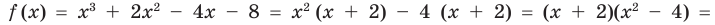
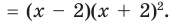
Поэтому 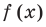 имеет корни:
имеет корни: 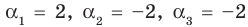 (поскольку
(поскольку 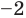 — корень кратности 2).
— корень кратности 2).
Проверим справедливость формулы (5). В нашем случае: 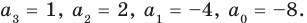 Тогда
Тогда
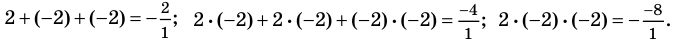
Как видим, все равенства выполняются, поэтому формулы Виета справедливы для данного многочлена.
Пример №4
Составьте квадратное уравнение, корнями которого являются квадраты корней уравнения 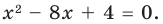
Решение:
► Обозначим корни уравнения 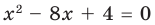 через
через 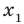 и
и 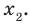 Тогда корнями искомого уравнения должны быть числа
Тогда корнями искомого уравнения должны быть числа 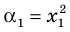 и
и 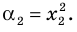 Поэтому искомое уравнение имеет вид
Поэтому искомое уравнение имеет вид 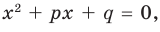 где
где
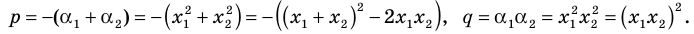
По формулам Виета имеем 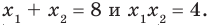 Отсюда находим, что
Отсюда находим, что 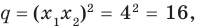 а
а 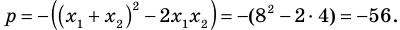 Таким образом, искомое уравнение имеет вид
Таким образом, искомое уравнение имеет вид 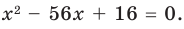
Схема Горнера
Делить многочлен 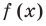 на двучлен
на двучлен 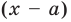 иногда удобно с помощью
иногда удобно с помощью
специальной схемы, которую называют схемой Горнера.
Пусть многочлен 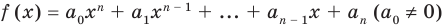 необходимо разделить на двучлен
необходимо разделить на двучлен 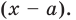 В результате деления многочлена
В результате деления многочлена 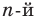 степени на многочлен первой степени получим некоторый многочлен
степени на многочлен первой степени получим некоторый многочлен 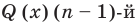 степени (то есть
степени (то есть 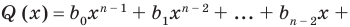
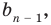 , где
, где 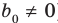 ) и остаток
) и остаток 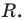 Тогда
Тогда 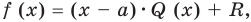 то есть
то есть
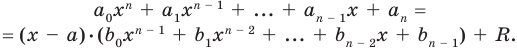
Левая и правая части полученного равенства тождественно равны, поэтому, перемножив многочлены, стоящие в правой части, можем приравнять коэффициенты при соответствующих степенях 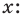
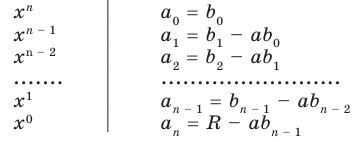
Найдем из этих равенств коэффициенты 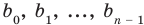 и остаток
и остаток 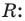

Как видим, первый коэффициент неполного частного равен первому коэффициенту делимого. Остальные коэффициенты неполного частного и остаток находятся одинаково: для того чтобы найти коэффициент 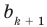 неполного частного, достаточно предыдущий найденный коэффициент
неполного частного, достаточно предыдущий найденный коэффициент 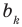 умножить на
умножить на 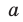 и добавить
и добавить 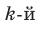 коэффициент делимого. Эту процедуру целесообразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.
коэффициент делимого. Эту процедуру целесообразно оформлять в виде специальной схемы-таблицы, которую называют схемой Горнера.

Пример №5
Разделите по схеме Горнера многочлен 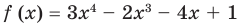 на двучлен
на двучлен 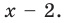
Решение:
► Запишем сначала все коэффициенты многочлена 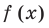 (если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:
(если в данном многочлене пропущена степень 2, то соответствующий коэффициент считаем равным 0), а потом найдем коэффициенты неполного частного и остаток по указанной схеме:

Таким образом, 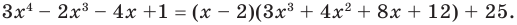
Пример №6
Проверьте, является ли 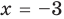 корнем многочлена
корнем многочлена 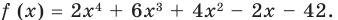
Решение:
► По теореме Безу остаток от деления многочлена 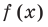 на
на 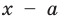 равен
равен 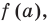 поэтому найдем с помощью схемы Горнера остаток от деления
поэтому найдем с помощью схемы Горнера остаток от деления 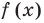 на
на 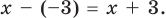

Поскольку 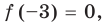 то
то 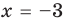 — корень многочлена
— корень многочлена 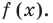
Нахождение рациональных корней многочлена с целыми коэффициентами
Теорема 4. Если многочлен с целыми коэффициентами 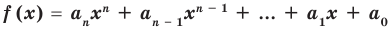 имеет рациональный корень
имеет рациональный корень 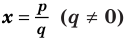 , то
, то 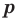 является делителем свободного члена
является делителем свободного члена 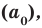 a
a 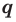 — делителем коэффициента при старшем члене
— делителем коэффициента при старшем члене 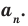
Если 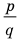 является корнем многочлена
является корнем многочлена 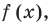 то
то 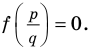 Подставляем
Подставляем
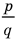 вместо
вместо 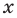 в
в 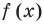 и из последнего равенства имеем
и из последнего равенства имеем
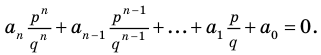 (1)
(1)
Умножим обе части равенства (1) на 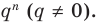 Получаем
Получаем
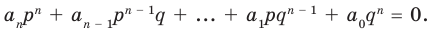 (2)
(2)
В равенстве (2) все слагаемые, кроме последнего, делятся на 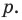 Поэтому
Поэтому 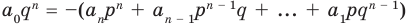 делится на
делится на 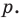
Но когда мы записываем рациональное число в виде 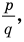 то эта дробь считается несократимой, то есть
то эта дробь считается несократимой, то есть 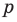 и
и 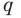 не имеют общих делителей. Произведение
не имеют общих делителей. Произведение 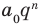 может делиться на
может делиться на 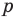 (если
(если 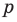 и
и 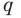 — взаимно простые числа) только тогда, когда
— взаимно простые числа) только тогда, когда 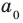 делится на
делится на 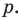 Таким образом,
Таким образом, 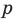 — делитель свободного члена
— делитель свободного члена 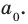
Аналогично все слагаемые равенства (2), кроме первого, делятся на 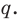 Тогда
Тогда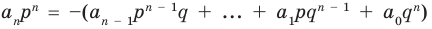 делится на
делится на 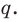 Поскольку
Поскольку 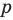 и
и 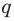 взаимно простые числа, то
взаимно простые числа, то 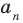 делится на
делится на 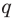 , следовательно,
, следовательно, 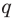 — делитель коэффициента при старшем члене.
— делитель коэффициента при старшем члене.
Отметим два следствия из этой теоремы. Если взять 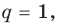 то корнем многочлена будет целое число
то корнем многочлена будет целое число 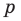 — делитель
— делитель 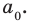 Таким образом, имеет место:
Таким образом, имеет место:
Следствие 1. Любой целый корень многочлена с целыми коэффициентами является делителем его свободного члена.
Если в заданном многочлене 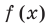 коэффициент
коэффициент 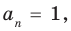 то делителями
то делителями 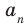 могут быть только числа
могут быть только числа 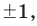 то есть
то есть 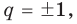 и имеет место:
и имеет место:
Следствие 2. Если коэффициент при старшем члене уравнения с целыми коэффициентами равен 1, то все рациональные корни этого уравнения (если они существуют) — целые числа.
Пример №7
Найдите рациональные корни многочлена 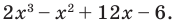
Решение:
► Пусть несократимая дробь 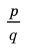 является корнем многочлена. Тогда
является корнем многочлена. Тогда 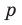 необходимо искать среди делителей свободного члена, то есть среди чисел
необходимо искать среди делителей свободного члена, то есть среди чисел 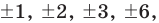 a
a 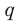 — среди делителей старшего коэффициента:
— среди делителей старшего коэффициента: 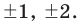
Таким образом, рациональные корни многочлена необходимо искать среди чисел 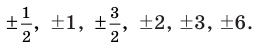 Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера.
Проверять, является ли данное число корнем многочлена, целесообразно с помощью схемы Горнера.
При 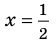 имеем следующую таблицу.
имеем следующую таблицу.
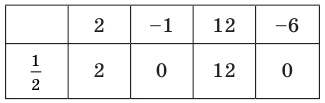
Кроме того, по схеме Горнера можно записать, что
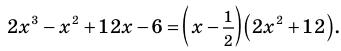
Многочлен 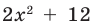 не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень
не имеет действительных корней (а тем более рациональных), поэтому заданный многочлен имеет единственный рациональный корень 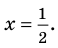
Пример №8
Разложите многочлен 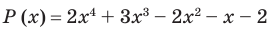 на множители.
на множители.
Решение:
► Ищем целые корни многочлена среди делителей свободного члена: 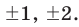
Подходит 1. Делим 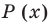 на
на  с помощью схемы Горнера.
с помощью схемы Горнера.
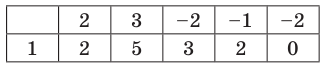
Тогда 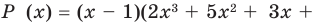
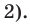
Ищем целые корни кубического многочлена 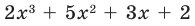 среди делителей его свободного члена:
среди делителей его свободного члена: 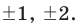 Подходит
Подходит 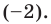 Делим на
Делим на 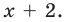

Имеем 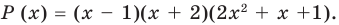
Квадратный трехчлен 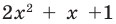 не имеет действительных корней и на линейные множители не раскладывается.
не имеет действительных корней и на линейные множители не раскладывается.
Ответ: 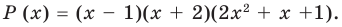
Отметим, что во множестве действительных чисел не всегда можно найти все корни многочлена (например, квадратный трехчлен 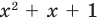 не имеет действительных корней). Таким образом, многочлен
не имеет действительных корней). Таким образом, многочлен 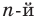 степени не всегда можно разложить на произведение линейных множителей. Но многочлен нечетной степени всегда можно разложить на произведение линейных и квадратных множителей, а многочлен четной степени — на произведение квадратных трехчленов.
степени не всегда можно разложить на произведение линейных множителей. Но многочлен нечетной степени всегда можно разложить на произведение линейных и квадратных множителей, а многочлен четной степени — на произведение квадратных трехчленов.
Например, многочлен четвертой степени раскладывается на произведение двух квадратных трехчленов. Для нахождения коэффициентов этого разложения иногда можно применить метод неопределенных коэффициентов.
Пример №9
Разложите на множители многочлен 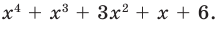
Решение:
► Попытка найти рациональные корни ничего не дает: многочлен не имеет рациональных (целых) корней.
Попытаемся разложить этот многочлен на произведение двух квадратных трехчленов. Поскольку старший коэффициент многочлена равен 1, то и у квадратных трехчленов возьмем старшие коэффициенты равными 1. То есть будем искать разложение нашего многочлена в виде:
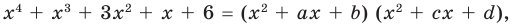 (3)
(3)
где 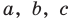 и
и 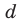 — неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях
— неопределенные (пока что) коэффициенты. Многочлены, стоящие в левой и правой частях этого равенства, тождественно равны, поэтому и коэффициенты при одинаковых степенях 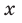 у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
у них равны. Раскроем скобки в правой части равенства и приравняем соответствующие коэффициенты. Это удобно записать так:
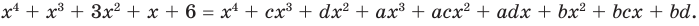
Получаем систему
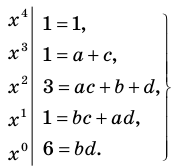 (4)
(4)
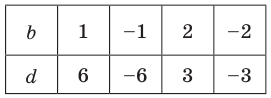
Попытка решить эту систему методом подстановки приводит к уравнению 4-й степени, поэтому попробуем решить систему (4) в целых числах. Из последнего равенства системы (4) получаем, что 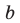 и
и 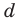 могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
могут быть только делителями числа 6. Все возможные варианты запишем в таблицу.
Коэффициенты 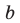 и
и 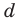 в равенстве (3) равноправны, поэтому мы не рассматриваем случаи
в равенстве (3) равноправны, поэтому мы не рассматриваем случаи 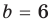 и
и 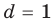 или
или 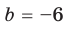 и
и 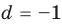 и т. д.
и т. д.
Для каждой пары значений 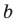 и
и 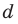 из третьего равенства системы (4) найдем
из третьего равенства системы (4) найдем 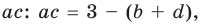 а из второго равенства имеем
а из второго равенства имеем 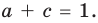 Зная
Зная 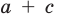 и
и 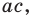 по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения
по теореме, обратной теореме Виета, находим а и с как корни квадратного уравнения. Найденные таким образом значения 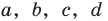 подставим в четвертое равенство системы (4)
подставим в четвертое равенство системы (4) 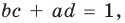 чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:
чтобы выбрать те числа, которые являются решениями системы (4). Удобно эти рассуждения оформить в виде таблицы:

Как видим, системе (4) удовлетворяет набор целых чисел 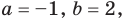
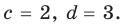 Тогда равенство (3) имеет вид
Тогда равенство (3) имеет вид
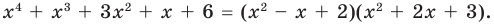 (5)
(5)
Поскольку квадратные трехчлены 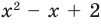 и
и 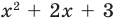 не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
не имеют не только рациональных, но и действительных корней, то равенство (5) дает окончательный ответ.
Деление многочлена на многочлен
Задача. Объём подарочных коробок, размеры которых даны в сантиметрах, можно смоделировать функцией 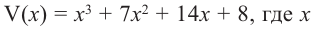 – положительное целое число и . Если высоты коробок можно определить при помощи линейной функции
– положительное целое число и . Если высоты коробок можно определить при помощи линейной функции 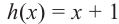 , то как можно выразить другие размеры коробки в виде многочлена? Вы сможете решить эту задачу, изучив правило деления многочлена на многочлен.
, то как можно выразить другие размеры коробки в виде многочлена? Вы сможете решить эту задачу, изучив правило деления многочлена на многочлен.
Исследование. Изучите, как правило деления многозначных чисел столбиком можно применить при делении многочлена.
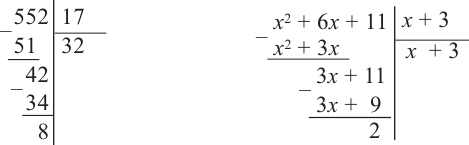
a) Для каждого из двух случаев укажите, какие числа и какие многочлены соответствуют понятиям делимое, делитель и частное.
b) Как был найден первый член при делении многочлена? Каковы сходные и отличительные черты данного деления и деления многозначных чисел?
c) Как вы убедились,что каждое из двух делений выполнено правильно?
Выражение вида 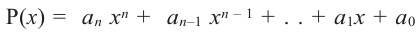 называется многочленом
называется многочленом 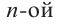 степени от одной переменной. Здесь
степени от одной переменной. Здесь 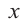 – переменная,
– переменная, 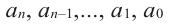 – определенные числа и
– определенные числа и 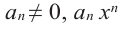 – старший член,
– старший член, 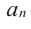 – коэффициент при старшем члене,
– коэффициент при старшем члене, 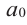 -свободный член. Многочлен можно разделить на многочлен аналогично правилу деления целых чисел столбиком.
-свободный член. Многочлен можно разделить на многочлен аналогично правилу деления целых чисел столбиком.
Деление целого числа па целое число можно проверить равенством
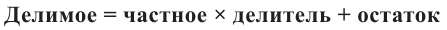
Аналогичное правило справедливо и при делении многочлена на многочлен. Если многочлен 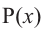 -делимое,
-делимое, 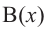 – делитель,
– делитель, 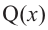 – неполное частное,
– неполное частное, 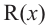 – остаток, то справедливо равенство
– остаток, то справедливо равенство
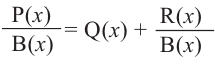 или
или 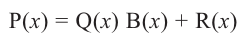 .
.
Здесь, степень многочлена 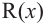 ниже степени многочлена
ниже степени многочлена 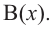 Если делителем является двучлен
Если делителем является двучлен 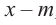 , то остатком может являться определенное число
, то остатком может являться определенное число 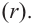
В этом случае: 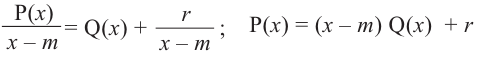
Пример №10
а) Разделите многочлен 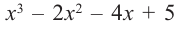 на двучлен
на двучлен 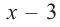 .
.
Ответ запишите в виде 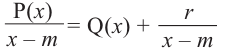
b) Определите множество допустимых значений переменной.
c) Выполните проверку.
Решение:
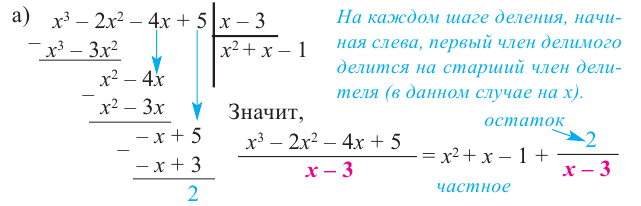
b) При этом 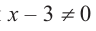 или
или 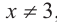 , иначе возникает деление на нуль.
, иначе возникает деление на нуль.
c) Должно выполняться тождество
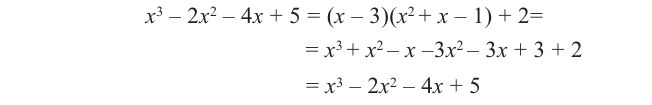
Пример №11
Разделите 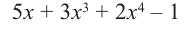 на многочлен
на многочлен 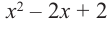 .
.
Решение:
запишем делимое в порядке убывания степеней. Введем в запись отсутствующие члены с коэффициентом равным 0. 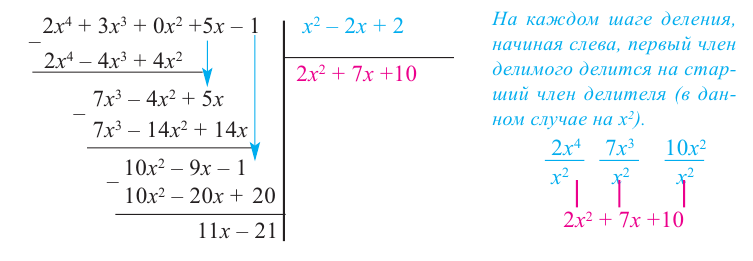
Пример №12
1) Исследуйте деление столбиком многочлена 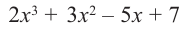 на двучлен
на двучлен 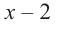 .
.
2) На каждом шаге деления делимое делится на старший член делителя, на 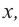 и результат записывается в частное. Установите, как можно найти первый член при делении на каждом из следующих шагов.
и результат записывается в частное. Установите, как можно найти первый член при делении на каждом из следующих шагов.
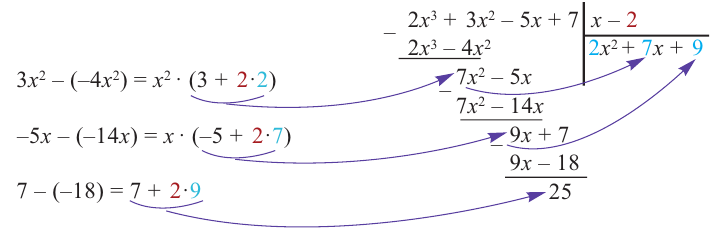 Правило синтетического деления многочлена на двучлен
Правило синтетического деления многочлена на двучлен 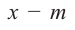 (схема Горнера)
(схема Горнера)
При делении многочлена на двучлен вида 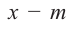 можно использовать метод, альтернативный делению столбиком – метод синтетического деления. При синтетическом делении, используя только коэффициенты, выполняется меньшее количество вычислений.
можно использовать метод, альтернативный делению столбиком – метод синтетического деления. При синтетическом делении, используя только коэффициенты, выполняется меньшее количество вычислений.
Пример №13
Разделите многочлен 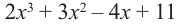 на двучлен
на двучлен 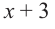 методом синтетического деления.
методом синтетического деления.
Решение:
коэффициенты делимого записываются в порядке убывания степеней (отсутствующий член записывается с коэффициентом равным нулю). Если двучлен имеет вид 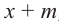 , то его записывают в виде
, то его записывают в виде 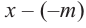 .
.
Запишем двучлен 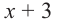 в виде
в виде 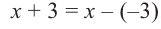 .
.
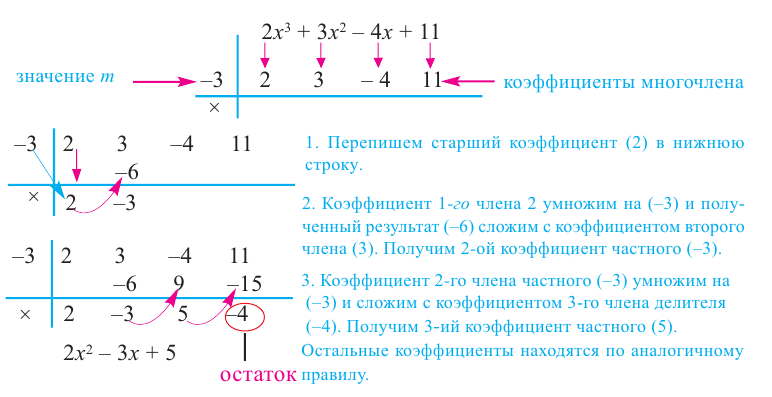
Таким образом, для делимого 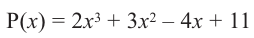 и делителя
и делителя 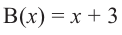 частным будет
частным будет 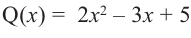 , а остатком
, а остатком 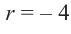 .
.
Деление можно записать в виде: 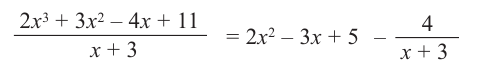 В общем случае, правило синтетического деления (или схема Горнера) многочлена и-ой степени на двучлен х -т приведено в таблице ниже.
В общем случае, правило синтетического деления (или схема Горнера) многочлена и-ой степени на двучлен х -т приведено в таблице ниже.
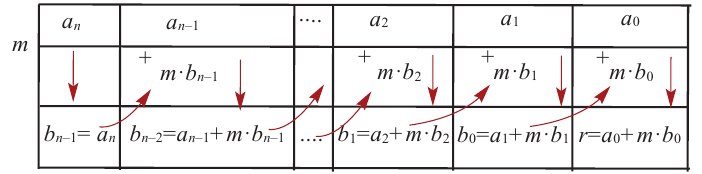
Теорема об остатке
Теорема об остатке (Теорема Безу)
Остаток от деления многочлена 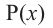 на двучлен
на двучлен 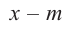 равен значению многочлена
равен значению многочлена 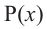 в точке
в точке 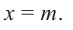
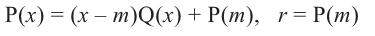
Доказательство: В равенстве 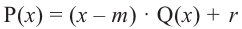 запишем
запишем 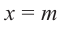 .
. 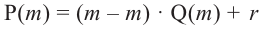 , тогда
, тогда 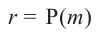 .
.
Пример №14
Найдите остаток от деления многочлена  на двучлен
на двучлен 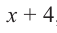 , применив теорему об остатке.
, применив теорему об остатке.
Решение: запишем делитель в виде 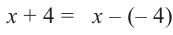 , тогда
, тогда 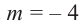 . По теореме об остатке получим, что остаток равен
. По теореме об остатке получим, что остаток равен 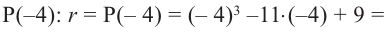
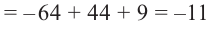 .
.
Проверим решение.
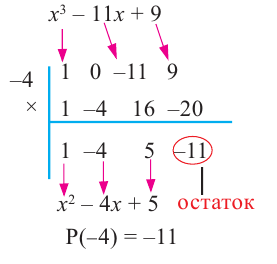
Теорема о разложении многочлена на множители
Значения переменной 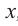 , которые обращают многочлен
, которые обращают многочлен 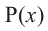 в нуль (т.е. корни уравнения
в нуль (т.е. корни уравнения 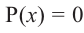 ), называются корнями (или нулями) многочлена.
), называются корнями (или нулями) многочлена.
Теорема. Если число 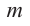 является корнем многочлена
является корнем многочлена 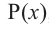 , то двучлен
, то двучлен 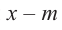 является множителем многочлена
является множителем многочлена 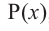 .
.
Действительно, если 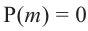 , то из равенства
, то из равенства 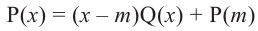 имеем
имеем 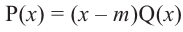 . Верно и обратное утверждение, т.е. если двучлен
. Верно и обратное утверждение, т.е. если двучлен 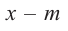 является множителем многочлена
является множителем многочлена 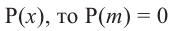 .
.
Пример №15
При помощи теоремы о разложении многочлена на множители определите, являются ли двучлены 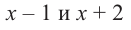 множителями многочлена
множителями многочлена 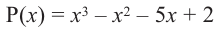 .
.
Решение: вычислим значение многочлена 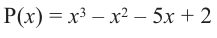 при
при 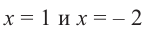 .
.
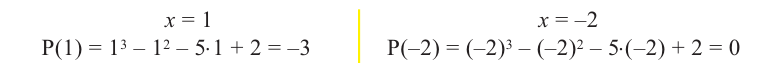
Значит, 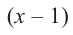 не является множителем, а
не является множителем, а 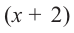 является одним из множителей данного многочлена.
является одним из множителей данного многочлена.
Пример №16
Зная, что 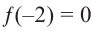 , разложите многочлен
, разложите многочлен 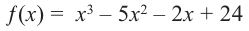 на множители.
на множители.
Решение: так как 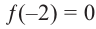 , то двучлен
, то двучлен 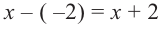 один из множителей многочлена
один из множителей многочлена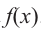 . Другой множитель найдем, используя метод синтетического деления.
. Другой множитель найдем, используя метод синтетического деления.
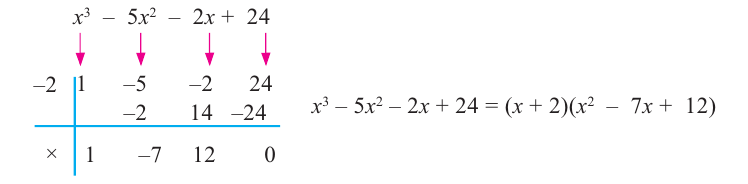
Учитывая, что 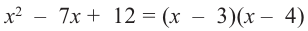 получим:
получим: 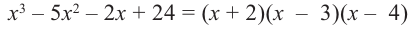 .
.
Отсюда получаем, что 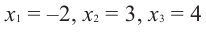 являются нулями многочлена.
являются нулями многочлена.
Примечание: Если многочлен задан в виде 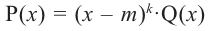 (здесь
(здесь 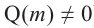 ), то число
), то число 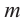 является
является 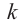 кратным корнем многочлена
кратным корнем многочлена 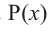 (повторяется
(повторяется 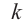 раз). Например, если разложение многочлена на множители имеет вид
раз). Например, если разложение многочлена на множители имеет вид 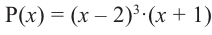 , то число
, то число 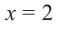 является корнем кратности 3.
является корнем кратности 3.
Нахождение рациональных корней
Теорема о рациональных корнях
Если для многочлена 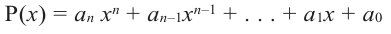 с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
с целыми коэффициентами существует рациональный корень, то этот корень имеет вид
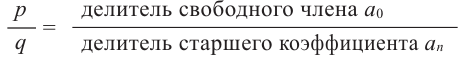
Доказательство. Пусть несократимая дробь 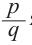 является корнем многочлена
является корнем многочлена 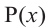 с целыми коэффициентами:
с целыми коэффициентами:
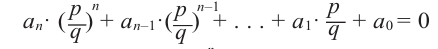
Умножим обе части равенства на 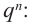
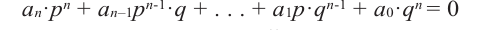
Так как в последнем равенстве каждый член, кроме члена 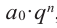 , содержит множитель
, содержит множитель 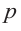 и каждый член, кроме члена
и каждый член, кроме члена 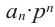 , содержит множитель
, содержит множитель 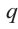 .то коэффициент
.то коэффициент 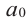 должен делится на
должен делится на 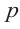 , а коэффициент
, а коэффициент 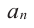 должен делится на
должен делится на 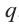 .
.
Пример №17
Найдите рациональные корни многочлена 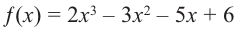 .
.
Решение: свободный член 6, старший коэффициент 2.
Для 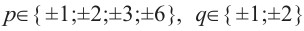 , запишем все возможные числа вида
, запишем все возможные числа вида 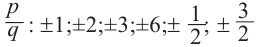
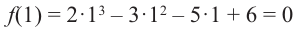 , т.е. одним из множителей является двучлен
, т.е. одним из множителей является двучлен 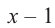 . Другие множители найдем, используя синтетическое деление:
. Другие множители найдем, используя синтетическое деление: 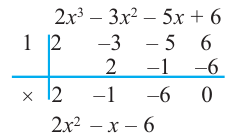
Так как, 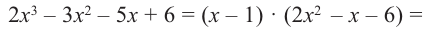
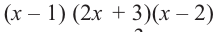 , получим, что
, получим, что 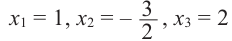 являются корнями многочлена.
являются корнями многочлена.
Следствие 1. Если старший коэффициент 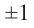 и многочлен имеет рациональный корень, то он является целым числом.
и многочлен имеет рациональный корень, то он является целым числом.
Следствие 2. Целые корни многочлена с целыми коэффициентами (если они имеются) являются делителями свободного члена.
Пример №18
Найдите корни многочлена 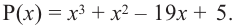
Решение: по теореме о рациональных корнях многочлена, целый корень данного многочлена (если он существует) надо искать среди делителей числа 5. Это числа ±5; ±1.
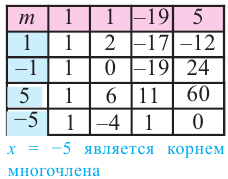
Запишем это короче при помощи синтетического деления и проверим, являются ли эти числа корнями многочлена.
Так как 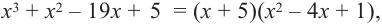 то, решив квадратное уравнение
то, решив квадратное уравнение 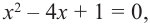 получим другие корни:
получим другие корни: 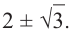 Значит данный многочлен третьей степени имеет три корня:
Значит данный многочлен третьей степени имеет три корня: 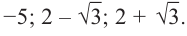
Внимание! Если коэффициенты многочлена являются рациональными числами, то для нахождения рациональных корней уравнения 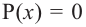 сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми. Например, для нахождения корней многочлена
сначала обе части уравнения надо умножить на такое число (отличное от нуля), чтобы коэффициенты стали целыми. Например, для нахождения корней многочлена
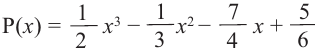 надо умножить все члены уравнения
надо умножить все члены уравнения 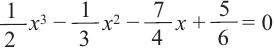 на 12, а затем решить полученное
на 12, а затем решить полученное
уравнение 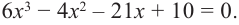
Для нахождения рациональных корней выполните следующие действия.
1. Записывается множество всех возможных дробей, числителями которых являются делители свободного члена, а знаменателями являются делители старшего коэффициента.
2. Из этих чисел выбирается число 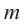 (обращающее значение многочлена в нуль), которое является корнем многочлена, т. е. определяется двучлен
(обращающее значение многочлена в нуль), которое является корнем многочлена, т. е. определяется двучлен 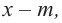 на который многочлен делится без остатка.
на который многочлен делится без остатка.
3. Для данного многочлена при помощи синтетического деления на двучлен 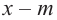 определяется другой множитель.
определяется другой множитель.
4. Если другой множитель является квадратным трехчленом или его можно разложить при помощи формул сокращенного умножения, находятся другие корни. Иначе все линейные множители находятся синтетическим делением.
5. Возможно, что ни одно число из списка не будет нулем многочлена. В этом случае многочлен не имеет рациональных корней. Например, рациональными корнями многочлена 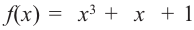 могут являться числа ±1.
могут являться числа ±1.
Проверим: 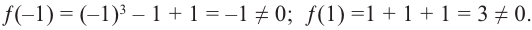 Значит, многочлен
Значит, многочлен 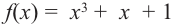 не имеет рациональных корней.
не имеет рациональных корней.
Основная теорема алгебры
Покажем на примере, что многочлен 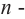 ой степени имеет
ой степени имеет 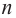 корней.
корней.
Пример №19
Найдите все корни многочлена 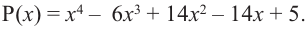
Решение: рациональными корнями данного многочлена (если они существуют), согласно правилу, могут являться числа ±1, ±5. Проверим:
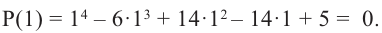
Значит, 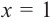 является корнем данного многочлена
является корнем данного многочлена 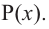 Другие корни найдем синтетическим делением.
Другие корни найдем синтетическим делением.
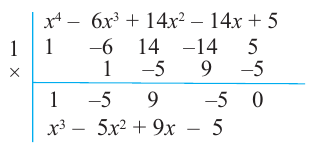
В выражении 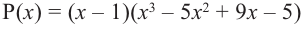 для множителя
для множителя 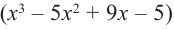 вновь применим теорему о рациональных корнях и синтетическое деление. Тогда
вновь применим теорему о рациональных корнях и синтетическое деление. Тогда 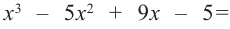
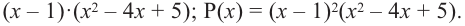 Решим уравнение
Решим уравнение 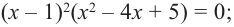
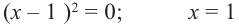 ( корень кратности 2);
( корень кратности 2);
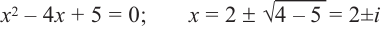
Корни: 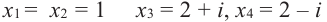
Во всех рассмотренных нами примерах уравнение 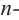 ой степени всегда имеет
ой степени всегда имеет 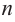 корней, включая кратные корни (действительных или комплексных).
корней, включая кратные корни (действительных или комплексных).
Теорема. Любой многочлен ненулевой степени имеет хотя бы один корень на множестве комплексных чисел.
Если 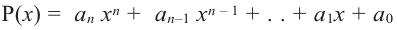 является многочленом ненулевой степени с комплексными коэффициентами, то согласно основной теореме алгебры, у него есть хотя бы один корень
является многочленом ненулевой степени с комплексными коэффициентами, то согласно основной теореме алгебры, у него есть хотя бы один корень 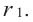 По теореме о разложении многочлена на множители получим
По теореме о разложении многочлена на множители получим 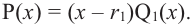 При этом многочлен
При этом многочлен 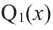 имеет степень
имеет степень 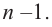 Если
Если 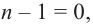 то
то 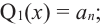 если
если 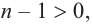 то согласно той же теореме, многочлен
то согласно той же теореме, многочлен 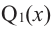 имеет хотя бы один корень. Обозначим его через
имеет хотя бы один корень. Обозначим его через 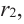 тогда справедливо разложение
тогда справедливо разложение 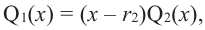 где
где 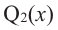 – многочлен степени
– многочлен степени 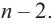 Значит, можно записать
Значит, можно записать 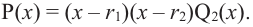 Аналогично, если
Аналогично, если 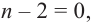 то
то 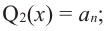 при
при 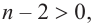 на основании той же теоремы, многочлен
на основании той же теоремы, многочлен 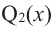 имеет хотя бы один корень. Обозначим его через
имеет хотя бы один корень. Обозначим его через 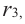 получим
получим 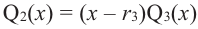 т. е. можно записать
т. е. можно записать 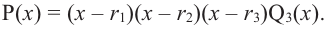
Продолжая процесс 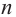 раз, получаем
раз, получаем 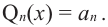 Тогда для многочлена
Тогда для многочлена 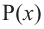 можно записать следующее разложение:
можно записать следующее разложение:
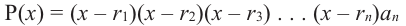
здесь числа  являются нулями многочлена
являются нулями многочлена 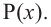 Эти нули могут и не быть различными.
Эти нули могут и не быть различными.
Следствие. Многочлен 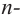 ой степени
ой степени 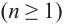 на множестве комплексных чисел имеет ровно
на множестве комплексных чисел имеет ровно 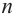 корней, включая кратные корни.
корней, включая кратные корни.
Отметим, что если комплексное число 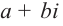 является корнем многочлена с действительными коэффициентами, то сопряженное комплексное число
является корнем многочлена с действительными коэффициентами, то сопряженное комплексное число 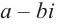 гак же является корнем данного многочлена.
гак же является корнем данного многочлена.
Любой многочлен с действительными коэффициентами можно представить в виде произведения двучленов вида 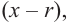 соответствующих действительным корням, и трехчленов вида
соответствующих действительным корням, и трехчленов вида 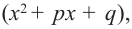 соответствующих сопряженным комплексным корням.
соответствующих сопряженным комплексным корням.
Отсюда можно сделать вывод, что многочлен нечетной степени с действительными коэффициентами всегда имеет действительные корни.
Пример №20
Запишите в виде произведения множителей многочлен наименьшей степени, если коэффициент при старшем члене равен 2, а корни равны 3 и 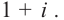
Решение: так как число 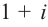 является корнем многочлена, то сопряженное комплексное число
является корнем многочлена, то сопряженное комплексное число 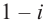 также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде
также является корнем этого многочлена. Тогда искомый многочлен можно записать в виде
- Заказать решение задач по высшей математике
Пример №21
При движении скоростной карусели в Лунапарке изменение высоты (в метрах) кабины от нулевого уровня за первые 5 секунд можно смоделировать функцией 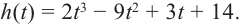 В какие моменты в течении 5 секунд после начала движения кабина карусели находилась на нулевом уровне?
В какие моменты в течении 5 секунд после начала движения кабина карусели находилась на нулевом уровне?
Решение: во всех случаях, кроме значений 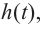 равных нулю, кабина карусели находится либо ниже, либо выше нулевого уровня. Значит, мы должны найти корни заданного многочлена. Применим правило нахождения рациональных корней.
равных нулю, кабина карусели находится либо ниже, либо выше нулевого уровня. Значит, мы должны найти корни заданного многочлена. Применим правило нахождения рациональных корней.
1. Проверим, является ли число 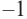 корнем.
корнем.
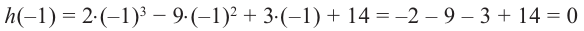
2. Число 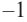 является корнем, значит одним из множителей данного многочлена является
является корнем, значит одним из множителей данного многочлена является 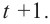 Другие корни найдем при помощи синтетического деления.
Другие корни найдем при помощи синтетического деления.
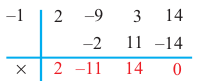
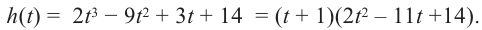
Учитывая, что 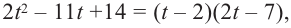 запишем многочлен в виде
запишем многочлен в виде 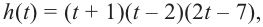 т. е.
т. е. 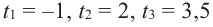 являются корнями уравнения. Значения
являются корнями уравнения. Значения 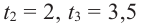 принадлежат временному интервалу в 5 секунд, и в этих моментах кабина карусели находилась на нулевом уровне. То, что корни найдены верно показывает график многочлена, построенный при помощи графкалькулягора.
принадлежат временному интервалу в 5 секунд, и в этих моментах кабина карусели находилась на нулевом уровне. То, что корни найдены верно показывает график многочлена, построенный при помощи графкалькулягора.
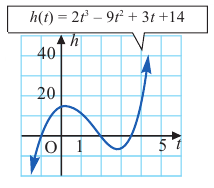
Функция-многочлен
График функции-многочлен
В стандартном виде функция – многочлен записывается как 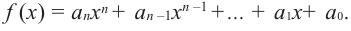 В частном случае, при
В частном случае, при 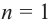 получаем линейную функцию (график – прямая линия), при
получаем линейную функцию (график – прямая линия), при 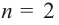 получаем квадратичную функцию (график- парабола). Любой многочлен определен на множестве действительных чисел и его графиком является непрерывная (сплошная) линия.
получаем квадратичную функцию (график- парабола). Любой многочлен определен на множестве действительных чисел и его графиком является непрерывная (сплошная) линия.
При возрастании значений аргумента по абсолютному значению многочлен ведет себя как функция старшего члена 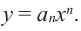 Ниже показаны примеры графиков функции – многочлен и их свойства.
Ниже показаны примеры графиков функции – многочлен и их свойства.
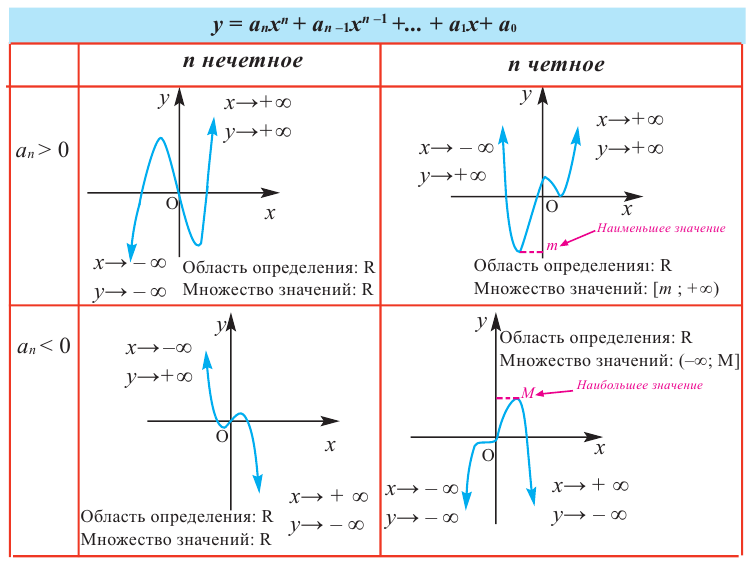
Пример №22
Определите характер поведения функции – многочлен в зависимости от степени и коэффициента при старшем члене при возрастании аргумента по абсолютному значению.
a) 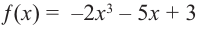 б)
б) 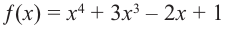
Решение: а) степень многочлена 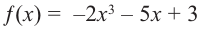 нечетная (равна 3). Коэффициент старшего члена равен
нечетная (равна 3). Коэффициент старшего члена равен 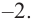 По таблице видно, что в данном случае при
По таблице видно, что в данном случае при 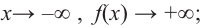 а при
а при 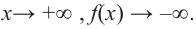
b) степень многочлена 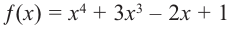 четная (равна 4). Коэффициент старшего члена равен 1. В данном случае при
четная (равна 4). Коэффициент старшего члена равен 1. В данном случае при 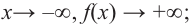 при
при 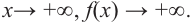
Пример №23
По графику определите как ведет себя функция – многочлен при неограниченном возрастании аргументов но абсолютному значению, четность или нечетность степени многочлена, знак коэффициента старшего члена.
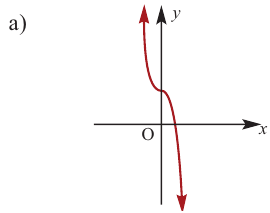
Решение:
при 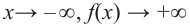
при 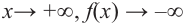
Многочлен нечетной степени
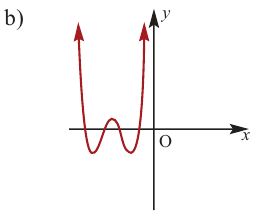
Решение:
при 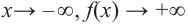
при 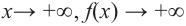
Многочлен четной степени
Отметим, что если 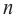 нечетно, то функция – многочлен имеет хотя бы один действительный нуль, если
нечетно, то функция – многочлен имеет хотя бы один действительный нуль, если 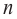 четно, то их вообще может и не быть.
четно, то их вообще может и не быть.
Алгоритм построения эскиза графика функции – многочлен.
1. Находятся точки пересечения графика с осями координат (если они есть). Эти точки отмечаются на координатной плоскости.
2. Вычисляются значения функции в некоторых точках между действительными нулями. Соответствующие точки отмечаются на координатной плоскости.
3. Определяется поведение графика при больших значениях аргумента по абсолютному значению.
4. На основе полученных данных строят схематически график.
Пример №24
Постройте график функции 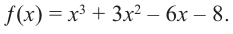
Решение:
1. Применим теорему о рациональных корнях. Разложим многочлен на множители и найдем нули функции.
По теореме возможные рациональные нули надо искать среди чисел, которые являются делителями числа 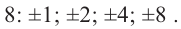
Проверим 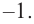
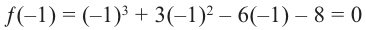
Значит, двучлен 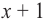 является одним из множителей. Остальные множители найдем синтетическим делением.
является одним из множителей. Остальные множители найдем синтетическим делением.
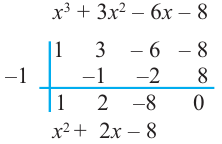
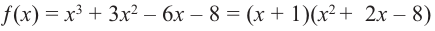
Зная, что 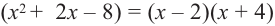 запишем все линейные множители многочлена:
запишем все линейные множители многочлена: 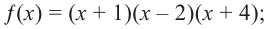
Отсюда находим нули 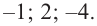 Т. е. график пересекает ось абсцисс в точках
Т. е. график пересекает ось абсцисс в точках 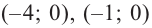 и
и 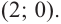 Так как
Так как 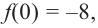 то точка
то точка 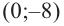 является точкой пересечения с осью
является точкой пересечения с осью 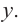 Отметим эти точки на координатной плоскости.
Отметим эти точки на координатной плоскости.
2. Найдем еще несколько значений функции в точках, не требующих сложных вычислений. Например, в точках 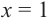 и
и 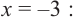
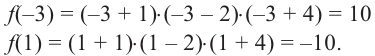
Отметим точки 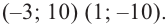
3. Определим, как меняется график при уменьшении или увеличении значений 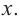 Степень при старшем члене равна 3, а коэффициент положителен, функция нечетная. Значит, при
Степень при старшем члене равна 3, а коэффициент положителен, функция нечетная. Значит, при 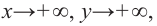 при
при 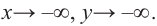
4. Соединим отмеченные точки и получим схематический график функции 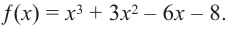
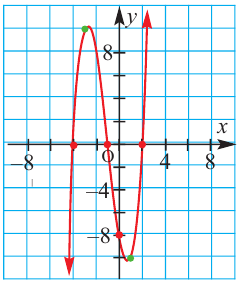
Рациональная функция
Рациональной функцией называется функция, которою можно представить в виде отношения двух многочленов:
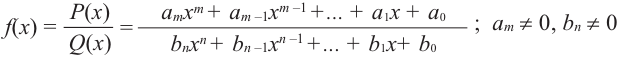
Самым простым примером рациональной функции является функция 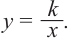
График функции 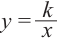 называется гиперболой.
называется гиперболой.
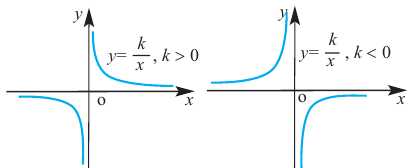
При стремлении значений 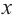 к нулю точки гиперболы стремятся к оси ординат, т е. к прямой
к нулю точки гиперболы стремятся к оси ординат, т е. к прямой 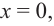 при неограниченном увеличении
при неограниченном увеличении 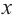 но абсолютному значению точки гиперболы неограниченно приближаются к оси абсцисс, т. е. к прямой
но абсолютному значению точки гиперболы неограниченно приближаются к оси абсцисс, т. е. к прямой 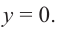 Прямая
Прямая 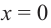 называется вертикальной асимптотой, а прямая
называется вертикальной асимптотой, а прямая 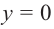 называется горизонтальной асимптотой гиперболы
называется горизонтальной асимптотой гиперболы 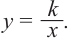 При параллельном переносе гиперболы
При параллельном переносе гиперболы 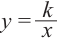 на вектор
на вектор 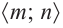 получается график функции
получается график функции 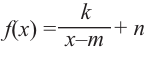 . В этом случае начало координат преобразуется в точку
. В этом случае начало координат преобразуется в точку 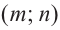 и вертикальной асимптотой становится прямая
и вертикальной асимптотой становится прямая 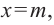 а горизонтальной- прямая
а горизонтальной- прямая 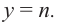
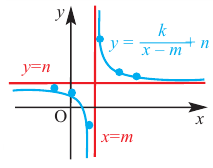
Пример №25
Постройте график функции 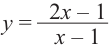
Решение: точки пересечения с осью 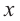 найдем из уравнения
найдем из уравнения 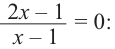
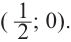
При 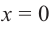 получим
получим 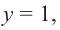 и график пересекает ось
и график пересекает ось 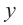 в точке
в точке 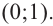 Разделим почленно числитель функции на знаменатель и запишем ее в виде
Разделим почленно числитель функции на знаменатель и запишем ее в виде 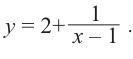 Прямая
Прямая 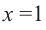 является вертикальной асимптотой, а прямая
является вертикальной асимптотой, а прямая 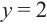 – горизонтальной асимптотой. Зададим таблицу значений для нескольких точек справа и слева от вертикальной асимптоты
– горизонтальной асимптотой. Зададим таблицу значений для нескольких точек справа и слева от вертикальной асимптоты
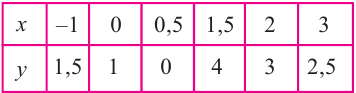
Отметим на координатной плоскости точки, соответствующие парам значений из таблицы и, учитывая горизонтальную и вертикальную асимптоту, изобразим ветви гиперболы, которые пересекают координатные оси в точках 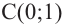 и
и 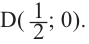
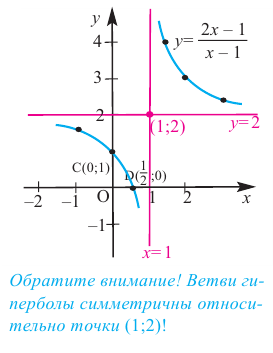
В общем случае, для построения графика рациональной функции надо найти точки пересечения с осями координат (если они есть) и ее асимптоты. Если выражение, которое задает рациональную функцию, имеет вид дроби, знаменатель которой обращается в нуль в точке 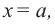 а числитель отличен от нуля, то данная функция имеет вертикальную асимптоту. Горизонтальные асимптоты для рациональной функции
а числитель отличен от нуля, то данная функция имеет вертикальную асимптоту. Горизонтальные асимптоты для рациональной функции 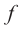 определяются в соответствии со степенью
определяются в соответствии со степенью 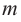 и
и 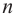 данных многочленов
данных многочленов 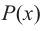 и
и 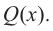
Для 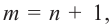 т. е. если степень многочлена в числителе на 1 единицу больше степени многочлена в знаменателе, частное, полученное при делении, имеет вид
т. е. если степень многочлена в числителе на 1 единицу больше степени многочлена в знаменателе, частное, полученное при делении, имеет вид 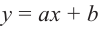 и является линейной функцией. При возрастании
и является линейной функцией. При возрастании 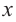 по абсолютному значению график функции приближается к данной прямой. В этом случае говорят, что прямая
по абсолютному значению график функции приближается к данной прямой. В этом случае говорят, что прямая 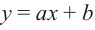 является наклонной асимптотой.
является наклонной асимптотой.
Пример №26
Найдите асимптоты и схематично изобразите график функции
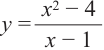
Решение: Точки пересечения с осью 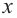 найдем из уравнения
найдем из уравнения 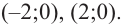 При
При 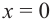 получим
получим 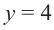 и график пересекает ось
и график пересекает ось 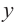 в точке
в точке 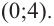 При
При 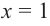 знаменатель обращается в нуль, а числитель отличен от нуля. Значит, прямая
знаменатель обращается в нуль, а числитель отличен от нуля. Значит, прямая 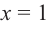 является вертикальной асимптотой. Горизонтальной асимптоты у данной функции нет
является вертикальной асимптотой. Горизонтальной асимптоты у данной функции нет 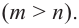 Разделив числитель на знаменатель, запишем функцию в виде:
Разделив числитель на знаменатель, запишем функцию в виде:
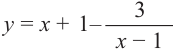
Для больших, но модулю, значений 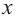 дробь
дробь 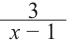 по абсолютному значению уменьшается и график заданной функции бесконечно приближается к прямой
по абсолютному значению уменьшается и график заданной функции бесконечно приближается к прямой 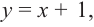 т. е. прямая
т. е. прямая 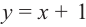 является наклонной асимптотой данной функции. Составим таблицу значений для некоторых точек слева и справа от вертикальной оси.
является наклонной асимптотой данной функции. Составим таблицу значений для некоторых точек слева и справа от вертикальной оси.
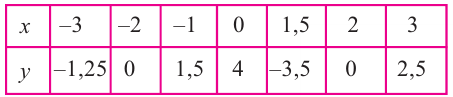
Отметим точки, координаты которых соответствуют парам из таблицы. Учитывая вертикальную и наклонную асимптоту, схематично изобразим график функции.
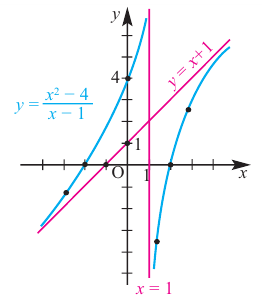
Многочлены в линейной алгебре
Многочленом от переменной х степени n называется выражение вида:
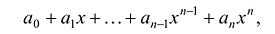 , где
, где 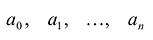 – действительные или комплексные числа, называемые коэффициентами, n – натуральное число, х – переменная величина, принимающая произвольные числовые значения.
– действительные или комплексные числа, называемые коэффициентами, n – натуральное число, х – переменная величина, принимающая произвольные числовые значения.
Если коэффициент 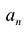 при
при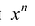 многочлена
многочлена 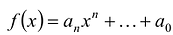 отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число n называется степенью многочлена,
отличен от нуля, а коэффициенты при более высоких степенях равны нулю, то число n называется степенью многочлена, 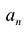 – старшим коэффициентом, а
– старшим коэффициентом, а 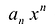 – старшим членом многочлена. Коэффициент
– старшим членом многочлена. Коэффициент 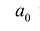 называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
называется свободным членом. Если все коэффициенты многочлена равны нулю, то многочлен называется нулевым и обозначается 0. Степень нулевого многочлена не определена.
Два многочлена называются равными, если они имеют одинаковую степень и коэффициенты при одинаковых степенях равны.
Суммой многочленов 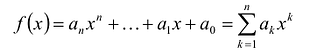 и
и 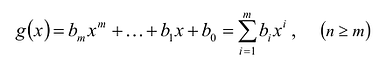 называется многочлен
называется многочлен
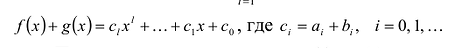
Произведением многочленов 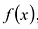 и
и 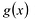 называется многочлен:
называется многочлен: 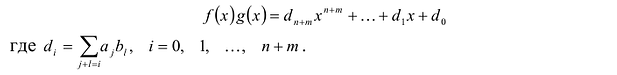
Легко проверить, что сложение и умножение многочленов ассоциативно, коммутативно и связаны между собой законом дистрибутивности.
Многочлен 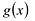 называется делителем многочлена
называется делителем многочлена 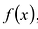 , если существует многочлен
, если существует многочлен 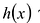 такой, что
такой, что 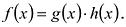
Теорема о делении с остатком
Для любых многочленов 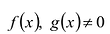 существуют многочлены
существуют многочлены 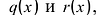 такие, что
такие, что 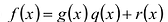 причем степень
причем степень 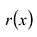 меньше степени g(x) или
меньше степени g(x) или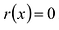 . Многочлены g(x) и r(x) определены однозначно.
. Многочлены g(x) и r(x) определены однозначно.
Многочлены g(x) и r(x) называются соответственно частным и остатком. Если g(x) делит  , то остаток
, то остаток 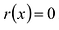 .
.
Число с называется корнем многочлена  , если
, если  .
.
Теорема Безу
Число с является корнем многочлена  тогда и только тогда, когда
тогда и только тогда, когда  делится на x – с.
делится на x – с.
Пусть с – корень многочлена  , т.е.
, т.е. . Разделим
. Разделим  на
на
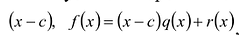 где степень r(х) меньше степени (x-с) которая равна 1. Значит, степень г(х) равна 0, т.е. r(х) = const. Значит,
где степень r(х) меньше степени (x-с) которая равна 1. Значит, степень г(х) равна 0, т.е. r(х) = const. Значит, 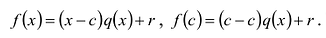 . Так как
. Так как  , то из последнего равенства следует, что r=0, т.е.
, то из последнего равенства следует, что r=0, т.е. 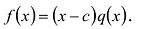
Обратно, пусть (х-с) делит  , т.е.
, т.е. 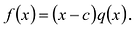 . Тогда
. Тогда 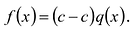
Следствие. Остаток от деления многочлена  на (x-с) равен
на (x-с) равен 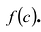 .
.
Многочлены первой степени называются линейными многочленами. Теорема Безу показывает, что разыскание корней многочлена  равносильно разысканию его линейных делителей со старшим коэффициентом 1.
равносильно разысканию его линейных делителей со старшим коэффициентом 1.
Многочлен  можно разделить на линейный многочлен х-с с помощью алгоритма деления с остатком, но существует более удобный способ деления, известный под названием схемы Горнера.
можно разделить на линейный многочлен х-с с помощью алгоритма деления с остатком, но существует более удобный способ деления, известный под названием схемы Горнера.
Пусть 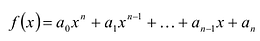 и пусть
и пусть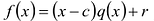 где
где 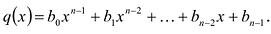 Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и правой частях последнего равенства, имеем:
Сравнивая коэффициенты при одинаковых степенях неизвестной с левой и правой частях последнего равенства, имеем:
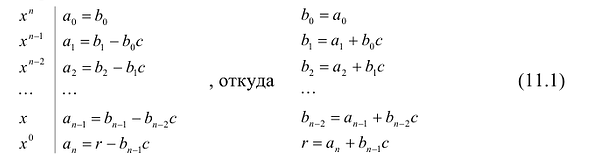
Число с-называется корнем кратности к многочлена  , если
, если 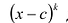 делит
делит  , но
, но 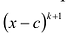 уже не делит
уже не делит  .
.
Чтобы поверить, будет ли число с корнем многочлена  и какой кратности, можно воспользоваться схемой Горнера. Сначала
и какой кратности, можно воспользоваться схемой Горнера. Сначала  делится на х-с, затем, если остаток равен нулю, полученное частное делится на х-с, и т.д. до получения не нулевого остатка.
делится на х-с, затем, если остаток равен нулю, полученное частное делится на х-с, и т.д. до получения не нулевого остатка.
Число различных корней многочлена не превосходит его степени.
Большое значение имеет следующая основная теорема.
Основная теорема. Всякий многочлен с числовыми коэффициентами ненулевой степени имеет хотя бы один корень (может быть комплексный).
Следствие. Всякий многочлен степени 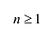 имеет в С (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.
имеет в С (множестве комплексный чисел) столько корней, какова его степень, считая каждый корень столько раз, какова его кратность.

где 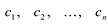 – корни
– корни  , т.е. во множестве С всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то:
, т.е. во множестве С всякий многочлен разлагается в произведение линейных множителей. Если одинаковые множители собрать вместе, то: 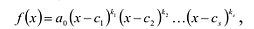 где
где 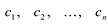 уже различные корни
уже различные корни  ,
, 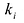 – кратность корня
– кратность корня 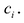
Если многочлен 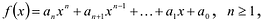 , с действительными коэффициентами имеет корень с, то число с также корень
, с действительными коэффициентами имеет корень с, то число с также корень 
Значит, у многочлена с действительными коэффициентами комплексные корни входят парами.
Следствие. Многочлен с действительными коэффициентами нечетной степени имеет нечетное число действительных корней.
Пусть 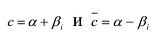 корни
корни  Тогда
Тогда  делится на х-с и
делится на х-с и 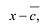 , но так как у
, но так как у 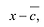 и х-с, нет общих делителей, то
и х-с, нет общих делителей, то  делится на произведение
делится на произведение 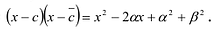
Утверждение 2. Многочлен с действительными коэффициентами степени 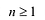 всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
всегда разлагается на множестве действительных чисел в произведение линейных многочленов, отвечающих его вещественным корням, и многочленов 2-ой степени, отвечающих паре сопряженных комплексных корней.
При вычислении интегралов от рациональных функций нам понадобится представление рациональной дроби в виде суммы простейших.
Рациональной дробью называется дробь где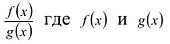 многочлены с действительными коэффициентами, причем многочлен
многочлены с действительными коэффициентами, причем многочлен 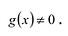 Рациональная дробь
Рациональная дробь  называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде
называется правильной, если степень числителя меньше степени знаменателя. Если рациональная дробь не является правильной, то, произведя деление числителя на знаменатель по правилу деления многочленов, ее можно представить в виде 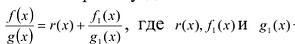 некоторые многочлены, а
некоторые многочлены, а 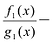 правильная рациональная дробь.
правильная рациональная дробь.
Лемма 1, Если  правильная рациональная дробь, а число
правильная рациональная дробь, а число 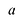 является вещественным корнем кратности
является вещественным корнем кратности 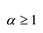 многочлена
многочлена 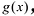 , т.е.
, т.е.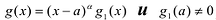 , то существует вещественное число A и многочлен
, то существует вещественное число A и многочлен 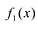 с вещественными коэффициентами, такие, что
с вещественными коэффициентами, такие, что 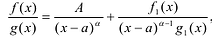 где дробь
где дробь 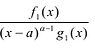 является правильной.
является правильной.
При этом несложно показать, что полученное выражение является рациональной дробью с вещественными коэффициентами.
Лемма 2. Если  правильная рациональная дробь, а число
правильная рациональная дробь, а число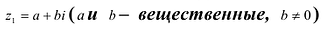 является корнем кратности
является корнем кратности 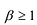 многочлена g(x), т.е.
многочлена g(x), т.е. 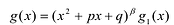 и если
и если 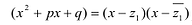 , то существуют вещественные числа M и N многочлен
, то существуют вещественные числа M и N многочлен 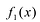 с вещественными коэффициентами, такие,
с вещественными коэффициентами, такие, 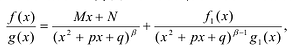 где дробь ,
где дробь , 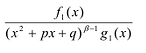 также является правильной.
также является правильной.
Рациональные дроби вида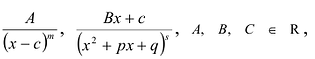
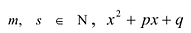 – трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
– трехчлен с действительными коэффициентами, не имеющий действительных корней, называются простейшими (или элементарными) дробями.
Всякая правильная рациональная дробь представима единственным образом в виде суммы простейших дробей.
При практическом получении такого разложения оказывается удобным так называемый метод неопределенных коэффициентов.
Он состоит в следующем:
При этом если степень многочлена 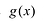 равна n, то в числителе после приведения к общему знаменателю получается многочлен степени n-1, т.е. многочлен
равна n, то в числителе после приведения к общему знаменателю получается многочлен степени n-1, т.е. многочлен 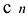 коэффициентами.
коэффициентами.
Число неизвестных 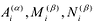 ‘ также равняется n:
‘ также равняется n: 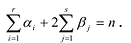
Таким образом, получается система n уравнений с n неизвестными. Существование решения у этой системы следует из приведенной выше теоремы.
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
- Линейное программирование
- Дифференциальное исчисление функций одной переменной
- Кривые второго порядка
- Евклидово пространство
- Матрица – виды, операции и действия с примерами
- Линейный оператор – свойства и определение
