Как составить многочлен жегалкина - Сайт, где вы сможете решить свои вопросы

Что нам стоит полином Жегалкина построить…

Время на прочтение
2 мин

Количество просмотров 129K

Думаю, каждый, кто изучал или изучает в университете дискретную математику, знаком с понятием многочлена Жегалкина.

Главная особенность этих многочленов состоит в том, что любую булеву функцию можно представить полиномом Жегалкина, причем единственным образом.

Чаще всего для построения полиномов Жегалкина студентам предлагаются два метода построения таких полиномов: метод неопределенных коэффициентов и метод эквивалентных преобразований.

Расчеты с использованием данных методов часто оказываются громоздкими. По невнимательности допустить ошибку не составляет труда.

Под катом приведен один удобный алгоритм, для построения полиномов Жегалкина, который студенты воспринимают «на ура», т.к. требует только выполнение «механических действий» без применения каких-либо умственных усилий. Краткое описание метода можно найти в Википедии, но на мой взгляд по нему не совсем понятно, как быстро проводить вычисления. Мне метод известен под названием «метод треугольника Паскаля».

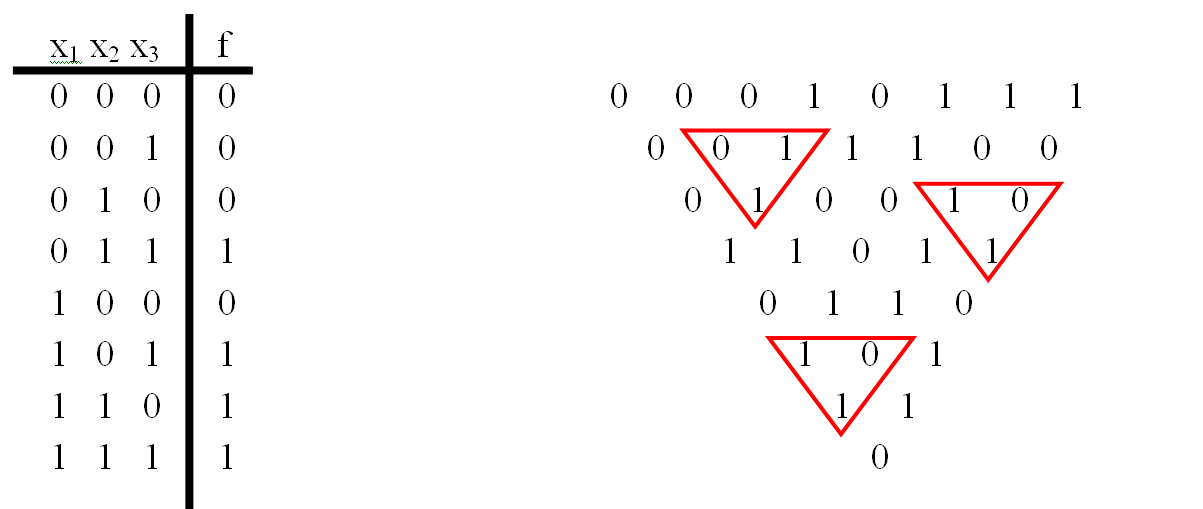
Порядок проведения вычислений проще показать на примере. Далее я буду по шагам показывать, как должен выглядеть расчет на бумаге (или как его удобно проводить).

Метод треугольника Паскаля

Требуется построить полином Жегалкина для функции f. Для примера, в качестве функции f возьмем функцию голосования .

Шаг 1. Строим таблицу значений функции (строки в таблице идут в порядке возрастания двоичных кодов). Таблицу лучше разместить в левой части листа.

Шаг 2. Построение треугольника.

Для этого берем вектор значения функции и выписываем его напротив первой строки таблицы:

Далее заполняем треугольник, складывая попарно соседние значения по модулю 2, результат сложения выписываем ниже.

Продолжаем вычисления, пока в строке не останется лишь одна цифра.

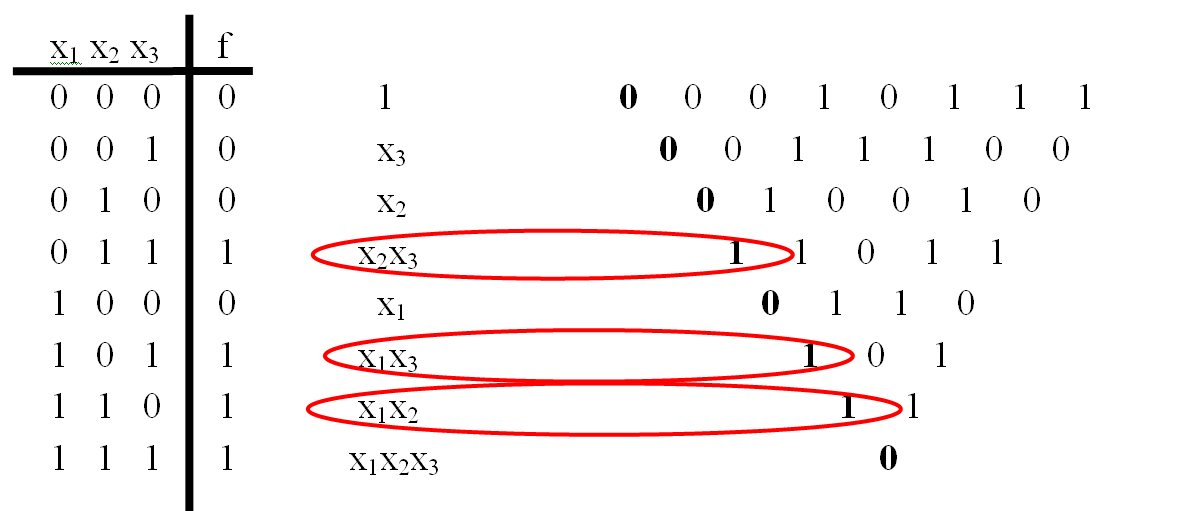
Шаг 3. Построение полинома Жегалкина.

Нас интересует левая сторона треугольника (значения выделены жирным):

Числа на левой стороне (выделены жирным шрифтом) треугольника есть коэффициенты полинома при монотонных конъюнкциях, соответствующих наборам значений переменных.

Теперь выпишем для наглядности эти конъюнкции. Конъюнкции выписываем по двоичным наборам в левой части таблицы по следующему принципу: если напротив переменной xi стоит 1, то переменная входит в конъюнкцию; в противном случае переменная отсутствует в конъюнкции. Набору (0,0,0) соответствует константа 1.

Если принцип получения конъюнкций понятен, то столбец с ними можно (даже лучше) не выписывать, а сразу переходить к построению полинома.

Для построения полинома нужны только конъюнкции из строк с единицами на левой стороне треугольника.

Это и есть конъюнкции, входящие в состав полинома Жегалкина. Осталось лишь выписать сам полином:
$f({{x}_{1}},{{x}_{2}},{{x}_{3}})={{x}_{1}}{{x}_{2}}oplus {{x}_{2}}{{x}_{3}}oplus {{x}_{1}}{{x}_{3}}.$

Если переменных в функции не 3, а 4 или больше, то метод работает без изменений, только увеличатся размеры таблиц. Тем не менее, в отличие от метода неопределенных коэффициентов, расчеты можно без особых усилий выполнить на листе бумаги.

Литература

К сожалению, мне не удалось найти и посмотреть источник, указанный в Википедии:
В.П. Супрун Табличный метод полиномиального разложения булевых функций // Кибернетика. — 1987. — № 1. — С. 116-117.

Источник

Полином Жегалкина — многочлен над полем ${mathbb {Z}}_{2}$ , то есть полином с коэффициентами вида 0 и 1, где в качестве произведения берётся конъюнкция, а в качестве сложения — исключающее или. Полином был предложен в 1927 году Иваном Жегалкиным в качестве удобного средства для представления функций булевой логики. В зарубежной литературе представление в виде полинома Жегалкина обычно называется алгебраической нормальной формой (АНФ).

Теорема Жегалкина — утверждение о существовании и единственности представления всякой булевой функции в виде полинома Жегалкина^[1].

Полином Жегалкина представляет собой сумму по модулю два попарно различных произведений неинвертированных переменных, где ни в одном произведении ни одна переменная не встречается больше одного раза, а также (если необходимо) константы 1^[1]. Формально полином Жегалкина можно представить в виде

${displaystyle P(X_{1},dots ,X_{n})=aoplus a_{1}X_{1}oplus a_{2}X_{2}oplus dots oplus a_{n}X_{n}oplus a_{12}X_{1}X_{2}oplus a_{13}X_{1}X_{3}oplus ldots oplus a_{1dots n}X_{1}dots X_{n},}$

${displaystyle a,ldots ,a_{1ldots n}in {0,1},}$

или в более формализованном виде как

${displaystyle P=aoplus bigoplus _{begin{array}{c}1leqslant i_{1}<ldots <i_{k}leqslant n\kin {overline {1,n}}end{array}}a_{i_{1},ldots ,i_{k}}wedge x_{i_{1}}wedge ldots wedge x_{i_{k}},quad a,a_{i_{1},ldots ,i_{k}}in {0,1}.}$

Примеры полиномов Жегалкина:

{displaystyle P=Xoplus YZoplus ABXoplus ABDYZ,}

Предпосылки[править | править код]

По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали:

Хотя бы одна функция, не сохраняющая 0.
Хотя бы одна функция, не сохраняющая 1.
Хотя бы одна нелинейная функция.
Хотя бы одна немонотонная функция.
Хотя бы одна несамодвойственная функция.

Этому требованию отвечает, в частности, система функций (конъюнкция, сложение по модулю два, константа 1). На её основе и строятся полиномы Жегалкина.

Существование и единственность представления[править | править код]

По теореме Жегалкина каждая булева функция единственным образом представляется в виде полинома Жегалкина. Теорема доказывается следующим образом. Заметим, что различных булевых функций от n переменных $2^{{2^{n}}}$ штук. При этом конъюнкций вида ${displaystyle x_{i_{1}}ldots x_{i_{k}}}$ существует ровно 2ⁿ, так как из n возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит 0 или 1, то есть существует $2^{{2^{n}}}$ различных полиномов Жегалкина от n переменных. Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.

Представление функции в виде полинома Жегалкина[править | править код]

С помощью эквивалентных преобразований ДНФ[править | править код]

По сравнению с ДНФ в полиноме Жегалкина отсутствуют операции ИЛИ и НЕ. Таким образом, полином Жегалкина можно получить из ДНФ, выразив операции ИЛИ и НЕ через операции сложение по модулю два, и константу 1. Для этого применяются следующие соотношения:

Ниже приведён пример преобразования ДНФ в полином Жегалкина:

{displaystyle XYvee {overline {X}},{overline {Y}}=XYoplus {overline {X}},{overline {Y}}oplus XY{overline {X}},{overline {Y}}=XYoplus {overline {X}},{overline {Y}}=XYoplus (Xoplus 1)(Yoplus 1)=}

{displaystyle quad =XYoplus XYoplus Xoplus Yoplus 1=Xoplus Yoplus 1.}

При преобразованиях использованы соотношения

С помощью эквивалентных преобразований СДНФ[править | править код]

СДНФ обладает тем свойством, что при любых значениях входных переменных в единицу обращается не более одного члена выражения. Для таких выражений операция дизъюнкции эквивалентна операции сложение по модулю два.

При преобразовании СДНФ в полином Жегалкина достаточно заменить все дизъюнкции на операции сложение по модулю два и избавиться от инверсий при помощи эквивалентного преобразования

С помощью карты Карно[править | править код]

Преобразование карты Карно в полином Жегалкина

Логическая функция трёх переменных , представленная в виде карты Карно, преобразуется в полином Жегалкина следующими шагами:

Рассматриваем все ячейки карты Карно в порядке возрастания количества единиц в их кодах. Для функции трёх переменных последовательность ячеек будет 000—100 — 010—001 — 110—101 — 011—111. Каждой ячейке карты Карно сопоставляем член полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1.
Если в рассматриваемой ячейке находится 0, переходим к следующей ячейке.
Если в рассматриваемой ячейке находится 1, добавляем в полином Жегалкина соответствующий член, инвертируем в карте Карно все ячейки, где этот член равен 1, и переходим к следующей ячейке. Например, если при рассмотрении ячейки 110 в ней оказывается единица, то в полином Жегалкина добавляется член AB и инвертируются все ячейки карты Карно, где A = 1 и B = 1. Если единице равна ячейка 000, то в полином Жегалкина добавляется член 1 и инвертируется вся карта Карно.
Процесс преобразования можно считать законченным, когда после очередной инверсии все ячейки карты Карно становятся нулевыми.

Метод треугольника[править | править код]

Основной источник: ^[2], ^[3]

Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных методом треугольника

Метод треугольника (часто называемый методом треугольника Паскаля) позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:

Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от 000…00 до 111…11.
Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
Ячейка в каждом последующем столбце получается путём суммирования по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке 111 соответствует член ABC, ячейке 101 — член AC, ячейке 010 — член B, ячейке 000 — член 1 и т. д.
Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.

Метод треугольника основан на теореме, предложенной В. П. Супруном, не связанной напрямую с треугольником Паскаля. В 1985 году метод двоичного треугольника было предложено использовать для преобразования вектора значений совершенной дизъюнктивной нормальной формы в вектор коэффициентов полинома Жегалкина для произвольной симметрической булевой функции. В 1987 году метод был расширен для произвольной булевой функции. Отметим, что метод треугольника позволяет строить полином Рида — Маллера^[en] с отрицательной поляризацией как для симметрических функций, так и для произвольных^{[источник не указан 1877 дней]}.

Метод БПФ[править | править код]

Построение полинома Жегалкина методом Паскаля

Наиболее экономным с точки зрения объёма вычислений и целесообразным для построения полинома Жегалкина вручную является метод быстрого преобразования Фурье (БПФ).

Строим таблицу, состоящую из 2^N столбцов и N + 1 строк, где N — количество переменных в функции. В верхней строке таблицы размещаем вектор значений функции, то есть последний столбец таблицы истинности.

Каждую строку полученной таблицы разбиваем на блоки (чёрные линии на рисунке). В первой строке блок занимает одну клетку, во второй строке — две, в третьей — четыре, в четвёртой — восемь и т. д. Каждому блоку в некоторой строке, который мы будем называть «нижний блок», всегда соответствует ровно два блока в предыдущей строке. Будем называть их «левый верхний блок» и «правый верхний блок».

Построение начинается со второй строки. Содержимое левых верхних блоков без изменения переносится в соответствующие клетки нижнего блока (зелёные стрелки на рисунке). Затем над правым верхним и левым верхним блоками побитно производится операция «сложение по модулю два», и полученный результат переносится в соответствующие клетки правой части нижнего блока (красные стрелки на рисунке). Эта операция проводится со всеми строками сверху вниз и со всеми блоками в каждой строке. После окончания построения в нижней строке оказывается строка чисел, которая является коэффициентами полинома Жегалкина, записанными в той же последовательности, что и в описанном выше методе треугольника.

Метод суммирования[править | править код]

Графическое представление коэффициентов полинома Жегалкина для функций с разным числом переменных

По таблице истинности легко вычислить отдельные коэффициенты полинома Жегалкина. Для этого нужно просуммировать по модулю 2 значения функции в тех строках таблицы, где переменные, отсутствующие в конъюнкции, принимают нулевые значения.

Предположим для примера, что нужно найти коэффициент при конъюнкции xz для функции трёх переменных f(x, y, z). В этой конъюнкции отсутствует переменная y. Найдём входные наборы, в которых переменная y принимает нулевое значение. Это наборы 0, 1, 4, 5 (000, 001, 100, 101). Тогда коэффициент при конъюнкции xz равен

${displaystyle a_{5}=f_{0}oplus f_{1}oplus f_{4}oplus f_{5}=f(0,0,0)oplus f(0,0,1)oplus f(1,0,0)oplus f(1,0,1).}$

Поскольку в свободном члене отсутствуют все переменные, то

$a_{0}=f_{0}.$

Для члена, куда входят все переменные, в сумму входят все значения функции:

${displaystyle a_{N-1}=f_{0}+f_{1}+f_{2}+ldots +f_{N-2}+f_{N-1}.}$

Представим графически коэффициенты полинома Жегалкина как суммы по модулю 2 значений функций в некоторых точках. Для этого построим квадратную таблицу, где каждый столбец представляет собой значение функции в одной из точек, а строка — коэффициент полинома Жегалкина. Точка на пересечении некоторого столбца и строки означает, что значение функции в данной точке входит в сумму для данного коэффициента полинома (см. рисунок). Назовём эту таблицу T_N, где N — число переменных функции.

Существует закономерность, которая позволяет получить таблицу для функции N переменных, имея таблицу для функции N − 1 переменных. Новая таблица T_N+1 компонуется как матрица 2 × 2 таблиц T_N, причём правый верхний блок матрицы очищается.

См. также[править | править код]

Алгебра Жегалкина

Примечания[править | править код]

↑ ¹ ² Капитонова Ю. В., Кривой С. Л., Летичевский А. А. Лекции по дискретной математике. — СПб., БХВ-Петербург, 2004. — ISBN 5-94157-546-7, с. 110—111.
↑ В. П. Супрун. Табличный метод полиномиального разложения булевых функций // Кибернетика. — 1987. — № 1. — С. 116—117.
↑ В. П. Супрун. Основы теории булевых функций. — М.: Ленанд / URSS. — 2017. — 208 с.

Литература[править | править код]

Яблонский С. В. Введение в дискретную математику. — М.: Наука. — 1986
Марченков С. С. Замкнутые классы булевых функций. — М.: Физматлит. — 2000
Супрун В. П. Основы теории булевых функций. — М.: Ленанд / URSS. — 2017.

Источник

Полином Жегалкина (англ. Zhegalkin polynomial) — полином с коэффициентами вида и , где в качестве произведения берётся конъюнкция, а в качестве сложения исключающее или. Полином был предложен в 1927 году И. И. Жегалкиным в качестве средства для представления функций булевой логики. Полином Жегалкина имеет следующий вид:

Содержание

1 Полнота
2 Существование и единственность представления (теорема Жегалкина)
3 Построение полинома Жегалкина
- 3.1 По таблице истинности
- 3.2 Преобразование дизъюнктивной нормальной формы
- 3.3 Метод треугольника
- 3.4 Преобразование Мёбиуса
4 См. также
5 Источники информации

Полнота

По теореме Поста, чтобы система булевых функций была полной, надо, чтобы в ней существовали

Хотя бы одна функция, не сохраняющая ;
Хотя бы одна функция, не сохраняющая ;
Хотя бы одна нелинейная функция;
Хотя бы одна немонотонная функция;
Хотя бы одна несамодвойственная функция.

Исходя из этого, система функций является полной:






Сохраняет 0
Сохраняет 1
Самодвойственная
Монотонная
Линейная

На основе этой системы и строятся полиномы Жегалкина.

Существование и единственность представления (теорема Жегалкина)

Теорема (Жегалкина):

Каждая булева функция единственным образом представляется в виде полинома Жегалкина.

Доказательство:

Заметим, что различных булевых функций от переменных штук. При этом конъюнкций вида существует ровно , так как из возможных сомножителей каждый или входит в конъюнкцию, или нет. В полиноме у каждой такой конъюнкции стоит или , то есть существует различных полиномов Жегалкина от переменных.

Теперь достаточно лишь доказать, что различные полиномы реализуют различные функции. Предположим противное. Тогда приравняв два различных полинома и перенеся один из них в другую часть равенства, получим полином, тождественно равный нулю и имеющий ненулевые коэффициенты. Тогда рассмотрим слагаемое с единичным коэффициентом наименьшей длины, то есть с наименьшим числом переменных, входящих в него (любой один, если таких несколько). Подставив единицы на места этих переменных, и нули на места остальных, получим, что на этом наборе только одно это слагаемое принимает единичное значение, то есть нулевая функция на одном из наборов принимает значение 1. Противоречие. Значит, каждая булева функция реализуется полиномом Жегалкина единственным образом.

Построение полинома Жегалкина

Существует несколько способов построения полинома Жегалкина.

По таблице истинности

Пусть для функции задана таблица истинности. Запишем сначала данную функцию в виде полинома Жегалкина с неопределёнными коэффициентами. Затем по очереди подставляем всевозможные наборы в порядке увеличения количества единиц и находим коэффициенты с учётом того, что , а . За каждую подстановку находим только один коэффициент.

Пример:
Дана функция и её таблица истинности:


0	0	0	0	0
0	0	0	1	0
0	0	1	0	0
0	0	1	1	0
0	1	0	0	0
0	1	0	1	0
0	1	1	0	1
0	1	1	1	0
1	0	0	0	1
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	1
1	1	0	1	0
1	1	1	0	1
1	1	1	1	0

Построим для неё полином Жегалкина:

Так как , то .
Далее подставляем все остальные наборы в порядке возрастания числа единиц, подставляя вновь полученные значения в следующие формулы:

следовательно

Таким образом, полином Жегалкина выглядит так:

Преобразование дизъюнктивной нормальной формы

Этот способ основан на том, что . Если функция задана в виде ДНФ, то можно сначала убрать дизъюнкцию, используя правило де Моргана, а все отрицания заменить прибавлением единицы по модулю два, после чего раскрыть скобки по обычным правилам, при этом учитывая, что четное число одинаковых слагаемых равно нулю (так как ), а нечетное число одинаковых слагаемых равно одному такому слагаемому. Либо же можно заменить дизъюнкцию по следующему правилу:
.

Если функция задана в СДНФ, то так как при любых значениях входных переменных в единицу обращается не более одного члена выражения, то достаточно просто заменить все дизъюнкции исключающим ИЛИ.

Пример:
Дана функция в ДНФ , построим полином Жегалкина.

Запишем функцию так:

;

Сгруппируем слагаемые и воспользуемся преобразованием (1):

Воспользуемся свойствами конъюнкции и , а также тем, что , и упростим выражение:

Ещё раз воспользуемся преобразованием (1):

Раскроем скобку по алгебраическим правилам:

Снова воспользуемся свойствами конъюнкции и исключающего ИЛИ:

Заменим отрицание на прибавление :

Раскроем скобки:

Выкинем парные слагаемые и получим окончательную формулу:

Метод треугольника

Метод треугольника позволяет преобразовать таблицу истинности в полином Жегалкина путём построения вспомогательной треугольной таблицы в соответствии со следующими правилами:

Строится полная таблица истинности, в которой строки идут в порядке возрастания двоичных кодов от до .
Строится вспомогательная треугольная таблица, в которой первый столбец совпадает со столбцом значений функции в таблице истинности.
Ячейка в каждом последующем столбце получается путём сложения по модулю 2 двух ячеек предыдущего столбца — стоящей в той же строке и строкой ниже.
Столбцы вспомогательной таблицы нумеруются двоичными кодами в том же порядке, что и строки таблицы истинности.
Каждому двоичному коду ставится в соответствие один из членов полинома Жегалкина в зависимости от позиций кода, в которых стоят единицы. Например, ячейке соответствует член , ячейке — член , ячейке — член , ячейке — член и т.д.
Если в верхней строке какого-либо столбца стоит единица, то соответствующий член присутствует в полиноме Жегалкина.

Фактически, этот метод является модификацией метода построения по таблице истинности, описанного выше. По сравнению с ним он удобнее тем, что расчёты занимают мало места и в них сложнее ошибиться, но метод треугольника требует бо́льшего количества операций.

Пример преобразования таблицы истинности в полином Жегалкина для функции трёх переменных показан на рисунке.

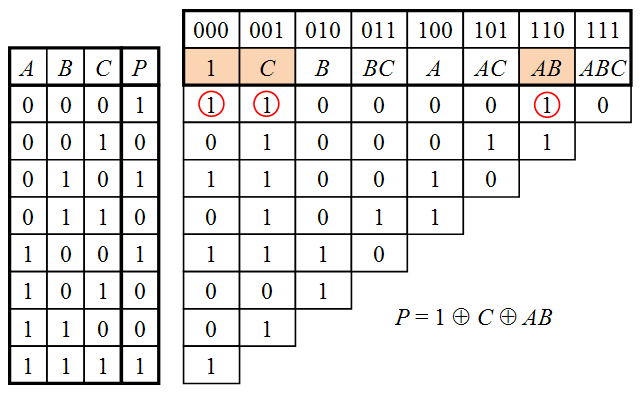
Чтобы получить формулу, по которой рассчитывается какой-либо коэффициент, нужно из клетки, в которой он записан, пройтись всеми возможными путями влево, до столбца таблицы истинности, делая ходы влево и влево-вниз, записать значения в конечных ячейках и сложить их все между собой по модулю 2.

Таким образом, в первом столбце сверху записан коэффициент ,

во втором — ,

в третьем — ,

в четвёртом —

и так далее, то есть при построении вспомогательной таблицы коэффициенты полинома просчитываются автоматически.

Преобразование Мёбиуса

Пусть задана булева функция .
Любая булева функция представима в виде полинома Жегалкина, притом единственным образом.

Пусть , и введем обозначение

Тогда полином Жегалкина можно записать как:
, где .

Множество коэффициентов можно рассматривать как функцию , заданной на множестве индексов , то есть .

Очевидно, функцию можно записать и следующим образом: если если если .

Тут запись если означает, что элелемент присутствует в соответствующем члене полинома только если .
Тогда если для какого-то , ,то в слагаемом будет существовать хотя бы один множитель, равный нулю, и такое слагаемое на сумму не повлияет.
Отсюда ясно, что
Найдем отображение (То есть такое, которое по заданной функции вычисляет значения всех коэффициентов).

обозначает, что “меньше” как последовательность бит

Теорема:

Пусть задана функция . Тогда функцию можно найти по формуле: .

Доказательство:

Докажем при помощи индукции по количеству единиц в векторе ( иначе говоря, по сумме ) и для удобства обозначим это количество единиц(сумму) .

1) База: если , то, очевидно

2) Пускай теорема справедлива для всех сумм . Покажем, что в таком случае она верна и для . По , а далее по предположению индукции видим: .

Рассмотрим сумму . Каждый элемент содержится в ней, только если , и для фиксированных и элемент встречается ровно столько раз, сколько существует , таких, что . Несложно увидеть, что таких существует ровно , то есть нечетное количество раз. Тогда .
Но тогда .

То есть при формула также выполняется, значит при любых выполняется .

Отображение также называется преобразованием Мёбиуса.

Видно, что и — это одно и тоже преобразование. Значит, если применить преобразование Мёбиуса к функции, а затем вновь применить то же преобразование к получившейся функции, тогда вновь получим исходную функцию . То есть преобразование Мёбиуса обратно самому себе, иными словами, является инволюцией.

См. также

Булевы функции
Полные системы функций, теорема Поста
ДНФ
КНФ

Источники информации

Cтатистика | Математика НГУ
Википедия — Полином Жегалкина
Е.Л Рабкин, Ю.Б. Фарфоровская, дискретная математика
Логачёв О.А, Сальников А.А., Ященко В.В. Булевы фунции в теории кодирования и криптологии — МЦНМО, 2004. – 470с. — ISBN 5-94057-117-4.

Источник

поэтому ее сокращенная ДНФ содержит всего 2 простые конъюнкции,

а она имеет вид f = x1 x3 x 2.

Следующий пример показывает использование карт Карно при п = 4:

x3, x4 /x1, x2	0 0	0 1	1 1	1 0
0 0	1	0	1	1
0 1	0	0	0	0
1 1	0	0	0	1
1 0	1	1	1	1
Здесь сокращенная ДНФ содержит 4 слагаемых (СДНФ содержит 8) и
имеет вид f = x2 x4 x3 x4	x1 x4 x1 x2 x3 .

При п = 5 использование карт Карно является несколько более сложным и здесь не приводится.

Обоснование приведенного алгоритма сокращения. Пусть для опреде-

ленности в карте Карно стоят рядом 2 единицы в первой строке и в первом и во втором столбцах. По алгоритму записи ДНФ функции по ее таблице истинности этим единицам в ДНФ соответствуют 2 дизъюнктных слагае-

мых: x1t1 x2t2 x3t3 x4t4 x1t1 x2t2 x3s3 x4s4 . По определению карты Карно (1-е условие)

впарах (t3, t4) и (s3, s4) либо t3 = t4, либо s3 = s4; для определенности, пусть

впервой паре – равенство, а во второй – неравенство. Тогда, вынося общие множители за скобки, получим:

x1t1 x2t2 x3t3 x4t4 x1t1 x2t2 x3s3 x4s4 x1t1 x2t2 x3t3 x4t4 x4s4 x1t1 x2t2 x3t3 1 0 x1t1 x2t2 x3t3 .

Такие же рассуждения применимы и к любому другому прямоугольнику из единиц в карте Карно.

Полиномом (многочленом) Жегалкина от п переменных называется функция, в которой для получения ее значений (из набора значений аргументов) используется фиксированная цепочка операций 3 видов: конъюнкций, сложений по модулю 2 и констант (т. е. нулей и единиц).

Ясно, что любой полином Жегалкина можно (после преобразований) записать в виде

P 0 1x1 2 x2	n xn n 1x1x2	n C2 xn 1xn	2n 1x1x2 xn. (2.6)
		n

Всего здесь 2п слагаемых. Напомним, что + сейчас означает сложение по модулю 2, коэффициенты 0 , 1, , 2n 1 являются константами (рав-

ными нулю или единице).

Например, полином Жегалкина от 3 переменных всегда можно привести к виду

P(x, y, z) 0 1x 2 y 3z 4xy 5xz 6 yz 7 xyz. (2.7)

Замечание. При помощи сложения по модулю 2 легко записать отрицание любой логической функции: K K 1 , в частности, х + 1 = x

Теорема. Любая логическая функция может быть представлена полиномом Жегалкина.

Доказательство. Любую функцию можно записать в виде ДНФ. Запишем двойное отрицание этой ДНФ (что не меняет функции). При помощи нижнего отрицания и правила Де Моргана избавимся от дизъюнкций. В оставшейся записи данной функции будут присутствовать только конъюнкции и отрицания. Каждое отрицание заменим на прибавление единицы. В получившейся записи функции на переменные будут действовать только конъюнкции, сложения по модулю 2 и присутствовать константы. Это и значит, что функция записана в виде полинома Жегалкина, и теорема доказана.

Замечания: 1) в доказательстве приведен алгоритм перехода от записи функции в виде ДНФ к ее записи в виде полинома Жегалкина.

Пример:

f(x, y, z) = xy x y y z xy x y y z = (xy + 1)((x + 1)(y + 1) + 1)((y + 1) z + 1) + 1 =

=(xy + 1)(xy + x+ y)(yz + z + 1) + 1 = (x+ y)(yz + z + 1) + 1 =

=xyz + yz + xz + yz + x + y + 1 = xyz + xz + x + y + 1;

2)напоминаем, что при сложении (по модулю 2) 1 + 1 = 0. Поэтому сумма четного числа одинаковых слагаемых всегда равна 0. Например, xyz + xyz + xyz = xyz;

3)надо уметь переходить к полиному Жегалкина не только от ДНФ (по алгоритму, приведенному в доказательстве теоремы), но и от таблицы истинности данной функции. Для такого перехода надо знать 2 алгоритма: метод неопределенных коэффициентов и «метод бабочки».

Метод неопределенных коэффициентов. Запишем сначала нашу функ-

цию в виде полинома Жегалкина с неопределенными коэффициентами, т. е. перепишем формулу (2.6), в частности, для функции 3 переменных – формулу (2.7). Затем в написанную формулу по очереди подставляем всевозможные наборы значений переменных и приравниваем полученные выражения соответствующим значениям функции из ее таблицы истинности.

Из полученных равенств, в которых неизвестными являются коэффициенты полинома Жегалкина, находим эти коэффициенты. Легко видеть, что за каждую подстановку мы находим ровно один коэффициент. Так как

число наборов равно числу коэффициентов (и равно 2п), то мы сможем найти все коэффициенты и, подставляя их в исходную формулу (2.6) (в частности, в формулу (2.7)), получим полином Жегалкина данной функции.

Метод бабочки. Пусть дана функция z = f (x1, x2,…, xп) от п переменных. В ее таблице истинности записаны 2п ее значений. Алгоритм метода бабочки заключается в последовательном проведении п операций, обычно называемых итерациями. 1-я итерация: рядом со столбцом значений данной функции записывается новый столбец; в верхнюю его половину (т. е. от 1-й строчки до строчки с номером 2п–1) переписываются числа из столбца значений функции, т. е числа f (0, x2,…, xп), а в нижнюю его половину (т. е. в строчках с номерами от 2п–1 + 1 до 2п) записываются суммы по модулю 2 соответствующих значений данной функции из верхней и нижней

половины таблицы, т. е. числа f (0, x2,…, xп) + f (1, x2,…, xп). Во 2-й итерации ту же процедуру проделывают отдельно с верхней и отдельно с ниж-

ней частью столбца, полученного в результате проведения 1-й итерации. В результате проведения второй итерации появляется новый столбец, у которого в верхней четверти записаны числа f (0, 0, x3,…, xп), во второй четверти – числа f (0, 0, x3,…, xп) + f (0, 1, x3,…, xп), в третьей четверти – числа f(0, 0, x3,…, xп) + f (1, 0, x3,…, xп), а в нижней четверти – числа

f(0, 0, x3,…, xп) + f (1, 0, x3,…, xп) + f (0, 1, x3,…, xп) + f (1, 1, x,…, xп).

Эта процедура повторяется п раз. При проведении последней, п-й, итерации в последнем, п-м, столбце в строках с номерами 1, 3, 5, …, 2п – 1 переписываются значения из предыдущего, п – 1–го столбца, а в строках с номерами 2, 4, 6,…, 2п записывается сумма (по модулю 2) того, что было записано в этой строке в п – 1–м столбце со значением, записанном в этом же п – 1–м столбце в предыдущей строке. По полученному п-му столбцу составляется полином Жегалкина данной функции: каждой единице этого столбца сопоставляется конъюнкция тех переменных, значения которых в строке с рассматриваемой единицей тоже равны единице, а затем эти конъюнкции переменных складываются по модулю 2. Последнее выражение и есть полином Жегалкина данной функции.

Например, f(x)= {01101001}.

x y z	f(x, y, z)	i1	i2	i3
0 0 0	0	0	0	0
0 0 1	1	1	1	1
0 1 0	1	1	1	1
0 1 1	0	0	1	0
1 0 0	1	1	1	1
1 0 1	0	1	1	0
1 1 0	0	1	0	0
1 1 1	1	1	0	0

В последнем столбце – 3 единицы, которым соответствуют наборы значений аргументов (0, 0, 1), (0, 1, 0) и (1, 0, 1) соответственно. Значит, в полиноме Жегалкина этой функции складываются три простых конъюнкции, каждая из которых содержит всего по одной переменной – x, y и z соответственно, и поэтому искомый полином имеет вид: f(x, y, z) = x+ y+ z.

Обоснование метода бабочки. Докажем по индукции, что указанный метод действительно приводит к полиному Жегалкина.

База индукции. Для всех 4 функций одной переменной (т. е. для 0, 1, х, x ) это утверждение проверяется непосредственно при помощи одной итерации над их таблицами истинности. Индукционный переход. Пусть это утверждение уже доказано для всех логических функций от п переменных (х1, х2, …, хп). Докажем, что тогда оно верно и для функции f от п+1 переменной, т. е. для z = f(х1, х2, …, хп, хп +1). Считаем, что таблица истинности этой функции записана стандартным образом, т. е. по возрастанию двоичных чисел, соответствующих наборам значений аргументов. Тогда в п-м столбце, полученном в результате п-й итерации, в строках с номерами 1, 3, 5, …, 2п –1 стоят числа, соответствующие значению 0 последнего аргумента: хп+1 = 0. Иными словами, в них стоят значения, соответствующие z = f(х1, х2, …, хп, 0), т. е. функции от п переменных. По индукционному предположению, по их значениям можно записать полином Жегалкина для этой функции, поэтому мы записываем этот полином (у которого простые конъюнкции не содержат переменной хп+1), а значения из этих строк переписываем без изменений в последний, (п + 1)-й столбец (т. е. для (п + 1)-й итерации). В том же п-м столбце в строках с номерами 2, 4, 6, …, 2п стоят числа, соответствующие тем же наборам значений аргументов, что и

встроках с номерами 1, 3, 5, …, 2п–1 (так как наборы значений аргументов

встроках с номерами 2k–1 и 2k отличаются только значениями последнего

аргумента: хп+1 = 0 и хп+1 = 1 соответственно). Поэтому, если мы уже получили для полинома Жегалкина простую конъюнкцию xk1 xk2 …xkm (km < n + 1),

рассматривая строку с нечетным номером для f(х1, х2, …, хп, 0) = 1, то в строке со следующим номером в последнем, (п + 1)-м, столбце должен стоять 0, так как иначе в полиноме Жегалкина нужно будет записать сумму (по модулю 2) 2 простых конъюнкций xk1 xk2 …xkm + xk1 xk2 …xkm xn 1, которая

при хп+1 = 1 и при любом наборе значений остальных переменных равна 0 (даже для тех наборов значений переменных, у которых соответствующая простая конъюнкция входит в полином Жегалкина с коэффициентом 1). Иными словами, если в столбце, соответствующем предпоследней итерации, стоят подряд две единицы, то в столбце последней итерации должны стоять 1 и 0. Это достигается сложением двух единиц предпоследнего столбца, что и требуется для доказательства индукционного перехода (так как 1 + 0 = 0 + 1 = 1, а 0 + 0 = 0, то рассуждения в остальных вариантах расположения значений в предпоследнем столбце очевидны).

Источник

Zhegalkin (also Žegalkin, Gégalkine or Shegalkin^[1]) polynomials (Russian: полиномы Жегалкина), also known as algebraic normal form, are a representation of functions in Boolean algebra. Introduced by the Russian mathematician Ivan Ivanovich Zhegalkin in 1927,^[2] they are the polynomial ring over the integers modulo 2. The resulting degeneracies of modular arithmetic result in Zhegalkin polynomials being simpler than ordinary polynomials, requiring neither coefficients nor exponents. Coefficients are redundant because 1 is the only nonzero coefficient. Exponents are redundant because in arithmetic mod 2, x² = x. Hence a polynomial such as 3x²y⁵z is congruent to, and can therefore be rewritten as, xyz.

Boolean equivalent[edit]

Prior to 1927, Boolean algebra had been considered a calculus of logical values with logical operations of conjunction, disjunction, negation, and so on. Zhegalkin showed that all Boolean operations could be written as ordinary numeric polynomials, representing the false and true values as 0 and 1, the integers mod 2. Logical conjunction is written as xy, and logical exclusive-or as arithmetic addition mod 2, (written here as x⊕y to avoid confusion with the common use of + as a synonym for inclusive-or ∨). The logical complement ¬x is then x⊕1. Since ∧ and ¬ form a basis for Boolean algebra, all other logical operations are compositions of these basic operations, and so the polynomials of ordinary algebra can represent all Boolean operations, allowing Boolean reasoning to be performed using elementary algebra.

For example, the Boolean 2-out-of-3 threshold or median operation is written as the Zhegalkin polynomial xy⊕yz⊕zx.

Formal properties[edit]

Formally a Zhegalkin monomial is the product of a finite set of distinct variables (hence square-free), including the empty set whose product is denoted 1. There are 2ⁿ possible Zhegalkin monomials in n variables, since each monomial is fully specified by the presence or absence of each variable. A Zhegalkin polynomial is the sum (exclusive-or) of a set of Zhegalkin monomials, with the empty set denoted by 0. A given monomial’s presence or absence in a polynomial corresponds to that monomial’s coefficient being 1 or 0 respectively. The Zhegalkin monomials, being linearly independent, span a 2ⁿ-dimensional vector space over the Galois field GF(2) (NB: not GF(2ⁿ), whose multiplication is quite different). The 2^2ⁿ vectors of this space, i.e. the linear combinations of those monomials as unit vectors, constitute the Zhegalkin polynomials. The exact agreement with the number of Boolean operations on n variables, which exhaust the n-ary operations on {0,1}, furnishes a direct counting argument for completeness of the Zhegalkin polynomials as a Boolean basis.

This vector space is not equivalent to the free Boolean algebra on n generators because it lacks complementation (bitwise logical negation) as an operation (equivalently, because it lacks the top element as a constant). This is not to say that the space is not closed under complementation or lacks top (the all-ones vector) as an element, but rather that the linear transformations of this and similarly constructed spaces need not preserve complement and top. Those that do preserve them correspond to the Boolean homomorphisms, e.g. there are four linear transformations from the vector space of Zhegalkin polynomials over one variable to that over none, only two of which are Boolean homomorphisms.

Method of computation[edit]

There are various known methods generally used for the computation of the Zhegalkin polynomial:

Using the method of indeterminate coefficients
By constructing the canonical disjunctive normal form
By using tables
Pascal method
Summation method
Using a Karnaugh map

The method of indeterminate coefficients[edit]

Using the method of indeterminate coefficients, a linear system consisting of all the tuples of the function and their values is generated. Solving the linear system gives the coefficients of the Zhegalkin polynomial.

Example[edit]

Given the Boolean function , express it as a Zhegalkin polynomial. This function can be expressed as a column vector

${displaystyle {vec {f}}={begin{pmatrix}1\0\1\0\1\0\0\1end{pmatrix}}}$

This vector should be the output of left-multiplying a vector of undetermined coefficients

${displaystyle {vec {c}}={begin{pmatrix}c_{0}\c_{1}\c_{2}\c_{3}\c_{4}\c_{5}\c_{6}\c_{7}end{pmatrix}}}$

by an 8×8 logical matrix which represents the possible values that all the possible conjunctions of A, B, C can take. These possible values are given in the following truth table:

${displaystyle {begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|}A&B&C&;;;;;;;;&1&C&B&BC&A&AC&AB&ABC\hline 0&0&0&&1&0&0&0&0&0&0&0\0&0&1&&1&1&0&0&0&0&0&0\0&1&0&&1&0&1&0&0&0&0&0\0&1&1&&1&1&1&1&0&0&0&0\1&0&0&&1&0&0&0&1&0&0&0\1&0&1&&1&1&0&0&1&1&0&0\1&1&0&&1&0&1&0&1&0&1&0\1&1&1&&1&1&1&1&1&1&1&1end{array}}}$

The information in the above truth table can be encoded in the following logical matrix:

${displaystyle S_{3}={begin{pmatrix}1&0&0&0&0&0&0&0\1&1&0&0&0&0&0&0\1&0&1&0&0&0&0&0\1&1&1&1&0&0&0&0\1&0&0&0&1&0&0&0\1&1&0&0&1&1&0&0\1&0&1&0&1&0&1&0\1&1&1&1&1&1&1&1end{pmatrix}}}$

where the ‘S’ here stands for “Sierpiński”, as in Sierpiński triangle, and the subscript 3 gives the exponents of its size: ${displaystyle 2^{3}times 2^{3}}$ .

It can be proven through mathematical induction and block-matrix multiplication that any such “Sierpiński matrix” $S_{n}$ is its own inverse.^{[nb 1]}

Then the linear system is

${displaystyle S_{3}{vec {c}}={vec {f}}}$

which can be solved for :

${displaystyle {vec {c}}=S_{3}^{-1}{vec {f}}=S_{3}{vec {f}}={begin{pmatrix}1&0&0&0&0&0&0&0\1&1&0&0&0&0&0&0\1&0&1&0&0&0&0&0\1&1&1&1&0&0&0&0\1&0&0&0&1&0&0&0\1&1&0&0&1&1&0&0\1&0&1&0&1&0&1&0\1&1&1&1&1&1&1&1end{pmatrix}}{begin{pmatrix}1\0\1\0\1\0\0\1end{pmatrix}}={begin{pmatrix}1\1\1oplus 1\1oplus 1\1oplus 1\1oplus 1\1oplus 1oplus 1\1oplus 1oplus 1oplus 1end{pmatrix}}={begin{pmatrix}1\1\0\0\0\0\1\0end{pmatrix}}}$

and the Zhegalkin polynomial corresponding to is .

Using the canonical disjunctive normal form[edit]

Using this method, the canonical disjunctive normal form (a fully expanded disjunctive normal form) is computed first. Then the negations in this expression are replaced by an equivalent expression using the mod 2 sum of the variable and 1. The disjunction signs are changed to addition mod 2, the brackets are opened, and the resulting Boolean expression is simplified. This simplification results in the Zhegalkin polynomial.

Using tables[edit]

Computing the Zhegalkin polynomial for an example function P by the table method

Let ${displaystyle c_{0},...,c_{2^{n}-1}}$ be the outputs of a truth table for the function P of n variables, such that the index of the $c_{i}$ ‘s corresponds to the binary indexing of the minterms.^{[nb 2]} Define a function ζ recursively by:

${displaystyle zeta (c_{i}):=c_{i}}$

${displaystyle zeta (c_{0},...,c_{k}):=zeta (c_{0},...,c_{k-1})oplus zeta (c_{1},...,c_{k})}$

Note that

${displaystyle zeta (c_{0},...,c_{m})=bigoplus _{k=0}^{m}{m choose k}_{2}c_{k}}$

where ${displaystyle {m choose k}_{2}}$ is the binomial coefficient reduced modulo 2.

Then

${displaystyle g_{i}=zeta (c_{0},...,c_{i})}$

is the i^th coefficient of a Zhegalkin polynomial whose literals in the i^th monomial are the same as the literals in the i^th minterm, except that the negative literals are removed (or replaced by 1).

The ζ-transformation is its own inverse, so the same kind of table can be used to compute the coefficients ${displaystyle c_{0},...,c_{2^{n}-1}}$ given the coefficients ${displaystyle g_{0},...,g_{2^{n}-1}}$ . Just let

${displaystyle c_{i}=zeta (g_{0},...,g_{i})}$

In terms of the table in the figure, copy the outputs of the truth table (in the column labeled P) into the leftmost column of the triangular table. Then successively compute columns from left to right by applying XOR to each pair of vertically adjacent cells in order to fill the cell immediately to the right of the top cell of each pair. When the entire triangular table is filled in then the top row reads out the coefficients of a linear combination which, when simplified (removing the zeroes), yields the Zhegalkin polynomial.

To go from a Zhegalkin polynomial to a truth-table, it is possible to fill out the top row of the triangular table with the coefficients of the Zhegalkin polynomial (putting in zeroes for any combinations of positive literals not in the polynomial). Then successively compute rows from top to bottom by applying XOR to each pair of horizontally adjacent cells in order to fill the cell immediately to the bottom of the leftmost cell of each pair. When the entire triangular table is filled then the leftmost column of it can be copied to column P of the truth table.

As an aside, note that this method of calculation corresponds to the method of operation of the elementary cellular automaton called Rule 102. For example, start such a cellular automaton with eight cells set up with the outputs of the truth table (or the coefficients of the canonical disjunctive normal form) of the Boolean expression: 10101001. Then run the cellular automaton for seven more generations while keeping a record of the state of the leftmost cell. The history of this cell then turns out to be: 11000010, which shows the coefficients of the corresponding Zhegalkin polynomial.^[3]^[4]

The Pascal method[edit]

Using the Pascal method to compute the Zhegalkin polynomial for the Boolean function . The line in Russian at the bottom says:
oplus – bitwise operation “Exclusive OR”

The most economical in terms of the amount of computation and expedient for constructing the Zhegalkin polynomial manually is the Pascal method.

We build a table consisting of 2^N columns and N+1 rows, where N is the number of variables in the function. In the top row of the table we place the vector of function values, that is, the last column of the truth table.

Each row of the resulting table is divided into blocks (black lines in the figure). In the first line, the block occupies one cell, in the second line — two, in the third — four, in the fourth — eight, and so on. Each block in a certain line, which we will call “lower block”, always corresponds to exactly two blocks in the previous line. We will call them “left upper block” and “right upper block”.

The construction starts from the second line. The contents of the left upper blocks are transferred without change into the corresponding cells of the lower block (green arrows in the figure). Then, the operation “addition modulo two” is performed bitwise over the right upper and left upper blocks and the result is transferred to the corresponding cells of the right side of the lower block (red arrows in the figure). This operation is performed with all lines from top to bottom and with all blocks in each line. After the construction is completed, the bottom line contains a string of numbers, which are the coefficients of the Zhegalkin polynomial, written in the same sequence as in the triangle method described above.

The summation method[edit]

Graphic representation of the coefficients of the Zhegalkin polynomial for functions with different numbers of variables.

According to the truth table, it is easy to calculate the individual coefficients of the Zhegalkin polynomial. To do this, sum up modulo 2 the values of the function in those rows of the truth table where variables that are not in the conjunction (that corresponds to the coefficient being calculated) take zero values.

Suppose, for example, that we need to find the coefficient of the xz conjunction for the function of three variables . There is no variable y in this conjunction. Find the input sets in which the variable y takes a zero value. These are the sets 0, 1, 4, 5 (000, 001, 100, 101). Then the coefficient at conjunction xz is

${displaystyle a_{5}=f_{0}oplus f_{1}oplus f_{4}oplus f_{5}=f(0,0,0)oplus f(0,0,1)oplus f(1,0,0)oplus f(1,0,1)}$

Since there are no variables with the constant term,

${displaystyle a_{0}=f_{0}}$

For a term which includes all variables, the sum includes all values of the function:

${displaystyle a_{N-1}=f_{0}oplus f_{1}oplus f_{2}oplus ...oplus f_{N-2}oplus f_{N-1}}$

Let us graphically represent the coefficients of the Zhegalkin polynomial as sums modulo 2 of values of functions at certain points. To do this, we construct a square table, where each column represents the value of the function at one of the points, and the row is the coefficient of the Zhegalkin polynomial. The point at the intersection of some column and row means that the value of the function at this point is included in the sum for the given coefficient of the polynomial (see figure). We call this table $T_{N}$ , where N is the number of variables of the function.

There is a pattern that allows you to get a table for a function of N variables, having a table for a function of N-1 variables. The new table ${displaystyle T_{N}+1}$ is arranged as a 2 × 2 matrix of $T_{N}$ tables, and the right upper block of the matrix is cleared.

Lattice-theoretic interpretation[edit]

Consider the columns of a table $T_{N}$ as corresponding to elements of a Boolean lattice of size 2^N . For each column f_M express number M as a binary number $M_{2}$ , then ${displaystyle f_{M}leq f_{K}}$ if and only if ${displaystyle M_{2}vee K_{2}=K_{2}}$ , where vee denotes bitwise OR.

If the rows of table $T_{N}$ are numbered, from top to bottom, with the numbers from 0 to ${displaystyle 2^{N}-1}$ , then the tabular content of row number R is the ideal generated by element f_R of the lattice.

Note incidentally that the overall pattern of a table $T_{N}$ is that of a logical matrix Sierpiński triangle. Also, the pattern corresponds to an elementary cellular automaton called Rule 60, starting with the leftmost cell set to 1 and all other cells cleared.

Using a Karnaugh map[edit]

Converting a Karnaugh map to a Zhegalkin polynomial.

The figure shows a function of three variables, P(A, B, C) represented as a Karnaugh map, which the reader may consider as an example of how to convert such maps into Zhegalkin polynomials; the general procedure is given in the following steps:

We consider all the cells of the Karnaugh map in ascending order of the number of units in their codes. For the function of three variables, the sequence of cells will be 000–100–010–001–110–101–011–111. Each cell of the Karnaugh map is associated with a member of the Zhegalkin polynomial depending on the positions of the code in which there are ones. For example, cell 111 corresponds to the member ABC, cell 101 corresponds to the member AC, cell 010 corresponds to the member B, and cell 000 corresponds to member 1.
If the cell in question is 0, go to the next cell.
If the cell in question is 1, add the corresponding term to the Zhegalkin polynomial, then invert all cells in the Karnaugh map where this term is 1 (or belonging to the ideal generated by this term, in a Boolean lattice of monomials) and go to the next cell. For example, if, when examining cell 110, a one appears in it, then the term AB is added to the Zhegalkin polynomial and all cells of the Karnaugh map are inverted, for which A = 1 and B = 1. If unit is in cell 000, then a term 1 is added to the Zhegalkin polynomial and the entire Karnaugh map is inverted.
The transformation process can be considered complete when, after the next inversion, all cells of the Karnaugh map become zero, or a don’t care condition.

Möbius transformation[edit]

The Möbius inversion formula relates the coefficients of a Boolean sum-of-minterms expression and a Zhegalkin polynomial. This is the partial order version of the Möbius formula, not the number theoretic. The Möbius inversion formula for partial orders is:

${displaystyle g(x)=sum _{y:yleq x}f(y)leftrightarrow f(x)=sum _{y:yleq x}g(y)mu (y,x)}$

,^[5]

where ${displaystyle mu (y,x)=(-1)^{|x|-|y|}}$ , |x| being the Hamming distance of x from 0. Since in the Zhegalkin algebra, the Möbius function collapses to being the constant 1.

The set of divisors of a given number x is also the order ideal generated by that number: . Since summation is modulo 2, the formula can be restated as

${displaystyle g(x)=bigoplus _{y:yin langle xrangle }f(y)leftrightarrow f(x)=bigoplus _{y:yin langle xrangle }g(y)}$

Example[edit]

As an example, consider the three-variable case. The following table shows the divisibility relation:

x	divisors of x
000	000
001	000, 001
010	000, 010
011	000, 001, 010, 011
100	000, 100
101	000, 001, 100, 101
110	000, 010, 100, 110
111	000, 001, 010, 011, 100, 101, 110, 111

Then

{displaystyle g(001)=f(000)oplus f(001)}

{displaystyle g(010)=f(000)oplus f(010)}

{displaystyle g(011)=f(000)oplus f(001)oplus f(010)oplus f(011)}

{displaystyle g(100)=f(000)oplus f(100)}

{displaystyle g(101)=f(000)oplus f(001)oplus f(100)oplus (101)}

{displaystyle g(110)=f(000)oplus f(010)oplus f(100)oplus f(110)}

{displaystyle g(111)=f(000)oplus f(001)oplus f(010)oplus f(011)oplus f(100)oplus f(101)oplus f(110)oplus f(111)}

The above system of equations can be solved for f, and the result can be summarized as being obtainable by exchanging g and f throughout the above system.

The table below shows the binary numbers along with their associated Zhegalkin monomials and Boolean minterms:

Boolean minterm	ABC	Zhegalkin monomial
	000	1
	001	C
	010	B
	011	BC
	100	A
	101	AC
	110	AB
	111	ABC

The Zhegalkin monomials are naturally ordered by divisibility, whereas the Boolean minterms do not so naturally order themselves; each one represents an exclusive eighth of the three-variable Venn diagram. The ordering of the monomials transfers to the bit strings as follows: given ${displaystyle a_{1}a_{2}a_{3}}$ and ${displaystyle b_{1}b_{2}b_{3}}$ , a pair of bit triplets, then ${displaystyle a_{1}a_{2}a_{3}leq b_{1}b_{2}b_{3}leftrightarrow a_{1}leq b_{1}wedge a_{2}leq b_{2}wedge a_{3}leq b_{3}}$ .

The correspondence between a three-variable Boolean sum-of-minterms and a Zhegalkin polynomial is then:

{displaystyle f(000){bar {A}}{bar {B}}{bar {C}}vee f(001){bar {A}}{bar {B}}Cvee f(010){bar {A}}B{bar {C}}vee f(011){bar {A}}BCvee f(100)A{bar {B}}{bar {C}}vee f(101)A{bar {B}}Cvee f(110)AB{bar {C}}vee f(111)ABC}

{displaystyle qquad qquad equiv g(000)oplus g(001)Coplus g(010)Boplus g(011)BCoplus g(100)Aoplus g(101)ACoplus g(110)ABoplus g(111)ABC}

The system of equations above may be summarized as a logical matrix equation:

${displaystyle {begin{pmatrix}g(000)\g(001)\g(010)\g(011)\g(100)\g(101)\g(110)\g(111)end{pmatrix}}={begin{pmatrix}1&&0&&0&&0&&0&&0&&0&&0\1&&1&&0&&0&&0&&0&&0&&0\1&&0&&1&&0&&0&&0&&0&&0\1&&1&&1&&1&&0&&0&&0&&0\1&&0&&0&&0&&1&&0&&0&&0\1&&1&&0&&0&&1&&1&&0&&0\1&&0&&1&&0&&1&&0&&1&&0\1&&1&&1&&1&&1&&1&&1&&1end{pmatrix}}{begin{pmatrix}f(000)\f(001)\f(010)\f(011)\f(100)\f(101)\f(110)\f(111)end{pmatrix}}}$

which N. J. Wildberger calls a Boole–Möbius transformation.

Below is shown the “XOR spreadsheet” form of the transformation, going in the direction of g to f:

${displaystyle f_{000}}$	${displaystyle f_{001}}$	${displaystyle f_{010}}$	${displaystyle f_{011}}$	${displaystyle f_{100}}$	${displaystyle f_{101}}$	${displaystyle f_{110}}$	${displaystyle f_{111}}$
${displaystyle g_{000}}$	${displaystyle g_{000}oplus g_{001}}$	${displaystyle g_{000}oplus g_{010}}$	${displaystyle g_{000}oplus g_{010}oplus g_{001}oplus g_{011}}$	${displaystyle g_{000}oplus g_{100}}$	${displaystyle g_{000}oplus g_{100}oplus g_{001}oplus g_{101}}$	${displaystyle g_{000}oplus g_{100}oplus g_{010}oplus g_{110}}$	${displaystyle g_{000}oplus g_{100}oplus g_{010}oplus g_{110}oplus g_{001}oplus g_{101}oplus g_{011}oplus g_{111}}$
${displaystyle g_{001}}$	${displaystyle g_{001}oplus g_{010}}$	${displaystyle g_{001}oplus g_{011}}$	${displaystyle g_{001}oplus g_{011}oplus g_{010}oplus g_{100}}$	${displaystyle g_{001}oplus g_{101}}$	${displaystyle g_{001}oplus g_{101}oplus g_{010}oplus g_{110}}$	${displaystyle g_{001}oplus g_{101}oplus g_{011}oplus g_{111}}$
${displaystyle g_{010}}$	${displaystyle g_{010}oplus g_{011}}$	${displaystyle g_{010}oplus g_{100}}$	${displaystyle g_{010}oplus g_{100}oplus g_{011}oplus g_{101}}$	${displaystyle g_{010}oplus g_{110}}$	${displaystyle g_{010}oplus g_{110}oplus g_{011}oplus g_{111}}$
${displaystyle g_{011}}$	${displaystyle g_{011}oplus g_{100}}$	${displaystyle g_{011}oplus g_{101}}$	${displaystyle g_{011}oplus g_{101}oplus g_{100}oplus g_{110}}$	${displaystyle g_{011}oplus g_{111}}$
${displaystyle g_{100}}$	${displaystyle g_{100}oplus g_{101}}$	${displaystyle g_{100}oplus g_{110}}$	${displaystyle g_{100}oplus g_{110}oplus g_{101}oplus g_{111}}$
${displaystyle g_{101}}$	${displaystyle g_{101}oplus g_{110}}$	${displaystyle g_{101}oplus g_{111}}$
${displaystyle g_{110}}$	${displaystyle g_{110}oplus g_{111}}$
${displaystyle g_{111}}$

[edit]

In 1927, in the same year as Zhegalkin’s paper,^[2] the American mathematician Eric Temple Bell published a sophisticated arithmetization of Boolean algebra based on Richard Dedekind’s ideal theory and general modular arithmetic (as opposed to arithmetic mod 2).^[6] The much simpler arithmetic character of Zhegalkin polynomials was first noticed in the west (independently, communication between Soviet and Western mathematicians being very limited in that era) by the American mathematician Marshall Stone in 1936^[7] when he observed while writing up his celebrated Stone duality theorem that the supposedly loose analogy between Boolean algebras and rings could in fact be formulated as an exact equivalence holding for both finite and infinite algebras, leading him to substantially reorganize his paper over the next few years.

Notes[edit]

^ As base case,

${displaystyle S_{0}:={begin{pmatrix}1end{pmatrix}}}$

${displaystyle (S_{0})^{2}={begin{pmatrix}1end{pmatrix}}=I_{0}}$

where $I_{n}$ is here taken to denote the identity matrix of size $2^{n}times 2^{n}$ . The inductive assumption is

${displaystyle (S_{n})^{2}=I_{n}}$ .

Then the inductive step is:

${displaystyle S_{n+1}:={begin{pmatrix}S_{n}&O\S_{n}&S_{n}end{pmatrix}}equiv {begin{pmatrix}1&0\1&1end{pmatrix}}otimes S_{n}}$ ,

where denotes the Kronecker product,

${displaystyle (S_{n+1})^{2}={begin{pmatrix}S_{n}&O\S_{n}&S_{n}end{pmatrix}}{begin{pmatrix}S_{n}&O\S_{n}&S_{n}end{pmatrix}}={begin{pmatrix}S_{n}S_{n}oplus OS_{n}&S_{n}Ooplus OS_{n}\S_{n}S_{n}oplus S_{n}S_{n}&S_{n}Ooplus S_{n}S_{n}end{pmatrix}}={begin{pmatrix}I_{n}&O\I_{n}oplus I_{n}&I_{n}end{pmatrix}}={begin{pmatrix}I_{n}&O\O&I_{n}end{pmatrix}}=I_{n+1}}$ ,

or, in terms of the Kronecker product:

${displaystyle S_{n+1}^{2}=(S_{1}otimes S_{n})(S_{1}otimes S_{n})=S_{1}^{2}otimes S_{n}^{2}=I_{1}otimes I_{n}=I_{n+1}}$ . ∎
^ A minterm is the Boolean counterpart of a Zhegalkin monomial. For an n-variable context, there are $2^{n}$ Zhegalkin monomials and $2^{n}$ Boolean minterms as well. A minterm for an n-variable context consists of an AND-product of n literals, each literal either being a variable in the context or the NOT-negation of such a variable. Moreover, for each variable in the context there must appear exactly once in each minterm a corresponding literal (either the assertion or negation of that variable). A truth table for a Boolean function of n variables has exactly $2^{n}$ rows, the inputs of each row corresponding naturally to a minterm whose context is the set of independent variables of that Boolean function. (Each 0-input corresponds to a negated variable; each 1-input corresponds to an asserted variable.)
Any Boolean expression may be converted to sum-of-minterms form by repeatedly distributing AND with respect to OR, NOT with respect to AND or OR (through the De Morgan identities), cancelling out double negations (cf. negation normal form); and then, when a sum-of-products has been obtained, multiply products with missing literals with instances of the law of excluded middle that contain the missing literals; then — lastly — distribute AND with respect to OR again.
Note that there is a formal correspondence, for a given context, between Zhegalkin monomials and Boolean minterms. However, the correspondence is not logical equivalence. For example, for the context {A, B, C}, there is a formal correspondence between the Zhegalkin monomial AB and the Boolean minterm , but they are not logically equivalent. (For more of this example, see the second table in the section “Möbius transformation”. The same set of bitstrings is used to index both the set of Boolean minterms and the set of Zhegalkin monomials.)

References[edit]

^ Steinbach, Bernd [in German]; Posthoff, Christian (2009). “Preface”. Written at Freiberg, Germany. Logic Functions and Equations – Examples and Exercises (1st ed.). Dordrecht, Netherlands: Springer Science + Business Media B. V. p. xv. ISBN 978-1-4020-9594-8. LCCN 2008941076.
^ ^a ^b Жега́лкин [Zhegalkin], Ива́н Ива́нович [Ivan Ivanovich] (1927). “O Tekhnyke Vychyslenyi Predlozhenyi v Symbolytscheskoi Logykye” О технике вычислений предложений в символической логике [On the technique of calculating propositions in symbolic logic (Sur le calcul des propositions dans la logique symbolique)]. Matematicheskii Sbornik (in Russian and French). Moscow, Russia. 34 (1): 9–28. Mi msb7433. Archived from the original on 2017-10-12. Retrieved 2017-10-12.
^ Suprun [Супрун], Valeriy P. [Валерий Павлович] (1987). “Tablichnyy metod polinomial’nogo razlozheniya bulevykh funktsiy” Табличный метод полиномиального разложения булевых функций [The tabular method of polynomial decomposition of Boolean functions]. Kibernetika [Кибернетика] (Cybernetics) (in Russian) (1): 116–117.
^ Suprun [Супрун], Valeriy P. [Валерий Павлович] (2017). “Osnovy teorii bulevykh funktsiy” Основы теории булевых функций [Fundamentals of the theory of Boolean functions]. М.: Lenand [Ленанд] / URSS (in Russian): 208.
^ “Möbius inversion”. Encyclopedia of Mathematics. 2021-02-17 [2011-02-07]. Archived from the original on 2020-07-16. Retrieved 2021-03-27.
^ Bell, Eric Temple (1927). “Arithmetic of Logic”. Transactions of the American Mathematical Society. 29 (3): 597–611. doi:10.2307/1989098. JSTOR 1989098.
^ Stone, Marshall (1936). “The Theory of Representations for Boolean Algebras”. Transactions of the American Mathematical Society. 40 (1): 37–111. doi:10.2307/1989664. ISSN 0002-9947. JSTOR 1989664.

Что нам стоит полином Жегалкина построить…

Метод треугольника Паскаля

Литература

Предпосылки[править | править код]

Существование и единственность представления[править | править код]

Представление функции в виде полинома Жегалкина[править | править код]

С помощью эквивалентных преобразований ДНФ[править | править код]

С помощью эквивалентных преобразований СДНФ[править | править код]

С помощью карты Карно[править | править код]

Метод треугольника[править | править код]

Метод БПФ[править | править код]

Метод суммирования[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Содержание

Полнота

Существование и единственность представления (теорема Жегалкина)

Построение полинома Жегалкина

По таблице истинности

Преобразование дизъюнктивной нормальной формы

Метод треугольника

Преобразование Мёбиуса

См. также

Источники информации

Boolean equivalent[edit]

Formal properties[edit]

Method of computation[edit]

The method of indeterminate coefficients[edit]

Example[edit]

Using the canonical disjunctive normal form[edit]

Using tables[edit]

The Pascal method[edit]

The summation method[edit]

Lattice-theoretic interpretation[edit]

Using a Karnaugh map[edit]

Möbius transformation[edit]

Example[edit]

[edit]

See also[edit]

Notes[edit]

References[edit]

Further reading[edit]

Вам также может понравиться

Как найти проститутку в семей

Как составить словарь по русскому языку для 5 класса

Как найти серийный номер на сайте apple

Добавить комментарий Отменить ответ