Как составить модель к задаче на движение

Наибольшую сложность в процессе решения
текстовой задачи представляет перевод текста с
естественного языка на математический. Чтобы
облегчить эту процедуру, строят вспомогательные
модели – схемы, таблицы, краткие записи и др.
Тогда процесс решения задачи можно
рассматривать как переход от одной модели к
другой: от словесной модели реальной ситуации,
представленной в задаче, к вспомогательной (от
неё – к математической, на которой и происходит
решение задачи) [2, с. 85].

Моделирование является неотъемлемой частью
каждого урока математики. Применяют модель в том
случае, чтобы ученикам было проще воспринимать
какой-либо предмет или ситуацию, которая описана
в задаче. У школьников не возникает страха
самостоятельно начать анализ задачи; если что-то
не получается, они используют другую модель,
повторно анализируют задачу.

Модель способствует правильному ходу мыслей
ребенка. При самостоятельной работе над задачей
прием моделирования помогает ученику быть более
активным, успешным, не боятся трудностей, которые
появляются на пути. Каждый ученик имеет свою
индивидуальность, поэтому именно он выбирает
собственный путь рассуждения, моделирования и
решения задач.

В четвёртых классах очень подробно изучаются
различные виды движения двух объектов: движение
в одном направлении, встречное движение,
движение в противоположных направлениях. При
любом подходе для лучшего понимания к изучению
этого процесса используют метод моделирования,
без которого нельзя освоить все тонкости
математики.

Можно воспользоваться различными видами
моделей при изучении процесса движения, которые
рассматриваются в качестве вспомогательных
моделей.

В начальной школе при решении задач на
движение, в случае, когда задача решается в два и
более действия эффективно применять
вспомогательные модели, которые позволяют
наглядно представить ситуацию, способствуют
осознанному приобретению знаний, умений и
навыков.

В период прохождения практики в МАОУ Лицее № 1
г. Красноярска было проведено анкетирование
на учащихся 4 «В» класса в количестве 21
человек, которое направлено на определение
вспомогательных моделей, используемых самими
учениками при решении текстовых арифметических
задач на движение. На основе результатов
анкетирования были сделаны выводы о том,
большинство обучающихся – 73% от числа
опрашиваемых, применяют схему как основную
вспомогательную модель при решении задач на
движение, что составляет 19 человек.

Для эффективного решения текстовых задач
целесообразней использовать различные виды
вспомогательных моделей. В данном случае краткая
запись неудобна в использовании, т.к. в
определенных ситуациях она не дает возможности
учащимся в необходимой мере представить себе
жизненную ситуацию, отраженную в задаче, уяснить
отношения между величинами в ней, зависимости
между данным и искомым, именно поэтому этот вид
модели не используется обучающимися
4 «В» класса.

Рассмотрим виды моделей, используемые при
решении текстовых задач на движение более
подробно.

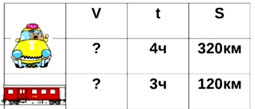
1. Таблица

Данная математическая модель помогает
упорядочить все данные в задаче для более
удобного восприятия. Наиболее удачным является
применение таблицы при решении задач на тройку
пропорциональных величин: скорость – время –
расстояние. Таблица используется, когда учащимся
необходимо рассчитать по формуле скорость, время
или расстояние.

Рис. 1

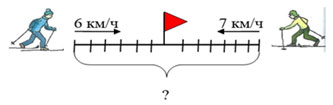
2. Чертёж

Этот вид модели удобно применять, когда
существуют удобные числовые данные в задаче,
позволяющие начертить отрезок заданной длины.
Ученики должны усвоить поэтапное выполнение
чертежа. Представленную модель можно
использовать при решении задач на движение двух
объектов с небольшими числовыми или
пропорциональными данными.

Рис.2

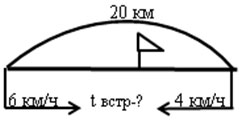
3. Схема

Схему используют на материале обратных задач,
применяемых различными способами. Данная модель
позволяет подняться на довольно высокую степень
абстрактности. Схема используется при решении
задач на движение двух объектов: встречное
движение, движение в одном направлении, движение
в противоположных направлениях, движение
вдогонку.

Рис.3

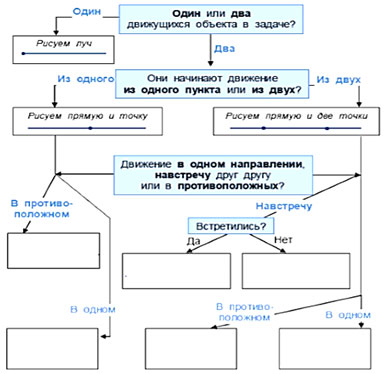
4. Блок-схема

Данный вид модели применяют в случаи
необходимости разбора задачи аналитическим
способом, начиная с вопроса. Блок-схему лучше
использовать в начале урока при знакомстве с
определенным видом задачи, что позволяет
установить, какой вид задачи рассматривается в
данный момент на уроке. При решении задач на
движение эту модель не используют как
вспомогательную модель к задаче [5, с. 109].

Рис.4

Чтобы свободно решать задачи, обучающийся
должен освоить разные виды моделей, научиться
выбирать модель, которая соответствует
поставленной цели, и переходить от одной формы к
другой.

Построение учащимися разных вспомогательных
моделей к одной и той же задаче ведет к
различному ходу рассуждений и, следовательно,
разным способам решения задачи.

Из приведённых вспомогательных моделей схема
является наиболее удобной при решении проблем по
ряду причин:

• может быть применена при решении задач с
  большими числами;
• может использоваться при решении задач с
  буквами;
• достаточно конкретна и полностью отражает
  внутренние связи и количественные отношения в
  задаче;
• позволяет подняться на довольно высокую
  степень абстрактности.

Библиографический список

1. Федеральный государственный образовательный
   стандарт начального общего образования. 2009 г.
   № 373.
2. Демидова Т.Е. Текстовые задачи и методы их
   решения [Текст] / Т.Е. Демидова, А.П. Тонких.
   М.: Изд-во МГУ, 201 г.
3. Нашахалова Н.В. Графическое моделирование
   текстовых задач на уроках математики в начальной
   школе [Электронный
   ресурс] / Н.В. Нашахалова // Математика:
   науч.-метод. журн. 2016. № 2. Режим доступа:
   https://docviewer.yandex.ru
4. Стойлова Л.П. Теоретические основы
   начального курса математики: учебное пособие для
   студ. Учреждений сред. проф.
   образования / Л.П. Стойлова., М.: Издательский
   центр «Академия», 2014. 272 с.
5. Толочко С.В. Проблемы организации работы с
   текстовыми задачами начальных классов / С.В. Толочко. Текст электронный // Педпортал:
   библиотека материалов для работников школы. URL:
   https://pedportal.net/starshie-klassy/algebra/problemy-organizacii-
   raboty-s-tekstovymi-zadachami-nachalnyh-klassov-1028106 (дата
   обращения: 15.10.2015). Текст: электронный.

Статья «Обучение моделированию на примере решения задач на  движение»

Учитель Ляпина И.А., ГБОУ СОШ №255, Адмиралтейский район города Санкт-Петербурга

Математические задачи

     Математическая задача – это маленькая поучительная история,

это небольшой рассказ, описывающий явление, событие, процесс

в жизни человека, его деятельность, с вопросом, на который нужно

дать ответ обоснованный, правильный (безошибочный), полный

(исчерпывающий). Именно эти слова говорю о задаче детям,

которых встречаю в 5м классе.

      Зачем решать задачи?  Этот вопрос задаю пятиклашкам.

Хороший вопрос, правда?

     Решая задачи, учащиеся овладевают теоретическими знаниями,

у м е н и е м   м ы с л и т ь – это умения: выделить полезную

информацию, пользоваться разными «языками» (словесный,

табличный, графический: диаграммы, графики, схематичный:

чертёж, блок-схема и т.д.), моделировать (переводить задачу со

словесного языка на графический), открывать «новые знания»,

на базе изученного способа решения, осуществлять самоконтроль,

прогнозировать и исследовать результат решения, вести дискуссию,

работать в команде и т.д.

    Функции задачи: обучающие, развивающие, воспитывающие,

контролирующие, но главное – формировать исследовательские

навыки и творческие способности, помочь овладеть

«инструментами» для решения задач, которые ставит жизнь не

только в школе.

     Один из таких «инструментов» – это моделирование (создание

модели).

     В УМК по математике 5-6 классов Н.Я. Виленкина и В.И.

Жохова, М.И. Башмакова, Г.В. Дорофеева и Л.Г. Петерсон

около 20% (примерно 5я часть) всех задач – это задачи на

движение: а) нахождение пропорциональных величин (расстояние,

скорость, время); б) одновременное движение двух объектов;

в) движение объекта по/против течения; г) круговое движение;

д) нахождение средней скорости.

     Впервые, учащиеся знакомятся с задачами на движение и

с понятием скорость в начальной школе, в 4м классе. В 5-6 классах

круг задач на движение расширяется, и задачи усложняются. В 7м

классе к арифметическому способу решения добавляется

алгебраический.

     Почему задач в учебниках так много?

     Мы и дети тоже постоянно в движении. Мы передвигаемся на

 автобусах, машинах, поездах, самолётах, велосипедах, пешком

каждый день. В нашей речи звучат слова: доехал быстро, опоздал,

догнал, вовремя, медленно, время в пути и т.д. Мы каждый день

решаем задачи на движение: во сколько нужно выйти, чтобы успеть

доехать до …, а если поехать не на автобусе, а на метро, то … и т.д.

То есть задачи на движение естественны для детей.

     Но для многих учащихся, как ни странно, эти задачи трудны.

     Почему трудны?

     В задачах присутствует понятие «скорость». Природу этой

величины детям понять сложно. Эта физическая величина

связывает две другие величины: расстояние (длина пути) и время,

за которое можно преодолеть это расстояние. Эти величины

привычны детям, так как их можно измерить инструментами,

приборами (часы, линейка) и оценить («внутренними часами»,

«глазами»). А скорость ребенок не может увидеть и измерить,

не может оценить. Даже слова быстрее, медленнее ребёнок

соотносит со временем. На вопрос о том, как вы понимаете

слова «велосипедист проедет быстрее это расстояние». Ребёнок

ответит за меньшее время. А почему за меньшее? Большинство

не сможет ответить.

     К тому же надо учесть, что запись величины скорость сложна

и непонятна: 12 километров в час (12 км/ч) или 20 метров в секунду

(20 м/с). Некоторым учащимся сложно найти в тексте и назвать

скорость объекта, к примеру, «Велосипедист за час проезжает

15 км, а за три часа сколько он проедет?». В данном случае

возникнуть сложности с заменой фразы «за час проезжает 15 км»

термином «скорость 15 км/ч».

Задачи на движение и моделирование.

     Процесс изучения задач на движение (одновременное движение

2х объектов) предполагает использовать модель, на которой можно

изобразить и изучить движение объектов, то есть промоделировать

ситуацию. Овладение операцией моделирования при решении задач

встречное движение, позволит учащимся использовать этот

«инструмент» для решения других задач (движение с отставанием,

движение вдогонку, движение в противоположных направлениях).

     Процесс моделирования предполагает умение анализировать

текст и переводить его на другой «язык» (со словесного на

символический: таблица, формула, чертеж и т.д.).

     «Ключевые моменты» при решении задачи – анализ текста,

создание модели, работа с моделью – это приводит к составлению

плана решения задачи. УРА!

        Что значит решить задачу?

        Решение  задачи  —  это:   а)  результат  (число,  слово,   выражение  и  т. д.), то есть ответ на вопрос задачи; б) процесс нахождения результата, то есть последовательность действий, совершаемых учащимися.

       Этапы процесса нахождения результата:

1) анализ текста задачи;

2) построение математической модели (перевод текста на язык математики);

3) установление отношений между условиями и требование задачи;

4) поиск способа решения задачи и составление плана решения;

5) выполнение действий по плану;

6) проверка решения задачи;

7) формулирование ответа задачи;

8) анализ способа решения задачи.

        Это общее представление процесса решения задачи.    

        1. Анализ текста задачи.

        Семантический  анализ.   Для  понимания  содержания  текста  необходимо:

а) выделить   и   осмыслит   некоторые  слова,  термины,  понятия,  конструкции  («если … то»,     «после того,  как»,    «когда … то»),    характеристики    объекта   (процесса,   явления,   события)  такие,   как  «некоторое»,  «любое»,  «каждый», «одинаковые», «такой же», «столько же», «всего» «поровну» и т. д.;

б) упростить    и    пересказать    текст    только  с  существенной   для   решения информацией;

в) выделить и назвать то,  о чём говорится в тексте  (объект, процесс, явление), и  что    должно    быть    найдено    (величину:    масса,    время,    объём    и   т. д.).

       Логический анализ заключается в замене терминов их определениями и для вывода следствий из условий задачи.

        Математический анализ текста направлен на работу:

1) с   условием   задачи:   выделить   объекты   (явления,    события,    процессы), величины,   их   характеризующие,   числовые   значения   величин,   отношения  между величинами и данные явные и неявные;

2) с требованием задачи: определить и назвать неизвестные характеристики

величин объекта (явления, события, процесса).

     Этот этап заканчивается не только осмыслением содержания задачи, но и «принятием» её учащимися, то есть решение задачи сделать целью своей деятельности.  [19]

        2. Построение математической модели.

        Результаты анализа текста фиксируются в форме, удобной для восприятия и работы:  высказывательная модель, логическая схема, условный рисунок, схематичный чертёж, таблица, диаграмма и т. д.

        Информацию,   полученную   при   анализе  текста,  удобно записать кратко, избавившись  от  несущественной информации,  оставив  систему взаимосвязей условий и требований — высказывательная модель (для детей краткое условие).

        Логическая  схема  ( к примеру,  граф) — эффективная  форма,   так как  все  объекты   присутствуют   одновременно,   выделены   отношения   между  ними, отсутствует избыточная информация.

        Рисунок     (условный) — это    вид     графической     информации;     несёт необходимый    минимум    информации  для    понимания   смысла,   развивает абстрактное   мышление;   часто   используется  в  начальной школе (1-2 класс).

        Чертёж   (схематический)    обеспечивает   целостное   восприятие   задачи, фиксирует  ход  рассуждения,  позволяет «увидеть» объекты, отношения; прост, нагляден,  удобен при поиске решения,  но к  схеме  предъявляются требования аккуратности, чёткости, читаемости, продуманности.

        Таблица может быть использована как модель (наиболее абстрактная), если в задаче есть взаимосвязанные величины.   Но поскольку она не показывает эти взаимосвязи,   то  учащийся   должен   владеть  знаниями  о  пропорциональных величинах.

        Формула — это   запись  с  помощью   математических  знаков  взаимосвязи  между компонентами и результатом действия.

        Технологии   моделирования,   то  есть  перевода   с  естественного  языка  на графический, учат строить модели жизненных ситуаций, с помощью которых и на которых возможно изучать окружающую реальность.  

       Этот этап заканчивается составлением модели — наглядного представления содержания задачи, величин, их зависимостей, явных и неявных.  [25]

     3. Установление отношений между условиями и требованием.

        На этом этане устанавливаются отношения между данными условия задачи, между данными вопроса задачи, между данными условия и вопроса

такие, как:

а) равенство,   часть/целое,  разность,  кратность,  часть одного числа от другого между одинаковыми объектами и их величинами;

б) зависимости между значениями разных величин, например,  формула         a b = c, которая    описывает    разнообразные    отношения    (связь   пройденного  пути,   времени,   скорости   равномерного   движения;     связь   выполненной   работы, времени,   производительности   труда;   связь  площади    прямоугольника,   его ширины, его длины и т. д.)

       Важно умение «увидеть» величины, между которыми есть взаимосвязи или «увидеть» зависимости между величинами; умение установить, как связаны эти величины;  умение записать эти отношения с помощью действий; установить последовательность действий, то есть выстроить план решения.

        4. Поиск способа решения задачи и составление плана решения.

        На   этом   этапе   поиск  может быть  осуществлён  следующими приёмами:  аналитическим (от вопроса к данным), синтетическим (от данных к вопросу) или анализ через синтез.

        Аналитический приём: зная, что требуется найти (вопрос задачи),

определяется, что нужно знать для ответа на вопрос, для чего выясняется, какие из данных есть в условии,  и если некоторые  данные отсутствуют  в условии, то определяется, что нужно знать, чтобы найти недостающие данные.

        Синтетический  приём:  имея  данные  и установив отношения между ними, находим новое данное; далее рассматриваем его и имеющиеся данные на предмет их взаимосвязи, установив её, находим следующее данное и т. д.

Процесс продолжается до тех пор, пока будет не найдено данное, являющееся ответом на вопрос задачи.

        План  включает  в  себя  последовательность  действий  с объяснением того, что узнаём, выполнив действие.

        5. Выполнение действий по плану.

        Действия   выполняются   по   порядку,   установленному   в  плане.   Запись решения   может   быть   выполнена   в   виде :  а) арифметического  выражения; б) записи   действий   с   пояснениями;   в) постановка  вопроса  с последующим действием; г) уравнения; д) сочетание этих способов.

        6. Проверка и оценка решения.

Модуль методических разработок.

     Кроме приобретения определённого набора знаний, необходимо

раскрыть и развить потенциал учащегося, создать условия и среду

для становление его как личности и реализации его способностей

и образовательных потребностей.

     Создание модуля методических разработок для обучения

решению задач на встречное движение («модуль») – это создание

среды, в которой учащийся проявит свою активность,

самостоятельность, реализует свой потенциал, добьётся успеха.

     Модуль включает в себя:

Шаг 1. Методическая разработка для урока: подготовка введения

задачи на встречное движение.

Шаг 2. Методическая разработка для урока: введение задачи на

встречное движение.

Шаг 3. Методическая разработка урока-игры.

Шаг 4. Методическая разработка урока развивающего контроля

спешности освоения способа решения задачи на встречное

движение.

Шаг 5. Творческий проект: создание сборника задач учащимися.

     Модуль включает в себя уроки, реализующие принципы:

1. системно-деятельностного подхода: урок открытия «новых

знаний», урок-игра, проектная деятельность, элементы

историзма, урок развивающего контроля;

1. минимакса, реализованный на уроке развивающего контроля,

уроке-игре;

1. психологического комфорта, реализованный на уроках через

выбор дз, через самоконтроль (по образцу) и внесение исправлений на уроке, через возможность выбора заданий по своим возможностям на уроках и во время контроля.

     Модуль создан в рамках УМК Н.Я. Виленкина и В.И. Жохова

«Математика. 5 класс»

     Шаг 1. Подготовка введения задачи на встречное движение.

     Решение задачи-исследования движения объекта (№124 в теме

«Шкалы и координаты») включает в себя: построение модели

(схематичный чертёж), работа с моделью (продемонстрировать

движение объекта, ответить на вопросы) и включение «новых

знаний» в систему знаний (модель, моделирование).

     Урок относится к типу урока открытия «новых знаний» через

создание проблемной ситуации.

     Шаг 2. Введение задачи на встречное движение.

     Задача №362 в теме «Буквенная запись свойств сложения и

Вычитания». Решение этой задачи – это применение теоретических

знаний по изучаемой теме на практическом примере, включает в

себя: формирование деятельности по построению модели задачи

(графической); использование модели для исследования и

открытия новых знаний (теоретических: скорость сближения,

время встречи) и включение в систему знаний.  

      Урок относится к типу урока открытия «новых знаний» через

 создания проблемной ситуации.

     Шаг 3. Урок-игра с элементами историзма.

     Цель: развитие мотивации учебной деятельности.

     Задачи: 1) создание ситуации успеха в учебной деятельности;

2) создание ситуации комфорта; 3) развитие коммуникативных

УУД.

     Играем четвёрками.

     Шаг 4. Урок развивающего контроля.

     Цель: успешная реализация знаний и умений по теме, которые

сформированы в результате его деятельности на уроке и дома.

     Тест и критерии оценивания реализуют принцип минимакса.

     Тест включает задания на сформированность: умения

анализировать текст, модель (схему); умения моделировать;

умения оформлять решение; умение осуществлять контроль.

Состоит из 6 заданий. Максимальное количество баллов 36.

Время выполнения 45 минут.

     Шаг 5. Творческий проект: создание учащимися сборника задач.

     Каждый учащийся выбирает тему (тип задачи на одновременное

движение 2х объектов), придумывает историю, после работы над

текстом, рисует историю.

     Проект предполагает обращение учащихся к учителям

словесности, изо, информатики.

     Итог проекта – это книжка (сборник задач) с историями и

рисунками учащихся 5 класса.

     Эта статья написана на базе диплома АППО «Работа с условием задачи на движение, как способ повышения качества обучения математики в 5-6 классах в школе с углублённым изучением предметов художественно-эстетического цикла»    СПб, 2017.

Литература  

1.        Асмолов А.Г. Системно- деятельностный подход в разработке стандартов нового поколения // Педагогика. – 2009 . – №2. – с.18-22

2.        Баранова И.В., Борчугова З.Г. и др. Математика. Учебник для 5 класса средних общеобразовательных школ. Дополнения к учебнику математика -5. –  СПб.:  СМИО Пресс, 2008.  

3.        Башмаков М.И.  Математика  5 класс  (в 2 частях). –  М.: Астрель, 2010.

4.        Башмаков М.И.  Математика  6  класс  (в 2 частях). – М.: Астрель, 2011.

5.        Бизухина И.Р. Деятельностный подход в обучении математики — путь повышения качества знаний учащихся основной школы: педагогический проект – Ульяновск, 2012 .  

6.        Виленкин Н.Я., Жохов В.И. и др. Математика 5 класс. – М.: Мнемозина, 2011.

7.        Виленкин Н.Я., Жохов В.И. и др. Математика 6 класс. – М.: Мнемозина, 2013.  

8.        Дорофеев  Г.В.,  Петерсон  Л.Г.  Математика   5  класс   (в  2  частях). – М.: Ювента, 2013.  

9.        Дорофеев Г.В.,   Петерсон Л.Г.   Математика   6  класс   (в  3  частях). – М.: Ювента, 2013.

10.         Зенкевич И.Г.  Эстетика урока математики: Пособие для учителей. – М.: Просвещение, 1981.

11.         Коротков, Э.М. Управление качеством образования / Э.М. Коротков. – М.: Академический проект, 2007.

12.         Международный стандарт ИСО 9000:2000. Управление качеством и обеспечение качества. Словарь.

Рассмотрим
большую группу задач, традиционно
считающихся трудными в обучении
школьников начальных классов, — это
задачи «на движение».

Трудность
этих задач для ребенка методически
обусловлена двумя причинами.

В
первую очередь, это содержательная
трудность. «Скорость» — это физическая
величина, связывающая две величины,
которые ребенок уже привык за период
предыдущего обучения воспринимать
каждую «саму по себе»: время и расстояние
(длина). Для осознания каждой из них
имеется либо визуальная опора (у длины,
которую можно непосредственно «оценить
глазом»), либо уже привычный за три года
обучения инструмент измерения — линейка,
часы. «Скорость» — это абстракция,
которую ребенок не может ни увидеть, ни
непосредственно измерить (т. е. «оценить»
хотя бы, как время). Сама запись «скорости»:
км/ч, м/мин — не имеет для ребенка никаких
аналогий, особенно сейчас, когда в
последней редакции традиционного
учебника математики не дается запись
дроби. И даже если она детям известна
(как в альтернативных учебниках), ее
способ чтения ничего не дает для понимания
смысла понятия «скорость».

Второй
причиной является технологическая
трудность. Долгие годы традиционный
курс математики впервые знакомил детей
со схемой задачи «в отрезках» именно
на задачах «на движение». Иными словами,
без всякой предварительной подготовки
к использованию графической символики
(обычно после 2—3 лет использования
задач краткой записи в качестве модели
при решении), ребенок должен был ее
освоить сразу на задачах с содержательно
трудным понятием «скорость». Эти задачи
появлялись во втором полугодии последнего
года обучения в начальной школе, поэтому
многие дети с таким трудом адаптируются
к ним— они просто не успевают так быстро
освоить одновременно новую величину с
ее сложностями и чертеж в отрезках.

С
точки зрения математической структуры
эти задачи не являются новым видом —
это задачи на пропорциональную
зависимость: расстояние (длина) прямо
пропорционально скорости и времени
движения; и обратно: скорость движения
обратно пропорциональна времени движения
при постоянном значении расстояния. Та
же зависимость наблюдается в задачах
«на куплю-продажу», «на площадь», «на
работу» и т. п. Однако многие учителя
полагают, что задачи «на движение»
представляют собой особую группу задач
нового вида, и при обучении их решению
нужны какие-то новые приемы. Докажем,
что заранее сформированное у ребенка
умение переводить словесно заданный
текст задачи на язык графики (в схему в
отрезках) является универсальным приемом
самостоятельной деятельности ребенка
при решении задачи на движение.

Задачи
«на движение», содержащие пропорциональные
величины, позволяют использовать как
таблицы, так и схематические чертежи,
причем последние являются, безусловно,
более наглядной моделью.

Прежде
чем приступить к решению задач, содержащих
такие величины, как «скорость», «время»
и «расстояние», необходимо разъяснить
учащимся само понятие скорости. При
этом следует опираться на опыт детей,
широко использовать практический и
наглядный методы.

Дети
часто употребляют в своей речи слова
«быстрее», «медленнее», не отдавая себе
отчета в том, что эти слова связаны со
скоростью (дети больше связывают их со
временем). Для разъяснения понятия
скорости можно задавать детям такие
вопросы:

— Кто
быстрее преодолеет данное расстояние:
автомобилист или велосипедист,
велосипедист или пешеход?

— Как
вы понимаете слова «быстрее пройдет
данное расстояние?»

— Чаще
всего ответ учащихся связан со временем:
«Пройдет за меньшее время».

— А
почему он пройдет за меньшее время? (Он
проходит в час расстояние большее.)
Значит,
его
скорость больше.

Понятие
о скорости конкретизируется в процессе
решения задач, например, таких:

Пешеход
за 3 ч прошел 15 км. В каждый час он проходил
одинаковое расстояние. Сколько километров
пешеход проходил в час?

Разбор
задачи следует сопровождать графической
моделью, на которой обозначаются данные
задачи: обозначим все расстояние отрезком
и отметим, что это расстояние он прошел
за 3 часа:

15
км

Поскольку
главная трудность при решении таких
задач состоит в том, что неподвижная
картинка является моделью равномерного
непрерывного процесса (движения), в
рисунок принято вводить стрелку,
символизирующую это движение и его
направление.

— Можно
ли найти на чертеже точку, в которой
окажется пешеход через час? Через 2 часа?

— Покажите,
откуда он вышел? Где пешеход окажется
через три часа?

— Что
можно сказать о длинах трех отрезков?
(Они
равные, так как за час пешеход проходил
одинаковое расстояние.)

— Как
найти это расстояние? (15:3.)

— А
можно ли узнать, сколько километров
пройдет пешеход за 4 ч (за 5 ч, за 6 ч)
двигаясь с той же скоростью?

— За
какое время он может пройти расстояние
в 35 км (40 км), если будет двигаться с той
же скоростью?

Поиск
ответов на такие вопросы поможет ученикам
глубже осознать пропорциональную
зависимость между скоростью, временем
и расстоянием.

Электропоезд
за 10 мин прошел 20 км, проходя каждую
минуту одинаковое расстояние. Сколько
километров проходил электропоезд в
одну минуту?

Спортсмен
преодолел 100 м за 10 с, пробегая за каждую
секунду одинаковое расстояние. Сколько
метров он пробегал за одну секунду?

При
решении таких задач учащиеся знакомятся
с различными единицами скорости,
усваивают, что скорость — это расстояние,
пройденное в единицу времени.

Для
закрепления понятия скорости можно
использовать и такие задания:

— Объясните,
как понимать следующие выражения:
«скорость самолета 810 км/ч», «скорость
электропоезда 120 км/ч», «скорость
лыжника18 км/ч», «космический корабль
летит со скоростью 7200 м/с».

Для
того чтобы учащиеся осознали зависимость
между скоростью, временем и расстоянием,
целесообразно рассматривать сразу по
три взаимообратные задачи, оформляя их
в таблицу.

Можно
предлагать задание:

Составьте
три взаимообратные задачи по этой
таблице.

Скорость	Время	Расстояние
?	4ч	20 км
5 км/ч	?	20 км
5 км/ч	4ч	?

Графическое
моделирование является наиболее
эффективным и целесообразным приемом
при решении большинства задач на
движение. Рассмотрим задачи:

Поезд
прошел некоторое расстояние за 10 час.
С какой скоростью шел поезд?

Строим
графическую модель:

?

10
ч

Одного
взгляда на чертеж достаточно, чтобы
обнаружить, что для ответа на вопрос не
хватает данных: не дано расстояние.

Скорость
велосипедиста 15 км/ч. Какое расстояние
он пройдет за 3 ч?

Типичной
ошибкой учащихся при решении данной
задачи является неправильный выбор
действия (15:3).

Построение
графической модели предупреждает эту
ошибку:

Чертеж
показывает, что для нахождения расстояния
нужно взять по 15 три раза: 15 • 3 = 45 (км).

Совершая
экскурсию по реке на катере, школьники
проплыли 66 км. При этом 2 ч они плыли со
скоростью 18 км/ч, а остальной путь — со
скоростью 15 км/ч. Сколько всего времени
находились в пути школьники?

Если
учитель планирует фронтальный разбор
этой задачи, он может воспользоваться
таблицей, которую заполняет в процессе
разбора текста с детьми. Графическая
модель к этой задаче является более
наглядной и удобной для выполнения в
тетради — по ней легко определить путь
решения:

Мотоциклист
ехал 3 ч со скоростью 60 км/ч и 2 ч со
скоростью 70 км/ч. Какое расстояние
проехал он за все это время?

В
процессе разбора текста и вычленения
данных целесообразно составить
графическую модель:

Опираясь
на чертеж, легко составить к этой задаче
выражение: 6 • 3 + 70 • 2.

Туристы
за день прошли пешком 18 км и проехали 2
ч на автобусе со скоростью 45 км/ч. Какой
путь проделали туристы за день?

Таблица
к данной задаче выглядит таким образом:

Скорость	Время	Расстояние
?	?	19 км
45 км/ч	2ч	?

При
разборе задачи она фактически не
работает, поскольку неизвестные скорость
и время в первой строке не нужны для
решения задачи, в то время как использование
графической модели поможет учащимся
быстро найти решение:

При
решении некоторых задач полезно часть
условия записать в виде таблицы, а затем
применить прием графического моделирования.

Из
двух городов, расстояние между которыми
1200 км, вышли одновременно навстречу
друг другу два поезда. Один из них может
пройти это расстояние за 20 ч, другой —
за 30 ч. Через сколько часов поезда
встретятся?

Скорость	Время	Расстояние
I —?	20 ч	1200 км
II — ?	30 ч	1200 км

Анализ
таблицы дает возможность найти скорость
поездов:

1.
1200 : 20 = 60 (км/час)

2.
1200 : 30 = 40 (км/час)

После
этого строится графическая модель:

Чертеж
дает наглядное представление о движении
поездов навстречу друг другу, облегчая
поиск дальнейшего пути решения.

Расстояние
от города до поселка велосипедист
проехал за 3 ч со скоростью 16 км/ч.
Возвращаясь обратно, он то же расстояние
проехал за 4 ч. С какой скоростью ехал
велосипедист на обратном пути?

Для
решения задачи можно использовать как
графическую модель, так и таблицу.

Графическая
модель:

Скорость	Время	Расстояние
16 км/ч	З ч	? одинаковое
?	4 ч	?

Визуальный
анализ рисунка подсказывает путь решения
задачи, при этом сразу, еще до решения
можно сказать, что скорость во втором
случае будет меньше ~- это подсказывает
рисунок.

После
решения задачи полезно обратить внимание
учащихся на взаимозависимость скорости
и времени (чем больше скорость, тем
меньше времени будет затрачено на
дорогу, и наоборот). Для этого можно
предложить сравнить скорость движения
велосипедиста и подумать, почему на
обратный путь велосипедист затратил
больше времени. (Потому,
что скорость была меньше.)

Особое
место в этой группе занимают задачи на
движение в противоположных направлениях
(на сближение и удаление).

При
их решении целесообразно использовать
графическую модель, так как она дает
наглядное представление о характере
движения и во многом облегчает поиск
решения задачи.

Два
пешехода одновременно вышли навстречу
друг другу. Через 4 ч они встретились.
Скорость первого пешехода 5 км/ч, скорость
второго — 6 км/ч. На каком расстоянии
первоначально находились пешеходы друг
от друга?

При
составлении графической модели необходимо
довести до понимания учеников тот факт,
что оба пешехода находились в пути
одинаковое время.

С
этой целью на подготовительном этапе
можно предложить ряд таких заданий:

Два
автомобиля выехали одновременно
навстречу друг другу и встретились
через 7 ч. Сколько времени находился в
пути каждый автомобиль?

Коля
и Таня вышли одновременно в школу каждый
из своего дома. Через 10 мин они встретились
в школе. Сколько минут был в пути Коля?
Сколько минут была в пути Таня?

Такого
рода задания помогут учащимся осознать
характерный момент задач на встречное
движение: одинаковое время в пути для
обоих сближающихся объектов (или
удаляющихся).

Графическая
модель уже визуально наводит учеников
на два способа решения этой задачи:

I.
1)5
-4
= 20 (км) II. 1)6
+ 5 = 11 (км/ч)

2)
6 + 4 = 24 (км) 2) 11 -4
= 44 (км)

3)
20 + 24 = 44 (км)

При
решении задачи вторым способом можно
ввести термин «скорость сближения»,
разъяснив его по графической модели.
Учитель может сдвигать одновременно
навстречу друг другу фигурки пешеходов,
каждый раз на одно деление. Это значит,
что прошел 1 час пути.

–
На сколько приблизились (сблизились)
друг к другу за 1 час пешеходы? (На5
+ 6=11
км/ч)

Обращаем
внимание детей на то, что складываются
скорости, поэтому в наименовании ответа
тоже скорость.

Далее
учащиеся рассуждают так: «За
1 ч пешеходы сблизились на 11 км; за 4 ч
они сблизятся на 11 -4
км».

Работая
с данной задачей, целесообразно
использовать различные методические
приемы и прежде всего рассмотреть задачи
обратные данной. Их можно предложить в
графическом виде, облегчающем детям
самостоятельное составление обратной
задачи:

Составьте
по чертежам три обратные задачи.

После
рассмотрения обратных задач можно
предложить учащимся вопросы:

— Ближе
к какому пункту произойдет встреча?

Если
в задаче даны обе скорости, то с помощью
готового чертежа или при его выполнении
полезно выяснить, почему пункт встречи
находится ближе (или дальше) к одному
из пунктов отправления, чем к другому.
Если сначала известна только одна из
скоростей, то данный вопрос полезно
задать уже после решения задачи.

— Какое
расстояние будет между пешеходами через
час после встречи, если они продолжали
двигаться в тех же направлениях?

Обратим
внимание детей на то, что «скорость
сближения» равна «скорости удаления».

— Могли
ли пешеходы встретиться в середине
пути?

— Кто
из них придет в конечный пункт первым?

Можно
использовать целый ряд приемов с целью
подготовки учащихся к решению более
сложных задач. Например, можно изменить
данные в условии задачи и предложить
детям составить задачу по такому чертежу:

— Поставьте
вопрос к задаче по рисунку (На
каком расстоянии друг от друга будут
находиться пешеходы через 4ч?) и решите
задачу.

Выполнение
задания такого рода формирует умение
читать чертеж, умение трансформировать
(видоизменять) условие и решать задачи
усложненного вида.

Аналогичный
прием постепенного усложнения условия
можно использовать и при решении задач
на удаление в противоположных направлениях.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Инфоурок

›

Математика

›Презентации›Презентация “Моделирование при обучении решению задач на движение”

Презентация “Моделирование при обучении решению задач на движение”

Математическое моделирование при решении задач на движение

Составление геометрических моделей

Медведева Галина Валериевна,

Учитель математики

МБОУ Ржавская СОШ

Допущения в задачах на движение Закон прямолинейного и равномерного движения

если нет специальных оговорок, то движение считают прямолинейным и равномерным скорость считается величиной положительной любой переход с одного режима движения на другой считается происходящим мгновенно

х = vt + х0 х – координата тела в момент времени t х0 – координата тела в начальный момент времени v – скорость движения тела

График прямолинейного и равномерного движения тела

1. Тело начинает движение сразу вместе с сюжетом задачи, из начального пункта 2. Тело начинает движение из пункта B, удаленного от О на расстояние х0 3. Тело начинает движение спустя некоторое время t0 от начала сюжета задачи 4. Тело начинает движение вместе с сюжетом задачи из другого пункта, удалённого от начального на х км, во встречном направлении

График прямолинейного и равномерного движения тела

Скорость первого тела в а раз меньше (больше) скорости второго тела S1 = хB – хA S2 = хD – хC S2 = аS1

Задача1. Из пункта А в пункт В выехал грузовик. Через час из пункта А выехал легковой автомобиль. Через 2 часа после выезда он догнал грузовик и прибыл в пункт В на 3 часа раньше грузовика. Сколько времени грузовик ехал от А до В?

Решение:
vа – скорость автомобиля vг – скорость грузовика
vг vа, хг = vг t, ха = vа t + х0

∆AOC ~ ∆FOG → OC : OG = AC : FG = 1 : 3 ∆COE ~ ∆GOD → OE:OD=CO:OG= 1 : 3 ∆AOE ~ ∆FOD → AE : FD = OE : OD = 1 : 3 DF = 9 BF = 12 Ответ. 12 ч.

Задача 2. Из пункта А в пункт В, удаленный от А на 10 км, выехали велосипедист и мотоциклист. Одновременно с ними из пункта В навстречу им вышел пешеход. Когда мотоциклист встретил пешехода, велосипедист отставал от мотоциклиста на 5 км. На сколько километров мотоциклист обгонит велосипедиста в тот момент, когда велосипедист встретит пешехода?

Решение: vп – скорость пешехода, vв – скорость велосипедиста,vм – скорость мотоциклиста,vп vв vм, хм = vм t, хв = vв t, хп = – vп t + 10

BA = 2DC, BA||DC → DС-средняя линия ∆АВЕ → BD = DЕ ∆ ABD = ∆FED → FE = AB →FE = 10 км Ответ. 10 км.

Задача 3. По сигналу дрессировщика два пони одновременно побежали равномерно вдоль внешней окружности арены цирка в противоположных направлениях. Первый пони бежал несколько быстрее второго и к моменту встречи пробежал на 5 м больше, чем второй. Продолжая бег, первый пони подбежал к дрессировщику, остававшемуся на том месте, от которого начали бежать пони, через 9 с после встречи со вторым пони, а второй – через 16 с после их встречи. Какова длина внешней окружности арены цирка?

Решение: v1 – скорость первого пони, v2 – скорость второго пони
v2

∆NOC ~ ∆HOA → NO : HO = NC : HA ∆NOB ~ ∆HOD → NO : HO = BN : HD→ NC : HA = BN : HD → 9 : HA = HA : 16 → HA = 12 NO : (NO + 5) = 9 : 12 → 12NO = 9NO + 45 → NO = 15, НО=20 → NH = 35 Ответ. 35 м.

Литература

1. 3000 конкурсных задач по математике / Е.Д.Кулагин и др. – Изд. 8-е, испр. – М.: Айрис-пресс, 2005.

2. Сборник задач для поступающих во втузы / В.К.Егерев, В.В.Зайцев, Б.А.Кордемский и др.; Под ред. М.И.Сканави. – 6-е изд. – М.: ООО «Издательский дом «ОНИКС 21 век»: ООО «Издательство «Мир и Образование», 2005.

3. Мясникова Т.Ф. Графическое моделирование в задачах на движение // Математика в школе, 2005. – № 5.

4. Хабибуллин К.Я. Моделирование ситуаций в процессе решения задач на движение // Математика в школе, 2003. – № 8.

5. Мардахаева Е.Л. Геометрические модели и задачи на движение // Математика в школе, 2010. – № 6.