Введение.
Умение решать текстовые задачи является одним из основных показателей уровня математического развития ребёнка, глубины усвоения им учебного материала. К сожалению, не
все учащиеся умеют и любят решать задачи. Это происходит потому, что дети не научены анализировать данные, видеть взаимосвязь между искомым и данным, структурировать ход решения. А при отсутствии потребности в глубоком осмыслении описанных в задаче связей у ребёнка формируется прочная привычка сводить решение к простому вычислению. Организация работы, заключающаяся в многократном прочитывании, устном анализе, составлении только краткой записи оказалась неинтересной и малоэффективной. Фронтальный анализ и решение задачи ограничивается правильными ответами двух-трёх человек, а остальные просто записывают готовые решения без глубокого понимания.
Так передо мной встала серьёзная проблема: как, используя традиционный УМК по математике ( программа М.И.Моро, М.А.Бантовой, Т.В.Бельтюковой ), анализировать задачу более продуктивно, чтобы она из просто арифметической превратилась в развивающую? Можно ли научить самостоятельно решать задачи каждого ученика?
Изучив теоретические подходы к обучению решать задачи, а также разнообразные практические приёмы, я пришла к выводу, что можно. Главное для каждого ученика на этом этапе – понять задачу, т.е. уяснить о чём эта задача, что в ней известно, что нужно узнать, как связаны между собой данные, каковы отношения между данными и искомыми параметрами и т.т. Для этого надо применять моделирование задачи и учить этому детей.
Цель моей работы: показать, что приём моделирования задачи позволяет сделать каждую задачу учебника развивающей, нестандартной, многогранной.
Задачи: – разработать методические рекомендации по использованию разных моделей при решении задач;
– накопление дидактического материала, используемого как для всего класса,
так и для индивидуальной работы учащихся;
Я предлагаю пособие, которое рекомендую использовать при изучении важной темы программы по математике: «Решение текстовых задач». Оно может оказать практическую помощь учителям, как в организации работы на уроке, так и в индивидуальной работе в классе и дома.
Методическое пособие содержит следующие разделы:
1. Справочный материал. Виды моделей задач. В нём я кратко рассказываю о видах моделей, которые применимы к задачам , и когда целесообразно с ними знакомить учащихся.
2.Методика работы с каждой моделью.
В пособии показана работа над задачей, используя приём моделирования. Приведены конкретные примеры и предложен фрагмент урока по теме. « Решение задач алгебраическим и арифметическим способом », используя приём моделирования.
3.Приложение. Дидактический материал.
Дидактический материал, который использую на уроке со всем классом, а также в индивидуальной работе.
Так что же такое моделирование? Моделирование-это процесс построения моделей
для каких-либо познавательных целей. Для простоты восприятия учеником какого-либо предмета или ситуации, описанной в задаче, я применяю модель. Постепенно моделирование стало неотъемлемой частью каждого урока математики в моём классе.
Систему работы по усвоению детьми моделирования задачи я разбиваю на три этапа:
1.Обучение детей преобразованию предметных действий в работающую модель.
2.Обучение детей составлению обратных задач к данной на основе работы с моделью.
3.Творческая работа детей над задачей на основе использования модели.
После систематической работы учащиеся добились следующих результатов: изучили
шесть видов моделей; научились применять в одной и той же задаче несколько видов моделей ( с целью выбора каждым учеником наиболее понятной ему модели );
сравнивать несколько моделей между собой ( с целью выбора наиболее рациональной );
выбирать наиболее подходящую к предложенной задаче. На основе моих наблюдений за детьми в процессе этой деятельности я пришла к выводу. Мои ученики не боятся самостоятельно начать анализ задачи; в случае неудачи они, используя другую модель, анализируют задачу вновь.
Следовательно, моделирование помогает вооружить ребёнка такими приёмами, которые позволяют ему при самостоятельной работе над задачей быть активным, успешным, не бояться трудностей. Каждый, не сравнивая себя с другими, выбирает собственный путь рассуждения, моделирования и, следовательно, решения задач.
Справочный материал. Виды моделей.
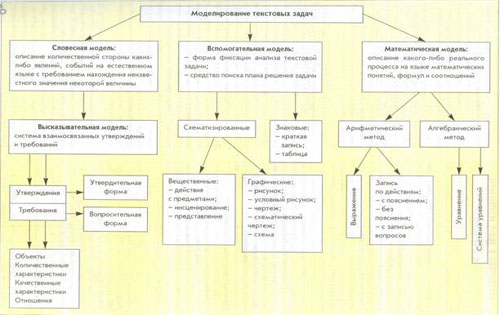
Вспомогательная модель.
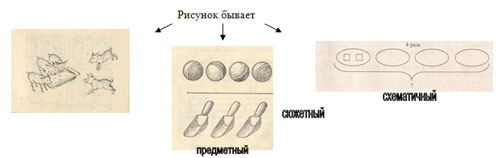
1. Рисунок. Знакомство с этой моделью начинаю в 1 классе Во-первых, рисование- любимый вид деятельности малышей, во-вторых, приём хорош для развития моторики рук, в-третьих, рисование является развивающим упражнением.
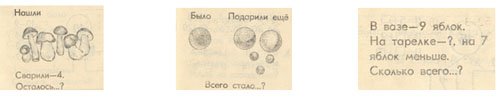
2.Краткая запись. С этой моделью начинаю работать в конце 1-го класса. Удачное введение краткой записи параллельно с рисунком.
3.Таблица. Знакомлю с этой моделью в конце 1-го, начале 2-го класса.
| Было | Вынесли | Осталось | Цена | Количество | Стоимость | v | t | s | ||
4.Чертёж. Применяю тогда, когда числовые данные в задаче удобные, позволяющие начертить отрезок заданной длины.

5.Схема. Знакомлю в начале 2-го класса. Подбор задач в этом классе позволяет применять эту модель на материале обратных задач, при решении задач разными способами.

6.Блок-схема (разбор задачи аналитическим способом, то есть с вопроса). Изучение этой модели возможно уже в конце 2-го класса, когда все предыдущие модели изучены хорошо, широко и системно используются на уроке
Методика работы с моделями.
1.Рисунок. Он должен изображать реальные предметы (кубики, платки, яблоки и т. д.), о которых говорится в задаче, или условные предметы в виде геометрических фигур.
Пример. Когда с полки сняли 2 книги, там осталось 4. Сколько книг лежало на полке сначала?
У. Сколько книг осталось на полке? 4
Изобразим.
![]()
У. Раньше книг было больше или меньше? Почему?
Д. Больше. Здесь нет книг, которые сняли с полки.
У. Знаем ли мы, сколько книг было сначала? Нет.
Покажем это скобкой или дугой и вопросительным знаком.

У. Почему книг стало меньше?
Д. С полки сняли две книги.
У. Изобразим две книги внизу, под скобкой.

У. Как узнать, сколько всего книг было на полке?
Д. Нужно сложить книги, которые остались на полке, и те, которые сняли.
1.1. Следующим шагом в работе над этой задачей будет составление новой модели –
это краткая запись и таблица. Краткая запись – представление в лаконичной форме содержание задачи, выполненное с помощью опорных слов.
|
Было |
Подарила |
Осталось |
|
? |
2к. |
5к. |
Было – ?
Подарила – 2к.
Осталось – 5к.
Слово «подарила» говорит младшему школьнику о том, что количество книг уменьшилось, значит, нужно производить вычитание. Так в сравнении дети видят какая из моделей позволяет проследить за количественными изменениями в задаче.
2.Таблица. Наиболее удачно применение таблицы при решении задач на тройку пропорциональных величин: цена – количество – стоимость; расход на 1 шт.- количество штук – общий расход; масса – количество – общая масса; скорость – время – расстояние; и т. д.
Пример. «Из двух городов, расстояние между которыми равно 1200 км, одновременно вышли навстречу друг другу два поезда. Один из них проходит это расстояние за 20ч., а другой – за 30 ч. Через сколько часов поезда встретятся?»
При решении задач на движение, учителя часто используют схематический чертёж.

2.1.Однако, такой чертёж может направить ученика по неверному пути, так как два времени могут подтолкнуть ребёнка к сложению соответствующих чисел, а затем к делению расстояния на полученный результат. Поэтому целесообразнее использовать таблицу.
|
скорость |
время |
расстояние |
|
|
1 поезд |
? |
20 ч. |
1200 км |
|
2 поезд |
? |
30 ч. |
1200 км |
2.2.После того как найдены скорости поездов, нужно выполнить схематический чертёж с целью осознания учащимися сути второй части задачи.
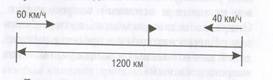
2.3.Данный чертёж даёт возможность учащимся представить и осознать задачную ситуацию, что, в свою очередь, помогает понять и закончить решение:60+40=100км/ч; 1200:100=12ч
Вот теперь дети сами могут составить модель задачи , используя таблицу, и выявить все ситуации, все данные и искомые.
|
скорость |
время |
расстояние |
|
|
1 поезд |
? |
20 ч. |
1200 км |
|
2 поезд |
? |
30 ч. |
1200 км |
|
1 и 2 поезда |
? |
? |
1200 км |
Опираясь на данную модель, путь решения задачи легко находится в процессе рассуждений как «от данных к вопросу», так и «от вопроса к данным».
3.Рассуждая «от данных к вопросу», получим схему (рис.1), которую называют моделью поиска решений данной задачи. Рассуждая «от вопроса к данным (блок-схема) модель будет иметь другой вид (рис.2.)
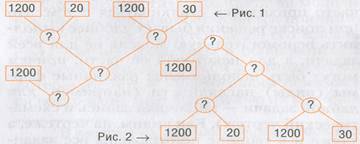
4. Схема –это чертёж, на котором все взаимосвязи и взаимоотношения величин передаются приблизительно, без соблюдения масштаба,
Пример. « Из двух кусков ткани сшили 18 одинаковых занавесок. В первом куске было 30 м , во втором – 24 м. Сколько занавесок сшили из каждого куска?»
Обычно условие записывают в таблицу.
|
Расход на одно платье |
Количество изделий |
Общий расход |
|
одинаковый |
? |
30 м |
Однако по этой модели рассуждение у детей вызывает затруднение. Детям трудно увидеть ,что нужно знать для определения расхода ткани на одну занавеску. Я рекомендую использовать такую схему.
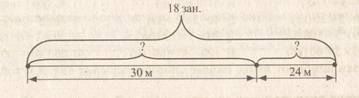
Понимание облегчается тем, что на схеме один и тот же отрезок изображает и (30+24)м ткани, и 18 занавесок.
5.Чертёж. Применяют эту модель, если числовые данные в задаче удобные, позволяющие начертить отрезок заданной длины. Ученики должны усвоить поэтапное выполнение чертежа.
Пример. « Когда шланг длинной 5 метров удлинили на несколько метров, то получился шланг длиной 8 метров. На сколько метров удлинили шланг?
Этапы работы.
Какой длины был сначала шланг? (5 м)
Какой длины вычерчиваем первый отрезок? (5см)
Что произошло со шлангом? (Увеличился на несколько метров.)
Как изменится отрезок?( Увеличится на несколько сантиметров.)
Какой длины стал шланг?(8м)
Какой длины станет наш отрезок?(8см)
Отметим на чертеже , насколько увеличился наш отрезок.
Что нужно узнать в задаче?
Как на нашей модели отмечено искомое?

Далее выбирается арифметическое действие.
Пример. « У Васи 2 машинки, а у Коли в 3 раза больше, чем у Васи. Сколько машинок к Коли? » Чертёж имеет такой вид.
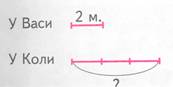
Далее выбирается арифметическое действие.
Фрагмент урока
Тема. Алгебраический и арифметический способ решения задач ( 2 класс )
Цель. – учить решать задачи разными способами;
– развивать умения сравнивать, анализировать, делать вывод;
– воспитание самостоятельности, творческой активности;
Ход урока.
1.Актуализация опорных знаний
– Составь разные задачи по выражению
28 – 16
– Выбери модели к этим задачам
Дети выходят к доске и из предложенных моделей выбирают следующие:

2. Освоение новых знаний
– Какая из ваших моделей подойдёт к этому уравнению?
28 – Х = 16
После сравнения и обсуждения дети выбирают
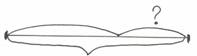
– Проговорите текст задачи. ( В магазине было 28 ящиков груш, когда несколько продали , осталось 16. Сколько ящиков груш продали?)
– Решим это уравнение. Какой компонент неизвестен? Как его найти?
Мы использовали уравнение для решения задачи . Это алгебраический способ решения задачи. ( Вывешиваю аншлаг слова алгебра. Поясняю, что алгебра – это раздел математики, который изучает буквенные выражения ,)
–А теперь решите эту задачу арифметическим способом ( Вывешиваю аншлаг слова
арифметика и поясняю, что это раздел математики, который изучает свойства чисел и действия над ними,)
На доске появляется такая запись
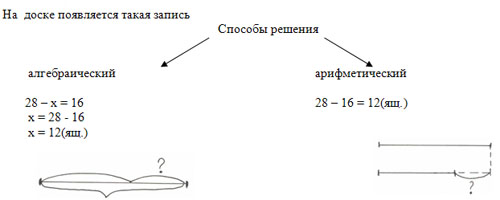
Делаем с ребятами вывод о том, что одну и ту же задачу можно решить разными способами .
-А как помогают модели в решении задачи? ( Помогают выбрать способ её решения )
Наряду с выше изложенным, педагог должен помнить, что одного составления модели к задаче недостаточно. Следует включать и обратные задания, а именно: составление текстов задач по модели. Учащиеся могут работать за партой и у доски, используя набор цифр.
Смотри приложение 1
Математика, 2 класс
Урок № 11. Модели задачи: краткая запись задачи, схематический чертёж
Перечень вопросов, рассматриваемых в теме:
- Как составить краткую запись и схематический чертеж к задаче?
- Как различать задачи на нахождение неизвестного уменьшаемого и на нахождение неизвестного вычитаемого?
Глоссарий по теме:
Компоненты вычитания – уменьшаемое, вычитаемое, разность.
Задача на нахождение неизвестного вычитаемого, в этой задаче находится вычитаемое (из уменьшаемого отнять разность)
Задача на нахождение неизвестного уменьшаемого, в этой задаче находится уменьшаемое (к разности прибавить вычитаемое)
Краткая запись – это коротко записанное условие задачи, последним в краткой записи пишется вопрос к задаче.
Схематический чертеж к задаче – это чертеж «в отрезках», схематическое изображение отношений между данными и искомым
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.28-29
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 18, 19
Теоретический материал для самостоятельного изучения
Научимся решать новые виды задач. Задача первая. На ветке было несколько птиц. Когда пять птиц улетели, на ветке осталось семь птиц. Сколько птиц было на ветке?
Сделаем краткую запись задачи. Было- ? Улетели- 5 пт. Осталось- 7 пт.
Сделаем схематический чертеж к задаче.

Начертим отрезок, который показывает, сколько птиц осталось, подпишем 7 птиц. Причертим к концу отрезка еще один отрезок, обозначающий улетевших птиц, подпишем 5 птиц. Сколько было птиц на ветке, неизвестно, поставим знак вопроса.
Рассмотрим краткую запись и чертёж к задаче
Каким действием будем решать задачу?
Правильно, чертёж нам подсказывает, что задача решается сложением, так как надо найти сумму отрезков.
Часть птиц улетели и часть осталось. Значит, мы находим уменьшаемое. А уменьшаемое находится действием сложением.
Запишем решение задачи.
7+5=12(пт.)
Ответ: 12 птиц.
Этот вид задачи называется на нахождение неизвестного уменьшаемого. Так как в этой задаче находим уменьшаемое.
Решим вторую задачу.
На клумбе было одиннадцать тюльпанов. Когда несколько тюльпанов завяло, то осталось шесть тюльпанов. Сколько тюльпанов завяло?
Сделаем краткую запись условия задачи и чертёж.
Было-11т. Завяло-? Осталось-6т.
Сделаем схематический чертеж.
6т. ?
11 т.
Начертим отрезок, обозначающий все тюльпаны. Подпишем его 11 тюльпанов. Отложим на отрезке отрезок равный оставшимся тюльпанам, подпишем 6 тюльпанов. Другой отрезок, обозначает, сколько тюльпанов завяло, это неизвестно, ставим знак вопроса.
Решим задачу. Узнать сколько тюльпанов завяло, значит надо узнать, на сколько тюльпанов стало меньше. Задача решается вычитанием. По чертежу видно, что неизвестна разность отрезков. Как называется число 11? Уменьшаемое. Как называется число 6? Разность. Неизвестно в задаче вычитаемое. Как найти вычитаемое? Из уменьшаемого вычесть разность.
11-6=5 (т.)
Ответ: 5 тюльпанов завяло.
Такой вид задач называется “на нахождение неизвестного вычитаемого”.Так как в этой задаче находим вычитаемое.
Сделаем вывод: правильно составленная краткая запись задачи подсказывает, каким компонентом является каждое число в задаче: уменьшаемым или вычитаемым. Правильно начерченный схематический чертеж подсказывает, каким действием решать задачу. По чертежу видно, что находим сумму или разность отрезков.
Тренировочные задания.
1. Решите задачу, выберите правильное решение
На стоянке было несколько машин. Когда уехало 8 машин, то осталось 7 машин. Сколько машин было на стоянке?
Варианты ответов:
1. 8-7=1 (м.)
2. 8+7=16 (м.)
3. 8+7=15 (м.)
Правильный вариант:
3. 8+7=15 (м.)
2. Вставьте подходящие слова в предложения
Чтобы найти неизвестное слагаемое, надо ______ вычесть известное слагаемое. Чтобы найти неизвестное __________, надо к разности прибавить вычитаемое. Чтобы найти вычитаемое, надо ________вычесть разность
Правильный вариант:
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое.
Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.
Чтобы найти вычитаемое, надо из уменьшаемого вычесть разность.
На прошлом уроке нами была установлена взаимозависимость между математическим языком и математической моделью. Теоретический базис заложен, так что теперь самое время переходить к практике. Далее мы подробнее рассмотрим составление математической модели и простые задачи, решаемые с помощью математической модели.
На первых порах тема может даваться с трудом. Но есть хорошая новость. Составление математической модели — это во многом навык.
Чем больше типовых задач вы нарешаете, тем проще вам будет ориентироваться в моделировании.
Этапы составления математической модели
Ранее мы описывали, что этапы составления математической модели включают в себя:
| 1. Наблюдение | 2. Моделирование | 3. Предсказание |
|---|---|---|
| Анализ задачи; на основе анализа подготовка частей будущей математической модели. | Логическое объединение частей и составление математической модели. | Использование составленной математической модели для заключений по вопросу задачи. |
С практической точки зрения наибольшую сложность представляют два первых этапа — наблюдение и моделирование. Чтобы их успешно завершать, необходимо умение правильно переводить текстовые утверждения на язык математики.
Что нужно хорошо понимать. На этапе наблюдения обычно переводятся части будущего алгебраического выражения. В процессе этапа моделирования эти части объединяются.
«Типовая задача»?
Еще раз подчеркнем, что задачи для седьмого класса, решаемые с помощью математической модели, являются типовыми. Что это означает? Они отличаются одинаковостью алгоритма решения.
Логика вычислений в них зациклена. А составление математической модели от задачи к задаче также следует одной схеме.
Например, пусть дана части задачи:
«Стоимость яблочного сока $x$ рублей, а томатного — $y$ рублей. Известно, что $5$ стаканов яблочного сока стоят столько же, сколько $6$ стаканов томатного…»
То, как составлена задача, подводит нас к двум концепциям — приравниванию и умножению. Опорным для решения будет следующее алгебраическое выражение:
$$5x=6y$$
Раз задача типовая, то выражения наподобие «$ax=by$» непременно встретятся еще раз, просто уже, так скажем, не в контексте сока. Вот почему мы выше говорили про то, что составление математической модели — это навык. Оно же умение отбросить текст и увидеть алгебру за ним.
Задачи на наблюдение и моделирование
Рассмотрим далее некоторые задачи, решаемые с помощью математической модели, в которых опущен этап наблюдения — где нет вывода ответа. Это поможет освоиться в основных типах учебных задач и научит выражать важные части текста алгебраически.
Операции сложения и вычитания
Задача. Первый рабочий выполняет порученное задание за $x$ часов, второй то же задание — за $y$ часов, при этом первый работает на три часа больше, чем второй.
Решение
Между производительностью двух рабочих можно установить отношение равенства, но с учетом условия «на три часа больше». Для начала составим каркасное тождество, которое дополним далее:
$$x=y$$
«Полноправно» приравнять данные переменные мы можем, только дополнив, что первый рабочий ($x$) работает на три часа больше. Интуитивно так и хочется переписать тождество следующим образом:
$$x+3=y$$
Однако это неверное составление математической модели для данной задачи. Мало того, что по условию очевидно неравенство $x>y$, так еще и тождество с частью «$x+3$» увеличивает разрыв между значениями $x$ и $y$ на лишние три раза.
Чтобы производительность рабочих все-таки приравнять, у первого, наоборот, нужно «отобрать» три часа и «отдать» их тому, кто работает быстрее:
$$x=y+3$$
Операции умножения и деления
Задача. На двух стройках трудится одинаковое количество рабочих. На первой стройке работает 5 бригад по $x$ человек в каждой, на второй стройке — 3 бригады по $y$ человек в каждой.
РЕШЕНИЕ
Первая стройка. В одной бригаде трудится $x$ человек. По условию таких бригад пять. Откуда получаем количество человек всего, трудящихся на первой стройке: $5x$.
Вторая стройка. Здесь же в одной бригаде трудится $y$ человек. По условию имеем три бригады. Следовательно количество работников, трудящихся на второй стройке: $3y$.
Также нам известно, что на двух стройках работает одно и то же количество рабочих. Остается данные части приравнять, чтобы получить тождество:
$$5x=3y$$
Вот, буквально мгновение — и мы вновь увидели составление математической модели коэффициентного типа «$ax=bx$».
Задачи, решаемые с помощью математической модели, со смешанной арифметикой
Задача. У Кати $x$ марок, а у Димы $y$ марок. Если Катя отдаст Диме 5 марок, то у Димы станет марок вдвое больше, чем останется у Кати.
РЕШЕНИЕ
Внимание на следующие части текста задачи:
| «Отдаст пять марок…» | «Вдвое больше» |
| Сложение/вычитание | Умножение/деление |
В зависимости от того, какая часть тождества отражает данные положения, операция может быть как прямой («Катя отдаст, $x-5$»), так и обратной («Дима возьмет, $y+5$).
Разделим составление математической модели задачи на два шага.
1. Катя отдает Диме 5 марок и у нее остается $x-5$ марок. Теперь у Димы $y+5$ марок.
2. В результате у Димы марок в два раза больше.
Однако нам нужно количество марок ребят приравнять. Раз у Димы их по условию задачи больше, то для равенства с количеством марок Кати у него их должно быть меньше. Значит, мы можем либо умножить количество марок Кати на 2, либо разделить количество марок Димы на 2:
| $$2(x-5)=y+5$$ | $$x-5=frac{y+5}{2}$$ |
Составление математической модели — полные задачи
Самое время усложнить содержание задач и ввести все этапы составления математической модели, включая этап планирования. Далее мы решим ряд показательных задач, где требуется дать ответ.
Задача. В двух залах кинотеатра 460 мест. Сколько мест в большом зале, если в нем в 3 раза больше мест, чем в малом?
РЕШЕНИЕ
Заметим, что в данном случае составление математической модели задачи будет вестись в двух направлениях. С одной стороны, устанавливается алгебраическое равенство между количеством мест в залах. С другой стороны, нам известна их сумма. Составим эти выражения.
Приравнивание. Пусть количество мест в большом зале равняется $x$. Вместо того, чтобы вводить лишнюю переменную $y$ для количества мест в малом зале, выразим места малого зала через уже введенную переменную $x$ — как $frac{x}{3}$. Это краткая модель записи:
$$y=frac{x}{3}$$
Сложение. Всего в залах 460 мест. Количество мест в большом зале $x$, в малом — $frac{x}{3}$, одна треть от мест в большом. Вместе:
$$x+frac{x}{3}=460$$
Задаче требуется ответ; этапы составления математической модели должны завершаться в полном объеме. С этой целью мы и взяли за «главную» переменную количество мест в большом зале. Остается решить уравнение выше.
$$frac{4}{3}x=460\x=345$$
Ответ: 345.
Составление математической модели — задачи на движение
Задача. От пристани отошел теплоход со скоростью 22 км/ч, а от другой пристани навстречу ему через три часа отошел теплоход со скоростью 26 км/ч. Расстояние между пристанями составляет 306 км. Сколько времени в пути был каждый из теплоходов до встречи?
Для решения нам понадобится формула пути:
$$S=vt$$
Этап наблюдения
Время в пути — искомый параметр, введем его в качестве переменной $t$.
Пусть $t_1$ — это количество времени, затраченное первым теплоходом на преодоление всего своего пути. Сколько при этом затратил времени второй теплоход? На три часа меньше, ведь по условию от пристани он отошел в сравнении с первым с задержкой:
$$t_1-3$$
Этап моделирования
Каркасная модель выглядит так:
$$v_{1}t_1+ v_{2}t_2=S,$$
где $S$ — расстояние между пристанями, $v_1$ — скорость первого теплохода, $v_2$ — скорость второго, $t_1$ и $t_2$ — соответствующее время в пути.
Откуда взялась модель? Зарисуем перемещение теплоходов, что бывает иногда очень полезно при решении задач на движение. Теплоходы двигаются навстречу друг другу. Значит, в сумме они проходят расстояние между пристанями.
Доработаем модель и добавим в нее имеющиеся у нас данные:
$$22t_1+26(t_{1}-3)=306$$
Этап предсказания
Остается решить уравнение, найти значение $t_1$ и вычесть из него 3, чтобы получить $t_2$.
$$22t_1+26t_1=306+78\t_1=8$$
Первый теплоход затратил 8 часов. Второй, соответственно, 5 часов.
Ответ: 8 и 5.
Решите сами!
Показать решение
Спрятать решение
🔵 РЕШЕНИЕ
Не очевидно, но за переменную $x$ удобно взять количество учащихся в старших классах. Почему — увидите далее.
Выразим количество учащихся в начальных и средних классах также через $x$. Для этого проанализируем утверждения, заданные условием задачи.
Утверждение первое: «В начальных классах учащихся в три раза больше, чем в старших». Раз их в три раза больше, то количество учеников в начальных классах через $x$ — это $3x$.
Утверждение второе: «В начальных классах учащихся в два раза меньше, чем в средних». Количество учащихся в начальных классах мы выразили ранее как $3x$. Сколько тогда учеников в средних классах? В два раза больше, то есть $2cdot{3x}=6x$.
Остается составить модель:
$$x+3x+6x=900$$
Решаем и находим количество учеников в старших классах ($x$):
$$10x=900\x=90$$
Откуда получаем, что в начальных классах учится 270 учеников ($3x$), а в средних классах — 540 учеников ($6x$).
Ответ: 270, 540, 90.
Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.
Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.
Пример:
Решение любой текстовой задачи можно разделить на несколько основных этапов:
- Работа с условием
- Составление математической модели
- Проверка ответа
Работа с условием
Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.
Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?
Иллюстрация:
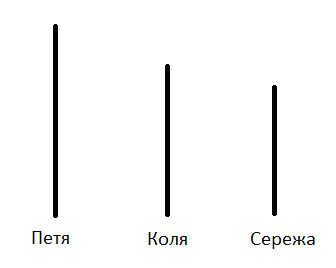
Из рисунка сразу понятен ответ: Петя выше всех.
Пример.
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?
Иллюстрация:
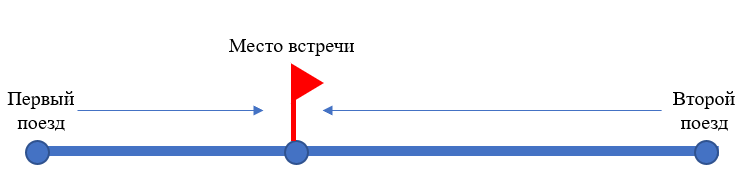
Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.
Составим математическую модель:
45х + 55х = 200
100х = 200
х = 2 ч
Ответ: 2 ч.
Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.
Математическая модель
Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.
x — число девочек
y — число мальчиков
| Реальная ситуация | Математическая модель |
|---|---|
| В классе поровну мальчиков и девочек | $ { x=y} $ |
| Девочек на 5 больше, чем мальчиков | $ { x=y+5, ; или; x-y=5,; или; x-5=y} $ |
| Мальчиков в 2 раза больше, чем девочек | $ { y=2x, ; или; frac{y}{2}=x,; или; frac{y}{x}=2} $ |
| Если в класс перейдут 3 мальчика, то девочек станет в два раза больше | $ { y=2(y+3)} $ |
Алгебраическая зависимость
Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.
При составлении уравнения особое значение играют используемые предлоги: «в» и «на».
Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?
Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.
Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.
Выразим рост мальчиков.
Петя выше Коли на 20 см: П – 20 = К
Сережа ниже Коли на 10 см: К = С + 10
Подставим в первое уравнение рост Коли: П – 20 = С + 10
Нам нужно найти, на сколько см Петя выше Сережи: П – С
П – 20 = С + 10
П – С = 20 + 10
П – С = 30
Получаем, что Петя выше Сережи на 30 см.
Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?
Решение:
Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.
Маша сделала в два раза больше снежинок, чем Коля: К = М/2
Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4
Вместе ребята сделали 12 снежинок: М + К + Р = 12
Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12
М = 4.
Маша сделала 4 снежинки.
Процентная зависимость
С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?
Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.
Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.
Так что же такое один процент?
Процент — это всегда доля какого-то числа.
100% — все число
50% — половина
25% — четверть
Чтобы найти 1%, необходимо поделить всё число на 100.
Пример:
Есть 100 яблок.
$ 1% ;от ;всех ;яблок; –frac{100}{100} = 1 ;яблоко. $
Есть 200 груш
$ 1% ;от ;всех ;груш; –frac{200}{100} = 2 ;груши. $
Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.
Пример:
200 груш — 100 %
2 груши — 1 %
Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.
$ frac{200}{2}=frac{100}{1} $
Исходя из правил работы с дробями, получаем правила работы с пропорцией.
1. Внутри одной дроби можно сокращать значения.
2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100
Эту тему мы еще подробно пройдем на курсе.
Рассмотрим несколько примеров работы с процентами в текстовых задачах.
Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов
Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?
Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек
Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?
Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?
На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:
Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880
Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880
Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.
Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.
п.1. Алгоритм решения задач с помощью систем уравнений
1. Обозначить неизвестные величины переменными («от смысла к буквам»).
2. По условию задачи записать уравнения, связывающие обозначенные переменные.
3. Решить полученную систему уравнений.
4. Истолковать результат в соответствии с условием задачи («от букв к смыслу»).
Например:
Найдите два положительных числа, если известно, что сумма квадратов этих чисел равна 185, а разность квадратов равна 57.
Шаг 1
«От смысла к буквам»:
Пусть x > 0 и y > 0 – задуманные числа.
Шаг 2
Уравнения по условию задачи:
( left{ begin{array}{ l } mathrm{x^2+y^2=185} & \ mathrm{x^2-y^2=57} & end{array}right. )
Шаг 3
Решение системы уравнений:
( left{ begin{array}{ l } mathrm{x^2+y^2=185} & \ mathrm{x^2-y^2=57} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{2x^2=185+57=242} & \ mathrm{2y^2=185-57=128} & end{array}right.Rightarrow )
( Rightarrow left{ begin{array}{ l } mathrm{x^2=121} & \ mathrm{y^2=64} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=pm 11} & \ mathrm{y=pm 8} & end{array}right. )
Шаг 4
«От букв к смыслу»:
Выбираем положительные корни $$ mathrm{x=11, y=8} $$ Задуманы числа 11 и 8.
п.2. Примеры
Пример 1. Диагональ прямоугольника равна 10 см. Если меньшую сторону прямоугольника увеличить на 2 см, а большую уменьшить на 2 см, то диагональ не изменится. Найдите стороны прямоугольника.
Пусть a и b – стороны прямоугольника, a > b. Диагональ через стороны выражается по теореме Пифагора. По условию получаем: $$ left{ begin{array}{ l } mathrm{a^2+b^2=10} & \ mathrm{(a-2)^2+(b+2)^2=10^2} & end{array}right. $$ Найдём линейную зависимость между a и b из уравнения: begin{gather*} mathrm{a^2+b^2=(a-2)^2+(b+2)^2}\ mathrm{a^2+b^2=a^2-4a+4+b^2+4b+4}\ mathrm{4a-4b=8Rightarrow a-b=2Rightarrow a=b+2} end{gather*} Подставим a в верхнее уравнение системы: ( mathrm{(b+2)^2+b^2=100} ) begin{gather*} mathrm{b^2+4b+4+b^2-100=0}\ mathrm{2b^2+4b-96=0Rightarrow b^2+2b-48=0Rightarrow (b+8)(b-6)=0}\ mathrm{b_1=-8, b_2=6} end{gather*} Выбираем положительный корень: b = 6
Тогда a = b + 2 = 8
Ответ: 8 см и 6 см.
Пример 2. (задача Диофанта, III в.) Отношение двух чисел равно 3, а отношение суммы квадратов этих чисел к их сумме равно 5. Найдите эти числа.
Пусть x и y – искомые числа. По условию: $$ left{ begin{array}{ l } mathrm{frac{x}{y}=3} & \ mathrm{frac{x^2+y^2}{x+y}=5} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{x=3y} & \ mathrm{x^2+y^2=5(x+y)} & end{array}right. $$ Подставляем верхнее уравнение в нижнее и решаем: begin{gather*} mathrm{(3y)^2+y^2=5(3y+y)Rightarrow 9y^2+y^2=20yRightarrow 10y^2-20y=0Rightarrow}\ mathrm{Rightarrow 10y(y-2)=0Rightarrow} left[begin{array}{ l } mathrm{y_1=0} & \ mathrm{y_2=2} & end{array}right. end{gather*} Т.к. y в первом уравнении системы стоит в знаменателе, он не может быть равен 0. Получаем: begin{gather*} left{begin{array}{ l } mathrm{x=3y=6} & \ mathrm{y=2} & end{array}right. end{gather*} Ответ: 6 и 2.
Пример 3. Двое рабочих могут выполнить работу за 12 дней. Если сначала один из них сделает половину всей работы, а потом остальное сделает другой, то им понадобится 25 дней. За сколько дней каждый рабочий может выполнить задание самостоятельно?
Пусть x и y – производительность каждого рабочего, A – работа.
По условию: $$ left{ begin{array}{ l } mathrm{frac{A}{x+y}=12} & \ mathrm{frac{A}{2x}+frac{A}{2y}=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{frac{A}{2}left(frac{1}{x}+frac{1}{y}right)=25} & end{array}right.Rightarrow left{ begin{array}{ l } mathrm{A=12(x+y)} & \ mathrm{A=frac{50}{frac{1}{x}+frac{1}{y}}=frac{50xy}{x+y}} & end{array}right. $$ Получаем уравнение: begin{gather*} mathrm{12(x+y)=frac{50xy}{x+y}Rightarrow 12(x+y)^2=50xyRightarrow 6(x+y)^2=25xy}\ mathrm{6(x^2+2xy+y^2)-25xy=0}\ mathrm{6x^2-13xy+6y^2=0 |:y^2}\ mathrm{6left(frac{x}{y}right)^2-13frac{x}{y}+6=0}\ mathrm{D=13^2-4cdot 6cdot 6=25=5^2, frac{x}{y}=frac{13pm 5}{12}=} left[begin{array}{ l } mathrm{frac23} & \ mathrm{frac32} & end{array}right. end{gather*} Пусть для определенности x > y. Тогда ( mathrm{frac{x}{y}=frac{3}{2}Rightarrow x=1,5y}. )
Работа: ( mathrm{A=12(x+y)=12(1,5y+y)=12cdot 2,5y=30y}. )
Второй рабочий может выполнить работу самостоятельно за: ( mathrm{frac{A}{y}=frac{30y}{y}=30} дней. )
Первый рабочий работает в 1,5 раза быстрей, ему понадобится ( mathrm{frac{30}{1,5}=20} дней. )
Ответ: 30 дней и 20 дней.
Пример 4. Бригада выполнила работу за 20 дней. Если бы в бригаде было на 4 человека больше, а рабочий день – на 1 ч дольше, то работа была бы выполнена за 10 дней. Если бы в бригаде было на 1 человека меньше, а рабочий день – на 1 ч короче, то работа была бы выполнена за 30 дней. Сколько человек было в бригаде, и сколько часов в день они работали?
Пусть A – вся работа, n – количество человек в бригаде, t – продолжительность рабочего дня. По условию: $$ left{ begin{array}{ l } mathrm{20nt=A} & \ mathrm{10(n+4)(t+1)=A} & \ mathrm{30(n-1)(t-1)=A} & end{array}right. $$ Исключаем A и получаем систему из двух уравнений: begin{gather*} left{begin{array}{ l } mathrm{20nt=10(n+4)(t+1)} & \ mathrm{20nt=30(n-1)(t-1)} & end{array}right.Rightarrow left{begin{array}{ l } mathrm{2nt=nt+4t+n+4} & \ mathrm{2nt=3(nt-t-n+1)} & end{array}right.Rightarrow\ Rightarrow left{begin{array}{ l } mathrm{nt=4t+n+4} & \ mathrm{nt=3t+3n-3} & end{array}right. end{gather*} Найдём линейную зависимость между n и t из уравнения: $$ mathrm{4t+n+4=3t+3n-3Rightarrow t-2n=-7Rightarrow t=2n-7}. $$ Подставим t в верхнее уравнение системы: begin{gather*} mathrm{n(2n-7)=4(2n-7)+n+4}\ mathrm{2n^2-7n=8n-28+n+4Rightarrow 2n^2-16n+24=0Rightarrow n^2-8n+12=0}\ mathrm{ (n-2)(n-6)=0Rightarrow} left[begin{array}{ l } mathrm{n_1=2} & \ mathrm{n_2=6} & end{array}right. end{gather*} Находим время ( mathrm{t=2n-7: } left[begin{array}{ l } left{begin{array}{ l } mathrm{n_1=2} & \ mathrm{t_1=-3} & end{array}right. &\ left{begin{array}{ l } mathrm{n_2=6} & \ mathrm{t_2=5} & end{array}right. end{array}right. )
Выбираем решение с ( tgt 0: left{begin{array}{ l } mathrm{n=6} & \ mathrm{t=5} & end{array}right. )
Ответ: 6 человек, 5 часов.
