Скачать материал
без ожидания

Скачать материал
без ожидания


- Сейчас обучается 272 человека из 65 регионов


- Сейчас обучается 393 человека из 62 регионов




Описание презентации по отдельным слайдам:
-

1 слайд
МОДЕЛИРОВАНИЕ КУБА
Для изготовления модели многогранника из плотной бумаги, картона или другого материала достаточно вырезать из этого материала многоугольники, равные граням многогранника, и затем склеить соответствующие ребра. Для удобства склейки многоугольники вырезают с клапанами, по которым и производится склейка.
Например, для изготовления модели куба нужно вырезать шесть квадратов с клапанами, как показано на рисунке и склеить их по соответствующим клапанам. -

2 слайд
МОДЕЛИРОВАНИЕ ПАРАЛЛЕЛЕПИПЕДА
Для изготовления модели прямоугольного параллелепипеда с ребрами 3, 4, 5 нужно вырезать пары прямоугольников с клапанами, показанных на рисунке, и склеить их по клапанам, прилегающих к равным сторонам.
Для изготовления модели наклонного параллелепипеда, гранями которого являются ромбы с острыми углами 60о нужно вырезать шесть таких ромбов с клапанами, как показано на рисунке, и склеить их по соответствующим клапанам. -

3 слайд
МОДЕЛИРОВАНИЕ ПРИЗМЫ
Для изготовления модели правильной треугольной призмы нужно вырезать два равных правильных треугольника с клапанами и три равных прямоугольника с клапанами, одна сторона которых равна стороне треугольника, как показано на рисунке, и склеить их по соответствующим клапанам.
Для изготовления модели правильной шестиугольной призмы нужно вырезать два равных правильных шестиугольника с клапанами и шесть равных прямоугольников с клапанами, одна сторона которых равна стороне шестиугольника, как показано на рисунке, и склеить их по соответствующим клапанам. -

4 слайд
МОДЕЛИРОВАНИЕ ПИРАМИДЫ
Для изготовления модели правильной треугольной пирамиды нужно вырезать правильный треугольник с клапанами и три равных равнобедренных треугольника с клапанами, одна сторона которых равна стороне правильного треугольника, как показано на рисунке, и склеить их по соответствующим клапанам.
Для изготовления модели правильной шестиугольной пирамиды нужно вырезать правильный шестиугольник с клапанами и шесть равных равнобедренных треугольника с клапанами, одна сторона которых равна стороне правильного шестиугольника, как показано на рисунке, и склеить их по соответствующим клапанам. -

5 слайд
МОДЕЛИРОВАНИЕ НЕВЫПУКЛЫХ МНОГОГРАННИКОВ
Для изготовления модели невыпуклого многогранника, изображенного на рисунке, нужно вырезать два равных невыпуклых многоугольника с клапанами, два равных квадрата и четыре равных прямоугольника с клапанами, как показано на рисунке, и склеить их по соответствующим клапанам. -

6 слайд
РАЗВЕРТКА МНОГОГРАННИКА
Если поверхность многогранника разрезать по некоторым ребрам и развернуть ее на плоскость так, чтобы все многоугольники, входящие в эту поверхность, лежали в данной плоскости, то полученная фигура на плоскости называется разверткой многогранника. Например, на рисунке изображены развертки куба и треугольной пирамиды. -

7 слайд
КУБ
Для изготовления модели многогранника из плотной бумаги, картона или другого материала достаточно изготовить его развертку и затем склеить соответствующие ребра. Для удобства склейки развертку многогранника изготавливают с клапанами, по которым и производится склейка. На рисунке показаны развертка куба с клапанами. -

8 слайд
ПАРАЛЛЕЛЕПИПЕД
На рисунке показаны развертки с клапанами прямоугольного параллелепипеда ребрами 3, 4, 5 и наклонного параллелепипеда, гранями которого являются ромбы с острыми углами 60о. -

9 слайд
ПРИЗМА
На рисунке показаны развертки треугольной и шестиугольной правильных призм. -

10 слайд
ПИРАМИДА
На рисунке показаны развертки треугольной и шестиугольной правильных пирамид. -

11 слайд
КОНСТРУКТОР
Другим способом моделирования многогранников является изготовление моделей многогранников с помощью конструктора, состоящего из многоугольников, сделанных из плотного материала с отгибающимися клапанами и резиновых колечек – основной крепежной детали конструктора. Подбирая соответствующим образом многоугольники в качестве граней многогранника и скрепляя их резиновыми колечками, можно получать модели различных многогранников. Для того, чтобы колечки лучше держались и не мешали друг другу, уголки многоугольников в конструкторе можно немного обрезать, как показано на рисунке. -

12 слайд
Упражнение 1
Укажите развертки куба.
Ответ. в), д), ж). -

13 слайд
Упражнение 2
Укажите развертки треугольной призмы.
Ответ. а), б), в), д), ж). -

14 слайд
Упражнение 3
Укажите развертки треугольной пирамиды.
Ответ. а), б), в), д). -

15 слайд
Упражнение 4
Укажите развертки четырехугольной пирамиды.
Ответ. а), б), д), е).
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 254 202 материала в базе
- Выберите категорию:
-
Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 22.11.2020
- 117
- 0
- 07.10.2020
- 100
- 0
- 12.09.2020
- 106
- 0
- 14.08.2020
- 225
- 3
- 07.07.2020
- 139
- 0
- 06.07.2020
- 106
- 0
- 22.05.2020
- 157
- 0
- 17.05.2020
- 171
- 0
Вам будут интересны эти курсы:
-
Курс профессиональной переподготовки «Маркетинг: теория и методика обучения в образовательной организации»
-
Курс повышения квалификации «Управление финансами: как уйти от банкротства»
-
Курс профессиональной переподготовки «Организация деятельности по подбору и оценке персонала (рекрутинг)»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Этика делового общения»
-
Курс повышения квалификации «Страхование и актуарные расчеты»
-
Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»
-
Курс повышения квалификации «Психодинамический подход в консультировании»
-
Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»
-
Курс повышения квалификации «Актуальные вопросы банковской деятельности»
-
Курс профессиональной переподготовки «Деятельность по хранению музейных предметов и музейных коллекций в музеях всех видов»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Осуществление и координация продаж»
-
Курс профессиональной переподготовки «Технический контроль и техническая подготовка сварочного процесса»
- Авторы
- Научный руководитель
- Файлы
- Литература
Ляховский К.С.
1
1 г. Котлас, ЧЧОУ «Школа-интернат № 1 среднего общего образования ОАО «Российские железные дороги», 4 класс
Бубнова Н.И. (Котлас, ЧОУ «Школа-интернат № 1 ;среднего общего образования ОАО «Российские железные дороги»)
1. Моро М.И., Волкова С.И. Для ;тех, кто любит математику. 4 ;класс ;/ Просвещение, 2017.
2. Волкова С.И. Математика и ;конструирование. 4 ;класс, 2014.
3. Атанасян Л.С., Бутузов В.Ф. Геометрия 7–9 ;классы: учеб. для ;образовательных учреждений. 5-е изд. – М.: Просвещение.
4. http://uslide.ru/geometriya/18852–razvyortki-kuba.html.
5. http://easyen.ru/load/m/3_klass/kub_ehlementy_kuba_grani_rebra_vershiny/377–1–0–13873.
6. https://ru.wikipedia.org/wiki.
Математика изучает объекты, явления, процессы окружающего мира во всех его проявлениях и взаимодействиях. Обустраивая окружающее пространство, человек всегда старается его упорядочить. Одна из часто встречаемых форм бытовых предметов – это прямоугольный параллелепипед. Его форму имеют: шкаф, телевизор, детские кубики, кусочки сахара… Длину, ширину и высоту прямоугольного параллелепипеда называют его измерением. Если все три измерения равны, то его называют кубом.
Знания о площади поверхности куба, его развертках, объёме полезны при расчётах количества обоев, паркета, краски при ремонте квартиры, кубометров леса при постройке дома… Поэтому тема «Куб и его развёртки» является актуальной.
Актуальность применения правил замощения плоскости подтверждает сказ о мастерах.
Двум мастерам было дано задание из одинаковых листов железа изготовить максимальное количество кубов, используя предложенную развертку куба. У первого мастера получилось 5 штук, второй же мастер, применив принципы замощения плоскости, сумел сделать в два раза больше кубов, тем самым показав возможность рационального использования материала
Цель исследования: получение новых знаний о кубе, его развертках и их практических применениях.
Задачи исследования:
1. Изучить элементы куба.
2. Исследовать развёртки куба.
3. Изготовить модели куба.
4. Выполнить замощение плоскости развёртками куба.
5. Изготовить пазлы.
Предмет исследования: куб.
Объект исследования: развёртки куба.
Гипотеза: знания о кубе и его развёртках помогают решать практические задачи.
Методы исследования: практический, наблюдение, опрос, анализ, обобщение, измерения, расчёты, изучение литературы и материалов сайтов.
Теоретический этап исследования
1. Куб и его элементы
По другому куб называют шестигранником или гексаэдром [6]. Куб имеет 6 граней Каждая грань куба – квадрат. У куба 8 вершин. Вершина куба – это самая отдалённая от центра куба точка, которая лежит на пересечении трёх его граней. Каждая вершина принадлежит только трём граням и только трём рёбрам. Куб имеет 12 рёбер. Ребро куба – это отрезок, образованный пересечением двух граней куба. Рёбра имеют одинаковую длину. Каждый конец ребра соединен с двумя соседними рёбрами под прямым углом [3].
Поверхность куба состоит из шести граней. Площадь поверхности куба – это сумма площадей всех граней.
Площадь одной грани куба при длине ребра «а» равна а2. Площадь поверхности куба можно выразить формулой S=6a2.
Площадь одной грани этого куба: 1 дм2, тогда площадь поверхности куба будет равна 6 дм2. Если разбить 1 дм2 на см2 и мм2, мы получим, что площадь поверхности данного куба будет равна 600см2 и 60 000мм2 соответственно.
Объём куба – это совокупность всех точек в пространстве, ограниченных гранями куба. Объём куба при длине ребра «а» можно выразить формулой V=a3.
Кубы с одинаковым размером граней, но сделанные из разных материалов имеют одинаковый объем, одинаковую площадь, но разную массу. Соответственно, кубы, изготовленные из разных материалов, но имеющие одинаковую массу, будут отличаться размерами.
Игральная кость – это популярный источник случайности, который широко применяется в азартных, настольных и ролевых играх.
Традиционная игральная кость – это кубик, который используется как средство генерирования случайных чисел. На каждую грань кубика нанесены числа от 1 до 6. Их принято располагать так, чтобы сумма чисел на противоположных гранях была равна семи. Целью кубика является демонстрация случайно определённого целого числа от одного до шести. Выпадение каждого числа является равновозможным благодаря правильной геометрической форме кубика.
2. Развёртки куба
Развёртка куба – это оболочка, позволяющая увидеть куб со всех сторон. Развертка куба состоит из 6 равных квадратов.
Изучение возможных вариантов развёртки куба, показало, что их всего 11 видов [4].
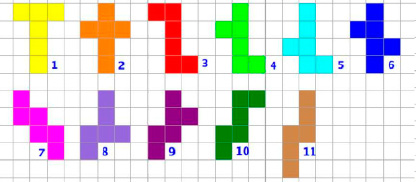
3. Замощение
Замощение – это покрытие всей плоскости или заполнение всего пространства неперекрывающимися фигурами [5].
Изучение куба показало, что плоскость можно покрыть целиком без пробелов его реберными развёртками одного вида. При этом несколько развёрток одного типа складываются в симметричный элемент орнамента, называемый плиткой, с помощью которой происходит замощение плоскости [2].
Выполнено замощение плоскости различными развёртками куба. Замощение плоскости развертками куба можно использовать при изготовлении пазлов.
Пазл – это увлекательная головоломка очень популярная у взрослых и незаменимый элемент в жизни каждого ребёнка. Пазлы для детей – это увлекательная игра, позволяющая развивать мелкую моторику, логическое мышление, воображение, память, усидчивость, терпение, целеустремленность.
Практический этап исследования
Практическая работа №1
Сделать модель куба из дерева с рёбрами 1 дм, из бумаги с ребром 1 дм. Из бумаги с ребром 1 см.
Заполнить таблицу.
|
Ребро |
Площадь поверхности |
Объём |
Масса |
|
|
Куб из дерева |
1 дм |
6 дм2 |
1 дм3 |
650 г |
|
Куб из бумаги |
1 дм |
6 дм2 |
1 дм3 |
50 г |
|
Куб из бумаги |
1 см |
6 см2 |
1 см3 |
0,5 г |
Вывод: площадь поверхности и объёма куба зависит от величины ребра и не зависит от материала. Масса куба зависит от размеров куба и материала, из которого он изготовлен (Приложение 1).
Практическая работа №2
Изготовить тренажёр по переводу единиц измерения площади. На бумажной модели куба разбить одну грань на квадратные сантиметры, на противоположной сделать надпись 100см2, другую грань разбить на квадратные миллиметры, на противоположной грани сделать надпись 10000 мм2. На пятой грани сделать надпись 1 дм2.
Результат: изготовлен тренажёр по переводу единиц измерения площади (Приложение 2).
Практическая работа №3
Изготовить 11 различных развёрток куба с длиной ребра 1дм. Обёртыванием бумажной модели куба убедиться, что все они являются развёртками куба.
Результат: даны названия развёрткам куба: «Буква Т», «Крестик», «Лежачая собачка», «Ружьё», «Стоячая собачка», «Пушка», «Загадочная», «Лесенки».
Проверено, что все 11 многоугольников являются развёртками куба (Приложение 3).
Практическая работа №4
Изготовить модель игральной кости с ребром 5 см. Подбрасыванием кости убедиться, что выпадение очков происходит с равной вероятностью.
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
Выпадение очков |
5 |
1 |
4 |
5 |
6 |
3 |
3 |
1 |
2 |
6 |
3 |
5 |
6 |
4 |
2 |
1 |
6 |
2 |
4 |
5 |
Вывод: выпадение очков происходит с равной вероятностью (Приложение 4).
Практическая работа №5
Замостить плоскость различными развёртками куба. Сделать пазлы.
Результаты:
1. Выполнены рисунки по замощению плоскости развёртками куба.
2. Изготовлены пазлы (Приложение 5).
Задача о нахождении кратчайшего расстояния по поверхности куба
В точке А на поверхности куба находится паук, в точке В муха. Найти кратчайшее расстояние по поверхности куба от паука к мухе.
Развертки куба помогают при решении различных задач. Одна из таких задач была предложена для решения воспитанникам нашей школы. Необходимо было указать кратчайший путь от паука, сидящего в точке А, к мухе, находящейся в точке В.
Был проведён опрос воспитанников по нахождению самого короткого пути по поверхности куба.Предложенные варианты ответов изображены цифрами.
|
№ опыта |
Длина линии |
|
1 |
25 см |
|
2 |
23 см |
|
3 |
21 см 5 мм |
|
4 |
20 см 5 мм |
|
5 |
21 см 4 мм |
Произвели измерения и вычислили длины путей, самый короткий путь оказался четвёртый. Это подтверждает развёртка куба. Самый короткий путь на развёртке – это отрезок АВ. Двигаться надо к точке на ребре куба, отстоящей от нижней грани на четверть ребра (Приложение 6).
Заключение
В результате работы были сделаны следующие выводы:
1. Куб – это геометрическое тело, являющееся правильным шестигранником, каждая грань которого представляет собой квадрат.
2. Куб небольшого размера, на каждую грань которого нанесены числа от 1 до 6, используется как средство генерирования случайных чисел.
3. Развёртки куба позволяют находить решения различных задач.
4. Применение различных развёрток куба и правил замощения плоскости способствуют созданию разнообразных орнаментов и рациональному использованию материала.
5. Замощение плоскости развертками куба можно использовать при изготовлении пазлов для детей, способствующих их полноценному и всестороннему развитию.
Приложения
Приложение 1
Модели куба

Приложение 2
Поверхность куба


Приложение 3
Развёртки куба




Приложение 4
Игральная кость



Приложение 5
Замощение плоскости



Приложение 6
Нахождение кратчайшего пути



Библиографическая ссылка
Ляховский К.С. КУБ И ЕГО РАЗВЁРТКИ // Старт в науке. – 2018. – № 5-6.
;
URL: https://science-start.ru/ru/article/view?id=1223 (дата обращения: 17.05.2023).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
Вот мы и подошли к созданию первой детали в Компас 3D. Предлагаю построить деталь, изображенную на рисунке ниже. (В конце есть видео процесса)
А вот ее чертеж.
Давайте рассмотрим эту деталь. Перед нами куб со сторонами 20 мм. У него имеется два отверстия с противоположных сторон. Одно отверстие имеет квадратное сечение с длиной сторон 10 мм. Второе – круглое сечение с диаметром 16. Оба отверстия глубиной 10 мм.
Исходя из этого имеем следующий план действий:
1. Создаем куб
2. Делаем вырез квадратного отверстия
3. Делаем вырез круглого отверстия
Приступим.
Создадим деталь. Заходим Файл – Создать … и выбираем Деталь.
Создание куба.
Для построения куба нам необходимо построить его сечение. Сечением куба является квадрат, поэтому нам необходимо создать эскиз с квадратом. Для этого выбираем любую из базовых плоскостей к примеру, синюю и жмем Эскиз.
Компас перешел в режим Эскиза, компактная панель изменила набор инструментов, а выбранная плоскость в рабочей области повернулась к нам нормалью. Если мы начали вращать и сбили эту ориентацию ее всегда можно вернуть, щелкнув правой кнопкой мыши в свободном месте и выбрав команду Нормаль к …
Теперь нам необходимо наполнить эскиз. На компактной панели выберем Геометрия.
В нижней части панели появятся различные инструменты: точка, линия, окружность и др. Их мы разберем позже. Нас интересует инструмент Прямоугольник. Нужно на него нажать левой кнопкой мыши и удерживать, откроется выпадающий список, в котором выберем Прямоугольник по центру и вершине
Сейчас мы можем либо поставить точку центра и вершины прямоугольна в рабочей области либо настроить его сначала в панели свойств, которая появилась в низу. Предлагаю воспользоваться втором вариантом. Так как нам нужно построить квадрат, то указываем размеры высоты и ширины одинаковыми по 20 мм, нажимаем Enter на клавиатуре, силуэт нашей фигуры перестроится в соответствии с размерами.
Сейчас нам осталось только указать центр прямоугольника. Подводим курсор к центру начала координат сработает привязка ближайшей точки. Жмем левую кнопку мыши. Вот наш квадрат и готов.
Можно нажать Esc на клавиатуре для отмены выбора инструмента Прямоугольник.
Теперь нам нужно выйти из Эскиза, нажав кнопку эскиз (либо на панели текущего состояния, либо в контекстной панели при щелчке левой кнопки мыши в свободном пространстве).
У нас имеется двухмерная фигура квадрат, которой нужно придать объем, чтобы она стала кубом. Для этого проверим чтоб в дереве модели наш эскиз был выбран, и выбираем в компактной панели Операцию выдавливания
Внизу появляется панель свойств, и мы настраиваем операцию (устанавливаем расстояние выдавливания 20 мм)
В зависимости от вводимых параметров в рабочей области изменяется фантом операции, отражающий влияние редактируемых параметров на конечный результат.
Жмем на панели свойств кнопку со стрелочкой (создать объект). Куб создан.
Вот и готов первый трехмерный объект. Осталось довести его до необходимого, а точнее сделать отверстия.
Создание квадратного отверстие.
Выбираем верхнюю грань нашего куба и создаем на ней эскиз.
Раз отверстие у нас квадратное, значит и сечение у него квадратное. Создаем в квадрат со сторонами 10 мм, абсолютно таким же образом как и в предыдущем эскизе. И также помещаем его центр в начале координат. Затем выходим из эскиза и выбираем на компактной панели операцию Вырезать выдавливанием
И настраиваем ее свойства как на рисунке
Проверяем как выглядит фантом нашей операции и если все устраивает жмем Создать объект.
Создание круглого отверстия.
Круглое отверстие нам необходимо создать на противоположной грани куба. Для этого вращаем нашу модель зажав колесико мыши, выбираем противоположную грань и создаем эскиз.
Выбираем в Геометрии инструмент Окружность. Настраиваем свойства, а точнее одно – диаметр, который у нас, в соответствии с чертежом, равен 16 мм.
Центр также устанавливаем в начало координат. Получился круг. Теперь можно выходить из эскиза и выбирать операцию Вырезать выдавливанием. Настраиваем свойства операции.
И уже как обычно, жмем Создать объект.
Вот у нас и получилась модель как на первом рисунке.
Что мы должны запомнить из этого занятия:
- Эскизы можно создавать на плоскостях и плоских гранях модели
- Существует две противоположные по действию формообразующие операции: операция выдавливания и вырезать выдавливанием.
- Построение сложной модели состоит из нескольких простых операций.
А сейчас предлагаю самостоятельно по вносить изменения в созданную модель, для этого необходимо щелкнуть правой кнопкой мыши на операцию или эскиз в дереве модели и выбрать редактировать.
Вот видео этого процесса.
До встречи.
Программа для рисования четырёхмерного куба
Время на прочтение
6 мин
Количество просмотров 82K
Начнём с объяснения, что же такое четырёхмерное пространство.
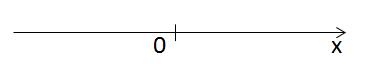
Это — одномерное пространство, то есть просто ось OX. Любая точка на ней характеризуется одной координатой.
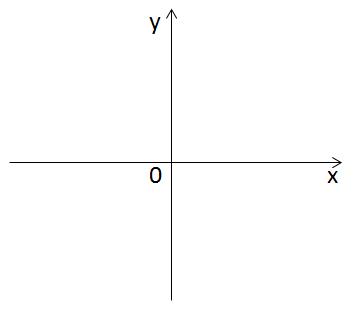
Теперь проведём ось OY перпендикулярно оси OX. Вот и получилось двумерное пространство, то есть плоскость XOY. Любая точка на ней характеризуется двумя координатами — абсциссой и ординатой.
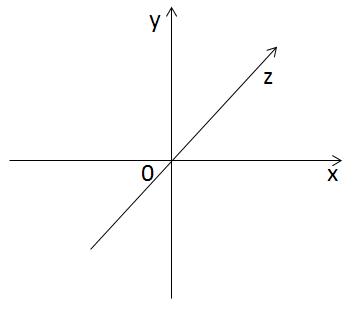
Проведём ось OZ перпендикулярно осям OX и OY. Получится трёхмерное пространство, в котором у любой точки есть абсцисса, ордината и аппликата.
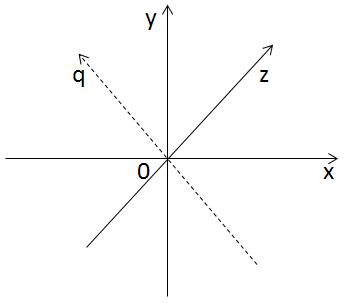
Логично, что четвёртая ось, OQ, должна быть перпендикулярной осям OX, OY и OZ одновременно. Но мы не можем точно построить такую ось, и потому остаётся только попытаться представить её себе. У каждой точки в четырёхмерном пространстве есть четыре координаты: x, y, z и q.
Теперь посмотрим, как появился четырёхмерный куб.
На картинке изображена фигура одномерного пространства — линия.
Если сделать параллельный перенос этой линии вдоль оси OY, а потом соединить соответствующие концы двух получившихся линий, получится квадрат.
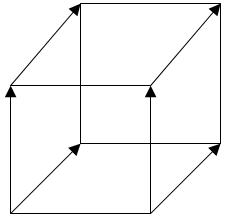
Аналогично, если сделать параллельный перенос квадрата вдоль оси OZ и соединить соответствующие вершины, то получится куб.
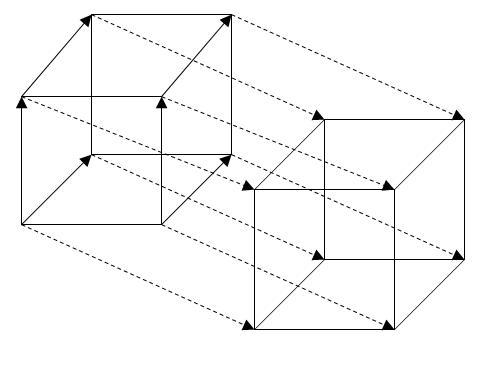
А если сделать параллельный перенос куба вдоль оси OQ и соединить вершины двух этих кубов, то мы получим четырёхмерный куб. Кстати, он называется тессеракт.
Чтобы нарисовать куб на плоскости, нужно его спроецировать. Наглядно это выглядит так:
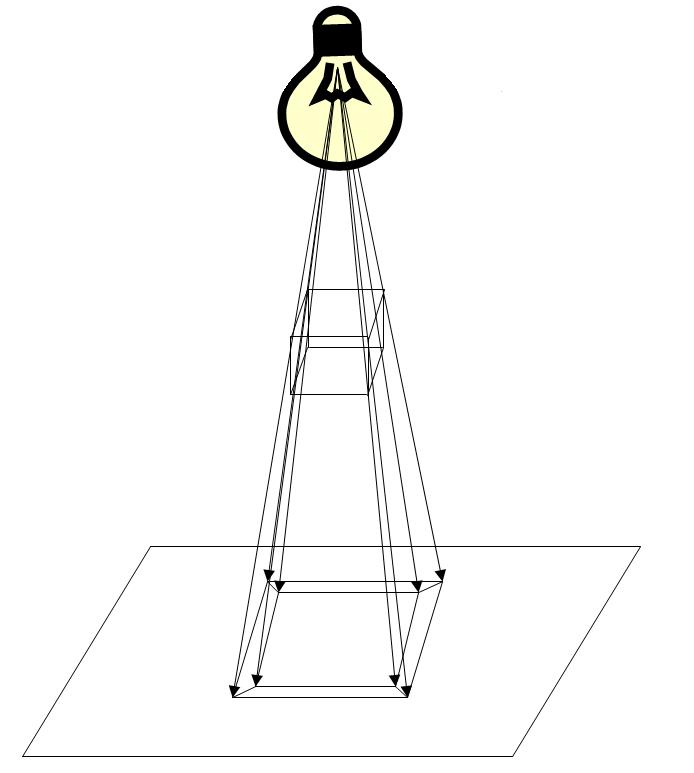
Представим, что в воздухе над поверхностью висит каркасная модель куба, то есть как бы «сделанная из проволоки», а над ней — лампочка. Если включить лампочку, обвести карандашом тень от куба, а потом выключить лампочку, то на поверхности будет изображена проекция куба.
Перейдём к немного более сложному. Ещё раз посмотрите на рисунок с лампочкой: как видите, все лучи сошлись в одной точке. Она называется точкой схода и используется для построения перспективной проекции( а бывает и параллельная, когда все лучи параллельны друг другу. Результат — не создаётся ощущения объёма, но она легче, и при том если точка схода достаточно сильно удалена от проецируемого объекта, то разница между этими двумя проекциями мало заметна). Чтобы спроецировать данную точку на данную плоскость, используя точку схода, нужно провести прямую через точку схода и данную точку, а потом найти точку пересечения получившейся прямой и плоскости. А для того, чтобы спроецировать более сложную фигуру, скажем, куб, нужно спроецировать каждую его вершину, а потом соответствующие точки соединить. Следует заметить, что алгоритм проекции пространства на подпространство можно обобщить для случая 4D->3D, а не только 3D->2D.
Как я уже говорил, мы не можем себе точно представить, как выглядит ось OQ, равно как и тессеракт. Зато мы можем получить ограниченное представление о нём, если мы спроецируем его на объём, а потом нарисуем это на экране компьютера!
Теперь поговорим о проекции тессеракта.
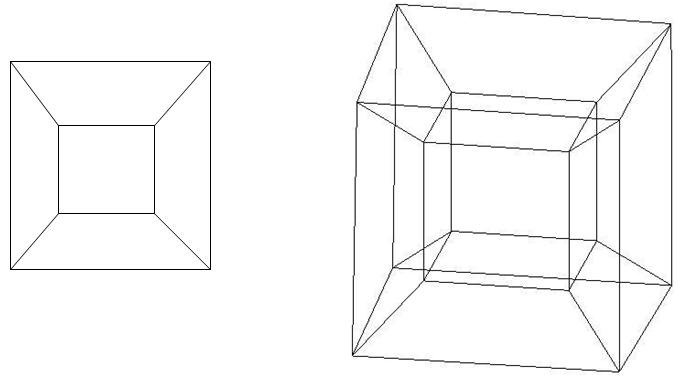
Слева находится проекция куба на плоскость, а справа — тессеракта на объём. Они довольно схожи: проекция куба выглядит как два квадрата, маленький и большой, один внутри другого, и у которых соответствующие вершины соединены линиями. А проекция тессеракта выглядит как два куба, маленький и большой, один внутри другого, и у которых соответствующие вершины соединены. Но мы все видели куб, и можем с уверенностью сказать, что и маленький квадрат, и большой, и четыре трапеции сверху, снизу, справа и слева от маленького квадрата, на самом деле являются квадратами, при чём равными. И у тессеракта тоже самое. И большой куб, и маленький куб, и шесть усечённых пирамид по бокам от маленького куба — это всё кубы, при чём равные.
Моя программа умеет не только рисовать проекцию тессеракта на объём, а ещё и вращать его. Рассмотрим, как делается это.
Для начала я вам расскажу, что такое вращение параллельно плоскости.
Представьте себе, что куб вращается вокруг оси OZ. Тогда каждая из его вершин описывает окружность вокруг оси OZ.
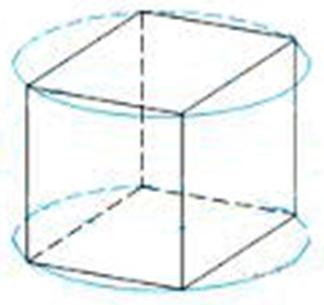
А окружность — фигура плоская. И плоскости каждой из этих окружностей параллельны между собой, и в данном случае параллельны плоскости XOY. То есть мы можем говорить не только о вращении вокруг оси OZ, а ещё и о вращении параллельно плоскости XOY.Как видим, у точек, которые вращаются параллельно оси XOY меняются только абсцисса и ордината, аппликата же остаётся неизменной И, вообще-то, мы можем говорить о вращении вокруг прямой только тогда, когда имеем дело с трёхмерным пространством. В двумерном всё вращается вокруг точки, в четырёхмерном — вокруг плоскости, в пятимерном пространстве мы говорим о вращении вокруг объёма. И если вращение вокруг точки мы можем себе представить, то вращение вокруг плоскости и объёма — что-то немыслимое. А если будем говорить о вращении параллельно плоскости, то тогда в любом n-мерном пространстве точка может вращаться параллельно плоскости.
Многие из вас, вероятно, слышали о матрице поворота. Умножив точку на неё, получим точку, повёрнутую параллельно плоскости на угол фи. Для двумерного пространства она выглядит так:
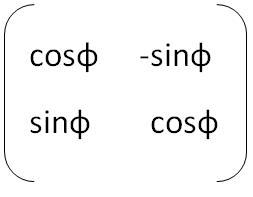
Как умножать: икс точки, повёрнутой на угол фи = косинус угла фи*икс первоначальной точки минус синус угла фи*игрек первоначальной точки;
игрек точки, повёрнутой на угол фи=синус угла фи*икс первоначальной точки плюс косинус угла фи*игрек первоначальной точки.
Xa`=cosф*Xa — sinф*Ya
Ya`=sinф*Xa + cosф*Ya
, где Xa и Ya — абсцисса и ордината точки, которую нужно повернуть, Xa` и Ya` — абсцисса и ордината уже повёрнутой точки
Для трёхмерного пространства это матрица обобщается следующим образом:

Вращение параллельно плоскости XOY. Как видим, координата Z не меняется, а меняются только X и Y
Xa`=cosф*Xa — sinф*Ya + Za*0
Ya`=sinф*Xa +cosф*Ya + Za*0
Za`=Xa*0 + Ya*0 + Za*1 (по сути, Za`=Za)

Вращение параллельно плоскости XOZ. Ничего нового,
Xa`=cosф*Xa + Ya*0 — sinф*Za
Ya`=Xa*0 + Ya*1 + Za*0 (по сути, Ya`=Ya)
Za`=sinф*Xa + Ya*0 + cosф*Za

И третья матрица.
Xa`=Xa*1 + Ya*0 + Za*0 (по сути, Xa`=Xa)
Ya`=Xa*0 + cosф*Ya — sinф*Za
Za`=Xa*0 + sinф*Ya + cosф*Za
А для четвёртого измерения они выглядят вот так:

Думаю, вы уже поняли, что на что множить, потому лишний раз расписывать не буду. Зато замечу, что она делает то же самое, что и матрица для поворота параллельно плоскости в трёхмерном пространстве! И та, и эта изменяют только ординату и аппликату, а остальные координаты не трогают, потому её можно использовать и в трёхмерном случае, просто не обращая внимания на четвёртую координату.
А вот с формулой проекции не всё так просто. Сколько я ни читал форумов, мне не подошёл ни один из способов проекции. Параллельная мне не подходила, так как проекция не будет выглядеть объёмной. В одних формулах проекции для нахождения точки нужно решить систему уравнений( а я не знаю, как научить компьютер их решать), другие я просто-напросто не понял… В общем, я решил придумать свой способ. Рассмотрим для этого проекцию 2D->1D.
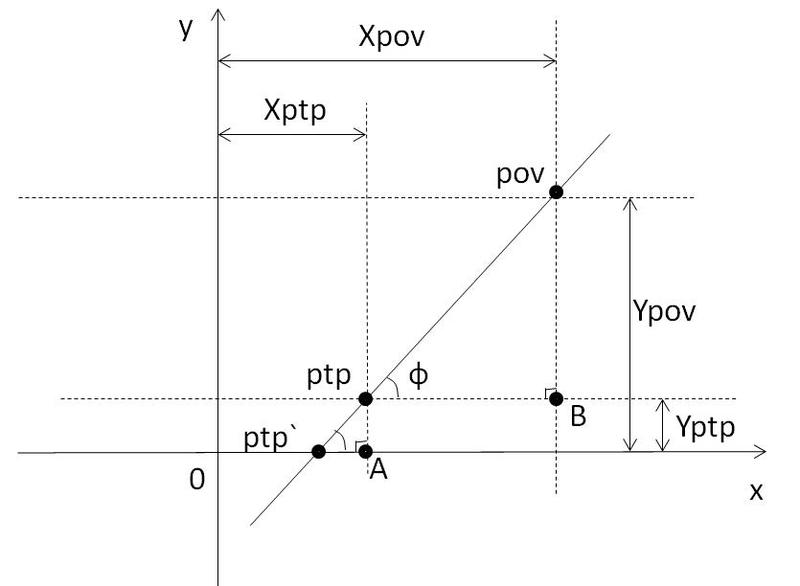
pov значит «Point of view» (точка зрения), ptp значит «Point to project» (точка, которую нужно спроецировать), а ptp` — это искомая точка на оси OX.
Углы povptpB и ptpptp`A равны как соответствующие( пунктирная линия параллельна оси OX, прямая povptp — секущая).
Икс точки ptp` равен иксу точки ptp минус длина отрезка ptp`A. Этот отрезок можно найти из треугольника ptpptp`A: ptp`A = ptpA/тангенс угла ptpptp`A. Мы можем найти этот тангенс из треугольника povptpB: тангенс угла ptpptp`A = (Ypov-Yptp)(Xpov-Xptp).
Ответ: Xptp`=Xptp-Yptp/тангенс угла ptpptp`A.
Я не стал подробно расписывать этот алгоритм тут, так как там куча частных случаев, когда формула несколько меняется. Кому это интересно — посмотрите в исходниках программы, там всё расписано в комментариях.
Для того, чтобы спроецировать точку трёхмерного пространства на плоскость, просто рассмотрим две плоскости — XOZ и YOZ, и для каждой из них решим эту задачу. В случае четырёхмерного пространства нужно рассмотреть уже три плоскости: XOQ, YOQ и ZOQ.
И наконец, про программу. Она действует так: инициализировать шестнадцать вершин тессеракта -> в зависимости от введённых пользователем команд повернуть его -> спроецировать на объём -> в зависимости от введённых пользователем команд повернуть его проекцию -> спроецировать на плоскость -> нарисовать.
Проекции и повороты я написал сам. Они работают по формулам, которые я только что описал. Библиотека OpenGL рисует линии, а так же занимается смешиванием цветов. А координаты вершин тессеракта вычисляются таким образом:
Координаты вершин линии с центром в начале координат и длинной 2 — (1) и (-1);
— ” — ” — квадрата — ” — ” — и ребром длинной 2:
( 1; 1 ), ( -1; 1), (1; -1) и (-1; -1);
— ” — ” — куба — ” — ” -:
( 1; 1; 1 ), ( -1; 1; 1), (1; -1; 1), (-1; -1; 1), ( 1; 1; -1 ), ( -1; 1; -1), (1; -1; -1), (-1; -1; -1);
Как можно было заметить, квадрат — это одна линия над осью OY и одна линия под осью OY; куб — это один квадрат спереди от плоскости XOY, и один за ней; тессеракт — это один куб по ту сторону объёма XOYZ, и один — по эту. Но куда легче воспринять это чередование единиц и минус единиц, если их записать в столбик
1; 1; 1
-1; 1; 1
1; -1; 1
-1; -1; 1
1; 1; -1
-1; 1; -1
1; -1; -1
-1; -1; -1
В первом столбце один и минус один чередуются. Во втором столбце сначала идёт два плюса, потом два минуса. В третьем — четыре плюс единицы, а потом четыре минус единицы. Это были вершины куба. У тессеракта их в два раза больше, и потому нужно было написать цикл для их объявления, иначе очень легко запутаться.
Моя программа так же умеет рисовать анаглиф. Счастливые обладатели 3D-очков могут наблюдать стереоскопическую картинку. В рисовании картинки нет ничего хитрого, просто рисуется две проекции на плоскость, для правого и левого глаз. Зато программа становится намного более наглядной и интересной, а главное — даёт лучшее представление о четырёхмерном мире.
Менее значительные функции — подсветка одной из граней красным, чтобы лучше можно было разглядеть повороты, а так же мелкие удобства — регуляция координат точек-«глаз», увеличение и уменьшение скорости поворота.
Архив с программой, исходником и инструкцией пользования: www.dropbox.com/s/xilxouqmgnsf6zs/%D0%A2%D0%B5%D1%81%D1%81%D0%B5%D1%80%D0%B0%D0%BA%D1%82.rar (нужно скачать и установить программу Dropbox: www.dropbox.com)
Исходник: docs.google.com/document/d/1sGjBTb-od84Qp_la0LS9tWFZL4aYk-1exUs0Za5_Uq0/edit
4.1 Геометрическая
модель куба
Куб задаётся
единственным параметром w –длина ребра
и состоит из восьми вершин: A11, A12, A13, A14
– вершины нижнего основания и A21, A22,
A23, A24 – вершины верхнего основания.
Пусть начало локальной системы координат
куба совпадает с его геометрическим
центром. Тогда координаты его вершин
будут вычисляться следующим образом:
A11=(-w/2,
-w/2, -w/2);
A12=(-w/2,
-w/2, w/2);
A13=(w/2,
-w/2, w/2);
A14=(w/2,
-w/2, -w/2);
A21=(-w/2,
w/2, -w/2);
A22=(-w/2,
w/2, w/2);
A23=(w/2,
w/2, w/2);
A24=(w/2,
w/2, -w/2);
Геометрическая
модель куба представлена на рисунке
4.1.

Рисунок 4.1 –
Геометрическая модель куба
4.2 Геометрическая
модель сферы
В графической базе
данных сфера представляется тройкой
вида (r, m, n), где r – радиус сферы, m –
количество разбиений на вертикальной
полуокружности при построении 0-го
меридиана (тот на котором расположены
точки на рисунке), n – количество разбиений
на горизонтальной окружности при
построении каждой из параллелей. Центр
локальной системы координат связывается
с геометрическим центром сферы.
Изображение сферы приведено на рисунке
4.2.
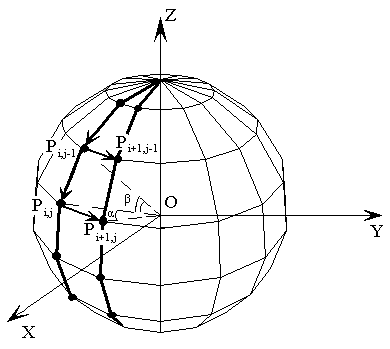
Рисунок 4.2 –
Геометрическая модель сферы
Для построения
сферы необходимо проделать следующие
шаги.
1. Построить точку
с координатами (0, 0, r) в локальной системе
координат сферы.
2. Построить 0-вой
меридиан. Каждая i-я точка 0-го меридиана
получается из предыдущей методом
вращения вокруг оси Х. Угол поворота
точки при построении 0-го меридиана
определяется как π/m. Координата следующей
точки определяется по формуле:
Pi=Pi-1*ПоворотOX(π/m).
(4.1)
Параллели получаются
вращением 0-го меридиана вокруг оси OZ
на угол 2π/n. Каждый следующий меридиан
получается из предыдущего по формуле:
Mi=Mi-1*ПоворотOZ(π/n).
(4.2)
4.3 Геометрическая
модель полусферы
Для построения
геометрической модели полусферы,
необходимо учесть 3 параметра: количество
разбиений по ширине (m), количество
разбиений по высоте (n) и радиус сферы
(r). Пусть основание полусферы лежит в
плоскости XOZ, а часть полусферы без
основания – со стороны положительного
направления оси OY.
Для аппроксимации
полусферы, необходимо построить n
ломаных, состоящих из m точек.
Первая точка первой
ломаной имеет координаты a11(0, r, 0),
координаты остальных m-1 точек будем
находить по формуле:
Aij+1=Aij*ПоворотOZ(-180/(m-1)).
(4.3)
Координаты точек
i-ой ломаной будем вычислять по формуле:
Ai+1j=Aij*ПоворотOY(-180/(n-1)).
(4.4)
Геометрическая
модель полусферы приведена на рисунке
4.3.

Рисунок 4.3 –
Геометрическая модель полусферы
4.4 Геометрическая
модель треугольной косоугольной
призмы
Данный объект
задаётся тремя параметрами: высота,
радиус окружности, в которую вписано
основание, смещение верхнего основания
относительно нижнего вдоль оси OX.
Обозначим эти параметры соответственно
буквами h, r и s.
Пусть центр нижнего
основания совпадает с началом локальной
системы координат, а часть призмы без
основания находится со стороны
положительного направления оси OZ. Первая
точка нижнего основания имеет координаты
A11=(0, r, 0). Тогда координаты остальных
точек нижнего снования будем находить
по следующей формуле:
A1i+1=
A1i*ПоворотOZ(360/3),
(4.5)
а координаты точек
нижнего основания – по формуле:
A2i+1=
A2i*ПоворотOZ(360/3)*Перемещение(s,
0, h). (4.6)
Вид геометрической
модели треугольной косоугольной
призмы приведен на рисунке 4.4.

Рисунок 4.4 –
Геометрическая модель треугольной
косоугольной призмы
4.5 Геометрическая
модель призмы с треугольным основанием
Данный объект
задаётся двумя параметрами: высота и
радиус окружности, в которую вписано
основание. Обозначим эти параметры
соответственно буквами h и r.
Пусть центр нижнего
основания совпадает с началом локальной
системы координат, а часть призмы без
основания находится со стороны
положительного направления оси OZ. Первая
точка нижнего основания имеет координаты
A11=(0,
r, 0). Тогда координаты остальных точек
нижнего снования будем находить по
следующей формуле:
A1i+1=
A1i*ПоворотOZ(360/3),
(4.7)
а координаты точек
верхнего основания – по формуле:
A2i+1=
A2i*ПоворотOZ(360/3)*Перемещение(0,
0, h). (4.8)
Вид геометрической
модели призмы с треугольным основанием
приведен на рисунке 4.5.

Рисунок 4.5 –
Геометрическая модель призмы с треугольным
основанием
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
