Регрессионную модель будем строить для прогнозирования и оценке демографии в России. Статистические данные динамики численности населения в России за 20 лет по годам, в период с 1999 по 2019 год возьмём из вики.
Таблица численности населения России с 1999 г. по 2019 г.
| X, год | Y, млн.чел. |
| 1999 | 147.5 |
| 2000 | 146.9 |
| 2001 | 146.3 |
| 2002 | 145.2 |
| 2003 | 145 |
| 2004 | 144.2 |
| 2005 | 143.5 |
| 2006 | 142.8 |
| 2007 | 142.2 |
| 2008 | 142 |
| 2009 | 141.9 |
| 2010 | 142.9 |
| 2011 | 142.9 |
| 2012 | 143.1 |
| 2013 | 143.3 |
| 2014 | 143.7 |
| 2015 | 146.3 |
| 2016 | 146.5 |
| 2017 | 146.8 |
| 2018 | 146.9 |
| 2019 | 146.8 |
В таблице переменная X – год, Y – численность населения в млн.
Для того чтобы построить линию тренда и получить уравнение регрессии, переходим на вкладку Вставка, выбираем диаграмму – точечная с гладкими кривыми и маркерами
Затем переходим на область диаграммы и правым кликом мыши вызываем меню и выбираем выбрать данные и выбираем диапазон данных для диаграммы
В результате должен получиться следующий график
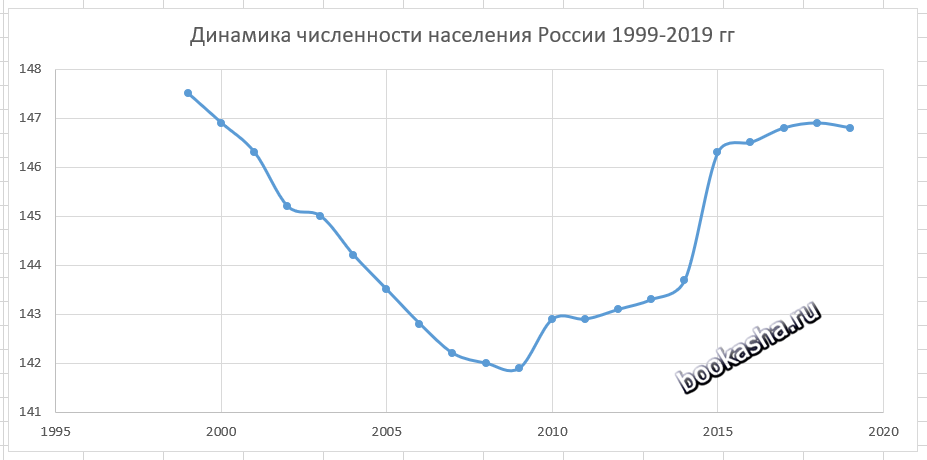
Анализируя полученный график, можно сделать вывод, что этот период характеризуется демографической ямой. С 1999 года по 2009 год численность населения падала в России, а с 2010 по 2018 год наблюдается рост численности населения, а c 2018 по 2019 гг. опять идёт небольшой спад численности населения. Рост численности населения в России, начиная с 2010 годом возможно связан с ведением программы материнского капитала в 2007 году, а также с присоединением Крыма в 2014 году.
Для получения уравнения регрессии для данной линии тренда, жмём плюс (элементы диаграммы) на области графика справа вверху -> линия тренда -> дополнительные параметры.
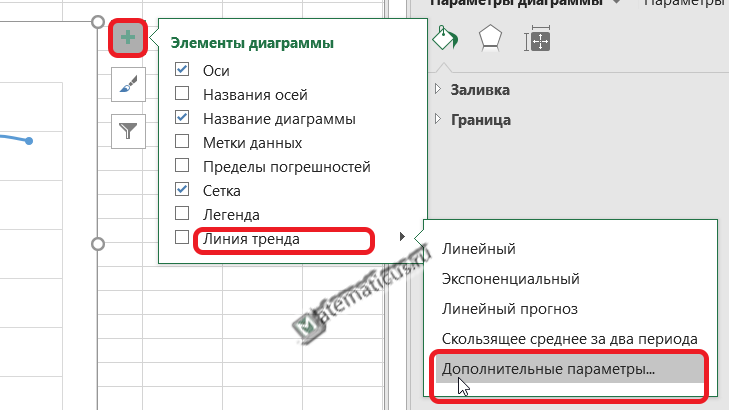
Здесь выбираем форму линии тренда и ниже ставим галочки — показать уравнение регрессии и показать на диаграмме величину достоверности аппроксимации, также указываем прогноз вперёд на один период, т.е. на 2020 год.
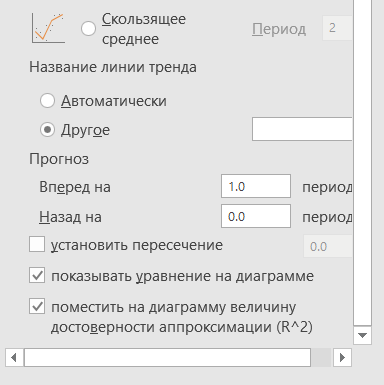
Выбираем полиномиальную линию тренда четвертой порядка (хотя выше 5 и 6 порядка, но они не всегда верно описывают модель), так как значение величины достоверности аппроксимации высокое по сравнению с линейной, экспоненциальной, логарифмической, степенной и т.д.
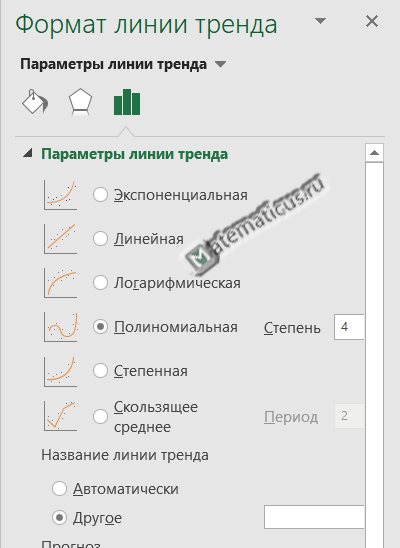
Уравнение регрессии:
y = -0.0005x4 + 4.2586x3 — 12830x2 + 2E+07x — 9E+09
Здесь, значение E означает 10 в какой-либо степени.
Например,
число 2E+07 эквивалентно числу 2*107=-20000000
— 9E+09=-9*109=-90000000000
Величина достоверности аппроксимации равна:
R² = 0.9587
С помощью полученного уравнения регрессии можно спрогнозировать население России на 2020 год.
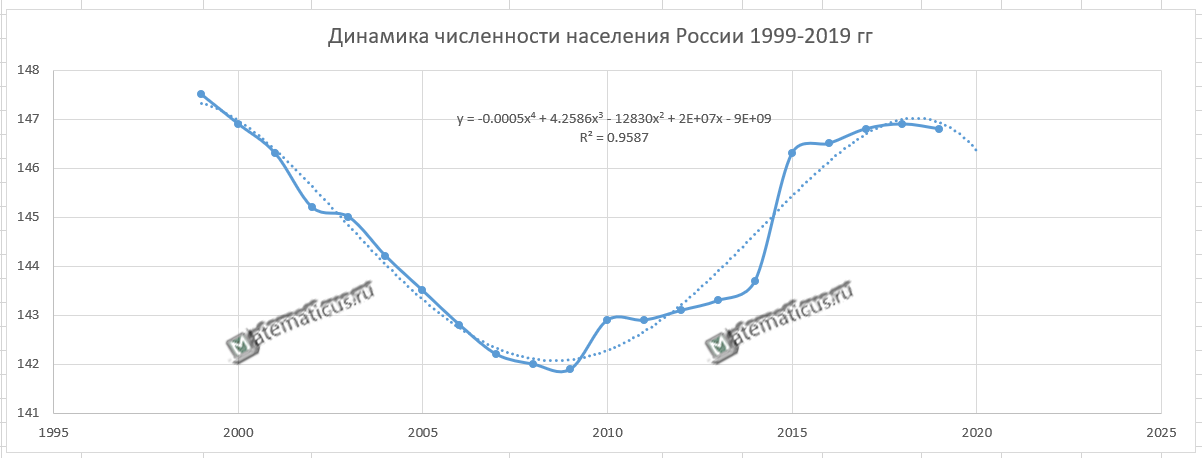
Анализируя график, можно сделать вывод что в 2020 году населения России снизится на 200-300 тыс.чел.
Таким же образом можно построить линию тренда для динамики численности населения России после ВОВ, начиная с 1946 по 2019 г.
| X | Y |
| 1946 | 97.5 |
| 1947 | 98.5 |
| 1948 | 99.2 |
| 1949 | 100.2 |
| 1950 | 102.1 |
| 1951 | 103 |
| 1952 | 104.6 |
| 1953 | 106.7 |
| 1954 | 108.4 |
| 1955 | 110.5 |
| 1956 | 112.3 |
| 1957 | 114 |
| 1958 | 115.7 |
| 1959 | 117.5 |
| 1960 | 119 |
| 1961 | 120.8 |
| 1962 | 122.4 |
| 1963 | 123.9 |
| 1964 | 125.2 |
| 1965 | 126.3 |
| 1966 | 127.2 |
| 1967 | 128 |
| 1968 | 128.7 |
| 1969 | 129.4 |
| 1970 | 130.1 |
| 1971 | 130.6 |
| 1972 | 131.3 |
| 1973 | 132.1 |
| 1974 | 132.8 |
| 1975 | 133.6 |
| 1976 | 134.6 |
| 1977 | 135.5 |
| 1978 | 136.5 |
| 1979 | 137.5 |
| 1980 | 138.1 |
| 1981 | 138.9 |
| 1982 | 139.6 |
| 1983 | 140.5 |
| 1984 | 141.6 |
| 1985 | 142.5 |
| 1986 | 143.5 |
| 1987 | 144.8 |
| 1988 | 146 |
| 1989 | 147.4 |
| 1990 | 147.7 |
| 1991 | 148.3 |
| 1992 | 148.5 |
| 1993 | 148.6 |
| 1994 | 148.4 |
| 1995 | 148.5 |
| 1996 | 148.3 |
| 1997 | 148 |
| 1998 | 147.8 |
| 1999 | 147.5 |
| 2000 | 146.9 |
| 2001 | 146.3 |
| 2002 | 145.2 |
| 2003 | 145 |
| 2004 | 144.2 |
| 2005 | 143.5 |
| 2006 | 142.8 |
| 2007 | 142.2 |
| 2008 | 142 |
| 2009 | 141.9 |
| 2010 | 142.9 |
| 2011 | 142.9 |
| 2012 | 143.1 |
| 2013 | 143.3 |
| 2014 | 143.7 |
| 2015 | 146.3 |
| 2016 | 146.5 |
| 2017 | 146.8 |
| 2018 | 146.9 |
| 2019 | 146.8 |
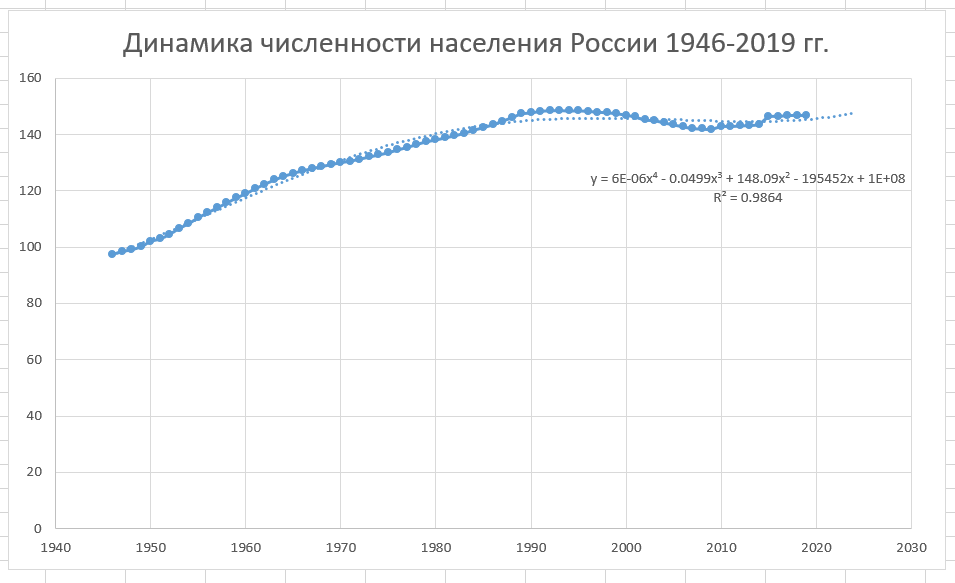
График динамики численности населения России после Великой Отечественной войны в период с 1946 по 2019 г.
![]() 5302
5302
Основы линейной регрессии
Время на прочтение
13 мин
Количество просмотров 122K
Здравствуй, Хабр!
Цель этой статьи — рассказать о линейной регрессии, а именно собрать и показать формулировки и интерпретации задачи регрессии с точки зрения математического анализа, статистики, линейной алгебры и теории вероятностей. Хотя в учебниках эта тема изложена строго и исчерпывающе, ещё одна научно-популярная статья не помешает.
! Осторожно, трафик! В статье присутствует заметное число изображений для иллюстраций, часть в формате gif.
Содержание
- Введение
- Метод наименьших квадратов
- Математический анализ
- Статистика
- Теория вероятностей
- Мультилинейная регрессия
- Линейная алгебра
- Произвольный базис
- Заключительные замечания
- Проблема выбора размерности
- Численные методы
- Реклама и заключение
Введение
Есть три сходных между собой понятия, три сестры: интерполяция, аппроксимация и регрессия.
У них общая цель: из семейства функций выбрать ту, которая обладает определенным свойством.
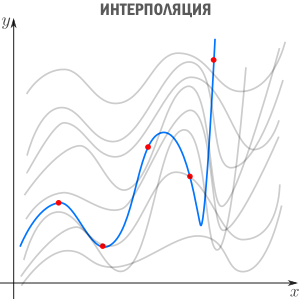
Интерполяция — способ выбрать из семейства функций ту, которая проходит через заданные точки. Часто функцию затем используют для вычисления в промежуточных точках. Например, мы вручную задаем цвет нескольким точкам и хотим чтобы цвета остальных точек образовали плавные переходы между заданными. Или задаем ключевые кадры анимации и хотим плавные переходы между ними. Классические примеры: интерполяция полиномами Лагранжа, сплайн-интерполяция, многомерная интерполяция (билинейная, трилинейная, методом ближайшего соседа и т.д). Есть также родственное понятие экстраполяции — предсказание поведения функции вне интервала. Например, предсказание курса доллара на основании предыдущих колебаний — экстраполяция.
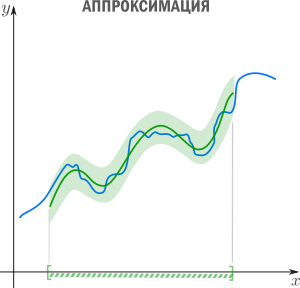 Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.
Аппроксимация — способ выбрать из семейства «простых» функций приближение для «сложной» функции на отрезке, при этом ошибка не должна превышать определенного предела. Аппроксимацию используют, когда нужно получить функцию, похожую на данную, но более удобную для вычислений и манипуляций (дифференцирования, интегрирования и т.п). При оптимизации критических участков кода часто используют аппроксимацию: если значение функции вычисляется много раз в секунду и не нужна абсолютная точность, то можно обойтись более простым аппроксимантом с меньшей «ценой» вычисления. Классические примеры включают ряд Тейлора на отрезке, аппроксимацию ортогональными многочленами, аппроксимацию Паде, аппроксимацию синуса Бхаскара и т.п.
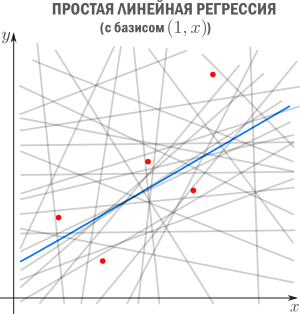 Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).
Регрессия — способ выбрать из семейства функций ту, которая минимизирует функцию потерь. Последняя характеризует насколько сильно пробная функция отклоняется от значений в заданных точках. Если точки получены в эксперименте, они неизбежно содержат ошибку измерений, шум, поэтому разумнее требовать, чтобы функция передавала общую тенденцию, а не точно проходила через все точки. В каком-то смысле регрессия — это «интерполирующая аппроксимация»: мы хотим провести кривую как можно ближе к точкам и при этом сохранить ее максимально простой чтобы уловить общую тенденцию. За баланс между этими противоречивыми желаниями как-раз отвечает функция потерь (в английской литературе «loss function» или «cost function»).
В этой статье мы рассмотрим линейную регрессию. Это означает, что семейство функций, из которых мы выбираем, представляет собой линейную комбинацию наперед заданных базисных функций
Цель регрессии — найти коэффициенты этой линейной комбинации, и тем самым определить регрессионную функцию
(которую также называют моделью). Отмечу, что линейную регрессию называют линейной именно из-за линейной комбинации базисных функций — это не связано с самыми базисными функциями (они могут быть линейными или нет).
Регрессия с нами уже давно: впервые метод опубликовал Лежандр в 1805 году, хотя Гаусс пришел к нему раньше и успешно использовал для предсказания орбиты «кометы» (на самом деле карликовой планеты) Цереры. Существует множество вариантов и обобщений линейной регрессии: LAD, метод наименьших квадратов, Ridge регрессия, Lasso регрессия, ElasticNet и многие другие.
Метод наименьших квадратов
Начнём с простейшего двумерного случая. Пусть нам даны точки на плоскости
и мы ищем такую аффинную функцию
 чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной
чтобы ее график ближе всего находился к точкам. Таким образом, наш базис состоит из константной функции и линейной
.
Как видно из иллюстрации, расстояние от точки до прямой можно понимать по-разному, например геометрически — это длина перпендикуляра. Однако в контексте нашей задачи нам нужно функциональное расстояние, а не геометрическое. Нас интересует разница между экспериментальным значением и предсказанием модели для каждого
поэтому измерять нужно вдоль оси
.
Первое, что приходит в голову, в качестве функции потерь попробовать выражение, зависящее от абсолютных значений разниц
. Простейший вариант — сумма модулей отклонений
приводит к Least Absolute Distance (LAD) регрессии.
Впрочем, более популярная функция потерь — сумма квадратов отклонений регрессанта от модели. В англоязычной литературе она носит название Sum of Squared Errors (SSE)
Метод наименьших квадратов (по англ. OLS) — линейная регрессия c
в качестве функции потерь.

Такой выбор прежде всего удобен: производная квадратичной функции — линейная функция, а линейные уравнения легко решаются. Впрочем, далее я укажу и другие соображения в пользу
.
Математический анализ
Простейший способ найти
— вычислить частные производные по
и
, приравнять их нулю и решить систему линейных уравнений
Значения параметров, минимизирующие функцию потерь, удовлетворяют уравнениям
которые легко решить
Мы получили громоздкие и неструктурированные выражения. Сейчас мы их облагородим и вдохнем в них смысл.
Статистика
Полученные формулы можно компактно записать с помощью статистических эстиматоров: среднего
, вариации
(стандартного отклонения), ковариации
и корреляции
Перепишем
как
где
это нескорректированное (смещенное) стандартное выборочное отклонение, а
— ковариация. Теперь вспомним, что коэффициент корреляции (коэффициент корреляции Пирсона)
и запишем

Теперь мы можем оценить все изящество дескриптивной статистики, записав уравнение регрессионной прямой так
Во-первых, это уравнение сразу указывает на два свойства регрессионной прямой:
Во-вторых, теперь становится понятно, почему метод регрессии называется именно так. В единицах стандартного отклонения
отклоняется от своего среднего значения меньше чем
, потому что
. Это называется регрессией(от лат. regressus — «возвращение») по отношению к среднему. Это явление было описано сэром Фрэнсисом Гальтоном в конце XIX века в его статье «Регрессия к посредственности при наследовании роста». В статье показано, что черты (такие как рост), сильно отклоняющиеся от средних, редко передаются по наследству. Характеристики потомства как бы стремятся к среднему — на детях гениев природа отдыхает.
Возведя коэффициент корреляции в квадрат, получим коэффициент детерминации
. Квадрат этой статистической меры показывает насколько хорошо регрессионная модель описывает данные.
, равный
, означает что функция идеально ложится на все точки — данные идеально скоррелированны. Можно доказать, что
показывает какая доля вариативности в данных объясняется лучшей из линейных моделей. Чтобы понять, что это значит, введем определения
— вариация исходных данных (вариация точек
).
— вариация остатков, то есть вариация отклонений от регрессионной модели — от
нужно отнять предсказание модели и найти вариацию.
— вариация регрессии, то есть вариация предсказаний регрессионной модели в точках
(обратите внимание, что среднее предсказаний модели совпадает с
).
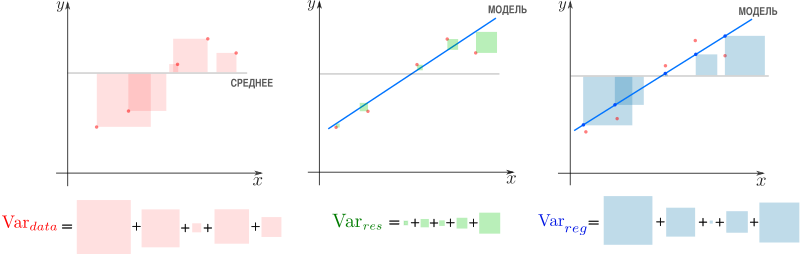
Дело в том, что вариация исходных данных разлагается в сумму двух других вариаций: вариации случайного шума (остатков) и вариации, которая объясняется моделью (регрессии)
или
Как видим, стандартные отклонения образуют прямоугольный треугольник.

Мы стремимся избавиться от вариативности, связанной с шумом и оставить лишь вариативность, которая объясняется моделью, — хотим отделить зерна от плевел. О том, насколько это удалось лучшей из линейных моделей, свидетельствует
, равный единице минус доля вариации ошибок в суммарной вариации
или доле объясненной вариации (доля вариации регрессии в полной вариации)
равен косинусу угла в прямоугольном треугольнике
. Кстати, иногда вводят долю необъясненной вариации
и она равна квадрату синуса в этом треугольнике. Если коэффициент детерминации мал, возможно мы выбрали неудачные базисные функции, линейная регрессия неприменима вовсе и т.п.
Теория вероятностей
Ранее мы пришли к функции потерь
из соображений удобства, но к ней же можно прийти с помощью теории вероятностей и метода максимального правдоподобия (ММП). Напомню вкратце его суть. Предположим, у нас есть
независимых одинаково распределенных случайных величин (в нашем случае — результатов измерений). Мы знаем вид функции распределения (напр. нормальное распределение), но хотим определить параметры, которые в нее входят (например
и
). Для этого нужно вычислить вероятность получить
датапоинтов в предположении постоянных, но пока неизвестных параметров. Благодаря независимости измерений, мы получим произведение вероятностей реализации каждого измерения. Если мыслить полученную величину как функцию параметров (функция правдоподобия) и найти её максимум, мы получим оценку параметров. Зачастую вместо функции правдоподобия используют ее логарифм — дифференцировать его проще, а результат — тот же.
Вернемся к задаче простой регрессии. Допустим, что значения
нам известны точно, а в измерении
присутствует случайный шум (свойство слабой экзогенности). Более того, положим, что все отклонения от прямой (свойство линейности) вызваны шумом с постоянным распределением (постоянство распределения). Тогда
где
— нормально распределенная случайная величина

Исходя из предположений выше, запишем функцию правдоподобия
и ее логарифм
Таким образом, максимум правдоподобия достигается при минимуме
что дает основание принять ее в качестве функции потерь. Кстати, если
мы получим функцию потерь LAD регрессии
которую мы упоминали ранее.
Подход, который мы использовали в этом разделе — один из возможных. Можно прийти к такому же результату, используя более общие свойства. В частности, свойство постоянства распределения можно ослабить, заменив на свойства независимости, постоянства вариации (гомоскедастичность) и отсутствия мультиколлинеарности. Также вместо ММП эстимации можно воспользоваться другими методами, например линейной MMSE эстимацией.
Мультилинейная регрессия
До сих пор мы рассматривали задачу регрессии для одного скалярного признака
, однако обычно регрессор — это
-мерный вектор
. Другими словами, для каждого измерения мы регистрируем
фич, объединяя их в вектор. В этом случае логично принять модель с
независимыми базисными функциями векторного аргумента —
степеней свободы соответствуют
фичам и еще одна — регрессанту
. Простейший выбор — линейные базисные функции
. При
получим уже знакомый нам базис
.
Итак, мы хотим найти такой вектор (набор коэффициентов)
, что
Знак “
” означает, что мы ищем решение, которое минимизирует сумму квадратов ошибок
Последнее уравнение можно переписать более удобным образом. Для этого расположим
в строках матрицы (матрицы информации)
Тогда столбцы матрицы
отвечают измерениям
-ой фичи. Здесь важно не запутаться:
— количество измерений,
— количество признаков (фич), которые мы регистрируем. Систему можно записать как
Квадрат нормы разности векторов в правой и левой частях уравнения образует функцию потерь
которую мы намерены минимизировать
Продифференцируем финальное выражение по
(если забыли как это делается — загляните в Matrix cookbook)
приравняем производную к
и получим т.н. нормальные уравнения
Если столбцы матрицы информации
линейно независимы (нет идеально скоррелированных фич), то матрица
имеет обратную (доказательство можно посмотреть, например, в видео академии Хана). Тогда можно записать
где
псевдообратная к
. Понятие псевдообратной матрицы введено в 1903 году Фредгольмом, она сыграла важную роль в работах Мура и Пенроуза.
Напомню, что обратить
и найти
можно только если столбцы
линейно независимы. Впрочем, если столбцы
близки к линейной зависимости, вычисление
уже становится численно нестабильным. Степень линейной зависимости признаков в
или, как говорят, мультиколлинеарности матрицы
, можно измерить числом обусловленности — отношением максимального собственного значения к минимальному. Чем оно больше, тем ближе
к вырожденной и неустойчивее вычисление псевдообратной.
Линейная алгебра
К решению задачи мультилинейной регрессии можно прийти довольно естественно и с помощью линейной алгебры и геометрии, ведь даже то, что в функции потерь фигурирует норма вектора ошибок уже намекает, что у задачи есть геометрическая сторона. Мы видели, что попытка найти линейную модель, описывающую экспериментальные точки, приводит к уравнению
Если количество переменных равно количеству неизвестных и уравнения линейно независимы, то система имеет единственное решение. Однако, если число измерений превосходит число признаков, то есть уравнений больше чем неизвестных — система становится несовместной, переопределенной. В этом случае лучшее, что мы можем сделать — выбрать вектор
, образ которого
ближе остальных к
. Напомню, что множество образов или колоночное пространство
— это линейная комбинация вектор-столбцов матрицы
—
-мерное линейное подпространство (мы считаем фичи линейно независимыми), линейная оболочка вектор-столбцов
. Итак, если
принадлежит
, то мы можем найти решение, если нет — будем искать, так сказать, лучшее из нерешений.
Если в дополнение к векторам
мы рассмотрим все вектора им перпендикулярные, то получим еще одно подпространство и сможем любой вектор из
разложить на две компоненты, каждая из которых живет в своем подпространстве. Второе, перпендикулярное пространство, можно характеризовать следующим образом (нам это понадобится в дальнейшем). Пускай
, тогда
равен нулю в том и только в том случае, если
перпендикулярен всем
, а значит и целому
. Таким образом, мы нашли два перпендикулярных линейных подпространства, линейные комбинации векторов из которых полностью, без дыр, «покрывают» все
. Иногда это обозначают c помощью символа ортогональной прямой суммы

где
. В каждое из подпространств можно попасть с помощью соответствующего оператора проекции, но об этом ниже.

Теперь представим
в виде разложения

Если мы ищем решение
, то естественно потребовать, чтобы
была минимальна, ведь это длина вектора-остатка. Учитывая перпендикулярность подпространств и теорему Пифагора
но поскольку, выбрав подходящий
, я могу получить любой вектор колоночного пространства, то задача сводится к
а
останется в качестве неустранимой ошибки. Любой другой выбор
сделает ошибку только больше.

Если теперь вспомнить, что
, то легко видеть
что очень удобно, так как
у нас нет, а вот
— есть. Вспомним из предыдущего параграфа, что
имеет обратную при условии линейной независимости признаков и запишем решение
где
уже знакомая нам псевдообратная матрица. Если нам интересна проекция
, то можно записать
где
— оператор проекции на колоночное пространство.
Выясним геометрический смысл коэффициента детерминации.

Заметьте, что фиолетовый вектор
пропорционален первому столбцу матрицы информации
, который состоит из одних единиц согласно нашему выбору базисных функций. В RGB треугольнике
Так как этот треугольник прямоугольный, то по теореме Пифагора
Это геометрическая интерпретация уже известного нам факта, что
Мы знаем, что
а значит
Красиво, не правда ли?
Произвольный базис
Как мы знаем, регрессия выполняется на базисных функциях
и её результатом есть модель
но до сих пор мы использовали простейшие
, которые просто ретранслировали изначальные признаки без изменений, ну разве что дополняли их постоянной фичей
. Как можно было заметить, на самом деле ни вид
, ни их количество ничем не ограничены — главное, чтобы функции в базисе были линейно независимы. Обычно, выбор делается исходя из предположений о природе процесса, который мы моделируем. Если у нас есть основания полагать, что точки
ложатся на параболу, а не на прямую, то стоит выбрать базис
. Количество базисных функций может быть как меньшим, так и большим, чем количество изначальных фич.
Если мы определились с базисом, то дальше действуем следующим образом. Мы формируем матрицу информации
записываем функцию потерь
и находим её минимум, например с помощью псевдообратной матрицы
или другим методом.
Заключительные замечания
Проблема выбора размерности
На практике часто приходится самостоятельно строить модель явления, то есть определяться сколько и каких нужно взять базисных функций. Первый порыв «набрать побольше» может сыграть злую шутку: модель окажется слишком чувствительной к шумам в данных (переобучение). С другой стороны, если излишне ограничить модель, она будет слишком грубой (недообучение).
Есть два способа выйти из ситуации. Первый: последовательно наращивать количество базисных функций, проверять качество регрессии и вовремя остановиться. Или же второй: выбрать функцию потерь, которая определит число степеней свободы автоматически. В качестве критерия успешности регрессии можно использовать коэффициент детерминации, о котором уже упоминалось выше, однако, проблема в том, что
монотонно растет с ростом размерности базиса. Поэтому вводят скорректированный коэффициент
где
— размер выборки,
— количество независимых переменных. Следя за
, мы можем вовремя остановиться и перестать добавлять дополнительные степени свободы.
Вторая группа подходов — регуляризации, самые известные из которых Ridge(
/гребневая/Тихоновская регуляризация), Lasso(
регуляризация) и Elastic Net(Ridge+Lasso). Главная идея этих методов: модифицировать функцию потерь дополнительными слагаемыми, которые не позволят вектору коэффициентов
неограниченно расти и тем самым воспрепятствуют переобучению
где
и
— параметры, которые регулируют «силу» регуляризации. Это обширная тема с красивой геометрией, которая заслуживает отдельного рассмотрения. Упомяну кстати, что для случая двух переменных при помощи вероятностной интерпретации можно получить Ridge и Lasso регрессии, удачно выбрав априорное распределения для коэффициента

Численные методы
Скажу пару слов, как минимизировать функцию потерь на практике. SSE — это обычная квадратичная функция, которая параметризируется входными данными, так что принципиально ее можно минимизировать методом скорейшего спуска или другими методами оптимизации. Разумеется, лучшие результаты показывают алгоритмы, которые учитывают вид функции SSE, например метод стохастического градиентного спуска. Реализация Lasso регрессии в scikit-learn использует метод координатного спуска.
Также можно решить нормальные уравнения с помощью численных методов линейной алгебры. Эффективный метод, который используется в scikit-learn для МНК — нахождение псевдообратной матрицы с помощью сингулярного разложения. Поля этой статьи слишком узки, чтобы касаться этой темы, за подробностями советую обратиться к курсу лекций К.В.Воронцова.
Реклама и заключение
Эта статья — сокращенный пересказ одной из глав курса по классическому машинному обучению в Киевском академическом университете (преемник Киевского отделения Московского физико-технического института, КО МФТИ). Автор статьи помогал в создании этого курса. Технически курс выполнен на платформе Google Colab, что позволяет совмещать формулы, форматированные LaTeX, исполняемый код Python и интерактивные демонстрации на Python+JavaScript, так что студенты могут работать с материалами курса и запускать код с любого компьютера, на котором есть браузер. На главной странице собраны ссылки на конспекты, «рабочие тетради» для практик и дополнительные ресурсы. В основу курса положены следующие принципы:
- все материалы должны быть доступны студентам с первой пары;
- лекция нужны для понимания, а не для конспектирования (конспекты уже готовы, нет смысла их писать, если не хочется);
- конспект — больше чем лекция (материала в конспектах больше, чем было озвучено на лекции, фактически конспекты представляют собой полноценный учебник);
- наглядность и интерактивность (иллюстрации, фото, демки, гифки, код, видео с youtube).
Если хотите посмотреть на результат — загляните на страничку курса на GitHub.
Надеюсь вам было интересно, спасибо за внимание.
Простая линейная регрессия — это метод, который мы можем использовать для понимания взаимосвязи между объясняющей переменной x и переменной отклика y.
В этом руководстве объясняется, как выполнить простую линейную регрессию в Excel.
Пример: простая линейная регрессия в Excel
Предположим, нас интересует взаимосвязь между количеством часов, которое студент тратит на подготовку к экзамену, и полученной им экзаменационной оценкой.
Чтобы исследовать эту взаимосвязь, мы можем выполнить простую линейную регрессию, используя часы обучения в качестве независимой переменной и экзаменационный балл в качестве переменной ответа.
Выполните следующие шаги в Excel, чтобы провести простую линейную регрессию.
Шаг 1: Введите данные.
Введите следующие данные о количестве часов обучения и экзаменационном балле, полученном для 20 студентов:
Шаг 2: Визуализируйте данные.
Прежде чем мы выполним простую линейную регрессию, полезно создать диаграмму рассеяния данных, чтобы убедиться, что действительно существует линейная зависимость между отработанными часами и экзаменационным баллом.
Выделите данные в столбцах A и B. В верхней ленте Excel перейдите на вкладку « Вставка ». В группе « Диаграммы » нажмите « Вставить разброс» (X, Y) и выберите первый вариант под названием « Разброс ». Это автоматически создаст следующую диаграмму рассеяния:
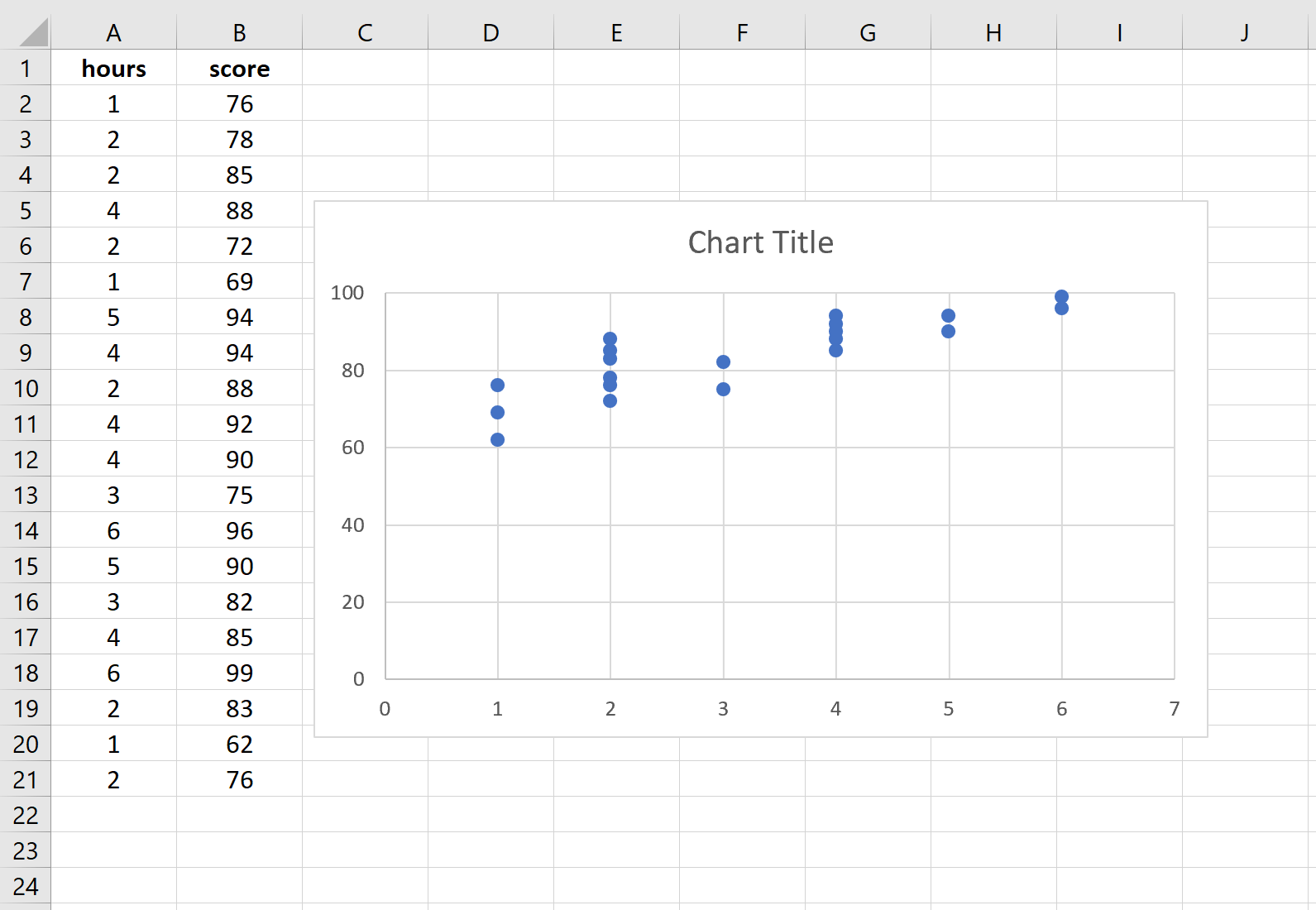
Количество часов обучения показано на оси x, а баллы за экзамены показаны на оси y. Мы видим, что между двумя переменными существует линейная зависимость: большее количество часов обучения связано с более высокими баллами на экзаменах.
Чтобы количественно оценить взаимосвязь между этими двумя переменными, мы можем выполнить простую линейную регрессию.
Шаг 3: Выполните простую линейную регрессию.
В верхней ленте Excel перейдите на вкладку « Данные » и нажмите « Анализ данных».Если вы не видите эту опцию, вам необходимо сначала установить бесплатный пакет инструментов анализа .

Как только вы нажмете « Анализ данных», появится новое окно. Выберите «Регрессия» и нажмите «ОК».
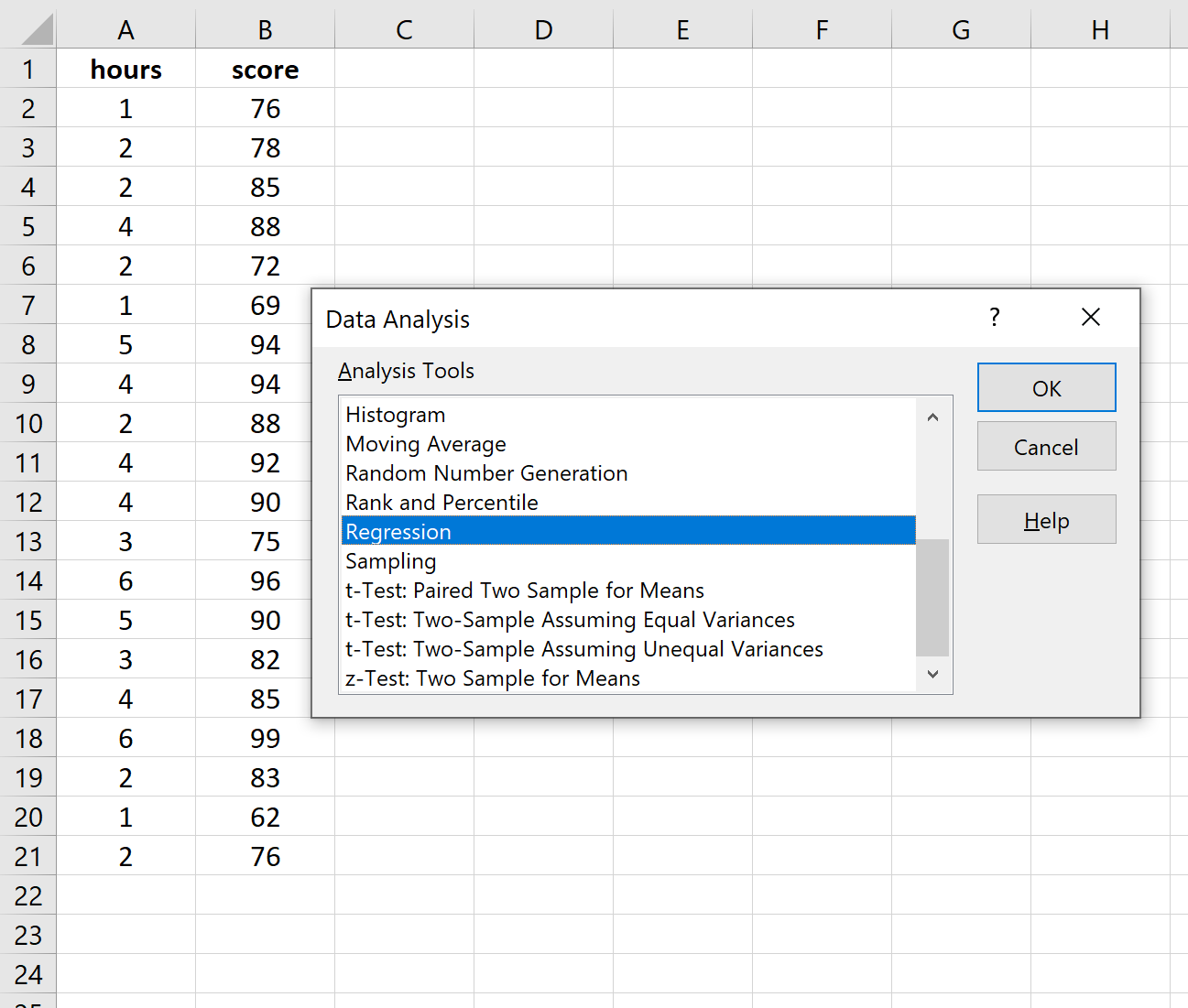
Для Input Y Range заполните массив значений для переменной ответа. Для Input X Range заполните массив значений для независимой переменной.
Установите флажок рядом с Метки , чтобы Excel знал, что мы включили имена переменных во входные диапазоны.
В поле Выходной диапазон выберите ячейку, в которой должны отображаться выходные данные регрессии.
Затем нажмите ОК .
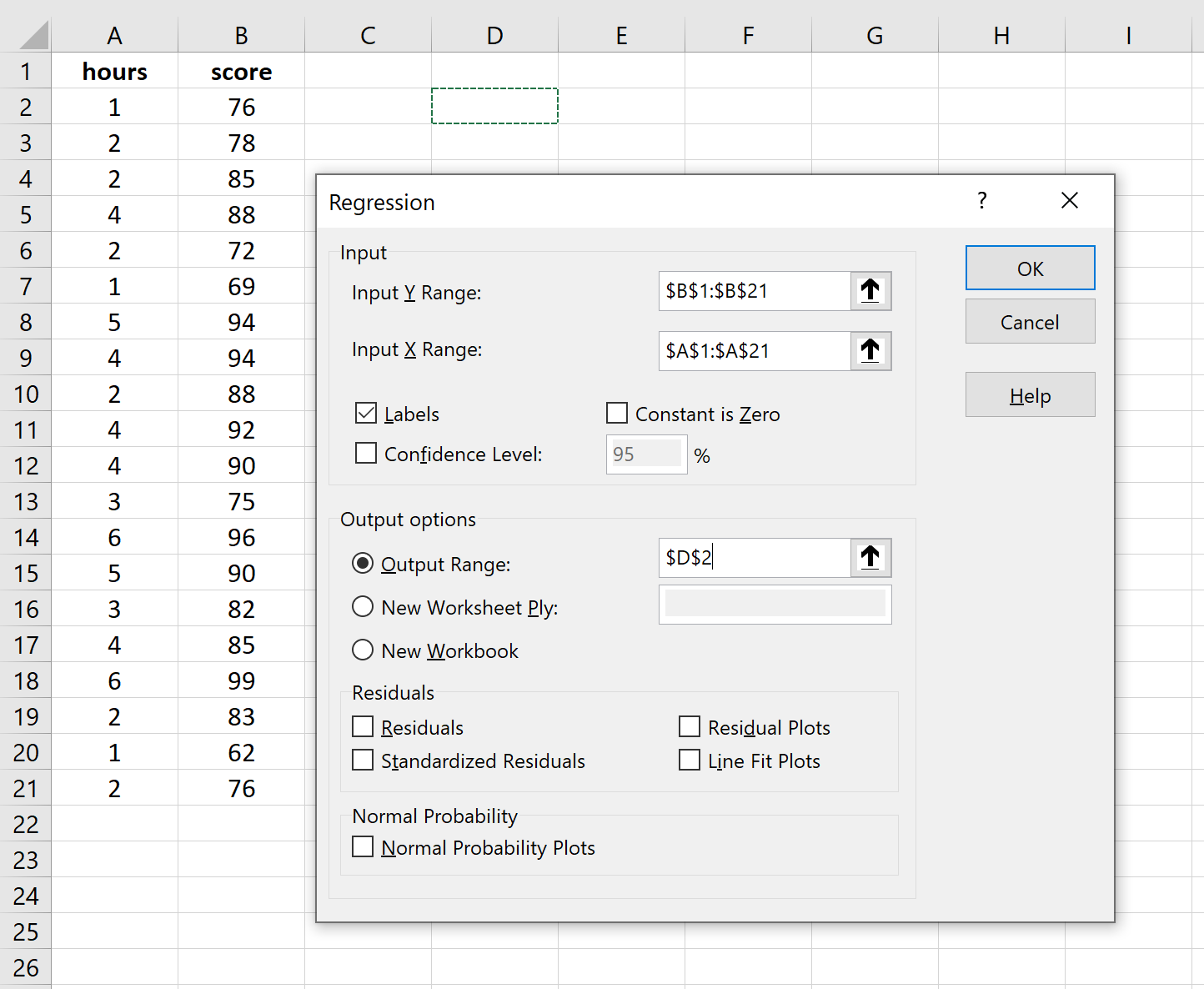
Автоматически появится следующий вывод:
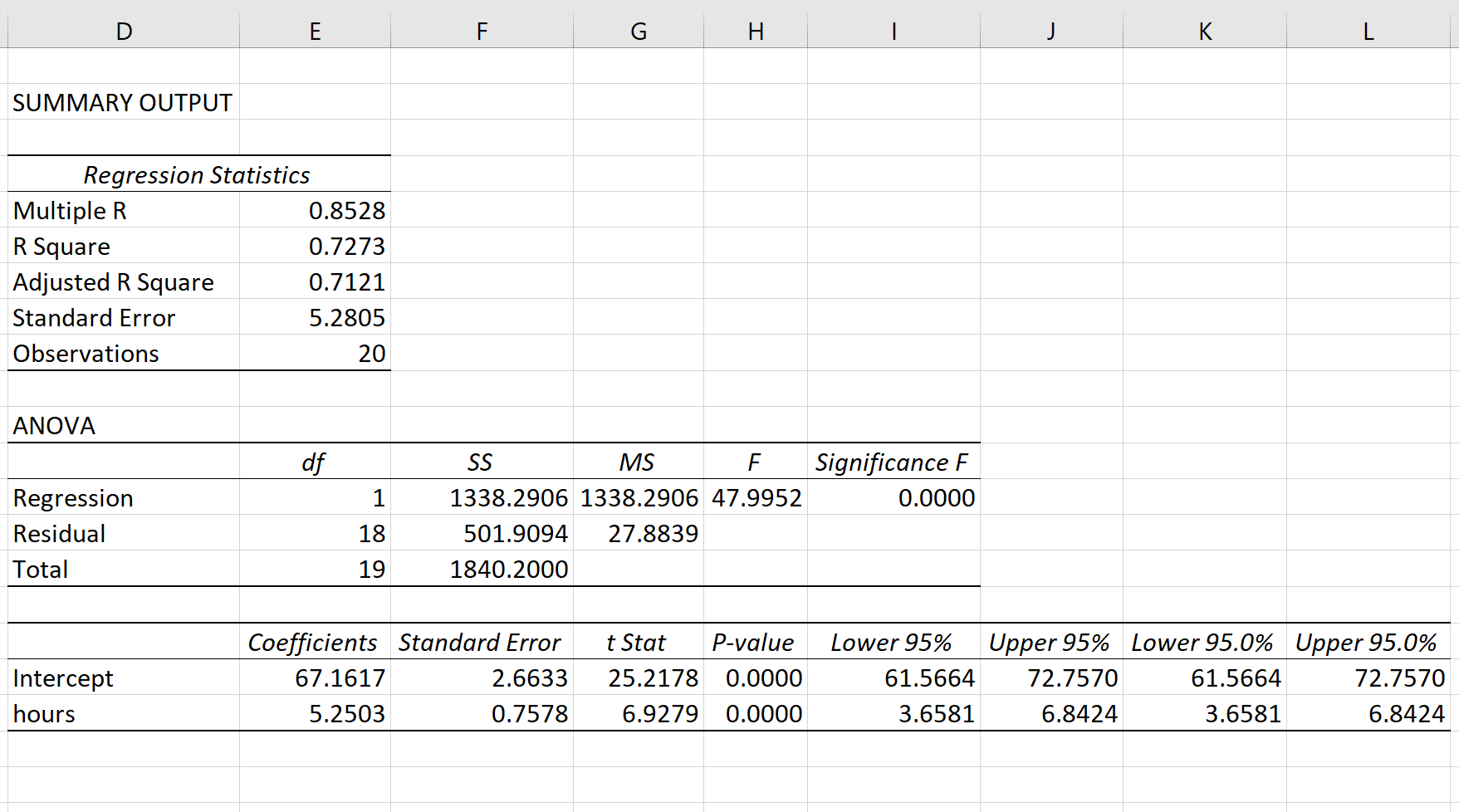
Шаг 4: Интерпретируйте вывод.
Вот как интерпретировать наиболее релевантные числа в выводе:
R-квадрат: 0,7273.Это известно как коэффициент детерминации. Это доля дисперсии переменной отклика, которая может быть объяснена объясняющей переменной. В этом примере 72,73 % различий в баллах за экзамены можно объяснить количеством часов обучения.
Стандартная ошибка: 5.2805.Это среднее расстояние, на которое наблюдаемые значения отходят от линии регрессии. В этом примере наблюдаемые значения отклоняются от линии регрессии в среднем на 5,2805 единиц.
Ф: 47,9952.Это общая F-статистика для регрессионной модели, рассчитанная как MS регрессии / остаточная MS.
Значение F: 0,0000.Это p-значение, связанное с общей статистикой F. Он говорит нам, является ли регрессионная модель статистически значимой. Другими словами, он говорит нам, имеет ли независимая переменная статистически значимую связь с переменной отклика. В этом случае p-значение меньше 0,05, что указывает на наличие статистически значимой связи между отработанными часами и полученными экзаменационными баллами.
Коэффициенты: коэффициенты дают нам числа, необходимые для написания оценочного уравнения регрессии. В этом примере оцененное уравнение регрессии:
экзаменационный балл = 67,16 + 5,2503*(часов)
Мы интерпретируем коэффициент для часов как означающий, что за каждый дополнительный час обучения ожидается увеличение экзаменационного балла в среднем на 5,2503.Мы интерпретируем коэффициент для перехвата как означающий, что ожидаемая оценка экзамена для студента, который учится без часов, составляет 67,16 .
Мы можем использовать это оценочное уравнение регрессии для расчета ожидаемого экзаменационного балла для учащегося на основе количества часов, которые он изучает.
Например, ожидается, что студент, который занимается три часа, получит на экзамене 82,91 балла:
экзаменационный балл = 67,16 + 5,2503*(3) = 82,91
Дополнительные ресурсы
В следующих руководствах объясняется, как выполнять другие распространенные задачи в Excel:
Как создать остаточный график в Excel
Как построить интервал прогнозирования в Excel
Как создать график QQ в Excel
Линейная регрессия
Сегодня пойдет речь о регрессии, как обучать и какие проблемы могут вам попасться при использовании таких моделей.
Для начала давайте введем удобные обозначения.
$mathbb{X} – text{пространство объектов}$
$mathbb{Y} – text{пространство ответов}$
$ x = (x^1, … x^n) – text{признаковое описание объекта}$
$ X = (x_i,y_i)^l_{i=1} – text{обучающая выборка} $
$ a(x) – text{алгоритм, модель} $
$ Q(a,X) – text{функция ошибки алгоритма a на выборке X} $
$ text{Обучение} – a(x) = text{argmin}_{a in mathbb{A}} Q(a,X)$
Но этого мало, давайте разберем, что такое функционал ошибки, семейство алгоритмов, метод обучения.
- Функционал ошибки Q: способ измерения того, хорошо или плохо работает алгоритм на конкретной выборке
- Семейство алгоритмов $mathbb{A}$: как выглядит множество алгоритмов, из которых выбирается лучший
- Метод обучения: как именно выбирается лучший алгоритм из семейства алгоритмов.
Пример задачи регрессии: предсказание количества заказов магазина
Пусть известен один признак – расстояние кафе от метро, а предсказать необходимо количество заказов. Поскольку количество заказов – вещественное число $mathbb{R}$, здесь идет речь о задаче регрессии.

По графику можно сделать вывод о существование зависимости между расстоянием от метро и количеством заказов. Можно предположить, что зависимость линейна, ее можно представить в видео прямой на графике. По этой прямой и можно будет предсказывать количество заказов, если известно расстояние от метро.
В целом такая модель угадывает тенденцию, то есть описывает зависимость между ответом и признаком.
При этом, разумеется ,она делает это не идеально, с некоторой ошибкой. Истинный ответ на каждом объекте несколько отклоняется от прогноза.
Один признак – это несерьезно. Гораздо сложнее и интереснее работать с многомерными выборками, которые описываются большим количеством признаков. В этом случае отобразить выборку и понять, подходит ли модель или нет, нельзя. Можно лишь оценить ее качество и по нему уже понять, подходит ли эта модель.
Описание линейной модели
Давайте обсудим, как выглядит семейство алгоритмов в случае с линейными моделями. Линейный алгоритм в задачах регрессии выглядит следующим образом
$$ a(x)=w_0 + sumlimits_{j=1}^d w_j x^j $$
где $w_0$ – свободный коэффициент, $x^j$ – признаки, а $w_j$ – их веса.
Если у нашего набора данных есть только один признак, то алгоритм выглядит так
$$ a(x)=w_0 + w x $$
Ничего не напоминает? Да, действительно это обычная линейная функция, известная с 7 класса.
$$ y = kx+b $$
В качестве меры ошибки мы не может быть выбрано отклонение от прогноза $Q(a,y)=a(x)-y$, так как в этом случае минимум функционала не будет достигаться при правильном ответе $a(x)=y$. Самый простой способ – считать модуль отклонения.
$$ |a(x)-y| $$
Но функция модуля не является гладкой функцией, и для оптимизации такого функционала неудобно использовать градиентные методы. Поэтому в качестве меры ошибки часто используют квадрат отклонения:
$$ (a(x)-y)^2 $$
Функционал ошибки, именуемый среднеквадратичной ошибкой алгоритма, задается следующим образом:
$$ Q(a,x) = frac{1}{l} sumlimits_{i=1}^l (a(x_i)- y_i)^2 $$
В случае линейной модели его можно переписать в виде функции (поскольку теперь Q зависит от вектора, а не от функции) ошибок:
$$ Q(omega,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 $$
Обучение модели линейной регрессии
Разберем том, как обучать модель линейной регрессии, то есть как настраивать ее параметры.
$$ Q(w,x) = frac{1}{l} sumlimits_{i=1}^l ( langle w_i,x_irangle- y_i) ^2 to min_{w}$$
То есть нам необходимо подобрать $w$, что бы линия могла описать наши данные. Или же задача состоит в нахождение таких $w$, что бы была минимальна ошибка $ Q(w,x)$
Матричная форма записи
Прежде, чем рассмотрим задачу о оптимизации этой функции, имеет смысл используемые соотношения в матричной форме. Матрица “объекты-признаки” $X$ составлена из признаков описаний все объектов выборки
$$ X = begin{pmatrix} x_{11} & … & x_{1d} … & … & … x_{l1} & … & x_{ld} end{pmatrix} $$
Таким образом, в $ij$ элементе матрицы $X$ записано значение $j$-го признака на i объекте обучающей выборки. Или короче говоря, каждая строчка – это объект, а каждый столбец – это признак.Так же понадобится вектор ответов y, который составлен из истинных ответов для всех объектов.
$$ y = begin{pmatrix} y_{1} … y_{l} end{pmatrix} $$
В этом случае среднеквадратичная шибка может быть переписана в матричном виде:
$$ Q(w,X) = frac{1}{l} || Xw-y ||^2 to min_{w}$$
Оптимизационный метод решения
Самый лучший метод – это численный метод оптимизации.
Не сложно показать, что среднеквадратичная ошибка – это выпуклая и гладкая функция. Выпуклость гарантирует существование лишь одного минимумам, а гладкость – существование вектора градиента в каждой точке. Это позволяет использовать метод градиентного спуска.
При использовании метода градиентного спуска необходимо указать начальное приближение. Есть много
подходов к тому, как это сделать, в том числе инициализировать случайными числами (не очень большими). Самый простой способ это сделать — инициализировать значения всех весов равными нулю:
$$ w^0=0 $$
На каждой следующей итерации, $t = 1, 2, 3, …,$ из приближения, полученного в предыдущей итерации $w^{t−1}$, вычитается вектор градиента в соответствующей точке $w^{t−1}$, умноженный на некоторый коэффициент $eta_t$, называемый шагом:
$$ w^t = w^{t-1} – eta_t Delta Q(w^{t-1},X) $$
Остановить итерации следует , когда наступает сходимость. Сходимость можно определять по-разному .В данном случае разумно определить сходимость следующим образом: итерации следует завершить, если разница
двух последовательных приближений не слишком велика:
$$ ||w^t – w^{t-1} ||<epsilon $$
Случай парной регрессии
В случае парной регрессии признак всего один, а линейная модель выглядит следующим образом:
$$ a(x)=w_0 + w x $$
где $w_1$ и $w_0$ – два параметра.
Среднеквадратичная ошибка принимает вид:
$$ Q(w_0,w_1,X) = frac{1}{l} sumlimits_{i=1}^l (w_1x_i+w_0 -y_i) ^2$$
Для нахождения оптимальных параметров будет применяться метод градиентного спуска, про который уже было сказано ранее. Чтобы это сделать, необходимо сначала вычислить частные производные функции ошибки:
$$frac{partial Q}{partial w_1} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)x_i$$
$$frac{partial Q}{partial w_0} = frac{2}{l} sumlimits_{i=1}^l (w_1x_i+w_0-y_i)$$
Следующие два графика демонстрируют применение метода градиентного спуска в случае парной регрессии. Справа изображены точки выборки, а слева — пространство параметров. Точка в этом пространстве обозначает конкретную модель (кафе)

График зависимости функции ошибки от числа произведенных операции выглядит следующим образом:

Выбор размера шага в методе градиентного спуска
Очень важно при использовании метода градиентного спуска правильно подбирать шаг. Каких-либо концерт- иных правил подбора шага не существует, выбор шага — это искусство, но существует несколько полезных закономерностей.

Если длина шага слишком мала, то метод будет неспешна, но верно шагать в сторону минимума. Если же
взять размер шага очень большим, появляется риск, что метод будет перепрыгивать через минимум. Более
того, есть риск того, что градиентный спуск не сойдется.
Имеет смысл использовать переменный размер шага: сначала, когда точка минимума находится еще да-
легко, двигаться быстро, а позже, спустя некоторое количество итерации — делать более аккуратные шаги.
Один из способов задать размер шага следующий:
$$ eta_t = frac{k}{t} $$
где $k$-константа, которую необходимо подобрать, а $t$ – номер шага.
import matplotlib.pyplot as plt # библиотека для отрисовки графиков import numpy as np # импортируем numpy для создания своего датасета from sklearn import linear_model, model_selection # импортируем линейную модель для обучения и библиотеку для разделения нашей выборки X = np.random.randint(100,size=(500, 1)) # создаем вектор признаков, вектора так как у нас один признак y = np.random.normal(np.random.randint(300,360,size=(500, 1))-X) # создаем вектор ответом plt.scatter(X, y) # рисуем график точек plt.xlabel('Расстояние до кафе в метрах') # добавляем описание для оси x plt.ylabel('Количество заказов')# добавляем описание для оси y plt.show()

# Делим созданную нами выборку на тестовую и обучающую X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y)
Давайте посмотрим какие параметры принимает LinearRegression.
fit_intercept – подбирать ли значения для свободного член $w_0$. True или False. Если ваши данные центрированны, то можете указать False. По умолчанию – True
normalize– нормализация данных перед обучением. Если fit_intercept=False то параметр будет проигнорирован. Если True – то данные перед обучением будут нормализованы при помощи L^2-Norm нормализации. По умолчанию – False
copy_X – True – копировать матрицу признаков. False – не копировать. **По умолчанию – **True
n_jobs – количество ядер используемых для сборки. Скорость будет существенно выше n_targets>1. По умолчанию – None
Параметры которые можно у модели:
coef_ – коэффициенты $w$, количество возвращаемых коэффициентов зависит от количества признаков. смотри пункт Описание линейной модели
intercept_ – свободный член $w_0$
Что бы предсказать значения необходимо вызвать функцию:
predict и передать массив из признаков.
Example: regr.predict([[40]])
regr = linear_model.LinearRegression() # создаем линейную регрессию #Обучаем модель regr.fit(X_train, y_train)
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
После выполнения кода, вам вернется ответ с установленными параметрами
LinearRegression(copy_X=True, fit_intercept=True, n_jobs=1, normalize=False)
# Посмотрим какие коэффициенты установила модель print('Коэфициент: n', regr.coef_) # Средний квадрат ошибки print("Средний квадрат ошибки: %.2f" % np.mean((regr.predict(X_test) - y_test) ** 2)) # Оценка дисперсии: 1 - идеальное предсказание. Качество предсказания. print('Оценка дисперсии:: %.2f' % regr.score(X_test, y_test))
Коэфициент:
[[-1.03950324]]
Средний квадрат ошибки: 325.63
Оценка дисперсии:: 0.70
# Посмотрим на получившуюся функцию print ("y = {:.2f}*x + {:.2f}".format(regr.coef_[0][0], regr.intercept_[0]))
# Посмотрим, как предскажет наша модель тестовые данные. plt.scatter(X_test, y_test, color='black')# рисуем график точек plt.plot(X_test, regr.predict(X_test), color='blue') # рисуем график линейной регрессии plt.show() # Покажем график

Давайте предскажем количество заказов, для нашего потенциального магазина. Скажем, что мы планируем построить магазин в 40 метрах от метро
290 заказов мы получим если построим магазин в 40 метрах от метро, но при этом качество предсказания всего лишь 71%, думаю не стоит доверять.
А что если, мы увеличим количество признаков?
Для этого воспользуемся встроенным датасетом make_regression из sklearn.
n_features – отвечает за количество признаков один нормальный другой избыточный
n_informative – отвечает за количество информативных признаков
n_targets – отвечает за размер ответов
noise – шум накладываемый на признаки
соef – возвращать ли коэффициенты
random_state – определяет генерацию случайных чисел для создания набора данных.
# Импортируем библиотеки для валидация, создания датасетов, и метрик качества from sklearn import cross_validation, datasets, metrics # Создаем датасет с избыточной информацией X, y, coef = datasets.make_regression(n_features = 2, n_informative = 1, n_targets = 1, noise = 5., coef = True, random_state = 2)
# Поскольку у нас есть два признака,для отрисовки надо их разделить на две части data_1, data_2 = [],[] for x in X: data_1.append(x[0]) data_2.append(x[1]) plt.scatter(data_1, y, color = 'r') plt.scatter(data_2, y, color = 'b')
<matplotlib.collections.PathCollection at 0x1134a6e10>

Можно заметить, что признак отмеченный красным цветом имеет явную линейную зависимость, а признак отмеченный синим, никакой информативность нам не дает.
# Разделение выборку для обучения и тестирования # test_size - отвечает за размер тестовой выборки X_train, X_test, y_train, y_test = cross_validation.train_test_split(X, y, test_size = 0.3)
# Создаем линейную регрессию linear_regressor = linear_model.LinearRegression() # Тренируем ее linear_regressor.fit(X_train, y_train) # Делаем предсказания predictions = linear_regressor.predict(X_test)
# Выводим массив для просмотра наших ответов (меток) print (y_test)
[ 28.15553021 38.36241814 -24.77820218 -61.47026695 13.02656201
23.87701013 12.74038341 -70.11132234 27.83791274 -14.97110322
-80.80239408 24.82763821 58.26281761 -45.27502383 10.33267887
-48.28700118 -21.48288019 -32.71074998 -21.47606913 -15.01435792
78.24817537 19.66406455 5.86887774 -42.44469577 -12.0017312
14.76930132 -16.65927231 -13.99339669 4.45578287 22.13032804]
# Смотрим и сравниваем предсказания print (predictions)
[ 22.32670386 40.26305989 -27.69502682 -56.5548183 18.47241345
31.86585663 6.08896992 -66.15105402 22.99937016 -12.65174022
-78.50894588 30.90311195 56.21877707 -47.81097232 8.98196478
-56.41188567 -24.46096716 -43.55445698 -17.99670898 -9.09225523
65.49657633 26.50900527 4.74114126 -39.28939851 -6.80665816
8.30372903 -15.27594937 -15.15598987 8.34469779 19.45159738]
# Средняя ошибка предсказания metrics.mean_absolute_error(y_test, predictions)
Для валидации можем выполнить перекрестную проверкую cross_val_score.
http://scikit-learn.org/stable/modules/generated/sklearn.model_selection.cross_val_score.html
Передадим, нашу линейную модель, признаки, ответы, количество разделений кросс-валидация
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 0.9792410447209384, Отклонение: 0.020331171766276405
# Создаем свое тестирование на основе абсолютной средней ошибкой scorer = metrics.make_scorer(metrics.mean_absolute_error)
linear_scoring = cross_validation.cross_val_score(linear_regressor, X, y, scoring=scorer, cv=10) print ('Средняя ошибка: {}, Отклонение: {}'.format(linear_scoring.mean(), linear_scoring.std()))
Средняя ошибка: 4.0700714987797, Отклонение: 1.0737104492890193
# Коэффициенты который дал обучающий датасет coef
array([38.07925837, 0. ])
# Коэффициент полученный при обучении linear_regressor.coef_
array([38.18191713, 0.81751244])
# обученная модель так же дает свободный член linear_regressor.intercept_
print ("y = {:.2f}*x1 + {:.2f}*x2".format(coef[0], coef[1]))
print ("y = {:.2f}*x1 + {:.2f}*x2 + {:.2f}".format(linear_regressor.coef_[0], linear_regressor.coef_[1], linear_regressor.intercept_))
y = 37.76*x1 + 0.17*x2 + -0.86
# Посмотрим качество обучения print('Оценка дисперсии:: %.2f' % linear_regressor.score(X_test, y_test))
Домашнее задание
Вы уже знаете как создать модель линейной регрессии, можете создать датасет.
Давайте посмотрим как влияет количество признаков на качество обучения линейной модели.
Скачайте этот файл, можете редактировать этот ноутбук, да бы уменьшить/увеличить количество признаков.
Будут вопросы пишите нам в Slack канал #machine_learning
Все курсы > Вводный курс > Занятие 14
Добро пожаловать на практическую часть вводного курса!
Прежде чем мы перейдем непосредственно к детальному изучению алгоритмов регрессии, несколько слов о том, какое вообще бывает машинное обучение.
Обучение с учителем и без
Про машинное обучение с учителем (Supervised Machine Learning) говорят в том случае, когда в данных, на которых мы обучаем модель, уже заложен некоторый результат. Это может быть конкретное число (например, окружность шеи в задаче регрессии) или принадлежность к определенному классу (тип заемщика в задаче классификации). Другими словами, в этих данных есть зависимая переменная y.
В случае, если такого результата нет, речь идет об обучении без учителя (Unsupervised Machine Learning). Такой тип алгоритмов встречается в задаче кластеризации, когда нужно выделить группу или кластер объектов, но сами эти кластеры заранее не известны (в отличие от классов при классификации).

Теперь давайте поговорим откуда мы будем брать данные.
Модуль datasets библиотеки Scikit-learn
В учебных целях мы будем использовать классические наборы данных, которые уже содержатся в библиотеке Scikit-learn в модуле datasets. Нас будут интересовать три набора данных:
- Данные по 506 районам Бостона. Модель будет предсказывать цену на жилье.
- Набор данных по 569 опухолевым образованиям, которые машина научится определять как злокачественные или доброкачественные.
- Данные по 150 образцам цветов ириса. Мы попросим алгоритм разделить эти цветы на виды (или кластеры), основываясь на их характеристиках.
Регрессия
По традиции вначале откроем ноутбук к этому занятию⧉
Этап 1. Загрузка данных — недвижимость в Бостоне

Вначале загрузим данные.
|
# импортируем данные и поместим их в переменную boston from sklearn.datasets import load_boston boston = load_boston() |
|
# определим тип данных type(boston) |
Наш набор данных является объектом Bunch, который в свою очередь, представляет собой подкласс питоновского словаря. Это значит, что его структуру мы можем увидеть с помощью метода .keys().
|
dict_keys([‘data’, ‘target’, ‘feature_names’, ‘DESCR’, ‘filename’]) |
В разделе data содержится информация о признаках (независимые переменные). В target содержится целевая (зависимая) переменная, в feature_names — наименование признаков, а DESCR содержит описание датасета.
Начнем с общего обзора. Для этого прочитаем описание.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
:Number of Instances: 506 :Number of Attributes: 13 numeric/categorical predictive. Median Value (attribute 14) is usually the target. :Attribute Information (in order): – CRIM per capita crime rate by town – ZN proportion of residential land zoned for lots over 25,000 sq.ft. – INDUS proportion of non-retail business acres per town – CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise) – NOX nitric oxides concentration (parts per 10 million) – RM average number of rooms per dwelling – AGE proportion of owner-occupied units built prior to 1940 – DIS weighted distances to five Boston employment centres – RAD index of accessibility to radial highways – TAX full-value property-tax rate per $10,000 – PTRATIO pupil-teacher ratio by town – B 1000(Bk – 0.63)^2 where Bk is the proportion of blacks by town – LSTAT % lower status of the population – MEDV Median value of owner-occupied homes in $1000’s :Missing Attribute Values: None |
Каждая единица данных — это район города Бостон. У нас есть информация об уровне преступности (CRIM), качестве воздуха (NOX), транспортной доступности (RAD), налогах (TAX), количестве учителей (PTRATIO), социальном положении населения (LSTAT) и некоторые другие показатели. Целевой переменной является медианная цена недвижимости в каждом из районов (MEDV). Именно ее нам и нужно научиться предсказывать.
Давайте выведем информацию по первым пяти районам. Так как читать сырые данные (в формате массива Numpy) не очень удобно, мы преобразуем их в формат DataFrame из библиотеки Pandas.
|
# для этого передадим функции DataFrame массив признаков boston.data # название столбцов возьмем из boston.feature_names boston_df = pd.DataFrame(boston.data, columns = boston.feature_names) # выведем первые пять районов с помощью функции head() boston_df.head() |

|
# теперь добавим в таблицу целевую переменную и назовем ее MEDV boston_df[‘MEDV’] = boston.target # снова воспользуемся функцией head() boston_df.head() |

Важно! По этическим соображениям разработчики библиотеки удалят датасет load_boston из последующих версий. В этом случае сделайте следующее.
Шаг 1. Скачайте файл boston.csv
Шаг 2. Загрузите файл в «Сессионное хранилище» в Google Colab.
Шаг 3. Запустите код ниже.
|
# на выходе вы получите уже сформированный датафрейм boston_df = pd.read_csv(‘/content/boston.csv’) boston_df.head() |
Посмотрим с каким типом переменных нам предстоит работать. От этого будет зависеть, какие статистические графики и инструменты мы будем применять при анализе данных.
|
# посмотрим с каким типом переменных нам предстоит работать # для этого есть метод .info() boston_df.info() |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
<class ‘pandas.core.frame.DataFrame’> RangeIndex: 506 entries, 0 to 505 Data columns (total 14 columns): # Column Non-Null Count Dtype — —— ————– —– 0 CRIM 506 non-null float64 1 ZN 506 non-null float64 2 INDUS 506 non-null float64 3 CHAS 506 non-null float64 4 NOX 506 non-null float64 5 RM 506 non-null float64 6 AGE 506 non-null float64 7 DIS 506 non-null float64 8 RAD 506 non-null float64 9 TAX 506 non-null float64 10 PTRATIO 506 non-null float64 11 B 506 non-null float64 12 LSTAT 506 non-null float64 13 MEDV 506 non-null float64 dtypes: float64(14) memory usage: 55.5 KB |
Как мы видим, все переменные, включая целевую, являются количественными (тип float). Помимо этого, мы можем посмотреть основные статистические показатели (summary statistics):
|
# для этого воспользуемся методом .describe() и округлим значения boston_df.describe().round(2) |

В частности, мы видим количество наблюдений (count), среднее арифметическое (mean), среднее квадратическое отклонение (std), минимальное (min) и максимальное (max) значения, а также первый (25%), второй (50%) и третий (75%) квартиль (второй квартиль это то же самое, что медиана) каждой количественной переменной. Подробнее об этом мы поговорим, когда будем изучать анализ данных на более продвинутом уровне.
Прекрасно, мы уже примерно понимаем, с чем нам предстоит работать.
Этап 2. Предварительная обработка данных
Данные редко поступают в идеальном виде. На этапе предварительной обработки данных (data pre-processing) нам необходимо понять:
- что мы будем делать с пропущенными значениями (missing values) и повторами (duplicates),
- как поступим с категориальными переменными (ведь компьютер не понимает, чем отличается одна категория от другой), и
- как не ухудшить модель из-за того, что диапазон или масштаб одной переменной сильно отличается от масштаба другой.
В работе с этим датасетом пока просто отметим, что пропущенные значения отсутствуют. Это видно из описания и, кроме того, мы можем посчитать пропущенные значения с помощью методов .isnull() и .sum().
|
CRIM 0 ZN 0 INDUS 0 CHAS 0 NOX 0 RM 0 AGE 0 DIS 0 RAD 0 TAX 0 PTRATIO 0 B 0 LSTAT 0 MEDV 0 dtype: int64 |
Этап 3. Исследовательский анализ данных
Теперь выполним то, что часто называют исследовательским или разведочным анализом данных (Exploratory Data Analysis, EDA). По большом счету, от нас требуется понять какие взаимосвязи мы можем выявить между переменными, чтобы потом построить модель.
Основной инструмент, который нам доступен на данный момент, это корреляция независимых переменных (признаков, описывающих каждый район) с зависимой, целевой переменной (ценами на жилье). Напомню, что мы говорим о сильной корреляции, когда значение приближается к 1 или −1, и о ее отсутствии, когда значение близко к нулю.
|
# посчитаем коэффициент корреляции для всего датафрейма и округлим значение corr_matrix = boston_df.corr().round(2) corr_matrix |

Такой способ представления корреляции называется корреляционной матрицей. В ней, в частности, мы видим (смотрите на последний столбец или строку), что переменные RM и LSTAT имеют достаточно сильную корреляцию с целевой переменной MEDV, 0,70 и −0,74, соответственно. Также умеренная корреляция наблюдается у переменных PTRATIO, TAX и INDUS.
Взаимосвязь двух переменных также можно визуализировать с помощью диаграммы рассеяния.
|
# подготовим данные (поместим столбцы датафрейма в переменные) x1 = boston_df[‘LSTAT’] x2 = boston_df[‘RM’] y = boston_df[‘MEDV’] |
|
# зададим размер и построим первый график plt.figure(figsize = (10,6)) plt.scatter(x1, y) # добавим подписи plt.xlabel(‘Процент населения с низким социальным статусом’, fontsize = 15) plt.ylabel(‘Медианная цена недвижимости, тыс. долларов’, fontsize = 15) plt.title(‘Социальный статус населения и цены на жилье’, fontsize = 18) |

|
# зададим размер и построим второй график plt.figure(figsize = (10,6)) plt.scatter(x2, y) # добавим подписи plt.xlabel(‘Среднее количество комнат’, fontsize = 15) plt.ylabel(‘Медианная цена недвижимости, тыс. долларов’, fontsize = 15) plt.title(‘Среднее количество комнат и цены на жилье’, fontsize = 18) |

Этап 4. Отбор и выделение признаков
После того, как мы собрали достаточно данных о взаимосвязи переменных, мы можем начать отбор наиболее значимых признаков (feature selection) и создание или выделение новых (feature extraction). В текущим исследовании, в частности, мы возьмем переменные RM, LSTAT, PTRATIO, TAX и INDUS, поскольку они имеют наиболее высокую корреляцию с целевой переменной MEDV. Создавать новые признаки мы пока не будем.
Поместим наши признаки в переменную X, а цены на жилье в переменную y.
|
X = boston_df[[‘RM’, ‘LSTAT’, ‘PTRATIO’, ‘TAX’, ‘INDUS’]] y = boston_df[‘MEDV’] |
Как мы видим, большая часть времени уходит именно на подготовительные этапы работы с данными, а не на обучение модели и составление прогноза. Это нормально. При работе с реальными данными их подготовка будет занимать еще больше времени.
Этап 5. Обучение и оценка качества модели
Теперь, когда мы загрузили, обработали и исследовали данные, а также отобрали наиболее значимые признаки, мы готовы к обучению модели. Вначале разобьем данные на обучающую и тестовую выборки.
|
# импортируем необходимый модуль from sklearn.model_selection import train_test_split # размер тестовой выборки составит 30% # также зададим точку отсчета для воспроизводимости X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 42) |
Посмотрим на размерность новых наборов данных:
|
# размерность обучающей print(X_train.shape, y_train.shape) # и тестовой выборки print(X_test.shape, y_test.shape) |
|
(354, 5) (354,) (152, 5) (152,) |
Теперь обучим модель и сделаем прогноз. Мы это уже делали на прошлом занятии.
|
# из набора линейных моделей библиотеки sklearn импортируем линейную регрессию from sklearn.linear_model import LinearRegression # создадим объект этого класса и запишем в переменную model model = LinearRegression() # обучим нашу модель model.fit(X_train, y_train) |
|
# на основе нескольких независимых переменных (Х) предскажем цену на жилье (y) y_pred = model.predict(X_test) # выведем первые пять значений с помощью диапазона индексов print(y_pred[:5]) |
|
[26.62981059 31.10008241 16.95701338 25.59771173 18.09307064] |
Осталось оценить качество модели. Посчитаем среднеквадратическую ошибку.
|
# импортируем модуль метрик from sklearn import metrics # выведем корень среднеквадратической ошибки # сравним тестовые и прогнозные значения цен на жилье print(‘Root Mean Squared Error (RMSE):’, np.sqrt(metrics.mean_squared_error(y_test, y_pred))) |
|
Root Mean Squared Error (RMSE): 5.107447670220913 |
Также рассчитаем новый для нас критерий качества — коэффициент детерминации (R2 или R-квадрат). R2 показывает, какая доля изменчивости целевой переменной объясняется с помощью нашей модели.
|
print(‘R2:’, np.round(metrics.r2_score(y_test, y_pred), 2)) |
В данном случае мы видим, что 65% изменчивости цены объясняется независимыми переменными, которые мы выбрали для нашей модели.
Конечно, обе эти метрики можно улучшить, и именно такими улучшениями мы и будем заниматься на последующих курсах.
Подведем итог
Сегодня мы выполнили первое полноценное исследование данных и построили модель. Мы (1) начали с того, что подгрузили данные из библиотеки Scikit-learn, (2) обработали и (3) исследовали данные, а также (4) отобрали наиболее значимые признаки. После этого мы (5) построили модель регрессии и оценили ее качество.
Вопросы для закрепления
Чем обучение с учителем отличается от обучения без учителя?
Посмотреть правильный ответ
Ответ: при обучении с учителем мы задаем нашей модели цель (y), к которой она должна стремиться в процессе оптимизации, при обучении без учителя такой цели нет.
Чем регрессия отличается от классификации?
Посмотреть правильный ответ
Ответ: регрессия предсказывает число, классификация относит объекты к определенному классу
Что показывает коэффициент детерминации?
Посмотреть правильный ответ
Ответ: коэффициент детерминации (R2) показывает долю изменчивости целевой переменной (y), которую мы можем объяснить с помощью нашей модели. Если R2 равен единице (100%), то наша модель полностью объясняет любые изменения в целевой переменной. Если R2 равен нулю (0%), наша модель никак не объясняет эти изменения.
Дополнительные упражнения⧉ вы найдете в конце ноутбука.
Теперь мы готовы к изучению алгоритма классификации.
Ответы на вопросы
Вопрос. Скажите, а почему вы всегда используете число 42, например, в random_state = 42 и в np.random.seed(42)?
Ответ. Никакой технической необходимости указывать число 42 нет, оно может быть любым.
Это число очень часто используется в проектах по Data Science и взято из романа Дугласа Адамса «Автостопом по галактике» (The Hitchhiker’s Guide to the Galaxy). По сюжету, один из героев книги ищет ответ на Главный вопрос жизни, вселенной и всего такого. Через семь с половиной миллонов лет непрерывных вычислений специально созданный для этих целей компьютер «Думатель» (Deep Thought) выдал ответ. Этим ответом и было число 42.
Если в Гугле ввести Answer to the Ultimate Question of Life, the Universe, and Everything, то в результате поиска появится калькулятор с числом 42.
Вопрос. Выполнив упражнение после [лекции], получил, как мне кажется, немного странный результат: RMSE уменьшилось, а $ R^2 $ увеличился. Не могли бы вы подсказать, нормально ли это? Заранее спасибо за ответ.
Ответ. Спасибо за вопрос. Да, это нормально. Уменьшение RMSE показывает, что наша модель ($ hat{y}_{(i)} $) стала меньше отклоняться от фактических значений ($y_{(i)}$).
Одновременно, после добавления новых признаков/зависимых переменных модель смогла лучше объяснить изменчивость целевой переменной (цены на жилье). Это отразилось на увеличении коэффициента детерминации $ R^2 $.
Продемонстрирую на формулах. Вот как мы рассчитываем RMSE.
$$ RMSE = sqrt{ frac {1}{n} sum_{i=1} (y_{(i)}-hat{y}_{(i)}) ^2 } $$
Мы считаем квадрат отклонения фактических значений от прогнозных, усредняем и извлекаем квадратный корень. Теперь давайте посмотрим на формулу $ R^2 $.
$$ R^2 = 1-frac {SS_{residuals}}{SS_{total}} = 1-frac{sum{(y_{(i)}-hat{y}_{(i)})^2}}{sum{y_{(i)}-bar{y}}} $$
В данном случае мы делим сумму квадратов отклонений от прогнозных значений $ SS_{residuals} $ на сумму квадратов отклонений от среднего $ SS_{total} $ и вычитаем получившийся результат из единицы. В Википедии⧉ есть хорошая иллюстрация этой метрики.

Обратите внимание, что RMSE и числитель в формуле $ R^2 $ — это почти одно и то же.
$$ SS_{residuals} = RMSE^2 times n $$
$$ R^2 = 1-frac {RMSE^2 times n}{SS_{total}} $$
Если мы уменьшаем RMSE, то соответственно уменьшаем числитель дроби и увеличиваем $R^2$. Другими словами, логично, что если мы смогли уменьшить RMSE (то есть наша модель лучше описывает данные), то она их и лучше объясняет.
Может показаться, что RMSE и $R^2$ дублируют друг друга с тем отличием, что RMSE измеряет ошибку в абсолютных значениях, а коэффициент детерминации объясняет изменчивость в процентах. Однако здесь есть один нюанс. Добавление новых признаков увеличивает, но никогда не уменьшает коэффициент детерминации. Для этого есть две причины:
- При любом количестве признаков знаменатель (то есть $SS_{total}$) остается неизменным, потому что зависит только от целевой переменной.
- Одновременно, при обучении модели (то есть подборе коэффициентов), алгоритм, если новый признак ухудшает $ R^2 $, может придать этому коэффициенту значение ноль и не включать его в финальную модель. Например, в модели $ hat{y} = beta_0 + beta_1 x_1 + beta_2 x_2 + beta_3 x_3 $ придать коэффициенту $beta_3$ значение ноль и, таким образом, исключить его. Значит числитель дроби может только уменьшаться, а $R^2$ только увеличиваться. Зачастую такое увеличение $R^2$ вызвано случаем и не улучшает качество модели.
Как следствие, возникает желание увеличивать количество признаков в погоне за большим коэффициентом детерминации. Для того чтобы этому противостоять, используется скорректированный $R^2$ (adjusted $R^2$).
$$ R^2_{adj} = 1-(1-R^2) times left(frac{n-1}{n-k-1} right) $$
где k — это количество признаков, а n — количество наблюдений.
При увеличении количества признаков знаменатель увеличивается, уменьшает дробь и, как следствие, понижает весь коэффициент детерминации. И только если новый признак действительно вносит существенный вклад в качество модели, новый скорректированный коэффициент детерминации вырастет.
Именно поэтому полезно измерять как RMSE, чтобы понимать, насколько ваша модель в абсолютных значениях отклоняется от факта, так и скорректированный $R^2$, чтобы понимать, с учетом количества признаков, насколько хорошо модель объясняет изменчивость целевой переменной.
Рассчитаем $ R^2_{adj} $ для модели из лекции.
|
# возьмем n и k для тестовых данных n, k = X_test.shape[0], X_test.shape[1] n, k |
|
# подставим их в формулу 1 – (1 – model.score(X_test, y_test)) * ((n – 1) / (n – k – 1)) |
Как вы видите, мы были «наказаны» (penalized) за наличие пяти признаков в модели. При построении модели из упражнения, думаю, коэффициент детерминации будет скорректирован еще сильнее.
