Как составить мольный баланс реакции

    Молярный баланс расщепления ДМД на промышленном катализаторе КДВ-15 при 370—390 °С (в %) приведен ниже  [c.83]

    Структура поля концентраций определяется, с одной стороны, геометрией зоны процесса, а с другой — структурой молярного баланса масс и баланса внутренней энергии двухфазной системы. [c.231]

    Составить молярный баланс эквивалентов анионов и катионов и вычислить погрешность анализа. [c.35]

    ПАРЦИАЛЬНЫЕ МОЛЯРНЫЕ БАЛАНСЫ [c.12]

    Парциальные молярные балансы. На безразмерных характеристиках реакций основаны расчеты так называемых парциальных молярных балансов, составляемых на 1 моль основного исходного реагента А. При этом начальный состав смеси также выражают через безразмерные величины, а именно мольные соотношения других веществ, в том числе инертных, к основному реагенту А  [c.15]

    Т. е. его выход равен степени полноты реакции. Следовательно, получаем уравнение парциального молярного баланса  [c.16]

    Рассчитаем парциальный молярный баланс реакции дегидратации этанола  [c.16]

    Более общий способ расчета парциальных давлений состоит в использовании мольных долей веществ, которые находят из парциальных молярных балансов [c.18]

    Имеем уравнения парциального молярного баланса  [c.19]

    Если объем реакционной смеси при газофазных реакциях изменяется, расчет состава несколько усложняется. Расчет можно провести с помощью введенного ранее коэффициента изменения объема 8, выражая через него Ра,о, Ру и Ха равновесные парциальные давления всех веществ. В термодинамике более принят способ парциальных молярных балансов, составляемых на 1 моль основного реагента А. [c.40]

    Составляем парциальный молярный баланс и находим Р/  [c.41]

    Если ИХ константы равновесия равны Крл и Кр,2. а равновесные выходы этилена и диэтилового эфира обозначим хв и Хс, то из “парциального молярного баланса находим  [c.42]

    Вывод уравнений, описывающих процессы физико-химических превращений опирается на законы термодинамики, с допущением существования локальных равновесий. Распределение видов компонентов в изучаемой гидрогеохимической системе (между жидкой и твердой фазой вступивших и не вступивших в реакции комплексообразования, сорбции, ионного обмена и т.д.) принципиально можно описать, основываясь на минимизации свободной энергии Гиббса, либо посредством термодинамических констант равновесия. В данном случае рассматривается последний подход, при котором уравнения выводятся на основе закона действующих масс согласно принципу молярного баланса [1]. [c.25]

    Поскольку уравнения массопереноса для всех компонентов имеют идентичную математическую форму, то после выбора первичных зависимых переменных для системы уравнений массопереноса, каждое из них может быть решено (относительно соответствующей первичной зависимой переменной) независимо от других уравнений системы. Первичными уравнениями здесь являются уравнения массопереноса, поскольку они включают пространственные производные и тем самым описывают протекание процесса в пространстве. Уравнения физико-химических равновесий и молярного баланса, выведенные с допущением существования локальных равновесий, рассматриваются в качестве вторичных, так как они описывают процессы в “точке” пространства. [c.36]

    Составьте парциальный молярный баланс для простой реакции из примера 1. Выведите уравнения парциальных давлений компонентов смеси в зависимости от начального давления бензола и общего давления, если извест-ло, что реакция проводится в газовой фазе без посторонних разбавителей и при начальном мольном отношении Hj СбНб=Рт. [c.20]

    Составляем парциальный молярный баланс реакции и находиы Р1  [c.41]

---

В
основе расчета любого процесса лежит
уравнение материального баланса.

Уравнение
материального баланса базируется на
законе сохранения массы вещества.

I
II
III

I
– сумма всех входящих материальных
потоков в элемент ХТС;

II
– сумма всех выходящих материальных
потоков из элемента ХТС;

III
– суммарные материальные потери в
элементе ХТС.

Различают
теоретический и практический материальные
балансы.

Теорерический
материальный баланс составляется на
заданную производительность с учетом
только стехиометрии реакции.

А+В=С+Д

G_A+G_B=G_C+G_Д

Практический
материальный баланс рассчитывают на
основе теоретического материального
баланса с учетом степени превращения,
селективности, выхода, соотношения
исходных реагентов, степени чистоты
сырья, количество растворителя или
инертного газа.

Уравнения
практического материального баланса:

1.

2.

3.

4.

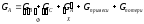
5.
(консекутивная
схема)

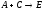
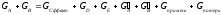
Отклонения
практического от теоретического баланса
обусловлены тремя основными факторами:

1. Термодинамический
   (реакции не идут до конца вследствие
   их обратимости);

2. Кинетический
   (реакции идут не до конца из-за падения
   скорости);

3. Механизмы
   реакции (обуславливает образование
   побочных продуктов и как следствие
   снижает селективность реакции).

Материальный
баланс может быть записан в виде
уравнения, таблицы или диаграммы.

Тепловой
баланс составляется с целью определения
теплового режима работы реактора.

Реактор
может работать в следующих тепловых
режимах:

1. Изотермический
   (температура на входе в реактор и на
   выходе одинакова);

2. Адиабатический
   (отсутствует теплообмен с окружающей
   средой);

3. Смешанный
   или политропный тепловой режим.

В
основе теплового баланса лежит закон
сохранения энергии, согласно которому

åQ_прих.
= åQ_расх.
+åQ_пот

åQ_прих
– характеризует
сумму всех входящих тепловых потоков;

åQ_расх
– сумма всех выходящих тепловых потоков;

±åQ_пот
– суммарные тепловые потери.

Для
изотермического режима уравнение
теплового баланса:

Q_реаг
±
Q_r.
±
Q_ф
±
Q_F
= Q_прод,+
Q_нагр.
+ Q_пот.

где
Q_реаг
– количество тепла, поступающего с
исходными реагентами;

Q_r
– тепло химических реакций;

Q_ф
– тепло фазовых переходов;

Q_нагр
– количество тепла, необходимое для
нагрева сырья до температуры реакции.

Q_пот
не должно превышать 5%.

В
отличие от материального баланса,
тепловой баланс не всегда сходится.

Приход
тепла:

Q_реаг
– тепло, входящее в реактор с исходными
реагентами;

Q_реаг=∑
Q_i

Q_реаг,
i
= G_i×Cp_i×T_i

где
G_i
– мольный поток i-го
реагента;

Cp_i
– теплоемкость i-го
реагента, (Дж·моль)/К;

–
тепло, выделяющееся (или поглощающееся)
в результате химических превращений:

G_i(j)

где
–
тепловой эффект химической реакции,
(Дж·моль)/К;

G_i(j)
– мольный поток i-го
реагента, участвующего в реакции (или
полученного j-го
продукта реакции);

–
тепло, выделяющееся (или поглощающееся)
в результате фазовых превращений
(испарение, конденсация, кристаллизация,
плавление, возгонка, растворение):

G_i(j)ф

где
G_i(j)ф
– мольный поток i-го
реагента (j-го
продукта), претерпевающегося фазовый
переход;

–
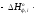энтальпия фазового перехода, кДж/моль
(справочная величина).

Расход
тепла:

Q_прод
– тепло, выходящее из реактора с
продуктами реакции;

Q_прод
Q_прод,
j

Q_прод,
j
= G_j×Cp_j×T_j

где
G_j
– мольный поток j-го
продукта реакции;

Cp_j
– теплоемкость j-го
продукта реакции, Дж/(моль·К);

T_j
– температура j-го
продукта реакции, К.

Q_нагр
– количество тепла, расходуемое на
нагревание исходных реагентов до
температуры реакции:

Q_нагр,i
= ∑[G_i×Cp_i×
(T_i,r
– T_i)]

где
G_i
– мольный поток i
– реагента, подвергаемый нагреву;

Cp_i
– теплоемкость i-
реагента, Дж/(моль·К);

T_i
– температура i-
реагента на входе в реактор;

T_i,r
– температура i-
реагента на выходе из реактора.

Q_пот
– тепловые потери (1 – 5% от прихода
тепла);

Q_пот
= (0,01–
0,05)∙Q_прих
,

±Q_F
– количество
тепла, отводимое (подводимое) от реактора
при помощи теплоносителя (хладоагента).
Тепловая нагрузка на реактор.

Исходя
из тепловой нагрузки на реактор,
рассчитывают необходимую поверхность
теплообмена F.

Q_F
рассчитывают по уравнению:

±Q_F
= Q_расх.
– Q_прих

,
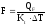м²
,

где
К_t
– коэффициент теплопередачи; ∆Т –
движущая сила теплопередачи (разность
между температурой реакции и температурой
теплоносителя).

После
нахождения поверхности теплообмена F
осуществляют ее анализ, сравнивая с
поверхностью теплообмена, имеющемся у
реактора.

F<F_r
(поверхность
реактора) – справочная величина;

F>F_r
– интенсифицируют процесс теплообмена
(изменяют К и ∆T)
или вводят дополнительные теплообменные
устройства.

F≈F_r
– неустойчивый тепловой режим, но
интенсифицировать его проще.

Тепловой
баланс записывается в виде уравнения,
диаграммы или таблицы.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Мольное соотношение: определение и примеры

На чтение 3 мин. Просмотров 491 Опубликовано 27.05.2021

В химической реакции соединения реагируют в заданном соотношении. Если соотношение несбалансированное, будет остаток реагента. Чтобы понять это, вам необходимо знать молярное отношение или мольное соотношение.

Содержание

1. Определение мольного отношения
2. Пример мольного отношения: сбалансированное уравнение
3. Пример несбалансированного уравнения

Определение мольного отношения

Мольное соотношение представляет собой соотношение между количествами в молях любых двух соединений, участвующих в химической реакции. Мольные отношения используются в качестве коэффициентов пересчета продуктов и реагентов во многих химических задачах. Мольное соотношение может быть определено путем изучения коэффициентов перед формулами в сбалансированном химическом уравнении.

Также известно как: Мольное соотношение также называется мольное отношение .

Пример мольного отношения: сбалансированное уравнение

Для реакция:
2 H ₂ (g) + O ₂ (g) → 2 H ₂ O (г)

Мольное соотношение между O ₂ и H ₂ O 1: 2. На каждый использованный 1 моль O ₂ образуется 2 моля H ₂ O.

Молярное соотношение между H ₂ и H ₂ O составляет 1: 1. На каждые 2 моля H ₂ образуется 2 моля H ₂ O. Если использовать 4 моля водорода, то получится 4 моля воды.

Пример несбалансированного уравнения

Другой пример , начнем с несбалансированного уравнения:

O ₃ → O ₂

При осмотре вы можете увидеть, что это уравнение не сбалансировано, потому что масса не сохраняется. В озоне (O ₃ ) больше атомов кислорода, чем в газообразном кислороде (O ₂ ). Вы не можете рассчитать мольное соотношение для несбалансированного уравнения. Уравновешивание этого уравнения дает:

2O ₃ → 3O ₂

Теперь вы можете использовать коэффициенты перед озоном и кислородом, чтобы найти мольное соотношение . Соотношение озона 2 к кислороду 3 или 2: 3. Как ты этим пользуешься? Допустим, вас просят определить, сколько граммов кислорода образуется, когда вы реагируете на 0,2 грамма озона.

1. Первый шаг – это узнать, сколько молей озона содержится в 0,2 грамма. (Помните, что это молярное соотношение, поэтому в большинстве уравнений соотношение для граммов не одно и то же.)
2. Чтобы преобразовать граммы в моль, найдите атомный вес кислорода в периодической таблице. На моль приходится 16,00 граммов кислорода.
3. Чтобы определить, сколько молей содержится в 0,2 грамма, решите:
   x моль = 0,2 грамма * (1 моль/16,00 граммов) .
   Вы получите 0,0125 моль.
4. Используйте мольное соотношение, чтобы определить, сколько молей кислорода производит 0,0125 моль озона:
   моль кислорода = 0,0125 моль озон * (3 моля кислорода/2 моля озона).
   Решив это, вы получите 0,01875 моль газообразного кислорода.
5. Наконец, преобразуйте количество молей газообразного кислорода в граммы для ответа:
   граммы газообразного кислорода = 0,01875 моль * (16. 00 граммов/моль)
   граммов газообразного кислорода = 0,3 грамма

Должно быть довольно очевидно, что вы могли подключить мольную долю прямо сейчас в этом конкретном примере, потому что только один тип атомов присутствует в обеих частях уравнения. Однако полезно знать процедуру, когда вы сталкиваетесь с более сложными проблемами, которые необходимо решить.

Молярное соотношение: определение и примеры

Молярное соотношение: определение и примеры — Науки

Содержание:

В химической реакции соединения реагируют в заданном соотношении. Если соотношение несбалансированное, будет остаток реагента. Чтобы понять это, вам нужно знать молярное соотношение или мольное соотношение.

Определение отношения молей

Мольное соотношение — это соотношение между количествами в молях любых двух соединений, участвующих в химической реакции. Мольные отношения используются в качестве коэффициентов пересчета продуктов и реагентов во многих химических задачах. Молярное соотношение может быть определено путем изучения коэффициентов перед формулами в сбалансированном химическом уравнении.

Также известен как: Молярное соотношение также называется мольное отношение.

Пример мольного отношения: сбалансированное уравнение

Мольное соотношение между O₂ и H₂О равно 1: 2. На каждый 1 моль O₂ используется, 2 моль H₂O образуются.

Мольное соотношение между H₂ и H₂O составляет 1: 1. На каждые 2 моль H₂ используется, 2 моль H₂O образуются. Если использовать 4 моля водорода, то получится 4 моля воды.

Пример несбалансированного уравнения

В качестве другого примера давайте начнем с несбалансированного уравнения:

При осмотре вы можете увидеть, что это уравнение не сбалансировано, потому что масса не сохраняется. В озоне больше атомов кислорода (O₃), чем в газообразном кислороде (O₂). Вы не можете рассчитать мольное соотношение для несбалансированного уравнения. Балансировка этого уравнения дает:

Теперь вы можете использовать коэффициенты перед озоном и кислородом, чтобы найти мольное соотношение. Соотношение озона 2 к кислороду 3 или 2: 3. Как вы это используете? Допустим, вас просят определить, сколько граммов кислорода образуется, когда вы реагируете на 0,2 грамма озона.

1. Первый шаг — определить, сколько молей озона содержится в 0,2 грамма. (Помните, что это молярное соотношение, поэтому в большинстве уравнений соотношение для граммов неодинаково.)
2. Чтобы преобразовать граммы в моль, найдите атомный вес кислорода в периодической таблице. На моль приходится 16,00 граммов кислорода.
3. Чтобы узнать, сколько родинок в 0,2 грамма, решите:
   х моль = 0,2 грамма * (1 моль / 16,00 грамма).
   У вас получится 0,0125 моль.
4. Воспользуйтесь мольным соотношением, чтобы определить, сколько молей кислорода производит 0,0125 моль озона:
   моль кислорода = 0,0125 моль озона * (3 моля кислорода / 2 моля озона).
   Решив это, вы получите 0,01875 моль газообразного кислорода.
5. Наконец, для ответа переведите количество молей газообразного кислорода в граммы:
   граммы газообразного кислорода = 0,01875 моль * (16,00 г / моль)
   граммы газообразного кислорода = 0,3 грамма

Должно быть довольно очевидно, что в этом конкретном примере вы могли сразу же ввести мольную долю, потому что в обеих частях уравнения присутствовал только один тип атомов. Тем не менее, полезно знать процедуру, когда вы сталкиваетесь с более сложными проблемами, которые необходимо решить.

Как решать задачи по химии. Расчет по уравнениям химических реакций.

Как решать задачи по химии? Как проводить простейшие расчеты по уравнениям химических реакций? Сколько выделяется газа, образуется воды, выпадает осадка или сколько получается конечного продукта реакций? Сейчас мы постараемся разобрать все нюансы и ответить на эти вопросы, которые очень часто возникают при изучении химии.

Решение задач в химии является неотъемлемой частью в изучении этой сложной, но очень интересной науки.

Алгоритм решения задач по химии

1. Прочитать условия задачи (если они есть). Да, об этом все знают — как же решить задачу без условий — но все же, для полноты инструкции, мы не могли не указать этот пункт.
2. Записать данные задачи. На этом пункте мы не будем заострять внимание, так как требования различных учебных заведений, учителей и преподавателей могут значительно отличаться.
3. Записать уравнение реакции. Теперь начинается самое интересное! Здесь нужно быть внимательным! Обязательно необходимо верно расставить коэффициенты перед формулами веществ. Если вы забудете это сделать, то все наши усилия буду напрасны.
4. Провести соответствующие расчеты по химическому уравнению. Далее рассмотрим, как же сделать эти самые расчеты.

Для этого у нас есть два пути, как решить задачу по химии. Условно, назовем их правильным (используя понятия количества вещества) и неправильным (используя пропорции). Конечно же, мы бы рекомендовали решать задачи правильным путем. Так как у неправильного пути имеется очень много противников. Как правило, учителя считают, что ученики, решающие задачи через пропорции, не понимают самой сути протекания процессов химических реакций и решают задачи просто математически.

Расчет по уравнениям химических реакций с использованием понятия количества вещества

Суть данного метода, состоит в том, что вещества реагируют друг с другом в строгом соотношении. И уравнение реакции, которое мы записали ранее, дает нам это соотношение. Коэффициенты перед формулами веществ дают нам нужные данные для расчетов.

Для примера, запишем простую реакцию нейтрализации серной кислоты и гидроксида натрия.

H_<2>SO_ <4>+ NaOH → Na_<2>SO_ <4>+ H_<2>O

H_<2>SO_ <4>+ 2NaOH → Na_<2>SO_ <4>+ 2H_<2>O

Исходя из этого уравнения, мы видим, что одна молекула серной кислоты взаимодействует с двумя молекулами гидроксида натрия. И в результате этой реакции получается одна молекула сульфата натрия и две молекулы воды.

Сейчас мы немного отступим от разбора задач, чтобы познакомиться с основными понятиями, которые пригодятся нам в решении задач по химии.

Рассчитывать количество молекул, например в 98 граммах серной кислоты — это не самое удобное занятие. Числа будут получаться огромными ( ≈ 6,022140857⋅10 23 молекул в 98 граммах серной кислоты) . Для этого в химии ввели понятие количества вещества (моль) и молярная масса.

1 Моль (единица измерения количества вещества) — это такое количество атомов, молекул или каких либо еще структурных единиц, которое содержится в 12 граммах изотопа углерода-12. Позднее выяснилось, что в 12 граммах вещества углерод-12 содержится 6,022140857⋅10 23 атомов. Соответственно, можно сказать, что 1 моль, это такая масса вещества, в которой содержится 6,022140857⋅10 23 атомов (или молекул) этого вещества.

Но ведь молекулы и атомы имеют различный состав и различное строение. Разные атомы содержат разное количество протонов и нейтронов. Соответственно 1 моль для разных веществ будет иметь разную массу, имея при это одинаковое количество молекул ( атомов). Эта масса называется молярной.

Молярная масса — это масса 1 моля вещества.

Используя данные понятия, можно сказать, что 1 моль серной кислоты реагирует с 2 молями гидроксида натрия, и в результате получается 1 моль сульфата натрия и 2 моль воды. Давайте запишем эти данные под уравнением реакции для наглядности.

beginH_<2>SO_ <4>& + & 2NaOH & → & Na_<2>SO_ <4>& + & 2H_<2>O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль end

Следом запишем молярные массы для этих веществ

begin H_<2>SO_ <4>& + & 2NaOH & → & Na_<2>SO_ <4>& + & 2H_<2>O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль \ 98 : г& & 40 : г & & 142 : г & & 18 : г end

Теперь, зная массу одного из веществ, мы можем рассчитать, сколько нам необходимо второго вещества для полного протекания реакции, и сколько образуется конечных продуктов.

Для примера, решим по этому же уравнению несколько задач.

Задача. Сколько грамм гидроксида натрия (NaOH) необходимо для того, чтобы 49 грамм серной кислоты (H₂SO₄) прореагировало полностью?

Итак, наши действия: записываем уравнение химической реакции, расставляем коэффициенты. Для наглядности, запишем данные задачи над уравнением реакции. Неизвестную величину примем за Х. Под уравнением записываем молярные массы, и количество молей веществ, согласно уравнению реакции:

begin49 : г & & X : г & & & & \ H_<2>SO_ <4>& + & 2NaOH & → & Na_<2>SO_ <4>& + & 2H_<2>O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль \ 98 : г& & 40 : г & & 142 : г & & 18 : г end

Записывать данные под каждым веществом — не обязательно. Достаточно это будет сделать для интересующих нас веществ, из условия задачи. Запись выше дана для примера.

Примерно так должны выглядеть данные, записанные по условиям задачи. Не претендуем на единственно правильное оформление, требования у всех разные. Но так, как нам кажется, смотрится все довольно наглядно и информативно.

Первое наше действие — пересчитываем массу известного вещества в моли. Для этого разделим известную массу вещества (49 грамм) на молярную массу:

4998=0,5 моль серной кислоты

Как уже упоминалось ранее, по уравнению реакции 1 моль серной кислоты реагирует с 2 моль гидроксида натрия. Соответственно с 0,5 моль серной кислоты прореагирует 1 моль гидроксида натрия.

n(NaOH)=0.5*2=1 моль гидроксида натрия

Найдем массу гидроксида натрия, умножив количество вещества на молярную массу:

1 моль * 40 г/моль = 40 грамм гидроксида натрия.

Ответ: 40 грамм NaOH

Как видите, в решении задачи по уравнению реакции нет ничего сложного. Задача решается в 2-3 действия, с которыми справятся ученики начальных классов. Вам необходимо всего лишь запомнить несколько понятий.

Решение задач по химии через пропорцию

Ну и расскажем про второй способ вычислений по уравнениям химических реакций — вычисления через пропорцию. Этот способ может показаться немного легче, так как в некоторых случаях можно пропустить стадию перевода массы вещества в его количество. Чтобы было более понятно, объясню на том же примере.

Так же, как и в прошлом примере, запишем уравнение реакции, расставим коэффициенты и запишем над уравнением и под уравнением известные данные.

Для этого способа, нам так же понадобится записать под уравнением реакции, следом за молярной массой, массу вещества, соответствующую его количеству по уравнению. Если проще, то просто перемножить две строки под уравнением реакции, количество моль и молярную массу. Должно получиться так:

begin49 : г & & X : г & & & & \ H_<2>SO_ <4>& + & 2NaOH & → & Na_<2>SO_ <4>& + & 2H_<2>O \ 1 : моль & & 2 : моль & & 1 : моль & & 2 : моль \ 98 : г& & 40 : г & & 142 : г & & 18 : г \ 98 : г & & 80 : г & & 142 : г & & 36 : г end

А теперь внимание, начинается магия! Нас интересует строка данных над уравнением, и самая нижняя строка под уравнением. Составим из этих данных пропорцию.

Далее находим неизвестное значение Х из пропорции и радуемся полученному значению:

Х=49*80/98=40 грамм

Как видим, получается тот же результат. Прежде всего, при решении задач в химии, главное все же — понимание химических процессов. Тогда решение задачи не станет для вас проблемой!

Расчеты массы вещества по уравнению химической реакции

Этот видеоурок доступен по абонементу

У вас уже есть абонемент? Войти

При решении расчетных химических задач необходимо умение производить вычисления по уравнению химической реакции. Урок посвящен изучению алгоритма расчетов массы (объема, количества) одного из участников реакции по известной массе (объему, количеству) другого участника реакции.