Содержание
Кривизна и кручение. Натуральные уравнения кривой
Краткие теоретические сведения
Кривизна кривой
Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.
Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec{r}=vec{r}(t)$, имеет в каждой точке определенную кривизну, причем
$$
|k(t)|=frac{|vec{r’}(t)times vec{r”}(t)|}{|vec{r'(t)}|^3}.
$$
Для кривой, заданной параметрически
$$ x=x(t), ,, y=y(t), ,, z=z(t), $$
кривизна в точке $P(t=t_0)$ находится по формуле:
$$
k^2(t_0)=frac{left| begin{array}{cc}
y’ & z’ \
y”& z” \
end{array}
right|^2+left| begin{array}{cc}
z’ & x’ \
z”& x” \
end{array}
right|^2+left| begin{array}{cc}
x’ & y’ \
x” & y” \
end{array}
right|^2}{Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3},
$$
где все производные вычисляются при $t=t_0$.
Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то векторы $vec{r’}(s)$ и $vec{r”}(s)$ перпендикулярны, причем $|vec{r’}(s)|=1$. Тогда выражение для кривизны принимает вид:
$$
k(s)= |vec{r”}(s)|.
$$
?
Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?
Для плоской кривой, лежащей в плоскости $(xy)$, кривизну можно найти по формулам:
$$
begin{array}{rl}
x=x(t), y=y(t):& k = displaystylefrac{|x’y”-x”y’|}{left((x’)^2+(y’)^2right)^{3/2}}, \
y=y(x):& k = displaystylefrac{|y”|}{left(1+(y’)^2right)^{3/2}}, \
rho=rho(varphi):& k = displaystylefrac{|rho^2+2(rho’)^2-rhorho”|}{left(rho^2+(rho’)^2right)^{3/2}}.\
end{array}
$$
Кручение
Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной.
$$
|varkappa (t)|=frac{|(vec{r’}(t), vec{r”}(t), vec{r”’}(t))|}{|vec{r’}(t)times vec{r”}(t)|^2}.
$$
В случае естественной параметризации
$$
|varkappa(s)|=frac{|(vec{r’}(s), vec{r”}(s), vec{r”’}(s))|}{k^2(s)}
$$
Для плоской кривой кручение равно нулю: $varkappa=0$!
Натуральные уравнения кривой
Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то кривизна и кручение будут являться функциями длины дуги
$$
k=k(s), quad varkappa=varkappa(s).
$$
Система этих двух соотношений называется натуральными уравнениями кривой.
Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).
Решение задач
Задача 1 (Феденко №351)
Найдите кривизну кривой:
$$
x=a,mbox{cos}^3t,,,y=a,mbox{sin}^3t.
$$
Задача 2 (Феденко №380)
Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mbox{sin}x$ в точке $A(pi/2,1)$ общие касательную и кривизну.
Задача 3 (Феденко №405)
Составьте натуральные уравнения кривой:
$$
x=a(mbox{cos},t+t,mbox{sin},t), ,, y=a(mbox{sin},t-t,mbox{cos},t).
$$
Краткое решение задачи 3
$$
s=frac{at^2}{2}.
$$
$$
k=frac{1}{at}.
$$
$$
t=frac{1}{ak} Rightarrow s= frac{1}{2ak^2}.
$$
Натуральные уравнения:
$$
k=frac{1}{at},,,s=frac{at^2}{2}
$$
или
$$
k^2=frac{1}{2as}.
$$
Феденко записывает ответы через радиус кривизны:
$R=frac{1}{k}$.
Задача 4 (Феденко №486, №514)
Найдите кривизну и кручение, составьте натуральные уравнения кривой:
$$
x=a,mbox{ch}t, , y=a,mbox{sh}t, , z=a, t.
$$
Решение задачи 4
Задачу можно решать двумя способами:
1 способ. Найти $k(t), varkappa(t), s(t)$.
2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec{r}=vec{r}(s)$. А далее найти $k(s)$ и $varkappa(s)$.
Воспользуемся первым способом.
begin{gather*}
vec{r}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , at},\
vec{r’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , a},\
vec{r”}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , 0}\
vec{r”’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , 0}.
end{gather*}
$$
Rightarrow quad k^2(t) = frac{1}{4a^2mbox{ch}^4t}.
$$
$$
Rightarrow quad k(t) = frac{1}{2a,mbox{ch}^2t}.
$$
begin{equation*}
varkappa(t) = frac{ left|
begin{array}{ccc}
a,mbox{sh}t & a,mbox{ch}t & a \
a,mbox{ch}t & a,mbox{sh}t & 0 \
a,mbox{sh}t & a,mbox{ch}t & 0 \
end{array}
right|}{a^4cdot 2mbox{ch}^2t} = frac{1}{2a,mbox{ch}^2t}.
end{equation*}
В задаче №473 была та же кривая и мы получили, что
$$s=asqrt{2},mbox{sh},t.$$
Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения:
begin{equation*}
s=asqrt{2},mbox{sh}t=asqrt{2},sqrt{mbox{ch}^2t-1} ,, Rightarrow ,, mbox{ch}^2t=frac{s^2}{2a^2}+1 ,, Rightarrow
end{equation*}
begin{equation*}
k(s)=varkappa(s)=frac{1}{2a,mbox{ch}^2t} = frac{a}{s^2+2a^2}.
end{equation*}
Вычисления сделаны для $a>0$.
Задача 5 (Феденко №496)
Найдите функцию $f(t)$, для которой данная кривая — плоская:
$$
vec{r}(t)={a,mbox{cos}t, , a,mbox{sin}t, , f(t)}
$$
Решение задачи 5
$$
begin{array}{lll}
x=a,mbox{cos}t,, &y=a,mbox{sin}t, , &z=f(t),\
x’=-a,mbox{sin}t, , &y’=a,mbox{cos}t, , &z’=f'(t),\
x”=-a,mbox{cos}t, , &y”=-a,mbox{sin}t, , &z”=f”(t),\
x”’=a,mbox{sin}t, , &y”’=-a,mbox{cos}t, , &z”’=f”'(t).
end{array}
$$
Для плоской кривой кручение равно нулю:
begin{equation*}
varkappa(t) = left|
begin{array}{rrr}
-a,mbox{sin}t & a,mbox{cos}t & f'(t) \
-a,mbox{cos}t & -a,mbox{sin}t & f”(t) \
a,mbox{sin}t & -a,mbox{cos}t & f”'(t) \
end{array}
right| = left( f'(t) + f”'(t) right)cdot2a^2=0.
end{equation*}
begin{equation*}
f'(t)=-f”'(t) quad Rightarrow quad f(t)=c_1+c_2,mbox{sin}t+c_3,mbox{cos}t.
end{equation*}
?
Как найти уравнение плоскости, в которой лежит кривая?
Известно, что плоская кривая лежит в своей соприкасающейся плоскости!
Второй способ — составить уравнение плоскости по трем точкам.
Натуральные уравнения — соотношения на кривизну и кручение бирегулярных кривых. Замечательное свойство натуральных уравнений в том, что по ним можно однозначно восстановить кривую.
Натуральные уравнения, уравнения, выражающие кривизну 







Натуральные уравнения плоских кривых[править | править код]
Пусть 





Натуральные уравнения в трехмерном пространстве[править | править код]
Пусть 






Мы видели, что если кривизна и кручение кривой в постоянны, то можно восстановить кривую (винтовую линию ) с данными
С точностью до движения в пространстве. Оказывается, этот факт справедлив и в общей ситуации, когда кривизна и кручение не являются постоянными.
Теорема. Пусть – любые регулярные функции, причем
. Тогда существует и притом единственная, с точностью до движения в пространстве, кривая, для которой
является кривизной, а
– кручением в точке, соответствующей дуге
.
1). Докажем сначала существование кривой. Рассмотрим систему уравнений, которой должны удовлетворять в силу формул Френе векторы касательной , главной нормали
, и бинормали
искомой кривой.

Пусть – начальные условия, причем векторы
образуют ортонормированный правый репер в точке кривой, отвечающей значению
. Поскольку функции
регулярны, то из общей теории ODE следует, что существует и единственно решение данной системы дифференциальных уравнений первого порядка с данными начальными условиями. Покажем, что решение
образует ортонормированный правый репер при любом
. Для этого вычислим
. Используя уравнения системы Френе, получим
Анализируя эту систему уравнений видим, что она удовлетворяется значениями С другой стороны, она удовлетворяется значениями
. Оба решения совпадают при
, следовательно, по теореме единственности, решения совпадают тождественно. Кроме того,
при всех
образуют правую тройку, так как детерминант, составленный из них, является непрерывной функцией и может принимать значения
или –1. Но в точке
он равен
, следовательно, и при всех
он должен быть равен +1.
После того, как восстановлен сопровождающий репер Френе искомой кривой, нетрудно восстановить и саму кривую : 
Проверим, что эта кривая имеет в качестве натуральных уравнений функции . Во-первых, ясно, что
является дугой на
, т. к.
Кривизна найденной линии равна
Кручение равно
2). Докажем единственность (с точностью до движения в ) найденной кривой. Пусть кривые
и
имеют одинаковые натуральные уравнения
и их сопровождающие реперы Френе кривых при
таковы :
и
. Существует матрица
, такая, что
Кроме того, нетрудно проверить, что если
– решение системы уравнений Френе, то
есть другое решение той же системы. В силу единственности решения,
при всех
. Интегрируя первое из этих уравнений, получим
, где
. Таким образом, кривая
получается из
движением в
,ч. т.д.
Литература. А. В. Погорелов. гл. 3, параграф 4.
| < Предыдущая | Следующая > |
|---|
Лекция 3
Формулы Френе.
Кривизна и кручение кривой в произвольной
параметризации. Винтовая линия.
Р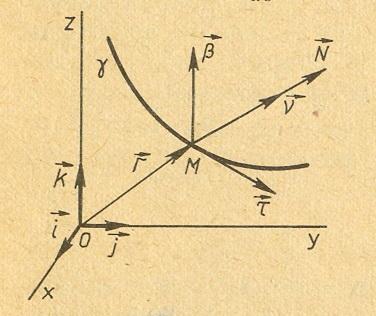
векторы
гладкой линии
заданной естественной параметризацией
.
1). Так как
то
(1)
2). Вектор
– единичный вектор гладкой нормали
параллелен
спрямляющей плоскости
3).
.
В (1) заменяем
и
по формулам (3) и (2). Получим
Подставим выражение
в (2).
4).
.
Дифференцируем по s:
=
.
Заменим
и
их выражениями по (3) и (4):
Формулы (3),(4),(5)
называются формулами Френе, которые
рассматривают связь между базисными
векторами сопровождающими треугольниками,
кручением и кривизной линии.
Определение 3.1.
Число
называется кручением линии
в точке М
на всей линии
.
Кручение есть функция параметра S.
Исходя из (5) и так
как
–
единичный вектор, то
.
Кручение больше 0 тогда и только тогда,
когда
и
противоположно направлены.
Геометрический
смысл кручения.
Модуль кручения
в данной точке кривой есть скорость
изменения направления функции b(S)
по отношению к естественному параметру
S.
Так как вектор b=b(S)
перпендикулярен соприкасающейся
плоскости, то абсолютная величина
кручения характеризует скорость
изменения положения соприкасающейся
плоскости по отношению к параметру S.
Если линия задана
в естественной параметризации, то
кривизна и кручение есть функция по
параметру S:
.Уравнения
такого вида называются натуральными
уравнениями кривой и характеризуют
кривую с точностью до движения, так как
если у двух кривых натуральные уравнение
совпадают, то кривые отличны только
положением в пространстве. Если у двух
кривых натуральные уравнения совпадают,
то на каждой из них существует естественная
параметризация, такая что в точках с
одинаковыми параметрами кривизна и
кручение одинаковы.
Вычислительная
формула для кручения линии заданной в
естественной параметризации.
–
продифференцируем
это равенство. Используем (5).
В
ыразим смешанное произведение
векторов производных:
формула
кручения (6)
Определение 3.2.
Линия называется плоской, если все её
точки принадлежат некоторой плоскости
.
Если во всех точках
гладкой плоской линии кручение равно
нулю.
Произвольная
параметризация.
Пусть кривая
задана произвольной параметризацией
своими параметрическими уравнениями:
Рассмотрим возможную
замену параметра t
на s,
причем функция s=h(t)
является допустимой заменой параметра
-1
:
-1
Найдем
Вектор
второй производной
параллелен
соприкасающейся плоскости, так как он
выражен через вектор
и
.
Рассмотрим векторное
произведение первой и второй производной.
Винтовая линия
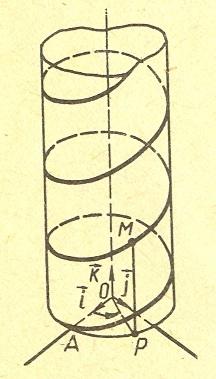
линия получена путем равномерного
вращения М
(х,у,z)
около оси Оz
и равномерного движения параллельно
оси Оz.
Является гладкой линией класса
.
Параметрические
уравнения винтовой линии:
Направляющая винтовой линии совпадает
с направляющей кругового цилиндра (ОХУ:
,
значит, винтовая линия лежит на прямом
круговом цилиндре с осью Оz.
Векторное уравнение
винтовой линии:
.
Используя формулу
,
имеем:
.
Таким образом,
.
Через М
проходит прямолинейная образующая МР
цилиндра, имеющая направляющий вектор
Так как
,
то винтовая линия пересекает все
образующие под постоянным углом (углом
между кривой и прямой называется угол
между касательной к этой кривой и данной
прямой).
Длина дуги винтовой
линии равна
.
Вектор главной
нормали:
Так как
(по формуле Френе), то
(k
– кривизна винтовой линии).
Главная нормаль
винтовой линии в точке М
есть
перпендикуляр к оси цилиндра, проведенный
через точку М,
т.к.
где Р
– проекция М
на ОХУ.
Вектор главной нормали направлен
противоположно вектору
Кручение винтовой
линии:
.
Знак кручения совпадает со знаком числа
b.
Винтовая линия
является частным случаем достаточно
широкого класса линий, называемых
кривыми Бертрана. Гладкая линия
называется кривой Бертрана, если для
нее существует другая гладкая линия
и такое отображение
,
что в каждой паре соответствующих точек
линии
и
имеют общую главную нормаль.
Соседние файлы в папке вопрос 14
- #
- #
- #
VMath
Инструменты сайта
Основное
Навигация
Информация
Действия
Содержание
Кривизна и кручение. Натуральные уравнения кривой
Краткие теоретические сведения
Кривизна кривой
Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.
Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec=vec(t)$, имеет в каждой точке определенную кривизну, причем $$ |k(t)|=frac<|vec(t)times vec(t)|><|vec|^3>. $$
Для кривой, заданной параметрически $$ x=x(t), ,, y=y(t), ,, z=z(t), $$ кривизна в точке $P(t=t_0)$ находится по формуле: $$ k^2(t_0)=frac<left| begin y’ & z’ \ y”& z” \ end right|^2+left| begin z’ & x’ \ z”& x” \ end right|^2+left| begin x’ & y’ \ x” & y” \ end right|^2><Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3>, $$ где все производные вычисляются при $t=t_0$.
Если кривая задана естественной параметризацией $vec=vec(s)$, то векторы $vec(s)$ и $vec(s)$ перпендикулярны, причем $|vec(s)|=1$. Тогда выражение для кривизны принимает вид: $$ k(s)= |vec(s)|. $$
Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?
Кручение
Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной. $$ |varkappa (t)|=frac<|(vec(t), vec(t), vec(t))|><|vec(t)times vec(t)|^2>. $$
В случае естественной параметризации $$ |varkappa(s)|=frac<|(vec(s), vec(s), vec(s))|> $$
Натуральные уравнения кривой
Если кривая задана естественной параметризацией $vec=vec(s)$, то кривизна и кручение будут являться функциями длины дуги $$ k=k(s), quad varkappa=varkappa(s). $$ Система этих двух соотношений называется натуральными уравнениями кривой.
Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).
Решение задач
Задача 1 (Феденко №351)
Найдите кривизну кривой: $$ x=a,mbox^3t,,,y=a,mbox^3t. $$
Задача 2 (Феденко №380)
Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mboxx$ в точке $A(pi/2,1)$ общие касательную и кривизну.
Задача 3 (Феденко №405)
Составьте натуральные уравнения кривой: $$ x=a(mbox,t+t,mbox,t), ,, y=a(mbox,t-t,mbox,t). $$
Краткое решение задачи 3
Натуральные уравнения: $$ k=frac<1>,,,s=frac <2>$$ или $$ k^2=frac<1><2as>. $$
Феденко записывает ответы через радиус кривизны: $R=frac<1>$.
Задача 4 (Феденко №486, №514)
Найдите кривизну и кручение, составьте натуральные уравнения кривой: $$ x=a,mboxt, , y=a,mboxt, , z=a, t. $$
Решение задачи 4
Задачу можно решать двумя способами:
1 способ. Найти $k(t), varkappa(t), s(t)$.
2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec=vec(s)$. А далее найти $k(s)$ и $varkappa(s)$.
В задаче №473 была та же кривая и мы получили, что $$s=asqrt<2>,mbox,t.$$ Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения: begin s=asqrt<2>,mboxt=asqrt<2>,sqrt<mbox^2t-1> ,, Rightarrow ,, mbox^2t=frac<2a^2>+1 ,, Rightarrow end begin k(s)=varkappa(s)=frac<1><2a,mbox^2t> = frac. end
Вычисления сделаны для $a>0$.
Задача 5 (Феденко №496)
Найдите функцию $f(t)$, для которой данная кривая — плоская: $$ vec(t)=t, , a,mboxt, , f(t)> $$
Решение задачи 5
Для плоской кривой кручение равно нулю: begin varkappa(t) = left| begin -a,mboxt & a,mboxt & f'(t) \ -a,mboxt & -a,mboxt & f”(t) \ a,mboxt & -a,mboxt & f”'(t) \ end right| = left( f'(t) + f”'(t) right)cdot2a^2=0. end begin f'(t)=-f”'(t) quad Rightarrow quad f(t)=c_1+c_2,mboxt+c_3,mboxt. end
Как найти уравнение плоскости, в которой лежит кривая?
Известно, что плоская кривая лежит в своей соприкасающейся плоскости! Второй способ — составить уравнение плоскости по трем точкам.
Приведение кривой второго порядка к каноническому виду
Пример №1 . Привести уравнение второго порядка к каноническому виду с помощью поворота и параллельного переноса осей координат. Построить кривую.
Пример №2 . Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой.
Алгоритм перехода кривой второго порядка к каноническому виду
Пример №1 . 4y=-6-sqrt(4x-x 2 )
sqrt(4x-x 2 ) = -(4y+6)
Возведем в квадрат
4x-x 2 = (4y+6) 2
Раскрывая скобки, получаем:
16y 2 +48y + 36 +x 2 -4x = 0
Далее решается калькулятором. Если самостоятельно решать, то получим:
4x-x 2 = (4y+6) 2
-(x 2 – 4x) = 2(y+3/2) 2
-(x 2 – 4x + 4) = (y+3/2) 2
-(x – 2) 2 = (y+3/2) 2
(y+3/2) 2 + (x – 2) 2 = 0
Пример №2 . x=1-2/3 sqrt(y 2 -4y-5)
Здесь надо сначала привести к нормальному виду.
3/2(x-1)=sqrt(y 2 -4y-5)
Возводим в квадрат
9/4(x-1) 2 =y 2 -4y-5
9/4x 2 -9/4*2x+9/4-y 2 +4y+5=0
9/4x 2 -9/2x-y 2 +4y+29/4=0
Далее можно решать как с калькулятором, так и без него:
9/4(x-1) 2 =y 2 -4y-5
9/4(x-1) 2 =y 2 -4y+4-4-5
9/4(x-1) 2 =(y 2 -2)-9
9/4(x-1) 2 -(y 2 -2) = -9
-1/4(x-1) 2 +1/9(y 2 -2) = 1
Калькулятор Обыкновенных Дифференциальных Уравнений (ОДУ) и Систем (СОДУ)
Порядок производной указывается штрихами — y”’ или числом после одного штриха — y’5
Ввод распознает различные синонимы функций, как asin , arsin , arcsin
Знак умножения и скобки расставляются дополнительно — запись 2sinx сходна 2*sin(x)
Список математических функций и констант :
• ln(x) — натуральный логарифм
• sh(x) — гиперболический синус
• ch(x) — гиперболический косинус
• th(x) — гиперболический тангенс
• cth(x) — гиперболический котангенс
• sch(x) — гиперболический секанс
• csch(x) — гиперболический косеканс
• arsh(x) — обратный гиперболический синус
• arch(x) — обратный гиперболический косинус
• arth(x) — обратный гиперболический тангенс
• arcth(x) — обратный гиперболический котангенс
• arsch(x) — обратный гиперболический секанс
• arcsch(x) — обратный гиперболический косеканс
[spoiler title=”источники:”]
http://math.semestr.ru/line/curve.php
http://mathdf.com/dif/ru/
[/spoiler]






