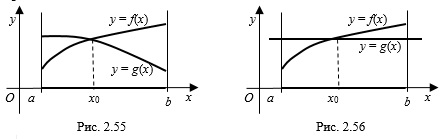Загрузить PDF
Загрузить PDF
График линейного или квадратного неравенства строится так же, как строится график любой функции (уравнения). Разница заключается в том, что неравенство подразумевает наличие множества решений, поэтому график неравенства представляет собой не просто точку на числовой прямой или линию на координатной плоскости. С помощью математических операций и знака неравенства можно определить множество решений неравенства.
-
1
Решите неравенство. Для этого изолируйте переменную при помощи тех же алгебраических приемов, которыми пользуетесь при решении любого уравнения.[1]
Помните, что при умножении или делении неравенства на отрицательное число (или член), поменяйте знак неравенства на противоположный. -
2
Нарисуйте числовую прямую. На числовой прямой отметьте найденное значение (переменная может быть меньше, больше или равна этому значению). Числовую прямую рисуйте соответствующей длины (длинную или короткую).
- Например, если вы вычислили, что
, на числовой прямой отметьте значение 1.
- Например, если вы вычислили, что
-
3
-
4
На числовой прямой заштрихуйте область, определяющую множество решений. Если переменная больше найденного значения, заштрихуйте область справа от него, потому что множество решений включает все значения, которые больше найденного. Если переменная меньше найденного значения, заштрихуйте область слева от него, потому что множество решений включает все значения, которые меньше найденного.[3]
- Например, если дано неравенство
, на числовой прямой заштрихуйте область справа от 1, потому что множество решений включает все значения больше 1.
Реклама
- Например, если дано неравенство
-
1
Решите неравенство (найдите значение
). Чтобы получить линейное уравнение, изолируйте переменную на левой стороне при помощи известных алгебраических методов.[4]
В правой части должна остаться переменнаяи, возможно, некоторая постоянная.
-
2
На координатной плоскости постройте график линейного уравнения. Для этого преобразуйте неравенство в уравнение и постройте график, как строите график любого линейного уравнения.[5]
Нанесите точку пересечения с осью Y, а затем при помощи углового коэффициента нанесите другие точки. -
3
-
4
Реклама
-
1
-
2
На координатной плоскости постройте график. Для этого преобразуйте неравенство в уравнение и постройте график, как строите график любого квадратного уравнения. Помните, что график квадратного уравнения является параболой.[9]
-
3
-
4
Выберите несколько контрольных точек. Чтобы определить, какую область заштриховать, выберите точки внутри и снаружи параболы.
-
5
Заштрихуйте соответствующую область. Чтобы определить, какую область заштриховать, в исходное неравенство подставьте значения
и
контрольных точек. Если при подстановке координат некоторой точки неравенство выполняется, заштрихуйте область, в которой лежит эта точка.[11]
Реклама
Советы
- Всегда упрощайте неравенство, прежде чем строить его график.
- Если вы не можете решить задачу, введите неравенство в графический калькулятор и попытайтесь справиться с задачей, действуя в обратном направлении.
Реклама
Об этой статье
Эту страницу просматривали 54 933 раза.
Была ли эта статья полезной?
Графический метод является одним из основных методов решения квадратных неравенств. В статье мы приведем алгоритм применения графического метода, а затем рассмотрим частные случаи на примерах.
Суть графического метода
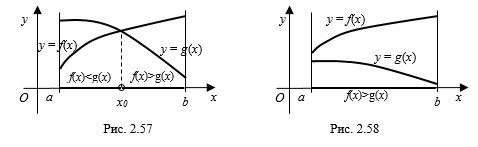
Метод применим для решения любых неравенств, не только квадратных. Суть его вот в чем: правую и левую части неравенства рассматривают как две отдельные функции y=f(x) и y=g(x), их графики строят в прямоугольной системе координат и смотрят, какой из графиков располагается выше другого, и на каких промежутках. Оцениваются промежутки следующим образом:
- решениями неравенства f(x)>g(x) являются интервалы, где график функции f выше графика функции g;
- решениями неравенства f(x)≥g(x) являются интервалы, где график функции f не ниже графика функции g;
- решениями неравенства f(x)<g(x) являются интервалы, где график функции f ниже графика функции g;
- решениями неравенства f(x)≤g(x) являются интервалы, где график функции f не выше графика функции g;
- абсциссы точек пересечения графиков функций f и g являются решениями уравнения f(x)=g(x).
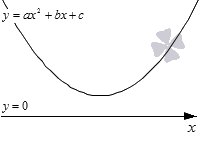
Рассмотрим приведенный выше алгоритм на примере. Для этого возьмем квадратное неравенство a·x2+b·x+c<0 (≤, >, ≥) и выведем из него две функции. Левая часть неравенства будет отвечать y=a·x2+b·x+c (при этом f(x)=a·x2+b·x+c), а правая y=0 (при этом g(x)=0).
Графиком первой функции является парабола, второй прямая линия, которая совпадает с осью абсцисс Ох. Проанализируем положение параболы относительно оси Ох. Для этого выполним схематический рисунок.
Решение с двумя корнями у квадратного трехчлена
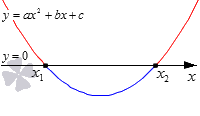
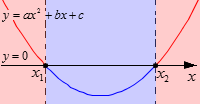
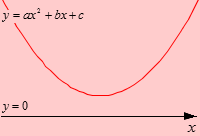
Ветви параболы направлены вверх. Она пересекает ось Ох в точках x1 и x2. Коэффициент а в данном случае положительный, так как именно он отвечает за направление ветвей параболы. Дискриминант положителен, что указывает на наличие двух корней у квадратного трехчлена a·x2+b·x+c . Корни трехчлена мы обозначили как x1 и x2, причем приняли, что x1<x2, так как на оси Ох изобразили точку с абсциссой x1 левее точки с абсциссой x2.
Части параболы, расположенные выше оси Ох обозначим красным, ниже – синим. Это позволит нам сделать рисунок более наглядным.
Выделим промежутки, которые соответствуют этим частям и отметим их на рисунке полями определенного цвета.
Красным мы отметили промежутки (−∞, x1) и (x2, +∞), на них парабола выше оси Ох. Они являются решением квадратного неравенства a·x2+b·x+c>0. Синим мы отметили промежуток (x1, x2), который является решением неравенства a·x2+b·x+c<0. Числа x1 и x2 будут отвечать равенству a·x2+b·x+c=0.
Сделаем краткую запись решения. При a>0 и D=b2−4·a·c>0 (или D’=D4>0 при четном коэффициенте b) мы получаем:
- решением квадратного неравенства a·x2+b·x+c>0 является (−∞, x1)∪(x2, +∞) или в другой записи x<x1, x>x2;
- решением квадратного неравенства a·x2+b·x+c≥0 является (−∞, x1]∪[x2, +∞) или в другой записи x≤x1, x≥x2;
- решением квадратного неравенства a·x2+b·x+c<0 является (x1, x2) или в другой записи x1<x<x2;
- решением квадратного неравенства a·x2+b·x+c≤0 является [x1, x2] или в другой записи x1≤x≤x2,
где x1 и x2 – корни квадратного трехчлена a·x2+b·x+c, причем x1<x2.
Решение с одним корнем у квадратного трехчлена
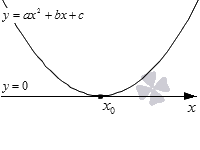
На данном рисунке парабола касается оси Oх только в одной точке, которая обозначена как x0. Ветви параболы направлены вверх, что означает, что a>0. D=0, следовательно, квадратный трехчлен имеет один корень x0.
Парабола расположена выше оси Oх полностью, за исключением точки касания координатной оси. Обозначим цветом промежутки (−∞, x0), (x0, ∞).
Запишем результаты. При a>0 и D=0:
- решением квадратного неравенства a·x2+b·x+c>0 является (−∞, x0)∪(x0, +∞) или в другой записи x≠x0;
- решением квадратного неравенства a·x2+b·x+c≥0 является (−∞, +∞) или в другой записи x∈R;
- квадратное неравенство a·x2+b·x+c<0 не имеет решений (нет интервалов, на которых парабола расположена ниже оси Ox);
- квадратное неравенство a·x2+b·x+c≤0 имеет единственное решение x=x0 (его дает точка касания),
где x0 – корень квадратного трехчлена a·x2+b·x+c.
Решение квадратного трехчлена, не имеющего корней
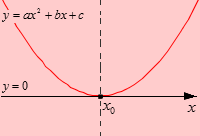
Рассмотрим третий случай, когда ветви параболы направлены вверх и не касаются оси Ox. Ветви параболы направлены вверх, что означает, что a>0. Квадратный трехчлен не имеет действительных корней, так как D<0.
На графике нет интервалов, на которых парабола была бы ниже оси абсцисс. Это мы будем учитывать при выборе цвета для нашего рисунка.
Получается, что при a>0 и D<0 решением квадратных неравенств a·x2+b·x+c>0 и a·x2+b·x+c≥0 является множество всех действительных чисел, а неравенства a·x2+b·x+c<0 и a·x2+b·x+c≤0 не имеют решений.
Нам осталось рассмотреть три варианта, когда ветви параболы направлены вниз. На этих трех вариантах можно не останавливаться подробно, так как при умножении обеих частей неравенства на −1 мы получаем равносильное неравенство с положительным коэффициентом при х2.
Алгоритм решения неравенств с использованием графического способа
Рассмотрение предыдущего раздела статьи подготовило нас к восприятию алгоритма решения неравенств с использованием графического способа. Для проведения вычислений нам необходимо будет каждый раз использовать чертеж, на котором будет изображена координатная прямая Oх и парабола, которая отвечает квадратичной функции y=a·x2+b·x+c. Ось Oу мы в большинстве случаев изображать не будем, так как для вычислений она не нужна и будет лишь перегружать чертеж.
Для построения параболы нам необходимо будет знать две вещи:
- направление ветвей, которое определяется значением коэффициента a;
- наличие точек пересечения параболы и оси абсцисс, которые определяются значением дискриминанта квадратного трехчлена a·x2+b·x+c.
Точки пересечения и касания мы будет обозначать обычным способом при решении нестрогих неравенств и пустыми при решении строгих.
Наличие готового чертежа позволяет перейти к следующему шагу решения. Он предполагает определение промежутков, на которых парабола располагается выше или ниже оси Oх. Промежутки и точки пересечения и являются решением квадратного неравенства. Если точек пересечения или касания нет и нет интервалов, то считается, что заданное в условиях задачи неравенство не имеет решений.
Теперь решим несколько квадратных неравенств, используя приведенный выше алгоритм.
Необходимо решить неравенство 2·x2+513·x-2 графическим способом.
Решение
Нарисуем график квадратичной функции y=2·x2+513·x-2 . Коэффициент при x2 положительный, так как равен 2. Это значит, что ветви параболы будут направлены вверх.
Вычислим дискриминант квадратного трехчлена 2·x2+513·x-2 для того, чтобы выяснить, имеет ли парабола с осью абсцисс общие точки. Получаем:
D=5132-4·2·(-2)=4009
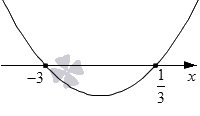
Как видим, D больше нуля, следовательно, у нас есть две точки пересечения: x1=-513-40092·2 и x2=-513+40092·2 , то есть, x1=−3 и x2=13.
Мы решаем нестрогое неравенство, следовательно проставляем на графике обычные точки. Рисуем параболу. Как видите, рисунок имеет такой же вид как и в первом рассмотренном нами шаблоне.
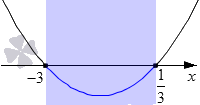
Наше неравенство имеет знак ≤. Следовательно, нам нужно выделить промежутки на графике, на которых парабола расположена ниже оси Ox и добавить к ним точки пересечения.
Нужный нам интервал −3, 13. Добавляем к нему точки пересечения и получаем числовой отрезок −3, 13. Это и есть решение нашей задачи. Записать ответ можно в виде двойного неравенства: −3≤x≤13.
Ответ: −3, 13 или −3≤x≤13.
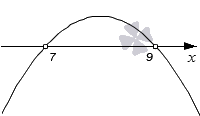
Решите квадратное неравенство −x2+16·x−63<0 графическим методом.
Решение
Квадрат переменной имеет отрицательный числовой коэффициент, поэтому ветви параболы будут направлены вниз. Вычислим четвертую часть дискриминанта D’=82−(−1)·(−63)=64−63=1. Такой результат подсказывает нам, что точек пересечения будет две.
Вычислим корни квадратного трехчлена: x1=-8+1-1 и x2=-8-1-1 , x1=7 и x2=9.
Получается, что парабола пересекает ось абсцисс в точках 7 и 9. Отметим эти точки на графике пустыми, так как мы работаем со строгим неравенством. После этого нарисуем параболу, которая пересекает ось Oх в отмеченных точках.
Нас будут интересовать промежутки, на которых парабола располагается ниже оси Oх. Отметим эти интервалы синим цветом.
Получаем ответ: решением неравенства являются промежутки (−∞, 7), (9, +∞).
Ответ: (−∞, 7)∪(9, +∞) или в другой записи x<7, x>9.
В тех случаях, когда дискриминант квадратного трехчлена равен нулю, необходимо внимательно подходить к вопросу о том, стоит ли включать в ответ абсциссы точки касания. Для того, чтобы принять правильное решение, необходимо учитывать знак неравенства. В строгих неравенствах точка касания оси абсцисс не является решением неравенства, в нестрогих является.
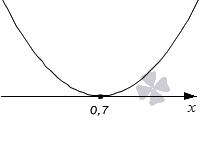
Решите квадратное неравенство 10·x2−14·x+4,9≤0 графическим методом.
Решение
Ветви параболы в данном случае будут направлены вверх. Она будет касаться оси Oх в точке 0,7, так как
Построим график функции y=10·x2−14·x+4,9. Ее ветви направлены вверх, так как коэффициент при x2 положительный, и она касается оси абсцисс в точке с абсциссой 0,7, так как D’=(−7)2−10·4,9=0, откуда x0=710 или 0,7.
Поставим точку и нарисуем параболу.
Мы решаем нестрогое неравенство со знаком ≤. Следовательно. Нас будут интересовать промежутки, на которых парабола располагается ниже оси абсцисс и точка касания. На рисунке нет интервалов, которые удовлетворяли бы нашим условиям. Есть лишь точка касания 0,7. Это и есть искомое решение.
Ответ: Неравенство имеет только одно решение 0,7.
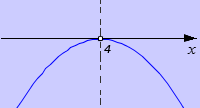
Решите квадратное неравенство –x2+8·x−16<0.
Решение
Ветви параболы направлены вниз. Дискриминант равен нулю. Точка пересечения x0=4.
Отмечаем точку касания на оси абсцисс и рисуем параболу.
Мы имеем дело со строгим неравенством. Следовательно, нас интересуют интервалы, на которых парабола расположена ниже оси Oх. Отметим их синим.
Точка с абсциссой 4 не является решением, так как в ней парабола не расположена ниже оси Ox. Следовательно, мы получаем два интервала (−∞, 4), (4, +∞).
Ответ: (−∞, 4)∪(4, +∞) или в другой записи x≠4.
Не всегда при отрицательном значении дискриминанта неравенство не будет иметь решений. Есть случаи, когда решением будет являться множество всех действительных чисел.
Решите квадратное неравенство 3·x2+1>0 графическим способом.
Решение
Коэффициент а положительный. Дискриминант отрицательный. Ветви параболы будут направлены вверх. Точек пересечения параболы с осью Oх нет. Обратимся к рисунку.
Мы работаем со строгим неравенством, которое имеет знак >. Это значит, что нас интересуют промежутки, на которых парабола располагается выше оси абсцисс. Это как раз тот случай, когда ответом является множество всех действительный чисел.
Ответ: (−∞, +∞) или так x∈R.
Необходимо найти решение неравенства −2·x2−7·x−12≥0 графическим способом.
Решение
Ветви параболы направлены вниз. Дискриминант отрицательный, следовательно, общих точек параболы и оси абсцисс нет. Обратимся к рисунку.
Мы работаем с нестрогим неравенством со знаком ≥, следовательно, интерес для нас представляют промежутки, на которых парабола располагается выше оси абсцисс. Судя по графику, таких промежутков нет. Это значит, что данное у условии задачи неравенство не имеет решений.
Ответ: Нет решений.
На этой странице вы узнаете
- Как мы ежедневно расставляем знаки неравенства в жизни?
- Как быстро определить верное обозначение точки на прямой?
- Как правильно чередовать знаки на числовой прямой?
Решая уравнение, мы стремимся к тому, чтобы обе части были равны. Но существуют такие примеры, где мы заведомо знаем, что два выражения не могут быть равны между собой. Они называются неравенствами.
Метод интервалов
Неравенство — это алгебраическое выражение, в котором одна сторона имеет отличное от другой значение. В неравенствах обычно одна сторона больше другой.
Для записи неравенств используют знаки > , < , ≥ , ≤ .
При этом “>” и “<” — это строгие знаки неравенства, а “≥” и “≤” — нестрогие знаки неравенства.
Их отличие в том, что нестрогие знаки неравенства включают граничные точки в итоговый промежуток, а строгие — нет.
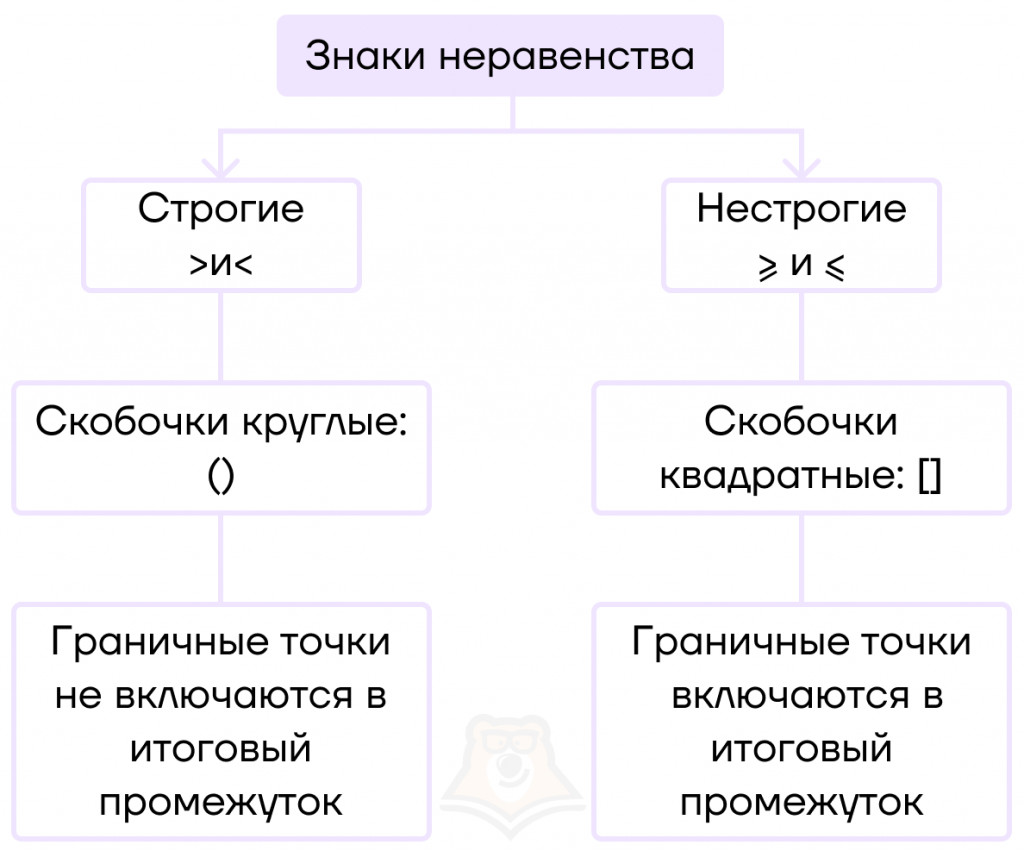
Посмотрим на привычные ситуации с точки зрения строгости знаков неравенства.
Например, возьмем известную игру “Камень, ножницы, бумага”.
Правила игры говорят нам, что камень всегда побеждает ножницы, а бумага побеждает камень. Если перенести это на язык неравенства, то получится:
Теперь зайдем в магазин цифровой техники и попробуем выбрать себе новый мобильный телефон. Задачка непростая, не так ли? Две разные модели могут настолько незначительно отличаться друг от друга своими характеристиками, что будут казаться почти одинаковыми. Тогда мы можем сказать, что они практически равны между собой, то есть неравенство нестрогое. Но один из них всё-таки понравился нам больше.
И каждый наш выбор, каждый шаг – это расстановка знака неравенства в настоящей жизни. Просто по бокам от него не цифры и переменные, а существующие ситуации и вещи.
Рассмотрим пример неравенства (х — 10)(х + 21) > 0.

Его можно решить несколькими способами. Например, вспомним, что положительным будет произведение двух положительных или двух отрицательных множителей, тогда получается совокупность из двух систем.
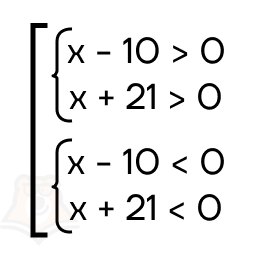
Однако этот способ решения очень трудоемкий и требует много времени. А если множителей будет больше, например, три или четыре, то время на решение в разы увеличивается.
Небольшой секрет тайм-менеджмента: как сократить время при решении неравенств? В таких случаях на помощь приходит метод интервалов.
Метод интервалов — специальный алгоритм решения для сложных неравенств вида f(x) > 0. При этом знак неравенства может быть любым.
Интервал — это промежуток на числовой прямой, ограниченный двумя различными числами.
Алгоритм решения неравенств методом интервалов
1 шаг. Перенести все части неравенства в одну сторону так, чтобы с другой остался только 0.
2 шаг. Найти нули функции, для этого необходимо решить уравнение f(x) = 0.
3 шаг. Начертить числовую прямую и отметить на ней все полученные корни. Таким образом, числовая прямая разобьется на интервалы.
4 шаг. Определить знаки на каждом интервале. Для этого необходимо подставить любое удобное значение в f(x) и определить, какой знак будет иметь функция на данном интервале.
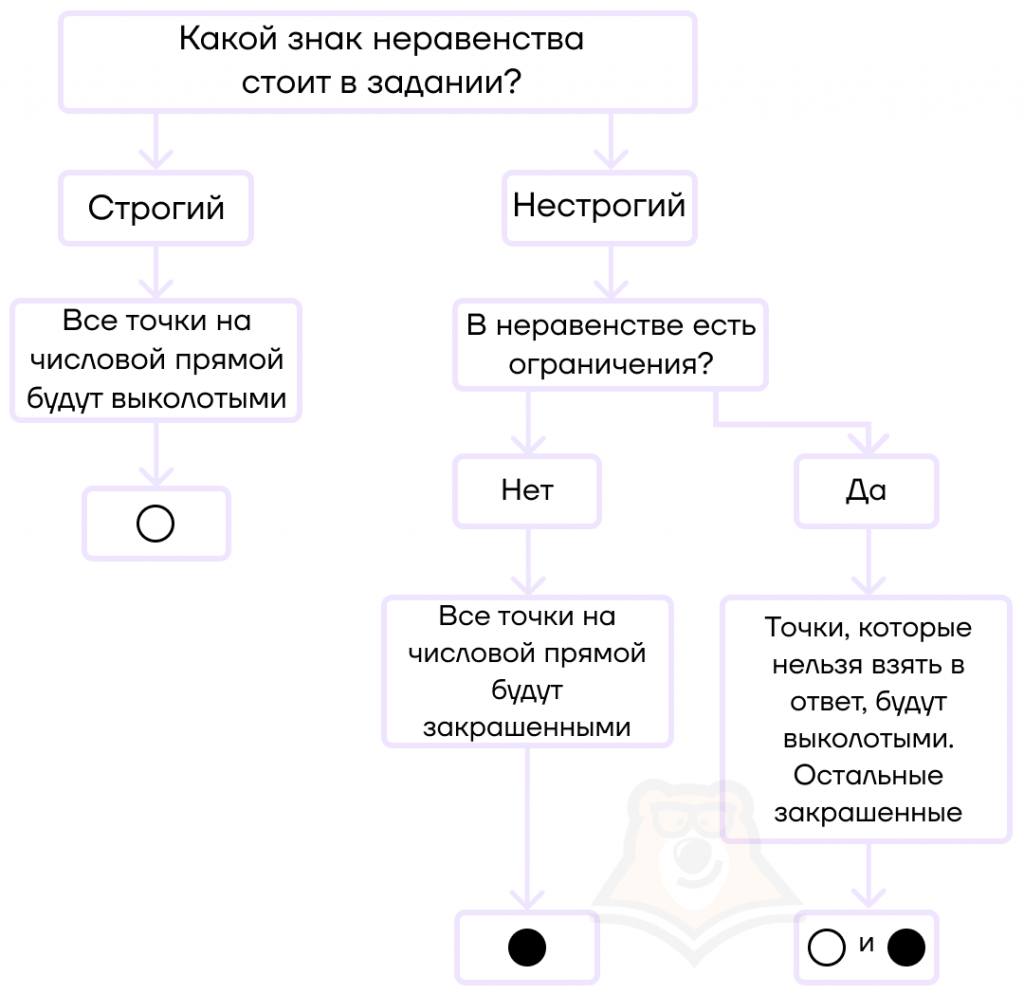
Расставляя полученные корни на прямой, необходимо отмечать их точками. При этом от того, какая отмечена точка (выколотая или закрашенная), будет зависеть ответ.
- Если в неравенстве стоит строгий знак неравенства, то все точки на прямой должны быть выколотыми.
Таким образом, граничные точки не будут включены в итоговый промежуток. Для записи таких точек используют круглые скобочки. Например, в промежуток (2;3) включаются все значения от 2 до 3, но не включаются граничные точки.
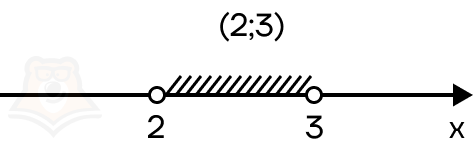
- Если в неравенстве стоит нестрогий знак неравенства, то найденные корни должны быть отмечены закрашенными точками.
Это означает, что мы включаем их в итоговый промежуток. Для записи таких точек используют квадратные скобочки. Например, в промежуток [2;3] включаются все значения от 2 до 3, в том числе и граничные точки.
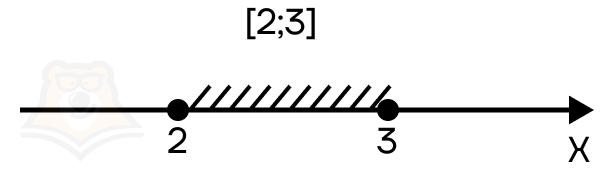
- Если в неравенстве появляются ограничения и некоторые точки нельзя взять в ответ, то такие точки должны быть выколотыми на числовой прямой, при этом знак самого неравенства может быть как строгим, так и нестрогим.
Например, если необходимо решить неравенство с дробью, то нули знаменателя на числовой прямой обязательно должны быть обозначены выколотыми точками.
В случае сомнений мы всегда можем проверить себя по простой схеме.
Вывод:
— если знак неравенства строгий, то все точки будут выколотыми;
— если знак неравенства нестрогий, то точки будут закрашенными, кроме тех точек, которые нельзя взять в ответ (например, они не удовлетворяют ОДЗ).
Стоит отметить, что непрерывная функция будет менять знак только в точках, в которых она равна 0. Подробнее узнать про смену знака функции можно в статье «Определение и график функции». Именно поэтому в методе интервалов мы ищем и отмечаем нули функции на прямой — только при переходе через них будет меняться знак функции.
При этом существует способ, с помощью которого можно быстро расставить знаки на прямой. Достаточно определить знак на одном из интервалов, а дальше чередовать знаки при переходе через каждую точку на прямой.
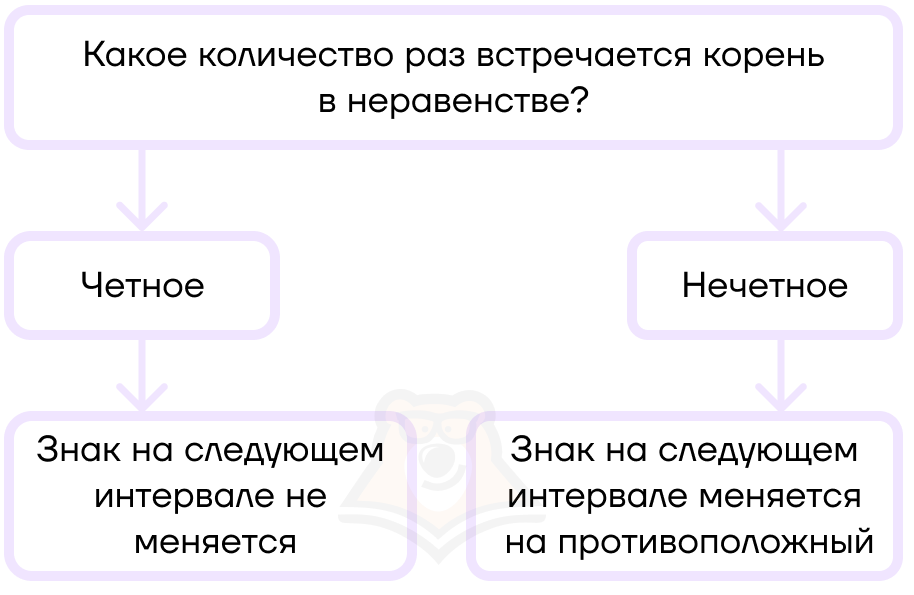
Правила чередования знаков:
- Если корень повторяется нечетное количество раз (то есть его степень нечетная), то знак при переходе на следующий интервал меняется.
- Если корень повторяется четное количество раз (его степень четная), то знак при переходе на следующий интервал не меняется.
Всегда будет нелишним перепроверить знак на каждом интервале, подставив значения в функцию, и убедиться в правильности расстановки знаков на прямой.
Но при расстановке можно пользоваться следующим алгоритмом, что значительно сократит время расстановки знаков.
Методом интервалов можно решить практически любое неравенство в задании 14 из ЕГЭ по профильной математике, также он может понадобиться в заданиях 8, 11 и 17 «профиля» или в задании 17 ЕГЭ по базовой математике.
На ОГЭ данным методом можно воспользоваться при решении неравенств из первой и второй частей — №13 и №20.
Так что осваивайте метод и 2 балла ЕГЭ или 3 балла ОГЭ будут у вас в кармане. Обязательно следуйте алгоритму решения неравенств методом интервалов, тогда вы точно решите неравенство верно.
Практика
Рассмотрим несколько примеров, чтобы на практике разобрать применение метода интервалов для решения неравенств.
Пример 1. Решить неравенство x2 + 8x — 33 > 0.
Шаг 1. Первым шагом необходимо найти нули функции, для этого приравниваем выражение слева к 0: x2 + 8x — 33 = 0.
Шаг 2. Находим корни уравнения, получаем х = 3 и х = -11.
Шаг 3. Расставляем полученные корни на числовой прямой. Поскольку знак неравенства строгий, то точки должны быть выколотыми:

Шаг 4. Дальше необходимо определить знаки на каждом интервале. Для этого подставим х = -12 в x2 + 8x — 33. Получаем:
(-12)2 + 8*(-12) — 33 = 144 — 96 — 33 = 15.
Получается положительное число, следовательно, интервал от минус бесконечности до -11 положительный. Поскольку все корни в неравенстве повторяются нечетное количество раз (по одному разу), то знаки чередуются.
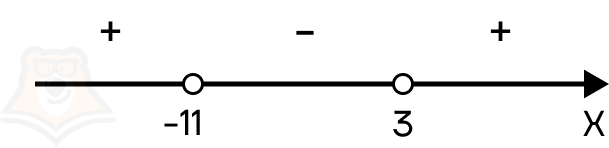
В ответ необходимо записать промежутки с положительным знаком, следовательно, ответом будет х ∈ (-∞; -11) U (3; +∞).
Пример 2. Решить неравенство (frac{2х^2 + 22х — 204}{(х-3)(х+5)} ≤ 0).
1. Находим нули функции.
Нули числителя: 2х2 + 22х — 204 = 0. Решая уравнение, получаем х = 6 и х = -17.
Нули знаменателя: (х — 3)(х + 5) = 0, следовательно, х = 3 и х = -5.
2. Расставляем полученные корни на числовой прямой. Нули числителя будут обозначены закрашенными точками, поскольку знак неравенства нестрогий. А вот нули знаменателя — выколотыми, поскольку знаменатель не может равняться 0, следовательно, и нули знаменателя не должны входить в итоговый промежуток.

3. Определяем знак на крайнем левом промежутке, подставляя х=-20 в дробь:
(frac{2(-20)^2 + 22(-20) — 204}{(-20 -3)(-20 +5)} = frac{2 * 400 — 440 — 204}{(-23) * (-15)} = 156345. )
Следовательно, промежуток положительный.
4. Поскольку каждый корень встречается один раз, то есть нечетное количество раз, то знаки будут чередоваться.

В ответ необходимо включить отрицательные промежутки. Следовательно, ответом будет х ∈ [-17; -5) U (3; 6].
Пример 3. Решить неравенство (frac{1}{х^2} ≥ frac{1}{х+2})
1. Первым делом следует отметить, что знаменатели не могут быть равны 0, следовательно, х2 ≠ 0 и х + 2 ≠ 0, отсюда получаем х ≠ 0 и х ≠ -2.
2. Теперь перенесем все части неравенства влево:
(frac{1}{х^2} — frac{1}{х+2} ≥ 0).
Приведем к общему знаменателю:
(frac{х + 2 — х^2}{х^2 (х + 2)} ≥ 0).
Для решения неравенства будет удобнее, если перед х2 в числителе будет стоять положительный знак, для этого умножим неравенство на -1.
При умножении неравенства на отрицательное число знак неравенства меняется на противоположный.
Получаем:
(frac{х^2 — х — 2}{х^2 (х + 2)} ≤ 0).
Теперь найдем нули функции.
Нули числителя: х2 — х — 2 = 0. Тогда х = -1 и х = 2.
Нули знаменателя: х = 0 и х = -2.
2. Расставим корни на числовой прямой, при этом нули числителя будут обозначены закрашенными точками, а нули знаменателя — выколотыми.

3. Определим знак на крайнем левом промежутке, подставив для этого х = -3 в дробь:
(frac{(-3)^2 — (-3) — 2}{(-3)^2 ((-3) + 2)} = frac{9 + 3 — 2}{9 * (-1)} = frac{10}{-9})
Промежуток отрицательный.
4. Дальше расставляем знаки, чередуя их. При этом следует заметить, что х = 0 — корень, повторяющийся четное количество раз (поскольку у х2 четная степень). Следовательно, при переходе через эту точку знак функции меняться не будет.

В ответ необходимо включить отрицательные промежутки, следовательно: х ∈ (-∞; -2) U [-1; 0) U (0; 2].
Давайте подведем итог. Для чего мы это изучили?
Конечно же, эти знания пригодятся на экзаменах, а также в решении школьных примеров с 8 класса по 11 класс.
Советуем после прочтения этой статьи попрактиковаться в рубрике «Проверь себя», чтобы закрепить полученные знания. После чего можете приступить к решению заданий посложнее, чтобы на экзамене у вас точно получилось решить подобные задания и набрать за них максимум баллов.
Фактчек
- Метод интервалов позволяет упростить решение любого неравенства, а также экономит время, которое ограничено на экзамене.
- Чтобы решить неравенство с помощью метода интервалов необходимо найти нули функции, расставить их на числовой прямой, а после определить знак каждого полученного интервала.
- Нули функции на прямой обозначаются точками, при этом закрашенные точки включают граничные значения в итоговый промежуток, а незакрашенные, напротив, исключают их из промежутка.
- Для определения знака на каждом интервале необходимо подставить любое значение из этого интервала в функцию.
- Для упрощения расстановки знаков можно пользоваться правилами чередования, определив знак только на одном интервале, а дальше менять знаки на каждом следующем. При этом если корень встречается в функции нечетное количество раз, то знак при переходе через эту точку на следующий интервал меняется, а если корень встречается четное количество раз, то знак на следующем интервале не меняется.
Проверь себя
Задание 1.
Какие знаки неравенства существуют?
- Строгие
- Нестрогие
- Строгие и нестрогие
- Больше и меньше
Задание 2.
Какой знак неравенства может встретиться в методе интервалов?
- Только больше или меньше.
- Только “больше или равно” или “меньше или равно”.
- Только “больше” и “больше или равно” или только “меньше” и “меньше или равно”.
- Любой.
Задание 3.
Какое утверждение верное?
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой закрашены.
- Если в неравенстве строгий знак неравенства, то точки на числовой прямой выколоты.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой закрашены, даже если в неравенстве есть ограничения.
- Если в неравенстве нестрогий знак неравенства, то все точки на числовой прямой выколоты.
Задание 4.
Какое утверждение верное?
- При переходе на числовой прямой на следующий интервал, знак на интервале всегда будет меняться.
- Если корень встречается в неравенстве четное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Если корень встречается в неравенстве нечетное количество раз, то при переходе через него на следующий интервал знак не меняется.
- Невозможно определить правильное чередование знаков на прямой, не подставляя значение из каждого интервала в функцию.
Задание 5.
Если в неравенстве строгий знак неравенства, то какие скобочки могут встретиться в ответе?
- Круглые
- Квадратные
- И круглые, и квадратные
- Ни один из перечисленных вариантов
Ответы: 1. — 3 2. — 4 3. — 2 4. — 2 5. — 1
Решение уравнений с помощью графиков
Решение линейных уравнений
Как ты уже знаешь, графиком линейного уравнения является прямая линия, отсюда и название данного вида.
Линейные уравнения достаточно легко решать алгебраическим путем – все неизвестные переносим в одну сторону уравнения, все, что нам известно – в другую и вуаля! Мы нашли корень.
Сейчас же я покажу тебе, как это сделать графическим способом.
Итак, у тебя есть уравнение: ( displaystyle 2{x} -10=2)
Как его решить?
Вариант 1, и самый распространенный – перенести неизвестные в одну сторону, а известные в другую, получаем:
( displaystyle 2x=2+10)
( displaystyle 2x=12)
Обычно дальше мы делим правую часть на левую, и получаем искомый корень, но мы с тобой попробуем построить левую и правую части как две различные функции в одной системе координат.
Иными словами, у нас будет:
( displaystyle {{y}_{1}}=2x)
( displaystyle {{y}_{2}}=12)
А теперь строим. Что у тебя получилось?
Как ты думаешь, что является корнем нашего уравнения? Правильно, координата ( displaystyle x) точки пересечения графиков:
Наш ответ: ( displaystyle x=6)
Вот и вся премудрость графического решения. Как ты с легкостью можешь проверить, корнем нашего уравнения является число ( displaystyle 6)!
Вариант 1. Напрямую
Просто строим параболу по данному уравнению: ( displaystyle {{x}^{2}}+2{x} -8=0)
Чтобы сделать это быстро, дам тебе одну маленькую подсказку: удобно начать построение с определения вершины параболы. Определить координаты вершины параболы помогут следующие формулы:
( displaystyle x=-frac{b}{2a})
( displaystyle y=-frac{{{b}^{2}}-4ac}{4a})
Ты скажешь «Стоп! Формула для ( displaystyle y) очень похожа на формулу нахождения дискриминанта» да, так оно и есть, и это является огромным минусом «прямого» построения параболы, чтобы найти ее корни.
Тем не менее, давай досчитаем до конца, а потом я покажу, как это сделать намного (намного!) проще!
Посчитал? Какие координаты вершины параболы у тебя получились? Давай разбираться вместе:
( displaystyle x=frac{-2}{2}=-1)
( displaystyle y=-frac{{{2}^{2}}-4cdot left( -8 right)}{4}=-frac{4+32}{4}=-9)
Точно такой же ответ? Молодец!
И вот мы знаем уже координаты вершины, а для построения параболы нам нужно еще … точек. Как ты думаешь, сколько минимум точек нам необходимо? Правильно, ( displaystyle 3).
Ты знаешь, что парабола симметрична относительно своей вершины, например:
Соответственно, нам необходимо еще две точки по левой или правой ветви параболы, а в дальнейшем мы эти точки симметрично отразим на противоположную сторону:
Возвращаемся к нашей параболе.
Для нашего случая точка ( displaystyle Aleft( -1;-9 right)). Нам необходимо еще две точки, соответственно, ( displaystyle x) можно взять положительные, а можно взять отрицательные? Какие точки тебе удобней?
Мне удобней работать с положительными, поэтому я рассчитаю при ( displaystyle x=0) и ( displaystyle x=2).
При ( displaystyle x=0):
( displaystyle y={{0}^{2}}+0-8=-8)
При ( displaystyle x=2):
( displaystyle y={{2}^{2}}+2cdot 2-8=0)
Теперь у нас есть три точки, и мы спокойно можем построить нашу параболу, отразив две последние точки относительно ее вершины:
Как ты думаешь, что является решением уравнения?
Правильно, точки, в которых ( displaystyle y=0), то есть ( displaystyle x=2) и ( displaystyle x=-4). Потому что ( displaystyle {{x}^{2}}+2{x} -8=0).
И если мы говорим, что ( displaystyle y={{x}^{2}}+2{x} -8), то значит, что ( displaystyle y) тоже должен быть равен ( displaystyle 0), или ( displaystyle y={{x}^{2}}+2{x} -8=0).
Просто? Это мы закончили с тобой решение уравнения сложным графическим способом, то ли еще будет!
Конечно, ты можешь проверить наш ответ алгебраическим путем – посчитаешь корни через теорему Виета или Дискриминант.
Что у тебя получилось? То же самое?
Вот видишь! Теперь посмотрим совсем простое графическое решение, уверена, оно тебе очень понравится!
Решение смешанных неравенств
Теперь перейдем к более сложным неравенствам!
Как тебе такое:
( displaystyle 4x<{{x}^{3}})?
Жуть, правда? Честно говоря, я понятия не имею, как решить такое алгебраически… Но, оно и не надо. Графически ничего сложного в этом нет! Глаза боятся, а руки делают!
Первое, с чего мы начнем, – это с построения двух графиков:
( displaystyle {{y}_{1}}=4x)
( displaystyle {{y}_{2}}={{x}^{3}})
Я не буду расписывать для каждого таблицу – уверена, ты отлично справишься с этим самостоятельно (еще бы, столько прорешать примеров!).
Расписал? Теперь строй два графика.
Сравним наши рисунки?
У тебя так же? Отлично!
Теперь расставим точки пересечения и цветом определим, какой график у нас по идее должен быть больше, то есть ( displaystyle {{y}_{2}}={{x}^{3}}).
Смотри, что получилось в итоге:
А теперь просто смотрим, в каком месте у нас выделенный график находится выше, чем график ( displaystyle {{y}_{1}}=4x)? Смело бери карандаш и закрашивай данную область! Она и будет решением нашего сложного неравенства!
На каких промежутках по оси ( displaystyle Ox) у нас ( displaystyle {{y}_{2}}={{x}^{3}}) находится выше, чем ( displaystyle {{y}_{1}}=4x)? Верно, ( displaystyle xin left( -2;0 right)cup left( 2;+infty right)).
Это и есть ответ!
Ну вот, теперь тебе по плечу и любое уравнение, и любая система, и уж тем более любое неравенство!
Уравнением линии на плоскости называют уравнение с двумя переменными 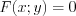



Уравнение окружности
Рассмотрим расположение окружности на координатной плоскости:
1) если уравнение окружности имеет вид 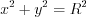


2) если уравнение окружности имеет вид 


Заметим, что неравенству 




Уравнение квадрата
Рассмотрим расположение квадрата на координатной плоскости:
1) если уравнение квадрата имеет вид 


2) если уравнение квадрата имеет вид 


Пересечение линий на плоскости
Рассмотрим две линии, заданные уравнениями 


Графическое решение уравнений и неравенств
1. Рассмотрим уравнение 



2. Использование монотонности функций при решении уравнений: если функция 





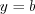
Например, число 

3. Использование монотонности функций при решении неравенств: если функция 
![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)



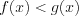

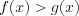
![(x_{0};b] LaTeX formula: (x_{0};b]](https://helpy.quali.me/uploads/formulas/402673c7d0139142c651324cae3880d5bb511595.1.1.png)
Графики функций на заданном отрезке могут и не пересекаться. Например, на рисунке 2.58 неравенство 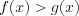
![[a;b] LaTeX formula: [a;b]](https://helpy.quali.me/uploads/formulas/490ffdf2e892c9664120bd901b5e45d8f13bfd5d.1.1.png)
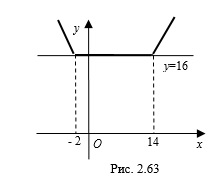
Пример 1. Найдите площадь фигуры, ограниченной прямыми 


Решение. Построим на координатной плоскости данные прямые (рис. 2.59).
Прямая 







Из рисунка 2.59 видим, что треугольник 
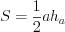

Найдем координаты точек пересечения прямых.
1. Найдем координаты точки 


2. Найдем координаты точки 


3. Найдем координаты точки 


Найдем длину отрезка 









Ответ: 
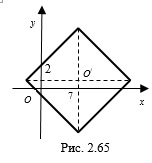
Пример 2. Найдите площадь фигуры, заданной на координатной плоскости системой неравенств
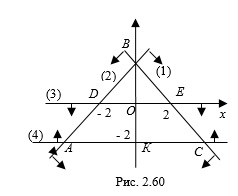
Решение. Построим гранич-ные прямые, соответствующие неравенствам заданной системы: 





Согласно рисунку 2.60 запишем: 

Найдем координаты точки 





Найдем площадь трапеции: 
Ответ: 
Пример 3. Найдите все целые значений параметра 

Решение. Заменим данное уравнение равносильной системой уравнений 
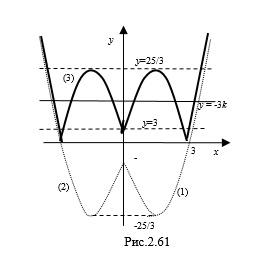
Построим схематически график функции 


1. Графиком функции 
Согласно формулам 







2. Рассмотрим функцию 




3. Построим график (3) функции 



Рассмотрим линейную функцию 






Ответ: 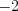
Пример 4. Найдите все значения параметра 

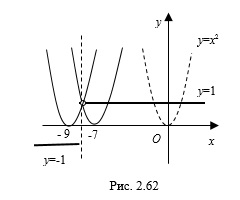
Решение. Решим уравнение графически, заменив его равносильной системой уравнений 
1. Построим схематически график функции 



Рассмотрим два случая:
1) если 


2) если 


2. Построим схематически график функции 

Парабола 














Ответ: 
Построим прямую 


![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png)
Ответ: ![a=-2sqrt[3]{2} LaTeX formula: a=-2sqrt[3]{2}](https://helpy.quali.me/uploads/formulas/1da946b3ee73655d5d103a1df7688b9505e43c78.1.1.png)
Пример 6. Найдите все значения параметра 
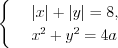
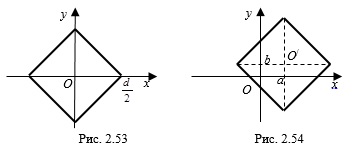
Решение. Имеем уравнение квадрата 

1. Построим квадрат с центром в точке 

Площадь квадрата найдем по формуле 





2. Построим окружность с центром в точке 

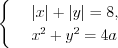






Ответ: 

Пример 7. Найдите площадь и периметр фигуры, заданной неравенством 
Решение. Данному неравенству удовлетворяют координаты всех точек плоскости, расположенных внутри квадрата 
Построим квадрат с центром в точке 



С другой стороны площадь квадрата находят по формуле 

Тогда 


Ответ: 

Решая уравнение или систему уравнений графически, точное решение найти бывает достаточно сложно, а то и вовсе не возможно. Поэтому этот метод чаще всего применяют в случае, когда необходимо определить количество корней уравнения или найти их приближенное значение.