Как составить несложный алгоритм

Как составить несложный алгоритм

Содержание

  • – Как написать алгоритм для новичков?
  • – Какой алгоритм простой?
  • – Какой алгоритм самый простой?
  • – Как создать алгоритм?
  • – Как писать алгоритмы с двумя числами?
  • – Что такое пример псевдокода?
  • – Каковы 5 свойств алгоритма?
  • – Какое еще слово означает алгоритм?
  • – Как вы используете алгоритм в предложении?

Как написать алгоритм для новичков?

Как построить алгоритм за шесть шагов

  1. Шаг 1: Определите цель алгоритма.
  2. Шаг 2: Получите доступ к историческим и текущим данным.
  3. Шаг 3: Выберите подходящие модели.
  4. Шаг 4: Точная настройка.
  5. Шаг 5: Визуализируйте свои результаты.
  6. Шаг 6: Непрерывный запуск вашего алгоритма.

Какой алгоритм простой?

Алгоритм набор инструкций по решению проблемы или выполнению задачи. Одним из распространенных примеров алгоритма является рецепт, который состоит из конкретных инструкций по приготовлению блюда или блюда. Каждое компьютеризированное устройство использует алгоритмы для выполнения своих функций.

Какой алгоритм самый простой?

Сортировка. Сортировка это простейший алгоритм, для которого больше всего подходит MapReduce. Как описано ранее, вычисление MapReduce следует шаблону распределенной сортировки, и, следовательно, наличие функций Map и Reduce идентичности автоматически обеспечивает сортировку входных данных.

Как создать алгоритм?

6 шагов по написанию любого алгоритма машинного обучения с нуля: пример использования Perceptron

  1. Получите базовое представление об алгоритме.
  2. Найдите несколько разных источников обучения.
  3. Разбейте алгоритм на части.
  4. Начнем с простого примера.
  5. Подтвердите с помощью надежной реализации.
  6. Напишите свой процесс.

Как писать алгоритмы с двумя числами?

Напишите алгоритм сложения двух чисел, введенных пользователем. Шаг 2: Объявите переменные num1, num2 и sum. Шаг 3: Считайте значения num1 и num2. Шаг 4: сложите num1 и num2 и присвойте результат сумма.

Что такое пример псевдокода?

Псевдокод – это искусственный и неформальный язык который помогает программистам разрабатывать алгоритмы. Псевдокод – это инструмент «текстового» детального (алгоритмического) проектирования. Правила псевдокода достаточно просты. Все утверждения, показывающие «зависимость», должны иметь отступ.

Каковы 5 свойств алгоритма?

Алгоритм должен иметь пять свойств:

  • Указан вход.
  • Указанный выход.
  • Определенность.
  • Эффективность.
  • Конечность.

Какое еще слово означает алгоритм?

Какое еще слово означает алгоритм?

процесс программанас
задача партия
код сценарий
двоичный функции
механика процедуры

Как вы используете алгоритм в предложении?

Алгоритм в предложении 🔉

  1. Многим ученым требовалось решить и описать алгоритм каждой решаемой ими проблемы, чтобы их приняли в компанию.
  2. Профессор Мэтью объяснил ученикам каждый алгоритм, чтобы они могли эффективно выполнять домашние задания самостоятельно.

Интересные материалы:

Сколько цветов вы видите в ответе?
Сколько турелей вы можете построить в Fallout 76?
Сколько у Apple в долгах?
Сколько у Bosch офисов?
Сколько у меня осталось места?
Сколько у вас привычек одновременно?
Сколько убийств – это мульти-убийство?
Сколько участков Чиа параллельно?
Сколько ударов в ультракомбо?
Сколько удвоить 1 доллар в день за 30 дней?

Источник

Если вы когда-либо слышали, что алгоритмы нужно знать всем разработчикам, но что это такое представляете с трудом – вам сюда.

Если хочешь подтянуть свои знания, загляни на наш курс «Алгоритмы и структуры данных», на котором ты:

  • углубишься в решение практических задач;
  • узнаешь все про сложные алгоритмы, сортировки, сжатие данных и многое другое.

Ты также будешь на связи с преподавателем и другими студентами.

В итоге будешь браться за сложные проекты и повысишь чек за свою работу 🙂

Интересно, хочу попробовать

Для опытных программистов некоторые понятия, в том числе и алгоритмы, настолько фундаментальны, что не возникает даже мыслей о том, что, то или иное определение может оказаться непонятным, сложным или вообще, пугающим, для новичка.

Алгоритм – вызывает ассоциации ни то с логарифмами, ни то с арифметикой.

И это слово действительно пришло из математики и использовалось для описания алгоритма Евклида, который применяется для нахождения наибольшего общего делителя двух целых чисел.

Если говорить нормальным языком, алгоритм – это пошаговая инструкция, где результат прошлого шага строго определен и используется в качестве входных данных для следующего шага.

Однако, поскольку в реальной жизни при написании программы совсем нечасто нужно искать общий делитель у целых чисел, раскладывать на множители и вообще думать о математиках, творивших в 300-е года до н.э., рассмотрим немного более жизненный пример применения алгоритмов.

Давайте представим, что телефонный справочник все еще актуален (да, тот бумажный, если вы их застали). Допустим, мы хотим набрать Николая Должанского. Принимая во внимание, что Николай есть в телефонном справочнике, мы можем найти его номер несколькими различными способами.

Метод полного перебора или линейный/последовательный поиск

Самый простой способ найти что-то в списке – пройти по нему по порядку, сравнивая с искомым значением. То есть:

1. Надежда Александрова –> не подходит

2. Николай Алексеев –> не подходит

…

И так далее, пока вы не найдете наконец Николая Должанского. Вероятно, понадобятся десятки и даже сотни операций сравнения. То есть, если вы захотите поболтать с Ярославом Яковлевым, то это займет порядком больше времени.

Как вы уже поняли, смысл алгоритма линейного поиска заключается в простом переборе значений от начала списка и до конца (или искомого результата). Это брутфорс. Этот алгоритм крайне прост и может возникнуть множество ситуаций, где его использование будет иметь смысл.

Например, если нужно найти телефон приятеля не в целой книге, а, предположим, на клочке бумаги, где помимо его номера всего десяток других записей – пройти список сверху вниз, в этом случае, будет умным решением.

Поиск по частям

У большинства людей просто не хватит терпения перебирать весь справочник. Поэтому они пойдут более прагматичным путем – будут разделять книгу на части.

Процесс деления на части предполагает сначала нахождение основной области, где, предположительно, находится искомое значение. Мы тут все еще ищем Николая Должанского.

Поиск начнем, перелистнув книгу на 30 страниц вперед. Мы увидим, что все фамилии начинаются на “Б”. Перейдем еще на 60 вперед и увидим “Г”. Достоверно известно, что “Г” находится прямо перед “Д”, а значит, Коля где-то рядом и с этого момента мы будем двигаться осторожнее.

Этот алгоритм описывает, как большинство людей ищут что-то в справочниках. Но поскольку мы, люди, часто выбираем неоптимальные пути решения задач, рассмотрим правильный подход к делению на части – бинарный алгоритм поиска.

Бинарный алгоритм поиска

Вот это уже звучит серьезно, да? На самом деле, ничего сложного. Бинарный поиск предполагает, что мы будем делить исходный массив данных пополам, отбрасывать ту часть, где искомого значения быть не может и делить остаток пополам снова, пока область поиска не сократится до минимально возможной.

В терминах телефонной книги, работа будет строиться следующим образом. Наш справочник содержит 400 страниц. Даже если мы все еще ищем Николая Должанского, который находится на 136 странице, мы можем воспользоваться бинарным поиском. Делим книгу пополам и по счастливой случайности попадаем прямо между буквами “М” и “Н” на 199 и 200 страницах соответственно. Мы знаем, что буква “Д” в алфавите находится перед “М”, так что справедливо будет утверждение:

Николай Должанский находится на странице между 0 и 199

Ту часть, что начинается с “Н” мы выбрасываем.

Далее, мы делим на две части первые 200 страниц телефонного справочника и видим, что попали мы прямо на страницу с буквой “Г”, а “Г”, как известно, идет перед “Д”. То есть нам снова стал известен неоспоримый факт:

Телефон Николая Должанского находится между 99 и 199 страницами

И вот, стартовав с 400 страниц, мы, всего через две операции сравнения, сократили область поиска на 3/4. Учитывая, что телефон Коли находится на 136 странице, нам предстоит сделать следующие операции:

[99-199] -> [99-149] -> [124-149] -> [124-137] -> [130-137] -> [133-137] -> [135-137] -> [136]

Еще 6 сравнений. Чтобы рассчитать количество операций необходимых для нахождения нужной страницы бинарным поиском, мы можем взять логарифм от количества страниц с основанием 2 и получим:

log2(400) = 8.644

то есть, округлив, в худшем случае – 9 операций сравнения. Рядом с исходным числом страниц, конечно, ерунда. Но давайте поговорим о по-настоящему серьезных книгах. Пусть в нашем справочнике будет не 400, а 4 000 000 страниц. Попробуйте представить, сколько операций сравнения нам потребуется? На самом деле, немного:

log2(4000000) = 21.932

то есть, 22 раза нужно будет провести сравнение частей справочника, прежде, чем 4 000 000 превратятся в 1.

Сравните скорость работы линейного и бинарного алгоритмов поиска для такого количества страниц.

Заключение

В общем, так и со всеми алгоритмами. Изучение алгоритмов – это изучение способов решать проблемы и задачи наиболее оптимальным путем. Алгоритм – это решение, рассмотренное со всех сторон и преобразованное в эдакий todo-list действий, которые нужно совершить, чтобы воспроизвести его.

И отдельная тема, это преобразование алгоритма в код на конкретном языке, ведь в разных языках алгоритмы (особенно поисковые) могут реализовываться по-разному. Иногда, это может быть уже встроенная в язык функция, которая выдаст нужный результат из массива одной строкой, а где-то понадобиться пара-тройка десятков строк.

И, для примера, вот так будет реализован бинарный поиск на Ruby:

def binary_search(target, list)
  position = (list.count / 2).floor
  mid = list[position]

  return mid if mid == target

  if(mid < target)
    return binary_search(target, list.slice(position + 1, list.count/2))
  else
    return binary_search(target, list.slice(0, list.count/2))
  end
end


puts binary_search(9, [1,2,3,4,5,6,7,8,9,10])

Другие статьи по теме

Изучаем алгоритмы: полезные книги, веб-сайты, онлайн-курсы и видеоматериалы

Источник

22

    1. Организация
      разветвлений в алгоритмах

Рассмотрим
сначала линейные алгоритмы.

Линейным
называется алгоритм, в схеме которого
вершины (блоки). связаны в одну линию.

Пример
1.1. Составить СА
для вычисления следующей функции:

y
= sin()cos()
+ e-x
cos() (1.1)

при
заданных значениях

x.

Вычислительный
процесс для данной функции может быть
организован

в
виде последовательности шагов, на каждом
из которых производятся следующие
вычисления:

1)
А1
= sin();

2)
A2
=
cos();

3)
A3
=
exp(-х);

4)
A4
=
cos();

5)
B1 =
A1A4;

6)
B2 =
A3A2;

7)
у = B1 +
B2.

СА,
представляющая данный вычислительный
процесс с учётом ввода исходных данных
и вывода вычисленного значенияy,
является
линейной (рис. 1.1; начальная и конечная
вершины не нумеруются). Его особенность
– то, что операторные блоки
(вершины)
2-5 можно располагать в произвольном
порядке; то же относится и к блокам 6 и
7.

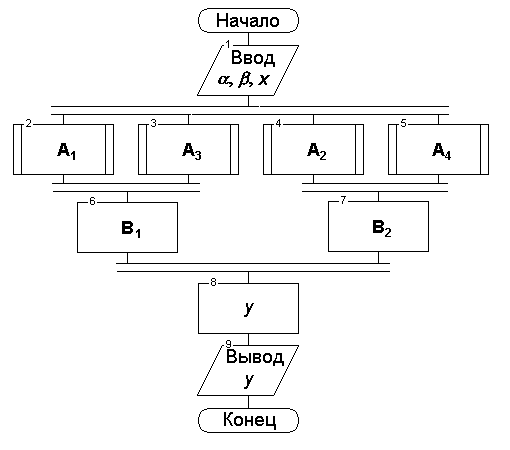
Рис.
1.1. Пример линейной СА (последовательная
реализация)

Независимость
СА от расположения отдельных блоков
означает, что реализуемые ими фрагменты
вычислительного процесса можно выпол-нить
одновременно (параллельно) при наличии
соответствующих аппарат-ных
средств. Одновременность выполнения
фрагментов обозначается на СА параллельными
линиями (рис. 1.2), при этом допускается
возможность расхождения связей на
выходах всех блоков.

Для
вычисления функций SIN,
COS
и EXP
используются стандартные подпрограммы
(СП), основанные, как правило, на
представлении этих функций в виде
полиномов (например, разложение в ряд
Тейлора [2]). Однако
эти СП реализуют нелинейные СА, содержащие
циклы –см. п. 1.2.

Таким
образом, линейность СА – понятие
относительное; при более подробном
рассмотрении СА может оказаться
нелинейной. В сколько-нибудь сложной
СА линейными могут быть только её
отдельные фрагменты.

Рис.
1.2. Параллельная реализация СА для
примера 1.1

Рассмотрим
далее схемы алгоритмов с разветвлением.

Разветвлением
мы будем называть фрагмент СА, содержащий
блок выбора альтернатив (например,
совокупность условных операторов) с
двумя или более выходами; по этим выходам
организуются связи с другими фрагментами
СА. Выбор
альтернатив осуществляется по простому
либо составному условию.

Пример
1.2. Составить СА
нахождения корней квадратного уравнения

au2
+ bu
+ c
= 0. (1.2)

Предварительно
запишем приведённое квадратное уравнение
с целью уменьшения числа параметров,
определяющих решения исходного уравнения:

u2
+ pu
+ q
= 0; (1.3)

здесь
p
= b/a,
q
= c/a
(a

0 !). (1.4)

Корни
приведённого квадратного уравнения
определяются по формуле

u1,2
=
–p/2

d, (1.5)

где
d
=
p2/4
– q.

(1.6)

В
зависимости от значений d
возможны 3 случая :

  • d>0.
    Решение содержит два вещественных
    корня

  • u1
    =
    –p/2
    + d,.
    u2
    =
    –p/2
    – d; (1.7)

  • d<0.
    Решение содержит два мнимых корня (u
    =
    x
    +
    iy,
    i
    = -1)

  • u1=
    –p/2
    + id,
    u2=
    –p/2
    – id (1.8)

  • d=0.
    Решение содержит один корень кратности
    два (два слившихся корня)

Проанализируем
поведение корней при изменении величины
и знака дискриминанта d
(рис.1.3):

1)
d<0
– корни перемещаются сим-метрично
по вертикали (мнимая ось);

2)
d>0 – корни перемещаются сим-метрично
по горизонтали (реальная ось);

3)
d=0
– граничная точка x=-p/2 при переходе с
вертикали на горизонталь.

u1
= u2
= –p/2. (1.9)

Рис.
1.3. Расположение корней

на
комплексной плоскости

(p>0;
r = d)

Анализ
такого рода необходим при построении
контрольного примера для отладки
программы или при ее тестировании.

Составляем
СА (рис. 1.4), исходя из следующей
последовательности шагов: вводим
исходные данные и вычисляем параметры
приведённого квадратного уравнения;
вычисляем значения корней в соответствии
с тремя возможными альтернативами,
используя условные блоки (вершины);
выводим результаты на экран (принтер).

Рис.1.4.
СА с ветвлением: а – основная схема; б –
вариант блока выбора.

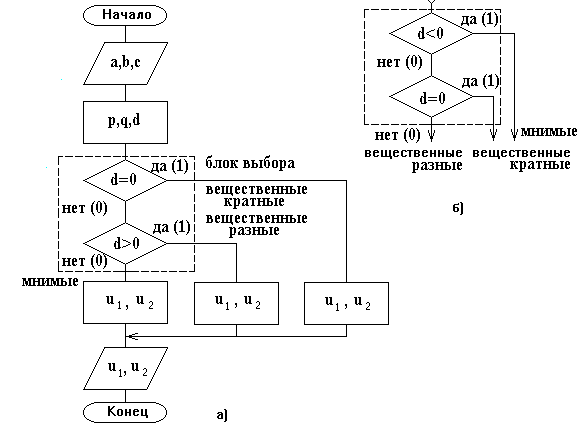
На
рис. 1.4а пунктиром выделен блок выбора
по условию, составленный из двух условных
вершин, этот блок позволяет представить
разветвление СА по трём альтернативным
направлениям в зависимости от значения
дискриминанта. Он может быть преобразован
в эквивалентный блок (рис. 1.4 б); анализ
этого блока показывает, что проверку
условия d=0
можно исключить из алгоритма, поскольку
в случае d=0
равные значения корней получаются
автоматически.

Рассмотрим
вопрос организации выбора направления
в СА с ветвлением подробнее.

На
рис. 1.5 приведены условные операторы и
их конфигурации в виде фрагментов СА,
а именно:

а)
if
<условие>
then
S (на
схеме – сокращённо I);

б)
if
<условие>
then
S1 else
S2 (на
схеме – сокращённо I);

в)
case
N of
1: S1;
2: S2;
… k: Sk
end (на
схеме – сокращённо C).

Здесь
Si
– оператор общего вида; он может быть
пустым либо составным, то есть включать
в себя последовательность операторов,
в том числе условный оператор.

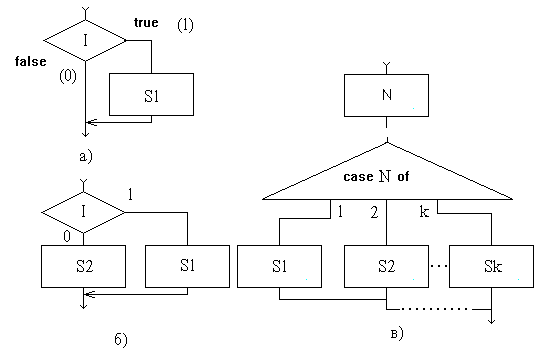
Рис.
1.5. Фрагменты СА для условных операторов
типа:

а,б
– if;
в – case .. of.

Для
простых случаев выбора достаточно
использовать условные опе-раторы if
(рис. 1.5,а и б). В
более сложных случаях Pascal предоставляет
мощное средство – оператор-переключатель
case .. of
(рис. 1.5в); аналогичное средство (switch)
имеется и в
языке C.

Ситуации,
в которых необходимо сделать сложный
выбор, описываются составными логическими
операторами, полученными композицией
простых условий (простых операторов).
Сложность выбора определяется следующими
факторами:

а)
много альтернатив с простыми условиями.
Пpи этом каждому альтеpнативному
напpавлению в СА выбора пpисваивается
свой десятичный номеp, начиная с 1;

б)
альтернативы – две, но выбор осуществляется
по сложному условию.

Возможно
сочетание этих факторов.

На
СА выбоp pеализуется двоичным деpевом
(полным либо неполным), в каждом узле
(условной веpшине) котоpого пpостейший
выбоp кодиpуется логическим 0, если
условие не выполняется (false),
и логической 1, если условие выполняется
(true).

Если
составить позиционный код на выходе из
блока выбоpа по каждому напpавлению в
соответствии с последовательным
пpохождением чеpез условные веpшины СА
свеpху вниз, то мы получим двоичный код
десятичного номера альтернативы,
уменьшенного на 1. Пpоpанжиpуем свеpху
вниз условные веpшины (ранг СА выбора
– это глубина узла дерева выбора,
увеличенная на 1); тогда количество
альтеpнатив n,
пpедоставляемых полным двоичным деревом,
опpеделяется его pангом r:
n=2r.
Возвpащаясь к pис.1.4, отметим, что в данном
случае мы имеем двухpанговое неполное
деpево выбоpа (r
= ] log2
3 [ = 2).

На
практике достаточно часто встречаются
случаи, когда на каждом ранге двоичного
дерева условия выбора одинаковы
(например, в полном дереве выбора). Для
описания такого рода ситуации достаточно,
чтобы логические функции выбора
альтернативы содержали столько
перемен-ных, каков ранг дерева выбора.

Пример
1.3. Пусть необходимо
оpганизовать выбоp из четырёх альтернатив,
пpичём на втором ранге условия одинаковы.

В
этом случае достаточно двух условий
В1 и В2 (В1 и В2 – булевы переменные), если
каждому из значений 0 (false)
и 1 (true)
этих условий сопоставить свою альтернативу
Ni – см. табл. 1.1, колонка А. Этой таблице
соответствует фpагмент СА, показанный
на pис.1.6; здесь рядом с номеpами альтеpнатив
указаны их коды (двоичные представления).

Таблица
1.1

B1

B2

А

0

0

N1

0

1

N2

1

0

N3

1

1

N4

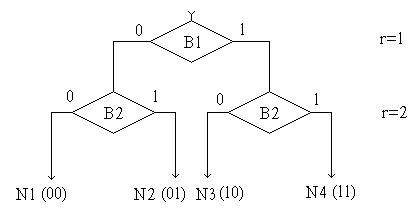
Рис.
1.6. Оpганизация выбоpа из четырех
альтеpнатив

В
таблицах альтернатив в столбце “А”
могут быть прочерки (не все альтернативы
используются) или одинаковые альтернативы
(иначе: одна и та же альтернатива
реализуется при нескольких наборах
значений условий). Первый случай
соответствует неполному дереву выбора
(n
<
2r);
второй случай
означает возможность объединения
листьев (конечных узлов дерева). В обоих
случаях необходимо попытаться
минимизировать логические выражения
и реализующие их схемы алгоритмов.

Рассмотрим
построение СА для блока выбора при
неполном дереве выбора.

Пример
1.4.
Пусть задано условие выбора вида С=В1В2,
где В1 и В2 – логические условия (В1, В2 –
булевы переменные) и 
– опеpация логического сложения по mod2.
Заполним таблицу истинности для функции
А (табл. 1.2); здесь в колонке для С
проставлены её логические значения
F(false)
и T(true),
определяющие выбоp из двух путей
(альтеpнатив), по котоpым pазветвляется
СА для заданного условия. На pис.1.7
пpиведен фрагмент схемы, построенный в
соответствии с таблицей 1.2, пpичём все
пути, имеющие одинаковое логическое
значение, объединены.

Таблица
1.2

B1

B2

C

0

0

F

0

1

T

1

0

T

1

1

F

Р
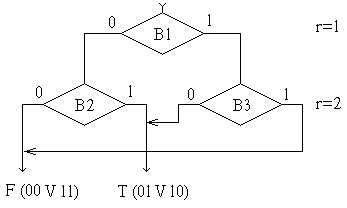ис.
1.7 СА выбоpа с объединением узлов при
полном дереве выбора

Если в какой-либо
ветви построенной схемы имеется
изобра-женный на pис. 1.8а фpагмент, то
данная булева пеpеменная Вi склеивается,
т. е. BiVBi дает логи-ческую константу 1;
это означает, что условная вершина на
участке a-b не нужна и её можно заменить
отpезком пpямой (рис 1.8б).

Аналогично
заполняется таблица истинности (если
она не задана) и по ней стpоится схема
алгоритма выбора, если задан составной
опеpатоp как логическая функция n
аpгументов; на каждом pанге, начиная со
второго, пpоводится объединение путей,
выбоp котоpых имеет одинаковые логические
значения.

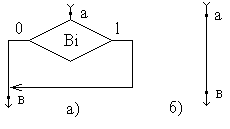
Рис.1.8
Частный случай выбора:

а
– исходный фрагмент БВ;

б
– упрощение фрагмента.

Покажем
способ постpоения схем выбоpа пpи r>2
на частном пpимеpе.

Пример
1.5. pеализации
логической функции
,
где B1, B2, B3 – некотоpые условия (булевы
переменные).

Введём
в исходную функцию пpомежуточную
пеpеменную
.
Тогда С=B1&Z, и эта функция pеализуется
в соответствии с приведенными выше
положениями в виде схемы pис.1.9а. Аналогично
pеализуется фpагмент схемы для пеpеменной
Z (pис.1.9б). Далее пpоизведем “сбоpку”
общей схемы, вставляя в веpшину Z (pис.1.9а)
соответствующий ей фpагмент из pис.1.9б,
и упpостим начертание pезультиpующей
схемы (pис.1.9в).

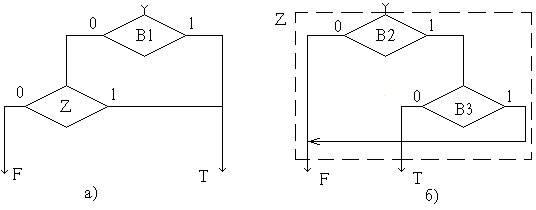
Рис.
1.9 Постpоение схемы выбоpа по условию

Пример
1.6. Пусть для
выбора существует 3 альтернативы N1, N2,
N3, определяемые
тремя простыми условиями В1,
B2, В3 (В1..В3 –
булевы переменные) в соответствии с
табл. 1.3. Требуется синтезировать СА для
блока выбора.

Перестроим
табл. 1.3 таким образом, чтобы каждой
альтернативе соответствовала своя
колонка (табл. 1.4), в которой для выбранного
набора В1В2В3 отмечен единицей тот факт,
что альтернатива реализу-ется,
а прочерком – что не реализуется. Тогда
Ni (i=)
можно считать выходными переменными
блока выбора, а саму таблицу можно
рассматривать как таблицу истинности
для системы трёх функций от трёх булевых
переменных. Далее можно использовать
известный под-ход […] для минимизации
такой системы и синтеза соответствующей
СА.

Таблица
1.3 Таблица1.4

B1

B2

B3

C

B1

B2

B3

N1

N2

N3

0

0

0

N1

0

0

0

1

—

—

0

0

1

N2

0

0

1

—

1

—

0

1

0

N1

0

1

0

1

—

—

0

1

1

N3

0

1

1

—

—

1

1

0

0

N3

1

0

0

—

—

1

1

0

1

N3

1

0

1

—

—

1

1

1

0

N3

1

1

0

—

—

1

1

1

1

N3

1

1

1

—

—

1

На
рис. 1.10а приведена начальная схема
алгоритма выбора, а на рис. 1.10б показана
СА выбора, полученная в результате
минимизации; под каждым альтернативным
выходом в скобках записаны соответству-ющие
им значения двоичных наборов В1В2В3 (X –
безразличное значение).

Отметим,
что в данном примере упрощения фрагментов
СА выбора могут быть получены чисто
схемным путем. Действительно, участок
a-b
может быть заменен прямой (см. рис. 1.8),
а участки c-d,
c-e,
c-в
можно преобразовать с учетом законов
дистрибутивности и коммутативности
как для переменных, так и для соответствующих
им условных вершин. Для упомянутых
участков имеем:

участок
c-d
–В2&B3VB2&B3
= B3(B2&B2) = B3;

участок
c-e
– В2&B3
= B3&B2;

участок
c-в
– В2&B3
= B3&B2.

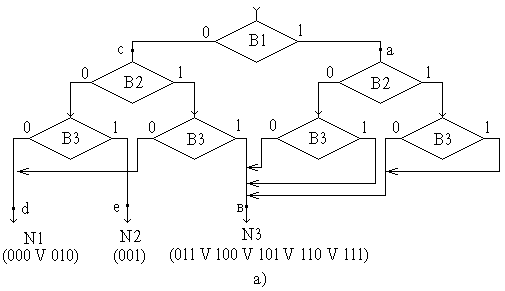
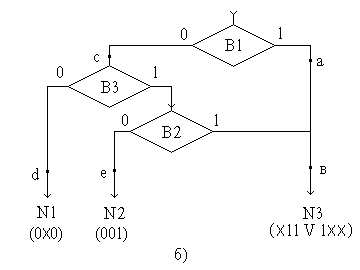
Рис.
1.10. Пример выбора нескольких альтернатив
по сложному условию: а – исходная СА
выбора; б – минимизированная схема.

В
заключение запишем фрагмент программы,
соответствующий миними-зированной СА
выбора. Переход от схемы выбора (рис.
1.10б) к условному оператору case
N
of
несложен и осуществляется следующим
образом: каждой альтернативе ставится
в соответствие свой десятичный номер
(слева направо в СА выбора), затем по
кодам альтернатив записываются логические
формулы, после чего формируется условный
оператор, в котором записы-ваются
полученные формулы (в качестве условий)
и операторы присваи-вания
параметру N
соответствующего десятичного номера;
далее следует (возможно, после операторов
общего вида)
оператор
case
N of.
Итак,
имеем:

if
(NOTB1)
AND (NOT B3)
then
N:=1
else

if
(NOT B1) AND
(NOT B2) AND B3 then
N:=2
else
N:=3;

case
N of

1:
S1;

2:
S2;

3:
S3

end

Отметим,
что к моменту вычисления N должны быть
определены значения B1,
B2,
B3.

Соседние файлы в папке Конспект лекций

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Блок-схема

Итак, опустив долгие и нудные восхваления Паскаля, которые так любят публиковать в своих статьях редакторы многих сайтов, приступим непосредственно к самому основному – к программированию.

В школах, как правило, изучение Паскаля начинают с решения простейших задач путем составления различных алгоритмов или блок-схем, которое многие так часто игнорируют, считая никому не нужной ерундой. А зря. Я, как и любой другой человек, хоть немного соображающий в программировании (не важно где – в Паскале, Си, Дельфи), могу уверить Вас – умение правильно и быстро составлять схемы является фундаментом, основой программирования.

Блок-схема — графическое представление алгоритма. Она состоит из функциональных блоков, которые выполняют различные назначения (ввод/вывод, начало/конец, вызов функции и т.д.).

Существует несколько основных видов блоков, которые нетрудно запомнить:

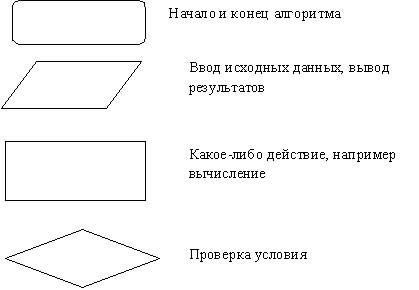
Некоторые виды блоков

Сегодняшний урок я решила посвятить не только изучению блок-схем, но также и изучению линейных алгоритмов. Как Вы помните, линейный алгоритм — наипростейший вид алгоритма. Его главная особенность в том, что он не содержит никаких особенностей. Как раз это и делает работу с ним простой и приятной.

Задача №1: «Рассчитать площадь и периметр прямоугольника по двум известным сторонам».

Данная задача не должна представлять особой трудности, так как построена она на хорошо известных всем нам формулах расчета площади и периметра прямоугольника, поэтому зацикливаться на выведении этих формул мы не будем.

Составим алгоритм решения подобных задач:

1) Прочитать задачу.
2) Выписать известные и неизвестные нам переменные в «дано». (В задаче №1 к известным переменным относятся стороны: a, b ;к неизвестным — площадь S и периметр P)
3) Вспомнить либо составить необходимые формулы. (У нас: S=a*b; P=2*(a+b))
4) Составить блок-схему.
5) Записать решение на языке программирования Pascal.

Запишем условие в более кратком виде.

Дано: a, b

Найти: S, P

Блок-схема:

Решение задачи №1. Блок-схема

Решение задачи №1

Структура программы, решающей данную задачу, тоже проста:

  • 1) Описание переменных;
  • 2) Ввод значений сторон прямоугольника;
  • 3) Расчет площади прямоугольника;
  • 4) Расчет периметра прямоугольника;
  • 5) Вывод значений площади и периметра;
  • 6) Конец.

А вот и решение:

Program Rectangle;
Var a, b, S, P: integer;
Begin
write('Введите стороны прямоугольника!'); 
readln(a, b);
S:=a*b;
P:=2*(a+b);
writeln('Площадь прямоугольника: ', S);
write('Периметр прямоугольника: ', P);
End.

Задача №2: Скорость первого автомобиля — V1 км/ч, второго – V2 км/ч, расстояние между ними S км. Какое расстояние будет между ними через T часов, если автомобили движутся в разные стороны? Значения V1, V2, T  и S задаются с клавиатуры.

Решение осуществляем, опять же, следуя алгоритму. Прочитав текст, мы переходим к следующему пункту. Как и во всех физических или математических задачах, это запись условий задачи:

Дано: V1, V2, S, Т
Найти: S1

Далее идет самая главная и в то же время самая интересная часть нашего решения – составление нужных нам формул. Как правило, на начальных стадиях обучения все необходимые формулы хорошо нам известны и взяты из других технических дисциплин (например, на нахождение площади различных фигур, на нахождение скорости, расстояния и т.п.).

Формула, используемая для решения нашей задачи, выглядит следующим образом:

S1=(V1+V2)*T+S

Следующий пункт алгоритма – блок-схема:

Решение задачи №2.Блок-схема

Решение задачи №2.

А также решение, записанное в Pascal :

Program Rasstoyanie;
Var V1, V2, S, T, S1: integer; {Ввод }
begin
write('Введите скорость первого автомобиля: '); 
readln(V1);
write('Введите скорость второго автомобиля: '); 
readln(V2);
write('Введите время: '); 
readln(T);
write('Введите расстояние между автомобилями: '); 
readln(S);
S1:=(V1+V2)*T+S;
writeln('Через ', t,'ч. расстояние ', S1,' км.');
End.

Вам может показаться, что две эти программы правильны, но это не так. Ведь сторона треугольника может быть 4.5, а не 4, а скорость машины не обязательно круглое число!  А Integer — это только целые числа. Поэтому при попытке написать во второй программе другие числа выскакивает ошибка:

Ошибка!

Обратите внимание в Паскале, как и в любом другом языке программирования десятичная дробь вводится с точкой, а не с запятой!

Чтобы решить эту проблему вам надо вспомнить какой тип в Pascal отвечает за нецелые числа. В этом уроке мы рассматривали основные типы. Итак, это вещественный тип — Real.  Вот, как выглядит исправленная программа:

Снимок экрана 2013 12 15 в 20.00.24 1024x545

Как видите, эта статья полезна для прочтения как новичкам, так и уже более опытными пользователям Pascal, так как составление блок-схем не только очень простое и быстрое, но и весьма увлекательное занятие.

Источник

Каждый человек на протяжении своей жизни решает множество задач разной сложности. Но даже самые простые из задач выполняются последовательно, то есть за несколько шагов. Эту последовательность можно назвать алгоритмом. Последовательности бывают разные, но начинать их изучение лучше всего с линейных.

Algo_970x90-20219-0c5b45.png

Прежде чем приступить к рассмотрению основной темы статьи, следует сделать краткое отступление и сказать несколько слов про алгоритмический язык.

Алгоритмический язык

Представьте, что человеку, работающему за компьютером, поставлена некая вычислительная задача. В языке программирования решение этой задачи выполняется с помощью алгоритмизации. Решение предполагает:
— разбиение на этапы;
— разработку алгоритма;
— составление программы решения на алгоритмическом языке;
— ввод данных;
— отладку программы (возможны ошибки — их надо исправить);
— выполнение на ПК;
— анализ результатов.

Алгоритмический язык является средством описания алгоритмов, а уже алгоритм, в свою очередь, представляет собой чёткое описание определённой последовательности действий, направленных на решение необходимой задачи.

Свойства алгоритма

Их несколько:
— конечность. Любой алгоритм должен быть завершённым, а окончание наступает после выполнения определённого числа шагов;
— однозначность, понятность. Не допускается разных толкований, неопределённости и двусмысленности — всё должно быть чётко и ясно, а также понятно исполнителю — и правила выполнения действий линейного алгоритма, и сами действия;
— результативность. Итог работы — результат, полученный за конечное число шагов;
— универсальность, массовость. Качественный алгоритм способен решать не одну задачу, а целый класс задач, имеющих схожую постановку/структуру.

Линейная структура

Любой алгоритм составляется из ряда базовых структур. Простейшей базовой структурой является следование — структура с линейными характеристиками. Из этого можно сформулировать определение.

Линейный алгоритм — это алгоритм, образуемый командами, которые выполняются однократно и именно в той последовательности, в которой записаны. Линейная структура, по сути, проста. Записать её можно как в текстовой, так и в графической форме.

Представим, что у нас стоит задача пропылесосить ковёр в комнате. В текстовой форме алгоритм будет следующим:
— принести пылесос к месту уборки;
— включить;
— пропылесосить;
— выключить;
— унести пылесос.

И каждый раз, когда нам надо будет пылесосить, мы будем выполнять один и тот же алгоритм.

Теперь поговорим про графическую форму представления.

Algo_970x90-20219-0c5b45.png

Блок-схема

Для изображения алгоритма графически используют блок-схемы. Они представляют собой геометрические фигуры (блоки), соединённые стрелками. Стрелки показывают связь между этапами и последовательность их выполнения. Каждый блок сопровождается надписью.

Рассмотрим фигуры, которые используются при визуализации типичной линейной последовательности.

Блок начала-конца:

Screenshot_1-1801-a35d16.png

Блок ввода-вывода данных (отображает список вводимых и выводимых переменных):

Screenshot_2-1801-52cab0.png

Арифметический блок (отображает арифметическую операцию/группу операций):

Screenshot_3-1801-df500e.png

Условный блок (позволяет описать условие). Алгоритмы с таким блоком используются при графической визуализации алгоритмов с ветвлением:

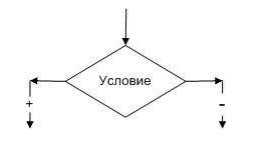
Screenshot_4-1801-3103cc.png

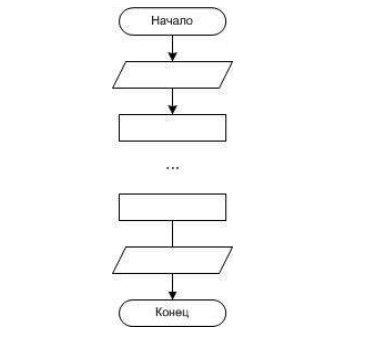
Условного блока нет в классическом линейном алгоритме, так как в нём, как уже было сказано ранее, все операции выполняются последовательно, то есть одна за другой. В линейном алгоритме размещение блоков выглядит следующим образом:

Screenshot_5-1801-f1511b.png

А вот, как решается задача по нахождению площади треугольника по формуле Герона. Здесь a, b, c – это длины сторон, S – площадь треугольника, P – периметр.

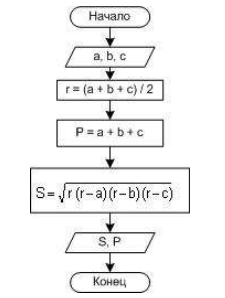
Screenshot_6-1801-c010e2.png

Следует обратить внимание, что запись «=» — это не математическое равенство, а операция присваивания. В результате этой операции переменная, стоящая слева от оператора, получает значение, которое указано справа. Значение не обязательно должно быть сразу определено (a = 3) — оно может вычисляться посредством выражения (a = b + z), где b = 1, a z = 2.

Примеры линейных алгоритмов

Если рассмотреть примеры решения на языке Pascal (именно этот язык до сих пор используется для изучения основ алгоритмизации и программирования), то можно увидеть следующую картину:

Screenshot_7-1801-f9ba66.png

И, соответственно, блок-схема программы линейной структуры будет выглядеть следующим образом:

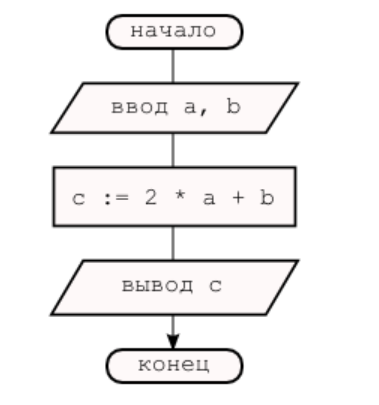
Screenshot_8-1801-8a0c1b.png

Как составить программу линейной структуры?

Порядок следующий:
— определите, что именно относится к исходным данными, а также каков типы/класс этих данных, выберите имена переменных;
— определите, каков тип данных будет у искомого результата, выберите название переменных (переменной);
— определите, какие математические формулы связывают результат и исходные данные;
— если требуется наличие промежуточных данных, определите класс/типы этих данных и выберите имена;
— опишите все используемые переменные;
— запишите окончательный алгоритм. Он должен включать в себя ввод данных, вычисления, вывод результатов.

На этом всё, в следующий раз рассмотрим на примерах программу разветвлённой структуры. Если же вас интересует тема алгоритмизации в контексте разработки программного обеспечения, ждём вас на профессиональном курсе OTUS!

Algo_970x550-20219-265dfd.png

Источники:
• https://inep.sfedu.ru/wp-content/uploads/2018/05/25/lection_27.pdf;
• https://www.sites.google.com/site/415ict/textbooks/prog-9/02-linejnyj-algoritm.

Источник

Добавить комментарий