Как составить номограмму

Старинное искусство номографии

Впервые увидел этот странный график в лаборатории университета. Невзрачный листок, ксерокопированный из старой книги, был наклеен на стену рядом с роторным испарителем. Листок, очевидно, использовали часто, но берегли, словно в нём содержалось какое-то древнее могучее заклинание… Впоследствии, схожего рода графики попадались мне и в других лабораториях, словно составляли неотъемлемую часть перегонки с вакуумом. Затем похожие рисунки встречались на страницах разной технической литературы. Их называли номограммы. Научиться ими пользоваться оказалось до смешного просто, но кто и как их в своё время сделал — оставалось загадкой.

Как выглядят номограммы и как они работают

Номограмма, что часто используется при перегонке с вакуумом приведена на рисунке ниже.

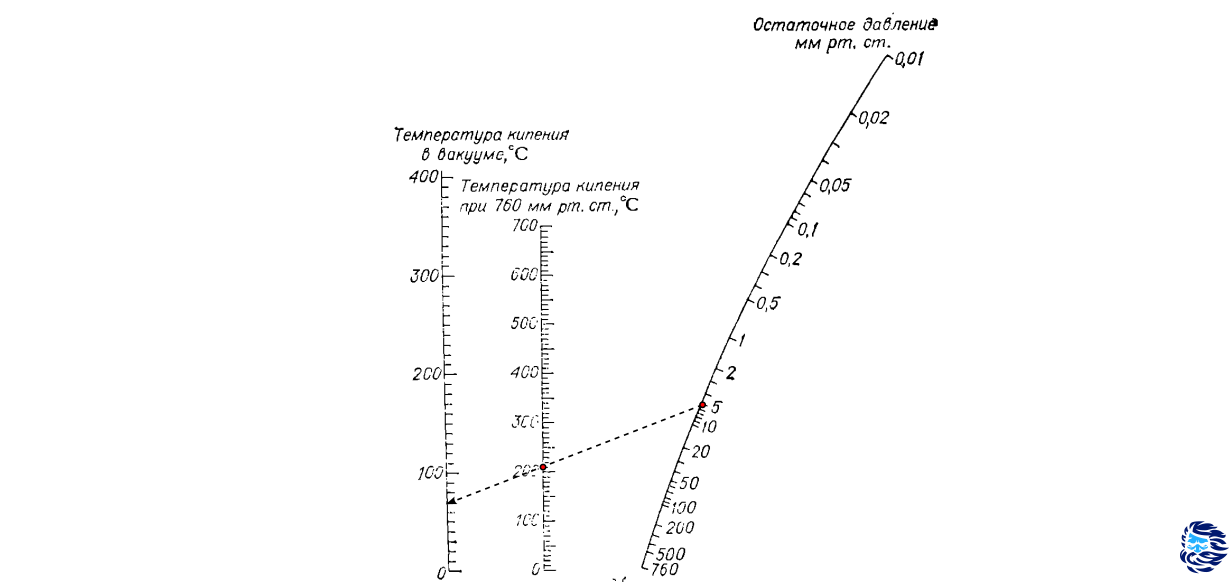
Допустим, вы провели реакцию в растворителе, а теперь собираетесь его удалить (выпарить), чтобы собрать продукт реакции. Растворитель улетучивается изнурительно медленно, а чтобы ускорить процесс, вы решаете его нагреть, но вот беда — греть раствор нежелательно, так как продукт реакции от нагревания может испортиться. Создав пониженное давление, вы уменьшите температуру кипения растворителя и сумеете его отделить не причинив вреда растворенному в нем веществу. При нормальном атмосферном давлении 760 мм ртутного столба вода кипит при 100 С, однако, при давлении 40 мм кипит уже при 34 С.

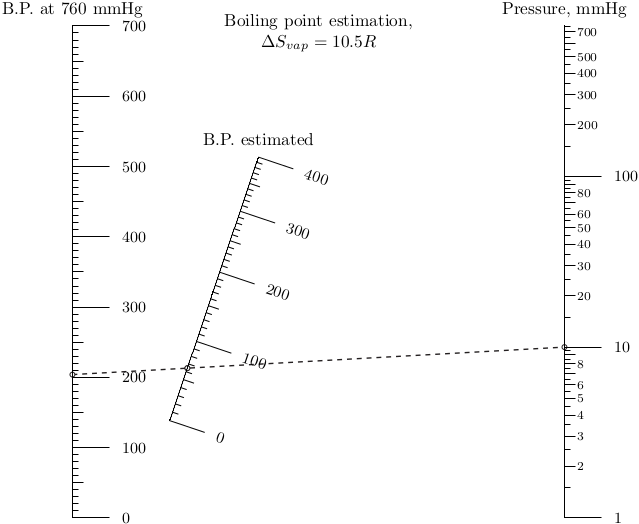
А как быть с гамма-бутиролактоном, который кипит при 204 С? Отмечаем на оси “Температура кипения при 760 мм” точку 204 С, выставляем на кривой оси “Остаточное давление” 5 мм, проводим прямую до пересечения с третьей осью. Ага, значит, в этих условиях наш растворитель начнет выкипать примерно при 70 С.

Это был пример достаточно простой номограммы. Ниже я привожу более сложную. Достоинство номограмм в том, что в них умещаются довольно сложные функциональные зависимости с несколькими переменными. В самом деле, сколько бы понадобилось обычных графиков вида для такой задачи?

Второй момент — эмпирические формулы бывают сложны для запоминания и неудобны. Вдруг неохота доставать смартфон, искать соответствующую программу, или же вообще тащить с собой компьютер. А так — вот в заводском помещении висит психрометр для замера влажности воздуха, вот номограмма — по ней легко прикинуть влажность.

Разбираемся и делаем свои номограммы

Основания общей теории номографических построений дал Морис Окань (1884—1891) — в его же работах впервые появился термин «номограмма». Книга Traité de nomographie. Théorie des abaques. Applications pratiques доступна онлайн. Это истоки. Более краткое современное изложение принципов номографии, по которому я учился делать номограммы читайте здесь — The Lost Art of Nomography by Ron Doerfler.

Итак, начнём!

Чтобы сделать номограмму определения температуры кипения при разных давлениях нам понадобится правило Трутона: молярная энтропия испарения разных веществ при нормальной температуре кипения является постоянной величиной. Затем, уравнение Клапейрона — Клаузиуса:

где — энтальпия испарения, — газовая постоянная.

Интегрируя последнее уравнение мы получаем:

где под мы обозначим давление 760 мм ртутного столба, а — температуру кипения при этом давлении. Нас интересует температура кипения при пониженном давлении .

Правило Трутона запишем так:

Подставив последнее выражение, получим расчётную формулу:

Её и следует привести в номограмму.

Построение номограмм с pynomo

Следующий шаг — устанавливаем питон-библиотеку pynomo. Тривиально:

pip install pynomo

Библиотека умеет строить различные номограммы из десяти стандартных блоков.

Нам понадобится стандартный блок номер 2 кодирующий зависимости вида:

где — какая-то одномерная функциональная зависимость. Разберём простой пример.

Пусть у нас есть лабораторная центрифуга, для которой мы хотим привести номограмму соответствия числа оборотов ротора в минуту (RPM) с достигаемым центробежным ускорением. Формула следующая:

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
"""
    rpm.py

    Simple nomogram of type 2: F1=F2*F3
"""
import sys
sys.path.insert(0, "..")
from pynomo.nomographer import *

N_params_RCF={
        'u_min':1000.0,
        'u_max':30000.0,
        'function':lambda u:u,
        'title':r'RCF, $times g$',
        'tick_levels':3,
        'tick_text_levels':1,
        'tick_side': 'left',
        'scale_type':'linear smart',
        'text_format': r"$%2.0f$",
                }

N_params_r = {'u_min': 1.0,
              'u_max': 5.0,
              'function': lambda u:u,
              'tick_levels': 3,
              'tick_text_levels': 1,
              'tick_side': 'left',
              'text_format': r"$%2.0f$",
              'title':r'R, cm',
              'extra_params': [
                {'u_min':  5.0,
                 'u_max': 10.0,                 
                 'tick_levels': 2,
                 'tick_text_levels': 1,
                 'tick_side': 'right',
                 'text_format': r"$%2.0f$",},
                {'u_min': 10.0,
                 'u_max': 40.0,
                 'scale_type': 'manual line',
                 'manual_axis_data': {10.0: r'10',
                                      12.0: r'12',
                                      14.0: r'14',
                                      16.0: r'16',
                                      20.0: r'20',
                                      24.0: r'24',
                                      30.0: r'30',
                                      40.0: r'40'},
                 },
                ],
            }

N_params_RPM={
        'u_min': 1000.0,
        'u_max':20000.0,
        'function':lambda u:u*u*1.1182e-5,
        'title':r'RPM',
        'tick_levels':3,
        'tick_text_levels':1,
        'scale_type':'linear smart',
        'text_format': r"$%2.0f$",
                }

block_1_params={
             'block_type':'type_2',
             'mirror_y':True,
             'width':10.0,
             'height':10.0,
             'f1_params':N_params_RCF,
             'f2_params':N_params_r,
             'f3_params':N_params_RPM,
             'isopleth_values':[['x',10.0,15200]],
             }

main_params={
              'filename':'RPM.pdf',
              'paper_height':10.0,
              'paper_width':10.0,
              'block_params':[block_1_params],
              'transformations':[('rotate',0.01),('scale paper',)],
              'title_str':r'$a=rtimes omega^2$'
              }
Nomographer(main_params)

Функция записывается строкой:

'function':lambda u:u*u*1.1182e-5,

Программа построит номограмму в файл RPM.pdf, ниже на рисунке.

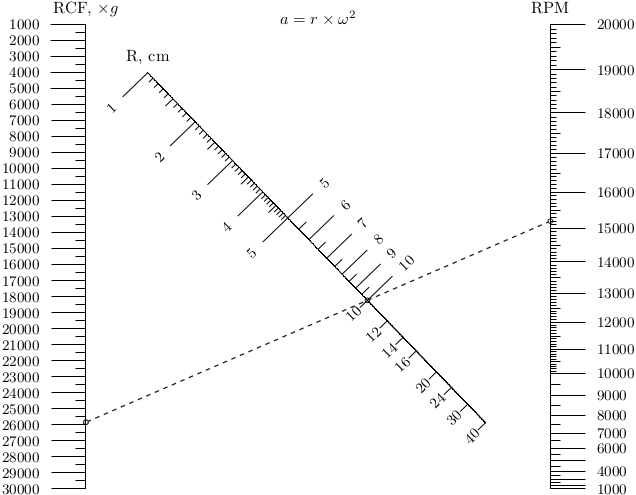
Пунктирная линия называется изоплета — она показывает, как пользоваться номограммой для расчёта достигаемого ускорения (в единицах g) при данной геометрии ротора (радиус вращения) и числа оборотов в минуту (RPM).

Почему этот график так работает? Смотрите чертеж.

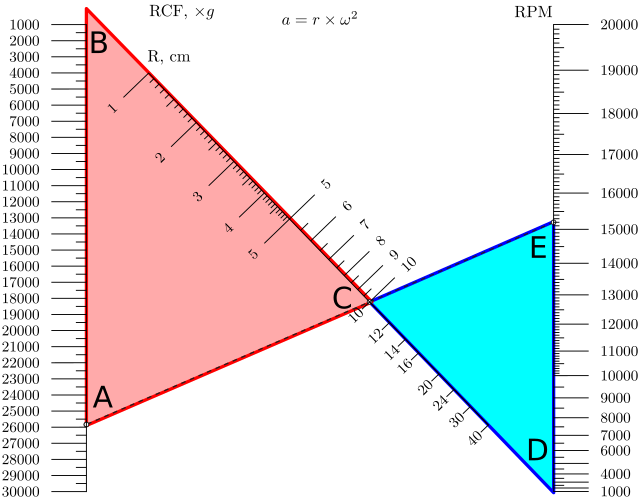
Из него видно, что треугольники ABC и CDE — подобны. Следовательно:

где L — длина BD, она задана. Пользуясь этим соотношением, можно построить шкалу на L.

Зная этот принцип, мы можем построить номограмму для соотношения

что даст нам номограмму для роторного вакуумного испарителя:

Усложняем номограмму

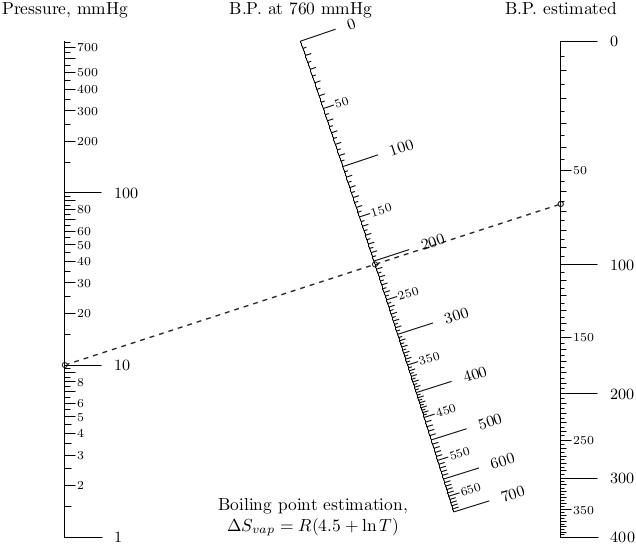
Теперь, разобравшись с простым примером, перейдем к более сложной зависимости. Воспользуемся уточненным правилом Trouton–Hildebrand–Everett:

В статье Some calculations for organic chemists: boiling point variation, Boltzmann factors and the Eyring equation. Tetrahedron Letters 41 (2000) 9879–9882 говорится, что для неё не так то просто создать номограмму. Вот и выясним!

Запишем новую зависимость для номограммы:

Она попадает под случай блока типа 10

Теперь ось в середине номограммы может быть не только прямолинейной. Записываем код.

from math import log
from pynomo.nomographer import *
import sys
sys.path.insert(0, "..")

Pressure = {
    'u_min':  1.0,
    'u_max': 760.0,
    'function': lambda u: log(u / 760.0),
    'title_y_shift': 0.55,
    'title': r'Pressure, mmHg',
    'tick_levels': 3,
    'tick_text_levels': 2,
    'scale_type': 'log smart',
}

BP_guess = {
    'u_min':  0.0,
    'u_max': 400.0,
    'function': lambda u: 1/(u + 273.15),
    'title_y_shift': 0.55,
    'title': r'B.P. estimated',
    'tick_levels': 4,
    'tick_text_levels': 2,
    'scale_type': 'linear smart',
}

BP_at_atm = {
    'u_min':  0.0,
    'u_max': 700.0,
    'function_3': lambda u: (u + 273.15)*(4.5 + log(u + 273.15)),
    'function_4': lambda u: -(4.5 + log(u + 273.15)),
    'title_y_shift': 0.55,
    'title': r'B.P. at 760 mmHg',
    'tick_levels': 4,
    'tick_text_levels': 2,
    'scale_type': 'linear smart',
}

block_1_params = {
    'block_type': 'type_10',
    'width': 10.0,
    'height': 10.0,
    'f1_params': Pressure,
    'f2_params': BP_guess,
    'f3_params': BP_at_atm,
    'isopleth_values': [[10, 'x', 204]]
}

main_params = {
    'filename': 'ex_type10_nomo_1.pdf',
    'paper_height': 10.0,
    'paper_width': 10.0,
    'block_params': [block_1_params],
    'transformations': [('rotate', 0.01), ('scale paper',)],
    'title_y': 0.55,
    'title_str': r'Boiling point estimation, $Delta S_{vap} = R(4.5 + ln T)$'
}

Nomographer(main_params)

Вуаля!

Заключение

Номограммы, как и работающие по схожему принципу логарифмические линейки и другие аналоговые устройства остались в далеком прошлом. Однако, не стоит о них совсем забывать — возможно, вы найдете им новые применения. Или, по крайней мере, найдете их интересным математическим развлечением. Пишите в комментариях о своем опыте.

Облачные серверы от Маклауд быстрые и безопасные.

Зарегистрируйтесь по ссылке выше или кликнув на баннер и получите 10% скидку на первый месяц аренды сервера любой конфигурации!

Всем привет, сегодня дед Иван расскажет вам от том, как построить номограмму по заданному уравнению (функция может быть в неявном виде, но всё-таки должна соответствовать некоторым требованиям, рассмотренным в этой статье) с использованием компьютерных программ (для построения графиков на плоскости я использую Graph). Поехали!

Вступление

Итак, что такое номограмма? Как говорит википедия, это графическое представление функции от нескольких переменных, позволяющее с помощью простых геометрических операций (например, прикладывания линейки) исследовать функциональные зависимости без вычислений. То есть, для заданных значений переменных можно найти значение функции без расчётов. Где это может пригодиться? Например, при определении значения функции, когда рассчитывать на калькуляторе это значение либо долго, либо невозможно (привет, интегралы👋). Ну или же просто для удобства: одно дело носить с собой калькулятор, а другое – сложенный несколько раз лист А4. Переходим непосредственно к изучению алгоритмов построения.

Случай 1: y=f(a, x)

Для построения номограммы сначала нужно выбрать диапазон возможных значений переменной x и параметра a (буквы могут быть разные, а параметром лучше сделать переменную, у которой меньше диапазон, либо требования к точности ниже). Затем приравнять параметр к какому-либо значению, после этого построить график функции y=f(a1, x) в заданном диапазоне x. Потом выбрать другое значение a и снова построить график. Когда параметр выйдет за границы выбранного диапазона, закончить работу. Думаю, здесь ничего сложного нет. Пример построения номограммы представлен на изображении. Хочу заметить, что начало координат можно сместить таким образом, чтобы график для заданных диапазонов переменных был только в одной четверти.

Случай 2: f(a, x, y)=0

Здесь мы имеем дело с функцией, заданной в неявном виде. Что делать? Все действия такие же, как в предыдущем случае, только для построения функции мы нажимаем кнопку x<y на верхней панели (Замечание: как в этом, так и в следующем методе значений функции может быть несколько, так как она в неявном виде).

Однако, есть ещё один метод построения. Он также используется, когда параметров несколько. Суть: можно попробовать привести функцию к виду (здесь мы рассматриваем наш случай неявной функции с одним параметром)

Для построения номограммы нам понадобится первая и вторая четверть координатной плоскости, при этом ось OX в одной четверти обозначает сами значения х, а в другой четверти – значения y (формирование значений y на оси мы выбираем сами, для этого задаём функцию y = f(x), и подставляем её туда, где есть y). Ось OY обозначает значение p. То есть мы строим график зависимости p и от x, и от y. Непонятно? Пример:

Итак, нужно построить номограмму определения значения y в диапазоне a = 1..3; x = -1.5..0.5.

Пусть p = y*ln(y), тогда приходим к системе

Попробуем построить графики

Как вам эта номограмма? По-моему, ужас. Что нужно поменять? Во-первых, пусть ось OY (вместо y написано p) пересекает ось ОХ в точке -1.5. Во-вторых, нужно изменить функцию значений y от х (потому что, например, при x = 0.5 и а = 1 найти y будет не очень удобно). Результат:

Здесь мы приняли, что y = -x-1. Теперь для любого значения x и a мы сможем определить значение y. Для примера, найдём значение y при a = 1, x = 0. Получили примерно 1.75.

Есть ещё одна фишка. В рассмотренном примере мы ввели параметр p. Но ведь могли ввести 2*p, p/2+10, p+4 и т.д. То есть графики можно масштабировать и смещать относительно оси OY (оси значений p).

Случай 3: f(a, b, x, y)=0

Чтобы построить номограмму для этого случая, уравнение нужно привести к виду h(параметр1, y) = g(параметр2, x) и приравнять обе части к p. В одной четверти будет график функции h, в другой – функции g. То есть что-то вроде этого:

Но что делать, если к такому виду уравнение f(a, b, x, y)=0 привести нельзя? Хм, тут многое зависит от самой функции и требованиям к номограмме. Можно x взять в качестве параметра, можно сделать несколько номограмм, каждая из которых составлена для определённого значения одного из параметров, можно попробовать использовать разложение в ряд.

Случай 4: f(a1, a2, …, aN, x, y) = 0

Итак, чтобы построить номограмму для этого случая, необходимо создать цепочку функций, которые, имея в качестве входных данных параметр, а также аргумент или предыдущую функцию в цепочке, приведут нас к значению y. Должно получиться так:

1. f1(параметр1, x, p1) = 0
2. f2(параметр2, p1, p2) = 0
3. f2(параметр3, p2, p3) = 0

K. fK(параметрK, pK-1, pK) = 0

N. fN(параметрN, pN-1, y) = 0

В первой строке задана функция p1 в неявном виде (как я раньше говорил, Graph сможет её построить, поэтому функция не обязана иметь явный вид). Во второй – функция p2 в неявном виде и т.д. Непонятно? Вот вам пример для трёх параметров:

Так как мы делим, x не равен 0, но 0 не входит в заданный отрезок, поэтому рассматривать случай x=0 не нужно. Дальше просто измените точку пересечения оси ОХ с осью OY, постройте графики, выполните масштабирование (осторожно, следите за ОДЗ) и градуировку оси значений y. Тяжело? Согласен, посмотрите сначала, как сделал это я:

Взгляните на уравнения графиков. Заметили p1, p2, p3? Эти функции я ввёл в программу для наглядности и для упрощения работы. Вот они сами:

Теперь вопрос: как выполнить градуировку значений y? Всё просто: подставьте значение по оси OY в крайнюю функцию (p3). Получившееся число и будет новым значением y. Почему пропустили другие функции? Предлагаю вам подумать самим и написать ответ в комментариях. Можете там же и написать, что делать в случае, когда параметров больше 4. Чтобы вы до конца смогли разобраться в теме, прикрепляю ссылку на крайнюю номограмму, открыть файл вы сможете программой Graph: Номограмма_3_параметра. Остались вопросы? Есть дополнения? Пишите, не стесняйтесь, но лучше ставьте лайки и подписывайтесь! Всем пока!

На форумах по Excel встречаются вопросы по построению различных номограмм.Но поиск ответов на данную тему оказался плачевным.Решил поделиться своими наработками.

Имеется изображение номограммы

Шаг 1. Составляем данные для построения горизонтальной оси номограммы.
(А2:В182)

Шаг 2. По данным (А2:В182) строим точечный график.

Шаг 3. Форматируем ось Y ( от 0 до 70)
Устанавливаем обратный порядок значений

Шаг 4. Форматируем ось Х ( от 1 до 10)
Логарифмическая шкала
Форматируем ряд “Горизонтальная ось”

Шаг 5.Добавляем подписи данных ряда “Горизонтальная ось”
Убираем Легенду.
Вставляем рисунок из файла в фон области построения.
Подгоняем размеры рисунка.
Убираем основную горизонтальную ось графика.

Шаг 6. Форматируем надписи ряда “Горизонтальная ось”

Шаг 7. Преобразуем ссылки ряда на диапазон ячеек в массив.
Выделить ряд диаграммы “Горизонтальная ось”.
В строке формул щелкнуть левой кнопкой мыши.
Нажмите <F9> и Enter.При этом ссылки на диапазон преобразуются
в массивы.

Шаг 8. В простейшем случае добавляем маркер и полосы прокрутки для
его управления

В файле” Номограмма 2″ оригинальное изображение номограммы заменено его копией,все кривые номограммы оцифрованы.
В ячейках D22:K22 расположены формулы кривых на номограмме.
В ячейке М21 производится выбор фильтра,а в ячейке М22 выводится рассчитанная по формулам величина A(db).

На листе2 приведен пример управления маркера мышью.
Для запуска макроса нажмите на кнопку.
Для остановки макроса дважды щелкните на ячейке.

Формулы,
используемые для расчета режима резания,
могут быть выражены графически, в виде
номограмм, что в ряде случаев значительно
упрощает расчет. Номограммы строятся
отдельно для каждой зависимости или в
форме комбинированных графиков. Весьма
удобно пользоваться комбинированным
графиком, где даются зависимости V = f
(n, D) и t0
= f (n, S), построение которых и требуется
выполнить.

5.1
Построение номограммы зависимости V =
f (D, n)

Зависимость
V = f (D, n) выражается формулой

V
= π·D·n·10^-3
м/мин

Номограмма
строится в логарифмических координатах.
По оси ординат откладывается скорость
резания lg V , по оси абсцисс – диаметр
детали lg D. Приняв π·n/1000 = С, получим V =
C·D. После логарифмирования получим:

lg
V = lg C + 1·lg D. При различных значениях n
получим, таким образом, ряд прямых линий,
наклоненных к оси абсцисс под углом 
= 45⁰.
Для удобства расчетов примем D = 100 мм,
тогда формула примет вид: V=π·n·10^-1м/мин.

Подставляя
в формулу различные значения чисел
оборотов (по станку), получим соответствующие
им значения V, сведенные в таблицу ниже.

Отложив
на оси абсцисс D = 100 мм, проведем
вертикальную линию, на которой отметим
точки, соответствующие значениям
найденных скоростей. Через эти точки
проведем линии под углом 
= 45⁰
к оси абсцисс.

Таким
образом, получим номограмму, представленную
в приложение В, для определения скорости
резания в зависимости от диаметра детали
и числа оборотов шпинделя станка: V = f
(D, n).

Таблица
5

5.2
Построение номограммы зависимости t₀
= f (S, n)

Зависимость
основного времени t₀
от n и S выражается формулой

t₀
= L_Р/n·S
мин,

где,
L_Р
– длина рабочего хода инструмента,
определяется по формуле

L_Р
= l₁
+ l + l₂,

где,
l – длина обработки, мм;

l₁
– врезание резца, мм;

l₂
– перебег резца, мм.

L_р
= 142 мм.

Номограмму
строят в логарифмических координатах.
По оси ординат откладывают основное
время lg t₀,
по оси абсцисс – подачу lg S.

Приняв
L/n = С, подставим в формулу

t₀
= С/S или t₀ =
C·S^-1.

Прологарифмируем
эту зависимость: lg t₀
= lg C – 1·lg S.

Это
уравнение прямой линии, проведенной
под углом 
= 45⁰
к оси абсцисс.

Для
различных значений n имеем ряд прямых
линий. При построении номограммы примем
S = 1,0 мм/об, при L_Р
=142 мм, тогда формула примет вид

t₀
= 142/1,0·n мин.

Подставляя
в формулу различные значения чисел
оборотов (по станку), получим соответствующие
им значения t₀,
сведенные в таблицу, приведенную ниже.

Таблица
6

Отложив
на оси абсцисс S = 1,0 мм/об, проведем
вертикальную линию и на ней отложим
точки, соответствующие значениям
найденного основного времени. Через
эти точки проведем линии под углом 45⁰
к оси абсцисс.

Таким
образом, получим номограмму, представленную
в приложение Г, для определения основного
времени в зависимости от подачи и числа
оборотов шпинделя станка: t₀
= f (n, S)

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #