Как составить обратное утверждение

Теория и практика методики обучения математике
показывают, что учащемуся недостаточно знать
лишь предметное содержание математического
факта для его полноценно усвоения. Требуется ещё
видеть и понимать способы организации этого
содержания, заложенные в логической структуре
изучаемого. Исходя из этого в математическом
факте, входящем в состав образовательной области
”математика”, целесообразно выделить
предметную и логическую составляющие.
Содержание предметной составляющей достаточно
долго являлось объектом пристального внимания
исследователей в области методики обучения
математике. Содержание же логической
составляющей в явном виде практически не
выделено. Математическое предложение является
одним из основных способов представления
предметной составляющей. Понимание особенностей
построения математического предложения даёт
возможность более осознанно усвоить заложенную
в нём информацию.

Важнейшая характеристика математического
предложения – его истинное значение (исключение,
как известно, составляют определения). С этой
точки зрения предложения делятся на два вида:
высказывание, обязательно истинное или ложное, и
высказывательная форма, истинность которой
зависит от значения переменных, взятых из
некоторого множества. Высказывания и
высказывательная формы проявляются в
математическом содержании в различных
вариантах. Это могут быть предложения
естественного языка или символические
конструкции – например числовые равенства и
неравенства: уравнение и неравенства с
переменными.

Математические предложения различаются и по
роли в предметном содержании. Рассматриваются в
основном три их вида: определения, аксиомы и
теоремы. Предложения различных видов могут иметь
сходную структуру. Разница – в подходе к их
истинности: определения не имеют истинного
значения; истинность аксиом принимается без
доказательств, истинность теорем доказывается.

Общие и частные предложения – одна из
важнейших и самых богатых по содержанию
компонент логической составляющей. Основной
дидактический потенциал этой логической
компоненты заключается в обосновании способов
доказательства и опровержения утверждений
общего и частного характера: правомерность
использования примеров (контрпримеров) для
аргументации, необходимость проведения
рассуждений в общем виде.

Глава 1. Обратные предложения и их роль в
математическом образовании.

1.1. Метод взаимно обратных задач.

Задачи обучения математике в средней школе
разнообразны. Закономерно встаёт вопрос: какими
должны быть методические пути и приёмы обучения,
какое предметное содержание нужно отбирать для
уроков, чтобы оптимально подойти к достижению
поставленных целей? Одним из таких путей
является использование метода взаимно обратных
задач. Под этим методом следует понимать
применение комплекса заданий: составление к
данной теореме обратного утверждения (или всех
возможных обратных утверждений) и проверку его
истинности; использования утверждения данной
теоремы при доказательстве обратной; выполнение
некоторого действия взаимно обратными
способами; параллельное выделение свойств
понятий и их признаков и т.д.

Одним из важных следствий применения
указанного метода является активизация
учебно-познавательной деятельности учащихся,
которым предоставляется возможность
самостоятельно формулировать теоремы,
составлять задачи, находить их решения,
исследовать нестандартные ситуации.
Использование метода взаимно обратных задач
позволяет интенсифицировать деятельность
учащихся, в то время как в практике обучения
часто используется экстенсивный путь: стараются
решать как можно больше задач, не вдаваясь в
глубокое исследование каждой из них. Между тем
опыт свидетельствует о том, что целесообразнее
вместо двух разных задач решить две взаимно
обратных задачи, вместо двух разных теорем
доказать две взаимно обратных теоремы, что
обогатит мыслительную деятельность учащихся
новыми приемами, способами действий. Получается
и выигрыш во времени: ученики работают с одними и
теми же отношениями и объектами условия и
заключения: чертёж тоже может быть один и тот же.
Приёмы, составляющие метод взаимно обратных
задач, позволяют осуществлять индивидуализацию
обучения, дифференцированный подход к ученикам.
Деятельность учащихся приобретает творческий
характер: приходится самостоятельно выдвигать
гипотезы и проверять их на правдоподобность;
опровергать неверные утверждения, приводить
контрпримеры. При этом знания становятся глубже
и прочнее. Развивается логическое мышление.

Содержание школьного курса математики
позволяет в полной мере использовать метод
взаимно обратных задач. Так, в геометрии вводится
понятие обратной теоремы. Кроме того, в учебнике
имеются задания сформулировать и доказать
теоремы, обратные утверждениям некоторых задач.
Всё это говорит о том, что в обучении геометрии
методу взаимно обратных задач должно уделяться
достаточное внимание.

1.2. Логическая структура сложного
предложения.

Логическая структура сложного предложения
является одной из важнейших компонент
логической составляющей математического
материала. Наиболее распространены в
математических текстах такие формы связи, как
конъюнктивная (“и”), дизъюнктивная (“или”),
импликативная (“если,…, то:”), а так же
отрицание. Понимание этого обстоятельства,
знание основных форм логической организации
текста могут существенно облегчить обучаемым
сознательное усвоение содержания данного
текста. В качестве примера можно привести
решение традиционной проблемы выбора между
пересечением и объединением промежутков при
решении системы либо совокупности уравнений или
неравенств. Трудности выбора практически
исчезают, если актуализировать логический смысл
союзов “и” и “или”. Союз “и” означает
конъюнкцию, которой является система уравнений
или неравенств, а союз ”или” символизирует
их дизъюнкцию (совокупность).

Логическая структура предложения часто бывает
скрыта. Для того чтобы её выделить, следует
переформулировать предложение. Примером может
служить стандартный текст геометрической
теоремы, допустим: в равнобедренном
треугольнике углы при основании равны.

В этом случае переформулировка также приводит
к импликативной структуре: если треугольник
равнобедренный, то в нём углы при основании
равны.

В результате становится лучше видно, что дано и
что требуется доказать, на какие исходные
утверждения опирается вывод.

Появляется также возможность осознанно
различать взаимно обратные утверждения.

Структура теоремы. Обратные предложения.

В математике каждое утверждение,
справедливость которого устанавливается путём
рассуждений, называется теоремой (от греческого
слова theorema – рассматриваю, обдумываю). Во всякой
теореме можно выделить разъяснительную часть,
условие и заключение. Разъяснительная часть
выделяется путём установления объектов и
отношений, на которых заданы условие и
заключение. Её можно изменять в некоторых
пределах за счёт условия.

Итак, структуру теоремы представляем следующим
образом: PI “если А, то В”, где P означает
разъяснительную часть, А – условие, а В –
заключение теоремы.

Теорему, обратную данной, принято определять
следующим образом. Если данная теорема
сформулирована в виде условного предложения
”если А, то В”, то обратной называется
теорема ”если В, то А”, т.е. такая, у которой
условием является заключение первой теоремы, а
заключением – её же условие.

Глава 2 Построение обратных предложений.

2.1. Получение обратных предложений.

Необходимо формировать у школьников приёмы
выделения условия и заключения теоремы (или
задачи на доказательство), учить их
формулировать встречающиеся утверждения в виде
”если…, то…”. Формирование этого приёма
происходит при решение задач, хотя сам приём
зачастую не осознаётся. Когда же выделение
условия и заключения является необходимым
этапом на пути к получению обратного
предложения, то внимание учащихся фиксируется на
нём целенаправленно. После того, как выделены
условие и заключение теоремы, легко
сформулировать обратное предложение

Пример. В параллелограмме диагонали,
пересекаясь, делятся пополам.

Здесь условие теоремы: р – четырёхугольник –
параллелограмм, диагонали его пересекаются;
заключение теоремы: q – точка пересечения
диагоналей делит каждую из них пополам. Чтобы
легче выделить условие и заключение теоремы её
часто формулируют в виде импликации, применяя
логический союз ”если:, то:”. Если
четырёхугольник – параллелограмм и диагонали
его пересекаются, то в точке пересечения они
делятся пополам. Известно, что, имея некоторую
теорему (p => q), назовём её прямой теоремой, можно
образовать новую теорему и не одну:

обратную: q => p;

противоположную:

обратную противоположной: .

Проиллюстрируем эти виды теорем на примере.

• если четырёхугольник параллелограмм, то
  диагонали его, пересекаясь, делятся пополам (p =>
  q)
• если в четырёхугольнике диагонали, пересекаясь,
  делятся пополам, то этот четырехугольник –
  параллелограмм (q => p)
• если четырёхугольник не параллелограмм, то его
  диагонали, пересекаясь, не делятся пополам ()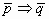
• если в четырёхугольнике диагонали, пересекаясь,
  не делятся пополам, то такай четырёхугольник не
  параллелограмм ().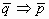

В данной иллюстрации все четыре теоремы истины,
в чём можно легко убедиться, проведя их
доказательство. Однако так бывает не всегда.
Между этими четырьмя видами теорем существует
тесная связь, именно:

а) (p => q) и ()
– одновременно И или Л;

б) (q => p) и ()
– также одновременно истины и ложны.

Каждую из этих эквивалентностей нетрудно
обосновать с помощью таблицы истинности. Так,
например, для второй эквивалентности имеем:

Взаимная связь теорем значительно облегчает
практику их изучения. Вот почему в любом курсе
математики нам встречаются обычно лишь прямая и
обратная теоремы, а остальные теоремы
встречаются редко.

Обратные теоремы могут быть неверными.

Обратные теоремы так же, как и прямые, могут
быть как верны, так и не верны. Поэтому
справедливость обратных теорем (как и прямых)
подлежит доказательству.

Верна или не верна обратная теорема, часто
зависит от того, как мы эту обратную теорему
сформулируем.

Возьмём, например, теорему: “диагонали ромба
взаимно перпендикулярны”. Если обратную теорему
сформулировать так: “четырёхугольник, диагонали
которого взаимно перпендикулярны, есть ромб”, то
эта теорема окажется неверной. Если же
сформулировать её так: “параллелограмм
диагонали, которого взаимно перпендикулярны,
есть ромб”, то она окажется верной.

Итак, обратную теорему мы можем строить двояким
образом: или взять в качестве заключения в
обратной теореме все условия, накладываемые на
объект в прямой теореме, а условием обратной
теоремы сделать только одно заключение прямой,
или взять в качестве заключения обратной теоремы
только часть условий, накладываемых на объект в
прямой теореме, а остальную часть условий прямой
теоремы вместе с её заключением сделать условием
обратной теоремы.

Чтобы у школьников не сложилось представление,
будто все обратные предложения верны, необходимо
подбирать и такие задачи, обратное утверждение к
которым оказывалось бы неверным. Например,
задача.

Докажите, что у равных треугольников АВС и А1 В1
С1 медианы, проведенные из вершин А и А1, равны.

Обратное утверждение: если медианы,
проведённые из вершины А и А1 треугольников АВС и
А1 В1 С1 равны, то эти треугольники равны.

Оно неверно. Контрпример к этому утверждению –
рисунок.

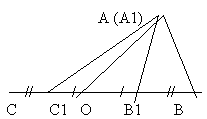
Ученикам нужно давать задания, чтобы выполняя
их, они самостоятельно убеждались в том, что
некоторые обратные предложения неверны.

Условие теорем (задач) может состоять из
нескольких частных условий (все они должны быть
четко выделены, в противном случае поиск
доказательства будет затруднён). Обратными
предложениями для таких теорем также считают те,
которые получаются путём замены одного или
нескольких условий заключением. Иными словами,
если прямая теорема имеет, например, вид “А и В, и
С, то D”, где А В, С и D – некоторые суждения, то
обратными ей являются предложения: “если D, то А и
В и С”, ” если А и D, то В и С”, “если B и D, то А и С”,
“если D и В, и С, то А”, “если А и D, и С, то В” и т.д.

Таким образом, если условие прямой теоремы
сложное, то можно сформулировать несколько
обратных предложений: некоторые из них (или все)
могут оказаться ложными.

Если требуется показать, что предложение “если
А, то В” неверно, достаточно доказать
возможность одновременного выполнения условий А
и не В, это значит – найти объект, для которого
имеет место условие А, но не выполняется В.

Теоремы, имеющие сложное заключение.

Большую дидактическую ценность представляют
теоремы, имеющие сложное заключение из
нескольких суждений, т.е. теоремы вида “если А, то
В1 и В2, и В3,…, Вn”. Обратное предложение будет
иметь такой вид: “если В1 и В2, и В3,…, и Вn, то А”.
Однако может оказаться, что условие в нём
избыточно. Поэтому перед учениками ставится
задача: среди В1, В2, В3,…,Вn найти минимальную
группу таких условий, из наличия которых будет
следовать А. При выполнении задания ученик
должен уметь строить контрпримеры. Без этого его
работа будет малоэффективной. Например, может
оказаться, что выбранная группа условий не
является достаточной для А, поэтому попытки
вывести А из этой группы, как следствие, к успеху
не приведут. Значит, ученик должен построить
контрпример.

Подобные теоремы, по существу, есть не что иное,
как совокупность нескольких теорем с
одинаковыми условиями. Сконструировать такую
теорему можно, предложив ученикам назвать,
например, свойства параллелограмма.

Пусть получим следующее: “Если
четырёхугольник АВСD – параллелограмм (О – точка
пересечения диагоналей), то 1. АВ = CD; 2. ВС = AD; 3. АО
=ОС; 4.BC//AD; 5.LA + LD =180; 6. LA
= LC; 7. треугольник ABC равен треугольнику CDA; 8. LOBC =
LODA”

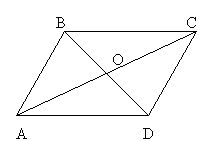
Из приведенных восьми условий ученики выбирают
группу таких, из которых будет следовать, что
четырёхугольник АВСD является параллелограммом.
Попутно они строят контрпримеры к некоторым
группам условий (из 1 – 8).

При доказательстве обратных теорем большую
помощь могут оказать исходные (прямые)
предложения.

Заключение.

Выполняя различные задания, о которых
говорилось выше, школьники приобретают умение
синтезировать условия для получения
необходимого результата, самостоятельно
конструируют новые для себя теоремы, учатся
отделять условие от заключения, не создавать
порочный круг в доказательстве, пользуясь ещё
недоказанным свойством как условием.

Такие задания, как показывает практика,
прекрасно активизируют познавательную
деятельность школьников. Строя контрпример, он
всякий раз должен учиться исследовать
достаточность взятых условий на правдоподобие.
Его деятельность приобретает продуктивный,
творческий характер.

Список литературы.

1. Градштейн И.С. Прямая и обратная теоремы М. Наука
   1972 г.
2. Погорелов А.В. Геометрия 7 – 11. М. Просвещение
3. Атанасян Л.С. Геометрия 7 – 9. М. Просвещение
4. Цукарь А.Я. Метод взаимно обратных задач в
   обучении математике. Н.,”Наука”., 1989 г.
5. ж/л Математика в школе № 2, 2003 г.
6. Оганесян В.А. и др. Методика преподавания
   математики в средней школе. Общая методика
   М.,”Просвещение”, 1980 г.

Муниципальное бюджетное общеобразовательное
учреждение

«Средняя общеобразовательная школа № 17

города Новоалтайска Алтайского края»

Урок геометрии в 7 классе

Тема: Прямая и обратная теорема

(урок обобщения знаний по  теме «Параллельные прямые»)

Учитель: Уварова Светлана Михайловна

г.Новоалтайск

2014г.

Урок геометрии в 7 классе

Учитель: Уварова С.М.(МБОУ «СОШ№17 г.Новоалтайска»)

Тема: Прямая и
обратная теорема

Тип урока: Урок
обобщения знаний по теме «Параллельные прямые»

Цели урока:

·      
Обобщить теоретический
материал I–II глав, способствовать прочному усвоению
учащимися изученного материала, пониманию логического построения геометрии,
развитию навыков применения теории к решению задач

·      
Развивать логическое
мышление учащихся, культуру речи, создавать условия для формирования их
познавательных, коммуникативных компетенций

·      
Воспитывать культуру
общения, любознательность, понимание необходимости и полезности изучения
математики. 

                                  
План урока

1.       
Оргмомент.

Записать число, тему урока

Записать в дневник домашнее задание

2.       
Целеполагание

3.       
Актуализация опорных
знаний (устная работа по готовым чертежам),

Постановка проблемы

4.       
Изучение материала «Прямая
и обратная теорема», фронтальная работа, определение понятий «свойство» и
«признак»

5.       
Практическая работа –
составление теорем, выражающих свойства матем. понятий ( работа в парах) с
последующей проверкой

          (
приложение 1)

6.       
Составление утверждений,
обратных данному. Контрпример.

7.       
Практическая работа в
парах: составление теорем, выражающих признаки матем. понятий (приложение 2)

8.       
Контроль.

– вопросы по теме (фронтально)

– Проверочная работа ( в тетрадях по готовым чертежам на доске)

9.       
Итог урока, рефлексия

Оформление:  

1. Эпиграфы:

«Математику уже затем учить надо, что она ум в порядок приводит»

                                                                         М.В.Ломоносов

«В математике все, что не обосновано до конца, расценивается как
абсолютно необоснованное»

                                                                        
А.Я.Хинчин

2. Стенд «Изучаем на уроке»:

         – Высказывание «Без доказательства истина в науке

           остается гипотезой»

– Толкование понятий  определение, аксиома, теорема, свойство,
признак, доказательство

           3. 
Магнитная или интерактивная доска, таблички с терминами:

                    Теорема,
свойство, признак, условие, заключение,   

                   
доказательство, рассуждение, аксиомы, определения,

                    теоремы

           4.
Демонстрационная таблица «Равнобедренный треугольник»

           5. На столах
у учащихся – раздаточный материал:

                на
карточках – условия и заключения изученных теорем для

               
составления свойств и признаков(прямых и обратных теорем)

           6. На
доске:

               –
Чертежи равнобедренных треугольников для работы с

                
теоремами

               –
Задания по готовым чертежам для самостоятельной работы

                  (
на закрытой доске или в презентации к уроку)

Ход урока

I.                
Оргмомент

     – Приветствие,
запись числа, темы урока

      – Запись
домашнего задания: Вопросы на с. 49, №154б,в, №162

II.  Целеполагание

Учитель: Мы
заканчиваем изучение II главы учебника. Сегодня –

                последний
урок перед контрольной работой.

                Является
ли новой для вас тема урока?

                Что
вы уже знаете по этой теме?

                Какие
ключевые слова можно в связи с этим вспомнить?

                Какие
цели поставим перед собой на урок?

Примерные ответы
учеников:

1)  
Закрепить и повторить весь
теоретический метериал

2)  
Научиться работать с
прямой и обратной теоремой, различать «свойство» и «признак»

Учитель обращает
внимание на эпиграф к уроку:

    «Математику уже затем учить надо, что она ум в порядок приводит»

                                        
                                М.В.Ломоносов

            
Попробуем же и мы, ребята, привести в порядок наши еще пока

          небогатые
знания.

III. Актуализация опорных знаний

1.  
Повторение теоретического
метериала

1) 
Что такое теорема?

2) 
 Что выражает теорема?

3) 
Из каких двух частей
обычно состоит ее формулировка?

4) 
Что такое доказательство?

5) 
На что можно опираться при
доказательстве?

По мере ответов ребят учитель составляет таблицу на магнитной доске или
демонстрирует слайд презентации:

                                                                                  

2.  Решение задач по
готовым чертежам

     – Есть ли на
чертеже равнобедренные треугольники? (Найти и доказать):

  1)                                                    2)

 3)
                                                        4)

                                   Р=19

   В задании №4
возможен ответ учащихся: да, треугольник

   равнобедренный,
так как у него углы при основании равны.

Проблема: Какой теоремой воспользовались?(возможны ошибки

при ответе)

-Если в треугольнике два угла равны, то он равнобедренный.

-Доказана ли нами такая теорема?

-Нет.

IV. Изучение нового материала

      1) Сформулиоуйте свойство равнобедренного
троеугольника со словами  «если, то»

        (Демонстрируется
таблица «Равнобедренный треугольник»)

      –  Если
треугольник равнобедренный, то углы при основании равны.

       -Выделите
условие и заключение этой теоремы.

       -Что такое
«свойство» фигуры?

       – Качество,
отличительная особенность чего-нибудь (из словаря

          Ожегова)
 

       -Что дано в
этой теореме, а что надо доказать? ( Дано, что треугольник равнобедренный, а
надо доказать его свойство, т.е. какой характеристикой еще обладает
равнобедренный треугольник)

       2) Как
составить теорему, обратную данной?

      – Надо
поменять условие и заключение теоремы.

       – Если два
угла треугольника равны, то он равнобедренный

    – Выделите
условие и заключение. Какой треугольник дан?

    – произвольный

    –  Что надо
доказать?

    – Что он
равнобедренный.

     – Как можно
назвать эту теорему?

    –Признак
равнобедренного треугольника.

    -Что такое
признак?

    – Это
показатель, примета, знак, по которым можно определить

        что-нибудь ( из словаря Ожегова)

 Учащиеся
предпринимают попытки доказательства теоремы, но

    безуспешно.

  Учитель: Для
доказательства этой теоремы нам не хватает знаний. Но  теорема верна, и мы убедимся
в этом на последующих уроках. А пока можем ли мы пользоваться этой теоремой?

-Нет

  Учитель

    –  обращает
внимание учащихся на слова А.Я.Хинчина

  «В математике все, что не обосновано до конца, расценивается как
абсолютно необоснованное»

    – А как можно
назвать научное предположение, которое пока не доказано?

 – Гипотеза.

– Значит, мы с вами
стоим на пороге маленького научного открытия.

   А как вообще
совершаются научные открытия?

– Наблюдение –
эксперимент, опыт – предположение (гипотеза) –

   доказательство-
научное положение(теория, теорема, закон и т.п.)

 3) Обратимся еще к
одному свойству равнобедренного треугольника

   – Если
треугольник равнобедренный, то биссектриса, проведенная из вершины, является
медианой и высотой.

( ученик доказывает теорему устно у доски на заготовленном ранее
чертеже равнобедренного треугольника или с помощью слайда презентации)

    – Составьте
обратное утверждение

  – Если
биссектриса треугольника является его медианой и высотой, то этот треугольник
равнобедренный.

 ( ученик доказывает теорему устно у доски на заготовленном ранее
чертеже равнобедренного треугольника или с помощью слайда)

    – Нет ли в
теореме лишнего условия?

    – Достаточно,
чтобы биссектриса являлась высотой, медиану мы в доказательстве не
использовали.

   – Итак, мы
рассмотрели две взаимно обратные теоремы, обе они верны.

      Что выражает
первая из этих теорем?

  – Свойство
равнобедренного треугольника.

 – Что выражает обратная ей теорема?

   – Признак равнобедренного
треугольника.

  – Значит, чем является теорема, обратная
свойству? А теорема, обратная

   признаку?

V. Практическая работа (в парах)

  Задание:

  Используя карточки
с условиями и заключениями теорем, изученных ранее, составить теоремы, выражающие
свойства фигур. ( 5 минут)

– Какие теоремы
получились?

    1) Если углы
смежные, то их сумма 180°.

    2) Если углы
вертикальные, то они равны

  3) Если
треугольники равны, то их соответственные углы и стороны равны

  4) Если
треугольник равнобедренный, то  углы при основании равны.

  5) Если
треугольник равнобедренный, то  биссектриса, проведенная к основанию, является
медианой и высотой.

  6) Если
треугольник равнобедренный, то  медиана, проведенная к основанию, является
биссектрисой и высотой

  7) Если
треугольник равнобедренный, то  высота, проведенная к основанию, является
биссектрисой и медианой

 VI.
Составление утверждений, обратных данному. Контрпример.

   – Составьте
утверждение, обратное свойству вертикальных углов.

    –Если углы
равны, то они вертикальные.

  – Верно ли это
утверждение?

        Ученики сами
пытаются опровергнуть это утверждение с помощью контрпримера:

-Приведите еще примеры неверных обратных утверждений.

                       (
о смежных углах)

  VII.
Практическая работа в парах.

    – Составьте из оставшихся карточек признаки
фигур.

– Первый признак
равенства треугольников

 – Второй признак
равенства треугольников

– Третий признак
равенства треугольников

– Если две прямые
перпендикулярны третьей прямой, то они параллельны.

-Составьте
утверждение, обратное первому признаку равенства треугольников

– Если
треугольники равны, то две стороны и угол между ними одного треугольника
соответственно равны двум сторонам и углу между ними другого треугольника.

– Верно ли это
утверждение? Докажите. Как его можно назвать?

– Свойство равных
треугольников

– Сформулируйте
известное нам более общее свойство равных треугольников.

– В равных
треугольниках соответственные углы и стороны равны.

VIII. Контроль

1. Фронтальный опрос

 – Какова структура теоремы?

 – Как составить
утверждение, обратное данному?

 – Всякая ли теорема
имеет обратную?

 – Как можно доказать
ложность утверждения?

 – Для каких теорем
первой части (свойства) практической работы верны

   обратные
утверждения? Как эти утверждения называются?

Выставляются оценки
активно работавшим ученикам

 2. Проверочная
работа

По готовым чертежам
определить, какая теорема проиллюстрирована и записать ее название в
соответствующую колонку:

Ответы:

           
Свойство:                                      Признак

                                      1
вариант

2) равноб.
треугольника                 1)3 признак равенства треугольников

3) равных
треугольников                4)  равнобедренного треугольника

5) вертикальных углов

                                        2
вариант

1) равноб.
треугольника                  2) 1 признак равенства треугольников

4) смежных
углов                             3) параллельных прямых

                                                           
5) равнобедренного треугольника

3.Самопроверка с
помощью ответов на экране

 IX.
Рефлексия

 – Ребята, на полях
своей тетради нарисуйте смайл, выражающий ваше настроение по результатам урока:

    Улыбка или сомнение или печаль,
затруднение

Приложение 1. Задания для работы в парах( разрезать)

углы
смежные                                              сумма углов равна 180°

углы
вертикальные                                      эти углы равны

две прямые
перпендикулярны                    эти прямые не пересекаются

к третьей прямой

треугольники
равны                                      их соответственные углы и

                                                                            стороны
равны

треугольник
равнобедренный                     углы при основании равны

треугольник
равнобедренный                    биссектриса, проведенная
к                                                                                                       

                                                                            основанию,
является медианой

                                                                      
и высотой

треугольник равнобедренный                     высота,
проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
медианой

треугольник
равнобедренный                    медиана, проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
высотой

две стороны и угол
между ними

одного треугольника
соответ-                           треугольники равны

ственно равны двум
сторонам и

углу между ними
другого треу-

гольника,

сторона и два
прилежащих к ней

угла одного
треугольника соот-                       треугольники равны

ветственно равны двум
сторонам

и углу между ними
другого тре-

угольника,

три стороны одного
треуголь-

ника соответственно
равны                                  треугольники равны

трем сторонам другого
треу-

гольника,

Приложение 2. Задания для работы в парах (разрезать)

углы
смежные,                                              сумма углов равна 180°

углы
вертикальные,                                     эти углы равны

две прямые
перпендикулярны                    эти прямые не пересекаются

к третьей прямой,

треугольники
равны,                                      их соответственные углы и

                                                                            стороны
равны

треугольник
равнобедренный,                     углы при основании равны

треугольник
равнобедренный,                    биссектриса, проведенная
к                                                                                                       

                                                                            основанию,
является медианой

                                                                      
и высотой

треугольник
равнобедренный,                    высота, проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
медианой

треугольник
равнобедренный,                    медиана, проведенная к основа-

                                                                     
нию, является биссектрисой и

                                                                      
высотой

две стороны и угол
между ними

одного треугольника
соответ-                           треугольники равны

ственно равны двум
сторонам и

углу между ними
другого треу-

гольника,

сторона и два прилежащих
к ней

угла одного
треугольника соот-                       треугольники равны

ветственно равны 
стороне

и  двум прилежащим к
ней углам

  другого
треугольника,

три стороны одного
треуголь-

ника соответственно
равны                                  треугольники равны

трем сторонам другого
треу-

гольника, 

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 1 сентября 2022 года; проверки требуют 6 правок.

Обратная теорема или обратное утверждение к данной теореме — это утверждение, в котором условие исходной теоремы (прямого утверждения) поставлено заключением, а заключение — условием.^[1]

Обратной к обратной теореме является исходная (прямая) теорема. Справедливость обоих взаимно обратных теорем означает, что выполнения условий любой из них необходимо и достаточно для справедливости заключения.^[1]

Каждая теорема может быть выражена в форме импликации , в которой посылка является условием теоремы, а следствие является заключением теоремы. Тогда теорема, записанная в виде является обратной к ней^[2].

Часто используется более общее определение обратной теоремы: если является прямой теоремой, то обратной называется не только теорема , но и теоремы , ^[3].

Если условие и/или заключение теоремы являются сложными суждениями, то обратная теорема допускает множество не равносильных друг другу формулировок.
Например, если условием теоремы является , а заключением :
, то для обратной теоремы существует пять форм:^[4]

1. 
2. 
3. 
4. 
5. 

Вообще говоря, обратная теорема может не быть истинной, даже если прямая теорема верна. Так, теорема «вертикальные углы равны» (иначе: «если углы вертикальные, то они равны»), как известно, верна. Но обратное к ней утверждение «если углы равны, то они вертикальные», вообще говоря, неверно.

Даже если обратное утверждение истинно, то его доказательство может быть гораздо сложнее доказательства прямого.
Например, теорема о четырёх вершинах была доказана в 1912 году, а её обратная только в 1998 году.

Свойства[править | править код]

Примеры[править | править код]

• Теорему Пифагора можно сформулировать следующим образом:

Если в треугольнике со сторонами длиной , и угол, противолежащий стороне , прямой, то a²+b²=c².

Обратная к этой теореме появляется в «Началах» Евклида (книга I, предложение 48), может быть сформулирована следующим образом:

Если в треугольнике со сторонами длиной , и выполняется , то угол, противолежащий стороне , прямой.

• Теорема Абеля и теорема Абеля — Таубера
• Теоремы о вершинах подерного треугольника
• Прямая и обратная предельная теорема
• В ином смысле: теоремы Шеннона для источника общего вида

Смотрите также[править | править код]

• Противоположная теорема

Примечания[править | править код]

Литература[править | править код]

• Эдельман С.Л. Математическая логика. — М.: Высшая школа, 1975. — 176 с.
• Гиндикин С.Г. Алгебра логики в задачах. — М.: Наука, 1972. — 288 с.
• Градштейн И.С. Прямая и обратная теоремы. Элементы алгебры логики. — М.: Наука, 1965. — 127 с.

Условные утверждения встречаются повсюду. В математике или где-либо еще нетрудно найти что-то вроде «Если P , то Q ». Условные утверждения действительно важны. Также важны операторы, которые связаны с исходным условным оператором путем изменения положения P , Q и отрицания оператора. Начиная с исходного оператора, мы получаем три новых условных оператора, которые называются обратным, противоположным и обратным.

Отрицание

Прежде чем мы определим обратное, противоположное и обратное условному выражению, нам нужно изучить тему отрицания. Каждое утверждение в логике либо истинно, либо ложно. Отрицание утверждения просто включает в себя вставку слова «не» в нужной части утверждения. Добавление слова «не» сделано для того, чтобы изменить статус истинности утверждения.

Это поможет посмотреть на примере. Утверждение «Прямоугольный треугольник равносторонний» имеет отрицание «Прямоугольный треугольник не является равносторонним». Отрицание «10 – четное число» означает утверждение «10 – не четное число». Конечно, в этом последнем примере мы могли бы использовать определение нечетного числа и вместо этого сказать, что «10 – нечетное число». Отметим, что истинность утверждения противоположна истине отрицания.

Мы рассмотрим эту идею в более абстрактной обстановке. Когда утверждение P истинно, утверждение «not P » ложно. Точно так же, если P ложно, его отрицание «not P » истинно. Отрицания обычно обозначаются тильдой ~. Поэтому вместо записи «not P » мы можем написать ~ P .

Обратное, Контрапозитивное и Обратное

Теперь мы можем определить обратное, противоположное и обратное условному утверждению. Мы начинаем с условного оператора «Если P , то Q.nds

• Обращение условного оператора: «Если Q , то P ».
• Противоположность условного утверждение: «Если не Q , то не P ».
• Обратное условному выражению – «Если не P , а не Q . ”

Мы увидим, как эти утверждения работать с примером. Предположим, мы начинаем с условного оператора «Если прошлой ночью шел дождь, значит, тротуар мокрый».

• Обратное условному выражению – «Если тротуар мокрый, значит, прошлой ночью шел дождь».
• Противоположным условному утверждению является «Если тротуар не мокрый, значит, вчера вечером дождя не было».
• Обратное условному выражению: «Если прошлой ночью не было дождя, значит, тротуар не мокрый.. ”

Логическая эквивалентность

Мы можем задаться вопросом, почему важно формировать эти другие условные операторы из нашего начального один. Внимательный взгляд на приведенный выше пример кое-что показывает. Предположим, что исходное утверждение «Если прошлой ночью шел дождь, значит, тротуар мокрый» верно. Какое из других утверждений также должно быть верным?

• Обратное утверждение: «Если тротуар мокрый, значит, прошлой ночью шел дождь» не обязательно верно. Тротуар может быть мокрым по другим причинам.
• Обратное утверждение: «Если прошлой ночью не было дождя, значит, тротуар не мокрый» не всегда верно. Опять же, то, что не было дождя, не означает, что тротуар не мокрый.
• Противоположное высказывание «Если тротуар не мокрый, значит, вчера вечером не было дождя» – верное утверждение.

То, что мы видим из этого примера (и то, что может быть доказано математически), – это то, что условное утверждение имеет то же значение истинности, что и его контрпозитив. Мы говорим, что эти два утверждения логически эквивалентны. Мы также видим, что условный оператор логически не эквивалентен своему обратному и обратному.

Поскольку условный оператор и его контрпозитив логически эквивалентны, мы можем использовать это в наших интересах, когда мы доказываем математические теоремы. Вместо того, чтобы напрямую доказывать истинность условного утверждения, мы можем использовать стратегию косвенного доказательства, заключающуюся в доказательстве истинности контрпозитива этого утверждения. Противопозитивные доказательства работают, потому что, если контрапозитив верен, из-за логической эквивалентности исходное условное утверждение также верно.

Оказывается, даже если обратное и inverse логически не эквивалентны исходному условному выражению, они логически эквивалентны друг другу. Этому есть простое объяснение. Мы начинаем с условного оператора «Если Q , то P ». Противоположным этому утверждению является «Если не P , то не Q ». Поскольку обратное является противоположностью обратного, обратное и обратное логически эквивалентны.