Математика, 2 класс
Урок № 10. Задачи, обратные данной
Перечень вопросов, рассматриваемых в теме:
- Что такое задачи, обратные данной?
- Как составлять и решать обратные задачи?
Глоссарий по теме:
Задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Основная и дополнительная литература по теме урока (точные библиографические данные с указанием страниц):
1. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1/ М. И. Моро, М. А. Бантова, Г. В. Бельтюкова и др. –8-е изд. – М.: Просвещение, 2017. – с.26, 27
2. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций/ Волкова А.Д.-М.: Просвещение, 2017, с. 16, 17
3. Математика. Рабочая тетрадь. 2 кл. 1 часть: учебное пособие для общеобразовательных организаций/ Волкова С.И.-М.: Просвещение, 2017.-с.31
Теоретический материал для самостоятельного изучения
Решим три задачи.
Составим по рисунку первую задачу.

В классе 10 девочек и 8 мальчиков. Сколько всего детей в классе?
Составим схематический рисунок.

Решим задачу:
10 + 8 = 18 (д.)
Ответ: 18 детей в классе.
Составим вторую задачу.

В классе 18 детей. Девочек 10, остальные-мальчики. Сколько мальчиков в классе?

Решим задачу:
18 – 10 = 8 (м.)
Ответ: 8 мальчиков в классе.
Составим третью задачу.

В классе 18 детей. Мальчиков 8, остальные – девочки. Сколько девочек в классе?

Решим задачу:
18 – 8 = 10 (д.)
Ответ: 10 девочек в классе.
Посмотрим еще раз на схемы к каждой задаче. Обратим внимание на то, что во всех задачах одинаковый сюжет, но то, о чем спрашивается в первой задаче стало известным во второй и третьей задачах, а узнать во второй задаче, сколько мальчиков и в третьей задаче сколько девочек в классе надо то, что известно в первой задаче.
Задачи, в которых известно то, о чем спрашивается в первой задаче и надо узнать то, что в первой задаче известно, называют обратными первой.
Сделаем вывод: задачи, обратные данной – считаются те задачи, в которых говорится об одних и тех же предметах, но известное и неизвестное меняются местами.
Тренировочные задания.
1. Решите задачу. Выберите задачи, обратные данной.
Кате подарили 8 воздушных шариков красного и синего цвета. Красных шариков было 5. Сколько синих шариков у Кати?
Варианты ответов:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
2. У Кати было 8 шариков. 3 шарика она подарила. Сколько шариков осталось у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
Правильные варианты:
1. Кате подарили 5 шариков красного цвета и 3 шарика синего цвета. Сколько шариков у Кати?
3. Кате подарили 8 воздушных шариков красного и синего цвета. Синих шариков было 3. Сколько красных шариков у Кати?
2 . Восстановите пропуски в задачах.
1.В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в ________?
2. В июне ____ дней. Из них 10 дней были пасмурными. Сколько______ дней было в июне?
3. В июне 30 дней. Ясными были ____ дней. Сколько ____ дней было в июне?
Варианты ответов:
30, 20, ясных, пасмурных, июне
Правильный вариант:
1. В июне было 10 пасмурных дней и 20 ясных дней. Сколько дней в июне?
2. В июне 30 дней. Из них 10 дней были пасмурными. Сколько ясных дней было в июне?
3. В июне 30 дней. Ясными были 20 дней. Сколько пасмурных дней было в июне?
Последовательность и продолжительность этапов
- Организационный момент – 2 мин.
- Актуализация опорных знаний – 5 мин.
- Самоопределение к деятельности (постановка темы и цели урока) – 8 мин.
- Гимнастика для глаз – 2 мин.
- Изучение нового материала. – 9 мин.
- Физкультминутка – 2 мин.
- Работа по теме урока (первичное закрепление знаний) – 7 мин.
- Домашние задание – 2 мин.
- Рефлексия учебной деятельности – 3 мин.
УМК: «Школа России».
Авторы учебника: «Математика» Моро М.И, Бантова М.И. и другие (1 часть); тетради: «Математика» Моро М.И., Волкова С.И. (1 часть).
Тема. Задачи, обратные данной.
Тип урока: изучение нового.
Цель урока:
формирование и развитие ценностного отношения обучающихся к совместной учебной деятельности по определению и практическому применению понятия «обратные задачи», установлению связи между прямой и обратной задачей.
Предметные результаты:
· Уметь узнавать и составлять обратные задачи.
· Уметь использовать в речи термин «обратная» задача.
· Знать структуру задачи.
· Уметь решать задачи в одно действие.
· Уметь выделять её части и анализировать содержание текстовой задачи.
· Уметь составлять краткую запись или схематический рисунок.
· Уметь выполнять вычисления изученных видов.
Метапредметные результаты:
Личностных УУД:
— Способность к самооценке на основе критерия успешности учебной деятельности; позитивному отношению к уроку математики, учебно-познавательный интерес к учебному материалу.
Регулятивных УУД:
— Уметь учащимися принимать и сохранять учебную задачу, планировать своё действие в соответствии с поставленной задачей; оценивать правиль-ность выполнения действия на уровне адекватной оценки; вносить необхо-димые коррективы в действие после его завершения на основе его оценки и учёта характера сделанных ошибок; овладение умениями проговаривать последовательность действий на уроке, умение формулировать цель урока с помощью учителя.
Познавательные УУД:
— Уметь осуществлять логические операции; описывать математические объекты; ориентироваться в своей системе знаний, строить небольшие математические высказывания.
УУД Коммуникативные:
— Уметь оформлять свои мысли в устной форме; слушать и понимать речь других; учиться работать в паре, формулировать собственное мнение и позицию.
Методы и формы работы: совместная с учителем учебно – познавательная деятельность, работа в парах, математическая игра, учебный (проблемный) диалог, самостоятельная работа, наблюдение за математическими объектами (моделирование (сравнение, анализ)).
Оборудование:
Для учителя: рабочая тетрадь, учебник, карточки для индивидуальной работы у доски.
Для учащихся: «Светофорчик», учебник, рабочая тетрадь, индивидуальный раздаточный материал (схемы для составления кратких записей к задачам, оценочные листы).
Ход урока:
I. Организационный момент. Психологический настрой.
Стихотворение «Урок математики»
Когда на математике я вижу море рук,
Мне кажется, что в класс пришли
Все доктора наук.
Решат задания правильно,
Все будет без проблем,
И в нашем школьном здании
Приятно будет всем.
Сложенье получается,
Задачки все решаются,
И дети улыбаются,
Хоть осень за окном.
А мячики, скакалочки,
Роботы, игралочки,
Проказы, забывалочки
Оставим на потом!
Девиз урока: Главное – внимание!
— Это девиз нашего урока. Как вы его понимаете? Чтобы понять новое или сделать научное открытие – надо быть внимательным!
— С каким настроением вы пришли на урок – покажите при помощи сигналов на «Светофорчике». СЛАЙД
— Откройте тетрадь и запишите число, классная работа.
— Ну, что – вперед за знаниями!
II. Актуализация опорных знаний.
1. Индивидуальная работа у доски (на местах работа в парах)
Закрепление знаний состава числа.
— У вас на столах есть карточки № 1. Повторим связь компонентов при сложении. 40+7=47 5+6=11
У доски 2 ученика.
Самостоятельная работа на местах в парах.
— Кто согласен, покажите зелёный сигнал «Светофора», а кто не согласен – красный. Оценочный лист.
2. Устный счёт
– А теперь будьте внимательны. Я зачитаю вам слова-понятия, а вы должны назвать общее слово, которое их объединяет: условие, вопрос, данные числа, искомое число. (Задача.)
— Что вы знаете о задаче? Назовите основные части задачи (условие, вопрос, решение, ответ). СЛАЙД
III. Самоопределение к деятельности (постановка темы и цели урока)
— Как вы думаете, зачем мы выполняли эти задания? (повторили связь компонентов при сложении, вспомнили части задачи)
Учитель закрепляет на доске карточку со словом «задачи».
– Сегодня вы узнаете новое о задачах. Вам самостоятельно предстоит сделать открытие.
Давайте распланируем нашу работу: что – сначала, а что потом.
План
1. Исследовать новое.
2. Сделать открытие.
3. Закрепить.
– Посмотрите на числа и расположите их в порядке возрастания. Каждому числу соответствует буква. Какое слово получилось? Поставьте буквы в порядке возрастания их высоты и узнаете слово.
— Какое слово получилось? (Задачи).
— Итак, чем мы будем сегодня заниматься на уроке? (Решать задачи).
Тема урока: задачи, обратные данной. КАРТОЧКУ НА ДОСКУ
— А обратные задачи, это какие?
— Попробуете сформулировать проблемный вопрос, который необходимо разрешить на уроке? (Узнать о том, что такое обратные задачи и проверить наши предположения). СЛАЙД
— Вот сегодня мы будем исследователями, понаблюдаем и разрешим данную проблему. Какие цели вы поставите на урок? Главная цель?
Цель: провести исследование задач, выявить сходства, отличия, дать определение этим задачам. КАРТОЧКУ НА ДОСКУ
IV. Гимнастика для глаз. СЛАЙД
— Ребята сейчас мы попадём на лесную полянку, где вам нужно глазками следить за движениями предметов.
V. Изучение нового материала.
Задачи на слайдах и на карточках у детей, схемы краткой записи для заполнения учащимися.
Сейчас мы поработаем в роли исследователей.
Прочитайте тексты. Это одна и та же задача? В чём сходство? О чем говорится в задаче? (О кленовых и дубовых листочках, сколько упало листочков на землю). В чём отличие?
1. На экскурсии в осеннем лесу Дима собрал 7 листочков, а Катя – 6 листочков. Сколько всего листочков собрали дети?
2. Катя и Дима собрали 13 листочков. У Кати было 6 листочков. Сколько листочков собрал Дима?
3. Катя и Дима собрали 13 листочков. Из них 7листочков были у Димы. Сколько листочков было у Кати?
Ребята, как называется явление в природе, когда падают листья?
– Прочитайте первую задачу. О чем говориться в задаче? Дубовых – 5 л., кленовых – 6 л., не знаем, сколько всего на земле листочков.
– Впишите самостоятельно на карточках данные, которые известны и неизвестны в задаче.
Д. — 5 л.
? л.
К. — 6 л.
Решите задачу № 1.
Эталон для взаимопроверки и взаимоконтроля. Оценочный лист.
– Прочитайте вторую задачу. О чем говориться в задаче? О кленовых и дубовых листочках, сколько упало листочков на землю.
– Чем задача похожа на предыдущую? Чем отличается от неё? В обеих задачах речь идёт о кленовых и дубовых листочках, и в той, и другой
задаче на земле 6 кленовых листочков. В первой задаче известно, что упало
5 дубовых листочков и нужно узнать, сколько всего упало на землю листочков с двух деревьев, во второй задаче известно общее количество листочков и нужно узнать, сколько на земле дубовых листочков
– Запишите кратко условие.
Д. — ? л.
11 л.
К. — 6 л.
Решите задачу № 2.
Эталон для взаимопроверки и взаимоконтроля. Оценочный лист.
– Что вы можете сказать о решениях этих задач?
– Прочитайте третью задачу. Как изменилось ее условие? Известно, сколько всего упало кленовых и дубовых листочков, и на земле кленовых листочков. Не знаем, сколько дубовых.
– Что надо узнать? Запишите задачу кратко.
Д. — 5 л.
11 л.
К. —? л.
Решите задачу № 3.
Эталон для взаимопроверки и взаимоконтроля. Оценочный лист.
– Внимательно посмотрите на условия этих трех задач. Что вы о них можете сказать? (Они похожи.)
– Что одинаково? (Данные, числа.)
— Чем отличаются?
– Внимательно посмотрите на решения задач. Что одинаково? (Числа.) — Чем отличаются? (Действиями: 1) + 2) – 3) – )
– Как назовем вторую и третью задачи? (Обратные первой.)
– Конечно, это обратные задачи.
— В какой форме мы записали задачи? (в форме краткой записи).
— А можно их оформить в виде схематического рисунка
— Кто может поделиться с Математиком, как понял, что такое обратная задача? (Задачи, в которых объект (число) и результат меняются местами (известное становится неизвестным, а неизвестное известным), называются обратными первой).
— Какую цель ставили? (узнать, что такое обратные задачи)
— Какой получили результат? (мы выяснили, что такое обратная задача и решили их).
— Что ещё нового мы узнали? В каком виде можно оформить кратко задачу? (схематический рисунок).
— Проверили мы наши предположения? Математик говорит, что вы молодцы.
V. Физминутка.
Ваня шел, шел, шел
И грибок нашел.
Раз грибок, два грибок
Положил в свой кузовок.
VI. Работа по теме урока (первичное закрепление знаний).
— Откройте учебник на стр. 26, № 2.
— Откройте тетрадь и запишите «Задача 2.»
– Прочитайте задачу. Запишите кратко на листах со схемами.
Л. – 3 р.
? р.
Ок. — 4 р.
— Решение и ответ задачи запишите в тетрадь самостоятельно. Один ученик читает решение вслух. Дети сигнализируют смайликами. Оценочный лист.
— Составьте обратные задачи (устно). Работа в парах. 1 пара проверка вслух.
Дети сигнализируют смайликами.
1 вариант: решает устно задачу с вопросом: Сколько поймал лещей?
2 вариант: решает устно задачу с вопросом: Сколько поймал окуней? Фронтальная проверка.
Эталон для взаимопроверки и взаимоконтроля. СЛАЙД
— Кому было легко решать задачи, покажите зелёный сигнал «Светофора».
— Кто затруднялся при работе с этим заданием, покажите жёлтый сигнал.
— С какой целью выполняли это упражнение из учебника? ( Закрепили умение решать задачи, учились устно составлять и решать обратные задачи).
VII. Домашнее задание.
№ 3, 4 с. 26
VIII. Итог урока
– Какая цель стояла в начале урока?
– Что нового вы узнали на уроке?
— Какие задачи называются обратными?
— Кто испытывал трудности при работе?
— Какие? Что нужно сделать, чтобы их устранить? IX. Рефлексия учебной деятельности.
- Какие качества ученика вам помогали в работе?
- Оцените свое отношение к результатам урока.
- Вы довольны результатами? Работой на уроке?
- Какое у вас настроение?
- Оцените свою работу на уроке при помощи «Светофорчика».
- Мы сегодня с вами хорошо поработали. Я вас благодарю: мне было с вами очень интересно!
- Главная
- Справочники
- Справочник по математике для начальной школы
- Задачи
- Обратные задачи
В обратной задаче одна из искомых величин становится известной, а одна из данных величин становится неизвестной.
Прямая задача:
У Тани было 3 зелёных шарика и 2 красных. Сколько всего шариков было у Тани?
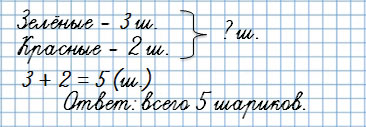
Первая обратная задача:
У Тани было 5 шариков, 3 шарика были зелёными, а остальные красные. Сколько красных шариков было у Тани?
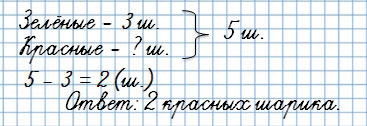
Ты видишь, что известная величина – красные шарики – стала неизвестной.
А неизвестная величина – общее количество шариков – стало известной.
Вторая обратная задача:
У Тани было 5 шариков, 2 шарика были красными, а остальные зелёные. Сколько зелёных шариков было у Тани?
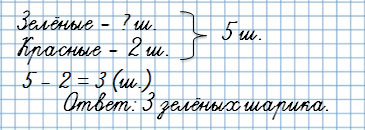
Ты видишь, что известная величина – зелёные шарики – стала неизвестной.
А неизвестная величина – общее количество шариков – стало известной.
ТАКИЕ ЗАДАЧИ НАЗЫВАЮТСЯ ОБРАТНЫМИ.
Советуем посмотреть:
Образцы оформления задачи
Цена. Количество. Стоимость
Скорость, время, расстояние
Задачи
Правило встречается в следующих упражнениях:
1 класс
Страница 48. Урок 25,
Петерсон, Учебник, часть 2
Страница 50. Урок 26,
Петерсон, Учебник, часть 2
Страница 53. Урок 27,
Петерсон, Учебник, часть 2
Страница 60. Урок 31,
Петерсон, Учебник, часть 2
Страница 63. Урок 32,
Петерсон, Учебник, часть 2
Страница 8. Урок 5,
Петерсон, Учебник, часть 3
Страница 25. Урок 13,
Петерсон, Учебник, часть 3
Страница 33. Урок 17,
Петерсон, Учебник, часть 3
Страница 65. Урок 33,
Петерсон, Учебник, часть 3
Страница 91. Повторение,
Петерсон, Учебник, часть 3
2 класс
Страница 31,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 39,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 85,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 88,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 36,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 45,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 16. ПР 1. Вариант 1,
Моро, Волкова, Проверочные работы
Страница 92,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 94,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 98,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
3 класс
Страница 19,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 20,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 27,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 35,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 64,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 29,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 71,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 101,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 35. Урок 13,
Петерсон, Учебник, часть 1
Страница 40. Урок 15,
Петерсон, Учебник, часть 1
4 класс
Страница 5,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 11,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 87,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 1
Страница 49,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 68,
Моро, Волкова, Рабочая тетрадь, часть 1
Страница 28,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 32,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 44,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 99,
Моро, Волкова, Степанова, Бантова, Бельтюкова, Учебник, часть 2
Страница 29,
Моро, Волкова, Рабочая тетрадь, часть 2
|
Что значит “обратная задача” в математике (1, 2, 3, 4 класс)? Как записать и решить обратную задачу, пример?
В математике обратная задача составляется на основании какой-либо имеющейся задачи. В обратных задачах искомые данные уже известны. Требуется найти одну из величин, которые были даны в условии исходной задачи. Пример 1 Исходная задача. В магазине яблоки стоят 120 рублей за 1 килограмм, а груши стоят 150 рублей за 1 килограмм. Требуется узнать, на сколько груши дороже яблок. Для решения этой задачи нужно найти разницу между 2 числами – стоимостью груш и стоимостью яблок. 150 – 120 = 30 (руб.) Таким образом, груши дороже яблок на 30 рублей. _ Обратная задача. Здесь нам будет известна разница в стоимости фруктов, то есть 30 рублей. Будем находить либо стоимость яблок, либо стоимость груш – то есть можно составить 2 разных обратных задачи. 1) Яблоки стоят 120 рублей, а груши на 30 рублей дороже. Сколько стоят груши? Решение: 120 + 30 = 150 (руб.) 2) Груши стоят 150 рублей, а яблоки на 30 рублей дешевле. Сколько стоят яблоки? Решение: 150 – 30 = 120 (руб.) Пример 2 Исходная задача. Покупатель хочет купить 500 грамм говядины, которая стоит 200 рублей за 1 килограмм. Сколько он должен заплатить? Для решения данной задачи нужно вспомнить соотношение между граммами и килограммами. 1 килограмм = 1000 грамм. 500 грамм – это ровно половина от 1000 грамм (или 1 килограмма): 500 / 1000 = 1/2. Таким образом, покупатель заплатит не 200 рублей, а только половину: 200 / 2 = 100 (руб.) _ Обратная задача. Здесь нам будет известна цена покупки, то есть 100 рублей. Можно найти, например, стоимость за 1 килограмм. Вот формулировка подобной задачи: Покупатель купил 500 грамм говядины за 100 рублей. Сколько стоит 1 килограмм говядины? Решение: 1) 1 килограмм – это 1000 грамм. 1000 / 500 = 2, то есть 1 килограмм будет в 2 раза больше, чем 500 грамм. 2) Стоимость 1 килограмма составляет 100 * 2 = 200 (руб.) модератор выбрал этот ответ лучшим
Математический термин “обратная задача” включает два слова. С существительным задача все понятно. Возникает вопрос: что значит обратная. Данное прилагательное по отношению к задаче можно определить как противоположная или ведущая назад, к исходному состоянию. Для того, чтобы составить обратную задачу, нужно иметь задачу исходную. И исходную задачу необходимо решить. Это нужно для того, чтобы использовать полученный результат в качестве исходных данных для обратной задачи. Если сказать еще проще, то то, что дано ( известно ) в исходной задача, в обратной ей нужно будет искать. А решение исходной задачи станет тем, что известно по условию обратной задачи. Это мое определение термину “обратная задача”, простого определения для начальной школы я не нашла. Проще пояснить на примерах. Исходная задача: Мама купила 5 пирожных и 7 кексов к чаю. Сколько всего кексов и пирожных купила мама? Решение 5+7=12 (шт.) выпечки купила мама. Обратная ей задача: Обратных задач можно в этом случае составить две: 1) Мама всего купила 12 пирожных и кексов к чаю, из них 5 пирожных. Сколько кексов купила мама? Решение 12-5=7 (к.) купила мама. 2) Мама всего купила 12 пирожных и кексов к чаю, из них 7 кексов. Сколько пирожных купила мама? Решение 12-7=5 (п.) купила мама.
Марина Вологда 3 года назад Обратная задача – это такая задача, в которой все искомые величины уже известны. Из этих известных величин и составляем обратную задачу. Например, нам дана задача: В автопарк заехало три красных машины и пять белых. Сколько всего машин заехало в автопарк? Решение: 3+5 = 8 машин. Составляем обратную задачу: 1) Сколько машин заехало в автопарк красного цвета, если известно, что всего машин было 8. А белых машин было 5. Решение: 8-5 = 3 машины красного цвета. 2) Известно, что в автопарк заехало 8 машин. Из них три были красного цвета. Остальные машины были белые. Сколько машин белого цвета? Решение: 8-3 = 5 машин белого цвета.
Алиса в Стране 3 года назад Многие из нас, наверное, уже забыли, что такое обратная задача, но на самом деле ничего сложного в ней нет. Приведу пример. Допустим, у нас есть расстояние (путь) и время, за которое человек его прошел, все мы знаем, как просто определить скорость, нужно расстояние (путь) разделить на время.
Так вот к этой элементарной задачке можно составить две обратные задачи: на определение пути (расстояния), если известна скорость и время (чтобы решить эту задачу, нужно скорость умножить на время):
Второй обратной задачей будет задача на определение времени, если известно расстояние (путь) и скорость (нужно путь поделить на скорость):
Не знаю, кто их назвал “обратными” потому что задача это всегда, как минимум, поиск третьего неизвестного по двум известным, и какая разница какое из них будет неизвестным. Составить их проще простого, просто поменять неизвестное с известным, ну и вероятно математическое действие будет другое – вместо сложения – вычитание, вместо деления – умножение (как и наоборот) Вот пример. У Васи было две конфеты, Валя дала Васе еще три конфеты, сколько у Васи конфет теперь? Ответ – пять. Якобы обратная задача. У Васи было пять конфет, две из которых были его, сколько конфет ему дала Валя что бы у него получилось пять? Ответ – три.
Zummy out off 3 года назад Обратная задача в математике – это такая задача, которая составляется по исходной задаче, но ответ исходной задачи включается в условие обратной задачи, а требуется найти то, что было одним из условий исходной задачи. Составление обратных задач тренирует «мозги» для решения задач в математике. Пример составления обратной задачи. Исходная задача. У Маши было 20 рублей, она купила тетрадь за 12 рублей. Сколько денег осталось у Маши? Решение: 20-12=8. Ответ: 8 рублей осталось у Маши. Обратная задача. В условие задачи надо включить сумму сдачи 8 руб. Составляем задачу: Маша купила тетрадь за 12 руб и у неё осталась сдача 8 руб. Сколько денег было у Маши до покупки тетради? Решение: 12+8=20. Ответ: 20 рублей было у Маши.
Бархатные лапки 3 года назад Обратная задача составляется на основе уже имеющейся решенной задачи. В обратной задаче требуется узнать то, что было известно в нашей задаче. Объясним, что такое обратная задача, на примере простейшей задачки для начальных классов. У Иры 10 яблок, у Маши 5 яблок. Нужно найти, сколько яблок у обоих девочек вместе. Это наша задача, решается она так: общее количество яблок равно: яблоки Иры плюс яблоки Маши = 5 + 10 + 15 Обратная задача к этой задаче: у двух девочек, Иры и Маши 15 яблок, сколько яблок у Иры, если у Маши 5 яблок. Решение: 15 – 5 = 10 яблок у Иры. Также обратную задачу можно составить и так: у Иры и Маши 15 яблок, сколько яблок у Маши, если у Иры 10 яблок. Решение: 15 – 10 = 5, у Маши 5 яблок.
KritikSPb 4 года назад Обратная задача в математике требует найти то, что было известно в первоначальной задаче. То есть обязательным условием составления обратной задачи является наличие прямо задачи, от которой и отталкиваются для составления обратной. Например, первоначально известно, что человеку нужно дойти из дома до магазина. Расстояние 10 км. Идёт он со скоростью 5 км в час. Через сколько времени он будет на месте? Решение: 10 / 5 = 2 часа. А теперь обратная задача: За два часа человек дошёл от дома до магазина. Определите расстояние, если известно, что скорость человека 5 км в час. Решение: 2 * 5 = 10 км. Для составления обратной задачи необходимо решить исходную.
Бекки Шарп 3 года назад Обратные задачи бывают в разных науках и в математике тоже. Обратная составляется на основании уже полученных данных. Когда то что требовалось найти уже известно. Например. У Миши было 7 яблок, а у Васи 8 яблок. Сколько всего было яблок у мальчиков. Решение: 7+8=15 (яблок) Обратная задача к нашей будет такая. Всего у Миши и Васи 15 яблок. У Миши – 7 яблок. Сколько у Васи яблок? Решение: 15-7=8 (яблок) Еще одна обратная задача к нашей. У Миши и Васи 15 яблок, у Васи – 8. Сколько яблок у Миши? Решение: 15-8=7 (яблок) Val111111 4 года назад Обратная задача- это когда то, что требовалось найти, теперь известно, а то, что было в дано нужно найти. Пример, есть три яблока. Два забрали. Сколько осталось? Обратная задачка: Забрали два яблока, осталось одно, сколько было? TheSun 3 года назад В обратной задаче неизвестным является дано, именно его и нужно найти. Но, при этом известен результат. Рассмотрим на примере. У Маши было 4 синих мяча и 3 зелёных мяча. Сколько всего у Маши мячей? 4+3=7 (шт.) мячей у Маши. Теперь обратная задача. У Маши всего 7 мячей. Из них синих мячей 4, а остальные мячи зелёного цвета. Сколько у Маши зелёных мячей? 7-4=3 (шт.) зелёных мяча у Маши. Знаете ответ? |
Тема
урока: Задачи, обратные данной.
Цель
урока: знакомство детей с новым математическим понятием: «обратные
задачи», установление связи между прямой и обратной задачей.
Предметные
результаты:
·
Уметь узнавать и составлять обратные задачи.
·
Уметь использовать в речи термин «обратная» задача.
·
Знать структуру задачи.
·
Уметь решать задачи в одно действие.
·
Уметь выделять её части и анализировать содержание текстовой
задачи.
·
Уметь составлять краткую запись или схематический рисунок.
·
Уметь выполнять вычисления изученных видов.
Метапредметные
результаты:
·
Личностных УУД: Способность к
самооценке на основе критерия успешности учебной деятельности; позитивному
отношению к уроку математики, учебно-познавательный интерес к учебному
материалу.
·
Регулятивных УУД: Уметь учащимися
принимать и сохранять учебную задачу, планировать своё действие в соответствии
с поставленной задачей; оценивать правильность выполнения действия на уровне
адекватной оценки; вносить необходимые коррективы в действие после его
завершения на основе его оценки и учёта характера сделанных ошибок; овладение
умениями проговаривать последовательность действий на уроке, умение
формулировать цель урока с помощью учителя.
·
Познавательные УУД: Уметь
осуществлять логические операции; описывать математические объекты;
ориентироваться в своей системе знаний, строить небольшие математические
высказывания.
·
УУД Коммуникативные: Уметь оформлять
свои мысли в устной форме; слушать и понимать речь других; учиться работать в
паре, формулировать собственное мнение и позицию.
Методы
и формы работы: совместная с учителем
учебно-познавательная деятельность, работа в парах, математическая игра,
учебный (проблемный) диалог,самостоятельная работа,наблюдение за
математическими объектами (моделирование (сравнение, анализ)).
I.
Организационный момент.
Психологический
настрой.
–
Сегодня я приглашаю вас в увлекательное путешествие по математическому лесу.
Наше путешествие будет идти под девизом, который написан на слайде. Прочитаем
его. (Слайд 2)
Чтоб
водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте-ка
Где бы нам не пригодилась
Математика.
–
Это девиз нашего урока. Как вы его понимаете? (Чтобы стать хорошим летчиком
капитаном, надо хорошо учиться. Преодолевать трудности, стараться самим
добывать знания.)
–
С каким настроением вы пришли на урок – покажите при помощи сигналов на
«Светофорчике».(Слайд 3)
– Откройте
тетрадь и зафиксируйте место и время нашей встречи.
–
Ну, что вперед за знаниями.
II.
Актуализация опорных знаний.
Первая
наша остановка «Соображай-ка»
1.
Индивидуальная работа у доски (на местах работа в парах)
Закрепление
знаний состава числа.
–
Посмотрите, какие чудесные математические ёлочки. Как вы думаете, какое задание
я вам хочу предложить?
–
У вас на столах есть карточки с математическими ёлочками. (Приложение
1)
–
Каждая пара веточек даёт в сумме число на макушке, числа на веточках могут быть
однозначные и двузначные.
(У
доски 3 ученика – вписывают числа в круги. (Приложение
5) Самостоятельная работа на местах в парах.)
– Кто
согласен, покажите зелёный сигнал «Светофора», а кто не согласен – красный.
–
С какой целью выполняли это задание? (повторили состав числа, способы
получения чисел 7, 11, 15).
2.
Устный счёт (Слайд 4)
–
На поляне растут математические грибы. Эти грибочки необычные они
волшебные. Посмотрите, какие числа записаны на шляпках грибов,
поставьте их в порядке убывания (уменьшения) и вы узнаете, какое слово
спряталось на грибочках. (Приложение
2) Ответ: 55, 50, 45, 35, 25, 15.
–
Что вы знаете о задаче? Назовите основные части задачи (условие, вопрос,
решение, ответ). (Слайд 5)
– Как
вы думаете, зачем мы выполняли это задание? (повторили порядок
чисел при счёте (в натуральном ряду, вспомнили части задачи)).
Учитель
закрепляет на доске карточку со словом «задачи».
III.
Гимнастика для глаз.
Остановка
«Глазково»
–
Ребята сейчас мы попадём на лесную игровую полянку, где вам нужно глазками
следить за движениями предметов. (Слайд 6)
IV.
Самоопределение к деятельности (постановка темы и цели урока).
–
Посмотрите, сегодня к нам на урок снова пришел Учёный Математик. (Слайд
7)
–
Как вы думаете, зачем он к нам пришёл? Что-то он не весёлый. Может быть
что-нибудь случилось? (У Математика в руках листочек с буквами).
–
Оказывается, Математик так спешил к нам, что пока бежал у него по листочку все
буквы рассыпались. Поможем Математику расшифровать слово? Поставьте буквы в
порядке возрастания их высоты и узнаете слово.
– Какое слово получилось? (Обратные). (Приложение
3)
–
Итак, чем мы будем сегодня заниматься на уроке? (Решать обратные задачи). (Слайд
8)
–
А обратные задачи, это какие?
–
Попробуйте сформулировать проблему, которую необходимо разрешить на уроке? (Узнать
о том, что такое обратные задачи и проверить наши предположения по этой
проблеме).
– Вот
сегодня мы будем исследователями, понаблюдаем и разрешим данную проблему.
Остановка
«Задачкино» (Слайд 9)
Задачи
на слайдах (схемы краткой записи для
заполнения учащимися (Приложение
4)).
–
Прочитайте тексты. Это одна и та же задача? В чём сходство? О чем говориться в
задаче? (О кленовых и дубовых листочках, сколько упало листочков на землю). В
чём отличие?
1. На
землю с деревьев упало 5 дубовых и 6 кленовых листочков. Сколько всего на земле
листочков?
2. В
лесу листопад. На землю с деревьев упало 11 листочков. Кленовых было 6. Сколько
на земле дубовых листочков?
3. В
лесу листопад. На землю с деревьев упало 11 листочков. Из них было 5 дубовых.
Сколько на земле кленовых листочков?
–
Прочитайте первую задачу. О чем говориться в задаче? (Дубовых – 5 л., кленовых
– 6 л., не знаем сколько всего на земле листочков).
–
Впишите самостоятельно на карточках данные, которые известны и неизвестны в
задаче.
![]()
–
Решите задачу №1.
Эталон
для взаимопроверки и взаимоконтроля. (Слайд 10)
–
Прочитайте вторую задачу. О чем говориться в задаче? (О кленовых и дубовых
листочках, сколько упало листочков на землю).
–
Чем задача похожа на предыдущую и чем отличается от неё? (В обеих задачах речь
идёт о кленовых и дубовых листочках, и в той, и другой
задаче
на земле 6 кленовых листочков В первой задаче известно, что упало
5
дубовых листочков и нужно узнать, сколько всего упало на землю листочков с двух
деревьев, во второй задаче известна общее количество листочков и нужно узнать,
сколько на земле дубовых листочков.)
–
Запишите кратко условие.
![]()
–
Решите задачу №2.
Эталон
для взаимопроверки и взаимоконтроля. (Слайд 10)
–
Что вы можете сказать о решениях этих задач?
–
Прочитайте третью задачу. Как изменилось ее условие? (Известно, сколько всего
упало кленовых и дубовых листочков, и на земле кленовых листочков. Не знаем,
сколько дубовых.)
–
Что надо узнать? Запишите задачу кратко.
![]()
–
Решите задачу №3.
Эталон
для взаимопроверки и взаимоконтроля. (Слайд 10)
– Внимательно
посмотрите на условия этих трех задач. Что вы о них можете сказать? (Они
похожи.)
–
Что одинаково? (Данные, числа.) – Чем отличаются?
–
Внимательно посмотрите на решения задач. Что одинаково? (Числа.) –
Чем отличаются? (Действиями:1) +; 2) -; 3) -.)
–
Как назовем вторую и третью задачи? (Обратные первой.)
–
Конечно, это обратные задачи.
–
В какой форме мы записали задачи? (в форме краткой записи).
– А
можно их оформить в виде схематического рисунка (Слайд 11)
–
Кто может поделиться с Математиком о том, как понял, что такое обратная задача?
(Задачи, в которых объект (число) и результат меняются местами (известное
становится не известным, а неизвестное известным), называются обратными
первой).
– Какую
цель ставили? (узнать, что такое обратные задачи)
–
Какой получили результат? (мы выяснили, что
такое обратная задача и решили их).
–
Что ещё нового мы узнали? В каком виде можно оформить кратко задачу?
(схематический рисунок).
–
Проверили мы наши предположения? Математик говорит, что вы молодцы.
V.
Работа по теме урока
–
Откройте учебник на стр. 26, № 2. (Слайд 12)
Остановка
«Речная»
– Откройте
тетрадь и запишите номер задания № 2.
–
Прочитайте задачу. Запишите кратко.
![]()
–
Решение и ответ задачи запишите самостоятельно.
–
Составьте обратные задачи (устно). (Коллективное составление с
комментированием).
1
вариант: решает задачу с вопросом: Сколько поймал лещей?
2
вариант: решает задачу с вопросом Сколько поймал окуней?
Самостоятельная
работа. Фронтальная проверка.
Эталон
для взаимопроверки и взаимоконтроля. (Слайд 13)
– Кому
было легко решать задачи, покажите зелёный сигнал «Светофора».
–
Кто затруднялся при работе с этим заданием, покажите жёлтый сигнал.
–
С какой целью выполняли это упражнение из учебника? (закрепили умение решать
задачи, учились устно составлять и решать обратные задачи).
VI.
Остановка «Отдыхайкино»
Учитель
показывает танцевальные движения. (Слайд 14)
1. Движения
ногами (сгибание и разгибание колен), руки на пояс.
2. Подняться
на носочки и поднимать медленно руки вверх.
3. Круговые
движения тазом (вправо, влево).
4. Повторить
1 танцевальное движение.
5. Хлопки
руками.
6. Повторить
1 танцевальное движение.
VII.
Работа над пройденным материалом
Остановка
«Узнайкино» (Слайд 15)
–
Откройте тетрадь с печатной основой с. 34 №19.
–
Прочитайте задание. Раскрасьте кружки с номерами обратных задач.
Докажите,
что вы их верно нашли.
–
Зачем мы выполняли это задание? Чему учились? (узнавать обратные задачи,
уметь отличить обратную от данной (прямой) задачи).
VIII.
Домашнее задание
1. Учебник:
стр. 26, № 3.
2. Р.
т.: стр. 34 № 18, № 19 (решить задачи).(Слайд 16)
IX.
Рефлексия учебной деятельности
–
Вспомните девиз нашего путешествия.
Чтоб
водить корабли.
Чтобы лётчиком стать
Надо прежде всего
Математику знать.
И на свете нет профессии,
Вы смекайте-ка
Где бы нам не пригодилась
Математика.
–
Мы сегодня с вами хорошо поработали, и я считаю, что из вас должны получиться
хорошие и летчики и капитаны и вы сможете для себя выбрать любую другую нужную
профессию. Математические знания важны для всех сфер деятельности.
–
Посмотрите, как смотрит на нас Математик. Он улыбается. Почему? (Доволен тем,
как мы поработали на уроке исследователями). (Слайд 17)
– Что
нового вы узнали на уроке? Чему научились?
–
Какие задачи называются обратными?
–
Кто испытывал трудности при работе?
–
Какие? Что нужно сделать, чтобы их устранить?
–
Оцените свою работу на уроке при помощи «Светофорчика». (Слайд 18)
–
Молодцы! Спасибо за работу на уроке. Наш помощник Учёный Математик благодарит
вас и вручает «медальки» за работу на уроке в виде цветных кленовых и дубовых
листочков: зелёный – активно работал на уроке, жёлтый –
хорошо работал, красный – работал на уроке, но нужна ещё
помощь.





