Время на прочтение
6 мин
Количество просмотров 76K
Данная статья представляет собой перевод введения в машинное обучение, представленное на официальном сайте scikit-learn.
В этой части мы поговорим о терминах машинного обучения, которые мы используем для работы с scikit-learn, и приведем простой пример обучения.
Машинное обучение: постановка вопроса
В общем, задача машинного обучения сводится к получению набора выборок данных и, в последствии, к попыткам предсказать свойства неизвестных данных. Если каждый набор данных — это не одиночное число, а например, многомерная сущность (multi-dimensional entry или multivariate data), то он должен иметь несколько признаков или фич.
Машинное обчение можно разделить на несколько больших категорий:
- обучение с учителем (или управляемое обучение). Здесь данные представлены вместе с дополнительными признаками, которые мы хотим предсказать. (Нажмите сюда, чтобы перейти к странице Scikit-Learn обучение с учителем). Это может быть любая из следующих задач:
- классификация: выборки данных принадлежат к двум или более классам и мы хотим научиться на уже размеченных данных предсказывать класс неразмеченной выборки. Примером задачи классификации может стать распознавание рукописных чисел, цель которого — присвоить каждому входному набору данных одну из конечного числа дискретных категорий. Другой способ понимания классификации — это понимание ее в качестве дискретной (как противоположность непрерывной) формы управляемого обучения, где у нас есть ограниченное количество категорий, предоставленных для N выборок; и мы пытаемся их пометить правильной категорией или классом.
- регрессионный анализ: если желаемый выходной результат состоит из одного или более непрерывных переменных, тогда мы сталкиваемся с регрессионным анализом. Примером решения такой задачи может служить предсказание длинны лосося как результата функции от его возраста и веса.
- обучение без учителя (или самообучение). В данном случае обучающая выборка состоит из набора входных данных Х без каких-либо соответствующих им значений. Целью подобных задач может быть определение групп схожих элементов внутри данных. Это называется кластеризацией или кластерным анализом. Также задачей может быть установление распределения данных внутри пространства входов, называемое густотой ожидания (density estimation). Или это может быть выделение данных из высоко размерного пространства в двумерное или трехмерное с целью визуализации данных. (Нажмите сюда, чтобы перейти к странице Scikit-Learn обучение без учителя).
Обучающая выборка и контрольная выборка
Машинное обучение представляет собой обучение выделению некоторых свойств выборки данных и применение их к новым данным. Вот почему общепринятая практика оценки алгоритма в Машинном обучении — это разбиение данных вручную на два набора данных. Первый из них — это обучающая выборка, на ней изучаются свойства данных. Второй — контрольная выборка, на ней тестируются эти свойства.
Загрузка типовой выборки
Scikit-learn устанавливается вместе с несколькими стандартными выборками данных, например, iris и digits для классификации, и boston house prices dataset для регрессионного анализа.
Далее мы запускам Python интерпретатор из командной строки и загружаем выборки iris и digits. Установим условные обозначения: $ означает запуск интерпретатора Python, а >>> обозначает запуск командной строки Python:
$ python
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> digits = datasets.load_digits()Набор данных — это объект типа «словарь», который содержит все данные и некоторые метаданных о них. Эти данные хранятся с расширением .data, например, массивы n_samples, n_features. При машинном обучении с учителем одна или более зависимых переменных хранятся с расширением .target. Для получения более полной информации о наборах данных перейдите в соответствующий раздел.
Например, набор данных digits.data дает доступ к фичам, которые можно использовать для классификации числовых выборок:
>>> print(digits.data)
[[ 0. 0. 5. ..., 0. 0. 0.]
[ 0. 0. 0. ..., 10. 0. 0.]
[ 0. 0. 0. ..., 16. 9. 0.]
...,
[ 0. 0. 1. ..., 6. 0. 0.]
[ 0. 0. 2. ..., 12. 0. 0.]
[ 0. 0. 10. ..., 12. 1. 0.]]а digits.target дает возможность определить в числовой выборке, какой цифре соответствует каждое числовое представление, чему мы и будем обучаться:
>>> digits.target
array([0, 1, 2, ..., 8, 9, 8])Форма массива данных
Обычно, данные представлены в виде двухмерного массива, такую форму имеют n_samples, n_features, хотя исходные данные могут иметь другую форму. В случае с числами, каждая исходная выборка — это представление формой (8, 8), к которому можно получить доступ, используя:
>>> digits.images[0]
array([[ 0., 0., 5., 13., 9., 1., 0., 0.],
[ 0., 0., 13., 15., 10., 15., 5., 0.],
[ 0., 3., 15., 2., 0., 11., 8., 0.],
[ 0., 4., 12., 0., 0., 8., 8., 0.],
[ 0., 5., 8., 0., 0., 9., 8., 0.],
[ 0., 4., 11., 0., 1., 12., 7., 0.],
[ 0., 2., 14., 5., 10., 12., 0., 0.],
[ 0., 0., 6., 13., 10., 0., 0., 0.]])Следующий простой пример с этим набором данных иллюстрирует, как, исходя из поставленной задачи, можно сформировать данные для использования в scikit-learn.
Обучение и прогнозирование
В случае с числовым набором данных цель обучения — это предсказать, принимая во внимание представление данных, какая цифра изображена. У нас есть образцы каждого из десяти возможных классов (числа от 0 до 9), на которым мы обучаем алгоритм оценки (estimator), чтобы он мог предсказать класс, к которому принадлежит неразмеченный образец.
В scikit-learn алгоритм оценки для классификатора — это Python объект, который исполняет методы fit(X, y) и predict(T). Пример алгоритма оценки — это класс sklearn.svm.SVC выполняет классификацию методом опорных векторов. Конструктор алгоритма оценки принимает в качестве аргументов параметры модели, но для сокращения времени, мы будем рассматривать этот алгоритм как черный ящик:
>>> from sklearn import svm
>>> clf = svm.SVC(gamma=0.001, C=100.)Выбор параметров для модели
В этом примере мы установили значение gamma вручную. Также можно автоматически определить подходящие значения для параметров, используя такие инструменты как grid search и cross validation.
Мы назвали экземпляр нашего алгоритма оценки clf, так как он является классификатором. Теперь он должен быть применен к модели, т.е. он должен обучится на модели. Это осуществляется путем прогона нашей обучающей выборки через метод fit. В качестве обучающей выборки мы можем использовать все представления наших данных, кроме последнего. Мы сделали эту выборку с помощью синтаксиса Python [:-1], что создало новый массив, содержащий все, кроме последней, сущности из digits.data:
>>> clf.fit(digits.data[:-1], digits.target[:-1])
SVC(C=100.0, cache_size=200, class_weight=None, coef0=0.0, degree=3,
gamma=0.001, kernel='rbf', max_iter=-1, probability=False,
random_state=None, shrinking=True, tol=0.001, verbose=False)Теперь можно предсказать новые значения, в частности, мы можем спросить классификатор, какое число содержится в последнем представлении в наборе данных digits, которое мы не использовали в обучении классификатора:
>>> clf.predict(digits.data[-1])
array([8])Соответствующее изображение представлено ниже:
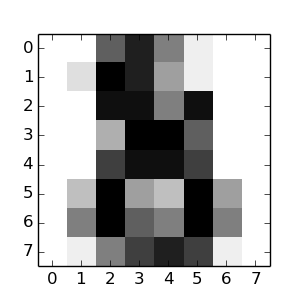
Как вы можете видеть, это сложная задача: представление в плохом разрешении. Вы согласны с классификатором?
Полное решение этой задачи классификации доступно в качестве примера, который вы можете запустить и изучить: Recognizing hand-written digits.
Сохранение модели
В scikit модель можно сохранить, используя встроенный модуль, названный pickle:
>>> from sklearn import svm
>>> from sklearn import datasets
>>> clf = svm.SVC()
>>> iris = datasets.load_iris()
>>> X, y = iris.data, iris.target
>>> clf.fit(X, y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0, degree=3, gamma=0.0,
kernel='rbf', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)
>>> import pickle
>>> s = pickle.dumps(clf)
>>> clf2 = pickle.loads(s)
>>> clf2.predict(X[0])
array([0])
>>> y[0]
0В частном случае применения scikit, может быть полезнее заметить pickle на библиотеку joblib (joblib.dump & joblib.load), которая более эффективна для работы с большим объемом данных, но она позволяет сохранять модель только на диске, а не в строке:
>>> from sklearn.externals import joblib
>>> joblib.dump(clf, 'filename.pkl') Потом можно загрузить сохраненную модель(возможно в другой Python процесс) с помощью:
>>> clf = joblib.load('filename.pkl') Обратите внимание, что joblib.dump возвращает список имен файлов. Каждый отдельный массив numpy, содержащийся в clf объекте, сеарилизован как отдельный файл в файловой системе. Все файлы должны находиться в одной папке, когда вы снова загружаете модель с помощью joblib.load.
Обратите внимание, что у pickle есть некоторые проблемы с безопасностью и сопровождением. Для получения более детальной информации о хранении моделей в scikit-learn обратитесь к секции Model persistence.
Все курсы > Вводный курс > Занятие 13
Работая с линейной регрессией в Scikit-learn, мы обучили нашу модель предсказывать обхват шеи по росту человека. Посмотрим на этот процесс еще раз.
Вначале, мы брали данные наших наблюдений (рост людей X и обхват шеи y) и строили модель (подбирали веса w). Затем, зная рост и веса модели, делали прогноз (ŷ). Качество модели мы оценивали по отклонению прогноза (ŷi) от реальных значений (yi).
В этом подходе все хорошо, кроме одного. Для обучения и проверки качества модели мы использовали одни и те же данные. Приведу хрестоматийную аналогию, чтобы объяснить почему так делать не стоит.
Пример студентов во время сессии

Как известно, от сессии до сессии живут студенты весело. Однако в какой-то момент сессия все-таки наступает, и перед учащимися встает вопрос подготовки к экзаменам. У них по большому счету есть два варианта:
- Первый вариант. Взять вопросы к экзамену у преподавателя, подготовить билеты и вызубрить их. Преимуществом такого подхода будут относительно небольшие трудозатраты. Нужно выучить только то, что написано в билетах. Недостатком будет то, что любой вопрос вне выученного конспекта поставит экзаменуемого в тупик.
- Второй вариант. Выучить сам предмет без привязки к билетам. Да, на вопросы билета человек может отвечать менее бодро, зато у него будет целостная картина того материала, который он, как надеются преподаватели, учил весь семестр.
Так вот при обучении модели у нас есть точно такой же выбор.
Обучающая и тестовая выборки
Если мы будем оценивать качество модели (например, с помощью корня из средней суммы расстояний, RMSE) на тех же данных, на которых обучали модель, то будем по большому счету заучивать билеты. Когда же нам встретятся новые данные, наш прогноз уже не будет таким замечательным.
Логичнее разделить данные на обучающую (training data) и тестовую (test data) выборки с тем, чтобы модель «знала предмет в целом» и не «проваливала экзамен из-за неожиданных вопросов преподавателя», т.е. не показывала низкого RMSE при встрече с новыми данными (новыми X и y).
Да, во втором случае мы скорее всего несколько снизим качество модели, потому что обучающая и тестовая выборки будут отличаться. Выигрышем же будет то, что в целом наша модель сможет делать более точные предсказания.
Проблема переобучения
С точки зрения данных проблему «заучивания билетов» еще называют переобучением модели (model overfitting). Когда мы учим и проверяем модель на одних и тех же данных, то по сути просим модель запомнить каждую единицу наших данных.
Также существует проблема недообучения (underfitting).
Если бы мы строили не линейную модель, а, например, полиномиальную (она выражена кривой), то нормально обученная модель отличалась бы от недообученной и переобученной следующим образом.
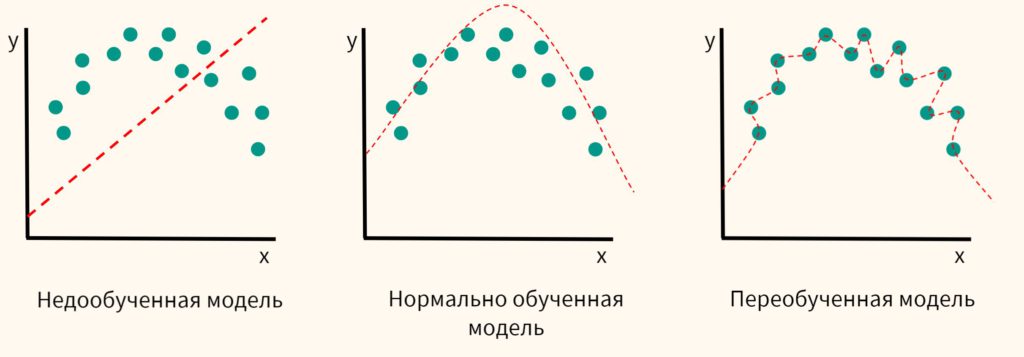
Разделение на обучающую и тестовую выборки в Scikit-learn
Вначале откроем ноутбук к этому занятию⧉
Вновь возьмем данные роста и обхвата шея. Только теперь не просто разделим данные на рост (X) и обхват шеи (y), но и каждый компонент в свою очередь разделим на две части, обучающую и тестовую.

Обучать мы будем на X_train и y_train, а делать прогноз и проверять качество модели на X_test и y_test. Вначале возьмем и подготовим наши данные.
|
# возьмем данные роста (X) и обхвата шеи (y) X = [1.48, 1.49, 1.49, 1.50, 1.51, 1.52, 1.52, 1.53, 1.53, 1.54, 1.55, 1.56, 1.57, 1.57, 1.58, 1.58, 1.59, 1.60, 1.61, 1.62, 1.63, 1.64, 1.65, 1.65, 1.66, 1.67, 1.67, 1.68, 1.68, 1.69, 1.70, 1.70, 1.71, 1.71, 1.71, 1.74, 1.75, 1.76, 1.77, 1.77, 1.78] y = [29.1, 30.0, 30.1, 30.2, 30.4, 30.6, 30.8, 30.9, 31.0, 30.6, 30.7, 30.9, 31.0, 31.2, 31.3, 32.0, 31.4, 31.9, 32.4, 32.8, 32.8, 33.3, 33.6, 33.0, 33.9, 33.8, 35.0, 34.5, 34.7, 34.6, 34.2, 34.8, 35.5, 36.0, 36.2, 36.3, 36.6, 36.8, 36.8, 37.0, 38.5] # импортируем библиотеку Numpy import numpy as np # преобразуем наш список X сначала в одномерный массив Numpy, а затем добавим второе измерение X = np.array(X).reshape(–1, 1) # список y достаточно преобразовать в одномерный массив Numpy y = np.array(y) |
Теперь произведем разделение с помощью функции train_test_split из библиотеки Scikit-learn.
|
# из модуля model_selection библиотеки sklearn импортируем функцию train_test_split from sklearn.model_selection import train_test_split # разбиваем данные на четыре части # названия переменных могут быть любыми, но обычно используют именно их # также задаем размер тестовой выборки (30%) и точку отсчета для воспроизводимости X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.3, random_state = 42) |
Выведем результат.
|
# выведем исходный размер массива признаков (X) X.shape |
|
# теперь посмотрим, что сделала функция train_test_split print(X_train.shape, X_test.shape) |
Далее мы снова построим нашу модель, но уже с учетом вышеописанного разделения на train и test (для простоты часто говорят именно так).
|
# из набора линейных моделей библиотеки sklearn импортируем линейную регрессию from sklearn.linear_model import LinearRegression # создадим объект этого класса и запишем в переменную model model = LinearRegression() # обучим нашу модель # т.е. найдем те самые веса или наклон и сдвиг прямой с помощью функции потерь # только теперь используем только обучающую выборку model.fit(X_train, y_train) |
Выведем коэффициенты (веса):
|
# выведем наклон и сдвиг с помощью атрибутов coef_ и intercept_ соответственно print(model.coef_, model.intercept_) |
|
[26.37316095] –9.809957964460885 |
Сделаем прогноз, но уже на тестовой выборке.
|
# на основе значений роста (Х) предскажем значения обхвата шеи y_pred = model.predict(X_test) # выведем первые пять значений с помощью диапазона индексов print(y_pred[:5]) |
|
[33.9694892 31.59590472 30.54097828 34.23322081 30.01351506] |
Посмотрим на результат, т.е. рассчитаем RMSE, снова по тестовой выборке.
|
# импортируем модуль метрик from sklearn import metrics # выведем корень среднеквадратической ошибки # в этот раз сравним тестовые и прогнозные значения окружности шеи print(‘Root Mean Squared Error (RMSE):’, np.sqrt(metrics.mean_squared_error(y_test, y_pred))) |
|
Root Mean Squared Error (RMSE): 0.5604831734149255 |
Результат несколько хуже, чем в прошлый раз (0,56 против 0,47), зато мы можем быть уверены, что модель готова к работе на всех данных, а не только на обучающих. Студент готов к самым неожиданным вопросам экзаменатора.
К сожалению, даже такое разделение имеет свои недостатки. Если тестовая выборка сильно отличается от обучающей, то оценка качества модели все равно будет некорректной. О том как преодолеть этот и некоторые другие недостатки мы поговорим в другой раз.
Вопросы и упражнения для закрепления
На какие четыре компонента разбивает данные функция train_test_split?
Посмотреть правильный ответ
Ответ: данные независимых переменных (признаков) и данные зависимой (целевой) переменной разбиваются каждые на обучающую и тестовую выборки. Получается четыре набора данных.
На каких данных мы строим прогноз и проверяем качество модели?
Посмотреть правильный ответ
Ответ: на тестовой выборке. Это позволяет избежать переобучения.
Дополнительные упражнения⧉ вы найдете в конце ноутбука.
Большое повторение
Итак, мы прошли два подготовительных раздела. Что мы узнали?
- В первую очередь, мы узнали, что такое модель машинного обучения, и чем она отличается от жестко прописанной компьютерной программы.
- Научились работать в программе Google Colab и освоили основы программирования на Питоне.
- Кроме того, мы изучили наборы данных, списки и словари.
- Добавив условия и циклы, мы начали писать первые программы.
- Все это заложило основу для анализа данных на Питоне.
- Во втором разделе, имея достаточно технических навыков, мы начали изучать данные с точки зрения их содержания. В частности, занимались описательной статистикой и статистическим выводом.
- Узнав о взаимосвязи переменных, мы начали строить первые модели.
- Затем мы изучили как компьютер подбирает веса и как можно представить данные в форме вектора или матрицы для удобства вычислений.
- Наконец, мы посмотрели, почему не стоит обучать и тестировать модели на одних и тех же данных.
Поздравляю!
Вы готовы к настоящей практической работе по построению моделей. В следующем, третьем, разделе мы изучим классические модели машинного обучения: регрессию, классификацию и кластеризацию. В последнем, четвертом, разделе, мы начнем решать существенно более сложные прикладные задачи.
Желаю успехов в дальнейшем обучении!
Добавлено 7 февраля 2020 в 02:02
В данной статье мы будем использовать для обучения многослойного перцептрона сгенерированные в Excel выборки, а затем посмотрим, как нейросеть работает с проверочными выборками.
Если вы хотите разработать нейронную сеть на Python, вы находитесь в правильном месте. Прежде чем углубиться в обсуждение о том, как использовать Excel для создания обучающих данных для вашей нейросети, для получения дополнительной информации посмотрите остальные статьи серии выше, в меню с содержанием.
Что такое обучающие данные?
В реальной жизни обучающие выборки состоят из данных измерений в сочетании с «решениями», которые помогут нейронной сети обобщить всю эту информацию в соответствующую связь вход-выход.
Например, предположим, что вы хотите, чтобы ваша нейронная сеть предсказывала вкусовые качества помидора на основе цвета, формы и плотности. Вы не представляете, как именно цвет, форма и плотность связаны с вкусностью, но вы можете измерить цвет, форму и плотность, и у вас есть вкусовые рецепторы. Таким образом, всё, что вам нужно сделать, это собрать тысячи и тысячи помидоров, записать их физические характеристики, попробовать каждый (лучшая часть), а затем поместить всю эту информацию в таблицу.
Каждая строка – это то, что я называю одной обучающей выборкой, и в ней четыре столбца: три из них (цвет, форма и плотность) являются столбцами входных данных, а четвертый – целевым выходным значением.
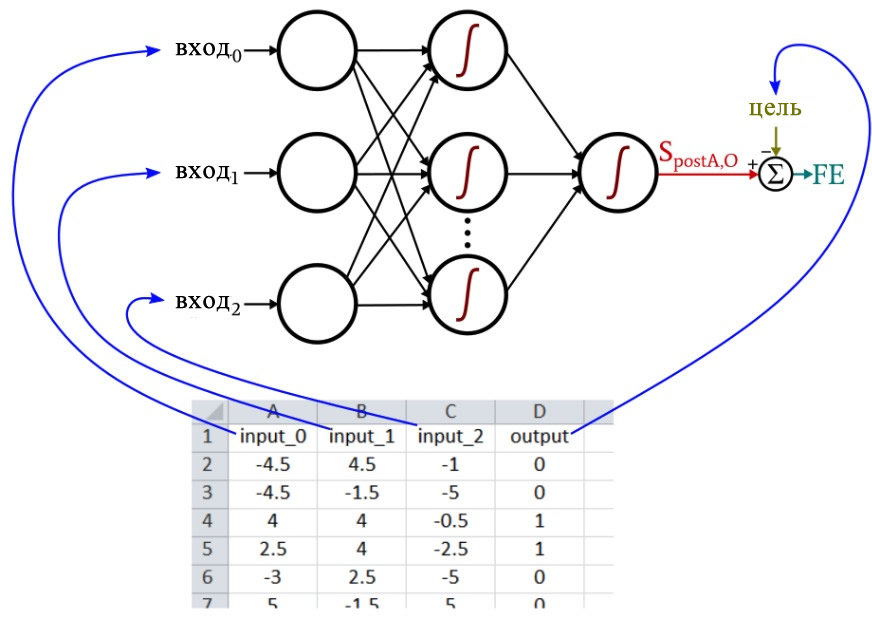
Во время обучения нейронная сеть найдет связь (если когерентная связь существует) между тремя входными значениями и выходным значением.
Оценка обучающих данных
Имейте в виду, что всё должно обрабатываться в числовом виде. Вы не можете в качестве входного параметра вашей нейронной сети использовать строку «сливовидная форма», а «аппетитный» не будет работать в качестве выходного значения. Вы должны количественно оценить ваши измерения и ваши классификации.
Для формы вы можете присвоить каждому помидору значение от –1 до +1, где –1 представляет собой идеальную сферу, а +1 означает крайне вытянутую форму. Что касается вкусовых качеств, вы можете оценивать каждый помидор по пятибалльной шкале от «несъедобного» до «восхитительного», а затем использовать унитарный код для сопоставления этих оценок с выходным вектором из пяти элементов.
Следующая диаграмма показывает, как этот тип кодирования используется для классификации выходных значений нейронной сети.
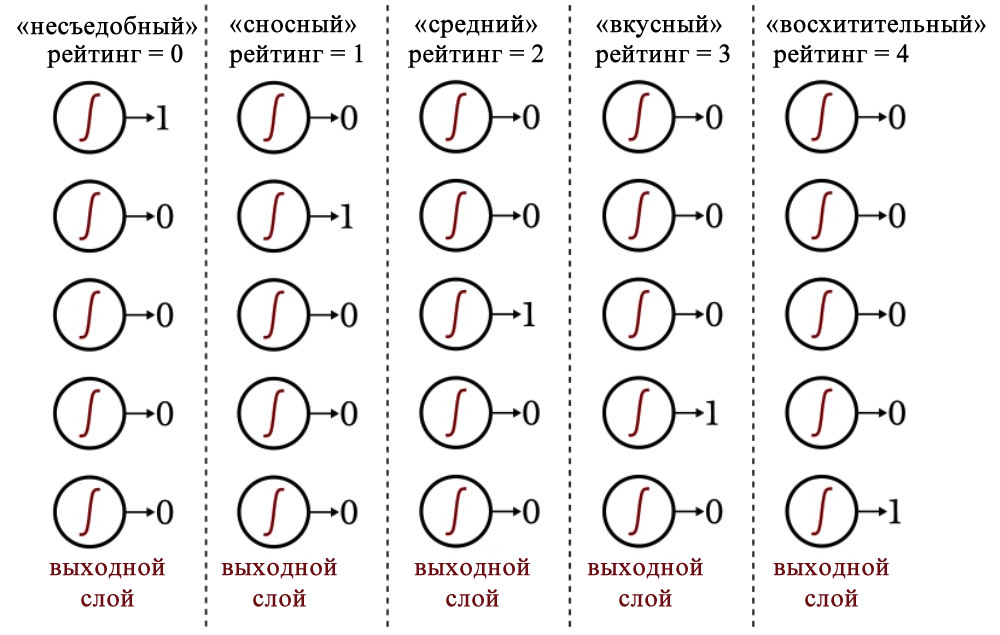
Выходная схема, использующая унитарный код, позволяет нам определить недвоичные классификации таким образом, чтобы это было совместимо с логистической сигмоидной функцией активации. Выходные данные логистической функции являются, по сути, двоичными, поскольку область перехода на графике является узкой по сравнению с бесконечным диапазоном входных значений, для которых выходное значение очень близко к минимальному или максимальному значению:
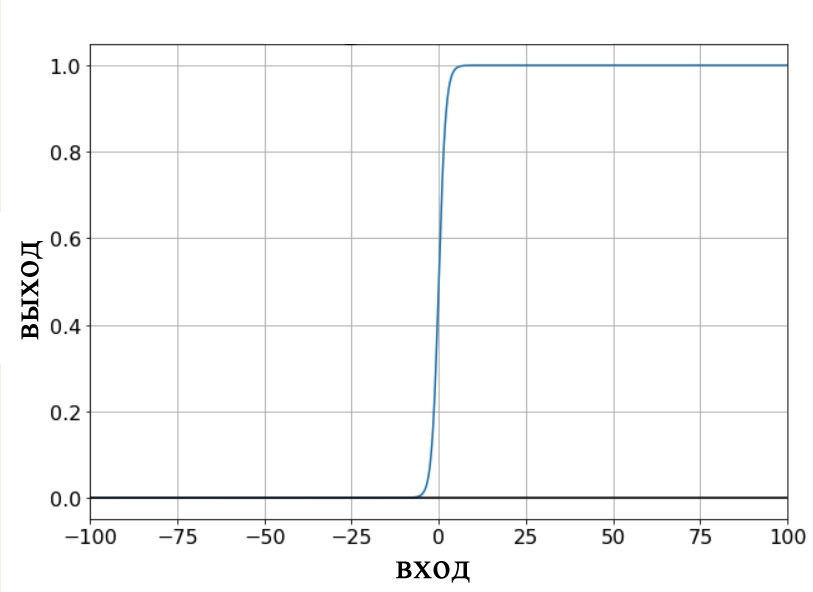
Таким образом, мы не хотим создавать эту нейросеть с одним выходным узлом, а затем предоставлять обучающие выборки, которые имеют выходные значения 0, 1, 2, 3 или 4 (или, если вы хотите оставаться в диапазоне от 0 до 1, это будут 0, 0,2, 0,4, 0,6 или 0,8), поскольку логистическая функция активации выходного узла будет устойчиво придерживаться минимального и максимального выходных значений.
Нейронная сеть просто не понимает, насколько нелепым было бы сделать вывод, что все помидоры либо несъедобны, либо восхитительны.
Создание набора обучающих данных
Нейронная сеть на Python, о которой мы говорили в части 12, импортирует обучающие выборки из файла Excel. Обучающие данные, которые я буду использовать для этого примера, организованы следующим образом:
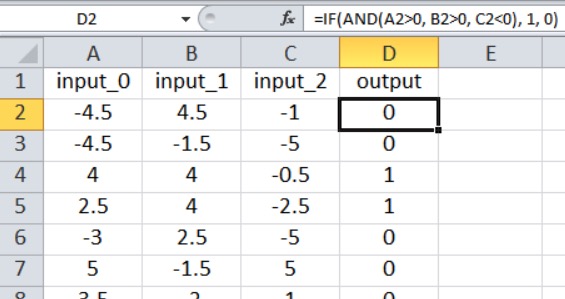
Наш текущий код для перцептрона ограничен одним выходным узлом, поэтому всё, что мы можем сделать, – это выполнить классификацию типа «истина/ложь». Входные значения – это случайные числа от –5 до +5, сгенерированные по формуле Excel:
=RANDBETWEEN(-10, 10)/2Как показано на скриншоте, результат рассчитывается следующим образом:
=IF(AND(A2>0, B2>0, C2<0), 1, 0)Таким образом, выходное значение равно true, только если input_0 больше нуля, input_1 больше нуля, а input_2 меньше нуля. В противном случае выходное значение равно false.
Это математическая связь вход-выход, которую перцептрон должен извлечь из обучающих данных. Вы можете создать столько выборок, сколько захотите. Для такой простой задачи, как эта, вы можете достичь очень высокой точности классификации с 5000 выборками и одной эпохой.
Обучение нейросети
Вам нужно установить входную размерность на три (I_dim = 3, если вы используете мои имена переменных). Я настроил нейросеть так, чтобы в ней было четыре скрытых узла (H_dim = 4), и выбрал скорость обучения 0,1 (LR = 0,1).
Найдите инструкцию training_data = pandas.read_excel(...) и введите название своей таблицы (если у вас нет доступа к Excel, библиотека Pandas также может читать файлы ODS). Затем просто нажмите кнопку «Run». Обучение с 5000 выборками занимает всего несколько секунд на моем ноутбуке.
Если вы используете полную программу «MLP_v1.py», которую я включил в часть 12, валидация(смотрите следующий раздел) начинается сразу после завершения обучения, поэтому перед тем, как приступить к обучению нейросети, вам необходимо подготовить данные валидации.
Валидация нейросети
Чтобы проверить эффективность нейросети, я создаю вторую электронную таблицу и генерирую входные и выходные значения, используя точно такие же формулы, а затем импортирую эти проверочные данные так же, как импортировал обучающие данные:
training_data = pandas.read_excel('MLP_Tdata.xlsx')
target_output = training_data.output
training_data = training_data.drop(['output'], axis=1)
training_data = np.asarray(training_data)
training_count = len(training_data[:,0])
validation_data = pandas.read_excel('MLP_Vdata.xlsx')
validation_output = validation_data.output
validation_data = validation_data.drop(['output'], axis=1)
validation_data = np.asarray(validation_data)
validation_count = len(validation_data[:,0])В следующем фрагменте кода показано, как выполнить базовую валидацию:
#####################
# проверка
#####################
correct_classification_count = 0
for sample in range(validation_count):
for node in range(H_dim):
preActivation_H[node] = np.dot(validation_data[sample,:], weights_ItoH[:, node])
postActivation_H[node] = logistic(preActivation_H[node])
preActivation_O = np.dot(postActivation_H, weights_HtoO)
postActivation_O = logistic(preActivation_O)
if postActivation_O > 0.5:
output = 1
else:
output = 0
if output == validation_output[sample]:
correct_classification_count += 1
print('Percentage of correct classifications:')
print(correct_classification_count*100/validation_count)Я использую стандартную процедуру прямого распространения для вычисления сигнала постактивации выходного узла, а затем использую оператор if/else для применения порогового значения, который преобразует значение постактивации в классификационное значение true/false.
Точность классификации вычисляется путем сравнения значения классификации с целевым значением для текущей выборки валидации, подсчета количества правильных классификаций и деления на количество выборок валидации.
Помните, что если вы закомментировали инструкцию np.random.seed(1), при каждом запуске программы веса будут инициализироваться различными случайными значениями, и, следовательно, точность классификации будет меняться от одного запуска к следующему. Я выполнил 15 отдельных запусков с параметрами, указанными выше, 5000 обучающих выборок и 1000 проверочных выборок.
Самая низкая точность классификации составила 88,5%, самая высокая – 98,1%, а средняя – 94,4%.
Заключение
Мы рассмотрели важную теоретическую информацию, относящуюся к обучающим данным нейронной сети, и провели первый эксперимент по обучению и валидации нашего многослойного перцептрона на языке Python. Я надеюсь, вам интересна эта серия статей о нейронных сетях – мы добились большого прогресса со времени первой статьи, и есть еще много, что нам нужно обсудить!
Теги
ExcelMLP, Multilayer Perceptron / Многослойный перцептронPythonЛогистическая функцияМашинное обучение / Machine LearningНейросеть / Нейронная сетьОбучающие данныеПерцептрон / PerceptronПрограммирование
В этой лекции сформулируем определения, связанные с обучающими выборками, использующимися для обучения нейронных сетей (или других методов машинного обучения).
Прежде всего, под ГЕНЕРАЛЬНОЙ совокупностью (population) понимается множество всех возможных прецедентов (объектов, ситуаций, событий, образцов и т.п.), при этом
под ВЫБОРКОЙ (sample, set) понимается конечный набор прецедентов, некоторым способом выбранных из множества ВСЕХ возможных прецедентов, т.е. это подмножество из генеральной совокупности.
ОБЩУЮ постановку задачи обучения по прецедентам (по примерам) можно сформулировать следующим образом:
ДАНО: конечное множество прецедентов (объектов, ситуаций, событий, образцов и т.п.), по каждому из которых собраны (измерены) некоторые данные (data).
Данные о прецеденте называют также его ОПИСАНИЕМ.
Совокупность ВСЕХ имеющихся описаний прецедентов называется ОБУЧАЮЩЕЙ ВЫБОРКОЙ.
ТРЕБУЕТСЯ: по частным данным выявить общие закономерности, зависимости, взаимосвязи, которые присущи не только этой конкретной выборке, но вообще всем прецедентам, в том числе тем, которые ещё не наблюдались.
ЗАМЕТИМ, что термины выборка (sample, set) и данные (data) взаимозаменяемы, при этом они иногда употребляются вместе как один термин ВЫБОРКА ДАННЫХ (data set).
Поговорим об описаниях.
Наиболее распространённым СПОСОБОМ описания прецедентов (объектов, ситуаций, событий, образцов и т.п.) является так называемое признаковое описание, суть которого заключается в фиксировании совокупности n показателей, которые можно каким-нибудь образом получить, например, измерить, вычислить, собрать статистику или каким-то другим образом получить для КАЖДОГО прецедента (объекта, ситуации, события, образца и т.п.).
ЗАМЕТИМ, что в случае, когда все n показателей числовые, то признаковые описания представляют собой числовые векторы размерности n.
Более того, признаковые описания называются обучающими векторами или обучающей парой {вход, выход}, где входом является многомерная совокупность показателей, а выход (может также быть многомерным) – рассчитывается, измеряется и т.д. для конкретной совокупности показателей.
ЗАМЕТИМ также, что прецеденты также могут описываться временнЫми рядами, сигналами, изображениями, информацией в текстовой форме и т.д.
Какие бы ни были признаковые описания, часто они требуют предварительной обработки с целью «улучшения» восприятия нейронной сетью (или другими алгоритмами машинного обучения).
Существует несколько способов такого улучшения «восприятия».
1. Нормировка выполняется в случаях, когда на различные входы подаются данные разной размерности. Например, на первый вход нейронной сети подаются значения от 0 до 1, а на второй – от 100 до 1000. если не производить нормировку, то значения на втором входе будут оказывать существенно бОльшее влияние на выход, чем значения на первом входе.
2. Квантование (от англ. quantization), представляющее собой разбиение на некоторое конечное число интервалов, выполняется над НЕПРЕРЫВНЫМИ величинами, для которых выделяется конечный набор дискретных значений. Например, квантование используют для задания частот звуковых сигналов при распознавании речи.
3. Фильтрация выполняется для «зашумленных» данных.
Полученная ВЫБОРКА (sample, set), т.е. конечный набор прецедентов (объектов, ситуаций, событий, образцов и т.п.) из генеральной совокупности делится на следующие части:
1. Непосредственно «Обучающая выборка» (training sample), которая представляет ту часть выборки, по которой производится настройка (оптимизация параметров) нейронной сети (или другого метода машинного обучения).
Для анализа результатов (в том числе определения наличия такого явления как переобучение, когда нейронная сеть (или другой метод машинного обучения) выдаёт хороший результат на примерах из обучающей выборки, но относительно плохо работает на примерах, не участвовавших в обучении (не входивших в обучающую выборку), что свидетельствует о низком качестве обобщения.
Хорошую эмпирическую оценку качества обучения нейронной сети (или другого метода машинного обучения) даёт проверка на независимых данных, т.е. на примерах (прецедентах), которые не использовались для обучения.
2. Тестовая (или контрольная) выборка (test sample) – та часть выборки, по которой оценивается качество обученной нейронной сети (или другого метода машинного обучения).
ЗАМЕТИМ, что оценку качества обученной нейронной сети (или другого метода машинного обучения), сделанную по тестовой выборке, можно применить для выбора наилучшей модели.
3. Проверочная выборка (validation sample) – та часть выборки, по которой осуществляется выбор наилучшей модели нейронной сети (или другого метода машинного обучения) из множества всех моделей, построенных по обучающей выборке.
Рассмотрим факторы, от которых зависит успешность обучения нейронной сети (или другого метода машинного обучения).
I. Нейронная сеть должна быть достаточно ГИБКОЙ, чтобы научиться правильно решать все примеры из обучающей выборки, поэтому в нейронной сети должно быть достаточное число нейронов и связей.
II. Обучающая выборка должна быть непротиворечивой, т. е. в обучающей выборке должны отсутствовать одинаковые входные векторы данных с соответствующими РАЗНЫМИ выходными.
В случае с противоречивыми данными нейронная сеть (или другой метод машинного обучения) не сможет качественно обучиться даже при увеличении числа слоёв и нейронов в слоях.
Появление таких конфликтных примеров может также означать недостаточность набора входных признаков, поскольку при расширении признакового пространства конфликтным примерам могут соответствовать разные значения добавляемого признака и критическая ситуация будет исчерпана.
В любом случае перед обучением необходимо проанализировать обучающую выборку и чаще всего противоречивость примеров решается путём исключения (удаления) конфликтных примеров из обучающей выборки.
Обучающая выборка должна быть репрезентативной, что означает, что данные должны иллюстрировать истинное положение вещей в предметной области.
III. После обучения нейронной сети (или другого метода машинного обучения) необходимо провести ее тестирование на тестовой (или даже контрольной) выборке для определения точности решения не входивших в обучающую выборку задач.
Точность правильного решения очень сильно зависит от репрезентативности обучающей выборки, когда обучающая выборка не охватывает всего множества ситуаций (выборка мала или просто узкоспециализирована). Например, при решении задачи классификации причиной большого числа ошибок может быть неодинаковое число примеров представителей разных классов классифицируемых объектов. Если выборка нерепрезентативна, то при тестировании нейронная сеть (или другой метод машинного обучения) будет достаточно хорошо распознавать примеры класса, для которого в обучающей выборке было много примеров, и относить к этому же классу примеры из другого класса только потому, что для него было мало примеров. Поэтому при решении задачи классификации необходимо, чтобы в обучающей выборке было примерно одинаковое число примеров для каждого класса.
В качестве упражнения предлагается записать в комментарии пример признакового описания для решения какой-нибудь интересной для Вас задачи. Какую при этом совокупность n показателей необходимо определить у прецедентов?
На предыдущем
занятии мы познакомились с алгоритмом обучения back propagation, но рассмотрели
его лишь в целом, чтобы мы с вами понимали принцип его работы. Теперь, пришло
время немного погрузиться в детали этого процесса и узнать:
-
как
оптимизировать алгоритм градиентного спуска для ускорения обучения; -
как
инициализировать начальные значения весовых коэффициентов; -
как
выполнять стандартизацию входных данных; -
как
готовить обучающую выборку и как ее подавать на вход сети; -
какую
функцию активации нейронов выбрать; -
когда
останавливать процесс обучения; -
какие
критерии качества обучения использовать.
Без знания этих
моментов, провести качественное обучение НС практически невозможно. Поэтому,
для полноты картины, мне придется дать некоторый теоретический материал, чтобы
вы могли ориентироваться в этих вопросах. Возможно, вам это покажется несколько
скучным, но, знаете, яркие эффекты – это лишь вершина айсберга, в основании
очень много подготовительного материала и кропотливой работы по проектированию
и обучению сетей. Так что, если вы решили пойти по этому пути и начать работать
в данной области, то без базовой математической подготовки, знания основных
моментов и наработки опыта, тут никуда.
Итак, начнем с
основной «рабочей лошадки» – алгоритма обратного распространения, который
базируется на алгоритме градиентного спуска. Но раз используется градиентный спуск,
то мы сразу получаем все его проблемы реализации. Главная – это попадание в
локальный минимум выбранного критерия качества E.
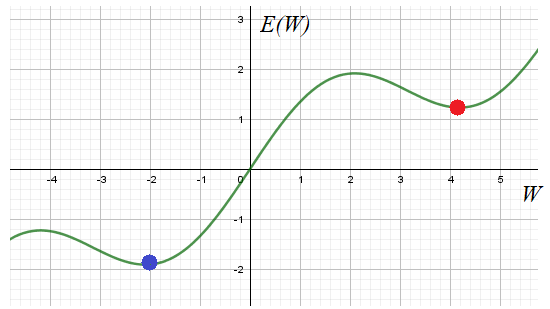
Общего решения
этой проблемы нет. Поэтому на практике запускают алгоритм обучения с разными
начальными значениями весовых коэффициентов. Тем самым мы, как бы выбираем
разные отправные точки на функции E в надежде, что одно из решений
достигнет глобального минимума. Хотя, точно узнать: достигли мы дна или нет не
представляется возможным. Поэтому процесс обучения останавливают, если
достигается требуемое качество работы НС.
Отсюда получаем рекомендацию
обучения №1:
Запускать алгоритм для разных начальных значений весовых
коэффициентов. И, затем, отобрать лучший вариант. Начальные значения генерируем
случайным образом в окрестности нуля, кроме тех, что относятся к bias’ам.
У вас может
возникнуть вопрос: почему начальные значения весов нужно брать малыми?
Смотрите, допустим, используется логистическая функция активации:
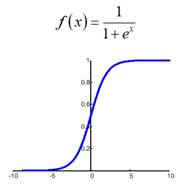
Если веса
изначально буду значимыми, то часто суммарный сигнал на входе нейронов будет
оказываться большим по модулю:
![]()
И мы попадаем на
пологий участок функции активации. К чему это потом приводит? В процессе
обучения градиент этого участка будет мал, а значит, веса будут медленно
изменяться, что приведет к торможению обучения НС в целом. Чтобы этого
избежать, мы, как раз и выбираем веса с малыми случайными значениями, и
оказываемся на более выгодном крутом участке кривой. Bias же (смещения
разделяющих гиперплоскостей) могут быть и с большими значениями, т.к. они
отвечают именно за смещение разделяющей гиперплоскости и оно может быть
значительным.
Другая проблема градиентных
алгоритмов – медленная сходимость на пологих участках функции:
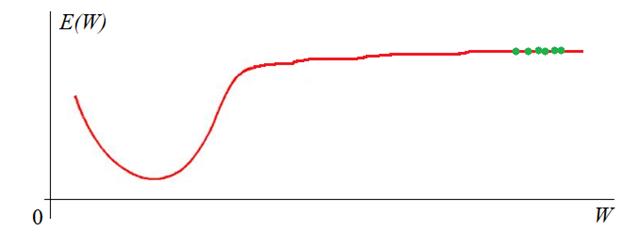
Для ее решения
было предложено множество подходов. Среди них наиболее известные, следующие:
-
оптимизация
на основе моментов (momentum); -
ускоренные
градиенты Нестерова (nesterov momentum); -
метод
Adagrad; -
методы
RMSProp и Adadelta; -
метод
Adam и NAdam.
О первых двух я
рассказывал на занятии по градиентному спуску:
Почему так важно
знать об этих методах оптимизации? Дело в том, что многие пакеты реализации и
обучения НС, например,
Keras или TFLearn
позволяют
использовать их для ускорения и улучшения обучения. Чаще всего применяется
оптимизация по Нестерову и Adam’у. Позже, когда мы будем рассматривать один
из этих пакетов, я покажу где и как настраиваются эти параметры.
Итак, рекомендация
обучения №2:
Запускаем алгоритм обучения с оптимизацией по Adam или Нестерову
для ускорения обучения НС.
Входные значения
Предположим, что
у нас имеется обучающая выборка с N наблюдениями:
|
Номер |
Входной |
Отклик |
|
1 |
|
|
|
2 |
|
|
|
… |
… |
… |
|
N |
|
|
Стоит ли нам
подавать значения ![]() этой
этой
выборки так как они есть? Так делать не рекомендуется. В общем случае, среди
этих величин могут оказаться большие значения и они нас сразу переместят в
область насыщения функции активации, где производная практически равна нулю:
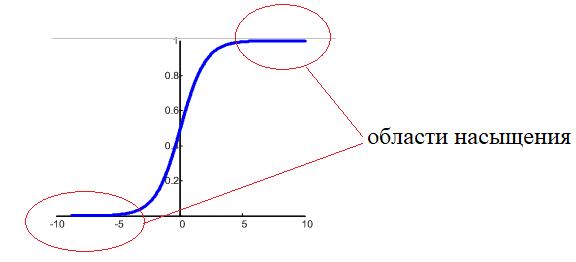
Поэтому на
практике выполняют предварительную стандартизацию входных значений, например,
по формуле:
![]()
Здесь max, min – максимальное
и минимальное значения входных данных по всему обучающему множеству. В
результате, входные данные при обучении будут находиться в диапазоне от 0 до 1.
И здесь
начинающие нейронщики часто делают одну важную ошибку. После обучения НС в
режиме ее эксплуатации забывают о нормализации данных на ее входах. Раз уж сеть
обучена на нормированных значениях, то и потом, при ее непосредственной работе,
данные также нужно нормировать. Об этом забывать не стоит. И, кроме того,
нормировку следует делать через те же самые параметры min и max, которые были
использованы в обучающей выборке! А не пересчитывать их заново!
Рекомендация
обучения №3:
Выполнять нормировку входных значений и запоминать нормировочные
параметры min, max из обучающей выборки.
Как создавать и подавать обучающую выборку
Следующий важный
вопрос: что из себя должна представлять обучающая выборка? Какие данные в нее
следует поместить? Ответить можно так: чем больше разных наблюдений будет при
обучении, тем выше качество работы сети. Здесь ключевое слово – разных,
то есть, выборка должна охватывать самые разные «ситуации» в процессе обучения
и эти «ситуации» должны появляться с равной частотой. Например, представьте,
что вы учитесь водить машину, но ваш инструктор выбирает перекрестки только со
светофором. Как думаете, сможете вы себя потом уверенно чувствовать на
нерегулируемых перекрестках? Вряд ли. Я бы не смог. С нейросетью также: если в
процессе эксплуатации будут попадаться входные данные, сильно отличающиеся от
обучающей выборки, то высока вероятность возникновения ошибки. Или, другой
пример. Ваш инструктор для «галочки» лишь показал как проезжать нерегулируемые
перекрестки, но вы все равно, в основном проезжали по регулируемым со
светофором. Здесь качество обучения также будет невысоким, т.к. навыка проезда
обычных перекрестков будет недостаточно. Поэтому желательно, чтобы в обучающей
выборке с равной частотой встречались самые разные данные, описывающие какие-то
характерные, особенные, частные ситуации.
Рекомендация обучения №4:
Помещать в обучающую выборку самые разнообразные данные примерно
равного количества.
Хорошо, с этим
разобрались, но какой объем обучающей выборки N следует брать? По
идее, чем больше, тем лучше. Например, в литературе отмечают, что при
классификации картинок (например, на мужчин и женщин, или кошек и собак и т.п.)
необходимо по 5 000 000 наблюдений для каждого класса, тогда можно
достичь хороших результатов различения. Если увеличить этот объем до
10 000 000, то есть шанс обучить нейросеть распознавать образы лучше
человека. Вас, возможно, удивят такие большие цифры? Да, это так, данные для
обучения – это как нефть «черное золото» для нашей экономики, они ценятся очень
высоко, а их подготовка может потребовать немалых ресурсов и времени. Это еще
одна причина, по которой нейронные сети лишь недавно завоевали свое место под
солнцем: раньше практически невозможно было получить столько реальных данных.
Теперь же, сеть Интернет, в частности, социальные сети, предоставляют весьма
богатый материал.
Итак,
предположим, что мы создали обучающую выборку и собираемся приступить к
обучению. Здесь возникает новый вопрос: как ее подавать на вход сети? В самом
простом варианте, мы сначала перемешиваем наблюдения в выборке (чтобы они шли в
случайном порядке), а затем поочередно подаем на вход. При этом для каждого
наблюдения выполняем корректировку весовых коэффициентов. Именно так мы делали
на предыдущем занятии.
Но это не самый
лучший вариант. Было замечено, что в процессе обучения часть наблюдений дают
небольшой положительный прирост весовых коэффициентов, часть – небольшой
отрицательный. В сумме они практически компенсируют друг друга и изменение
весов практически не происходит. И лишь некоторая часть наблюдений из выборки
приводит к их заметному изменению. Чтобы не «крутить» вхолостую весовые
коэффициенты, коррекцию выполняют не сразу для каждого наблюдения, а после
прогонки через сеть некоторого их количества. Такое множество получило название
batch или, в
последнее время чаще стали говорить mini–batch. А вся выборка
получила название эпоха. Так вот, прогоняя mini-batch через сеть,
суммируют локальные градиенты на каждом нейроне (я думаю вы помните, что это
такое из предыдущего занятия), а затем, корректируют веса по результирующей их
сумме. В процессе такого суммирования небольшие положительные и отрицательные
значения будут скомпенсированы и останется полезное смещение, которое и приведет
к изменению весов в пределах mini-batch.
Такая идея
позволила сократить время обучения в разы, что очень важно, так как для больших
НС общее время обучения составляет иногда дни, недели и даже месяцы. Поэтому
сокращение этого времени в несколько раз открывает новые горизонты применения
НС.
Когда
целесообразно разбивать выборку на серию mini-batch? Считается, что
для этого общее число выборки должно составлять от нескольких тысяч и более.
Если наблюдений меньше, порядка тысячи, то ее можно воспринимать как один
единственный mini-batch.
Итак, мы
получаем рекомендацию обучения №5:
Наблюдения на вход сети подавать случайным образом, корректировать веса после серии наблюдений, разбитых на mini-batch.
Значение
критерия качества вычисляется только после прогонки всей эпохи. Если оно нас не
устраивает (как правило, так и есть), то наблюдения снова тасуются случайным
образом и обучение продолжается. В конце каждой эпохи снова и снова
пересчитывается критерий качества. Получается такой график:
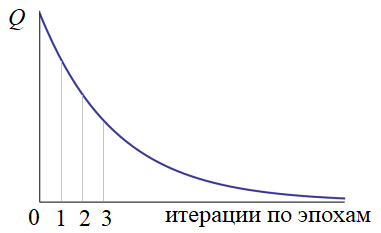
Конечно, это
идеализированный график. В реальности он, конечно, не такой гладкий и
монотонный. Нередки случаи когда он может внезапно возрастать. Но об этом мы
поговорим в другой раз. На следующем продолжим
рассматривать эти, достаточно важные вопросы, без знания которых начинать
работать с нейросетями не имеет особого смысла.
