Составление дополнительного ограничения (сечения Гомори)
Пусть
оптимальный план, полученный
симплекс-методом для задачи (5.1)-(5.3),
следующий:
![]()
и получен на базисе
![]() Тогда последняя симплексная таблица
Тогда последняя симплексная таблица
имеет следующий вид:
Таблица 5.1
Приведённая
к базису симплексная таблица для задачи
целочисленного программирования

Предположим,
что
![]() дробное;
дробное;
тогда некоторое![]() также дробное (в противном случае задача
также дробное (в противном случае задача
не имеет целочисленного решения).
Обозначим через![]() и
и![]() целые части чисел
целые части чисел![]() и
и![]() ,
,
т.е. наибольшие целые числа, не
превосходящие числа![]() и
и![]() .
.
Тогда величины дробных частей![]() и
и![]() чисел
чисел![]() и
и![]() определяются как разности:
определяются как разности:
![]() где
где
![]()
и
![]()
Например,
![]()
![]() .
.
Так
как по условию
![]() – неотрицательные целые числа, то и
– неотрицательные целые числа, то и
разность![]() также целое неотрицательное число.
также целое неотрицательное число.
Преобразуя
это неравенство в уравнение, вычитая
из его левой части целую неотрицательную
дополнительную переменную
![]() умножим уравнение на –1, добавим к
умножим уравнение на –1, добавим к
последней симплексной таблице и, применяя
симплексный метод (желательно
двойственный), находим новый план. Если
он не является целочисленным, то по
последней симплексной таблице составляем
новое дополнительное ограничение.
Если
в оптимальном плане задачи (5.1)-(5.3)
несколько дробных
![]() то дополнительное ограничение составляют
то дополнительное ограничение составляют
дляmax![]() .
.
Это ускоряет процесс получения
оптимального целочисленного решения.
Рассмотрим
геометрический смысл введения
дополнительного ограничения (см. рис.
5.2). Пусть в точке A
многогранника
решений Q
функция Z
достигает максимального значения
Z(A)=max,
но координаты точки A
– дробные. Тогда введенные ограничения
по целочисленности I
и II
от области
Q
отсекают область
![]() с угловой точкой
с угловой точкой![]() ,
,
координаты которой целочисленные и в
которой линейная функция достигает
максимального значения.
Рис.5.2.
Геометрический смысл ограничения Гомори
Метод
Гомори рассмотрим на примере следующей
задачи.
Пример
5.1. Найти
максимальное значение функции
|
|
(5.5) |
при
условиях
|
|
(5.6) |
|
|
(5.7) |
|
|
(5.8) |
Дать геометрическую
интерпретацию решения задачи.
Решение.
Для определения оптимального плана
задачи (5.5)-(5.8) сначала находим оптимальный
план задачи (5.5)-(5.7):
Таблица 5.2
Симплекс-таблица,
приведённая к базису
![]()
-
x1
x2
x3
x4
x5
1
1
1
0
0
13
1
-1
0
1
0
6
-3
1
0
0
0
9
3
2
0
0
1
0
![]() базис
базис
![]()
план
![]() – неоптимальный,
– неоптимальный,
![]() .
.
Таблица 5.3
Симплекс-таблица,
приведённая к базису
![]()
-
x1
x2
x3
x4
x5
0
2
1
-1
0
7
1
-1
0
1
0
6
0
-2
0
3
1
27
0
5
0
-3
0
-18
![]() ,
,
![]() – неоптимальный,
– неоптимальный,
базис
![]() ,
,
![]() .
.
Таблица 5.4
Симплекс-таблица,
приведённая к базису
![]()
-
x1
x2
x3
x4
x5
0
1
1/2
-1/2
0
7/2
1
0
1/2
½
0
19/2
0
0
1
2
1
34
0
0
-5/2
-1/2
0
-71/2
Оптимальный
план
![]() ,
,
базис![]() .
.
Этот оптимальный план не является
оптимальным планом задачи (5.5)-(5.8),
поскольку две компоненты![]() и
и![]() имеют нецелочисленное значение. При
имеют нецелочисленное значение. При
этом дробные части этих чисел![]() равны между собой. Поэтому для одной из
равны между собой. Поэтому для одной из
этих переменных составляется дополнительное
ограничение. Составим, например, такое
ограничение для переменной![]() (чаще берут первую строку). Из последнейсимплекс-таблицы
(чаще берут первую строку). Из последнейсимплекс-таблицы
имеем:
![]() .
.
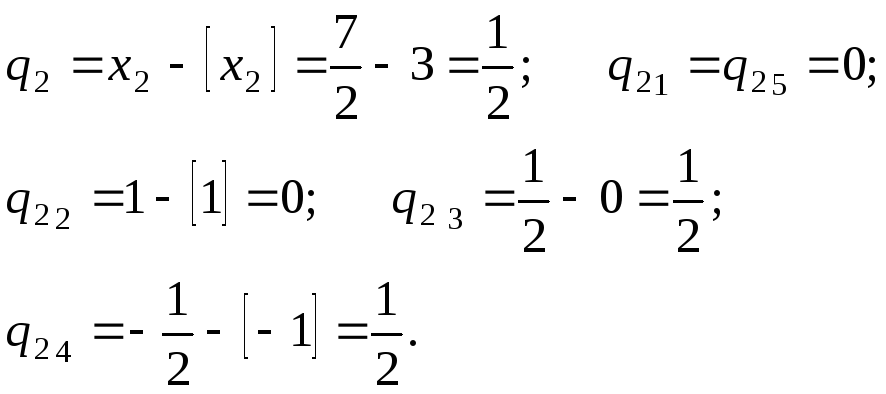
Таким
образом, к системе ограничений задачи
(5.5)-(5.7) добавляем неравенство
![]()
т. е.
|
|
(5.9) |
Теперь
находим максимальное значение функции
(5.5) при выполнении условий (5.6), (5.7) и
(5.9). В условие (5.9) вводим дополнительную
переменную
![]() :
:
Таблица
5.5
Ввод
в симплекс-таблицу дополнительной
переменной
![]()
-
x1
x2
x3
x4
x5
x6
0
1
0
0
1
0
0
0
1/2
1/2
1
1
-1/2
1/2
2
1
0
0
1
0
0
0
0
-1
7/2
19/2
34
1
0
0
-5/2
-1/2
0
0
-71/2
![]() Выберем
Выберем
![]() .
.![]()
базис.
Таблица 5.6
Приведение
симплекс-таблицы к базису
![]()
-
x1
x2
x3
x4
x5
x6
0
1
0
0
1
0
0
0
1
0
-1
1
0
0
0
1
0
0
1
0
-1/2
1/2
2
-1
4
9
32
1
0
0
-2
0
0
-1/2
-35
Базис
![]() .
.![]() .
.
Запишем
оптимальный план для исходной задачи:
![]()
При этом плане значение целевой функции
равно
![]() .
.
Геометрическая
интерпретация решения задачи.
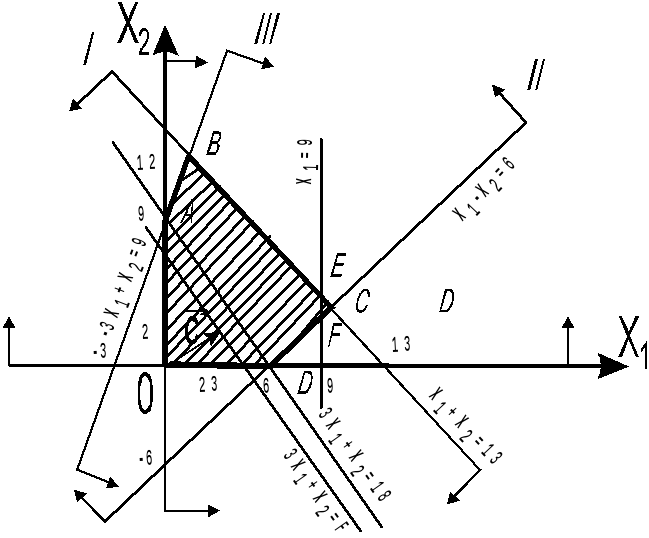
Рис.5.3. Геометрическая
интерпретация решения задачи
Областью
допустимых решений задачи (5.5)-(5.7) является
многоугольник ОАВСD
(рис. 5.3). Из рисунка видно, что максимальное
значение целевая функция принимает в
точке
![]() т.е.
т.е.![]() является оптимальным планом. Так как
является оптимальным планом. Так как
этот план не является оптимальным планом
задачи (5.5)-(5.8) (числа![]() и
и![]() –
–
дробные), то вводится дополнительное
ограничение
![]()
Исключая
из этого неравенства
![]() и
и![]() подстановкой вместо них соответствующих
подстановкой вместо них соответствующих
значений из уравнений системы ограничений
(5.6), получим![]() .
.
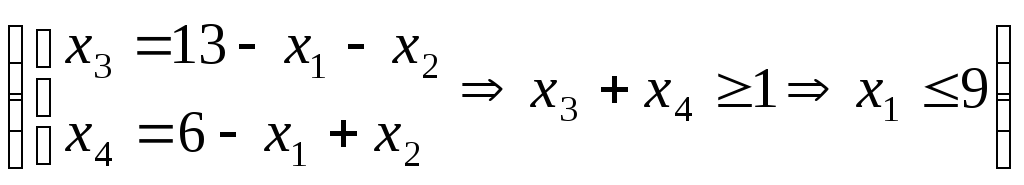 .
.
Этому
неравенству соответствует полуплоскость,
ограниченная прямой
![]() отсекающей отмногоугольника
отсекающей отмногоугольника
ОАВСD
треугольник
EFC.
Как
видно из рисунка, областью допустимых
решений полученной задачи является
многоугольник OABEFD.
В точке E(9;4)
этого многоугольника целевая функция
данной задачи принимает максимальное
значение. Так как координаты точки Е
– целые числа и неизвестные
![]() и
и![]() принимают целочисленные значения при
принимают целочисленные значения при
подстановке в уравнения (5.6) значений![]() и
и![]() то
то![]() является оптимальным планом задачи
является оптимальным планом задачи
(5.5)-(5.8). Это следует и из таблицы
симплекс-метода.
Замечание
к использованию метода Гомори: если в
первоначальный базис задачи входили
искусственные векторы, то при составлении
дополнительного ограничения искусственные
переменные необходимо опустить.
Вопросы для
самопроверки
-
Области применения
целочисленного программирования. -
Постановка задачи
целочисленного программирования. -
Графический
способ решения задачи целочисленного
программирования. -
Алгоритм метода
Гомори. -
Правило
составления дополнительного ограничения
(сечения Гомори). -
Геометрический
смысл введения сечения Гомори.
Соседние файлы в папке Учебники и пособия
- #
- #
Содержание:
Исследование различных процессов, в том числе и экономических, обычно начинается с их моделирования, т.е. отражения реального процесса через математические соотношения. При этом составляются уравнения или неравенства, которые связывают различные показатели (переменные) исследуемого процесса, образуя систему ограничений. В этих процессах выделяются такие переменные, меняя которые можно получить оптимальное значение основного показателя данной системы (прибыль, доход, затраты и т.д.). Соответствующие методы, позволяющие решать указанные задачи, объединяются под общим названием «математическое программирование» или математические методы исследования операций.
Математическое программирование включает в себя такие разделы математики, как линейное, нелинейное и динамическое программирование. Сюда же относят и стохастическое программирование, теорию игр, теорию массового обслуживания, теорию управления запасами и некоторые другие.
Математическое программирование – это раздел высшей математики, посвященный решению задач, связанных с нахождением экстремумов функций нескольких переменных, при наличии ограничений на переменные.
Методами математического программирования решаются задачи о распределении ресурсов, планировании выпуска продукции, ценообразования, транспортные задачи и т.д.
Построение математической модели экономической задачи включает следующие этапы:
- выбор переменных задачи;
- составление системы ограничений;
- выбор целевой функции.
Переменными задачи называются величины 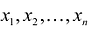
Система ограничений включает в себя систему уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов или других экономических или физических условий, например, положительности переменных и т.п.
Целевой функцией называют функцию переменных задачи, которая характеризует качество выполнения задачи, и экстремум которой требуется найти.
Общая задача математического программирования формулируется следующим образом: найти экстремум целевой функции: 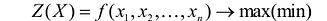 и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:
и соответствующие ему переменные при условии, что эти переменные удовлетворяют системе ограничений:
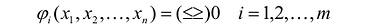
Если целевая функция и система ограничений линейны, то задача математического программирования называется задачей линейного программирования и в общем виде может быть записана следующим образом:
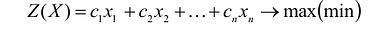
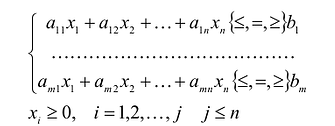
Данная запись означает следующее: найти экстремум целевой функции задачи и соответствующие ему переменные X = (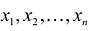 ). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.
). при условии, что эти переменные удовлетворяют системе ограничений и условиям неотрицательности.
Допустимым решением (планом) задачи линейного программирования называется любойX = (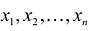 ). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.
). удовлетворяющий системе ограничений и условиям неотрицательности. Множество допустимых решений (планов) задачи образует область допустимых решений.
Оптимальным решением (планом) задачи линейного программирования называется такое допустимое решение задачи, при котором целевая функция достигает экстремума.
Задача линейного программирования
В общем случае задача линейного программирования записывается так, что ограничениями являются как уравнения, так и неравенства, а переменные могут быть как неотрицательными, так и произвольно изменяющимися. В случае, когда все ограничения являются уравнениями и все переменные удовлетворяют условию неотрицательности, задачу линейного программирования называют канонической. Каноническая задача линейного программирования в координатной форме записи имеет вид:
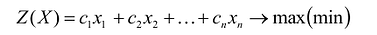
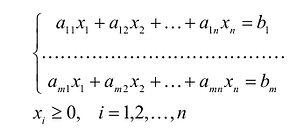
Используя знак суммирования эту задачу можно записать следующим образом:
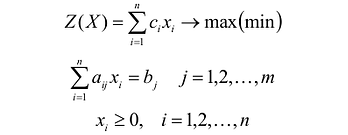
Каноническая задача линейного программирования в векторной форме имеет вид:
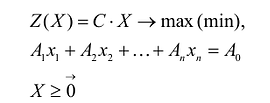
В данном случае введены векторы:
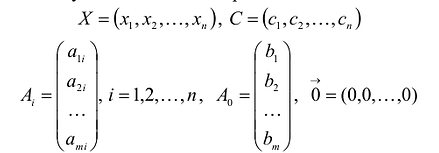
Здесь С – X – скалярное произведение векторов С и X.
Каноническая задача линейного программирования в матричной форме записи имеет вид:
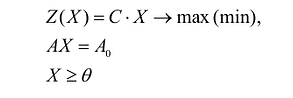
где:
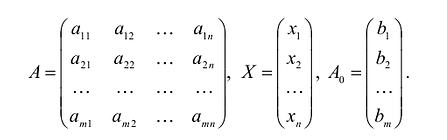
Здесь А – матрица коэффициентов системы уравнений, X -матрица-столбец переменных задачи; 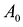 – матрица-столбец правых частей системы ограничений.
– матрица-столбец правых частей системы ограничений.
Нередко используются задачи линейного программирования, называемые симметричными, которые в матричной форме записи имеют вид:
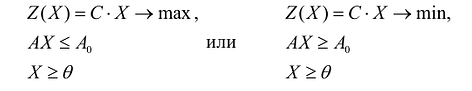
Приведение общей задачи линейного программирования к канонической форме
В большинстве методов решения задач линейного программирования предполагается, что система ограничений состоит из уравнений и естественных условий неотрицательности переменных. Однако, при составлении математических моделей экономических задач ограничения в основном формулируются системы неравенств, поэтому возникает необходимость перехода от системы неравенств к системе уравнений. Это может быть сделано следующим образом. К левой части линейного неравенства:
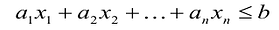 прибавляется величина
прибавляется величина 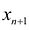 такая, что переводит неравенство в равенство
такая, что переводит неравенство в равенство 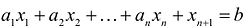 , где:
, где: 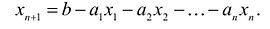
Неотрицательная переменная  называется дополнительной переменной.
называется дополнительной переменной.
Основания для возможности такого преобразования дает следующая теорема.
Теорема. Каждому решению  неравенства
неравенства 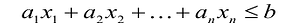 соответствует единственное решение
соответствует единственное решение 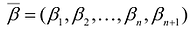 уравнения:
уравнения: 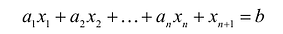 и неравенства
и неравенства 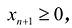 и, наоборот, каждому решению
и, наоборот, каждому решению  уравнения:
уравнения: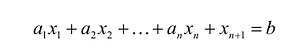 и неравенства
и неравенства  соответствует единственное решение
соответствует единственное решение 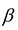 неравенства:
неравенства: 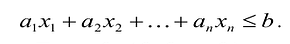
Доказательство. Пусть  – решение неравенства
– решение неравенства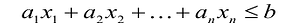 . Тогда:
. Тогда: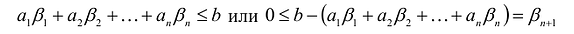
Если в уравнение 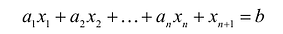 вместо переменных подставить значения
вместо переменных подставить значения 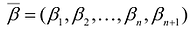 , получится:
, получится:
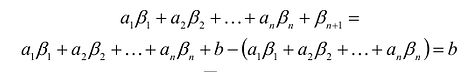
Таким образом, решение  удовлетворяет уравнению:
удовлетворяет уравнению: 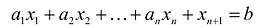 и неравенству
и неравенству  .
.
Доказана первая часть теоремы.
Пусть  удовлетворяет уравнению
удовлетворяет уравнению 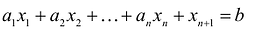 и неравенству
и неравенству  , т.е.
, т.е. 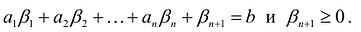 . Отбрасывая в левой части равенства неотрицательную величину
. Отбрасывая в левой части равенства неотрицательную величину 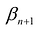 , получим:
, получим: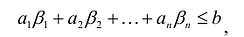
т.е.  удовлетворяет неравенству:
удовлетворяет неравенству: 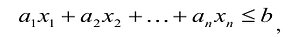 что и требовалось доказать.
что и требовалось доказать.
Если в левую часть неравенств системы ограничений вида 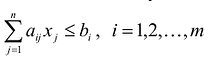
добавить переменную 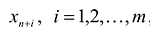 , то получится система ограничений – уравнений
, то получится система ограничений – уравнений 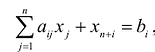
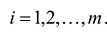 В случае, если система неравенств-ограничений имеет вид
В случае, если система неравенств-ограничений имеет вид 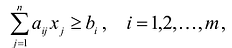 , то из левой части неравенств-ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную
, то из левой части неравенств-ограничений нужно вычесть соответствующую неотрицательную дополнительную переменную 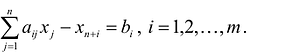
Полученная таким образом система уравнений-ограничений, вместе с условиями неотрицательности переменных, т.е. 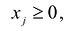
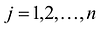 и целевой функцией является канонической формой записи задачи линейного программирования.
и целевой функцией является канонической формой записи задачи линейного программирования.
Дополнительные переменные вводятся в целевую функцию с нулевыми коэффициентами и поэтому не влияют на ее значения.
В реальных практических задачах дополнительные неизвестные имеют определенный смысл. Например, если левая часть ограничений задачи отражает расход ресурсов на производство продукции в объемах 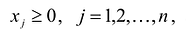 , а правые части – наличие производственных ресурсов, то числовые значения дополнительных неизвестных
, а правые части – наличие производственных ресурсов, то числовые значения дополнительных неизвестных 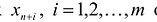 и означают объем неиспользованных ресурсов i-го вида.
и означают объем неиспользованных ресурсов i-го вида.
Иногда возникает также необходимость перейти в задаче от нахождения минимума к нахождению максимума или наоборот. Для этого достаточно изменить знаки всех коэффициентов целевой функции на противоположные, а в остальном задачу оставить без изменения. Оптимальные решения полученных таким образом задач на максимум и минимум совпадают, а значения целевых функций при оптимальных решениях отличаются только знаком.
Множества допустимых решений
Множество точек называется выпуклым, если оно вместе с любыми двумя своими точками содержит их произвольную выпуклую линейную комбинацию.
Выпуклой линейной комбинацией произвольных точек 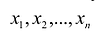 Евклидова пространства
Евклидова пространства 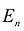 называется сумма
называется сумма 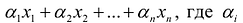 – произвольные неотрицательные числа, сумма которых равна 1.
– произвольные неотрицательные числа, сумма которых равна 1.
Геометрически это означает, что если множеству с любыми двумя его произвольными точками полностью принадлежит и отрезок, соединяющий эти точки, то оно будет выпуклым. Например, выпуклыми множествами являются прямолинейный отрезок, прямая, круг, шар, куб, полуплоскость, полупространство и др.
Точка множества называется граничной, если любая окрестность этой точки сколь угодно малого размера содержит точки, как принадлежащие множеству, так и не принадлежащие ему.
Граничные точки множества образуют его границу. Множество называется замкнутым, если оно содержит все свои граничные точки.
Ограниченным называется множество, если существует шар с радиусом конечной длины и центром в любой точке множества, содержащий полностью в себе данное множество. В противном случае множество будет неограниченным.
Пересечение двух или более выпуклых множеств будет выпуклым множеством, так как оно отвечает определению выпуклого множества.
Точка выпуклого множества называется угловой, если она не может быть представлена в виде выпуклой линейной комбинации двух других различных точек этого множества.
Так, угловые точки треугольника – его вершины, круга – точки окружности, ее ограничивающие, а прямая, полуплоскость, плоскость, полупространство, пространство не имеют угловых точек.
Выпуклое замкнутое ограниченное множество на плоскости, имеющее конечное число угловых точек, называется выпуклым многоугольником, а замкнутое выпуклое ограниченное множество в трехмерном пространстве, имеющее конечное число угловых точек, называется выпуклым многогранником.
Теорема. Любая тонка многоугольника является выпуклой линейной комбинацией его угловых точек.
Теорема. Область допустимых решений задачи линейного программирования является выпуклым множеством.
Уравнение целевой функции при фиксированных значениях самой функции является уравнением прямой линии (плоскости, гиперплоскости и т.д.). Прямая, уравнение которой получено из целевой функции при равенстве ее постоянной величине, называется линией уровня.
Линия уровня, имеющая общие точки с областью допустимых решений и расположенная так, что область допустимых решений находится целиком в одной из полуплоскостей, называется опорной прямой.
Теорема. Значения целевой функции в точках линии уровня увеличиваются, если линию уровня перемещать параллельно начальному положению в направлении нормали и убывают при перемещении в противоположном направлении.
Теорема. Целевая функция задачи линейного программирования достигает экстремума в угловой точке области допустимых решений; причем, если целевая функция достигает экстремума в нескольких угловых точках области допустимых решений, она также достигает экстремума в любой выпуклой комбинации этих точек.
Опорное решение задачи линейного программирования, его взаимосвязь с угловыми точками
Каноническая задача линейного программирования в векторной форме имеет вид:
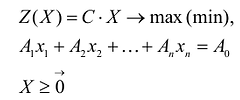
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.
Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное 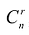 , где n – число неизвестных, r- ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
, где n – число неизвестных, r- ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.
Опорным решением задачи линейного программирования называется такое допустимое решение  , для которого векторы условий, соответствующие положительным координатам
, для которого векторы условий, соответствующие положительным координатам  линейно независимы.
линейно независимы.
Число отличных от нуля координат опорного решения не может превосходить ранга r системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).
Если число отличных от нуля координат опорного решения равно m, то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше т, такое решение называется вырожденным.
Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.
Теорема. Любое опорное решение является угловой точкой области допустимых решений.
Теорема. Любая угловая точка области допустимых решений является опорным решением.
Пример:
Графический метод решения задачи линейной оптимизации рассмотрим на примере задачи производственного планирования при n = 2.
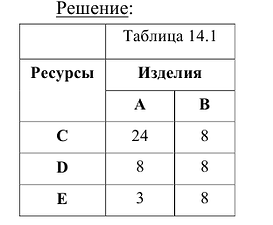
Предприятие изготавливает изделия двух видов А и В. Для производства изделий оно располагает сырьевыми ресурсами трех видов С, D и Е в объемах 600, 480 и 240 единиц соответственно. Нормы расхода ресурсов на единицу продукции каждого вида известны и представлены в табл. 14.1
Прибыль от реализации изделия А составляет 40 млн. руб., а изделия В – 50 млн.руб. Требуется найти объемы производства изделий А и В, обеспечивающие максимальную прибыль.
Построим математическую модель задачи, для чего обозначим 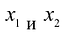 – объемы производства изделий А и В соответственно.
– объемы производства изделий А и В соответственно.
Тогда прибыль предприятия от реализации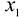 изделий А и
изделий А и 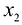 изделий В составит:
изделий В составит:
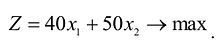
Ограничения по ресурсам будут иметь вид:
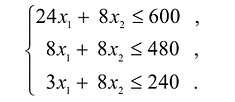
Естественно, объемы производства должны быть неотрицательными 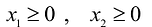
Решение сформулированной задами найдем, используя геометрическую интерпретацию. Определим сначала многоугольник решений, для чего систему ограничений неравенств запишем в виде уравнений и пронумеруем их:
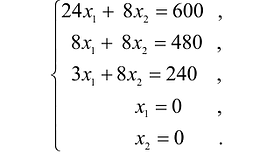
Каждое из записанных уравнений представляет собой прямую на плоскости, причем 4-я и 5-я прямые являются координатными осями.
Чтобы построить первую прямую, найдем точки ее пересечения с осями координат: 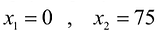 а при
а при 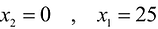 .
.
Далее нас интересует, по какую сторону от прямой будет находиться полуплоскость, соответствующая первому неравенству. Чтобы определить искомую полуплоскость, возьмем точку O(0,0) подставив ее координаты в неравенство, видим, что оно удовлетворяется. Так как точка O(0,0) лежит левее первой прямой, то и полуплоскость будет находиться левее прямой
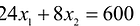 . На рис 14 , расположение полуплоскости относительно первой прямой отмечено стрелками.
. На рис 14 , расположение полуплоскости относительно первой прямой отмечено стрелками.
Аналогично построены 2-я и 3-я прямые и найдены полуплоскости, соответствующие 2-му и 3-му неравенству. Точки, удовлетворяющие ограничениям 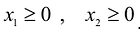 , находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.
, находятся в первом квадранте. Множество точек, удовлетворяющих всем ограничениям одновременно, является ОДР системы ограничений. Такой областью на графике (рис. 14.1) является многоугольник ОАВС.
Любая точка многоугольника решений удовлетворяет системе ограничений задачи и, следовательно, является ее решением. Это говорит о том, что эта задача линейной оптимизации имеет множество допустимых решений, т.е. моговариантпа. Нам же необходимо найти решение, обеспечивающее максимальную прибыль.
Чтобы найти эту точку, приравняем функцию к нулю и построим соответствующую ей прямую. Вектор-градиент прямой функции
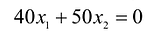 имеет координаты
имеет координаты 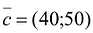
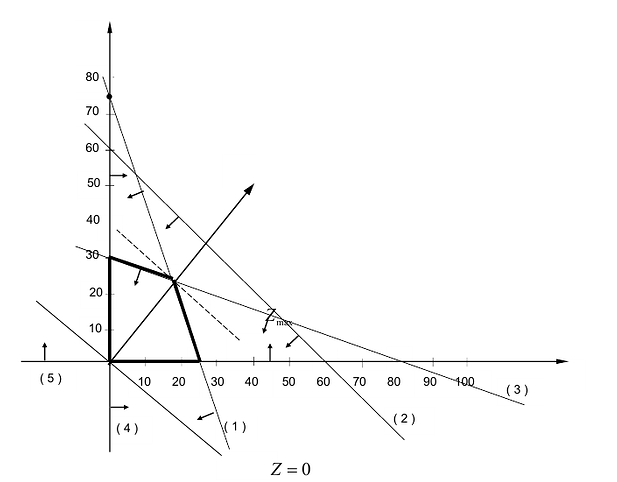
Рис. 14.1
Изобразим вектор на графике и построим прямую функции перпендикулярно вектору на рис. 14.1. Перемещая прямую функции параллельно самой себе в направлении вектора, видим, что последней точкой многоугольника решений, которую пересечет прямая функции, является угловая точка В. Следовательно, в точке В функция достигает максимального значения. Координаты точки В находим, решая систему уравнений, прямые которых пересекаются в данной точке.
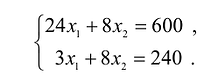
Решив эту систему, получаем, что 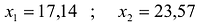
Следовательно, если предприятие изготовит изделия в найденных объемах, то получит максимальную прибыль, равную:
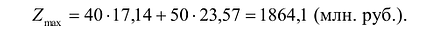
Алгоритм решения задачи линейного программирования графическим методом таков:
- Строится область допустимых решений;
- Строится вектор нормали к линии уровня с точкой приложении в начале координат;
- Перпендикулярно вектору нормали проводится одна из линий уровня, проходящая через начало координат;
- Линия уровня перемещается до положения опорной прямой. На этой прямой и будут находиться максимум или минимум функции.
В зависимости от вида области допустимых решений и целевой функции задача может иметь единственное решение, бесконечное множество решений или не иметь ни одного оптимального решения. 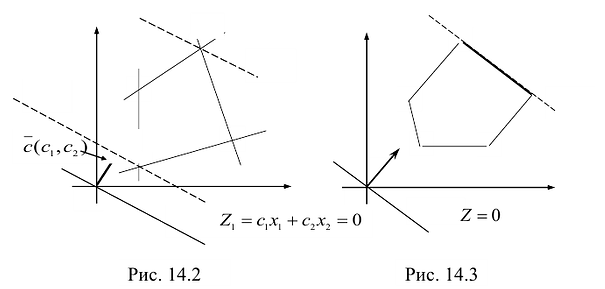
На рис. 14.3 показан случай, когда прямая функции параллельна отрезку АВ, принадлежащему ОДР. Максимум функции Z достигается в точке А и в точке В, а, следовательно, и в любой точке отрезка АВ, т.к. эти точки могут быть выражены в виде линейной комбинации угловых точек А и В.
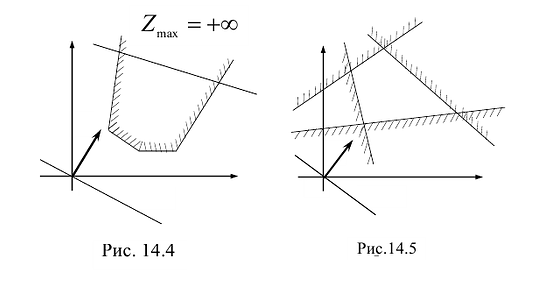
На рисунке 14.4 изображен случай, когда система ограничений образует неограниченное сверху множество. Функция Z в данном случае стремится к бесконечности, так как прямую функции можно передвигать в направлении вектора градиента как угодно далеко, а на рисунке 14.5 представлен случай несовместной системы ограничений.
Основные понятия симплексного метода решения задачи линейного программирования.
Среди универсальных методов решения задач линейного программирования наиболее распространен симплексный метод (или симплекс-метод), разработанный американским ученым Дж.Данцигом. Суть этого метода заключается в том, что вначале получают допустимый вариант, удовлетворяющий всем ограничениям, но необязательно оптимальный (так называемое начальное опорное решение); оптимальность достигается последовательным улучшением исходного варианта за определенное число этапов (итераций). Нахождение начального опорного решения и переход к следующему опорному решению проводятся на основе применения рассмотренного выше метода Жордана-Гаусса для системы линейных уравнений в канонической форме, в которой должна быть предварительно записана исходная задача линейного программирования; направление перехода от одного опорного решения к другому выбирается при этом на основе критерия оптимальности (целевой функции) исходной задачи.
Симплекс-метод основан на следующих свойствах задачи линейного программирования:
- Не существует локального экстремума, отличного от глобального. Другими словами, если экстремум есть, то он единственный.
- Множество всех планов задачи линейного программирования выпукло.
- Целевая функция ЗЛП достигает своего максимального (минимального) значения в угловой точке многогранника решений (в его вершине). Если целевая функция принимает свое оптимальное значение более чем в одной угловой точке, то она достигает того же значения в любой точке, являющейся выпуклой линейной комбинацией этих точек.
- Каждой угловой точке многогранника решений отвечает опорный план ЗЛП.
Рассмотрим две разновидности симплексного метода: симплекс-метод с естественным базисом и симплекс-метод с искусственным базисом (или М-метод).
- Заказать решение задач по высшей математике
Симплекс-метод с естественным базисом
Для применения этого метода задача линейного программирования должна быть сформулирована в канонической форме, причем матрица системы уравнений должна содержать единичную подматрицу размерностью mхm. В этом случае очевиден начальный опорный план (неотрицательное базисное решение).
Для определенности предположим, что первые m векторов матрицы системы составляют единичную матрицу. Тогда очевиден первоначальный опорный план: 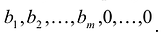
Проверка на оптимальность опорного плана проходит с помощью критерия оптимальности, переход к другому опорному плану — с помощью преобразований Жордана-Гаусса и с использованием критерия оптимальности.
Полученный опорный план снова проверяется на оптимальность и т.д. Процесс заканчивается за конечное число шагов, причем на последнем шаге либо выявляется неразрешимость задачи (конечного оптимума нет), либо получаются оптимальный опорный план и соответствующее ему оптимальное значение целевой функции.
Признак оптимальности заключается в следующих двух теоремах.
Теорема 1. Если для некоторого вектора, не входящего в базис, выполняется условие:
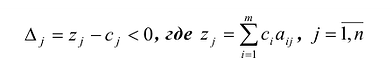
то можно получить новый опорный план, для которого значение целевой функции будет больше исходного; при этом могут быть два случая:
- если все координаты вектора, подлежащего вводу в базис, неположительны, то задача линейного программирования не имеет решения;
- если имеется хотя бы одна положительная координата у вектора, подлежащего вводу в базис, то можно получить новый опорный план.
Теорема 2. Если для всех векторов выполняется условие 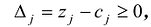 то полученный план является оптимальным.
то полученный план является оптимальным.
На основании признака оптимальности в базис вводится вектор Ак, давший минимальную отрицательную величину симплекс-разности: 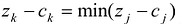
Чтобы выполнялось условие неотрицательности значений опорного плана, выводится из базиса вектор  , который дает минимальное положительное отношение:
, который дает минимальное положительное отношение:
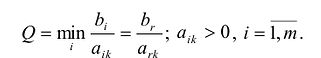
Строка 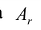 называется направляющей, столбец
называется направляющей, столбец 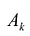 и элемент
и элемент 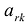 — направляющими (последний называют также разрешающим элементом).
— направляющими (последний называют также разрешающим элементом).
Элементы вводимой строки, соответствующей направляющей строке, в новой симплекс-таблице вычисляются по формулам:
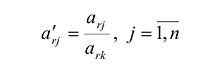
а элементы любой другой i-й строки пересчитываются по формулам:
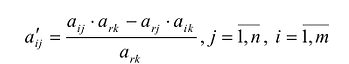
Значения базисных переменных нового опорного плана (показатели графы «план») рассчитываются по формулам:
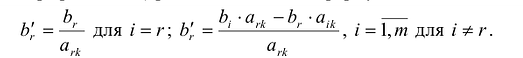
Если наименьшее значение Q достигается для нескольких базисных векторов, то чтобы исключить возможность зацикливания (повторения базиса), можно применить следующий способ.
Вычисляются частные, полученные от деления всех элементов строк, давших одинаковое минимальное значение Q на свои направляющие элементы. Полученные частные сопоставляются по столбцам слева направо, при этом учитываются и нулевые, и отрицательные значения. В процессе просмотра отбрасываются строки, в которых имеются большие отношения, и из базиса выводится вектор, соответствующий строке, в которой раньше обнаружится меньшее частное.
Для использования приведенной выше процедуры симплекс -метода к минимизации линейной формы 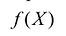 следует искать максимум функции
следует искать максимум функции 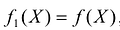 затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
затем полученный максимум взять с противоположным знаком. Это и будет искомый минимум исходной задачи линейного программирования.
Симплексный метод с искусственным базисом (М-метод)
Симплексный метод с искусственным базисом применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи линейного программирования, записанной в канонической форме.
М-метод заключается в применении правил симплекс-метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной задачи линейного программирования таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае её максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки А, теперь будут зависеть от числа М. Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения M-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Теория двойственности
Любой задаче линейного программирования можно сопоставить сопряженную или двойственную ей задачу. Причем, совместное исследование этих задач дает, как правило, значительно больше информации, чем исследование каждой из них в отдельности.
Любую задачу линейного программирования можно записать в виде:
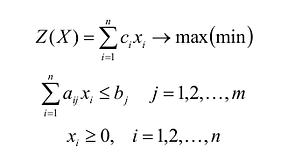
Первоначальная задача называется исходной или прямой.
Модель двойственной задачи имеет вид:
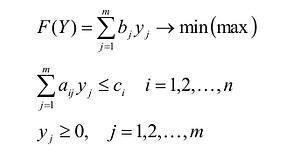
Переменные двойственной задачи 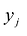 называют объективно обусловленными оценками или двойственными оценками.
называют объективно обусловленными оценками или двойственными оценками.
Связь исходной и двойственной задач заключается, в частности, в том, что решение одной из них может быть получено непосредственно из решения другой. Каждая из задач двойственной пары фактически является самостоятельной задачей линейного программирования и может быть решена независимо от другой.
Двойственная задача по отношению к исходной составляется согласно следующим правилам:
- Целевая функция исходной задачи формулируется на максимум, а целевая функция двойственной задачи – на минимум, при этом в задаче на максимум все неравенства в функциональных ограничениях имеют вид <, а в задаче на минимум – вид
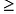
- Матрица
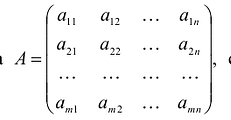 , составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица
, составленная из коэффициентов при неизвестных в системе ограничении исходной задачи, и аналогичная матрица 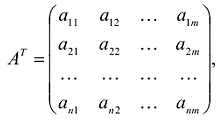 , в двойственной задаче получаются друг из друга транспонированием;
, в двойственной задаче получаются друг из друга транспонированием; - Число переменных в двойственной задаче равно числу функциональных ограничений исходной задачи, а число ограничений в системе двойственной задачи – числу переменных в исходной задаче;
- Коэффициентами при неизвестных в целевой функции двойственной задачи являются свободные члены в системе ограничений исходной задачи, а правыми частями в ограничениях двойственной задачи – коэффициенты при неизвестных в целевой функции исходной задачи;
- Каждому ограничению одной задачи соответствует переменная другой задачи: номер переменной совпадает с номером ограничения; при этом ограничению, записанному в виде неравенства <, соответствует переменная, связанная условием неотрицательности.
Если функциональное ограничение исходной задачи является равенством, то соответствующая переменная двойственной задачи может принимать как положительные, так и отрицательные значения.
Математические модели пары двойственных задач могут быть симметричными и несимметричными. В несимметричных двойственных задачах система ограничений исходной задачи задается в виде равенств, а двойственной – в виде неравенств, причем переменные в двойственной задаче могут быть и отрицательными. В симметричных двойственных задачах система ограничений как исходной, так и двойственной задачи задается в виде неравенств, причем на двойственные переменные налагается условие неотрицательности.

где:
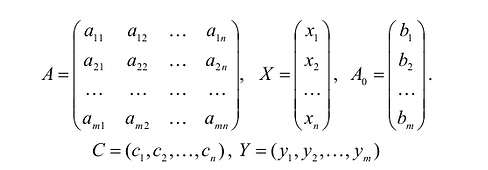
Рассмотрим пример, показывающий, как в реальной экономической ситуации появляются взаимно двойственные задачи линейного программирования.
На некотором предприятии после выполнения годового плана возник вопрос: как поступить с остатками сырья? Из оставшегося сырья можно наладить производство продукции и реализовать его или продать сырье.
Предположим, что имеется два вида сырья 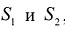 , остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров:
, остатки которого составляют соответственно 35 и 20 единиц. Из этого сырья можно наладить производство трех видов товаров: 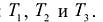
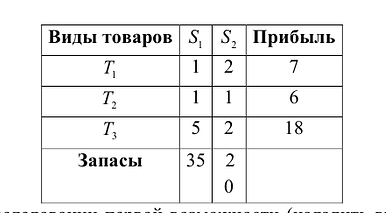
При исследовании первой возможности (наладить выпуск товаров 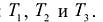 ) возникает вопрос о плане выпуска, который задается тремя переменными
) возникает вопрос о плане выпуска, который задается тремя переменными 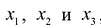 , которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:
, которые соответствуют количеству произведенного товара. Эти переменные должны удовлетворять условиям:
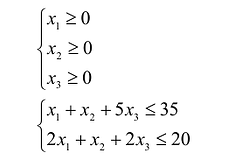
Прибыль, которую получит предприятие от реализации товара, составит:
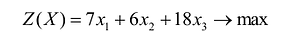
В интересах предприятия эту прибыль максимизировать.
Это прямая задача.
Объективно обусловленными оценками двойственной задачи 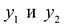 будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже
будут цены, по которым целесообразно продавать излишки сырья, т.е. при продаже сырья по ценам ниже 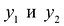 предприятие будет терпеть убытки.
предприятие будет терпеть убытки.
Справедливое требование со стороны продающего предприятия состоит в следующем: если взять сырье, идущее на производство единицы товара 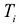 то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).
то выручка от его продажи должна быть не меньше, чем прибыль от реализации готового изделия (в противном случае нет смысла продавать сырье – целесообразнее изготовить товар и получить прибыль от его реализации).
Это требование можно представить в виде системы неравенств: 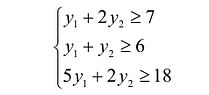
В левой части каждого неравенства предполагаемая выручка от продажи сырья, необходимого для производства единицы товара  а в правой – прибыль от реализации этой единицы товара.
а в правой – прибыль от реализации этой единицы товара.
Что касается покупателя, то он заинтересован в минимизации расходов на покупку сырья, т.е. величины 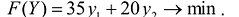
Теоремы двойственности
Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач: можно либо найти оптимальное решение другой задачи, не решая ее, либо установить его отсутствие.
Возможны следующие случаи:
- обе задачи из пары двойственных имеют оптимальные решения;
- одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.
Первая теорема двойственности.
Для двойственных задач линейного программирования имеет место один из взаимоисключающих случаев:
- В прямой и двойственной задачах имеются оптимальные решения, при этом значения целевых функций на оптимальных решениях совпадают:
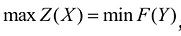
- В прямой задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена сверху. При этом у двойственной задачи будет пустое допустимое множество.
- В двойственной задаче допустимое множество не пусто, а целевая функция на этом множестве не ограничена снизу. При этом у прямой задачи допустимое множество оказывается пустым;
- Обе из рассматриваемых задач имеют пустые допустимые множества.
Вторая теорема двойственностн (теорема о дополняющей нежесткости):
Пусть 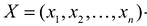 – допустимое решение прямой задачи, а
– допустимое решение прямой задачи, а 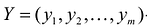 допустимое решение двойственной задачи.
допустимое решение двойственной задачи.
Для того, чтобы они были оптимальными решениями соответствующих взаимодвойственных задач, необходимо и достаточно, чтобы выполнялись следующие соотношения:
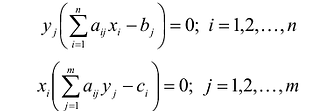
Эти условия устанавливают связь между оптимальными значениями прямой и двойственной задач и позволяют, зная решение одной из них, находить решение другой задачи.
Теорема об оценках:
Значения переменных 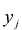 в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов
в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов 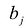 системы ограничений – неравенств прямой задачи на величину
системы ограничений – неравенств прямой задачи на величину 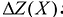 :
:
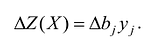
Диапазон изменения компонент вектора В, в котором сохраняется оптимальный базис, называется областью устойчивости оптимальных оценок.
Экономический смысл первой теоремы двойственности следующий. План производства X и набор ресурсов Y оказываются оптимальными тогда и только тогда, когда прибыль от реализации продукции, определенная при известных заранее ценах продукции 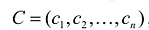 , равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов
, равна затратам на ресурсы по «внутренним» (определяемым только из решения задачи) ценам ресурсов 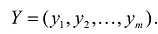 Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов
Для всех других планов прибыль от продукции всегда меньше или равна стоимости затраченных ресурсов 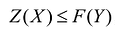 , т.е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина Z(X)~ F(Y) характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.
, т.е. ценность выпущенной продукции не превосходит суммарной оценки затраченных ресурсов. Значит, величина Z(X)~ F(Y) характеризует производственные потери в зависимости от рассмотренной производственной программы и выбранных оценок ресурсов.
- Дифференциальное исчисление функций одной переменной
- Исследование функции
- Пространство R”
- Неопределённый интеграл
- Линейный оператор – свойства и определение
- Многочлен – виды, определение с примерами
- Квадратичные формы – определение и понятие
- Системы линейных уравнений с примерами
Решение задачи линейного программирования методом Гомори
Введение
Задачи, которые мы решали ранее всегда давали целочисленный ответ. Это происходило
потому, что исходные данные были подобраны специальным образом. Но так бывает не всегда.
Гораздо чаще в ответе получаются дробные величины – например, нужно произвести 2,5 единицы
изделия A и 3,44 единицы изделия B. Допустимо ли такое решение? Тут все зависит от
условий задачи. Если мы производим, например, муку и сахар в килограммах – такое решение
вполне допустимо. 2,5 единицы изделия A – это 2 килограмма 500 грамм муки, а 3,44 единицы
изделия B это 3 килограмма 440 грамм сахара. Однако представьте, что изделие A – это компьютеры,
а изделие B – это MP3-плееры. Как можно произвести 3,44 единицы MP3-плеера? Очевидно, что
никак. В таких случаях говорят, что необходимо решить задачу целочисленного
линейного программирования, подразумевая, что в ответе обязательно должны получиться
целые числа.
Для решения целочисленных задач был разработан специальный метод под названием Метод
Гомори. На самом деле, метод Гомори это всего лишь “надстройка” над обычным симплекс-методом,
который мы изучили в прошлых главах. Идея метода Гомори заключается в том, что можно решить
задачу обычным симплекс-методом, получив (возможно) нецелочисленное решение, а потом для каждой
нецелочисленной переменной добавить “поправочное” ограничение, которое во-первых, сделает эту
переменную целочисленной, а во-вторых, минимальным образом повлияет на значение целевой функции.
Полезная страница? Сохрани или расскажи друзьям
Алгоритм метода Гомори
Итак, понятно, что нам необходимо сначала просто решить задачу симплекс-методом, а затем для
каждой нецелочисленной переменной в решении немного “подправить” ее значение. То есть, схема метода
Гомори примерно следующая:
- Решить исходную производственную задачу обычным симплекс-методом;
- Убедиться, что ответ получился нецелочисленным. Если он целочисленный, то задача решена;
- Умножить значения в последней строке (строка F) на -1;
- Пока в ответе остались нецелочисленные переменные, делать следующее:
- Среди нецелочисленных значений в получившемся решении выбрать переменную, для которой
необходимо составить дополнительное ограничение (как это сделать будет объяснено в нижеприведенном
примере); - К исходной задаче добавить специальным образом составленное ограничение для выбранной переменной
(опять же, в примере будет показано, как именно это сделать). Это приведет к появлению еще одной
вспомогательной переменной; - К полученной задаче применить один этап симплекс-метода, причем убрать появившуюся вспомогательную
переменную, и добавить какую-то из исходных (какую именно также будет объяснено в примере). - Предыдущий шаг (шаг 4) необходимо выполнять, пока все решение не станет целочисленным. Метод Гомори
гарантирует, что на каком-либо шаге это точно произойдет.
Решение производственной задачи методом Гомори
Решим методом Гомори ту же самую производственную задачу, которую решали ранее Симплекс-методом,
но изменим в ней одно число – чтобы решение с использованием Симплекс-метода получилось нецелочисленным:
| Ресурс | Изделие A | Изделие B | Изделие C | Сколько ресурса на складах |
| R1 | 1 | 2 | 3 | 35 |
| R2 | 4 | 3 | 2 | 45 |
| R3 | 3 | 1 | 1 | 40 |
| Прибыль | 4 | 5 | 6 |
Как обычно, запишем систему ограничений нашей задачи и целевую функцию в виде неравенств.
Обозначим за $x_A, x_B$ и $x_C$ количество производимых изделий A, B и C, соответственно. Так
как весь процесс был подробно описан ранее, приведем только результат:
$$begin{array}{l}
left{ {begin{array}{*{20}{c}}
{{x_A} + 2{x_B} + 3{x_C} le 35}\
{4{x_A} + 3{x_B} + 2{x_C} le 45}\
{3{x_A} + {x_B} + {x_C} le 40}
end{array}} right.\
{x_A},{x_B},{x_C} ge 0\
F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C} to max
end{array}$$
Чтобы начать решать производственную задачу симплекс-методом, необходимо наши неравенства
превратить в равенства. Для этого добавим к каждому из ограничений дополнительные неотрицательные
переменные ${x_1},{x_2},{x_3}$:
$$begin{array}{l}
left{ {begin{array}{*{20}{c}}
{{x_A} + 2{x_B} + 3{x_C} + {x_1} = 35}\
{4{x_A} + 3{x_B} + 2{x_C} + {x_2} = 45}\
{3{x_A} + {x_B} + {x_C} + {x_3} = 40}
end{array}} right.\
{x_A},{x_B},{x_C},{x_1},{x_2},{x_3} ge 0\
F({x_A},{x_B},{x_C}) = 4{x_A} + 5{x_B} + 6{x_C} to max
end{array}$$
Как и в прошлых разделах, найдем “начальное решение”. В производственной задаче в качестве
начального решения лучше всего выбрать такое, когда не производится ни одной единицы товара, то
есть, $x_A,x_B,x_C=0$. При этом исходя из ограничений, получаем $x_1=35,x_2=45,x_3=40$. Такое решение
можно записать в виде $(0,0,0,35,45,40)$ – то есть, в скобках просто последовательно перечислить
переменные (сначала “основные”, а потом “введенные нами”).
Запишем симплекс-таблицу. Как это делается было подробно объяснено тут.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_1$ | 1 | 2 | 3 | 1 | 0 | 0 | 35 |
| $x_2$ | 4 | 3 | 2 | 0 | 1 | 0 | 45 |
| $x_3$ | 3 | 1 | 1 | 0 | 0 | 1 | 40 |
| F | -4 | -5 | -6 | 0 | 0 | 0 | 0 |
Итерация 1
Прежде чем выполнять очередную итерацию, необходимо проверить, может быть, наше решение
уже оптимально, и ничего делать не нужно? Для этого необходимо проверить, есть ли в последней
строке отрицательные элементы. Есть. Их три. Следовательно, наше решение не оптимально.
Выберем самое большое по модулю отрицательное значение -6 в столбце $x_C$, эту переменную необходимо
добавить к нашему базису (то есть, ввести ее в одну из строк слева). Но тогда одну из
переменных текущего базиса ($x_1,x_2,x_3$) необходимо убрать. Чтобы узнать, какую,
необходимо найти для каждой базисной переменной (каждой строки) отношение свободного
члена (значения в столбце B) к коэффициенту в строке $x_C$ (переменной, которую, как мы
решили выше, необходимо ввести в базис). Обратите внимание, что это отношение должно существовать,
и оно должно быть положительно. Если это не так, мы просто пропускаем соответствующую строку
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | $frac{B}{x_C}$ | |
| $x_1$ | 1 | 2 | 3 | 1 | 0 | 0 | 35 | $frac{35}{3}approx11,67$ |
| $x_2$ | 4 | 3 | 2 | 0 | 1 | 0 | 45 | $frac{45}{2}=22,5$ |
| $x_3$ | 3 | 1 | 1 | 0 | 0 | 1 | 40 | $frac{40}{1}=40$ |
| F | -4 | -5 | -6 | 0 | 0 | 0 | 0 |
Мы нашли отношения для каждой строки, и для первой строки отношение получилось наименьшим.
Поэтому именно данную строку (то есть, переменную $x_1$) необходимо убрать из базиса, заменив,
как мы определили выше, переменной $x_C$. Как это сделать? Прежде всего, найдем значение
элемента на пересечении найденной строки и найденного столбца. Он равен 3 (в таблице выше он
подчеркнут). И нам нужно всю найденную строку на этот элемент поделить:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ | |
| $x_2$ | 4 | 3 | 2 | 0 | 1 | 0 | 45 |
| $x_3$ | 3 | 1 | 1 | 0 | 0 | 1 | 40 |
| F | -4 | -5 | -6 | 0 | 0 | 0 | 0 |
Обратите внимание, из первой строки исчезло название строки – $x_1$. Это потому, что
$x_1$ – больше не базисная переменная. Она была бы базисной, если бы был столбец $x_1$,
в котором была бы одна единица, а остальные нули. Но такого столбца больше нет. Теперь
первая строка не выражает никакой базисной переменной. Нам же необходимо, чтобы базисной
стала переменная $x_C$. Первое требование к базисным переменным для нее выполняется –
есть столбец $x_C$, и у него в первой строке число 1. Но вот остальные числа не равны
нулю. Так давайте их сделаем такими.
- Чтобы во второй строке, в столбце $x_C$ число 2 превратить в ноль, вычтем из второй строки две первых.
- Чтобы в третьей строке, в столбце $x_C$ число 1 превратить в ноль, вычтем из третьей строки первую.
- Чтобы в последней строке, в столбце $x_C$ число -6 превратить в ноль, добавим к последней строке шесть первых.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ |
| $x_2$ | $4-2cdotfrac{1}{3}$ | $3-2cdotfrac{2}{3}$ | $2-2cdot1$ | $0-2cdotfrac{1}{3}$ | $1-2cdot0$ | $0-2cdot0$ | $45-2cdotfrac{35}{3}$ |
| $x_3$ | $3-frac{1}{3}$ | $1-frac{2}{3}$ | 1-1 | $0-frac{1}{3}$ | 0-0 | 1-0 | $40-frac{35}{3}$ |
| F | $-4+6cdotfrac{1}{3}$ | $-5+6cdotfrac{2}{3}$ | $-6+6cdot1$ | $0+6cdotfrac{1}{3}$ | $0+6cdot0$ | $0+6cdot0$ | $0+6cdotfrac{35}{3}$ |
Проводим математические действия и получаем итоговую таблицу.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ |
| $x_2$ | $frac{10}{3}$ | $frac{5}{3}$ | 0 | $-frac{2}{3}$ | $1$ | $0$ | $frac{65}{3}$ |
| $x_3$ | $frac{8}{3}$ | $frac{1}{3}$ | 0 | $-frac{1}{3}$ | 0 | 1 | $frac{85}{3}$ |
| F | -2 | -1 | 0 | 2 | 0 | 0 | 70 |
Теперь первая строка у нас выражает базисную переменную $x_C$, так как действительно,
в столбце $x_C$ одно значение равно 1, а остальные – 0. Итерация выполнена.
Итерация 2
Прежде чем выполнять очередную итерацию, необходимо проверить, оптимально ли наше решение?
В последней строке есть отрицательные элементы, следовательно, наше решение не оптимально.
Выберем самое большое по модулю отрицательное значение -2 в столбце $x_A$, эту переменную необходимо
добавить к нашему базису, а одну из переменных текущего базиса ($x_C,x_2,x_3$) необходимо
убрать. Чтобы узнать, какую, необходимо найти для каждой базисной переменной отношение свободного
члена к коэффициенту в строке $x_A$ (переменной, которую, как мы решили выше, необходимо ввести в базис).
Обратите внимание, что это отношение должно существовать, и оно должно быть положительно. Если это
не так, мы просто пропускаем соответствующую строку
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | $frac{B}{x_A}$ | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ | $frac{35}{3}:frac{1}{3}=35$ |
| $x_2$ | $frac{10}{3}$ | $frac{5}{3}$ | 0 | $-frac{2}{3}$ | 1 | 0 | $frac{65}{3}$ | $frac{65}{3}:frac{10}{3}=frac{65}{10}=6,5$ |
| $x_3$ | $frac{8}{3}$ | $frac{1}{3}$ | 0 | $-frac{1}{3}$ | 0 | 1 | $frac{85}{3}$ | $frac{85}{3}:frac{8}{3}=frac{85}{8}=10,625$ |
| F | -2 | -1 | 0 | 2 | 0 | 0 | 70 |
Мы нашли отношения для каждой строки, и для переменной $x_2$ отношение получилось наименьшим.
Поэтому именно данную переменную необходимо убрать из базиса, заменив,
как мы определили выше, переменной $x_A$. Прежде всего, найдем значение элемента на пересечении
найденной строки и найденного столбца. Он равен $frac{10}{3}$. И нам нужно всю найденную строку
на этот элемент поделить:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}$ | $frac{2}{3}$ | 1 | $frac{1}{3}$ | 0 | 0 | $frac{35}{3}$ |
| 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | $frac{65}{10}$ | |
| $x_3$ | $frac{8}{3}$ | $frac{1}{3}$ | 0 | $-frac{1}{3}$ | 0 | 1 | $frac{85}{3}$ |
| F | -2 | -1 | 0 | 2 | 0 | 0 | 70 |
Из второй строки исчезло название строки – $x_2$. Это потому, что
$x_2$ – больше не базисная переменная. Нам же необходимо, чтобы базисной
стала переменная $x_A$. Первое требование к базисным переменным для нее выполняется –
есть столбец $x_A$, и у него во второй строке число 1. Но вот остальные числа не равны
нулю. Так давайте их сделаем такими.
- Чтобы в первой строке, в столбце $x_A$ число $frac{1}{3}$ превратить в ноль, вычтем из первой строки вторую, умноженную на $frac{1}{3}$.
- Чтобы в третьей строке, в столбце $x_A$ число $frac{8}{3}$ превратить в ноль, вычтем из третьей строки вторую, умноженную на $frac{8}{3}$
- Чтобы в последней строке, в столбце $x_A$ число -2 превратить в ноль, добавим к последней строке две вторых.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | $frac{1}{3}-frac{1}{3}cdot1$ | $frac{2}{3}-frac{1}{3}cdotfrac{1}{2}$ | $1-frac{1}{3}cdot0$ | $frac{1}{3}-frac{1}{3}cdot(-frac{1}{5})$ | $0-frac{1}{3}cdotfrac{3}{10}$ | 0 | $frac{35}{3}-frac{1}{3}cdotfrac{65}{10}$ |
| 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | $frac{65}{10}$ | |
| $x_3$ | $frac{8}{3}-frac{8}{3}cdot1$ | $frac{1}{3}-frac{8}{3}cdotfrac{1}{2}$ | $0-frac{1}{3}cdot0$ | $-frac{1}{3}-frac{8}{3}cdot(-frac{1}{5})$ | $0-frac{8}{3}cdotfrac{3}{10}$ | $1-frac{8}{3}cdot0$ | $frac{85}{3}-frac{8}{3}cdotfrac{65}{10}$ |
| F | $-2+2cdot1$ | $-1+2cdotfrac{1}{2}$ | $0+2cdot0$ | $2+2cdot(-frac{1}{5})$ | $0+2cdotfrac{3}{10}$ | $0+2cdot0$ | $70+2cdotfrac{65}{10}$ |
Проводим математические действия и получаем итоговую таблицу.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 11 |
| F | 0 | 0 | 0 | $frac{8}{5}$ | $frac{3}{5}$ | 0 | 83 |
Теперь вторая строка у нас выражает базисную переменную $x_A$, так как действительно,
в столбце $x_A$ одно значение равно 1, а остальные – 0. Итерация выполнена.
Итерация 3
Прежде чем выполнять очередную итерацию, необходимо проверить, оптимально ли наше решение?
В последней строке нет отрицательных элементов, следовательно, наше решение оптимально. Если записать
значения интересующих нас переменных $x_A,x_B,x_C$, то получим, что $x_A=frac{13}{2};x_B=0;x_C=frac{19}{2}$.
Значения получились нецелые. Следовательно, необходимо применить метод Гомори. По методу Гомори
нам необходимо добавить еще одно ограничение к нашей задаче. Сперва необходимо определить, для какой
нецелой переменной мы будем составлять дополнительное ограничение. У нас две нецелых переменных – $x_C$ и $x_A$.
Чтобы определить, для какой именно, необходимо найти дробные части чисел, стоящих в соответствующих строках, столбце B.
- Число, стоящее в строке $x_C$, столбце B равно $frac{19}{2}$. Можно записать его как $9frac{1}{2}$. Его
дробная часть равна $frac{1}{2}$ - Число, стоящее в строке $x_A$, столбце B равно $frac{13}{2}$. Можно записать его как $6frac{1}{2}$. Его
дробная часть равна $frac{1}{2}$
Среди данных дробных частей нужно найти наибольшую, и именно для этой переменной мы будем составлять
дополнительное ограничение. Однако у нас дробные части получились равными, поэтому просто берем первую – $x_C$.
Составляем для переменной $x_C$ ограничение. Оно будет иметь вид:
$$q_C-q_{CA}cdot{x_A}-q_{CB}cdot{x_B}-q_{CC}cdot{x_C}-q_{C1}cdot{x_1}-q_{C2}cdot{x_2}-q_{C3}cdot{x_3}leq0$$
Для любой другой переменной будет точно такая же формула, только в ней индексы у коэффициентов $q$ будут не
$C$, а какие-то другие
Разберемся что тут что. Очевидно, что $x_A,x_B,x_C,x_1,x_2,x_3$ – переменные нашей задачи. Для нахождения
коэффициентов $q$ будем использовать числа первой строки, так как именно там содержатся данные по нашей
переменной $x_C$. Значение $q_C$ это просто дробная часть числа в строке $x_C$ и столбце свободных членов B. Значение
этой клетки равно $frac{19}{2}=9frac{1}{2}$. Очевидно, что целая часть здесь 9, а дробная $frac{1}{2}$.
Следовательно, $q_C=frac{1}{2}$.
- Значение коэффициента $q_{CA}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_A$.
Там находится число 0, и очевидно, что его дробная часть также равна 0. $q_{CA}=0$ - Значение коэффициента $q_{CB}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_B$.
Там находится число $frac{1}{2}$, и очевидно, что его дробная часть также равна $frac{1}{2}$. $q_{CB}=frac{1}{2}$ - Значение коэффициента $q_{CC}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_C$.
Там находится число 1, и очевидно, что его дробная часть равна 0. $q_{CC}=0$ - Значение коэффициента $q_{C1}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_1$.
Там находится число $frac{2}{5}$, и очевидно, что его дробная часть также равна $frac{2}{5}$. $q_{C1}=frac{2}{5}$ - Значение коэффициента $q_{C2}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_2$.
Там находится число $-frac{1}{10}$. Для отрицательных чисел дробная часть определяется немного не так, как
для положительных, и равна разности нашего числа и следующего целого отрицательного числа, меньшего, чем нашего.
Для числа $-frac{1}{10}$ следующее меньшее целое отрицательное число это $-1$, и, следовательно, $q_{С2}=-frac{1}{10}-(-1)=frac{9}{10}$ - Значение коэффициента $q_{C3}$ это дробная часть числа, находящегося в строке $x_C$, столбце $x_3$.
Там находится число 0, и очевидно, что его дробная часть также равна 0. $q_{C3}=0$
Подставив найденные коэффициенты, получим еще одно ограничение:
$$frac{1}{2}-frac{1}{2}cdot{x_B}-frac{2}{5}cdot{x_1}-frac{9}{10}cdot{x_2}leq0$$
Однако это ограничение в виде неравенства, а у нас все ограничения в виде равенств. Поэтому превратим данное
ограничение в равенство, добавив еще одну неотрицательную переменную $x_4$:
$$-frac{1}{2}cdot{x_B}-frac{2}{5}cdot{x_1}-frac{9}{10}cdot{x_2}+x_4=-frac{1}{2}$$
Занесем данное ограничение еще одной строкой в симплекс-таблицу, кроме того, не забудем, что появился новый
столбец $x_4$, а также изменим знак последней строки – так всегда делается при начале работы по методу Гомори:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 0 | 11 |
| $x_4$ | 0 | $-frac{1}{2}$ | 0 | $-frac{2}{5}$ | $-frac{9}{10}$ | 0 | 1 | $-frac{1}{2}$ |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Теперь продолжаем работать по практически обычному симплекс-методу. Правда теперь будет отличаться правило
определения того, какую переменную необходимо убрать из базиса, а какую оставить. По правилам метода Гомори,
убирать надо всегда только что введенную переменную, то есть, $x_4$. А вот чтобы определить, какую необходимо ввести,
необходимо найти частные от деления значений последней строки (F) на значения предпоследней строки (так как
именно в ней переменная $x_4$). Найдем эти частные (кроме только что введенной переменной $x_4$ и столбца B, а
также тех столбцов, где приходится делить на ноль):
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 0 | 11 |
| $x_4$ | 0 | $-frac{1}{2}$ | 0 | $-frac{2}{5}$ | $-frac{9}{10}$ | 0 | 1 | $-frac{1}{2}$ |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
| $frac{F}{x_4}$ | – | 0 | – | 4 | $frac{2}{3}$ | – | – | – |
Наименьшее значение мы получили для столбца с переменной $x_B$ – 0. Следовательно именно переменную $x_B$
необходимо ввести в базис. Определяем, какое число стоит на пересечении строки $x_4$ и столбца $x_B$ – это
число $-frac{1}{2}$. Поэтому делим всю строку $x_4$ на это число:
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | $frac{1}{2}$ | 1 | $frac{2}{5}$ | $-frac{1}{10}$ | 0 | 0 | $frac{19}{2}$ |
| $x_A$ | 1 | $frac{1}{2}$ | 0 | $-frac{1}{5}$ | $frac{3}{10}$ | 0 | 0 | $frac{13}{2}$ |
| $x_3$ | 0 | -1 | 0 | $frac{1}{5}$ | $-frac{4}{5}$ | 1 | 0 | 11 |
| 0 | 1 | 0 | $frac{4}{5}$ | $frac{9}{5}$ | 0 | -2 | 1 | |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Из четвертой строки исчезло название строки – $x_4$. Это потому, что
$x_4$ – больше не базисная переменная. Нам же необходимо, чтобы базисной
стала переменная $x_B$. Первое требование к базисным переменным для нее выполняется –
есть столбец $x_B$, и у него в четвертой строке число 1. Но вот остальные числа не равны
нулю. Так давайте их сделаем такими.
- Чтобы в первой строке, в столбце $x_B$ число $frac{1}{2}$ превратить в ноль, вычтем из первой строки четвертую, умноженную на $frac{1}{2}$.
- Чтобы во второй строке, в столбце $x_B$ число $frac{1}{2}$ превратить в ноль, вычтем из второй строки четвертую, умноженную на $frac{1}{2}$
- Чтобы в третьей строке, в столбце $x_B$ число $-1$ превратить в ноль, добавим к третьей строке четвертую
- Последнюю строку не трогаем, так как в последней строке, столбце $x_B$ и так ноль
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | $0-frac{1}{2}cdot0$ | $frac{1}{2}-frac{1}{2}cdot1$ | $1-frac{1}{2}cdot0$ | $frac{2}{5}-frac{1}{2}cdotfrac{4}{5}$ | $-frac{1}{10}-frac{1}{2}cdotfrac{9}{5}$ | $0-frac{1}{2}cdot0$ | $0-frac{1}{2}cdot(-2)$ | $frac{19}{2}-frac{1}{2}cdot1$ |
| $x_A$ | $1-frac{1}{2}cdot0$ | $frac{1}{2}-frac{1}{2}cdot1$ | $0-frac{1}{2}cdot0$ | $-frac{1}{5}-frac{1}{2}cdotfrac{4}{5}$ | $frac{3}{10}-frac{1}{2}cdotfrac{9}{5}$ | $0-frac{1}{2}cdot0$ | $0-frac{1}{2}cdot(-2)$ | $frac{13}{2}-frac{1}{2}cdot1$ |
| $x_3$ | 0+0 | -1+1 | 0+0 | $frac{1}{5}+frac{4}{5}$ | $-frac{4}{5}+frac{9}{5}$ | 1+0 | 0-2 | 11+1 |
| $x_B$ | 0 | 1 | 0 | $frac{4}{5}$ | $frac{9}{5}$ | 0 | -2 | 1 |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Проводим математические действия и получаем итоговую таблицу.
| $x_A$ | $x_B$ | $x_C$ | $x_1$ | $x_2$ | $x_3$ | $x_4$ | B | |
| $x_C$ | 0 | 0 | 1 | 0 | -1 | 0 | 1 | 9 |
| $x_A$ | 1 | 0 | 0 | $-frac{3}{5}$ | $-frac{3}{5}$ | 0 | 1 | 6 |
| $x_3$ | 0 | 0 | 0 | 1 | 1 | 1 | -2 | 12 |
| $x_B$ | 0 | 1 | 0 | $frac{4}{5}$ | $frac{9}{5}$ | 0 | -2 | 1 |
| F | 0 | 0 | 0 | $-frac{8}{5}$ | $-frac{3}{5}$ | 0 | 0 | -83 |
Проверяем, получили ли мы целочисленное решение. Да, получили. Мы получили решение $x_A=6,x_B=1,x_C=9$, причем
значение целевой функции (правая нижняя клетка таблицы с противоположным знаком) равно 83, что, кстати, совпадает
со значением целевой функции в исходной (нецелочисленной) задачи. Поэтому, можно сказать, что переход к целочисленности не изменяет значения дохода фирмы. Так, однако бывает не всегда, и чаще всего доход фирмы при переходе к целочисленности немного падает.
Выводы
Так как мы получили целочисленное решение, то задача решена. Если бы какие-то из переменных снова были бы
нецелочисленными, процесс нужно было бы повторить – найти одну из нецелочисленных переменных, составить для нее
дополнительное ограничение, получив еще одну вспомогательную переменную, а затем сделать шаг симплекс-метода, уберя
ее из базиса. После какого-то шага мы бы точно получили целочисленное решение (как и в этом случае).
Мы научились решать производственную задачу, и умеем выдавать такой результат, который обеспечивает
максимальную прибыль. Однако при этом мы совсем не учитываем остатки на складах. То есть, мы конечно гарантируем,
что используем не больше ресурсов, чем есть, однако вполне возможно, что на складах останутся излишки. Что обычно
делают предприятия, если у них на складах образуются излишки ресурсов? На самом деле, можно много чего сделать:
- Можно их продать, и тем самым повысить прибыль (целевую функцию);
- Можно поменять одни ресурсы на другие (если такое возможно), и, может быть, тогда прибыль увеличится;
- Можно обдумать выпуск нового товара, который потребляет как раз тот ресурс, которого у нас излишек.
Может быть, тогда наша прибыль увеличится.
Обычное решение производственной задачи не дает ответов на вопросы подобного рода. Однако существуют методы, позволяющие получить такие ответы. Один из этих методов – решение “двойственной” задачи. Его мы рассмотрим в следующем разделе.
Полезное по теме
- Примеры решений задач ЛП в целых числах
- Решенные контрольные по линейному программированию
- Заказать решение целочисленной задачи ЛП
Раньше и трава была зеленее
Всю жизнь все при решении неравенств и уравнений в ЕГЭ по профильной математике писали ОДЗ (Область Допустимых Значений), понимая под этим ограничения, накладываемые на аргумент «непростыми» функциями типа квадратного корня или логарифма. И не было проблем. Пока в сеть не попали разъяснения методиста из Кемеровской области.
За ТАКОЕ точно снизят
Семинар Трушкиной Т.П., методиста из Кемеровской области, наделал много шума. Оказалось, что на ЕГЭ по математике можно получит 0 баллов за задачу, даже имея верный ответ и верную последовательность рассуждений. Все из-за неправильного использования понятия «ОДЗ». Первое, что ясно совершенно точно: если вы выписали «ОДЗ» «не полностью» — прощайтесь с баллами за задачу. Если вы решили выписать лишь ограничения, вносимые логарифмической функцией, а условие отличия знаменателя от нуля оставить на потом («ну они ведь и далее сохранятся, «переход равносилен»»), и назвали эти «неполные» ограничения словом ОДЗ — то это 0 баллов. И можно было даже не браться за задачу =(
Если хотите пользоваться равносильными переходами — пользуйтесь, никто это не запрещает. Но тогда ОДЗ вам вообще ни к чему — работайте спокойно через систему условий, и будет вам счастье.
Скажите детям — пусть они ОДЗ выбросят!
Но даже при правильном, полностью выписанной ОДЗ, есть риск нарваться на неприятности. Эксперт заявляет: в школьных учебниках по математике понятие области допустимых значений (ОДЗ) определен лишь для функций. Поэтому использовать это понятие при решении уравнений и неравенств не рекомендуется. Однако использование ОДЗ в неравенствах и уравнениях активно использовалось преподавателями ВУЗов, в том числе при работе со школьниками, постепенно «мигрировало» в методички и сборники по подготовке к ЕГЭ, и теперь уже прочно укоренилось в умах репетиторов, учителей и абитуриентов. Как показывает практика, полностью выписанные ограничения на переменную под заголовком «ОДЗ» не ведут к снижению баллов на ЕГЭ по профильной математике. Тем не менее, эксперт не рекомендует использовать эту конструкцию.
«Коллеги, лучше вообще ничего не писать; Скажите детям — пусть они ОДЗ выбросят!» — столько эмоций на пустом, казалось бы, месте.
Эксперт рекомендует накладывать ограничения на переменную, при этом никак это не «озаглавливать». При это заголовки типа «ограничения», «условия», «важные замечания» и т.п. возбраняться не должны.
А что говорят интернет-гуру?
Специалисты в области подготовки к ЕГЭ по профильной математике разделились во взглядах. Многие известные Ютуб-блогеры (Борис Трушин, Wild Mathing) придерживаются того мнения, что полностью выписанная ОДЗ ни в коем случае к снижению баллов не приведет. Однако выписаны ограничения, действительно, должны быть полностью. То есть если у вас, например, имеется неравенство с логарифмом, да который ещё и стоит в знаменателе дроби — будьте любезны, потребуйте, чтобы аргумент логарифма был положителен, основание положительно и отлично от единицы, а также чтобы знаменатель вашей дроби был отличен от нуля.
То, что за верно выписанную ОДЗ вам не снизят баллы, подтверждают и официальные методические рекомендации по оцениванию выполнения заданий с развернутым ответом ЕГЭ по профильной математике от РосОбрНадзора. Ниже приведен пример работы с верно выписанной ОДЗ. Работа оценена на максимальный балл. К ОДЗ никто не придирался.
Если Вам нужна методичка для экспертов по оцениванию работ ЕГЭ по профильной математике — можете написать нам в сообщения сообщества ВК. Подскажем, где скачать.
И как же быть?
- Если Вы привыкли использовать ОДЗ — используйте, но пишите его полностью. Если снизят — идите на апелляцию. Методичка по оцениванию — вам в помощь.
- Если Вы умеете работать с равносильными переходами — вы красавчик =) Это самый безопасный вариант. Но писанины будет… Запасайтесь бланками заранее.
- Если не устраивают предыдущие два пункта — озаглавьте ОДЗ словом «ограничения» или вообще никак не называйте. Это безопасно, даже если забудете какое-то важное условие.
А где пруфы?
Ну, если вам мало всего выше написанного — смотрите полную запись вебинара.
Автор текста: Арсений Филин
Оптимизация с ограничениями — это процесс оптимизации целевой функции с учётом некоторых ограничений[en] с некоторыми переменными. Целевая функция является функцией потерь, энергетической функцией, которая минимизируется, функцией вознаграждения, или функцией полезности, которая максимизируется.
Связь с задачами удовлетворения ограничений[править | править код]
Задача оптимизации с ограничениями является сильным обобщением классической задачи удовлетворения ограничений[1]. Задача оптимизации с ограничениями является задачей удовлетворения ограничений, в которой добавлена целевая функция, требующая оптимизации. Много алгоритмов разработано для работы с оптимизационной частью задачи.
Общая форма[править | править код]
Общая задача минимизации с ограничениями можно записать следующим образом:
где 




В некоторых задачах целевая функция, фактически, равна сумме функций цены, каждая из которых штрафует за выход на точку, в которой мягкие ограничения[en] (ограничения, которые предпочтительны, но не обязательно должны выполняться) нарушаются.
Методы решения[править | править код]
Многие алгоритмы оптимизации без ограничений могут быть применены в случае присутствия ограничений, часто путём использования метода штрафов. Однако, шаги поиска, предпринимаемые в методах без ограничений, могут оказаться неприемлемыми для задач с ограничениями, приводящими к потере сходимости. Этот эффект называют эффектом Маратоса[2].
Ограничения-равенства[править | править код]
Метод подстановки[править | править код]
Для очень простых задач, скажем, для функции от двух переменных с единственным линейным ограничением (равенством), наиболее практичным подходом является применение подстановки[3]. Идея заключается в подстановке ограничения в целевую функцию для создания композиции функций, которая включает эффект ограничения. Например, представим, что целью является максимизация функции 







Множитель Лагранжа[править | править код]
Если задача имеет лишь ограничения-равенства, может быть использован метод множителей Лагранжа для преобразования задачи в задачу без ограничений, в которой число переменных равно исходному числу переменных плюс исходное число ограничений. Альтернативно, если все все ограничения являются равенствами и все линейны, они могут быть решены относительно некоторых переменных в терминах других (одни переменные могут быть выражены через другие), а затем подставлены в целевую функцию, получая задачу без ограничений с меньшим числом переменных.
Ограничения-неравенства[править | править код]
С ограничениями-неравенствами задача может быть описана в терминах геометрических условий оптимальности, условий Фрица Джона[en] и условий Каруша — Куна — Таккера, при которых могут быть решены простые задачи.
Линейное программирование[править | править код]
Если целевая функция и все жёсткие ограничения линейны и некоторые из жёстких ограничений являются неравенствами, то задача является задачей линейного программирования. Задача может быть решена симплекс-методом, который обычно работает за полиномиальное от размера задачи время (но эта скорость не гарантирована) или методами внутренней точки, которые гарантированно работают за полиномиальное время.
Нелинейное программирование[править | править код]
Если целевая функция или некоторые из ограничений нелинейны, а некоторые из ограничений являются неравенствами , то задача является задачей нелинейного программирования.
Квадратичное программирование[править | править код]
Если все жёсткие ограничения линейны и некоторые из них являются неравенствами, но целевая функция квадратична, то задача является задачей квадратичного программирования. Это один из типов нелинейного программирования. Эту задачу можно решать за полиномиальное время методом эллипсоидов, если целевая функция выпукла. В противном случае задача может оказаться NP трудной.
ККТ условия[править | править код]
В случае неравенств ККТ подход для нелинейного программирования обобщает метод множителей Лагранжа. Он может быть применён при условии дифференцируемости и выпуклости.
Метод ветвей и границ[править | править код]
Задачи оптимизации с ограничениями могут быть решены методом ветвей и границ. Это алгоритмы перебора, запоминающие цену лучшего решения, найденного при выполнении и использующий её для отсечения ветвей поиска. Более точно, когда алгоритм находит частичное решение, которое нельзя расширить до образования решения с лучшей ценой, чем запомненная цена, алгоритм возвращается вместо попыток расширить решение.
При предположении, что цену следует минимизировать, эффективность этих алгоритмов зависит от того, как вычисляется цена , которая может быть получена при расширении частичного решения. Если алгоритм возвращается при поиске, часть возможных вариантов поиска пропускается. Чем ниже оценочная цена, тем лучше работает алгоритм, поскольку при низкой оценке мы более вероятно найдём решение лучше, чем уже встретили.
С другой стороны, эта оценочная цена не может быть ниже фактической цены, которая может быть получена путём расширения решения, так как в противном случае алгоритм может выполнить возврат, хотя решение в ветви может быть лучше, чем найденное ранее. Как результат, алгоритму требуется верхняя граница цены, которую можно получить при расширении частичного решения, и эта верхняя граница должна быть как можно меньше.
Вариант этого подхода, называемый методом Хансена, использует интервальные методы[4]. Метод по умолчанию реализует прямоугольные ограничения.
Выбор ограничивающих функций[править | править код]
Одним из способов получения этой верхней границы для частичного решения является рассмотрение каждого мягкого ограничения отдельно. Для каждого мягкого ограничения предполагается максимальное возможное значение для неназначенных переменных. Сумма этих значений является верхним значением, поскольку мягкие ограничения не могут принимать большие значения. Это потому, что максимальные значения могут получиться в результате вычисления в различных точках – мягкое ограничение может принимать максимальное значение в точке 

Поиск матрёшки[править | править код]
Этот метод[5] работает с помощью алгоритма ветвей и границ на 



В частности, оценка решения для неназначенных переменных 
Имеется сходство между поиском матрёшки и динамическим программированием. Подобно динамическому программированию поиск матрёшки решает подзадачи для решения основной задачи. Однако, в то время как динамическое программирование прямо комбинирует результаты, полученные при решении подзадачи, чтобы получить решение основной задачи, поиск матрёшки использует их только как границы в течение поиска.
Сегментное исключение[править | править код]
Алгоритм сегментного исключения[en] может быть приспособлен для оптимизации с ограничениями. Заданная переменная может быть удалена из задачи заменой всех мягких ограничений, её содержащих, новым мягким ограничением. Цена этого нового ограничения вычисляется в предположении максимального значения для всех удаляемых переменных. Формально, если 



Сегментное исключение работает с произвольным упорядочением переменных. Любая переменная ассоциирована с набором ограничений, который все ограничения, имеющие более высокий порядок. Сегментное исключение работает с последней переменной к первой. Для каждой переменной все ограничения сегмента заменяются как описано выше для исключения переменной. Результирующее ограничение затем помещается в подходящий набор.
См. также[править | править код]
- Метод наименьших квадратов с ограничениями[en]
- Распределённая оптимизация в ограничениях[en]
- Удовлетворение ограничений
- Программирование в ограничениях
- Целочисленное программирование
- Метод штрафов
Примечания[править | править код]
- ↑ Rossi, van Beek, Walsh, 2006, с. 3–12.
- ↑ Sun, Yua, 2010, с. 541.
- ↑ Prosser, 1993, с. 338–346.
- ↑ Leader, 2004.
- ↑ Verfaillie, Lemaître, Schiex, 1996.
Литература[править | править код]
- Gérard Verfaillie, Michel Lemaître, Thomas Schiex. Russian doll search for solving constraint optimization problems // AAAI/IAAI. — 1996. — Т. 1..
- Wenyu Sun, Ya-Xiang Yua. Optimization Theory and Methods: Nonlinear Programming. — Springer, 2010. — ISBN 978-1441937650.
- Mike Prosser. Constrained Optimization by Substitution // Basic Mathematics for Economists. — New York: Routledge, 1993. — ISBN 0-415-08424-5.
- Jeffery J. Leader. Numerical Analysis and Scientific Computation. — Addison Wesley, 2004. — ISBN 0-201-73499-0.
Литература для дальнейшего чтения[править | править код]
- Dimitri P. Constrained Optimization and Lagrange Multiplier Methods. — New York: Academic Press, 1982. — ISBN 0-12-093480-9.
- Francesca Rossi, Peter van Beek, Toby Walsh. Chapter 1 – Introduction. — Elsevier, 2006. — Т. 2. — С. 3–12. — (Handbook of Constraint Programming). — doi:10.1016/s1574-6526(06)80005-2.
- Rina Dechter. Constraint Processing. — Morgan Kaufmann, 2003. — ISBN 1-55860-890-7.



