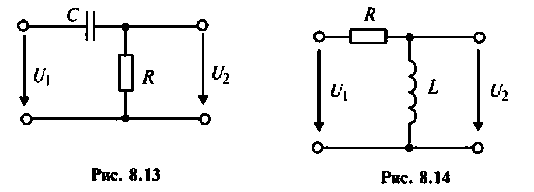
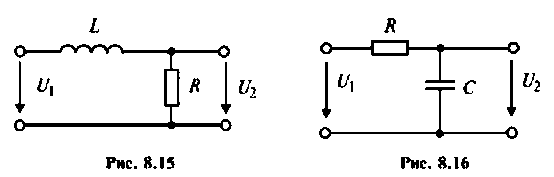
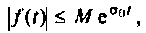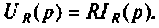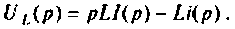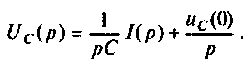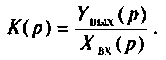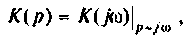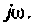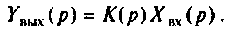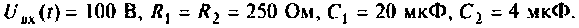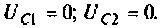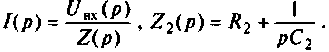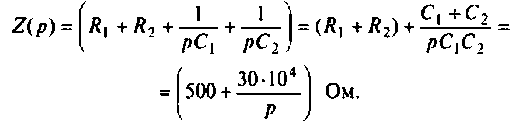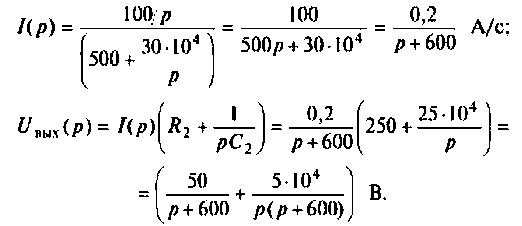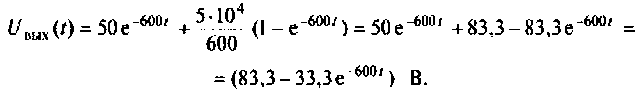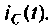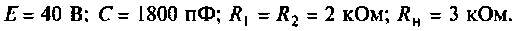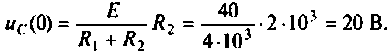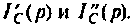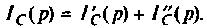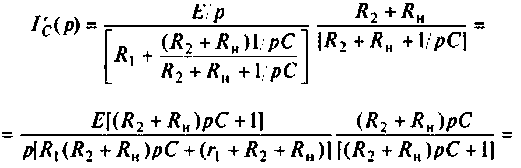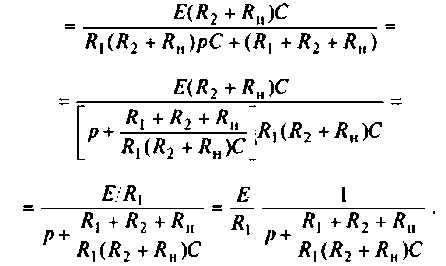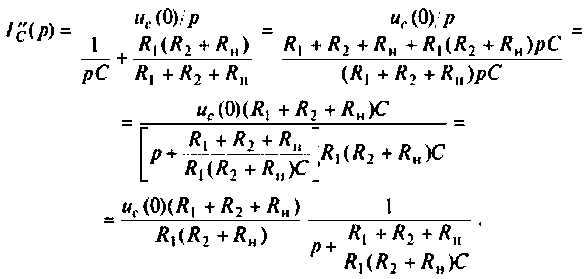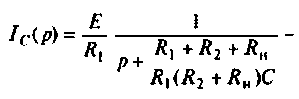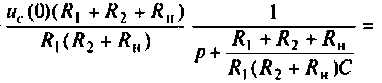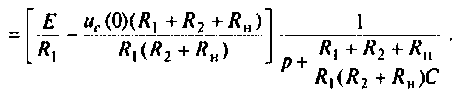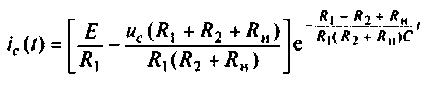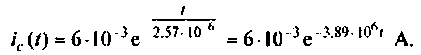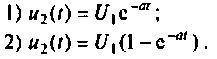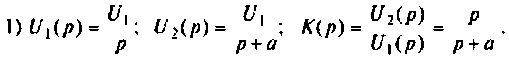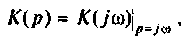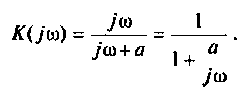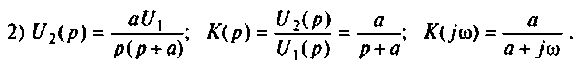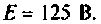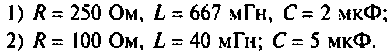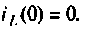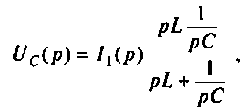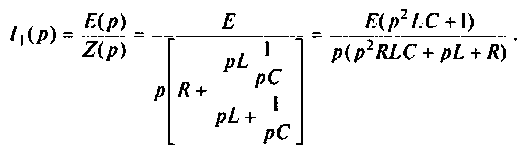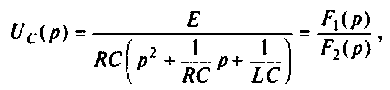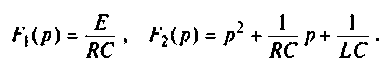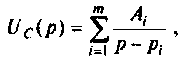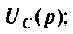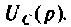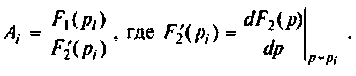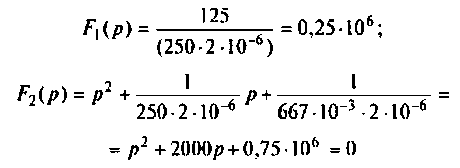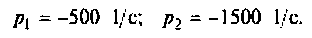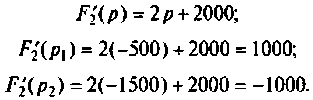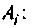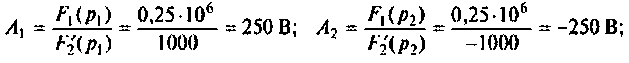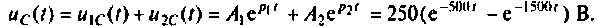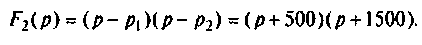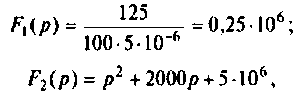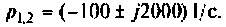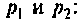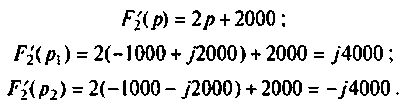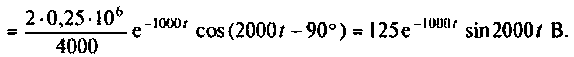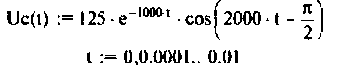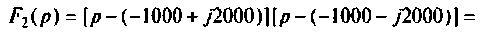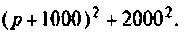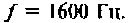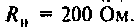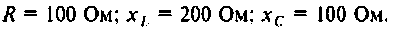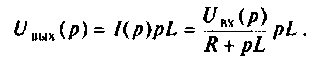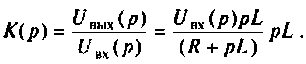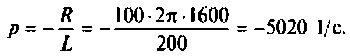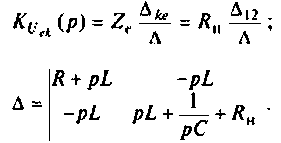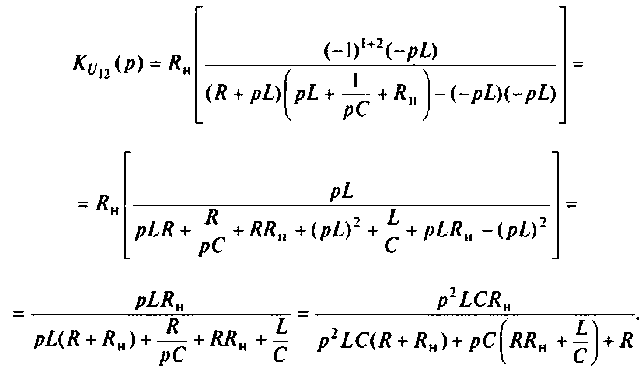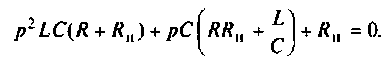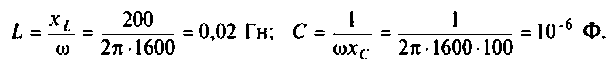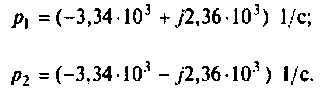7.3.1. Операторное уравнение.
Пусть дано линейное
дифференциальное уравнение -го порядка с постоянными
коэффициентами
. (1)
Требуется найти решение уравнения
(1) для при
начальных условиях
,
. (2)
Пусть является решением (1),
удовлетворяющее начальным условиям (2). Тогда после подстановки этой функции в
(1) мы получим тождество. Значит, функция, стоящая в левой части (1), и функция
имеют
одно и то же -изображение:

В силу следствия 1 § 7.2
.
Поэтому, используя свойство
линейности изображения, получаем

.
Для краткости записи обозначим ,
. Тогда
. (3)
Уравнение (3) будем называть вспомогательным
уравнением или изображающим уравнением, или операторным
уравнением.
Отметим, что коэффициент при в (3) получается из
левой части (1) формальной заменой производных на степени
. Обозначим этот коэффициент
через
.
Легко видеть, что этот
коэффициент является левой частью характеристического уравнения для дифференциального
уравнения (1) (см. (2) § 1.16). Тогда изображение решения находим в виде
, (4)
где
.
Если начальные условия нулевые,
т. е. ,
то формула (4) запишется
. (4′)
Если теперь по изображению (4)
или (4′) мы найдем оригинал, то в силу теоремы единственности это и будет
искомое решение .
Пример 1. Решить уравнение
,
.
По формуле (4′) имеем
,
так
как .
Разложим изображение на простейшие дроби

Отсюда
.
Мы получили решение только для
. Легко проверить,
что оно удовлетворяет нашему уравнению и при . Впрочем, этот факт следует из общих
соображений, на которых мы не останавливаемся. Это замечание относится и к
примерам 2-4.
Можно также воспользоваться
теоремой 12 § 7.2 ,
,
;
– простые нули многочлена
:
.
Пример 2. ,
,
.
Составим вспомогательное
уравнение:
,
.
Отсюда

Многочлен имеет простые нули
,
. На основании
теоремы 12 § 7.2 имеем:
,
,
,
,
,
,
,
.
При решении дифференциального
уравнения иногда удобно использование формулы Дюамеля (см. (15) § 7.2).
Будем рассматривать уравнение (1)
при нулевых начальных условиях: . К этому случаю всегда можно свести
задачу заменой искомой функции по формуле

Допустим, известно решение
уравнения (1) при правой части, равной единице, и нулевых начальных условиях.
Операторное уравнение для данной задачи имеет вид
, (5)
где
–
изображение решения указанной задачи. Из равенства (4′) и
(5) находим
. (6)
Согласно формуле Дюамеля
или
учитывая, что ,
получаем

Отсюда решение уравнения (1) при
нулевых начальных условиях будет иметь вид

где
–
решение уравнения (1) при и нулевых начальных условиях.
Пример 3. Решить уравнение
,
.
Решим вначале задачу Коши для
уравнения
,
.
Составим операторное уравнение:
,
.
Отсюда
.
Замечание. Так как правая часть
уравнения имеет
специальный вид, то решение этого уравнения можно проводить и обычным образом
(см. § 1.18).
По формуле (7)
.
Записываем операторное уравнение
(Tp2
+ p)Y(p)
= kX(p)
и
передаточную функцию системы:
.
Полиномы числителя и знаменателя имеют
вид:
.
Характеристическое
уравнение разомкнутой системы D(p)
= 0, то есть,
.
Корни этого характеристического
уравнения действительные:
.
Пример 5.2.
Используя
дифференциальное уравнение предыдущего
примера, найти характеристическое
уравнение и его корни для замкнутой
системы.
Подставляя
передаточную функцию разомкнутой
системы
в формулу (5.6), получаем характеристическое
уравнение замкнутой системы:
.
Его
корни:
Они
могут быть как действительными (4 k
T
< 1), так и комплексными
(4
k
T
> 1) .
5.2. Критерий Гурвица. Устойчивость системы по Гурвицу выясняется с помощью характеристического уравнения. Составляется специальный определитель – определитель Гурвица. Правило следующее.
Намечают
n строк и n
столбцов (n – степень
характеристического уравнения). В первый
строке ставят все нечетные коэффициенты:
a1, a3,
a5. По главной
диагонали, начиная с коэффициента a1,
слева-вниз-направо располагают
последовательно все остальные
коэффициенты. Столбцы, начиная с главной
диагонали, заполняются вверх по
нарастающим индексам, вниз – по убывающим.
Все коэффициенты с индексами ниже нуля
и выше степени уравнения, заменяют
нулями.
Определители
Гурвица 5-го, 4-го, 3-го и 2-го порядков
выглядят следующим образом.
n
= 5 n = 4 n = 3 n =
2
Для устойчивости
системы необходимо, чтобы все коэффициенты
характеристического уравнения и все
определители были положительными.
Получим условия
устойчивости для конкретных уравнений.
-
Характеристическое
уравнение 2-й степени:
a0p2+a1p+a2
= 0 .
Ему соответствует
определитель Гурвица 2-го порядка:
=
a1a2
– a0
· 0
= a1a2.
2
= a1a2
.
Условие
устойчивости: a0,
a1,
a2
> 0;
2
> 0,
т.е.
a1a2
> 0.
-
Характеристическое
уравнение 3-й степени:
a0p3
+ a1p2
+ a2p
+ a3
= 0.
Ему соответствует
определитель Гурвица 3-го порядка:
= a1(a2a3
– a10)
– a3(a0a3
– 0·0)+0(a0a1
– a2·0).
Δ3
= a1a2a3
– a0a23.
Условие
устойчивости: a0,
a1,
a2,
a3
>
0; Δ3
>
0, или, сокращая на a3,
a1a2
– a0a3
> 0.
-
Характеристическое
уравнение 4-й степени:
a0p4
+ a1p3
+ a2p2
+ a3p
+ a4
= 0 .
Ему соответствует
определитель Гурвица 4-го порядка:
= а1
– а3
+ 0 – 0 .
Δ4
=
a1a2a3a4
–
a21a24
– a0a23a4
.
Условие
устойчивости:
a0,
a1,
a2,
a3,
a4
>
0, Δ4
>
0, или
сокращая
на
a4,
a1a2a3
–
a21a4
–
a0a23
>
0 .
-
Характеристическое
уравнение 5-й степени:
a0p5
+ a1p4
+ a2p3
+ a3p2
+ a4p
+ a5
= 0 .
Опуская процедуру
вычисления определителя, выпишем сразу
условие устойчивости:
a0,
a1,
a2,
a3,
a4,
a5 >
0,
(a1a2
– a0a3)(a3a4
– a2a5)
– (a1a4
– a0a5)2
> 0 .
Можно составлять
определители Гурвица и для характеристических
уравнений более высокой степени, получая
соответствующие условия устойчивости.
Однако, объем вычислений нарастает с
увеличением степени характеристического
уравнения, поэтому считается приемлемым
пользоваться критерием Гурвица для
характеристических уравнений степени
не выше пятой.
Определитель
Гурвица позволяет найти коэффициент
усиления на границе устойчивости.
Коэффициент усиления – это свободный
член характеристического уравнения,
его индекс равен степени уравнения.
Границей устойчивости будет условие
Δ = 0. Откуда и вычисляется
коэффициент усиления.
Пример 5.3.
Дана система,
характеристическое уравнение которой
имеет вид :
T1
T1T2T3p3
+ (T1T2
+ T1T3
+ T2T3)p2
+ (T1
+ T2
+ T3)p
+ 1 + k
= 0 .
Выяснить,
будет ли система устойчивой, если T1
= 1, T2
= 2, T3
= 3, k
= 19 ? Каким
должен быть коэффициент усиления на
границе устойчивости?
Записываем
характеристическое уравнение 3-й степени
в общем виде, сопоставляем его с заданным
и заключаем:
a0=
T1T2T3
,
a2=
T1+T2+T3
,
a1=
T1T2+T1T3+T2T3
,
a3=1+k
.
Все
коэффициенты больше нуля, но надо
проверить, будет ли определитель Гурвица
больше нуля. Подставив числа в неравенство
a1a2
– a0a3
> 0,
обнаруживаем, что оно не выполняется:
66 – 120 < 0. Определитель оказался
отрицательным. Следовательно, система
неустойчива.
На
границе устойчивости a1a2
– a0a3
= 0.
Подставляя числа, имеем: 11·6 = 6 (1 + k).
Коэффициент усиления на границе
устойчивости k
= 10.
Пример
5.4.
Выяснить,
будет ли устойчивой система с
характеристическим уравнением
5p4
+ p
+ 2 = 0 .
Сопоставив
данное уравнение с его общим видом,
получаем:
a0
= 5, a1
=
a2
=
0, a3
=
1, a4
=
2.
По
условию
устойчивости
a1a2a3
– a12a4
– a0a32
> 0. Это
не выполняется:
-5∙12
< 0. Система неустойчива, хотя все
коэффициенты положительные.
Пример
5.5.
Звенья, передаточные
функции которых
и
,
соединяются
последовательно. Выяснить, будет ли
такая система устойчивой? Какую величину
имеет постоянная времени T0
на границе устойчивости замкнутой
системы?
Находим передаточную
функцию разомкнутой системы
.
Ее
знаменатель, приравненный к нулю, есть
характеристическое уравнение. После
сокращения на T0
характеристическое уравнение выглядит
так:
T12p3
+
T2p2
+
p
= 0 .
Сопоставляя
с записью характеристического уравнения
в общем виде, делаем вывод:
a0
= T12,
a1
= T2,
a2
= 1, a3
= 0.
Для
уравнения 3-й степени условия устойчивости
требуют, чтобы
a0,
a1,
a2,
a3
> 0 , a1a2
–
a0a3
> 0 .
Это
соблюдается: T12
, T2
, 1 > 0 ,
T2
– 0 ∙ T12
> 0 . Следовательно, разомкнутая система
устойчива.
Составим
характеристическое уравнение замкнутой
системы. Это будет сумма полиномов
числителя и знаменателя, приравненная
к нулю:
T0
T12p3
+ T0T2p2
+ T0(k1k2
+ 1)p
+ k1k2
= 0.
Выписываем
коэффициенты:
a0
= T0T12,
a1
= T0
T2
,
a2
= T0(k1k2
+ 1) , a3
= k1k2
.
Выясняем
устойчивость:
T0T12,
T0T2
,
T0(k1k2
+ 1) , k1k2
>
0 .
Замкнутая система
будет устойчивой, если
T0T2
(k1k2
+ 1) – k1k2
T12
>
0 .
На
границе устойчивости определитель
равен нулю, из чего заключаем:
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Содержание:
Операторный метод расчета переходных процессов:
Для решения линейных дифференциальных и интегродифференциальных уравнений в теории электрических цепей нашел широкое применение так называемый операторный метод, основанный на преобразованиях Лапласа.
Сущность этого метода заключается в том что функции вещественного переменного t преобразуются в функции комплексного переменного
Переход от функции вещественного переменного t к функции комплексного переменного p осуществляется с помощью прямого преобразования Лапласа
Обратный переход от функции комплексного переменного р к функциям вещественного переменного t осуществляется на основании обратного преобразования Лапласа
Функцию 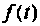
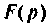
Напомним, что для того чтобы функция 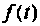
- удовлетворяла условиям Дирихле;
- была равна нулю для отрицательных значений t, т. е. при
- в интервале
не возрастала быстрее, чем некоторая показательная функция
где 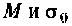
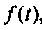
Применение свойств преобразования Лапласа в сочетании с теоремой разложения дает возможность составить таблицы изображений и оригиналов, облетающие и ускоряющие нахождение оригиналов по изображениям [4, 26]. Применение операторного метода совместно с компьютерными математическими программными средами делает анализ и расчет электрических цепей доступным, быстрым и интересным.
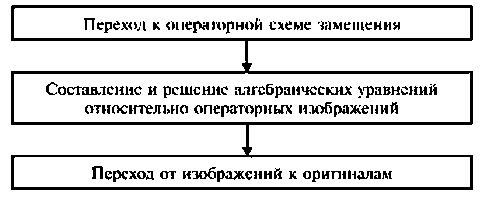
Особенностью метода является необходимость выполнения трех этапов:
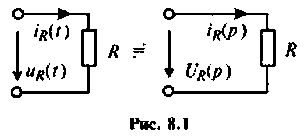
Эквивалентные операторные схемы замещения элементов
Активное сопротивление:
На рис. 8.1 изображена схема замещения в операторном виде участка цепи с активным сопротивлением. Для этого участка цепи связь между операторным напряжением и током записывается в виде
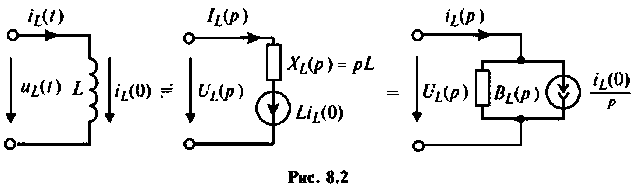
Индуктивность:
Для участка цепи с индуктивностью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.2.
Связь между операторным напряжением и током записывается в виде
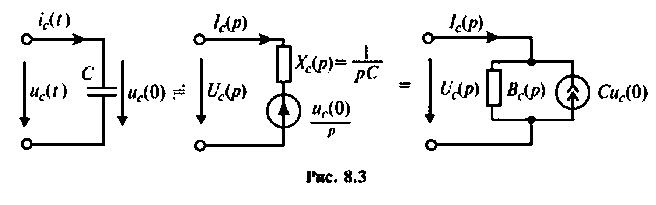
Емкость:
Для участка цепи с емкостью при ненулевых начальных условиях операторная схема замещения изображена на рис. 8.3.
Связь между напряжением и током устанавливает соотношение
В эквивалентных операторных схемах для индуктивности и емкости с ненулевыми начальными условиями возникают дополнительные источники ЭДС 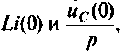
Порядок расчета:
- определяют независимые начальные условия;
- составляют эквивалентную операторную схему замещения для послекоммутационной цепи;
- составляют систему уравнений в операторной форме в соответствии с выбранным рациональным методом расчета эквивалентной схемы замещения и решают ее относительно изображений неизвестных величин;
- для нахождения оригиналов неизвестных величин используют таблицы соответствия, формулы теоремы разложения, компьютерные программные среды и др.
Операторные функции электрических цепей
Основные операторные функции:
Операторной функцией цепи называется отношение изображения по Лапласу выходной величины 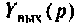
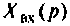
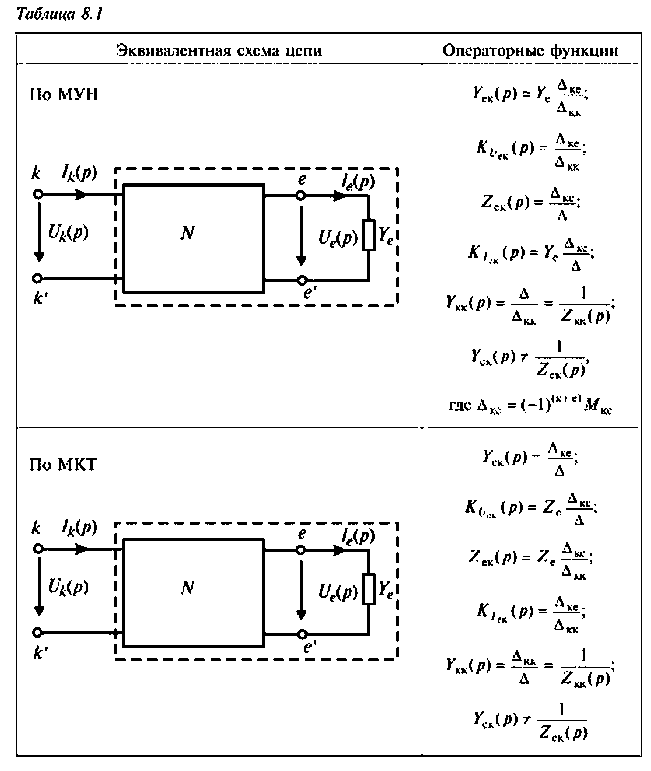
Операторная функция зависит только от параметров цепи и ее схемы. Различают входные и передаточные операторные функции. В табл. 8.1 приведены соотношения для расчета операторных функций сложных цепей.
Для расчета операторных функции можно применять все методы расчета комплексных функций
т. е. комплексная функция является частным случаем операторной при замене оператора 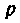
Анализ переходных процессов в цепях с помощью операторных функций
По известной операторной функции цепи и операторному изображению воздействия можно найти реакцию цепи на это воздействие
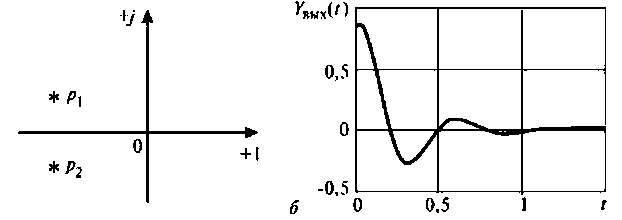
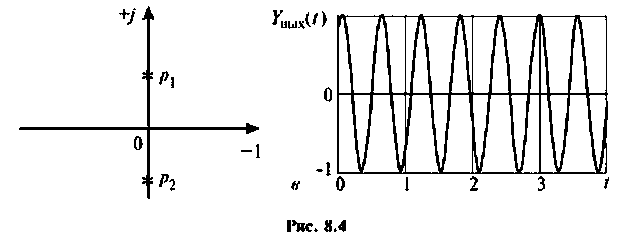
На рис. 8.4 (а—в) приведены временные диаграммы переходных процессов, а также полюсно-нулевое представление на комплексной плоскости.
По расположению полюсов операторной функции можно судить о характере переходное процесса:
- если все полюсы расположены только на отрицательной вещественной полуоси, то переходный процесс в цепи носит апериодический характер;
- если имеются сопряженные полюсы в левой полуплоскости, то переходный процесс носит характер затухающих колебаний;
- если все полюсы расположены только на отрицательной мнимой оси, то переходный процесс в цепи носит характер незатухающих колебаний.
Примеры решения задач
Пример 8.4.1.
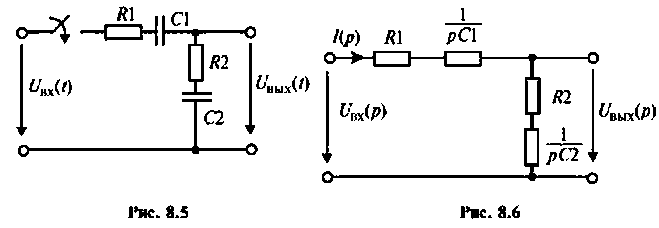
В интегродифференцирующем контуре постоянного тока (рис. 8.5), применяемом для коррекции ЭЦ и САУ. определить напряжение 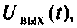
Решение
Определяют независимые начальные условия — напряжения на емкостях. До коммутации ключ был разомкнут, напряжение на емкостях отсутствовало:
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.6).
Находят изображение напряжения 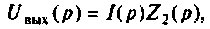
Сопротивление всей цепи определяется выражением
Тогда:
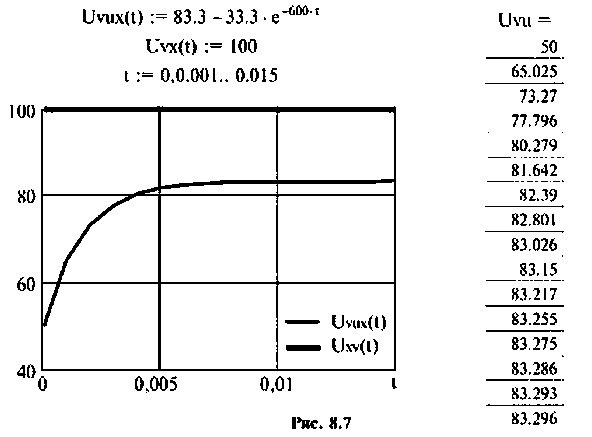
По данному изображению находят оригинал (рис. 8.7) напряжения 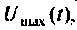
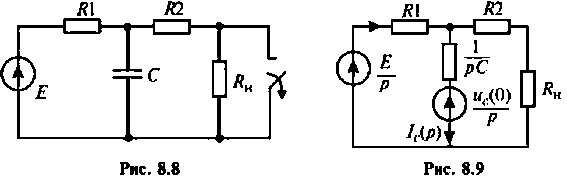
Пример 8.4.2.
К пассивному RС-фильтру нижних частот подключается нагрузка 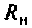
Дано:
Решение
Определяют независимые начальные условия – напряжение на емкости
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.9).
Операторный ток 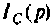
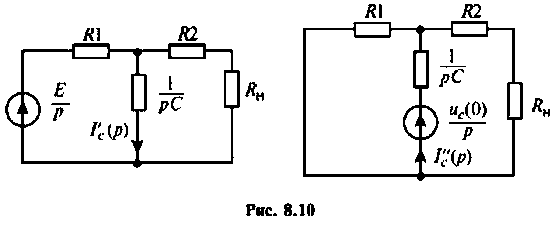
Операторные схемы, соответствующие частичным токам, изображены на рис. 8.10.
Искомый ток
Определяют частичный ток
Аналогично определяют частичный ток
Искомый ток
По данному изображению 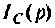
Подставляя числовые значения величин, получают
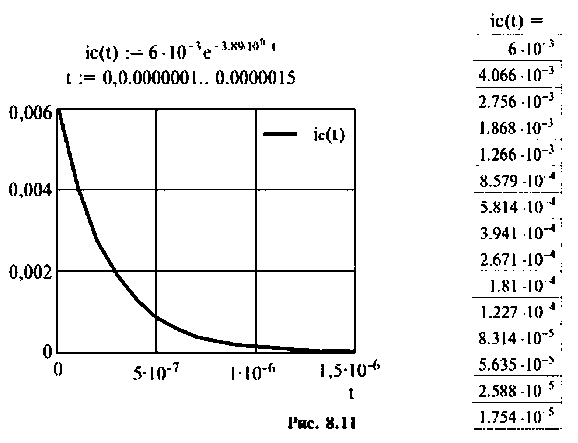
Строят график тока 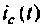
Выводы. До коммутации напряжение на емкости определялось падением напряжения на сопротивлении 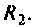
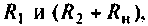
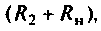
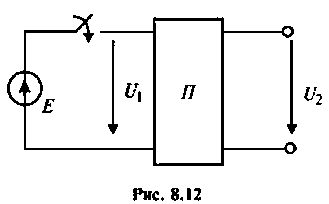
Пример 8.4.3.
Рассчитать коэффициент передачи по напряжению пассивной цепи (рис. 8.12) и составить ее схему так, чтобы при подключении на вход источника постоянной ЭДС 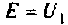
Решение
Применяя преобразования Лапласа, находят изображения
Из прямых преобразований Лапласа и Фурье следует, что
тогда
Если принять 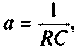
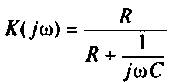
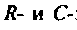
Если принять 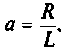
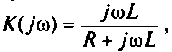
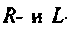
Если принять 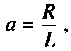
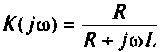
Если принять 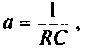
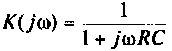
Пример 8.4.4.
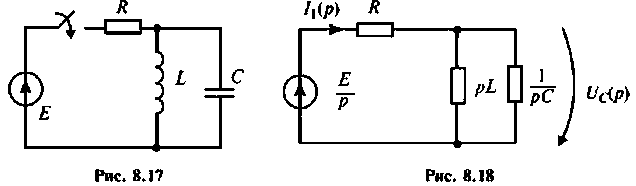
Параллельный колебательный контур (рис. 8.17) включается на постоянное напряжение
Определить напряжение на конденсаторе и построить его опюру, если:
Решение
Определяют независимые начальные условия: напряжение на конденсаторе 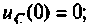
Строят эквивалентную операторную схему замещения после коммутации (рис. 8.18).
Находят изображение напряжения на конденсаторе
где
Тогда
где
По данному изображению находят оригинал по теореме разложения дробно-рациональной функции
где 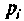
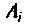
При простых (некратных) полюсах 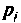
а) Для первого варианта значений:
Полюсы изображения 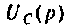
Вычисляют производную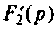
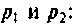
Вычисляют начальные значения компонент
Следовательно,
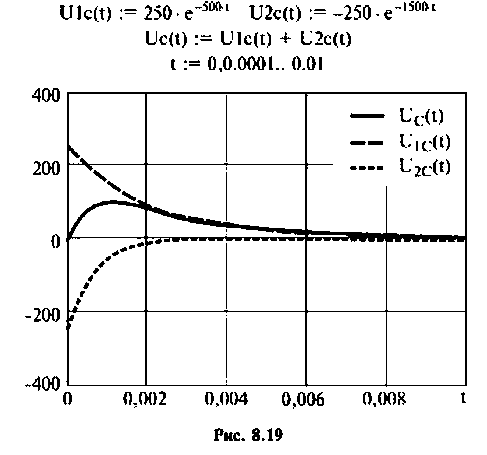
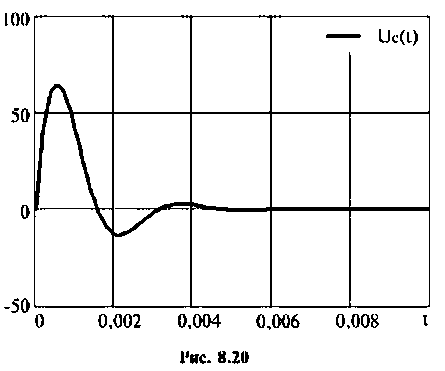
Графики напряжения на конденсаторе и его компонентов получены в среде Mathcad и показаны на рис. 8.19.
Тоn же результат может быть получен по таблице преобразования Лапласа (табл. 8.2, п. 8), если знаменатель изображения напряжения на конденсаторе представить в виде
б) Для второго варианта числовых значений:
а полюсы
Находят производную от 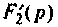
Следовательно,
По теореме разложения определяют
где
или
График изменения напряжения 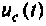
Тот же результат может быть получен по таблице преобразования Лапласа (см. табл. 8.2, п. 13), если знаменатель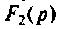
Примечание. Результаты этого примера сравните с результатами примера 6.3. Оцените достоинства и недостатки классического и операторного методов расчета переходных процессов.
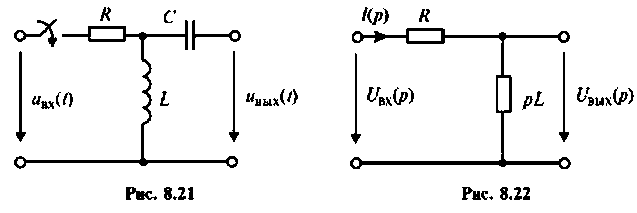
Пример 8.4.5.
После замыкания ключа четырехполюсник (рис. 8.21) используется для работы на частоте
Определить:
а) коэффициент передачи по напряжению 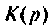
б) характер переходного процесса по кривой переходного процесса.
Дано:
Решение
В режиме холостого хода
Изображают эквивалентную операторную схему замещения. На рис. 8.22 приведена операторная схема замещения при нулевых начальных условиях.
Находят изображение напряжения на выходе
Откуда
Определяют полюсы операторной функции из уравнения 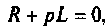
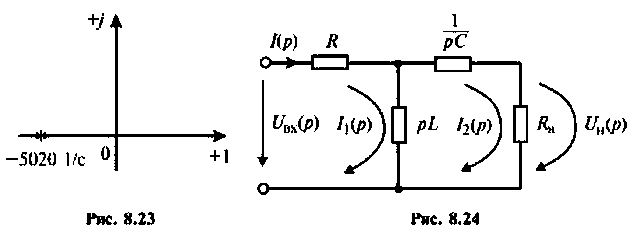
Переходной процесс в цепи имеет апериодический характер, что видно из расположения полюсов на комплексной плоскости (рис, 8.23).
В режиме нагрузки
Изображают эквивалентную операторную схему замещения после коммутации (рис. 8.24).
Определяют операторную функцию 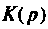
Определяют полюсы операторной функции из уравнения
Для этога вначале вычисляют L и С.
Находят корни уравнения:
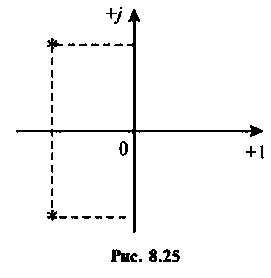
Переходный процесс в цепи имеет характер затухающих колебаний, что видно из расположения полюсов на комплексной плоскости (рис. 8.25).
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Цепи с распределенными параметрами
- Электрическая энергия, ее свойства и применение
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
- Классический метод расчета переходных процессов
- Анализ переходных и установившихся процессов методом интеграла свертки
Сущность операторного метода заключается в том, что функции вещественной переменной t, которую
называют оригиналом, ставится в соответствие функция комплексной переменной
, которую называют изображением.
В результате этого производные и интегралы от оригиналов заменяются алгебраическими
функциями от соответствующих изображений (дифференцирование заменяется умножением
на оператор р, а интегрирование – делением на него), что в свою очередь определяет
переход от системы интегро-дифференциальных уравнений к системе алгебраических
уравнений относительно изображений искомых переменных. При решении этих уравнений
находятся изображения и далее путем обратного перехода – оригиналы. Важнейшим
моментом при этом в практическом плане является необходимость определения только
независимых начальных условий, что существенно облегчает расчет переходных процессов
в цепях высокого порядка по сравнению с классическим методом.
Изображение заданной функции
определяется в соответствии с
прямым преобразованием Лапласа:
 . . |
(1) |
В сокращенной записи соответствие между изображением и оригиналом обозначается,
как:

Следует отметить, что если оригинал увеличивается с ростом t,
то для сходимости интеграла (1) необходимо более быстрое убывание модуля . Функции, с которыми встречаются
на практике при расчете переходных процессов, этому условию удовлетворяют.
В качестве примера в табл. 1 приведены изображения некоторых характерных функций,
часто встречающихся при анализе нестационарных режимов.
Таблица 1. Изображения типовых функций
Оригинал  |
Изображение  |
| A |  |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Некоторые свойства изображений
- Изображение суммы функций равно сумме изображений слагаемых:
- При умножении оригинала на коэффициент на тот же коэффициент умножается
изображение:

.
С использованием этих свойств и данных табл. 1, можно показать, например,
что

Изображения производной и интеграла
В курсе математики доказывается, что если , то
, где
– начальное значение функции
.
Таким образом, для напряжения на индуктивном элементе можно записать
или при нулевых начальных условиях
.
Отсюда операторное сопротивление катушки индуктивности
.
Аналогично для интеграла: если , то

С учетом ненулевых начальных условий для напряжения на конденсаторе можно записать:

Тогда

или при нулевых начальных условиях

откуда операторное сопротивление конденсатора

Закон Ома в операторной форме
Пусть имеем некоторую ветвь (см. рис. 1), выделенную
из некоторой

сложной цепи. Замыкание ключа во внешней цепи приводит к переходному процессу,
при этом начальные условия для тока в ветви и напряжения на конденсаторе в общем
случае ненулевые.
Для мгновенных значений переменных можно записать:

Тогда на основании приведенных выше соотношений получим:

Отсюда
 , , |
(2) |
где 
участка цепи.
Следует обратить внимание, что операторное сопротивление соответствует комплексному сопротивлению
ветви в цепи синусоидального
тока при замене оператора р на .
Уравнение (2) есть математическая запись закона Ома для участка цепи с источником
ЭДС в операторной форме. В соответствии с ним для ветви на рис. 1 можно нарисовать
операторную схему замещения, представленную на рис. 2.

Законы Кирхгофа в операторной форме
Первый закон Кирхгофа: алгебраическая сумма изображений токов,
сходящихся в узле, равна нулю

Второй закон Кирхгофа:алгебраическая сумма изображений ЭДС, действующих в контуре, равна алгебраической сумме изображений напряжений на пассивных элементах этого контура

При записи уравнений по второму закону Кирхгофа следует помнить о необходимости
учета ненулевых начальных условий (если они имеют место). С их учетом последнее
соотношение может быть переписано в развернутом виде

В качестве примера запишем
выражение для изображений токов в цепи на рис. 3 для двух случаев: 1 –
; 2 –
.
В первом случае в соответствии с законом Ома 
Тогда

и
Во втором случае, т.е. при
, для цепи на рис. 3 следует составить
операторную схему замещения, которая приведена на рис. 4. Изображения токов
в ней могут быть определены любым методом расчета линейных цепей, например,
методом контурных токов:

откуда ;
и
.
Переход от изображений к оригиналам
Переход от изображения искомой величины к оригиналу может быть осуществлен
следующими способами:
1. Посредством обратного преобразования Лапласа

которое представляет собой решение интегрального уравнения (1) и сокращенно
записывается, как:
.
На практике этот способ применяется редко.
2. По таблицам соответствия между оригиналами и изображениями
В специальной литературе имеется достаточно большое число формул соответствия,
охватывающих практически все задачи электротехники. Согласно данному способу
необходимо получить изображение искомой величины в виде, соответствующем табличному,
после чего выписать из таблицы выражение оригинала.
Например,
для изображения тока в цепи на рис. 5 можно записать

Тогда в соответствии с данными табл. 1

что соответствует известному результату.
3. С использованием формулы разложения
Пусть изображение искомой переменной определяется
отношением двух полиномов

где .
Это выражение может быть представлено в виде суммы простых дробей
 , , |
(3) |
где – к-й корень уравнения
.
Для определения коэффициентов умножим левую и правую части
соотношения (3) на ( ):

При

Рассматривая полученную неопределенность типа по правилу Лопиталя, запишем

Таким образом,

Поскольку отношение 
то учитывая, что 
 . . |
(4) |
Соотношение (4) представляет собой формулу разложения. Если один из корней
уравнения равен нулю, т.е.
, то уравнение (4) сводится к
виду

В заключение раздела отметим, что для нахождения начального и конечного
значений оригинала можно использовать
предельные соотношения

которые также могут служить для оценки правильности полученного изображения.
Литература
- Основы теории цепей: Учеб. для вузов /Г.В.Зевеке, П.А.Ионкин, А.В.Нетушил,
С.В.Страхов. –5-е изд., перераб. –М.: Энергоатомиздат, 1989. -528с. - Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи. Учеб. для студентов электротехнических, энергетических и приборостроительных
специальностей вузов. –7-е изд., перераб. и доп. –М.: Высш. шк., 1978. –528с. - Теоретические основы электротехники. Учеб. для вузов. В трех т. Под
общ. ред. К.М.Поливанова. Т.1. К.М.Поливанов. Линейные электрические цепи
с сосредоточенными постоянными. –М.: Энергия- 1972. –240с.
Контрольные вопросы
- В чем заключается сущность расчета переходных процессов операторным методом?
- Что такое операторная схема замещения?
- Как при расчете операторным методом учитываются ненулевые независимые начальные
условия? - Какими способами на практике осуществляется переход от изображения к оригиналу?
- Для чего используются предельные соотношения?
- Как связаны изображение и оригинал в формуле разложения? Какие имеются варианты
ее написания? -
С использованием теоремы об
активном двухполюснике записать операторное изображение для тока через катушку
индуктивности в цепи на рис. 6. - С использованием предельных соотношений и решения предыдущей задачи найти
начальное и конечное значения тока в ветви с индуктивным элементом.
Ответ: 
Ответ: .
Операторные уравнения
Пример операторного уравнения:
где — оператор, — функция.
Функция , которая удовлетворяет операторному уравнению
[ L f=lf ]
, называется собственной функцией оператора. Число (не переменная) l называется собственным значением оператора.
где — собственное значение, — собственная функция оператора.
Например, рассмотрим оператор дифференцирования:
- f=e^{kx}
widehat{L}f = frac{d}{dx}e^{kx} = underset{substack{ downarrow l}} {k}e^{kx}=lf
Вывод: функция f является собственной функцией оператора, собственное значение k.
- f = x^2
widehat{L}f = frac{d}{dx}x^2 = 2x = frac{2}{x}fneq lf
Вывод: функция f не является собственной, так как не соответствует операторному уравнению (l содержит в себе переменную).
Основная задача квантовой химии сводится к нахождению собственных функций и собственных значений оператора полной энергии для молекул.
Содержание
- Является ли собственная функция единственной для оператора, или у него может быть несколько собственных функций?
- Пусть есть разные операторы. Будут ли их собственные функции разными или они могут быть одинаковыми?
- Всегда ли разным собственным функциям отвечают разные собственные значения?
- Физический смысл собственного значения
- Проблема точных и средних значений физических величин. Энергия известна точно или это вероятностная величина?
Является ли собственная функция единственной для оператора, или у него может быть несколько собственных функций?
Рассмотрим оператор дифференцирования:
widehat{L}=frac{d}{dx}
e^{kx} longrightarrow e^x,e^{2x},…,e^{kx}
Собственное значение — k.
Для оператора может существовать различное множество собственных функций. Причем собственные функции самосопряженного оператора ортогональны друг другу и образуют базис пространства функций.
Пусть есть разные операторы. Будут ли их собственные функции разными или они могут быть одинаковыми?
Если операторы коммутируют друг с другом , то они имеют общую систему собственных функций. Собственные функции коммутирующих операторов одни и те же.
Всегда ли разным собственным функциям отвечают разные собственные значения?
Рассмотрим оператор дифференцирования:
widehat{L} = frac{partial}{partial{x}}
f = e^{kx} qquad widehat{L}f = ke^{kx} = kf, quad l_1 =k g = ye^{kx} qquad widehat{L}g = kye^{kx} = kg, quad l_2 =k gneq fqquad l_1=l_2
Собственные волновые функции для которых собственное значения одинаковые называются вырожденными.
Физический смысл собственного значения
Запишем операторное уравнение:
widehat{L}f=lf
Умножим левую и правую часть равнения на комплексно-сопряженную функцию f^*:
f^*widehat{L}f=f^*lf
Проинтегрируем:
Собственное значение есть значение физической величины (из 5 постулата). Т.е. для оператора полной энергии системы (гамильтониана H) — собственное значение Е есть значение физической величины полной энергии системы.
1 следствие: константа Е в уравнении Шредингера является полной энергией системы.
widehat{H}Psi = EPsi
2 следствие: Для любого состояния системы можно найти его энергию.
Проблема точных и средних значений физических величин. Энергия известна точно или это вероятностная величина?
Физическая величина определяется интегралом:
1) Ψ — собственная, тогда физическая величина l — точное значение;
2) Ψ — не собственная:
Ψ — не собственная:
Физическая величина вычисляемая по 5 постулату является точной, если волновая функция является собственной функцией оператора.
Если волновая функция не является собственной функцией оператора, то физическая является средней.
2 следствия:
- энергия любой системы может быть определена точно (это не средняя величина)
widehat{H}Psi=EPsi
- физические величины, соответствующие коммутирующим операторам могут быть одновременно определены с любой степенью точности. И обратное: если операторы не коммутируют, то их физические величины не могут быть одновременно точно определены.










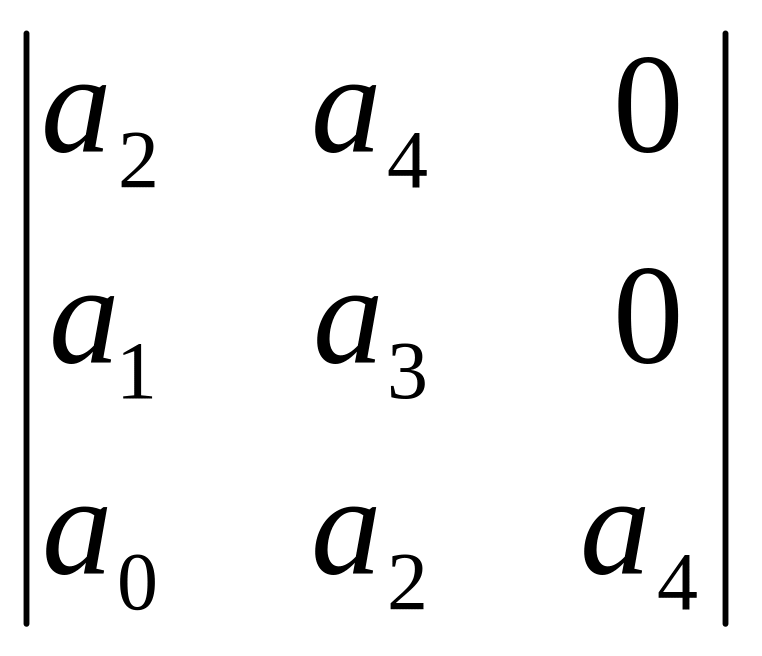

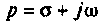
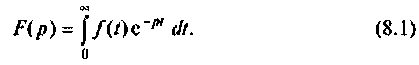
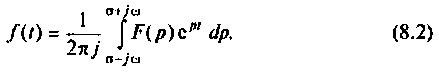
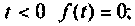
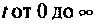 не возрастала быстрее, чем некоторая показательная функция
не возрастала быстрее, чем некоторая показательная функция