Появление в
математике новых понятий, а значит, и
новых терминов, обозначающих эти понятия,
предполагает их определение.
Определением
обычно называют предложение, разъясняющее
суть нового термина (или обозначения)
Как правило, делают
это
на основе ранее введенных понятий.
Например, прямоугольник можно определить
так: «Прямоугольником называется
четырехугольник, у которого все углы
прямые». В этом определении есть две
части- определяемое понятие (прямоугольник)
и определяющее понятие (четырехугольник,
у которого все углы прямые). Если
обозначить через а первое понятие, а
через b
– второе, то данное определение можно
представить в таком виде:
а есть
(по определению) b.
Слова
«есть (по определению)» обычно заменяют
символом
![]() , и тогда определение выглядит так: а
, и тогда определение выглядит так: а![]() b
b
Читают:
«а равносильно b
по определению». Можно прочитать эту
запись еще и так: «а тогда и только тогда,
когда b».
Определения,
имеющие такую структуру, называются
явными. Сформулировать их можно
по-разному. В математике используют
определения через род и видовое отличие,
генетические, индуктивные и другие.
Примером
определения через род и видовое отличие
является определение прямоугольника,
данное выше. В генетических
определениях указывается способ
образования определяемого объекта.
Например, шар – это геометрическая
фигура, получаемая в результате вращения
полукруга вокруг диаметра. В индуктивных
определениях указываются некоторые
основные объекты теории и правила,
позволяющие получать новые из уже
имеющихся. Примером такого определения
может служить определение арифметической
прогрессии: «Арифметической прогрессией
называется числовая последовательность,
каждый член которой, начиная со второго,
равен предыдущему, сложенному с одним
и тем же числом».
Но
чаще всего в математике используются
определения через род и видовое отличие.
Рассмотрим подробнее структуру этих
определений.
Обратимся
опять к определению прямоугольника,
вернее, к его второй части – определяющему
понятию. В нем можно выделить:
1) понятие
«четырехугольник», которое является
родовым по отношению к понятию
«прямоугольник»,
2)
свойство «иметь все углы прямые», которое
позволяет выделить из всевозможных
четырехугольников один вид – прямоугольники;
поэтому его называют видовым отличием.
Вообще
видовое отличие- это свойства (одно или
несколько), которые позволяют выделять
определяемые объекты из объема
родового понятия.
Итоги нашего
анализа можно представить в виде схемы

Заметим,
что в наглядном представлении структуры
определения через род и видовое
отличие мы допустили некоторые неточности.
Во-первых, слова «родовое понятие»
означают, что речь идет о родовом понятии
по отношению к определяемому.
Во-вторых, не совсем ясно, что означает
знак «+», который, как известно,
используется для обозначения сложения
чисел. Смысл этого знака станет понятным
немного позже, когда мы рассмотрим
математический смысл союза «и». А пока
познакомимся с еще одной возможностью
наглядного представления определения
через род и видовое отличие. Если
определяемое понятие обозначить буквой
а, определяющее буквой b,
родовое
понятие (по отношение к определяемому)
-буквой с,
а
видовое отличие – буквой Р,
то
определение через род и видовое отличие
можно представить так:
а
![]()

Почему видовое
отличие обозначено заглавной буквой,
мы узнаем несколько позже.
Нам
известно, что любое понятие имеет объем.
Если понятие а
определено
через род и видовое отличие (2), то о его
объеме – множестве А
–
можно сказать, что в нем содержатся
такие объекты, которые принадлежат
множеству С
(объему
родового понятия с)
и
обладают свойством Р:
А= {х
| х
![]() С и Р(х)}.
С и Р(х)}.
Например,
если дано определение: «Острым углом
называется угол, который меньше
прямого»,- то объем понятия «острый
угол» – это подмножество множества всех
углов плоскости, которые обладают
свойством «быть меньше прямого».
Так
как определение понятия через род и
видовое отличие является по существу
условным соглашением о введении нового
термина для замены какой-либо совокупности
известных терминов, то об определении
нельзя сказать, верное оно или неверное;
его не доказывают и не опровергают.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вспомним кратко основные определения функции в математике.
Функция — это зависимость переменной « y » от
независимой переменной « x ».
Функцию можно задать через формулу (аналитически). Например:
у = 2x
- « x » называют независимым аргументом функции;
- « y » зависимой переменной или значением функции.
Вместо « x » (аргумента функции) в формулу «у = 2x» подставляем произвольные числовые значения
и по заданной формуле вычисляем
значение « y ».
Подставим несколько числовых значений вместо « x » в формулу «у = 2x» и запишем результаты в таблицу.
| x | y = 2x | ||||||
|---|---|---|---|---|---|---|---|
| x = −2 | у = 2 · (−2) = −4 | ||||||
| x = 0 | y = 2 · 0 = 0 | ||||||
x =
|
y = 2 ·
= 1 |
||||||
| x = 3 | y = 2 · 3 = 6 |
Запомните!
![]()
Область определения функции — это множество числовых значений, которые можно подставить вместо « x » (аргумента функции).
Обозначают область определения функции как:
D(y)
Вернемся к нашей функции «у = 2x» и найдем её область определения.
Посмотрим ещё раз на таблицу функции «y = 2x», где
мы подставляли произвольные числа вместо « x », чтобы найти « y ».
| x | y = 2x | ||
|---|---|---|---|
| −2 | −4 | ||
| 0 | 0 | ||
|
1 | ||
| 3 | 6 |
Так как у нас не было никаких ограничений на числа, которые можно подставить вместо « x », можно утверждать,
что вместо « x » мы могли подставлять любое действительное число.
Другими словами, вместо « x » можно подставить любые числа, например:
- −2
- 0
- 10
- 30,5
- 1 000 000
- и так далее…
Запомните!
![]()
Областью определения функции называют множество чисел,
которые можно подставить вместо « x ».
В нашей функции «у = 2x» вместо « x »
можно подставить любое число, поэтому область определения функции «у = 2x» — это любые действительные числа.
Запишем область определения функции «у = 2x» через математические обозначения.
у = 2x
D(y): x — любое действительное число
Ответ выше написан словами без использования специального математического языка. Заменим лишние слова на
математические символы.
Для этого вспомним понятие числовой оси.
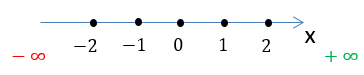
Заштрихуем область на числовой оси, откуда можно брать значения для « x » в функции «у = 2x».
Так как в функции
«у = 2x» нет ограничений для « x »,
заштрихуем всю числовую ось от минус бесконечности «−∞» до плюс бесконечности
«+∞».
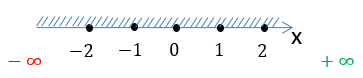
Запишем результат по правилам записи неравенств.

D(y): x ∈ (−∞ ; +∞)
Запись выше читается как: « x » принадлежит промежутку от минус бесконечности
до плюс бесконечности.
Запишем окончательный ответ для области определения функции.
Ответ:
D(y): x ∈ (−∞ ; +∞)
По-другому промежуток
« x ∈ (−∞ ; +∞) » можно записать
как
«x ∈ R».
Читается «x ∈ R» как: « x » принадлежит всем действительным числам».
Записи « x ∈ (−∞ ; +∞) » и
«x ∈ R» одинаковы по своей сути.
Область определения функции с дробью
Разберем пример сложнее, когда в задании на поиск области определения функции есть дробь с « x » в знаменателе.
Разбор примера
Найдите область определения функции:
Задание «Найдите область определения функции» означает, что нам нужно определить все числовые значения, которые может принимать « x »
в функции
« f(x) = ».
По законам математики из школьного курса мы помним, что на ноль делить нельзя.
Иначе говоря,
знаменатель (нижняя часть дроби) не может быть равен нулю.
Переменная « x » находится в знаменателе функции «f(x) = ».
Так как на ноль делить нельзя, запишем, что знаменатель не равен нулю.
x + 5 ≠ 0
Решим полученное линейное уравнение.
Получается, что « x » может принимать любые числовые значения кроме «−5».
На числовой оси заштрихуем все доступные значения для « x ».
Число «−5» отмечено
«пустой»
точкой на числовой оси, так как не входит в область допустимых значений.
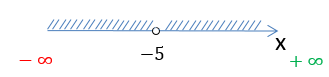
Запишем заштрихованную область на числовой оси через знаки неравенства.
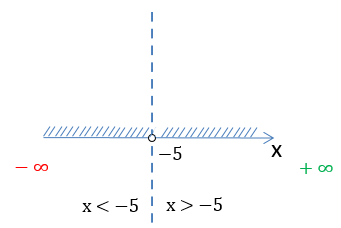
Запишем промежутки через математические символы. Так как число «−5» не входит
в область определения функции, при записи ответа рядом с ним будет стоять
круглая скобка.
Вспомнить запись ответа через математические символы можно в уроке
«Как записать ответ неравенства».

x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Запишем окончательный ответ для области определения функции
«f(x) = ».
Ответ:
D(y): x ∈ (−∞ ; −5) ∪ (−5 ; +∞)
Область определения функции с корнем
Рассмотрим другой пример. Требуется определить область определения функции, в которой содержится квадратный корень.
Разбор примера
Найти область определения функции:
y = √6 − x
Из урока «Квадратный корень» мы помним,
что подкоренное выражение корня чётной степени должно быть больше или равно нулю.
Найдём, какие значения может принимать « x » в функции
«у = √6 − x».
Подкоренное выражение
«6 − x» должно быть больше или равно нулю.
6 − x ≥ 0
Решим линейное неравенство по правилам урока «Решение линейных неравенств».
6 − x ≥ 0
−x ≥ −6 | ·(−1)
x ≤ 6
Запишем полученный ответ, используя числовую ось и математические символы. Число «6» отмечено
«заполненной»
точкой на числовой оси, так как входит в область допустимых значений.
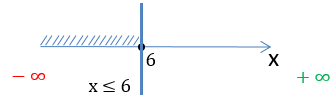
x ∈ (−∞ ; 6]
Запишем окончательный ответ для области определения функции
«y = √6 − x» .
Так как число «6» входит
в область определения функции, при записи ответа рядом с ним будет стоять
квадратная скобка.
Ответ:
D(y): x ∈ (−∞ ; 6]
Правило для определения области определения функции
Запомните!
![]()
Чтобы найти область определения функции нужно проверить формулу функции по двум законам школьного курса математики:
- на ноль делить нельзя (другими словами, знаменатели дробей с « x » не должны быть равны нулю);
- подкоренные выражения корней чётной степени должны быть больше или равны нулю.
При нахождении области определения функции необходимо всегда задавать себе два вопроса:
- есть ли в функции дроби со знаменателем, в котором есть « x »?
- есть ли корни четной
степени с « x »?
Если на оба вопроса вы получаете отрицательный ответ, то область определения функции — это все действительные числа.
Рассмотрим пример поиска области определения функции с корнем и дробью.
Разбор примера
Найдите область определения функции:
Идем по алгоритму. Задаём себе первый вопрос, есть ли в функции дробь с « x » в знаменателе. Ответ: да, есть.
В функции «
f(x) = √x + 3 +
»
есть дробь «
»,
где « x » расположен в знаменателе. Запишем условие, что знаменатель
« x 2 − 9 »
не может быть равен нулю.
Решаем квадратное уравнение через
формулу квадратного уравнения.
x1;2 =
x2 − 9 ≠ 0
x1;2 =
| −0 ± √02 − 4 · 1 · (−9) |
| 2 · 1 |
x1;2 ≠
x1;2 ≠
x1;2 ≠
x1;2 ≠ ±3
Запомним полученный результат. Задаем себе
второй
вопрос.
Проверяем, есть ли в формуле функции
«
f(x) = √x + 3 +
»
корень четной степени.
В формуле есть квадратный корень «
√x + 3
».
Подкоренное выражение «x + 3»
должно быть больше или равно нулю.
x + 3 ≥ 0
Решим линейное неравенство.
x + 3 ≥ 0
x ≥ −3
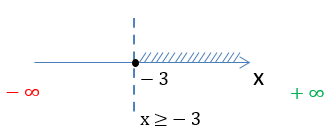
Объединим полученные ответы по обоим вопросам:
- знаменатель дроби
«
» не равен нулю ; - подкоренное выражение «
√x + 3
» должно быть больше или равно нулю.
Объединим все полученные результаты на числовых осях.
Сравнивая полученные множества, выберем только те промежутки, которые удовлетворяют обоим условиям.
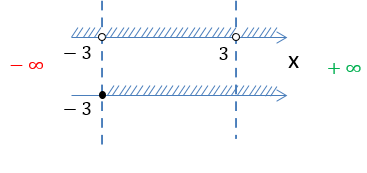
Выделим красным заштрихованные промежутки, которые совпадают на обеих числовых осях.
Обратим внимание, что числа «−3» и «3» отмечены «пустыми» точками и не входят в итоговое решение.
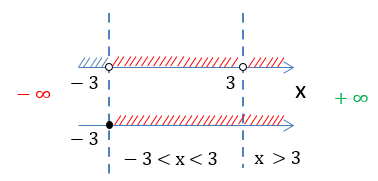
Получаем два числовых
промежутка «−3 < x < 3» и «x > 3», которые являются областью определения функции
«f(x) = √x + 3 + ».
Запишем окончательный ответ.
Ответ:
D(y): x ∈ (−3 ; 3) ∪ (3 ; +∞)
Примеры определения области определения функции
Разбор примера
Найти область определения функции:
y = 6√x +
5√1 + x
Для поиска области определения функций задаем себе
первый вопрос.
Есть ли знаменатель, в котором содержится « x »?
Ответ: в формуле функции
«y = 6√x +
5√1 + x»
нет дробей.
Задаем
второй вопрос.
Есть ли в функции корни четной степени?
Ответ: в функции есть корень шестой степени:
«6√x».
Степень корня — число «6». Число «6» — чётное,
поэтому подкоренное выражение корня «6√x»
должно быть больше или равно нулю.
x ≥ 0
В формуле функции «y = 6√x +
5√1 + x»
также есть корень пятой степени
«5√1 + x
».
Степень корня «5» — нечётное число, значит, никаких ограничений на подкоренное выражение
«1 + x»
не накладывается.
Получается, что единственное ограничение области определения функции
«y = 6√x +
5√1 + x»
— это ограничение подкоренного выражения
«6√x».
x ≥ 0
Нарисуем область определения функции на числовой оси и запишем ответ.
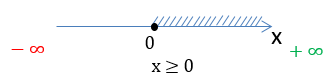
Ответ:
D(y): x ∈ [0 ; +∞)
Разбор примера
Найдите область определения функции:
Есть ли в функции знаменатель, в котором содержится « x »? В заданной функции подобных знаменателей два.
Выделим знаменатели с « x » красным цветом.
Запишем условие, что каждый из знаменателей не должен быть равен нулю.
| √x + 2 ≠ 0 | |
| x2 − 7x + 6 ≠ 0 |
Обозначим их номерами «1» и
«2» и решим каждое уравнение отдельно.
| √x + 2 ≠ 0 (1) | |
| x2 − 7x + 6 ≠ 0 (2) |
Решаем первое уравнение.
√x + 2 ≠ 0 (1)
Если значение квадратного корня
«√x + 2 ≠ 0» не должно быть равно нулю,
значит, подкоренное выражение
«x + 2 ≠ 0»
также не должно быть равно нулю.
√x + 2 ≠ 0 (1)
x + 2 ≠ 0
x ≠ −2
Теперь решим уравнение под номером «2», используя
формулу квадратного уравнения.
x1;2 =
x2 − 7x + 6 ≠ 0 (2)
x1;2 =
| −(−7) ± √(−7)2 − 4 · 1 · 6 |
| 2 · 1 |
x1;2 =
x1;2 =
x1;2 =
Запишем все полученные ответы в порядке возрастания вместе под знаком системы, чтобы их не забыть.
Знаменатели с « x »
мы проверили. Настала очередь
проверить
формулу функции
на
наличие корней четной степени .
В формуле функции
«f(x) =
+
»
есть два корня
«√x − 4» и
«√x + 2». Их подкоренные
выражения должны быть больше или равны нулю.
Решим полученную
систему неравенств.
Нарисуем полученные решения на числовой оси. Выберем заштрихованный промежуток, который есть на обеих числовых осях.
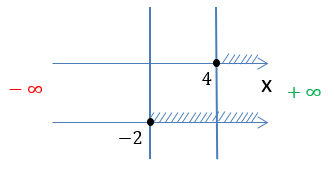
Выпишем результат решения системы неравенств.
x ≥ 4
Объединим в таблицу ниже полученные ответы по обеим
проверкам:
- проверка, что знаменатели
дробей
с « x »
не равны нулю; - проверка, что
подкоренные выражения корней четной степени должно быть больше или равны нулю.
| Условие проверки | Результат |
|
Результат проверки, что знаменатели дробей с « x » не равны нулю |
|
|
Результат проверки, что подкоренные выражения должно быть больше или равны нулю |
x ≥ 4 |
Нарисуем полученные результаты проверок на числовых осях, чтобы определить, какая заштрихованная область удовлетворяет
всем полученным условиям.
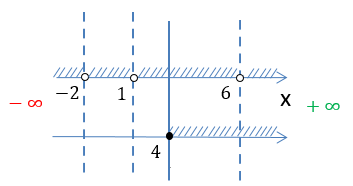
Запишем окончательный ответ для области определения функции
«f(x) =
+
»
с использованием математических символов.
Ответ:
D(y): x ∈ [4 ; 6) ∪ (6; +∞)
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
17 декабря 2016 в 18:02
Татьяна Цыганова

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Цыганова
Профиль
Благодарили: 0
Сообщений: 1
Найти ОДЗ функции у=?(р1+р2х+x2)
Я не могу понять за какое число воспринимать p1, p2
0
Спасибо
Ответить
17 декабря 2016 в 19:10
Ответ для Татьяна Цыганова
Евгений Фёдоров

Профиль
Благодарили: 0
Сообщений: 60

Евгений Фёдоров
Профиль
Благодарили: 0
Сообщений: 60
x2 + p2x + p1 ? 0.
0
Спасибо
Ответить
24 февраля 2016 в 20:29
Влад Алексеев

Профиль
Благодарили: 0
Сообщений: 1

Влад Алексеев
Профиль
Благодарили: 0
Сообщений: 1
Постройте график функции y=-
. Укажите область определения функции
0
Спасибо
Ответить
25 февраля 2016 в 8:10
Ответ для Влад Алексеев
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
Область определения функции: знаменатель не равен 0.
x+1?0
x?-1
Графиком является гипербола, смещеная влево относительно оси Y.
0
Спасибо
Ответить
5 февраля 2018 в 14:30
Ответ для Влад Алексеев
Кирилл Косован

Профиль
Благодарили: 0
Сообщений: 1

Кирилл Косован
Профиль
Благодарили: 0
Сообщений: 1
0
Спасибо
Ответить
11 февраля 2018 в 15:44
Ответ для Влад Алексеев
Татьяна Мирная

Профиль
Благодарили: 0
Сообщений: 1

Татьяна Мирная
Профиль
Благодарили: 0
Сообщений: 1
у=-
0
Спасибо
Ответить
7 октября 2015 в 21:21
Катерина Яроцкая

Профиль
Благодарили: 0
Сообщений: 1

Катерина Яроцкая
Профиль
Благодарили: 0
Сообщений: 1
Помогите найти область определения функции

0
Спасибо
Ответить
12 сентября 2016 в 15:59
Ответ для Катерина Яроцкая
Евгений Колосов

Профиль
Благодарили: 12
Сообщений: 197

Евгений Колосов
Профиль
Благодарили: 12
Сообщений: 197
К сожалению, картинка не отражается.
0
Спасибо
Ответить
«Братский
педагогический колледж»
Кафедра педагогики, психологии и методики начального образования
Учебно-методические материалы
по МДК.01.04
Теоретические основы начального курса математики с методикой
преподавания
Раздел: Математические понятия.
Составитель: Белоглазова Л.В.
Данный материал
написан в соответствии с программой профессионального модуля «Преподавание по
программам начального образования».
Структура темы
включает в себя материал для теоретических занятий, практические занятия,
задания для самостоятельной работы студентов, список рекомендуемой для изучения
литературы, вопросы для самоконтроля.
Профессиональная
направленность материала достигается посредством определенного отбора
теоретического материала и методических подходов к его изложению, путем
включения заданий, выполняемых младшими школьниками (они в основном взяты из
действующих учебников математики для начальных классов). В основу обучения
положен системно – деятельностный подход, что отражает требования ФГОС НОО условиям
и результатам освоения начального курса математики.
Тема:
Математические понятия
1.1.
Математические понятия. Объем и содержание понятия
Цель: Получить
представления о понятии, его существенных и несущественных признаках, объеме и содержании
понятия, о понятии рода и вида
План:
1. Группы
понятий, изучаемых в начальной школе.
2. Понятие
как форма мышления.
3. Существенное
и несущественное свойства для объекта.
4. Объем и
содержание понятия.
5. Понятие
рода и вида.
Группы понятий, изучаемых в начальной
школе.
В начальном курсе математики изучаются понятия, представленные в виде четырех
групп. Первая группа понятий связана с числами и операциями над ними: число,
сложение, слагаемое, больше и др. Во вторую включены алгебраические понятия:
выражение, равенство, уравнение и др. Третью составляют геометрические понятия:
прямая, отрезок, треугольник, прямоугольник и др. Четвертую группу образуют
понятия, связанные с величинами и их измерением.
Чтобы изучать такое обилие самых разных понятий надо
иметь представление о понятии как логической категории и особенностях
математических понятий.
Понятие как форма мышления. Понятие – это
форма мышления, отражающая объекты (предметы или явления) в их существенных
общих свойствах. Языковая форма понятия – это слово или группа слов.
Составить понятие об объекте – это значит уметь
отличать его от других сходных с ним объектов. Главная особенность
математических понятий – математические объекты, о которых составляется
понятие, в реальности не существуют, они созданы умом человека, они результат
абстрагирования. Например, в геометрии изучают форму и размеры предметов, не
принимая во внимание другие их свойства: цвет, массу, твердость и др.
Чтобы овладеть общими подходами к изучению понятий в
начальном курсе математики, учителю необходимы знания об объеме и содержании
понятия, об отношениях между понятиями и о видах определений понятий.
Существенное и несущественное свойства для
объекта.
Всякий математический объект обладает определенными свойствами. Например,
квадрат имеет четыре стороны, четыре прямых угла, равные диагонали и др.
Среди свойств объекта различают существенные и
несущественные. Существенное свойство для объекта присуще для него и без
этого свойства объект не может существовать. Несущественное свойство для
объекта не присуще для него и без этого свойства объект может существовать.
Например, понятие «квадрат»:
![]() существенные
существенные
свойства – четыре вершины, диагонали перпендикулярны, четыре вершины и др.;
![]() несущественные
несущественные
свойства – две стороны горизонтальные, нарисован на бумаге и др. Если квадрат
повернуть, то стороны будут располагаться по-другому, но объект останется
квадратом.
Объем и содержание понятия. Когда
говорят о математическом понятии, то имеют в виду множество объектов,
обозначаемых одним термином (словом или группой слов). Например, говоря о
квадрате, имеют в виду все геометрические фигуры, которые можно назвать
квадратами.
Объем понятия – это множество
всех объектов, обозначаемых одним термином (множество бесконечное).
Любое понятие имеет не только объем, но и содержание.
Содержание понятия – это
множество всех существенных свойств объекта, присущих этому понятию (множество
конечное).
Например, понятие «квадрат»:
объем понятия – это бесконечное множество различных
квадратов;
содержание понятия – все существенные свойства: «имеет
четыре прямых угла», «имеет четыре стороны», «имеет четыре вершины», «имеет
равные стороны» и др.
Понятие рода и вида. Нельзя
усвоить понятие, не осознав его взаимосвязь с другими понятиями. Поэтому важно
знать, в каких отношениях могут находиться понятия, уметь устанавливать эти
связи.
Пусть понятия обозначаются буквами латинского
алфавита: a, b, c, …, z. Заданы два понятия a и b, их
объем соответственно А и В.
Если ![]() , то понятие а – видовое
, то понятие а – видовое
по отношению к понятию в, а понятие в – родовое по отношению к понятию
а.
Например,
объемы понятий «квадрат» и «прямоугольник» находятся в отношении включения.
Поэтому понятие «квадрат» – видовое по отношению к понятию «прямоугольник», а
понятие «прямоугольник» – родовое по отношению к понятию «квадрат».
Если А = В, то говорят, что понятия aub тождественны.
Например, тождественны понятия «равносторонний
треугольник» и «равноугольный треугольник», так как их объемы совпадают.
Рассмотрим подробнее отношение рода и вида
между понятиями.
Во-первых, понятия рода и вида
относительны: одно и то же понятие может быть родовым по отношению к
одному понятию и видовым по отношению к другому. Например, понятие
«прямоугольник» – родовое по отношению к понятию «квадрат» и видовое по
отношению к понятию «четырехугольник».
Пример
цепочки видовых и родовых отношений между понятиями:
Квадрат
Ì
прямоугольник Ì
параллелограмм Ì
четырехугольник Ì
многоугольник
Во-вторых, для данного понятия часто
можно указать несколько родовых понятий. Так, для понятия «прямоугольник» родовыми являются
понятия «четырехугольник», «параллелограмм», «многоугольник». Среди них можно
указать ближайшее. Для понятия «прямоугольник» ближайшим является понятие
«параллелограмм».
В-третьих, видовое понятие
обладает всеми свойствами родового понятия. Например, квадрат,
являясь видовым понятием по отношению к понятию «прямоугольник», обладает
всеми свойствами, присущими прямоугольнику.
Итак, для понятия часто можно указать несколько
родовых понятий; видовое понятие обладает всеми свойствами родового понятия. Например,
для понятия «квадрат» родовые понятия – «прямоугольник», «параллелограмм»,
«четырехугольник» и др. Квадрат обладает свойствами, присущими прямоугольнику.
Так как объем понятия – множество, то удобно,
устанавливая отношения между объемами понятий, изображать их при помощи кругов
Эйлера.
Установим,
например, отношения между следующими парами понятий а и в, если:
1)
а – «прямоугольник», b – «ромб»;
2)
а – «многоугольник», b – «параллелограмм»;
3)
а – «прямая», b – «отрезок».
В случае 1) объемы
понятий пересекаются, но не одно множество не является подмножеством другого
(рис. 27). Следовательно, можно утверждать, что данные понятия а и b не находятся в
отношении рода и вида.
В случае 2) объемы
данных понятий находятся в отношении включения, но не совпадают – не всякий
параллелограмм является многоугольником, но не наоборот (рис. 28).
Следовательно, можно утверждать, что понятие «параллелограмм» – видовое по
отношению к понятию «многоугольник», а понятие «многоугольник» – родовое по
отношению к понятию «параллелограмм».
В случае 3) объемы
понятий не пересекаются, так как ни про один отрезок нельзя сказать, что он
является прямой, и ни одна прямая не является отрезком (рис.29). Следовательно,
данные понятия не находятся в отношении рода и вида.



О
понятиях «прямая» и «отрезок» можно сказать, что они находятся в отношении целого и
части: отрезок – часть прямой, а не ее вид. И если видовое понятие обладает
всеми свойствами родового понятия, то часть не обязательно обладает всеми
свойствами целого. Например, отрезок не обладает такими свойствами прямой, как
бесконечность.
Вопросы для самоконтроля:
– Назовите группы понятий, изучаемых в начальной
школе.
– Определите, что такое «понятие».
– Какие свойства для объекта являются существенными и
несущественными?
–
Что такое объем и содержание понятия.
–
Определите понятие рода и вида.
Список
литературы
1. Стойлова
Л.П. Математика: Учебник для студ. высш. пед. учеб. заведений. – М:
Издательский центр «Академия», 2008. – 424 с.
2. Спирина
М.С. Дискретная математика: учебник для студ. учреждений сред. проф.
образования. – М: Издательский центр «Академия», 2010. – 368 с.
1.2.
Определение
понятий. Требование к определению понятия
Цель: Усвоить структуру
определения понятия, видов определений в начальном курсе математики, требований
к определениям понятий.
План:
1. Определение
понятия.
2. Структура
явного определения. Условные определения.
3. Требования
к определениям понятий.
4. Определение понятий в
начальной школе.
Определение
понятия.
Появление в математике новых понятий, а значит, и новых терминов, обозначающих
эти понятия, предполагает их определение.
Определением обычно называют предложение,
разъясняющее суть нового термина (или обозначения). Определение
понятия – логическая операция, раскрывающая его содержание.
Как правило, делают это на основе ранее
введенных понятий. Например, прямоугольник можно определить так:
«Прямоугольником называется четырехугольник, у которого все углы прямые». В
этом определении есть две части – определяемое понятие (прямоугольник) и
определяющее понятие (четырехугольник, у которого все углы прямые). Если
обозначить через а первое понятие, а через b – второе, то данное
определение можно представить в таком виде:
а есть (по определению) b.
Слова «есть (по определению)» обычно заменяют
символом <=>, и тогда определение
onр.
выглядит так:
а<=> b
onр.
Читают: «а равносильно b по определению». Можно
прочитать эту запись еще и так: «а тогда и только тогда, когда b».
Структура явного определения. Условные
определения. Определения, имеющие такую структуру,
называются явными. Рассмотрим их подробнее.
Обратимся опять к определению
прямоугольника, вернее, к его второй части – определяющему понятию. В нем можно
выделить:
1)понятие «четырехугольник», которое является родовым по отношению к
понятию «прямоугольник»,
2)свойство «иметь все углы прямые», которое позволяет выделить из
всевозможных четырехугольников один вид – прямоугольники; поэтому его называют
видовым отличием.
Вообще видовое отличие – это свойства (одно
или несколько), которые позволяют выделять определяемые объекты из объема
родового понятия.
Итоги нашего анализа можно
представить в виде схемы

Заметим, что в
наглядном представлении структуры определения через род и видовое отличие мы
допустили некоторые неточности. Во-первых, слова «родовое понятие» означают,
что речь идет о родовом понятии по отношению к определяемому. Во-вторых, не
совсем ясно, что означает знак «+», который, как известно, используется для обозначения
сложения чисел. Смысл этого знака станет понятным немного позже, когда мы
рассмотрим математический смысл союза «и».
Нам известно, что
любое понятие имеет объем. Если понятие а определено через род и видовое отличие, то о
его объеме – множестве А – можно сказать, что в нем содержатся такие объекты,
которые принадлежат множеству С (объему родового понятия с) и обладают свойством Р.
Например, если дано
определение: «Острым углом называется угол, который меньше прямого», – то объем
понятия «острый угол» -это подмножество множества всех углов плоскости, которые
обладают свойством «быть меньше прямого».
Так как определение понятия через род и видовое
отличие является по существу условным соглашением о введении нового
термина для замены какой-либо совокупности известных терминов, то об
определении нельзя сказать, верное оно или неверное; его не доказывают и не
опровергают.
Требования к определениям понятий. Но, формулируя определения, придерживаются ряда правил.
Назовем основные требования к определению понятий.
Определение
должно быть соразмерным. Это означает, что
объемы определяемого и определяющего понятий должны совпадать. Это правило
вытекает из того, что определяемое и определяющее понятия взаимозаменяемы.
Например, несоразмерно такое определение
квадрата: «Квадратом называется четырехугольник, у которого все стороны
равны». Действительно, объем определяемого понятия – множество квадратов. Объем
определяющего понятия – множество четырехугольников, все стороны которых равны,
а это множество ромбов. Но не всякий ромб есть квадрат, т.е. объемы
определяемого и определяющего понятия не совпадают, и, следовательно, данное
определение несоразмерно.
В
определении (или их системе) не должно быть порочного круга.
Это означает, что
нельзя определять понятие через само себя (в определяющем понятии не должно
содержаться определяемого термина) или определять его через другое, которое, в
свою очередь, определять через него.
Например, содержат порочный круг определения:
«Равные треугольники – это треугольники, которые равны», «Касательная к
окружности – это прямая, которая касается окружности».
Так как в математике рассматривают не просто
отдельные понятия, а их систему, то данное правило запрещает порочный круг и в
системе определений. В соответствии с ним нельзя определять понятие а, выбрав в качестве
родового понятия с, а понятие с – через понятие а.
Например, если определить окружность как границу
круга, а круг как часть плоскости, ограниченную окружностью, то мы будем иметь
порочный круг в определениях данных понятий.
Объект должен
существовать. Это означает, что нельзя определить тот объект,
который нереален.
Например,
«Прямоугольным треугольником называется треугольник, у которого все углы
прямые», такой объект нереален, т.к. нет такого прямоугольного треугольника, у
которого все углы прямые
Определение
должно быть ясным.
Требование
означает оно многое. Так как требуется, чтобы значения терминов, входящих в
определяющее понятие, были известны к моменту введения определения нового
понятия.
Например, нельзя определять прямоугольник как
параллелограмм с прямым углом, если понятие «параллелограмм» еще не
рассмотрено.
К условиям ясности определения относят также
рекомендацию включать в видовое отличие лишь столько свойств, сколько необходимо
и достаточно для выделения определяемых объектов из объема родового понятия.
Рассмотрим, например,
такое определение прямоугольника: «Прямоугольником называется четырехугольник,
у которого все углы прямые и противоположные стороны равны».
Нетрудно убедиться в
том, что это определение соразмерное и в нем нет порочного круга. Но можно
доказать, что свойство «в прямоугольнике противоположные стороны равны» вытекает
из свойства «в прямоугольнике все углы прямые». В этом случае считают, что в
данном определении прямоугольника второе свойство избыточное.
Таким образом, чтобы определение было ясным,
желательно, чтобы оно не содержало избыточных свойств в определяющей части,
т.е. таких свойств, которые могут быть выведены из других, включенных в это
определение. Однако иногда для простоты изложения это правило нарушают.
Для обеспечения ясности определения важно
также наличие понятия, родового по отношению к определяемому. Пропуск родового
понятия делает определение несоразмерным. Неприемлемо, например, такое
определение квадрата: «Квадрат – это когда все стороны равны».
К сказанному следует добавить, что, формулируя
определение, надо стремиться в определяющем указывать не просто родовое по отношению
к определяемому понятие, а ближайшее. Это часто позволяет сократить количество
свойств, включаемых в видовое отличие.
Например, если для определения квадрата в
качестве родового выбрать понятие «четырехугольник», то тогда надо будет
включать в видовое отличие два свойства: «иметь все прямые углы» и «иметь все
равные стороны». В результате получим определение: «Квадратом называется
четырехугольник, у которого все углы прямые и все стороны равны».
Если же в качестве родового выбрать ближайшее
для квадрата родовое понятие – прямоугольник, то получим более короткое определение
квадрата: «Квадратом называется прямоугольник, у которого все стороны равны».
Завершая рассмотрение определений понятий через род и
видовое отличие, назовем ту последовательность действий, которую мы должны
соблюдать, если хотим воспроизвести определение знакомого понятия или построить
определение нового:
1. Назвать определяемое понятие (термин).
2. Указать ближайшее
родовое (по отношению к определяемому) понятие.
3. Перечислить свойства, выделяющие определяемые объекты из объема
родового, т. е. сформулировать видовое отличие.
4. Проверить, выполнены ли правила определения понятия (соразмерно ли
оно, нет ли порочного круга и т.д.).
Определение понятий в начальной школе. При изучении
математики в начальных классах определения через род и видовое отличие
используют редко. Связано это как с особенностями курса, так и с возможностями
детей. Но понятий в начальном курсе математики очень много – об этом мы
говорили в самом начале параграфа. Как же их определяют?
При изучении
математики в начальной школе чаще всего используют так называемые неявные определения. В их
структуре нельзя выделить определяемое и определяющее. Среди них различают контекстуальные и остенсивные.
В контекстуальных определениях
содержание нового понятия раскрывается через отрывок текста, через контекст,
через анализ конкретной ситуации, описывающей смысл вводимого понятия. Посредством
контекста устанавливается связь определяемого понятия с другими, известными, и
тем самым косвенно раскрывается его содержание. Примером контекстуального
определения может быть определение уравнения и его решения, приведенное в
учебнике математики для II класса (Моро М.И., Бантова М.А. Математика: Учеб.
для 2 класса трехлетней начальной школы. – М.: Просвещение, 1987. – С. 196).
Здесь после записи □ + 6 = 15 и перечня чисел 0, 5, 9, 10 идет текст: «К какому
числу надо прибавить 6, чтобы получилось 15? Обозначим неизвестное число
латинской буквой х (икс):
х + 6 = 15 – это
уравнение.
Решить уравнение –
значит найти неизвестное число. В данном уравнении неизвестное число равно 9,
так как 9 + 6 = 15.
Объясни, почему числа
0, 5 и 10 не подходят».
Из приведенного текста
следует, что уравнение – это равенство, в котором есть неизвестное число. Оно
может быть обозначено буквой л: и это число надо найти.
Кроме того, из этого текста следует, что решение уравнения – это число, которое
при подстановке вместо х обращает уравнение в верное равенство.
Остенсивные
определения – это определения путем показа. Они используются для
введения терминов путем демонстрации объектов, которые этими терминами
обозначают. Например, таким способом можно определить в начальной школе понятия
равенства и неравенства:
2-7 > 2-6 9-3
= 27
78 – 9 < 78 6-4
= 4-6
37 + 6>37 17-5
= 8 + 4
Это
неравенства Это равенства
Остенсивные
определения, как и контекстуальные, характеризуются некоторой незавершенностью.
Действительно, определение посредством показа не выделяет числовые равенства
(неравенства) из других предложений, в нем не указываются свойства, характерные
для данных понятий. Они только связывают термины с определяемыми объектами.
Поэтому после контекстуального или остенсивного определения понятия необходимо
дальнейшее изучение свойств так определенных объектов.
Вопросы для
самоконтроля:
– Поясните термин «определение понятия».
– Какова структура явного определения?
– Какое определение считается условным?
– Перечислите требования к определениям понятий,
поясните их суть.
Какие существуют виды определений понятий в начальной
школе, что они означают?
Список
литературы
3. Стойлова
Л.П. Математика: Учебник для студ. высш. пед. учеб. заведений. – М:
Издательский центр «Академия», 2008. – 424 с.
4. Спирина
М.С. Дискретная математика: учебник для студ. учреждений сред. проф.
образования. – М: Издательский центр «Академия», 2010. – 368 с.
Практическое
занятие
Тема: Определение родовых отношений между
понятиями. Решение задач на распознавание понятий
Цель: На основе
систематизации теоретических знаний о видах и структуре определений понятий
раскрыть логико-математическую структуру типичных для школьного курса
математики определений понятий; освоить основные учебные действия, необходимые
для усвоения понятий.
План:
1. Теоретическое обобщение знаний о понятиях
2. Решение упражнений
3. Самостоятельная работа
Вопросы:
– Группы понятий, изучаемых в начальной школе.
– Понятие как форма мышления.
– Существенное и несущественное свойства для объекта.
–
Объем и содержание понятия.
–
Понятие рода и вида.
– Определение понятия.
– Структура явного определения.
– Условные определения.
– Требования к определениям понятий.
– Процесс составления задачи на распознавание понятия.
Решение упражнений
Указания: Вспомните, что
такое объем, существенные и несущественные свойства понятия, отношение рода и вида
между понятиями, какие требования к определениям должны выполняться и выполните
задания.
1. Начертите три геометрические фигуры, принадлежащие
объему понятия:
а)
параллелограмм; б) трапеция; в) равнобедренный треугольник.
2.
Назовите пять существенных свойств понятия:
а)
параллелограмм; б) трапеция; в) равнобедренный треугольник.
3.
Каков объем понятия:
а)
однозначное число; б) натуральное число?
4.
Какое из следующих утверждений верное? Ответ объясните.
а)
Всякое свойство квадрата присуще прямоугольнику.
б)
Всякое свойство прямоугольника присуще квадрату.
5.
Находятся ли в отношении рода и вида следующие пары понятий:
а)
многоугольник и четырехугольник;
б)
угол и острый угол;
в)
луч и прямая;
г)
круг и окружность?
6. Среди понятий, изучаемых в начальном курсе
математики, есть такие, как «четное число», «треугольник», «многоугольник»,
«число», «трехзначное число», «прямой угол», «сумма», «слагаемое», «выражение».
Есть ли среди них понятия, находящиеся в отношении рода и вида?
7. Есть ли логические ошибки в следующих определениях?
Если можете, то исправьте их.
а) Прямоугольником называется четырехугольник, у
которого противоположные стороны равны.
б) Биссектрисой угла называется прямая, делящая угол
пополам.
в) Сложением называется действие, при котором числа
складываются.
г) Квадратом называется прямоугольник с равными
сторонами.
Самостоятельная работа
Задание 1. В каких из
приведенных ниже определений математических понятий имеются ошибки?
Указание: Если в
определении есть ошибка, то укажите ее причину, исправьте ее, если это
возможно. Для верного определения сформулируйте эквивалентное ему определение.
Результаты оформите в таблицу.
I.
Вариант
II. Вариант
|
1 |
Биссектрисой |
1 |
Прямоугольником |
|
2 |
Сложением |
2 |
Диаметром |
|
3 |
Прямоугольником |
3 |
Касательной |
|
4 |
Остроугольным |
4 |
Параллелограммом |
|
5 |
Смежными |
5 |
Решением |
|
6 |
Равнобедренным |
6 |
Тупоугольным |
Оформление
выполненного задания
|
№ п/п |
Ошибка понятия |
Правильное понятия |
Эквивалентное |
|
1. |
|||
|
2. |
|||
|
3. |
|||
|
4. |
|||
|
5 |
|||
|
6. |
Задание
2. Выполните логический анализ определений, приведенных
ниже понятий:
|
1. |
Квадрат |
1. |
Числовое |
|
2. |
Угол |
2. |
Прямоугольник |
|
3. |
Умножение |
3. |
Окружность |
|
4. |
Прямоугольный |
4. |
Многоугольник |
|
5. |
Неравенство |
5. |
Уравнение |
|
6. |
Двузначное |
6. |
Цифра |
Указание:
Вспомните определение понятия (или прочитайте его в учебнике), определите его
вид, род, видовые отличия и результат оформите в таблицу.
|
№ п/п |
Определение понятия |
Термин |
Род |
Видовые отличия |
Вид понятия |
|
1. |
|||||
|
2. |
|||||
|
3. |
|||||
|
4. |
|||||
|
5. |
|||||
|
6. |
Задание
3. Выполните действие подведения под определение
объекта. Результат оформите таблицей, записав сначала 1) определение понятия;
2) его свойства; 3) логическую связь между свойствами. Примеры объектов,
подлежащих распознаванию, привести самим.
Самостоятельная
работа студентов
Задание. Составить и выполнить задания на
распознавание математических понятий в начальных классах (рассмотреть не менее
10 понятий).
Сроки выполнения: решение задач на
распознавание на практическом занятии.
Рекомендации по выполнению задания:
1.
Записать
автора учебника математики и класс.
2.
Выявить
понятия, которым даются определения.
3.
Определить
родовое понятие и существенные признаки.
4.
Составить
задачи на распознавание выявленных понятий.
5.
Решить
задачи на распознавание понятий, фиксируя наличие признаков и делая вывод:
|
1. |
1. |
|||
|
+ |
2. |
– |
||
|
2. |
3. |
Список
литературы
1. Истомина
Н.Б. Методика обучения математике в начальных классах: Учеб. пособие для студ.
сред. и высш. пед. учеб. заведений. – М: Издательский центр «Академия», 2001.
2. Петерсон
Л.Г. Математика. 4 класс. Часть 1. – М.: Издательство «Ювента», 2011.
3. Петерсон
Л.Г. Математика. 3 класс. Часть 1. – М.: Издательство «Ювента», 2011.
4. Моро М.И.
Математика. 1 класс.Учеб. для общеобразоват. учреждений с прил. на электр.
носителе. В 2 ч. Ч. 1. – М.: Просвещение, 2011.
5. Моро М.И.
Математика. 1 класс.Учеб. для общеобразоват. учреждений с прил. на электр.
носителе. В 2 ч. Ч. 2. – М.: Просвещение, 2011.
6. Чекин А.Л.
Математика: 1 класс: Учебник: В 2 ч. – М.: Академкнига/Учебник, 2011.
7. Стойлова
Л.П. Математика: Учебник для студ. высш. пед. учеб. заведений. – М:
Издательский центр «Академия», 2002. – 424 с.
Форма
контроля:
Представление заданий на практическом занятии 1
Развитие личности средствами математики невозможно без овладения ею определённой системой научных знаний. Одной из главных составляющих системы научных знаний любого предмета, в том числе и математики, являются понятия. Не оперируя понятиями, нельзя сформулировать ни один закон и без усвоения соответствующих понятий не может быть ни усвоения законов, ни усвоения теорий. Это обусловливает ведущую роль понятий при формировании в сознании учащихся системы научных знаний в соответствующей предметной области. Процесс формирования системы знаний выступает как процесс овладения понятиями.
Оперирование понятиями требует от учащихся активной мыслительной деятельности, поскольку только в этом случае можно обеспечить глубокое понимание сущности изучаемых предметов и явлений теории, отражённой в системе научных понятий. Умение мыслить включает и умение оперировать понятиями. Процесс усвоения понятий влияет и на развитие логического мышления учащихся, так как именно они составляют его фундамент.
Таким образом, развивающие функции обучения математике реализуются и в процессе овладения понятиями. Умственное развитие ребёнка при обучении математике можно рассматривать и как развитие его способностей к осмыслению понятий, оперированию ими и конструированию новых понятий. Перечисленные способности и являются, в сущности, показателями математического развития ученика.
В процессе обучения математики перед учителем стоит задача — формирование понятийного аппарата темы.
Понятие — форма мышления, в которой отражены существенные (отличительные) свойства объектов изучения. Понятие считается правильным, если оно верно отражает реально существующие объекты.
Каждое понятие имеет содержание и объем. С помощью определения раскрывается содержание понятия, а с помощью классификации — объем.
Содержание понятия — это множество всех существенных признаков данного понятия.
Объем понятия — множество объектов, к которым применимо данное понятие.
Рассмотрим пример. Понятие треугольник соединяет в себе виды различных треугольников и свойство, которое его характеризует: наличие трех сторон, трех вершин, трех углов. Объем данного понятия — виды треугольников; содержание — существенные свойства.
Таким образом, освоение понятий связано с выделением свойств.
Свойство – это то, что каким-то образом характеризует вещь и не требует для своего описания более одной вещи.
Существенные (характеристические) свойства — это такие свойства, каждое из которых необходимо, а все вместе достаточны для характеристики объектов, принадлежащих понятию. Однако не каждое необходимое условие является достаточным и не каждое достаточное условие является необходимым. Например, равенство двух углов является необходимым условием для того, чтобы эти углы были вертикальные, но не является достаточным. Процесс конструирования понятий заключается в поиске такого числа необходимых условий, которое было бы достаточно для однозначного определения требуемого класса вещей. Совокупность этих условий и принимают за содержание понятия.
К существенным свойствам понятия относятся те свойства, без которых понятие (объект для понятия) априори не может существовать. Свойства являются основой для выделения и обобщения предметов, составляющих множество. В литературе можно встретить термин «существенные признаки». Но слово «признак» в школьном курсе математики несет другую смысловую нагрузку, поэтому будет целесообразным употреблять именно слово «свойство». Можно встретить следующее понимание существенных свойств объекта для понятия: свойство объекта является существенным в том случае, если отдельно взятое свойство необходимо, а взятые в совокупности свойства достаточны для отделения данного понятия от остальных. Но такая трактовка термина «существенные» в большей степени характеризует не отдельные свойства, а определенный набор свойств. Поэтому правильнее будет использовать первую из приведенных трактовок.
В качестве примера выделим следующие существенные свойства ромба:
- является четырехугольником;
- является параллелограммом;
- все его стороны равны;
- имеет равные противоположные углы;
- диагонали в точке пересечения делятся пополам;
- диагонали лежат на биссектрисах углов ромба и т.д.
Как говорилось ранее, объект может иметь много таких свойств, поэтому часто используется набор свойств, достаточный для выделения данного объекта.
Достаточный набор существенных свойств – это набор существенных свойств объекта, достаточный для того, чтобы выделить некоторое множество объектов из всех остальных.
Например, в случае с ромбом достаточный набор свойств может включать в себя следующие свойства: быть параллелограммом и иметь все равные стороны. Другой достаточный набор существенных свойств, по которым можно выделить ромб из множества объектов, – это то, что объект является параллелограммом и имеет диагонали, делящие его углы пополам. Таких наборов существенных свойств для объекта можно подобрать множество. Они являются признаками понятия или формируют определение понятия.
В модуле 1 мы отмечали, что в математике преимущественно используется логический подход к трактовке понятия. С точки зрения логики каждое понятие характеризуется термином, смыслом и значением.
Термин (имя) – это языковое выражение, которое используется для обозначения определенных объектов.
К данным объектам относятся предметы, свойства, отношения, процессы, явления и т.д. Объекты могут быть материальными или идеальными (созданными воображением человека). Значением термина (имени) является объект, обозначенный этим термином (именем). Смысл или концепт имени – это способ, с помощью которого термин обозначает предмет. С помощью примера попробуем разобраться, что представляют собой значение и смысл термина (имени). Например, значением для термина «Александр Сергеевич Пушкин», является определенный человек, который носил это имя. Смыслов данный термин может иметь несколько: «знаменитый писатель», «автор романа «Евгений Онегин» и т.д. Если рассматривать только термин, то, во-первых, имеется в виду некий объект, который называется этим термином – значение имени. Во-вторых, имеется в виду объективное содержание, которое выражается этим термином – смысл термина. Термин «клетка» с точки зрения биологии и химии будет иметь смысл частицы живого организма, а на уроке математики он будет обозначать частицу разграфленной определенным образом тетради. При этом в биологии и химии значение «клетки» будет идентичным, но смысл будет несколько отличаться, так как описываться на этих предметах «клетка» будет по-разному и ее свойства будут изучаться с разных точек зрения.
Математические понятия также характеризуются термином, смыслом и значением. Терминами понятий обозначаются объекты, которые изучает математика. Значениями понятий являются идеи. Смысл понятий может быть передан определением, признаком, описанием свойств объектов, существенных для понятия, системой аксиом. Один и тот же предмет может иметь несколько разных имен. Например, именами числа 3 являются языковые выражения «1+1 + 1», «», «
», «корень уравнения 6-х=3» Данные выражения обозначают один и тот же предмет – число 3 – т.е. имеют одно и то же значение, но при этом они имеют разный смысл. Смысл имени «
» заключается в том, что именуемое число может быть получено путем извлечения арифметического квадратного корня из числа 9, а смысл имени «корень уравнения 6-х=3» заключается в том, что именуемое число можно получить путем решения простейшего уравнения.
Также следует отметить, что один и тот же математический объект может иметь несколько смыслов. Например, модуль числа обладает как аналитическим, так и геометрическим смыслом. Объект может иметь смысл (определить можно все, что угодно), но при этом не иметь значения (объект может не существовать). И не смотря на то, что в процессе обучения математике термины «смысл» и «значение» применяются, но на вопрос: «Имеет ли смысл и значение равенство », – все учителя и учащиеся отвечают по-разному. Безусловно, равенство имеет смысл, так как выражения, стоящие в правой и левой части равенства, имеют смысл (область определения уравнения как предиката), но значения у них нет.
Такую связь между термином, значением и смыслом можно изобразить в виде семантического треугольника (треугольника Фреге):
Связь между вершинами данного треугольника может быть неоднозначна. Это можно наблюдать и в математике: одно значение понятия может обозначаться разными терминами, а одному термину может соответствовать несколько значений, не смотря на то, что для математики присуще однозначность.
Например, в школьном курсе математики для термина «многоугольник» значением может являться часть плоскости, ограниченная замкнутой простой ломаной, и сама эта ломаная. Такая же ситуация наблюдается с термином «угол». Поэтому в процессе обучения при введении понятия будет правильным показать эту неоднозначность, а рассматривая понятие, указывать, в каком смысле и значении его следует понимать.
С точки зрения методики обучения каждое математическое понятие характеризуется объемом и содержанием. Рассмотрим, как данные характеристики понятия в математике соотносятся с аналогичными характеристиками понятия в логике.
Объем понятия – множество объектов, которые можно выделить и обобщить в понятии.
Содержание понятия – совокупность свойств объектов, которые являются существенными для данного понятия.
А значит, объем математического понятия – это и есть множество значений понятия (представителей, образов), а содержание отражает смысл понятия, которое описывается разными существенными для понятия свойствами. Но свойств может быть много, поэтому выделяют основное содержание – достаточный набор свойств, т.е. все те свойства, каждое из которых, взятое отдельно, необходимо, а взятые в совокупности достаточны для отличия данного понятия от других.
На каждой новой ступени развития понятий образуются новые связи между понятиями. Так, сокращение содержания понятия C(C1 ⊃ C2) приводит к расширению его объема V(V1⊂ V2). Эта операция была названа обобщением понятия. Например, если из содержания понятия «равносторонний треугольник» удалить свойство «равенство всех сторон», то множество треугольников, соответствующих новому содержанию, станет «шире» – будет содержать множество всех равносторонних треугольников в качестве подмножества.
Расширение содержания понятия C(C1⊂ C2) влечет за собой сужение его объема V(V1⊃V2). Это явление называется ограничением (специализацией) понятия. Примером подобной операции является переход от понятия тождественных преобразований к понятию сокращения дробей. Изучение отношений между выпуклыми четырехугольниками и окружностями привело к возникновению понятия вписанного в окружность четырехугольника. В результате во множестве выпуклых четырехугольников выделяется множество вписанных в окружность четырехугольников, для которых характерно более сложное содержание, но меньший объем по сравнению с множеством выпуклых четырехугольников.
Сформированность понятия у учащегося определяется его способностью выделять все существенные свойства данного понятия в их целостной совокупности, умением определять внутренние и внешние связи данного понятия с другими понятиями, а также умением осмыслить понятие в системе понятий. В качестве примера рассмотрим следующую фразу: «Муха села на варенье». Как правило, когда человек слышит или произносит эту фразу, ему представляется красивая картинка. Оперируя понятиями эту фразу можно прокомментировать следующим образом: «Элемент множества мух стал принадлежать множеству всех элементов, существенным свойством которых является «сидеть на варенье». Разумеется, что в повседневной жизни человек так не мыслит.
В обыденной жизни человек чаще оперируют предпонятиями.
Если объем одного понятия содержится в объеме другого, то второе понятие называется родовым по отношению к первому понятию, а первое называется видовым по отношению ко второму. Например, понятие ромб является родовым по отношению к понятию квадрат. Введение понятия через ближайший род и видовые заключается в следующем:
- указывается род, в который входит определяемое понятие;
- указываются видовые отличия и связь между ними.
Родовым понятием выступает понятие параллелограмма, из которого определяемое понятие выделяется посредством одного видового отличия (равенство смежных сторон).
В отношении объемов различают следующие виды понятий:
- равнозначные (объемы понятий полностью совпадают);
- пересекающиеся (объемы понятий частично пересекаются);
- понятия, находящиеся в отношении включения (объем одного понятия содержится в объеме другого понятия).
Формирование понятий
Формирование понятий — сложный психологический процесс, который осуществляется и протекает по следующей схеме:
Процесс формирования понятий состоит из мотивации введения понятия, выделения его существенных свойств, усвоения определения, применения понятия, понимания связи изучаемого понятия с ранее изученными понятиями.
Формирование понятия осуществляется в несколько этапов:
- мотивация (на данном этапе педагог должен подчеркнуть важность изучения понятия, активизировать целенаправленную деятельность учащихся, пробудить интерес к изучению понятия с помощью привлечения средств нематематического содержания, выполнения специальных упражнений, объясняющих необходимость развития математической теории);
- выявление существенных свойств понятия (деятельность учащихся направлена на выполнение упражнений, с целью выделения существенных свойства изучаемого понятия);
- формулировка определения понятия (деятельность учащихся направлена на распознавание объектов, принадлежащих понятию, конструирование объектов, относящихся к объему понятия).
Определение понятия
Для изучения объекта и формирования понятия очень важным является умение давать определение понятию.
Определение понятия (дефиниция) представляет собой логическую операцию, которая раскрывает основное содержание понятия или смысл термина. В зависимости от способа раскрытия основного содержания выделяют следующие типы определений:
- невербальные (остенсивные);
- вербальные.
Вербальные определения включают в себя:
- явные определения – определения, в основе которых лежит родовая принадлежность и видовые отличия объекта;
- неявные определения: аксиоматические (определения, описываемые системой аксиом) и описательные (определения, в основе которых лежат существенные свойства объекта).
На уроках математики в 1– 4-х и частично в 5 – 6-х классах в большей степени применяются остенсивные и описательные определения понятий. Остенсивные определения понятий вводятся на чувственной ступени познания. Описательные определения понятий вводятся на эмпирическом уровне рациональной ступени познания и описывают объекты с помощью моделей, посредством изучения частных случаев, выделения отдельных существенных свойств. Например, учитель вводит термин «треугольник», изображая треугольник на доске.
Иногда в начальной школе приходится сталкиваться с явными определениями, когда, например, дается определение квадрата как прямоугольника с равными сторонами.
В средней школе чаще всего используются вербальные определения, но явные определения также часто встречаются. Реже приходится сталкиваться с неявными описательными определениями. Примером может служить понятие непрерывной функции, или аксиоматические понятия, которые задают понятия посредством выполнения определенных свойств, описанных в аксиомах. В курсе геометрии такими понятиям являются понятия точки, прямой, длины, площади, объема и т.д.
В явном определении, которое осуществляется на основе рода и видовых отличий, даны определяемое понятие и определяющее, объемы которых равны. Часто только такой вид определений относят к определениям и только к ним применяют логико-математический анализ, речь о котором пойдет ниже.
Мы уже рассматривали связь между родом и видом. Обобщим сказанное выше:
- множество всех объектов, к которому можно применить данное понятие, образует класс;
- один класс является высшим (т.е. является родом) по отношению к другому классу (виду) в том случае, если он включает в себя вместе со всеми элементами данного класса элементы другого класса;
- отношение рода и вида является одним из основных отношений между понятиями и лежит в основе наиболее распространенного типа определений;
- понятия, находящиеся в известных отношениях друг с другом, образуют систему;
- один и тот же раздел школьного курса математики может быть описан с точки зрения различных систем понятий.
С точки зрения логики определение через род и видовые отличия является эквиваленцией. Структура явного определения включает такие элементы, как термин, род, видовое (видовые) отличие(я) и логические связи. Способ выделения видовых отличий определяет вид явного определения. Выделяют следующие виды явного определения: через описание характеристических свойств, конструктивные или генетические (задан способ построения или происхождения объекта), рекурсивные (указываются базисные объекты некоторого множества и правила, позволяющие получить новые объекты этого же множества), отрицательные (объект задается через отсутствие у него определенных свойств).
Связи между родом и видовыми отличиями всегда являются конъюнктивными, тогда как связи между видовыми отличиями могут быть как конъюнктивными, так и дизъюнктивными.
Учитывая тип логической связи видовых отличий, выделяют конъюнктивные и дизъюнктивные определения.
Выполнение логического анализа явного определения понятия подразумевает последовательное выполнение следующих операций:
- распознавание вида определения;
- запись его логической структуры.
Обе эти операции носят название логико-математического анализа определения. Под математическим анализом определения понимается раскрытие математического содержания каждого элемента.
В качестве примера рассмотрим определение, которое дается квадрату:
Структура данного определения может быть представлена следующим образом:
Подробно эту запись можно прочитать следующим образом: объект х является квадратом (имеет свойство «быть квадратом») тогда и только тогда, когда х принадлежит множеству прямоугольников и обладает свойством «все стороны равны».
В школьном курсе математики часто можно встретить определения, термином для которых является сочетание слов (корень квадратного уравнения, биссектриса угла треугольника) или отдельные слова, выражающие связи или отношения между объектами (смежные углы, параллельные прямые и т.д.). В этом случае определение рассматривается на множестве пар и троек. В частности, для медианы треугольника множество М представляет собой множество пар отрезков X и треугольников Y, а структуру его можно записать следующим образом:
A (x, y) ⇔ ∀ (x, y) ∊ M ⋀ B (x, y) ⋀ C (x, y)
где М = X x Y
На основании выделенных свойств представим определение в виде «алгоритма»:
Медиана треугольника:
- отрезок в треугольнике;
- соединяет вершину треугольника с точкой стороны, противоположной вершине;
- данная точка является серединой стороны;
- данная точка называется основанием медианы.
Такая запись позволяет точно определить учебный материал, необходимый для актуализации перед введением понятия. Также благодаря такой записи учащимся легче усвоить определения, так как в ней выделены существенные свойства понятия (первым выделено родовое понятие), наличие которых необходимо проверить у объекта, чтобы отнести его к понятию. Фактически данная запись представляет собой алгоритм, следуя которому, можно определить, является ли данный объект понятием (использовать такой алгоритм целесообразно при выполнении заданий на распознавание). Поэтому такую запись можно назвать как «запись определения в алгоритмизированном виде».
Для других видов определений логико-математический анализ определенно не выполняется. Устанавливается вид определения, для аксиоматического определения выделяются аксиомы, описывающие неопределяемые понятия, связи с уже изученными темами, что позволяет определить знания, которые необходимо актуализировать.
Требования к определениям
Существуют формально-логические требования корректности явных определений. К таким требованиям относятся следующие:
- Определение должно быть соразмерным, т.е. объем определяемого понятия должен быть равен объему определяющего понятия. Если данное равенство не соблюдается, может быть допущена логическая ошибка.
- Определение не должно содержать круга. Например, Градус был определен как величина угла, составляющего часть прямого угла. Значит «Прямой угол – это угол, содержащий 900», являться определением не может.
- Определение должно раскрывать необходимый набор свойств понятия и иметь четкую и ясную формулировку. Так утверждение «Лень – мать всех пороков» является поучительным, но не является определением лени.
- Определять объект лучше через ближайший род. При определении понятия необходимо приводить примеры объектов, ему не удовлетворяющих, и показать, что определение не является бессодержательным. В школьном курсе рассматриваются ситуации, когда теорема существования доказывается после определения.
Определение считается корректным, если выполняются два условия:
- отсутствует порочный круг и связанная с ним возможность исключения нововведенных терминов («Решение уравнения — это то число, которое является его решением»);
- отсутствует омонимия: каждый термин встречается не более одного раза в качестве определяемого.
К процессу обучения математике также предъявляется ряд методологических требований:
- определение понятия следует формулировать только после того, как предмета всесторонне изучен;
- предмет следует изучать в развитии, а не в статике;
- учитывать критерий практики и принцип конкретности истины.
Классификация понятий
Процесс определения понятия тесно связан с такой характеристикой, как содержание понятия. Объем понятия раскрывается посредством классификации.
Классификация – это систематическое распределение некоторого множества по классам, возникающее в результате последовательного деления.
Операция деления представляет собой логическую операцию, которая раскрывает объем понятия путем выделения в нем возможных видов объекта.
Например, всех учащихся 11 класса можно разделить на тех, кто планирует поступать в вуз, и на тех, кто не собирается это делать.
Основанием деления понятия является свойство, в соответствии с которым выделяются подмножества объема понятия (виды понятия). В приведенном выше примере основанием деления является свойство: «планирует поступать в вуз ».
При осуществлении классификации важен выбор основания деления: разные основания создают разные классификации одного и того же понятия. Например, приняв за основания деления количество равных сторон, все параллелограммы можно разделить на ромбы и параллелограммы, имеющие неравные смежные стороны, а если за основание деления принять наличие прямого угла, то все параллелограммы можно разделить на прямоугольники и параллелограммы, не являющиеся прямоугольниками.
Классификация может основываться на существенных свойствах (естественная классификация) и на несущественных (вспомогательная классификация). При естественной классификации, когда известно, к какой группе принадлежит элемент, можно судить о его свойствах. Например, Д. И. Менделеев, благодаря тому, что расположил химические элементы в зависимости от их атомного веса, открыл закономерности в их свойствах и создал Периодическую систему, которая позволяет предсказывать свойства еще не открытых химических элементов.
Выделяют два вида деления:
Деление по видоизменению признака – это деление, при котором свойство, которое является основанием деления, присуще объектам выделенных видов в разной степени. Например, в зависимости от количества сторон все многоугольники можно разделить на треугольники, четырехугольники и n-угольники.
Дихотомическое деление – это деление, при котором данное понятие делится на два вида в зависимости от наличия или отсутствия у него некоторого свойства.
Например, классификацию треугольников можно выполнить по двум основаниям:
- по признаку наибольшего угла треугольника (но не по величине угла);
- по равенству двух сторон.
В первом примере деление – это деление по видоизменению свойства, а во втором – дихотомическое деление. В результате обоих делений все треугольники сначала будут разделены на остроугольные, прямоугольные, тупоугольные (один угол является тупым), после чего каждое из полученных множеств будет разделено на два подмножества. В результате всех делений будет получено шесть классов:
- остроугольные разносторонние;
- остроугольные равнобедренные;
- прямоугольные разносторонние;
- прямоугольные равнобедренные;
- тупоугольные разносторонние;
- тупоугольные равнобедренные.
Операция деления требует соблюдения следующих правил:
- деление должно быть соразмерным, т.е. выделенные классы при их объединении должны образовывать исходное множество (сумма объемов видовых понятий должна быть равна объему родового понятия);
- проводить деление можно только по одному основанию;
- пересечение классов должно быть пусто;
- классы не должны быть пустыми.
Часто выделяют еще одно требование: деление должно быть непрерывным (хотя при выполнении требования под пунктом 2 данное требование и так должно выполняться).
Например, нельзя делить члены предложения на подлежащее, сказуемое и второстепенные члены (что часто можно наблюдать в школе на уроках русского языка). Сначала необходимо выделить главные и второстепенные члены предложения, а уже затем делить каждый из них.
Список источников:
- Бочаров, В. А. Основы логики: учебник / В. А. Бочаров, В. И. Маркин. – М.: ИД «Форум»; Инфра-М, 2008.
- Выготский Л.С. Лекции по педологии. Ижевск: Изд-во Удмуртского университета, 2001.
- Гетманова А.Д. Логика: учебник для педагогических учебных заведений. М., 1998.
- Гусев В.А., Орлов В.В., Панчищина В.А. Методика обучения геометрии. Учеб. пособие для студ. высш. пед. учеб. заведений Под ред. В. А. Гусева. — М.: Издательский центр «Академия». — 368 с.
- Лященко Е.И. Лабораторные и практические работы по методике преподавания математике: учебное пособие для студентов физ.-мат. спец. пед. ин.-тов. М.: Просвещение, 1988.
- Методика и технология обучения математике [Текст] : курс лекций : учебное пособие для вузов / [Н. Л. Стефанова, Н. С. Подходова, В. В. Орлов и др. ; под науч. ред. Н. Л. Стефановой, Н. С. Подходовой]. – Москва : Дрофа, 2005. – 415 с.
- Методика обучения математике в 2 ч.: учебник для академического бакалавриата / Н. С. Подходова [и др.] ; под ред. Н. С. Подходовой, В. И. Снегуровой. — М. : Издательство Юрайт, 2017.
- Подходова Н.С., Кожокарь О.А., Фефилова Е.Ф. Реализация ФГОС ОО: новые решения в обучении математике // Учебно-методическое пособие для высших учебных заведений, ведущих подготовку по направлению 44.03.01/Учебное пособие с грифом УМО.Санкт- Петербург,Архангельск.КИРА, 2014.- 225с.
- Саранцев, Г. И. Методика обучения математике в средней школе: учеб. пособие для студ. мат. спец. пед. вузов и ун-тов / Г. И. Саранцев. – М.: Просвещение, 2002.
- Саранцев. Г. И. Формирование математических понятий в средней школе / Г. И. Саранцев // Математика в школе. – 1998. – № 6 – С. 27 – 30.
- Темербекова, А. А. Методика обучения математике : учеб. пособие для студ. высш. учеб. заведений / И. В. Чугунова, Г. А. Байгонакова, А. А. Темербекова .— Горно-Алтайск : РИО ГАГУ, 2013 .— 365 с.
- Теоретические основы обучения математике в средней школе : Учебное пособие для вузов / [Т. А. Иванова, Е. Н. Перевощикова, Т. П. Григорьева, Л. И. Кузнецова] ; Под ред. Т. А. Ивановой; МО РФ. – Нижний Новгород : Издательство Нижегородского государственного педагогического университета, 2003. – 318 с.
- Фрегге Г. Логика и логическая семантика. М.: Аспект Пресс, 2000.
- Фундаментальное ядро содержания общего среднего образования / под ред. В. В. Козлова, А. М. Кондакова. – М.: Просвещение, 2011.
Для того, чтобы понять, что такое область определения функции, необходимо знать области определения основных элементарных функций. Для этого нужно разбираться в определенных понятиях и находить весомые аргументы и методы решения, что и предложено данной статьей. Будут рассмотрены различные сложнейшие комбинации функций вида y=x+x-2 или y=5·x2+1·x3, y=xx-5 или y=x-15-3. Рассмотрим теорию и решим несколько примеров с подобными заданиями, чтобы вам больше не нужно было определять все это онлайн.
Что значит найти область определения
После того как функция задается, указывается ее область определения. Иначе говоря, без области определения функция не рассматривается. При задании функции вида y=f(x) область определения не указывается, так как ее ОДЗ для переменной x будет любым. Таким образом, функция определена на всей области определения.
Область определения и область значения можно найти и для кубического корня (куб. √), к примеру, для x+2.
Ограничение области определения
Область определения функции или ООФ рассматривается еще в школьном курсе алгебры. У действительных чисел она может быть (0, +∞) или такой [−3, 1)∪[5, 7). Еще по виду функции можно визуально узнавать ее ОДЗ. Рассмотрим, на что может указывать наличие области определения:
- при имеющемся знаменателе необходимо производить деление такого типа функции как y=x+2·xx4-1;
- при наличии переменной под знаком корня необходимо обращать внимание на сложение корня четной степени типа y=x+1 или y=23·x+3x;
- при наличии переменной в основании степени с отрицательным или нецелым показателем такого типа, как y=5·(x+1)-3, y=-1+x113, y=(x3-x+1)2, которые определены не для всех чисел;
- при наличии переменной под знаком логарифма или в основании вида y=lnx2+x4 или y=1+logx-1(x+1) причем основание является числом положительным, как и число под знаком логарифма;
- при наличии переменной, находящейся под знаком тангенса и котангенса вида y=x3+tg2·x+5 или y=ctg(3·x3-1), так как они существуют не для любого числа;
- при наличии переменной, расположенной под знаком арксинуса или арккосинуса вида y=arcsin(x+2)+2·x2, y=arccosx-1+x, область определения которых определяется ни интервале от -1 до 1.
При отсутствии хотя бы одного признака, область определения приходится искать другим образом (и это не с калькулятором). Рассмотрим пример функции вида y=x4+2·x2-x+12+223·x. Видно, что никаких ограничений она не имеет, так как в знаменателе нет переменной.
Правила нахождения области определения
Для примера рассмотрим функцию типа y=2·x+1. Для вычисления ее значения можем определить x. Из выражения 2·x+1 видно, что функция определена на множестве всех действительных чисел. Рассмотрим еще один пример для подробного определения.
Если задана функция типа y=3x-1, а необходимо найти область определения, тогда понятно, что следует обратить внимание на знаменатель. Известно, что на ноль делить нельзя. Отсюда получаем, что 3x-1знаменатель равняется нулю при х=1, поэтому искомая область определения данной функции примет вид (−∞, 1)∪(1, +∞) и считается числовым множеством.
На рассмотрении примера y=x2-5·x+6 видно, что имеется подкоренное выражение, которое всегда больше или равно нулю. Значит запись примет вид x2−5·x+6≥0. После решения неравенства получим, что имеются две точки, которые делят область определения на отрезки, которые записываются как (−∞, 2]∪[3, +∞).
При подготовке ЕГЭ и ОГЭ можно встретить множество комбинированных заданий для функций, где необходимо в первую очередь обращать внимание на ОДЗ. Только после его определения можно приступать к дальнейшему решению.
Область определения суммы, разности и произведения функций
Перед началом решения необходимо научиться правильно определять область определения суммы функций. Для этого нужно иметь следующее утверждение:
Когда функция ff считается суммой n функций f1, f2, …, fn, иначе говоря, эта функция задается при помощи формулы y=f1(x)+f2(x)+…+fn(x), тогда ее область определения считается пересечением областей определения функций f1, f2, …, fn. Данное утверждение можно записать как:
D(f)=D(f1)D(f2)…D(fn)
Поэтому при решении рекомендуется использование фигурной скобки при записи условий, так как это является удобным способом, чтобы понимать понимания перечисления числовых множеств.
Найти область определения функции вида y=x7+x+5+tgx.
Решение
Заданная функция представляется как сумма четырех: степенной с показателем 7,степенной с показателем 1, постоянной, функции тангенса.
По таблице определения видим, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞), D(f3)=(−∞, +∞), причем область определения тангенса включает в себя все действительные числа, кроме π2+π·k, k∈Z.
Областью определения заданной функции f является пересечение областей определения f1, f2, f3 и f4. То есть для функции существует такое количество действительных чисел, куда не входит π2+π·k, k∈Z.
Ответ: все действительные числа кроме π2+π·k, k∈Z.
Чтобы найти область определения произведения функций необходимо применять правило:
Когда функция f считается произведением n функций f1, f2, f3 и fn, тогда существует такая функция f, которую можно задать при помощи формулы y=f1(x)·f2(x)·…·fn(x), тогда ее область определения считается областью определения для всех функций.
Запишется D(f)=D(f1)D(f2)…D(fn)
Найти область определения функции y=3·arctg x·ln x.
Решение
Правая часть формулы рассматривается как f1(x)·f2(x)·f3(x), где за f1 является постоянной функцией, f2 является арктангенсом, f3 – логарифмической функцией с основанием e. По условию имеем, что D(f1)=(−∞, +∞), D(f2)=(−∞, +∞) и D(f3)=(0, +∞). Мы получаем, что
D(f)=D(f1)D(f2)D(fn)=(-∞, +∞)(-∞, +∞)D(0, +∞)=(0, +∞)
Ответ: область определения y=3·arctg x·ln x – множество всех действительных чисел.
Необходимо остановиться на нахождении области определения y=C·f(x), где С является действительным числом. Отсюда видно, что ее областью определения и областью определения f совпадающими.
Функция y=C·f(x) – произведение постоянной функции и f. Область определения – это все действительные числа области определения D(f). Отсюда видим, что область определения функции y=C·f(x) является -∞, +∞D(f)=D(f).
Естестввенным образом получили, что область определения y=f(x) и y=C·f(x), где C является некоторое действительное число, совпадают. Это видно на примере определения корня y=x считается [0, +∞), потому как область определения функции y=-5·x – [0, +∞).
Области определения y=f(x) и y=−f(x) совпадают , что говорит о том, что его область определения разности функции такая же, как и область определения их суммы.
Найти область определения функции y=log3x−3·2x.
Решение
Необходимо рассмотреть как разность двух функций f1 и f2.
f1(x)=log3x и f2(x)=3·2x. Тогда получим, что D(f)=D(f1)D(f2).
Область определения записывается как D(f1)=(0, +∞). Приступим к области определения f2. В данном случае она совпадает с областью определения показательной, тогда получаем, что D(f2)=(−∞, +∞).
Для нахождения области определения функции y=log3x−3·2x получим, что
D(f)=D(f1)D(f2)=(0, +∞)-∞, +∞
Ответ: (0, +∞).
Необходимо озвучить утверждение о том, что областью определения y=anxn+an-1xn-1+…+a1x+a0 является множество действительных чисел.
Рассмотрим y=anxn+an-1xn-1+…+a1x+a0, где в правой части имеется многочлен с одной переменной стандартного вида в виде степени n с действительными коэффициентами. Допускается рассматривать ее в качестве суммы (n+1)-ой функции. Область определения для каждой из таких функций включается множество действительных чисел, которое называется R.
Найти область определения f1(x)=x5+7×3-2×2+12.
Решение
Примем обозначение f за разность двух функций, тогда получим, что f1(x)=x5+7×3-2×2+12 и f2(x)=3·x-ln 5. Выше было показано, что D(f1)=R. Область определения для f2 является совпадающей со степенной при показателе –ln5, иначе говоря, что D(f2)=(0, +∞).
Получаем, что D(f)=D(f1)D(f2)=-∞, +∞(0, +∞)=(0, +∞).
Ответ: (0, +∞).
Область определения сложной функции
Для решения данного вопроса необходимо рассмотреть сложную функцию вида y=f1(f2(x)). Известно, что D(f) является множеством всех x из определения функции f2, где область определения f2(x) принадлежит области определения f1.
Видно, что область определения сложной функции вида y=f1(f2(x)) находится на пересечении двух множеств таких, где x∈D(f2) и f2(x)∈D(f1). В стандартном обозначении это примет вид
x∈D(f2)f2(x)∈D(f1)
Рассмотрим решение нескольких примеров.
Найти область определения y=ln x2.
Решение
Алгоритм решения этого уравнения или функции следующий.
Данную функцию представляем в виде y=f1(f2(x)), где имеем, что f1 является логарифмом с основанием e, а f2 – степенная функция с показателем 2.
Для решения необходимо использовать известные области определения D(f1)=(0, +∞) и D(f2)=(−∞, +∞).
Тогда получим систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-∞, +∞x2∈(0, +∞)⇔⇔x∈(-∞, +∞)x2>0⇔x∈(-∞, +∞)x∈(-∞, 0)∪(0, +∞)⇔⇔x∈(-∞, 0)∪(0, +∞)
Искомая область определения найдена. Вся ось действительных чисел кроме нуля является областью определения.
Ответ: (−∞, 0)∪(0, +∞).
Найти область определения функции y=(arcsin x)-12.
Решение
График решения следующий.
Так как дана сложная функция, необходимо рассматривать ее как y=f1(f2(x)), где f1 является степенной функцией с показателем -12, а f2 функция арксинуса, теперь необходимо искать ее область определения. Необходимо рассмотреть D(f1)=(0, +∞) и D(f2)=[−1, 1]. Теперь найдем все множества значений x, где x∈D(f2) и f2(x)∈D(f1). Получаем систему неравенств вида
x∈D(f2)f2(x)∈D(f1)⇔x∈-1, 1arcsin x∈(0, +∞)⇔⇔x∈-1, 1arcsin x>0
Для решения arcsin x>0 необходимо прибегнуть к свойствам функции арксинуса. Его возрастание происходит на области определения [−1, 1], причем обращается в ноль при х=0, значит, что arcsin x>0 из определения x принадлежит промежутку (0, 1].
Преобразуем систему вида
x∈-1, 1arcsin x>0⇔x∈-1, 1x∈(0, 1]⇔x∈(0, 1]
Область определения искомой функции имеет интервал равный (0, 1].
Ответ: (0, 1].
Постепенно подошли к тому, что будем работать со сложными функциями общего вида y=f1(f2(…fn(x)))). Область определения такой функции ищется из x∈D(fn)fn(x)∈D(fn-1)fn-1(fn(x))∈D(fn-2)…f2(f3(…(fn(x)))∈D(f1).
Найти область определения y=sin(lg x4).
Решение
Заданная функция может быть расписана, как y=f1(f2(f3(x))), где имеем f1 – функция синуса, f2 – функция с корнем 4 степени, f3 – логарифмическая функция.
Имеем, что по условию D(f1)=(−∞, +∞), D(f2)=[0, +∞), D(f3)=(0, +∞). Тогда областью определения функции – это пересечение множеств таких значений, где x∈D(f3), f3(x)∈D(f2), f2(f3(x))∈D(f1). Получаем, что
x∈D(f3)f3(x)∈D(f2)f2(f3(x))∈D(f1)⇔x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞
Условие lg x4∈-∞, +∞ аналогично условию lg x∈[0, +∞), значит
x∈(0, +∞)lg x∈[0, +∞)lg x4∈-∞, +∞⇔x∈(0, +∞)lg x∈[0, +∞)lg x∈[0, +∞)⇔⇔x∈(0, +∞)lg x∈[0, +∞)⇔x∈(0, +∞)lg x≥0⇔⇔x∈(0, +∞)lg x≥lg 1⇔x∈(0, +∞)x≥1⇔⇔x∈[1, +∞)
Ответ: [1, +∞).
При решении примеров были взяты функции, которые были составлены при помощи элементарных функций, чтобы детально рассмотреть область определения.
Область определения дроби
Рассмотрим функцию вида f1(x)f2(x). Стоит обратить внимание на то, что данная дробь определяется из множества обеих функций, причем f2(х) не должна обращаться в ноль. Тогда получаем, что область определения f для всех x записывается в виде x∈D(f1)x∈D(f2)f2(x)≠0.
Запишем функцию y=f1(x)f2(x) в виде y=f1(x)·(f2(x))-1. Тогда получим произведение функций вида y=f1(x) с y=(f2(x))-1. Областью определения функции y=f1(x) является множество D(f1), а для сложной y=(f2(x))-1 определим из системы вида x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f2)f2(x)≠0.
Значит, x∈D(f1)x∈D(f2)f2(x)∈(-∞, 0)∪(0, +∞)⇔x∈D(f1)x∈D(f2)f2(x)≠0.
Найти область определения y=tg(2·x+1)x2-x-6.
Решение
Заданная функция дробная, поэтому f1 – сложная функция, где y=tg(2·x+1) и f2 – целая рациональная функция, где y=x2−x−6, а область определения считается множеством всех чисел. Можно записать это в виде
x∈D(f1)x∈D(f2)f2(x)≠0
Представление сложной функции y=f3(f4(x)), где f3 –это функция тангенс, где в область определения включены все числа, кроме π2+π·k, k∈Z, а f4 – это целая рациональная функция y=2·x+1 с областью определения D(f4)=(−∞, +∞). После чего приступаем к нахождению области определения f1:
x∈D(f4)2·x+1∈D(f3)⇔x∈(-∞, +∞)2x+1≠π2+π·k, k∈Z⇔x≠π4-12+π2·k, k∈Z
Еще необходимо рассмотреть нижнюю область определения y=tg(2·x+1)x2-x-6. Тогда получаем, что
x∈D(f1)x∈D(f2)f2(x)≠0⇔x≠π4-12+π2·k, k∈Zx∈-∞, +∞x2-x-6≠0⇔⇔x≠π4-12+π2·k, k∈Zx≠-2x≠3
Ответ: множество действительных чисел, кроме -2, 3 и π4-12+π2·k, k∈Z.
Действия с корнями
Корни в математике, в частности, функцию с корнем можно определить следующим образом:
y=n√x. N здесь — натуральное число, большее за единицу.
Область определения корня зависит от того, каков показатель: четный или нечетный.
Если n является четным числом (n=2m). Это значит, что область определения представляет собой множество всех неотрицательных действительных чисел.
Если показатель корня — нечетное число, большее за единицу (n=2m+1 и m принадлежит к n), то областью определения корня будет множество всех действительных чисел.
Также важным является вопрос, как складывать корни.
Сложение и вычитание корней возможно при условии наличия одинакового подкоренного выражения. К примеру, сложение и вычитание корней возможно 2√3 и 4√3. Можно ли складывать корни или вычитать в случае 2√3 и 2√5? Ответ — нет.
Как решать корни во втором случае? Вы можете упростить подкоренное выражение и привести их корни к одинаковому подкоренному выражению. После этого вы сможете как считать корни, так и вычитать корни.
К основным действиям с корнями относят:
- умножение корней;
- деление корней;
- корень минус корень или плюс.
Область определения логарифма с переменной в основании
Определение логарифма существует для положительных оснований не равных 1. Отсюда видно, что функция y=logf2(x)f1(x) имеет область определения, которая выглядит так:
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
К аналогичному заключению можно прийти, когда функцию можно изобразить в таком виде:
y=logaf1(x)logaf2(x), a>0, a≠1. После чего можно приступать к области определения дробной функции.
Область определения логарифмической функции – это множество действительных положительных чисел, тогда области определения сложных функций типа y=logaf1(x) и y=logaf2(x) можно определить из получившейся системы вида x∈D(f1)f1(x)>0 и x∈D(f2)f2(x)>0. Иначе эту область можно записать в виде y=logaf1(x)logaf2(x), a>0, a≠1, что означает нахождение y=logf2(x)f1(x) из самой системы вида
x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0logaf2(x)≠0=x∈D(f1)f1(x)>0x∈D(f2)f2(x)>0f2(x)≠1
Обозначить область определения функции y=log2·x(x2-6x+5).
Решение
Следует принять обозначения f1(x)=x2−6·x+5 и f2(x)=2·x, отсюда D(f1)=(−∞, +∞) и D(f2)=(−∞, +∞). Необходимо приступить к поиску множества x, где выполняется условие x∈D(f1), f1(x)>0, x∈D(f2), f2(x)>0, f2(x)≠1. Тогда получаем систему вида
x∈(-∞, +∞)x2-6x+5>0x∈(-∞, +∞)2·x>02·x≠1⇔x∈(-∞, +∞)x∈(-∞, 1)∪(5, +∞)x∈(-∞, +∞)x>0x≠12⇔⇔x∈0, 12∪12, 1∪(5, +∞)
Отсюда видим, что искомой областью функции y=log2·x(x2-6x+5) считается множнство, удовлетворяющее условию 0, 12∪12, 1∪(5, +∞).
Ответ: 0, 12∪12, 1∪(5, +∞).
Область определения показательно-степенной функции
Показательно-степенная функция задается формулой вида y=(f1(x))f2(x). Ее область определения включает в себя такие значения x, которые удовлетворяют системе x∈D(f1)x∈D(f2)f1(x)>0.
Эта область позволяет переходить от показательно-степенной к сложной вида y=aloga(f1(x))f2(x)=af2(x)·logaf1(x), где где a>0, a≠1.
Найти область определения показательно-степенной функции y=(x2-1)x3-9·x.
Решение
Примем за обозначение f1(x)=x2−1 и f2(x)=x3-9·x.
Функция f1 определена на множестве действительных чисел, тогда получаем область определения вида D(f1)=(−∞, +∞). Функция f2 является сложной, поэтому ее представление примет вид y=f3(f4(x)), а f3 – квадратным корнем с областью определения D(f3)=[0, +∞), а функция f4 – целой рациональной,D(f4)=(−∞, +∞). Получаем систему вида
x∈D(f4)f4(x)∈D(f3)⇔x∈(-∞, +∞)x3-9·x≥0⇔⇔x∈(-∞, +∞)x∈-3, 0∪[3, +∞)⇔x∈-3, 0∪[3, +∞)
Значит, область определения для функции f2 имеет вид D(f2)=[−3, 0]∪[3, +∞). После чего необходимо найти область определения показательно-степенной функции по условию x∈D(f1)x∈D(f2)f1(x)>0.
Получаем систему вида x∈-∞, +∞x∈-3, 0∪[3, +∞)x2-1>0⇔x∈-∞, +∞x∈-3, 0∪[3, +∞)x∈(-∞, -1)∪(1, +∞)⇔⇔x∈-3, -1∪[3, +∞)
Ответ: [−3, −1)∪[3, +∞)
В общем случае
Для решения обязательным образом необходимо искать область определения, которая может быть представлена в виде суммы или разности функций, их произведений. Области определения сложных и дробных функций нередко вызывают сложность. Благодаря выше указанным правилам можно правильно определять ОДЗ и быстро решать задание на области определения.
Таблицы основных результатов
Весь изученный материал поместим для удобства в таблицу для удобного расположения и быстрого запоминания.
| Функция | Ее область определения |
|
Сумма, разность, произведение функций f1, f2,…, fn |
Пересечение множеств D(f1), D(f2), …, D(fn) |
|
Сложная функция y=f1(f2(f3(…fn(x)))) В частности, y=f1(f2(x)) |
Множество всех x, одновременно удовлетворяющих условиям x∈D(fn),fn(x)∈D(fn-1),fn-1(fn(x))∈D(fn-2),… ,f2(f3(…fn(x)))∈D(f1) x∈D(f2),f2(x)∈D(f1) |
Расположим функции и их области определения.
| Функция | Ее область определения |
|
Прямая пропорциональность y=k·x |
R |
| Линейная y=k·x+b | R |
|
Обратная пропорциональность y=kx |
-∞, 0∪0, +∞ |
| Квадратичная y=a·x2+b·x+c | R |
| y=anxn+an-1xn-1+…+a1x+a0 | R |
| Целая рациональная | R |
| y=C·f(x), где C – число | D(f) |
|
Дробная y=f1(x)f2(x) В частности, если f1(x), f2(x) – многочлены |
Множество всех x, которые одновременно удовлетворяют условиям f2(x)≠0 |
| y=f(x)n, где n – четное | x∈D(f1), f(x)≥0 |
|
y=logf2(x)f1(x) В частности, y=logaf1(x) В частности, y=logf2(x)a |
x∈D(f1), f1(x)>0,x∈D(f2), f2(x)>0, f2(x)≠1 x∈D(f1), f1(x)>0 x∈D(f2), f2>0, f2(x)≠1 |
| Показательно-степенная y=(f1(x))f2(x) | x∈D(f1), x∈D(f2), f1(x)>0 |
Отметим, что преобразования можно выполнять, начиная с правой части выражения. Отсюда видно, что допускаются тождественные преобразования, которые на область определения не влияют. Например, y=x2-4x-2 и y=x+2 являются разными функциями, так как первая определяется на (−∞, 2)∪(2, +∞), а вторая из множества действительных чисел. Из преобразования y=x2-4x-2=x-2x+2x-2=x+2 видно, что функция имеет смысл при x≠2.
