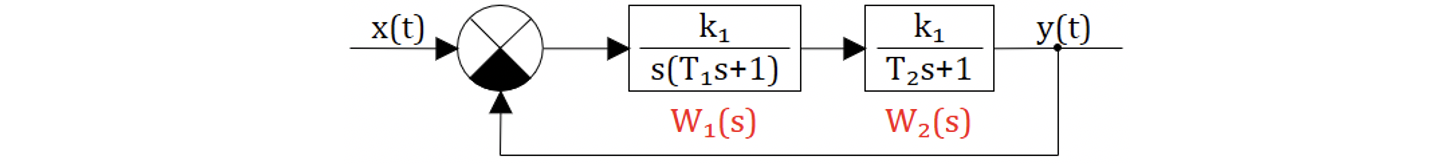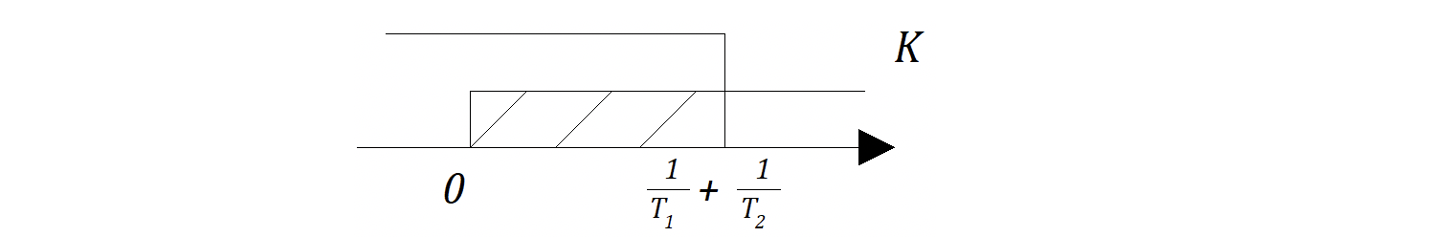Как составить определитель гурвица

Как составить определитель гурвица

Предыдущие лекции по теории автоматического управления можно посмотреть здесь:

1. Введение в теорию автоматического управления.2. Математическое описание систем автоматического управления 2.1 — 2.3, 2.3 — 2.8, 2.9 — 2.13.

3. ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНЬЕВ И СИСТЕМ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ РЕГУЛИРОВАНИЯ. 3.1. Амплитудно-фазовая частотная характеристика: годограф, АФЧХ, ЛАХ, ФЧХ. 3.2. Типовые звенья систем автоматического управления регулирования. Классификация типовых звеньев. Простейшие типовые звенья. 3.3. Апериодическое звено 1–го порядка инерционное звено. На примере входной камеры ядерного реактора. 3.4. Апериодическое звено 2-го порядка. 3.5. Колебательное звено. 3.6. Инерционно-дифференцирующее звено. 3.7. Форсирующее звено.  3.8. Инерционно-интегрирующее звено (интегрирующее звено с замедлением). 3.9. Изодромное звено (изодром). 3.10 Минимально-фазовые и не минимально-фазовые звенья. 3.11 Математическая модель кинетики нейтронов в «точечном» реакторе «нулевой» мощности.

4. Структурные преобразования систем автоматического регулирования.

5. Передаточные функции и уравнения динамики замкнутых систем автоматического регулирования (САР).

6.1. Понятие об устойчивости САР. Теоремы Ляпунова.

В теории «Управления техническими системами» общепринято понятие качество управления, состоящее из трех основных составляющих:

  • устойчивость САР (или запасы устойчивости);

  • точность САР;

  • качество переходного процесса.

 Необходимо заметить, что если не обеспечена устойчивость замкнутой САР, то говорить о точности и, тем более, о качестве переходного процесса – бессмысленно.

      Поэтому понятие «устойчивость» – важнейшее понятие для САР.

      Приведем «механическую» аналогию понятия «устойчивость» 

Рисунок 6.1.1 а) абсолютно устойчивое положение, б) неустойчивое положение, в) нейтральное (безразличное) положение.

Рисунок 6.1.1 а) абсолютно устойчивое положение, б) неустойчивое положение, в) нейтральное (безразличное) положение.

В положении а) при отклонении шарика от нижнего положения он обязательно вернется в свое устойчивое положение (низ «воронки»).

В положении б) малейшее отклонение шара от состояния равновесия приведет к «скатыванию» его вниз; т.е. шар не вернется сам назад на вершине «горки».

В положении в) при воздействии на шар он начнет перемещаться в горизонтальном направлении и, если нет трения, то шар будет двигаться с постоянной скоростью.

 Если реальная замкнутая САР имеет свойства, аналогичные а), то она «хорошая», если б) – «совсем плохая».   Нужно так проектировать САР, чтобы ее свойства были похожи на а), т.е. если какое-то возмущающее воздействие отклонит систему от равновесия, то система управления обязана вернуть техническую систему в состояние равновесия.

Ранее мы водили передаточную функуию для по возмущающему воздействию для замкнутой САР (см. формулу 5.4 в предыдущей лекции). Уравнения динамики замкнутой САР, описываемую в переменных «вход-выход»:

D(p)cdot y(t)=k cdot N(p) cdot x(t) mathbf{(6.1.1)}

Решения для такого уравнения будет являтся суммой двух функций:y(t)=y_{соб}(t)+y_{вын}(t), где y_{соб}(t)– собственное решение, при x(t)=0и вынужденное y_{вын}(t)решение вызванное воздействием.

Решим характеристическое уравнение (подробнее смотри здесь…)

D(lambda) = 0 mathbf{(6.1.2)}a_ncdot lambda^n_n+a_{n-1}cdot lambda^{n-1}_{n-1}+...+a_1cdot lambda_1+a_0 =0

 Решая уравнение (6.1.2), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения lambda_j, тогда собственное решение примет вид:

y_{соб}(t)=sum_{j=1}^n c_jcdot e^{lambda_jcdot t} mathbf{(6.1.3)}

В зависимости от значения lambda_jвозможно несколько вариантов вида функуции. На рисунке 6.1.2 представлены варинаты поведения функции вида c_jcdot e^{lambda_jcdot t}в случае когда lambda_j in Rявляется реальными числом или комплексным числом lambda_j in C.

Рисунок 6.1.2 Возможная вид решения

Рисунок 6.1.2 Возможная вид решения

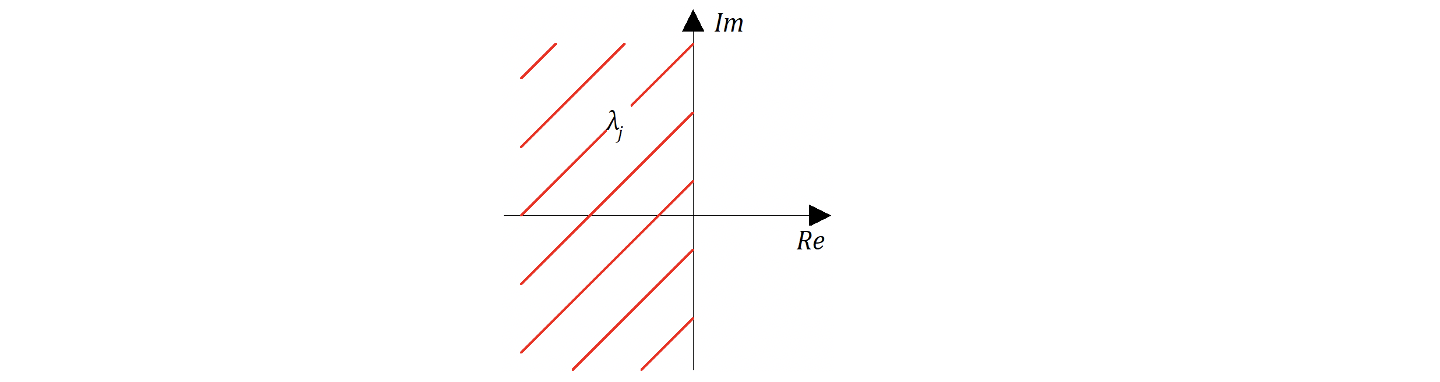
Анализ вышеприведенных рисунков показывает, что система может вернуться в исходное состояние, если все составляющие с_jcdot e^{lambda_jcdot t } при trightarrow infty будут стремиться к нулю.  А для этого показатель степени должен быть отрицательным.  Поэтому условием устойчивости является отрицательное значение реальной части корней Re[lambda_j]<0т.е. необходимо чтобы корни характеристического уравнения лежали в левой полуплоскости.  

Рисунок 6.1.3 Расположение корней характеристического уравнения

Рисунок 6.1.3 Расположение корней характеристического уравнения

Если корни комплексные, то процесс колебательный, если корни реальные, то процес аперодический (затухающий). Причем ось ординат  соответствует границам устойчивости (Re [ lambda_i]=0)(апериодической или колебательной). Таким образом, вопрос об устойчивости или неустойчивости замкнутой (и разомкнутой) САР определяется по расположению корней соответствующего характеристического уравнения.

Для не замкнутой САР вместо D(lambda) устойчивость определяется корнями характеристического уравнения знаменателя передаточной функции L(lambda)в предыдущей лекции мы выводили формулу рассчета передаточной фунции замкунутой САР, по предаточной функции разомкнутоф САР: D(s)=L(s)+Kcdot N(s)

 Таким образом, вопрос об устойчивости или неустойчивости замкнутой и разомкнутой САР определяется по расположению корней соответствующего характеристического уравнения.

left [ begin{align} D(lambda)=0 - для замкнутой САР \L(lambda) =0 - для разомкнутой САР end{align} mathbf{(6.1.3)}right.

Если все корни характеристического уравнения лежат (расположены) в левой полуплоскости – линейная (или линеаризованная) САР устойчива.

 Необходимо заметить, что коэффициенты уравнения D(lambda)=0совпадают с коэффициентами многочлена (полинома)  D(s)=0 следовательно     полюса замкнутой САР тождественно совпадают с корнями характеристического уравнения   lambda_j=s_j  , где  lambda_j– корни характеристического уравнения; s_j– полюса перредаточной функции.

Напомним, полюсом передаточной функции называется значение её аргумента, при котором знаменатель функции обращается в ноль.

Используя приблизительно такие же рассуждения сходимости степенных функций Ляпуновым были сформулированы 3 теоремы об устойчивости линейных САР: 

  1. Если все корни характеристического уравнения или полюса передаточной функции САР расположены в левой полуплоскости, то линеаризованная САР обязательно вернется в исходное состояние при снятии внешнего воздействия, выведшего эту САР из состояния равновесия. Следовательно САР – устойчива.

  2. Если хотя бы один полюс (или корень характеристического уравнения) передаточной функции САР расположен в правой полуплоскости (при всех остальных в левой полуплоскости), линейная (линеаризованная) САР никогда не вернется в исходное (равновесное) состояние при снятии внешнего воздействия, которое вывело данную САР из исходного состояния равновесия.   Следовательно САР – неустойчива.

  3. Если хотя бы один из полюсов передаточной функции САР (корней   характеристического уравнения) находится на мнимой оси (при всех остальных в левой полуплоскости) об устойчивости линеаризованной САР ничего сказать нельзя, т.к. учет нелинейных (отброшенных) членов в динамике САР может дать любой результат (устойчива или неустойчива).

Резюмируя вышесказанное, отметим, что:

 Наиболее простым способом определения устойчива или неустойчива САР (как замкнутая, так и разомкнутая) является решение уравнения D(s)=0для замкнутой САР (или L(s)=0 для разомкнутой САР) или решение характеристического уравнения D(lambda)=0илиL(lambda)– для разомкнутой САР).

Если САР задана в переменных состояния, то вопрос об устойчивости САР определяется матрицей А – собственной матрицей:

left { begin{align} x'=Acdot x+Bcdot u \ y =C cdot x + D cdot u end{align} mathbf{(6.1.5)}right.

Если собственные числа матрицы А лежат в левой полуплоскости – САР устойчива; если хотя бы одно собственное число лежит в правой полуплоскости – линейная САР неустойчива.

Собственные числа (согласно разделу «Линейная алгебра») находятся из уравнения:

det[A -Ecdot lambda] =0 mathbf{(6.1.6)}

где: A– матрица размера n times n; E– единичная матрица

E = begin{bmatrix} 1 &0 &cdots & 0 \ 0 & 1 &cdots & 0 \ vdots &vdots &ddots &vdots \ 0 &0 &0 &1 end{bmatrix}

Это означает, что уравнение принимает:

left | begin{matrix} a_{11}-lambda_1 &a_{12} &cdots & a_{1n} \ a_{21} & a_{22} - lambda_2 &cdots & a_{2n} \ vdots &vdots &ddots &vdots \ a_{n1} &a_{n2} &cdots &a_{nn}-lambda_n end{matrix} right |=0 mathbf{(6.1.7)}

решая, находим lambda_j

Фактически уравнения (6.1.6) и (6.1.7) – характеристические уравнения САР. Поэтому, если САР задана в переменных состояния, то характеристический полином D(s)при задании САР в переменных «вход-выход» может быть определен как:

D(s)=left [ begin{align} det[A -E cdot s] = 0 - если размерность матрицы A четная \det[Ecdot s -A]=0 - если размерность матрицы A нечетная end{align} right.

Чисто математически задача определения устойчивости сводится к решению степенного уравнения D(s)=0 или к проблеме нахождения собственных чисел матрицы А.

6.2. Необходимые условия устойчивости линейных и линеаризованных САР.

Наиболее просто необходимое условие устойчивости линейных (линеаризованных) САР формулируется для систем, записанных в переменных «вход-выход», причем оно применяется в одинаковой «редакции» как для замкнутых, так и для разомкнутых САР.   Это условие доказывается с использованием характеристического полинома D(s) – для замкнутых САР, или L(s) – для разомкнутых САР. Сделаем вывод на основании D(s)  

Разложим многочлен D(s) на элементарные линейные сомножители :

D(s)=a_ncdot s^n+a_{n-1}cdot s^{n-1}+...+a_1cdot s+a_0D(s)=a_ncdot(s-s_1)cdot(s-s_2)cdot ...cdot(s-s_n) mathbf{(6.2.1)}

где: s_1,s_2,s_3...s_n– полюса передаточной функции замкнутой САР.

Предположим, что a_n>0и что все полюса s_jрасположены в левой полуплоскости:   

left | begin{align} s_1 &= -|alpha_1 | \s_2&=-|alpha_2|+icdotbeta_2; \s_3&=-|alpha_2|-icdot beta_2;\s_4&=-|alpha_3|+icdotbeta_3;\ s_5&=-|alpha_3|-icdotbeta_3;\&............ end{align} right.

где: s_1– действительный полюс; s_2cdots s_5–  – комплексно-сопряженные полюса.

Подставим значения s_1 cdots s_nв выражение 6.2.1 заметим, что если перемножать любые две скобки в выражении 6.2.1, которые содержат комплексно сопряженные скобки например (s-s_2)cdot(s -s_3)мы получим выражение типа: s^2+2cdot alpha_jcdot s+alpha_j^2+beta_j^2.

В первой скобке мы получим выражение: (s-s_1)=(s+alpha_1);Таким образом мы получаем только полжительные коэффициенты полинома D(s). Таким образом можно сформулировать необходимое условие устойчивости линейных САР:

Необходимым условием устойчивости линейных САР является положительность всех коэффициентов в полиноме D(s) – для замкнутых САР, или в L(s)– для разомкнутых САР.

Для систем 1-го и 2-го порядка необходимое условие является и достаточным.

Но для систем, имеющих порядок , выполнение необходимого условия невсегда является достаточным.

Тем не менее, необходимое условие «очень удобно», т.е. если хотя бы один коэффициент в D(s) отрицателен, то однозначно – САР неустойчива.

Если необходимое условие выполнено (a_j>0), то если порядок матрицы больше 2 (n>2)необходимо либо вычислить корни характеристического уравнения (полюса передаточной функции), либо используя какой-либо из критериев устойчивости сделать соответствующий вывод об устойчивости САР.  

6.3. Алгебраический критерий устойчивости Гурвица. 

Как отмечалось выше, устойчивость любой САР можно определить, вычислив значение всех полюсов (или корней соответствующего характеристического уравнения). Однако далеко не все способны без компьютера (калькулятора) решить степенное уравнение выше квадратного (кубическое и т.д.). 

Критерий Гурвица, являющийся частным случаем критерия Раусса, позволяет не решая уравнений типа D(s)=0или D(lambda)=0сделать вывод об устойчивости САР на основании «несложных» вычислений с использованием коэффициентов характеристического полинома.

Представим полином D(s)в измененном виде:

D(s)=a_0cdot s^n+ a_1cdot s^{n-1}+ ...+ a_{n-1}cdot s +a_n mathbf{(6.3.1)}

Данное выражение полинома позволяет соcтавить матрицу Гурвица, для этого:

  1. по главной диагонале по главной диагонали слева направо выставляются коэффициенты характеристического уравнения от a_1до a_n;

  2. от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;

  3. на место коэффициентов с индексами меньше нуля или больше nставатся нули:

Г = begin{bmatrix} a_1 &a_3 &a_5 &cdots & 0 &0 \ a_0 & a_2 &a_4 &cdots &0 &0\0 &a_1 &a_3 &cdots &0 &0\ vdots &vdots &vdots &ddots &vdots &vdots \0 &0 &0 &cdots &a_{n-1} &0 \ 0 &0 &0 &cdots &a_{n-2} &a_n end{bmatrix}

Составив эту матрицу можно сфомулировать критерий:

Для того, чтобы замкнутая САР (или разомкнутая) была устойчивой, необходимо и достаточно, чтобы были положительны все n главных определителей Гурвицевой матрицы Г.

left { begin{align} Delta_1 &= a_1>0; \ Delta_2 &= left |begin{matrix} a_1 &a_3\ a_0 &a_2 end{matrix} right |>0; \ Delta_3 &= left | begin{matrix}a_1 &a_3 &a_5 \ a_0 &a_2 &a_2 \ 0 &a_1 &a_3 end{matrix} right |>0; \ cdots \ Delta_{n} &= Delta_{n-2}cdot a_n >0. end{align} right.

Если все определители больше нуля, то линейная САР устойчива.

Если все определители больше нуля и a_n=0то САР находится на апереодической границе устойчивости.

Если все определители, кроме Delta_{n-1}больше нуля, а опеределитель Delta_{n-1} =0 и a_nneq0Р , то САР находится на колебательного границы устойчивости.

Пример 1

Определить, устойчива или нет следующая система САР:

Рисунок 6.3.1 САР для анализа устойчивости

Рисунок 6.3.1 САР для анализа устойчивости

Найдем главную передаточную функцию замкнутой САР:

Ф(s)=frac{W(s)}{W_{oc}(s)}=frac{10cdot s+1}{(4cdot s^2+s+1)cdot left [1+frac{10cdot s+1}{4cdot s^2+s+1}cdot frac{1}{s+1} right]}=\ =frac{(10cdot s+1)cdot(s+1)}{(s+1)cdot(4cdot s^2+s+1)+(10cdot s+1)}=frac{(10cdot s+1)cdot(s+1)}{underbrace{4cdot s^3+5cdot s^2+12cdot s+2}_{D(s)}}

Все коэффициенты полинома D(s)– положительные:

D(s)=underbrace{4}_{a_0}cdot s^3+underbrace{5}_{a_1}cdot s^2+underbrace{12}_{a_2}cdot s+underbrace{2}_{a_3}

А значит САР может быть устойчива. Составим матрицу Гурвица, и найдем ее определители:

Г=begin{bmatrix} 5 &2 &0\ 4 &12 &0 \ 0 &5 & 2 end{bmatrix}Rightarrow left { begin{align} Delta_1 &=5>0; \ Delta_2 &= left | begin{matrix} 5 &2\ 4&12 end{matrix} right | =5cdot12-4cdot2=52>0 \ Delta_3 &= 52 cdot 2>0; end{align} right.

Все определители матрицы Гурвица больше нуля, следовательно САР устойчива.

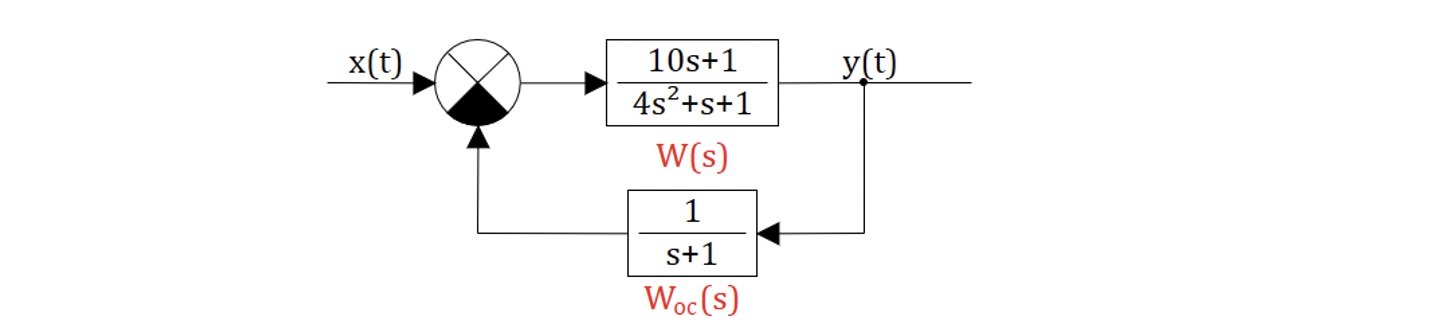
Пример 2

Используя критерий Гурвица, выполнить анализ устойчивости следующей САР:

Рисунок 6.3.2 САР для анализа устойчивости

Рисунок 6.3.2 САР для анализа устойчивости

Общая передаточная функция разомкнутой системы САР:

W(s) =frac{overbrace{k_1cdot k_2}^K}{scdot(T_1cdot s+1)cdot(T_2cdot s+1)}

Корни знаменателя передаточной функцийй размкнутой САР:

s_1=-frac{1}{T_1}; s_2 =-frac{1}{T_2}; s_3 =0

Поскольку s_3=0разомкнутая САР находится на границе устойчивости.

Передаточная функция замкнутой САР:

Ф(s)=frac{W_1(s)cdot W_2(s)}{1+W_1(s)cdot W_2(s)}RightarrowФ(s)=frac{overbrace{k_1cdot k_2}^K}{scdot(T_1cdot s+1)cdot(T_2cdot s+1)+underbrace{k_1cdot k_2}_K}=underbrace{frac{K}{T_1cdot T_2cdot s^3+(T_1+T_2)cdot s^2+s+k}}_{D_s}D(s)=underbrace{T_1cdot T_2}_{a_0}cdot s^3+underbrace{(T_1+T_2)}_{a_1}cdot s^2+underbrace{1}_{a_2}cdot s+underbrace{k}_{a_3}

Выражения для матрицы Гурвица:

Г=begin {bmatrix}(T_1+T_2) & K & 0\ T_1cdot T_2 &1 &0\ 0 &(T_1+T_2)& K end{bmatrix}

Главные определители матрицы Гурвица:

left {begin{align} Delta_1&=T_1+T_2 >0\ Delta_2&=T_1+T_2-Kcdot T_1cdot T_2 >0\ Delta_3 &=Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right.

Очевидно из формулы для определиттеля Delta_3 следует что для устойчивости САР необходимо чтобы K>0

Рисунок 6.3.3. Условие устойчивости по

Рисунок 6.3.3. Условие устойчивости по

В случае когда постоянные времени положительны T_1>0, T_2>0 условие устойчивости можно вычислить получить из выражения для второго определителя:

T_1+T_2 - Kcdot T_1cdot T_2 >0Rightarrow k< frac{1}{T_1}+frac{1}{T_2}

Рисунок 6.3.4 Полные условия устойчивости

Рисунок 6.3.4 Полные условия устойчивости

Полученный результат свидетельствует, что если T_1=const, T_2=const, то для того, чтобы САР была устойчивой, необходимо, чтобы выполнит следующие условия:

0<K<frac{1}{T_2}+frac{1}{T_1}

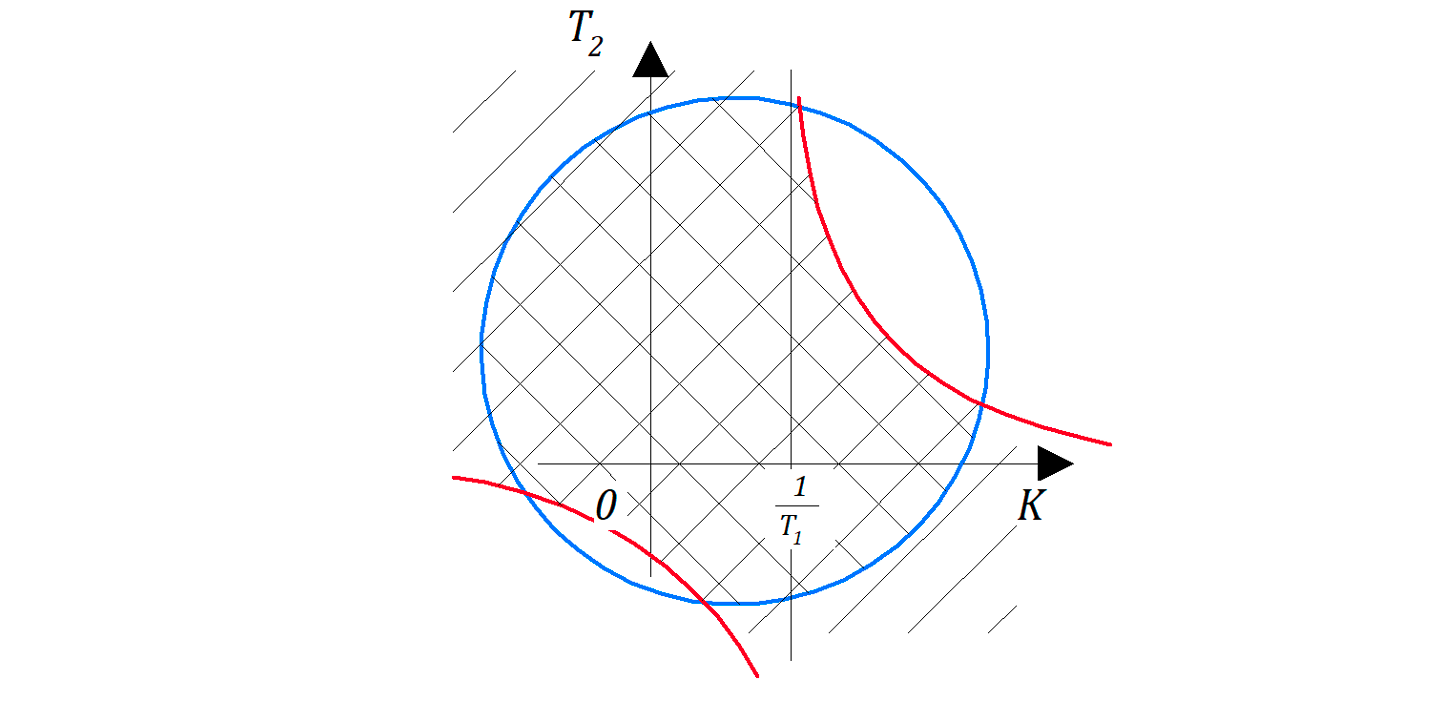
Усложним задачу: предположим, что в системе САР изображенной на рис. 6.3.2 возможно варьировать (изменять) коэффициент усиления Kи постоянную времени, например, T_2В этом случае область устойчивости может быть отображена в виде фигуры в координатах T_2-K

Рисунок 6.3.5 Область устойчивости

Рисунок 6.3.5 Область устойчивости

Система неравенств такая же, что и выше, для определителей матрицы Гурвица:

left {begin{align} Delta_1&=T_1+T_2 >0\ Delta_2&=T_1+T_2-Kcdot T_1cdot T_2 >0\ Delta_3 &=Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right. Rightarrowleft {begin{align} & T_1+T_2 >0\ & T_1+T_2-Kcdot T_1cdot T_2 >0\& Kcdot(T_1+T_2- Kcdot T_1cdot T_2)>0 end{align} right. Rightarrow K< left ( frac{1}{T_1}+frac{1}{T_2} right ) Rightarrow frac{1}{T_2}>K-frac{1}{T_1} RightarrowRightarrow left { begin{align} T_2<frac{1}{K-frac{1}{T_1}} если K>frac{1}{T_1}\ T_2>frac{1}{frac{1}{T_1}-K} если K<frac{1}{T_1} end{align} right.

Рисунок 6.3.6. Область устойчивости для САР с переменными T2 и К

Рисунок 6.3.6. Область устойчивости для САР с переменными T2 и К

Примеры из видео можно взять здесь..

Продолжение темы устойчивости:

6.4 Частотный критерий устойчивости Михайлова.

6.5. Частотный критерий Найквиста

6.6. Понятие об областях устойчивости

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 октября 2021 года; проверки требуют 6 правок.

Критерий устойчивости Гурвица — один из способов анализа линейной стационарной динамической системы на устойчивость, разработанный немецким математиком Адольфом Гурвицом. Наряду с критерием Рауса является представителем семейства алгебраических критериев устойчивости, в отличие от частотных критериев, таких, как критерий устойчивости Найквиста — Михайлова. Достоинством метода является принципиальная простота, недостатком — необходимость выполнения операции вычисления определителя, которая связана с определенными вычислительными тонкостями (например, для больших матриц может появиться значительная вычислительная ошибка).

Формулировка[править | править код]

Метод работает с коэффициентами характеристического уравнения системы. Пусть W(s)={frac {Y(s)}{U(s)}} — передаточная функция системы, а {displaystyle U(s)=0} — характеристическое уравнение системы. Представим характеристический полином {displaystyle U(s)} в виде

{displaystyle U(s)=a_{0}s^{n}+a_{1}s^{n-1}+...+a_{n}}

где s — комплексный аргумент.

Из коэффициентов характеристического уравнения строится определитель Гурвица Delta по алгоритму:

  1. по главной диагонали слева направо выставляются все коэффициенты характеристического уравнения от {displaystyle a_{1}} до {displaystyle a_{n}};
  2. от каждого элемента диагонали вверх и вниз достраиваются столбцы определителя так, чтобы индексы убывали сверху вниз;
  3. на место коэффициентов с индексами меньше нуля или больше n ставятся нули.

Размерность матрицы Гурвица определяется максимальной степенью при s в характеристическом уравнении (то есть n).

Или явно[1]

{displaystyle Delta ={begin{vmatrix}a_{1}&a_{3}&a_{5}&ldots &0\a_{0}&a_{2}&a_{4}&ldots &0\0&a_{1}&a_{3}&ldots &0\0&a_{0}&a_{2}&ldots &0\vdots &vdots &vdots &ddots &vdots \ldots &ldots &ldots &ldots &a_{n}end{vmatrix}}}

Тогда согласно критерию Гурвица:

Для того, чтобы динамическая система была устойчива, необходимо и достаточно, чтобы все n главных диагональных миноров определителя Гурвица были положительны, при условии {displaystyle a_{0}>0}. Эти миноры называются определителями Гурвица.

(Пример определителя Гурвица для характеристического уравнения пятой степени.)

Анализируя условие критерия Гурвица, можно заметить его избыточность. Число неравенств можно уменьшить в два раза, используя теорему Льенара — Шипара. Впрочем, в вычислительном отношении сложность критерия уменьшается не существенно, так как при вычислении минора высокого порядка чаще всего необходимо вычисление миноров низших порядков.

Достоинства и недостатки[править | править код]

Недостаток критерия Гурвица — малая наглядность. Достоинство — удобен для реализации на ЭВМ. Его часто используют для определения влияния одного из параметров САУ на ее устойчивость. Так равенство нулю главного определителя {displaystyle Delta _{n}=Delta _{n-1}=0} говорит о том, что система находится на границе устойчивости. При этом либо {displaystyle Delta _{n}=0} — при выполнении остальных условий система находится на границе апериодической устойчивости, либо предпоследний минор {displaystyle Delta _{n-1}=0} — при положительности всех остальных миноров система находится на границе колебательной устойчивости. Параметры САУ определяют значения коэффициентов уравнения динамики, следовательно изменение любого параметра K_{i} влияет на значение определителя {displaystyle Delta _{n-1}}. Исследуя это влияние можно найти, при каком значении K_{i} определитель {displaystyle Delta _{n-1}} станет равен нулю, а потом — отрицательным. Это и будет предельное значение исследуемого параметра, после которого система становится неустойчивой.

К вопросу об автоматизации метода[править | править код]

Метод Гурвица достаточно удобен для определения устойчивости звеньев при помощи ЭВМ. При этом, однако, следует учитывать, что применение критерия для систем с порядком выше 5 может привести к значительным ошибкам, поскольку вычисление определителей высоких порядков является достаточно сложной операцией и приводит к накоплению ошибок вычислений.

Ниже приведён пример автоматизации работы метода с использованием одного из самых распространённых языков для технических вычислений MATLAB версии 5.3 с его синтаксисом.

Представленная ниже функция выполняет все необходимые вычисления. Для работы её необходимо поместить в текстовый файл с расширением .m и именем, совпадающим с именем самой функции, в данном случае имя файла должно быть raus_gur.m. 

function [Ust, Mnrs, Mtrx] = raus_gur(D)
% Определение устойчивости системы методом Рауса-Гурвица, заданной при
% помощи следующей передаточной функции.
% 
%          B(s)   
%   W(s) = ----,
%          D(s)     
% 
% Здесь D(s) - характеристический полином.
% 
% D(s) = a0*s^n + a1*s^(n-1) + a2*s^(n-2) + ... + an 
%  
%   a0, a1, a2, ..., an - коэффициенты полинома D.
% 
% 
% Обращение к функции RAUS_GUR может быть выполнено двумя способами:
% 
%   Способ 1.
% 
%   [Ust, Mnrs, Mtrx]  = raus_gur(D);
% 
%   Входные параметры:
% D - вектор коэффициентов знаменателя (характеристический полином)
% 
%   Выходные параметры:
% Ust - строковое значение, сообщающее устойчива система или неустойчива
%  
% Mnrs - вектор значений миноров от меньшего размера к большему,
% которые необходимо вычислить для оценки устойчивости по методу Рауса-Гурвица.
% Согласно методу Рауса-Гурвица, система устойчива, если все миноры положительны.
% Вычисления значения внешнего минора не имеют смысла, так как его знак
% всегда будет совпадать со знаком предыдущего минора.
% 
% Mtrx - полная матрица Рауса-Гурвица для данного полинома.
% 
%   Способ 2.
% 
%   [Ust, Mnrs, Mtrx]  = raus_gur(W);
% 
%   Входные параметры:
% W - объект класса LTI (см. описание Control System Toolbox)  
% 
% Выходные параметры аналогичны вышеописанным.
% 
% 
% Ориентирована на работу в версии MATLAB 2022a

if isa(D,'tf')
   [~,D]=tfdata(D,'v');
end
n=length(D)-2;
Dr=[D zeros(1,n)];
A=flipud(reshape(Dr,2,[]));
Mtrx=cell2mat(arrayfun(@(x)(circshift(A',x))',(0:n/2)',"UniformOutput",false));
Mnrs=cell2mat(arrayfun(@(x)det(Mtrx(1:x,1:x)),(2:n)',"UniformOutput",false));
Z='';
if any(Mnrs<0)
    Z='не ';
end
Ust=['система ',Z,'устойчива'];
end

Пример[править | править код]

Пусть дана передаточная функция:

{displaystyle operatorname {W} (s)={frac {Y(s)}{U(s)}}={frac {5cdot s+4}{{{s}^{5}}+16cdot {{s}^{4}}+95cdot {{s}^{3}}+260cdot {{s}^{2}}+324cdot s+144}}}

Тогда вызов приведенной выше функции будет выглядеть следующим образом:

format shortG

[A, B, C] = raus_gur([1 16 95 260 324 144])
А результат вычислений:
A =

    ‘система устойчива’

B =

   1260

   2.4696e+05

   6.3504e+07

C =

    16   260   144     0     0

     1    95   324     0     0

     0    16   260   144     0

     0     1    95   324     0

     0     0    16   260   144

     0     0     1    95   324

A сообщает, что система устойчива.

Вектор В содержит значения диагональных определителей от 2×2 до 4×4, первый элемент не имеет значения, а значение внешнего определителя всегда будет иметь тот же знак, что и предыдущий. Согласно методу Гурвица, чтобы система была устойчива, все эти определители должны оказаться положительными.

Матрица С — сам определитель Гурвица.

Эту функцию вполне можно использовать в математических пакетах, имеющих схожий с MATLAB синтаксис или после небольшой переделки.

Система находится на границе апериодической устойчивости, если {displaystyle a_{n}=0}.
Система находится на границе колебательной устойчивости, если определитель Гурвица с индексом (n-1) будет равным 0.

См. также[править | править код]

  • Критерий устойчивости Рауса
  • Критерий устойчивости Найквиста — Михайлова
  • Теорема Рауса — Гурвица
  • Маркеры устойчивости линейных динамических систем

Примечания[править | править код]

  1. ↑ Гантмахер Ф. Р. Теория матриц. — 5-е изд. — М.: Физматлит, 2010. — С. 463. — 560 с. — ISBN 978-5-9221-0524-8.

Литература[править | править код]

Четаев Н. Г. Устойчивость движения. — М: Наука, 1965. — 234 с.

Ссылки[править | править код]

Источник

Определение устойчивости по критерию Гурвица

Для
устойчивости системы необходимо и
достаточно, чтобы все миноры определителя
Гурвица были положительны.
По
коэффициентам характеристического
уравнения составляется определитель
Гурвица.

Для
этого по главной диагонали делителя
выписываются все коэффициенты
характеристического уравнения, начиная
со второго (т.е. а1,
а2,
а3,
… ,аn
), затем вверх записываются коэффициенты
с возрастающим индексом, а вниз – с
убывающим индексом.

Например,
для третьего коэффициента в главной
диагонали а3
вверх
записываются а4,
а5
(индекс возрастает), а вниз – а2,
а1,
а0.
На остальные оставшиеся места вписываются
нули.

Д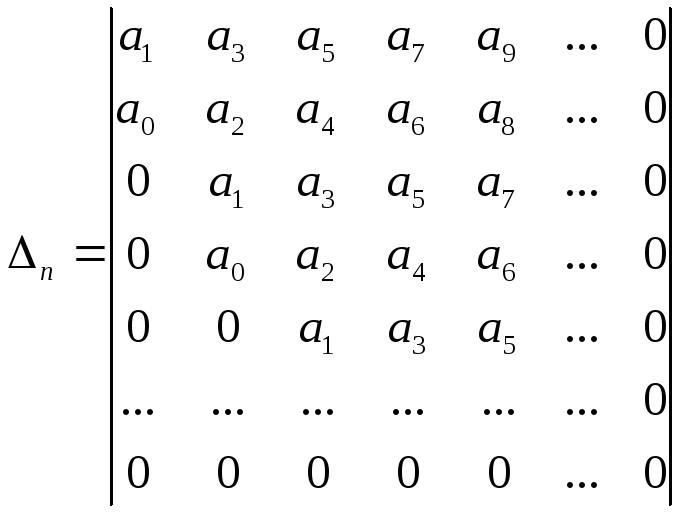ля
проверки правильности заполнения
определителя Гурвица необхо­димо
учесть, что по строкам чередуются
коэффициенты с нечётными и чёт­ными
индексами. Так первая строка – нечётные
а1
а3
а5
а7…,
вторая строка – четные а0а2
а4
а6
и т.д.

Покажем
вычисление миноров в определителе
Гурвица для системы 6-го порядка.

Последний
определитель обычно не рассчитывается.
В данном случае
.
Если выполняется первое необходимое
условие устойчивости (все а>0), то при>0всегда
положителен.

Пусть
необходимо определить устойчивость
системы пятого порядка. Тогда а6=0
>0

неравенства принимают вид:

Если
необходимо определить устойчивость
системы четвертого порядка, то
неравенства принимают вид:

Для
устойчивости системы третьего порядка
достаточно

.

Для
систем седьмого порядка определение
устойчивости по Гурвицу обычно не делают
из-за громоздкости расчетов.

ПРИМЕР
1. Определить устойчивость САУ по критерию
Гурвица по следующему характеристическому
уравнению:

.

Решение.
1. Все коэффициенты характеристического
уравнения положительные. Значит
необходимое условие устойчивости
выполняется.

2.
Составляется определитель Гурвица

Определяют
значения миноров согласно неравенствам:

Ответ.
Все миноры определителя Гурвица
положительны, значит вещественная часть
корней характеристического уравнения
отрицательна и, согласно теореме
Ляпунова, САУ устойчива.

Критерий устойчивости Рауса

Для
устойчивости систем необходимо и
достаточно, чтобы все коэффициенты
первого столбца таблицы Рауса были
положительны.

Таблица
Рауса составляется по правилам:

а)
в первой строке таблицы Рауса записываются
соответственно коэффициенты а0,а2,а4
….;

б)
во второй строке таблицы Рауса записываются
соответственно коэффициенты а1,а3,а5
….;

в)
коэффициенты третьей строки таблицы
Рауса вычисляются по формулам:

г)
коэффициенты четвертой строки таблицы
Рауса определяются по формулам:

д)
коэффициенты n-й
строки таблицы Рауса вычисляются по
формулам

где
i
– номер столбца; j
– номер строки.

ПРИМЕР
2. Определить устойчивость САУ по критерию
Рауса по характеристическому уравнению
примера 1.

Решение.
1. Вычисляют третью строку таблицы Рауса:

2.
Определяют четвертую строку:

3.
Вычисляют пятую строку:

4.
Определяют шестую строку:

По
результатам расчета составляют таблицу
Рауса.

Таблица
1

Таблица
Рауса

№ строки

R

1
столбец

2
столбец

3
столбец

1

2

3

4

5

6

Ответ:
коэффициенты первого столбца положительны.
Система устойчивая.

Источник

Критерии устойчивости Рауса–Гурвица и Михайлова
(геометрический критерий устойчивости)

Пусть имеем линейное дифференциальное уравнение с постоянными вещественными коэффициентами:

a_0y^{(n)}+a_1y^{(n-1)}+ldots+a_ny=0quad (a_0,a_1,ldots,a_n=text{const},~a_0&gt;0).

(1)

Нулевое решение yequiv0 уравнения (1) асимптотически устойчиво, если все корни характеристического уравнения

f(lambda)equiv a_0lambda^n+a_1lambda^{n-1}+ldots+a_n=0

(2)

имеют отрицательные вещественные части.

Критерий Рауса—Гурвица. Для того чтобы все корни уравнения (2) имели отрицательные вещественные части, необходимо и достаточно, чтобы были положительными все главные диагональные миноры матрицы Гурвица

begin{pmatrix}a_1&a_0&0&0&0&0&{}&0\ a_3&a_2&a_1&a_0&0&0&{}&0\ a_5&a_4&a_3&a_2&a_1&a_0&cdots&0\ cdots&cdots &cdots &cdots &cdots &cdots &cdots&cdots\ 0&0&0&0&0&0&{}&a_n end{pmatrix}!.

(3)

Матрица Гурвица составляется так. По главной диагонали выписываются коэффициенты многочлена (2), начиная с a_1 и оканчивая a_n. Столбцы состоят поочередно из коэффициентов только с нечетными или только с четными индексами, причем в число последних включается коэффициент a_0. Все остальные элементы матрицы, отвечающие коэффициентам с индексами, большими n или меньшими 0, полагаются равными нулю. Главные диагональные миноры матрицы Гурвица имеют вид

Delta_1=a_1,quad Delta_2=begin{vmatrix}a_1&a_0\a_3&a_2end{vmatrix},quad Delta_3=begin{vmatrix}a_1&a_0&0\a_3&a_2&a_1\a_5&a_4&a_3end{vmatrix},quad ldots,quad Delta_n=begin{vmatrix}a_1&a_0&0&{}&0\a_3&a_2&a_1&{}&0\a_5&a_4&a_3&{}&0\ cdots&cdots&cdots&cdots&cdots\ 0&0&0&{}&a_nend{vmatrix}.

Таким образом, условие Гурвица гласит: для устойчивости решения yequiv0 уравнения (1) необходимо и достаточно, чтобы выполнялись соотношения

Delta_1&gt;0,quad Delta_2&gt;0,quad ldots,quad Delta_n&gt;0.

(4)

Так как Delta_n=a_nDelta_{n-1}, то условие Delta_n&gt;0 может быть заменено требованием a_n&gt;0.

Пример 1. Исследовать на устойчивость нулевое решение уравнения

y''''+5y'''+13y''+19y'+10y=0.

(11)

Решение. Составляем характеристическое уравнение

f(lambda)equiv lambda^4+5lambda^3+13lambda^2+19lambda+10=0

Здесь a_0=1,~a_1=5,~a_2=13,~a_3=19,~a_4=10. Выписываем диагональные миноры Гурвица

Delta_1=5&gt;0,~ Delta_2=begin{vmatrix}5&1\19&13end{vmatrix}=46&gt;0,~ Delta_3=begin{vmatrix}5&1&0\19&13&5\0&10&19end{vmatrix}=424&gt;0,~ Delta_4=begin{vmatrix}5&1&0&0\19&13&5&1\0&10&19&13\0&0&0&10end{vmatrix}=4240&gt;0,

Итак, Delta_1&gt;0,~Delta_2&gt;0,~Delta_3&gt;0,~Delta_4&gt;0. Следовательно, тривиальное решение yequiv0 уравнения (5) асимптотически устойчиво.

Вычисление можно, например, организовать так. Составляем сначала старший минор Гурвица Delta_n. По нему легко выписываются все младшие миноры Delta_{n-1},ldots,Delta_1. Затем начинаем вычислять последовательно Delta_1,,Delta_2 и т.д. Если встретился отрицательный минор, решение неустойчиво и дальнейший подсчет не нужен.

Геометрический критерий устойчивости (критерий Михайлова)

Рассмотрим линейное дифференциальное уравнение n-го порядка с постоянными вещественными коэффициентами

a_0y^{(n)}+a_1y^{(n-1)}+ldots+a_ny=0.

(1)

Его характеристическое уравнение

f(lambda)equiv a_0lambda^{n}+a_1lambda^{n-1}+ldots+a_n=0.

(2)

Критерий Михайлова позволяет решить вопрос о расположении корней характеристического уравнения (2) на комплексной плоскости и, следовательно, решить вопрос об устойчивости нулевого решения уравнения (1). Полагая lambda=iomega, получаем

f(iomega)= u(omega)+iv(omega),

где

u(omega)=a_n-a_{n-2}omega^2+a_{n-4}omega^4-ldots,quad v(omega)=a_{n-1}omega-a_{n-3}omega^3+ldots

Геометрический критерий устойчивости Михайлова

Величину f(iomega) при заданном значении параметра omega можно изобразить в виде вектора на комплексной плоскости Ouv с началом в начале координат.

При изменении omega в интервале (-infty,+infty) конец этого вектора опишет некоторую кривую — так называемую кривую Михайлова (рис. 45). Так как функция u(omega) четная, то кривая Михайлова симметрична относительно оси Ou и поэтому достаточно строить часть кривой, отвечающую изменению параметра omega от 0 до +infty.

Если многочлен f(lambda) степени n имеет m корней с положительной вещественной частью и n-m корней с отрицательной, то угол varphi поворота вектора f(iomega) при изменении omega от 0 до +infty равен varphi=(n-2m)frac{pi}{2}.

Ясно, что для устойчивости решения уравнения (1) необходимо и достаточно, чтобы m=0.

Критерий Михайлова. Для устойчивости нулевого yequiv0 решения уравнения (1) необходимо и достаточно, чтобы

1) вектор f(iomega) при изменении omega от 0 до +infty совершил поворот на угол varphi=nfrac{pi}{2}, т.е. сделал frac{n}{4} оборотов против часовой стрелки;

2) годограф f(iomega) при изменении omega от 0 до +infty не проходил через начало (0;0).

Отсюда следует, что для устойчивости решения уравнения (1) необходимо, чтобы все корни уравнений u(omega)=0, v(omega)=0 были вещественными и перемежающимися друг с другом, т.е. между любыми двумя корнями одного уравнения должен находиться корень другого уравнения.

Пример 1. Исследовать на устойчивость нулевое решение yequiv0 уравнения

y^{mathsf{IV}}+y'''+4y''+y'+y=0.

Решение. Составляем характеристический многочлен

f(lambda)=lambda^4+lambda^3+4lambda^2+lambda+1.

Далее,

f(iomega)=omega^4-iomega^3-4omega^2+iomega+1,quad u(omega)=omega^4-4omega^2+1,quad v(omega)=-omega^3+omega=omega(1-omega)(1+omega).

Построим кривую (рис.46) begin{cases}u=u(omega),\ v=v(omega),end{cases}0leqslantomega&lt;+infty.

begin{array}{|c|c|c|c|c|}hline omega&0&sqrt{2-sqrt{3}}&1&sqrt{2+sqrt{3}}\ hline u&1&0&-2&0\ hline v&0&+&0&-\ hlineend{array}quad lim_{omegato+infty}frac{v}{u}=0.

Угол поворота радиуса-вектора varphi=4{cdot}frac{pi}{2}=(n-2m)frac{pi}{2}. Отсюда n-2m=4 и так как n=4, то m=0, т.е. все корни характеристического уравнения лежат в левой полуплоскости. Значит, тривиальное решение yequiv0 асимптотически устойчиво.

График кривой, заданной параметрически

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник
Автор статьи

Демьян Бондарь

Эксперт по предмету «Автоматизация технологических процессов»

преподавательский стаж — 5 лет

Задать вопрос автору статьи

Формулировка, преимущества и недостатки критерия Гурвица

Определение 1

Критерий Гурвица – это способ анализа стационарной динамической системы на устойчивость, который был разработан немецким ученым Адольфом Гурвицем.

Наряду с критерием Рауса, критерий Гурвица представляет семейство алгебраических критериев устойчивости системы. Его главное достоинство – принципиальная простота, а главный недостаток заключается в том, что существует необходимость выполнения операции вычисления определителя, связанной с многочисленными вычислительными тонкостями. Данный метод определения устойчивости связан с коэффициентами характеристического уравнения. Предположим, что:

$W(s) = Y(s)/U(s) $- передаточная функция.

Логотип baranka

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

U(s) – характеристическое уравнение рассматриваемой системы.

Теперь представим характеристический полином U(s) в следующем виде:

Рисунок 1.

где, s – комплексный аргумент.

Затем строится определитель Гурвица из коэффициентов характеристического уравнения системы по следующему алгоритму:

  1. По правой диагонали слева направо выставляются все коэффициенты характеристического уравнения системы.
  2. От каждого элемента диагонали вверх и вниз достраиваются столбцы определителя таким образом, чтобы индексы убывали сверху вниз.
  3. На место коэффициентов, у которых индекс меньше нуля или больше n, ставятся нули.

Размерность таблицы Гурвица определяется максимальной степенью s в характеристическом уравнении.

Рисунок 2.

« Устойчивость систем: критерий Гурвица» 👇

Тогда, в соответствии с критерием Гурвица для того, чтобы динамическая система была устойчива, необходимо, чтобы все n главных диагональных миноров определителя Гурвица были положительными, при условии, что a0 > 0. Если проанализировать условия критерия Гурвица, то заметна его избыточность. Количество неравенств может быть уменьшено в два раза, для чего используется теорема Льенара-Шипара.

Еще один недостаток критерия Гурвица – его малая наглядность. А достоинство заключается в том, что он удобен для реализации на электронно-вычислительной машине. Он часто используется для определения влияния одного из параметров системы автоматического управления на уровень ее устойчивости. Например, равенство главного определителя нулю говорит о том, что система находится на границе устойчивости. Параметры автоматической системы управления определяют значения коэффициентов динамического уравнения, таким образом изменение любого параметра системы влияет на значение определителя.

Решение задачи при помощи критерия Гурвица

Допустим задана автоматическая система управления, структурная схема которой изображена на рисунке ниже.

Схема автоматической системы управления. Автор24 — интернет-биржа студенческих работ

Рисунок 3. Схема автоматической системы управления. Автор24 — интернет-биржа студенческих работ

Сначала необходимо получить для нее передаточные функции и определить соотношение параметров, которые обеспечивают ее устойчивость. По задающему воздействию передаточная функция разомкнутой системы будет иметь следующий вид:

Рисунок 4.

По возмущающему воздействию передаточная функция разомкнутой системы будет выглядеть следующим образом:

Рисунок 5.

Передаточная функция разомкнутой цепи выглядит следующим образом:

Рисунок 6.

Допустим:

$К = К1К2Кос$ – коэффициент передачи разомкнутой цепи.

Тогда:

Рисунок 7.

По задающему воздействию передаточная функция замкнутой системы выглядит следующим образом:

Рисунок 8.

По возмущающему воздействию передаточная функция замкнутой системы имеет следующий вид:

Рисунок 9.

Характеристический полином автоматической системы управления, то есть знаменатель любой из передаточных функций замкнутой системы, выглядит следующим образом:

Рисунок 10.

Где:

  • $а0=1+Кр$
  • $а1 = Т1+Т2+Тос$
  • $а2 = Т1(Т2+Тос)+Т2Тос$
  • $а3 = Т1Т2Тос$

Видно, что характеристический полином замкнутой системы автоматического управления равняется сумме числителя и знаменателя передаточной функции разомкнутой цепи. Так как все коэффициенты характеристического полинома больше нуля, то в соответствии с условием устойчивости все сводится к следующему неравенству:

Рисунок 11.

Полученное неравенство показывает, что устойчивость системы автоматического управления в конце нарушится в случае неограниченного увеличения коэффициента передачи при любых положительных значениях постоянных времени. Предельная величина значения коэффициента передачи, при котором автоматическая система управления теряет устойчивость называется граничным, а для рассматриваемого примера рассчитывается следующим образом:

Рисунок 12.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Добавить комментарий