Понятие
ориентированного графа лежит в основе
решения многих прикладных задач, имеющих
непосредственное отношение к задачам
логистики. Одной из таких задач является
построение минимального остовного
дерева сети. При
изучении сетей возникает названная
задача, т. е. задача соединения всех
узлов сети с помощью путей наименьшей
длины. Примером такой задачи является
проектирование сети дорог между
населенными
пунктами, где дороги, соединяющие два
пункта, могут проходить через
другие населенные пункты. Наиболее
экономичный проект должен минимизировать
общую длину дорог.
Ребро
графа G(X,
Т) называется ориентированным,
или дугой,
если одну вершину считают началом, а
другую концом этого ребра
На
рисунке дугу обозначают стрелкой. Дугу
с началом в вершине xi
и концом в вершине xj
записывают
(xi,
xj).
Определение2.7.
Граф, все ребра которого ориентированы,
называется
ориентированным
графом.
Число дуг, исходящих
из вершины ориентированного графа xi,
называется полустепенью
исхода
вершины xi,
число дуг, входящих в вершину xi,
− полустепенью
захода
вершины xi.
Вершина
xi
называется источником,
если ее полустепень захода равна нулю,
и стоком,
если ее полустепень исхода равна нулю.
Рассмотрим
ориентированный граф на рисунке 2.25.
Полустепень исхода вершины х1
равна 1, полустепень захода этой вершины
– 2, степень вершины х1
равна
3. Вершина х3
является
источником, вершина х2
–
стоком.
|
|
|
|
Рис. 2.25 |
Рис. 2.26 |
Определение
2.8.
Последовательность дуг (x1,
x2),
(x2,
x3),
…, (xk-1,
xk),
в
которой
конец предыдущей дуги совпадает с
началом следующей, называется
маршрутом
от
x1
до
xk
.
Маршрут,
в котором первая и последняя вершины
совпадают, называется замкнутым.
Пример
2.6.
Рассмотрим ориентированный граф (рис.
2.26). Он имеет множество
маршрутов, например: (х1,
х2),
(х2,
х6),
(х6,
х7),
(х7,
х3),
(x3,
х2),
(х2,
x6),
(х6,
х5),
(х5,
х1).
Этот
маршрут является замкнутым.
Маршрут,
в котором все вершины различны, называется
путем
от
x1
до
xk.
Если
существует путь из вершины xi
в
вершину xj,
то
говорят, что xj
достижима
из
xi.
Замкнутый
путь называется контуром.
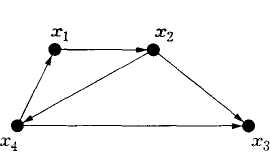
Рассмотрим
ориентированный граф (рис. 2.27). Он имеет
пути (х4,
х1),
(х1,
х2),
(х2,
х3)
и (x1,
х2);
(х2,
х4),
(х4,
х3),
а также один контур (х4,
x1),
(х1,
х2),
(х2,
х4).
Вершина хз
достижима из вершины х1.
Полным
ориентированным графом называется
граф G(X,
Т),
в котором каждая
пара вершин соединена в точности одной
дугой.
Ориентированный
граф, изображенный на рис.2.28, является
полным.
|
|
|
|
Рис. 2.27 |
Рис. 2.28 |
Ориентированный
граф G(X.T)
можно задать
с помощью матрицы инцидентности.
Пусть x1,
x2,
…, хn
— вершины
графа, 11,
12,
…, lm
— дуги графа.
Определение
2.9. Матрицей
инцидентности ориентированного графа
G(X,
T)
называется
матрица Вn
х m,
у которой
элемент bij
равен 1, если
дуга lj
исходит из
вершины xi,
равен (−1), если
дуга lj
входит в
вершину xi;
равен 0, если дуга lj
и вершина xi
не инцидентны.
Пример 2.7.
Для ориентированного графа, изображенного
на рис. 2.29,
матрица
инцидентности имеет следующий вид:
|
1 -1 0 0
4 |
x1
|
|
Рис. 2.29 |
Построение
минимального остовного дерева сети. В
экономических приложениях графы принято
называть сетями, а их вершины
— узлами. Каждому ребру (дуге) придают
некоторое числовое значение, которое
в зависимости от смысла задачи может
обозначать расстояние, пропускную
способность, время и т. д. С каждым видом
сети связан определенный тип потоков
например, поток нефти в нефтепроводах,
автомобильные потоки в сети
городских дорог).
Определение
2.10.
Остовным
деревом сети
называется дерево, содержащее
все узлы сети.
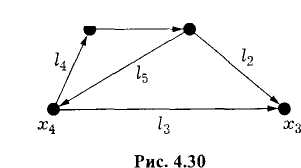
Пример
2.8.
Рассмотрим сеть с пятью узлами (рис.
2.30, а). Для этой сети
можно построить множество остовных
деревьев. Некоторые примеры таких
остовных деревьев
изображены на рис. 2.30, б-е.

|
x5
x4 x3 x2 x1
|
x5
x4 x3 x2 x1
|
|
а |
б |
|
x5
x4 x3 x2 x1
|
x5
x4 x3 x2 x1
|
|
в |
г |
|
x5
x4 x3 x2 x1
|
x5
x4 x3 x2 x1
|
|
д |
е |
При
изучении сетей возникает задача
построения минимального остовного
дерева, т. е. задача соединения всех
узлов сети с помощью путей наименьшей
длины. Примером такой задачи является
проектирование сети дорог между
населенными
пунктами, где дороги, соединяющие два
пункта, могут проходить через
другие населенные пункты. Наиболее
экономичный проект должен минимизировать
общую длину дорог.
Рассмотрим
процедуру построения минимального
остовного дерева. Введем
обозначения:
X
= {
х1,
х2
, …, хn}
—
множество узлов сети;
Ck
—
связное множество узлов сети, соединенных
алгоритмом после выполнения
k-ой
итерации;
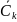
— множество
узлов сети, не соединенное с узлами
множества Ck
после
выполнения
k-ой
итерации;
Минимальное
остовное дерево строят по следующему
алгоритму:
-
выбирают
произвольный узел сети хi:
С1
=
хi
,
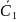
=
X
{х}; -
выбирают
из оставшихся узлов узел Xj,
ближайший
к множеству узловС1:
С2
= Xi,.xj,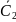
= X
{xi,
Xj}; -
выбирают
из множестваузел, ближайший к узлам множества
С2,включают
его в множество С2
и исключают из множества.
За
конечное число шагов будут обработаны
все узлы сети и построено минимальное
остовное дерево: Сn
=
X,
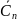
=
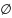
.
|
|
|
|
а |
3
3 б |
|
3
3
5
6
|
8
6 3
|
|
3
3 в |
г |
|
|
|
|
д |
е |
|
|
|
|
ж |
|
|
Рис. 2.31 |
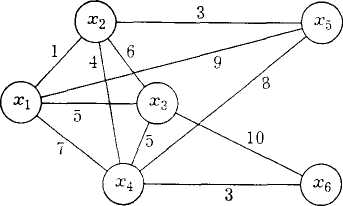
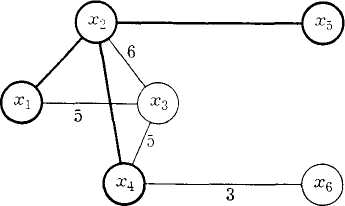
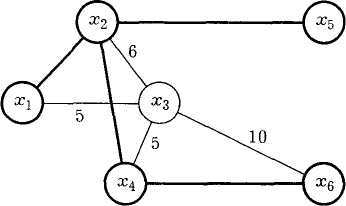
Пример
2.9. Телевизионная
компания планирует подключение к
кабельной сети
пяти новых районов. Структура планируемой
сети и расстояния между пунктами
(в км) заданы на рис. 2.31, а.
Требуется
спланировать кабельную сеть наименьшей
длиной.
Проведем
пошаговое построение минимального
остовного дерева для данной
сети. Со =
,
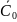
= {
х1,
х2,
х3,
х4,
х5,
х6}.
Начнем
с узла x1.
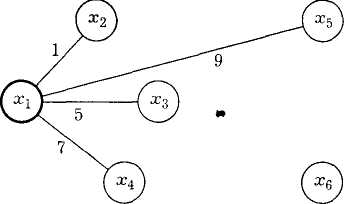
Итерация
1 (рис.
2.31, б):
С1
= {х1}.
= {х2,
х3,
х4,
х5,
х6},
min(1,5,7,9)
= 1.
ближайший
узел к множеству С1
—
узел х2.
Добавляем его к остовному дереву с
ребром длиной 1 км.
Итерация
2 (рис.
2.31, в):
С2
= {х1
, х2}.
= {х3,
х4,
х5,
х6}.
min(3,4,5,6,7,9)
= 3.
ближайший
узел к множеству С2
— узел х5.
Добавляем его к остовному дереву с
ребром длиной 3 км.
Итерация
3 (рис.
2.31, г):
С3
= {х1,
х2,
х5}.

= {х3,
х4,
х6}.
min(4,5,6,7,8)
= 4.
ближайший
узел к множеству Сз — узел х4.
Добавляем
его к остовному дереву с ребром длиной
4 км.
Итерация
4 (рис.
2.31, д):
С4
= {x1,
х2,
х4,
х5},
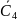
= {х3,
х6},
min(3,5,6)
= 3.
ближайший
узел к множеству С4
— узел х6.
Добавляем
его к остовному дереву с ребром длиной
3 км.
Итерация
5 (рис.
2.31, е):
С5
= {x1,
х2,
х4,
х5,
х6},

= {х3},
min(5,6,10)
= 5.
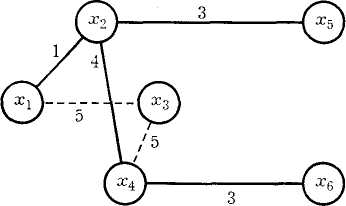
Ближайший
узел к множеству С5
— узел х3.
Добавляем
его к остовному дереву с ребром длиной
5 км. При этом возможно два альтернативных
соединения (х1,
х3)
и (х4,
х3)
длиной
5 км. Процесс построения минимального
остовного дерева завершен (рис. 32, ж).
Итак,
С6
= X
=
{
x1,
х2,
х3,
х4,
х5,
х6},
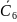
=
.
Минимальная
длина телевизионного кабеля составит
1 + 3 + 4 + 3 + 5 = 16 км.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Ориентированный граф — один из видов графа, структуры, состоящей из вершин и путей между ними. Используется в математике и программировании. Проще всего представить граф в виде карты с городами: вершины — это города, а пути — дороги между ними. В ориентированном графе все дороги односторонние.
Что такое графы и какими они бывают
Графы — это абстракция для представления отношений между сущностями. С ее помощью можно описать дорожную карту, сеть из нескольких модулей, программу и пр. Сам граф описывается как точки и соединяющие их отрезки либо с помощью математических формул.
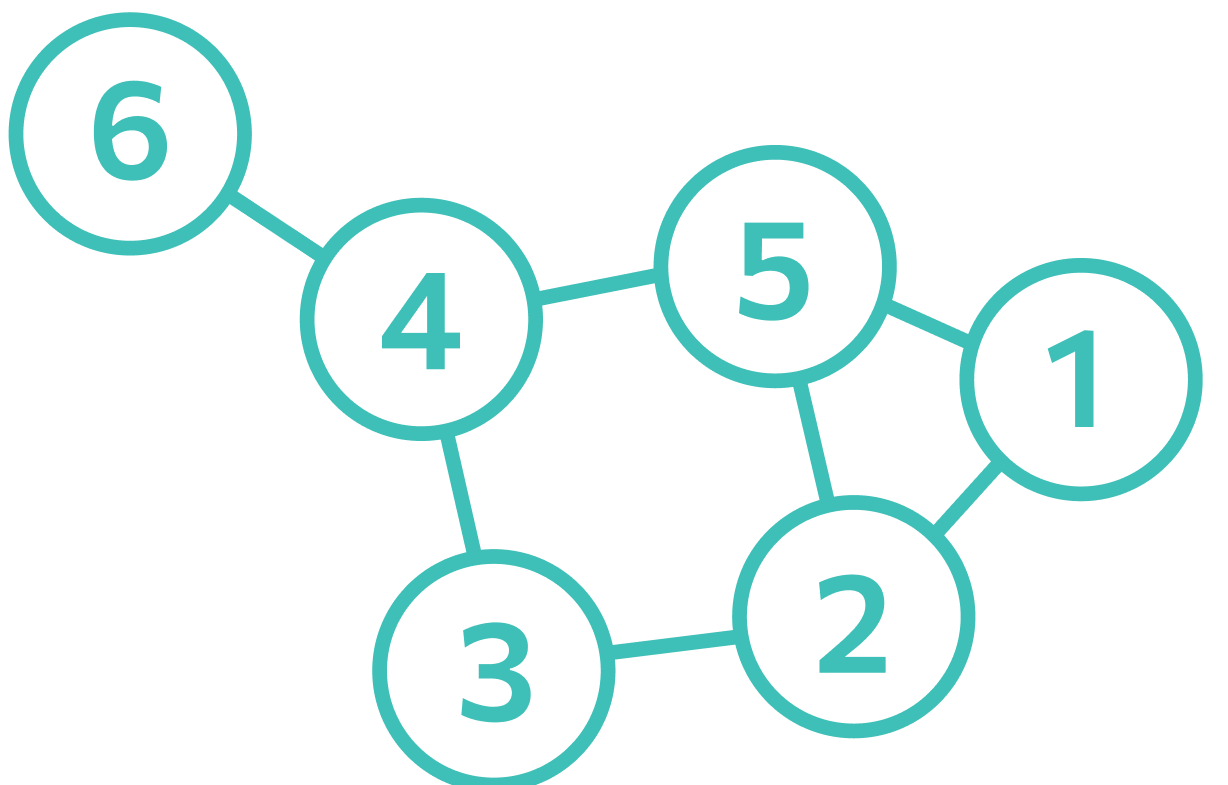
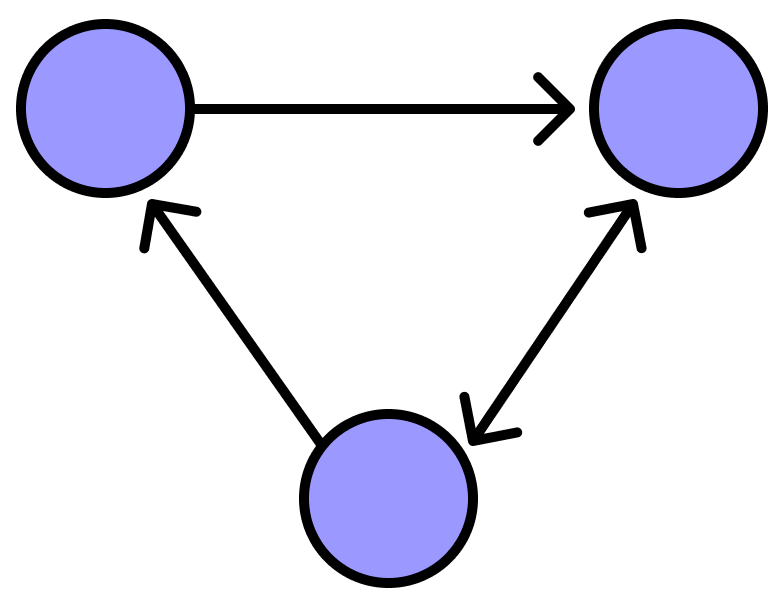
Отрезки между вершинами могут быть неориентированными, а могут иметь направление. Если ребро имеет направление, его изображают не отрезком, а стрелкой между двумя точками. Ориентированным называют такой граф, у которого все пути направленные.
Фактически направление означает, в каком порядке можно обходить структуру. По неориентированным путям можно проходить в любую сторону — от вершины A к вершине B и наоборот. А если путь ориентированный, по нему можно идти только в направлении стрелки.
В ориентированном графе по всем отрезкам можно проходить только в одну сторону. Если она из линий выглядит как двойная стрелка, она считается двумя «дорогами», направленными в разные стороны.
Для чего нужны ориентированные графы
На основе графов создают модели тех или иных процессов, событий, взаимоотношений или объектов.
Графы как концепция используются в точных, естественных и гуманитарных науках: от физики и химии до экономики или социологии. С их помощью описывают разнообразные процессы, связи, структуры. Это может быть и схема работы алгоритма, и визуализация социальных взаимоотношений — практически любая структура, которую можно представить как набор элементов и связей между ними.
Поэтому привести полный список примеров использования графов невозможно. Ситуации, в которых может понадобиться граф, встречаются даже в таких дисциплинах, как археология или диспетчерское обслуживание полетов.
Они могут использоваться даже в логических и математических задачах, в головоломках.
Кто пользуется ориентированными графами
- Математики и другие ученые, которые описывают с их помощью явления.
- Инженеры, так как электронные сети и другие похожие схемы тоже можно представить как графы.
- Разработчики, которые пользуются графами как структурой данных или модулей. Структуры бывают нужны при разработке искусственного интеллекта и реализации некоторых алгоритмов.
Понятия, связанные с графами
Это основные термины, связанные с графами в целом. Ниже мы поговорим о понятиях, которые касаются непосредственно ориентированных графов.
- Вершина — одна из точек, из которых состоит граф.
- Ребро — отрезок между двумя вершинами, которым они соединяются.
- Путь — способ пройти от одной вершины к другой без повторения ребер.
- Простой путь — путь, где вершины не повторяются.
- Цикл — участок графа, где вершины образуют замкнутую систему. Визуально это выглядит как многоугольник.
- Связный граф — такой, в котором из любой вершины есть путь к другой.
- Дерево — связный граф, где нет циклов. Эту абстракцию часто используют в программировании для хранения данных и при машинном обучении.
- Полный граф — граф, где все вершины соединены друг с другом.
- Петля — ребро, которое ведет из вершины в нее же. У такого ребра совпадают начало и конец.
Термины для ориентированных графов
Если граф ориентированный и все ребра у него имеют «направление прохода», то при его описании нужны дополнительные понятия.
- Степень выхода вершины ориентированного графа — то, сколько путей-стрелок «выходит» из вершины.
- Степень входа — соответственно, количество «входящих» в вершину стрелок.
- Изолированная вершина — такая, у которой степени входа и выхода равны 0.
- Источник — вершина, у которой степень входа равна 0, а степень выхода больше 0.
- Сток — наоборот, вершина, у которой степень выхода равна 0, а степень входа больше 0.
- Ориентированный цикл — цикл, который состоит из направленных ребер. При этом он по-прежнему должен создавать замкнутый путь.
- Полный ориентированный граф — ориентированный граф, у которого каждая пара вершин соединена ровно одним ориентированным ребром. Это почти то же самое, что простой полный граф, только его ребра должны иметь направление.
Как графы представляются в программировании
Визуальное представление графа, в том числе ориентированного, хорошо понятно человеку. Но компьютер не понимает такую структуру, поэтому в программировании графы реализуют иначе. Их кодируют с помощью одного из двух способов: матрицы смежности или списка смежности.
Матрицы смежности. Матрица — это понятие из математики. Оно означает набор связанных между собой чисел, который представляют в виде двумерной таблицы. Матрицы используются во многих математических формулах и в множестве отраслей, в том числе при описании графа.
Матрица смежности — это способ представить граф в виде подобной таблицы. У нее N столбцов и N строк, где N — количество вершин в графе. Столбцы и строки имеют те же названия или номера, что и вершины.
Заполняется матрица так: если из вершины A в вершину B ведет ребро, то на пересечении строки A и столбца B в таблицу ставится единица. Такое повторяется для всех ребер, а оставшиеся ячейки заполняются нулями.
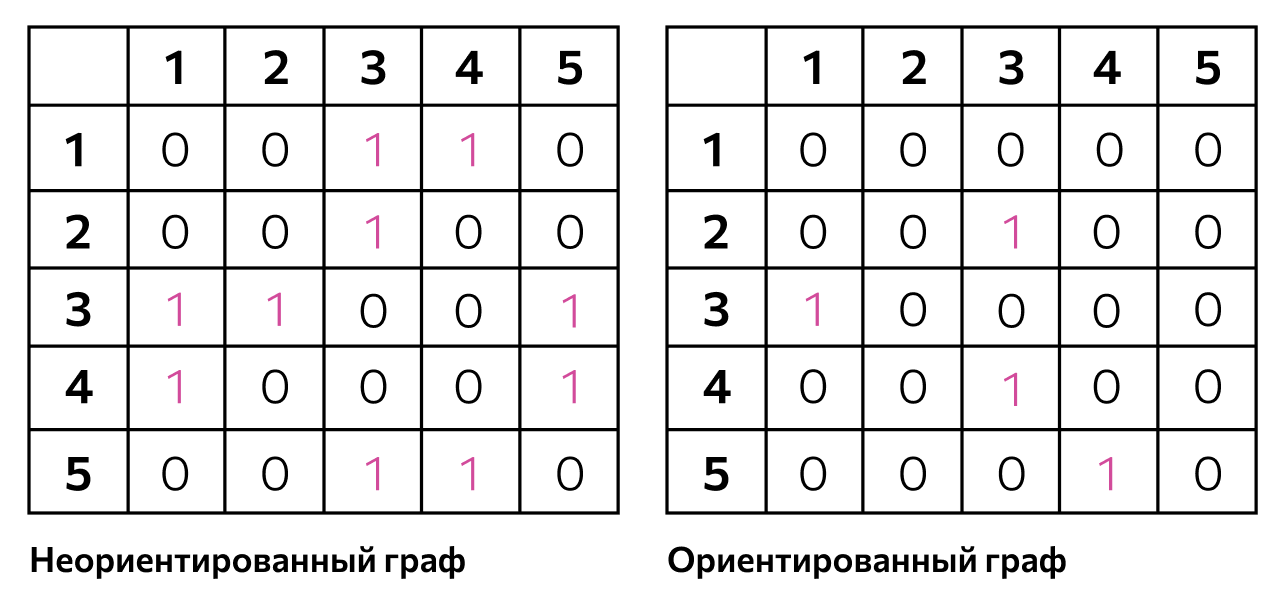
Такой способ описания подходит для ориентированных и неориентированных графов. Это работает, потому что ячейка n[A][B] и ячейка n[B][A] — разные. Благодаря этому можно передать на матрице направления ребер.
Подход используют, если граф плотный: количество ребер примерно равно количеству вершин, возведенному в квадрат. Иначе нулей будет слишком много, и матрица получится громоздкой.
Списки смежности. Это второй способ. Он менее нагляден, но занимает меньше места в памяти. Его используют, если количество ребер намного меньше, чем количество вершин в квадрате, — так называемый разреженный граф. Матрица будет заполненной нулями. Для хранения в памяти компьютера это критично: полезной информации мало, зато структура отнимает много ресурсов. Поэтому при малом количестве ребер используют список.
Список смежности — это N массивов данных, где N — количество вершин. На каждую вершину приходится один массив: в нем содержится имя этой вершины и список ее «соседей». То есть у каждой вершины есть список тех, что соединены с ней ребром.
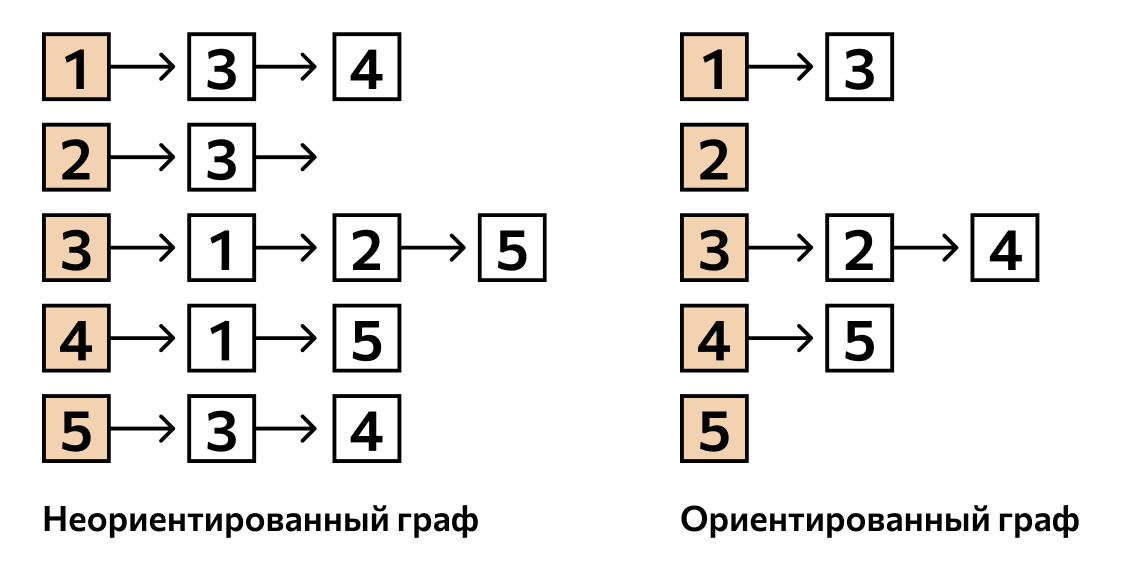
Метод списков смежности опять же подходит и для ориентированных, и для неориентированных графов. Во втором случае списки будут длиннее, потому что соединения придется указывать дважды: A—B — это не только путь из A в B, но и путь из B в A. Поэтому его придется добавить и в массив для A, и в массив для B.
В этом способе представления удобнее узнавать о соседях вершины. Также он занимает меньше памяти, и алгоритмы проходят по нему быстрее. Но он плохо подходит для плотных графов.
Алгоритмы с использованием ориентированных графов
Ориентированные графы используются в десятках алгоритмов в разных сферах IT. Это в первую очередь машинное обучение, анализ данных и другие направления, где используются большие и абстрактные структуры информации. Но встретить графы можно и в других сферах.
Разберем несколько примеров, чтобы вы могли понять, в каких задачах программирования могут применяться ориентированные графы.
Поиск в глубину. Это метод обхода графа, где цель алгоритма — пройти максимально глубоко от первой вершины. Алгоритм подсчитывает расстояние между разными вершинами.
Обход начинается с одной из вершин. Затем алгоритм перемещается в другие вершины по ребрам и помечает каждую из пройденных как посещенную, если ему удается пройти ее без циклов. Для каждой новой вершины шаг повторяется, если она не была посещена раньше. Алгоритм возвращается назад, если в одной из вершин не оказалось ребер, которые вели бы из нее куда-то еще.
Поиск в ширину. Тоже метод обхода графа, частично похожий на предыдущий. Алгоритм обходит вершины, начиная с первой заданной. Но делает он это иначе. Если при поиске в глубину алгоритм последовательно шел «вглубь» графа, то здесь он по очереди переходит к каждому из «соседей» начальной точки. Каждый «сосед» помечается как пройденный. Когда пути из начальной точки закончатся, алгоритм перейдет к обходу «соседей» по такой же методике.
Этот алгоритм помогает, например, найти самый короткий путь передачи данных. Его можно использовать и в других задачах, в том числе при машинном обучении.
Топологическая сортировка. Сортировка — распространенная задача в программировании, для которой существуют десятки известных алгоритмов. Топологическая сортировка на графах — один из них.
Алгоритм нумерует вершины графа так, чтобы из вершины с меньшим номером всегда выходили ребра, ведущие в вершину с большим номером. Такое может понадобиться, например, при упорядочивании сложных структур.
Задача 2-SAT. Это еще одна интересная практическая задача — подстановка значений в формулу таким образом, чтобы она оказалась верной. Формула представляется в виде графа импликаций, где у каждой переменной две вершины — x и !x (не x). Между вершинами проставляются связи в зависимости от условий задачи. Если оказывается, что из x есть путь в !x, а из !x одновременно с этим есть путь в x, то задача решения не имеет.
Алгоритм подходит для решения задач, где неизвестные переменные могут принимать одно из двух противоположных значений. Например, составление расписания спортивных игр: каждая команда должна по разу сыграть с другими командами, может играть дома или на выезде. В реальном мире задач, которые отвечают таким требованиям, намного больше.

Ориентированный граф (кратко орграф) — (мульти) граф, рёбрам которого присвоено направление. Направленные рёбра именуются также дугами, а в некоторых источниках и просто рёбрами. Граф, ни одному ребру которого не присвоено направление, называется неориентированным графом или неорграфом.
Основные понятия[править | править код]
Формально, орграф 



Дуга 




Орграф, полученный из простого графа ориентацией рёбер, называется направленным. В отличие от последнего, в произвольном простом орграфе две вершины могут соединяться двумя разнонаправленными дугами.
Направленный полный граф называется турниром.
Связность[править | править код]
Маршрутом в орграфе называют чередующуюся последовательность вершин и дуг, вида 
Путь есть маршрут в орграфе без повторяющихся дуг, простой путь — без повторяющихся вершин. Если существует путь из одной вершины в другую, то вторая вершина достижима из первой.
Контур есть замкнутый путь.
Для полумаршрута снимается ограничение на направление дуг, аналогично определяются полупуть и полуконтур.
Орграф сильно связный, или просто сильный, если все его вершины взаимно достижимы;
односторонне связный, или просто односторонний, если для любых двух вершин, по крайней мере, одна достижима из другой;
слабо связный, или просто слабый, если при игнорировании направления дуг получается связный (мульти)граф;
Максимальный сильный подграф называется сильной компонентой; односторонняя компонента и слабая компонента определяются аналогично.
Конденсацией орграфа 



Дополнительные определения[править | править код]
Направленный ациклический граф или комок есть бесконтурный орграф.
Ориентированный граф, полученный из заданного сменой направления рёбер на противоположное, называется обратным.
Изображение и свойства всех орграфов с тремя узлами[править | править код]
Легенда: С — слабый, ОС — односторонний, СС — сильный, Н — является направленным графом, Г — является гамаком (ациклический), Т — является турниром
| 0 дуг | 1 дуга | 2 дуги | 3 дуги | 4 дуги | 5 дуг | 6 дуг |
 пустой, Н, Г пустой, Н, Г |
 Н, Г Н, Г |
 |
 ОС ОС |
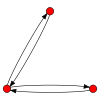 CC CC |
 CC CC |
 полный, CC полный, CC
|
|---|---|---|---|---|---|---|
 ОС, Н, Г ОС, Н, Г |
 CC, Н, Т CC, Н, Т |
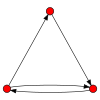 CC CC |
||||
 C, Н, Г C, Н, Г |
 ОС, Н, Г, Т ОС, Н, Г, Т |
 ОС ОС |
||||
 C, Н, Г C, Н, Г |
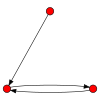 ОС ОС |
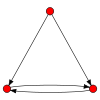 ОС ОС |
Применение орграфов[править | править код]
Орграфы широко применяются в программировании как способ описания систем со сложными связями. К примеру, одна из основных структур, используемых при разработке компиляторов и вообще для представления компьютерных программ — граф потоков данных.
Бинарные отношения[править | править код]

орграф отношения делимости
Бинарное отношение над конечным носителем может быть представлено в виде орграфа. Простым орграфом представимы антирефлексивные отношения, в общем случае требуется орграф с петлями. Если отношение симметрично, то его можно представить неориентированным графом, а если антисимметрично, то направленным графом.
Прочее[править | править код]
Алгоритм Суурбалле — алгоритм нахождения двух непересекающихся (не имеющих общих рёбер) путей в ориентированном графе с неотрицательными весами, так что оба пути связывают ту же самую пару вершин и имеют минимальную общую длину.
Литература[править | править код]
- Харари Ф. Теория графов. — М.: УРСС, 2003. — 300 с. — ISBN 5-354-00301-6.
- Оре, Ойстин. Теория графов. — М.: УРСС, 2008. — 352 с. — ISBN 978-5-397-00044-4.
- Альфред В. Ахо, Моника С. Лам, Рави Сети, Джеффри Д. Ульман. Компиляторы: принципы, технологии и инструменты, 2 издание = Compilers: Principles, Techniques, and Tools. — 2 изд. — М.: «Вильямс», 2008. — ISBN 978-5-8459-1349-4.
Не понимаете теорию графов? Эта статья для вас. Расскажем об основных элементах теории графов и рассмотрим применение теории.

Теория графов представляет собой один из наиболее важных и интересных, но в то же время один из самых сложных и непонятных разделов в информатике.
Понимание и использование графов делает нас более квалифицированными специалистами. По крайней мере, так должно быть. Граф – это множество вершин V и множество рёбер E, содержащих упорядоченную пару G=(V, E).
Пытаясь изучать теорию графов и реализовать некоторые алгоритмы, многие программисты просто прекращают этим заниматься, потому что считают данное занятие слишком скучным.
Лучший способ освоить что-то – понять, как и где оно применяется. В этой статье мы покажем различные примеры применения теории графов, проиллюстрировав каждый из них.
Пусть эта статья покажется слишком детальной для опытных программистов, но, поверьте, подробные объяснения гораздо эффективнее сжатых определений.
Содержание:
- Семь мостов Кёнигсберга
- Представление графов: введение
- Представление графов и бинарных деревьев (пример Airbnb)
- Представление графов: заключение
- Пример Twitter: проблема доставки твитов
- Алгоритмы на графах: введение
- Обход графа: DFS и BFS
- Uber и задача кратчайшего пути (алгоритм Дейкстры)
Семь мостов Кёнигсберга
Начнём с того, с чем чаще всего сталкивается программист, читающий книгу про теорию графов – история про мосты и островы Калининграда. В Калининграде было семь мостов, соединяющих два больших острова, окруженных рекой Преголя, и две части материка, разделенные той же рекой.
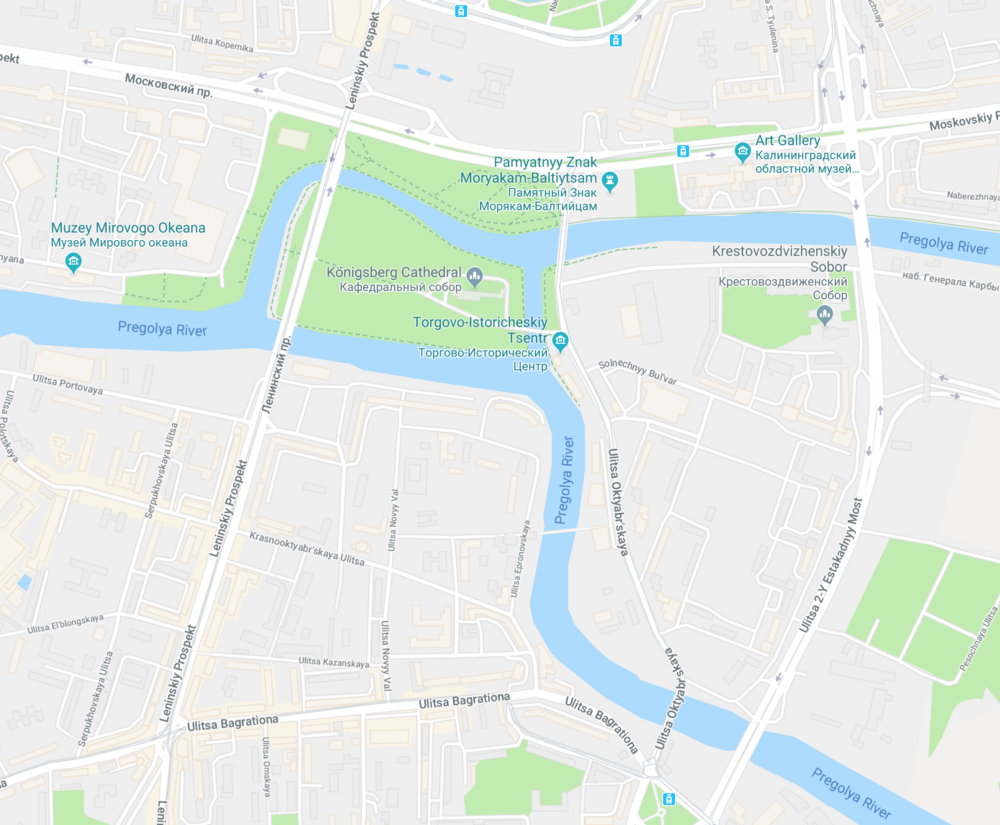
В 18 веке это был Кёнигсберг, город Пруссии, и на этой территории было гораздо больше мостов. Задача или просто головоломка состояла в том, что необходимо было найти такой маршрут, который проходил через каждый мост ровно один раз. Вот иллюстрированный вид семи мостов Кёнигсберга в 18 веке:
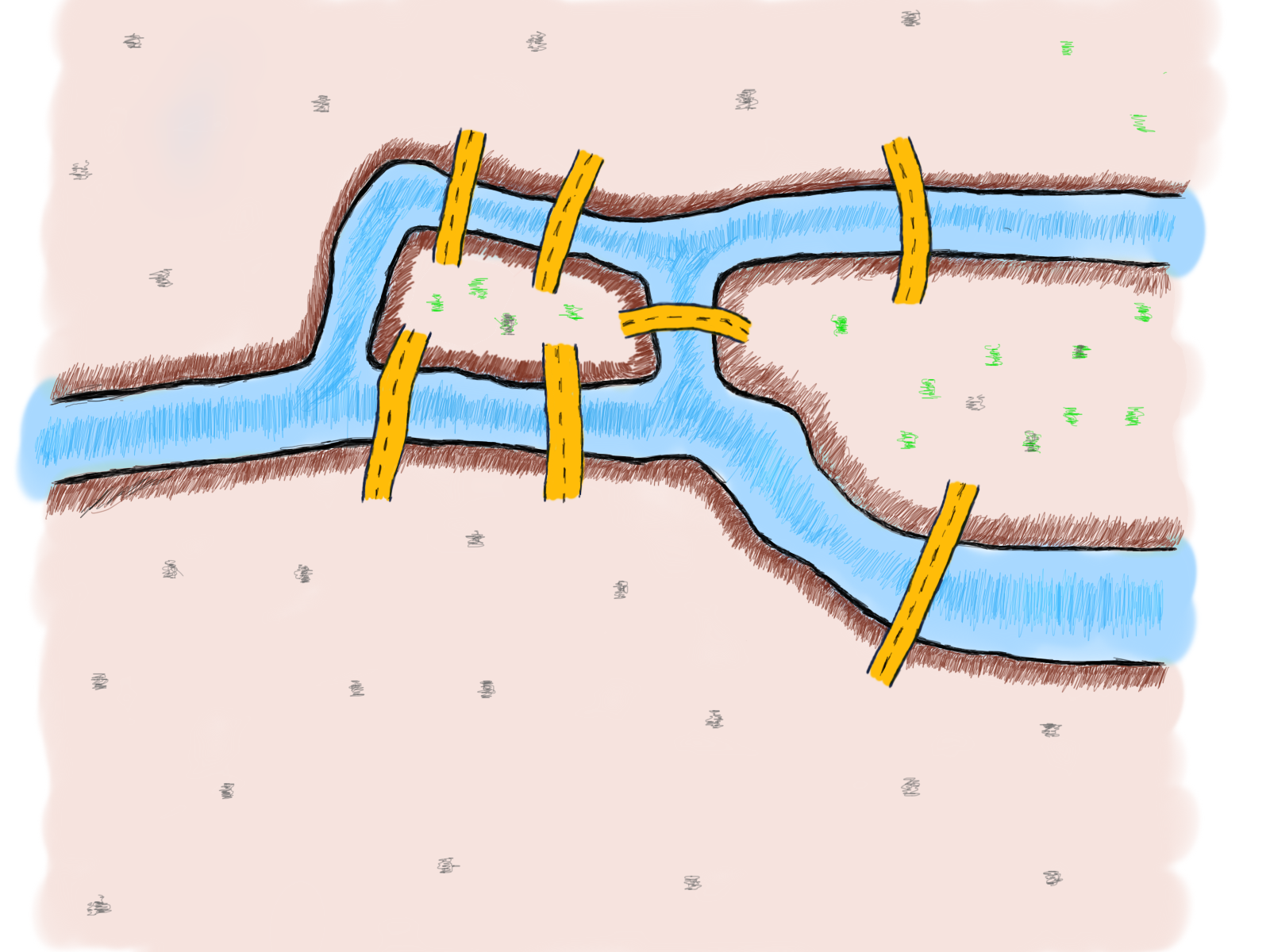
Попробуйте решить эту головоломку. Посмотрите, сможете ли вы пройти по всем мостам ровно один раз.
- Непосещённых мостов быть не должно.
- Пройти по мосту можно только один раз.
Если вы знакомы с этой задачей, то знаете, что это невозможно. Даже если вы очень сильно пытались, в конечном итоге вам пришлось сдаться.

Иногда разумно сдаться быстро. Именно так решил эту проблему Эйлер – он сдался довольно скоро. Вместо того, чтобы пытаться решить головоломку, он пытался объяснить, почему это невозможно.
Давайте попробуем понять, как Эйлер думал, и как он нашёл решение.
Начнем с представления невозможного
Есть четыре разных места: два острова и две части материка. И семь мостов. Интересно узнать, существует ли какая-либо закономерность в отношении количества мостов, связанных с островами или материком (мы будем использовать термин “земля” для обозначения четырех различных мест)?
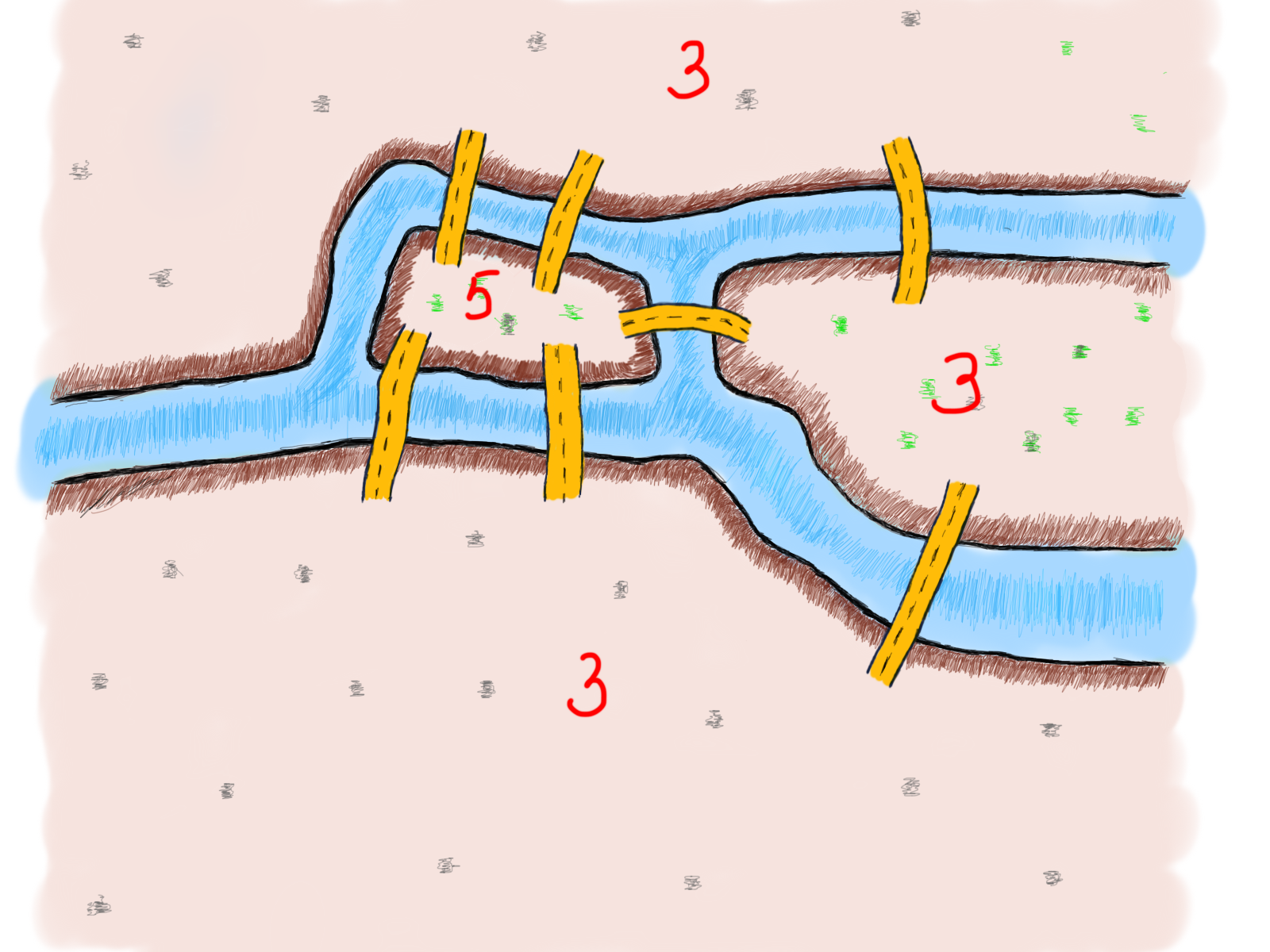
На первый взгляд кажется, что это похоже на какой-то шаблон. Есть нечётное количество мостов, связанных с каждой землёй. Если нужно пересечь каждый мост один раз, то вам достаточно зайти на землю и сойти с неё, если она имеет два моста.
На рисунке выше видно, что если вы заходите на землю, проходясь по одному мосту, вы всегда можете покинуть землю, пройдя по её второму мосту. Всякий раз, когда появляется третий мост, вы не сможете покинуть землю, как только войдёте в нее.
Если вы попытаетесь обобщить это рассуждение для одного участка земли, то увидите, что в случае чётного количества мостов всегда можно покинуть землю, а в случае нечётного – нет.
Изменим условие
Давайте добавим новый мост, чтобы узнать, как изменится количество общих соединённых мостов, и решит ли он проблему:
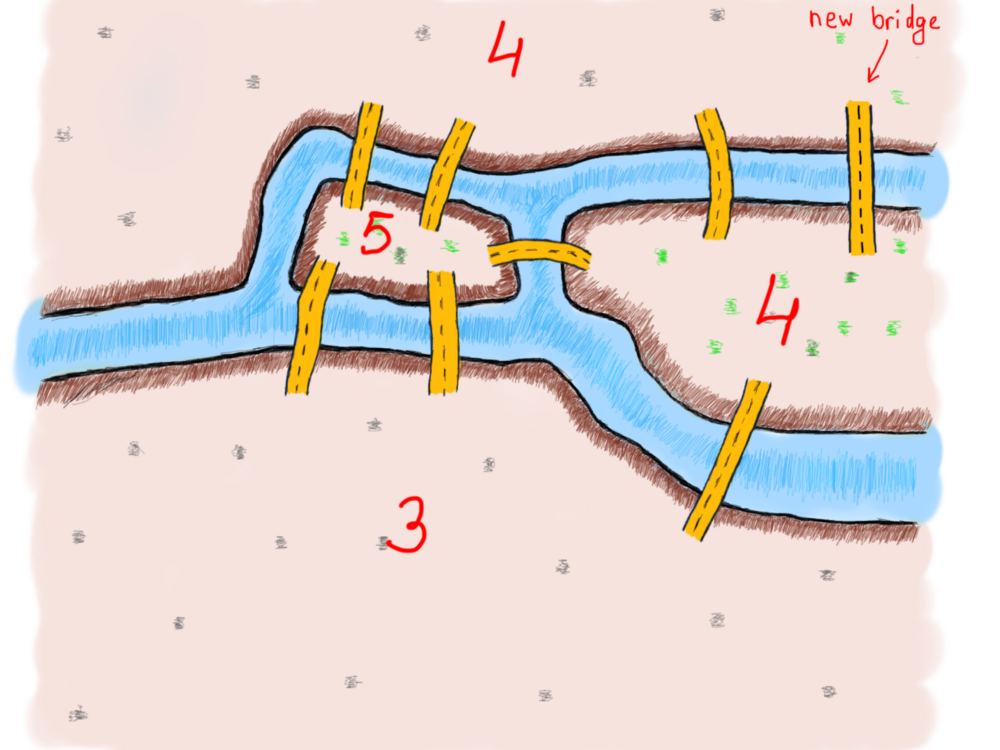
Теперь, когда у нас есть два четных (4 и 4) и два нечетных (3 и 5) числа мостов, соединяющих четыре части земли, давайте нарисуем новый маршрут с добавлением этого нового моста.
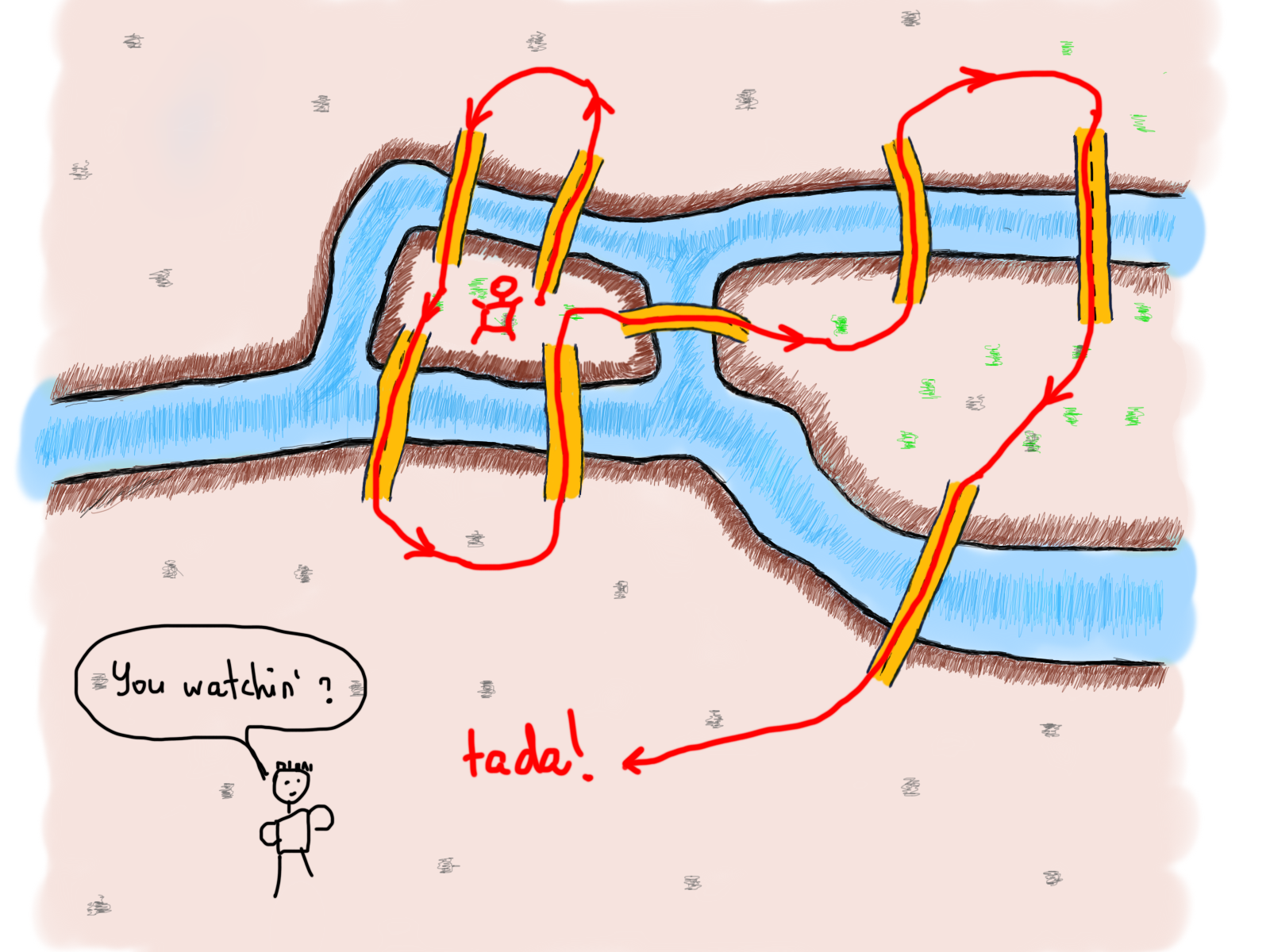
Переходим к графам
Мы увидели, что число чётных и нечётных мостов сыграло свою роль в определении возможного решения. Возникает вопрос. Количество мостов решает проблему? И должно ли это работать во всех случаях? Оказывается, это не так. Вот что сделал Эйлер. Он нашёл способ показать, что количество мостов имеет значение. Что более интересно, также имеет значение количество участков земли с нечётным количеством соединённых мостов. Именно тогда Эйлер начал преобразовывать земли и мосты в то, что мы знаем как графы. Вот как может выглядеть граф этой задачи (обратите внимание, что временно добавленного моста нет).
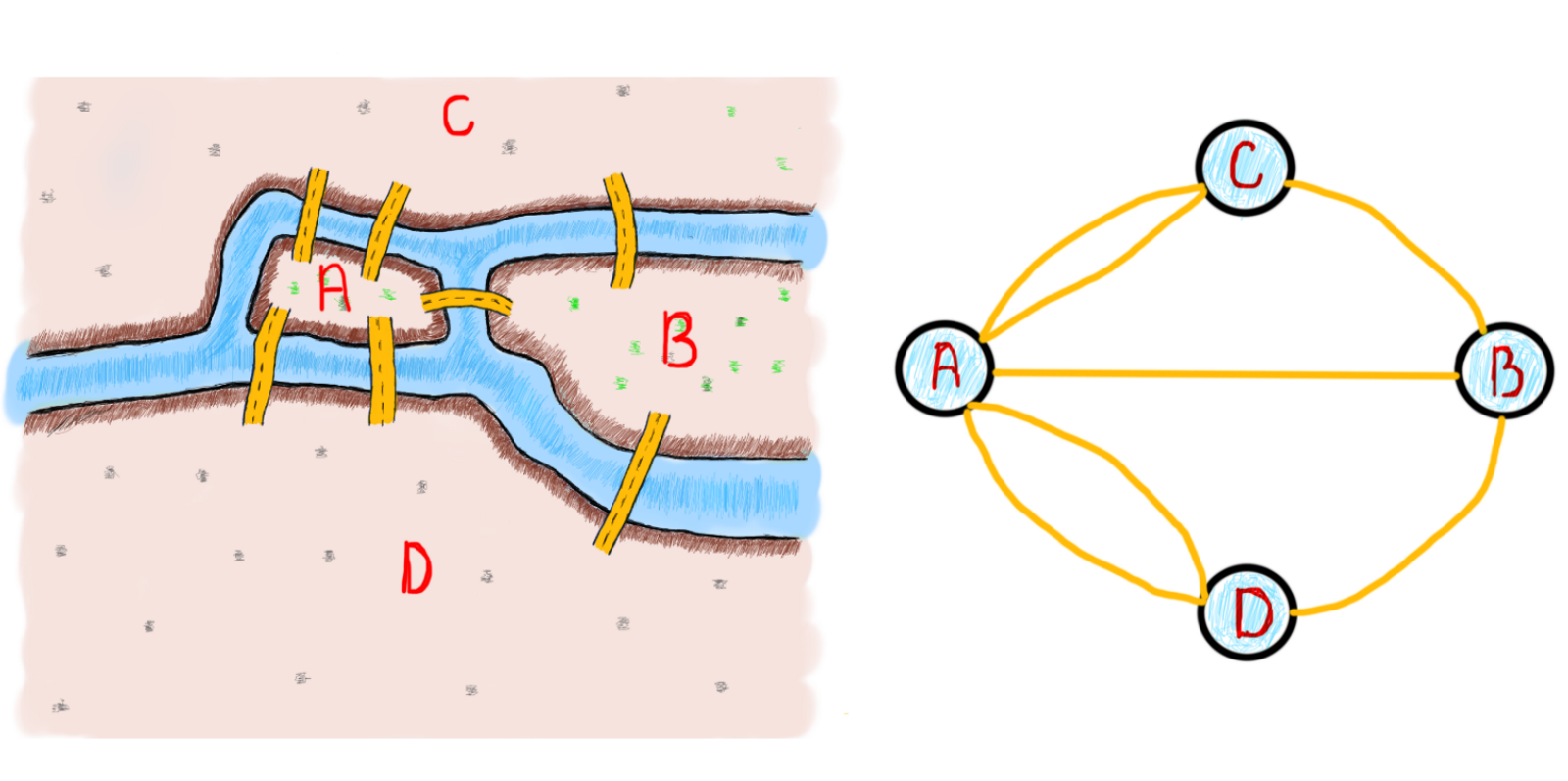
Важно отметить обобщение/абстрагирование задачи. Всякий раз, когда вы решаете определённую задачу, самое главное – обобщить решение. Конкретно в этом случае задача Эйлера состояла в том, чтобы обобщить эту задачу для решения подобных в будущем. Визуализация также помогает рассматривать проблему под другим углом. Изображения ниже – различные представления одной и той же задачи Кёнигсбергского моста.
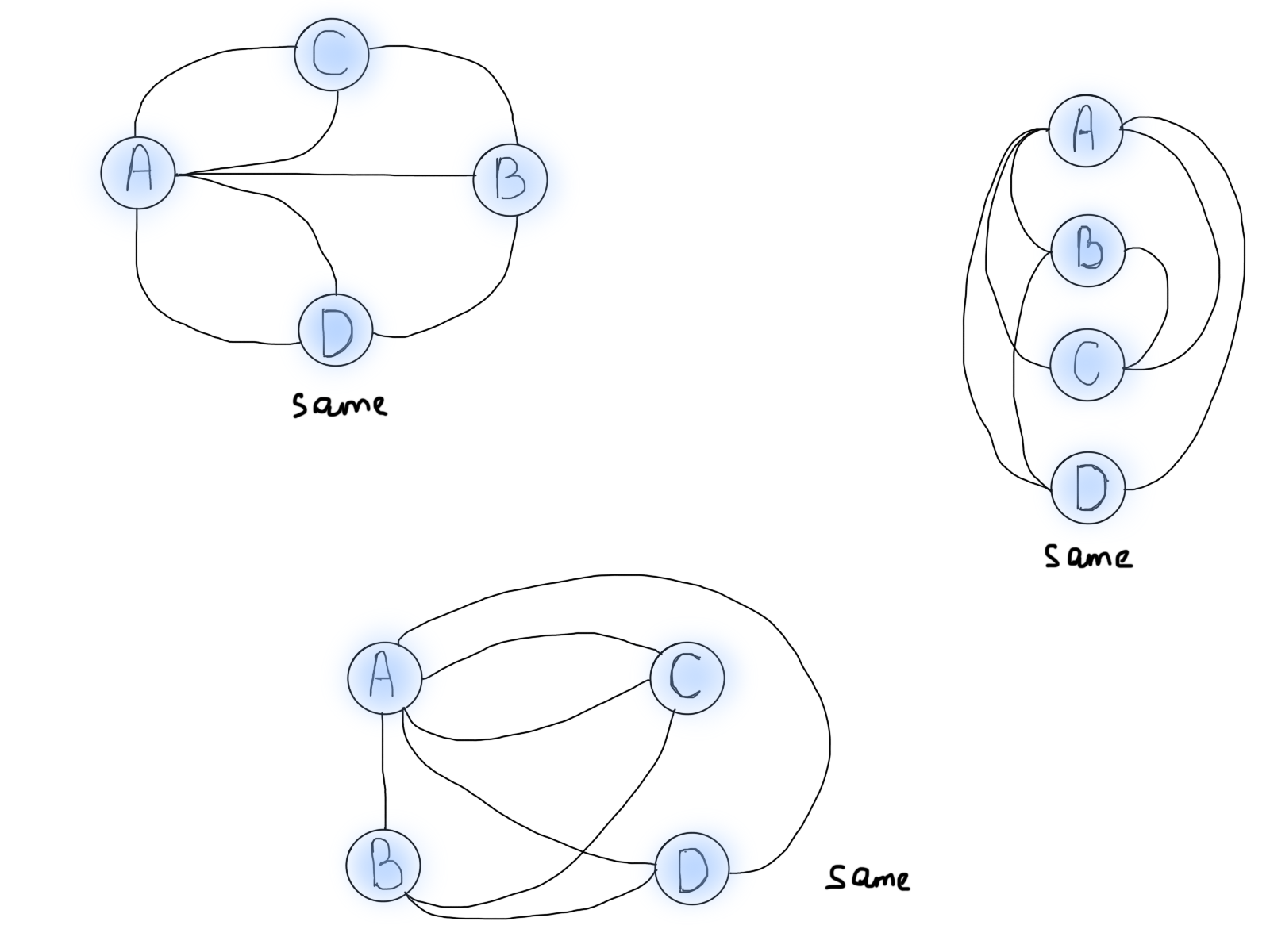
Итак, графы – хороший выбор для визуализации задачи
Но сейчас нам нужно выяснить, как проблема Кёнигсбергских мостов может быть решена с использованием графов. Обратите внимание на количество линий, выходящих из каждого круга. С этого момента то, что мы называли “кругами”, будем называть вершинами, а “линии” – рёбрами.
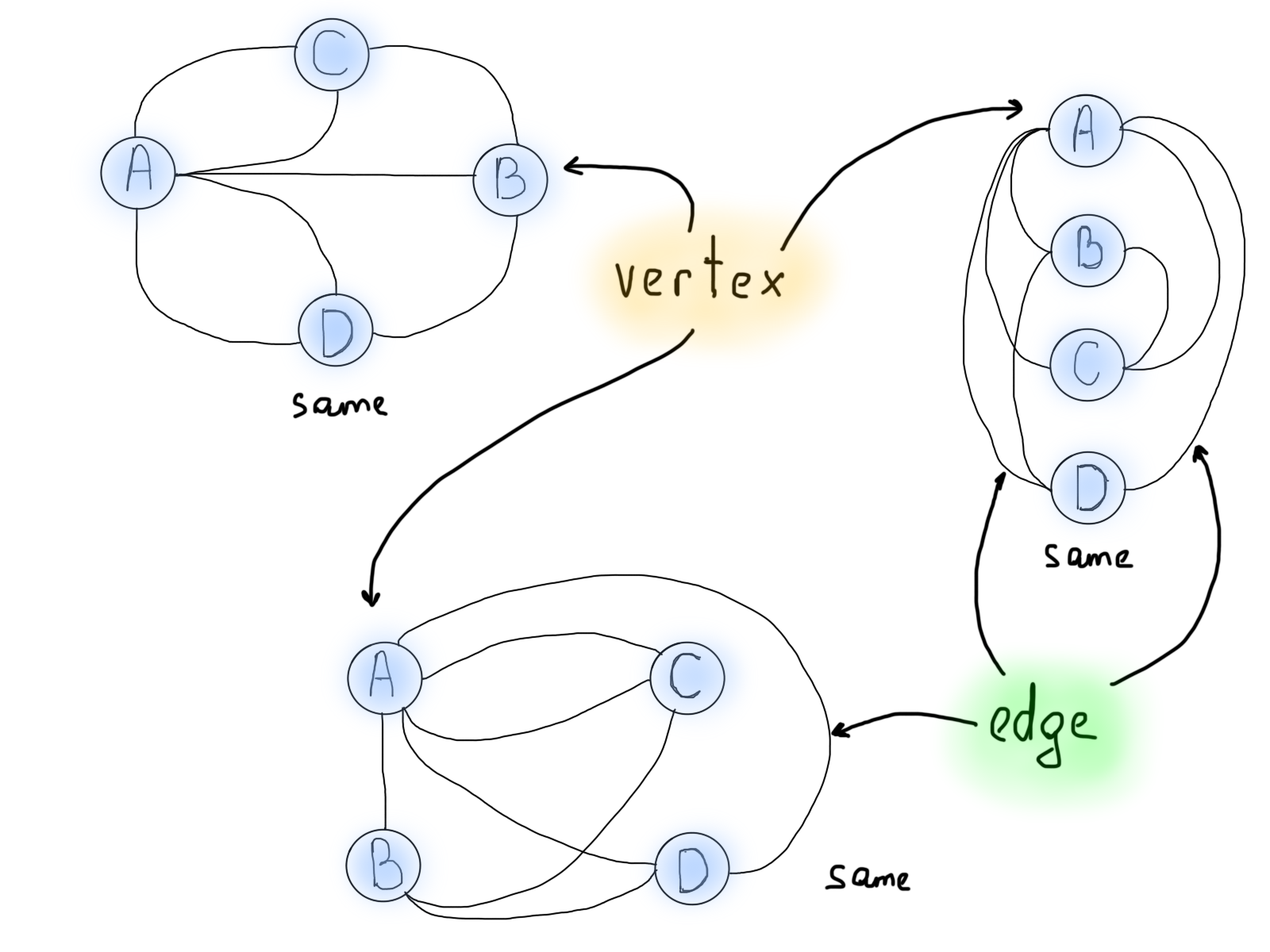
Следующим важным моментом является так называемая степень вершины, число рёбер, связанных с вершиной. В нашем примере выше число мостов, связанных с землёй, может быть выражено как степень вершины.
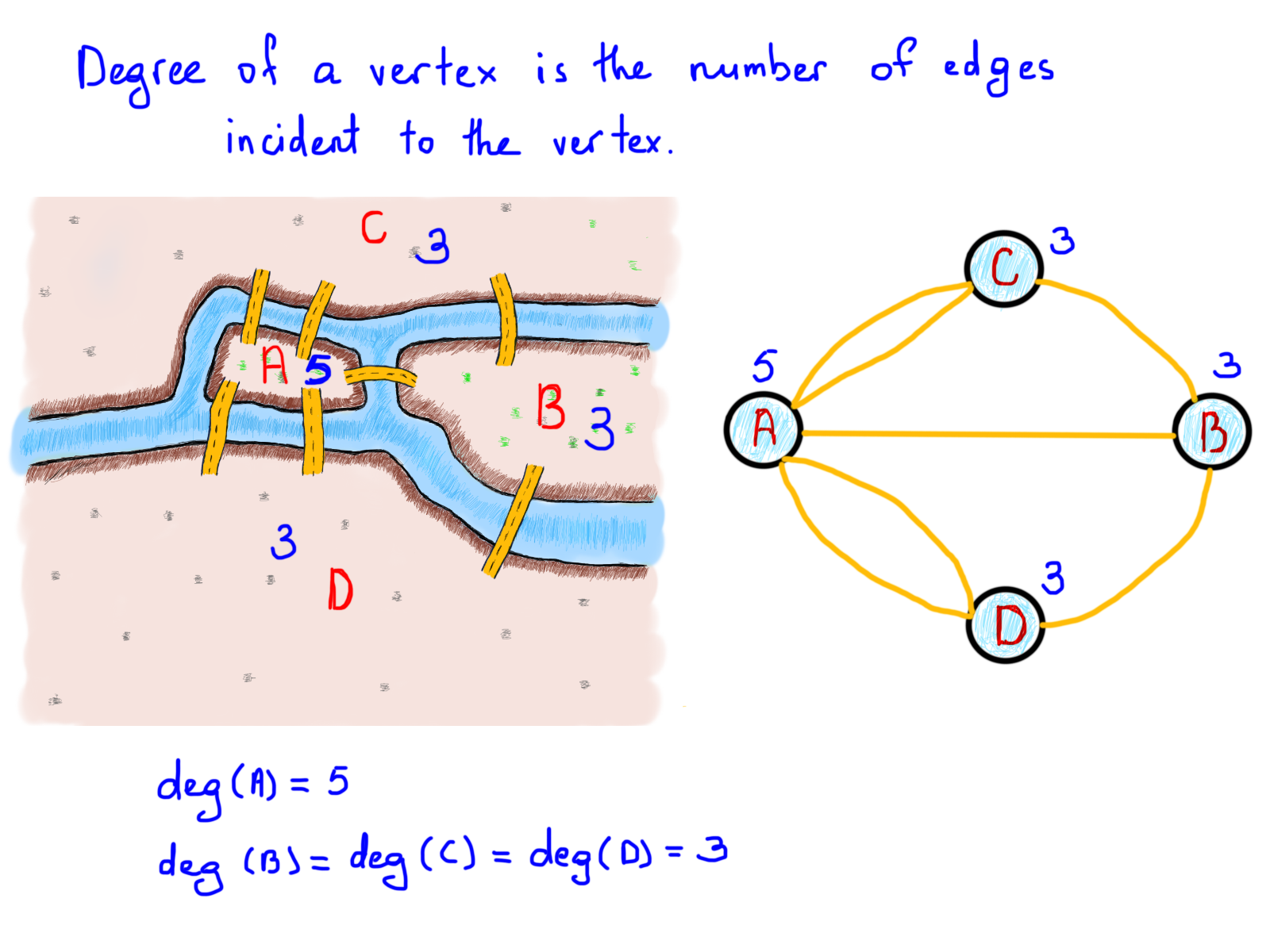
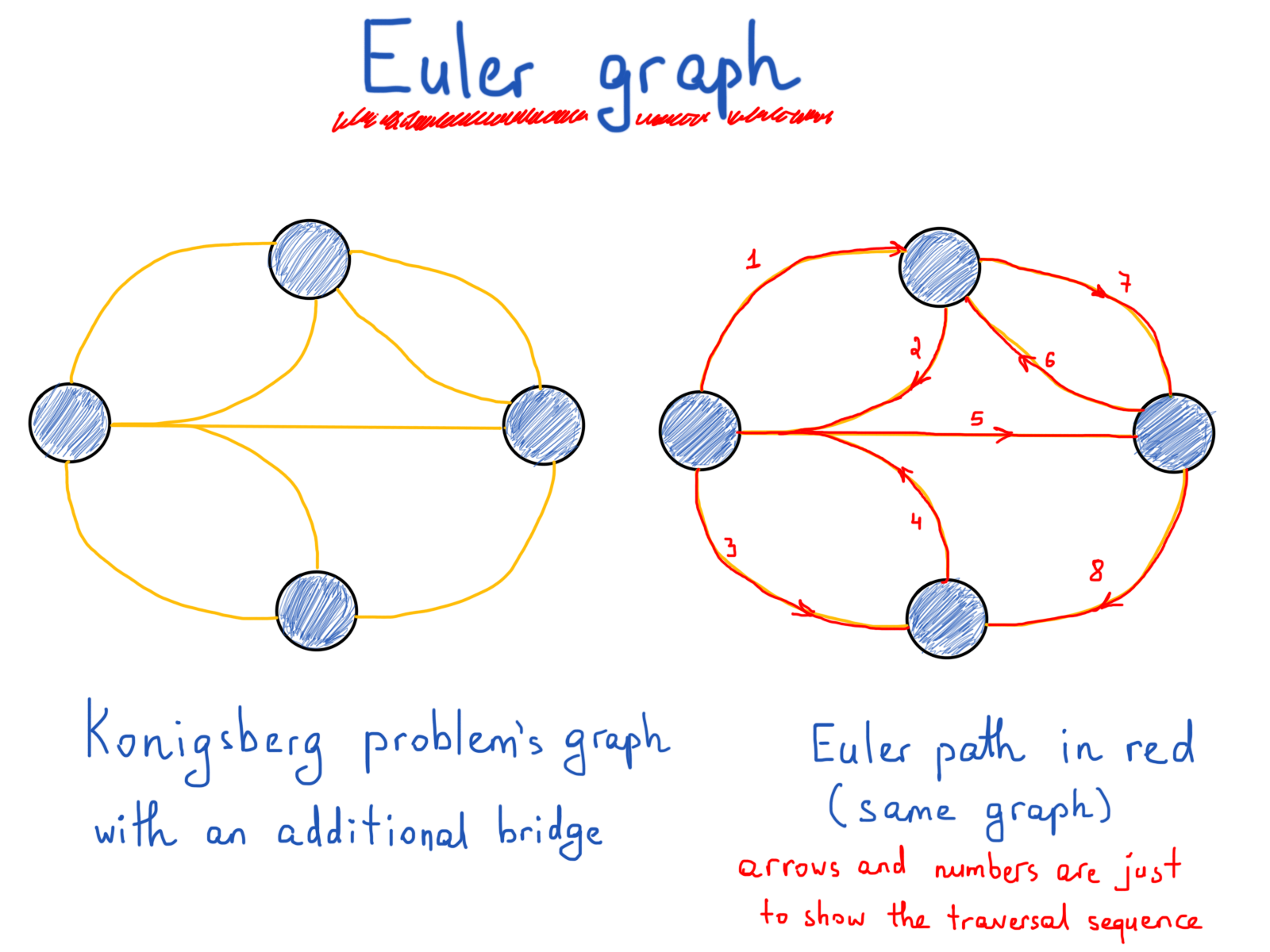
В своем стремлении Эйлер показал, что возможность прохода графа (города) по каждому ребру (мосту) один и только один раз строго зависит от степеней вершин (земель). Путь, состоящий из таких ребер, называется (в его честь) путем Эйлера. Длина пути Эйлера – это количество ребер.
Определение
Путь Эйлера конечного неориентированного графа G(V, E) является таким путём, что каждое ребро G появляется на нём один раз. Если G имеет путь Эйлера, то он называется графом Эйлера.
Теорема
Конечный неориентированный связный граф – это граф Эйлера тогда и только тогда, когда ровно две вершины имеют нечётную степень, или все вершины имеют чётную степень.
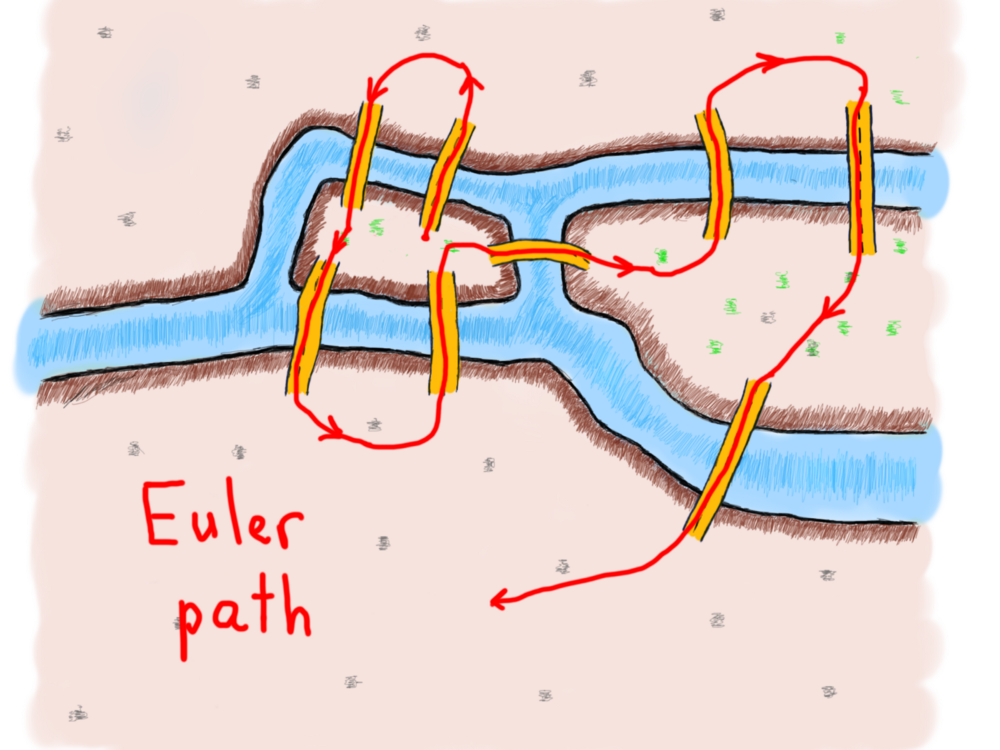
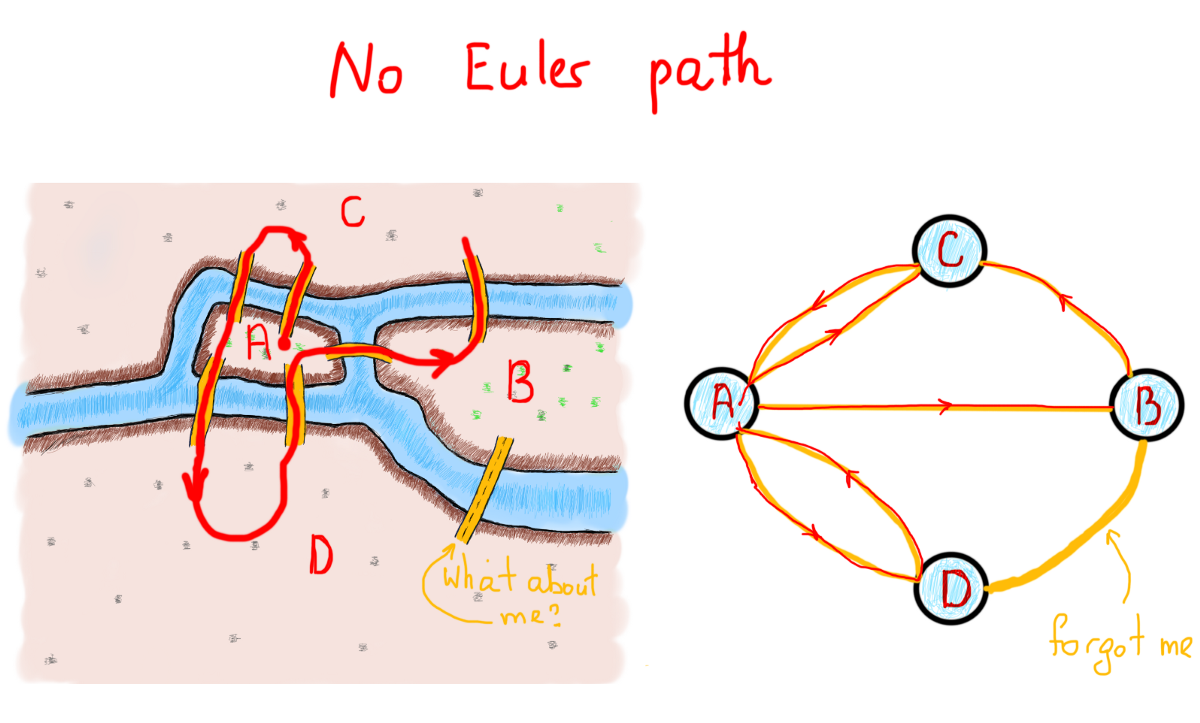
Новые термины
Прежде всего, давайте рассмотрим новые термины, встретившиеся в теореме и определении выше:
- Конечный граф – граф с конечным количеством рёбер и вершин.
- Бесконечный граф – граф, конец которого в определённом направлении(ях) простирается до бесконечности.
- Неориентированный граф – граф, рёбра которого не имеют определённого направления.
- Ориентированный граф – граф, рёбра которого имеют определённое направление.
- Связный граф – граф, в котором отсутствуют недостижимые вершины (вершины, не связанные с остальными).
- Несвязный граф – граф, в котором существуют недостижимые вершины.
Некоторые из этих терминов мы затронем в следующих пунктах.
Графы могут быть ориентированными и неориентированными.
Это одно из интересных свойств графов. К примеру, возьмём Facebook и Twitter. “Дружба” в Facebook может быть легко представлена как неориентированный граф. Например, если Алиса является другом Боба, то Боб тоже является другом Алисы. Нет конкретного направления, оба дружат друг с другом.
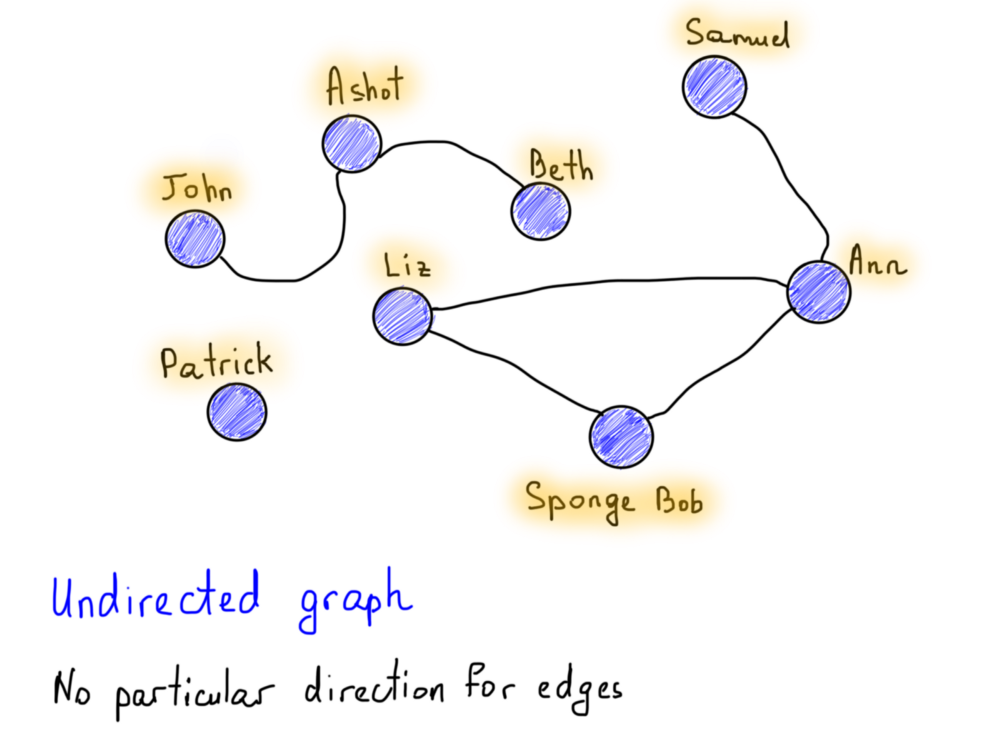
Также обратите внимание на вершину, помеченную как Patrick: она особенная (нет друзей), т. к. отсутствуют рёбра. Это всё ещё часть графа, но в таком случае мы скажем, что этот граф несвязный (то же самое относится к Джону, Ашоту и Бету, поскольку они взаимосвязаны друг с другом, но отделены от других). В связном графе не существует недостижимых вершин, должен существовать путь между каждой парой вершин.
Вопреки примеру Facebook, если Алиса фолловит Боба в Twitter, это не означает, что Боб фолловит Алису. Таким образом, “follow” должен иметь индикатор направления, показывающий, какая вершина (пользователь) имеет направленное ребро (фолловит) к другой вершине (другого пользователя).
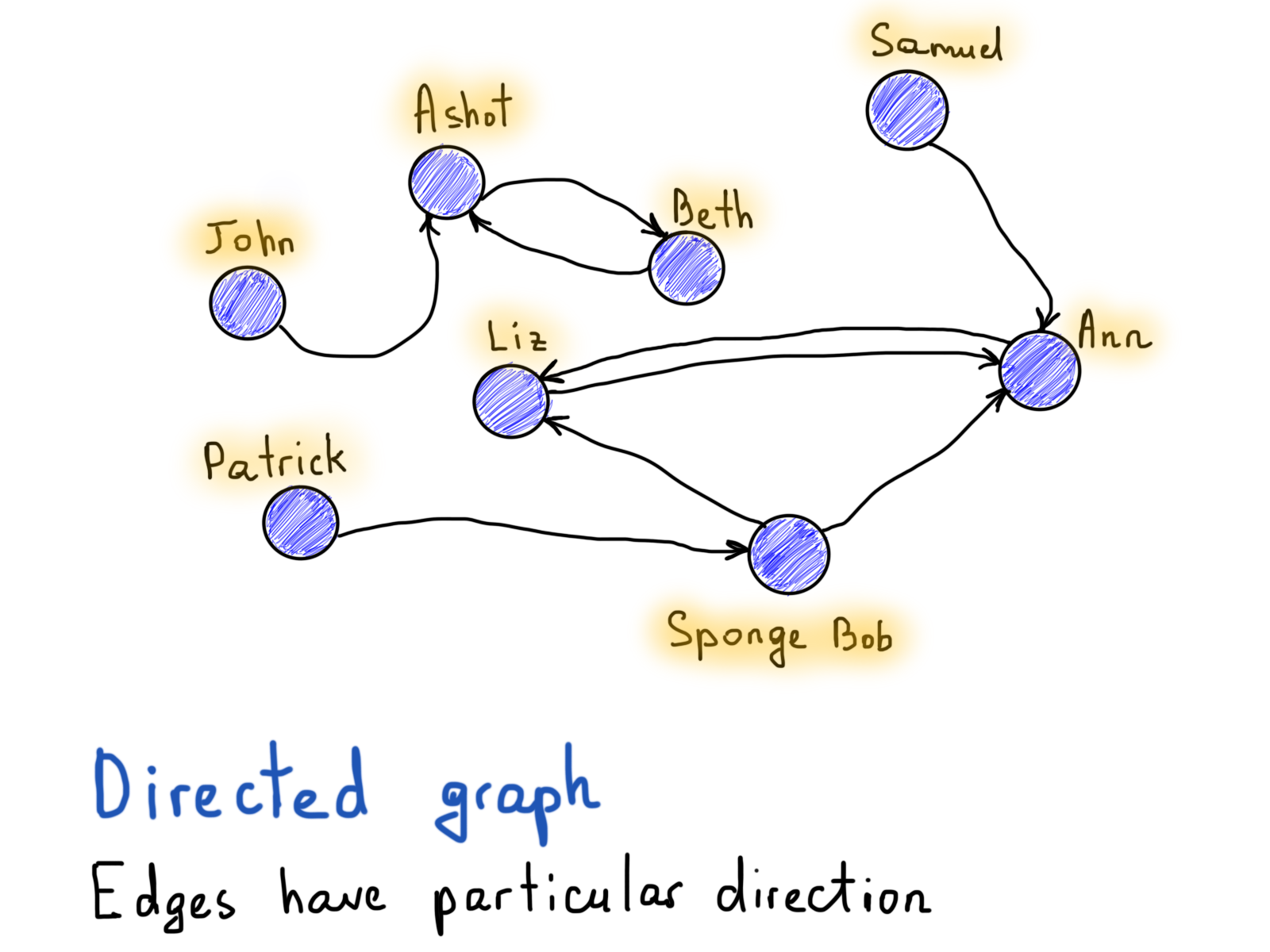
Вернёмся к графу Эйлера
Итак, почему мы обсуждали проблему Кёнигсбергских мостов и графы Эйлера в первую очередь? Это не так скучно, и, исследуя задачу и вышеизложенное решение, мы коснулись основных элементов графов (вершина, ребро, виды графов и т. п.), избегая сухого теоретического подхода. И нет, мы ещё не закончили с графами Эйлера и проблемой выше.
Теперь мы должны перейти к представлению графов на компьютерном уровне, поскольку это в большей степени интересует нас, программистов. Представляя граф в программе, мы сможем разработать алгоритм отслеживания пути графа, и, следовательно, выяснить, является ли он графом Эйлера.
Представление графов: введение
Это довольно утомительная задача, поэтому будьте терпеливы. Помните противостояние массивов и связных списков? Используйте массивы, если вам нужен быстрый доступ к элементу, используйте списки, если вам нужна быстрая вставка/удаление элемента и т.д. Вряд ли вы когда-нибудь сталкивались с проблемой, например, “как представить списки”. В случае графов фактическое представление действительно беспокоит, потому что сначала вы должны решить, как именно вы собираетесь представить граф. И поверьте, вам это не понравится. Список смежности, матрица смежности, или, может быть, список рёбер?
Бинарное дерево
Прежде всего, начнём с дерева. Должно быть, вы видели бинарное дерево по крайней мере один раз.
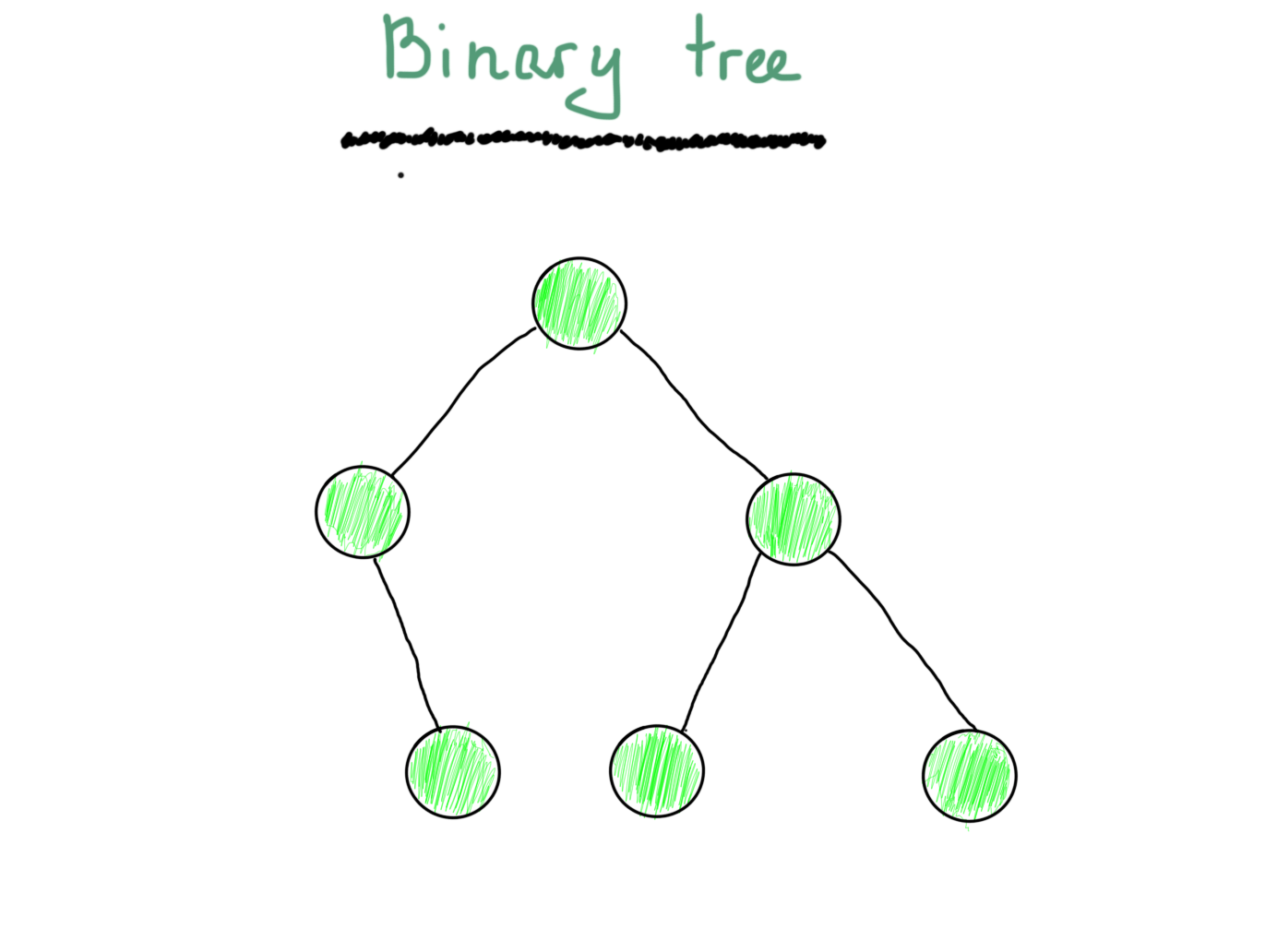
Просто потому, что оно состоит из вершин и рёбер, это граф. Вы также можете вспомнить, как обычно представлено бинарное дерево.
struct BinTreeNode
{
T value; // don't bother with template<>
TreeNode* left;
TreeNode* right;
};
class BinTree
{
public:
// insert, remove, find, bla bla
private:
BinTreeNode* root_;
};
Это может показаться слишком простым для людей, знакомых с бинарными деревьями, однако всё же стоит проиллюстрировать это, чтобы все понимали, о чём идёт речь (обратите внимание, что мы всё ещё имеем дело с псевдокодом).
BinTreeNode<Apple>* root = new BinTreeNode<Apple>("Green");
root->left = new BinTreeNode<Apple>("Yellow");
root->right = new BinTreeNode<Apple>("Yellow 2");
BinTreeNode<Apple>* yellow_2 = root->right;
yellow_2->left = new BinTreeNode<Apple>("Almost red");
yellow_2->right = new BinTreeNode<Apple>("Red");
Если вы только начинаете разбираться с деревьями, внимательно прочитайте псевдокод выше, а затем следуйте инструкциям на рисунке ниже.
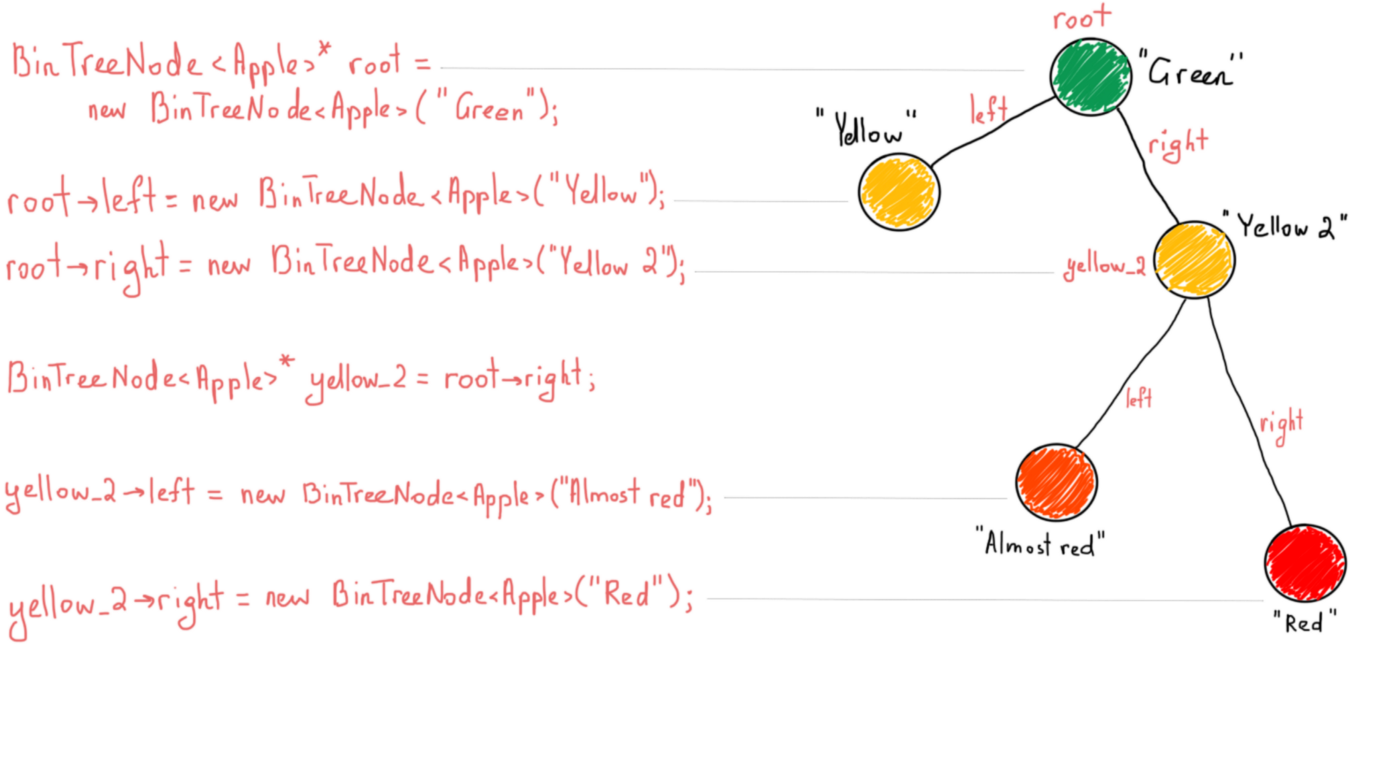
Бинарное дерево поиска
Бинарное дерево – это просто сочетание узлов, каждый из которых имеет левый и правый дочерние узлы. Бинарное дерево поиска полезно, поскольку оно применяет одно простое правило, которое позволяет быстро искать нужные значения. Бинарные деревья поиска держат свои значения в отсортированном порядке. Наиболее важным в деревьях является то, что они удовлетворяют свойству бинарного поиска. Значение каждого узла должно быть больше любого значения в левом поддереве и меньше любого ключа в правом поддереве.
Стоит отметить интересный момент относительно фразы “больше”, который имеет решающее значение для понимания того, как работает бинарное дерево поиска. Всякий раз, когда вы изменяете свойство на “больше или равно”, ваше дерево будет иметь возможность сохранять повторяющиеся значения при вставке новых узлов, в противном случае, оно будет держать только узлы с уникальными значениями. Проиллюстрируем простое бинарное дерево поиска.
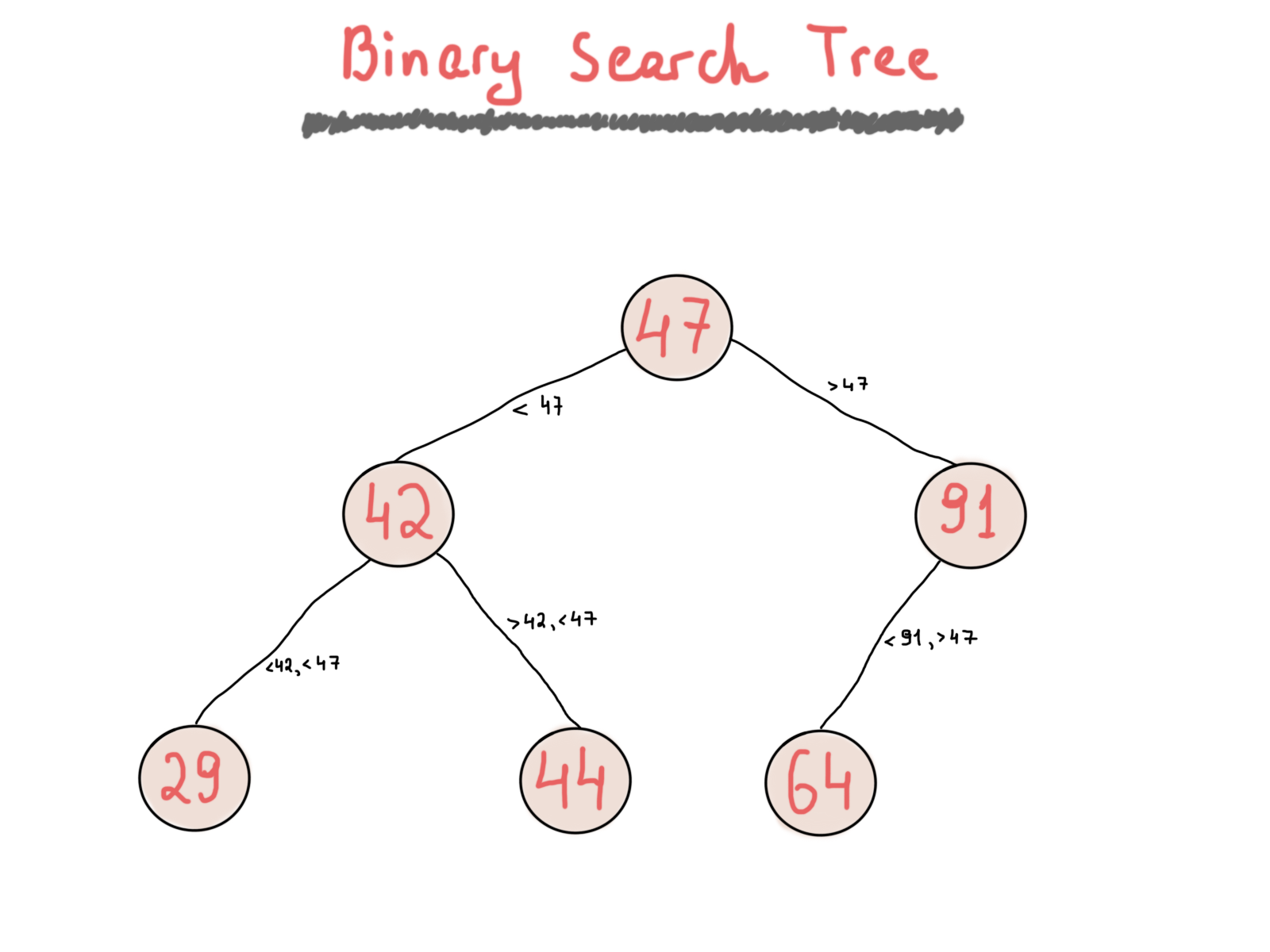
Представление графов и бинарных деревьев (пример Airbnb)
Деревья – очень полезные структуры данных. Возможно, вы не реализовывали дерево с нуля в своих проектах. Но вы, вероятно, использовали их, даже не замечая. Давайте рассмотрим искусственный, но ценный пример и попытаемся ответить на вопрос “зачем”: “зачем использовать бинарное дерево поиска?”.
Как вы могли заметить, в бинарном дереве поиска есть поиск. Таким образом, всё, что нуждается в быстром поиске, следует поместить в бинарное дерево поиска. “Следует” не значит “надо”. Важно помнить, что главное – это решить задачу с помощью правильных инструментов. Существует много ситуаций, в которых простой связный список со сложностью O(N) будет лучше бинарного дерева со сложностью O(logN).
Как правило, мы будем использовать библиотеку BST, скорее всего std::map или std::set в C++. Однако в этом уроке мы вольны изобретать собственное колесо. BST реализована практически в любом современном языке программирования. Вы можете найти их в соответствующей документации вашего любимого языка.
Переходим к Airbnb
Приближаясь к “реальному примеру”, вот проблема, которую мы попытаемся решить – Airbnb Home Search.
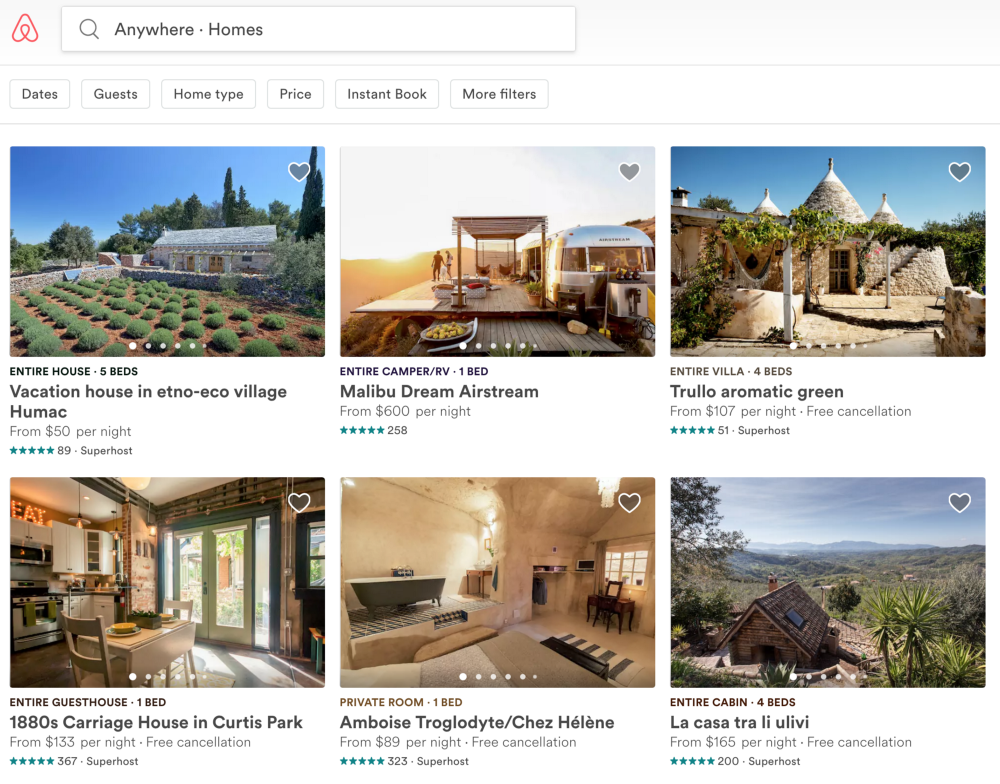
Как мы можем быстро искать дома на основе некоторого запроса с множеством фильтров? Это сложная задача. Она становится труднее, если учитывать то, что Airbnb хранит 4 миллиона списков.

Таким образом, когда пользователи ищут дома, есть шанс, что они могут “коснуться” 4 миллионов записей, хранящихся в базе данных. Конечно, результаты ограничены “топ-листами“, показанными на домашней странице сайта, и пользователь почти никогда не бывает слишком любопытен, чтобы просмотреть миллионы списков. Предположим, что пользователь находит хороший дом, просмотрев не более 1000 предложений.
Наиболее важным фактором здесь является количество пользователей онлайн, т.к. от этого зависят структуры данных, выбор базы данных и архитектура проекта в целом. Очевидно, что если мы имеем только 100 пользователей, то можем не беспокоиться об этом вообще.
Если количество онлайн пользователей превышает миллион, мы должны продумать каждое решение в проекте. Именно поэтому компании нанимают лучших специалистов, стремясь к совершенству в предоставлении услуг.
Google, Facebook, Airbnb, Netflix, Amazon, Twitter и многие другие имеют дело с огромным количеством данных, и правильный выбор для обслуживания миллионов байт данных каждую секунду начинается с найма хороших инженеров. Всё, что нужно таким компаниям – это инженер, способный решать проблемы самым быстрым и эффективным способом.
Итак, вот классический пример. Пользователь посещает домашнюю страницу (мы по-прежнему говорим об Airbnb) и пытается отфильтровать все предложения, чтобы найти наилучшее соответствие. Как бы мы справились с этой проблемой?
Рассчитываем объём занимаемой памяти
Давайте начнём с нескольких предположений:
- Мы имеем дело с данными, объём которых подходит под нашу ОЗУ
- Наша ОЗУ достаточно большая
Сколько памяти потребуется для хранения текущих данных? Если мы имеем дело с 4 миллионами единиц данных, и, если мы, вероятно, знаем размер каждой единицы, можно получить требуемый размер памяти: 4M * sizeof(one_unit).
Рассмотрим объект “дом” и его свойства. По крайней мере, рассмотрим те свойства, с которыми мы будем иметь дело при решении проблемы (“дом” – это наша единица). Мы будем представлять его как структуру C++ в некотором псевдокоде. Вы можете легко преобразовать его в объект схемы MobgoDB или ещё во что-нибудь. Мы просто обсуждаем имена и типы свойств (подумайте об использовании bitfields или bitsets для экономии пространства).
// feel free to reorganize this struct to avoid redundant space
// usage because of aligning factor
// Remark 1: some of the properties could be expressed as enums,
// bitset is chosen for as multi-value enum holder.
// Remark 2: for most of the count values the maximum is 16
// Remark 3: price value considered as integer,
// int considered as 4 byte.
// Remark 4: neighborhoods property omitted
// Remark 5: to avoid spatial queries, we're
// using only country code and city name, at this point won't consider
// the actual coordinates (latitude and longitude)
struct AirbnbHome
{
wstring name; // wide string
uint price;
uchar rating;
uint rating_count;
vector<string> photos; // list of photo URLs
string host_id;
uchar adults_number;
uchar children_number; // max is 5
uchar infants_number; // max is 5
bitset<3> home_type;
uchar beds_number;
uchar bedrooms_number;
uchar bathrooms_number;
bitset<21> accessibility;
bool superhost;
bitset<20> amenities;
bitset<6> facilities;
bitset<34> property_types;
bitset<32> host_languages;
bitset<3> house_rules;
ushort country_code;
string city;
};
Очевидно, эта структура не является совершенной. Она создана на основе фильтров Airbnb с помощью списков свойств, которые должны удовлетворить поисковые запросы. Это просто пример.
Рассматриваем объект AirbnbHome подробнее
Теперь мы должны вычислить, сколько байт в памяти займёт каждый объект AirbnbHome.
Имя дома
Имя это wstring, поддерживающий множество языков, что означает, что каждый символ занимает 2 байта. Посмотрев на дома Airbnb, можно сказать, что имя должно занимать меньше 100 символов. Мы будем считать 100 символов как максимальное значение => имя весит 200 байт.
Фотографии
Фотографии хранятся в хранилищах, таких как Amazon S3 (насколько я знаю, это предположение верно для Airbnb, но опять же, Amazon S3 – это просто предположение).
URL фотографий
Учитывая тот факт, что не существует стандартного ограничения на URL-адреса, возьмём 2000 символов. Поэтому, учитывая, что в каждом объявлении есть 5 фотографий в среднем, это займёт ~ 10 кб.
ID фотографий
Обычно службы хранения обслуживают контент с одинаковыми базовыми URL-адресами, такими как http (s): //s3.amazonaws.com/ bucket / object, то есть существует общий шаблон для URL-адресов, и нам нужно хранить только фактические идентификаторы фотографий. Предположим, мы используем уникальный генератор идентификаторов, который возвращает уникальный идентификатор строки в 20 байт, где фотообъекты и шаблон URL для определенной фотографии выглядят как https://s3.amazonaws.com/some-know-bucket/unique-photo-id. Это хорошо экономит пространство, поэтому для хранения строк пяти id фотографий нам потребуется всего 100 байт памяти.
ID хоста
Тот же “трюк” (выше) может быть выполнен с помощью host_id, то есть идентификатора пользователя, который размещает дом. Это занимает 20 байт памяти. И, наконец, мы возьмём bitset размером до 32 бит для объекта размером 4 байта и bitset размером от 32 до 64 бит для объекта размером 8 байт.

Услуги
В каждом объявлении хранится список предоставляемых услуг, например, телевидение, интернет, детектор дыма и так далее. Касательно количества услуг, мы будем придерживаться 20, т.к. это количество установлено на странице фильтров Airbnb. bitset сэкономит нам место, если мы должным образом распорядимся удобствами. Например, если в доме есть все вышеупомянутые удобства, мы просто установим значение в соответствующую ячейку в bitset.
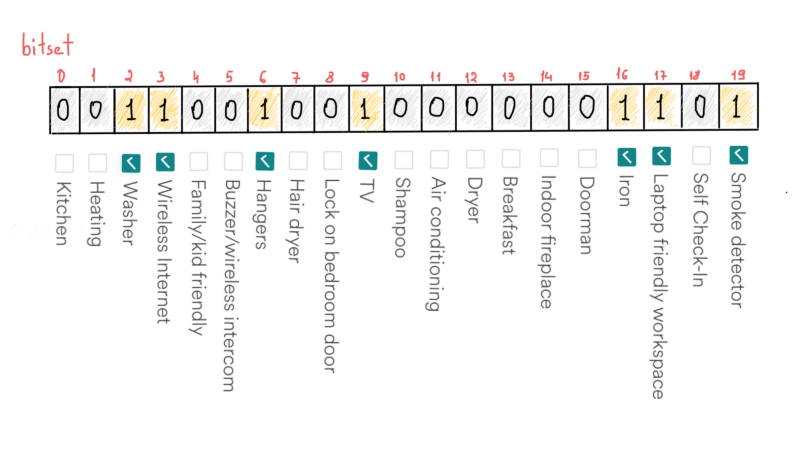
Например, если у дома есть стиральная машина:
bool HasWasher(AirbnbHome* h)
{
return h->amenities[2];
}
Или немного более профессионально:
const int KITCHEN = 0;
const int HEATING = 1;
const int WASHER = 2;
//...
bool HasWasher(AirbnbHome* h)
{
return (h != nullptr) && h->amenities[WASHER];
}
bool HasWasherAndKitchen(AirbnbHome* h)
{
return (h != nullptr) && h->amenities[WASHER] && h->amenities[KITCHEN];
}
bool HasAllAmenities(AirbnbHome* h, const std::vector<int>& amenities)
{
bool has = (h != nullptr);
for (const auto a : amenities) {
has &= h->amenities[a];
}
return has;
}
Правила дома, тип дома
Та же идея (которую мы реализовали для поля удобств), только для типа дома и правил дома.
Код страны, название города
Как уже упоминалось в комментариях кода выше, мы не будем хранить широту и долготу, чтобы избежать геопространственных запросов. Вместо этого мы сохраняем код страны и название города, чтобы сузить поиск по местоположению. Код страны может быть представлен как 2, 3 символа или 3 цифры. Мы сохраним числовое представление и будем использовать ushort для него. К (не)счастью, существует гораздо больше городов, чем стран, поэтому мы не можем использовать код города. Вместо этого мы будем хранить фактическое название города, сохраняя в среднем 50 байт для названия города и для исключительных случаев, таких как город с 85-буквенным названием.
Мы лучше используем дополнительную логическую переменную, которая указывает, что это тот конкретный сверхдлинный город (не пытайтесь его произнести). Таким образом, учитывая дополнительные расходы памяти на строки и векторы, мы добавим дополнительные 32 байта (на всякий случай) к окончательному размеру структуры. Мы также предположим, что мы работаем в 64-битной системе, хотя мы выбрали очень компактные значения для int и short.
// Note the comments
struct AirbnbHome
{
wstring name; // 200 bytes
uint price; // 4 bytes
uchar rating; // 1 byte
uint rating_count; // 4 bytes
vector<string> photos; // 100 bytes
string host_id; // 20 bytes
uchar adults_number; // 1 byte
uchar children_number; // 1 byte
uchar infants_number; // 1 byte
bitset<3> home_type; // 4 bytes
uchar beds_number; // 1 byte
uchar bedrooms_number; // 1 byte
uchar bathrooms_number; // 1 byte
bitset<21> accessibility; // 4 bytes
bool superhost; // 1 byte
bitset<20> amenities; // 4 bytes
bitset<6> facilities; // 4 bytes
bitset<34> property_types; // 8 bytes
bitset<32> host_languages; // 4 bytes, correct me if I'm wrong
bitset<3> house_rules; // 4 bytes
ushort country_code; // 2 bytes
string city; // 50 bytes
};
Итог подсчёта
Итак, 420 байт + дополнительные 32 байта = 456 байт. Округлим до 500 байт. Таким образом, каждый объект занимает до 500 байт, а для всех списков – 500 байт * 4 миллиона = 1,86ГБ ~ 2ГБ.
Переходим к следующей подзадаче
Теперь самая сложная часть задачи. Выбор правильной структуры данных для этой проблемы –(максимально эффективная фильтрация списков) не самая сложная задача. Самая трудная задача – поиск списков с помощью множества фильтров, заданных пользователем. Если бы был только один фильтр, эту задачу можно было бы легко решить. Предположим, что всё, что волнует пользователя, это цена, поэтому всё, что нам нужно – это найти объекты AirbnbHome с ценами, подходящими под заданный диапазон. Если мы будем использовать бинарное дерево поиска, вот как это будет выглядеть.
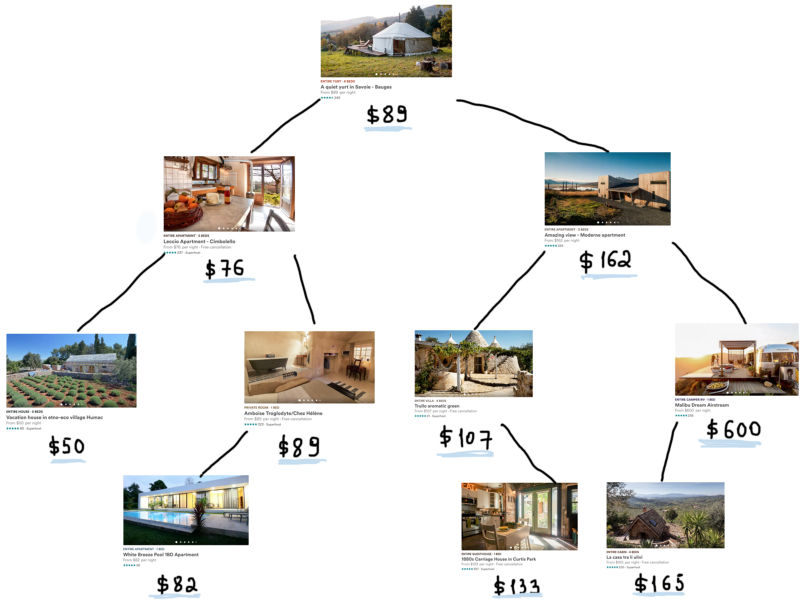
Если представить себе все 4 миллиона объектов, то это дерево вырастет очень сильно. Между прочим, дополнительные расходы памяти также растут, т.к. мы используем дерево для хранения объектов. Поскольку каждый родительский узел указывает на левый и правый дочерние элементы, он добавляет до 8 дополнительных байт каждому дочернему элементу (при условии, что это 64-разрядная система). Для 4 миллионов объектов это примерно 62МБ, что по сравнению с текущими 2ГБ выглядит довольно скромно.
Дерево на последнем рисунке показывает, что сложность алгоритма поиска любого элемента будет O(log N).
Вычислительная сложность алгоритмов
В большинстве случаев найти сложность алгоритма довольно просто. Прежде всего, стоит отметить, что мы всегда рассматриваем наихудший случай, т.е. максимальное количество операций, которые делает алгоритм для получения положительного результата (для решения проблемы).
Предположим, что массив содержит 100 несортированных элементов. Сколько сравнений потребуется, чтобы найти элемент (также принимая во внимание, что необходимый элемент может отсутствовать)? Для этого потребуется до 100 сравнений, т.к. мы должны сравнить значение каждого элемента с заданным значением. И, несмотря на то, что искомый элемент может быть первым в массиве (что приводит к единственному сравнению), мы рассмотрим только худший случай (элемент либо отсутствует, либо находится на последней позиции).
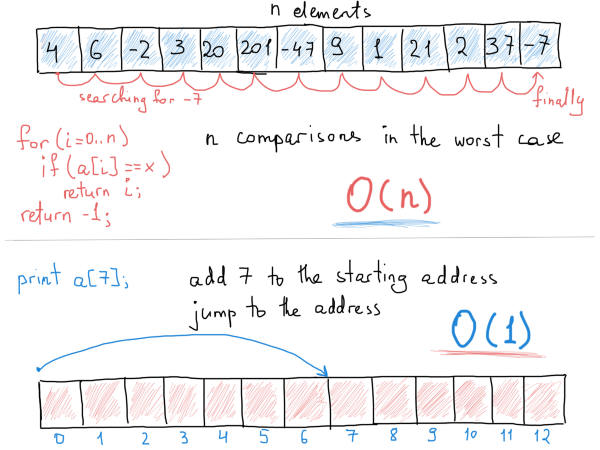
Смысл вычисления алгоритмической сложности заключается в нахождении зависимости между количеством операций и размером входных данных.
Например, массив из примера выше имел 100 элементов, и точно такое же количество операций потребовалось для нахождения нужного элемента. Если количество элементов массива увеличится до 1423, то количество операций точно так же увеличится до 1423. Таким образом, в данном примере зависимость получается линейной. Количество операций возрастает с увеличением количества элементов. Доступ к любому элементу массива занимает константное время, т.е. О(1). Это объясняется структурой массива. Переход к конкретному элементу требует только вычисления его позиции относительно первого элемента.
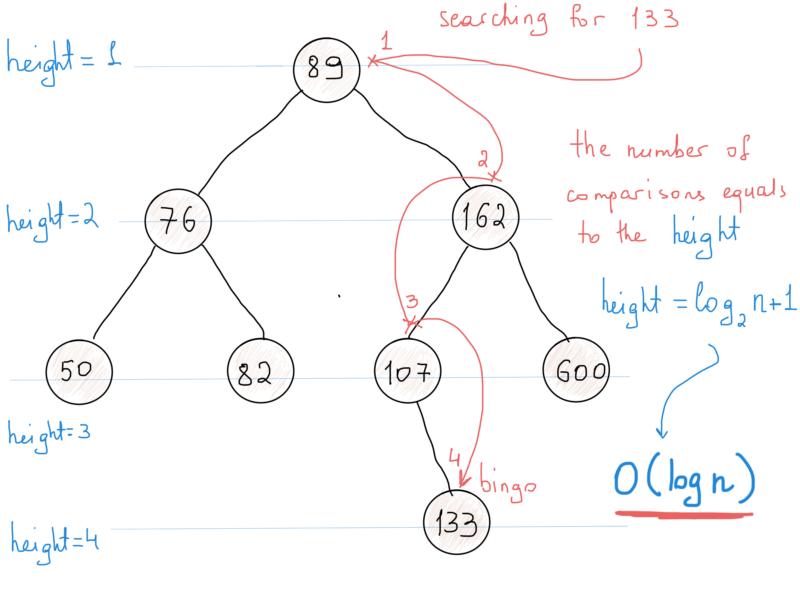
Ясно одно: бинарное дерево поиска хранит свои узлы в отсортированном порядке. Итак, какова будет вычислительная сложность алгоритма поиска элемента в бинарном дереве? Нужно рассчитать количество операций, необходимых для нахождения элемента (для худшего случая).
Посмотрите на иллюстрацию выше. Когда мы начинаем поиск с корня, первое сравнение может привести к трём разным результатам.
- Искомый узел найден.
- Сравнение применяется к дочернему элементу слева, если искомое значение меньше значения текущего узла.
- Сравнение применяется к дочернему элементу справа, если искомое значение больше значения текущего узла.
На каждом шаге мы вдвое уменьшаем количество узлов, которые необходимо рассматривать. Количество операций (т.е. сравнений), необходимых для нахождения элемента в BST, равно высоте дерева. Высота дерева – это количество узлов на самом длинном пути. В нашем случае это 4. И высота равна logN (с основанием 2) + 1, как показано на рисунке. Таким образом, сложность поиска – О(logN + 1) = O(logN). Это означает, что поиск в 4 миллионах узлов требуется log4000000 = ~ 22 сравнения в худшем случае.
Вернёмся к дереву
Время доступа элемента в двоичном дереве поиска – O(logN). Почему бы не использовать хеш-таблицы? Они имеют постоянное время доступа к элементу, поэтому разумно использовать их почти везде.

В этой задаче мы должны принять во внимание важное требование.
Мы должны быть в состоянии сделать поиск по заданному диапазону цен, например, поиск домов с ценами от $80 до $162. В BST легко получить все узлы в диапазоне, просто проходя по дереву и обновляя счётчик. Для хеш-таблицы это будет сложно сделать, поэтому в данном случае следует придерживаться BST.
Хотя есть еще один момент, который заставляет нас переосмыслить хеш-таблицы. Густота. Цены не будут расти “всегда”, большинство домов находятся в одном ценовом диапазоне. Посмотрите на скриншот, гистограмма показывает нам реальную картину цен, миллионы домов находятся в одном диапазоне (+/- $18 – $212), у них такая же средняя цена. Простые массивы могут сыграть хорошую роль. Предполагая, что индекс массива – цена, и значение – список домов, мы можем получить доступ к любому ценовому диапазону за константное время (ну, почти константное). Вот как это выглядит:
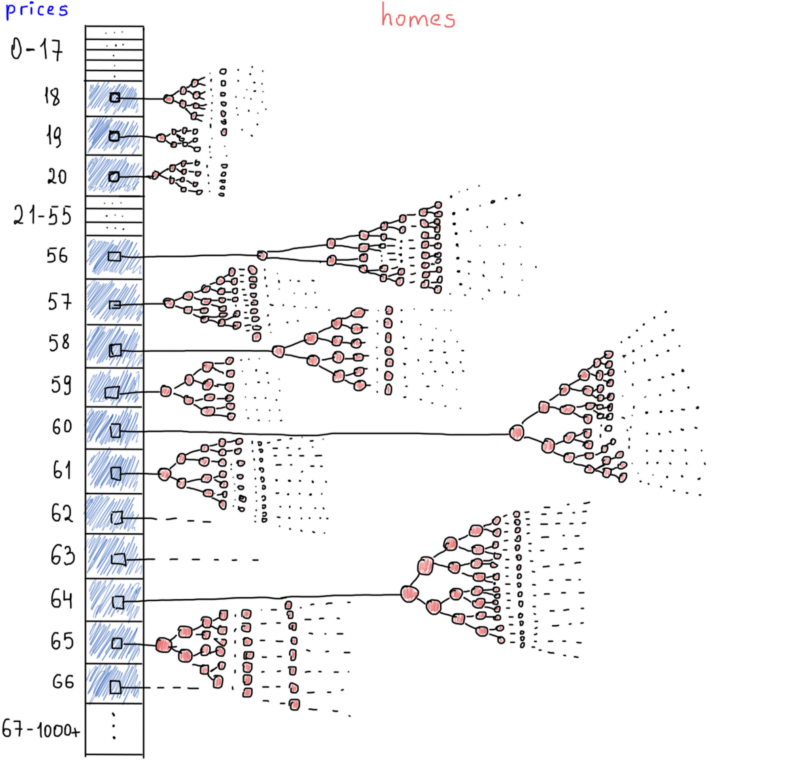
Как и хэш-таблица, мы получаем доступ к каждому набору домов по цене. Все дома с одинаковой ценой сгруппированы в отдельное бинарное дерево. Это также сэкономит нам некоторое пространство, если мы храним домашние идентификаторы вместо целого объекта, определенного выше (структура AirbnbHome). Наиболее вероятным сценарием является сохранение всех объектов, заполненных объектами, в домашнем идентификаторе хеш-таблицы для домашнего полного объекта и хранении другой хэш-таблицы, которая отображает цены с идентификаторами домов.
Поэтому, когда пользователи запрашивают ценовой диапазон, мы получаем домашние идентификаторы из таблицы цен, сокращаем результаты до фиксированного размера (т. е. разбиваем на страницы, обычно около 10 – 30 элементов на одной), извлекаем полные объекты домов, используя каждый идентификатор объекта.
Балансировка имеет решающее значение для BST, потому что это единственная гарантия выполнения операций с деревом за O(logN).
Проблема несбалансированного BST очевидна при вставке элементов в сортированном порядке. В конце концов, дерево становится просто связанным списком, что, очевидно, приводит к линейным операциям времени. Забудьте об этом, предположим, что все наши деревья идеально сбалансированы. Еще раз взгляните на иллюстрацию выше. Каждый элемент массива представляет собой большое дерево.
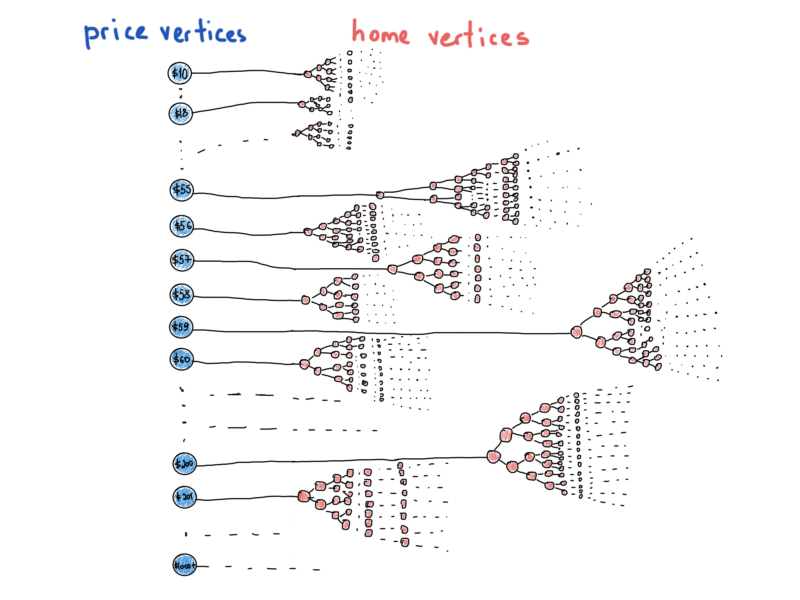
Это уже более похоже на граф. Эта иллюстрация представляет собой наиболее замаскированные структуры данных и графы, которые приводят нас к следующему разделу.
Представление графов: заключение
Плохая новость относительно представления графов заключается в том, что не существует единственно истинного представления графа. Вот почему не существует std::graph в библиотеках. У нас уже был шанс представить “специальный” граф под названием бинарное дерево поиска. Суть в том, что всякое дерево – это граф, но не каждый граф – дерево. Последняя иллюстрация показывает нам, что у нас есть много деревьев под одной абстракцией, “цены против домов“, и некоторые из вершин отличаются по своему типу, цены – это вершины графа, имеющие значение цены и относящиеся ко всему дереву id домов, которые удовлетворяют конкретной цене. Это больше похоже на гибридную структуру данных, чем на простой граф, который мы привыкли видеть в учебниках.
Это ключевой момент в представлении графов.
Не существует фиксированной структуры данных для представления графа (в отличие от BST с их узлами и левыми/правыми дочерними элементами). Вы можете представить граф наиболее удобным для вас способом (наиболее удобным для конкретной задачи), главное, чтобы вы “видели” это как граф. Под этим мы подразумеваем применение алгоритмов на графах.
Что касается N-арного дерева, это скорее будет напоминать граф.
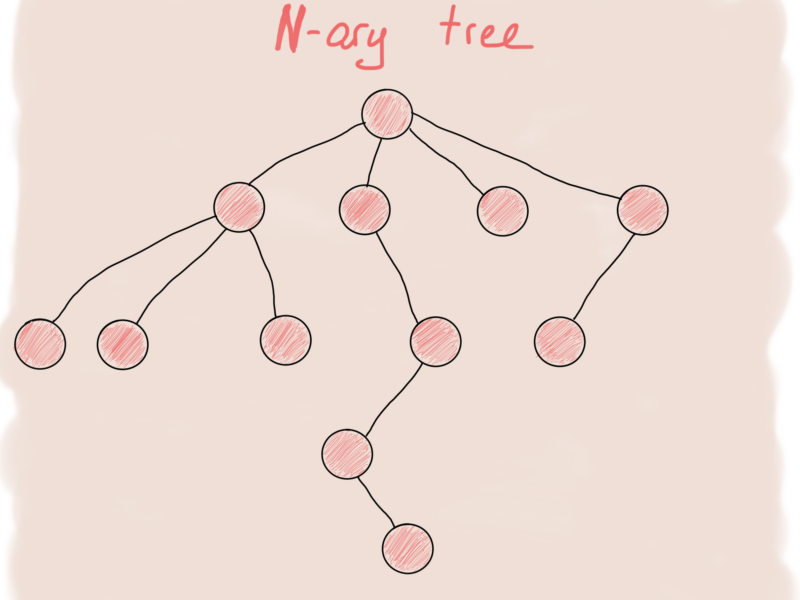
И первое, что приходит в голову, чтобы представить узел N-арного дерева, это что-то вроде этого:
struct NTreeNode
{
T value;
vector<NTreeNode*> children;
};
Эта структура представляет собой единственный узел дерева. Полное дерево выглядит примерно так:
// almost pseudocode
class NTree
{
public:
void Insert(const T&);
void Remove(const T&);
// lines of omitted code
private:
NTreeNode* root_;
};
Этот класс является абстракцией одного узла дерева с именем root_. Это всё, что нам нужно, чтобы построить дерево любого размера. Это исходная точка дерева. Для добавления нового узла дерева нам нужно выделить ему память и добавить этот узел в корень дерева.
Граф и дерево
Граф очень похож на n-арное дерево, только с небольшой разницей.
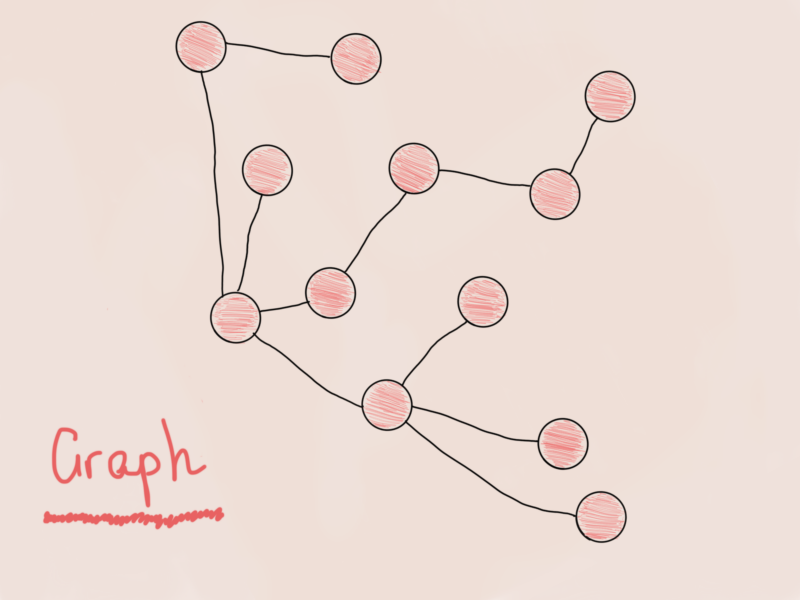
Это граф? Нет. Я имею в виду да, но это то же самое N-арное дерево из предыдущей иллюстрации, просто перевёрнутое. Как правило, когда вы видите дерево (даже если это яблоня, лимонное дерево или бинарное дерево поиска), вы можете быть уверены, что это граф. Итак, разрабатывая структуру для вершины графа, мы можем создать ту же структуру:
struct GraphNode
{
T value;
vector<GraphNode*> adjacent_nodes;
};
Достаточно ли этого для создания полноценного графа?
Нет. И вот почему. Посмотрите на эти два графа из предыдущих иллюстраций и найдите разницу:
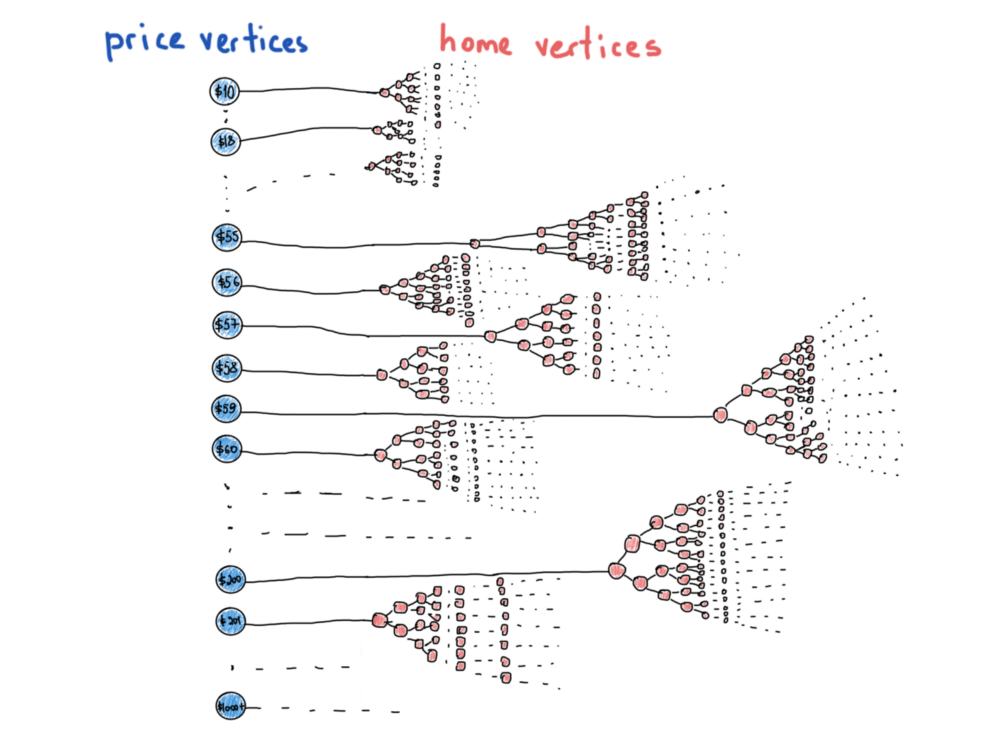
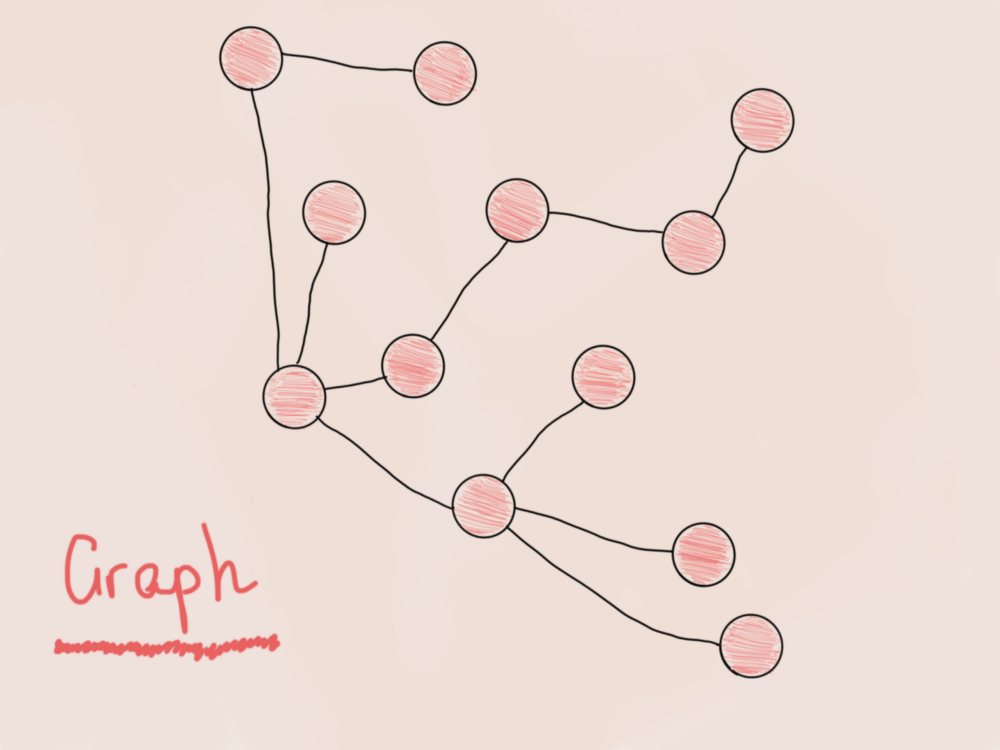
Граф на рисунке слева не имеет единой точки входа (это скорее лес, чем одно дерево). Граф на рисунке справа не имеет недостижимых вершин. Звучит знакомо.
Граф является связным, если существует путь между каждой парой вершин.
Очевидно, что не существует пути между каждой парой вершин для графа “цены vs. дома” (если это не очевидно из иллюстрации, просто предположите, что цены не связаны друг с другом). Поскольку это просто пример, чтобы показать, что мы не в состоянии построить граф с одной структурой GraphNode, есть случаи, когда нам приходится иметь дело с такими несвязанными графами. Взгляните на этот класс:
class ConnectedGraph
{
public:
// API
private:
GraphNode* root_;
};
Подобно тому, как N-арное дерево строится вокруг одного узла (корневого), связный граф также может быть построен вокруг “корневой” вершины. Говорят, что деревья “укоренены”, т.е. у них есть начальная точка. Связный граф может быть представлен как корневое дерево (с несколькими дополнительными свойствами), это очевидно, но имейте в виду, что фактическое представление может отличаться от алгоритма к алгоритму, от проблемы к проблеме даже для связного графа. Однако, учитывая природу графов, несвязанный граф может быть представлен следующим образом:
class DisconnectedGraphOrJustAGraph
{
public:
// API
private:
std::vector<GraphNode*> all_roots_;
};
Для обходов графа, таких как BFS/DFS, вполне естественно использовать древовидное представление. Однако такие случаи, как поиск кратчайшего пути требуют другого представления графа. Помните граф Эйлера? Чтобы отследить “эйлерность” графа, мы должны проследить путь Эйлера внутри него. Это означает, что сначала мы должны посетить все вершины только один раз путём обхода каждого ребра, и когда проход заканчивается, а мы имеем необработанные рёбра, то граф не имеет пути Эйлера, и поэтому не является графом Эйлера.
Существует более быстрый метод проверки.
Мы можем проверить степени вершин (предположим, что каждая вершина хранит свою степень), и, как говорится в определении, если граф имеет вершины нечетной степени, и их не ровно два, то это не граф Эйлера. Сложность такой проверки O (|V|), где |V| – количество вершин графа. Довольно быстро, не так ли? Неважно, мы просто пройдемся по графу, вот и всё. Ниже вы найдёте как представление графа, так и функцию Trace(), возвращающую путь.
// A representation of a graph with both vertex and edge tables
// Vertex table is a hashtable of edges (mapped by label)
// Edge table is a structure with 4 fields
// VELO = Vertex Edge Label Only (e.g. no vertex payloads)
class ConnectedVELOGraph {
public:
struct Edge {
Edge(const std::string& f, const std::string& t)
: from(f)
, to(t)
, used(false)
, next(nullptr)
{}
std::string ToString() {
return (from + " - " + to + " [used:" + (used ? "true" : "false") + "]");
}
std::string from;
std::string to;
bool used;
Edge* next;
};
ConnectedVELOGraph() {}
~ConnectedVELOGraph() {
vertices_.clear();
for (std::size_t ix = 0; ix < edges_.size(); ++ix) {
delete edges_[ix];
}
}
public:
void InsertEdge(const std::string& from, const std::string& to) {
Edge* e = new Edge(from, to);
InsertVertexEdge_(from, e);
InsertVertexEdge_(to, e);
edges_.push_back(e);
}
public:
void Print() {
for (auto elem : edges_) {
std::cout << elem->ToString() << std::endl;
}
}
std::vector<std::string> Trace(const std::string& v) {
std::vector<std::string> path;
Edge* e = vertices_[v];
while (e != nullptr) {
if (e->used) {
e = e->next;
} else {
e->used = true;
path.push_back(e->from + ":-:" + e->to);
e = vertices_[e->to];
}
}
return path;
}
private:
void InsertVertexEdge_(const std::string& label, Edge* e) {
if (vertices_.count(label) == 0) {
vertices_[label] = e;
} else {
vertices_[label]->next = e;
}
}
private:
std::unordered_map<std::string, Edge*> vertices_;
std::vector<Edge*> edges_;
};
Конечно, вы можете легко усовершенствовать этот код, чтобы он удовлетворял всем вашим потребностям.
Пример Twitter: проблема доставки твитов
Вот ещё одно представления графа, называемое матрицей смежности, которое может быть полезно в ориентированных графах (вспомните пример с фолловерами Twitter).
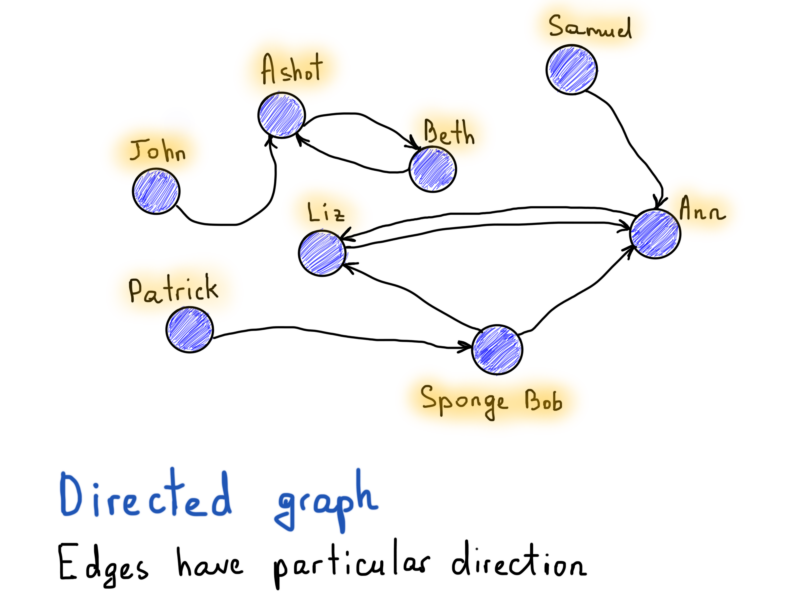
В этом примере есть 8 вершин. Итак, всё, что нам нужно представить, это матрица |V| x |V| (|V| количество строк и |V| количество столбцов). Если есть направленное ребро от v до u, то элемент, находящийся в [v][u] равен единице. Иначе он равен нулю.
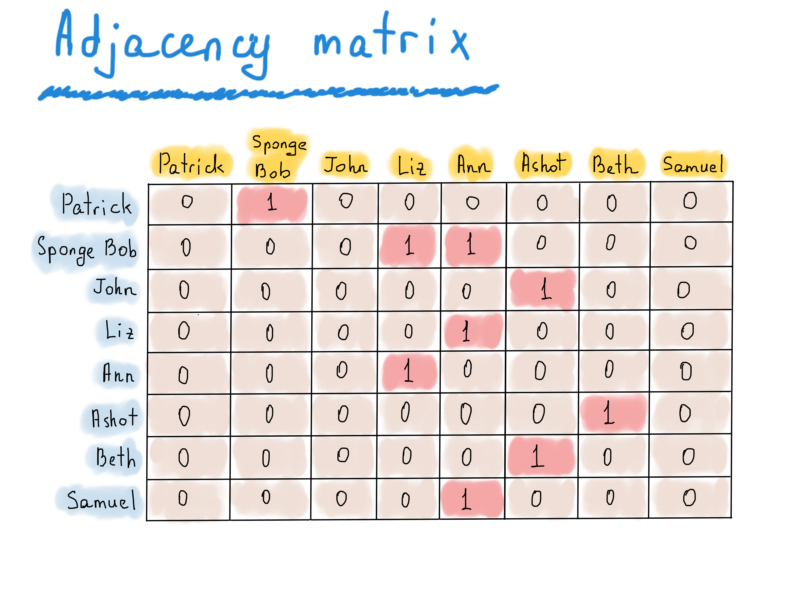
Как вы можете видеть, эта матрица слишком скудна, ее единственный плюс – это быстрый доступ к элементу. Чтобы увидеть, фолловит ли Патрик Губку Боба, мы должны просто проверить значение матрицы [Patrick] [Sponge Bob]. Чтобы получить список подписчиков Ann, мы просто обрабатываем всю колонку Ann. Матрицы смежности можно использовать для неориентированных графов, и вместо одного значения, если существует ребро из V в U, мы должны установить оба значения, равными единице, например, если adj_matrix[v][u] = 1, то и adj_matrix[u][v] должен равняться единице. Матрица смежности неориентированного графа симметрична относительно главной диагонали.
Обратите внимание, что вместо хранения единиц и нулей в матрице смежности мы можем хранить там что-то “более полезное”, например, весовые коэффициенты.
Одним из лучших примеров может быть граф с информацией о расстоянии от вершины до вершины.
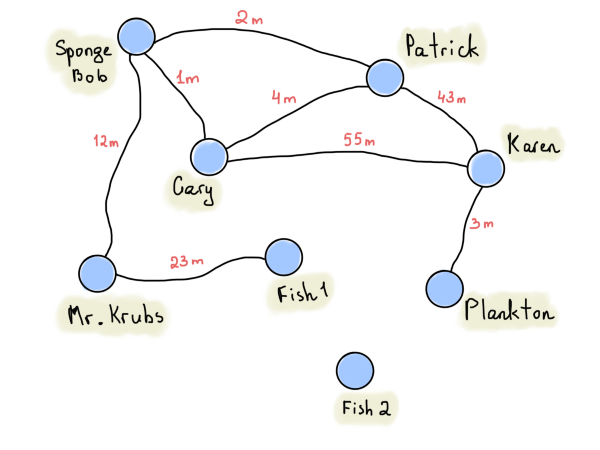
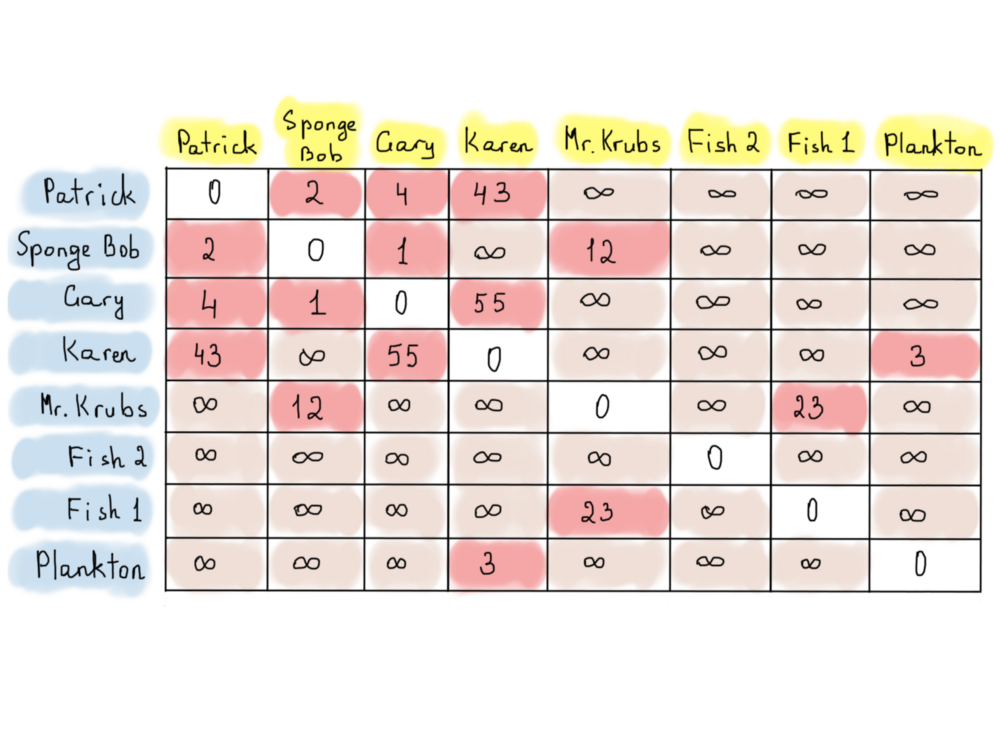
На приведённом выше графе представлены расстояния между домами Патрика, Губки Боба и других (такой граф называется взвешенным). Мы ставим знаки бесконечности, если между вершинами нет прямого маршрута. Это не означает, что маршруты вообще отсутствуют, и в то же время это не означает, что маршруты обязательно должны быть.
Использование матрицы смежности для хранения графа фолловеров кажется хорошим решением, однако не стоит забывать, что в Twitter сейчас существует порядка 300 миллионов пользователей, поэтому хранить матрицу смежности для каждого из них занимает около 300 * 300 * 1 байт. То есть ~ 82000 терабайт, что составляет ~ 1024 * 82000 гигабайт. Bitsets? BitBoard может нам немного помочь, уменьшив требуемый размер до ~ 10000 терабайт. Всё ещё слишком много. Очевидно, матрица смежности – плохой выбор, т.к. заставляет использовать больше места, чем необходимо. Вот почему использование списка ребер, инцидентных вершинам, может оказаться полезным. Дело в том, что матрица смежности позволяет нам хранить информацию о том, подписан человек на другого или нет, а нам нужно знать информацию только о подписчиках, что-то вроде этого:
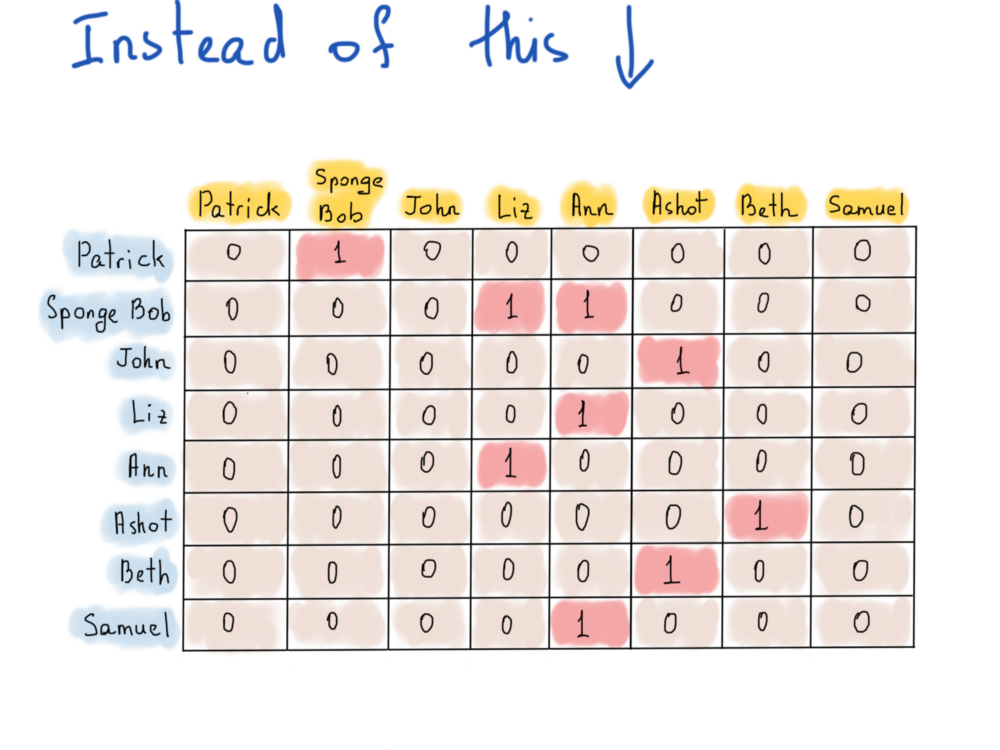
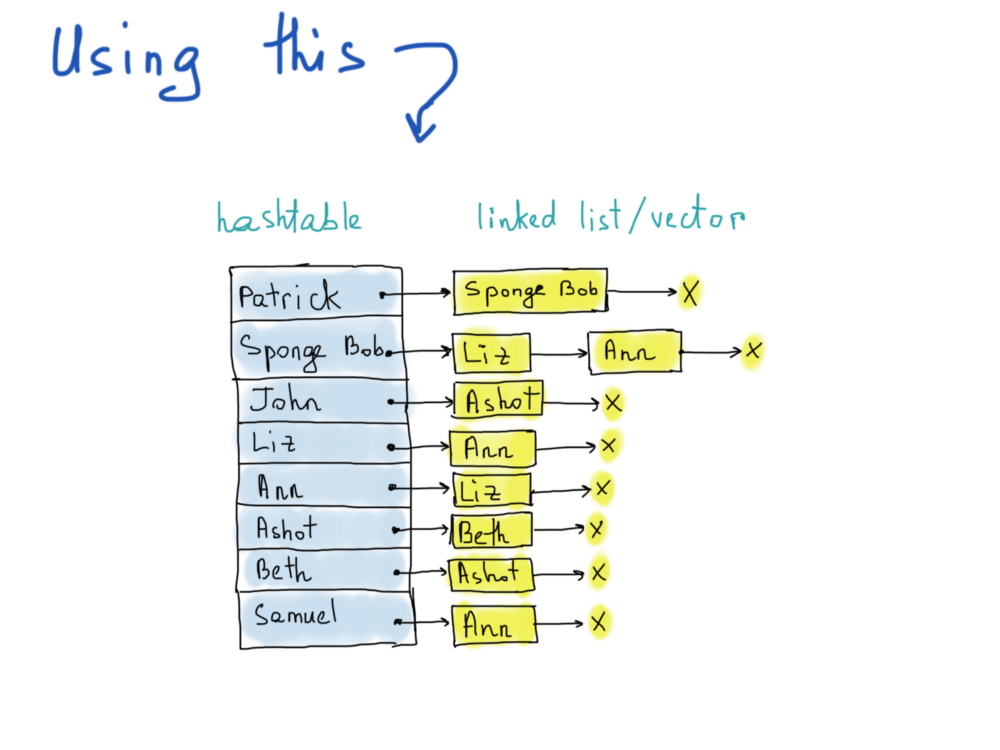
Иллюстрация справа называется списком смежности.
Каждый список описывает множество соседних вершин в графе. Кстати, фактическая реализация графа как списка смежности, опять же, отличается. На рисунке мы выделили использование хеш-таблицы, что разумно, так как доступ к любой вершине будет O(1), а для списка соседних вершин мы не упомянули точную структуру данных, отклоняясь от связанных списков к векторам. Выбор за вами.
Дело в том, чтобы выяснить, фолловит ли Патрик Liz, мы должны получить доступ к хеш-таблице (константное время) и просмотреть все элементы в списке, сравнивающие каждый элемент с элементом “Liz” (линейное время). Линейное время не так уж и плохо, потому что нам нужно перебрать только фиксированное количество вершин, смежных с “Патриком”. Итак, нам нужно как минимум 300 миллионов записей хеш-таблиц, каждая из которых указывает на вектор. Неизвестно сколько элементов точно должен содержать вектор, т.к. отсутствует статистика. Погуглив, можно обнаружить, что среднее количество подписчиков ~ 707.
Поэтому, если учесть, что каждая запись хэш-таблицы указывает на массив из 707 id пользователей (каждый весит 8 байт), предположим, что служебные данные хэш-таблицы – это только её ключи, которые являются id пользователей, поэтому сама хэш-таблица занимает 300 миллионов * 8 байт. В целом, у нас есть 300 миллионов * 8 байт для хэш-таблицы + 707 * 8 байт для каждой хэш-таблицы, то есть 300 миллионов * 8 * 707 * 8 байтов ~ 12 терабайт. Нельзя сказать, что этот объём идеален, но, во всяком случае, это лучше, чем 10 000 терабайт.
Честно говоря, нельзя точно сказать, что 12 терабайт является разумным числом.
Однако, учитывая тот факт, что сервер с 32 гигабайтами оперативной памяти в среднем стоит 30 долларов за месяц, то для 12 терабайт потребуется как минимум 385 таких серверов, плюс пара серверов управления (для распределения данных). Округлим до 400. Получим, что аренда серверов будет стоить около $12000 в месяц.
Учитывая тот факт, что данные должны быть реплицированы, и что что-то всегда может пойти не так, мы утроим количество серверов, а затем снова добавим некоторые серверы управления, допустим, нам нужно по крайней мере 1500 серверов, что будет стоить нам $45000 ежемесячно. Предположим, что это хорошее решения для Twitter.
Что в Twitter главное?
Я имею в виду, технически, какова его самая большая проблема? Вы не будете одиноки, если скажете, что это быстрая доставка твитов. Допустим, что Патрик написал твит о еде. Все его последователи должны получить этот твит в разумные сроки. Сколько времени это займёт? Мы можем предполагать что угодно и использовать любые абстракции, которые мы хотим, но мы заинтересованы в реальных системах, так что давайте копать. Вот что обычно происходит, когда кто-то постит твит:
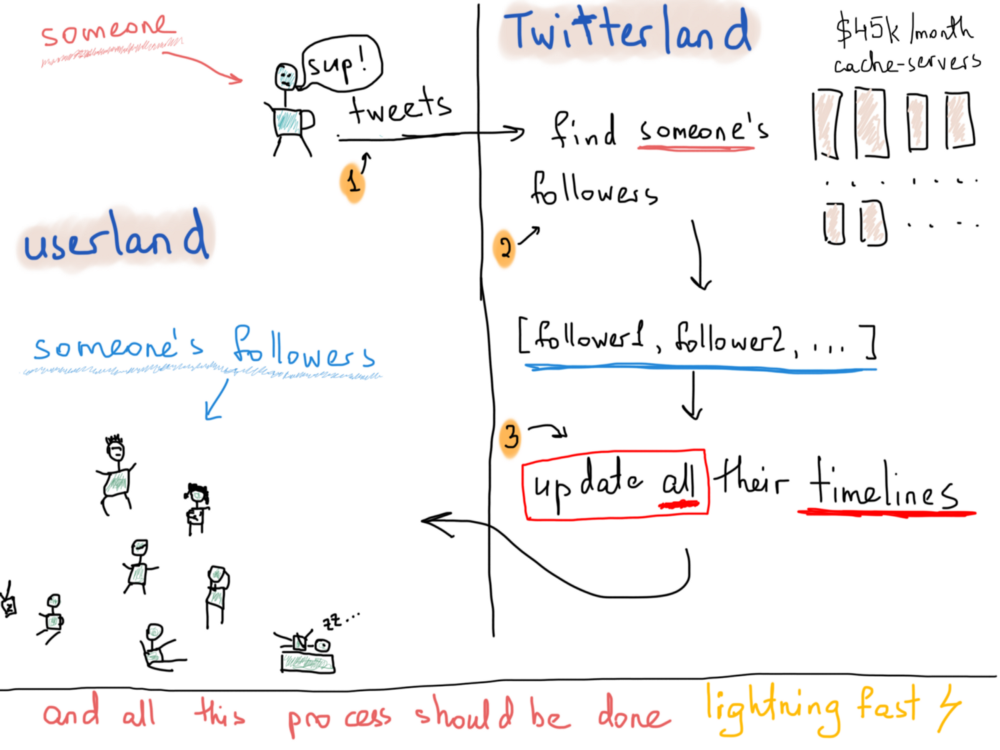
Опять же, мы не знаем о том, сколько времени требуется для доставки одного твита, чтобы он дошёл до всех фолловеров, но по общедоступной статистике мы можем увидеть, что ежедневно постится около 500 миллионов твитов.
Таким образом, процесс, изображённый выше, происходит 500 миллионов раз каждый день.
Нельзя найти какую-либо информацию по скорости передачи твитов. Можно предположить, что это время занимает около пяти секунд. Но обратите внимание на “тяжёлые случаи”: знаменитости с более, чем миллионом фолловеров. Они могут писать о своем замечательном завтраке в домике на пляже, но Twitter будет стараться изо всех сил, чтобы доставить этот супер-полезный контент миллионам фолловеров.
Предыдущий граф (с хэш-таблицей и кучей списков) позволяет нам эффективно находить всех пользователей, которых фолловит конкретный пользователь. Но это не позволяет нам эффективно найти всех пользователей, которые фолловят одного конкретного пользователя, в этом случае мы должны сканировать все ключи хеш-таблицы. Поэтому мы должны построить еще один граф, который является симметрично противоположным тому, который мы построили для подписок. Этот граф снова будет состоять из хэш-таблицы, содержащей все 300 миллионов вершин, каждая из которых указывает на список смежных вершин (структура остаётся той же), но на этот раз список смежных вершин будет представлять фолловеров (подписчиков).
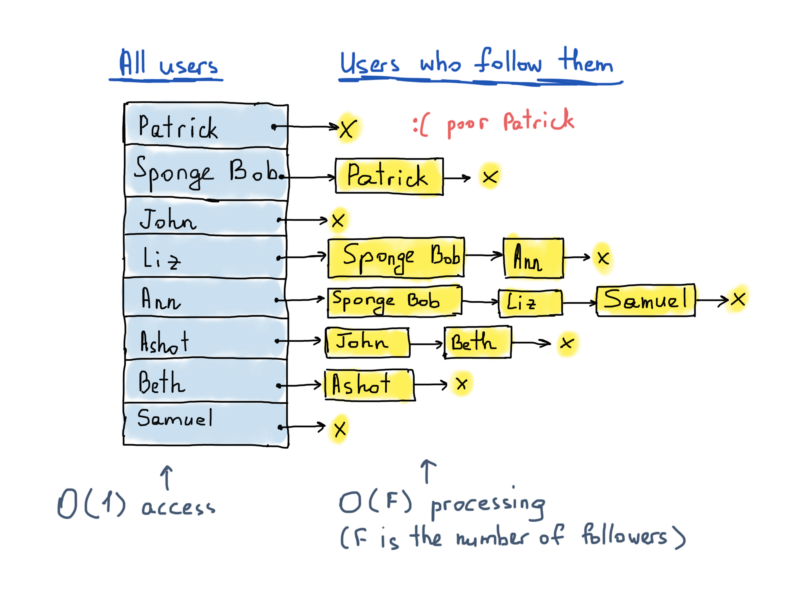
Таким образом, основываясь на этой иллюстрации, когда Liz постит новый твит, Губка Боб и Ann должны заметить этот твит в своей ленте через какое-то время. Общий метод для достижения этой цели – сохранение отдельных структур для ленты каждого пользователя. В случае 300+ миллионов пользователей Twitter, мы могли бы предположить, что есть по крайней мере 300+ миллионов лент (для каждого пользователя). В принципе, всякий раз, когда пользователь постит твит, мы должны получить список подписчиков пользователя и обновить ленту каждого из них. Лента может быть представлена в качестве связного списка или АВЛ-дерева.
// 'author' represents the User object, at this point we are interested only in author.id
//
// 'tw' is a Tweet object, at this point we are interested only in 'tw.id'
void DeliverATweet(User* author, Tweet* tw)
{
// we assume that 'tw' object is already stored in a database
// 1. Get the list of user's followers (author of the tweet)
vector<User*> user_followers = GetUserFollowers(author->id);
// 2. insert tweet into each timeline
for (auto follower : user_followers) {
InsertTweetIntoUserTimeline(follower->id, tw->id);
}
}
Это всего лишь основная идея, которую мы абстрагировали от фактического представления ленты, и, конечно, мы можем сделать доставку быстрее, если мы используем многопоточность.
Это имеет решающее значение для “тяжелых случаев”, потому что среди миллионов последователей те, которые находятся ближе к концу, обрабатываются позже, чем те, которые находятся ближе к началу списка.
// Warning: a bunch of pseudocode ahead
void RangeInsertIntoTimelines(vector<long> user_ids, long tweet_id)
{
for (auto id : user_ids) {
InsertIntoUserTimeline(id, tweet_id);
}
}
void DeliverATweet(User* author, Tweet* tw)
{
// we assume that 'tw' object is already stored in a database
// 1. Get the list of user's (tweet author's) followers's ids
vector<long> user_followers = GetUserFollowers(author->id);
// 2. Insert tweet into each timeline in parallel
const int CHUNK_SIZE = 4000; // saw this somewhere
for (each CHUNK_SIZE elements in user_followers) {
Thread t = ThreadPool.GetAvailableThread(); // somehow
t.Run(RangeInsertIntoTimelines, current_chunk, tw->id);
}
}
Поэтому, когда пользователи обновляют свою ленту, они получают новый твит.
Справедливости ради следует сказать, что мы просто коснулись верхушки айсберга реальных проблем в Airbnb или Twitter. Это занимает действительно много времени у талантливых инженеров, чтобы достичь таких больших результатов в сложных системах, таких как Twitter, Google, Facebook, Amazon, Airbnb и других. Просто имейте это в виду, читая эту статью.
Смысл демонстрации проблем доставки твитов заключается в том, чтобы показать реальное применение графов, но пока без использования алгоритмов.
Мы обсуждали дома Airbnb и эффективную фильтрацию, прежде чем заканчивать графические представления, и главной очевидной вещью была неспособность эффективно фильтровать дома с несколькими ключами фильтра. Есть ли что-нибудь, что можно было бы сделать с помощью алгоритмов на графах? Мы не можем точно сказать, но, по крайней мере, мы можем попробовать. Что, если мы представим каждый фильтр как отдельную вершину?
Буквально каждый фильтр, даже все цены от $10 до $1000 + все названия городов, коды стран, удобства (телевизор, Wi-Fi и все остальные), будет представлен как отдельная вершина графа.
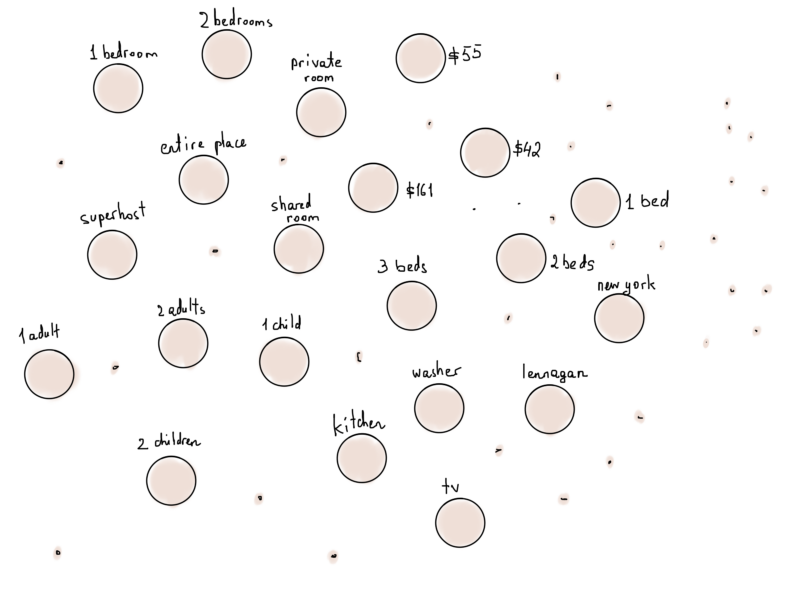
Мы даже можем немного усовершенствовать этот набор, сгруппировав удобства по определённым типам.
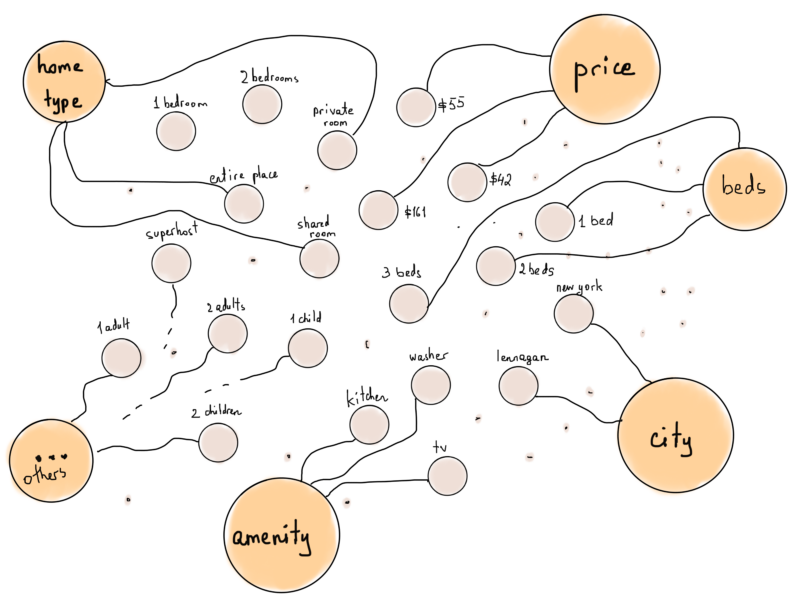
Теперь, что если мы представляем Airbnb дома как вершины, а затем соединим каждый дом с фильтрами, которые ему соответствуют?
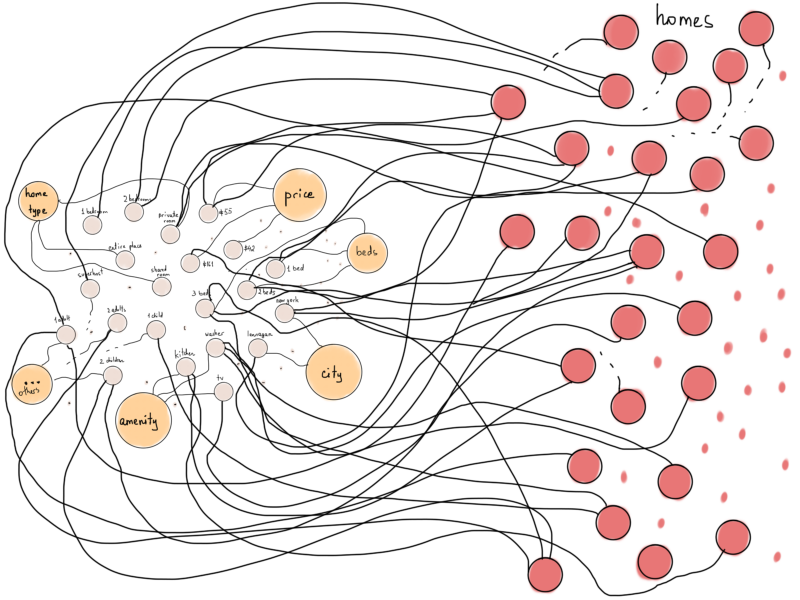
Изменение этой иллюстрации делает её более похожей на специальный тип графа, называемый двудольным графом.
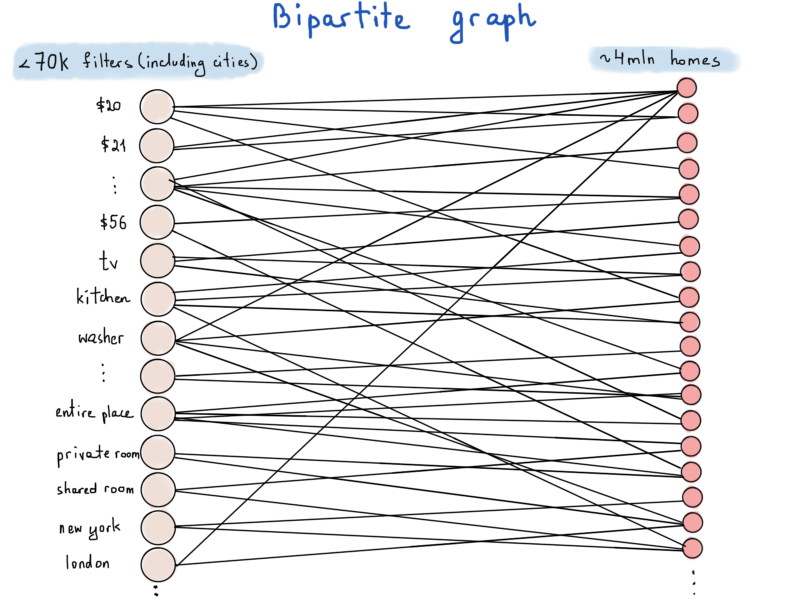
Алгоритмы на графах: введение
Двудольный граф или биграф — это граф, множество вершин которого можно разбить на две части таким образом, что каждое ребро графа соединяет какую-то вершину из одной части с какой-то вершиной другой части, то есть не существует ребра, соединяющего две вершины из одной и той же части. — Википедия.
Задача
Любая обработка графа может быть классифицирована как алгоритм графа. Вы в буквальном смысле можете реализовать функцию, выводящую все вершины графа. Большинство из нас боится алгоритмов, о которых идёт речь в учебниках. Давайте попробуем применить алгоритм Хопкрофта-Карпа для сопоставления двудольных графов к нашей задаче фильтрации домов Airbnb:
Дан двудольный граф домов Airbnb (H) и фильтров (F), где каждый элемент (вершина) H может иметь более одного соседними элементами (вершины) F (с общим ребром). Найти подмножество H, состоящее из вершин, смежных с вершинами в подмножестве F.
Алгоритм Хопкрофта — Карпа — алгоритм, принимающий на вход двудольный граф и возвращающий максимальное по мощности паросочетание, то есть наибольшее множество рёбер, таких что никакие два не имеют общую вершину. — Википедия.
Читатели, знакомые с этим алгоритмом, уже знают, что это не решает нашу проблему, потому что определение требует, чтобы никакие два ребра не имели общей вершины.
Рассмотрим пример иллюстрации, где есть всего 4 фильтра и 8 домов (ради простоты).
- Дома обозначаются буквами от A до H, фильтры выбираются случайным образом.
- Дом a имеет цену ($50) и 1 кровать, (это все, что мы получили за эту цену).
- Все дома от A до H имеют цену $50 за ночь и 1 кровать, но немногие из них имеют “Wi-Fi” и/или “телевизор”.
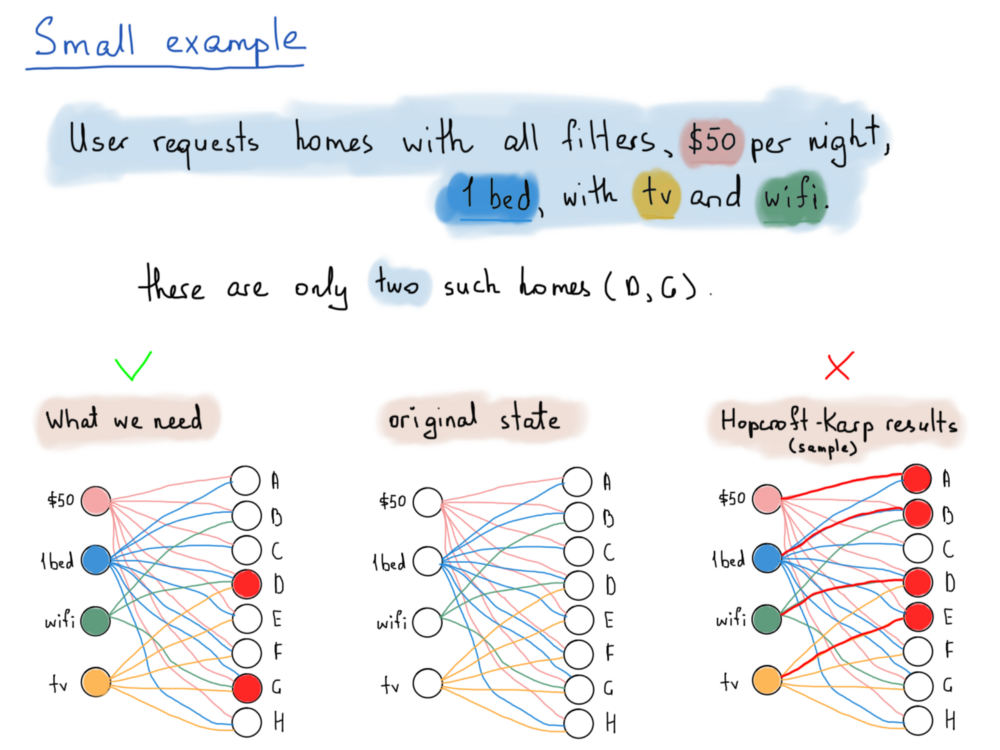
Решение нашей задачи требует наличия рёбер с общими вершинами, ведущих к различным вершинам домов, которые попадают в одно и то же подмножество фильтров, тогда как алгоритм Хопкрофта-Карпа устраняет такие рёбра с общими конечными точками и создает рёбра, инцидентные вершинам обоих подмножеств.
Взгляните на иллюстрацию выше: всё, что нам нужно, это дома D и G, которые удовлетворяют всем четырем значениям фильтров.
Нам нужно получить все совпадающие ребра, которые имеют общую конечную точку.
Мы могли бы разработать алгоритм для этого подхода, но его время обработки, возможно, не имеет отношения к потребностям пользователей (пользователям необходим мгновенный результат). Вероятно, было бы быстрее создать сбалансированное бинарное дерево поиска с несколькими ключами сортировки, почти как файл индекса базы данных, который отображает первичные / внешние ключи с набором удовлетворяющих записей.
Алгоритм Хопкрофта-Карпа (и многие другие) основан на алгоритмах обхода графов DFS (Depth First Search – обход в глубину) и BFS (Breadth First Search – обход в ширину).
Если честно, фактическая причина использования в этом примере алгоритма Хопкрофта-Карпа заключается в скрытом переключении на обходы графов, бинарных деревьев.
// struct ListNode {
// ListNode* next;
// T item;
// };
void TraverseRecursive(ListNode* node) // starting node, most commonly the list 'head'
{
if (!node) return; // stop
std::cout << node->item;
TraverseRecursive(node->next); // recursive call
}
void TraverseIterative(ListNode* node)
{
while (node) {
std::cout << node->item;
node = node->next;
}
}
Почти то же самое происходит с бинарными деревьями: вы выводите значения узла, затем переходите к двум следующим узлам. Здесь возникает три разных варианта:
- Вывести значение текущей вершины, затем перейти в левую дочернюю вершину, затем перейти в правую дочернюю вершину.
- Перейти в левую дочернюю вершину, вывести значение текущей вершины, затем перейти в правую дочернюю вершину.
- Перейти в левую дочернюю вершину, затем перейти в правую дочернюю вершину и вывести значение текущей вершины.
// struct TreeNode {
// T item;
// TreeNode* left;
// TreeNode* right;
// }
// you cann pass a callback function to do whatever you want to do with the node's value
// in this particular example we are just printing its value.
// node is the "starting point", basically the first call is done with the "root" node
void PreOrderTraverse(TreeNode* node)
{
if (!node) return; // stop
std::cout << node->item;
PreOrderTraverse(node->left); // do the same for the left sub-tree
PreOrderTraverse(node->right); // do the same for the right sub-tree
}
void InOrderTraverse(TreeNode* node)
{
if (!node) return; // stop
InOrderTraverse(node->left);
std::cout << node->item;
InOrderTraverse(node->right);
}
void PostOrderTraverse(TreeNode* node)
{
if (!node) return; // stop
PostOrderTraverse(node->left);
PostOrderTraverse(node->right);
std::cout << node->item;
}
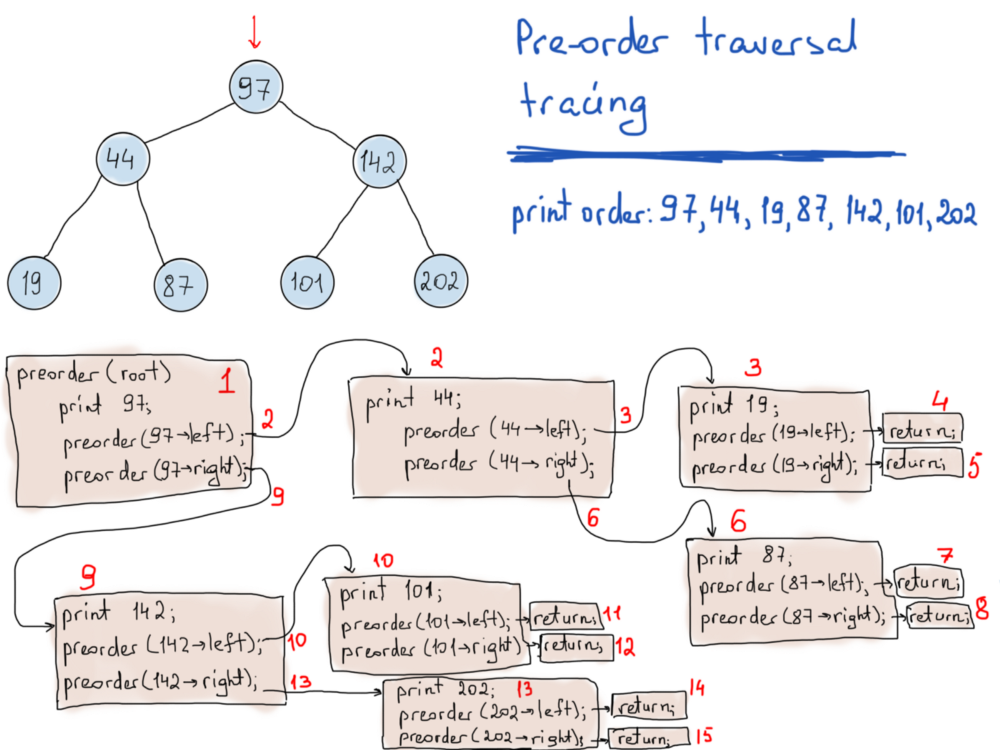
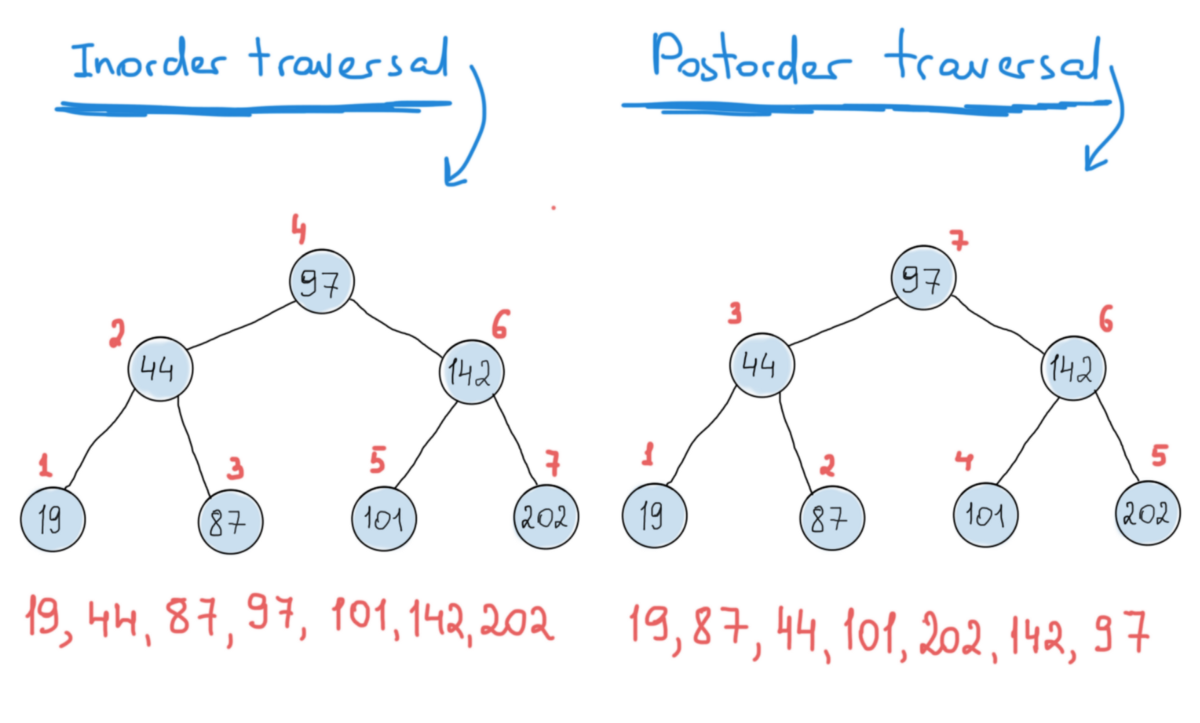
Насчёт рекурсии
Очевидно, что рекурсивные функции выглядят очень элегантно. Однако каждый раз, когда мы вызываем функцию рекурсивно, это означает, что мы выделяем под неё дополнительную память. Вот почему рекурсивные вызовы являются нерациональными (дополнительное пространство под стек и многочисленные вызовы функций) и даже опасными (переполнение стека). В критически важных системах программирования (самолеты, NASA и т.д.) рекурсия полностью запрещена.
Обход графа: DFS и BFS
Самые распространённые алгоритмы для графов
Если вы не знакомы с этой проблемой, подумайте о некоторой структуре данных, которую вы могли бы использовать для хранения узлов при обходе дерева. Мы разработаем два основных алгоритма обхода графа, то есть поиск в глубину (DFS) и поиск в ширину (BFS).
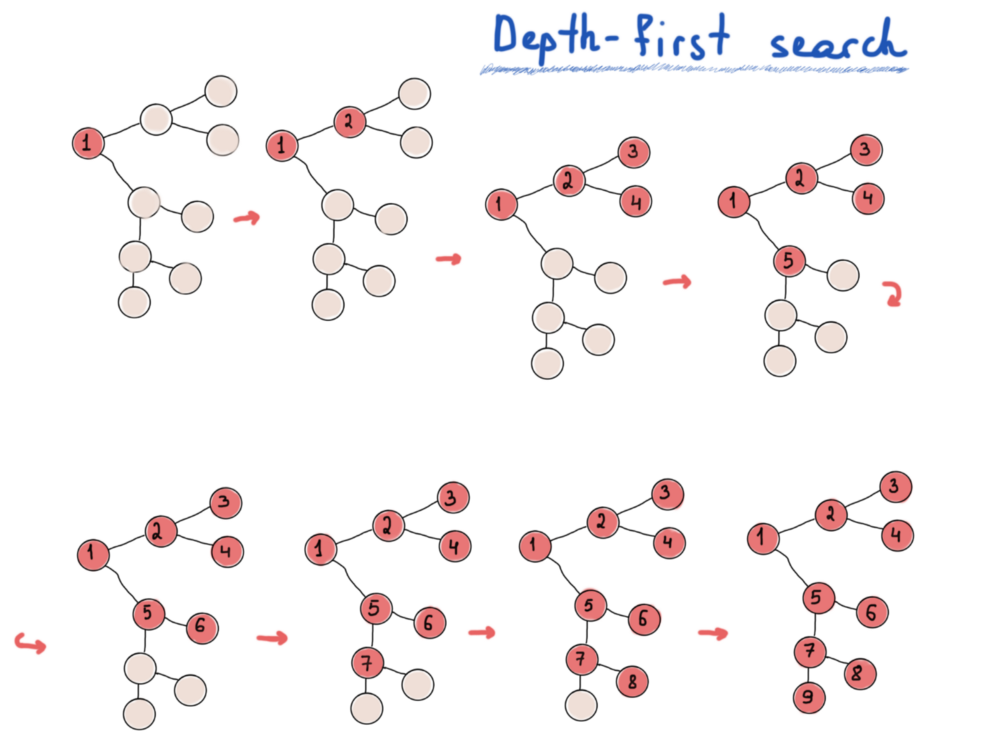
Поиск в глубину исследует самые дальние вершины, поиск в ширину исследует ближайшие.
- Поиск в глубину – больше действий, меньше мыслей.
- Поиск в ширину – хорошо осмотритесь, прежде чем идти дальше.
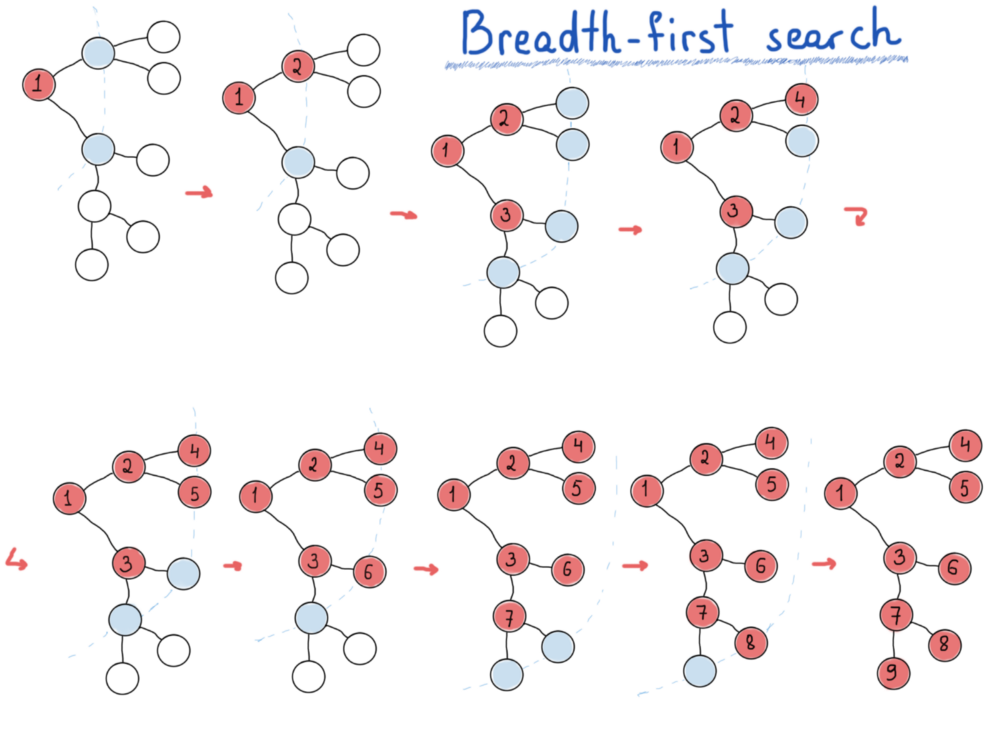
BFS – это то, что нам нужно, если мы хотим выводить вершины графов поэтапно. Для этого нам понадобится очередь (структура данных) для хранения “уровня” графа при выведении (или посещении) его “родительского уровня”. На предыдущей иллюстрации вершины, помещённые в очередь, имеют голубой цвет.
На каждом уровне вершины извлекаются из очереди, и, посещая каждую выбранную вершину, мы должны вставить её дочерние элементы в очередь (для следующего уровня). Следующий код достаточно прост, чтобы уловить основную идею BFS. Предполагается, что граф связан.
// Assuming graph is connected
// and a graph node is defined by this structure
// struct GraphNode {
// T item;
// vector<GraphNode*> children;
// }
// WARNING: untested code
void BreadthFirstSearch(GraphNode* node) // start node
{
if (!node) return;
queue<GraphNode*> q;
q.push(node);
while (!q.empty()) {
GraphNode* cur = q.front(); // doesn't pop
q.pop();
for (auto child : cur->children) {
q.push(child);
}
// do what you want with current node
cout << cur->item;
}
}
Имейте в виду, что реализация обхода изменяется в зависимости от того, как вы представляете граф.
DFS и BFS являются важными инструментами для решения проблем, касаемых графов. В то время как DFS имеет элегантную рекурсивную реализацию, имеет смысл избавить этот алгоритм от рекурсии. Для реализации BFS без рекурсии мы использовали очередь, для DFS вам понадобится стек. Однако неосвещённой остаётся ещё одна проблема: нахождение кратчайшего пути между вершинами графа. Поэтому, мы переходим к заключительному разделу статьи.
Uber и задача кратчайшего пути (алгоритм Дейкстры)
С его 50 миллионами пользователей и 7 миллионами водителей (источник), одна из самых важных вещей, которая имеет решающее значение для нормального функционирования Uber – это способность эффективно сочетать водителей с пользователями. Проблема начинается с местоположения.
Серверная часть должна обрабатывать миллионы пользовательских запросов, отправляя каждый из запросов одному или нескольким водителям поблизости. Хоть проще и иногда даже рациональнее отправлять запрос пользователя всем водителями, находящимся поблизости, всё же потребуется предварительная обработка.
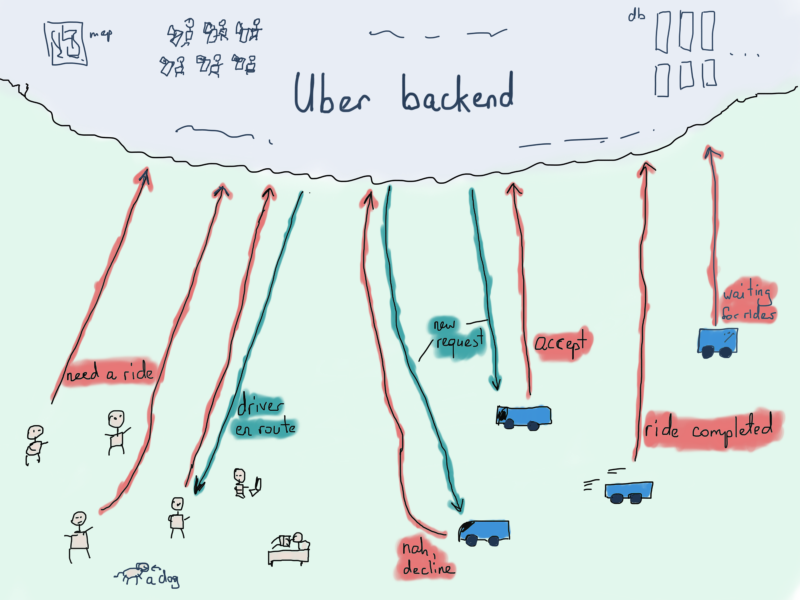
Кроме обработки входящих запросов и нахождения области местоположения на основе координат пользователя, а затем нахождения водителей с ближайшими координатами, нам также нужно найти правильного водителя для поездки. Чтобы избежать обработки геопространственных запросов (получение близлежащих автомобилей путем сравнения их текущих координат с координатами пользователя), предположим, у нас уже есть сегмент карты с пользователем и несколькими автомобилями поблизости.
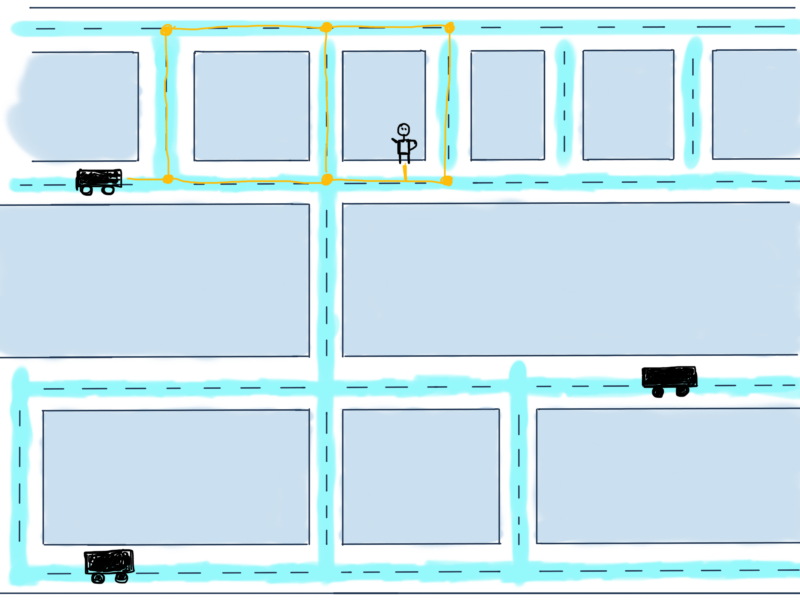
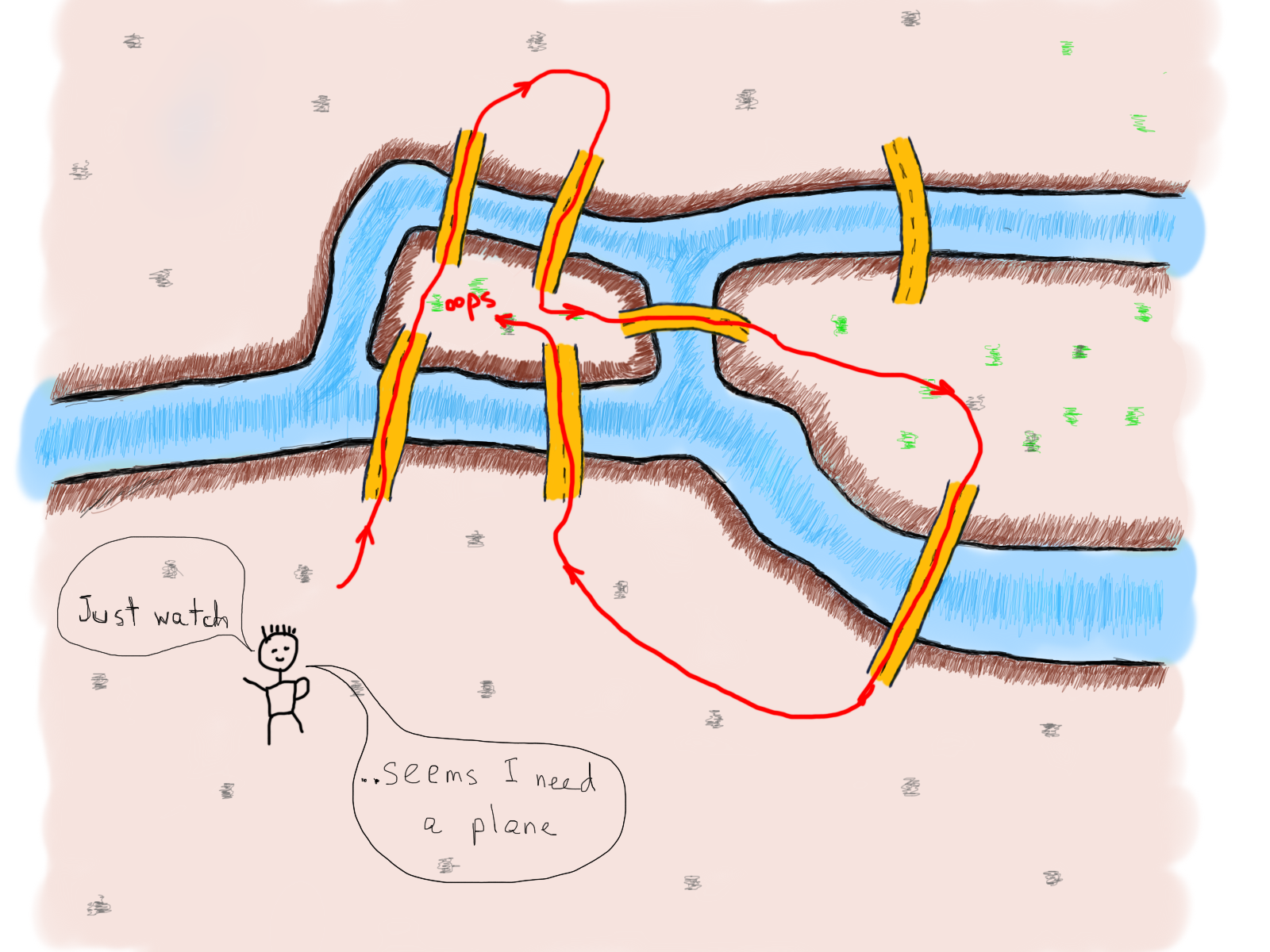
Возможные пути от автомобиля к пользователю обозначены желтым. Задача заключается в том, чтобы рассчитать минимальное расстояние между автомобилем и пользователем, другими словами, найти кратчайший путь между ними.
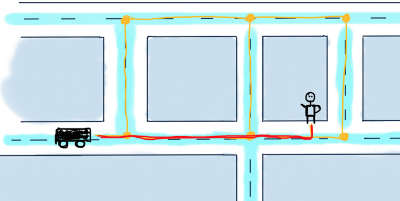
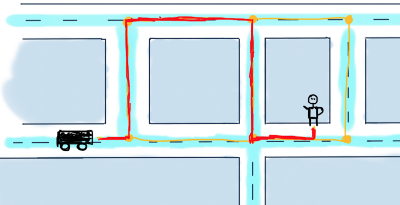
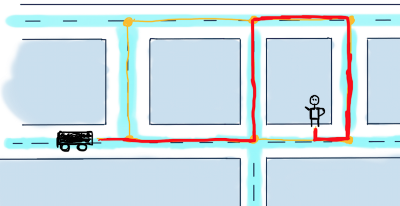
Представим этот сегмент в виде графа:
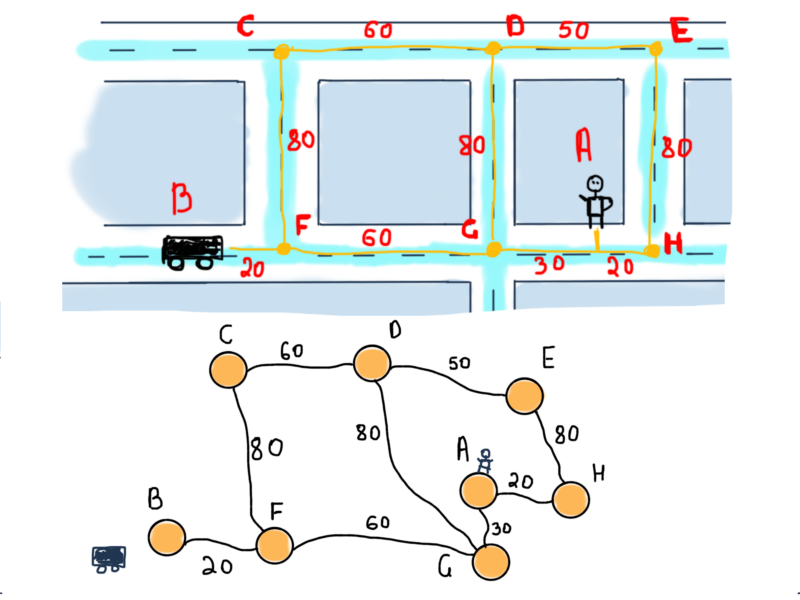
Это неориентированный взвешенный граф. Чтобы найти кратчайший маршрут между вершинами B (автомобиль) и А (пользователь), мы должны найти маршрут между ними, состоящий из ребер с возможно минимальными значениями.
Алгоритм действий
- Отметьте все вершины непосёщенными. Создайте структуру всех непосещённых вершин.
- Присвойте каждой вершине значение расстояние до этой вершины. Первой вершине присвойте ноль.
- Для текущей вершины рассмотрите непосещённые соседние вершины и вычислите расстояния до каждой с учётом текущей вершины. Сравните новое вычисленное расстояние с текущим назначенным значением и назначьте меньшее. Например, если текущая вершина А имеет вес 6, а ребро, связывающее её с соседом B, имеет длину 2, то расстояние до B через А будет 6 + 2 = 8.
- Когда мы закончим рассматривать всех соседей текущей вершины, отметьте текущую вершину как посещенную и удалите её из структуры непосещённых вершин. Эта вершина больше никогда не будет задействована.
- Если вершина назначения была отмечена как посещённая (при планировании маршрута между двумя определенными вершинами), остановитесь. Алгоритм завершен.
- В противном случае выберите непосещённую вершину, отмеченную наименьшим предварительным расстоянием, установите её в качестве новой текущей вершины и вернитесь к шагу 3.
Применяя это к нашему примеру, мы начнем с вершины B (автомобиль) в качестве начального узла. Для первых двух шагов:
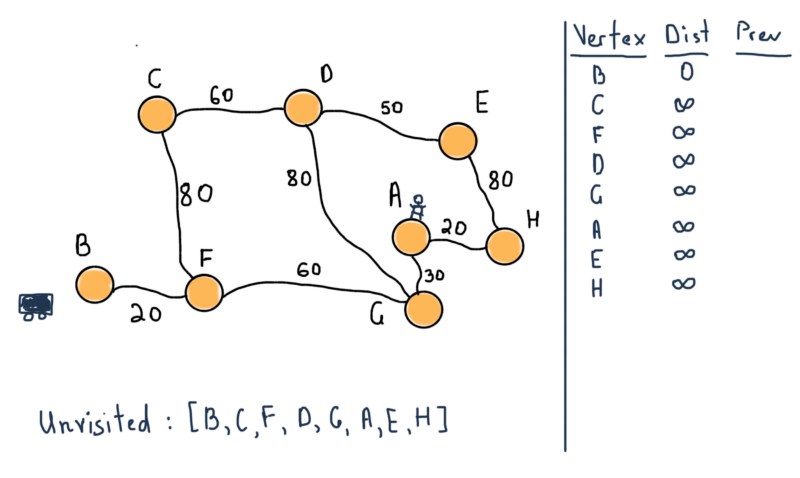
В нашей структуре непосещённых вершин находятся все вершины. Также обратите внимание на таблицу, в правой части иллюстрации. Для всех вершин там будут все самые короткие расстояния от B и предыдущей (отмеченной “Prev”) вершины, которые ведут к вершине. Например, от B до F расстояние = 20, за предыдущую вершину мы считаем B.
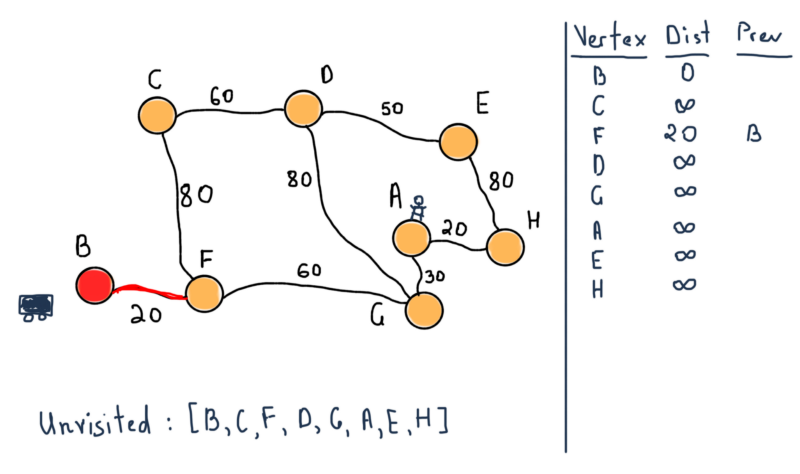
Мы помечаем B как посещённую вершину и переходим к соседней – F.
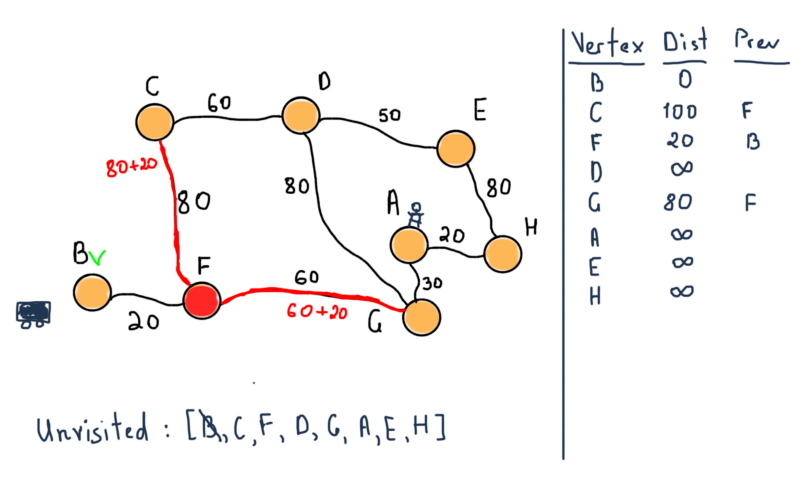
Теперь мы помечаем F как посещённую и выбираем следующую вершину, до которой расстояние минимально. Это вершина G.
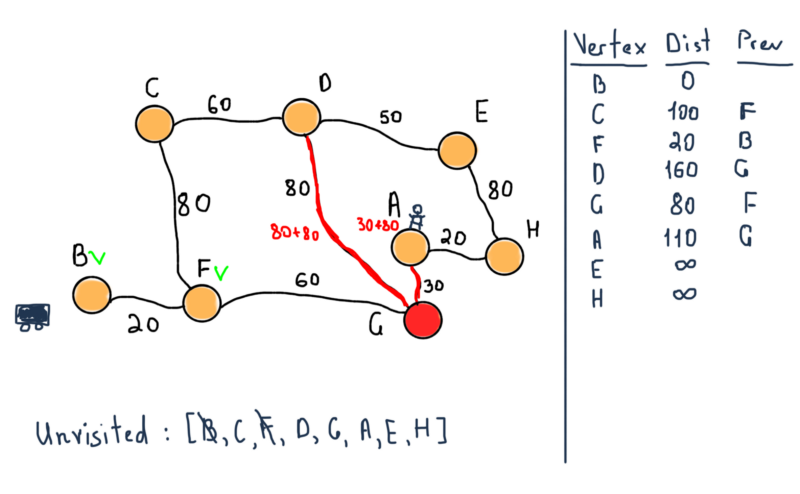 Как указано в алгоритме, если вершина назначения отмечена посещенной (при планировании маршрута между двумя определенными узлами, как в нашем случае), то мы можем остановиться. Таким образом, наш следующий шаг останавливает алгоритм со следующими значениями.
Как указано в алгоритме, если вершина назначения отмечена посещенной (при планировании маршрута между двумя определенными узлами, как в нашем случае), то мы можем остановиться. Таким образом, наш следующий шаг останавливает алгоритм со следующими значениями.
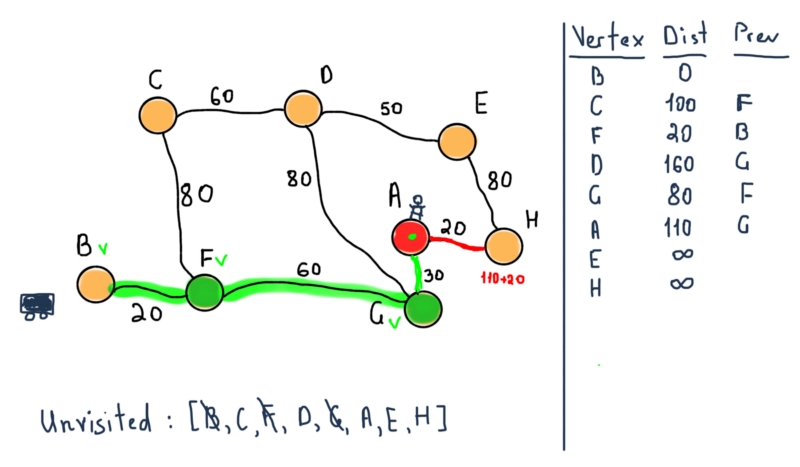 Таким образом, у нас есть как кратчайшее расстояние от B до A, так и маршрут через вершины F и G.
Таким образом, у нас есть как кратчайшее расстояние от B до A, так и маршрут через вершины F и G.
Заключение
В этой статье мы подробно рассмотрели основы теории графов. Как вы могли заметить, графы являются неотъемлемой частью программной инженерии, и, если вы претендуете на хорошую должность, вы обязаны разбираться во всём этом. Надеемся, что эта статья стала для вас хорошим фундаментом для дальнейшего изучения алгоритмов.
Оригинал
Материалы по теме:
- 10 алгоритмов на графах в гифках
- Математика для программиста: советы, разделы, литература
- Как научиться решать алгоритмические задачи?
- Искусственный интеллект и всё, о чем вы боялись спросить