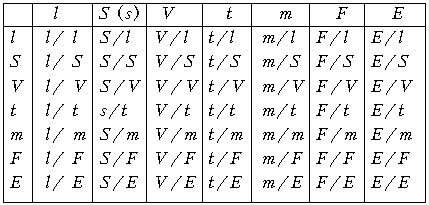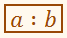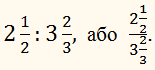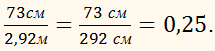Как составить отношение в физике

Пропорции и соотношения в физических задачах.

Автор: Аметова Эльмас Зеккиевна, учитель физики высшей категории МБОУ «Вилинская СОШ №2 с русским и крымскотатарским языками обучения» Бахчисарайского района Республики Крым.

Знания по физике становятся необходимыми в различных сферах деятельности человека. Решение физических задач – едва ли не главная часть физических знаний. Профессор Лев Давидович Ландау сказал: “Учебник физики должен состоять из одних задач. При их решении происходит усвоение физических знаний”. Но есть проблемы, одна из которых: неумение учащимися применять математические знания для решения физических задач. Практически все задачи по физике можно легко решать, используя математический аппарат. Но иногда то, что допустимо при решении задач по физике, недопустимо в общей математической практике.

Мне хотелось бы разобрать решения задач с использованием пропорций, отношений и соотношений из следующих физических тем: “Равновесие рычага”, “Уравнение Менделеева-Клапейрона. Внутренняя энергия идеального газа”, “Закон всемирного тяготения”, “Закон прямолинейного распространения света” и “Механические колебания. Математический маятник”.

Впервые интерес к пропорции, возникающей при делении отрезка в крайнем и среднем отношении, возникает в античной науке. Об этом свидетельствуют древнеегипетские храмы, знаменитые пирамиды (III тысячелетие до н.э.), также гробницы Менеса, дворцы в Персии и другое множество архитектурных сооружений древности. Необходимость возникновения и развития понятий пропорциональности и отношения отрезков, площадей и других величин появилась при построении упомянутых памятников древности.

Важную роль в создании понятия “пропорция” сыграл древнегреческий математик, астроном и механик Евдокс ( IV век до нашей эры). Слово «пропорция» ввел в употребление Цицерон в 1 веке до н.э., который буквально означал аналогия, соотношение.

Пропорция (от лат. proportio – «соотношение») – это отношение между двумя или более соразмерными величинами. Термин «пропорция» используется в математике, архитектуре, медицине, кулинарии, строительстве, химии, физике, природе, музыке и других областях науки и искусства. В создании образной выразительности в костюме огромную роль играют отношения и пропорции частей формы одежды. Пропорция-это равенство двух отношений. Если это равенство содержит переменную, значение которой надо найти, то оно является уравнением.

Запись пропорции.

Пропорцию с помощью букв записывают так: a:b=с:d или .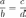

Хочется упомянуть о так называемом «золотом сечением». Золотым сечением называли математики древности и средневековья деление отрезка, при котором длина всего отрезка так относится к длине его большей части, как длина большей части к меньшей, и это отношение равно 8:5=5:3 =1,6. (8=5+3).

Основное свойство пропорции гласит, что в правильной пропорции произведение крайних членов равно произведению средних членов.

Отличным примером применения пропорции является задача на использование правила равновесия рычага (Архимеда).

Рассмотрим задачу на рычаг.

На концах рычага действуют силы 2 и 18 Н. Длина рычага 1 м. Где находится точка опоры, если рычаг – в равновесии? (Весом рычага пренебречь).

Преобразовав пропорцию и используя ее новый вид (уравнение), определили длины плеч рычага.

Еще есть соотношение (или просто отношением). Это некоторая взаимосвязь между сущностями нашего мира. Это могут быть числа, физические величины, предметы, продукты, явления, действия и даже люди.

В математике соотношение чаще употребляется как «отношение того-то к тому-то». Например, соотношение четырёх цилиндров и двух кубов в математике будет читаться как «отношение четырех кубов к двум цилиндрам»

Рассмотрим задачу из геометрической оптики.

На какой высоте H находится лампа над горизонтальной поверхностью стола, если тень от вертикально поставленного на стол карандаша высотой h= 0,15 м оказалась равной x= 0,1м при расстоянии от основания карандаша до основания перпендикуляра, опущенного из центра лампы на поверхность стола ℓ= 0,9 м?

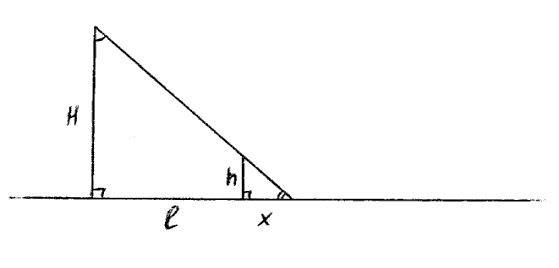
Как видим, чтобы измерить высоту потолка или столба не обязательно лезть на него, достаточно построить правильное соотношение.

В 10-м классе мы решали задачу на закон всемирного тяготения. Оказалось, что у этой задачи есть 2 способа решения. Остановимся на них.

Задача про космонавта.

Космонавт, находясь на Земле, притягивается к ней с силой 700 Н. С какой силой он будет притягиваться к Марсу, находясь на его поверхности, если радиус Марса примерно в 2 раза, а масса в 10 раз меньше чем у Земли?

Видно, что гораздо проще и интересней использовать не метод подстановки, а метод составления отношения величин друг к другу. Столько сокращений сразу! Главное: не перепутать основную дробь с другими! И ведь опять – пропорция!

Подобным образом можно решить задачу про маятники.

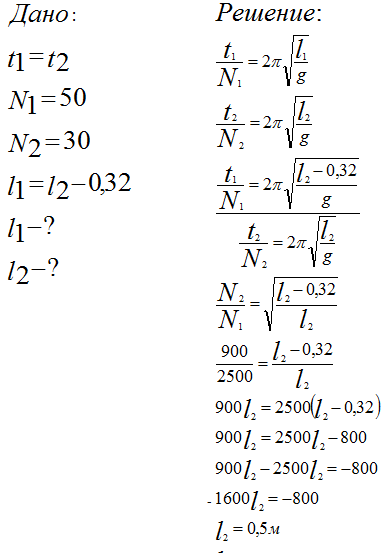
За одно и то же время один математический маятник делает 50 колебаний, а второй 30. Найти их длины, если один из них на 0, 32 м короче другого.

Как видно, можно без измерительных приборов и с помощью пропорций определить длину математического маятника. Здесь была использована формула периода колебаний математического маятника (через его длину ускорение свободного падения) и зависимость периода от числа колебаний и времени.

Во многих задачах, на первый взгляд, слишком много неизвестных. Кажется, что такая задача не может быть решена. Но если в задаче стоит вопрос о том, во сколько раз одна величина больше или меньше другой, то, скорее всего, все вспомогательные величины, которые мы введем для того, чтобы было проще, рассуждать на заключительном этапе, когда мы будем рассчитывать отношение, сократятся.

Уравнения с одним неизвестным во время решения задач по физике появляются при использовании законов, правил, определений или непосредственно выведенных применительно к той или иной задаче формул. В школьной физике большинство уравнений могут быть сведены к уравнениям, которые содержат неизвестные величины в первой степени. Достаточно редко встречаются уравнения второй степени и крайне редко третьей. Другое дело, что записанные в своем первоначальном виде, уравнения часто являются довольно громоздкими, и требуется большой опыт для того, чтобы выразить из них неизвестные величины. К сожалению, именно неумение выполнить тождественные преобразования уравнений, очень часто не позволяет школьникам правильно решить задачу и получить удовольствие от изучения физики. Из ошибок, которые наиболее часто делаются школьниками, следует особо сказать о тех, которые связаны с неумением производить операции с алгебраическими дробями. При решении уравнения допускается выполнять только тождественные преобразования, т.е. такие, которые не приводят к изменению решений первоначального уравнения.

Применение отношения при решении задач молекулярной физики.

Рассмотрим пример. Дано уравнение PV = m/µ RT, нужно вычислить неизвестную µ. Более половины учащихся самостоятельно сделать это не могут, хотя на математике долго изучают делитель, делимое, частное. Самый простой способ выражения неизвестной – это метод пропорций (крест на крест) т. е. при переносе из одной части уравнения в другую меняем расположение µ = mRT/PV. Такой способ успешно используется многими учителями.

До сих пор мы рассмотрели все случаи, когда делятся друг на друга одинаковые величины. В следующей же задаче мы будем делить друг на друга разные величины.

При ее решении образуется система уравнений, причем ее можно решить двумя методами.

Первый метод – это метод подстановки, при котором неизвестная величина, входящая в одно из уравнений, выражается, так как при решении уравнения с одним неизвестным. Затем полученное выражение для этой неизвестной величины подставляется вместо нее во второе уравнение. Этот метод часто приводит к громоздким выражениям. При этом можно совершить множество ошибок.

Суть второго метода в том, что уравнения системы складываются, вычитаются, умножаются или делятся друг на друга. То есть над правыми и над левыми частями уравнений производятся одинаковые действия. Это нужно для сокращения неизвестных величин после выполнения некоторых действий над ними. Этот метод является более эффективным, но в данном случае требуется сообразительность и опыт.

Рассмотрим применение этих методов в следующей задаче.

В баллоне объемом 2 л находится гелий. Внутренняя энергия гелия равна 300 Дж. Определите давление в сосуде.

Здесь важно было определить, что на что делить и заметить одинаковые величины в уравнении Менделеева – Клапейрона и формуле внутренней энергии газа! Кстати, можно делить импульс на кинетическую энергию, даже силу Кулона взаимодействия электрических зарядов на силу всемирного тяготения, то есть фактически один закон на другой! В “многоэтажных” выражениях, когда одна дробь делится на другую, необходимо различать основную дробь и дополнительные, знак равенства следует ставить точно напротив основной дроби. При решении уравнения допускается выполнять только тождественные преобразования, т.е. такие, которые не приводят к изменению решений первоначального уравнения.

И еще. Умение построить правильное отношение— важный навык при решении задач.

Использовать математику в физике – это настоящее искусство! Но, чем заниматься методом подстановки, проще делить одно выражение на другое, причем можно делить и разные физические величины. Мои материалы могут пригодиться школьникам и молодым учителям на уроках физики. А сколько еще тем мы не рассмотрели! Описанные алгоритмы, при их активном использовании на уроках позволяют существенно сократить время на приобретения учащимися навыка решения задач. Алгоритмы универсальны и могут применяться в любой теме курса физики. Можно один раз затратить учебное время на обучение решению задач, а затем вводить только новые законы и закономерности. И еще: все-таки, есть своя красота в физических задачах!

Список использованных источников:

1. Поль Дирак http://dmpokrov.livejournal.com/403285.html

2. Лев Давидович Ландау: Обучение студентов Майя Бессараб. Москва. «Октопус» 2008 г. 61 с.

3. Глава из книги И.И.Гарина «Ангелы библиотек». 2017 г. 660с. Автор И.И.Гарин. https://www.proza.ru/2017/03/10/804

4. Книга «Начала», автор Евклид, издательство «Лириком» год 2012. 446 страниц

5. «Теория отношений Евдокса и теория сечений Дедекинда» Струнилина К. teh–krasina.ru›…NSO…teorija_otnoshenij…i_teorija…

6. Никольский. С.М. Математика -6 класс. С.М.Никольский, М.К.Потапов, Н.Н.Решетникова Москва: «Просвещение” 2014 год, 256 с.

7. Сборник задач по физике для 7-9 классов – Лукашик В.И., Иванова Е.В. Москва “Просвещение” 2011:

8. Исаков Александр Яковлевич. И 85 Физика. Решение задач ЕГЭ. Часть 8. Оптические явления. Кам-чат ГТУ, 2013. 195 с.7

9. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. (Под ред. Николаева В.И., Парфентьевой Н.А). Физика-10: учебник для общеобразовательных учреждений с приложением на электронном носителе: базовый и профильный уровни М.: Просвещение, 2014, 416 с.

10. Сборник задач и упражнений по физике под ред. Рымкевич -2011 г. 158 с.

11. Демидова М.Ю., Грибов В.А., Лукашева Е.В., Чистякова Н.И. «Физика ЕГЭ 2016». Издательство «Экзамен», 2016 г. 294 с.

Осмысление понятия «удельная величина»

Л.Н.РАГУЛИНА,
школа № 266, г. Москва

aaragulina@mail.ru

Осмысление понятия «удельная
величина»

Мышление – это деятельность «чтобы
узнать»,
а о вещах ничего нельзя узнать, не проследив,
что они делают и что с ними делается.

П.Я.Гальперин

В процессе обучения физике разумность
деятельности является наиважнейшей задачей.
Примером построения образа, выработки умения
«вращать» его мысленно, рассматривая с разных
сторон, под разными углами является формирование
понятия удельной величины. Удельные величины
(т.е. доли) рассматриваются в течение всего курса
физики и представляют собой в обобщённом виде
отношение двух физических величин:

– удельная теплоёмкость ~ Q/m;

– удельная электропроводность ~ R/l,
~ R/S;

– удельная теплота сгорания топлива L/m;

– удельная теплота парообразования /m;

– удельная энергия связи в ядре E_N
= E/N.

Так как разумность действия
подразумевает ориентацию на существенные
свойства и отношения, то развёртывание наполняет
эти соотношения разнообразным смыслом. Например,
целесообразно предложить учащимся составить
таблицу из отношений физических величин и
развернуть их, т.е. охарактеризовать на примерах
из собственного опыта.

Примеры выполнения задания

Отношения разнородных величин

• m/ V: масса отварного
  картофеля/объём воды; масса полученного
  творога/объём молока; масса резинового
  шарика/объём вдуваемого воздуха.

• V/ m: объём тарелки/масса супа;
  объём древесины/масса полученной бумаги; объём
  шкафа/масса одежды.

• m/t: масса яблок/время роста; масса
  банана/время съедания; масса куска сахара/время
  растворения. (Это уже не скорости. – Ред.)

• t/V: время расчёсывания
  волос/объём волос; время таяния льда/объём льда;
  время/объём песка в песочных часах.

• E/t: затраченная энергия/время
  тренировки; энергия аккумулятора/время работы
  плеера; энергия зарядки мобильного
  телефона/время работы.

• S/V: площадь пожара/объём воды;
  площадь поверхности головы/объём волос; площадь
  поля/объём жидких удобрений.

• S/m: площадь разрушений/масса
  взрывчатки; площадь Красной площади/масса
  собравшихся людей; площадь парка/масса
  памятников.

Отношения однородных величин:

• S₁/S₂: площадь
  сцены/площадь люка;

• t₁/t₂: время урока
  физики/всё время пребывания в школе;

• V₁/V₂: объём
  нефти/объём бензина;

• E₁/E₂: энергия,
  потребляемая в Москве/энергия, потребляемая в
  России;

• m₁/m₂: масса
  ягод/масса сахара;

• l₁/l₂: длина
  строки/длина всей статьи.

Придуманные образы и наполнение
отношений смыслом являются превращёнными
формами жизненных ситуаций учащихся. После
такого обдумывания отношений величин легко
ввести понятие удельной теплоёмкости в 8-м классе
на уроке «Количество теплоты и удельная
теплоёмкость».

Ход урока

Учитель. Когда мы рассматривали
движение шарика по наклонной плоскости, то
установили, что в отсутствие сопротивления
движению полная механическая энергия
сохраняется. Но при наличии трения этот закон не
выполняется, т.к. изменяются состояния тел: когда
механическая энергия убывает, обычно тела
нагреваются. Приведите примеры.

Учащиеся. Удар молотка о
свинцовую плиту; натирание ластиком крышки
стола; сгибание и разгибание проволоки.

Учитель. Могут происходить и
другие изменения. Например, при вылетании пробки
из бутылки с газированной водой под давлением
газа газ охлаждается. При размельчении тела
наоборот нагреваются. Аналогичные явления
происходят при плавлении или отвердевании
вещества. Что меняется во всех этих примерах в
веществе, из которого состоят тела?

Учащиеся. Взаимодействие молекул,
изменение характера их движения, т.е. внутренняя
энергия.

Учитель. Изменение внутренней
энергии может происходить не только при
совершении работы. Например, при остывании
горячей воды в стакане никакой работы не
совершается, а внутренняя энергия убывает.
Происходит просто передача тепла. Для
характеристики этого процесса введено понятие
количества теплоты Q. Исследуем, от чего оно
зависит. Если в ванну с холодной водой добавить
стакан кипятка, то увеличение температуры будет
незаметным. А когда стакан кипятка окажет
существенное влияние?

Учащиеся. Когда массы тел
соизмеримы.

Учитель. Значит, изменение
внутренней энергии зависит от массы тела. Как
можно охарактеризовать эту зависимость?

Учащиеся. Изменение внутренней
энергии прямо пропорционально массе тела.

Учитель. Другими словами, на
каждую долю массы тела приходится определённое
изменение внутренней энергии. А теперь возьмём
две совершенно равные массы воды. Но в одном
сосуде вода горячая, а в другом холодная.
Поставим на одинаковые плитки. Какая вода будет
нагреваться дольше до кипения?

Учащиеся. Холодная.

Учитель. Что это означает?

Учащиеся. Холодной воде требуется
больше сообщить тепла.

Учитель. Значит и изменение
внутренней энергии холодной воды будет больше.
Сделайте вывод.

Учащиеся. Изменение внутренней
энергии прямо пропорционально изменению
температуры тела. То есть на каждый градус
температуры приходится определённое изменение
внутренней энергии.

Учитель. Замечу, что чем выше
температура тела, тем дольше оно остывает.
Возьмём тела одинаковой массы, нагретые до
одинаковой температуры. Пронаблюдаем, под каким
из цилиндров: латунным, железным или алюминиевым
расплавится больше воска. (Демонстрация.)
Сделайте вывод.

Учащиеся. Под цилиндрами
расплавилось разное количество воска. Значит
цилиндры отдали разное количество теплоты.
Отсюда следует, что изменение внутренней энергии
зависит от рода вещества.

Учитель. Для характеристики
тепловых свойств веществ используют удельную
теплоёмкость. Её выражают в Дж/(кг Ч град).
Учёные определили удельную теплоёмкость многих
веществ. Это свойство зависит от температуры, но
очень незначительно, так что эту зависимость мы
не будем учитывать. Что показывает удельная
теплоёмкость?

Учащиеся. Количество теплоты,
необходимое для нагревания 1 кг вещества на 1 °С.
Или количество теплоты, выделившегося при
остывании 1 кг вещества на 1 °С.

Учитель. Обобщим: от чего зависит
изменение внутренней энергии?

Учащиеся. От массы, разности
температур, рода вещества.

Учитель. Для вычисления
количества теплоты, передаваемого или
отдаваемого телом, существует формула: Q = cm
(t₂ – t₁). Теперь обратимся к
таблице удельных теплоёмкостей:

– У какого вещества самая большая
удельная теплоёмкость? самая маленькая? что это
означает?

– Можно ли на пламени свечи вскипятить
ведро воды? Почему?

– Можно ли передать некоторое
количество теплоты, не вызывая этим повышение
его температуры?

– Как быстрее остудить горячий чай:
бросить в него сахар сразу или подождав 5 мин?
Растворение сахара идёт с поглощением тепла.

– Одинаковое ли количество теплоты
необходимо для нагревания газа до одной и той же
температуры в сосудах, закрытых поршнем, если в
одном сосуде поршень перемещается, а в другом
неподвижен?

– Какое тело нагреется до более
высокой температуры: кусок свинца или стали той
же массы, если по ним ударить молотком одинаковое
число раз с одинаковой силой?

Как показывает практика, единожды тщательно
отработанное понятие удельной величины не
вызывает в дальнейшем изучении физики никаких
трудностей при введении понятий: удельная
теплота плавления, парообразования, сгорания и
другие.

Людмила Николаевна Рагулина окончила
Ленинградский ГПИ им. А.И.Герцена в 1976 г. по
специальности «Физика», учитель физики высшей
квалификационной категории, педагогический стаж
29 лет. Работала в основном в СВАО г. Москвы в
школах № 247, 1122, 266. Отличник народного
просвещения, ветеран труда, кустовой методист
округа «Лианозово», лауреат конкурса «Лучшие
учителя России» 2006 г., неоднократно награждалась
грамотами городского комитета, МДО и др. Только
за последние 4 года её ученики 12 раз побеждали в
олимпиадах и конкурсах проектов. Под
руководством профессора МГУ им. М.В.Ломоносова,
д.п.н. Ю.А.Самоненко проводит в школе
диссертационное исследование на тему «Создание
комфортной обучающей среды с усилением
методологического компонента в
естественнонаучном образовании школьников».
Главная идея работы – внедрение деятельностного
подхода в образовании с использованием
здоровьесберегающих технологий, с учётом
психологических и поведенческих нарушений
детской психики и хронического или
эпизодического стресса.Сейчас на завершающем
этапе находится методическая разработка
элективного курса по физике I ступени
«Гимнастика ума». В этом курсе на простых
примерах дети научаются рассуждать и
самостоятельно исследовать явления. Среди
выпускников есть учёные, преподаватели не только
средних школ, но и таких вузов, как МФТИ, РУДН и
даже Кембриджского университета. Муж Александр
– художник-реставратор, обе дочери защитили
степени магистров, внучке Машеньке уже годик.
Людмила Николаевна любит шить и вязать – но где
взять на это время?

ОТНОШЕНИЕ СИЛ

ВИДЕО УРОК

Отношение величин
приходится находить при решении множества самых разнообразных задач. Это способ
сопоставления однородных величин, который состоит в том, что при сравнении
величин стараются ответить на вопрос во 
сколько  раз одна из них больше
другой.

Отношение чисел.

Как уже отмечалось,
частное от деления одного числа на другое называется также их отношением.
Таким образом, частное и отношение обозначают одно и то же понятие. Однако,
когда говорят <<частное>>, имеют в виду одно число, полученное в
результате деления двух данных чисел. Когда же говорят <<отношение>>,
имеют в виду пару чисел, соединённых знаком деления.

ПРИМЕР:

Если разделить  10  на  2, получим:

10 : 2 = 5.  

В данном  случае
говорят, что частное от деления  10  на  2  равно  5, говорят
также, что отношение  10
 к  2  равно  5. Но
само отношение данных чисел записывают в виде 
10 : 2, или  ¹⁰/₂. Понятно,
что числа  10
: 2  и  5  равны, поэтому и говорят, что отношение – то
же самое, что и частное.

 ПРИМЕР:

Цена – это отношение стоимости товара к количеству
единиц. Если за  5 кг  яблок
заплатили  100 руб, то цена товара будет отношением  100  к  5, то есть

100 : 5 = 20.

ПРИМЕР:

²/₈ – это отношение
показывает, что  2  составляет  ¹/₄  часть от 
8, так как:

²/₈ = ¹/₄.

⁴/₂₀ – это отношение
показывает, что  4  составляет  ¹/₅  часть от 
20, так как:

⁴/₂₀ = ¹/₅ = 0,2.

Отношением называется число, которое показывает, во
сколько раз одна величина больше другой, или какую часть одна величина составляет
от другой.

Для обозначения отношения
используют дробную черту или двоеточие – деления  (:). В  общем
виде отношение записывают так:

Числа  a  і  b  называются членами отношения.
Первый член  a называется предыдущим, а второй член  b –
последующим.

ПРИМЕР:

В отношении

4 : 5,

число  4  есть предыдущий член, 5 –
последующий.

Так как отношение
двух чисел с помощью деления, то для него справедливы все свойства частного.

Основное свойство отношения.

Значение отношения не изменится, если его члены умножить
или разделить на одно и то же число, отличное от нуля.

Членами отношения
могут быть любые числа, только последующий член не может быть равен нулю. Поэтому
возможны и такие отношения:

Чтобы найти
отношение одноименных величин (длин, масс и т. д.), необходимо выразить их в
одной и той же единице измерения – в противном случае полученный результат для
сравнения величин использовать нельзя.

ПРИМЕР:

Найти отношения  73
см  к 
2,92 м:

Сокращение членов отношения и
замена отношения дробных чисел отношением целых чисел.

Используя основное свойство
отношения, выполняем два преобразования:

– сокращение членов отношения;

– замену отношения дробных чисел отношением целых
чисел.

Как это выполняется,
видно из следующих примеров.

ПРИМЕР:

Сократить члены отношения:

48 : 32 = 3 : 2.

ПРИМЕР:

Заменить отношение дробных чисел отношением целых чисел:

1¹/₂ : ²/₃ = ³/₂ : ²/₃

= ⁹/₆ : ⁴/₆ = 9 : 4. 

Мы привели дроби к общему знаменателю, а затем умножили
предыдущий и последующий члены отношения на их общий знаменатель  (на 6).                        

При сравнении величин мы можем найти два таких отношения,
в которых предыдущий член одного будет следующим членом другого и наоборот.
Такие два отношения называются обратными. Произведение обратных отношений
равно единицы.

Отношение величин.

Отношение однородных величин равно отношению чисел,
получающихся при измерении этих величин одной и той же единицей; оно не зависит
от выбора единицы измерения.

Иногда говорят об
отношении разнородных величин. Например, говорят об отношении пути ко времени,
массы к объёму и т. д. отношение разнородных величин есть величина. Так,
отношение пути ко времени есть скорость, отношение массы к объёму – плотность и
т. д. значение отношения разнородных величин зависит от выбора единицы
измерения.

ПРИМЕР:

Если путь равен  20
м, а время, затраченное на его прохождение, равно  5
сек, то отношение пути ко времени равно  4
м/сек. Оно выражает скорость движения в 
м/сек. Если тот же путь измерить в километрах, а время – в часах, то
отношение пути ко времени будет равно:

0,02 : ¹/₇₂₀ = 14,4 (км/час).

Оно выражает ту же скорость в  км/час:

4 м/сек = 14,4 км/час.

ЗАДАЧА:

Найдите отношение величин:

1,2 м  и  40 см.

РЕШЕНИЕ:

Прежде чем искать отношения величин, приведём все члены к одной и той же
единице измерения. Переведём метры в сантиметры. В  1 м  100 см. Поэтому, чтобы
перевести  1,2 м  в сантиметры, умножим  1,2  на  100.

1,2 ∙ 100 = 120 см.

Теперь найдём отношение величин  120  и 
40:

¹²⁰/₄₀ = ³/₁.

Итак, 1,2 м 
относится к  40 см, как  3  относится к  1.

ЗАДАЧА:

Найдите отношение величин:

2 кг  и  500 г.

РЕШЕНИЕ:

Прежде чем искать отношения величин, приведём все члены к одной и той же
единице измерения. Переведём килограммы в граммы. В  1 кг  1000 г. Поэтому, чтобы
перевести  2 килограмма  в граммы, умножим  2  на  1000.

2 ∙ 1000 = 2000 г.

Теперь найдём отношение величин  2000  и 
500:

²⁰⁰⁰/₅₀₀ = ⁴/₁.

Итак, 2 кг 
относится к  500 г, как  4  относится к  1.

ЗАДАЧА:

Найдите отношение величин:

50 см  и  2 дм.

РЕШЕНИЕ:

Прежде чем искать отношения величин, приведём все члены к одной и той же
единице измерения. Переведём дециметры в сантиметры. В  1 дм  10 см. Поэтому, чтобы
перевести  4 дециметра  в сантиметры, умножим  4  на  10.

4 ∙ 10 = 40 см.

Теперь найдём отношение величин  50  и 
40:

⁵⁰/₄₀ = ⁵/₄.

Итак, 50 см  относятся
к  4 дм, как  5  относится к 
4.

ЗАДАЧА:

Количество  шоколадных конфет, которые находятся в пакете,
относятся до количества карамелек как  3 : 5.
Укажите число, которым может быть выражено количество шоколадных конфет и
карамелек.

25;  32; 
30;  36.

РЕШЕНИЕ:

Пусть  3х – количество шоколадных конфет, тогда  5х
кг – количество карамелек.

3х + 5х = 8х.

Поэтому, количество конфет должно быть кратно  8,
то есть  32
 конфеты

ЗАДАЧА:

На  200 руб  можно
купить  4
кг  яблок. Сколько килограммов картошки
можно купить на эти деньги, если картофель в 
5
раз дешевле яблок ?

РЕШЕНИЕ:

1 способ решения.

Если  4 кг  яблок
стоят  200
руб, то можно узнать, сколько стоит  1 кг  яблок. Для
этого всю стоимость (200 руб) разделим на количество килограммов (4 кг).

200 : 4 = 50 (руб).

50
рублей стоит  1 килограмм яблок. Но так как картофель дешевле яблок
в  5
раз, то цена  1 кг  картофеля
будет:

50 руб : 5 = 10 руб.

Тогда на  200 руб  можно купить
картофеля

200 : 10 = 20 (кг).

ОТВЕТ:  на  200
руб  можно купить  20
кг  картофеля.

2 способ решения.

Если картофель дешевле яблок в  5 раз,
а яблок можно купить на  200 рублей  4 кг, значит, картофеля можно купить в  5
раз больше:

4 кг ∙ 5 =
20 кг.

ОТВЕТ: 

на  200 руб  можно
купить  20
кг  картофеля.

ЗАДАЧА:

Масса ящика с огурцами составляет  36
кг. Масса пустого ящика 
равна  2 кг 400
г. Найдите отношение огурцов к массе ящика.

РЕШЕНИЕ:

Если ящик с огурцами весит  36
кг, а пустой ящик весит  2 кг 400 г,
то можно найти вес огурцов:

36 кг – 2 кг 400 г = 33 кг 600 г.

Переведём значения, выраженные в килограммах и граммах в
килограммы:

33 кг 600 г = 33,6 кг,

2 кг 400 г = 2,4 кг.

Теперь найдём отношение массы огурцов к массе пустого
ящика:

33,6 : 2,4 = 14.

ЗАДАЧА:

В школьную библиотеку привезли новые учебники для  7-9
классов, по  125 штук для каждого класса. Все книги имеют одинаковый
размер. В книжном шкафу  6 полок. На каждой полке помещается  20
учебников. Сколько шкафов можно полностью заполнить
новыми учебниками.

РЕШЕНИЕ;

Так как классов всего 
3 (7, 8, 9 классы), и каждому классу привезли по  125
учебников, то можно узнать, сколько всего привезли учебников в библиотеку.

125 ∙ 3 = 375 штук

375
учебников привезли в библиотеку, следовательно, 375
учебников нужно разместить в книжном шкафу.

Так как в книжном шкафу 
6
полок и на каждую полку помещается  20 учебников, то можно узнать, сколько учебников помещается
в книжном шкафу.

20 учебников ∙ 6 = 120 учебников.

Так как мы определили количество учебников, которые нужно
разместить в книжном шкафу  (375
учебников), и известно сколько учебников помещается в
один шкаф, то можно узнать сколько шкафов потребуется для размещения этих
учебников. Для этого количество всех учебников разделим на число учебников,
которое помещается в один шкаф.

375 : 120 = 3 (остаток 15).

ЗАДАЧА:

Туристическая путёвка стоит  45000
рублей. В стоимость путёвки входит проезд и проживание. Проезд стоит  9000
рублей. Какую часть от всей стоимости путёвки составляет проживание ?

РЕШЕНИЕ:

Если путёвка стоит 
45000
рублей, а проезд  9000 рублей, то от стоимости путёвки нужно отнять стоимость
проживания. Таким образом мы узнаем стоимость проживания:

45000 – 9000 = 36000 руб.

Чтобы определить, какую часть от всей стоимости
путёвки составляет проживание, найдём отношение стоимости проживания к общей
стоимости путёвки.

ОТВЕТ:

Проживание составляет  0,8 часть от общей стоимости
путёвки

Изучение физики в школе длится несколько лет. При этом ученики сталкиваются с проблемой, что одни и те же буквы обозначают совершенно разные величины. Чаще всего этот факт касается латинских букв. Как же тогда решать задачи?

Пугаться такого повтора не стоит. Ученые постарались ввести их в обозначение так, чтобы одинаковые буквы не встретились в одной формуле. Чаще всего ученики сталкиваются с латинской n. Она может быть строчной или прописной. Поэтому логично возникает вопрос о том, что такое n в физике, то есть в определенной встретившейся ученику формуле.

Что обозначает прописная буква N в физике?

Чаще всего в школьном курсе она встречается при изучении механики. Ведь там она может быть сразу в дух значениях – мощность и сила нормальной реакции опоры. Естественно, что эти понятия не пересекаются, ведь используются в разных разделах механики и измеряются в разных единицах. Поэтому всегда нужно точно определить, что такое n в физике.

Мощность — это скорость изменения энергии системы. Это скалярная величина, то есть просто число. Единицей ее измерения служит ватт (Вт).

Сила нормальной реакции опоры — сила, которая оказывает действие на тело со стороны опоры или подвеса. Кроме числового значения, она имеет направление, то есть это векторная величина. Причем она всегда перпендикулярна поверхности, на которую производится внешнее воздействие. Единицей измерения этой N является ньютон (Н).

Что такое N в физике, помимо уже указанных величин? Это может быть:

• постоянная Авогадро;

• увеличение оптического прибора;

• концентрация вещества;

• число Дебая;

• полная мощность излучения.

Что может обозначать строчная буква n в физике?

Список наименований, которые могут за ней скрываться, достаточно обширен. Обозначение n в физике используется для таких понятий:

• показатель преломления, причем он может быть абсолютным или относительным;

• нейтрон — нейтральная элементарная частица с массой незначительно большей, чем у протона;

• частота вращения (используется для замены греческой буквы «ню», так как она очень похожа на латинскую «вэ») — число повторения оборотов за единицу времени, измеряется в герцах (Гц).

Что означает n в физике, кроме уже указанных величин? Оказывается, за ней скрываются основное квантовое число (квантовая физика), концентрация и постоянная Лошмидта (молекулярная физика). Кстати, при вычислении концентрации вещества требуется знать величину, которая также записывается латинской «эн». О ней будет идти речь ниже.

Какая физическая величина может быть обозначена n и N?

Ее название происходит от латинского слова numerus, в переводе оно звучит как «число», «количество». Поэтому ответ на вопрос о том, что значит n в физике, достаточно прост. Это количество любых предметов, тел, частиц — всего, о чем идет речь в определенной задаче.

Причем «количество» — одна из немногих физических величин, которые не имеют единицы измерения. Это просто число, без наименования. Например, если в задаче идет речь о 10 частицах, то n будет равно просто 10. Но если получается так, что строчная «эн» уже занята, то использовать приходится прописную букву.

Формулы, в которых фигурирует прописная N

Первая из них определяет мощность, которая равна отношению работы ко времени:

N = А : t.

В молекулярной физике имеется такое понятие, как химическое количество вещества. Обозначается греческой буквой «ню». Чтобы его сосчитать, следует разделить количество частиц на число Авогадро:

ν = N : N_А.

Кстати, последняя величина тоже обозначается столь популярной буквой N. Только у нее всегда присутствует нижний индекс — А.

Чтобы определить электрический заряд, потребуется формула:

q = N × e.

Еще одна формула с N в физике – частота колебаний. Чтобы ее сосчитать, нужно их число разделить на время:

ν = N : t.

Появляется буква «эн» в формуле для периода обращения:

Т = t : N.

Формулы, в которых встречается строчная n

В школьном курсе физики эта буква чаще всего ассоциируется с показателем преломления вещества. Поэтому важным оказывается знание формул с ее применением.

Так, для абсолютного показателя преломления формула записывается следующим образом:

n = с : v.

Здесь с — скорость света в вакууме, v — его скорость в преломляющей среде.

Формула для относительного показателя преломления несколько сложнее:

n₂₁ = v₁ : v₂ = n₂ : n₁,

где n₁ и n₂ — абсолютные показатели преломления первой и второй среды, v₁ и v₂ — скорости световой волны в указанных веществах.

Как найти n в физике? В этом нам поможет формула, в которой требуется знать углы падения и преломления луча, то есть n₂₁= sin α : sin γ.

Чему равно n в физике, если это показатель преломления?

Обычно в таблицах приводятся значения для абсолютных показателей преломления различных веществ. Не стоит забывать, что эта величина зависит не только от свойств среды, но и от длины волны. Табличные значения показателя преломления даются для оптического диапазона.

Среда	Абсолютный показатель преломления
воздух	1,00029
лед	1,31
вода	1,33298
спирт этиловый	1,36
сахар	1,56
алмаз	2,419

Итак, стало ясно, что такое n в физике. Чтобы не осталось каких-либо вопросов, стоит рассмотреть некоторые примеры.

Задача на мощность

№1. Во время пахоты трактор тянет плуг равномерно. При этом он прилагает силу 10 кН. При таком движении в течение 10 минут он преодолевает 1,2 км. Требуется определить развиваемую им мощность.

Перевод единиц в СИ. Начать можно с силы, 10 Н равны 10000 Н. Потом расстояние: 1,2 × 1000 = 1200 м. Осталось время — 10 × 60 = 600 с.

Выбор формул. Как уже было сказано выше, N = А : t. Но в задаче нет значения для работы. Для ее вычисления пригодится еще одна формула: А = F × S. Окончательный вид формулы для мощности выглядит так: N = (F × S) : t.

Решение. Вычислим сначала работу, а потом – мощность. Тогда в первом действии получится 10 000 × 1 200 = 12 000 000 Дж. Второе действие дает 12 000 000 : 600 = 20 000 Вт.

Ответ. Мощность трактора равна 20 000 Вт.

Задачи на показатель преломления

№2. Абсолютный показатель преломления у стекла равен 1,5. Скорость распространения света в стекле меньше, чем в вакууме. Требуется определить, во сколько раз.

В СИ переводить данные не требуется.

При выборе формул остановиться нужно на этой: n = с : v.

Решение. Из указанной формулы видно, что v = с : n. Это значит, что скорость распространения света в стекле равна скорости света в вакууме, деленному на показатель преломления. То есть она уменьшается в полтора раза.

Ответ. Скорость распространения света в стекле меньше, чем в вакууме, в 1,5 раза.

№3. Имеются две прозрачные среды. Скорость света в первой из них равна 225 000 км/с, во второй — на 25 000 км/с меньше. Луч света идет из первой среды во вторую. Угол падения α равен 30º. Вычислить значение угла преломления.

Нужно ли переводить в СИ? Скорости даны во внесистемных единицах. Однако при подстановке в формулы они сократятся. Поэтому переводить скорости в м/с не нужно.

Выбор формул, необходимых для решения задачи. Потребуется использовать закон преломления света: n₂₁= sin α: sin γ. А также: n = с : v.

Решение. В первой формуле n₂₁ — это отношение двух показателей преломления рассматриваемых веществ, то есть n₂ и n₁. Если записать вторую указанную формулу для предложенных сред, то получатся такие: n₁= с : v₁ и n₂ =с : v₂. Если составить отношение двух последних выражений, получится, что n₂₁ = v₁ : v₂. Подставив его в формулу закона преломления, можно вывести такое выражение для синуса угла преломления: sin γ = sin α × (v₂ : v₁).

Подставляем в формулу значения указанных скоростей и синуса 30º (равен 0,5), получается, что синус угла преломления равен 0,44. По таблице Брадиса получается, что угол γ равен 26º.

Ответ. Значение угла преломления — 26º.

Задачи на период обращения

№4. Лопасти ветряной мельницы вращаются с периодом, равным 5 секундам. Вычислите число оборотов этих лопастей за 1 час.

Переводить в единицы СИ нужно только время 1 час. Оно будет равно 3 600 секундам.

Подбор формул. Период вращения и число оборотов связаны формулой Т = t : N.

Решение. Из указанной формулы число оборотов определяется отношением времени к периоду. Таким образом, N = 3600 : 5 = 720.

Ответ. Число оборотов лопастей мельницы равно 720.

№5. Винт самолета вращается с частотой 25 Гц. Какое время потребуется винту, чтобы совершить 3 000 оборотов?

Все данные приведены с СИ, поэтому переводить ничего не нужно.

Необходимая формула: частота ν = N : t. Из нее необходимо только вывести формулу для неизвестного времени. Оно является делителем, поэтому его полагается находить делением N на ν.

Решение. В результате деления 3 000 на 25 получается число 120. Оно будет измеряться в секундах.

Ответ. Винт самолета совершает 3000 оборотов за 120 с.

Подведем итоги

Когда ученику в задаче по физике встречается формула, содержащая n или N, ему нужно разобраться с двумя моментами. Первый — из какого раздела физики приведено равенство. Это может быть ясно из заголовка в учебнике, справочнике или слов учителя. Потом следует определиться с тем, что скрывается за многоликой «эн». Причем в этом помогает наименование единиц измерения, если, конечно, приведено ее значение. Также допускается еще один вариант: внимательно посмотрите на остальные буквы в формуле. Возможно, они окажутся знакомыми и дадут подсказку в решаемом вопросе.